Determination of Material and Interaction Properties of Granular Fertilizer Particles Using DEM Simulation and Bench Testing

Abstract

The discrete element method (DEM) is an effective tool for obtaining qualitative and quantitative information on particle motion, which aids in the design and optimization of agricultural equipment structures. The accuracy of the DEM simulation parameters significantly impacts the simulation results. This study employed a combination of high-speed camera measurement, DEM simulation, and validation tests to determine the material and interaction property parameters for fertilizer particles. The basic parameters (triaxial size, bulk density, density, and coefficient of static friction) and coefficients of restitution between fertilizer and material were measured for three fertilizer varieties. There was a significant difference in the angle of repose between various material plates and fertilizer particles. The calibration values of coefficients of restitution and coefficients of rolling friction between fertilizer particles were optimized using the Box–Behnken method. The angle of repose was significantly affected by the coefficient of static friction and the coefficient of rolling friction between the fertilizer particles. The determined values for the coefficient of restitution, coefficient of static friction, and coefficient of rolling friction between the fertilizer particles were 0.323, 0.381, and 0.173, respectively. The error in the angle of the repose test was less than 3.0%, and the variation coefficient for each row consistency was less than 1.68 percentage points under the optimal simulation parameters. DEM simulations of the angle of repose and each row consistency variation coefficient test using the measured parameters can accurately predict the experimental results. The findings of this paper provide a theoretical basis for the DEM study of fertilizer particles.

1. Introduction

Fertilizer has provided balanced nutrition and improved soil chemical and physical properties. Precision fertilizer application is an effective way to increase crop yield and quality [1]. Granular compound fertilizer, which contains nutrients such as N, P₂O₅, and K₂O and is adaptable for mechanized fertilization application, is widely used in agricultural production. Due to the current environmental issues and farmers’ economic needs, precision fertilization relying on fertilizer feeders has become a key component in crop cultivation [2].

With the characteristics of low moisture absorption, high fluidity, and good bonding, it is necessary to have a further understanding of the characteristics of granular compound fertilizer to aid in the design of fertilizer feeders and the understanding of the relationship between fertilizer particles and the feeder. The physical properties of granular compound fertilizer particles mainly include shape, 3-D size, particle friction coefficients, stiffness, and coefficient of restitution. However, due to the complexity of granular compound fertilizer properties, designing a fertilizer feeder still relies heavily on experience and experimental methods, which can be both costly and time-consuming [3]. To reduce the cost and time required for optimal equipment design, the discrete element method (DEM) has been considered an effective simulation method for dealing with granular particles in agriculture [4]. Previous researchers have designed fertilizer spreaders based on the DEM approach [5,6,7,8]. Coetzee et al. [9] investigated the effects of fertilizer feed position, feed rate, and disc structure on the spread pattern of a centrifugal fertilizer using the DEM model. Liedekerke et al. [10] applied DEM simulations to analyze the impacts of fertilizer physical properties on the spread pattern of spinning disc spreaders. Additionally, DEM modeling was proposed to optimize the structure of a dual-band fertilizer applicator and a multi-fertilizer mixing device [11,12]. DEM simulation has proven to be a useful tool for solving agricultural engineering problems and obtaining quantitative information on particles [13].

In the DEM simulation process, the accuracy of simulation parameters determines the accuracy and reliability of results. Some simulation parameters, such as the static friction coefficient, rolling friction coefficient, and coefficient of restitution, are basic and key parameters required in DEM simulations. These coefficients have been determined by methods such as numerical analysis and bench testing. Horabik et al. [14] reported the coefficient of restitution of peas, soybeans, and rapeseed using high-speed camera technology. Huang et al. [15] determined the coefficients of restitution of rapeseed for collisions between rapeseed and harvesting equipment. Wang et al. [16] investigated the coefficient of rolling friction of maize particles and found that the angle of repose was a suitable index to verify the accuracy of the simulation model. Furthermore, Liu et al. [17] analyzed the boundary parameters of the DEM simulation of urea particles and indicated that the static friction coefficient between urea particles and plates significantly affected the simulation results. Lu et al. [18] optimized the DEM simulation parameters of the static friction coefficient between bud seeds and stainless plate and the rolling friction coefficient between bud seeds. Irazábal et al. [19] investigated bounded rolling friction for spherical discrete element particles, and Persson and Frenning [20] analyzed the effects of rolling friction on the shear behavior of granular particles.

Although previous research has analyzed some characteristics of granular fertilizers and fertilizer spreaders that have been optimally designed based on DEM simulations, the parameters of granular fertilizers are mainly empirical, and some boundary parameters remain unclear due to the limitations of experimental conditions. In this work, we investigated the particle static friction coefficient, rolling friction coefficient, and restitution coefficient of granular compound fertilizer by bench testing using a high-speed camera and DEM simulations. The angle of repose and fertilizer performance results were utilized to verify the accuracy of the simulation parameters. This work can improve the accuracy of the simulation model for granular compound fertilizer and aid in the design of fertilizer spreaders.

2. Materials and Methods

2.1. Test Method of Material and Interaction Properties of Granular Fertilizer Particle

2.1.1. Shape and Size Analysis of Granular Fertilizer

In this work, we tested three types of granular compound fertilizers that are widely used in crop production. These types are Zhushang (Summit Fertilizer Company Limited, Qingdao, China), Zhonghua (Sinochem Fertilizer Company Limited, Linyi, Shandong, China), and Sanning (Sanning Fertilizer Company Limited, Yichang, Hubei, China), as shown in Table 1. We measured the triaxial dimensions, namely length (L), width (W), and thickness (T), using a digital vernier caliper with an accuracy of 0.01 mm, and the size distribution is shown in Figure 1 with samples of 100 particles. Table 1 represents the triaxial size for three types granular compound fertilizer.

Table 1. Triaxial size of various types of granular compound fertilizer.

Fertilizer Types	Nutrient Ratio (%)	Length (mm)	Width (mm)	Thickness (mm)	Equivalent Diameter (mm)	Sphericity (%)	Bulk Density (kg m−3)
Zhushang	N:P2O5:K2O = 20:9:11	4.24 ± 0.40	3.77 ± 0.24	3.35 ± 0.29	3.76 ± 0.21	89.21 ± 5.67	941.90
Zhonghua	N:P2O5:K2O = 15:15:15	4.52 ± 0.46	4.04 ± 0.36	3.63 ± 0.35	4.04 ± 0.31	89.68 ± 5.42	799.00
Sanning	N:P2O5:K2O = 15:15:15	3.55 ± 0.25	3.43 ± 0.22	3.32 ± 0.22	3.43 ± 0.22	96.80 ± 2.04	826.00
Average	-	4.10	3.75	3.43	3.74	91.90	865.97

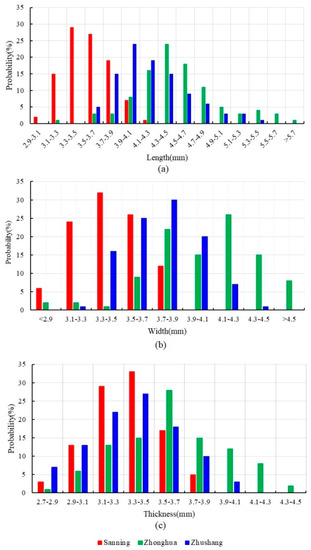
Figure 1. Triaxial size of various granular fertilizers: (a) length of fertilizer, (b) width of fertilizer, and (c) thickness of fertilizer.

Figure 1 shows that the triaxial dimensions of granular compound fertilizer follow a normal distribution. There were significant differences in the triaxial dimensions among the three types of granular compound fertilizer. The length and width of the Sanning type were lower than those of the Zhonghua and Zhushang types. The length, width, and thickness mainly varied between 3.5–5.1 mm, 3.3–4.3 mm, and 2.9–4.1 mm, respectively. The sphericity of these types was over 89%, indicating that the granular compound fertilizer was elliptical.

2.1.2. Density

The density of fertilizer particles was measured by the weighting method. An appropriate amount of fertilizer particles with a known mass was poured into a measuring cylinder with 500 mL of distilled water. The liquid level reading of the measuring cylinder was recorded with five replications. The average density of fertilizer particles was obtained as 1542 kg/m³.

2.1.3. Coefficient of Restitution

The test principle of the coefficient of restitution is presented in Figure 2. The coefficient of restitution is defined as the absolute ratio of the instantaneous velocity after collision to that before collision. When a particle was dropped from a height (h), the coefficient of restitution was calculated using Equation (1).

$$e=\frac{v}{v_0}=\sqrt{\frac{v_x^2+v_y^2+v_z^2}{2gh}}$$

(1)

where e is the coefficient of restitution; v is an instantaneous velocity after a collision, m s⁻¹; v₀ is an instantaneous velocity before a collision, m s⁻¹; v_x, v_y, and v_z are the velocity in x-direction, y-direction, and z-direction, respectively; and h is the dropping height, m.

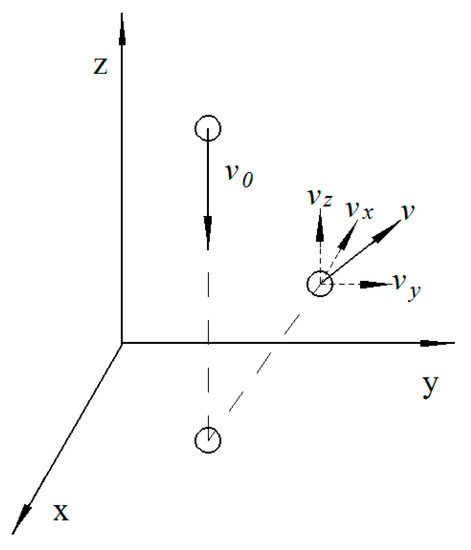
Figure 2. Test principle of collision recovery coefficient.

Figure 3 shows the process for measuring the coefficient of restitution. The experimental setup consists of a mirror (1), a first coordinate plane (2), a second coordinate plane (3), a base plate (4), a vacuum nozzle (5), a test plate (7), and a high-speed camera (8). In the experimental setup, the angle between the first and second coordinate planes was 90°, and the angle between the first coordinate plane and the mirror was 135°. The first and second coordinate planes were used to measure the particle coordinates in the three-axis directions. The velocities of the two planes were obtained through a mirror (1) and a high-speed camera (FASTCAM Mini UX100; Photron Limited; Tokyo, Japan). The particle, held by a vacuum nozzle (5), was dropped freely from a height (h). The test plate (7) materials included ABS (Acrylonitrile-butadiene-styrene copolymer), 304 stainless steel, and aluminum. The particle movement trajectories were extracted from images. The programming process for extracting the trajectory is shown in Figure 4. The velocities and coefficients of restitution were obtained by extracting the particle trajectory.

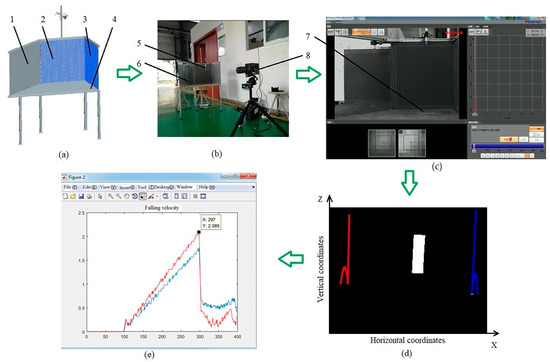
Figure 3. Measurement method of particle velocity: (a) particle rebound test platform, (b) test system, (c) particle movement images, (d) particle movement trajectory, (e) tracking particle velocity, (1) mirror, (2) first coordinate plane, (3) second coordinate plane, (4) base plate, (5) vacuum nozzle, (6) particle rebound platform, (7) test plate, and (8) high-speed camera.

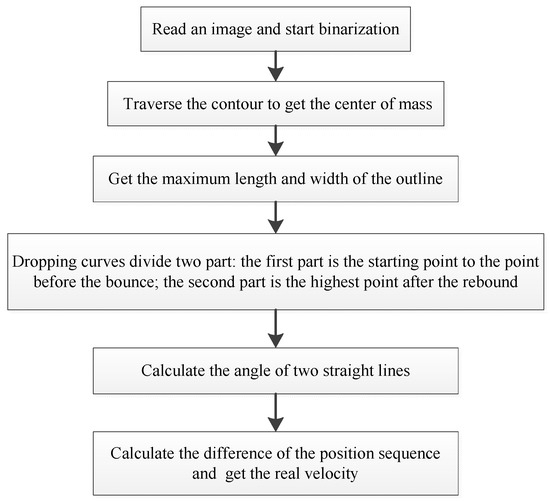
Figure 4. Programming process of extracting trajectory.

2.1.4. Coefficient of Static Friction

The multifunctional comprehensive test platform (Figure 5) was utilized to measure the coefficient of static friction. The platform consisted of a 304 stainless steel (or acrylonitrile-butadiene-styrene copolymer, aluminum) test plate, which was bonded to the inclined plate. Initially, the fertilizer particles were placed at the upper end of the inclined test plate, and then the drive rod was rotated to gradually raise the inclined plate. When the fertilizer particle began to slide, the rotation of the drive rod was halted, and the inclination angle (θ) was recorded. The coefficient of static friction was calculated as μ = tanθ. The measured coefficients of static friction between fertilizer particles and 304 stainless steel, acrylonitrile-butadiene-styrene copolymer, and aluminum were found to be in the range of 0.47–0.51, 0.45–0.50, and 0.47–0.50, respectively.

Figure 5. Multifunctional comprehensive test platform.

2.2. DEM Simulation and Validation Experiment Method

2.2.1. Particle-Contact Model

EDEM 2018 (provided by DEM Solutions Limited, Edinburgh, UK) was used to verify the accuracy of the simulation parameters. The behavior of granular particles is governed by interactions between particles and between particles and surfaces. The surface of granular fertilizer particles was sooth and the hardness of fertilizer particles was high. Thus, the Hertz–Mindlin (no-slip) model, as shown in Figure 6, was chosen as the particle contact model, and the granular compound fertilizer was modeled as a hard-sphere model in the simulation. The particle-contact model was based on the triaxial dimensions.

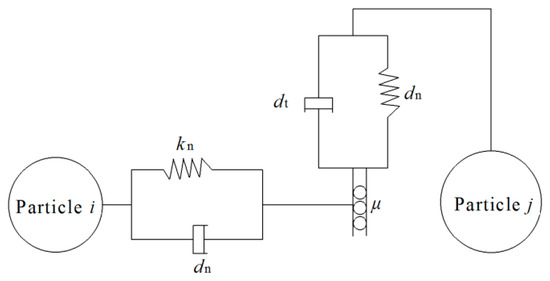
Figure 6. Particle-contact model.

In the DEM formulation, the particle dynamics equations defined the translational and rotational motion of particles. These equations could be expressed as follows:

$$m_i\ddot{\upsilon }=m_{i}g+{\displaystyle \sum _{j=1}^{\mathrm{n}}\left(F_{\mathrm{n}}+F_{\mathrm{n}}^{\mathrm{d}}+F_{\mathrm{t}}+F_{\mathrm{t}}^{\mathrm{d}}\right)}$$

(2)

where m_i is the mass of particle i, $\ddot{\upsilon }$ is the particle’s centroid acceleration, $g$ is the vector of gravitational acceleration, $F_{\mathrm{n}}$ and $F_{\mathrm{t}}$ is the normal force and tangential force, respectively, and $F_{\mathrm{n}}^{\mathrm{d}}$ and $F_{\mathrm{t}}^{\mathrm{d}}$ is the normal damping force and tangential damping force, respectively.

The normal force $F_{\mathrm{n}}$ was defined as follows:

$$F_{\mathrm{n}}=\frac{4}{3}{E}^{*}{\left(R^{*}\right)}^{\frac{1}{2}}{\delta }_{\mathrm{n}}^{\frac{3}{2}}$$

(3)

where $E^{*}$ was the equivalent elastic modulus, $R^{*}$ was the equivalent radius, and ${\delta }_{\mathrm{n}}^{}$ was the normal overlap amount.

$$F_{\mathrm{n}}^{\mathrm{d}}=-2\sqrt{\frac{5}{6}}\frac{{\ln }^{\gamma }}{\sqrt{{\left({\ln }^{\gamma }\right)}^2+{\mathsf{\pi }}^2}}\sqrt{S_{\mathrm{n}}{m}^{*}}{{\upsilon }^{\prime }}_{\mathrm{n}}$$

(4)

where γ was the coefficient of restitution, S_n was the normal stiffness, $m^{*}$ was the equivalent mass, and ${{\upsilon }^{\prime }}_{\mathrm{n}}$ was the relative normal velocity.

$$F_{\mathrm{t}}=-S_{\mathrm{n}}{\delta }_{\mathrm{t}}$$

(5)

where, ${\delta }_{\mathrm{t}}$ was the tangential overlap amount.

$$F_{\mathrm{t}}^{\mathrm{d}}=-2\sqrt{\frac{5}{6}}\frac{{\ln }^{\gamma }}{\sqrt{{\left({\ln }^{\gamma }\right)}^2+{\mathsf{\pi }}^2}}\sqrt{S_{\mathrm{t}}{m}^{*}}{{\upsilon }^{\prime }}_{\mathrm{t}}$$

(6)

where S_t was the tangential stiffness, and ${{\upsilon }^{\prime }}_{\mathrm{t}}$ was the relative tangential velocity.

$$I_i\dot{\omega }={\displaystyle \sum _{j=1}^{\mathrm{n}}\left(T_{\mathrm{t}}+T_{\mathrm{r}}\right)}$$

(7)

$$T_{\mathrm{t}}=R_i\left(F_{\mathrm{t}}+F_{\mathrm{t}}^{\mathrm{d}}\right)$$

(8)

where, $I_i$ was the moment of the inertia of particle I, $\dot{\omega }$ was the angular acceleration, $T_{\mathrm{t}}$ was the tangential torque, $T_{\mathrm{r}}$ was the rolling friction torque, $R_i$ and was the distance from the barycenter of particle i to the contact point.

$$T_{\mathrm{r}}=-\beta R_r\left|F_{\mathrm{n}}\right|\frac{{\omega }^{\prime }}{\left|{\omega }^{\prime }\right|}$$

(9)

where β was the rolling friction coefficient, $R_r$ was the effective rolling contact radius, and $\omega \prime$ was the relative angular velocity of two particles in contact.

2.2.2. DEM Simulation Model

The 3D model of the fertilizer is depicted in Figure 7, where the fertilizer particle is constructed by filling overlapping spheres to satisfy the particle parameters specified in Table 1. According to the particle size distribution, the particle size distribution coefficient ranged from 0.9 to 1.1. The main simulation parameters include particle characteristics and particle-material parameters, as listed in Table 2.

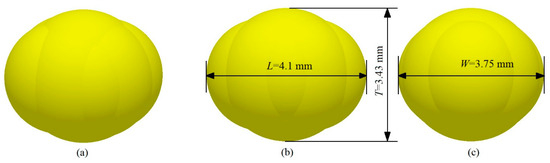
Figure 7. 3D model parameters of fertilizer: (a) 3D model; (b) front view; and (c) lateral view.

Table 2. Parameters used in the DEM simulations.

Parameters	Fertilizer	304 Stainless Steel	ABS	Aluminum	Plastic	Source/Method of Measurement
Poisson’s ratio	0.25	0.3	0.394	0.36	0.47	[14]
Shear modulus (Pa)	2.8 × 107	7.9 × 1010	8.9 × 108	6.85 × 1010	2.9 × 109	[21]
Density (kg m−3)	1542	7 930	1 060	2707	1350	Measured for fertilizer and [21] for other materials
Coefficient of restitution
Particle-particle	0.3–0.4 *	-	-	-	-
Particle-material	-	0.35	0.52	0.32	0.45	Measured
Coefficient of static friction
Particle-particle	0.30–0.40 *	-	-	-	-
Particle-material	-	0.45–0.55 *	0.45–0.55 *	0.45–0.55 *	0.3	Measured
Coefficient of rolling friction
Particle-particle	0.10–0.20	-	-	-	-
Particle-material	-	0.1	0.1	0.1	0.1	[22]
Gravitational acceleration (m s−2)	9.81

Note: * represents the uncertain DEM simulation values.

2.2.3. DEM Simulation Design

As some parameters were measured or from previous research [14,22], the values of uncertain parameters included the coefficient of restitution, the coefficient of static friction, the coefficient of rolling friction between fertilizer particles, and the coefficient of static friction of fertilizer-plate material. The four factors with three levels of experimental design were carried out using the Box-Behnken method. The coding of factors is shown in Table 3. The Design-Expert version 13.0 was used to analyze the regression model and variance.

Table 3. Coding of factors.

Parameter	−1	0	1
Coefficient of restitution of fertilizer-fertilizer (x1)	0.30	0.35	0.40
Coefficient of static friction of fertilizer-fertilizer (x2)	0.30	0.35	0.40
Coefficient of static friction of fertilizer-plate material (x3)	0.45	0.50	0.55
Coefficient of rolling friction of fertilizer- fertilizer (x4)	0.10	0.15	0.20

2.2.4. Simulation Method and Validation Experiment of Angle of Repose

The angle of repose is an important parameter for verifying the accuracy of the parameters. The angle of repose was tested using the hollow cylinder method, which consists of a hollow cylinder and a bottom plate. The bottom plate material included 304 stainless steel, acrylonitrile-butadiene-styrene copolymer (ABS), and aluminum. The diameter and height of the hollow cylinder were 42 mm and 126 mm, respectively. The procedure for the hollow cylinder test was as follows in the simulations: 5000 fertilizer particles were poured into the cylinder, and the particle surface was flattened first (Figure 8a). Second, the cylinder was lifted at a speed of 50 mm per second, causing the particles to flow out of the cylinder and contact the bottom plate. Finally, when the particles were stable, a cone-shaped pile was formed, as shown in Figure 8b. Each group of tests was repeated four times.

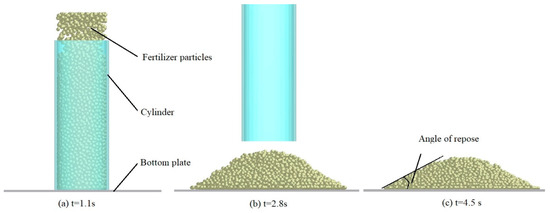
Figure 8. DEM simulation of the hollow cylinder test method.

In the validation experiment, the cylinder (5) was lifted by the lifting frame of a universal material testing machine (3). The lifting velocity was controlled by the hydraulic system in the universal material testing machine (3), which was operated through the controller (4) and PC (2). In front of the universal material testing machine (3), a high-speed camera system (1) was positioned to capture images of the cone-shaped pile (Figure 9). Each treatment was repeated five times.

Figure 9. Angle of repose setup: (1) high-speed camera, (2) PC, (3) universal material testing machinery, (4) controller, (5) cylinder, and (6) lifting frame.

Figure 10 presents the image processing method for measuring the repose angle. The repose angle in both DEM simulations and bench tests was measured using MATLAB. The original image was imported into MATLAB software (Version 2012R), and then the image was subjected to gray processing and binary processing. The outlines of the particles were extracted, and a fitting line for the repose angle was obtained. The repose angle was calculated according to Wang et al. [16].

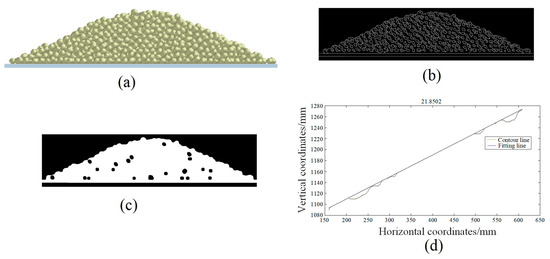
Figure 10. Image processing of repose angle: (a) original image, (b) gray processing, (c) binary processing, (d) fitting line of repose angle.

2.2.5. Validation Experiment of Fertilization Uniformity

To further validate the accuracy of simulation parameters, the fertilization process of a fertilizer metering device was investigated using DEM simulation (Figure 11b) and bench tests (Figure 11a). The Zhonghua fertilizer was tested in the bench test. The fertilizer metering device was designed by our research group and consisted of a fertilizer box (1), fertilizer metering mechanism (2), and fertilizer tube (3). The fertilizer metering mechanism (2) was a key component of the fertilizer metering device and consisted of three spiral groove-type fertilizer feeding wheels. Three rows of fertilizer were discharged by the three spiral groove-type fertilizer feeding wheels through fertilizer tubes. The fertilizer mass was measured at the 10–50 rpm rotational speed of the fertilizer metering mechanism for both the DEM simulation and bench test. The fertilization mass in each fertilizer tube was collected. The coefficient of variation for each row was calculated to evaluate the uniformity of fertilization across the three rows. The coefficient of variation for each row (cv) was calculated as follows:

$$\left\{\begin{array}{l}cv=\frac{SD}{\overline{X}}\times 100\%\\ SD={\left\{{\displaystyle \sum _{i=1}^n\left[{(X_i-\overline{X})}^2\right]/(n-1)}\right\}}^{\frac{1}{2}}\\ \overline{X}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{X}_i}\begin{array}{cc}& (i=1,2,3)\end{array}\end{array}\right.$$

(10)

where, cv was the coefficient of variation for each row, %; SD was the standard deviation of fertilization mass, g; $X_i$ was the fertilization mass of the ith fertilizer tube, g; $\overline{X}$ was the average fertilization mass for each fertilizer tube, g; and n was the total number of samples.

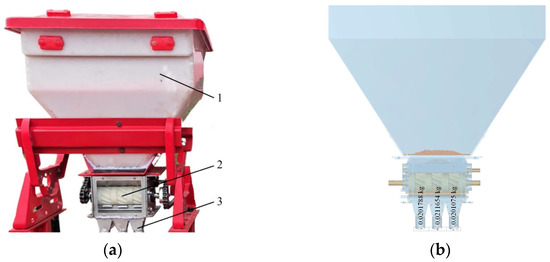
Figure 11. Fertilization performance setup. (a) experiment setup and (b) simulation setup, (1) fertilizer box, (2) fertilizer metering mechanism, (3) fertilizer tube.

3. Results and Analysis

3.1. Coefficient of Restitution and Angle of Repose of Experimental Study

Table 4 presents the coefficients of restitution (COR) for granular compound fertilizer against different types of materials. The CORs between the fertilizer particle and various plate materials showed significant differences. The COR between the fertilizer particle and ABS was markedly larger than the CORs between the fertilizer particle and 304 stainless steel and aluminum. The coefficient of restitution decreased with increasing dropping height, and the deviation was within 0.03 for the same material. No significant difference in COR was observed for fertilizer types or dropping height. The COR between the fertilizer particle and 304 stainless steel, ABS, and aluminum was 0.35, 0.52, and 0.32, respectively.

Table 4. Coefficient of restitution for granular compound fertilizer against different types of materials.

Fertilizer Types	Type of Contact Surface	Dropping Height (mm)
		100	200	300
Zhushang	Acrylonitrile-butadiene-styrene copolymer	0.524	0.520	0.518
	304 stainless steel	0.381	0.379	0.364
	Aluminum	0.380	0.330	0.326
Zhonghua	Acrylonitrile-butadiene-styrene copolymer	0.533	0.523	0.522
	304 stainless steel	0.350	0.346	0.330
	Aluminum	0.331	0.322	0.311
Sanning	Acrylonitrile-butadiene-styrene copolymer	0.523	0.517	0.490
	304 stainless steel	0.376	0.375	0.357
	Aluminum	0.346	0.321	0.312
Average	Acrylonitrile-butadiene-styrene copolymer	0.527	0.520	0.510
	304 stainless steel	0.369	0.367	0.350
	Aluminum	0.352	0.324	0.316
F value	Fertilizer types	0.088
	Material type	305.62 **
	Dropping height	0.613

Note: ** represent significantly different at the 0.01 probability level.

The angle of repose between fertilizer particles and 304 stainless steel, ABS, and aluminum is shown in Table 5. The average angle of repose between fertilizer particles and 304 stainless steel, ABS, and aluminum was 33.78°, 31.34°, and 30.70°, respectively.

Table 5. Angle of repose between fertilizer particle and plate material.

Type of Contact Surface	Angle of Repose (°)
	Test 1	Test 2	Test 3	Test 4	Test 5	Average
304 stainless steel	32.80	33.24	32.04	34.16	36.68	33.78
Acrylonitrile-butadiene-styrene copolymer	31.40	31.15	31.03	32.93	30.18	31.34
Aluminum	31.02	28.47	33.73	29.5	30.44	30.70

3.2. Parameters Determination in DEM Simulation

Table 6 represents the effects of the coefficient of restitution (x₁), the coefficient of static friction (x₂), the coefficient of rolling friction (x₃) between fertilizer particles, and the coefficient of static friction of fertilizer-plate material (x₄) on the angle of repose in the simulation results between fertilizer particles and 304 stainless steel. The reduced quadratic model was established between the angle of repose and parameters as Equation (11).

$$\begin{array}{l}y=30.63+0.0079x_1+1.62x_2-0.5606x_3+5.40x_4-0.4856x_1{x}_3-0.6025x_2{x}_4-0.6338x_3{x}_4\\ -1.26x_2^2-0.0717x_3^2-0.8186x_4^2\end{array}$$

(11)

Table 6. Simulation scheme and results between fertilizer particle and 304 stainless steel.

Test Number	Test Factors				Angle of Repose (°)
	x1	x2	x3	x4
1	−1	1	0	0	31.75 ± 3.09
2	0	−1	0	−1	21.73 ± 3.08
3	−1	0	0	1	33.69 ± 1.49
4	0	0	−1	−1	24.74 ± 3.16
5	0	1	1	0	31.92 ± 0.98
6	1	−1	0	0	27.25 ± 2.37
7	0	−1	0	1	34.21 ± 0.96
8	0	0	0	0	31.00 ± 3.11
9	−1	−1	0	0	28.00 ± 1.36
10	0	−1	1	0	27.14 ± 2.06
11	0	1	−1	0	32.52 ± 1.97
12	0	1	0	−1	23.45 ± 2.18
13	0	0	1	−1	24.15 ± 2.76
14	1	0	−1	0	30.91 ± 0.87
15	−1	0	−1	0	30.58 ± 1.00
16	0	0	−1	1	37.40 ± 4.37
17	0	0	0	0	30.69 ± 1.20
18	−1	0	1	0	29.99 ± 1.16
19	0	0	0	0	31.54 ± 2.08
20	0	−1	−1	0	26.46 ± 2.99
21	0	1	0	1	33.52 ± 0.81
22	0	0	1	1	34.28 ± 1.31
23	1	0	0	1	35.53 ± 1.75
24	1	0	1	0	28.38 ± 2.04
25	1	1	0	0	31.03 ± 2.10
26	0	0	0	0	31.03 ± 0.27
27	1	0	0	−1	25.40 ± 0.43
28	−1	0	0	−1	24.39 ± 1.87
29	0	0	0	0	29.99 ± 1.49

Variance analysis for the reduced quadratic model is shown in Table 7. The p-value of the quadratic model was less than 0.001, and the adequacy precision was 21.578, indicating that the quadratic model reflected the relationship between the angle of repose and simulation parameters. Furthermore, the angle of repose was significantly affected by the coefficient of static friction and the coefficient of rolling friction between fertilizer particles.

Table 7. ANOVA of quadratic model.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	402.23	10	40.22	29.98	<0.0001 **
x1	0.0008	1	0.0008	0.0006	0.9814
x2	31.41	1	31.41	23.42	0.0001 **
x3	3.77	1	3.77	2.81	0.1109
x4	349.46	1	349.46	260.5	<0.0001 **
x1x3	0.9433	1	0.9433	0.7032	0.4127
x2x4	1.45	1	1.45	1.08	0.3119
x3x4	1.61	1	1.61	1.2	0.2882
x2x2	10.62	1	10.62	7.92	0.0115 *
x3x3	0.0346	1	0.0346	0.0258	0.8742
x4x4	4.51	1	4.51	3.36	0.0834
Residual	24.15	18	1.34
Lack of fit	22.85	14	1.63	5.05	0.0648
Pure error	1.29	4	0.3234
Total	426.38	28

Note: * and ** represent significantly different at the 0.05 and 0.01 probability level, respectively.

The simulation parameters were optimized to achieve an objective angle of repose of 33.78°, which was obtained from the hollow cylinder bench test. Using numerical optimization analysis, the coefficients of restitution, static friction, and rolling friction between fertilizer particles were determined to be 0.323, 0.381, and 0.173, respectively. The coefficient of static friction between fertilizer particles and 304 stainless steel was 0.453.

3.3. Parameters Verification between DEM Simulation and Bench Test

To verify the accuracy of EDM simulation parameters, the optimal simulation parameters of fertilizer particles and fertilizer particles with 304 stainless steel were imported into the EDEM software (Version 2018). The average angle of repose was found to be 34.02° in the DEM simulation, indicating a relative error of only 0.72% between the DEM simulation and experiment (Figure 12a). When the coefficient of static friction between fertilizer particles and both aluminum and ABS copolymers was set to 0.5, the relative errors of the coefficient of static friction between fertilizer particles and aluminum and acrylonitrile-butadiene-styrene copolymers were 2.44% and 3.22%, respectively (Figure 12b,c). Qualitative comparisons were also made between the simulation and bench test to analyze the coefficient of variation for each row of the fertilizer metering device. Figure 12d shows that the relative error of the coefficient of variation for each row between the simulation and bench test was less than 1.68 percentage points, indicating a good agreement between the experimental and simulation results.

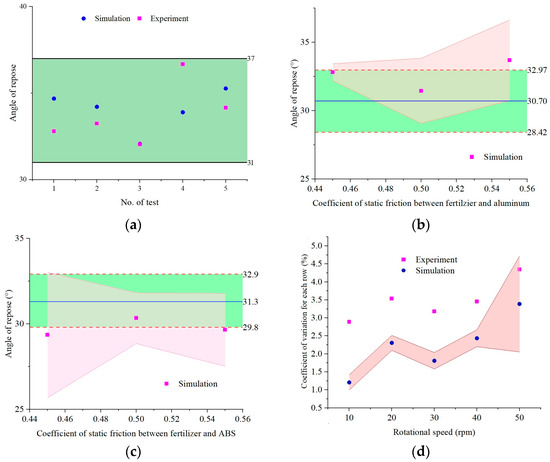
Figure 12. Simulation parameters verification results. (a) Angle of repose verification between simulation and experiment, (b) effects of coefficient of static friction between fertilizer particle and aluminum on angle of repose, (c) effects of coefficient of static friction between fertilizer particle and ABS on the angle of repose, and (d) coefficient of variation for each row verification between simulation and experiment. Note: The light red zone represents the error bar, and the green zone represents the experimental value.

4. Discussion

4.1. Fertilizer Particle and Interaction Properties Determination Method

Accurate simulation results rely on the calibration of appropriate parameters for the DEM simulation model. The coefficients of restitution, static friction, and rolling friction for both particle-particle and particle-material interactions were significant DEM simulation parameters. The coefficient of restitution is a measure of the energy transferred between particles and the surface of impact [23]. It is expressed as the ratio of the rebound velocity to the initial velocity. The coefficient of restitution between particle and plate is tested between fertilizer particle and plate using two coordinate planes and a high-speed camera in this research. Therefore, the coefficient of restitution between fertilizer particles and 304 stainless steel, ABS, and aluminum was obtained to be 0.35, 0.52, and 0.32 using bench test. However, determining the coefficient of restitution between fertilizer particles is challenging due to the uncertain movement direction and unpredictable collision. We used simulation optimization to determine the coefficient of restitution between fertilizer particles, and the coefficient of restitution between fertilizer particles was determined to be 0.323 in this simulation experiment.

The coefficients of static friction and rolling friction are important parameters that influence particle behavior. The coefficient of static friction between particles and a plate can be obtained using a platform, as demonstrated by Wang et al. [24]. However, determining the static friction between particle-particle interactions and the coefficient of rolling friction through experimental methods is challenging. A common approach to improving simulation accuracy and reducing computational requirements is to select some significant parameters. Su Y. [25] found that combinations of factors were important parameters using a Plackette–Burman experimental design. We used the Box–Behnken method to determine static friction between particle-particle interactions and the coefficient of rolling friction. We found that the coefficients of static friction and rolling friction between fertilizer particles significantly affected the angle of repose. An increase in the coefficient of rolling friction led to an increase in the angle of repose. Our findings were consistent with those from other studies (Wang et al. [16]). Song et al. [26] optimized the DEM models for fertilizer particles by training a radial basis function neural network, and the approximate model’s prediction accuracy was less than 5%. In our research, the coefficient of restitution between particles and other materials, and static friction between particles and other materials were determined by bench test. The coefficient of restitution, coefficient of static friction, and coefficient of rolling friction between fertilizer particles were determined by simulation optimization. By conducting experimental measurements in combination with simulation optimization, the interactive parameters between fertilizer particles and between fertilizer particles and other materials were determined. A DEM simulation model of fertilizer particles was constructed to accurately represent their real characteristics.

4.2. Accuracy Analysis of Simulation Parameters

The angle of repose is a commonly used parameter to evaluate the accuracy of simulation parameters [23]. The accuracy of the simulation parameters is assessed by comparing the angle of repose obtained between the simulation and experimental data, typically by measuring the accumulation of particles.

Our study indicated that the revolving cylinder method was applied to test the angle of repose in both simulation and bench tests, and the relative error between the simulation and experiment was found to be less than 3.0%. Zhou et al. [27] and Yan et al. [28] utilized the fixed funnel method to test the angle of repose for maize and soybeans. These studies confirmed the effectiveness of the angle of repose as a parameter for ensuring higher accuracy in determining particle properties. This implied that the angle of repose was an effective evaluation index to test the accuracy of DEM simulation and helped to construct the DEM model.

To further verify the accuracy and applicability of the DEM simulation parameters for fertilizer particles, the coefficient of variation for each row was measured using a fertilizer metering device in this research. The fertilizer feeding process was consistent between the simulation and bench test. The relative error of each row consistency variation coefficient was found to be less than 1.68 percentage points, and both values were below 5.0%. This verification indicated that the fertilizer DEM modeling method and the simulation parameters obtained above are accurate and can be applied in simulations of fertilizer spreaders. These results demonstrated that accurately determining simulation parameters enabled the creation of precise DEM simulation models, which were beneficial in understanding the fertilizer feeding process, fertilizer particle movement characteristics, and optimizing the structural parameters of the fertilizer feeder.

5. Conclusions

This work aimed to determine the parameters of fertilizer particles and fertilizer interactions for DEM simulation in order to ensure the accuracy of the fertilizer particle model. The simulation model has been validated by comparing it with experimental and numerical results. The conclusions were as follows:

(1) Experimentally, the triaxial size, bulk density, and density of three fertilizer varieties were measured, along with the coefficients of restitution and static friction between the fertilizers and different materials. The coefficients of restitution between the fertilizer particle and 304 stainless steel, ABS, and aluminum were 0.35, 0.52, and 0.32, respectively. The angles of repose between fertilizer particles and 304 stainless steel, ABS, and aluminum were 33.78°, 31.34°, and 30.70°, respectively.

(2) Numerically, the DEM modeling of fertilizer particles based on the triaxial size was established and the fertilizer particle model was closer to the actual fertilizer size. The angle of repose was an effective parameter to assess the accuracy of DEM simulation parameters and was found to be significantly influenced by the coefficient of static friction and the coefficient of rolling friction between fertilizer particles. The determined values of the coefficient of restitution, coefficient of static friction, and coefficient of rolling friction between fertilizer particles were 0.323, 0.381, and 0.173, respectively. The coefficient of static friction between fertilizer particles and 304 stainless steel, aluminum, and ABS was 0.453, 0.5, and 0.5, respectively.

(3) The accuracy of simulation parameters was verified by comparing the angle of repose and the coefficient of variation for each row between the DEM simulation and bench test. The relative error of the angle of repose and the coefficient of variation for each row between the simulation and experiment was less than 3.0% and 1.68 percentage points, respectively. This verified the feasibility and effectiveness of the DEM simulation parameters for fertilizer particles proposed in this research. This research can provide the accurate parameters, including fertilizer particles and particle plates, needed to construct a DEM model. The interaction between fertilizer particles and the component of fertilizer spreader, the analysis of fertilizer particle motion characteristics, and the optimization of the fertilizer spreader can be further studied.