Abstract
We re-examine the theory of electronic and vibrational circular dichroism spectroscopy in terms of the formalism of frequency-dependent molecular polarizabilities. We show the link between Fermi’s gold rule in circular dichroism and the trace of the complex electric dipole–magnetic dipole polarizability. We introduce the C++ code polar to compute the molecular polarizability complex tensors from quantum chemistry outputs, thus simulating straightforwardly UV-visible absorption (UV-Vis)/electronic circular dichroism (ECD) spectra, and infrared (IR)/vibrational circular dichroism (VCD) spectra. We validate the theory and the code by referring to literature data of a large group of chiral molecules, showing the remarkable accuracy of density functional theory (DFT) methods. We anticipate the application of this methodology to the interpretation of vibrational spectra in various measurement conditions, even in presence of metal surfaces with plasmonic properties. Our theoretical developments aim, in the long run, at embedding the quantum-mechanical details of the chiroptical spectroscopic response of a molecule into the simulation of the electromagnetic field distribution at the surface of plasmonic devices. Such simulations are also instrumental to the interpretation of the experimental spectra measured from devices designed to enhance chiroptical interactions by the surface plasmon resonance of metal nanostructures.
1. Introduction
The steady and exciting development of quantum chemistry and, notably, density functional theory (DFT) methods has greatly enhanced our capabilities in understanding molecular spectra [1]. Current quantum chemistry computer codes can be used very reliably to assign the features observed in molecular spectra to electronic or vibrational transitions, with increasingly accurate levels of theory [2,3,4,5,6,7,8,9]. Notable advances in tools available for computational spectroscopy have appeared in the recent literature [10,11,12,13,14,15,16,17,18,19]. These are commonly based on existing quantum chemistry engines, and their development often enhances the accuracy of the existing approaches. For instance, the harmonic approximation can be improved to deal with anharmonic effects [20,21,22,23]. Within the rich and evolving scenario of computational spectroscopy, it is interesting to discuss approaches complementary to those most often employed to simulate spectra, which have been in use for a long time, and basically consist in weighted sums of selected lineshape functions [24] (ultimately, the weights of such sums are related to transition moments computed by quantum chemistry—see, for instance, [25]). In fact, one of the aims of the developments of our work is the embedding of the quantum-mechanical details of the chiroptical spectroscopic response of a molecule (which requires its complex electric dipole–magnetic dipole polarizability) within the simulation of the electromagnetic field distribution at the surface of plasmonic devices. Such simulations are instrumental to the interpretation of the experimental spectra measured from devices designed to enhance chiroptical interactions by the surface plasmon resonance of metal nanostructures [26]. The role of molecular polarizability is well recognized in the field of linear and non-linear spectroscopy, and led to the development of insightful computational tools for non-linear optics (e.g., [27,28,29]). Interestingly, polarizability was also introduced in the context of electronic CD aiming to calculate CD spectra of large molecules from the polarizability characterization of fragments [30].
We have investigated polarizability from the principles of quantum mechanics and light–matter interaction [31] adopting the notation used in [24]. The paper is organized as follows. We first illustrate the connection of CD with the polarizability tensor to obtain the relevant equations which relate the quantum mechanical transition rate to the trace of molecular polarizability (i.e., Equation (9)). Thereafter we show the use of the polar code, which has been written to implement such equations, for both electronic and vibrational transitions, based on the transition matrix elements obtained from quantum chemistry codes such as Gaussian [5]. For the benchmark of the electronic polarizability we consider a set of rigid molecules, thus avoiding conformational issues (which are irrelevant to the present study). Hence, -conjugated molecules offer a rich playground, with reliable reference theoretical and experimental data available for comparison. For vibrational polarizability, we have considered another set of small and rigid chiral molecules, which have been very well characterized in the VCD literature, both experimentally and theoretically. In the final part of this work, we show how the Intensity Carrying Modes, which were pioneered by Torii et al. in the context of vibrational polarizability and IR spectroscopy [32,33], can be smoothly extended to VCD spectroscopy as well.
Before describing our results, let us introduce the needed complex polarizabilities , , and . This notation resembles the one adopted in theoretical investigations of antennas (e.g., [34]). It is also a notation that fits computer coding, and has fostered the development of the polar program. In the context of chiroptical spectroscopy, the tensor is often denoted [35]. Similarly, the tensor represents the magnetic susceptibility [35,36]; the electric polarizability is typically written as [35]. We remark that the electric dipole–magnetic dipole polarizability was repeatedly written as sum over states in the literature [35,37,38,39,40], even though with different purposes and different notation. In the present work, we neglect the dipole–quadrupole contribution (denoted [35]), which is relevant in presence of anisotropic systems and/or gradients of the electric field. Such contribution, which can be relevant, e.g., in plasmonics, can be evaluated in perspective by a natural extension of the proposed approach.
The proposed method to simulate molecular spectra is essentially a post-processing of outputs from standard quantum chemistry packages (e.g., Gaussian in the present case, but interfaces to other packages can be introduced straightforwardly). This approach is general, and it is meant to support the simulation of spectra in selected experimental conditions without the need of re-computing the molecular response from quantum chemistry. This also alleviates modifications at level of the source code of the adopted quantum chemistry engine. Moreover, the calculation of the polarizability elements is a crucial step in the implementation of effective chiral media within nano-optical electromagnetic simulations.
2. Results
The theoretical description of CD phenomena entails both electric and magnetic effects. In a detailed review [24], Schellman presented the theoretical description of circular dichroism and optical rotation for molecules in solution state. The central role is played by the perturbation operator associated to left-handed (−) and right-handed (+) circularly polarized light, which is defined through the electric () and the magnetic () dipole operators. By making use of the results illustrated in Ref. [24], for a given transition between states 0 and k, the expectation value of such operators is the following:
where and are the electric and magnetic field amplitudes of the impinging light wave, is the electric transition dipole moment, and is the magnetic transition dipole moment. I represents the light intensity, c is the speed of light, and indicates the complex number . Schellman’s review [24] adopts cgs units. For the reasons discussed by McWeeny [41], in this work we prefer using atomic units for the numerical values of polarizabilities and we consider the SI system for the description of the electromagnetic field. For the sake of simplicity, we disregard solvent effects and adopt electromagnetic waves in vacuum. Therefore, the intensity of the electromagnetic wave required by Schellman’s treatment (Equation (6) in Ref. [24]) is given by , where the magnetic () and electric field () amplitudes are related one another by the relation [42]. The electromagnetic energy absorbed per unit time as a consequence of the transitions promoted by the electromagnetic perturbation at frequency is given by [24]:
where is the density of states for the transition, and it is normalized, i.e., . By substituting Equation (1) into Equation (2), one obtains:
To connect Equation (3) with the molecular polarizability tensors, it is instrumental to write the inner products among the transition dipoles (Equation (1)) as traces of outer products:
We recall that the tensor (outer) product of two vectors and has matrix elements . Therefore, the dot product can be seen as .
For a molecule with eigenstates and transition energies from the ground state , the electric polarizability can be written as a sum over states, with opposite sign damping in the resonance term (first term) and off-resonance term (second term) [35,43,44,45]:
By recognizing in the second line of Equation (5), the numerators as the outer products of the transition electric dipoles (namely, and ), one can compactly write the polarizability tensor as follows:
By introducing the formal substitution (, ) in the expression of the electric polarizability given by Equation (5), one can devise the expression of the complex electric dipole–magnetic dipole polarizability :
With a similar reasoning, the following expression can be written for the magnetic dipole polarizability tensor :
Near resonance conditions with the transition, Equations (6)–(8) can be used to relate the trace of molecular polarizabilities to the transition rate given by Equation (3) (see Appendix A for details):
As well-known, we recall that the imaginary part of relates to absorption phenomena, and the real part to dispersive ones. Because of the presence of the purely imaginary magnetic dipole transition moment in the expression of , the absorption and dispersive terms in are the real and the imaginary parts of , respectively (see also Equation (A7) in Appendix A). When neglecting vibronic effects, the transitions introduced in Equations (6)–(8) are taken as vertical electronic transitions, and they can be conveniently computed by, e.g., TDDFT. This is the approach adopted by the polar code.
In summary, by the calculation of frequency-dependent polarizabilities, Equation (9) can be used:
- (i)
- to simulate UV-Vis absorption spectra in the absence of vibronic effects:
- (ii)
- to simulate electronic CD (ECD) spectra [24]:and
- (iii)
- to simulate the dissymmetry factor g, which is the ratio of CD () to ordinary absorption () [24]:
To simulate IR and VCD spectra, one has to evaluate the molecular polarizabilities by considering the transitions as vibrational. If one focuses on the vibrational transitions in the mid-IR range, within the double harmonic approximation, the sum over states is restricted to one-quantum transitions over the 3N-6 vibrational modes of the system, based on mechanical harmonicity. Therefore, by making the formal change in Equations (6)–(8), one directly obtains the desired result:
where is the vibrational quantum of the a-th normal mode). Moreover, the matrix elements of the electric and magnetic dipole over one-quantum vibrational transitions can be evaluated according to the following expressions [46,47], based on electrical harmonicity assumption:
In Equation (14), is the transformation matrix relating the Cartesian nuclear displacements to the normal coordinate . Wilson’s matrix [48] is often named in VCD literature, and individual indexes are adopted to label the atom and the ith Cartesian component of the nuclear displacement (). This double index notation is cumbersome when writing loops in programs. For this reason, we prefer to merely list the Cartesian nuclear displacements along a vector with components: .
The real vectors collect the Atomic Polar Tensors (APTs) [49,50,51]. The matrix element represents the change of the kth Cartesian component of the electric dipole caused by a change in nuclear position along the coordinate (). The real vectors collect the Atomic Axial Tensors (AATs) [49,50,51]. The matrix element represents the change in the kth Cartesian component of the magnetic dipole caused by a change in the nuclear velocity . By making use of Equation (14), one obtains the following expressions for the dipole and rotatory strengths of the vibrational transition:
Further details about the evaluation of Equation (13) are given in Appendix B. The relation of molecular polarizabilities with Lambert-Beer’s law and the concept of cross section is given in Appendix C.
3. Discussion
3.1. Polarizability Due to Electronic Transitions and UV-Vis Absorption
As an initial benchmark for the polar implementation, we report in Figure 1 the results of its application on TDDFT outputs of the benzene molecule computed for increasing values of the number of excited states (N). The correctness of polar implementation is checked against independent results obtained from frequency-dependent linear response theory (i.e., CPKS equations). The latter approach is implemented in Gaussian09 and computes the polarizability avoiding the sum over states. It can be noted that the convergence of polar results to the CPKS results is smooth over a wide range of photon energies. No appreciable differences are observed when the number of states in the sum of Equation (5) is large enough (in our case N = 1000). The static limit of the polarizability is known to be proportional to the volume occupied by core and valence electrons, both for atoms [52] and molecules [53]. For this reason, to reach convergence with respect to CPKS results, one needs to include enough electronic excitations in the sum over states expansion of , so to make sure that also contributions from core-excitations are present. As expected, convergence is faster when approaching resonance conditions (e.g., close to 7 eV in Figure 1a), for which single transitions dominate the sum over states expression of the polarizability.
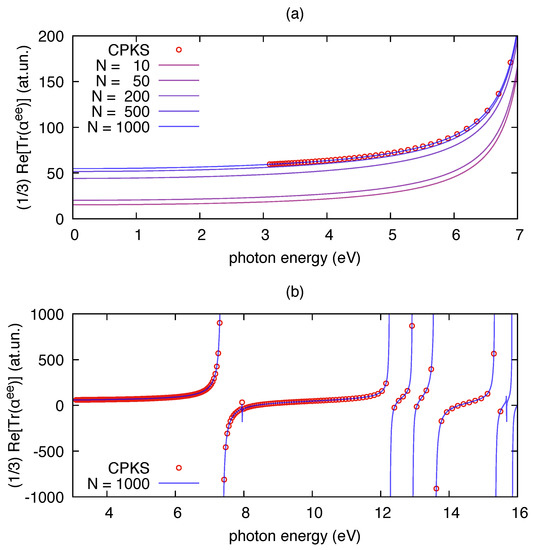
Figure 1.
The real part of the isotropic invariant of the electric dipole polarizability of benzene () computed by polar from a time-dependent density functional theory(TDDFT) calculation at B3LYP/6-31G(d,p) level: (a) far from the resonance range; and (b) close to the resonance range. The dots in both panels have been computed by the CPKS scheme available in Gaussian09 for applied electric fields at given frequencies. The results from the sum over states implemented by polar (Equation (5)) are shown with solid lines for increasing values of the number of states N included in the sum. The damping used in the polar calculations is = 0.001 eV.
In a further independent check, we have validated polar against the reported values of the complex electric dipole polarizability of 4,4’-diaminoazobenzene [54]. A direct numerical comparison is difficult in this case due to the different quantum chemistry code used here (Gaussian09) and in [54] (ADF). To approach the computational conditions of Haghdani et al. [54], we adopted for 4,4’-diaminoazobenzene the PBE functional and the cc-pVTZ basis set. Our results, reported in Figure 2, nicely compare with those reported in Figure 3b of Ref. [54]: the maximum value of the imaginary part of is about 1000 bohr and the maximum value of the real part of is about 600 bohr. We also note that the shapes and linewidths of both the real and imaginary parts of the isotropic electric polarizability in Figure 2 are very close to those reported in Figure 3b of Ref. [54].
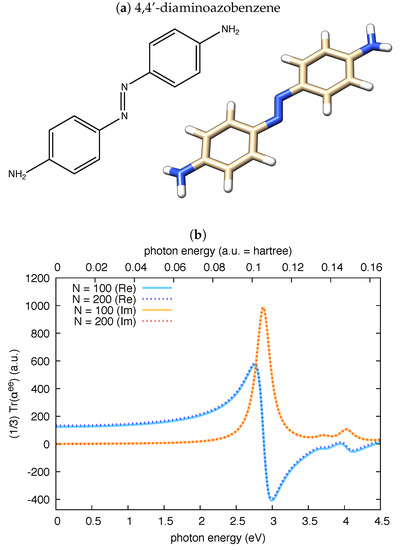
Figure 2.
The real and imaginary parts of the isotropic invariant of the electric dipole polarizability of 4,4’-diaminoazobenzene () computed by polar from a TDDFT calculation at PBE/cc-pVTZ level: (a) the chemical structure of 4,4’-diaminoazobenzene and the graphical representation of the computed equilibrium structure, which is essentially planar, with the -NH groups slightly pyramidalized; and (b) the results obtained by the polar code for two choices of N, demonstrating good convergence at states in this photon energy range. To approach the conditions used in [54], the damping for polar calculations is to 0.24 eV.
3.2. The Electric Dipole–Magnetic Dipole Polarizability and ECD
Turning to chiral molecules and chiroptical spectroscopy, the tensor becomes of relevance. To validate polar for this kind of calculations, we address in Figure 3 the case of hexahelicene. This is a representative molecule of the class of helicenes, which are -conjugated systems consisting of ortho-fused benzene rings and have many possible applications [55]. They are characterized by inherent helical chirality, and possess interesting spectroscopic properties [56,57,58,59,60,61].
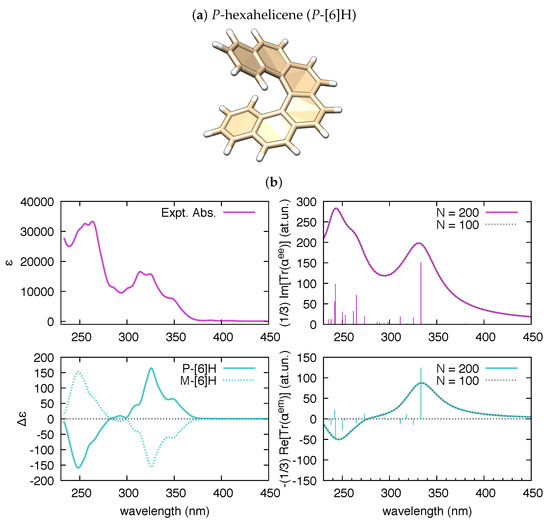
Figure 3.
(a) Graphical representation of the equilibrium structure of P-hexahelicene (data from B3LYP/6-31G(d,p) DFT calculation); and (b) comparison of the experimental UV-Vis absorption of hexahelicene and the electronic circular dichroism(ECD) spectra of P-hexahelicene and M-hexahelicene (from [60]) vs. the corresponding spectra simulated by polar ( = 0.5 eV) based on results from TDDFT calculations (200 states, B3LYP/6-31G(d,p)).
As shown in Figure 3, the trace of the polarizability tensor evaluated by polar on the basis of TDDFT calculations nicely match with the sign and relative magnitude of the rotatory strengths reported by Gaussian09 within the same TDDFT calculation. In comparison with hexahelicene, we have considered the hexamer model of a helically coiled graphene nanoribbon of recent synthesis [62] (HGNR-6), which is also a -conjugated system with inherent chirality (see Figure 4a). Interestingly, if we compare hexahelicene with HGNR-6 (for the same P-helicity), we obtain the same sign of the rotatory strength for the optically more active low energy transition (computed at 391 nm in HGNR-6, see Figure 4b). Notably, being -conjugation more extended in HGNR-6 than in hexahelicene, this causes a significant red-shift of the wavelength of such transition, and higher values of its rotatory strength. This is evident by comparing Figure 3b and Figure 4b. Furthermore, following the assignment of this low energy transition in hexahelicene to a helical sense-responsive feature (H-type band) [60], and by observing that the associated rotatory strengths have the same sign in P-hexahelicene and P-HGNR-6, we infer that such low-energy transition (computed at 391 nm) is of H-type also in HGNR-6.
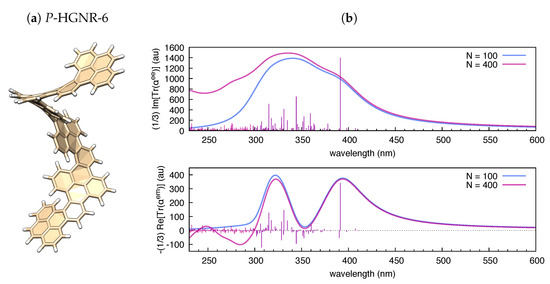
Figure 4.
(a) Graphical representation of the equilibrium structure of P-HGNR-6 (data from B3LYP/6-31g(d,p) DFT calculation); and (b) electronic absorption and circular dichroism of P-HGNR-6 simulated by polar ( = 0.5 eV) based on results from TDDFT calculations (B3LYP/6-31G(d,p); and states).
We have finally considered a third inherently chiral -conjugated molecule, the higher fullerene C, which belongs to point group symmetry [63] (see Figure 5). Similar to the case of another chiral fullerene, C [12,64,65,66,67,68], UV-Vis absorption and CD spectroscopies were among the techniques which were instrumental also in the discovery and characterization of C. Here, we limit ourselves to C, for which the assignment of the absolute configuration was carried out by means of DFT methods in reference [69].

Figure 5.
(a) The optimized structure of C used to compute the electric dipole–magnetic dipole polarizability reported in the top part of (c); and (b) the ()--C configuration of C which was assigned in [69] to the experimental CD spectrum represented in the bottom part of (c). The color scheme of (a,b) helps in distinguishing pentagons from hexagons in the fullerene. The experimental CD spectrum is taken from Ref. [69]. To simulate ( = 0.35 eV), we fed polar with data from a TDDFT calculation (B3LYP/6-31G(d,p) level, 400 states).
3.3. Vibrational Polarizabilities and IR/VCD Spectroscopies
To benchmark the vibrational contributions to molecular polarizabilities provided by polar, we begin by considering in the static limit. Such a quantity is straightforwardly provided by the Gaussian code in standard vibrational frequency calculations, and for small molecules (CH, CF, and CCl) it is also available from published independent calculations [70] and experiments [71]. As shown in Table 1, the numerical data provided by polar have the same quality as those reported by Gaussian, and compare reasonably with other theoretical data and experimental results.

Table 1.
Vibrational electric polarizabilities of CH, CF, and CCl (data are in atomic units [41]; B3LYP/aug-cc-pVTZ DFT calculations for Columns 1 and 2—present work). The minor discrepancy between Columns 1 and 2 is due to slight differences in the numerical values of the physical constants involved in the calculations (i.e., polar in Column 1 vs. Gaussian in Column 2). This is proved by the ratios of the values in Columns 1 and 2 being 1.0072, independently of the molecule.
Parallel to the case of the electronic polarizability, where the imaginary part of relates to UV-Vis absorption spectroscopy and the real part of relates to circular dichroism (CD) spectroscopy, the calculation of the frequency-dependent vibrational polarizabilities and paves the way to the simulation of IR and VCD spectra, respectively. It is known that VCD and IR (to a minor extent) are fairly sensitive to structural changes in flexible molecules [72,73] and to the equilibrium among conformers [74,75,76,77]. Even though it is possible to handle molecular flexibility in VCD (e.g., see Ref. [78] for a recent approach), in our validation of polar, we decided to consider rigid molecules, for the sake of simplicity. We selected four chiral molecules with unique conformations, which offers a more straightforward comparison with the experimental IR and VCD spectra. The application of polar to molecules with many conformations is a conceptually straightforward task, which could be considered in future versions of the code. The experimental VCD and IR spectra of (1S)-Fenchone ((1S) -FEN), (1S)-Camphor ((1S)-CAM), (1S)-2-Methylenefenchone ((1S)-MEFEN) and (1S)-2-Methylenecamphor ((1S)-MECAM) were investigated in [79], and the main features of the spectra where assigned with the help of DFT calculations. The satisfactory comparison between frequency-dependent polarizabilities and experimental IR and VCD spectra of the four molecules is presented in Figure 6 and Figure 7.
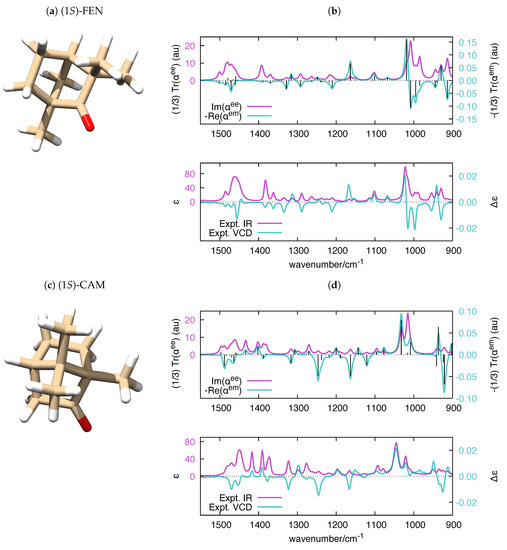
Figure 6.
(a,c) The equilibrium structure of (1S)-FEN and (1S)-CAM, respectively; and (b,d) polar-simulated IR and VCD spectra of (1S)-FEN and (1S)-CAM ( = 10 cm), respectively, compared to their experimental counterparts [79]. The vertical black bars in the top panels are proportional to the rotatory strengths computed by Gaussian (). To ease the comparison with the experimental data, the wavenumber axis of the simulated polarizabilities has been uniformly scaled by the empirical factor 0.98. DFT calculations were carried out at the B3LYP/aug-cc-pVTZ level.
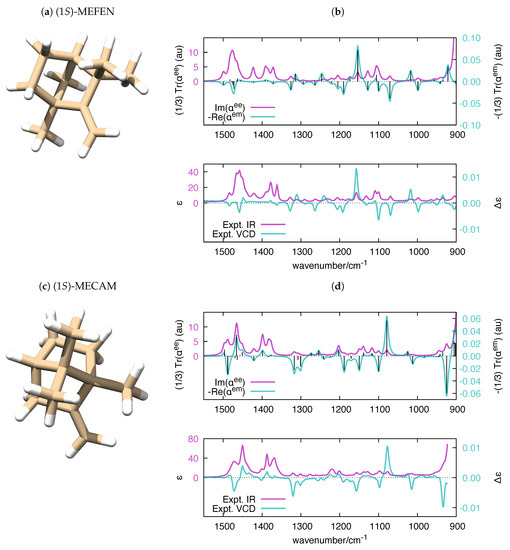
Figure 7.
(a,c) The equilibrium structure of (1S)-MEFEN and (1S)-MECAM, respectively; and (b,d) polar-simulated IR and VCD spectra of (1S)-MEFEN and (1S)-MECAM ( = 10 cm), respectively, compared to their experimental counterparts [79]. The vertical black bars in the top panel are proportional to the rotatory strengths computed by Gaussian (). To ease the comparison with the experimental data, the wavenumber axis of the simulated polarizabilities has been uniformly scaled by the empirical factor 0.98. DFT calculations were carried out at the B3LYP/aug-cc-pVTZ level.
The dissymmetry factor g plays an important role in VCD spectroscopy [80,81]. The g factor analytically correlates with the concept of robustness [82,83], which was introduced in VCD by Nicu and Baerends [84]. This useful parameter characterizes the soundness of the numerical prediction of VCD intensities and signs, and its use has been extended by Góbi and Magyarfalvi through the dissymmetry factor [85]. For these reasons, we have decided to compare in Figure 8 the function computed by polar with the corresponding experimental quantity measured for 1S-CAM, taken as a representative reference. Both the order of magnitude and the spectral shape of the computed match reasonably well with the experimental results, which we take as a solid benchmark of the implementation of the polar code.
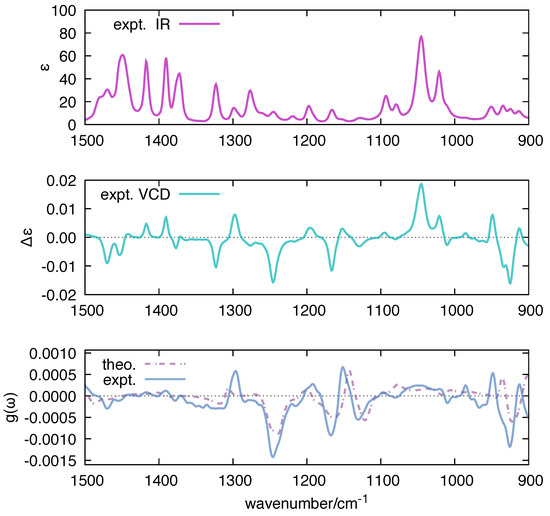
Figure 8.
Comparison between the experimental g-ratio of 1S-CAM and the g-ratio calculated by polar based on Equation (12) ( = 10 cm). DFT calculations on 1S-CAM have been carried out at B3LYP/aug-cc-pVTZ level; for ease of comparison with experimental data, the wavenumbers computed by DFT were scaled by 0.98.
To further validate the calculation of the transition magnetic dipole moments and the rotatory strengths performed by polar, we have computed the transition dipole moments and the g-ratios of methyloxirane (Figure 9), a well-known small and rigid chiral molecule which was investigated in the past by three of us [82]. The above quantities have been compared with the corresponding g-ratios that can be straightforwardly determined from the dipole and rotatory strengths extracted (in cgs units) from the typical output of a VCD calculation made by Gaussian. We collect in Table 2 the satisfactory comparison between the g-ratios computed by polar and those determined from the Gaussian output.
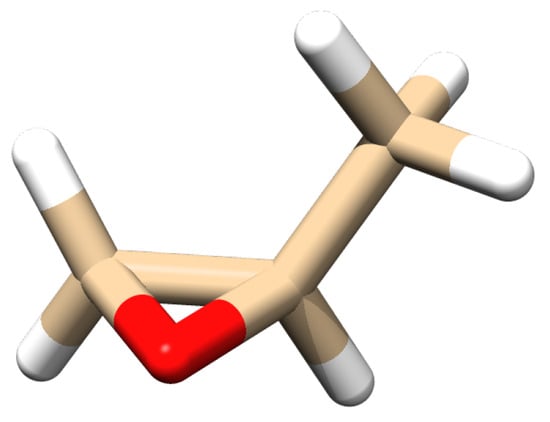
Figure 9.
Representation of the equilibrium structure of (R)-methyloxirane computed by DFT at the B3LYP/aug-cc-pVQZ level of theory.

Table 2.
Comparison of the results from a VCD calculation carried out with Gaussian09 on (R)-methyloxirane at the B3LYP/aug-cc-pVQZ level, and the results obtained by a corresponding polar calculation based on the numerical data contained in the *.fchk file associated with the Gaussian calculation. Column (a) is the wavenumbers computed by Gaussian09 and polar are not distinguishable at the shown precision. The APTs and AATs stored in the *.fchk file are used by polar to compute the dipole and rotatory strengths (Columns (b) and (c)) in atomic units (see Equation (14) and Section 4 for details), from which we computed the dissymmetry ratios listed in Column (d)—please note the use of SI for the electromagnetic field, which implies the factor in atomic units [41]. The dipole and rotatory strengths computed by Gaussian09 (Columns (e) and (f)) are used to compute the dissymmetry ratios (cgs system) reported in Column (g).
3.4. Introducing Intensity-Carrying Modes in VCD
Among the observations pointed out in [79], we highlight that “the intensities, both in absorption and in VCD, are generally larger for FEN than for MEFEN and for CAM than for MECAM”. Indeed, the inspection of Figure 6a and Figure 7a confirms that the polarizabilities of the carbonyl-containing molecules FEN and CAM display larger values than MEFEN and MECAM. To directly point out the role of the carbonyl group in causing the intensity increase in both VCD and IR calculations, we compute the Intensity Carrying Modes (ICM) of the four molecules. This useful concept was introduced by Torii et al. in the framework of IR and Raman spectroscopy [32,33], connected to vibrational polarizabilities (and hyperpolarizabilities) [33], and later extended to Raman Optical Activity (ROA) by Luber et al. [86]. However, to the best the authors’ knowledge, the use of ICM in the context of VCD is unprecedented. Therefore, it is worth recalling the notation used for IR spectroscopy, and extend it to VCD.
ICMs are introduced as collective nuclear displacements along which the IR intensity (or Raman or ROA intensity) is maximized. This leads to an eigenvalue problem [33,86] for the matrix, which, in the case of IR spectroscopy, can be expressed through the dipole derivatives with respect to the nuclear displacement Cartesian coordinates (; ):
For a given matrix (either for IR, Raman, or ROA), the eigenvalue problem
provides the eigenvalues associated with the maximized intensities, and the related nuclear displacements coefficients that describe a selected kth ICM [33,86].
If one evaluates the dipole strength in terms of APTs (Equation (14)), one can easily justify the expression of the matrix provided in Equation (16):
with
We mention that Torii’s approach to ICM [33] makes use of internal coordinates instead of Cartesian nuclear displacements. This is just a matter of choice in the representation of the nuclear displacements, and it does not affect the conclusions reached in this Section.
Equation (18) shows that the dipole strength of a given vibrational transition () is a quadratic form in the coefficients of the nuclear displacement of the associated normal mode (). Clearly, Torii’s approach to ICM [33] seeks the eigenvalues of the matrix (Equation (16)), which is exactly the matrix of the quadratic form associated to the dipole strength reported in Equation (18). This observation justifies a similar approach for IR and VCD, provided that a suitable matrix is defined also for the latter case. Following the strategy described for IR, to define ICM in VCD one may proceed by looking for a quadratic form associated with the rotatory strength . By making use of Equation (14), one can express the rotatory strength in terms of APTs and AATs as follows:
The last identity in Equation (19) provides the expression of the quadratic form suitable for VCD, characterized by a matrix . We note that this matrix is not symmetric. However, the result of the summation in Equation (19) cannot be distinguished from the symmetric version below, which is preferred for numerical convenience:
with
From the inspection of Equation (20), we conclude that ICMs suitable for VCD can be found by seeking the stationary values of the rotatory strength as a function of the nuclear displacement coefficients (subject to normalization of the vector of coefficients). Similar to the case of IR spectroscopy [33], this leads to the eigenvalue problem for the matrix defined by Equation (20).
We implemented the calculation of ICM in polar, for both IR and VCD spectroscopy, considering the matrices given by Equations (18) and (20). The eigenvalues resulting from the solution of Equation (17) are collected in Table 3 (for IR) and in Table 4 (for VCD). We observe that the number of non-zero eigenvalues of is three (as previously found by Torii [33]), while it is six for . As pointed out by Luber et al. in discussing Raman and ROA ICMs [86], the rank of the matrix indeed equals the number of independent components of the polarizability. Similarly, in VCD, we have three independent components of the electric and magnetic dipoles, which justifies the rank of being six. Furthermore, since the sum of the rotatory strengths is zero [47] (i.e., ), this justifies the fact that the sum of the eigenvalues is approximately zero, within the numerical accuracy affordable by the selected computational method.

Table 3.
IR Intensity Carrying Modes (ICM)s of the four chiral compounds for which the corresponding simulated and experimental spectra are reported in Figure 6 and Figure 7. The APTs and AATs required for the evaluation of ICMs have been computed at the B3LYP/aug-cc-pVTZ level of theory. All numerical data are given in the atomic units of the matrix.

Table 4.
VCD Intensity Carrying Modes (ICM)s of the four chiral compounds for which the corresponding simulated and experimental spectra are reported in Figure 6 and Figure 7. The APTs and AATs required for the evaluation of ICMs have been computed at the B3LYP/aug-cc-pVTZ level of theory. All numerical data are given in the atomic units of the matrix.
The inspection of the data reported in Table 3 fully justifies the observation made in Ref. [79] that the IR intensities of FEN and CAM are overall stronger than MEFEN and MECAM (respectively). The eigenvalues of the IR-ICMs of the carbonyl-containing compounds FEN and CAM are quite similar, but they are remarkably larger than those of MEFEN and MECAM. Moreover, the inspection of the animations of the associated eigenmodes (Supplementary Materials) reveals that for and (which are the most IR-active ICMs of FEN and CAM) the carbonyl group is significantly involved: mode 1 has a large C=O stretching content, whereas mode 2 shows a significant C=O bending content. It is thus clear that the presence of carbonyl explains the stronger activity in the IR of FEN and CAM compared to MEFEN and MECAM (as expected).
Turning now our attention to VCD, the ICM eigenvalues reported in Table 4 reveal, similar to IR, the presence in FEN and CAM of two significant positive eigenvalues (), which pair up with their negative counterparts . The inspection of the associated eigenmodes (Supplementary Materials) reveals also for VCD the involvement of stretching/bending carbonyl motions occurring in-phase () or out-of-phase () with respect to skeletal distortions of the rest of the molecule. Therefore, based on the analysis of VCD-ICMs of the four molecules, we can provide a clue for the IR and VCD strengths of FEN and CAM being stronger than MEFEN and MECAM, as observed in [79]. Indeed, the direct involvement of carbonyl motions in the stronger ICMs is responsible for the observed differences in both IR and VCD.
4. Materials and Methods
All the polarizability calculations reported here were carried out through the polar code developed in this work. polar allows the numerical evaluation of the three polarizability tensors , , as a function of the photon frequency . Both electronic and vibrational polarizabilities can be computed. polar is written in the C++ language, and adopts complex numbers for better code readability.
Electronic polarizabilities are evaluated as sum over vertical electronic transitions (Equations (6)–(8)). The required input data are the excitation energies of a selected set of excited states , and the associated electric (magnetic) transition dipoles (). The output file of an ordinary TDDFT calculation made by Gaussian code [5] can be parsed by polar to gather all information required to operate. By writing additional parsers, polar can be straightforwardly interfaced to other quantum chemistry packages.
The calculation of vibrational polarizabilities by Equation (13) requires the quantities computed by Gaussian in a standard VCD job. These are the Hessian of the energy vs. the Cartesian nuclear displacements, and the derivatives of the electric and magnetic dipole vs. the Cartesian nuclear displacements (the latter two quantities are also, respectively, named APTs and AATs, see for instance [49,50,51]). By using the Hessian matrix, polar solves the secular equation to obtain the vibrational frequencies () and the normal modes, which are required to compute the dipole derivatives vs. normal coordinates () from APTs and AATs. The Hessian, APTs, and AATs are stored by Gaussian in the formatted checkpoint file (*.fchk) and are read by polar before addressing the evaluation of vibrational polarizabilities. For convenience, since Gaussian checkpoint and output files report computed data in atomic units, we adopt the same convention in polar. The quite useful and neat paper by McWeeny [41] can help the reader in converting all the quantities reported here from atomic to SI units. We merely remind here the following identities (where is the symbol for the Hartree, the symbol for the Bohr, and is the electric permittivity):
Since the atomic units of the electric and magnetic fields are and [41], it is straightforward to show that .
The DFT and time-dependent density functional theory(TDDFT) calculations reported in this work have been carried out with Gaussian09 Rev. D.01 [5]. Because of the scattered nature of the literature reference data employed in this work to validate polar, we had to chose individual functionals and basis sets, as best suited to carry out the required comparison. Therefore, in the caption of each figure or table presenting computational data, we report the selected functional and basis set.
5. Conclusions
The polar code makes the simulation of CD spectra straightforward through the evaluation of the trace of the frequency-dependent electric dipole–magnetic dipole molecular polarizability, . polar allows simulating both ECD and VCD spectra based on the quantum chemical outputs routinely produced by the Gaussian code [5]. These calculations allow for the validation of polar thanks to the available literature data.
As a remarkable byproduct, our theoretical analysis of the molecular polarizabilities also allows one to easily compute the dissymmetry factor , which compares well with the experimental counterpart of camphor, as reported in Figure 8. Finally, we have extended Torii’s Intensity Carrying Modes [32,33] to the context of VCD spectroscopy. This provides an informative approach to the understanding of the origin of VCD intensities.
Moreover, the complex polarizabilities computed by polar are of relevance to spectroscopic applications in the presence of controlled distributions of electromagnetic fields that can be realized via nano-optical engineering in order to enhance the chiroptical response [87,88,89]. In this framework, the molecular calculations can serve both the purpose of introducing the chiral medium into the electromagnetic simulations via effective medium approaches and of evaluating the weight of the quadrupolar contributions in the CD spectra because of the presence of specific field gradients.
Author Contributions
Conceptualization, M.T., C.Z, G.P. and P.B.; Software, M.T.; Validation, G.L., S.A. and M.T.; Data curation, M.T. and C.Z.; Writing—original draft preparation, M.T.; and Writing—review and editing, C.Z., G.L., S.A., G.P., P.B. and M.T.
Funding
This research was funded by the Italian Ministry of Education, Universities and Research (MIUR) through the PRIN 2015 program (Project No. 2015FSHNCB “Plasmon-enhanced vibrational circular dichroism”).
Acknowledgments
M.T. acknowledges James Cheeseman (Gaussian Inc., Wallingford, Connecticut, USA) for useful details about the formatted checkpoint produced by Gaussian09 rev D.01.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AAT | Atomic Axial Tensor |
| APT | Atomic Polar Tensor |
| CD | circular dichroism |
| CPKS | coupled perturbed Kohn Sham equations |
| DFT | density functional theory |
| ECD | electronic circular dichroism |
| TDDFT | time-dependent density functional theory |
| VCD | vibrational circular dichroism |
Appendix A. Analysis of Polarizabilities in Resonance Condition
By taking the trace of Equations (6)–(8), and by considering Equation (4), one straightforwardly obtains the following:
where . We notice that these identities hold because the dipole operators are Hermitian operators, which implies , and (similar identities hold for and as well). This implies that the resonance and off-resonance terms of Equation (A1) are related to each other by complex conjugation, as expected [43]:
In resonance condition (), the quantity is small. Therefore, one can consider just the resonance terms in the sum over states expansion (A2), obtaining:
By recalling that and are real quantities, one can expand the expression for the real and imaginary parts of the and tensors, obtaining:
Similarly, by considering that is imaginary, one obtains:
We recall that the Lorentzian lineshape , typical of absorption spectroscopy [90], has the following expression:
This lineshape function is normalized so that , similar to in Equation (2). In the imaginary parts of Equation (A4) and in the real part of Equation (A5), one can easily identify the Lorentzian lineshape (i.e., ). Therefore, we conclude the following:
where we have identified in Equation (A7) with the Lorentzian lineshapes showing up in Equations (A4) and (A5). This is possible also because both and are normalized functions.
Appendix B. Polarizability as a Sum over Vibrational States
By evaluating the electric dipole transition elements showing up in Equation (13) through the use of Equation (14), one obtains the vibrational contribution to the electric polarizability as follows:
When considering the static limit (), and neglecting damping effects (), one recovers the result previously obtained by Castiglioni et al. in terms of electric dipole derivatives [71,91]:
Appendix C. Relation with Lambert–Beer law
For convenience, we recall here the connection between the transition rate and the Lambert–Beer law by which absorption experiments are usually interpreted (for consistency with the rest of this work, we adopt SI units, which, when needed, consistently lead to atomic units [41]. For this reason, instead of the molecular absorbivity , we use here the molecular cross section (whose dimension is an area):
A is the absorbance, l the sample length, and C represents the number of absorbing molecules per unit volume (number concentration). The differential form of the Lambert–Beer law, corresponding to the differential absorption caused by light traversing the differential path , is the following:
Hence, the intensity loss due to absorption within the path is:
We remark that represents the energy loss per unit time over the cross section S of the light beam, and it is caused by the rate of energy absorbed by the molecule, , times the number of molecules within the volume , divided by the cross section S of the light beam:
References
- Barone, V. Computational Strategies for Spectroscopy: From Small Molecules to Nano Systems; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- TURBOMOLE V6.2 2010, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, Since 2007. Available online: http://www.turbomole.org (accessed on 1 November 2019).
- Gordon, M.S.; Schmidt, M.W. Chapter 41—Advances in Electronic Structure Theory: GAMESS a Decade Later; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1167–1189. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Aidas, K.; Angeli, C.; Bak, K.L.; Bakken, V.; Bast, R.; Boman, L.; Christiansen, O.; Cimiraglia, R.; Coriani, S.; Dahle, P.; et al. The Dalton quantum chemistry program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 269–284. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.G.A.; Burns, L.A.; Sirianni, D.A.; Nascimento, D.R.; Kumar, A.; James, A.M.; Schriber, J.B.; Zhang, T.; Zhang, B.; Abbott, A.S.; et al. Psi4NumPy: An Interactive Quantum Chemistry Programming Environment for Reference Implementations and Rapid Development. J. Chem. Theory Comput. 2018, 14, 3504–3511. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Zerara, M. pyVib, a computer program for the analysis of infrared and Raman optical activity. J. Comput. Chem. 2008, 29, 306–311. [Google Scholar] [CrossRef]
- Bannwarth, C.; Grimme, S. A simplified time-dependent density functional theory approach for electronic ultraviolet and circular dichroism spectra of very large molecules. Comput. Theor. Chem. 2014, 1040–1041, 45–53. [Google Scholar] [CrossRef]
- Bannwarth, C.; Grimme, S. Electronic Circular Dichroism of Highly Conjugated π-Systems: Breakdown of the Tamm–Dancoff/Configuration Interaction Singles Approximation. J. Phys. Chem. A 2015, 119, 3653–3662. [Google Scholar] [CrossRef]
- Ren, S.; Caricato, M. Multi-state extrapolation of UV/Vis absorption spectra with QM/QM hybrid methods. J. Chem. Phys. 2016, 144, 184102. [Google Scholar] [CrossRef]
- Barone, V. The virtual multifrequency spectrometer: A new paradigm for spectroscopy. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 86–110. [Google Scholar] [CrossRef]
- Fusè, M.; Egidi, F.; Bloino, J. Vibrational circular dichroism under the quantum magnifying glass: From the electronic flow to the spectroscopic observable. Phys. Chem. Chem. Phys. 2019, 21, 4224–4239. [Google Scholar] [CrossRef] [PubMed]
- Frediani, L.; Andreussi, O.; Kulik, H.J. Coding solvation: Challenges and opportunities. Int. J. Quantum Chem. 2019, 119, e25839. [Google Scholar] [CrossRef]
- Chiariello, M.G.; Raucci, U.; Coppola, F.; Rega, N. Unveiling anharmonic coupling by means of excited state ab initio dynamics: Application to diarylethene photoreactivity. Phys. Chem. Chem. Phys. 2019, 21, 3606–3614. [Google Scholar] [CrossRef] [PubMed]
- Galimberti, D.R.; Bougueroua, S.; Mahé, J.; Tommasini, M.; Rijs, A.M.; Gaigeot, M.P. Conformational assignment of gas phase peptides and their H-bonded complexes using far-IR/THz: IR-UV ion dip experiment, DFT-MD spectroscopy, and graph theory for mode assignment. Faraday Discuss. 2019, 217, 67–97. [Google Scholar] [CrossRef] [PubMed]
- Pezzotti, S.; Galimberti, D.R.; Gaigeot, M.P. Deconvolution of BIL-SFG and DL-SFG spectroscopic signals reveals order/disorder of water at the elusive aqueous silica interface. Phys. Chem. Chem. Phys. 2019, 21, 22188–22202. [Google Scholar] [CrossRef] [PubMed]
- Bloino, J.; Biczysko, M.; Barone, V. Anharmonic Effects on Vibrational Spectra Intensities: Infrared, Raman, Vibrational Circular Dichroism, and Raman Optical Activity. J. Phys. Chem. A 2015, 119, 11862–11874. [Google Scholar] [CrossRef] [PubMed]
- Micciarelli, M.; Conte, R.; Suarez, J.; Ceotto, M. Anharmonic vibrational eigenfunctions and infrared spectra from semiclassical molecular dynamics. J. Chem. Phys. 2018, 149, 64115. [Google Scholar] [CrossRef]
- Micciarelli, M.; Gabas, F.; Conte, R.; Ceotto, M. An effective semiclassical approach to IR spectroscopy. J. Chem. Phys. 2019, 150, 184113. [Google Scholar] [CrossRef]
- Zuehlsdorff, T.J.; Montoya-Castillo, A.; Napoli, J.A.; Markland, T.E.; Isborn, C.M. Optical spectra in the condensed phase: Capturing anharmonic and vibronic features using dynamic and static approaches. J. Chem. Phys. 2019, 151, 74111. [Google Scholar] [CrossRef]
- Schellman, J.A. Circular dichroism and optical rotation. Chem. Rev. 1975, 75, 323–331. [Google Scholar] [CrossRef]
- Kawiecki, R.W.; Devlin, F.; Stephens, P.J.; Amos, R.D.; Handy, N.C. Vibrational circular dichroism of propylene oxide. Chem. Phys. Lett. 1988, 145, 411–417. [Google Scholar] [CrossRef]
- Hu, L.; Huang, Y.; Pan, L.; Fang, Y. Analyzing intrinsic plasmonic chirality by tracking the interplay of electric and magnetic dipole modes. Sci. Rep. 2017, 7, 11151. [Google Scholar] [CrossRef] [PubMed]
- Mukamel, S.S. Principles of Nonlinear Optical Spectroscopy; Includes Index: New York, NY, USA; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Toury, T.; Zyss, J.; Chernyak, V.; Mukamel, S. Collective Electronic Oscillators for Second-Order Polarizabilities of Push-Pull Carotenoids. J. Phys. Chem. A 2001, 105, 5692–5703. [Google Scholar] [CrossRef]
- Tretiak, S.; Mukamel, S. Density Matrix Analysis and Simulation of Electronic Excitations in Conjugated and Aggregated Molecules. Chem. Rev. 2002, 102, 3171–3212. [Google Scholar] [CrossRef] [PubMed]
- Kessler, J.; Bouř, P. Transfer of Frequency-Dependent Polarizabilities: A Tool To Simulate Absorption and Circular Dichroism Molecular Spectra. J. Chem. Theory Comput. 2015, 11, 2210–2220. [Google Scholar] [CrossRef] [PubMed]
- Moscowitz, A. Theoretical Aspects of Optical Activity Part One: Small Molecules. Adv. Chem. Phys. 1962, 4, 67–112. [Google Scholar] [CrossRef]
- Torii, H.; Ueno, Y.; Sakamoto, A.; Tasumi, M. Infrared Intensity-Carrying Modes and Electron-Vibration Interactions in the Radical Cations of Polycyclic Aromatic Hydrocarbons. J. Phys. Chem. A 1999, 103, 5557–5566. [Google Scholar] [CrossRef]
- Torii, H. Intensity-carrying modes important for vibrational polarizabilities and hyperpolarizabilities of molecules: Derivation from the algebraic properties of formulas and applications. J. Comput. Chem. 2002, 23, 997–1006. [Google Scholar] [CrossRef]
- Lee, K.S.H. Relations between electric and magnetic polarizabilities and other related quantities. Radio Sci. 1987, 22, 1235–1238. [Google Scholar] [CrossRef]
- Barron, L.D. Molecular Light Scattering and Optical Activity, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Arrighini, G.P.; Maestro, M.; Moccia, R. Magnetic Properties of Polyatomic Molecules. I. Magnetic Susceptibility of H2O, NH3, CH4, H2O2. J. Chem. Phys. 1968, 49, 882–889. [Google Scholar] [CrossRef]
- Pelloni, S.; Lazzeretti, P. On the determination of the diagonal components of the optical activity tensor in chiral molecules. J. Chem. Phys. 2014, 140, 74105. [Google Scholar] [CrossRef] [PubMed]
- Ruud, K.; Helgaker, T. Optical rotation studied by density-functional and coupled-cluster methods. Chem. Phys. Lett. 2002, 352, 533–539. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Cheeseman, J.R.; Frisch, M.J. Calculation of Optical Rotation Using Density Functional Theory. J. Phys. Chem. A 2001, 105, 5356–5371. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Frisch, M.J.; Devlin, F.J.; Stephens, P.J. Hartree-Fock and Density Functional Theory ab Initio Calculation of Optical Rotation Using GIAOs: Basis Set Dependence. J. Phys. Chem. A 2000, 104, 1039–1046. [Google Scholar] [CrossRef]
- McWeeny, R. Natural Units in Atomic and Molecular Physics. Nature 1973, 243, 196. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Pearson: Boston, MA, USA, 2013; Re-Published by Cambridge University Press in 2017. [Google Scholar]
- Buckingham, A.D.; Fischer, P. Phenomenological damping in optical response tensors. Phys. Rev. A 2000, 61, 035801. [Google Scholar] [CrossRef]
- Mukamel, S. Causal versus noncausal description of nonlinear wave mixing: Resolving the damping-sign controversy. Phys. Rev. A 2007, 76, 021803. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Sowiński, T. Quantum electrodynamics of qubits. Phys. Rev. A 2007, 76, 062106. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Fowler, P.W.; Galwas, P.A. Velocity-dependent property surfaces and the theory of vibrational circular dichroism. Chem. Phys. 1987, 112, 1–14. [Google Scholar] [CrossRef]
- Buckingham, A.D. Introductory lecture. The theoretical background to vibrational optical activity. Faraday Discuss. 1994, 99, 1–12. [Google Scholar] [CrossRef]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; Dover Books on Chemistry; Dover Publ.: New York, NY, USA, 1980. [Google Scholar]
- Stephens, P.J. Theory of vibrational circular dichroism. J. Phys. Chem. 1985, 89, 748–752. [Google Scholar] [CrossRef]
- Stephens, P.J. Gauge dependence of vibrational magnetic dipole transition moments and rotational strengths. J. Phys. Chem. 1987, 91, 1712–1715. [Google Scholar] [CrossRef]
- Nicu, V.P.; Neugebauer, J.; Wolff, S.K.; Baerends, E.J. A vibrational circular dichroism implementation within a Slater-type-orbital based density functional framework and its application to hexa- and hepta-helicenes. Theor. Chem. Acc. 2008, 119, 245–263. [Google Scholar] [CrossRef]
- Politzer, P.; Jin, P.; Murray, J.S. Atomic polarizability, volume and ionization energy. J. Chem. Phys. 2002, 117, 8197–8202. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Polarizability and volume. J. Chem. Phys. 1993, 98, 4305–4306. [Google Scholar] [CrossRef]
- Haghdani, S.; Davari, N.; Sandnes, R.; Åstrand, P.O. Complex Frequency-Dependent Polarizability through the π→π* Excitation Energy of Azobenzene Molecules by a Combined Charge-Transfer and Point-Dipole Interaction Model. J. Phys. Chem. A 2014, 118, 11282–11292. [Google Scholar] [CrossRef]
- Gingras, M. One hundred years of helicene chemistry. Part 3: Applications and properties of carbohelicenes. Chem. Soc. Rev. 2013, 42, 1051–1095. [Google Scholar] [CrossRef]
- Bürgi, T.; Urakawa, A.; Behzadi, B.; Ernst, K.H.; Baiker, A. The absolute configuration of heptahelicene: A VCD spectroscopy study. New J. Chem. 2004, 28, 332–334. [Google Scholar] [CrossRef]
- Abbate, S.; Lebon, F.; Longhi, G.; Fontana, F.; Caronna, T.; Lightner, D.A. Experimental and calculated vibrational and electronic circular dichroism spectra of 2-Br-hexahelicene. Phys. Chem. Chem. Phys. 2009, 11, 9039–9043. [Google Scholar] [CrossRef]
- Nakai, Y.; Mori, T.; Inoue, Y. Theoretical and Experimental Studies on Circular Dichroism of Carbo[n]helicenes. J. Phys. Chem. A 2012, 116, 7372–7385. [Google Scholar] [CrossRef]
- Johannessen, C.; Blanch, E.; Villani, C.; Abbate, S.; Longhi, G.; Agarwal, N.; Tommasini, M.; Lightner, D. Raman and ROA spectra of (-)- and (+)-2-Br-Hexahelicene: Experimental and DFT studies of a π-conjugated chiral system. J. Phys. Chem. B 2013, 117. [Google Scholar] [CrossRef] [PubMed]
- Abbate, S.; Longhi, G.; Lebon, F.; Castiglioni, E.; Superchi, S.; Pisani, L.; Fontana, F.; Torricelli, F.; Caronna, T.; Villani, C.; et al. Helical sense-responsive and substituent-sensitive features in vibrational and electronic circular dichroism, in circularly polarized luminescence, and in Raman spectra of some simple optically active hexahelicenes. J. Phys. Chem. C 2014, 118, 1682–1695. [Google Scholar] [CrossRef]
- Zanchi, C.; Lucotti, A.; Cancogni, D.; Fontana, F.; Trusso, S.; Ossi, P.; Tommasini, M. Functionalization of nanostructured gold substrates with chiral chromophores for SERS applications: The case of 5-Aza[5]helicene. Chirality 2018, 30, 875–882. [Google Scholar] [CrossRef] [PubMed]
- Daigle, M.; Miao, D.; Lucotti, A.; Tommasini, M.; Morin, J.F. Helically Coiled Graphene Nanoribbons. Angew. Chem. Int. Ed. 2017, 56, 6213–6217. [Google Scholar] [CrossRef] [PubMed]
- Manolopoulos, D.E. Proposal of a chiral structure for the fullerene C76. J. Chem. Soc. Faraday Trans. 1991, 87, 2861–2862. [Google Scholar] [CrossRef]
- Diederich, F.; Ettl, R.; Rubin, Y.; Whetten, R.L.; Beck, R.; Alvarez, M.; Anz, S.; Sensharma, D.; Wudl, F.; Khemani, K.C.; et al. The Higher Fullerenes: Isolation and Characterization of C76, C84, C90, C94, and C70O, an Oxide of D5h-C70. Science 1991, 252, 548–551. [Google Scholar] [CrossRef]
- Ettl, R.; Chao, I.; Diederich, F.; Whetten, R.L. Isolation of C76, a chiral (D2) allotrope of carbon. Nature 1991, 353, 149. [Google Scholar] [CrossRef]
- Orlandi, G.; Poggi, G.; Zerbetto, F. The circular dichroism spectrum of C76. A quantum chemical study. Chem. Phys. Lett. 1994, 224, 113–117. [Google Scholar] [CrossRef]
- Goto, H.; Harada, N.; Crassous, J.; Diederich, F. Absolute configuration of chiral fullerenes and covalent derivatives from their calculated circular dichroism spectra. J. Chem. Soc. Perkin Trans. 2 1998, 8, 1719–1724. [Google Scholar] [CrossRef]
- Kessinger, R.; Crassous, J.; Herrmann, A.; Rüttimann, M.; Echegoyen, L.; Diederich, F. Preparation of Enantiomerically Pure C76 with a General Electrochemical Method for the Removal of Di(alkoxycarbonyl)methano Bridges from Methanofullerenes: The Retro-Bingel Reaction. Angew. Chem. Int. Ed. 1998, 37, 1919–1922. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R. Absolute Configuration of D2-Symmetric Fullerene C84. J. Am. Chem. Soc. 2002, 124, 3804–3805. [Google Scholar] [CrossRef] [PubMed]
- Bishop, D.M.; Gu, F.L.; Cybulski, S.M. Static and dynamic polarizabilities and first hyperpolarizabilities for CH4, CF4, and CCl4. J. Chem. Phys. 1998, 109, 8407–8415. [Google Scholar] [CrossRef]
- Gussoni, M.; Rui, M.; Zerbi, G. Electronic and relaxation contribution to linear molecular polarizability. An analysis of the experimental values. J. Mol. Struct. 1998, 447, 163–215. [Google Scholar] [CrossRef]
- Heshmat, M.; Baerends, E.J.; Polavarapu, P.L.; Nicu, V.P. The Importance of Large-Amplitude Motions for the Interpretation of Mid-Infrared Vibrational Absorption and Circular Dichroism Spectra: 6,6’-Dibromo-[1,1’-binaphthalene]-2,2’-diol in Dimethyl Sulfoxide. J. Phys. Chem. A 2014, 118, 4766–4777. [Google Scholar] [CrossRef] [PubMed]
- Passarello, M.; Abbate, S.; Longhi, G.; Lepri, S.; Ruzziconi, R.; Nicu, V.P. Importance of C*–H Based Modes and Large Amplitude Motion Effects in Vibrational Circular Dichroism Spectra: The Case of the Chiral Adduct of Dimethyl Fumarate and Anthracene. J. Phys. Chem. A 2014, 118, 4339–4350. [Google Scholar] [CrossRef] [PubMed]
- Miyazawa, M.; Kyogoku, Y.; Sugeta, H. Vibrational circular dichroism studies of molecular conformation and association of dipeptides. Spectrochim. Acta Part A Mol. Spectrosc. 1994, 50, 1505–1511. [Google Scholar] [CrossRef]
- Wang, F.; Polavarapu, P.L.; Schurig, V.; Schmidt, R. Absolute configuration and conformational analysis of a degradation product of inhalation anesthetic Sevoflurane: A vibrational circular dichroism study. Chirality 2002, 14, 618–624. [Google Scholar] [CrossRef]
- Polavarapu, P.L. Renaissance in chiroptical spectroscopic methods for molecular structure determination. Chem. Rec. 2007, 7, 125–136. [Google Scholar] [CrossRef]
- Izumi, H.; Ogata, A.; Nafie, L.A.; Dukor, R.K. Structural determination of molecular stereochemistry using VCD spectroscopy and a conformational code: Absolute configuration and solution conformation of a chiral liquid pesticide, (R)-(+)-malathion. Chirality 2009, 21, E172–E180. [Google Scholar] [CrossRef]
- Böselt, L.; Sidler, D.; Kittelmann, T.; Stohner, J.; Zindel, D.; Wagner, T.; Riniker, S. Determination of Absolute Stereochemistry of Flexible Molecules Using a Vibrational Circular Dichroism Spectra Alignment Algorithm. J. Chem. Inf. Model. 2019, 59, 1826–1838. [Google Scholar] [CrossRef]
- Longhi, G.; Abbate, S.; Gangemi, R.; Giorgio, E.; Rosini, C. Fenchone, Camphor, 2-Methylenefenchone and 2-Methylenecamphor: A Vibrational Circular Dichroism Study. J. Phys. Chem. A 2006, 110, 4958–4968. [Google Scholar] [CrossRef] [PubMed]
- Polavarapu, P.L.; Covington, C.L. Comparison of Experimental and Calculated Chiroptical Spectra for Chiral Molecular Structure Determination. Chirality 2014, 26, 539–552. [Google Scholar] [CrossRef] [PubMed]
- Polavarapu, P.L. Determination of the Absolute Configurations of Chiral Drugs Using Chiroptical Spectroscopy. Molecules 2016, 21, 1056. [Google Scholar] [CrossRef] [PubMed]
- Longhi, G.; Tommasini, M.; Abbate, S.; Polavarapu, P. The connection between robustness angles and dissymmetry factors in vibrational circular dichroism spectra. Chem. Phys. Lett. 2015, 639. [Google Scholar] [CrossRef]
- Longhi, G.; Tommasini, M.; Abbate, S.; Polavarapu, P.L. Corrigendum to “The connection between robustness angles and dissymmetry factors in vibrational circular dichroism spectra” [Chem. Phys. Lett. 639 (2015) 320–325]. Chem. Phys. Lett. 2016, 648, 208. [Google Scholar] [CrossRef]
- Nicu, V.P.; Baerends, E.J. Robust normal modes in vibrational circular dichroism spectra. Phys. Chem. Chem. Phys. 2009, 11, 6107–6118. [Google Scholar] [CrossRef]
- Góbi, S.; Magyarfalvi, G. Reliability of computed signs and intensities for vibrational circular dichroism spectra. Phys. Chem. Chem. Phys. 2011, 13, 16130–16133. [Google Scholar] [CrossRef]
- Luber, S.; Reiher, M. Intensity-Carrying Modes in Raman and Raman Optical Activity Spectroscopy. ChemPhysChem 2009, 10, 2049–2057. [Google Scholar] [CrossRef]
- Tang, Y.; Cohen, A.E. Optical Chirality and Its Interaction with Matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.V.; Lapthorn, A.J.; Kelly, S.M.; Barron, L.D.; Gadegaard, N.; Kadodwala, M. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef]
- Pellegrini, G.; Finazzi, M.; Celebrano, M.; Duò, L.; Biagioni, P. Chiral surface waves for enhanced circular dichroism. Phys. Rev. B 2017, 95, 241402. [Google Scholar] [CrossRef]
- Pitha, J.; Jones, R.N. A Comparison Of Optimization Methods For Fitting Curves To Infrared Band Envelopes. Can. J. Chem. 1966, 44, 3031–3050. [Google Scholar] [CrossRef]
- Castiglioni, C.; Gussoni, M.; Del Zoppo, M.; Zerbi, G. Relaxation contribution to hyperpolarizability. A semiclassical model. Solid State Commun. 1992, 82, 13–17. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).