Light-Weighted Password-Based Multi-Group Authenticated Key Agreement for Wireless Sensor Networks

Abstract

Security is a critical issue for medical and health care systems. Password-based group-authenticated key agreement for wireless sensor networks (WSNs) allows a group of sensor nodes to negotiate a common session key by using password authentication and to establish a secure channel by this session key. Many group key agreement protocols use the public key infrastructure, modular exponential computations on an elliptic curve to provide high security, and thus increase sensor nodes’ overhead and require extra equipment for storing long-term secret keys. This work develops a novel group key agreement protocol using password authentication for WSNs, which is based on extended chaotic maps and does not require time-consuming modular exponential computations or scalar multiplications on an elliptic curve. Additionally, the proposed protocol is suitable for multiple independent groups and ensures that the real identities of group members cannot be revealed. The proposed protocol is not only more secure than related group key agreement protocols but also more efficient.

1. Introduction

A security association which manages security in a network layer is an important matter and it involves the establishment of a shared security key between two end points to support secure associations [1]. Wireless sensor networks (WSNs) consist of a large number of sensor nodes, which cannot support heavy computations, extensive communications or extensive storage and have limited bandwidth. They can be applied in many environments, such as medical monitors, military reconnaissance and communication, and others. WSNs are deployed to allow a legitimated user to login to the network and access data. The sensor node authentication has become one of the important security issues [2]. Group authenticated key agreements for WSNs enable a group of sensor nodes to authenticate each other and to establish a common key for securely communicating over public sensor networks. Group authenticated key agreement protocols typically fall into two categories, which are group key agreement protocols without public keys and group key agreement protocol using public keys. The former realize authentication and negotiates a group key using shared weak passwords or a shared long-term secret key [3,4,5,6], while the latter realize authentication and negotiate a common group key using public key systems [7,8,9]. Most group key agreement protocols that use public keys have higher security than those without. However, they depend on time-consuming modular exponential computations and scalar multiplications on an elliptic curve, and thus are not suitable for sensor networks. Recently, several group-authenticated key agreement approaches have been presented. Unfortunately, most of these protocols were developed for two communication entities (two-party) or three communication entities (three-party), and can only be extended to a group key agreement protocol with difficulty. Thus, most authenticated key agreement protocols are difficult to extend to multi-group authenticated key agreement for WSNs.

A multi-group key agreement protocol for WSNs allows communicating entities (sensor nodes) to belong to multiple groups, and enables each group to establish an independent group session key. A key hypergraph [9,10,11] is a graph where each vertex represents a party and each hyper-edge represents a relation among parties who to share a key. For instance, group members SN₁, SN₂, SN₃, SN₄ and SN₅ involve groups {SN₁, SN₂, SN₃}, {SN₃, SN₄, SN₅}, and {SN₁, SN₂, SN₃, SN₄, SN₅} and establish group keys used for secure communication. Then its key hypergraph can be denoted as G = {V, E}, where V = {SN₁, SN₂, SN₃, SN₄, SN₅} is a finite set of vertices and E = {e₁ = {SN₁, SN₂, SN₃}, e₂ = {SN₃, SN₄, SN₅}, e₃ = {SN₁, SN₂, SN₃, SN₄, SN₅}} is a set of subsets of V, as presented in Figure 1.

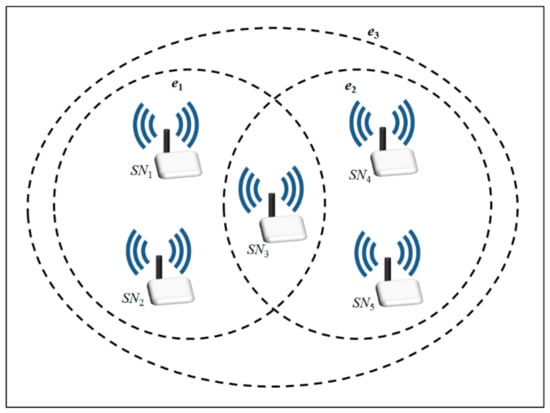
Figure 1. In a key hypergraph, one sensor node is allowed to belong to multiple independent groups.

Key management issues are also considered to have a major impact on the security scale of WSNs [12]. Recently, several group-authenticated key agreement approaches have been presented for WSNs. For example, in 2007, Jeong and Lee [9] proposed a group-authenticated key agreement protocol that uses a public key system to build a session key; these group key approaches can be extended for hypergraphs and are suitable for use with multiple groups [9,10,11].

Users also need extra storage, such as radio frequency identification (RFID) tags, flash drives, smart cards and so on, to store public/private key pairs. In 2006, Abdalla et al. [3] developed a password-based group-authenticated key exchange that can be executed in a constant number of rounds. In the same year, Dutta and Barua [13] proposed a password-based encrypted group-authenticated key agreement protocol. Although these approaches do not require the maintenance of public key systems, all communicating users share the same password so these protocols do not protect the privacy of users. In 2013, Lee et al. [14] proposed a password-based group-authenticated key agreement protocol for the integrated electronic patient record (EPR) information system, which enabled users to have their own passwords. A multi-server authentication protocol based on dynamic identity is proposed by Sood et al. [15]. Amin et al. [16] demonstrated that Xue et al.’s protocol [17] is not protected against the user anonymity problem and cannot resist user impersonation and session key discloser attack. In 2017, Lin et al. [18] applied an extended chaotic map to present password-less group authentication key agreement which improves the computation efficiency for the simple group password-based authenticated key agreement (SGPAKE) proposed by Lee et al [19]. Although most limitations in the field of security have been overcome, the above protocols require many time-consuming modular exponential computations or scalar multiplications on elliptic curves and so are inefficient and unsuitable for use in many practical scenarios. Moreover, most of them are difficult to extend to multiple groups.

Recently, a number of key agreement protocols based on chaotic maps were proposed, which have improved computational efficiency. Using Chebyshev chaotic maps has been shown to be more efficient than cryptography using modular exponential computations and scalar multiplications on elliptic curves [20,21,22,23,24,25,26,27,28,29]. However, Chebyshev chaotic maps and their enhancement are affected by the discrete logarithm problem and the Diffie–Hellman problem [30,31,32,33]. In addition, most of them were developed for two communication entities (two-party) or three communication entities (three-party), and can only be extend to group key agreement protocol with difficulty.

In our analysis, we present a novel password-based multi-group authenticated key agreement protocol for WSNs that was based on the extended chaotic map-based Diffie–Hellman problem. The main contributions of this paper are:

(1). The proposed protocol enables one sensor node to belong to several mutually independent groups and ensures group key security. Additionally, the real identities of group members cannot be revealed.

(2). Accordingly, the proposed protocol is suitable for multiple groups and ensures users’ anonymity. It overcomes not only the limitations of previously proposed protocols and has a lower computational cost, but also offers greater security and is suitable for WSNs.

The remainder of this paper is organized as follows. The primitives used are described in Section 2. The proposed extended chaotic map-based multi-group authenticated key agreement protocol is illustrated in Section 3. In Section 4, we presented the security analysis and overall comparison. The conclusions are drawn in Section 5.

2. Preliminaries

This section lists notations and describes the underlying primitives used in this paper. The underlying primitives include Chebyshev polynomials, enhanced Chebyshev chaotic maps, the extended chaotic map-based discrete logarithm and Diffie–Hellman problems [30,31,32,33] which are described as follows and Table 1 lists the symbol system applied by the proposed solution.

Table 1. The symbol system applied by the proposed solution.

Symbol	Definition
SNi	The sensor node for $i=1,2,\dots ,n$.
IDi	The identity of sensor node i (SNi.)
pwi	The password of sensor node i (SNi.)
AS	The trusted authentication server.
h(.)	One-way hash function.
A→B: M	A sends messages (M) to B by a common channel.
A⇒B: M	A sends message (M) to B by a secure channel.
M1||M2	Message 1(M1) concatenates to message 2(M2).

2.1. Chebyshev Polynomials

The Chebyshev polynomials of degree n are defined as:

$$\{\begin{array}{l}{T}_0(x)=1;\\ T_1(x)=x; \mathrm{and}\\ T_n(x)=2x{T}_{n-1}(x)-T_{n-2}(x),\mathrm{for} n \ge 2,\end{array}$$

(1)

and the first few Chebyshev polynomials are

$$\{\begin{array}{l}{T}_2(x)=2x^2-1,\\ T_3(x)=4x^3-3x,\\ T_4(x)=8x^4-8x^2+1.\end{array}$$

(2)

2.2. Semigroup Property

We have T_r(T_s(x)) = T_rs(x) for different r and s, where −1 ≤ x ≤ 1. The core idea of semi-group is similar to the Diffie–Hellman problem. Semi-group implies that there is not a specific order for r and s. This property comes from Chebyshev polynomials. However, −1 ≤ x ≤ 1 is not enough to provide high security in terms of the diversity of x, and Zhang extends the mapping range from (−1,1) to (−∞, ∞) [33]. In other words, the scheme with a semi-group property has similar security to that of the Diffie–Hellman key exchange [34].

2.3. Enhanced Chebyshev Polynomials

In order to enhance the property of the Chebyshev chaotic map, Zhang [19] proved that the semi-group property holds for Chebyshev polynomials defined on interval $(-\infty ,+\infty )$. This paper uses the following enhanced Chebyshev polynomials:

$$T_n\left(x\right)=2x{T}_{n-1}\left(x\right)-T_{n-2}\left(x\right) mod p for n\ge 2.$$

(3)

The enhanced Chebyshev polynomials meet the semi-group property. Then,

$$T_r\left(T_s\left(x\right)\right)\equiv T_{rs}\left(x\right)\equiv T_s\left(T_r\left(x\right)\right) mod p.$$

(4)

2.4. Extended Chaotic Map-based Discrete Logarithm (ECM-DL) Problem

Given x, y, and p, it is not computationally feasible to find the satisfied integer r,

$$\mathrm{y}=T_r\left(x\right) mod p.$$

(5)

2.5. Extended Chaotic Map-based Diffie-Hellman (ECM-DH) Problem

Given T_u(x) mod p, T_v(x) mod p, T(•), x, and p, where u, v ≥ 2, $x\in (-\infty ,+\infty )$, and p is a large prime number, the calculations are not feasible.

$$T_{uv}\left(x\right)\equiv T_u\left(T_v\right))\equiv T_v\left(T_u\right)) mod p.$$

(6)

3. Proposed Multi-Group Authenticated Key Agreement Protocol for WSNs

This section presents a group authenticated key agreement protocol using extended chaotic maps for hypergraphs. The proposed protocol enables one user to belong to several independent groups, ensures group key security, and protects the real identities of group members. The proposed protocol is composed of four phases, which are the initialization phase, registration phase, the authentication and key agreement phase and the password change phase, and it is implemented as follows.

3.1. Initialization Phase

Step 1:

The authentication server AS randomly selects mk as its master key.

Step 2:

AS computes pk_s = T_mk(x) mod p, where x is a random number and p is a large prime number.

Step 3:

AS publishes parameters (pk_s, T(.), x, p).

3.2. Registration Phase

Step 1: SN_i$\Rightarrow$S:{ID_i, pw_i}

The sensor node SN_i chooses his/her identity ID_i and password pw_i, and sends {ID_i, pw_i, Group_i} to AS over a secure channel, where Group_i = (G_i1, G_i2,…,G_iN) and G_i1, G_i2,…,G_iN are groups that SN_i belong to.

Step 2: Upon receiving the register message from SN_i, The trusted authentication server (AS) computes HID_i = h(ID_i ||mk), Q_i = h(ID_i || pw_i) and stores (HID_i, Q_i, Group_i).

3.3. Authentication and Key Agreement Phase

This phase, as shown in Figure 2, enables sensor nodes SN_i for i = 1,2,…,n to authenticate each other and to negotiate session keys for each group with the help of AS. First, sensor node SN_i sends its password pw_i to AS, which is encrypted with a secret key of SN_i and AS. After AS successfully authenticates SN_i, AS assists these sensor nodes in agreeing a common secret key as their group session key. The details are worked as follows.

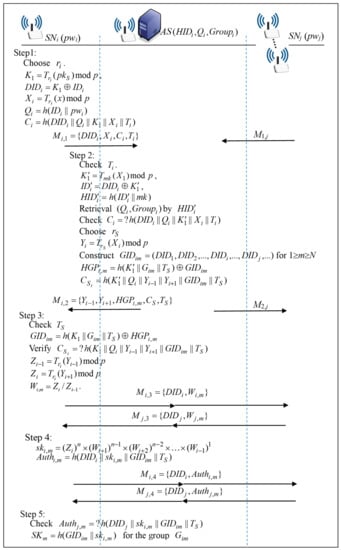
Figure 2. The proposed multi-group authenticated key agreement protocol for wireless sensor networks (WSNs).

Step 1. SN_i→AS : M_i,1 = {DID_i, X_i, C_i, T_i}

Each sensor node SN_i chooses a nonce r_i, computes K₁ = T_ri(pk_S) mod p, DID_i=K₁$\oplus$ID_i, X_i = T_ri(x) mod p, Q_i=h(ID_i||pw_i), C_i = h(DID_i||Q_i||K₁||X_i||C_i,||T_i), where T_i is the current timestamp, and sends M_i,1 = {DID_i, X_i, C_i, T_i} to AS.

Step 2. AS→SN_i :M_i,2 = {Y_i-1, Y_i+1, HGP_i,m, C_S, T_S}

After receiving M_i,1, AS checks the validity of T_i. If successful, AS computes K₁^’ = T_mk(X₁) mod p, ID_i^’ = DID_i$\oplus$K₁^’, HID_i^’ = h(ID_i^’||m_k), retrieves (Q_i, Group_i) by HID_i^’, and checks C_i = h(DID_i||Q_i||K₁^’||X_i||T_i). If successful, AS chooses a nonce r_S, computes Y_i = T_rs(X_i) mod p, constructs a group identity GID_im = (DID₁, DID₂,…,DID_i,…,DID_j,…) by using sensor nodes’ temporal identity DID_i and calculates HGP_i,m = h(K₁^’||G_im||T_S)⊕GID_im, CS_i = h(K₁^’||Q_i||Y_i-1||y_i+1||GID_im||T_S) for i = 1,2,…,n, where T_S is the current timestamp and SN_i is a group member of G_im for m = 1,2,…,N, and sends M_i,2 = {Y_i-1, Y_i+1, HGP_i,m, C_S, T_S} to U_i.

Step 3. SN_i→* : M_i,3 = {DID_i ,W_i,m}

SN_i checks T_S, calculates GID_im = h(K₁||G_im||T_S)⊕ HGP_i,m and verifies CS_i = h(K₁||Q_i||Y_i-1||y_i+1||GID_im||T_S). If successful, SN_i computes Z_i-1 = ${{T}}_{r_i}$ (Y_i-1) mod p, Z_i = $T_{r_i}$ (Y_i+1) mod p and W_i,m = Z_i / Z_i-1, and broadcasts M_i,3 = {DID_i ,W_i,m}.

Step 4. SN_i→* : M_i,4 = {DID_i ,Auth_i,m}

After receiving M_i,3 for $j\ne i$, if SN_i computes sk_i,m = (Z_i)ⁿ×(W_i+1)^n-1×(W_i+2)^n-2×…×(W_i-1)¹ and key confirmation Auth_i,m = h(DID_i||sk_i,m||GID_im||T_S), and broadcasts M_i,4 = {DID_i ,Auth_i,m}.

Step 5. Finally, SN_i authenticates SN_j by checking Auth_i,m = h(DID_i||sk_i,m||GID_im||T_S) for j$\ne$i, and computes sk_m = h(GID_im||sk_i,m) for the group G_im.

3.4. Password Change Phase

A legal sensor nodes SN_i changes its password by performing the following steps.

Step 1. SN_i→AS : M_i,1 = {DID_i, X_i, C_i, T_i}

SN_i chooses a nonce r_i, computes K₁ = T_ri(pk_S) mod p, DID_i = K₁$\oplus$ID_i, X_i = T_ri(x) mod p, Q_i = h(ID_i||pw_i), Q_{i_new} = h(ID_i||pw_{i_new}), D_i = h(K₁||T_i)$\oplus$Q_{i_new}, E_i = h(DID_i||Q_i||Q_{i_new}||K₁||X_i||T_i), where T_i is the current timestamp, and sends M_i,1 = {DID_i, X_i ,D_i, E_i, T_i} to AS.

Each sensor node SN_i chooses a nonce r_i, computes K₁ = T_ri(pk_S) mod p, DID_i = K₁$\oplus$ID_i, X_i = $T_{r_i}$ (x) mod p, Q_i = h(ID_i||pw_i), C_i = h(DID_i||Q_i||K₁||X_i||C_i,||T_i), where T_i is the current timestamp, and sends M_i,1 = {DID_i, X_i, C_i, T_i} to AS.

Step 2. AS→SN_i :M_i,2 = {V_Si, T_S}

After receiving M_i,1, AS checks the validity of T_i. If successful, AS computes K₁^’ = T_mk(X₁) mod p, ID_i^’ = DID_i$\oplus$K₁^’, HID_i^’ = h(ID_i^’||m_k), retrieves (Q_i, Group_i) by HID_i^’, computes Q^’_{i_new} = D_i$\oplus$h(K₁||T_i) and checks E_i = h(DID_i||Q_i||Q^’_{i_new}||K^’₁||X_i||T_i). If successful, AS replaces Q_i with Q^’_{i_new}, and calculates V_Si = h(K₁^’||Q_i||Q^’_{i_new}||K^’₁||X_i||T_s), where T_s is the current timestamp, and sends M_i,2 = {V_Si, T_S} to SN_i. Finally, SN_i makes sure that AS has updated SN_i’s verification data in S’s database by validating T_s and checking V_Si = h(K₁||Q_i||Q_{i_new}||K^’₁||X_i||T_s).

4. Security Analysis

The security analyses on the correctness, session key security, perfect forward security, mutual authentication, and privacy protection are provided; it also resists password guessing, known-key attacks, and sensor node capture attacks.

4.1. Correctness

All legal users have the same secret sk_i,m since SN_i computes

$$\begin{array}{ll}s{k}_{i,m}& ={(Z_i)}^n\cdot {(W_{i+1,m})}^{n-1}\cdot {(W_{i+2,m})}^{n-2}\cdot \dots \cdot {(W_{i-1,m})}^1\\ & ={(Z_i)}^n\cdot {(\frac{Z_{i+1}}{Z_i})}^{n-1}\cdot {(\frac{Z_{i+2}}{Z_{i+1}})}^{n-2}\cdot \dots \cdot {(\frac{Z_{i-1}}{Z_{i-2}})}^1\\ & =Z_1\cdot Z_2\cdot Z_3\cdot \dots \cdot Z_n\\ & =T_{r_1\cdot r_2\cdot r_S}(x)\mathrm{mod}p\cdot T_{r_2\cdot r_3\cdot r_S}(x)\mathrm{mod}p\cdot T_{r_3\cdot r_4\cdot r_S}(x)\mathrm{mod}p\cdot \dots \cdot T_{r_n\cdot r_1\cdot r_S}(x)\mathrm{mod}p.\end{array}$$

Thus, these sensor nodes can obtain a common session key SK_m = h(GID_im||sk_i,m) for the group G_im.

4.2. Session Key Security

Given $T_{r_i}$ (x_o) mod p (= $T_{r_i{r}_s}$ (x) mod p) and $T_{r_{i+1}}$ (x_o) mod p (= $T_{r_{i+1}{r}_s}$ (x) mod p), where x₀ denotes T_rs(x) mod p, Y_i = T = T_r•ri+1(x_o) mod p (= T_riri+1rs(x) mod p) cannot be determined, because of the ECM-DH problem. The values of r₁,r₂,…,r_n and r_s are randomly selected and mutually independent in each protocol execution, so the secret sk_i,m and the session key SK_m fail to be determined without knowledge of r_s and r_i for 1 ≤ i ≤ n, where $s{k}_{i,m}=T_{r_1\cdot r_2\cdot r_S}(x)\cdot T_{r_2\cdot r_3\cdot r_S}(x)\cdot \dots \cdot T_{r_n\cdot r_1\cdot r_S}(x)\mathrm{mod}p$ and SK_m = h(GID_im||sk_i,m) for the group G_im. Hence, the session key security is based on the ECM-DH problem and is therefore considered not computationally feasible.

4.3. Perfect Forward Security

In the proposed protocol, since r₁,r₂,…,r_n and r_s are randomly selected and independent among protocol executions, a compromised password pw_i does not yield any previous session keys SK_m = h(GID_im||sk_i,m) for G_im, where $s{k}_{i,m}=T_{r_1\cdot r_2\cdot r_S}(x)\mathrm{mod}p\cdot T_{r_2\cdot r_3\cdot r_S}(x)\mathrm{mod}p\cdot \dots \cdot T_{r_n\cdot r_1\cdot r_S}(x)\mathrm{mod}p$. The session key security is based on the ECM-DH problem. Accordingly, the proposed protocol provides perfect forward security.

4.4. Mutual Authentication

In the proposed group key agreement scheme, only legal sensor node SN_i who has the correct ID_i and pw_i can compute C_i = h(DID_i||Q_i||K₁||X_i||C_i,||T_i), where Q_i = h(ID_i||pw_i). AS then authenticates sensor node by checking C_i = h(DID_i||Q_i||K₁||X_i||C_i,||T_i). Also, sensor node authenticates AS by checking CS_i = h(K₁||Q_i||Y_i-1||Y_i+1||GID_im||T_S). Additionally, only legal SN_i in G_i,m can compute $s{k}_{i,m}=T_{r_1\cdot r_2\cdot r_S}(x)\cdot T_{r_2\cdot r_3\cdot r_S}(x)\cdot \dots \cdot T_{r_n\cdot r_1\cdot r_S}(x)\mathrm{mod}p$. Then, SN_i authenticates SN_j by checking Auth_i,m = h(DID_i||sk_i,m||GID_im||T_S) for j$\ne$i. Therefore, the participants of the proposed protocol authenticate each other.

4.5. Privacy Protection

In the proposed protocol, DID_i implicitly involves the identity of SN_i, ID_i, where DID_i = K₁$\oplus$ID_i. Attackers cannot derive ID_i from DID_i because ID_i is protected by K₁ and the security of K₁ (= T_rmk mod p) is based on the ECM-DH problem. Additionally, the group identity GID_im = (DID₁, DID₂,…,DID_i,…,DID_n) is protected by h(K₁||G_im||T_s) (or K₁). No one can derive GID_im from the revealed message HGP_im, where HGP_im = h(K₁||G_im||T_s)$\oplus$GID_im. Another group member SN_i cannot recognize the group members of G_im to which SN_i does not belong. Thus, the proposed protocol ensures users’ privacy protection.

4.6. Resistance to Undetectable On-Line Password-Guessing Attacks

In the proposed protocol, an adversary SN_i^* cannot compute the correct C_i = h(DID_i||h(ID_i||pw_i)||K₁||X_i||T_i) without SN_i’s identity ID_i, where K₁ = T_ri(pk_S) mod p, DID_i = K₁$\oplus$ID_i, X_i = T_ri(x) mod p and T_i is the timestamp, and so such an adversary fails to send out M_i,1 = {DID_i, X_i, C_i, T_i} in Step 1. Additionally, SN_i^* who has ID_i and is disguised as SN_i guesses a password pw_i^*, computes C_i^* = h(DID_i||Q_i^*||K₁||X_i||T_i), where Q_i^* = h(ID_i||pw_i^*) and sends M^*_i,1 = {DID_i, X_i, C_i^*, T_i} to S in Step 1. After receiving M^*_i,1, AS will detect this failed password-guessing by checking C_i = h(DID_i||Q_i||K₁’||X_i||T_i) in Step 2, where K^’₁ = T_mk(X₁) mod p, ID_i^’ = DID_i$\oplus$K₁^’, HID^’_I = h(ID^’_i||mk), Q_i = h(ID_i||pw_i). Therefore, the proposed protocol is secure against undetectable on-line password-guessing attacks.

4.7. Resistance to Off-Line Password-Guessing Attacks

In the authentication and key agreement phase of the proposed protocol, only messages C_i = h(DID_i||Q_i||K₁||X_i||C_i||T_i) in M_i,1 and CS_i = h(K₁||Q_i||Y_i-1||Y_i+1||GID_im||T_S) in M_i,2 contain password pw_i, where Q_i = h(ID_i||pw_i). However, pw_i is protected by K₁, and the one-way property of hash functions. Similarly, in the password change phase of the proposed protocol, only messages D_i = h(K₁||T_i)$\oplus$Q_{i_new} and E_i = h(DID_i||Q_i||Q_{i_new}||K₁||X_i||T_i) in M_i,1 and CS_i = h(K₁||Q_i||Y_i-1||Y_i+1||GID_im||T_S) in M_i,2 contain password pw_i, where K₁ = T_ri(pk_S) mod p, DID_i = K₁$\oplus$ID_i, Q_i = h(ID_i||pw_i) and Q_{i_new} = h(ID_i||pw_{i_new}). However, pw_i and pw_{i_new} are protected by K₁ and the one-way property of hash functions. No information helps to confirm the correctness of the guessed passwords, so off-line password-guessing attacks are unsuccessful against the proposed protocol.

4.8. Known-Key Security

The session keys SK_m = h(GID_im||sk_i,m), generated in various runs, are mutually independent, where $s{k}_{i,m}=T_{r_1\cdot r_2\cdot r_S}(x)\cdot T_{r_2\cdot r_3\cdot r_S}(x)\cdot \dots \cdot T_{r_n\cdot r_1\cdot r_S}(x)\mathrm{mod}p$, since r₁,r₂,…,r_n and r_S are randomly selected by SN₁, SN₂,…, SN_n and AS, respectively, and are independent across protocol executions. Thus, the proposed group key agreement protocol exhibits known-key security.

4.9. Resistance to Sensor Node Capture Attacks

In the proposed scheme, each sensor node SN_i has its secrets (ID_i, pw_i). An attacker A who has captured SN_j and obtained ID_j cannot derive other sensor node SN_i’s secrets (ID_i, pw_i), and thus cannot impersonate SN_i and AS.

5. Performance Analyses and Comparisons

The performance of the proposed protocol in communication was compared with that of related approaches. Table 2 presents a performance comparison of the group authenticated key agreement (GAKA) protocols of Abdalla et al. [3], Kim et al. [7], Boyd and Nieto [8], and Dutta and Barua [13] and the protocol that was proposed herein, where T_chao denotes the time required to execute a Chebyshev chaotic map operation; T_sym denotes the time required to execute a symmetric encryption/decryption operation; T_exp denotes the time required to execute a modular exponential operation, T_sign/veri denotes the time required to execute a signing/verifying operation in the public key system, and T_chao < T_sym < T_exp (≈ T_sign/veri) [35,36].

Table 2. Comparisons of other related protocols and the proposed protocol.

Protocols	P1	P2	P3	P4	P5
Abdalla et al. [3]	$3n{T}_{exp}+3n{T}_{sym}$	All users share a password	Yes	No	No
Dutta and Barua [13]	$3n{T}_{exp} + \left(n+3\right)T_{sym}$	All users share a password	Yes	No	No
Kim et al. [7]	$2n{T}_{sign/veri}+n{T}_{exp}$	PKI based	No	Yes	No
Boyd and Nieto [8]	$n{T}_{sign/veri}+\left(2n-2\right)T_{exp}$	PKI based	No	No	No
Lee et al. [14]	$4n{T}_{exp}+n{T}_{sym}$	A private password	Yes	No	No
Proposed GAKA	$3n{T}_{chao}$	A private password	Yes	Yes	Yes

P1: computations; P2: mutual authentication; P3: no user’s public key; P4: for multiple groups; P5: providing users privacy protection.

The first comparison concerned computations. These GAKA protocols [3,7,8,13,14] require many time-consuming modular exponential computations or scalar multiplications on elliptic curves to realize authentication and negotiate group keys. Only the proposed GAKA protocol was developed using extended chaotic map operations and did not have a heavy computational burden. Thus, the proposed GAKA protocol was more efficient than the other GAKA protocols.

The second comparison concerned the realization of user authentication in each protocol. The protocols of Kim et al. [7] and Boyd and Nieto [8] realize authentication using users’ public keys. The GAKA protocols of Abdalla et al. [3], Dutta and Barua [13], and Lee et al. [14] as well as the proposed GAKA protocol realize authentication using users’ passwords. However, in the GAKA protocols of Abdalla et al. [3] and Dutta and Barua [13], all users share the same password so their protocols do not ensure users’ privacy.

The third comparison concerned whether the protocol required the maintenance of users’ public keys. The protocols of Kim et al. [7] and Boyd and Nieto [8] employ users’ public keys, and thus require extra equipment to store long-term secret keys and the results of time-consuming exponential computations in clients. The GAKA protocols of Abdalla et al. [3], Dutta and Barua [13], and Lee et al. [14] as well as the proposed GAKA protocol are password-based authentication protocols. Each user remembers only his weak password without the need for any extra equipment to store long-term secret keys.

The fourth comparison involved whether the protocol was suitable for hypergraphs. The GAKA protocols [3,7,8,13] consider only a single group, and are difficult to extend to multiple groups. The protocol of Kim et al. [7] and the proposed GAKA protocol enable communicating entities to belong to multiple groups, and so are effective for hypergraphs.

The final comparison involved whether the protocol provided the anonymity of users. The GAKA protocols [3,7,8,13,14] reveal users’ identities, and fail to protect user privacy. Only the proposed GAKA protocol did not reveal users’ identities, and so protected users’ anonymity.

Table 3 lists the simulation environment, including used hardware/software specifications and algorithms. Figure 3 illustrates simulation results for the response time of related protocols and the proposed one for n = 5, 10, 15,…, 30. Due to the use of extended Chebyshev chaotic map operations, the proposed protocol required less response time than related protocols.

Table 3. Simulation environment.

Hardware/Software Specification
Intel CPU i7 CPU 3.2GHz 8G Memory Windows 10 Scala programming language
Used Algorithms
Asymmetric en/decryption algorithm: RSA Symmetric en/decryption algorithm: AES Extended Chebyshev chaotic maps

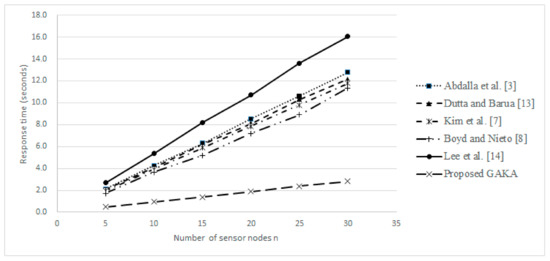
Figure 3. The response time of related protocols and the proposed one.

6. Conclusions

This work presented an efficient and secure group authenticated key agreement protocol for WSNs, which enabled sensor nodes to belong to multiple independent groups. The proposed protocol used extended chaotic map operations, did not require time-consuming computations, and thus was more computationally efficient than other group-authenticated key agreement protocols. Moreover, it did not require the maintenance of users’ public keys or extra equipment for storing a long-term secret key, and resisted potential attacks and provided more functionality than comparable approaches. The proposed protocol is not only suitable for WSNs, but also can be implemented in the current environment involving database systems, file sharing systems, broadcasting radio/TV systems, and others.