Multi-Constraint Optimized Planning of Tasks on Virtualized-Service Pool for Mission-Oriented Swarm Intelligent Systems

Abstract

With the emergence of swarm intelligent systems, especially the swarming of aircraft and ground vehicles, cooperation in multiple dimensions has becoming one of the great challenges. How to dynamically schedule the resources within a swarm intelligent system and optimize the execution of tasks are all vital aspects for such systems. Focusing on this topic, in this paper, one new task planning mechanism with multiple constraints is proposed to solve such dynamic programming problems. Concretely, several fundamental models, covering three-level task models and resource-service pool models, are put forward and defined first. Considering the limitations of swarm systems running within complicated cyber-physical space, multi-dimension constraints for tasks scheduling and execution are further modeled and established. On this basis, we mapped this planning problem to an optimization searching problem, and then proposed a Genetic-Algorithm-based mechanism. All these works have been verified with simulated cooperation scenes. Experimental results show that this new mechanism is efficient to solve such resource-related and mission-oriented cooperation problems in complicated environments.

1. Introduction

Along with the rapid development of information technologies, such as embedded systems, Artificial Intelligence, Internet of Things, Cloud computing and so on [1,2], diverse intelligent systems and application domains have been emerging increasingly, in particular, Connected Intelligent Vehicles (CIVs) and Intelligent Transportation Systems (ITS), Unmanned Aerial Vehicles (UAVs) and combat cloud, etc. More recently, such intelligent systems have been presenting amazing intelligent capabilities. As an aid to individual intelligence, varied communication technologies, such as 5G and data link, have made such systems more and more networked. In addition, these technologies made it possible to construct new Swarm Intelligent Systems (SIW), which operate with a decentralized, collective and self-organized mode, and are always service-oriented [3,4]. This is one important coming trend. Such systems will be stronger because the deep connection of intelligent systems allow coordinating and cooperating through the whole system, from different levels and using multiple aspects. Typically, there are three cooperation problems that concern researchers: the behavior-level cooperation (e.g., between CIVs [5,6,7] or Numerical Control Machines [8]), the computation-level cooperation (e.g., within a satellite fleet or edge clouds [9]), and the mission-level cooperation (e.g., within a fleet of robots or flights [10,11]).

Obviously, mission-level cooperation should be the most complicated of these three aforementioned problems, and as we know, the mission-level cooperation for robot fleet has been a concern and has been studied in recent decades. Its main connotation refers to the fact that a specific mission will be accomplished through a group of smart objects automatically and cooperatively, every member of which achieve dedicated collective actions. In fact, this kind of cooperation is always restricted by several different factors, covering the constraints of time, location, distance, energy, payloads and so on. For instance, There are several typical scenes. Automatic machines within an automating production line collaborate with each other to finish the product processing [12]. Of course, this kind of cooperation between these machines is mainly down to rhythmical coordination, without considering dynamical constraints. However, the cooperation of mobile robots within a fleet, typically UAV fleet, is often more different and complex. This is because to accomplish one mission collectively, the cooperation procedure will be closely related to several important aspects, for instance, allocating sub-missions rationally to fleet members, the behavior cooperation, capabilities of the fleet members, open environment, and other cyber-physical factors [13,14,15,16,17].

Today, along with the rapid development of embedded hardware/software and network technologies, such problems have been becoming more complicated for some complex applications of swarm robots that come with several constraints, e.g., combat cloud. Beyond performing sub-missions synergistically, such swarm applications always need to deeply cooperate with each other via sharing their local resources. The advantage of this manner is significant. Through more fine-grained scheduling and reconfiguring of various resources of swarm systems, it will promote the reliability, robustness and flexibility of swarm cooperation as well as the performance. Essentially, it has evolved to be one problem with more constraint dimensions than that of traditional mission cooperation, and its main thought is also somewhat similar to that of cloud computing. After considering these new features and the challenges to use heterogeneous resources cooperatively and efficiently, in this paper, optimized planning models and methods between sub-missions and resources for swarm systems are mainly studied. The main contributions of this paper include models of multi-level task, virtualized service and multiple constraints in cyber-physical environment, and in particular, a service pool-based task-service planning mechanism.

The rest of this paper is organized as follows. In Section 2, the relevant literature is presented. Then, several related fundamental models of multi-level task, service and its capability are proposed and defined in Section 3. Section 4 includes the main contribution of this study, where a new Genetic Algorithm (GA)-based planning mechanism is designed and expressed in detail. All these designs of this work are verified via simulation in Section 5. In Section 6, research conclusions are drawn and our ongoing work is sketched out.

2. Related Work and Literature

Recently, studies on Swarm Intelligence (SI) and its applications has been increasingly arousing the interest of more and more researchers [18,19,20]. Typically, the theories and mechanisms about architectures, models, algorithms and systems are the main concerns.

2.1. Swarm Intelligence Theories

As the foundation of various swarm intelligent systems, theories of Swarm Intelligence have attracted a lot of attention from both academia and industry in nearly thirty years. Typically, there were two basic models of swarm behavior in the early age of research: Boids [21] and self-propelled particles [22], and also several well-known methods, such as pulse-coupled oscillators, stochastic diffusion search, ant colony optimization, particle swarm optimization, Pseudo-Boolean Optimization, evolutionary computation, and Multi-Agent-System (MAS) etc. Based on these pioneering fundamental contributions, new theories and applications have recently been springing up [23], especially with the rapid emerging of intelligent IoT systems. For example, after exploring the swarm intelligence-based features of IoT-based systems, Ouarda presented a reference swarm-based architectural model that enables the cooperation among devices in IoT systems [24]. On the basis of the study about ACODA (Ant Colony Optimization on a Distributed Architecture), Ilie et al. proposed a multi-agent distributed framework for Swarm Intelligence that can be used to sole graph search problems on a computer network [25]. With modeling cooperative smart objects as multiple agents, Fortino et al. proposed an agent-oriented and event-based framework, and then implemented all designs within the JADE middleware [26]. Salama designed an architecture for a Swarm Intelligence Based Mobile Cloud Computing Model, and employed a Parallel Particle Swarm Optimization to enhance the access time for the mobile cloud computing services in the domain of E-commerce [27]. The thoughts and methods of swarm intelligence have been also applied to improve the capabilities of self-organized or adaptive systems. For instance, Zhang et al. concluded the principles and optimization approaches [28], and Wong et al. surveyed how to employ these techniques to enhance the learning ability of adaptive systems [29].

2.2. Mechanisms for Mission-Level Cooperation

Mission cooperation is the fundamental capability for any mission-oriented swarm intelligent systems, and the study of this aspect is a continuously evolutive challenge. Essentially, mission cooperation is a problem that includes two typical steps: mission planning (or task allocation) and sub-mission scheduling (or task scheduling) [30,31]. Most of these visible studies mainly focus on these two aspects. For efficient allocation tasks among multiple UAVs during a mission, Kurdi et al. proposed a new autonomous bio-inspired approach that allows each UAV to adjust the task assignment according to its individual status and mission parameters, which was inspired by the nature of locust elastic behavior [32]. For the UAV air combat task assignment problem, Chen et al. established a task allocation model and put forward a discrete particle swarm optimization algorithm [33]. After organizing the robot’s knowledge in a three-level architecture, Marc et al. proposed solution method for task planning and execution in uncertainty or open environments [34]. Considering task cooperation among multiple UAV teams, Hu et al. proposed a hierarchical task assignment method with clustering algorithms, integer linear programming and ant colony algorithm, which reduced the computational complexity of the task assignment problem considerably [35]. Crosby et al. proposed an industrial robotics framework integrates two level planning: a mission planner in multiple robots and a task planner in each robot [36].

The mission cooperation of (heterogeneous) mobile robots is in fact always more complicated, because there exist much more cyber-physical factors which affect the robots’ behavior and the execution of sub-missions. Hence, such problems are often treated as a multi-constraint or multi-objective optimized problem. For instance, under temporal and ordering constraints, Leofante proposed an approach that unites the power of Optimization Modulo Theories with the flexibility of an on-line executive, providing optimal solutions for task planning, and runtime feedback on their execution [37]. Choi et al. presented decentralized methods on the basis of the consensus-based bundle algorithm for allocating tasks to a network of heterogeneous agents [38]. Similarly, Dong et al. also studied the optimization method of decentralized task assignment for heterogeneous UAVs [39].

2.3. Resource Sharing and Virtualization

How to efficiently organize and share underlying resources on-demand for mission-oriented swarm intelligent systems is another vital problem [1,40]. As well known, technologies that are concerned with resource sharing, virtualization, and service are very useful for swarm systems, through which the cooperation will be enhanced efficiently from the resource level [41,42]. Essentially, distributed resource sharing is the foundation for distributed computing and cloud computing, and has been studied widely. For instance, Rezaei et al. studied a distributed resource sharing mechanism and approach for low-latency wireless Ad Hoc networks, to optimize the allocation of resources and the performance [43]. Xu et al. proposed a double auction-based cloud resource allocation and pricing model for resolving the resource allocation between cloud service providers (CSPs) and users [44]. Yin et al. proposed a distributed resource sharing scheme, in which the software defined network (SDN) network is employed to make decisions by coordinating fog nodes and adjust the volume of data for pre-processing [45]. Meanwhile, virtualization and servitization of physical resources have become one effective approach to improve resource sharing for modern distributed systems, such as clouds and IoTs. For bridging the gap between complex manufacturing tasks and underlying resources, Liu et al. proposed novel multi-granularity resource virtualization and sharing strategies, including a resource clustering algorithm and cloud service specifications [46]. Naranjo et al. presented an energy-efficient adaptive scheduler for Vehicular Fog Computing (VFC), focusing on the optimization of energy by leveraging the heterogeneity of foglets [47]. As one cyber-physical example, tactical cloud is a novel conception composed of a fleet of heterogeneous aircraft that cooperate below the resource level [48]. In such a cloud, all resources, both internal ones of each individual aircraft, such as computation, storage, networking, and payloads (radar, missile, etc.), and the traditional coarse-grained resource—aircraft itself, are all sharable and always encapsulated into cloud services [49]. Such new manners of operating takes advantage of cloud computing, and it is obvious that expanding the resources of on-demand sharing and servitization capabilities of swarm intelligent systems will make the cooperation more flexible, powerful, efficient and better optimized.

Although all visible contributions are somewhat different from the connotation of our work, the ideas or approaches of these works are still important and referential, in particular the resources, virtualization, service pool, allocation methods, etc.

3. Cooperation Architecture and Models

3.1. Virtualized-Service and Event Based Cooperation Architecture

As aforementioned, deep cooperation permeates the whole system, from tasks at the top level to heterogeneous resources at the bottom level. Obviously, although mapping one task to certain resources is possible, it is hard to carry out every task by scheduling corresponding resources directly. The main reason is the properties of each resource are too simple and crude to manage and schedule; furthermore, these distributed heterogeneous resources are always used in different manners. Thus, one main step for this work is to establish a general schedulable model that encapsulates diverse distributed resources with the idea of Infrastructure as a Service (IaaS) [50]. On this basis, it is necessary to establish relevant task planning and execution mechanisms. Considering these features and requirements, we proposed a cooperation architecture with the essential concepts of resource encapsulation and virtualized service. The whole structure and information/control flows are shown in Figure 1. At the bottom, all physical resources are basically separated into four types, namely the platform resource (e.g., robots and UAVs, also called the carrier resource), processing resource (e.g., diverse processors and storage), payload resource (e.g., camera and LiDAR.), and data resources that are valuable information shared among members. All these resources are encapsulated with a unified service model that will be detailed in the following sections. Furthermore, all such encapsulated resources will be exposed to applications as schedulable services living within a virtualized service pool. The management agent of service pool is event-based, and handles any cooperation events. Its functionalities involve the automatic management of all services, assessment of the capabilities of services, and scheduling of special services.

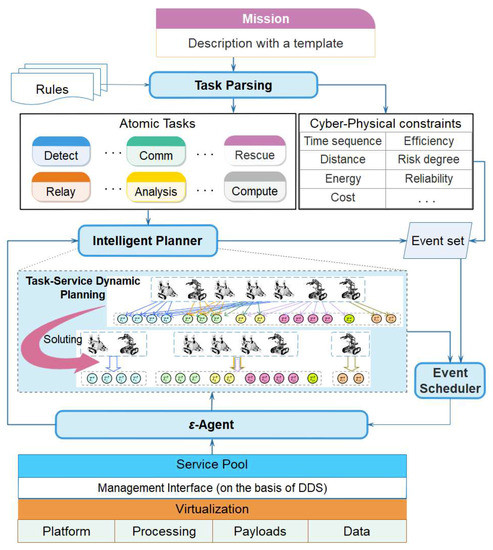
Figure 1. Virtualized-Service and Event-based Cooperation Architecture.

Task parsing component is at the top layer, and includes a three-level task model described in next subsection. According to parsing rules, this component resolves one mission into a set of atomic tasks and a set of cyber-physical constraints. The core part of this architecture is the intelligent planner. This component will, firstly, evaluate whether all requested services can provide required capabilities. If satisfied, it will then try to find out one feasible optimal map from the task set to the service pool under multiple cyber-physical constraints. If there exists such a solution, it will further generate the event set with respect to these constraints. Event scheduler on each member of one swarm system finally schedules certain services in accordance with the events being triggered. The information and control flows for this architecture are also implied in Figure 1.

3.2. Hierarchical Task Model

In this proposed architecture, one hierarchical task model is employed for automatically task parsing and allocating. This model composes of three layers from top to bottom: Mission M, Sub-Mission T, and Atomic Task $\tau$, which are detailed in Table 1. A Mission M is that the action goal one swarm system should achieve, and is described by a structural template. According to parsing rules and policies, the set of Sub-Mission T and constraints implied within M can be further generated. Each Sub-Mission T represents a concrete type of function, such as area detecting, communication relaying, and so on. All these Sub-Missions are constrained by a group of conditions, typically covering the time sequence, efficiency, cost, etc. Furthermore, every Sub-Mission is finally resolved into a set of Atomic Tasks, which are all of the same type inherited from the parent Sub-Mission. Each Atomic Task $\tau$ has only one indecomposable function, and during the scheduling, it is mapped to several service instances. These service instances are instantiated with particular parameters, especially, event(s) to trigger this task and be triggered by this task.

Table 1. Definitions of the Proposed Hierarchical Task Model.

Para	Definition	Para	Definition
Mission M
$M.id$	identification number.	$M.beh$	the behavior parameters of M.
$M.reg$	region parameters of M.	$M.btw$	behavior time window $[t_s,t_e]$ of M.
$M.info$	XML-based description of M.	$M.rule$	parsing rules of M.
Sub-Mission T
$T.id$	identification number.	$T.\rho$	the priority of T.
$T.reg$	region parameters of T.	$T.etw$	execution time window $[t_s,t_e]$ of T.
$T.tar$	target object (s) of T.	$T.act$	the action of T.
$T.pre$	direct predecessor sub-missions of T.	$T.suc$	direct successor sub-missions of T.
$T.cons$	constraints of T.	$T.ea$	expected earning from the execution of T.
Atomic Task $\tau$
$\tau .id$	identification number.	$\tau .pid$	$id$ of the parent sub-mission of $\tau$.
$\tau .reg$	region parameters of $\tau$.	$\tau .etw$	execution time window $[t_s,t_e]$ of $\tau$.
$\tau .tar$	target object of $\tau$.	$\tau .act$	the action of $\tau$.
$\tau .cons$	constraints of $\tau$.	$\tau .ea$	expected earning from $\tau$.
$\tau .te$	event (s) to trigger $\tau$.	$\tau .t{e}^{\prime }$	event (s) triggered by $\tau$.
Service $\epsilon$
$\epsilon .Cid$	id of the carrier of $\epsilon$.	$\epsilon .typ$	type of $\epsilon$.
$\epsilon .Val$	value of $\epsilon$.	$\epsilon .MaxV$	Maximum velocity of $\epsilon$.
$\epsilon .MaxD$	Maximum reachable distance of $\epsilon$.	$\epsilon .MaxLW$	Maximum load weight of $\epsilon$, only for a carrier, namely a member of a swarm system.
$\epsilon .mtbf$	MTBF of $\epsilon$ itself.	$\epsilon .bttr$	BTTR of $\epsilon$ itself.
$\epsilon .Cap$	capability of $\epsilon$.	$\epsilon .Reli$	reliability of $\epsilon$ itself.
$\epsilon .cV$	current velocity of $\epsilon$.	$\epsilon .cD$	current reachable distance of $\epsilon$.
$\epsilon .cLW$	current load weight of $\epsilon$.	$\epsilon .cPos$	current position of $\epsilon$.
$\epsilon .cSta$	current status of $\epsilon$.	$\epsilon .exec\_IF$	schedulable interface of $\epsilon$.

Additionally, an event E is defined as a tuple $<id,source,target,type,para>$, where $source$ and $target$ are the sender and receiver of this event separately, $type$ indicates this is a point-to-point event (valued 0) or broadcast event (valued 1), and $para$ composes of specific parameters.

3.3. Service and Service Pool Model

As discussed above, resource virtualization is a critical aspect for this architecture, which will improve the usage of resources and the mission efficiency of swarm systems. Therefore, various physical resources, covering the platform resource, processing resource, payload resource, and data resources, as shown in Figure 1, are virtualized and encapsulated into services, and all these services are gathered into a service pool. To represent these different resources uniformly, we firstly design a unified service model $\epsilon$. This model is defined as a four-tuple $<id,b\_prop,d\_prop,ins\_para>$, where $id$ is an identity within the global pool, $b\_prop$ and $d\_prop$ are static properties and dynamic properties respectively, and $ins\_para$ is the set of parameters inherited from a corresponding $\tau$ for instantiating this service. Concretely, each element is defined as the following. Of course, the definitions of these elements will vary with the types of services.

$b\_prop:=<Cid,typ,Val,MaxV,MaxD,MaxLW,mtbf,bttr>$

$d\_prop:=<Cap,Reli,cV,cD,cLW,cPos,cSta>$

$ins\_para:=<\tau .id,exec\_IF>$.

Based on this model, the dynamical efficiency of each service can be fundamentally assessed from several aspects. For example, the availability $\alpha$, reliability $\gamma$, and the comprehensive service ability $\xi$ of $\epsilon$ can be evaluated by Formulas (1)–(3), separately. It is clear that $\alpha$ and $\gamma$ of $\epsilon$ are all closely related to the carrier of $\epsilon$, except the platform service. In addition, Formula (3) shows that $\xi$ is a combinational function of several factors $x_i$ and its weight $w_i$. For example, $\xi$ of one fighter can be defined as $f=ln(S\times P_e\times K_m\times P_n)+lnQ$, where S is the maximum voyage distance, $P_e$ is the penetration coefficient, $K_m$ is the long-range weapon coefficient, $P_n$ is the navigation ability, and Q is the $MaxLW$ [51]. For specific swarm system, the definition of this function should be different.

$$\begin{array}{c}\epsilon .\alpha =\frac{\epsilon .mtbf}{\epsilon .mtbf+\epsilon .bttr}\times {\epsilon }^{\prime }.\alpha where{\epsilon }^{\prime }.id=\epsilon .Cid\hfill \end{array}$$

(1)

$$\begin{array}{c}\epsilon .\gamma =\epsilon .Reli\times {\epsilon }^{\prime }.Reliwhere{\epsilon }^{\prime }.id=\epsilon .Cid\hfill \end{array}$$

(2)

$$\begin{array}{c}\epsilon .\xi =f(x_i,w_i)(i=1,2,...,m)\hfill \end{array}$$

(3)

For one swarm system, there exists a global service pool that is composed of local service pools of individual members within this system. In addition, in each member, a $\epsilon$-Agent is deployed to manage the service pool, interact with the intelligent planner and local event scheduler. Considering the topic of this paper, all details about service, service pool, and $\epsilon$-Agent are not presented here, but the advantage of such model is obvious.

4. Design of Multi-Constraint Optimized Genetic Algorithm

As described above, there are several different heuristic algorithms for task planning, such as Particle Swarm Optimization (PSO), Simulated Annealing (SA), Integer Programming (IP), Genetic Algorithm and so on. According to the requirements of multidimensional constraints and to find the best solution approximatively and rapidly, in this paper, we further proposed one novel mechanism with the classic Genetic Algorithm (GA). The selection of GA is mainly because its features are more suitable for such complex optimal problems than others. In the following, several new models and mechanisms about chromosome coding, optimized operators, and fitness function are studied and designed.

4.1. Clustering-Based Gene-Encoding Model of Tasks and Services

The design of chromosome is very important for improving the efficiency of GA. According to the service relevance among atomic tasks, we proposed a variable-length binary encoding model after clustering these tasks. It means that all atomic tasks with service intersections should be grouped into one same chromosome, and all unrelated tasks should be allocated in different chromosomes. One main advantage of this approach is that it can greatly reduce the time cost when searching an optimized global solution $\pi$.

Figure 2 shows the fundamental model of the chromosome piece for task ${\tau }_i$. As shown in this figure, this chromosome piece is composed of n segments, from $C{S}_{i1}$ to $C{S}_{in}$, and each of these segment owns a different type of service from others. $X_{ik}(k=1,2,...,n)$ is the amount of a special required type service, and correspondingly, $Y_{ik}(k=1,2,...,n)$ is the total amount of such type services available. If $Y_{ik}$ is greater than $X_{ik}$, it means that this type of services are sufficient for this atomic task. The binary value of each bit within the chromosome indicates whether the corresponding service is allocated to ${\tau }_i$, “1” means $True$ and “0” means $False$. Thus, the resolving of this problem is equivalent to finding a feasible code that satisfies a group of constraints.

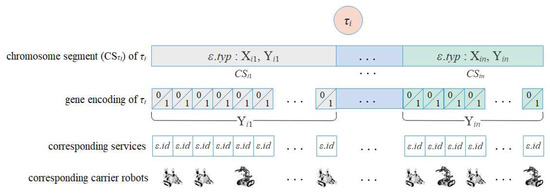
Figure 2. Chromosome Piece and its Coding for ${\tau }_i$.

4.2. Multi-Dimension Constraints in Cyber-Physical Domain

Given that swarm systems operate automatically in physical space, the task-service planning process must be subject to multidimensional constraints. Here, all these constraints are divided into two typical types: capability constraints and efficiency constraints. The former is employed to assess whether the current capability of the service pool can meet the requirements for the successful execution of all atomic tasks, while the latter is mainly used to find an optimized efficiency solution $\pi$.

4.2.1. Constraints for Fundamental Capabilities

After analyzing the cyber-physical characteristics, several capability constraints are briefly summarized and listed in this section.

Constraint 1 (Service Amount): Assuming a task set ${\zeta }_{type}^{\tau }$, where each task ${\tau }_i$ requests some amount of several services, belonging to different service type denoted as $type$, and $type$ type service corresponds to the $C{S}_{ik}$ in the chromosome piece of ${\tau }_i$, then, only when ${\sum }_{i=first\left(\tau \right).id}^{last\left(\tau \right).id}\left(X_{ik}\right)\le \sum \left(Y_{ik}\right)$ is satisfied, there possibly exists a feasible solution $\pi$ for ${\zeta }_{type}^{\tau }$.

Constraint 2 (Task Feasible): For any task ${\tau }_i$, only when the amount of each type service left for it is greater than it required, ${\tau }_i$ is feasible.

Constraint 3 (Service Types): Assuming a service set ${\zeta }_{{\tau }_i}^{\epsilon }$ required by ${\tau }_i$, where the types of all services are need by ${\tau }_i$, then, only if each type of required services is in ${\zeta }_{{\tau }_i}^{\epsilon }$, ${\tau }_i$ is realizable.

Constraint 4 (Global Service Capability): For all tasks of mission M, only when Constraint 1–Constraint 3 are all satisfied, these tasks are realizable, namely, it is possible to find a plan for M.

Constraint 5 (Reachable Range): For a distance-related service $\epsilon$, such as robot, missile etc., if the sum of its $\epsilon .MaxD$ and $MaxD$ of $\epsilon .Cid$ is greater than the distance from $\epsilon .Cid$ to the position of $\tau .tar$, where service $\epsilon$ is allocated to $\tau$, then, that is to say that $\epsilon$ is usable to $\tau .tar$.

Constraint 6 (Global Reachable Range): When a platform service is scheduled to orderly move to different targets, correspondingly, performing a series of services it carried, the global reachable range $cD$ of this service must be not smaller than the sum of distances of planned positions of these adjacent targets.

Constraint 7 (Service Time Window): Every service must be performed in a predetermined time window, which depends on $MaxV$, $cPos$ of this service and its carrier.

It should be cleared that a platform service is also a carrier service. Its reachable range mainly depends on the fuel or battery allowance, and sometime, the round trip must be considered. For other carried services, the reachable range is always a compound value as indicated within Constraint 5. Only when these constraints are all satisfied, is it possible to find a feasible task-service solution $\pi$. Namely, these constraints can be used to adjudge whether the capability of current service pool is sufficient, and also, verify whether every solution found is valid.

4.2.2. Conditions for Optimizing the Efficiency

With the fundamental constraints above, several optimization constraints are further proposed for finding a nice solution $\pi$. In fact, for the genetic algorithm, the composition of these constraints constitutes the fitness function.

Condition 1 (Amount of Platform Services ${\mathbf{A}}_{\mathbf{PS}}$): $A_{PS}$ is the amount of carrier services for a special solution, which is equal to the number of robots that perform the mission M cooperatively. When there exist different solutions, the solution with fewer carrier services should be given priority.

Condition 2 (Time Cost ${\mathbf{A}}_{\mathbf{TC}}$): When a solution is found, its $A_{TC}$ can be calculated according to a group of arguments, covering every service and its target. Generally, the smaller $A_{TC}$ means a mission is performed more efficiently.

Condition 3 (Global Distance ${\mathbf{A}}_{\mathbf{GD}}$): $A_{GD}$ is the whole distance all robots will cruise. It is obvious that this value represents the efficiency and cruising cost for a mission.

Condition 4 (Damage Cost ${\mathbf{A}}_{\mathbf{DC}}$): $A_{DC}$ indicates the possible cost of damaged resources during the execution of a planned solution. This value reflects the evaluated overhead of a special solution, depending on the status of environment.

Condition 5 (Mission Earning ${\mathbf{A}}_{\mathbf{ME}}$): $A_{ME}$ represents the achievement degree of one mission, in other words, the average success rate of vital services.

With these conditions, we can further design a weighted function $F\left(\right)$ to evaluate the performance of one solution $\pi$. This function is defined as Formula (4), where each ${\beta }_{xx}$ is a float weight factor between 0 and 1, and $f_n\left(\right)$ is a function for normalizing the value of each variable into the same magnitude as defined in Formula (5). According to different execution policies, the value of each ${\beta }_{xx}$ can be adjusted adaptively. As described, $F\left(\right)$ is in fact the fitness function of GA.

$$\begin{array}{cc}F\left(\pi \right)=\sum _{xx=PS}^{ME}{\beta }_{xx}\times f_n\left(A_{xx}\right)\hfill & \hfill xx=\{PS,TC,GD,DC,ME\}\end{array}$$

(4)

$$\begin{array}{c}{f}_n\left(x\right)=\frac{x-x_{min}}{x_{max}-x_{min}}\times 100\hfill \end{array}$$

(5)

4.3. Task Planning Oriented Genetic Algorithm

4.3.1. Multiple Population Based on Task Cluster

As analyzed above, all related tasks are aggregated together according to the service relevance, forming a group of independent task clusters. The so-called service relevance here has two meanings: the direct relevance and indirect relevance. Assuming two tasks ${\tau }_i$ and ${\tau }_j$ require the same type of service, then, ${\tau }_i$ and ${\tau }_j$ are considered to be directly related. For two direct related tasks ${\tau }_i$ and ${\tau }_j$, if task ${\tau }_m$ is directly related with ${\tau }_i$, but not related with ${\tau }_j$, ${\tau }_m$ and ${\tau }_j$ are seen as indirect related. All tasks that are service related will be put into the same cluster. In addition, the chromosome segments of tasks in same cluster will be assembled together, as a fundamental chromosome for an evolutionary population. Thus, an original large solution space is decomposed into multiple subspaces, which will greatly reduce the complexity and cost of the full solution procedure.

Of course, after employing the conception of task cluster, there will also introduce two-level solutions: the local solution for each chromosome and global solution for one planning problem. It is easy to prove that for one globally solvable problem, it must be locally solvable, i.e., as long as there is a global solution for a problem, it must exist a set of local solutions. Therefore, the solving procedure can be separated into the following four steps.

• Step 1: For every population $P_j(j=1,2,...,nnisthetotalnumberofpopulations)$, search all possible solutions under Constraint 2–Constraint 6, and form its corresponding solution set ${\zeta }_{P_j}^{\pi }$; If there does not exist a set ${\zeta }_{P_j}^{\pi }$ that is $null$, all populations are solvable, go to next, otherwise return $False$.
• Step 2: Iterate through the combinations of local solutions among all $P_j$, and add the globally solvable solutions into the set ${\zeta }_{global}^{\pi }$; If ${\zeta }_{global}^{\pi }$ is not $null$, then, go to next, otherwise, there is no feasible solution, return $False$.
• Step 3: Evaluate the efficiency of all solutions in ${\zeta }_{global}^{\pi }$ using an instantiated function $F\left(\pi \right)$ as shown in Formula (4).
• Step 4: Select one optimal solution from ${\zeta }_{global}^{\pi }$ and return.

It can be said that service relevance based on task clustering is the first step for optimizing this problem, and the other obvious advantage of this method is the potential for improving the computing efficiency via parallel hardware.

4.3.2. Optimized GA Operators under Multiple Constraints

(1) Constrained population initialization

As we all know, in GA, the first generation of population is always initialized randomly. The main advantage of this manner is that the diversity of population can be well guaranteed, similar to biological evolution. Of course, its disadvantage is also obvious that this manner may result in a long convergence time or even the failure of convergence. For this reason, we propose an initialization method with some constraints. Firstly, we employ a service status vector $\lambda$ to record the status of all services in the pool, where $\left|\lambda \right|$ is equal to the size of service pool, and each element $\lambda \left[i\right](i=1,2,...,|\lambda \left|\right)$ is initialized to be 0 (means available). When $\lambda \left[i\right]$ is allocated to a chromosome bit, its value will be set to 1. Then, we employ Constraint 8 to supervise the assigning procedure of a chromosome bit. it is obvious that via adjusting the value of $\delta$, the randomness and certainty can be balanced.

Constraint 8 (Supervisory Assign): During initializing chromosomes of each populations, if and only if it exists at least one available service that corresponds to this bit, this bit can be set to 1 with a probability $\delta$.

(2) Hybrid selection operator

Although the Roulette-wheel-selection is the typical mechanism in traditional genetic algorithms, it is not appropriate for this study because in the crossover and mutation operation, optimal individuals are easy to be eliminated, and the convergence speed of this mechanism is slow. To get rid of these potential problems, we designed a hybrid selection operator that gives full play to the advantages of both Binary Tournament selection and Elitist selection. As is well known, the obvious advantage of Binary Tournament selection is that it enables excellent individuals to enter the next generation of population with a greater probability, which is meaningful to speed up the evolution. On this basis, we further exploit the advantages of Elitist selection that it always replaces a certain number of individuals in the offspring population with some optimal individuals in the parent population. This is very important to guarantee the convergence. Of course, too much substitution will destroy the diversity of the offspring population, which may lead to the local optimal solution. Therefore, this proposed operator just replace the worst individuals in the offspring population with the best of its parent.

(3) Constrained adaptive crossover operator

To guide evolution in the direction of convergence, we designed a constrained adaptive crossover operator on the basis of adaptive crossover and one-point crossover [52]. Firstly, the adaptive crossover will dynamically adjust the crossover probability according to the maximum value, minimum value and average value of fitness of individuals in current population. In addition, as the average fitness value of the evolving population increases, the crossover rate decreases. In this study, we adopt Formula (6) to calculate the probability of crossover $P_c$, where $f_{max}$, $f_{avg}$, and $f_{min}$ represent the maximum, average, and minimum fitness values separately. Secondly, to guarantee the diversity of individuals and also the structure of cluster-based chromosome, this operator will cross two individuals in chromosome pieces, rather than bits. Additionally, the two offspring produced by crossover will compete with these two parents to enter the next generation population, the better two individuals will be selected into new generated population.

$$P_c=\left\{\begin{array}{cc}{\displaystyle \frac{P_{c1}\times (f_{avg}-f^{\prime })+P_{c2}\times (f^{\prime }-f_{min})}{f_{avg}-f_{min}}}\hfill & \hfill f^{\prime }<f_{avg}\\ {\displaystyle \frac{P_{c2}\times (f_{avg}-f^{\prime })+P_{c3}\times (f^{\prime }-f_{avg})}{f_{max}-f_{avg}}}\hfill & \hfill f^{\prime }\ge f_{avg}\end{array}\right.$$

(6)

(4) Effectiveness-oriented mutation operator

Mutation is an important operation for a genetic algorithm, which can promote the randomness of individuals and avoid falling into local optimization. In this design, this operator has been given a new function, amending chromosome pieces that do not meet Constraint 1 as much as possible to satisfy the requirements. For new generated individuals, this operator will check each chromosome piece $C{S}_{ik}$ for task ${\tau }_i$. If it finds any piece that does not satisfy Constraint 1 and Constraint 2, namely the amount of service allocated to special type task is not just equal to the amount required, it will edit some bits of related pieces of this individual randomly, of course, under Constraint 1–Constraint 4. The advantage of this operation is that it can increase the number of effective individuals significantly.

5. Verification Experiments and Analysis

On the basis of models and mechanisms mentioned above, we implemented all these designs within a distributed simulator on Windows OS. All resources a swarm system covered are stored as entries in different resource tables within a MySQL database. Meanwhile, we employ Data Distribution Service (DDS) as the fundamental communication middleware. All other designs are implemented with $C++$. Focusing on the topic of optimized task-service planning, the correctness and performance of proposed methods are mainly simulated and verified in special scenes. In the following, several typical experiments and the results are described in detail.

5.1. Verification of Planning Mechanism and GA Operators

To verify this planning mechanism, we firstly construct a scenario as shown in Figure 3, where seven robots cooperate to fight a fire. This mission is parsed into five atomic tasks $t_1$–$t_5$ for 5 different target places with 4 type of services, as exhibited in Table 2. Each robot carries a different number and type of fire-fighting resources: water ($\epsilon .typ=1$), carbon dioxide fire extinguisher ($\epsilon .typ=2$), dry powder fire extinguisher ($\epsilon .typ=3$), foam fire extinguisher ($\epsilon .typ=4$), fan fire extinguisher ($\epsilon .typ=5$), sand fire extinguisher ($\epsilon .typ=6$), rock powder extinguishing ($\epsilon .typ=7$). The properties of each task, the distribution of all resources, and the parameters of robots are detailed in Table 2, Table 3, and Table 4, separately. Based on these settings, the performance of planning mechanism is verified from different aspects, especially, the chromosome coding, population size, and three proposed operators.

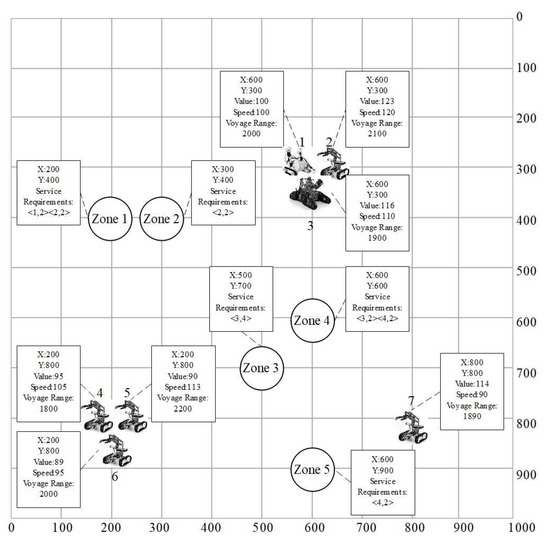
Figure 3. A Simulated Scene for Cooperative Fire Fighting by Swarm Robots.

Table 2. Descriptions of 5 Atomic Tasks.

ID	${\mathit{t}}_{\mathit{s}}$	${\mathit{t}}_{\mathit{e}}$	X	Y	Service Requirements	Risk	Value
1	2	5	200	400	<1,2><2,2>	0.1	1000
2	3	5	300	400	<2,2>	0.1	700
3	5	9	500	700	<3,4>	0.1	900
4	6	10	600	600	<3,2><4,2>	0.1	800
5	9	13	600	900	<4,2>	0.1	900

Table 3. Distribution of Resources on Six Robots.

$\mathit{\epsilon }.\mathit{id}$	$\mathit{\epsilon }.\mathit{Cid}$	$\mathit{\epsilon }.\mathit{typ}$	$\mathit{\epsilon }.\mathit{Cap}$	$\mathit{\epsilon }.\mathit{id}$	$\mathit{\epsilon }.\mathit{Cid}$	$\mathit{\epsilon }.\mathit{typ}$	$\mathit{\epsilon }.\mathit{Cap}$	$\mathit{\epsilon }.\mathit{id}$	$\mathit{\epsilon }.\mathit{Cid}$	$\mathit{\epsilon }.\mathit{typ}$	$\mathit{\epsilon }.\mathit{Cap}$
1	1	1	5	2	1	1	5	3	1	1	5
4	1	1	5	5	1	1	5	6	1	2	6
7	1	2	6	8	2	2	6	9	2	2	6
10	2	2	6	11	2	2	6	12	3	3	7
13	3	3	7	14	3	3	7	15	3	3	7
16	3	3	7	17	3	3	7	18	3	3	7
19	2	4	5	20	2	4	5	21	4	4	5
22	4	4	5	23	4	4	5	24	4	5	7
25	4	5	7	26	5	5	7	27	5	5	7
28	5	5	7	29	5	5	7	30	5	5	7
31	6	6	4	32	6	6	4	33	6	6	4
34	6	6	4	35	7	7	1

Table 4. Parameters of Robots.

ID	Mode	X	Y	Value	Speed	Voyage Range
1	1	600	300	100	100	2000
2	1	600	300	123	120	2100
3	1	600	300	116	110	1900
4	1	200	800	95	105	1800
5	1	200	800	90	113	2200
6	1	200	800	89	95	2000
7	1	800	800	114	90	1890

Because all these tasks are related, both directly and indirectly, to each other, only one task cluster is established. Figure 4 presents the chromosome code of 41 bits in length for this scene, which means that the size of solution space is equal to $2^{41}$. Furthermore, we design a more complex scene with 9 tasks and 7 services. The result of task cluster-based chromosome coding for this scene is shown in Figure 5, where there are 3 segments of 47 bits, 14bits, and 1 bit in length, respectively. These segments corresponds to three solution spaces, the size of which are $2^{47}$, $2^{14}$, and 2, separately. Obviously, the total size of these three space is $(2^{47}+2^{14}+2)$, rather than the original larger one $2^{62}$. It is the main advantage of such cluster-based mechanism that the solution time cost can be reduced significantly, especially when parallel solving is possible. It should be noted that in both Figure 4 and Figure 5, the values of all bits of both coded chromosomes are fixed, indicating in fact two feasible solutions by our planning algorithm.

Figure 4. A single Chromosome Coded for 5 Tasks and 4 Services.

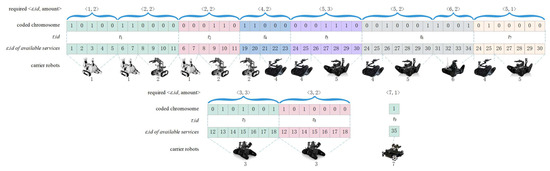
Figure 5. Three Chromosome Segments Coded for 9 Tasks and 7 Services.

As we know, the size of population is the first important factor for GA, which affects the quality of solutions and the convergence speed. After experimenting this parameter 100 times on such scene, we found that when the population size was about 50, the fitness values of optimal solutions and the convergence speed would be well balanced, as shown in Figure 6 and in Figure 7. This conclusion is worthy of reference to determine a proper population scale before solving a special problem.

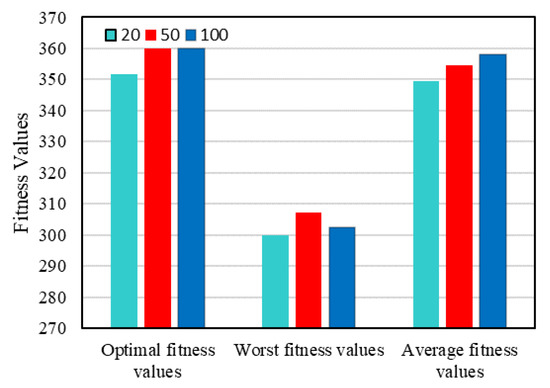
Figure 6. The relation of Population Size and Fitness Value.

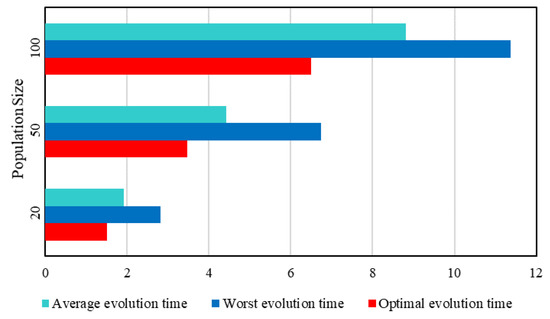
Figure 7. The relation of Population Size and Convergence Speed.

Furthermore, the effectiveness of three operators are verified. The performance of selection operator is shown in Figure 8, where R_O, R_W, and R_A represents Optimal fitness, Worst fitness, and Average fitness of Binary Tournament selection respectively, and H_O, H_W, and H_A are that for hybrid selection. From Figure 8, we can observe that the hybrid selection operator performs better than traditional Binary Tournament selection. With this hybrid selection operator, more better solutions can be evolved, and the convergence speed is also faster. Figure 9 shows the compared results between traditional crossover denoted as (O_*) and designed adaptive crossover denoted as (A_*), with fixed parameters of Formula (6): $P_{c1}=0.85$, $P_{c2}=0.6$, and $P_{c3}=0.45$. From these results, we can also find the new operator is effective to find optimal solutions, but the convergence speed is somewhat slow. This is mainly because such procedure has been artificially interfered, typically Formula (6). Figure 10 presents the effect of Effectiveness-oriented mutation, denoted as (ECM_*). We can find that this operator can promote the performance of both getting better fitness and accelerating the evolving speed, just similar to that of Figure 8. Figure 11 shows the final performance with the proposed mechanism combining all these new operators. The results of 100 experiments are shown in Figure 12. From this Figure, we know that feasible solutions can be obtained at every time, and in 97 experiments the fitness values approximating the optimal value 360 are achieved. Of course, there still exist three experiments that converge to some suboptimal solutions. This is a normal case for a genetic algorithm, and is acceptable because, primarily, this problem must be solvable at each time.

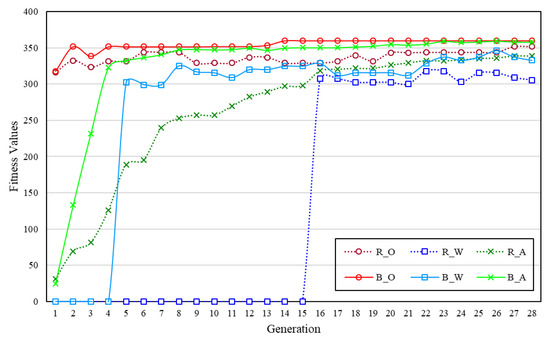
Figure 8. Compare of Roulette Selection and Hybrid Selection.

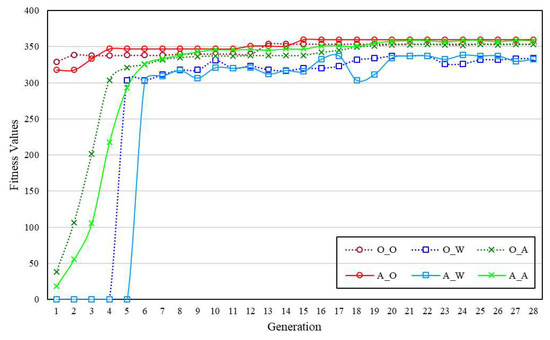
Figure 9. Compare of Traditional Crossover and Constrained Adaptive Crossover.

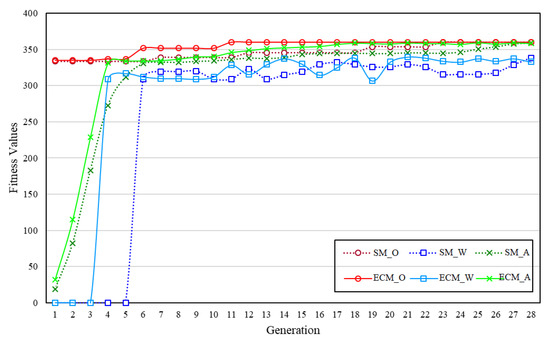
Figure 10. Compare of Traditional Mutation and Effectiveness-oriented Mutation.

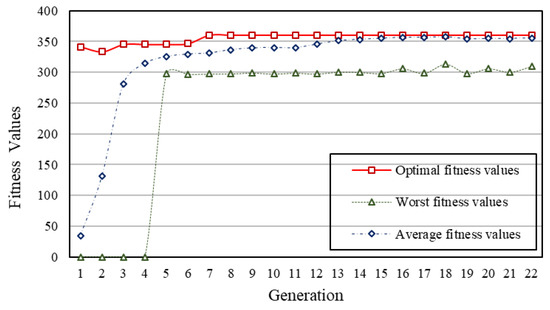
Figure 11. The Performance of this Proposed Planning Mechanism.

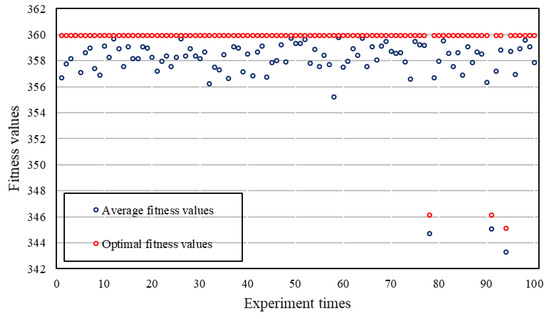
Figure 12. Optimal Fitness Values in 100 Experimental Results.

5.2. Solving Ability Analysis

The verification of the solving ability is to check whether this algorithm can find out effective solutions and further some optimal ones when there indeed exist such feasible answers within a solution space. For this purpose, we establish a solution verification mechanism with a traversal algorithm, and the architecture is shown in Figure 13.

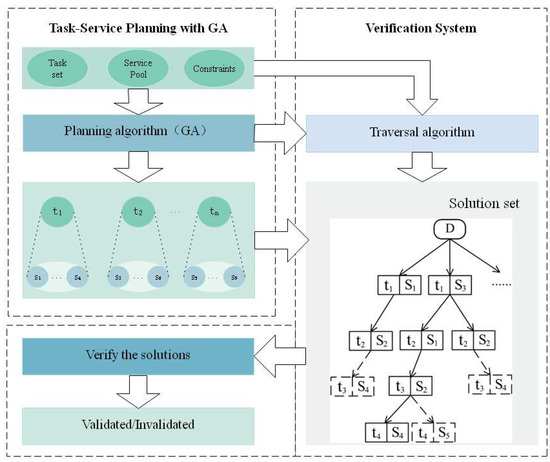
Figure 13. Verification Architecture with a Traversal Algorithm.

With this method, several experiments have been conducted. As we can imagine, with the increase of the number of tasks andrequired sharing resources, the solution space increases dramatically. As shown in Figure 14, the costs of planning mechanism we proposed always keep low and stable, while that of the traversal algorithm increases exponentially. Additionally, with 100 experiments of several different scenes, we can observe that this proposed algorithm can find out feasible solutions correctly, and the average ratio of optimal solution is about $93\%$, as detailed in Table 5. These data also indicates that this new GA algorithm can guarantee the capability of solving, although there is no well guarantee that the best solution can be found every time. Thus, we can conclude from Figure 14 and Table 5 that this algorithm has good convergence ability and fast convergence speed, which are all vital performance aspects for swarm intelligent systems.

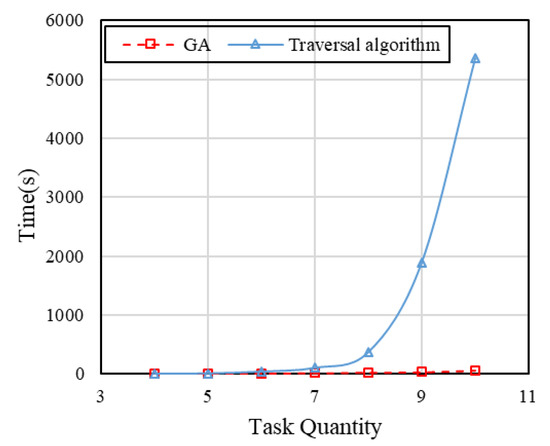
Figure 14. Solving Costs with Increasing Number of Related Tasks.

Table 5. Results of Verification.

Group ID	Number of Tasks	Times	Probability of Solutions	Optimal Ratio
1	4	100	100%	90%
2	4	100	100%	95%
3	5	100	100%	87%
4	5	100	100%	97%
5	7	100	100%	97%
6	7	100	100%	95%

6. Conclusions

Swarm Intelligent systems have been becoming one new and important form in the age of the Internet of Everything, and cooperation among such systems are a vital intelligence aspect that has lately gained great research interest. Considering the problem about task planning and allocation on hierarchical and heterogeneous resources in a swarm system, a new service virtualization-based task planning architecture is proposed, and further, a multi-constraint optimized planning genetic algorithm is designed. This design differs from current task allocation methods mainly in two aspects: First, the assignment of tasks is based on the internal resources of systems, not just the systems themselves. Ssecond, multi-dimensional cyber-physical constraints are introduced for solving such an optimization problem.

Typical Experiments show that this novel mechanism is effective and efficient for cooperative intelligent systems. Concretely, virtualization is one effective manner that can mask the heterogeneity of resources, and virtualized services provide more regular encapsulated attributes, unified interface, and particularly, the execution capability that can be scheduled by software Agent. The main feature of multi-constraint-based task planning method we proposed is that it is suitable to solve this kind of complicated optimization problems, and takes the advantage of GA by extending operators. Experimental results, including the solvability proved by the traversal algorithm, have demonstrated that the convergency of algorithm and its speed, the quality of solution can be guaranteed well, although these aspects are vital problems for traditional GA. In addition, when the parallel computing is supported, e.g., by multi-cores or distributed processors, the performance will be improved significantly.

Our ongoing and future studies on this topic have been extending to the scope of adaptive management of service pool, event generation and scheduling, the parallel mechanism for swarm planning, and also constructing of test bed systems.