Abstract
In recent years, healthcare has attracted much attention, which is looking for more and more data analytics in healthcare to relieve medical problems in medical staff shortage, ageing population, people living alone, and quality of life. Data mining, analysis, and forecasting play a vital role in modern social and medical fields. However, how to select a proper model to mine and analyze the relevant medical information in the data is not only an extremely challenging problem, but also a concerning problem. Tuberculosis remains a major global health problem despite recent and continued progress in prevention and treatment. There is no doubt that the effective analysis and accurate forecasting of global tuberculosis prevalence rates lay a solid foundation for the construction of an epidemic disease warning and monitoring system from a global perspective. In this paper, the tuberculosis prevalence rate time series for four World Bank income groups are targeted. Kruskal–Wallis analysis of variance and multiple comparison tests are conducted to determine whether the differences of tuberculosis prevalence rates for different income groups are statistically significant or not, and a novel combined forecasting model with its weights optimized by a recently developed artificial intelligence algorithm—cuckoo search—is proposed to forecast the hierarchical tuberculosis prevalence rates from 2013 to 2016. Numerical results show that the developed combination model is not only simple, but is also able to satisfactorily approximate the actual tuberculosis prevalence rate, and can be an effective tool in mining and analyzing big data in the medical field.
1. Introduction
Currently, the world faces a considerable health burden related to tuberculosis (TB), which is an infectious bacterial disease caused by Mycobacterium tuberculosis, typically exerting adverse effects not only on the lungs, but also on other bodily organs. TB is transmitted from person to person via small droplets of sputum and saliva expelled when an infectious patient coughs or sneezes [1]. Declared a major worldwide health problem by the World Health Organization (WHO), TB induces ill-health among millions of people each year, and ranks as the second leading cause of death from infectious disease after human immunodeficiency virus (HIV) [2]. Nonetheless, TB is the most prevalent airborne infectious cause of death, inducing approximately three million deaths each year, principally among young adults in the globally poorest nations [3,4,5,6,7,8,9].
Smart cities have been paid attention, and its status consolidates as one of the fanciest areas of research today. Hence, [10] makes a case for a cautious rethink of the very rationale and relevance of the debate, and in the paper [11], the origins of what is termed normative bias in smart cities research are identified and a case is made for a holistic, scalable, and human-centered smart cities research agenda. Smart healthcare applications are one part of a smart city, which involve domain and data understanding for physician- and patient-centric healthcare, data preprocessing, and modeling using natural language processing and (big) data analytic techniques, and model evaluation and knowledge deployment through information infrastructures [12].
TB is often associated with behavioral factors and demographics, including occupation, age, tobacco and alcohol consumption, poor nutrition, and household crowding [13,14,15,16,17,18]. Recently, WHO has begun to promote efforts to address social determinants as an important component of global tuberculosis control [19]. Recently, the improvement of medical conditions [20], the improvement of optimal control strategy [21], classification algorithm, and signal processing algorithm [22,23], have been widely used in the medical field, meanwhile, big data and data analysis techniques are applied to disease diagnosis [24], such that the accuracy of diagnosis results has been significantly improved, and have contributed to preventing the incidence of tuberculosis diseases. Much of the epidemiological TB literature relies on notified cases, and relatively few involve measurements and trend predictions of TB prevalence [25]. However, the approaches related to the prediction of TB prevalence rates are less than ideal, and these possible tools deserve further exploration. Accurate tuberculosis prevalence rate forecasting is of vital importance to global tuberculosis prevention and control. Advances made in predicting tuberculosis events may be used to anticipate high and low risk years or future tuberculosis epidemics. In recent-year forecasts, future disease trends or comparisons of competing disease control policies commonly estimate results using dynamic transmission models, which represent the mechanisms of transmission, natural history, and health system interactions that generate tuberculosis outcomes. The studies shown in Table 1 described standard tuberculosis modeling approaches and examined specific modeling approaches. However, little systematic investigation has been done on the assumptions made by published tuberculosis models. If these assumptions are not valid, the results of these studies could be biased [26].

Table 1.
The different forecasting approaches of tuberculosis (TB).
According to the above discussion, this paper seeks to use a combined model to estimate and forecast the prevalence of TB. We mainly focus on hierarchical tuberculosis prevalence rate data according to four World Bank income groups. The association between tuberculosis prevalence rates and income levels is examined by means of nonparametric analysis of variance (ANOVA). In addition, nonlinear regression analysis is first applied to hierarchically forecast tuberculosis prevalence rates; then, a combination forecasting strategy, whose weights are further optimized by the cuckoo search algorithm, based on machine learning, is proposed. Cuckoo search-based combined models are constructed in this paper to improve forecasting accuracy as much as possible and, thus, provide meaningful evidence and information about the potential trends and future evaluation of the burden of tuberculosis, i.e., incidence, prevalence, and mortality. In conclusion, the major distinction of this study is that hierarchical tuberculosis prevalence rates are innovatively analyzed and forecasted. Furthermore, an innovative combination forecasting model based on regression analysis and an artificial intelligence optimization method is proposed.
In the future, big data and data analysis technology will be widely used in disease surveillance, decision-making, health management, and other fields, which is the focus of current intelligent medical care. In this paper, data analysis is used to analyze and forecast the tuberculosis prevalence rates. Through repeated analysis of tuberculosis data, combined with the data of tuberculosis prevalence rates and professional literature, a hybrid combined forecasting model is proposed, verified repeatedly and, finally, the CS-combined model is used to forecasting the trend of prevalence rates of intelligent medical products.
The remainder of this paper is organized as follows: Section 2 introduces related methodologies, including the Kruskal–Wallis test, regression analysis, combination forecasting strategy, and the cuckoo search algorithm. In Section 3, we present numerical examples and forecasting results. Section 4 reports the related conclusions of this study.
2. Related Methodology
Curve fitting is the process of constructing a curve, or mathematical function, which has the best fit to a series of data points, possibly subject to constraints. This section introduces different methods of curve fitting.
2.1. Kruskal–Wallis (KW) Test
The Kruskal–Wallis (KW) method is presented as a nonparametric technique to detect whether different samples originate from the same probability distribution [35,36,37,38]. Since no normality assumption is made, the KW test is based on an analysis of medians instead of means.
Assume a set of p random variables, Xk (), are selected from different populations. Define as the median of Xk. The null hypothesis H0 and the alternative hypothesis H1 of the KW test can be expressed as follows [35]:
If the null hypothesis is rejected, then the p random variables are assumed to be drawn from more than a single population. For detailed information on the KW test, please refer to Reference [38].
2.2. Regression Analysis
Regression analysis is a statistical tool used to investigate relationships between variables with the procedure of model construction, coefficient estimation, and statistical inference [35]. The method of least squares estimation aims to minimize the summed squares of the residuals, defined via
where is observed response value, is the fitted response value, and n is the number of data points included in the fit process.
The R-square statistic is a measure to indicate the extent to which the total variation of the dependent variable is explained by the regression model. It is defined as the ratio of the sum of squares of regression and the total sum of squares, which can be expressed as [39]:
Since it takes into consideration the degrees of freedom, the adjusted R-square statistic is more reasonable for indicating regression performance, which is defined as
where n denotes the number of response values and m is the number of fitted coefficients. An adjusted R-square value closer to one indicates that a greater proportion of variance is accounted for by the regression model.
In addition, two error evaluation criteria are calculated to assess forecasting accuracy—namely, mean absolute percentage error (MAPE) indicator receives one value for a specific forecasting accuracy and the root mean square error (RMSE) is used to measure the deviation between the forecasting value and the actual value—calculated as follows:
where N is the number of forecasting periods, is the actual value at time i, and denotes the corresponding forecasted value.
2.3. Cuckoo Search (CS) Optimization
Cuckoo search is a novel metaheuristic optimization algorithm based on the obligate brood parasitic behavior of some cuckoo species in combination with Lévy flight behavior [40]. Three idealized rules are applied by Yang and Deb [40,41], and the aim is to use the new and potentially better solutions (cuckoos) to replace the not-so-good solution in the nests. The interested readers can refer to References [40,41] for details of the cuckoo search algorithm. A shortened description of the process of the cuckoo search algorithm is provided in Appendix A.
2.4. Combined Forecasting Method
The combined forecasting method, which assigns a weighted coefficient to each individual method proportional to its past forecasting performance, can improve the final forecasting performance by taking advantage of individual forecasting methods that perform differently depending on the datasets, the forecast horizons, and their capability of capturing nonlinearity. The combined forecast model can be represented as
where is the final forecast at time t, is the forecast value of ith model at time t, is the corresponding weight assigned to the ith model, and m is the number of the individual models utilized. The formulation of the combined forecast model can be realized in various ways. In this study, the weights are determined based on an artificial intelligence method. Figure 1 depicts the flowchart of the proposed combined forecasting model based on the cuckoo search algorithm to optimize the weights.
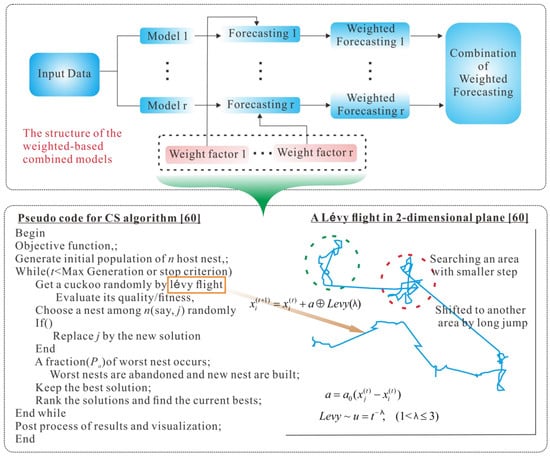
Figure 1.
Flowchart of the proposed combined forecasting model based on the cuckoo search algorithm.
2.5. Radial Basis Function Neural Networks
The RBF neural network is a forward network model with good performance [42], global approximation, and is free from the local minima problems. In this paper, the RBF neural work is used to estimate the parameter of polynomial regression.
It has three layers: an input layer, a hidden layer with a non-linear RBF activation function, and a linear output layer, which is a two-layer feed-forward neural network.
The network output y is a vector with m components, determined in terms of the n components of the input vector x by the following formula:
where are the radial-basis functions, and Nh is the number of hidden-layer neurons. The hidden-layer-to-outputs interconnection weights are given by . The threshold offset is denoted by .
Generally, the hidden neuron of an RBF network employs a Gaussian form for the activation function, which is given as:
where are centers, and the are widths or variances. For simplicity, the centers and variances are pre-defined and fixed. The above equation can be transformed to the matrix form below:
where Ψ(x) = and W is the weights matrix.
Y = WTΨ(x),
2.6. Data Analysis
The hierarchical tuberculosis prevalence rate dataset, applied in the simulation, was downloaded from the website of the World Health Organization (WHO) [43]. As described in Section 1, prevalence is one of main indicators used to assess the burden of tuberculosis. When survey data are not available, estimates of prevalence are derived from estimates of incidence and the duration of disease.
The tuberculosis prevalence rate refers to the number of cases of tuberculosis (all forms) in a population at a given point in time (the middle of the calendar year), expressed as the rate per 100,000 people, including cases of tuberculosis in people with HIV. In this study, we pay close attention to tuberculosis prevalence rates at the global level with respect to the World Bank income groups.
According to the information on its official website, the World Bank classifies economies as low income, middle income (subdivided into lower-middle and upper-middle), or high income, based on gross national income (GNI) per capita. Low income and middle income economies are sometimes referred to as developing economies. Each year, on 1 July, the World Bank revises the classification of world economies. As of 1 July 2013, the World Bank income classifications by gross national income (GNI) per capita are as shown in Table 2.

Table 2.
Income classifications by gross national income (GNI) per capita according to the World Bank.
For nearly 17 years since WHO’s declaration of tuberculosis as a global public health emergency, major progress has been made towards 2017 global targets set within the context of the millennium development goals (MDGs). Table 3 presents a time series of tuberculosis prevalence rates (incidence of tuberculosis and incidence of tuberculosis by HIV-positive cases) at the global level for the four different World Bank income groups—namely, high income, upper-middle income, lower-middle income, and low income—from 2000 to 2016.

Table 3.
Tuberculosis prevalence rates for the four income groups from 2000 to 2016.
As we can see from Table 2, generally speaking, lower income status is accompanied with higher tuberculosis prevalence rates. For the high income group, tuberculosis prevalence rates from 2000 to 2016 decreased rapidly. Additionally, the tuberculosis prevalence rate in 2000 was 52% less than the 2000 rate. The tuberculosis prevalence rates for upper-middle income group gradually descended across the seventeen years from 2000 to 2016. The prevalence rate reached 87 cases per 100,000 population in 2016, representing a decrease of 24.35% since 2000. For lower-middle income and low income groups, the tuberculosis prevalence rates exhibited similar patterns of decline: first slow and then quickly falling, with decreases of 21.24% and 37.12%, respectively, compared to the rates in 2000. The reduced prevalence rates for all income groups demonstrate continuous progress being made in the global fight against tuberculosis.
For better modeling, this paper uses the KW test to verify whether tuberculosis prevalence rates are different among the four different income groups. Table 4 displays the pairwise comparison results. Each row of the table represents one test, and there is one row for each pair of groups. In total, there are six pairs of groups. The entries in each row indicate the mean ranks being compared, the estimated difference in mean ranks, and a confidence interval for the difference with 95% confidence. For example, the first row shows that the mean rank tuberculosis prevalence rate for the high income group minus the mean rank tuberculosis prevalence rate for the upper-middle income group is estimated to be −17, with a 95% confidence interval for the true difference of the mean ranks of [−34.4219, 0.4219]. The confidence interval does not contain zero, so the difference is significant at the 0.05 level. Consequently, we can draw the conclusion that the mean rank tuberculosis prevalence rate for the high income group is significantly different from those megabank rates for all other income groups, as measured by all the 95% confidence intervals listed from the second row to the fourth row (i.e., none contains zero). Similarly, the mean tuberculosis prevalence rate for the upper-middle income group is also significantly different from those for the lower-middle, as well as the low income groups.

Table 4.
Results of multiple comparison test.
All in all, through the multiple comparison test yielding the results shown in Table 3, we collect further detailed information about the pairwise difference of tuberculosis prevalence rates among the four World Bank income groups. Pairwise analyses conclude that significant differences in mean tuberculosis prevalence rates among income groups exist, except between the mean tuberculosis prevalence rates of the lower-middle income and the low income groups.
2.7. Structure of the Proposed Integrated Forecasting Framework
Mathematical models (in Table 1) consist of compartments which represent sets of individuals grouped by disease status. The links between compartments represent transitions from one state of disease to another state and different compartments can be included or excluded according to the assumptions of the mathematical models. However, the combined model based on polynomial regression proposed in this paper aims at the incidence of TB; no other assumptions are needed in the modeling process. In the process of forecasting, it avoids the deviation of forecasting results caused by the invalid assumptions of the mathematical model. This is different from the mathematical models whose goal of a combined model is to model a non-linear relationship between the independent and dependent variables (technically, between the independent variable (year) and the conditional mean of the dependent variable (tuberculosis rates), and the combined forecasting model is the same as other common forecasting models, which mainly reflects the statistical regularity of diseases from data.
Hierarchical tuberculosis prevalence rate data were collected from the World Health Organization (WHO) and the data were collected into four economic groups: high income, upper-middle income, lower-middle income, and low income groups. Given these data, we first employ the KW test to check whether tuberculosis prevalence rates are significantly different among the four income groups.
After the hierarchical tuberculosis prevalence rate data analysis, the TB time series data is input into the five different regression models. The overall flowchart of the proposed integrated model is depicted in Figure 1.
The parameters of the different regression models are determined by employing an RBF neural network; the RBF neural network is used to fit unknown function. Given a nonlinear function, such as y = aebx, the parameters of the function a and b are not known. To determine them, first randomly generate two trial parameters of a and b. With these two parameters, y is calculated by y = aebx, and is used as the output data of the RBF neural network. Thus, the RBF neural network establishes approximate and exact regression analysis.
With the different regressions determined, a combined forecasting model is employed. The combined forecasting model is based on multiple different forecasting models for the same problem. It can be a combination of several quantitative methods or a combination of several qualitative methods. In this paper, a quantitative method is used to combine six regression models. The main purpose of combination is to make full use of the information provided by various forecasting models. To improve the forecasting accuracy as much as possible, this paper uses the cuckoo search algorithm to optimize and determine the combination weights in the combined model.
It is worth noting that there are four steps of future forecasting, h = 4, for the different income groups studied in this paper, with the forecasting values from 2013 to 2016.
3. The Model Processing and Analysis Forecasting Result
Original yearly records of tuberculosis prevalence rate are measured and published by the World Health Organization [43], which is our main data resource. In this section, the tuberculosis prevalence rates from four different income groups are used to estimate the performance of the proposed novel combined model. The proposed novel combined model is compared with other forecasting models, namely, Poly, Sin, Reci-Poly, Reci-Exp, Power2-Poly2, and Power2-Exp2.
3.1. The Data Description and the Forecasting Modeling for Each Income Group
Considering that tuberculosis prevalence rates are associated with income groups, we seek to make full use of the hierarchical tuberculosis prevalence rates. Thus, for each income group, we construct six different types of regression models with good adjusted R-square values. The tuberculosis prevalence rates from 2000 to 2012 are used for model construction and coefficient estimation. Linear and nonlinear regression models, such as the quadratic polynomial model, the two-term exponential model, the sum-of-sines model, and the Gaussian model, are repeatedly used for the different income groups. It is worth noting that the adjusted R-square value is regarded as the appropriate metric to evaluate the model’s goodness-of-fit. That is to say, we prefer to select regression models with adjusted R-square values as large as possible. Tuberculosis prevalence rates from 2013 to 2016 are forecasted for each income group, respectively.
In addition, for each income group, a total of six individual regression models are combined to forecast tuberculosis prevalence rates from 2013 to 2016, and the weights of the combination forecasting model are optimized by the cuckoo search algorithm. Below, the results of the individual and combination forecasting models are presented in great detail.
- (1)
- With respect to tuberculosis prevalence rates for the high income group, we first construct two regression models based on the original dataset using the quadratic polynomial model (Poly2) as well as the sum-of-two-sines model (Sin2). In addition, the original tuberculosis prevalence rates are transformed by taking reciprocals and then the quadratic polynomial model (Reci-Poly2) and the two-term exponential model (Reci-Exp2) are applied to characterize the data using a global fit. Finally, the original time series is transformed by taking base-2 logarithms and then the quadratic polynomial model (Power2-Poly2), as well as the one-term Gaussian model (Power2-Gauss1), are built.
- (2)
- In regard to tuberculosis prevalence rates for upper-middle income group, the seven types of forecasting models are the quadratic polynomial model (Poly2), the single sine model (Sin1), the reciprocal transformation plus quadratic polynomial model (Reci-Poly2) or the two-term exponential model (Reci-Exp2), the base-2 logarithm transformation with the quadratic polynomial model (Power2-Poly2), or the two-term exponential model (Power2-Exp2), and the combination model (CS-Combined).
- (3)
- Taking the tuberculosis prevalence rates for the lower-middle income group into account, the quadratic polynomial model (Poly2), the single sine model (Sin1), reciprocal transformation plus the quadratic polynomial model (Reci-Poly2), or the two-term exponential model (Reci-Exp2), the base-2 logarithm transformation with the quadratic polynomial model (Power2-Poly2), or the two-term exponential model (Power2-Exp2), as well as the combination model (CS-Combined) sequentially comprise a total of seven types of forecasting models.
- (4)
- With regard to the tuberculosis prevalence rates for the low income group, as described above, the cubic polynomial model (Poly2), the single sine model (Sin1), the reciprocal transformation plus the quadratic polynomial model (Reci-Poly2), or the two-term exponential model (Reci-Exp2), the base-2 logarithm transformation with the quadratic polynomial model (Power2-Poly2), or the two-term exponential model (Power2-Exp2), as well as the combination model (CS-Combined), are constructed sequentially.
3.2. Analysis of the Modeling Result for Tuberculosis Prevalence Rate in Each Income Group
According to the above analysis, in this part, we further analyze the tuberculosis prevalence rate forecasting results of four different income groups. Note that the corresponding inverse transformations are implemented to obtain final forecasting values. The coefficients of each regression model are estimated by the least-squares method, and the adjusted R-square (A-R2) of each regression model is calculated. Finally, the combination model is formed based on the six individual regression models, whose weights are optimized by the cuckoo search algorithm, which is denoted as “CS-Combined”. The reason why the aforementioned six regression models are chosen in our combined approach, is that these models have higher adjusted R-square values than other competing models. Appendix C plots the fit curves of all seven types of forecasting models while including details of the regression equations and adjusted R-squares.
Combined models which integrate the results of six individual regression models are often utilized in the forecasting field. In order to obtain the optimal weight coefficients of the individual models, a novel deciding weight method based on the cuckoo search is developed to determine the optimal combination weights. The optimization is as follows.
According to the cuckoo’s process of hatching bird eggs, the CS algorithm is described as follows:
Step 1 Defines the objective function , initializes the function, and randomly generates the initial position of n nests (i = 1, 2, …, n) to set parameters such as population size, problem dimension, maximum discovery probability P, and maximum iterative times;
Step 2 Chooses the fitness function and calculates the objective function value of each bird’s nest position, and obtains the current optimal function value;
Step 3 Records the optimal function value of the previous generation, and uses the formula (5.10) to update the position and state of the other nests;
Step 4 The existing position function value is compared with the previous generation optimal function value and, if it is better, the current optimal value is changed;
Step 5 After the location update, compare the random number with P. If , randomly change , otherwise, it will not change. Finally, keep the best of a group of nest positions ;
Step 6 If the maximum number of iterations or the minimum error requirement is not reached, return to step 2, otherwise, continue to the next step;
Step 7 Output the global optimal combination weight.
As demonstrated in Appendix C (Figure A1), all six individual regression models provide remarkable goodness-of-fit, with adjusted R-squares all above 0.93. Thus, the selection of regression models is proper and effective. From Appendix C (Figure A1), there are clearly significant improvements for combined model forecasts compared with the results of other forecasting models for high income group. The annual high income group tuberculosis prevalence rate from 2013 to 2016 years was forecasted by CS-combined model. The forecasting results show that the SSE (sum square error), RMSE (root mean square error) are 3.38 and 0.9587, respectively. The forecasting values are close to the actual value. It is indicated that the CS-combined model has better forecasting performance, which has high popularization and application in forecasting the tuberculosis prevalence rate. It can provide a reference basis for the prevention and control measures of TB in the world.
Appendix C (Figure A2) plots the fitting and forecasting curves and presents related regression equations and goodness-of-fit for the upper-middle income group. From Appendix C (Figure A2), it can be concluded that the estimated fitting equations are able to fit the dataset quite well; the adjusted R-squares of the six regression models all being above 0.99. Appendix C (Figure A2) demonstrated that the sum square error, root mean square error, R-square, and adj R-square of the CS-combined forecasting model established by the upper-middle income group tuberculosis prevalence rate from 2000 to 2012 were 5.35, 0.5972, 0.9968, and 0.9966, respectively. This indicates that the forecasting efficiency of the combined model is better than the other model, which can achieve higher forecasting requirements and be used for extrapolation forecasting. The forecasting can help provide reference for the formulation of tuberculosis prevalence rate control measures in upper-middle income group.
The related fitting and forecasting curves for the lower-middle income group are drawn in Appendix C (Figure A3), which demonstrates that all six regression models fit the dataset very well, with adjusted R-square values greater than 0.99. As indicated in Appendix C (Figure A3), the forecasting results of tuberculosis prevalence rate for lower-middle income group from 2013 to 2016 was 258.3/100,000; 252.6/100,000; 246.9/100,000; and 241.2/100,000, showing a downward trend year by year. The forecasting results of CS-combined showed that sum square error is 1.957, and root mean square error is 0.6651. The CS-combined model fitting accuracy criteria (R-square) indicated that the fitting accuracy of CS-combined model is 0.9998, and the fitting curve almost coincides with the actual tuberculosis prevalence rate curve. The fitting effect is better than the other models and can be used for forecasting the lower-middle income group tuberculosis prevalence rate.
The low income group with fitting and forecasting curves is plotted in Appendix C (Figure A4). According to Appendix C (Figure A4), the individual regression models all have remarkable goodness-of-fit with adjusted R-square values greater than 0.99. Appendix C (Figure A4) shows that the CS-combined model is used to fit tuberculosis prevalence rate time series for low income group during 2000–2012. The data of tuberculosis prevalence rate from 2013 to 2016 are forecasted by CS-combined model. The fitting value and forecasting value of the CS-combined model for 2000–2016 are basically the same as the actual tuberculosis prevalence rate, which is very similar to the actual value, and shows that the fitting and forecasting results are better than individual regression models.
3.3. Forecasting Results of Individual and Combined Models
In this section, forecasting results of both individual and combined methods are presented. The real values and forecasting values for the four different income groups from 2013 to 2016, generated by all seven forecasting models, are listed in Appendix B.
From Table 5, it can be concluded that the absolute values of the differences between the real values and the forecasting values, by means of the combined forecasting model, are no greater than four. Moreover, one-third of the twelve forecasting values derived from the proposed combination forecasting model are exactly equal to their real values. Thus, related analysis sufficiently reflects the superiority of the proposed combination forecasting model based on artificial intelligence optimization.

Table 5.
Root mean square error (RMSE) and mean absolute percentage error (MAPE) values of forecasting models.
Figure 2 presents the stack bars of forecast errors, including MAPE and RMSE, of the seven forecasting models for the four income groups. Note that, in Figure 2, the MAPE value is represented as a percentage.
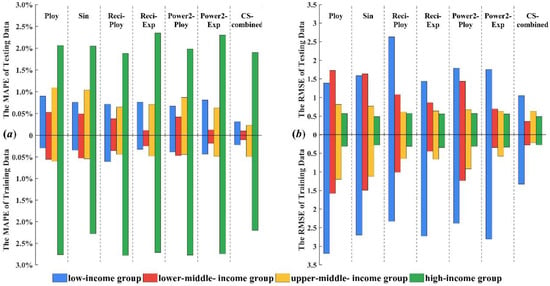
Figure 2.
Stack bars of forecast errors for the four income groups.
From Figure 2 and Table 5 we can see that the combined forecasting model can further improve forecast accuracy compared with individual regression models as evidenced by it always achieving the lowest forecast error. Based on the fitting results of six polynomial regression models from 2000 to 2012, the combined weight of each model is calculated according to the combined model theory. In order to get the optimal combined weight, cuckoo algorithm is used to optimize the combination weight and the forecasting results (2013–2016) of CS-combined model is calculated by the optimal combination weight.
The CS-combined model was established for the tuberculosis prevalence rate in high income population, which fitted the trend of the original tuberculosis prevalence rate. The forecasting accuracy of CS-combined model is higher than the other model and could be used for the forecasting tuberculosis epidemic trend in high income group. The forecasting results show that the incidence of tuberculosis in the high income group has been declining year by year since 2013 and the decline in 2013–2016 fluctuated between 2% and 4%. The tuberculosis prevalence rate in upper-middle income group in 2013–2016 showed a decreasing trend. For the forecasting results of upper-middle income group from 2013 to 2016, the RMSE and MAPE of CS-combined forecasting model were 0.6307 and 0.4883% respectively, which indicated that the CS-combined model has better forecasting performance and can meet higher forecasting requirements. From another point of view, the CS-combined model can be used for other diseases forecasting. For the lower-middle income group, the RMSE and MAPE of CS-combined model are 0.2113% and 0.2270%, respectively. The forecasting result of CS-combined model indicates that the tuberculosis prevalence rate from 2013 to 2016 is also declining. The forecasting results of tuberculosis prevalence rate for low income group from 2013 to 2016 showed that RMSE and MAPE were 0.3556% and 0.1028%, respectively, and the forecasting values were close to the actual values, which indicate that the CS-combined model has good forecasting performance and application in the tuberculosis prevalence rate forecasting. The forecasting results of the combined model could be used for the prevention and control of tuberculosis in low income group, and provide reference for formulating measures. The above analysis shows that global tuberculosis control strategies and measures have obtained significant achievements, which effectively curb the trend of tuberculosis prevalence rate.
Remark: The CS-combined model proposed in this paper can improve the forecasting accuracy, which combines the advantages of a variety of models and overcomes the influence of the characteristics of the tuberculosis prevalence rate time series on the forecasting results, such as fluctuating trend, small sample, randomness, and non-linearity. Therefore, the combination model in the forecasting and analysis of tuberculosis prevalence rate trend shows good forecasting performance. Therefore, infectious disease control has great significance.
3.4. Analysis of the Performance of Each Model
To further estimate and analyze the performance of the proposed combined tuberculosis prevalence rate forecasting model, the forecasting availability [40] and the DM (Diebold–Mariano) test [44], which evaluate the forecasting performance, are discussed in this part.
- (1)
- Table 6 shows the results of the DM test. We can reject the null hypothesis and it is deemed that the difference between the prediction abilities of two models is significant. The significance level for a study is chosen before data collection, and typically set to 1%, 5%, 10% [45,46]. The corresponding significance level is as follows:
 Table 6. Diebold–Mariano (DM) test of five different models for four different income groups.
Table 6. Diebold–Mariano (DM) test of five different models for four different income groups.- (a)
- If |DM| > 1.65 the null hypothesis is rejected at a 10% level, otherwise, if |DM| ≤ 1.65 we accept the null hypothesis.
- (b)
- If |DM| > 1.96 the null hypothesis is rejected at a 5% level, otherwise, if |DM| ≤ 1.96 we accept the null hypothesis.
- (c)
- If |DM| > 2.58 the null hypothesis is rejected at a 1% level, otherwise, if |DM| ≤ 2.58 we accept the null hypothesis.
For example, the results of low income group indicate that the combined model is different than Reci-ploy2 at the 10% significance level for training process, for the testing process, the |DM| value of Reci-ploy2 is 2.146856 at the 5% significance level, and the |DM| value of Ploy2, Sin2, Reci-exp2, Power2-ploy2, and Power2-Exp2 are 1.809601, 1.695902, 1.642031, 1.487737, and 1.524198 at the 10% significance level in tuberculosis prevalence rate forecasting. The upper limits at the different significance levels are smaller than the DM statistics in four income groups in tuberculosis prevalence rates. The combined model successfully overcomes some limitations of the individual forecasting models and effectively improves the forecasting accuracy. These results indicate that the proposed combined model is more valid and significantly superior to the other models. Thus, it is obvious that the proposed combined model is superior to the other six individual regression models. Accordingly, the proposed combined forecasting model can satisfactorily approximate the observed tuberculosis prevalence rate.
- (2)
- Table 7 indicates that the first-order and second-order forecasting availabilities offered by the proposed combined model outperform six individual regression models for the four income groups in tuberculosis prevalence rate forecasting. For example, for the low income group, the first-order forecasting availabilities offered by each forecasting model are 0.998405, 0.998663, 0.99874, 0.998651, 0.998815, 0.998572, and 0.999445, respectively, while their second-order values are 0.998403, 0.998662, 0.99874, 0.99865, 0.998814, 0.998571, and 0.999445, respectively.
 Table 7. Forecasting availability of five different forecasting models for four different income group.
Table 7. Forecasting availability of five different forecasting models for four different income group.
Remark: The results indicate that the proposed combined model is more valid and significantly superior to the other models. Accordingly, the proposed combined forecasting model can satisfactorily approximate the observed tuberculosis prevalence rate.
4. Conclusions
Concerning the association of income status and prevalence rate, a non-parametric Kruskal–Wallis test is performed, and the matrix derived from the test demonstrates that there are significant differences in tuberculosis prevalence rates among pairwise income groups, except between the lower-middle income and the low income group.
In addition, individual regression models are constructed to fit the tuberculosis prevalence rates from 1999 to 2012 for the four income groups. The quadratic polynomial model, the two-term exponential model, the sum-of-sines model, and the Gaussian model, are repeatedly used to forecast the tuberculosis prevalence rates from 2013 to 2016, with two types of variable transformations: taking reciprocals and base-2 logarithms. All selected individual regression models have satisfactory goodness-of-fit with adjusted R-squares all greater than 0.96. Combined forecasting models are proposed based on six individual regression models, and the weights are optimized by the cuckoo search algorithm, which is based on machine learning. From the extensive simulation results, it can be concluded that for each of the four income groups, the proposed combination forecasting models based on artificial intelligence optimization always provide better forecast accuracy than the individual regression models. As a result, these findings provide substantial information about the effectiveness and stability of the proposed combination forecasting model in the forecasting of hierarchical tuberculosis prevalence rates.
Future healthcare is research on the interaction between patient-centered healthcare and all pillar industries, which uses data science to store, capture, and mine the relationship between medical data and patients. This is, in fact, a new era of radical innovation based on big data and data analysis applications, capable of exploiting leading-edge approaches in data analysis and data mining, which include the idea that the analysis of big data is conducted and designed to better understand healthcare, analyses on healthcare data, and deal with various social issues in the adoption of telematics in medicine and healthcare. In this paper, we mainly focus on analysis and forecasting data of tuberculosis prevalence rate. Through repeated analysis of tuberculosis data, combined with the data of tuberculosis prevalence rates and professional literature, a hybrid combined forecasting model is proposed, verified repeatedly and, finally, the trend of prevalence rates of intelligent medical products.
Based on these developments, this paper contributes significantly in the body of data of tuberculosis prevalence rates, and publishes a combined forecasting model and data analysis methodologies in the field of tuberculosis prevalence rates.
The following points are a summary of the main contents of this paper:
- (1)
- the KW test is used to validate the different among four kinds of income group;
- (2)
- different forecasting models are set up for each income group;
- (3)
- a CS-combined model is proposed in this paper, which incorporates the advantages of each forecasting model.
The numerical results show that the CS-combined model is effective in forecasting the tuberculosis prevalence rate, and the forecasting results have important guiding significance for tuberculosis prevention and control.
Author Contributions
J.W. carried on the validation and visualization of experiment results; C.W. carried on programming and writing of the whole manuscript; J.W. and Y.Z. provided the overall guide of conceptualization and methodology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ANOVA | analysis of variance |
| A-R2 | adjusted R-square value |
| CDF | cumulative distribution function |
| CS | cuckoo search |
| CS-Combined | combination model with cuckoo search algorithm |
| DM | Diebold–Mariano |
| DOTS | directly observed treatment, short-course |
| GNI | gross national income |
| HIV | human immunodeficiency virus |
| KW method | Kruskal–Wallis method |
| MAPE | mean absolute percentage error |
| MDGs | millennium development goals |
| Poly2 | quadratic polynomial model |
| Poly3 | cubic polynomial model |
| Power2-exp2 | base-2 logarithm transformation and two-term exponential model |
| Power2-gauss1 | base-2 logarithm transformation and one-term Gaussian model |
| Power2-ploy2 | base-2 logarithm transformation and quadratic polynomial model |
| RBFNN | radical basis function neural network |
| Reci-exp2 | reciprocal transformation and two-term exponential model |
| Reci-poly2 | reciprocal transformation and quadratic polynomial model |
| RMSE | root mean square error |
| SCDF | empirical cumulative distribution function |
| Sin1 | single sine model |
| Sin2 | sum of two-sines model |
| TB | tuberculosis |
| WHO | World Health Organization |
Appendix A
| Algorithm A1 The shortened process of the cuckoo search algorithm. |
| Algorithm: CS. |
| Input: |
| —A sequence of training data. |
| Output: |
| —The returned value with the best fitness in the search domain. |
| Parameters: |
| n—Number of nests. |
| —Discovery rate of alien eggs/solutions. |
| Ub—Upper bounds of the search domain. |
| Lb—Lower bounds of the search domain. |
| —Objective function. |
| MaxGeneration—Maximum number of generations. |
| 1: /* Generate an initial population of n host nests */ |
| */2: FOR EACHi: DO |
| 3: |
| 4: END FOR |
| 5: = 1; |
| 6: WHILE (iter<MaxGeneration) DO |
| 7: /* Get a cuckoo randomly (sayi) by Lévy flights. */ |
| 8: /* Evaluate its quality/fitness . */ |
| 9: /* Choose a nest among n (say j) randomly. */ |
| 10: IF THEN1 |
| 11: /* Replace j by the new solution. */ |
| 12: END IF |
| 13: /* Abandon a fraction () of the worse nests. */ |
| 14: /* Build new ones at new locations via Lévy flights. */ |
| 15: /* Keep the best solutions. */ |
| 16: /* Rank the solutions and find the current best. */ |
| 17: iter = iter + 1; |
| 18: END WHILE |
| 19: RETURN |
Appendix B

Table A1.
Real values and forecasting values of the seven models for the four income groups.
Table A1.
Real values and forecasting values of the seven models for the four income groups.
| high income group | Year | Real Value | Ploy3 | Sin2 | Reci-ploy2 | Reci-exp2 | Power2-ploy2 | Power2-Exp2 | CS-Combined |
| 2013 | 13.4 | 13.7982 | 13.7975 | 13.7675 | 13.8679 | 13.7832 | 13.8473 | 13.7744 | |
| 2014 | 13.4 | 13.3229 | 13.1230 | 13.3254 | 13.3623 | 13.3213 | 13.3441 | 13.1150 | |
| 2015 | 12.4 | 12.8430 | 12.6257 | 12.8926 | 12.8163 | 12.8616 | 12.8080 | 12.6540 | |
| 2016 | 12.5 | 12.3586 | 12.3331 | 12.4701 | 12.2187 | 12.4049 | 12.2313 | 12.4212 | |
| upper-middle income group | Year | Real value | Poly2 | Sin1 | Reci-ploy2 | Reci-exp2 | Power2-ploy2 | Power2-Exp2 | CS-combined |
| 2013 | 95 | 96.2026 | 96.1404 | 95.6352 | 95.7721 | 95.9307 | 95.6058 | 95.2133 | |
| 2014 | 92 | 92.7685 | 92.7337 | 92.4706 | 92.6712 | 92.6135 | 92.5328 | 92.1231 | |
| 2015 | 89 | 89.0584 | 89.0884 | 89.2538 | 89.5291 | 89.1424 | 89.4174 | 89.2615 | |
| 2016 | 87 | 85.0723 | 85.2137 | 86.0167 | 86.3721 | 85.5437 | 86.2845 | 86.7775 | |
| lower-middle income group | Year | Real value | Poly2 | Sin1 | Reci-ploy2 | Reci-exp2 | Power2-ploy2 | Power2-Exp2 | CS-combined |
| 2013 | 258 | 259.6904 | 259.6018 | 258.8620 | 258.8623 | 259.3924 | 258.4081 | 258.3227 | |
| 2014 | 253 | 253.0490 | 252.9959 | 252.5304 | 252.9670 | 252.9045 | 252.5490 | 252.6082 | |
| 2015 | 247 | 245.9936 | 246.0191 | 246.0649 | 247.0764 | 246.1485 | 246.6981 | 246.8826 | |
| 2016 | 241 | 238.5242 | 238.6817 | 239.5091 | 241.2176 | 239.1550 | 240.8832 | 241.1815 | |
| low income group | Year | Real value | Poly2 | Sin2 | Reci-ploy2 | Reci-exp2 | Power2-ploy2 | Power2-Exp2 | CS-combined |
| 2013 | 297 | 302.1288 | 301.5349 | 300.8472 | 301.6497 | 301.2547 | 301.9486 | 299.5565 | |
| 2014 | 288 | 289.4075 | 289.0711 | 289.3481 | 289.1197 | 289.0349 | 289.4911 | 287.4155 | |
| 2015 | 276 | 276.1888 | 276.3133 | 278.0348 | 276.3462 | 276.6887 | 276.8117 | 276.0947 | |
| 2016 | 266 | 262.4727 | 263.2969 | 266.9637 | 263.4011 | 264.2757 | 263.9669 | 265.5636 |
Appendix C
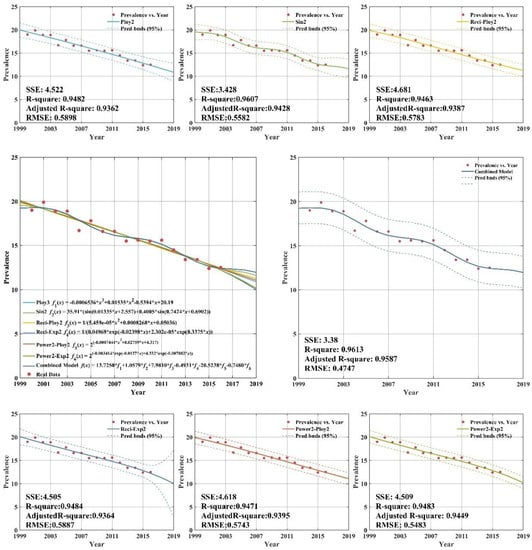
Figure A1.
Fitting and forecasting curves for the high income group.
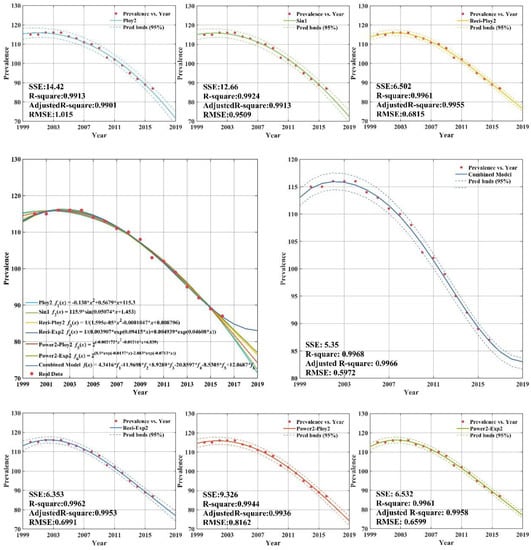
Figure A2.
Fitting curves and forecasting for the upper-middle income group.
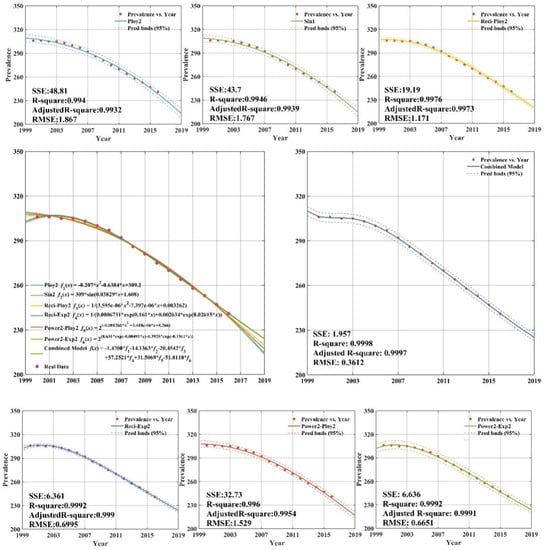
Figure A3.
Fitting and forecasting curves for the lower-middle income group.
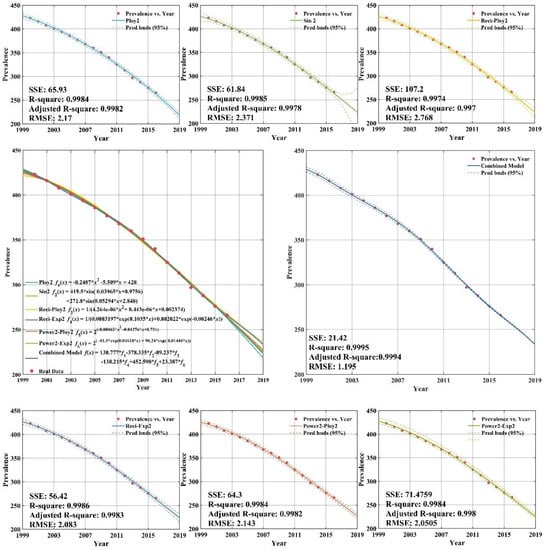
Figure A4.
Fitting and forecasting curves for the low income group.
References
- Guernier, V.; Guegan, J.F.; Deparis, X. An evaluation of the actual incidence of tuberculosis in French Guiana using a capture-recapture model. Microbes Infect. 2006, 8, 721–727. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Tuberculosis Report 2013; World Health Organization: Geneva, Switzerland, 2013. [Google Scholar]
- Bhunu, C.P.; Mushayabasa, S.; Smith, R.J. Assessing the effects of poverty in tuberculosis transmission dynamics. Appl. Math. Model. 2012, 36, 4173–4185. [Google Scholar] [CrossRef]
- Neville, K.; Bromberg, A.; Bromberg, R.; Bank, S.; Hanna, B.A.; Ross, W.N. The third epidemic: Multi-drug resistant tuberculosis. Chest 1994, 105, 45–48. [Google Scholar] [CrossRef] [PubMed]
- Lambregts-van Weezenbeek, C.S.; Veen, J. Control of drug-resistant tuberculosis. Tubercle Lung Dis. 1995, 76, 455–459. [Google Scholar] [CrossRef]
- Yew, W.W.; Chau, C.H. Drug-resistant tuberculosis in the 1990s. Eur. Respir. J. 1995, 8, 1184–1192. [Google Scholar] [CrossRef] [PubMed]
- World Health Organisation. Anti-Tuberculosis Drug Resistance in the World: The WHO/IUTLD Global Project on Anti-Tuberculosis Drug Resistance Surveillance 1994–1997; WHO: Geneva, Switzerland, 1997. [Google Scholar]
- Farmer, P.; Kim, J.Y. Community based approaches to the control of multidrug resistant tuberculosis: Introducing ‘‘DOTS-plus’’. Br. Med. J. 1998, 317, 671–674. [Google Scholar] [CrossRef]
- Dye, C.; Maher, D.; Weil, D.; Espinal, M.; Raviglione, M. Targets for global tuberculosis control. Int. J. Tuberc. Lung Dis. 2006, 10, 460–462. [Google Scholar] [PubMed]
- Lytras, M.D.; Visvizi, A. Who Uses Smart City Services and What to Make of It: Toward Interdisciplinary Smart Cities Research. Sustainability 2018, 10, 1998. [Google Scholar] [CrossRef]
- Spruit, M.; Lytras, M. Applied Data Science in Patient-centric Healthcare. Telemat. Inf. 2018, 35, 643–653. [Google Scholar] [CrossRef]
- Anna, V.; Miltiadis, D.L. Rescaling and refocusing smart cities research: From mega cities to smart villages. J. Sci. Technol. Policy Manag. 2018, 9, 134–145. [Google Scholar]
- WHO. Global Tuberculosis Control: Surveillance, Planning, Financing; World Health Organization: Geneva, Switzerland, 2007. [Google Scholar]
- WHO. Forty-Fourth World Health Assembly, Resolutions and Decisions; World Health Organization: Geneva, Switzerland, 1991. [Google Scholar]
- Dye, C.; Scheele, S.; Dolin, P.; Pathania, V.; Raviglione, M.C. Global burden of tuberculosis: Estimated incidence, prevalence, and mortality by country. J. Am. Med. Assoc. 1999, 282, 677–686. [Google Scholar] [CrossRef]
- Dye, C.; Bassili, A.; Bierrenbach, A.L. Measuring tuberculosis burden, trends, and the impact of control programmes. Lancet Infect. Dis. 2008, 8, 233–243. [Google Scholar] [CrossRef]
- Dye, C. Tuberculosis 2000–2010: Control, but not elimination. Int. J. Tuberc. Lung Dis. 2000, 4, S146–S152. [Google Scholar] [PubMed]
- Dye, C.; Floyd, K. Disease Control Priorities in Developing Countries, 2nd ed.; Oxford University Press: New York, NY, USA, 2006; pp. 289–312. [Google Scholar]
- Yu, C.Y.; Li, X.X.; Yang, H.; Li, Y.H.; Xue, W.W.; Chen, Y.Z.; Tao, L.; Zhu, F. Assessing the Performances of Protein Function Prediction Algorithms from the Perspectives of Identification Accuracy and False Discovery Rate. Int. J. Mol. Sci. 2018, 19, 183. [Google Scholar] [CrossRef] [PubMed]
- Temesgen, D.A.; Kassa, S.M. Optimal Control Strategy for TB-HIV/AIDS Co-Infection Model in the Presence of Behaviour Modification. Processes 2018, 6. [Google Scholar] [CrossRef]
- Yang, T.; Liu, S.; Liu, W.; Guo, J.; Wang, P. Noise Enhanced Signal Detection of Variable Detectors under Certain Constraints. Entropy 2018, 20, 470. [Google Scholar] [CrossRef]
- Livieris, I.; Kanavos, A.; Tampakas, V.; Pintelas, P. An Ensemble SSL Algorithm for Efficient Chest X-ray Image Classification. J. Imaging 2018, 4, 95. [Google Scholar] [CrossRef]
- Rasanathan, K.; SivasankaraKurup, A.; Jaramillo, E.; Lonnroth, K. The social determinants of health: Key to global tuberculosis control. Int. J. Tuberc. Lung Dis. 2011, 15, S30–S36. [Google Scholar] [CrossRef] [PubMed]
- Lytras, M.D.; Raghavan, V.; Damiani, E. Big data and data analytics research: From metaphors to value space for collective wisdom in human decision making and smart machines. Int. J. Semant. Web Inf. Syst. 2017, 13, 1–10. [Google Scholar] [CrossRef]
- Harling, G.; Castro, M.C. A spatial analysis of social and economic determinants of tuberculosis in Brazil. Health Place 2014, 25, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Menzies, N.A.; Wolf, E.; Connors, D. Progression from latent infection to active disease in dynamic tuberculosis transmission models: A systematic review of the validity of modelling assumptions. Lancet Infect. Dis. 2018. [Google Scholar] [CrossRef]
- Cohen, T.; Colijn, C.; Finklea, B.; Murray, M. Exogenous re-infection and the dynamics of tuberculosis epidemics: Local effects in a network model of transmission. J. R. Soc. Interface 2007, 4, 523–531. [Google Scholar] [CrossRef] [PubMed]
- Brookspollock, E.; Cohen, T.; Murray, M. The impact of realistic age structure in simple models of tuberculosis transmission. PLoS ONE 2010, 5, e8479. [Google Scholar]
- Wearing, H.J.; Rohani, P.; Keeling, M.J. Appropriate models for the management of infectious diseases. PLoS Med. 2005, 2, e174. [Google Scholar]
- Klotz, A.; Harouna, A.; Smith, A.F. Forecast analysis of the incidence of tuberculosis in the province of Quebec. BMC Public Health 2013, 13, 400. [Google Scholar]
- Feng, Z.; Huang, W.; Castillo-Chavez, C. On the Role of Variable Latent Periods in Mathematical Models for Tuberculosis. J. Dyn. Differ. Equ. 2001, 13, 425–452. [Google Scholar] [CrossRef]
- Colijn, C.; Cohen, T.; Murray, M. Emergent heterogeneity in declining tuberculosis epidemics. J. Theor. Biol. 2007, 247, 765–774. [Google Scholar] [PubMed]
- Ozcaglar, C.; Shabbeer, A.; Vandenberg, S.L. Epidemiological models of Mycobacterium tuberculosis complex infections. Math. Biosci. 2012, 236, 77–96. [Google Scholar] [CrossRef] [PubMed]
- White, P.J.; Garnett, G.P. Mathematical modelling of the epidemiology of tuberculosis. Adv. Exp. Med. Biol. 2010, 673, 127–140. [Google Scholar] [PubMed]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hajek, J.; Sidak, Z.; Sen, P.K. Theory of Rank Tests; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Adelantado, F.; Verikoukis, C. Detection of malicious users in cognitive radio ad hoc networks: A non-parametric statistical approach. Ad Hoc Netw. 2013, 11, 2367–2380. [Google Scholar] [CrossRef]
- Carpenter, R.G. Principles and Procedures of Statistics with Special Reference to the Biological Sciences. Ann. N. Y. Acad. Sci. 1960, 682, 283–295. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering optimization by Cuckoo Search. Int. J. Math. Model Numer. Optim. 2010, 1, 330–343. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Levy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Cantwell, D. Using Radial Basis Function Networks and Hyper-Cubes for Excursion Classification in Semi-Conductor Processing Equipment. U.S. Patent US9262726, 17 January 2016. [Google Scholar]
- Incidence Data by World Bank Income Groups (Last updated: 2017-10-07). Available online: http://apps.who.int/gho/data/view.main.57038ALL?lang=en (accessed on 17 September 2018).
- Xiao, L.; Shao, W.; Wang, C.; Zhang, K.; Lu, H. Research and application of a hybrid model based on multi-objective optimization for electrical load forecasting. Appl. Energy 2016, 180, 213–233. [Google Scholar] [CrossRef]
- Craparo, R.M. Significance level. In Encyclopedia of Measurement and Statistics; Salkind, N.J., Ed.; SAGE Publications: Thousand Oaks, CA, USA, 2007; pp. 889–891. ISBN 1-412-91611-9. [Google Scholar]
- Sproull, N.L. Hypothesis testing. In Handbook of Research Methods: A Guide for Practitioners and Students in the Social Science, 2nd ed.; Scarecrow Press, Inc.: Lanham, MD, USA, 2002; pp. 49–64. ISBN 0-810-84486-9. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).