Abstract
In this work, fully-resolved rotor-fuselage interactional aerodynamics is used as the forcing term in a model based on the Euler-Bernoulli equation, aiming to simulate helicopter tail-boom vibration. The model is based on linear beam analysis and captures the effect of the blade-passing as well as the effect of the changing force direction on the boom. The Computational Fluid Dynamics (CFD) results were obtained using a well-validated helicopter simulation tool. Results for the tail-boom vibration are not validated due to lack of experimental data, but were obtained using an established analytical approach and serve to demonstrate the strong effect of aerodynamics on tail-boom aeroelastic behavior.
1. Introduction
Interactional effects between the main rotor and the fuselage are commonplace in rotorcraft. In particular, at low advance ratios of the main rotor, its wake can interact with the main fuselage and the empennage. The higher the helicopter weight, the stronger the rotor wake, and therefore interactional aerodynamics can be significant. Leishman [1,2] carried out experiments on the topic and there are several numerical studies too. Nevertheless, amongst the current research reports there is little information on the effect of these aerodynamic interactions on the vibration and deformation of the tail-boom structure. This interaction is expected to be significant if a long tail-boom is used or if the employed structure is light with substantial weight added at the end of the boom due to the presence of the tail rotor, its rotor-head, the intermediate gear-box, fin and horizontal stabilizer. One can expect that the tail boom loads are not high, but estimating the vibration level is important for design and fatigue analysis of the boom. Therefore, this work aims to investigate the effect of unsteady aerodynamics on the vibration and deformation of a helicopter tail-boom. In contrast to earlier works [3] where the rotor aerodynamics is represented by blade-element methods, Computational Fluid Dynamics (CFD) is used here to compute the unsteady flow, and then the aerodynamic loads are used in conjunction with a simple structural model. The use of CFD allows for the details of the unsteady flow spectrum to be captured and preserved in the flow around the tail-boom.
In terms of modeling the structure of the tail-boom, it was decided here to keep the model simple, based on the Euler-Bernoulli equation for coupling with CFD via embedding the model in the framework of a CFD solver. The Euler-Bernoulli equation for various end conditions allows for analytical or approximate solution of the natural and forced vibrations of uniform and non-uniform beams [4,5,6,7,8,9].
Detailed empennage models with structural optimization were considered in [10], where complete Finite Element Method (FEM) models are demonstrated for computing the natural mode shapes and frequencies of the structure. In [11], maintaining the non-dimensional amplitude of the forces against several lifting conditions were analyzed with the FEM approach. Nevertheless, these works did not proceed to compute the effects of wake aerodynamics on the tail boom.
To determine the transverse vibrations of an Euler-Bernoulli uniform beam in the present study, an approximate analytical approach is used, based on the approach of [12]. According to [12], a solution of the Euler-Bernoulli can be presented as a series of spatial and time coordinates. The forced vibrations are computed using an approximation of the tail boom load obtained from CFD calculation of rotor-fuselage configuration.
The selected test case is motivated by the Ansat light helicopter (Kazan Helicopters Public Stock Company, Kazan, Russia), although the results obtained serve to demonstrate the employed method and correspond to a generic interaction case. The aerodynamic predictions of the helicopter fuselage aerodynamics are validated against wind tunnel tests.
2. Fuselage Aerodynamics
The first step of this work is the simulation of the flow around the isolated “clean” fuselage. The Helicopter Multi-Block (HMB) solver is established in the field of rotorcraft aerodynamics and it is based on the discretization of the Unsteady Reynolds Averaged Navier-Stokes (URANS) equation on multi-block structured grids. The solver allows for sliding and overset grids and has a variety of solution methods for flows at low or very high Mach number. A mesh deformation method based on a combination of the Trans-Finite Interpolation and the Spring-Analogy method allows for aero-elastic cases to be studied. Also, a sliding-mesh method is implemented so that test cases with relative motions of different parts of the geometry can be modeled. The HMB method has been validated for a range of rotorcraft applications [13,14,15,16,17,18] and has demonstrated good accuracy and efficiency for very demanding flows. The parallel implementation makes use of the Message Passing Interface library for inter-processor communication and of parallel I/O for saving and reading data from out-of-core storage. The HMB method has so far been used for the analysis of rotors, wind turbines, propellers and cavities and has demonstrated good scalability for up to 10 k cores. This was of course achieved using a fine mesh. A summary of the method in HMB is presented in reference [13]. The code can also use actuator disks or virtual blade models to simulate the effect of the main rotor on the fuselage.
Although the solver is able to use Detached-Eddy Simulation (DES) and Large-Eddy Simulation (LES) models, the URANS equations were used in this work. This was justified by the rather limited regions of flow separation encountered during computations. In general, different models of turbulence, including the Spalart-Allmaras one-equation model, the k-ω (SST) 2-equation model and transition models of turbulence are available in HMB solver.
The geometry of the isolated fuselage corresponds to an early Ansat-P model of the Ansat helicopter produced by the Kazan Helicopters. The wind tunnel model (Figure 1a) was manufactured based on the computer model, used for CFD modeling. The aerodynamic analysis of this model was considered in references [19,20], and were studied using the open test section (2.25 m diameter) closed circuit, low speed, wind tunnel T-1K of the KNRTU-KAI Aerohydrodynamics department.
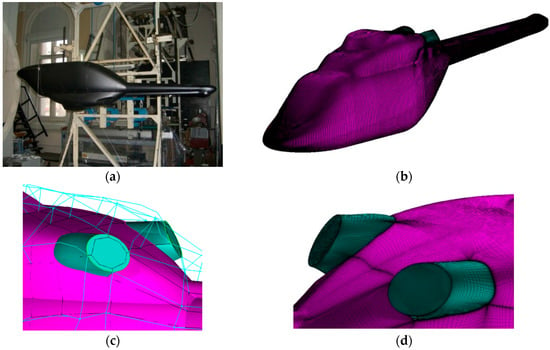
Figure 1.
(a) Ansat-P fuselage model in the T-1K wind tunnel of KNRTU-KAI, (b) surface grid for fuselage, (c) multi-block topology, and (d) surface mesh near exhausts.
For the grid around the Ansat-P fuselage, the (ICEM)-hexa software of ANSYSTM mesh generation tool has been used. The length of the wind tunnel model (Figure 1a) was = 1.8 m. The computational grid for this model contained 964 blocks and 13.5 × 106 cells. The surface grid and grid details are shown in Figure 1b–d.
The topology and surface grid near the area of the engine exhausts is also presented on the same figure. Care has been taken to represent the geometry of the wind tunnel models as accurately as possible, regardless of the minor edits that the laser-scans of the models needed in order to be converted to air-tight surfaces suitable for CFD.
In terms of turbulence modeling, the k-ω model [21] was employed. Experimental and CFD analyses were conducted at Reynolds number of 4.4 × 106 and Mach number of 0.1.
Figure 2 suggests a good agreement between CFD and experimental results for the lift () and drag () coefficients in the considered range of pitch angles.
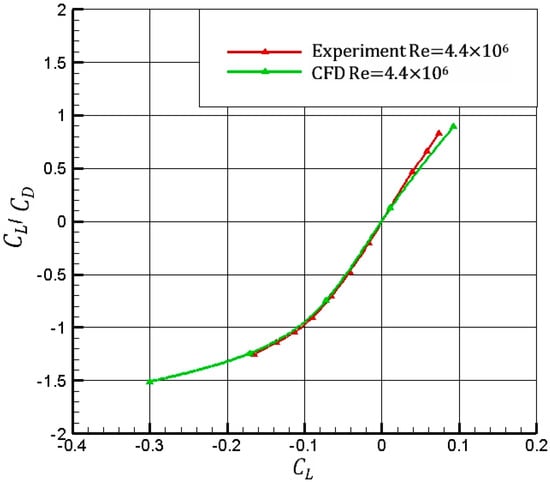
Figure 2.
Computational Fluid Dynamics (CFD) and experimental drag coefficients vs. lift coefficient for Ansat-P model.
More detailed information about grid sensitivity studies and the HMB code validation vs. experimental data is presented in [14,19,20].
The next step was the simulation of the flow around the rotor model in hover [22]. The CFD code validation was performed against the experimental data of Caradonna and Tung [23] that are extensively used within the helicopter community. Figure 3 shows the satisfactory agreement of CFD results for the pressure coefficient () distribution with experimental data ( 0.612, collective pitch of 8 degrees) at two values of the rotor dimensionless radius .
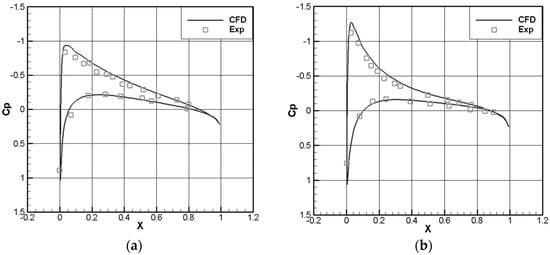
Figure 3.
Pressure coefficients along the rotor section: (a) = 0.68, (b) = 0.96.
3. Rotor-Fuselage Computations
Rotor-fuselage flow simulations are also considered in this paper. For the simulation of the rotor over the fuselage, a sliding surface is constructed that divides the computational domain into two parts (Figure 4). The movable upper part corresponds to the rotor, that includes four-blades made of NACA 23012 airfoils with the root cut-off r = 0.2R, where R is the radius of the rotor. A simplified elliptical hub is used. The geometry of the upper part is inclined to allow forward tilting of the rotor.
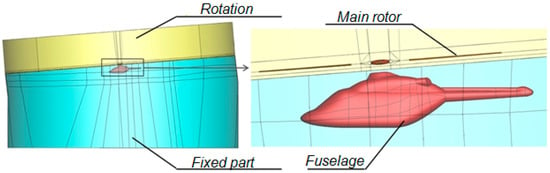
Figure 4.
Far and near view of the computation domain.
The CFD grids are constructed using the ICEM-hexa software of ANSYSTM. The topology of the blocks and the parameters of the computational grids correspond to what was used for the isolated fuselage of the helicopter. The fixed part of the mesh contains 688 blocks and 9 × cells.
The computational grid of the rotor was assembled in several stages. At the first stage, the computational grid for a quarter of the computational domain (for one blade) was generated, as shown in Figure 5. The computational grid for each blade comprises 144 blocks and 6 × cells.
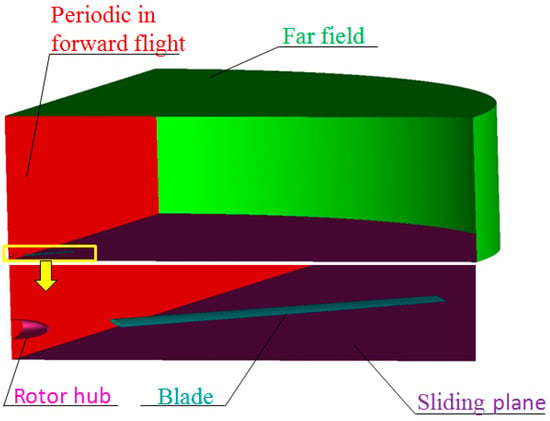
Figure 5.
Sliding plane arrangement near the main rotor hub.
The boundary conditions are shown in Figure 5. Only a single blade was meshed, but using periodic conditions between blades allows for the full rotor to be considered by copying and rotating the mesh of a single blade around the azimuth (Figure 6). This method simplifies the process of constructing the computational grid for the main rotor and keeps constant the characteristics of the computational grid for each blade.
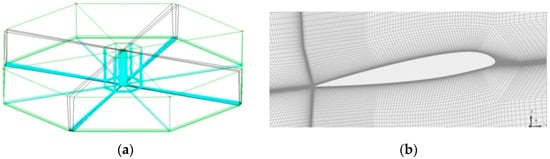
Figure 6.
Multi-block topology (a) and mesh section (b).
After assembling of all elements, the computational grid had 1144 blocks and 33 × 106 cells. The simulation concerns forward flight for a 1:6 scaled helicopter model, and all geometric and flight parameters are presented in Table 1.

Table 1.
Main rotor parameters.
The following assumptions were made:
- -
- Rigid blades;
- -
- No flapping motion of the blades, only pitch input is considered;
- -
- No lead-lag.
Changing the cyclic pitch of the rotor is achieved by deforming the computational grid. The employed method is described in [13].
The simulation was unsteady, and with a time step corresponding to 1 degree in rotor azimuth. An example of the surface pressure distribution at the azimuth of ψ = 80° is shown in Figure 7.
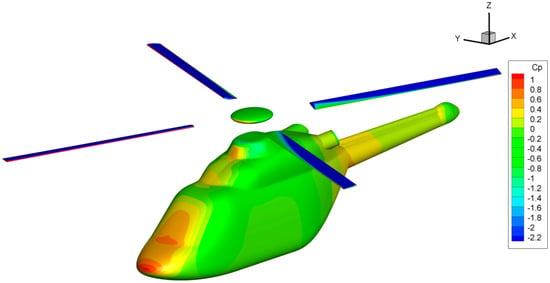
Figure 7.
Surface pressure coefficient on the fuselage and blades at the conditions of Table 1.
Analysis of the results was carried out using Tecplot 360™, and normal vectors to the surface of the body oriented towards the outside were computed.
Variation of the pressure distribution over the surface of the fuselage and the rotor blades leads to variable fuselage drag () and rotor thrust () coefficients, which are computed by:
where is the free stream dynamic pressure, is the dynamic pressure at the blade tip, is the reference fuselage area, is the drag force, and the rotor thrust. The oscillation amplitude values of the coefficient of drag of the fuselage are about 13% around the mean (Figure 8).
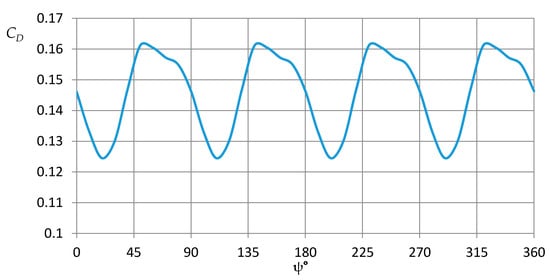
Figure 8.
Fuselage drag as function of the blade azimuth.
The average value of drag in the presence of a fuselage of the rotor is higher compared with the simulation results of an isolated flow fuselage. Increased drag of 46.6% is seen, which correlates with the results obtained by using a simplified actuator-disk model [24] (Δ = 45.6% at the value of thrust coefficient = 0.0128).
The value of the thrust coefficient also changes during the rotation of the rotor (Figure 9). The oscillation amplitude reaches 2.25% of the mean.
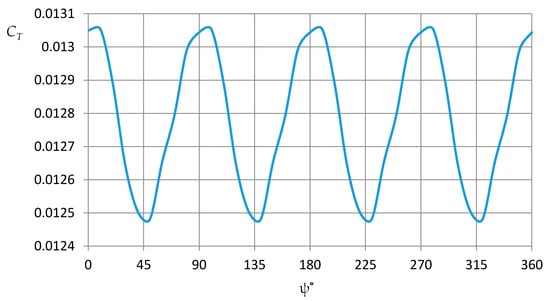
Figure 9.
Main rotor thrust as function of the blade azimuth.
The rotation of the rotor has a strong effect on the fuselage. Figure 10 presents diagrams of loading of the tail boom at different azimuthal positions of the rotor.
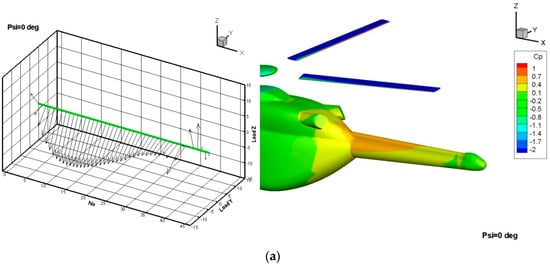
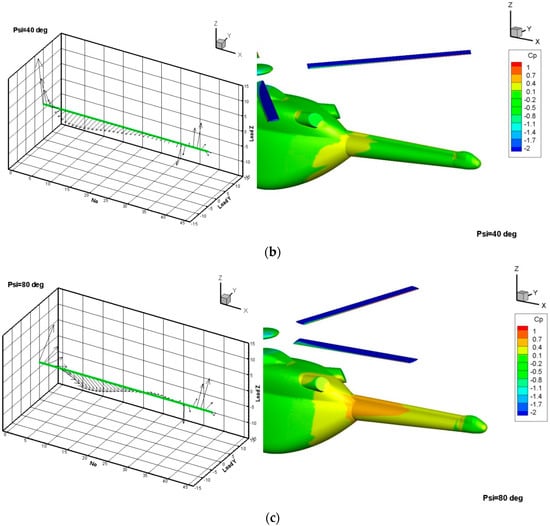
Figure 10.
Load Z and Load Y present sectional forces along the tail boom projected in the vertical (Z) and lateral directions for different azimuthal positions: (a) ψ = 0°, (b) ψ = 40°, (c) ψ = 80°.
The aerodynamic load acting on the tail boom is shown in Figure 11 in terms of vertical force coefficient that was computed according to the expression:
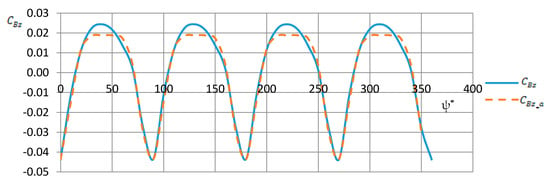
Figure 11.
Vertical aerodynamic load on the tail boom, as a function of the azimuth of the main rotor blades.
Figure 11 shows that the effect of the rotor on the tail boom is characterized by rapid loading changes. The main oscillation frequency corresponds to the blade passing frequency.
The variation of can be approximated by a function
where , , , rad (N = 4 is the number of blades). Using a harmonic function (cosine) in expression (2) captures the periodic character of the tail-boom load. The parameter allows for correction of the peak to peak amplitude and the parameters determine the shift of the function with respect to the azimuth axis. The parameters were fitted to ensure The function is shown in Figure 11 in comparison to the function .
4. Mathematical Model of Tail Boom Vibrations
The tail boom of the helicopter is susceptible to vibration. Several factors contribute to this; in particular, the impact of the main and tail rotor loads. An approximate analytical method for simulation of the tail boom vibrations is considered here.
The mathematical formulation of the problem is bound by the following limitations and assumptions: (1) The tail boom is considered to be of a constant diameter thin-walled cylindrical structure with continuously distributed mass (no concentrated mass points), so that the total mass of the beam is equal to the one of the light helicopter boom (but also adding the horizontal tail, transmission and other design elements); (2) The tail boom is rigidly fixed at the fuselage end and the other end is free; (3) The mathematical model of vibrations (vertically directed) without viscous damping is determined by the Euler-Bernoulli equation with one spatial coordinate and variable tail boom geometry along the tail boom span.
Under these assumptions, the equation of the tail boom deformation is described by equation [4,7,12]:
Here x is the longitudinal coordinate; t is the time coordinate; is the flexural rigidity (E is Young’s modulus, is a moment of inertia); is the transverse vertical deformation; is the mass per unit length. The normal (vertical) component of the force acting on the surface of the tail boom per unit length is given by
Here is the normal force coefficient; L is length of the beam. The boundary conditions for the Equation (3) can be written as
According to [12], the solution of Equation (3) with boundary conditions (5) can be written in the form
Here the functions and can be determined by using constraints of the physical and mathematical formulation of the vibration task: the function determines the natural and the function determines forced tail boom vibrations. Substitution of (6) in Equation (3) leads to the expression:
Here , .
From the last expression, a system of two equations can be obtained:
Boundary conditions for the Equation (8) can be written as
For Equation (9), the boundary conditions are taken in the form
The Equation (8) can be rewritten in a dimensionless form
with boundary conditions
Similarly, Equation (9) can be written as:
with boundary conditions
The dimensionless variables in (13) and (14) are determined by the expressions
where is a reference time. The right part of (13) according to (4) can be written as
Here is a normalized transversal load coefficient, and is a constant.
According to [4,7,12], the solution of Equation (11) can be presented in the form
where , are dimensionless functions. Substitution of (16) in (11) yields the system of equations
The coefficients are determined by the relations [4,7,12]:
where ,…
The solution of the system (17) with the boundary conditions of (12) can be written as
Here,
and
So, the solution of Equation (11) has the form [4,7,12]
Figure 12 shows the basic functions () for the simulated conditions. One can note that the shape of calculated functions corresponds to the reference data (see, for example [4]).
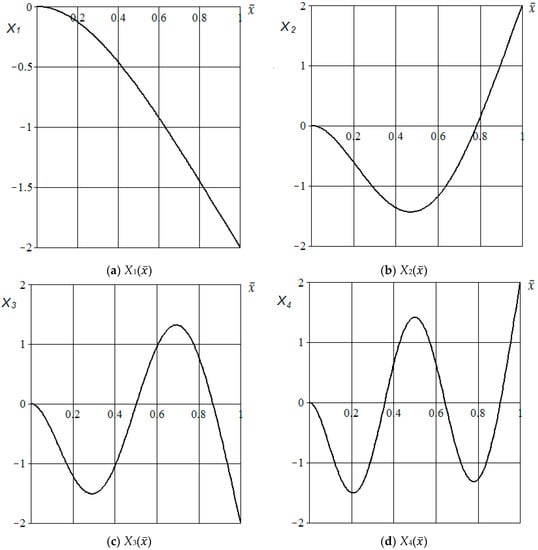
Figure 12.
The basic functions .
The solution of Equation (13) can be written as [12]
where the function is approximated by the series
Substituting (20) in (13) and after some transformations result in
that is a system of equations
with boundary conditions
The functions and are determined by the expressions:
Thus, based on the functions and the general solution of the Equation (3) can be presented in the form of (6), (16) and (20) with a finite number of terms of the series expansion.
From the solution above, it follows that, in this study, the normalized functions and determine the natural and forced vibrations, respectively, for the equivalent uniform beam.
5. Calculation of the Tail Boom Vibrations
The geometric parameters and physical tail boom material properties are presented in Table 2 and approximately correspond to parameters of a full scale light helicopter.

Table 2.
Tail boom parameters.
The formulation adopted in this paper does not account for a non-uniform tail boom surface. For this reason, computations of forced vibrations were conducted for several equivalent uniform tail booms with diameter and mass per unit length, obtained from:
where is a small parameter, kg/m is a mass of internal tail boom construction elements per unit length. Table 3 presents the values of the parameters, mass and geometry used for forced vibration simulations.

Table 3.
Equivalent mass and diameter of tail boom.
The beam moment of inertia is determined, taking into account properties of the stringers used typically for such beams. The moment of inertia of the stringers is determined by the expression:
so that the total moment of inertia of the tail boom is
Based on the results of the CFD simulation of the rotor-fuselage interaction, the normal force coefficient was determined in the form , where are trigonometric functions. From Figure 10, it follows that , , . The results of Figure 11 and the function (expression (2)) were used to determine the function . In this case, the function has to satisfy to the condition . So, an approximation of the function in (15) was taken here as
where Hz is the main rotor frequency, is the angular rotor frequency, and .
One should note here that, for the employed main rotor frequency of 6.023 Hz, the time step corresponding to 1 degree in rotor azimuth is s, that satisfies the condition . The peak value of the normal force coefficient for the considered simulation parameters corresponds to a peak vertical tail boom load of about 30 N per meter of tail boom length.
Using the basic functions , one can determine the function for the forced tail boom vibrations (analytical transformations and calculations were performed using Maple 17™ software).
One can note here that the behavior of the function is determined primarily by the first two components and The eigenfrequencies and depend on the geometry parameter . Nevertheless, in this work, all components , were used to determine . Thus, a general behavior of the function depends on the interaction of the eigen and forced vibrations. Figure 13 shows the functions and for the different values of parameter . The time behavior of the functions and is predominantly determined by the frequencies and respectively, and the amplitude of the total function depends on the mass and geometry data. For variant 4, the function demonstrates resonance due to the second blade passing harmonic 2Nf being equal to the second eigenfrequency and .
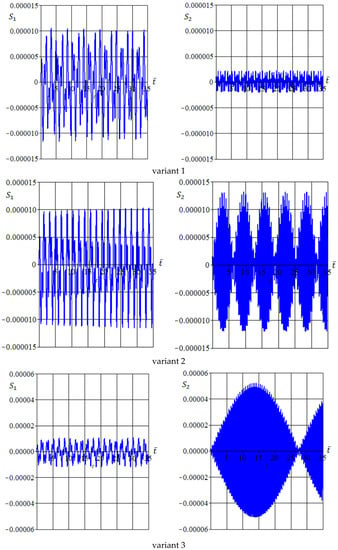
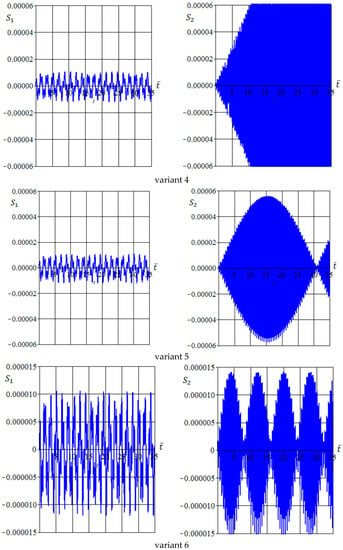
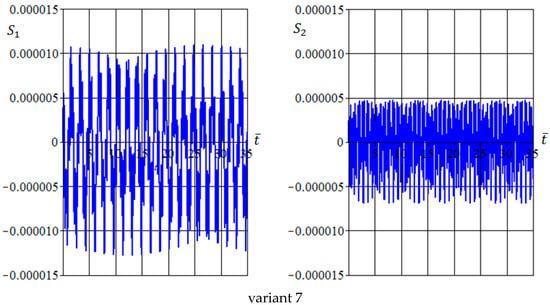
Figure 13.
Functions (left column) and (right column) for different values (variant numbers).
From Figure 13, it follows that, for variants 1 and 7, the amplitude of the forced tail boom oscillations is determined by the term and one can expect that the dominant frequency of oscillations corresponds to the eigenfrequency (. On the contrary, for variants 2–6, the amplitude of the forced oscillations is determined by the term and the dominant frequency of oscillations corresponds to the eigenfrequency (.
Figure 14 shows the function for the forced oscillations of the free tail boom end (data are presented in mm) for different values of the parameter except of the resonance variant 4).
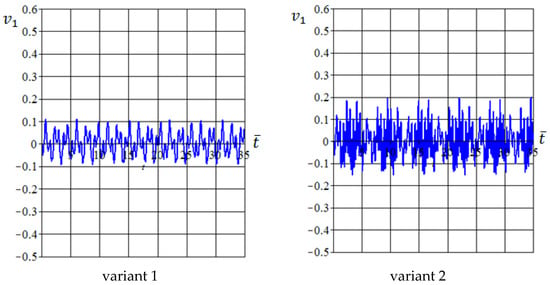
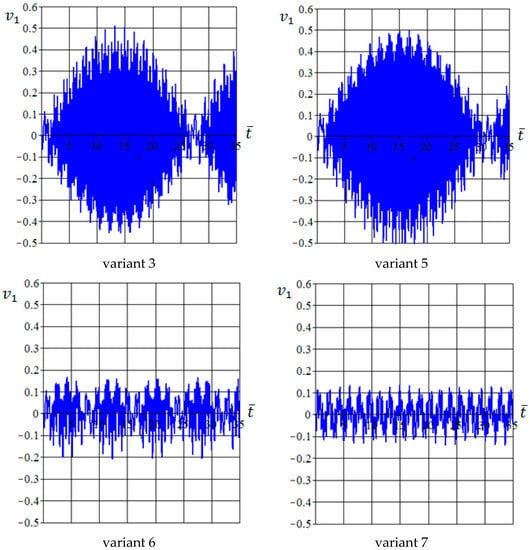
Figure 14.
Forced free end tail boom oscillations (in mm) at different values (variant numbers).
In general, one can note that the interaction between eigen and forced vibrations leads to two oscillation types having short () and long () dimensionless periods. Thus, all considered variants can be divided into two cases. Case I includes variants 1 and 6, for which , and case II includes variants 2–5, for which .
For case I, the short period of oscillations is determined by the eigenfrequency ( and oscillations of the free tail boom end have approximately constant amplitudes of about 0.1 mm (peak to peak relative deviation is approximately 50 microstrains). In general, this value of the oscillation amplitudes corresponds to estimations of paper [11] for static deformations of a light helicopter tail boom.
For all variants of case II, the short period of the oscillations is determined by the eigenfrequency ( and the long (interactional) oscillations period depends on the parameter value. For variant 2, the period of interactional oscillations is approximately equal to (0.417 s) and (0.603 s) for variant 6. Maximum amplitude of the interactional oscillations is about 0.2 mm (peak to peak deviation is about 100 microstrains).
The period and amplitude of interactional oscillations increased as the value of approaches the value. For variant 3, the dimensionless period of interactional oscillations is approximately equal to (2.016 s), and for variant 5 takes place (2.35 s). The maximum amplitude of the interactional oscillations for variants 3 and 5 is about 0.5 mm (peak to peak deviation is approximately 250 microstrains).
6. Conclusions
The effect of the unsteady aerodynamics on the forced vibration and deformation of a helicopter tail-boom was considered. CFD modeling was used to compute the unsteady flow around the main rotor-fuselage, and then the aerodynamic loads were used in conjunction with the analytical structural model, based on the Euler-Bernoulli equation with one spatial coordinate. A solution of the Euler-Bernoulli was presented as a series of spatial and time coordinates, including four harmonics. The normal force coefficient acting on the tail boom surface was approximately determined based on CFD results for the rotor-fuselage interaction case. The aerodynamics were obtained assuming rigid tail boom.
The results of simulations showed that the amplitudes of the forced oscillations due to the main rotor blade rotation are relatively small. However, for a long operational flight period, deformations can become essential from the point of view of initiation of metal cracks, and delamination of structural beam elements made of composite materials.
For certain geometric parameters of the tail boom, the results demonstrate a resonance effect if the second blade passing harmonic is equal to the second tail boom eigenfrequency.
The tail boom was modeled as a thin-walled cylindrical structure with continuously distributed mass (no concentrated mass points). In the future, the proposed vibration model will be generalized for cylindrical structures with concentrated masses along their length.
Acknowledgments
The support of this work via the “State Tasks of the Education Ministry of Russia” grant (No. 9.1577.2017/PCH) is gratefully acknowledged.
Author Contributions
Alexander Kusyumov and George N. Barakos conceived the idea, designed and wrote the paper. Andrey Batrakov conducted CFD modeling, Sergey Kusyumov calculated tail boom deformations. Sergey Mikhailov co-designed and revised the paper.
Conflicts of Interest
The authors declare no conflict of interests.
Nomenclature
| T = rotor thrust | L = tail boom length |
| D = fuselage drag | = vertical load coefficient |
| = pressure coefficient | E = Young’s modulus |
| = rotor thrust coefficient | = moment of inertia |
| = fuselage drag coefficient | = mass per unit length |
| = tip Mach number | = per unit length tail boom force |
| N = number of blades | = normal force coefficient |
| = free stream dynamic pressure | = vertical deformation |
| = blade tip dynamic pressure | = natural deformation |
| R = rotor radius | = forced deformation |
| = normalized rotor radius | Greek symbols |
| x = longitudinal tail boom coordinate | = beam material density |
| t = time coordinate | ψ = rotor azimuth angle |
| = reference fuselage area | ω = angular velocity of rotor |
References
- Crouse, L.; Leishman, J.; Bi, N. Theoretical and Experimental Study of Unsteady Rotor/Body Aerodynamic Interactions. J. Am. Helicopter Soc. 1990, 37, 55–65. [Google Scholar] [CrossRef]
- Sydney, A.; Leishman, J.G. Measurements of Rotor/Airframe Interactions in Ground Effect under Simulated Brownout Conditions. In Proceedings of the American Helicopter Society 69th Annual Forum, Phoenix, AZ, USA, 21–23 May 2013. [Google Scholar]
- Meerwijk, L.; Brouwer, W. Real-Time Helicopter Simulation Using the Blade Element Method. In Proceedings of the 17 European Rotorcraft Forum, Berlin, Germany, 24–27 September 1991. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 5rd ed.; Computers & Structures, Inc.: Berkeley, CA, USA, 2003; pp. 365–424. ISBN 978-0070113923. [Google Scholar]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill International Edition: New York, NY, USA, 2001; pp. 374–458. ISBN 0-07-041345-2. [Google Scholar]
- Weaver, W.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1990; pp. 422–433. ISBN 0-471-632287. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 5rd ed.; Addison-Wesley Publishing Company: Boston, MA, USA, 1995; pp. 721–739. ISBN 978-0-13-212819-3. [Google Scholar]
- Hsu, J.-C.; Lai, H.-Y.; Chen, C.K. Free Vibration of Non-Uniform Euler-Bernoulli Beams with General Elastically End Constraints Using a Domain Modified Decomposition Method. J. Sound Vib. 2008, 318, 965–981. [Google Scholar] [CrossRef]
- Coskun, S.B.; Atay, M.T.; Ozturk, B. Transverse Vibration Analysis of Euler-Bernoulli Beams Using Analytical Approximate Techniques. In Advances in Vibration Analysis Research; Ebrahimi, F., Ed.; InTech: Vienna, Austria, 2011; pp. 1–22. ISBN 978-953-307-209-8. [Google Scholar]
- Staley, J.A.; Sciarra, J.J. Coupled Rotor/Airframe Vibration Prediction Methods. In Proceedings of the Specialists Meeting on Rotorcraft Dynamics, Moffet Field, CA, USA, 13–15 February 1974; NASA Ames Res. Center Rotorcraft Dyn.: Moffett Field, CA, USA, 1974; pp. 81–90. [Google Scholar]
- Rose, J.B.R.; Vetrivel, S. Structural Design and Analysis of Cost Effective Rotorcraft for Recovery Purposes. Int. J. Eng. Trends Technol. (IJETT) 2014, 10, 225–229. [Google Scholar] [CrossRef]
- Krylov, А.N. Vibrationships, Shipbuilding Literature Edition ed; ONTINKTP: Leningrad-Moscow, USSR, 1936; pp. 326–365. (In Russian) [Google Scholar]
- Steijl, R.; Barakos, G.; Badcock, K. A Framework for CFD Analysis of Helicopter Rotors in Hover and Forward Flight. Int. J. Numer. Methods Fluids. 2006, 51, 819–847. [Google Scholar] [CrossRef]
- Batrakov, A.; Garipova, L.; Kusyumov, A.; Mikhailov, S.; Barakos, G. CFD Computational Fluid Dynamics Modeling of Helicopter Fuselage Drag. J. Aircraft 2015, 52, 1634–1643. [Google Scholar] [CrossRef]
- Dehaeze, F.; Baverstock, K.D.; Barakos, G.N. CFD simulation of flapped rotors. Aeronaut. J. 2015, 119, 1561–1583. [Google Scholar] [CrossRef]
- Woodgate, M.A.; Pastrikakis, V.A.; Barakos, G.N. Method for calculating rotors with active gurney flaps. J. Aircraft 2016, 53, 605–626. [Google Scholar] [CrossRef]
- Carrion, M.; Woodgate, M.; Steijl, R.; Barakos, G. Implementation of All-Mach Roe-type Schemes in Fully Implicit CFD Solvers—Demonstration for Wind Turbine Flows. Int. J. Numer. Methods Fluids 2013, 73, 693–728. [Google Scholar] [CrossRef]
- Lawson, S.; Barakos, G.N. Review of Numerical Simulations for High-Speed, Turbulent Cavity Flows. Prog. Aerosp. Sci. 2011, 47, 186–216. [Google Scholar] [CrossRef]
- Kusyumov, A.; Mikhailov, S.; Garipov, A.; Nikolaev, E.; Barakos, G. CFD Simulation of Fuselage Aerodynamics of the “ANSAT” Helicopter Protype. Trans. Control Mech. Syst. 2012, 1, 318–324. [Google Scholar]
- Batrakov, A.S.; Kusyumov, A.N.; Mikhailov, S.A.; Pakhov, V.V. A Study in Helicopter Fuselage Drag. In Proceedings of the 39th European Rotorcraft Forum, Moscow, Russia, 3–6 September 2013. [Google Scholar]
- Wilcox, D.C. Re-assessment of the Scale-Determining Equation for Advanced Turbulence Models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Garipova, L.I.; Batrakov, A.S.; Kusyumov, A.N.; Mikhailov, S.A.; Barakos, G. Estimates of Hover Aerodynamics Performance of Rotor Model. Russ. Aeronaut. 2014, 57, 234–244. [Google Scholar] [CrossRef]
- Caradonna, F.X.; Tung, C. Experimental and Analytical Studies of a Model Helicopter Rotor in Hover. In Proceedings of the 6th European Rotorcraft and Powered Lift Aircraft Forum, Bristol, UK, 16–19 September 1980. [Google Scholar]
- Batrakov, A.S.; Kusyumov, A.N.; Barakos, G. Simulation of Flow around Fuselage of Helicopter Using Actuator Disc Theory. In Proceedings of the 29 ICAS Conference, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).