Abstract
In wideband radar systems, the performance of motion parameters estimation can significantly affect the performance of object detection and the quality of inverse synthetic aperture radar (ISAR) imaging. Although the traditional motion parameters estimation methods can reduce the range migration (RM) and Doppler frequency migration (DFM) effects in ISAR imaging, the computational complexity is high. In this paper, we propose a new fast non-parameter-searching method for motion parameters estimation based on the cross-correlation of adjacent echoes (CCAE) for wideband LFM signals. A cross-correlation operation is carried out for two adjacent echo signals, then the motion parameters can be calculated by estimating the frequency of the correlation result. The proposed CCAE method can be applied directly to the stretching system, which is commonly adopted in wideband radar systems. Simulation results demonstrate that the new method can achieve better estimation performances, with much lower computational cost, compared with existing methods. The experimental results on real radar datasets are also evaluated to verify the effectiveness and superiority of the proposed method compared to the state-of-the-art existing methods.
1. Introduction
The wideband linear frequency modulation (LFM) signal is widely used in modern wideband radar systems. Compared with the narrow-band LFM signal, it can achieve much better quality in inverse synthetic aperture radar (ISAR) imaging, due to the higher range resolution [1,2,3,4]. However, the motions of the target often cause range migration (RM) and Doppler frequency migration (DFM) effects in the received signals, which will degrade the imaging quality. Therefore, the object’s motion parameters should be estimated and compensated before imaging [5,6,7,8]. Besides, the accuracy of motion parameters estimation also affects the performance of target tracking and identification. Thus, high precision motion parameters estimation is necessary and attracts much more attention in modern wideband radar systems [1,2,3,4,5,6,7,8,9].
For wideband radars, the estimation methods of motion parameters can be divided into two types: parameter-searching methods and non-parameter-searching methods. A parameter-searching method maximizes or minimizes some criterion by searching the motion parameters step by step. Many of the traditional range alignment methods [4,8,10,11,12,13,14,15,16] in inverse synthetic aperture radar (ISAR) imaging are parameter-searching methods, such as spatial domain realignment [8], adaptive joint time-frequency technique [10] and minimum entropy method [15,16]. Spatial domain realignment [8] defines a correlation function between two envelops of echo signals with delays. The amount of envelope shift is determined by searching the delay to obtain the maximum of the correlation function. In [10], the radar echo signal is projected to a set of basis functions, which are constructed with different parameters. A searching procedure is conducted to maximize the projection value, and then, the motion parameters are estimated. The minimum entropy method introduces a 1D entropy function to determine the degree of alignment between radar echoes [15,16]. As the delay, which minimizes the entropy, is searched with the step determined by the bandwidth of the transmitted signal, the accuracy of the estimated parameters is limited by the delay step. To perform high precision motion parameters estimation, the Radon–Fourier transform (RFT) method is proposed for multi-pulse energy accumulation [9,17,18]. The RFT method is a multidimensional searching method and achieves a good performance of motion parameters estimation because of long coherent integration time. A common drawback of these parameter-searching methods is that their computation is highly complex, when they are applied in the wideband radar systems.
In the non-parameter-searching methods, the keystone transform (KT) is able to eliminate the RM effect based on long time coherent integration technology [19,20,21]. However, the DFM induced by acceleration cannot be removed by KT. In [22], a non-searching ISAR range alignment method based on minimizing the entropy of the average range profile (ARP) is proposed. An iterative procedure is utilized to estimate the delays of envelops, of which the precision is determined by the range resolution. Meanwhile, an interpolation is employed on the envelops to improve the estimation precision. However, the iterative procedure and the interpolation operation significantly increase the computational complexity. Moreover, the phase information is not used for estimation in [22]. In [23], a novel estimation algorithm of motion parameters is proposed for ISAR imaging, based on KT and the adjacent cross-correlation function (ACCF). Then, a fast non-parameter-searching method based on ACCF is proposed for target motion estimation, target detection and ISAR imaging [24,25,26,27,28]. There are two differences between the two methods in [23] and in [24,25,26,27,28]. The first one is that the KT is not utilized in [24,25,26,27,28], and the other one is that the choice of the scaling factors is improved in [28]; thus, better performance is obtained under low SNR conditions. Compared with the RFT method, the ACCF method [24,25] can achieve similar performance with much lower computational cost. However, it can be applied only to the uncompressed received (UR) signal, whose bandwidth is equal to that of the transmitted wideband LFM signal. In order to reduce the processing bandwidth and the sampling rate of the analog-to-digital converter, the stretching processing is commonly used in most of the wideband LFM radars, and therefore, the ACCF method cannot be applied in these radar systems.
In this paper, a novel and fast estimation method based on the cross-correlation of adjacent echoes (CCAE) is proposed. Specifically, the cross-correlation operation is performed on two adjacent echo signals, then the motion parameters are calculated by estimating the frequency of the correlation result. The proposed new method is a non-parameter-searching method and can be directly applied to the stretched signals. Since the SNR of the stretched signal is higher than that of the UR signal, better root-mean-square error (RMSE) performance can be achieved by applying the CCAE method to the stretched signals. When estimating the velocity using two echo signals, the FFT operation is needed only once in the CCAE method. Thus, the computational complexity of the proposed CCAE method is much lower than that of the existing methods. Numerical simulations demonstrate that the proposed CCAE method can be applied in real wideband LFM radars.
The rest of this paper is organized as follows. In Section 2, the model of the stretched signal is presented. In Section 3, the proposed fast non-parameter-searching CCAE method is presented first, and then, the root mean square error (RMSE) of the proposed CCAE method is derived in closed form. In Section 4, the details of the experiments conducted on simulation and real data are presented. Finally, we conclude this paper in Section 5.
2. Signal Model
In this paper, the scatterer model of the wideband LFM signal is used. It is assumed that the target is in the far field and the incident wave is a plane wave. The scatterers are located on the line of sight. The range profile of target in wideband radar is illustrated in Figure 1. In stretching processing, the wideband echo signal reflected by the scatterers is mixed with the local wideband LFM signal. For single scatterer, the mixing result is a single frequency signal, whose frequency is determined by the round trip time of the scatterer. For multiple scatterers, the mixing result is composed of multiple signals with different frequencies. Therefore, the wideband echo signal is converted to a narrowband signal, of which the bandwidth is determined by the length of the target. After performing FFT operation, this stretched narrowband signal can be transformed to a range profile along the radar line of sight (RLOS), as shown in the bottom of Figure 1. The parameters that will be frequently used in later derivation are listed in Table 1.
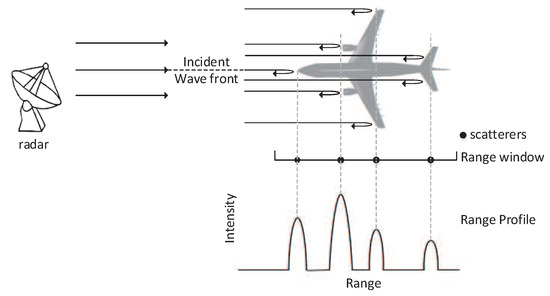
Figure 1.
Target’s range profile of wideband radar.

Table 1.
Notations.
The transmitted signal of the wideband LFM radar can be modeled as:
where denotes the rectangle pulse shape, t the fast time, T the pulse width and the radar center frequency. is the chirp rate of the LFM signal, where B is the swept bandwidth of the LFM signal.
The UR signal of the wideband LFM radar can be represented as:
where P denotes the number of scatterers, the scattering coefficient of the p-th scatterer and the time delay from the radar to the p-th scatterer. is the slow time, where m is the pulse number, and is the pulse repetition interval (PRI). denotes the signal term of , is the Gaussian noise with mean zero and variance . The time delay can be expressed as:
where is the distance from the radar to the p-th scatterer at slow time . Due to the wide bandwidth of the signal, the data size of the uncompressed signal is considerably large, which leads to a high computational complexity. Therefore, in wideband radar systems, the stretching operation is often used to reduce the data size.
The local reference signal for stretching operation can be written as:
where is the duration of the reference signal, which is usually slightly larger than the width of the transmitted pulse, so that it covers the received signal. The stretched signal is obtained by multiplication:
where is the signal term of the and is the noise. In practical wideband radar systems, the sampling frequency of the stretched signal is much lower than that of the UR signal. Thus, the data size of the stretched signal is much smaller than that of the UR signal. When parameter estimation is performed on the stretched signal, the computational complexity decreases significantly. The proposed motion parameters estimation method can be applied to both UR and stretched signals. In the following section, the idea of “stretching” processing is first illustrated to show the availability of the CCAE method to the UR signal, then the algorithm of the proposed CCAE estimation method is derived using the stretched signal model.
3. Estimation of Motion Parameters Based on the CCAE Method
3.1. “Stretching” Idea of the Proposed CCAE Method
In radar systems, when a target is tracked, the range profile of the target varies from pulse to pulse because of the rotational and the translational motions of the target. In this paper, the rotation of the target is not taken into consideration. However, within the interval of two adjacent transmitted pulses, the change in motion parameters is generally small. Therefore, the range profiles of two adjacent echo signals are highly correlated [29]. Consequently, the energy of two adjacent echoes can be accumulated. Thus, the motion parameters may be estimated by the correlation result of adjacent echoes.
The idea of the proposed method is shown in Figure 2, where the UR signal is utilized for the convenience of illustration. It is already known that the stretching operation can transform a wideband echo signal into a narrow-band signal. In the CCAE method, considering one of the two adjacent echo signals (e.g., the echo at slow time ) as the “local reference” signal, the other one (e.g., the echo at slow time ) is “stretched” into a single tone signal. The frequency of the “stretched” signal contains the information of the distance differences between the slow time and . The motion parameters can be estimated according to the distance differences. In the next subsection, the CCAE method is derived mathematically to prove the idea.
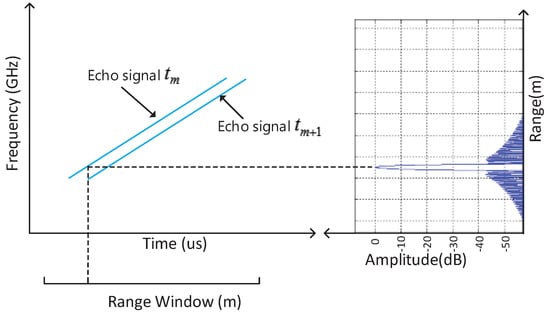
Figure 2.
The “stretching” idea of the proposed cross-correlation of adjacent echoes (CCAE) method.
3.2. Proposed CCAE Algorithm
At the beginning, we apply the conjugate multiplication to both UR signals and stretched signals. Then, it is seen that the conjugate multiplication result of the UR signals is similar to that of the stretched signals. The UR signal at slow time is multiplied with the conjugate of the adjacent UR signal at slow time :
where:
where the superscript denotes the conjugate of x and the superscript indicates that the multiplication is performed on the UR signals. In Equation (6), the first term, i.e., the self-term , is the product of adjacent echoes from the same scatterer, the second term, i.e., the cross-term , is the product of adjacent echoes from different scatterers and the third term is the noise after conjugate multiplication.
Similarly, when the conjugate multiplication is performed on the stretched signals, we can obtain:
where:
is the noise added to the stretched signal after conjugate multiplication. The first two terms of the right-hand side of Equation (10) are the same in Equation (6), where the exponential term contains the information of the distance difference between the slow time and . The difference lies in that the data rate of the stretched signal is lower than that of the UR signal, and the noise bandwidth is smaller, resulting in the SNR of the stretched signal being higher than that of the UR signal. Consequently, the stretched signal is adopted in the following derivation.
In Equations (7) and (8), there are two rectangular window functions. The lengths of the two functions are equal, while their positions are different. In other words, the nonzero parts of the two window functions do not completely overlap. This will cause loss in signal energy. The length of the non-overlapping part is determined by the target’s motion, i.e.,
where .
In common radar applications, the ratio of the non-overlapping part’s length to the length T of the transmitted signal (i.e., ) is much less than one. For example, if ms and ms, then the length of the target is 50 m and velocity 6000 m/s. Computation of the maximum value of by m gives the ratio %. Thus, the influence of the non-overlapping part can be considered negligible. Then, by substituting Equation (3) into Equation (10) and applying the FFT operation to Equation (10) for energy focusing, one gets:
where , , are the FFT results of , and , respectively, i.e.,
where is the wavelength corresponding to the center frequency . In Equations (14) and (15), the exponential terms are constant phase terms, which have no impact on estimating the frequency of the spectrum, i.e., Equation (13). For simplicity, the sinc functions are extracted for further discussion in the following sections.
Define:
Let it be assumed that the peak position of is . When , Equation (16) is the same as the sinc function in Equation (14). Since all scatterers are assumed to locate along the line of sight, the distance difference between and is the same for every scatterer of the target. Namely, and for . The energy of all scatterers will accumulate on one peak, which can be regarded as the main peak of the spectrum. When , because of the differences in the combinations of p and q, the distance difference will bring a number of frequency components into the spectrum. The amplitudes of these spectral lines are much less than that of the main spectral line . As seen from Equations (12) and (14), the main peak position of the spectrum is determined by the distance difference of the target between slow time and . Therefore, the target parameters can be obtained by estimating the frequency of the main peak position. This can be implemented by using the frequency estimation methods, such as FFT and Newton’s method [30]. The estimated frequency can be expressed as:
Unlike the estimation methods based on the coherent integration strategy, the proposed CCAE method is a fast non-parameter-searching estimation method, where the estimated parameters can be output in real time. In the following paragraphs, we discuss the algorithm of estimating the velocity and higher order parameters, respectively.
3.2.1. Estimation of Velocity
Assuming that only the velocity is taken into consideration and that the velocities of different scatterers within a target are the same, the motion of the target can be written as:
where denotes the distance between the p-th scatterer and the radar at instant, the initial distance between the p-th scatterer and the radar and v the velocity of the target. The acceleration of the target a is set to zero. Thus, the estimated frequency can be rewritten as:
Consequently, using two echo signals, we can estimate the velocity by the following equation:
3.2.2. Estimation of Higher Order Parameters
It is seen from Equation (17) that the estimated frequency of the cross-correlation result is determined by the difference in the target’s distance between the two pulses. To estimate high-order motion parameters, the differential operation or curve fitting operation can be applied to the cross-correlation results. For example, a second-order differential operation can be applied to estimate the jerk, with which the acceleration can be obtained using the result of the first-order differential operation. Another approach for simultaneous estimation of velocity, acceleration and other higher order parameters is to employ the curve fitting method, such as the least-square method. However, high-order parameter estimation requires more pulses, and consequently, the output delay increases. It is worth noting that the objective of the proposed CCAE method is to estimate the motion parameters in real time, i.e., the estimated results should be output with minimum delay. Therefore, for estimation of high-order motion parameters, we mainly focus on acceleration estimation in this paper. Considering the acceleration, Equation (18) is rewritten as:
Then, the estimated frequency of Equation (17) can be expressed as:
It is seen that the estimated frequency is a slow time varied function. The acceleration can be calculated out by and (i.e., three echo signals are used).
Then, the velocity can be obtained with at slow time and a, where can always be set to the time of the first pulse:
3.3. Implementation of the Proposed CCAE Method
As described above, the velocity of the target can be estimated by the proposed CCAE method using only two echo signals. To estimate the acceleration or even higher order parameters, three or more echo signals are required. The flowchart of the proposed CCAE method is shown in Figure 3, including the following steps:
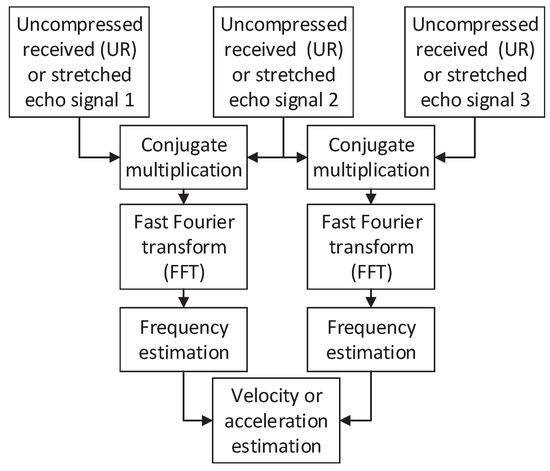
Figure 3.
The flowchart of the proposed cross-correlation of adjacent echoes (CCAE) method.
- The first UR or stretched signal is multiplied with the conjugate of the second UR or stretched signal. For acceleration estimation, the second echo signal is also multiplied with the third echo signal.
- The FFT operation is performed on the multiplication results for energy accumulation.
- Estimate the frequencies of the above FFT results.
Although the ACCF method [24,25] also adopts the conjugate multiplication, it is basically different from the proposed CCAE method. In the ACCF method, first, pulse compression is applied to the two adjacent UR signals by the FFT operation, and then, a conjugate multiplication is performed with the pulse compression results. Then, for velocity estimation, the correlation result is transformed into the time domain by an IFFT operation. If we only estimate the velocity of the target by using two echo signals, the ACCF method requires the FFT (or IFFT) operation three times, while the proposed method only requires once. Besides, the ACCF method can be applied to only the UR signals, while the proposed CCAE method can be applied to both UR and stretched signals.
3.4. Performance Analysis
The SNR of the wideband signal is defined as in [23,31,32]. If the mean of the in Equation (2) is zero and the variance is , then the SNR of can be written as , where A is the signal amplitude. Because of the stretching operation and analog-to-digital conversion, the bandwidth of the noise will decrease. If the sampling frequency is , then the noise bandwidth of the stretched signal decreases by the ratio . Consequently, the SNR of the stretched signal, i.e., Equation (5), can be written as:
In Equation (10), the first two terms contain the signal, and the third one is regarded as the noise term, which is composed of three terms, i.e., , and . It is clear that and satisfy the Gaussian distribution, and satisfy double Gaussian distribution [33]. There is no exact PDF for this distribution so far. However, this distribution can be approximately regarded as a Gaussian distribution in most cases [33,34]. Therefore, the noise term in Equation (10) is approximate to the Gaussian noise. In addition, the means of these three terms are zero, and the variances of them are , and , respectively. Hence, the SNR of is:
The velocity of the target is obtained by estimating the main peak position of the sinc function in Equation (13). This procedure can be considered similar to that of the frequency estimation of a complex sinusoidal signal . For a complex sinusoidal signal with unknown amplitude, phase and frequency [35], the RMSE of frequency estimation can be expressed as:
where is the sampling interval, N the number of samples and the SNR of the sinusoidal signal [35]. According to the above definition, the RMSE of velocity of the proposed method is:
When N is large, the equation can be written as:
It is seen from Equation (29) that the estimation performance is affected by the PRI, the SNR of the UR signal and the bandwidth B. When the acceleration is taken into consideration, the acceleration is obtained by subtracting two i.i.d variables and in Equation (23). The RMSE of the acceleration can be obtained according to Equation (23):
Similarly, according to Equation (24), the velocity is calculated using the subtracted value of the two i.i.d variables and a. Thus, the RMSE of the velocity can be expressed as:
The energy loss is not considered in the above derived RMSEs. In Section 3.2, it is pointed out that the non-overlapping part of the conjugate multiplication result induces the loss of signal energy. The loss can be figured out to be small, which has little influence on the estimation performance. According to Equation (25), conjugate multiplication causes a decrease in SNR, consequent to which the performance of the proposed method also suffers. However, since the noise bandwidth of the stretched signal is reduced to be much smaller than that of the UR signal, the SNR of the stretched signal is higher than that of the UR signal. Therefore, better estimation performance can be achieved by applying the CCAE method to the stretched signals.
In this paper, the cross-correlation operation is performed on the two adjacent echo signals. Actually, the cross-correlation can performed on any two echo signals. When the two echo signals are taken with an interval , the “” in Equation (29) should be modified as “”. As a result, the RMSE will decrease to . In other words, the performance of the proposed method can be improved through increasing the interval of the echo signals. However, when the interval becomes too large, the correlation between the two echo signals decreases, as a consequence of which the accuracy of parameters estimation decreases. Therefore, for this study, the two adjacent signals are used for parameters estimation.
4. Simulations and Real Data Processing
In this section, the proposed CCAE method is first evaluated with different simulation parameters. In Section 4.2, the performance of the CCAE method is compared with that of the ACCF method at different SNRs. Finally, the CCAE method is verified using real radar data.
4.1. Evaluation of the Proposed CCAE Method
In this subsection, simulations are performed to evaluate the proposed CCAE method on stretched signals. The CPU frequency of the computer is 3.30 GHz, and the memory size is 8 GB. The transmitted signal is an LFM waveform, and additive white Gaussian noise is added to the UR signal. Table 2 lists the detailed simulation parameters. The target is set as a multi-scatterer model containing 10 scatterers, and the length of the target is about 9 m. The velocity is 100 m/s, and the acceleration is set to zero.

Table 2.
Simulation parameters of the evaluation of the proposed CCAE method.
The energy concentration of the proposed CCAE method is investigated at a high SNR level, i.e., 30 dB. The spectrum of the cross-correlation result is shown in Figure 4, which shows that the energy of different scatterers is focused on one position. The estimated velocity of the proposed method is 99.9 m/s.
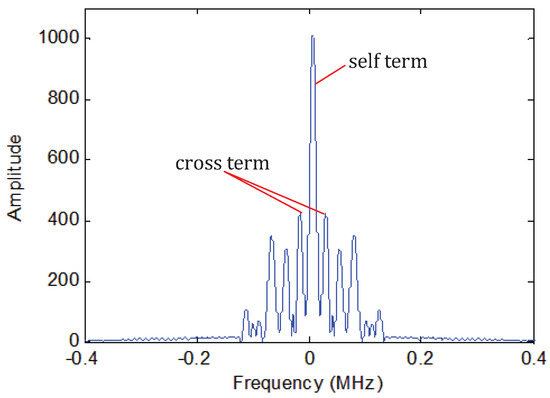
Figure 4.
The spectrum of the cross-correlation result.
Next, we compare the performances of the proposed CCAE method with different bandwidths and PRIs, under different SNR conditions. The SNR varies from −30 dB to 2 dB. Under each SNR, 1000 Monte Carlo simulations have been carried out. Figure 5 shows the RMSE results. It is observed that when the bandwidth or the PRI increases, the RMSE decreases. To achieve the same RMSE, the test case with GHz and ms requires the lowest SNR, and hence, it has the best performance. Under the same SNR, the RMSE performance of the case with GHz, ms is about 3 dB lower than the case with GHz, ms and the case with GHz and ms. The performance difference is about 6 dB between the case with GHz, ms and the case with GHz, ms.
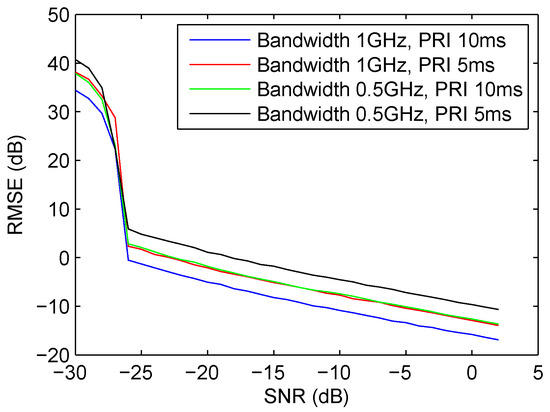
Figure 5.
The performances of the proposed CCAE method with different parameters.
4.2. Comparison with the ACCF Method
In this subsection, we compare the performance of the proposed CCAE method with the ACCF method [24,25] at different SNRs, which varies from −30 dB to 2 dB. One thousand Monte Carlo simulations are also carried out for each SNR condition. The other simulation parameters are listed in Table 3. In this experiment, the stretched signals and UR signals are both used in the proposed CCAE method, and the UR signals are used in the ACCF method, which can only be applied to the UR signals.

Table 3.
Simulation parameters of the comparison with the adjacent cross-correlation function (ACCF) method.
We first evaluate the performance of the case, in which only velocity is taken into account. The velocity of the target is set to 100 m/s. Two pulse echoes are used only for velocity estimation. In Figure 6, it is seen that the estimated RMSEs of CCAE method on UR signals are similar to that of ACCF on UR signals, and the performance of CCAE on stretched signals is the best. As mentioned in Section 3.4, the noise term is approximately regarded as a Gaussian noise, hence there is a gap between the theoretical and simulation results, which can be seen from Figure 6. However, on average, the RMSE gap is about 0.0543 dB for UR signals and 0.0179 dB for stretched signals. This shows that the noise approximation is reasonable.
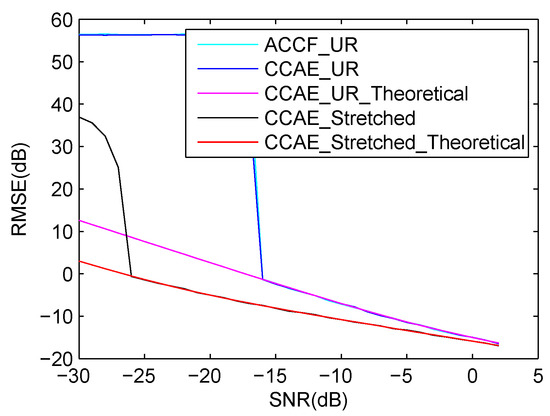
Figure 6.
RMSE comparison of velocity estimation by using CCAE on stretched signals, CCAE on uncompressed received (UR) signals and adjacent cross-correlation function (ACCF) on UR signals (without acceleration).
Furthermore, it is noted that the RMSEs of the CCAE deteriorate largely when the SNR is low. In low SNR cases, the amplitude of the self-term in the correlation result may be smaller than the noise amplitude. This may cause the failure of the peak search, so that the RMSEs deteriorate. In the parameter estimation problem, a threshold SNR means that the performance may deteriorate largely when the input SNR is lower than the threshold value. The threshold SNR is lower, the performance is better. In this experiment, the threshold SNR of CCAE/ACCF on UR signals is about −16 dB, higher than that of CCAE on stretched signals (about −26 dB). Generally, the theoretical RMSE is derived with the assumption that the spectrum peak can be successfully found. Therefore, there is no threshold SNR in the theoretical RMSE.
We further evaluate the performances of the two methods with a second-order motion model. The velocity of the target is 100 m/s, and the acceleration is 10 m/s2. Three pulses are used for velocity and acceleration estimation, the other parameters being the same as those of the previous experiments. The estimated acceleration results are shown in Figure 7, from which we can see that the RMSE performance of CCAE on UR signals is better than that of ACCF on UR signals. It can also be seen that the threshold SNR of CCAE on UR signals is smaller than that of ACCF on UR signals, i.e., −16 dB versus −8 dB. As has already been analyzed in Section 3.4, SNR decreases after cross-correlation. To estimate the acceleration, the conjugate multiplication has to be used twice in the ACCF method, but only once in the CCAE method. Therefore, the performance loss is more in the ACCF method than in the CCAE method. In addition, the performance of CCAE on stretched signals is better than that of CCAE on UR signals, due to the higher SNR of stretched signals.
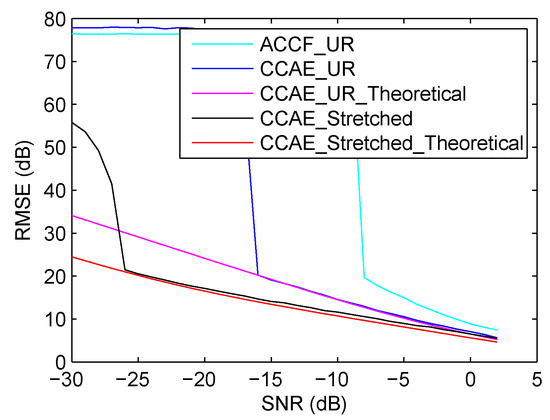
Figure 7.
RMSE comparison of acceleration estimation by using CCAE on stretched signals, CCAE on UR signals and ACCF on UR signals (with acceleration).
When the acceleration is considered, the velocity estimation results by using CCAE on stretched signals, CCAE on UR signals and ACCF on UR signals are compared in Figure 8. It can be seen that the RMSE of the ACCF method is also larger than the proposed method. In this experiment, the threshold SNRs of the three test methods are −26 dB, −16 dB and −4 dB, respectively. To estimate the velocity, the estimated acceleration should be used to eliminate its influence. Thus, the performance of the velocity estimation is related to the performance of the acceleration estimation. As the performance of estimated acceleration is worse, the performance of velocity estimation of the ACCF method also becomes worse. From a comparison of Figure 6 and Figure 8, for the proposed CCAE method, it can be seen that the RMSE of the estimated velocity with acceleration is a bit higher than that without acceleration. This is because the velocity is calculated by subtracting two i.i.d variables. This can be confirmed by comparing Equations (29) and (31).
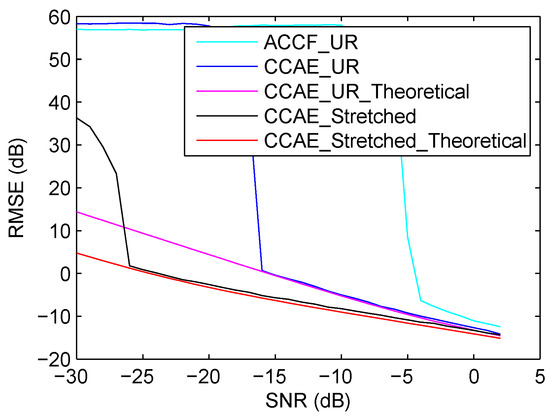
Figure 8.
RMSE comparison of velocity estimation by using CCAE on stretched signals, CCAE on UR signals and ACCF on UR signals (with acceleration).
In Figure 6, Figure 7 and Figure 8, there exist performance gaps between the simulation and the theoretical results of the CCAE method. The differences are mainly caused by the noise approximation, which is analyzed in Section 3.4. The RMSE gap in Figure 7 and Figure 8 is bigger than that in Figure 6. The reason is that acceleration estimation is implemented by performing CCAE twice. This leads to a noise term subtracted from two double Gaussian noises. When approximating this subtraction noise to be a Gaussian distribution, the error is increased. Thus, the RMSE gap between the simulation and the theoretical results in Figure 7 and Figure 8 is larger than that in Figure 6. In summary, for the CCAE method, the RMSEs of the estimated acceleration and velocity are both close to the theoretical RMSEs, which proves the effectiveness of the proposed method.
The total time costs of the 1000 Monte Carlo simulations for all of the SNR cases are listed in Table 4. It is seen that the time cost of the CCAE on stretched signals is much less than that of CCAE on UR signals and ACCF on UR signals. The reason is two-fold: first, the data size of the UR signal is larger than the stretched signal; second, the number of FFT operation required by the ACCF method is more than that of the CCAE method.

Table 4.
Comparison of the time cost between CCAE on stretched signals, CCAE on UR signals and ACCF on UR signals.
4.3. Verification with Real Data
Two sets of real data, obtained from the wideband LFM radar systems, are applied for the verification of the proposed method. The parameters of the two datasets are shown in Table 5, where PRI means pulse repetition interval. The targets are satellites in space. They fly along the radar line of sight, first toward the radar, then leave. For real radar data, the signals are stretched, and the SNR values cannot be obtained. Nevertheless, the noise power can be estimated by averaging the power of the spectrum outside the target’s position, and the signal power can be calculated via subtracting the noise power from the power of the stretched signal. In this way, the average estimated SNRs of the two real data sets are −5.99 dB and −7.58 dB, respectively.

Table 5.
Parameters of radars.
Figure 9 illustrates the spectrums of the cross-correlation results of the two datasets. Figure 10a and Figure 11a show the estimated velocities in comparison with the real velocities of the targets. The absolute values of differences between the estimated velocities and the real velocities of the targets are shown in semilog scale in Figure 10b and Figure 11b. It is seen that the estimated results are consistent with the real velocities for both datasets. The RMSE of the estimated velocity is 0.0561 m/s in the first dataset and 0.2842 m/s in the second dataset.
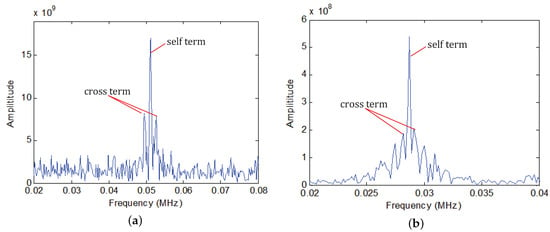
Figure 9.
The spectrums of the cross-correlation results. (a) The spectrum of the cross-correlation result of radar Dataset 1. (b) The spectrum of the cross-correlation result of radar Dataset 2.
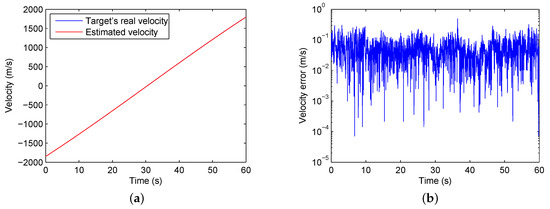
Figure 10.
Estimation results of Dataset 1. (a) The estimated velocity and the target’s real velocity (due to the high speed of the target and the high precision of the estimated velocity, the two lines overlap). (b) The absolute values of differences between the estimated velocities and the target’s real velocities.
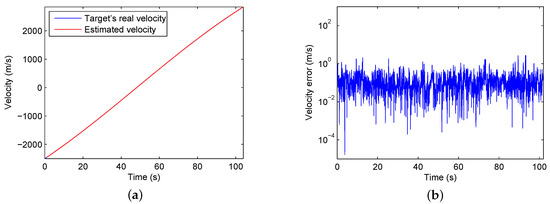
Figure 11.
Estimation results of Dataset 2. (a) The estimated velocity and real velocity of the target (due to the high speed of the target and the high precision of the estimated velocity, the two lines overlap). (b) The absolute values of differences between the estimated velocities and the target’s real velocities.
Finally, the proposed CCAE method is applied to range alignment in the ISAR imaging procedure, with a civil aircraft as the target. Figure 12a shows the target’s range profiles of wideband radar at different slow times (i.e., pulse number). Due to the target’s motion, the range profile of the target moves across the range cells, which is called the range migration (RM). Thus, the range profiles at difference slow times are not aligned. As a result, the energy of the different range profiles cannot be focused to generate a high quality image. Therefore, the motion compensation is necessary for ISAR imaging. In this experiment, motion compensation is performed using the proposed CCAE method. After motion compensation, the range profiles of different slow times are aligned, as shown in Figure 12b. With motion compensation, the RM effect is eliminated, resulting in a focused ISAR image (Figure 13). These results with real data demonstrate that the proposed method is effective in practical radar systems.
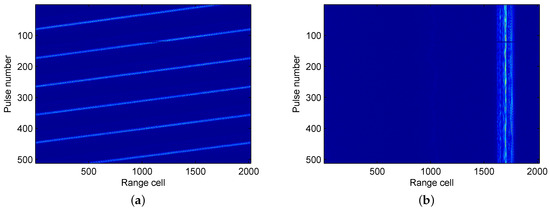
Figure 12.
The range profiles of the target. (a) The range profiles with the range migration (RM) effect. (b) The range profiles after range alignment by the proposed CCAE method.
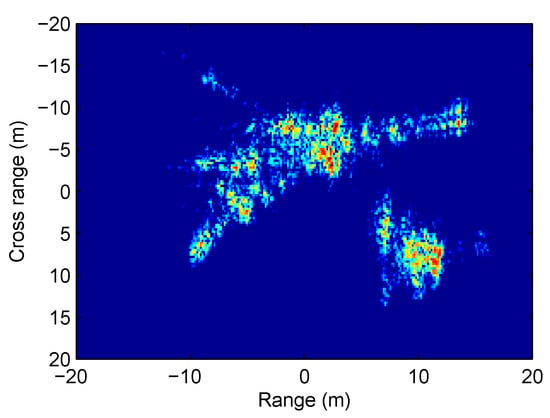
Figure 13.
The result of inverse synthetic aperture radar (ISAR) imaging after range alignment.
5. Conclusions
In this paper, a new fast motion parameters estimation method based on CCAE for wideband LFM radars is presented. First, the conjugate multiplication is performed on two adjacent signals. Then, the velocity is obtained by estimating the frequency of the signal, i.e., the correlation result. The acceleration can be estimated by using three echo signals. The proposed CCAE method can be applied to the UR signals or the stretched signals. When estimating the velocity using two echo signals, the FFT operation is required only once in the proposed method, and the estimated parameters can be output in real time. Simulation results show that the new method provides better RMSE performances than the state-of-the-art existing method for both velocity and acceleration estimation, with much less computational cost. Besides, the RMSEs of the simulation data are close to the theoretical RMSEs of the proposed method. Real radar datasets are also evaluated to verify the effectiveness of the proposed method. The proposed fast estimation method of motion parameters can be applied to range alignment in ISAR imaging.
Acknowledgments
The research was supported by the National High-tech R&D Program of China, the Open-End Fund National Laboratory of Automatic Target Recognition (ATR), the Open-End Fund of BITTT Key Laboratory of Space Object Measurement and the National Natural Science Foundation of China (Grant No. 62101196).
Author Contributions
Yi-Xiong Zhang, Zhen-Miao Deng and Cheng-Fu Yang conceived and designed the experiments; Ru-Jia Hong performed the experiments; Yun-Jian Zhang analyzed the data; Cheng-Fu Yang and Sheng Jin contributed reagents/materials/analysis tools; Yi-Xiong Zhang and Ru-Jia Hong wrote the paper; Yi-Xiong Zhang, Zhen-Miao Deng and Cheng-Fu Yang modified the paper.
Conflicts of Interest
The authors declare that the grant, scholarship and/or funding mentioned in the Acknowledgments section do not lead to any conflict of interest. Additionally, the authors declare that there is no conflict of interest regarding the publication of this manuscript.
References
- Skolnik, M.I. Introduction to radar. In Radar Handbook; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Berizzi, F.; Mese, E.D.; Diani, M.; Martorella, M. High-resolution ISAR imaging of maneuvering targets by means of the range instantaneous Doppler technique: Modeling and performance analysis. IEEE Trans. Image Process. 2001, 10, 1880–1890. [Google Scholar] [CrossRef] [PubMed]
- Suo, P.C.; Tao, S.; Tao, R.; Nan, Z. Detection of high-speed and accelerated target based on the linear frequency modulation radar. IET Radar Sonar Navig. 2014, 8, 37–47. [Google Scholar] [CrossRef]
- Wehner, D.R. High Resolution Radar; Artech House, Inc.: Norwood, MA, USA, 1987. [Google Scholar]
- Werness, S.A.; Carrara, W.G.; Joyce, L.; Franczak, D.B. Moving target imaging algorithm for SAR data. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 57–67. [Google Scholar] [CrossRef]
- Chen, V.C.; Qian, S. Joint time-frequency transform for radar range-Doppler imaging. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 486–499. [Google Scholar] [CrossRef]
- Peng, S.B.; Xu, J.; Peng, Y.N.; Xiang, J.B. Parametric inverse synthetic aperture radar manoeuvring target motion compensation based on particle swarm optimiser. IET Radar Sonar Navig. 2011, 5, 305–314. [Google Scholar] [CrossRef]
- Chen, C.C.; Andrews, H.C. Target-motion-induced radar imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, 16, 2–14. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier transform for radar target detection III: Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Wang, Y.; Ling, H.; Chen, V.C. ISAR motion compensation via adaptive joint time-frequency technique. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 670–677. [Google Scholar] [CrossRef]
- Wang, J.; Kasilingam, D. Global range alignment for ISAR. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 351–357. [Google Scholar] [CrossRef]
- Li, J.; Wu, R.; Chen, V.C. Robust autofocus algorithm for ISAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1056–1069. [Google Scholar]
- Wu, H.; Grenier, D.; Delisle, G.Y.; Fang, D.G. Translational motion compensation in ISAR image processing. IEEE Trans. Image Process. 1995, 4, 1561–1571. [Google Scholar] [PubMed]
- Xing, M.; Wu, R.; Lan, J.; Bao, Z. Migration through resolution cell compensation in ISAR imaging. IEEE Geosci. Remote Sens. Lett. 2004, 1, 141–144. [Google Scholar] [CrossRef]
- Son, J.S.; Thomas, G.; Flores, B. Range-Doppler Radar Imaging and Motion Compensation; Artech House: Norwood, MA, USA, 2001. [Google Scholar]
- Xi, L.; Guosui, L.; Ni, J. Autofocusing of ISAR images based on entropy minimization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1240–1252. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier transform for radar target detection, I: Generalized Doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.G.; Peng, S.B.; Yu, J.; Peng, Y.N.; Qian, L.C. Radar maneuvering target motion estimation based on generalized Radon-Fourier transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- Perry, R.; Dipietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for SAR ground moving-target imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.G.; Peng, Y.N. Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, L.; Yu, Y.; Tao, Q.; Zhu, Z. Robust ISAR range alignment via minimizing the entropy of the average range profile. IEEE Geosci. Remote Sens. Lett. 2009, 6, 204–208. [Google Scholar]
- Li, Y.; Xing, M.; Su, J.; Quan, Y.; Bao, Z. A new algorithm of ISAR imaging for maneuvering targets with low SNR. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 543–557. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. A fast maneuvering target motion parameters estimation algorithm based on ACCF. IEEE Signal Process. Lett. 2015, 22, 270–274. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Kong, L.; Yi, W. Fast Non-Searching Method for Maneuvering Target Detection and Motion Parameters Estimation. IEEE Trans. Signal Process. 2016, 64, 2232–2244. [Google Scholar] [CrossRef]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s distribution: Principle, implementation, properties, and performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar] [CrossRef]
- Luo, S.; Bi, G.; Lv, X.; Hu, F. Performance analysis on Lv distribution and its applications. Digit. Signal Process. 2013, 23, 797–807. [Google Scholar] [CrossRef]
- Li, X.; Kong, L.; Cui, G.; Yi, W.; Yang, Y. ISAR imaging of maneuvering target with complex motions based on ACCF–LVD. Digit. Signal Process. 2015, 46, 191–200. [Google Scholar] [CrossRef]
- Shui, P.L.; Xu, S.W.; Liu, H.W. Range-spread target detection using consecutive HRRPs. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 647–665. [Google Scholar] [CrossRef]
- Abatzoglou, T.J. A fast maximum likelihood algorithm for frequency estimation of a sinusoid based on Newton’s method. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 77–89. [Google Scholar] [CrossRef]
- Xia, X.G. A quantitative analysis of SNR in the short-time Fourier transform domain for multicomponent signals. IEEE Trans. Signal Process. 1998, 46, 200–203. [Google Scholar]
- Xia, X.G.; Chen, V.C. A quantitative SNR analysis for the pseudo Wigner-Ville distribution. IEEE Trans. Signal Process. 1999, 47, 2891–2894. [Google Scholar]
- O’Donoughue, N.; Moura, J.M.F. On the Product of Independent Complex Gaussians. IEEE Trans. Signal Process. 2012, 60, 1050–1063. [Google Scholar] [CrossRef]
- Ma, N.; Goh, J.T. Ambiguity-function-based techniques to estimate DOA of broadband chirp signals. IEEE Trans. Signal Process. 2006, 54, 1826–1839. [Google Scholar]
- Rife, D.; Boorstyn, R. Single tone parameter estimation from discrete-time observations. IEEE Trans. Inf. Theory 1974, 20, 591–598. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).