Abstract
This paper analyzes the underlying complexity and non-linearity of electroencephalogram (EEG) signals by computing a novel multi-scale entropy measure for the classification of seizure, seizure-free and normal EEG signals. The quality factor (Q) based multi-scale entropy measure is proposed to compute the entropy of the EEG signal in different frequency-bands of interest. The Q -based entropy (QEn) is computed by decomposing the signal with the tunable-Q wavelet transform (TQWT) into the number of sub-bands and estimating K-nearest neighbor (K-NN) entropies from various sub-bands cumulatively. The optimal selection of Q and the redundancy parameter (R) of TQWT showed better robustness for entropy computation in the presence of high- and low-frequency components. The extracted features are fed to the support vector machine (SVM) classifier with the wrapper-based feature selection method. The proposed method has achieved accuracy of 100% in classifying normal (eyes-open and eyes-closed) and seizure EEG signals, 99.5% in classifying seizure-free EEG signals (from the hippocampal formation of the opposite hemisphere of the brain) from seizure EEG signals and 98% in classifying seizure-free EEG signals (from the epileptogenic zone) from seizure EEG signals, respectively, using the SVM classifier. We have also achieved classification accuracies of 99% and 98.6% in classifying seizure versus non-seizure EEG signals and the individual three classes, namely normal, seizure-free and seizure EEG signals, respectively. The performance measure of the proposed multi-scale entropy has been found to be comparable with the existing state of the art epileptic EEG signals classification methods studied using the same database.
1. Introduction
Worldwide, around 60 million people are affected by epilepsy disorder, indicating frequent occurrence of seizure events due to hyper-synchronous firing of neuron clusters [1]. Electroencephalogram (EEG) signals are frequently used as a convenient and inexpensive tool for the diagnosis of epilepsy. Manual monitoring of EEG signals for the detection of epileptic seizure is a time-consuming task even for highly-trained neurologists. Thus, automated methods of seizure detection based on advanced signal processing techniques will significantly reduce the burden of monitoring lengthy EEG signals by clinicians. Many studies have been carried out in developing automated systems, which extract discriminative features for the classification of epileptic EEG signals [2,3]. Classification of epileptic seizure EEG signals has been performed by exploiting the underlying non-stationarity and nonlinearity of EEG signals in previous studies. In [2], the authors used the area of the phase space representations of the intrinsic mode functions (IMFs) as features and achieved a classification accuracy of 98.67% in classifying seizure-free and seizure EEG signals. In [3], bandwidth contributions due to amplitude and frequency modulations of IMFs have been considered as features for the classification of non-seizure and seizure EEG signals and achieved classification accuracy of 99.5–100%. Epileptic seizure EEG signal classification has been performed by extracting area features from the second order difference plot and analytic signal representation of IMFs extracted from EEG signals using empirical mode decomposition (EMD) [4]. Non-stationary signal decomposition techniques and time-frequency domain analysis for the classification of epileptic EEG signals have been studied extensively. In [5], the features extracted from time-frequency distributions, namely Wigner–Ville distribution and short time Fourier transform (STFT), are used for the classification of epileptic seizure EEG signals with the artificial neural-network classifier. They achieved 100% classification accuracy when classifying seizure EEG signals from normal EEG signals. Acharya et al. [6] have extracted texture features from scalogram images of EEG signals with higher order spectra (HOS) features and classified seizure, seizure-free and normal EEG signals with a classification accuracy of 96%. In [7], the authors applied wavelet transform on EEG signals to decompose into sub-bands and computed statistical features from these sub-bands. The data dimension was reduced using linear discriminant analysis (LDA), independent component analysis (ICA) and principal component analysis (PCA) followed by support vector machine (SVM) and obtained the highest classification of 100% in classifying seizure and normal classes of EEG signals. In [8], epileptic seizure EEG signals have been classified using discrete wavelet transform and generalized fractal dimensions method. In [9], the authors decomposed EEG signals using tunable-Q wavelet transform (TQWT) and extracted Kraskov entropy (measured from the mathematical expression of K-nearest neighbors (K-NN) entropy) features from the decomposed sub-band signals to classify seizure and seizure-free EEG signals. They achieved classification accuracy of 97.75% with the least squares support vector machine (LS-SVM) classifier. In [10], the authors decomposed EEG signals using TQWT and extracted spectral features from the TQWT decomposed sub-band signals followed by the bagging algorithm to classify epileptic EEG signals. They achieved classification accuracy of 98.40% in classifying seizure, seizure-free and the normal classes of EEG signals. The classification of epileptic seizure EEG signals has been carried out by several other nonlinear features, namely recurrence quantification analysis (RQA) [11], Hurst exponent [12] and approximate entropy (ApEn) [13]. Local binary pattern (LBP)-based methods have been suggested in recent studies for the classification of epileptic seizure EEG signals. In [14], one-dimensional (1D) LBP-based features are extracted for the classification of epileptic seizure EEG signals and obtained classification accuracy of 95.67% when classifying seizure, seizure-free and the normal classes of EEG signals. In [15], the authors have developed a method based on the LBP of the Gabor filter-decomposed EEG signals followed by the nearest neighbor classifier and classified seizure-free and seizure EEG signals with a classification accuracy of 98.33%. In a recent study [16], key-point-based LBP has been used for the classification of seizure EEG signals. The authors obtained classification accuracy of 98.80% with a standard deviation (SD) of 0.11% in classifying seizure, seizure-free and normal groups of EEG signals. In [17], the authors modeled EEG signals by the linear prediction (LP) process, and the energy of the modeling error was used for the epileptic seizure EEG signal classification task. They achieved classification accuracy of 94% in classifying seizure and seizure-free EEG signals. Epileptic seizure EEG signal classification has been performed using the fractional LP model in [18]. They computed signal energy and fractional LP error energy as features for the classification of seizure-free and seizure EEG signals with the SVM classifier and obtained 95.33% classification accuracy in classifying seizure and seizure-free EEG signals. The PCA has been used with the cosine radial basis function (RBF) neural network for the classification of epileptic EEG signals in [19], and the authors yielded classification accuracy of 96.6% in classifying seizure, seizure-free and normal EEG signals. The short-term maximum Lyapunov exponent (STLmax) has been estimated from the EEG recordings of intractable epilepsy patients in [20]. They estimated low STLmax in the focal area of the brain during the pre-ictal or inter-ictal state. In [21], the authors processed one hour-long pre-ictal segments and estimated the STLmax profiles from them. They modeled spatial STLmax maps with the combination of two Gaussian functions to extract parameters of the fitted models, which in turn helped to extract quantitative information about the spatial distribution of the STLmax. For three out of four patients, the authors found low STLmax levels in the brain regions of seizure origination. In [22], the authors have used permutation entropy (PE)-based [23] spatio-temporal analysis for EEG synchronization activity in 24 patients suffering from absence seizures and 40 healthy subjects. They found a higher PE value for fronto-temporal areas, and it showed a lower value when computed from the parietal/occipital area. In [24], the authors proposed the permutation Rényi entropy (PEr) for the classification of seizure and seizure-free EEG signals of patients diagnosed with childhood absence epilepsy. Their proposed algorithm performed better than conventional PE.
In this paper, we have presented a new method for the classification of seizure, seizure-free and normal classes of EEG signals. The proposed method computes the complexity of the analyzed signals in multi-level oscillatory scales. Entropy features have been used extensively as a measure of the complexity in biomedical signal processing [25,26,27,28]. Traditional measures of entropies, namely Shannon entropy [29], Kolmogorov–Sinai (K-S) entropy [30], approximate entropy (ApEn) [31] and sample entropy (SEn) [32], quantify the complexity of time series. These methods measure the complexity of the time series in a single scale, which may not be able to quantify the underlying dynamics of real time series [33]. The signals generated from complex biological systems consist of more than one spatiotemporal scales [33]. In [33], the authors have proposed multi-scale entropy (MSEn), which computed SEn over different scales of a signal as a measure of complexity. The multi-scale version of SEn has been utilized for the complexity measure of multivariate EEG signals in [34]. In [35], the authors proposed multi-scale PE for the classification of epileptic events in EEG signals and distinguishing healthy controls from patients. The underlying idea of MSEn is based on coarse graining (computation of the average over an increasing number of samples), which computes a smaller value of entropy following the increment of the time scale [36]. The MSEn approach, proposed in [33], introduces oscillations due to the presence of significant side-lobes in the finite impulse response (FIR) filter of varying transfer function length. In [36], the authors replaced the FIR filter by the low-pass Butterworth filter to rectify the problem of aliasing associated with FIR filter frequency response. As an improvement of MSEn, intrinsic mode entropy (IMEn) [37] is proposed based on EMD, which computes complexity in high frequency scales of the signal, as well as being robust to dominating low-frequency components by combining the group of IMFs. The concept of multilevel filtering has been applied in the EMD domain [38] and in the flexible analytic wavelet transform (FAWT) [39] domain [40]. However, in some cases, the EMD method failed to extract low-energy components from the analyzed time series [41], and hence, low-energy components are absent in the time-frequency plane. Secondly, the EMD method may not be suitable for signals consisting of singularities and localized waves [42]. Keeping in mind the above constraints of existing multi-scale entropy measures, we have proposed a novel multi-scale K-NN entropy measure based on the multi-level filtering approach using the TQWT [43]. The K-NN entropy has been used as a discriminative feature in the area of biomedical signal processing [9,25]. However, in the current study, it has been presented that the conventional K-NN entropy feature is not sufficient enough to provide good classification accuracy in classifying three EEG classes, namely seizure, seizure-free and normal. Thus, in this work, the conventional K-NN entropy has been enhanced with multi-scale filtering using TQWT, which provided a significant discrimination among seizure, seizure-free and normal EEG signals. Recently, in [44], the authors proposed multivariate sub-band fuzzy entropy based on TQWT and applied their proposed entropy for the discrimination of focal and non-focal EEG signals. In this paper, the TQWT-based multi-scale K-NN entropy is computed by generating sub-bands (SBs) of the signal to be analyzed by proper selection of the quality factor (Q), the redundancy parameter (R) and the number of levels of decomposition (J) using TQWT, followed by computation of K-NN entropy for the cumulative addition of each sub-band signal. Optimal performance can be achieved in this method by optimal selection of the Q and R parameters. The MSEn measures are used to distinguish seizure EEG signals from normal and seizure-free EEG signals automatically. Figure 1 presents the block diagram of the proposed method.
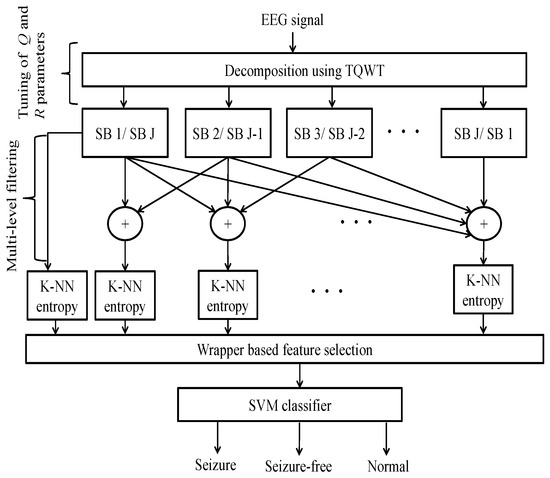
Figure 1.
Block diagram of the proposed epileptic EEG classification method.
The remainder of the paper is organized as follows. A brief description of K-NN entropy, TQWT-based multi-scale K-NN entropy and the details of the EEG database used are provided in Section 2, Section 3 and Section 4, respectively. Section 5 briefly describes the feature selection method and classifier used in this study. Section 6 presents the results obtained using the proposed method, Section 7 discusses the effectiveness of the proposed method in discriminating the normal, seizure-free and seizure classes of EEG signals, and the paper concludes in Section 8.
2. K-Nearest Neighbor Entropy Estimation
The K-NN estimate of the differential entropy of a d-dimensional random variable Y with unspecified density function is defined as [45,46]:
where N is the number of samples of the random variable Y and is the digamma function expressed as follows [46]:
where is mathematically defined as .
Here, is the distance between the sample of random variable Y and its K nearest neighbors in d-dimensional space.
denotes the volume of a d-dimensional unit ball. For the Euclidean norm, is defined as [45]:
In order to study the estimation of K-NN entropy for a highly random signal in the presence of a dominant low-frequency component with different weights, we have studied the similar example used to estimate the sample entropy in [37]. It has been found that K-NN entropy estimation is highly affected by the low-frequency signal component of the analyzed signal. Even though the analyzed signal is highly random, the K-NN entropy estimates the value closer to the K-NN entropy estimate of the dominant low-frequency component present in that analyzed signal.
Figure 2 shows the K-NN entropy estimates with varying nearest neighbors for dominant low-frequency component signal , highly random signal (Gaussian noise) and their weighted sums expressed as . It is clear from the figure that though is highly random in nature, the K-NN entropy estimate of (with increased value of the weight parameter w) is closer to the K-NN entropy estimate of . Therefore, the conventional measure of K-NN entropy may not be well suitable for physiological signals where the dominance of low-frequency trends is high. Therefore, a multilevel filtering approach prior to the computation of entropy is necessary for the discriminant analysis of biomedical signals. In the next section, we propose the multilevel filtering concept using TQWT for the computation of multi-scale K-NN entropy.
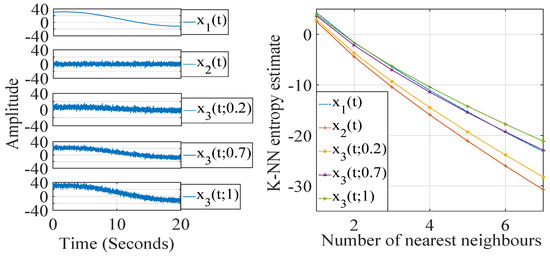
Figure 2.
Random signals with increasing weights of dominant low-frequency component and their K-NN entropy estimates.
3. TQWT-Based K-NN Entropy
In this work, we have analyzed the signals using TQWT prior to the computation of K-NN. The TQWT is built with the help of the two-channel filter bank method. Let the low-pass and high-pass scale factors of the two-channel filter bank be denoted by and , respectively. The low-pass filter frequency response is mathematically expressed as [43]:
The high-pass filter frequency response can be formulated as [43]:
where is considered as the Daubechies filter frequency response [43]. The high-pass scale factor and low-pass scale factor are to be selected in order to follow the condition [43].
The Q and R of TQWT are mathematically expressed as:
Detailed mathematical expressions of Q, R, center frequency () and the bandwidth (B) of TQWT are provided in [43].
The computation algorithm of Q-based entropy (QEn) can be summarized as follows:
- Sub-band signals denoted as are reconstructed by applying the inverse TQWT operation.
- To measure the complexity at multiple oscillatory levels, K-NN entropy has been computed on the signals, generated by cumulatively summing the reconstructed sub-band signals. We have formulated two kinds of multilevel filtering approaches as follows:
- (a)
- Detailed sub-band to approximate sub-band: The multilevel filtering starts from the highest oscillatory level sub-band to the dominant low-frequency trend sub-band . Finally, can be mathematically formulated as follows:where corresponds to highest oscillatory sub-band and corresponds to the dominant low-frequency trend, is the scale factor and l is the number of nearest neighbors.
- (b)
- Approximate sub-band to the detailed sub-band: The multilevel filtering starts from the dominant low-frequency trend sub-band to the highest oscillatory level sub-band . Finally, can be expressed as follows:where corresponds to the dominant low-frequency trend and corresponds to the highest oscillatory sub-band, denotes the scale factor and l represents number of nearest neighbors. In this work, we have set for K-NN entropy estimation.
In Figure 3 and Figure 4, we have graphically presented the frequency responses of successive scale factors corresponding to different values of Q parameters for this operation. In these figures, S1, S2, and so on, represent Scale 1, Scale 2, and so on, respectively.
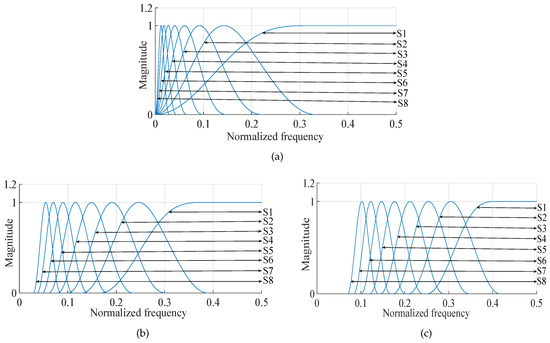
Figure 3.
TQWT-based multi-scale filtering operation starting from the detailed sub-band to the approximate sub-band: (a) for , , ; (b) for , , ; (c) for , , .
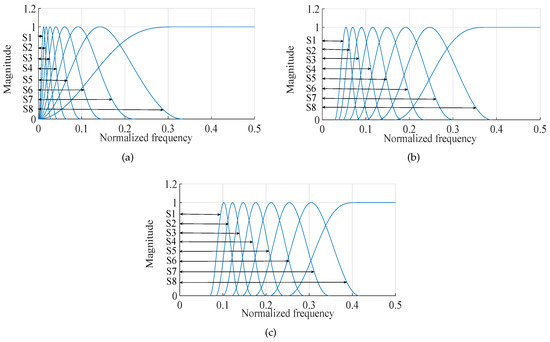
Figure 4.
TQWT-based multi-scale filtering operation starting from the approximate sub-band to the detailed sub-band: (a) for , , ; (b) for , , ; (c) for , , .
4. EEG Dataset
The public EEG database is provided by the University of Bonn, Germany [47]. The database has five sets known as Z, O, N, F and S. Each of these sets contains 100 single-channel recordings of EEG signals with a sampling rate of 173.61 Hz and a duration of 23.6 s. The sets Z and O contain the surface EEG recording, acquired from five healthy volunteers in eyes-open and eyes-closed conditions, respectively, using the standard 10–20 electrode placement scheme. Hence, the EEG signals of sets Z and O are considered as normal EEG signals. Sets N and F contain seizure-free intracranial EEG signals, whereas set S contains intracranial seizure EEG signals. The three sets, namely N, F and S, were recorded from five epileptic patients in their presurgical evaluation of epilepsy. The EEG signals of set N were acquired from the hippocampal formation, opposite hemisphere of the brain. The EEG signals of set F were recorded from the epileptogenic zone. In Table 1, we have summarized the information of the above-mentioned EEG database. Figure 5 shows sample EEG signals belonging to the S, F, N, Z and O sets. In this study, we have performed six classification problems as follows:

Table 1.
Information of the EEG datasets publicly made available by the University of Bonn, Germany [47].
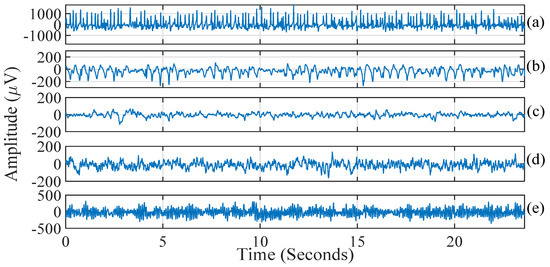
Figure 5.
Sample EEG signals: (a) seizure (S); (b) seizure-free (F); (c) seizure-free (N); (d) normal eyes-open (Z); (e) normal eyes-closed (O).
- (S-Z): classification of two classes, namely seizure (S) EEG signals and normal eyes-open (Z) EEG signals.
- (S-O): classification of two classes, namely seizure (S) EEG signals and normal eyes-closed (O) EEG signals.
- (S-N): classification of two classes, namely seizure (S) EEG signals and seizure-free (N) EEG signals.
- (S-F): classification of two classes, namely seizure (S) EEG signals and seizure-free (F) EEG signals.
- (S-FNZO): classification of two classes, namely seizure (S) EEG signals and non-seizure (F, N, Z and O) EEG signals.
- (S-FN-ZO): classification of three classes, namely seizure (S) EEG signals, seizure-free (F and N) EEG signals and normal (Z and O) EEG signals.
5. Classification of EEG Records
After finding the MSEn features from the EEG signals, they are classified into three different categories, namely normal, seizure-free and seizure.
We have selected the optimal set of MSEn features using the wrapper-based feature selection method [48] and classified using the SVM [49] classifier with the radial basis function (RBF) kernel [50].
The classification performance measurement metrics [51], namely accuracy (Acc), sensitivity (Sens) and specificity (Spec), are obtained using the ten-fold cross-validation method [51,52]. The ten-fold cross-validation method has been used widely to get unbiased performance of the classifier in the area of bio-medical signal processing [50,51]. All of the classification tasks along with wrapper-based feature selections have been performed using the WEKA machine learning toolbox (Weka 3.6.13, University of Waikato, Hamilton, New Zealand) [53]. For all of the classification tasks, the cost parameter of SVM is set to one and gamma parameter of the RBF kernel to (default in WEKA).
6. Experimental Results
In this section, we have presented the performance evaluation of the proposed multi-scale K-NN entropy features for epileptic EEG classification. In Figure 6 and Figure 7, the multilevel filtered signals of the seizure EEG signals (a–i) and their corresponding frequency spectrums (j–r) are presented. The distinguishing ability of the conventional K-NN entropy feature and proposed multi-scale K-NN entropy features have been tested using the confidence interval plot (99% confidence level) of the three mentioned classes (normal, seizure-free, seizure) in Figure 8a–c.
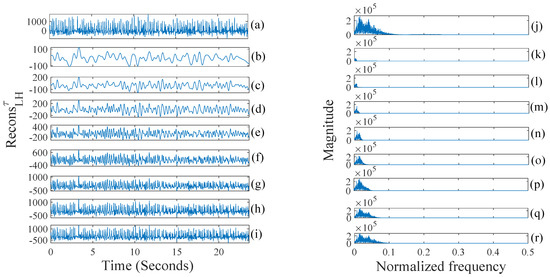
Figure 6.
(a) Seizure EEG signal; (b)–(i) proposed multilevel filtered (, and ) versions of it (); and (j)–(r) are their corresponding spectrums.
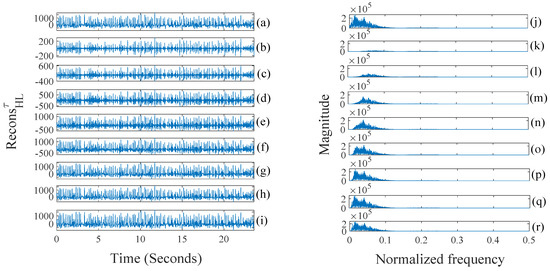
Figure 7.
(a) Seizure EEG signal; (b)–(i) proposed multilevel filtered (, and ) versions of it (); and (j)–(r) are their corresponding spectrums.
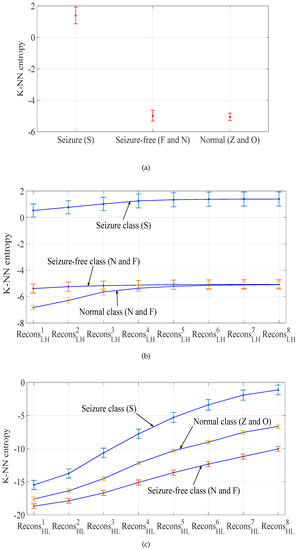
Figure 8.
(a) Confidence interval plot (with 99% confidence) of conventional K-NN entropy features obtained from EEG signals (Butterworth high-pass filtered with cut-off frequency 0.1 Hz); (b) confidence interval plot (with 99% confidence) of TQWT-based multi-scale entropy (; ; ) for three classes (normal, seizure-free and seizure); (c) confidence interval plot (with 99% confidence) of TQWT-based multi-scale entropy (; ; ) for three classes (normal, seizure-free and seizure).
In Figure 8a, the confidence interval plot of K-NN entropy features for three classes is shown. We have computed K-NN entropies of high-pass filtered EEG signals with cut-off frequency of 0.1 Hz, instead of raw EEG signals. The EEG signal samples in this database are integers, and in many cases, the Euclidean distances between nearest neighbor samples and the current sample are zero. In that case, K-NN entropies of raw EEG signals are not a finite quantity, and hence, high-pass filtered EEG signals are considered. It can be observed from Figure 8a that the confidence interval of the seizure class has a clear separation with the other two classes (seizure-free and normal), but the confidence interval of seizure-free and normal EEG signals overlaps significantly. This limits the applicability of K-NN entropy to clearly distinguish three classes. Figure 8b shows the confidence interval plot of three classes using our proposed features. It is clear from Figure 8b that the confidence intervals of seizure-free and normal classes are well separated in only the first two levels ( and ). We have also plotted the confidence interval of three classes using the proposed feature in Figure 8c, where all three classes are well separated in terms of their confidence intervals at each level. Thus, the proposed multi-scale K-NN entropy is robust to the dominant low-frequency component in the signal. In Table 2, the mean and SD of the proposed MSEn features, namely and , are presented. This indicates that the SD computed using the proposed method for normal categories of EEG signals are smaller than expected, due to the absence of abnormalities in the signals. In Table 3, we have presented the classification performance using the conventional K-NN entropy feature computed from high-pass filtered (cut-off frequency = 0.1 Hz) EEG signals. Though we achieved reasonably good classification accuracies for most of the classification problems, the classification accuracy for seizure, seizure-free and normal (S-FN-ZO) EEG signals is 64.8%, which is significantly low. As compared to conventional K-NN entropy, the performance of the proposed multi-scale K-NN entropy features is very promising. In Table 4, we have presented the the classification performance measures using our proposed method. In our method, the parameter (Q) is varied to get better discrimination among three classes. The number of decomposition levels of TQWT are set to 8 and 16, respectively, to put forward the importance of the number of sub-bands in the proposed MSEn based classification. In most of the classification tasks, we have achieved better classification results by considering . For , and , we have achieved significant improvement in classification accuracies for the majority of classification tasks, namely S-Z, S-O, S-N and S-FN-ZO, using the proposed feature. The highest classification accuracy of 100% is obtained for both classification tasks, namely S-Z and S-O. We have obtained the highest classification accuracy of 98.6% and 99.5% for S-FN-ZO and S-N, respectively. For the S-F classification task, the highest classification accuracy reported is 98% using the (, and ) feature. The classification performance using proposed feature is also noteworthy. For the S-FNZO classification task, the highest classification accuracy of 99% is achieved using the proposed feature (, and ). It is clear from Table 3 and Table 4 that there is significant improvement in classification accuracies for most of the considered classification tasks, except S-Z. In Table 5, we have summarized the comparison of the proposed method with the existing methods using the same EEG database. In most of the classification tasks, our proposed MSEn has shown comparable performance with the existing state of the art methods reported in Table 5.

Table 2.
Mean and SD of the extracted MSEn features (, , ).

Table 3.
Classification results using the conventional K-NN entropy feature.

Table 4.
Summary of the classification results for various tuning parameters.

Table 5.
Comparison of the proposed method with the existing methods studied using the same EEG dataset.
7. Discussion
The performance of the proposed multi-scale K-NN entropy is enhanced using the TQWT-based [43] multilevel filtering approach. The multi-level filtering based on TQWT has some major benefits. For analyzing signals of an oscillatory nature, a higher value of the Q factor is well suited. This is because with the increased value of the Q factor, the generated wavelets will be more oscillatory with increased center frequency and relatively narrow frequency responses. On the other hand, for a lower value of Q factors, the generated wavelets are less oscillatory and posses a wider frequency response as compared to their center frequencies. Thus, a lower value of the Q factor may be chosen for non-oscillatory transient signals [44]. These properties of the Q factor motivated us to use TQWT in our multi-scale analysis.
In this work, the multi-scaling operation is carried out starting from the low-frequency component and gradually introducing high frequency components cumulatively in successive scales. This is useful when analyzed signals have dominant high-frequency components. In multi-scaling with a lower scale factor, the reconstructed signal components after accumulation do not posses high-frequency components. Thus, with a lower scale factor, the complexity of low-frequency components can be computed. We have also performed the multi-scaling operation in the reverse direction, starting from the very high-frequency component signal and added low-frequency components in successive scales. This enables us to analyze high-frequency components of the signals without including the low-frequency component, which is predominant. As a result, the use of TQWT-based multilevel filtering enhances the discriminating ability of the conventional K-NN entropy features. In the previous studies, the TQWT framework together with K-NN entropy [9] and spectral features [10] have been proposed for epileptic EEG classification. The proposed method in this paper presents a generalized form of K-NN entropy in the TQWT framework, which has also been studied for the classification of seizure and seizure-free EEG signals [9]. Moreover, the proposed entropy feature has been applied for multiple classification problems associated with epileptic EEG signals. The proposed method also incorporates the feature selection technique before classifying EEG signals using the SVM classifier.
The highest performance of the proposed MSEn is achieved by optimal selection of input parameters Q, R and J. If any input parameter changes, the corresponding effect will be seen in the TQWT filter-bank, which in turn leads to a different multi-level filtering, and the computed entropy values will change accordingly. We have distinguished three classes (seizure, seizure-free and normal) with 99% confidence using confidence interval plots, which gives a clear separation between the classes. In this work, we have achieved the highest three-class classification accuracy of 98.60% (detailed to approximation multi-scale filtering) for , which is comparable with the existing classification methods using the same database in Table 5. The advantage of the proposed method is that it can discriminate the EEG classes by optimal selection of the Q and R parameters. It should be noted that intracranial seizure (dataset S) and seizure-free (datasets F and N) EEG recordings are clean signals due to their way of recording, thus having a high signal to noise ratio [63]. The seizure and seizure-free EEG signals from scalp EEG recordings may be more susceptible to noise, thus requiring an additional noise reduction process [64] before the feature extraction step to improve the classification performance. Due to the presence of the multi-level filtering step, our method is also suitable for the analysis of scalp EEG signals. Hence, our proposed method can be used for the classification of epileptic seizure EEG signals irrespective of the method used to record the EEG signals. The proposed multi-scale K-NN entropy can be applied for diagnostic application of diseases using electrocardiogram (ECG), electromyogram (EMG) and respiratory signals. The proposed framework in this paper can be used for automated diagnosis of abnormalities using biomedical signals.
8. Conclusions
In this paper, a new entropy measure Q-based K-NN entropy ( and ) has been proposed to compute K-NN entropy at different frequency scales of the EEG signal. The proposed method works better for analysis of the high frequency scale of the signal and is robust to dominant local trends with optimal selection of the Q and R parameters, which makes the proposed entropy measure more generalized. Higher values of Q are chosen for multi-scale analysis to analyze oscillatory signals. However, the selection of the Q and R parameters is application specific. Our proposed method achieved improvement in classification accuracies using multi-scale K-NN entropy features over conventional K-NN entropy features. In future, this proposed entropy can be used as a feature for the analysis and classification of other physiological signals. This proposed algorithm needs to be tested with long duration EEG recordings with more patients before using it for clinical applications.
Author Contributions
Ram Bilas Pachori and U. Rajendra Acharya designed the research problem; Abhijit Bhattacharyya performed the experiments and analyzed the data; Abhijit Bhattacharyya and Abhay Upadhyay interpreted the experimental results and wrote the manuscript. All the authors edited the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Witte, H.; Iasemidis, L.D.; Litt, B. Special issue on epileptic seizure prediction. IEEE Trans. Biomed. Eng. 2003, 50, 537–539. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B. Classification of epileptic seizures in EEG signals based on phase space representation of intrinsic mode functions. Expert Syst. Appl. 2015, 42, 1106–1117. [Google Scholar] [CrossRef]
- Bajaj, V.; Pachori, R.B. Classification of seizure and nonseizure EEG signals using empirical mode decomposition. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1135–1142. [Google Scholar] [CrossRef] [PubMed]
- Pachori, R.B.; Sharma, R.; Patidar, S. Classification of normal and epileptic seizure EEG signals based on empirical mode decomposition. In Complex System Modelling and Control through Intelligent Soft Computations; Zhu, Q., Azar, A.T., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 367–388. [Google Scholar]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Epileptic seizure detection in EEGs using time-frequency analysis. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Yanti, R.; Zheng, J.W.; Krishnan, M.M.R.; TAN, J.H.; Martis, R.J.; Lim, C.M. Automated diagnosis of epilepsy using CWT, HOS and texture parameters. Int. J. Neural Syst. 2013, 23, 1350009. [Google Scholar] [CrossRef] [PubMed]
- Subasi, A.; Gursoy, M.I. EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Syst. Appl. 2010, 37, 8659–8666. [Google Scholar] [CrossRef]
- Uthayakumar, R.; Easwaramoorthy, D. Epileptic seizure detection in EEG signals using multifractal analysis and wavelet transform. Fractals 2013, 21, 1350011. [Google Scholar] [CrossRef]
- Patidar, S.; Panigrahi, T. Detection of epileptic seizure using Kraskov entropy applied on tunable-Q wavelet transform of EEG signals. Biomed. Signal Process. Control 2017, 34, 74–80. [Google Scholar] [CrossRef]
- Hassan, A.R.; Siuly, S.; Zhang, Y. Epileptic seizure detection in EEG signals using tunable-Q factor wavelet transform and bootstrap aggregating. Comput. Methods Progr. Biomed. 2016, 137, 247–259. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Sree, S.V.; Chattopadhyay, S.; Yu, W.; Ang, P.C.A. Application of recurrence quantification analysis for the automated identification of epileptic EEG signals. Int. J. Neural Syst. 2011, 21, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Chua, C.K.; Lim, T.C.; Dorithy; Suri, J.S. Automatic identification of epileptic EEG signals using nonlinear parameters. J. Mech. Med. Biol. 2009, 9, 539–553. [Google Scholar] [CrossRef]
- Srinivasan, V.; Eswaran, C.; Sriraam, N. Approximate entropy-based epileptic EEG detection using artificial neural networks. IEEE Trans. Inf. Technol. Biomed. 2007, 11, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Kaya, Y.; Uyar, M.; Tekin, R.; Yıldırım, S. 1D-local binary pattern based feature extraction for classification of epileptic EEG signals. Appl. Math. Comput. 2014, 243, 209–219. [Google Scholar] [CrossRef]
- Kumar, T.S.; Kanhangad, V.; Pachori, R.B. Classification of seizure and seizure-free EEG signals using local binary patterns. Biomed. Signal Process. Control 2015, 15, 33–40. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Pachori, R.B.; Kanhangad, V.; Panigrahi, B. Automated diagnosis of epilepsy using key-point based local binary pattern of EEG signals. IEEE J. Biomed. Health Inform. 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Altunay, S.; Telatar, Z.; Erogul, O. Epileptic EEG detection using the linear prediction error energy. Expert Syst. Appl. 2010, 37, 5661–5665. [Google Scholar] [CrossRef]
- Joshi, V.; Pachori, R.B.; Vijesh, A. Classification of ictal and seizure-free EEG signals using fractional linear prediction. Biomed. Signal Process. Control 2014, 9, 1–5. [Google Scholar] [CrossRef]
- Ghosh-Dastidar, S.; Adeli, H.; Dadmehr, N. Principal component analysis-enhanced cosine radial basis function neural network for robust epilepsy and seizure detection. IEEE Trans. Biomed. Eng. 2008, 55, 512–518. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Morabito, F.C.; Principe, J.C. Visualization of the short term maximum Lyapunov exponent topography in the epileptic brain. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 4257–4260. [Google Scholar]
- Mammone, N.; Principe, J.C.; Morabito, F.C.; Shiau, D.S.; Sackellares, J.C. Visualization and modeling of STLmax topographic brain activity maps. J. Neurosci. Methods 2010, 189, 281–294. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Morabito, F.C. Analysis of absence seizure EEG via Permutation entropy spatio-temporal clustering. Proceedingd of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; pp. 1417–1422. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Duun-Henriksen, J.; Kjaer, T.W.; Morabito, F.C. Differentiating interictal and ictal states in childhood absence epilepsy through permutation Rényi entropy. Entropy 2015, 17, 4627–4643. [Google Scholar] [CrossRef]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. An efficient automated technique for CAD diagnosis using flexible analytic wavelet transform and entropy features extracted from HRV signals. Expert Syst. Appl. 2016, 63, 165–172. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Patidar, S.; Pachori, R.B.; Acharya, U.R. Automated diagnosis of coronary artery disease using tunable-Q wavelet transform applied on heart rate signals. Knowl. Based Syst. 2015, 82, 1–10. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Chen, Z.; Tian, X.; Du, S.; Huang, R. Approximate entropy and support vector machines for electroencephalogram signal classification. Neural Regen. Res. 2013, 8, 1844. [Google Scholar] [PubMed]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591. [Google Scholar] [CrossRef]
- Pincus, S. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Costa, M.; Goldberger, A.; Peng, C. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Labate, D.; La Foresta, F.; Morabito, G.; Palamara, I.; Morabito, F.C. Entropic measures of EEG complexity in Alzheimer’s disease through a multivariate multiscale approach. IEEE Sens. J. 2013, 13, 3284–3292. [Google Scholar] [CrossRef]
- Labate, D.; Palamara, I.; Mammone, N.; Morabito, G.; La Foresta, F.; Morabito, F.C. SVM classification of epileptic EEG recordings through multiscale permutation entropy. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–5. [Google Scholar]
- Valencia, J.; Porta, A.; Vallverdú, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Amoud, H.; Snoussi, H.; Hewson, D.; Doussot, M.; Duchêne, J. Intrinsic mode entropy for nonlinear discriminant analysis. IEEE Signal Process. Lett. 2007, 14, 297–300. [Google Scholar] [CrossRef]
- Pachori, R.B.; Hewson, D.; Snoussi, H.; Duchêne, J. Postural time-series analysis using empirical mode decomposition and second-order difference plots. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 537–540. [Google Scholar]
- Bayram, I. An analytic wavelet transform with a flexible time-frequency covering. IEEE Trans. Signal Process. 2013, 61, 1131–1142. [Google Scholar] [CrossRef]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. Use of accumulated entropies for automated detection of congestive heart failure in flexible analytic wavelet transform framework based on short-term HRV signals. Entropy 2017, 19, 92. [Google Scholar] [CrossRef]
- Peng, Z.; Peter, W.T.; Chu, F. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Gupta, A.; Joshi, S. On the concept of intrinsic wavelet functions. In Proceedings of the International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 22–25 July 2014; pp. 1–5. [Google Scholar]
- Selesnick, I. Wavelet transform with tunable Q-factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.B.; Acharya, U.R. Tunable-Q wavelet transform based multivariate sub-band fuzzy entropy with application to focal EEG signal analysis. Entropy 2017, 19, 99. [Google Scholar] [CrossRef]
- Veselkov, K.A.; Pahomov, V.I.; Lindon, J.C.; Volynkin, V.S.; Crockford, D.; Osipenko, G.S.; Davies, D.B.; Barton, R.H.; Bang, J.W.; Holmes, E.; et al. A metabolic entropy approach for measurements of systemic metabolic disruptions in patho-physiological states. J. Proteome Res. 2010, 9, 3537–3544. [Google Scholar] [CrossRef] [PubMed]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Sharma, M.; Pachori, R.B.; Sircar, P.; Acharya, U.R. A novel approach for automated detection of focal EEG signals using empirical wavelet transform. Neural Comput. Appl. 2016, in press. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.B. A multivariate approach for patient specific EEG seizure detection using empirical wavelet transform. IEEE Trans. Biomed. Eng. 2017, in press. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation And Model Selection; International Joint Conference on Artificial Intelligence: Montreal, QC, Canada, 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Tzallas, A.; Tsipouras, M.; Fotiadis, D. Automatic seizure detection based on time-frequency analysis and artificial neural networks. Comput. Intell. Neurosci. 2007, 2007, 80510. [Google Scholar] [CrossRef] [PubMed]
- Peker, M.; Sen, B.; Delen, D. A novel method for automated diagnosis of epilepsy using complex-valued classifiers. IEEE J. Biomed. Health Inform. 2016, 20, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. Automatic EEG seizure detection using dual-tree complex wavelet-Fourier features. Expert Syst. Appl. 2014, 41, 2391–2394. [Google Scholar] [CrossRef]
- Orhan, U.; Hekim, M.; Ozer, M. EEG signals classification using the K-means clustering and a multilayer perceptron neural network model. Expert Syst. Appl. 2011, 38, 13475–13481. [Google Scholar] [CrossRef]
- Samiee, K.; Kovács, P.; Gabbouj, M. Epileptic seizure classification of EEG time-series using rational discrete short-time Fourier transform. IEEE Trans. Biomed. Eng. 2015, 62, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Rivero, D.; Dorado, J.; Rabunal, J.R.; Pazos, A. Automatic epileptic seizure detection in EEGs based on line length feature and artificial neural networks. J. Neurosci. Methods 2010, 191, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Molinari, F.; Sree, S.V.; Chattopadhyay, S.; Ng, K.H.; Suri, J.S. Automated diagnosis of epileptic EEG using entropies. Biomed. Signal Process. Control 2012, 7, 401–408. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhou, W.; Li, S.; Cai, D. Epileptic EEG classification based on extreme learning machine and nonlinear features. Epilepsy Res. 2011, 96, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Al Ghayab, H.R.; Li, Y.; Abdulla, S.; Diykh, M.; Wan, X. Classification of epileptic EEG signals based on simple random sampling and sequential feature selection. Brain Inform. 2016, 3, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Bhati, D.; Sharma, M.; Pachori, R.B.; Gadre, V.M. Time–frequency localized three-band biorthogonal wavelet filter bank using semidefinite relaxation and nonlinear least squares with epileptic seizure EEG signal classification. Digit. Signal Process. 2017, 62, 259–273. [Google Scholar] [CrossRef]
- Ahirwal, M.K.; Kumar, A.; Singh, G.K. Analysis and testing of PSO variants through application in EEG/ERP adaptive filtering approach. Biomed. Eng. Lett. 2012, 2, 186–197. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).