Abstract
Nowadays, the accurate identification of natural frequencies and damping ratios play an important role in smart civil engineering, since they can be used for seismic design, vibration control, and condition assessment, among others. To achieve it in practical way, it is required to instrument the structure and apply techniques which are able to deal with noise-corrupted and non-linear signals, as they are common features in real-life civil structures. In this article, a two-step strategy is proposed for performing accurate modal parameters identification in an automated manner. In the first step, it is obtained and decomposed the measured signals using the natural excitation technique and the synchrosqueezed wavelet transform, respectively. Then, the second step estimates the modal parameters by solving an optimization problem employing a genetic algorithm-based approach, where the micropopulation concept is used to improve the speed convergence as well as the accuracy of the estimated values. The accuracy and effectiveness of the proposal are tested using both the simulated response of a benchmark structure and the measurements of a real eight-story building. The obtained results show that the proposed strategy can estimate the modal parameters accurately, indicating than the proposal can be considered as an alternative to perform the abovementioned task.
1. Introduction
Over the last years, retrieving information about the behavior of civil structures under different scenarios is a task of paramount importance, since an inadequate design may not be able to stand the normal vibrations produced by the operational conditions, causing economic, structural, and human catastrophes. In this regard, the estimation of modal parameters, such as natural frequencies and damping ratios, of civil structures has become an important tool because they can reflect their dynamic behavior under natural and artificial excitations. Modal parameters are widely used in applications such as seismic design for civil and earthquake engineering [1,2,3], vibration control [4], condition and damage assessment [5,6,7], and development or update of analytical models [8,9]. Hence, their accurate estimation allows providing more reliable and suitable information of the structure, improving the performance and results of the aforementioned applications.
In order to obtain the modal parameters of a civil structure, it must be excited either using human-made equipment or naturally-produced vibrations. The former involves the utilization of hammers, drop weight or shakers; however, the in-test structure must be closed in order to allow the realization of the tests. Moreover, the energy available from these sources limits their utilization in real-life structures. For these reasons, the utilization of natural sources (e.g., vibrations produced by wind, traffic loadings, and small seismic waves) is usually preferred because: (i) they can properly excite a civil structure regardless of its size; (ii) the normal operation is not interrupted; and (iii) they are the typical vibrations that every civil structure is subjected during its service period [10]. In this regard, as these types of sources are of a non-stationary nature, producing a noisier response than the one obtained using human-made equipment, the modal parameter identification (MPI) becomes a challenging task, since the noise levels compromise the results accuracy [11] if classical algorithms are employed.
During the last two decades, a branch of algorithms have been specifically designed for performing the MPI of civil structures using ambient vibrations, including fast Fourier transform (FFT)-based methods [12,13], the autoregressive model-based models [14,15], random decrement technique (RDT) [16], natural excitation technique combined with the eigensystem realization algorithm (NExT-ERA) [17,18], and stochastic subspace identification (SSI) methods [19,20], among others. Despite the excellent results obtained using the abovementioned techniques, some difficulties remain unsolved. For example, FFT-based methods have problems when they process non-stationary and noisy signals; further, the detection of closely-spaced modes is troublesome. The use of autoregressive models requires an appropriate selection of the algorithm to estimate the model coefficients, since the accuracy of the estimated results relies on the coefficients [21]. Regarding RDT, the accuracy of the technique might be affected when non-stationary signals are processed [22]. On the other hand, although SSI and NExT-ERA can deal better with noise-corrupted signals, the detection of closely-spaced modes usually requires selecting a higher order in the estimated model, which might generate false or spurious frequency components [23,24], making necessary the utilization of further stages to detect and separate the real frequencies from the fictitious ones.
In order to lessen the abovementioned difficulties, other advanced approaches such as the wavelet transform (WT) and the empirical mode decomposition (EMD) have been explored to perform the MPI of civil structures. WT has become an important tool in MPI, because it can be used to analyze nonlinear and non-stationary signals, characteristics found in the measured signals [25,26]; however, a carefully selection of the mother wavelet and its parameters must be done in order to ensure a good time-frequency resolution. Moreover, it is sensitive to noisy signals [26]. On the other hand, the EMD method is an adaptive scheme, which is designed to process nonlinear and non-stationary signals according to the frequencies contented in the time-series signal. Its utilization, however, is limited in the MPI because of the so-called mode mixing effect, which is the assignment of more than one frequency to each frequency band, limiting the accurate estimation of the modal parameters [27]. Although different improvements to the EMD method have been proposed to mitigate this effect [27,28], the developed techniques still have problems when they deal with noisy signals. From this point of view, other signal processing techniques should be explored in order to perform the MPI in an accurate and reliable way. MPI of real-life structures, especially large ones, is complicated; in fact, a single computational technique may not be sufficient. The works developed by [28,29,30,31] show that the utilization of multi-paradigm approaches can lead to develop methodologies capable of dealing with noisy signals, as well as to improve accuracy, efficiency, and stability of the resulting algorithm. Recently, a methodology based on the utilization of the synchrosqueezed wavelet transform (SWT) in combination with Hilbert transform (HT), and Kalman Filter (FK) is proposed for MPI [11]. The work proposed in that article uses SWT to decompose the signal into its individual modes; then; for each mode, and it is applied HT to obtain its instantaneous amplitude, which is used to estimate both the natural frequency and damping ratio. It should be pointed out that the methodology has to make use of KF in order to smooth the obtained instantaneous amplitude since any imperfection in this signal could potentially cause a miscalculation of these values. KF requires setting different parameters to obtain the best possible result, making necessary to design a procedure to find out these values, which change depending on the nature of the sensors used to acquire the signal. Evidently, sometimes they can be difficult to reach in a practical way, thus deteriorating the accuracy and reliability of the modal parameters value. For these reasons, it should be desirable to develop a new methodology that does not require designing calibration procedures to ensure the best possible result, and also to improve the accuracy of the modal parameters values. In particular, as the damping ratios usually have a very small value, the accurate estimation of the damping ratio is a complicated issue [32]. In the literature, many problems that involve the search and selection of the best-suited parameters for specific models have been solved by means of optimization algorithms, where genetic algorithms (GA) have demonstrated to be an efficient tool for solving these problems [33].
Taking advantages of the multi-paradigm approaches, this paper proposes a new methodology based on the utilization of the SWT fused with GA to identify natural frequencies and damping ratios of civil structures. In general, it uses two steps to estimate the modal parameters of civil structures. In Step 1, the mode extraction is performed by using the NExT and SWT algorithms, where NExT converts the measured response into a free-decay one and SWT decomposes the converted signal into its fundamental components. In Step 2, the natural frequencies and damping ratios of every mode are calculated using a GA-based approach, where a fusion of novel objective functions for the estimation of natural frequencies and damping ratios is proposed. It is worth noting that the appropriate selection of the search space and the utilization of the micropopulation concept will reduce the required time to estimate the optimal solution, allowing its obtaining in a practical way. In order to validate the efficacy and performance of the proposed methodology, two study cases are carried out. For the first one, the benchmark of the International Association for Structural Control American Society of Civil Engineers Structural Health Monitoring (IASC-ASCE SHM) Task Group, which consists of a four-story 2 × 2 bay 3D steel frame structure is used, where the simulated response obtained from a finite element analysis (FEA) model is processed to obtain its modal parameters. The obtained results are compared with other methodologies [11,34,35]. Regarding the second study case, the real measurements obtained from an eight-story steel frame subjected to white noise input in a shaking table test are also processed to estimate its modal parameters.
2. Methodology
Figure 1 shows a schematic diagram of the proposal to perform the MPI of civil structures. The proposal is based on two steps. In Step 1, the measured vibration signal is converted in a free-decay response and separated into individual mono-components using the NExT and SWT methods, respectively. In Step 2, the natural frequency (NF) and damping ratio (DR) of each individual component is calculated in an automatic manner using an optimization scheme solved by a GA-based approach. The fundamental concepts of the aforementioned techniques and their use in the proposal are described in the following subsections.

Figure 1.
Proposed methodology block diagram (GA, genetic algorithms).
2.1. Step 1: Estimation of the Individual Modes
2.1.1. Free-Decay Form Estimation
NExT method was proposed by James et al. [36] to estimate and extract the response (a free-decay one) produced broadband dynamic excitations using the acquired response samples. It presents a slightly improved capability to deal better with noisy signals, which allows obtaining better free-decay responses unlike random decrement technique [37]. For this reason, NExT method has been employed in this work and in several applications, such as health monitoring [38,39,40]. This method assumes that any civil structure, subjected to broadband signals as excitation source, can be represented by the following motion equation:
where M, C, and K are the mass, damping, and stiffness matrices, respectively; x and y are the measurement positions. Analyzing the aforementioned equation, it is seen that the cross-correlation function fulfills the homogenous equation of motion; hence, it can be treated as the free-damped response of the structure. is estimated by using the following equation:
where x and y are the reference signal and the in-test signal, respectively, N is the length of the signals, and k is the variable index that goes from 0 to 2N−1.
2.1.2. Mode Extraction
Once the free-decay vibration of measured signal, , is obtained using the NExT method, the SWT is employed to decompose it in its individual mono-components, xi(t), which correspond to the excited modes of the analyzed structure. SWT is capable of analyzing nonlinear, transient, and non-stationary signals. Further, it has been proven to be a reliable tool to detect components in highly noisy environments without compromising the quality of the retrieved individual modes [11,41].
In general, the SWT of a time signal is obtained in four steps [42]. Firstly, the continuous WT (Wf(a,b)) of the signal is calculated; secondly, using the obtained wavelet coefficients, the phase transform, ωf, is employed to estimate the instantaneous frequency of the in-test signal by means of:
where Wf, a, and b are the wavelet coefficient, scale and time offset, respectively. Later, the calculated wavelet coefficients Wf(a,b) are reassigned to the time-frequency domain. Hence, every point (a,b) is converted to another point (ωf(a,b),b) using an operator named synchrosqueezed (Tf). This operation allows enhancing the frequency location and is defined as:
where Δω = ωl − ωl−1 and Δa = ak − ak−1.
Finally, each individual mono-component, xi(t), of the original signal, detected in the previous step, is recovered as follows:
where is a constant calculated as:
where ψ is the wavelet mother selected and ^ denotes the Fourier transform of ψ. An in-depth explanation of SWT can be found in [42]. It should be pointed out that if the frequency value of the mode is desired, tools like the Fourier or Hilbert Transforms must be used [11].
2.2. Step 2: Modal Parameters Identification
Once divided the time signal into its fundamental modes or mono-components using SWT, a mathematical expression, which describes the behavior of each obtained mode is necessary. The obtained mono-components present a free-decay response; hence, the following equation can be used:
where Ai, fi, and ζi are the amplitude, frequency and damping ratio values of the i-th mode, respectively. In general, the search of these parameters for modeling a real signal can be solved by proposing an optimization scheme.
GA is one of the most employed methods to solve optimization problems, since global optimal solutions can be found [30]. A flow chart of the stages required for implementation of the GA is shown in Figure 2. In Step 1, the initial population is generated, usually randomly, to ensure a diversity of potential solutions. In Step 2, the population is evaluated in one or more objective functions in order to find the best individuals and their fitness values, which are used in the next Step 3. In this step, it is checked if the population fulfills the criterion established to end the algorithm execution. If the population cannot be considered as the solution, an additional step (Step 4) must be executed, where the genetic operators (reproduction, crossover, and mutation) are applied to obtain a new population. The reproduction employs the best individuals, which have the highest fitness value, to be part of the new population. On the other hand, the crossover operation uses the current best individuals to create new ones employing several crossover points, at the same position in the used individuals. The delimited parts are swapped to create the new individuals. A crossover probability value is used to select the order of swap. Finally, the mutation modifies specific position values according to a mutation probability value. It should be noticed that the abovementioned operators manipulate the individuals in bit manner, i.e., the operations are performed in a bit-to-bit basis. Once the new population is created, they are evaluated and tested until the stop criterion is reached. When the algorithm finalizes its execution, the final population is designated as the problem solutions (Step 5).
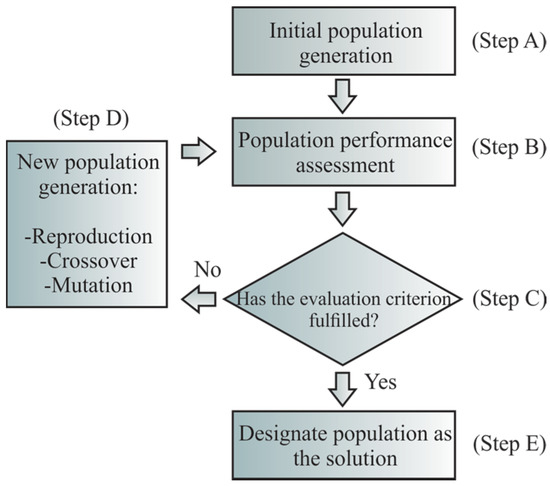
Figure 2.
Flow chart of the GA execution.
GA uses many potential solutions or individuals, usually about 100, to estimate the solution [43]. This can produce a low convergence speed in the best scenario, or can cause a premature convergence or stagnation, which means that the estimated value is close enough to the solution (not an optimal solution); but its value does not change through the generations [33]. In order to lessen the abovementioned limitations, the concept of micro-GA has been presented by [44], which consists of utilizing a very small population, usually four or five individuals per generation [45]. This allows ensuring that the used time to evaluate the population is less than the required by the classical GA; further, the convergence and the diversity required are guaranteed by using the same operators than the classical GA. For this reason, micro-GA is used in this work.
Figure 3 illustrates the graphical description of the micro GA-based approach proposed for performing the MPI. Employing the advantages of micro-GA, in this work, four individuals are used since they provide an adequate compromise between diversity and computational time required to find the solution. On the other hand, the design space, i.e., the values that the natural frequencies and damping ratios can take, is also set. Table 1 summarizes the range of possible values for both the natural frequency and damping ratios, which will be estimated by the proposed micro-GA scheme. It should be noticed that in these ranges the natural frequencies and damping ratios values of civil structures can be found [46]. Thus, this range will allow obtaining the optimal solutions. Each individual has a length of 32 bits, the first 16 bits are used for the candidate natural frequency, whereas the last 16 bits contain the candidate damping ratio. The initial values of the population are generated randomly, ensuring that they are in a normal distribution in order to guarantee a diversity of potential solutions.

Figure 3.
Proposed micro-GA scheme for the modal parameter identification (MPI).

Table 1.
Range of values used for every modal parameter.
Once generated the initial population, the next step is to evaluate their performance. Recalling Equation (7), it is observed that the produced signal depends of two variables: frequency and damping ratio. The amplitude of each mode is taken as the first value of the recovered signal, which corresponds with the maximum amplitude of signal. Therefore, it is necessary to use different functions to evaluate the impact of the subtle changes in the values of frequency and damping ratio in the final solution. For evaluating the natural frequency value, the following equations are proposed:
where f1 represents the correlation of each mono-component estimated by the micro-GA (ym) using Equation (7) and by SWT (y); and f2 is the correlation of the envelopes of each mono-component obtained by the micro-GA (gm) and by SWT (g). The envelope of each signal is obtained as follows:
where yh is the Hilbert Transform of y [47]. Finally, f3 represents the histograms difference of the signals y and ym.
It is important to mention that the correlation measures the similarity between two signals and the histogram gives the shape and distribution of the signal. Therefore, the combination of these equations provides useful information for the detection of the subtle changes that are produced when the estimated values are close to their exact counterparts. For this reason, the following objective function is proposed to optimize the natural frequency value:
where w1, w2, and w3 are ponderation weights used to set a level of importance of each function, fi, of the objective function. It was found, from previous experimentations, that 0.5, 0.45, and 0.05 for w1, w2, and w3, respectively, were the best values since they allow estimating the natural frequency value with the lowest error, indicating that correlation between the two signals provides the most information to obtain an accurate frequency value.
On the other hand, in order to evaluate the damping ratio value, the envelope of the in-test signal and the one constructed are employed. Thus, the following evaluation function is proposed:
Therefore, Equation (13) allows setting the following objective function:
Once the obtained values with the proposed objective functions in Equations (12) and (14) are evaluated, the next step is to verify the criterion for stopping the generation of new populations. In this regard, it is used the maximization criterion of the objective functions, since it is desired to calculate the highest correlation value, because it will indicate that the signal, constructed with Equation (7), has the most resemblance with the mono-component obtained by SWT. If the criterion is not achieved; then, it is necessary to create a new population based on the current one. To this purpose, the best individual, the one that produces the signal with the highest correlation value with respect of the in-test one, is used directly as the first individual of the new generation. The other individuals are created using the crossover operator with the best individual of the former generation and the two remaining individuals. After investigating the number of different crossover points, the four-point crossover is used in this paper with a small mutation probability value, since this value must reflect its real-life counterpart [48,49]. Further, both the crossover and mutation probabilities are usually selected according to the desired application [50]. In this work, it is found that 0.5 and 0.007 are the crossover and mutation probability values that allow obtaining the best results. The abovementioned procedure is repeated until no improvements of the correlation value in a certain value of iterations, and for each retrieved mode by SWT. It should be pointed out that the combination of the abovementioned objective functions, Equations (12) and (14), allows avoiding the utilization of schemes to smooth the envelop, since it is only used for comparison purposes in the proposed approach, unlike the work presented in [11], which uses it as a fundamental part of the estimation of the modal parameters formulas, making the proposal inherently more robust to the aforementioned variations of the envelop form.
3. Numerical Assessment of the New Methodology Performance
The validation of the efficacy and performance of the proposed methodology for identifying and quantifying the modal parameters (NF and DR), the phase I of the benchmark problem developed by the IASC-ASCE structural health monitoring task group is used [51]. It consists of a FE-based code of a four-story 2 × 2 bay 3D steel frame constructed at the University of British Columbia (UBC), located at Vancouver, the British Columbia, Canada. Figure 4 shows the overall dimensions of the structure and the location of the sixteen sensors used to measure vibration data during the excitation. The structure was excited using broadband input signals applied in both horizontal directions (x and y). Using a sampling frequency of 1000 Hz, 20 s of the structure response were acquired resulting in 20,000 samples. Every mode has a damping ratio of 1%. The measured vibration response of sensors 7 (x-direction) and 6 (y-direction) are selected to carry out the analysis. Figure 5 depicts the acquired signals in the x- and y-directions by the abovementioned sensors, respectively.
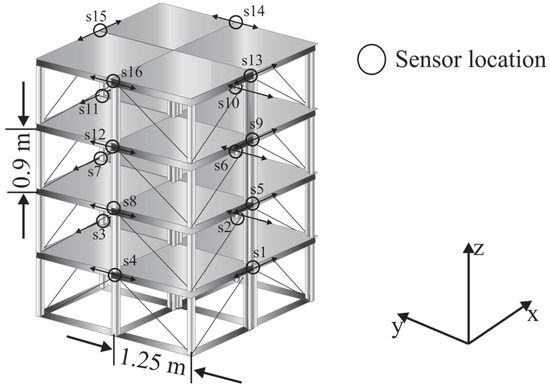
Figure 4.
Benchmark structure used and the location of the used sensors.

Figure 5.
Measured signals in the: (a) x- and (b) y-directions.
Following the proposed methodology, which is implemented in MATLAB, the measured vibration signals of sensors 7 and 6 are converted to their free-decay response employing NExT method. Recalling from Section 2, the method uses reference signals. Caicedo [52] suggests that these signals should be far away of the in-test ones. In this regard, sensors 15 (x-direction) and 14 (y-direction) fulfill with the aforementioned suggestion and, hence, they are used as the references. In this example, only 2000 samples of obtained signal are selected because they allow obtaining the free-decay response correctly; thus, the original signal transformed to a new signal of 2.0 s. Figure 6 shows the obtained free responses for the x- and y-directions. Then, the obtained free-decay responses in the x- and y-directions are separated in individual modes using the SWT, each with a single frequency corresponding to one modal response. The Gaussian wavelet is employed as wavelet mother since it provides the best time-frequency resolution [11].
Figure 6.
Estimated free damped response in the: (a) x- and (b) y-directions.
Once the individual modes using the SWT are obtained, the natural frequencies and damping ratios are calculated using the micro-GA approach. Figure 7 and Figure 8 illustrate the convergence graphs for the NF, DR, and correlation value for the x- and y-direction, respectively. It is seen that the estimated values reach the optimal solution when the correlation values are 0.9, indicating that modes estimated by SWT-micro-GA scheme are remarkable similar to the ones extracted by SWT. Further, it is seen that for all the modal parameters, their values are reached within 80 generations, indicating that the convergence rate is fast, making evident that the proposed objective functions, along with the micropopulation concept, allows increasing the convergence rate. A graphical illustration of the similarities is shown in Figure 9, where it is confirmed in a visual way that both modes are very similar.
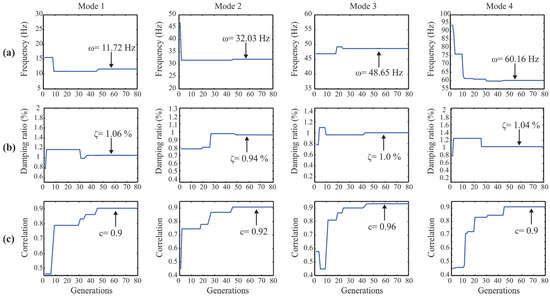
Figure 7.
Convergence graphs of the: (a) natural frequency; (b) damping ratio; and (c) correlation value for the x-direction modes.
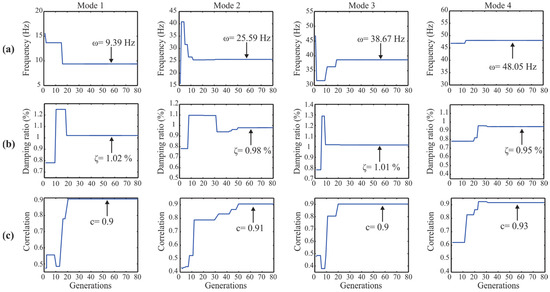
Figure 8.
Convergence graphs of the: (a) natural frequency; (b) damping ratio; and (c) correlation value for the y-direction modes.
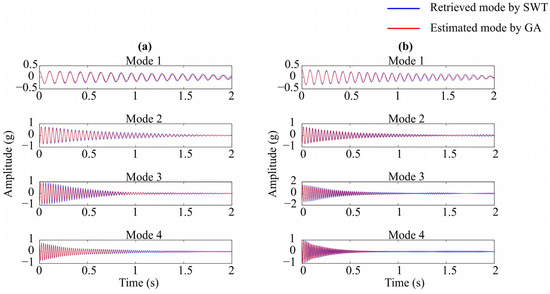
Figure 9.
Estimated modes by the GA-based approach in the: (a) x- and (b) y-directions.
Table 2 summarizes modal parameters calculated using the proposal and the ones estimated by the FEA model. Additionally, the estimated natural frequencies and damping ratios using the methodologies proposed by Li et al. [34], Amini and Hedayati [35], and Perez-Ramirez et al. [11] are presented. In general, the results presented in this table show that the proposal can identify and estimate the first eight modes detect by the FEM model in an accurate way. In particular, the NF value is very close to the theoretical one, as the maximum deviation is found to be about 0.5%. These results show that the objective function, described by Equation (12), can be considered as an adequate maximization function. On the other hand, the results obtained by Perez-Ramirez et al. [11] and Li et al. [34] show that the same eight NF are also found with their proposals. It is worth noting that the former uses the complex mode indicator function as a signal processing tool; however, the maximum deviation was found to be about of 23%, indicating that this function may not be able to deal with noisy and time-variant signal properly. On the contrary, the results estimated by the former show that this methodology can be considered as accurate, as the deviations are quite similar to the ones obtained by the proposal. Even when the maximum deviation (0.33%) is lower than the one obtained with this proposal, more NF modes have a significant lower deviation compared with the aforementioned methodology. The work reported by Amini and Hedayati [35] use the sparse component analysis, a blind source separation technique, to analyze the response. It is evident that they cannot estimate the third NF of the y-direction. By the presented results, it is seen that this methodology cannot be considered as accurate, as the maximum deviation is higher than 10%. It is important to mention that they only analyze the y-direction; hence, the other four natural frequencies of the x-direction are not considered.

Table 2.
Identified modal parameters of the benchmark structure shown in Figure 4. (FEA: finite element analysis.)
In addition, the obtained results allow to affirm that the damping ratios values estimated by the proposal are more accurate than the ones calculated by Amini and Hedayati [35] and Perez-Ramirez et al. [11], since a maximum error for the proposal and the other two works are: 6%, 12% and 15%, respectively. In particular, the proposal outperforms the methodology of the former reference by achieving an error reduction of over 50%. This reduction can be achieved as the proposal uses the envelope values in a qualitative way, that is, how similar are the two envelopes, making them inherent more robust to any slightly spike that can be presented. On the contrary, the methodology of Perez-Ramirez et al. [11] is more susceptible to these spikes, as the value is an integral part of the equations used to obtain the DR value. It can be seen that the approach used by Amini and Hedayati [35], show that the used methodology can successfully estimate the DR with a reasonable accuracy, indicating that their methodology has a better performance to estimate the aforementioned values. The main objective of Li et al. [34] is to find the best FE-based model; thus, the authors do not estimate the damping ratios of structure. From these works, it is evident that the ones that use multi-paradigm approaches lead to better estimations of the modal parameters. Further, it is worth noting that Su et al. [53] mentioned that for obtaining an accurate value, it should be present a maximum error of 2% and 20% for natural frequency and damping ratio, respectively. In this regard, the proposed methodology contributes to demonstrate the abovementioned statement, as the obtained results can be considered as accurate.
In summary, the obtained results demonstrate that the proposal is an excellent tool to identify and quantify the NF and DR. This is proven as the errors between the obtained values and the theoretical counterparts do not exceed 0.5% and 0.6%, respectively. Moreover, the validity of the proposed objective function is also demonstrated, as the correlation value of the estimated modes compared to the original ones is higher than 0.9.
4. Application to an Eight-Story Building
In order to evaluate the performance of the proposed methodology under real-life conditions, the eight-story steel frame experimental data are used to estimate its natural frequencies and damping ratios. A graphical illustration of the structure is shown in Figure 10. The building has H-shaped columns with dimensions of 1.5 m × 1.1 m × 9.44 m (width, length, and height). Additionally, lead plates of 250 kg are piled on each floor; hence, each floor has a total mass of 325 kg. The base of the building was subjected to white noise excitation in the long-span direction. This structure is located in the National Center for Research on Earthquake Engineering, Taiwan, and is also used by Su et al. [53]. The responses were measured using eight velocity sensors distributed on the eight stories and located at the center of each floor. The sensor employs a sampling rate of 200 Hz during 100 s, thus each signal contains 20,000 samples. The measured vibration response of sensor 4 is used indistinctly to estimate the modal parameters of the structure. Figure 11 depicts the signal measured by sensor 4.
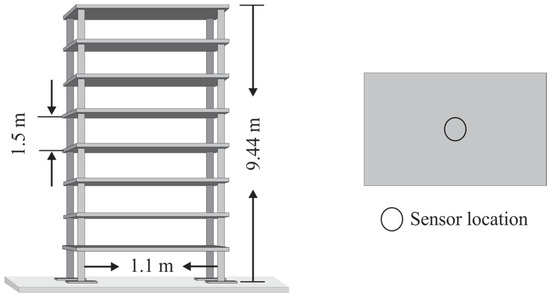
Figure 10.
General overview of the eight-story building analyzed.
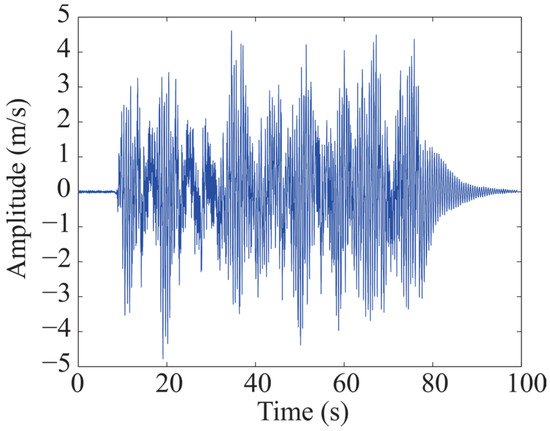
Figure 11.
Sensor used for estimating the modal parameters of the eight-story building.
Using the proposal, the acquired vibration data are transformed to the to free-damped vibration form using NExT method. In an analogous way to the previous example, sensor 8 is used as the reference signal to estimate the free-decay response, since this sensor is far away from selected sensor 4 to estimate the modal parameters of structure. In this case, sensor 8 satisfies this specification recommended by Caicedo [52]. In this example, 1000 samples signal are selected to estimate the free-damped vibration form. This means that the original signal is converted to a new signal of 5.0 s, as shown in Figure 12. This number of samples is sufficient to estimate the free-damped form. Then, once obtained the free-damped response, it is processed by SWT in order to extract the individual modes contained in the signal, which are illustrated in Figure 13.
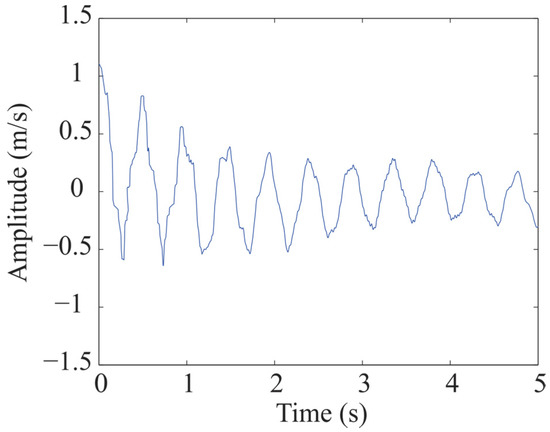
Figure 12.
Free-damped response estimated for the eight-story building.
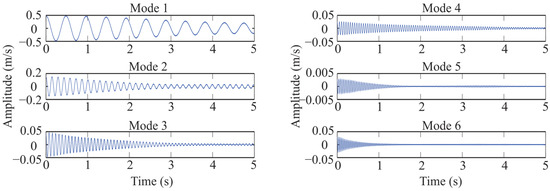
Figure 13.
Individual modes recovered by synchrosqueezed wavelet transform (SWT).
Finally, the micro-GA approach is used to obtain the natural frequencies and damping ratios of extracted modes, obtained in the previous step, of the analyzed building. Table 3 presents the values of estimated natural frequencies and damping ratios values using the proposal and FEA. Further, the estimated modal parameters of eight-story steel frame using the methodologies proposed by Su et al. [53] and Perez-Ramirez et al. [11] are also presented. It is observed that these methodologies present similar results to the estimated by FEA model, which indicates that they can be considered as accurate; however, it is important to mention that the methodology proposed by Su et al. [53] requires calibration for each structure analyzed, limiting an automatic estimation of the parameters. On the other hand, it is also seen a slightly difference between the estimated DR values using the methodologies proposed by Su et al. [53], Perez-Ramirez et al. [11], and the values obtained with the proposal. It should be noticed that for this case, there are no reference values for the DR; thus, the comparison is performed in a qualitative way, that is, how similar are the values obtained with the different methodologies. In general, it can be seen that the proposal obtains similar values compared with those obtained by Su et al. [53]. The difference between the values obtained by Perez-Ramirez et al. [11] and the proposal is due to that the KF still delivers a signal with some spikes that affect its quality, deteriorating the estimated results by HT, as the mathematical operations used for obtaining the value (a derivative) can be affected by the spikes, even a slightly one. On the contrary, the proposed methodology demonstrates to be efficient to perform the MPI of automatic manner, as neither requires the proper selection of the AR model number (Su et al. [53]) nor the fine tuning of the KF parameters (Perez-Ramirez et al. [11]).

Table 3.
Estimated natural frequencies and damping ratios of the eight-story steel frame.
5. Conclusions
In this work, a new methodology based the utilization of an optimization algorithm, the micro-GA, fused with SWT for detecting and estimating the natural frequencies and damping ratios values of civil structures in an automatic manner is presented. In order to demonstrate the efficiency of the proposal, two study cases are presented: (1) a benchmark problem, a numerical model selected from the literature with aiming at comparison with other methodologies; and (2) a real-life eight-story building.
The results for the numerical simulation show that the presented methodology is effective in detecting and quantifying the modal parameters of structure, since the obtained errors for natural frequencies and damping ratios have a maximum value of 0.5% and 6%, respectively. This is confirmed since the proposed methodology detects all the modal parameters of the benchmark problem with a remarkably improved accuracy, unlike the abovementioned methodologies, indicating that the proposed novel objective functions that involve the use of the correlation, histogram, and envelope, as well as its weights proved to be effective to solve the MPI. It is worth noting that the proposal allows obtaining an error reduction of over 50% compared to the results presented in [11]. Particularly, it should be pointed out that this proposal only uses the envelope in a quantitative way, i.e., to estimate how similar is the proposed signal with the reference one, whereas the work presented in [11] uses the envelope to directly estimate the modal parameters, making necessary the utilization of schemes to smooth the envelope. On the other hand, by means of the micropopulation concept, the proposal also demonstrated to be fast as only 80 generations were required to estimate the modal parameters values.
In the eight-story building example, the results show that the proposal is efficient for identifying and estimating the ND and DR values of the building using dynamic vibrations, a challenging routine, as the measured signals can be time-varying or transient, as well as noisy, confirming that proposed objective functions are efficient to deal with this task. Additionally, the results show that proposed methodology does not require a previous knowledge of structure or an initial value or specialized calibration for estimating the modal parameters with accuracy unlike the methodology proposed by Su et al. [53].
As a future work, it is necessary to explore the convenience to adapt the proposed methodology to analyze the response of building that have adaptive capabilities, such as smart structures or structures that deal with varying loads.
Acknowledgments
This work was supported in part by the Mexican Council of Science and Technology (CONACyT) by the scholarship 289377 and by the SEP-CONACyT CB-2015/254697 project. The authors appreciate to the National Center for Research on Earthquake Engineering for providing the data of the eight-story building.
Author Contributions
Carlos Andres Pererz-Ramirez and Arturo Yosimar Jaen-Cuellar conceived and designed the methodology. Carlos Andres Pererz-Ramirez, Juan Pablo Amezquita-Sanchez, Aurelio Dominguez-Gonzalez, and Martin Valtierra-Rodriguez performed the experiments and analyzed the obtained results. All authors contributed to the preparation of the manuscript, and Roque Alfredo Osornio-Rios, Juan Pablo Amezquita-Sanchez, and Rene De Jesus Romero-Troncoso revised the manuscript and provided useful intellectual content.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Pei, Q.; Li, L. Modal parameter identification of civil engineering structures under seismic excitations. Adv. Mater. Res. 2014, 859, 163–166. [Google Scholar] [CrossRef]
- Çelebi, M.; Kashima, T.; Ghahari, S.F.; Abazarsa, F.; Taciroglu, E. Responses of a tall building with US code-type instrumentation in Tokyo, Japan—To events before, during and after the Tohoku earthquake of March 11, 2011. Earthq. Spectra 2015, 32, 497–522. [Google Scholar] [CrossRef]
- Coffield, A.; Adeli, H. Irregular steel building structures subjected to blast loading. J. Civ. Eng. Manag. 2016, 22, 17–25. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Boduroğlu, M.H. Active tendon control of torsionally irregular structures under near-fault ground motion excitation. Comput. Aided Civ. Infrastruct. Eng. 2013, 28, 718–736. [Google Scholar] [CrossRef]
- Jiang, X.; Adeli, H. Pseudospectra, MUSIC, and dynamic wavelet neural network for damage detection of highrise buildings. Int. J. Numer. Methods Eng. 2007, 71, 606–629. [Google Scholar] [CrossRef]
- Gangone, M.V.; Whelan, M.J.; Janoyan, K.D. Wireless monitoring of a multi-span bridge superstructure for diagnostic load testing and system identification. Comput. Aided Civ. Infrastruct. Eng. 2011, 26, 560–579. [Google Scholar] [CrossRef]
- Osornio-Rios, R.A.; Amezquita-Sanchez, J.P.; Romero-Troncoso, R.J.; Garcia-Perez, A. MUSIC-ANN analysis for locating structural damages in a truss-type structure by means of vibrations. Comput. Aided Civ. Infrastruct. Eng. 2012, 27, 687–698. [Google Scholar] [CrossRef]
- Foti, D.; Gattulli, V.; Potenza, F. Output-only identification and model updating by dynamic testing in unfavorable conditions of a seismically damaged building. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 659–675. [Google Scholar] [CrossRef]
- Skafte, A.; Aenlle, M.L.; Brincker, R. A general procedure for estimating dynamic displacements using strain measurements and operational modal analysis. Smart Mater. Struct. 2016, 25, 025020. [Google Scholar] [CrossRef]
- Peeters, B.; Maeck, J.; De Roeck, G. Vibration-based damage detection in civil engineering: excitation sources and temperature effects. Smart Mater. Struct. 2001, 10, 518–527. [Google Scholar] [CrossRef]
- Perez-Ramirez, C.A.; Amezquita-Sanchez, J.P.; Adeli, H.; Valtierra-Rodriguez, M.; Camarena-Martinez, D.; Romero-Troncoso, R.J. New methodology for modal parameters identification of smart civil structures using ambient vibrations and synchrosqueezed wavelet transform. Eng. Appl. Artif. Intell. 2016, 48, 1–12. [Google Scholar] [CrossRef]
- García-Palencia, A.J.; Santini-Bell, E. A two-step model updating algorithm for parameter identification of linear elastic damped structures. Comput. Aided Civ. Infrastruct. Eng. 2013, 28, 509–521. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, Y.L.; Xiao, X. Multiscale modeling and model updating of a cable-stayed bridge. I: Modeling and influence line analysis. J. Bridge Eng. 2015, 20, 04014112. [Google Scholar] [CrossRef]
- Li, J.; Ruiz-Sandoval, M.; Spencer, B.F., Jr.; Elnashai, A.S. Parametric time-domain identification of multiple-input systems using decoupled output signals. Earthq. Eng. Struct. Dyn. 2014, 43, 1307–1324. [Google Scholar] [CrossRef]
- Niu, Y.; Fritzen, C.-P.; Jung, H.; Buethe, I.; Ni, Y.-Q.; Wang, Y.-W. Online simultaneous reconstruction of wind load and structural responses—Theory and application to Canton Tower. Comput. Aided Civ. Infrastruct. Eng. 2015, 30, 666–681. [Google Scholar] [CrossRef]
- Górski, P. Investigation of dynamic characteristics of tall industrial chimney based on GPS measurements using Random Decrement Method. Eng. Struct. 2014, 83, 30–49. [Google Scholar] [CrossRef]
- Wethyavivorn, B.; Surit, S.; Apichatyakul, C.; Lerdsivanon, N. Model verification of Thai historic masonry monuments. J. Perform. Construct. Facil. 2016, 30, 04014188. [Google Scholar] [CrossRef]
- Marulanda, J.; Caicedo, J.M.; Thomson, P. Modal identification using mobile sensors under ambient excitation. J. Comput. Civ. Eng. 2017. [Google Scholar] [CrossRef]
- Bursi, O.S.; Kumar, A.; Abbiati, G.; Ceravolo, R. Identification, model updating, and validation of a steel twin deck curved cable-stayed footbridge. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 703–722. [Google Scholar] [CrossRef]
- Nohutcu, H.; Demir, A.; Ercan, E.; Hokelekli, E.; Altintas, G. Investigation of a historic masonry structure by numerical and operational modal analyses. Struct. Des. Tall Spec. Build. 2015, 24, 821–834. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal processing techniques for vibration-based health monitoring of smart structures. Arch. Comput. Meth. Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Ceravolo, R.; Abbiati, G. Time domain identification of structures: Comparative analysis of Output-Only Methods. J. Eng. Mech. 2013, 139, 537–544. [Google Scholar] [CrossRef]
- Dorvash, S.; Pakzad, S.N. Effects of measurement noise on modal parameter identification. Smart Mater. Struct. 2012, 21, 065008. [Google Scholar] [CrossRef]
- Zhang, G.; Tang, B.; Tang, G. An improved stochastic subspace identification for operational modal analysis. Measurement 2012, 45, 1246–1256. [Google Scholar] [CrossRef]
- Adeli, H.; Kim, H. Wavelet-Based Vibration Control of Smart Buildings and Bridges; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, Z.-C.; Chen, G.-D. Analytical mode decomposition of time series with decaying amplitudes and overlapping instantaneous frequencies. Smart Mater. Struct. 2013, 22, 095003. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Perez-Ramirez, C.A.; Amezquita-Sanchez, J.P.; Romero-Troncoso, R.J.; Garcia-Perez, A. Novel down-sampling empirical mode decomposition approach for power quality analysis. IEEE Trans. Ind. Electr. 2016, 63, 2369–2378. [Google Scholar] [CrossRef]
- Bao, C.; Hao, H.; Li, Z.-X. Multi-stage identification scheme for detecting damage in structures under ambient excitations. Smart Mater. Struct. 2013, 22, 045006. [Google Scholar] [CrossRef]
- Qarib, H.; Adeli, H. A new adaptive algorithm for automated feature extraction in exponentially damped signals for health monitoring of smart structures. Smart Mater. Struct. 2015, 24, 125040. [Google Scholar] [CrossRef]
- Musafere, F.; Sadhu, A.; Liu, K. Towards damage detection using blind source separation integrated with time-varying auto-regressive modeling. Smart Mater. Struct. 2016, 25, 015013. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. A new music-empirical wavelet transform methodology for time–frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Proc. 2015, 45, 55–68. [Google Scholar] [CrossRef]
- Jaen-Cuellar, A.Y.; Romero-Troncoso, R.J.; Morales-Velazquez, L.; Osornio-Rios, R.A. PID-controller tuning optimization with genetic algorithms in servo systems. Int. J. Adv. Robot. Syst. 2013, 10, 324. [Google Scholar] [CrossRef]
- Li, P.J.; Xu, D.W.; Zhang, J. Probability-based structural health monitoring through Markov chain Monte Carlo sampling. Int. J. Struct. Stab. Dyn. 2016, 16, 1550039. [Google Scholar] [CrossRef]
- Amini, F.; Hedayati, Y. Underdetermined blind modal identification of structures by earthquake and ambient vibration measurements via sparse component analysis. J. Sound Vib. 2016, 366, 117–132. [Google Scholar] [CrossRef]
- The Natural Excitation Technique (NExT) for Modal Parameter Extraction from Operating Wind Turbines. Available online: http://prod.sandia.gov/techlib/access-control.cgi/1992/921666.pdf (accessed on 15 November 2016).
- Giraldo, D.; Caicedo, J.M.; Song, W.; Mogan, B.; Dyke, S.J. Modal identification through ambient vibration: A comparative study. In Proceedings of the 2006 IMAC-XXIV: Conference & Exposition on Structural Dynamics Conference, San Louis, MO, USA, 30 January–2 February 2009.
- Moser, P.; Moaveni, B. Design and deployment of a continuous monitoring system for the dowling hall footbridge. Exp. Tech. 2011, 37, 15–26. [Google Scholar] [CrossRef]
- Zhang, G.; Ma, J.; Chen, Z.; Wang, R. Automated eigensystem realization algorithm for operational modal analysis. J. Sound Vib. 2014, 333, 3550–3563. [Google Scholar] [CrossRef]
- Dammika, A.J.; Kawarai, K.; Yamaguchi, H.; Matsumoto, Y.; Yoshioka, T. Analytical damping evaluation complementary to experimental structural health monitoring of bridges. J. Bridge Eng. 2015, 20, 04014095. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Synchrosqueezed wavelet transform-fractality model for locating, detecting, and quantifying damage in smart highrise building structures. Smart Mater. Struct. 2015, 24, 065034. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. App. Comput. Harm. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Chakravarty, S.; Mittra, R.; Williams, N.R. Application of a microgenetic algorithm (MGA) to the design of broad-band microwave absorbers using multiple frequency selective surface screens buried in dielectrics. IEEE Tran. Antennas Propag. 2002, 50, 284–296. [Google Scholar] [CrossRef]
- Krishnakumar, K. Micro-genetic algorithms for stationary and non-stationary function optimization function. In Proceedings of the SPIE Intelligent Control and Adaptive Systems, Philadelphia, PA, USA, 1 November 1989; Volume 1196.
- Dennis, B.H.; Dulikravich, G.S. Optimization of magneto-hydrodynamic control of diffuser flows using micro-genetic algorithms and least-squares finite elements. Finite Elem. Anal. Des. 2001, 37, 349–363. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Pearson Education: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Hilbert, D. Begrundung der kinetischen Gastheorie. Math. Ann. 1912, 72, 562–577. [Google Scholar] [CrossRef]
- Adeli, H.; Cheng, N.-T. Integrated genetic algorithm for optimization of space structures. J. Aerosp. Eng. 1993, 6, 315–328. [Google Scholar] [CrossRef]
- Greenwell, R.N.; Angus, J.E.; Finck, M. Optimal mutation probability for genetic algorithms. Math. Comput. Model. 1995, 21, 1–11. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. Syst. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. Phase I IASC-ASCE structural health monitoring benchmark problem using simulated data. J. Eng. Mech. 2004, 130, 3–15. [Google Scholar] [CrossRef]
- Caicedo, J.M. Practical guidelines for the Natural Excitation Technique (NExT) and the Eigensystem Realization Algorithm (ERA) for modal identification using ambient vibration. Exp. Tech. 2011, 35, 52–58. [Google Scholar] [CrossRef]
- Su, W.C.; Huang, C.S.; Chen, C.H.; Liu, C.Y.; Huang, H.C.; Le, Q.T. Identifying the modal parameters of a structure from ambient vibration data via the stationary wavelet packet. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 738–757. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).