Featured Application
The numerical methods described in this paper can be used in the automatic creation of artificial datasets of audio mixes, as real-world mixes are both scarce and costly to produce. Such datasets can be used for a variety of applications, such as material for signal analysis, audio stimuli in psychoacoustic testing or as a population of solutions to be optimised, thus forming the basis of an automatic mixing system. Within this paper, the application of interest is testing the robustness of tempo estimation to re-mixing.
Abstract
The creation of multitrack mixes by audio engineers is a time-consuming activity and creating high-quality mixes requires a great deal of knowledge and experience. Previous studies on the perception of music mixes have been limited by the relatively small number of human-made mixes analysed. This paper describes a novel “mix-space”, a parameter space which contains all possible mixes using a finite set of tools, as well as methods for the parametric generation of artificial mixes in this space. Mixes that use track gain, panning and equalisation are considered. This allows statistical methods to be used in the study of music mixing practice, such as Monte Carlo simulations or population-based optimisation methods. Two applications are described: an investigation into the robustness and accuracy of tempo-estimation algorithms and an experiment to estimate distributions of spectral centroid values within sets of mixes. The potential for further work is also described.
1. Introduction
The mixing of audio signals is a complicated optimisation problem, in which an audio engineer must consider a vast number of technical and aesthetic considerations in order to achieve the desired result. Traditionally, many tasks in audio mixing are performed on a mixing console. Typically, such a device consists of a series of channel strips, one representing each audio track, on which various operations can be performed such as adjustments in equalisation, panning and overall level. While this format is useful for allowing a hands-on interaction with the audio content, it is not the most direct or efficient way of exploring these parameters and discovering mixes in the process.
One legacy of this console design philosophy is that, in the literature, it has become commonplace to define a mix as the sum of the input tracks, subject to control vectors for gain, panning, equalisation etc., [1,2,3]. Subsequently, a number of publications [4,5,6] have referred to a mix of n tracks as a point in an n-dimensional vector space, with each axis as the gain of a given track. While effective in certain cases, and certainly straightforward to visualise, this definition produces a solution space which is sub-optimal when searching for mixes.
The following are equations used to define a mix, according to various previous works. Note that the nomenclature has not been changed from the original texts. Equation (1) was used by [1], stating simply that a mix is the sum of all individual channels.
This definition seems logical and even trivial, if inspired by a summing mixer, and has become the foundation for a series of more elaborate definitions, such as adding a gain vector, a to each track, allowing for time-dependent changes to the track gains, simulating the movement of individual faders [2].
In a review paper from 2011 [3], Equation (3) was used, adding generic control vectors c which modulate the input signals x. These control vectors allow for a variety of results, such as polarity correction, delay correction, panning and source separation, depending on their implementation.
Each of these equations considers the mix as the sum of the input tracks, although there is little agreement on terminology or nomenclature in this general definition. What is important to realise here is that these expressions characterise not strictly the mix itself but the output of a summing mixer, or conventional fader-based mixing console. As will be shown in Section 2, the set of unique mixes is a subset of this set, as illustrated by Equation (4). We refer to this subset as the mix-space, introduced in [7]. It is this space that a mixing console should directly explore, rather than the gain-space. Section 2 presents an updated definition of the term mix, which produces concise solution spaces by exploring only the parameter space , avoiding the redundancies in g, which represents the gain vector of the system.
The primary contributions of this work are as follows: (a) the mix-space as a theoretical framework in which existing audio mixes can be examined, in contrast to the gain-space, and (b) methods for the generation of audio mixes in the mix-space. These contributions are described in Section 2.
The creation of artificial datasets relating to music mixing practice helps to overcome one of the main obstacles in the field of mix analysis, which is the lack of available data and the cost associated with gathering new data from mix engineers. Thus far, it has been difficult to make statistical inference about music mixing practice as available studies have only had access to small datasets of user-generated audio mixes, with few exceptions [8].
2. Theoretical Framework
Adjustment of track level, pan position and equalisation are common in audio processing. While level and pan are fundamental operations in multichannel mixing, equalisation is one of the most commonly used processors. Together, these three operations form a basic channel strip. As such, the scope of this paper considers these three operations.
2.1. Track Gains
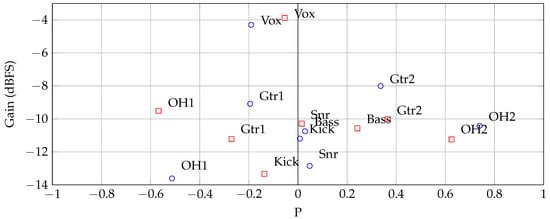
Consider the trivial case where two audio signals are to be mixed, where only the absolute levels of each signal can be adjusted. In Figure 1, the gains of two signals are represented by x and y, where both are positive-bound. Consider the point p as a configuration of the signal gains, i.e., . From this point, the values of x and y are both increased in equal proportion, arriving at the point . The magnitude of p is less than that of () yet since the ratio of x to y is identical, the angles subtended by the vectors from the y-axis are equal (). In the context of a mix of two tracks, what this means is that the volume of is greater than p, yet the blend of input tracks is the same.
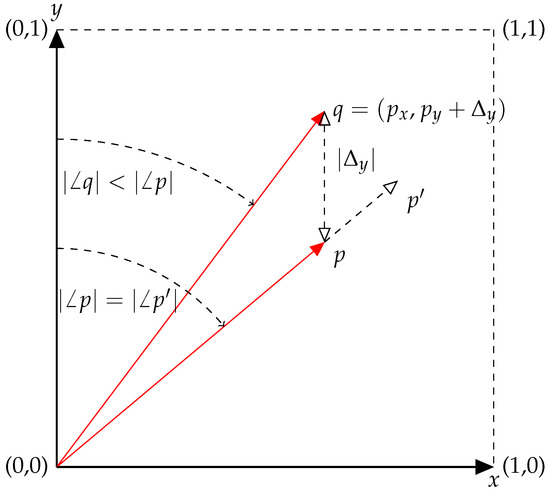
Figure 1.
Points p, and r, in 2-track gain space. Note that the audio output at points p and is the same ‘mix’.
As an alternate to Equation (1), a mix can be thought of as the relative balance of audio signals. From this definition, the points p and are the same mix, only is being presented at a greater volume. If the listener has control over the master volume of the system, then any difference between p and becomes ambiguous.
Definition 1.
Mix: an audio stream constructed by the superposition of others in accordance with a specific blend, balance or ratio.
From p, the level of fader y can be increased by , arriving at q. In this particular example, the value of was chosen such that . However, for any , . Therefore, q clearly represents a different mix to either p or . Consequently, the definition of a mix is clarified by what it is not: when two audio streams contain the same blend of input tracks but the result is at different overall amplitude levels, these two outputs can be considered the same mix. For this mixing example, where there are signals, represented by n gain values, the mix is dependant on variables; in this case, the angle to the vector. The norm of the vector is simply proportional to the overall loudness of the mix.
Figure 2a shows a similar structure, with . Here, the point is also an extension of p. As in Figure 1, q is located by increasing the value of y from the point p and . Here, the values of each angle are explicitly determined and displayed. All three vectors share the equatorial angle of 60. The polar angle of p and is 50, while the polar angle of q is less than this, at ≈37. As in the two-dimensional case, it is the angles which determine the parameters of the mix and the norm of the vector is related to the overall loudness.

Figure 2.
Graphical representation of three mixes in mix-space. While shown for three tracks, this is generalisable to any number of tracks n, using hyperspherical coordinates. (a) Mix at a point in 3-track gain space. Note that the audio output at points p and is the same ‘mix’, despite the vectors having different lengths in this space; (b) For a 3-track mixture, while the cube () represents all outputs of a summing mixer, the surface of the sphere () represents all possible mixes.
While Figure 1 and Figure 2a show a space of track gains, there is clearly a redundancy of mixes in this space. What is ultimately desired is a space of mixes.
Definition 2.
Mix-space: a parameter space containing all the possible audio mixes that can be achieved using a defined set of processes.
It becomes apparent that a Euclidean space with track gains as basis vectors is not an efficient way to represent a space of mixes, according to Definition 2. This explains why Equation (1) would not be appropriate when searching for mixes. If, in Figure 2a, a set of m points randomly selected on were chosen, the number of mixes could be less than m, as the same mix could be chosen multiple times at different overall volumes. A set of m randomly selected points on a sphere of any radius () would result in a number of mixes equal to m. This surface is represented in Figure 2b, which shows the portion of a unit-sphere in positively-unbounded , upon which exist all possible mixes of three tracks.
While both the 2-content of (surface area) and the 3-content of the enclosing , (volume) both, strictly, contain an infinite amount of points, the reduced dimensionality of makes it a more attractive content to use in optimisation, as is a subset of (in this context, content can be considered as “hypervolume”. See http://mathworld.wolfram.com/Content.html). As a consequence, the mix-space, , is a more compact representation of audio mixes than the gain-space, g.
While the examples so far have used polar and spherical coordinates, for and respectively, to extend the concept to any n dimensions, hyperspherical coordinates are used. The conversion from Cartesian to hyperspherical coordinates is given below in Equation (5). The inverse operation, from hyperspherical to Cartesian, is provided in Equation (6), based on [11]. Here, is the gain of the jth track out of a total of n tracks. The angles are represented by . By convention, is the equatorial angle, over the range radians, while all other angles range over radians.
Figure 3 represents a comparable 4-track mixing exercise, as described in [7]. The four audio sources were specifically chosen for this example (vocals, guitar, bass and drums) and assigned to , , and respectively. Consequently, the set of mixes is represented by a 3-sphere of radius r. Due to the deliberate assignment of tracks in this example, the parameters and represent a set of inter-channel balances which, due to the specific relationships of instruments, have importance to musicians and audio engineers: determines the balance of bass to drums, the rhythm section in this case; describes the projection of this balance onto the axis, i.e., the blend of guitar to rhythm section, and finally, describes the balance of the vocal to this backing track.
Figure 3.
Schematic representation of a four-track mixing task, with track gains , and the semantic description of the three terms, when adjusted from 0 to . Figure taken from [7].
From here, the parameter space comprising the angular components of the hyperspherical coordinates of a ()-sphere in a n-dimensional gain-space, is referred to as a ()-dimensional mix-space. More simply, this can be stated by saying the mix-space is the surface of a hypersphere in gain-space. In the case of music mixing, only the positive values of g are of interest. Subsequently, the interesting region of the mix-space is only a small proportion of the total hypersurface. This fraction is .
As each point in represents a unique mix, the process of mixing can be represented as a path through the space. In Figure 4a, a random walk begins at the point marked ‘∘’ in the 2D mix-space (the origin [0,0], which corresponds to a gain vector of [1,0,0]). The model for the walk is a simple Brownian motion (http://people.sc.fsu.edu/~jburkardt/m_src/brownian_motion_simulation/brownian_motion_simulation.html). After 30 s, the walk is stopped and the final point reached is marked ‘×’. The gain values for each of the three tracks are shown in Figure 4b and it is clear that the random walk is on a 2-sphere, as anticipated. The time-series of gain values is shown in Figure 4c. Note that , so for positive g the region explored is as represented in Figure 2b.
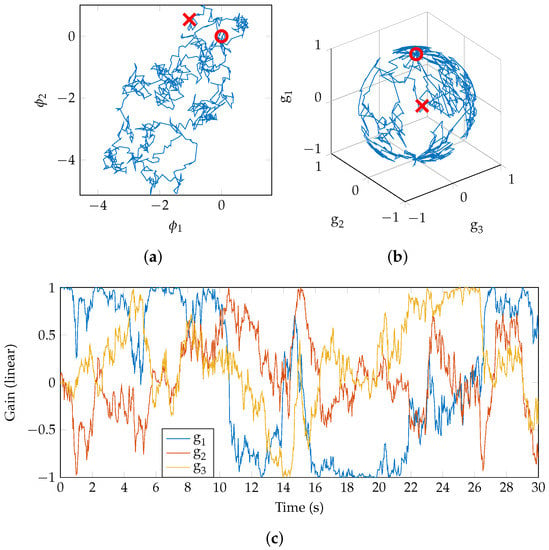
Figure 4.
A time-varying mix can be considered as a path in the mix-space. Here, a random time-varying mix is generated by means of a random walk. (a) Random walk in mix-space; Brownian motion, halted after 30 s; (b) Random walk from Figure 4a converted to gain-space; (c) Time series of gain values for each of the three tracks.
When presented in isolation, such a random mix, whether static or time-varying, may be unrealistic. It is hypothesised that real mix engineers do not carry out a random walk but a guided and informed walk, from some starting point (“source”) to their ideal final mix (“sink”). For further discussion of these terms, see [7], which uses the mix-space as a framework for the analysis of a simple 4-track mixing experiment. The power in these methods comes from generating a large number of mixes, more so than realistically could be obtained from real-world examples, and estimating parameters using statistical methods. Further generation and statistical analysis of time-varying mixes is left to further work.
2.2. Generating Gain Vectors by Sampling the Mix-Space
A set of mixes can be generated by choosing points in the mix-space. In selecting a suitable parametric distribution, it is important to note that linear distributions, such as the normal distribution, are not appropriate as the domain in question is not linear but a spherical surface. The statistics of such distributions are described by a number of equivalent terms in the literature, such as circular, spherical or directional statistics. In order to generate points close to a desired position on the -sphere, points are generated from a von-Mises–Fisher (vMF) distribution. The probability density function of the vMF distribution for a random n-dimensional unit vector is given by
where and the normalisation constant is given by
Here, is the modified Bessel function of the first kind at order v. The parameters and are called the mean direction and concentration parameter, respectively. The greater the value of , the higher the concentration of the distribution around the mean direction , resulting in lower variance. The distribution is unimodal for and is uniform on for . Further details can be found in [12,13]. The SphericalDistributionsRand (https://github.com/yuhuichen1015/SphericalDistributionsRand) code, based on the work of [14], was used to generate points according to a vMF distribution. In the context of audio mixes, (where ) represents the mix about which others are distributed, akin to the mean in a normal distribution. The term represents the diversity of mixes generated, analogous (but inversely proportional) to variance. An example is shown in Figure 5, where three distributions are drawn from a 2-sphere.
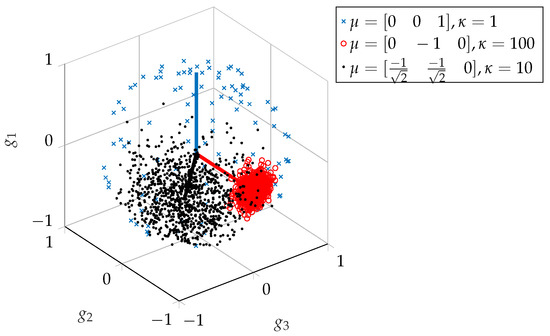
Figure 5.
Three sets of mixes, drawn from the mix-space. This shows the effect of varying the concentration parameter , that a larger value results in less diversity.
2.2.1. Simple Mixing Model
From here, the example mixing session described is an 8-track session, containing vocals, guitars, bass and drums [15]. For tracks, the gains required for the equal-loudness mix (once all audio tracks have been normalised in perceived loudness) are distributed around the following —each track gain is equal to , such that .
Previous studies have indicated that, while a good initial guess, presenting each track at equal loudness is not an ideal final mix. As suggested by three recent PhD theses on the topic [15,16,17], vocals are often the loudest element in a mix. To this equal loudness configuration, a vocal boost is added according to p.157 of [16], i.e., a boost of 6.54 dB. This addition of 6.54 dB to the vocal track produces the following vector, where track 8 is vocals.
If the previous vector was, then it is clear that this point is no longer on the unit 7-sphere. To project the point back onto the unit 7-sphere, the vector is normalised by dividing by the (Euclidean) norm, resulting in the following.
This vector is the new on the unit 7-sphere about which a set of mixes will be generated. The result is shown in Figure 6a. Each mix generated draws a gain value for each track such that the norm is equal to 1. Note that the median values closely match the vector , as expected. Of course, there may not exist a mix which has these median values. This specific value of was chosen to avoid generating negative gains, achieved through trial and error. For a distribution which produces negative gains, the absolute value could be taken to avoid inverting the phase of the tracks. Ignoring phase, a gain of g is perceptually equal to , meaning that the shape of the distribution would be altered if negative gains were included.
2.2.2. Perceptual Mixing Model
Rather than a simple vocal boost, what is required is a more informed choice of instrument levels. In [7], a simple 4-track mixing exercise was reported, where participants created mixes of vocals, guitars, bass and drums using only volume faders. This experiment was expanded to an 8-track format, as in this paper, and is reported in [15]. Participants were asked the same task, only this time stereo-panning and a basic 3-band EQ was added. The median instrument levels obtained from this experiment are shown in Equation (8). Since participants had the ability to pan sources; the median levels were available for left and right channels separately, which are shown in Equations (10) and (11). Figure 6b shows the mixes obtained when the target vector is based on these median track levels, known as . It can be seen that the levels of bass guitar and kick drum are higher than average, while drum overheads have been attenuated. Vocals are set high in the mix, as seen in the mono experiment [7,15] and other previous studies [16,17]. Matlab code for generating sets of mixes, as in Figure 6, is available for download (https://github.com/alexwilson101/PopulateMixSpace).
2.3. Track Panning
Thus far, only mono mixes have been considered, where all audio tracks are summed to one channel. In creative music production, it is rare that mono mixes are encountered. The same mathematical formulations of the mix-space can be used to represent panning. Consider Figure 4, which shows track gains in the range . Should these be replaced with track pan positions (with and 1 corresponding to extreme left and right pan positions, for example) then the mix-space (or “pan-space”) can be used to generate a position for each track in the stereo field. To avoid confusion with the earlier use of , the pan-space is denoted by , although the formalism is identical.
However, the mix-space for gains () takes advantage of the fact that a mix (in terms of track gains only) is comprised of a series of inter-channel gain ratios, meaning that the radius r is arbitrary and represents a master volume. In terms of track panning, one obtains a series of inter-channel panning ratios, the precise meaning of which is not intuitive. Additionally, the radius would still be required to determine the exact pan position of the individual tracks. Therefore, the pan-space describes the relative pan positions of audio tracks to one another.
For a simple example with only two tracks, the meaning of and is relatively simple to understand. Consider the unit circle in a plane where the Cartesian coordinates represent the pan positions of two tracks, as shown in Figure 7. Mix A is at the point : both tracks are panned at the same position. As this is a circle with arbitrary radius, , then the radius controls how far positive (right) the two tracks are panned, from 0 (centre) to (far right). Mix B does the same but towards the left channel. One may ask whether A and B are identical “panning-mixes”, as p and in Figure 1 were identical “level-mixes”?
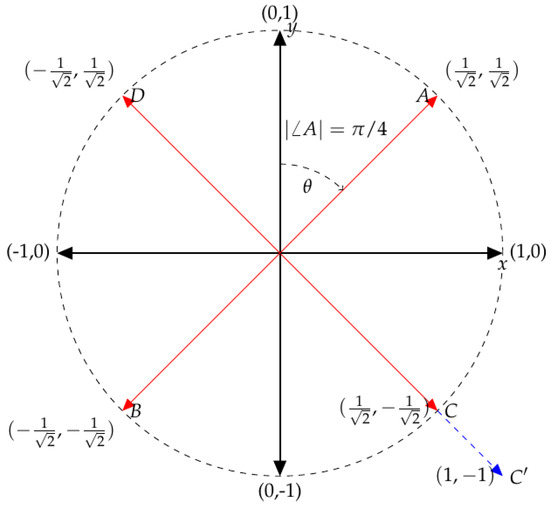
Figure 7.
Panning of two tracks, represented as a 1-sphere. The panning mix is determined by the angle with acting as a scaling variable, adjusting the overall width of the mix. For example, is a wider version of C.
Now consider mix C, where one track is panned left and the other right. Mix D is simply the mirror image of this. Are these to be considered as the same mix, or as different mixes? Here, adjusts the distance between the two tracks, from both centre when , to when (as indicated by mix ). Does a change in change the mix, or is it simply the same mix only wider/narrower? Overall, the angle adjusts the panning mix and is used to obtain absolute positions in the stereo field, at a particular width-scale (i.e., to zoom in or zoom out).
2.3.1. Method 1—Separate Left and Right Gain Vectors
The method for random gains (see Section 2.2) was used to create separate mixes for the left and right channels of a stereo mix. In absolute terms, hard-panning only exists when the gain in one channel is 0 (perceptually, the impression of hard-panning can be achieved when the difference between one channel and the other is sufficiently large [18]). Since the vocal boost prevents any vocal gain of zero, the panning of the vocals is much less wide than the other tracks. Additionally, since was chosen to prevent any negative gains, there are few zero-gain instances; therefore, there is a lack of hard-panning. Figure 8a,b show the gain settings produced and a boxplot of the resulting pan positions is shown in Figure 8c, where the inter-quartile range extends to ±0.4 for the seven instrument tracks and about ±0.2 for the vocals. The estimated density of pan positions for each track is shown, illustrating the relatively narrow vocal panning. As expected, these estimated density functions are Gaussian, to a good approximation.
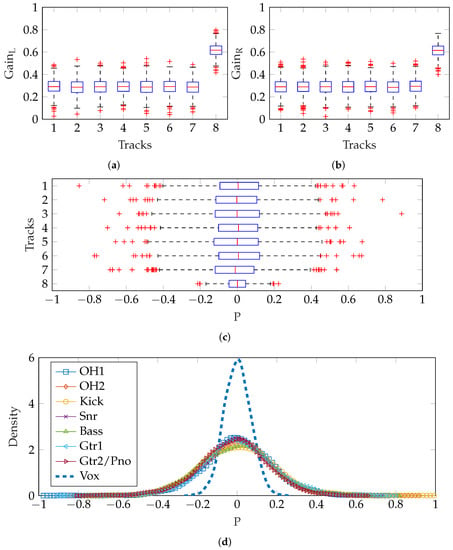
Figure 8.
Panning method 1—separate vMF distributions for and , both using Equation (7). (a) Boxplot of track gains for left channel, using Equation (7); (b) Boxplot of track gains for right channel, using Equation (7); (c) Boxplot of pan positions for each track; (d) Probability density of pan positions for each track.
Rather than using the same for both left and right channels, a unique choice of and can be made, as described in Section 2.2.2. The vectors used are shown in Equations (10) and (11). When summed to mono, this is equivalent to Equation (8).
Figure 9 shows the difference in gains produced for left and right channels. There were some negative track gains produced: when generating audio mixes, the absolute magnitude of the gain was used to avoid phase inversions which would alter spatial perception of the stereo overhead pair. It is clear that the similarity of vocals gains in left and right channels produces a limited variety of pan positions close to the central position, as shown in Figure 9c,d. Other instruments are panned with mean position and variance in accordance with the experimental results [15].

Figure 9.
Panning method 1b—separate vMF distributions for left and right channels but using unique vectors, shown in Equations (10) and (11). (a) Boxplot of track gains for left channel, using Equation (10); (b) Boxplot of track gains for right channel, using Equation (11); (c) Boxplot of pan positions for each track. Where , this is caused by negative track gains; (d) Probability density of pan positions for each track.
2.3.2. Method 2—Separate Gain and Panning
This method involved generating random mono mixes as Section 2.2 (using Equation (7) and then generating pan positions separately. A was created for a vMF distribution. This vector was based on experimental results reported in [15], which showed that, generally, overheads and guitars were widely panned while kick, snare, bass and vocals were positioned centrally.
This then needs to be a unit vector for it to be used in creating vMF-distributed points. Consequently, the precise values are not critically important, as it is the relative pan positions that are reflected in the normalised vector and which would be used to adjust the scaling of these relative positions.
Three different values for were used, which illustrates how this parameter controls the distribution of panning. The results are shown in Figure 10, where the influence of is clear. When , the distribution of pan positions approaches uniform over the sphere, and so the median pan positions are close to 0 (central position in the stereo field) for all tracks, regardless of . As increases, the distribution of pan positions is narrower, more concentrated on the specific pan positions specified in .

Figure 10.
Panning method 2—generating vMF distributions in panning space. As expected, increasing (concentration parameter) results in a narrower range of pan positions for each track, around the target vector Equation (13).
Figure 11 shows an example of two mixes created using this method. The gains and pan positions of each track are displayed. It is clear that the instruments are typically panned close to the positions specified in the pan vector (Equation (13). In this example, ; increasing this parameter would produce wider mixes, while a decrease would produce a less wide mix.
2.4. Track Equalisation
Similarly to how the mix can be considered as a series of inter-channel gain ratios, when the frequency-response of a single audio track is split into a fixed number of bands, the inter-band gain ratios can be used to construct a tone-space using the same formulae. For three bands, with gain of low, middle and high bands in the filter being , and respectively, the problem is comparable to the 3-track mixing problem shown in Figure 2a. Again, one can convert this to spherical coordinates (by EquationS (5) and obtain , yet, in this case, the values of control the EQ filter applied, and is the total amplitude change produced by equalisation (to avoid confusion, is used in place of when referring to equalisation). As before, if all three bands are increased or decreased by the same proportion, then the tone of the instrument does not change apart from an overall change in presented amplitude, . Analogous to its use in track gains, the value of adjusts the balance between and , while adjusts the balance of to the previous balance.
In Figure 12, five points are randomly chosen in the tone-space. These co-ordinates are converted to three band gains as before, except that, in order to centre on a gain vector of , , which is in this example. Of course, this method can be used for any number of bands.
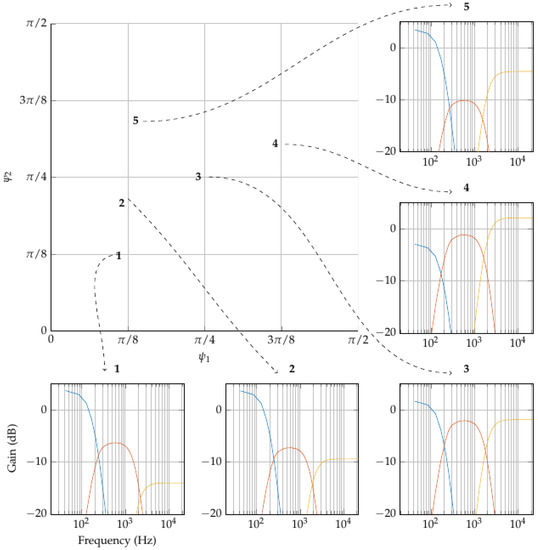
Figure 12.
Five randomly-chosen examples of 3-band equalisation, chosen from the tone-space. As , the gain of the high band decreases. As , the gain of the low band increases at the expense of the other two bands; their balance is determined by .
With this method, one must assume that an audio track has equal amplitude in each band, which is rarely the case. When is increased on a hi-hat track, there may be little effect, compared to a bass guitar. Therefore, the loudness change is a function of and the spectral envelope of the track, prior to equalisation. This is not considered here and is left to further work.
3. Applications
Being able to generate artificial datasets of audio mixtures in the mix-space has a variety of applications. Two such applications are described here. The procedure is similar for both experiments: an audio mix is created using a generated gain vector and raw multitrack audio, resulting in a generated mix from which audio signal features may be determined. Feature extraction used the MIRtoolbox [19], version 1.6.1. Equations (7) and (8) were used to create two sets of mixes. These experiments use sets of 500 mixes, rather than 1000 as outlined in earlier sections. It can be shown that the distributions of audio signal features do not change much beyond 500 mixes [15]. The reduced computation time is advantageous in these examples.
The test audio in these experiments is 30-second segments of the songs “Burning Bridges”, “I’m Alright” and “What I Want” as used in previous studies [8,15], available from the Mixing Secrets free multitrack download library (http://www.cambridge-mt.com/ms-mtk.htm). The raw multitrack audio was reduced to the required eight tracks and each track was normalised in perceived loudness according to a modified form of ITU BS.1770 [20]. The songs “I’m Alright” and “What I Want” feature a track of piano as track #7, in place of ‘Gtr 2’.
3.1. Testing the Robustness of Tempo Estimation Algorithms to Changes in the Mix
In the absence of any time-stretching processes, the tempo of each mix should be identical for a given song. As a result, if the tempo of alternate mixes is estimated and any disagreement is found, this suggests limitations in the tempo-estimation algorithm. In this section, the process of estimating tempo across a large set of artificial mixes is presented as a means of assessing the performance of tempo-estimation algorithms. Two such algorithms are tested herein: the classic and metre-based [21] implementations of mirtempo in the MIRtoolbox. In short, the classic tempo estimation algorithm performs onset detection based on the amplitude envelope of the audio. Periodicities in the detected onsets are determined by finding peaks in the autocorrelation function. The metre method additionally takes into account the metrical hierarchy of the audio, allowing for a more consistent tempo-tracking. Whichever tempo-estimation is used, the resultant tempo is the mean value over the 30-second audio segment. Panning and equalisation were not considered here as tempo was estimated from a mono signal.
Figure 13a and Figure 14a show the results for “Burning Bridges”, where it is clear that the classic method performs poorly. The correct tempo of 100 bpm is estimated for only a small percentage of the mixes while all others are estimated close to 133 bpm (see Figure 14a). This leads to a high mean squared error (MSE) as shown in Table 1. A similar flaw is evident for “I’m Alright” where the tempo is again overestimated by roughly 33% for both mix distributions (see Figure 13b and Figure 14b). This indicates a consistent error in the tempo-estimation routine, which is being revealed by these mix distributions. The metre-based method performs much better, estimating the correct tempo in almost all cases and exhibiting a lower MSE, with only a small amount of absolute error (0.1–0.2 bpm). The performance of the classic tempo-estimation method is improved for “What I Want”, where both methods are found to have a high level of accuracy, as shown in Figure 13c and Figure 14c. For both distributions, the metre-based version produces clusters of solutions for “What I Want”, although the tempo represented by largest cluster is consistent.
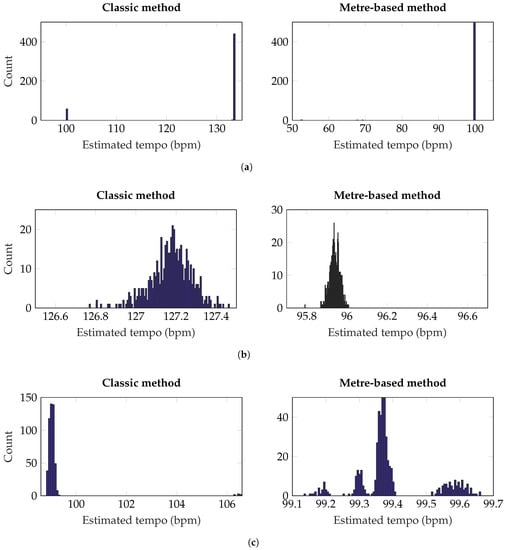
Figure 13.
Estimated tempo for three songs, 500 mixes each using Equation (7). In each histogram, the data is split into 100 bins. Overall, performance is better for the metre-based method, as it demonstrates greater accuracy and improved robustness to changes in the mix. (a) “Burning Bridges”—The correct tempo is ≈100 bpm; (b) “I’m Alright”—The correct tempo is ≈96 bpm; (c) “What I Want”—The correct tempo is ≈99 bpm.
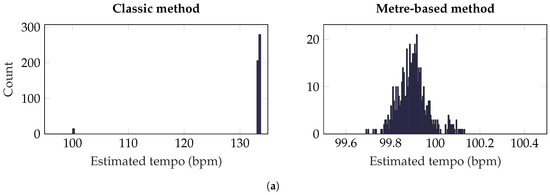
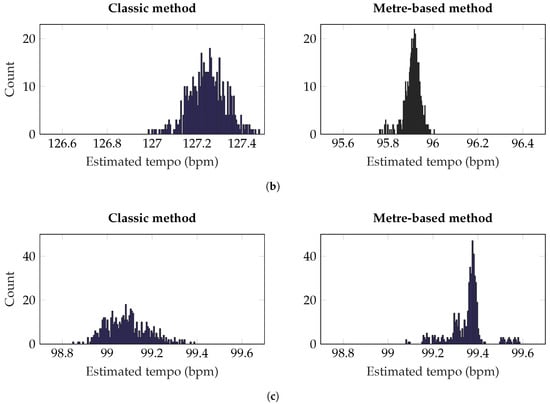
Figure 14.
Estimated tempo for three songs, 500 mixes each using Equation (8). In each histogram, the data is split into 100 bins. Overall, performance is better for the metre-based method, as it demonstrates greater accuracy and improved robustness to changes in the mix; (a) “Burning Bridges”—The correct tempo is ≈100 bpm; (b) “I’m Alright”—The correct tempo is ≈96 bpm; (c) “What I Want”—The correct tempo is ≈99 bpm.

Table 1.
Summary of tempo estimation accuracy results. Shown is the mean squared error (MSE) in each set of 500 mixes.
It is conceivable that no tempo-estimation algorithm is able to obtain the correct result in all cases. What this experiment reveals is that there is also variation within the mixes of a given song, with some mixes providing the correct tempo and other mixes yielding error, with different estimation methods showing varying levels of robustness to mixing practice.
3.2. Estimation of Spectral Centroid in Sets of Mixes
It is common to use the spectral centroid as a feature to describe the timbre of an audio signal, specifically as an approximation to perceptual brightness [22,23,24]. However, where the spectral centroid of a mixed recording is evaluated, it is not clear that the value obtained is typical of the recording as a whole, or if it simply relates to that specific mix of the recording. This is especially problematic in an object-based audio broadcast, where no reference mix exists. This applies to any signal feature, not just the spectral centroid. As studies of features across multiple alternate mixes are still rare in the literature [8,25,26], this issue has not been adequately investigated.
A previous work by the authors [8] reports on the spectral centroid of 1501 user-generated mixes of 10 songs. The number of mixes per song ranges from 97 to 373. The estimated probability distributions of spectral centroid are shown (among other signal features relating to amplitude, timbre and spatial properties), indicating that the median spectral centroid can vary by song, although it is still possible for significant overlap in distributions to exist.
The work in this section investigates the distributions of the spectral centroid that occur for artificial mixes drawn from different mix-space distributions. Equation (7) describes a simple model for mixes while Equation (8) shows the result of a perceptual level-balancing experiment. What is it about the mix that changes when these levels are adjusted? In this section, an estimation of the median spectral centroid produced by these two sets of mixes is made using Monte Carlo methods.
The experiment was conducted as follows. Using Equation (7) and , a set of 500 gain vectors was generated. For each of these vectors, a mix was created and the spectral centroid was measured. This resulted in 500 measurements of spectral centroid, the density of which was estimated using Kernel Density Estimation (KDE). This procedure was repeated for a second set of 500 mixes, generated using Equation (8) and . The estimated density distribution of both is plotted in Figure 15. These distributions were compared using a Wilcoxon rank sum test, which tests the null hypothesis that the distributions of both samples are equal. This null hypothesis was rejected in each case, as shown by the p-values in each subplot of Figure 15 ( in each case).
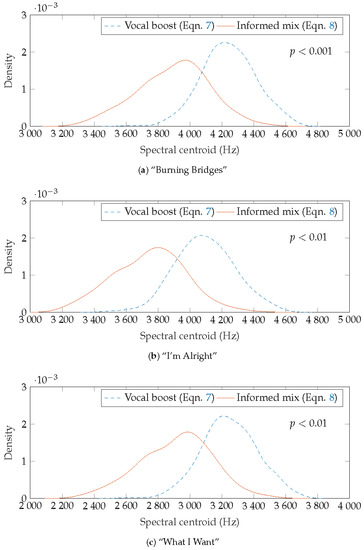
Figure 15.
Probability distribution of spectral centroid as a function of mix-space parameters; (a) “Burning Bridges”; (b) “I’m Alright”; (c) “What I Want”.
The significant difference between the medians of the two groups illustrates that there is a coarse perceptual difference in timbre, generally, between mixes drawn from the two distributions. This is true for all three songs considered. Of course, whether or not there is a significant difference between the medians of the two groups depends on the chosen parameters: the vectors must be perceptually different but if is low enough, then the distributions will overlap, regardless of the choice of (recall that as , the distribution approaches uniformity). The choice of depends on the application.
The higher spectral centroid in the simple equal-gain-with-vocal-boost approach (Equation (7)) is caused by an overestimation in the level of the drum overheads and vocal, and an underestimation of the level of bass and kick drum, when compared to the results of the perceptual test (Equation (8)). The distributions of the spectral centroid for these artificially-generated mixes were compared to the distributions of the spectral centroid for user-generated mixes, as were reported in previous work by the authors [8]. For “Burning Bridges” and “What I Want”, the peak of the distribution compares well to the user-generated mixes (approx 3.8 kHz and 3.2 kHz respectively). In the case of “I’m Alright”, Equation (7) yields a better match to real mixes (approx 4.2 kHz); however, the 373 user-generated mixes of this song from [8] did contain a large proportion of highly amateur, potentially low-quality, mixes. For further comparison of artificial mixes and user-generated mixes, see [15].
This experiment shows that a set of mixes can be obtained by sampling the mix-space but that perceptually-relevant mixes are more likely to be obtained if some level of human guidance is fed into the system. The parametric mixing model for this experiment did not feature panning or equalisation. It has been shown that the addition of equalisation broadens the distribution of spectral centroid values, as would be expected given the wider variety of instrument tone [15].
4. Discussion
4.1. Artificial Datasets for Testing of Processes
The theoretical framework presented in this paper provides for a space of mixes that can be explored, using evolutionary computing, machine learning or similar computational methods. Applications of this include the creation of an initial population of solutions to be used in the search of balance-mixes [9] and electric guitar tones [10], both using interactive genetic algorithms. These approaches have yielded positive results, as the user is able to search the space effectively and find the desired solution.
For subjective testing, the methods presented in this paper have the advantage that each mix is generated at a constant perceived loudness, as the magnitude of the gain vector can be set to a constant (such as in Equation (4). In both [9,10], which used an interactive genetic algorithm, test participants were asked to rate subjectively the solutions presented. Being generated at a consistent loudness level allowed for fair evaluations, while avoiding the additional computational time required for specific loudness-normalisation to be applied to each generated mix. This allows a more free exploration of the solution space, since audio stimuli can be generated in real-time using this method.
Currently, newly-developed algorithms for tempo estimation, key estimation etc., are evaluated during specific challenges, such as the MIREX audio tempo estimation challenge (http://www.music-ir.org/mirex/wiki/2017:Audio_Tempo_Estimation), using standard datasets of audio recordings. We propose that sets of artificially generated mixes be considered as a standard test, in order to examine the level of robustness to mixing practice, as in Section 3.1.
4.2. Signal Analysis of Audio Mixing Practices
Of course, more conventional experiments can be analysed in this framework. In a level-balancing task, where participants were asked to set track gains to their desired levels, the resulting gains can be converted to the mix-space and analysed therein [7]. This allows differences in cohorts to be investigated: thus far, the different mixes produced by headphone or loudspeaker users has been investigated [15] in addition to checking if changing the initially presented rough mix influences the mixing-decisions [7], a hypothesis also supported by later work [6].
A recent work analysed the audio mixes of broadcast audio stems (dialogue, foreground sound effects, background sound effects and music) as produced by hearing-impaired listeners [27]. This 4-track mixing scenario is equivalent to that represented by Figure 3. The changes in level made to each mix stem were reported in a bar chart, showing an increase in dialogue level and a decrease in the level of the other three stems. From a mix-space perspective, we know that these two strategies are equivalent. The mixes created from such an experiment can be more effectively analysed in a 3-dimensional mix-space, in which it could be more clear how different cohorts (such as hearing-impaired listeners) would balance the four tracks in different ways. If the needs of the user demand a change to the audio mix, as in the case of increasing speech intelligibility, then the path from the current mix to the desired mix may be more easily determined in the mix-space.
As object-based audio broadcast becomes commonplace, audio signal feature extraction algorithms will need to be robust to changes in the audio object, be it changes in amplitude, panning, equalisation, or other parameters. It has been shown that the measured value of pulse clarity (a measure of how easy it is to pick out the underlying rhythm of a mix [28]) varies with object loudness, typically decreasing as the mix moves into regions of the mix-space where the relative level of vocals is increased [15].
5. Conclusions
A method for the creation of artificial audio mixes has been presented. This has been achieved by the parametric generation of points in a novel “mix-space”, a concise representation of three audio processing activities: level-balancing, stereo-panning and equalisation.
This method has been used for a number of application thus far: in creating an initial population for evolutionary algorithms [9,10] and two simple experiments estimating the values of audio signal features using Monte Carlo techniques. This has revealed limitations in tempo-estimation algorithms. This paper suggests that, in the future, such algorithms need to be robust to changes in instrument level and other mixing practices. This will allow such routines to be applied to an object-based paradigm of audio broadcast, where no reference mix may exist on which to determine the value of the feature.
Future work is required to further generalise the presented models to audio mixing practices, such as dynamic range processing, as well as implementing a fully-parametric model of time-varying mixes and the related statistical analysis.
Author Contributions
Portions of the work described in this paper are from the PhD thesis of A.W., under the supervision of B.M.F. A.W. conceived and designed the experiments; A.W. performed the experiments; A.W. and B.M.F. analyzed the data; A.W. contributed materials/analysis tools; A.W. and B.M.F. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. No funding sponsors had a role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Gonzalez, E.; Reiss, J. Improved control for selective minimization of masking using Inter-Channel dependancy effects. In Proceedings of the 11th International Conference on Digital Audio Effects (DAFx-08), Espoo, Finland, 1–4 September 2008. [Google Scholar]
- Tsilfidis, A.; Papadakos, C.; Mourjopoulos, J. Hierarchical perceptual mixing. In Proceedings of the 126th AES Convention, Munich, Germany, 7–10 May 2009. [Google Scholar]
- Reiss, J.D. Intelligent systems for mixing multichannel audio. In Proceedings of the IEEE 17th International Conference on Digital Signal Processing, Corfu, Greece, 6–8 July 2011. [Google Scholar]
- Cartwright, M.; Pardo, B.; Reiss, J. Mixploration: Rethinking the audio mixer interface. In Proceedings of the ACM 19th International Conference on Intelligent User Interfaces, Haifa, Israel, 24–27 February 2014. [Google Scholar]
- Terrell, M.; Simpson, A.; Sandler, M. The mathematics of mixing. J. Audio Eng. Soc. 2014, 62, 4–13. [Google Scholar] [CrossRef]
- Jillings, N.; Stables, R. A semantically powered digital audio workstation in the browser. In Proceedings of the Audio Engineering Society International Conference on Semantic Audio, Erlangen, Germany, 22–24 June 2017. [Google Scholar]
- Wilson, A.; Fazenda, B.M. Navigating the Mix-Space: Theoretical and practical level-balancing technique in multitrack music mixtures. In Proceedings of the 12th Sound and Music Computing Conference, Maynooth, Ireland, 24–26 October 2015. [Google Scholar]
- Wilson, A.; Fazenda, B. Variation in Multitrack Mixes: Analysis of Low-level Audio Signal Features. J. Audio Eng. Soc. 2016, 64, 466–473. [Google Scholar] [CrossRef]
- Wilson, A.; Fazenda, B. An evolutionary computation approach to intelligent music production, informed by experimentally gathered domain knowledge. In Proceedings of the 2nd AES Workshop on Intelligent Music Production, London, UK, 13 September 2016. [Google Scholar]
- Wilson, A. Perceptually-motivated generation of electric guitar timbres using an interactive genetic algorithm. In Proceedings of the 3rd Workshop on Intelligent Music Production, Salford, UK, 14 September 2017. [Google Scholar]
- Blumenson, L.E. A Derivation of n-Dimensional Spherical Coordinates. Am. Math. Mon. 1960, 67, 63–66. [Google Scholar] [CrossRef]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 494. [Google Scholar]
- Chen, Y.H.; Wei, D.; Newstadt, G.; DeGraef, M.; Simmons, J.; Hero, A. Statistical estimation and clustering of group-invariant orientation parameters. In Proceedings of the IEEE 18th International Conference on Information Fusion, Washington, DC, USA, 6–9 July 2015. [Google Scholar]
- Wilson, A. Evaluation and Modelling of Perceived Audio Quality in Popular Music, towards Intelligent Music Production. Ph.D. Thesis, University of Salford, Salford, UK, 2017. [Google Scholar]
- Pestana, P. Automatic Mixing Systems Using Adaptive Audio Effects. Ph.D. Thesis, Universidade Catolica Portuguesa, Lisbon, Portugal, 2013. [Google Scholar]
- De Man, B. Towards a Better Understanding of Mix Engineering. Ph.D. Thesis, Queen Mary, University of London, London, UK, 2017. [Google Scholar]
- Lee, H.; Rumsey, F. Level and time panning of phantom images for musical sources. J. Audio Eng. Soc. 2013, 61, 978–988. [Google Scholar]
- Lartillot, O.; Toiviainen, P. A matlab toolbox for musical feature extraction from audio. In Proceedings of the 10th International Conference on Digital Audio Effects (DAFx-07), Bordeaux, France, 10–15 September 2007. [Google Scholar]
- Pestana, P.D.; Reiss, J.D.; Barbosa, A. Loudness measurement of multitrack audio content using modifications of ITU-R BS.1770. In Proceedings of the 34th AES Convention; Audio Engineering Society, Rome, Italy, 4 May 2013. [Google Scholar]
- Lartillot, O.; Cereghetti, D.; Eliard, K.; Trost, W.J.; Rappaz, M.A.; Grandjean, D. Estimating Tempo and metrical features by tracking the whole metrical hierarchy. In Proceedings of the 3rd International Conference on Music & Emotion (ICME3), Jyväskylä, Finland, 11–15 June 2013. [Google Scholar]
- Von Bismarck, G. Timbre of steady sounds: A factorial investigation of its verbal attributes. Acta Acust. United Acust. 1974, 30, 146–159. [Google Scholar]
- Grey, J.M.; Gordon, J.W. Perceptual effects of spectral modifications on musical timbres. J. Acoust. Soc. Am. 1978, 63, 1493–1500. [Google Scholar] [CrossRef]
- McAdams, S.; Winsberg, S.; Donnadieu, S.; De Soete, G.; Krimphoff, J. Perceptual scaling of synthesized musical timbres: Common dimensions, specificities, and latent subject classes. Psychol. Res. 1995, 58, 177–192. [Google Scholar] [CrossRef] [PubMed]
- De Man, B.; Leonard, B.; King, R.; Reiss, J. An analysis and evaluation of audio features for multitrack music mixtures. In Proceedings of the 15th International Society for Music Information Retrieval Conference, Taipei, Taiwan, 27–31 October 2014. [Google Scholar]
- Wilson, A.; Fazenda, B.M. 101 Mixes: A statistical analysis of mix-variation in a dataset of multitrack music mixes. In Proceedings of the 139th AES Convention, Audio Engineering Society, New York, NY, USA, 29 October–1 November 2015. [Google Scholar]
- Shirley, B.G.; Meadows, M.; Malak, F.; Woodcock, J.S.; Tidball, A. Personalized object-based audio for hearing impaired TV viewers. J. Audio Eng. Soc. 2017, 65, 293–303. [Google Scholar] [CrossRef]
- Lartillot, O.; Eerola, T.; Toiviainen, P.; Fornari, J. Multi-feature modeling of pulse clarity: Design, validation and optimization. In Proceedings of the 9th International Society for Music Information Retrieval Conference, Philadelphia, PA, USA, 14–18 September 2008. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).