Investigation of an Ironless Permanent Magnet Linear Synchronous Motor with Cooling System

Abstract

In this paper, a novel ironless linear synchronous motor with a cooling system is proposed. Firstly, the topology of this ironless linear synchronous motor with a cooling system is introduced. Flux density in the cooling system is obtained analytically by the separation of variables method according to the boundary conditions. The eddy current braking force induced by the cooling system is calculated and validated by finite element method. Then, the influence of the motor parameters on the eddy current braking force is investigated. At last, a prototype is manufactured and some experiments are carried out with the prototype. The experiment results are validated by finite element analyzed results.

1. Introduction

Permanent magnet linear synchronous motors (PMLSM) are arguably best suited for use in ultra-precision positioning, numerical control machining, and processing areas. PMLSMs have many advantages such as high force density, high dynamic performance, low thermal losses, and most importantly, the high precision and accuracy associated with the simplicity in mechanical structure. Traditionally, the iron-core PMLSM gained more attraction because of the highly-developed motor thrust [1]. However, the thrust ripple, which is the main disadvantage of an iron-core permanent magnet linear synchronous motor, results in periodic force oscillation with respect to the mover position.

For some special applications, low thrust ripple and high precision position control are needed. In this case, the permanent magnet linear synchronous motor with an ironless winding seems to be the most suitable electrical machine. However, in order to achieve high force density, PMLSMs with ironless windings are usually supplied with high current density, which may generate excessive heat in windings and lead to a rapid and high temperature increase. The heat induced by the winding can cause insulation deterioration, structure deformation, and permanent magnet demagnetization, or even lead to the failure of the machine [2], which seriously restricts the thrust density and limits the application of PMLSM. Meanwhile, the temperature increase can influence the resistance of windings and magnetic performance of permanent magnets, which will lead to a decrease of thrust output and make the machine unable to reach the desired characteristics [3,4,5]. Therefore, it is essential to investigate the PMLSM with a cooling system in order to inhibit the effects of the temperature increase.

Many studies on the cooling system and thermal analysis have been carried out for permanent magnet motors [3,5,6,7,8]. However, analysis of the influence of the cooling system on the PMLSM has received less attention. In this work, a novel ironless linear synchronous motor with a cooling system is proposed. Compared to other PMLSMs with a cooling system, the primary winding of the novel ironless PMLSM is divided into two layers, and the cooling system is located between the two layers. Flux density is obtained analytically by the separation of variables method according to the boundary conditions. For the linear synchronous motor with a cooling system, the eddy current braking force induced in the cooling system is a main reason for the thrust ripple. In this paper, analysis and calculation of the eddy current braking force of an ironless linear synchronous motor with a cooling system is investigated. At last, a prototype is manufactured and some experiments are carried out with the prototype. Furthermore, the experiment results are compared with the finite element analyzed results for validation.

2. Topology of the Novel Ironless LSM with Cooling System

The ironless permanent magnet linear synchronous motor investigated in this paper is shown in Figure 1. This ironless PMLSM consists of a mover with ironless winding and a stator with U-shaped yoke with a face-to-face Halbach magnet array mounted on it. A permanent magnet Halbach array is used to establish strong and sinusoidal magnetic field. Similar to permanent magnet rotary motors, the thrust is generated by the interaction between permanent magnetic field and travelling magnetic field, while the synchronous speed of the motor is the same as the speed of the travelling magnetic field. The primary winding is divided into two layers, and the cooling system is located between the two layers. Water flows through the cooling jacket and the heat generated by the permanent magnet linear synchronous motor is taken away by the cooling water.

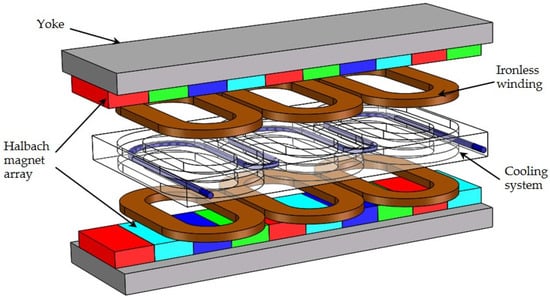
Figure 1. The novel ironless linear synchronous motor with cooling system.

3. Magnetic Field Analysis and Calculation of the Eddy Current Braking Force

3.1. Magnetic Field Produced by the Halbach Magnet Array

Figure 2 shows the analytical model of the PMLSM for the magnetic field analysis. The sources of the permanent magnet array are expressed in the form of a Fourier series, so that higher order harmonics can be taken into consideration. As the doubled-sided linear motor has a symmetric structure along the y-axis, only one side is selected as the analysis region. To simplify, some assumptions are made, as follows [9,10,11,12]:

• All regions are extended infinitely in the x-direction
• Permanent magnets are periodically distributed along the x-axis
• The permeability of the yoke is infinite and the permeability of the permanent magnet material is equal to the permeability of free space
• The effects of the slots inside the cooling jacket are ignored

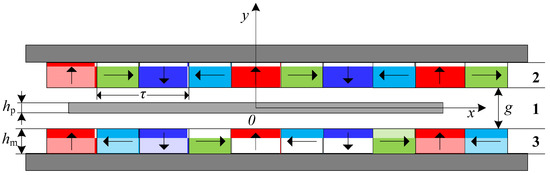
Figure 2. The analytical model of the permanent magnet linear synchronous motors (PMLSM).

If the transverse edge effects are temporarily ignored, i.e., the eddy currents are considered to flow only in the z-direction, the actual 3-D problem is then reduced to a 2-D one [13,14,15].

The analytical model is divided into three regions as shown in Figure 2. In region 1, the magnetic vector potential satisfies the Laplace equation, in region 2 and 3, the magnetic vector potential satisfies the Poisson equation.

$$\{\begin{array}{l}\frac{{\partial }^2{A}_{\mathrm{z}1}}{\partial x^2}+\frac{{\partial }^2{A}_{\mathrm{z}1}}{\partial y^2}=0\\ \frac{{\partial }^2{A}_{\mathrm{z}2}}{\partial x^2}+\frac{{\partial }^2{A}_{\mathrm{z}2}}{\partial y^2}=-{\mathsf{\mu }}_0\frac{\partial M_{\mathrm{x}}}{\partial x}\\ \frac{{\partial }^2{A}_{\mathrm{z}3}}{\partial x^2}+\frac{{\partial }^2{A}_{\mathrm{z}3}}{\partial y^2}={\mathsf{\mu }}_0\frac{\partial M_{\mathrm{x}}}{\partial x}\end{array}$$

(1)

where ${\stackrel{\rightharpoonup }{J}}_{\mathrm{M}}=\nabla \times \stackrel{\rightharpoonup }{M}$, A_z is the z-axis component of the vector magnetic potential, J_M is equivalent magnetizing current density.

$$\{\begin{array}{l}\stackrel{\rightharpoonup }{M}=M_{\mathrm{x}}\stackrel{\rightharpoonup }{i}+M_{\mathrm{y}}\stackrel{\rightharpoonup }{j}\\ M_{\mathrm{x}}={\displaystyle \sum _{n=1}^{\infty }\frac{4B_{\mathrm{r}}}{\left(2n-1\right){\mathsf{\pi }\mathsf{\mu }}_0}}\cos \frac{\left(2n-1\right){\mathsf{\pi }\mathsf{\alpha }}_{\mathrm{p}}}{2}\sin \frac{\left(2n-1\right)\mathsf{\pi }x}{\tau }\\ M_{\mathrm{y}}={\displaystyle \sum _{n=1}^{\infty }\frac{4B_{\mathrm{r}}}{\left(2n-1\right){\mathsf{\pi }\mathsf{\mu }}_0}}\sin \frac{\left(2n-1\right){\mathsf{\pi }\mathsf{\alpha }}_{\mathrm{p}}}{2}\cos \frac{\left(2n-1\right)\mathsf{\pi }x}{\tau }\end{array}$$

(2)

Equation (1) satisfies the boundary conditions (3).

$$\{\begin{array}{l}{B}_{\mathrm{y}1}{|}_{y=\frac{1}{2}g}=B_{\mathrm{y}2}{|}_{y=\frac{1}{2}g}\\ H_{\mathrm{y}2}{|}_{y=\frac{1}{2}g}-H_{\mathrm{y}1}{|}_{y=\frac{1}{2}g}=M_{\mathrm{x}}\\ B_{\mathrm{y}1}{|}_{y=-\frac{1}{2}g}=B_{\mathrm{y}2}{|}_{y=-\frac{1}{2}g}\\ H_{\mathrm{y}2}{|}_{y=-\frac{1}{2}g}-H_{\mathrm{y}1}{|}_{y=-\frac{1}{2}g}=-M_{\mathrm{x}}\\ H_{\mathrm{y}2}{|}_{y=\frac{1}{2}g+h_{\mathrm{m}}}=M_{\mathrm{x}}\\ H_{\mathrm{y}2}{|}_{y=-\frac{1}{2}g-h_{\mathrm{m}}}=-M_{\mathrm{x}}\end{array}$$

(3)

According to the boundary condition (3), Variable Separation Method is used to solve the differential equations in the regions. The magnetic fields induced by permanent magnets can be derived as follows. The correctness of the analytical calculation of the Halbach array field distribution has been verified in our previous work [15].

$$B_{\mathrm{y}1}=B_{\mathrm{ym}}\cosh \left(\frac{\mathsf{\pi }}{\mathsf{\tau }}y\right)\cos \left(\frac{\mathsf{\pi }}{\mathsf{\tau }}x\right)$$

(4)

$$\begin{array}{ll}{B}_{\mathrm{ym}}=-\frac{\mathsf{\pi }}{\mathsf{\tau }}& \{\frac{K-\left[K\cosh \left(\frac{\mathsf{\pi }}{\mathsf{\tau }}\frac{g}{2}\right)+T\sinh \left(\frac{\mathsf{\pi }}{\mathsf{\tau }}\frac{g}{2}\right)\right]\cosh \left[\frac{\mathsf{\pi }}{\mathsf{\tau }}\left(\frac{g}{2}+h_m\right)\right]}{\sinh \left[\frac{\mathsf{\pi }}{\mathsf{\tau }}\left(\frac{g}{2}+h_m\right)\right]}\\ & \hspace{1em}+K\sinh \left(\frac{\mathsf{\pi }}{\mathsf{\tau }}\frac{g}{2}\right)+T\cosh \end{array}$$

(5)

where g is the length of the air-gap, h_m is the thickness of the magnet, and h_p is the thickness of the cooling jacket.

$$\{\begin{array}{l}K=\frac{4\mathsf{\tau }{B}_{\mathrm{r}}}{{\mathsf{\pi }}^2}\cos \left(\frac{{\mathsf{\pi }\mathsf{\alpha }}_{\mathrm{p}}}{2}\right)\\ T=-\frac{4\mathsf{\tau }{B}_{\mathrm{r}}}{{\mathsf{\pi }}^2}\sin \left(\frac{{\mathsf{\pi }\mathsf{\alpha }}_{\mathrm{p}}}{2}\right)\end{array}$$

3.2. The Eddy Current Density

As the demagnetization effect of the eddy current in the cooling jacket is ignored, Equation (4) can be regarded as the expression of the flux density in the cooling jacket. In Figure 2, the magnetic vector potential in the cooling jacket also satisfies the following equation

$$\frac{{\partial }^2{A}_{\mathrm{z}}}{\partial x^2}+\frac{{\partial }^2{A}_{\mathrm{z}}}{\partial y^2}=j\mathsf{\omega }\mathsf{\mu }\mathsf{\sigma }{A}_{\mathrm{z}}$$

(6)

where ω is the angular frequency, μ is the permeability of the cooling plate, σ is the conductivity of the cooling plate.

Transforming (6) to a time domain equation as follows

$$\frac{{\partial }^2{A}_{\mathrm{z}}}{\partial x^2}+\frac{{\partial }^2{A}_{\mathrm{z}}}{\partial y^2}=\mathsf{\mu }\mathsf{\sigma }\frac{\partial A_{\mathrm{z}}}{\partial t}$$

(7)

At t = 0, the magnetic vector potential satisfies the following boundary conditions.

$$\{\begin{array}{l}{B}_{\mathrm{y}}{|}_{y=\frac{1}{2}{h}_{\mathrm{p}}}=B_{\mathrm{ym}}\cosh \left(\frac{\pi }{\tau }\frac{1}{2}{h}_{\mathrm{p}}\right)\cos \left(\frac{\pi }{\tau }x\right)\\ B_{\mathrm{y}}{|}_{y=-\frac{1}{2}{h}_{\mathrm{p}}}=B_{\mathrm{ym}}\cosh \left(-\frac{\pi }{\tau }\frac{1}{2}{h}_{\mathrm{p}}\right)\cos \left(\frac{\pi }{\tau }x\right)\end{array}$$

(8)

The general solution of (7) can be solved by Variable Separation Method as follows

$$\begin{array}{r}{A}_{\mathrm{z}}=C_1[e^{-\mathsf{\alpha }y}\sin \left(\mathsf{\omega }t-\frac{\mathsf{\pi }}{\mathsf{\tau }}x-\mathsf{\beta }y+{\mathsf{\theta }}_1\right)\\ \hspace{1em}+e^{\mathsf{\alpha }y}\sin \left(\mathsf{\omega }t-\frac{\mathsf{\pi }}{\mathsf{\tau }}x+\mathsf{\beta }y+{\mathsf{\theta }}_1\right)]\end{array}$$

(9)

where

$$\{\begin{array}{l}\mathsf{\alpha }=\mathsf{\gamma }\cos \mathsf{\phi }\\ \mathsf{\beta }=\mathsf{\gamma }\sin \mathsf{\phi }\\ {\mathsf{\gamma }}^2=\sqrt{{\left(\mathsf{\pi }/\mathsf{\tau }\right)}^4+{\left(\mathsf{\omega }\mathsf{\mu }\mathsf{\sigma }\right)}^2}\\ \mathsf{\phi }=\frac{1}{2}\arctan \left(\frac{\mathsf{\omega }\mathsf{\mu }\mathsf{\sigma }}{{\left(\mathsf{\pi }/\mathsf{\tau }\right)}^2}\right)\end{array}$$

According to the boundary conditions (8), Variable Separation Method is applied to solving the Equation (7).

$$\{\begin{array}{l}{\mathsf{\theta }}_1=-\arctan \left(\tanh \left(\frac{\mathsf{\alpha }{h}_{\mathrm{p}}}{2}\right)\tan \left(\frac{\mathsf{\beta }{h}_{\mathrm{p}}}{2}\right)\right)\\ C_1=\frac{B_{\mathrm{ym}}\cosh \left(\frac{\mathsf{\pi }{h}_{\mathrm{p}}}{2\mathsf{\tau }}\right)}{\frac{\mathsf{\pi }}{\mathsf{\tau }}\sqrt{2\cosh \left(\mathsf{\alpha }{h}_{\mathrm{p}}\right)+2\cos \left(\mathsf{\beta }{h}_{\mathrm{p}}\right)}}\end{array}$$

(10)

In the cooling jacket, the magnetic vector potential, magnetic field density, and eddy current density meet the following relationship

$$\{\begin{array}{l}{H}_x=\frac{1}{\mathsf{\mu }}\frac{\partial A_{\mathrm{z}}}{\partial y}\\ H_{\mathrm{y}}=-\frac{1}{\mathsf{\mu }}\frac{\partial A_{\mathrm{z}}}{\partial x}\\ J_{\mathrm{z}}=\frac{\partial H_{\mathrm{y}}}{\partial x}-\frac{\partial H_{\mathrm{x}}}{\partial y}\end{array}$$

(11)

By substituting (9) into (11), the expression of the eddy current density can be written as

$$\begin{array}{r}{J}_{\mathrm{z}}=-\frac{2C_1\mathsf{\alpha }\mathsf{\beta }}{\mathsf{\mu }}[e^{-\mathsf{\alpha }y}\cos \left(\mathsf{\omega }t-\frac{\mathsf{\pi }}{\mathsf{\tau }}x-\mathsf{\beta }y+{\mathsf{\theta }}_1\right)\\ +e^{\mathsf{\alpha }y}\cos \left(\mathsf{\omega }t-\frac{\mathsf{\pi }}{\mathsf{\tau }}x+\mathsf{\beta }y+{\mathsf{\theta }}_1\right)]\end{array}$$

(12)

3.3. The Eddy Current Braking Force

According to previous analysis, the normal flux density in the cooling plate can be written as

$$B_{\mathrm{y}}=C_1{m}_1[e^{-\mathsf{\alpha }y}\cos \left(\mathsf{\omega }t-\frac{\mathsf{\pi }}{\mathsf{\tau }}x-\mathsf{\beta }y+{\mathsf{\theta }}_1\right)+e^{\mathsf{\alpha }y}\cos \left(\mathsf{\omega }t-\frac{\mathsf{\pi }}{\mathsf{\tau }}x+\mathsf{\beta }y+{\mathsf{\theta }}_1\right)]$$

(13)

At any time, differential form of the tangential eddy current braking force is

$$d{F}_{\mathrm{x}2}=B_{\mathrm{y}}{J}_{\mathrm{z}}{l}_{\mathrm{w}}dxdy$$

(14)

where l_w is the horizontal width of the cooling plate.

Figure 3 shows the analytical model of eddy current braking force. From t = 0, the expression of the eddy current braking force induced in the cooling jacket can be written as follows

$$\begin{array}{ll}{F}_{\mathrm{x}2}& ={\displaystyle \iint d{F}_{\mathrm{x}2}dxdy}\\ & =\frac{2{C_1}^2\mathsf{\pi }\mathsf{\alpha }\mathsf{\beta }{l}_{\mathrm{w}}}{{\mathsf{\mu }}_0\mathsf{\tau }}{\displaystyle {\int }_{-\frac{L_{\mathrm{p}}}{2}-vt}^{\frac{L_{\mathrm{p}}}{2}-vt}{\displaystyle {\int }_{-\frac{h_{\mathrm{p}}}{2}}^{\frac{h_{\mathrm{p}}}{2}}[e^{-\mathsf{\alpha }y}\cos \left(-\frac{\mathsf{\pi }}{\mathsf{\tau }}x-\mathsf{\beta }y+{\mathsf{\theta }}_1\right)}}+{e^{\mathsf{\alpha }y}\cos \left(-\frac{\mathsf{\pi }}{\mathsf{\tau }}x+\mathsf{\beta }y+{\mathsf{\theta }}_1\right)]}^{2}dxdy\\ & =\frac{2{C_1}^2\mathsf{\pi }{l}_{\mathrm{w}}}{{\mathsf{\mu }}_0\mathsf{\tau }}\left[\mathsf{\beta }\sinh \left(\mathsf{\alpha }{h}_{\mathrm{p}}\right)+\mathsf{\alpha }\sin \left(\mathsf{\beta }{h}_{\mathrm{p}}\right)\right]L_{\mathrm{p}}+\frac{{C_1}^2{C}_2\mathsf{\alpha }\mathsf{\beta }{l}_{\mathrm{w}}}{{\mathsf{\mu }}_0}\sin \left(\frac{\mathsf{\pi }}{\mathsf{\tau }}{L}_{\mathrm{p}}\right)\sin \left(2\mathsf{\omega }t+{\mathsf{\theta }}_2\right)\end{array}$$

(15)

where

$$\{\begin{array}{l}{C}_2=\sqrt{{C_3}^2+4{h_{\mathrm{p}}}^2+2C_3\sin \left({\mathsf{\theta }}_3-\mathsf{\phi }\right)}\\ {\mathsf{\theta }}_2=2{\mathsf{\theta }}_1+\arctan \frac{C_3\cos \left({\mathsf{\theta }}_3-\mathsf{\phi }\right)}{C_3\cos \left({\mathsf{\theta }}_3-\mathsf{\phi }\right)+2h_{\mathrm{p}}}\\ C_3=\sqrt{2\cosh \left(2\mathsf{\alpha }{h}_{\mathrm{p}}\right)-2\cos \left(2\mathsf{\beta }{h}_{\mathrm{p}}\right)}/\gamma \\ {\mathsf{\theta }}_3=\arctan \left(\coth \left(\mathsf{\alpha }{h}_{\mathrm{p}}\right)\tan \left(\mathsf{\beta }{h}_{\mathrm{p}}\right)\right)\end{array}$$

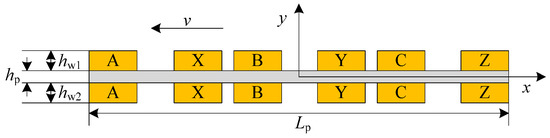
Figure 3. The analytical model of eddy current braking force.

From Equation (15), it can be noticed that the eddy current braking force includes two parts, the constant component and the volatile component. The amplitude and fluctuation of the eddy current braking force are determined by the size of the cooling jacket and the motor’s speed.

4. Simulation Verification

4.1. Simulation Verification

A 2-D finite element simulation model of the ironless linear synchronous motor with cooling system was established based on the Maxwell equations in Ansoft, as shown in Figure 4. By using FEM, the eddy current braking force induced in the cooling system was calculated and compared with the analytical results. Table 1 shows parameters dimension of the finite element simulation model of the PMLSM.

Figure 4. The finite element simulation model of the PMLSM.

Table 1. Parameters dimension of the finite element simulation model of the PMLSM.

Parameter	Symbol	Value	Unit
length of air-gap	g	10.5	mm
pole pitch	τ	24	mm
lateral width of the cooling jacket	lw	80	mm
amplitude values of fundamental harmonic	Bym	0.8	T
thickness of the cooling jacket	hp	2	mm
length of the cooling jacket	Lp	100	mm
thickness of the top-layer coil	hw1	3.5	mm
thickness of the under-layer coil	hw2	3.5	mm

Figure 5 shows the comparison of the eddy current braking force F_x2 of the ironless linear synchronous motor with cooling system between theoretical analysis and FEM simulation. As the effects of high order harmonics and the end effects are taken into consideration in the simulation model, the force ripple of the simulation result is larger than the analytical result. As a whole, the analytical results are in good agreement with the simulation results.

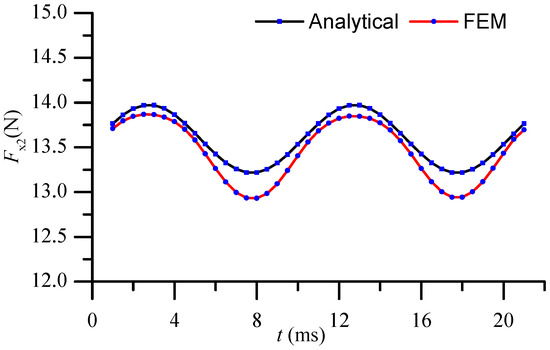
Figure 5. Comparison of eddy current braking force F_x2 between analytical and simulation.

Figure 6 shows the structure of the cooling jacket with slots. Figure 7 shows the comparison of the eddy current braking force F_x2 of the ironless linear synchronous motor with cooling system between the slots are ignored and considered. The two curves are basically consistent with each other. When the slots on the cooling jacket are considered, it can be observed from Figure 7 that the average of the eddy current braking force decreases, and the fluctuation amplitude increases. In Figure 7, the maximum error between the two curves is about 0.8 N, only 6% of the average of the eddy current braking force, within acceptable limits.

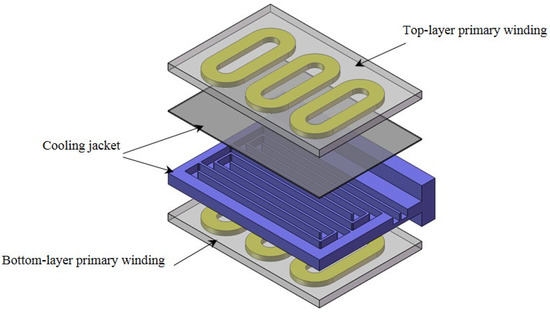
Figure 6. The cooling jacket with slots.

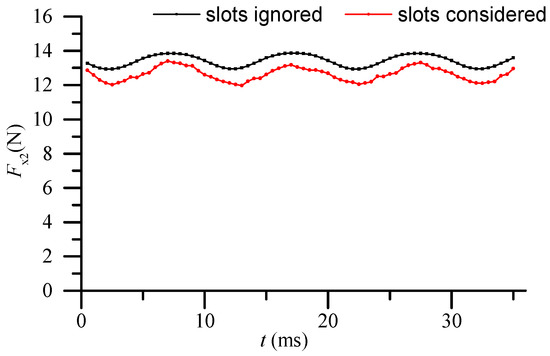
Figure 7. Comparison of eddy current braking force F_x2 between slots ignored and slots considered.

4.2. Influence of the Motor Parameters on the Eddy Current Braking Force

According to Equation (15), it can be observed that the eddy current braking force is consists of the constant component (F_x21) and the volatile component (F_x22). The two-eddy current braking force densities are defined as Equations (16) and (17), respectively.

$$f_{\mathrm{x}1}=\frac{F_{\mathrm{x}21}}{h_{\mathrm{p}}{L}_{\mathrm{p}}{l}_{\mathrm{w}}}$$

(16)

$$f_{\mathrm{x}2}=\frac{F_{\mathrm{x}22}}{h_{\mathrm{p}}{L}_{\mathrm{p}}{l}_{\mathrm{w}}}$$

(17)

The force density f_x1 reflects the size of the eddy current brake force and the force density f_x2 reflects the fluctuation of the eddy current brake force.

It can be observed from Figure 8a, f_x1 increases slowly along with the increase of h_p. As the change of h_p is limited, f_x1 basic remain the same value as the change of h_p. Therefore, the eddy current brake force density can be seen as constant along with the change of h_p. By contrast, f_x2 increases linearly along with the increase of h_p as shown in Figure 8b. In order to reduce the eddy current brake force's volatility, the thickness of the cooling jacket should be reduced. It should be pointed out that, the total braking force mainly comes from the electromagnetic braking force, while eddy current only contributes a fraction to the total braking force. Improving the thickness of the cooling jacket can strengthen primary motor cooling capacity and increase the current value of the primary winding, thus increasing the electromagnetic braking force as well as the total braking force. Therefore, the selection of the thickness of the cooling jacket should be given priority over all the other factors.

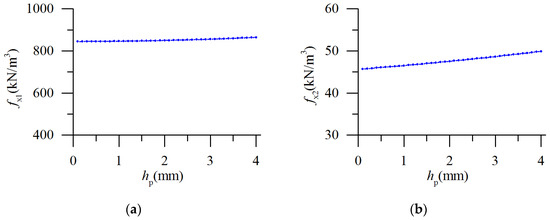
Figure 8. The curves of the two-eddy current braking force density along with the change of h_p. (a) The curve of f_x1 along with the change of h_p; (b) The curve of f_x2 along with the change of h_p.

From Equation (15), it can be observed that the volatile component of the eddy current brake force associated with the value of L_p/τ. It can be observed from Figure 9a, f_x1 remains relatively constant no matter what the value of L_p/τ is. However, in Figure 9b, f_x2 attenuates according to the sine law along with the increase of L_p/τ, and reaches the minimum when the length of the cooling jacket equals the integer times the pole pitch. Consequently, for the design of the motor, the length of the cooling jacket should be the integer times the pole pitch.

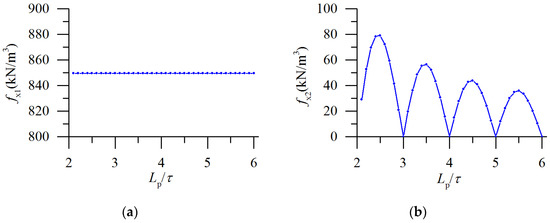
Figure 9. The curves of the two-eddy current braking force density along with the change of L_p/τ. (a) The curve of f_x1 along with the change of L_p/τ; (b) The curve of f_x2 along with the change of L_p/τ.

5. Prototype and Experiments

An ironless linear synchronous motor with a cooling system was designed and produced in laboratory based on the previous study, as shown in Figure 10. The test platform of the LSM (linear synchronous motor) is established with the prototype, as shown in Figure 11. Some experiments were carried out with the prototype and the experiment results are validated by finite element analyzed results.

Figure 10. Photos of the prototype. (a) The coils and cooling jacket; (b) The stator; (c) The prototype motor.

Figure 11. The test platform of the LSM.

By using the prototype, the no-load back-EMF (electromotive force) waveform of the PMLSM was measured, as shown in Figure 12. It can be observed that the three phase no-load back-EMF waveforms were of good sinusoidal shape. Figure 13 shows the comparison of the no-load back-EMF waveform between simulation result and experiment result. It can be observed from Figure 13 that the two curves are consistent with each other and the difference between the peak values of the two curves is about 5% of the average of peak value, within acceptable limits.

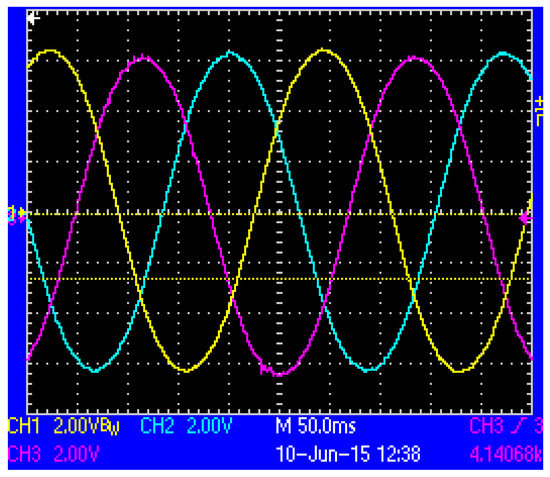
Figure 12. The measured no-load back-EMF waveform.

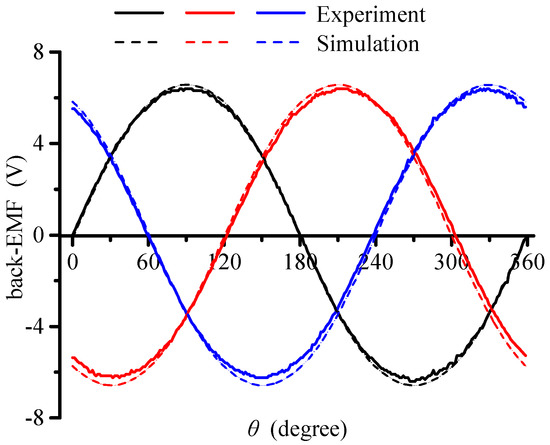
Figure 13. Comparison of the no-load back-EMF waveform between the simulation result and experiment result.

Figure 14 shows the comparison of the static thrust waveform between simulation result and experiment result. It can be observed from Figure 14 that the peak value of the simulation result is 202.9 N and the peak value of the experiment result is 194.6 N, so the difference between the two curves is 8.3 N, about 4% of the average. The error is mainly caused by factors such as the actual machining accuracy, the actual installation precision, and so on.

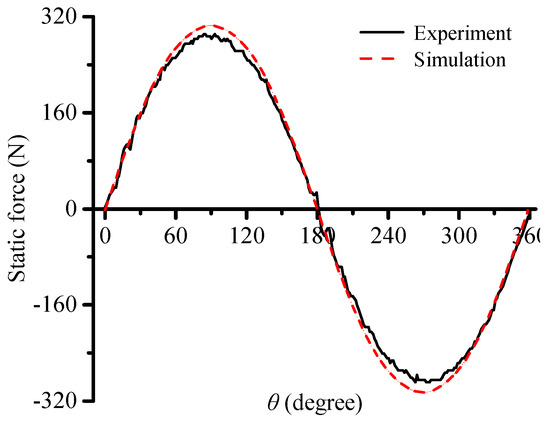
Figure 14. Comparison of the static thrust waveform between simulation result and experiment result.

6. Conclusions

In this work, an ironless linear synchronous motor with a cooling system was proposed. The topology of the ironless linear synchronous motor with a cooling system was first introduced. The expression of the flux density in the cooling jacket was solved analytically and the eddy current braking force induced in the cooling system was investigated and validated by finite element method. The influence of the motor parameters on the eddy current braking force was investigated. At last, a prototype was designed and manufactured, and some characteristics of the linear synchronous motor were measured and validated. The feasibility of the design has been proven by the comparison of the characteristics of the linear synchronous motor between simulation and experiments. The thrust ripple and thermal characterization of the prototype will be investigated in future work.