Abstract
We theoretically study the photoelectron angular distribution (PAD) from the two-photon single ionization of H and He by femtosecond and attosecond extreme-ultraviolet pulses, based on the time-dependent perturbation theory and simulations with the full time-dependent Schrödinger equation. The PAD is formed by the interference of the s and d continuum wave packets, and, thus, contains the information on the relative phase δ and amplitude ratio between them. We find that, when a spectrally broadened femtosecond pulse is resonant with an excited level, the PAD substantially changes with pulse width, since the competition between resonant and nonresonant ionization paths, leading to δ distinct from the scattering phase shift difference, changes with it. In contrast, when the Rydberg manifold is excited, and for the case of above-threshold two-photon ionization, δ and the PAD do not depend much on pulse width, except for the attosecond region. Thus, the Rydberg manifold and the continuum behave similarly in this respect. For a high-harmonic pulse composed of multiple harmonic orders, while the value of δ is different from that for a single-component pulse, the PAD still rapidly varies with pulse width. The present results illustrate a new way to tailor the continuum wave packet.
1. Introduction
Two-photon ionization (2PI), or multi-photon ionization more generally, has consistently been receiving a great deal of attention for decades (see e.g., [1–11]). Also these processes have been used in a variety of applications in laser optics and spectroscopy. It is well known that the two-photon photoelectron angular distributions (PAD) are directly related to the relative amplitudes and the relative phase between different partial waves [8,12–16]. However, these earlier works dealt with the laser pulses in the optical range whose pulse width is very long in comparison with the modern standard of femosecond laser technology. The advent of extreme ultraviolet (EUV) [17,18] and X-ray [19,20] free-electron lasers (FELs) as well as intense ultrashort high-harmonic sources has led to renewed interest in two-photon processes in the EUV to X-ray regimes (see, e.g., [11,21–28]). Photoelectron angular distribution is nowadays extensively studied by the velocity map imaging technique (see e.g., [29,30]). These new light sources have also enabled two-photon ionization (2PI) of species with a deep ionization potential such as He [31–35] and N2 [36].
Single-color two-photon single ionization of a helium atom, apart from a hydrogen atom, may be one of the simplest two-photon processes. For theoretical study, see, for example, the work by Nikolopoulos et al. [37], van der Hart and Bingham [38], and references cited therein. On the experimental side, Kobayashi et al. [32] were the first to observe this process and used it for an autocorrelation measurement of high-order harmonic pulses, and Moshammer et al. [35] recently used it for an autocorrelation measurement of the EUV FEL pulses provided by the SPring-8 Compact SASE Source (SCSS) test accelerator [18]. The absolute two-photon ionization cross sections of He were measured using an intense high harmonic source [31] as well as the SCSS test accelerator [39]. Hishikawa et al. [40] recently investigated two- and three-photon ionization of He at the SCSS test accelerator by photoelectron spectroscopy using a magnetic bottle spectrometer. Though not single-color, the PAD from multi-color above-threshold ionization of He has recently been reported [41,42].
Two-photon single ionization of H and He produces a continuum electron wave packet, which is a superposition of s and d partial waves. The photoelectron angular distribution provides information about the ratio of amplitudes for the s and d partial waves and their relative phase. Extracting a phase shift difference from the PAD that is observed from a photoexcited state is a well-established method. For example, Haber et al. [29] excited the ground state helium atom to the 1snp Rydberg states by high-order harmonics and measured the PAD emitted from these excited states using IR and UV lasers as ionizing pulses. A similar experiment was also performed by O’Keeffe et al. [43] using synchrotron radiation for the excitation and a laboratory laser for the ionization. Both these experiments confirmed that the relative phase extracted from measured PADs resulting from sequential two-color excitation and ionization agrees well with the theoretically predicted scattering phase shift difference.
We have recently studied the PAD from two-photon single ionization of He by femtosecond (fs) EUV pulses theoretically [44]. In the case of resonance-enhanced 2PI, the resonant ionization path via resonant levels and the nonresonant path via nonresonant intermediate levels coexist [2]. We have shown [44] that a feature peculiar to the few fs regime is the competition between the two paths, leading to a relative phase δ between s and d that is distinct from the value expected from the corresponding scattering phase shifts, which is otherwise intrinsic to the target atom or molecule. This extra phase δex can be controlled by the pulse width, which manifests itself in a pulse width dependence of the PAD. This will eventually open a new avenue to the coherent control of the continuum wave packets. (In this connection, see [45] for the control of the resonant two-color two-photon excitation yield and [46] for the control of the photoelectron angular distributions of the nonperturbative resonant multi-photon ionization with ultrashort polarization-shaped pulses. See also a very recent review article for photoelectron angular distributions [47].)
In this paper, we extend the study and investigate the dependence of the PAD and δex on pulse parameters in more detail. In our previous study [44], we have chosen He as a target atom for the following reasons: first, its single-electron excitation energies, e.g., 21.218 eV for 1s2p 1P and 23.087 eV for 1s3p 1P [48], coincide with the 13th and 15th harmonic photon energies of a Ti:Sapphire laser, respectively, and also with the typical wavelength range (50–61 nm) of EUV FELs such as the Spring-8 Compact SASE Source (SCSS) [18], the Free-electron LASer at Hamburg (FLASH) [17], and FERMI [49]. Second, its simple electronic structure allows for exact time-dependent numerical analysis [50–54], in great contrast to alkali atoms. Basically the same effect, however, is also expected for other atomic and molecular species. In the present study, in addition to He, we examine the case of a hydrogen atom, for which simulations are much less demanding and the scattering phase shift is precisely known as the Coulomb phase shift. We also investigate the case where the photon energy is close to the ionization threshold and show that the transition from 2PI involving Rydberg-manifold excitation to above-threshold 2PI is smooth. The Rydberg manifold behaves in a similar manner to the continuum, even when only a modest numbers of levels are excited by the pulse.
Intense high-order harmonic and self-amplified spontaneous emission (SASE) FEL pulses are rarely a single coherent pulse; the former is often a train of a few pulses temporally separated by a half cycle of the driving laser, and the latter fluctuate from shot to shot [55–59]. Hence, we examine how such a multi-component nature, either coherent or chaotic, affects the PAD.
This paper is organized as follows. In Section 2, we discuss the PAD by a Gaussian pulse, based on the second-order perturbation theory and TDSE simulations. Then, in Section 3, we examine the PAD by high harmonic pulses containing multiple harmonic orders and the effects of the chaotic nature of SASE FEL pulses. Conclusions are given in Section 4.
2. Gaussian Pulse
2.1. Time-Dependent Perturbation Theory
In this subsection, let us do a simple analysis on how the relative importance of the resonant and nonresonant paths depends on pulse width, based on the second-order time-dependent perturbation theory within the common rotating wave approximation. The dynamic Stark effect is negligible for pulse parameters used in the present study. We consider the process where a laser pulse with a central frequency ω and a pulse envelope f(t), linearly polarized in the z direction, promotes an atomic electron from an initial state |i⟩ to a final continuum state |f⟩ through two-photon absorption. The complex amplitude cf of the final state after the pulse in the interaction picture can be written as,
where μmn denotes the dipole transition matrix element between states m and n, ∆m = ωm − (ωi + ω), ∆f = ωf − (ωm + ω) with ωm being the energy eigen-value of state m, and the sum runs over all the intermediate bound and continuum states m. One can equivalently express Equation (1) by Equation (3) of [45] using the Fourier transform of f(t). Although a rectangular pulse is often assumed in previous work [2] and textbooks, we take, as a more realistic choice, a Gaussian profile
, with E0 and T being the field amplitude and the pulse width, respectively. More precisely, T is related to the full-width-at-half-maximum (FWHM) pulse width T1/2 as
.
For the case of ωf = ωi + 2ω, in particular, one can perform the integrals in Equation (1) analytically to obtain a physically transparent expression:
where
denotes Dawson’s integral [60], which tends to x near the origin and 1/2x for x → ∞. Only resonant states within the spectral width of the pulse contribute to the first term, corresponding to the resonant path. In particular, if a single intermediate level r is resonant with the pulse spectrum, Equation (2) can be rewritten as,
On the other hand, the asymptotic behavior of F (x) suggests that all the intermediate states except for the exact resonance (∆m = 0) participate in the second term, as expected for nonresonant paths. While either term dominates for a relatively long pulse (ps and ns), assuming that resonant excitation is not saturated, we can expect that the two terms are comparative for sufficiently short pulses and that their relative importance, which may be expressed as arg cf, varies with T. In such a situation, the amplitude ratio cS/cD between the final S and D continuum states is complex, since the branching ratio
of the transitions from the intermediate P states m to each state depends on m. While the actual outgoing wave packets involve the contribution from the final states with ωf ≠ ωi + 2ω, it is instructive to write arg cS/cD using Equation (3) as follows:
with
. Here we have assumed that F (∆mT) ≈ (2∆mT)−1 for all the other intermediate states. Hence, the competition between the resonant and nonresonant paths affects the interference between the outgoing S and D wave packets and manifests itself in the photoelectron angular distribution that depends on the pulse width.
2.2. Photoelectron Angular Distribution
The photoelectron angular distribution from 2PI of H and He is given by [12],
where σ is the total cross section, θ is the angle between the laser polarization and the electron velocity vector, and β2 and β4 are the anisotropy parameters associated with the second- and fourth-order Legendre polynomials, respectively. The interference of the S and D wave packets produces a photoelectron angular distribution,
where
and
are the real amplitudes that have absolute values of |cS| and |cD|, respectively, and can be either positive or negative in principle, and δl is the phase of the partial wave, or the apparent phase shift. The apparent phase shift difference,
consists of a part δsc intrinsic to the continuum eigen wave-functions (scattering phase shift difference), which has previously been studied both theoretically [61–63] and experimentally [29], and the extra contribution δex = arg cS/cD (if
), π − arg cS/cD (if
) from the competition of the two paths. This situation presents a contrast to the case of the photo-ionization from photo-excited states [29], where the nonresonant path is absent and only δsc is present (δ = δsc).
The amplitude ratio
and δ are related with the anisotropy parameters as [64],
It should be noticed that, when one extracts W and δ from β2 and β4, one cannot distinguish between (W, δ) and (−W, π − δ). One cannot distinguish between δ and −δ, either. Hence, in what follows, let us take W as positive, i.e., W = |cS/cD| and define the value of δ within the range [0, π]. Then, δsc in Equation (7) should be replaced by |δsc| or π − |δsc| for appropriate interpretation in some cases (see the discussion on Figure 1 below).
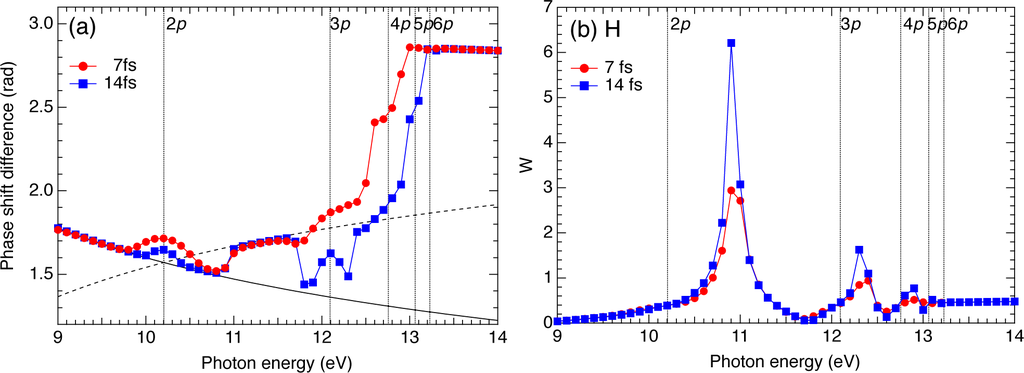
Figure 1.
Photon-energy dependence of (a) the relative phase (phase-shift difference) δ and (b) the amplitude ratio W between the s and d wave packets for a pulse width of 7 fs (circles) and 14 fs (squares). The target atom is hydrogen. Thin sold and dashed lines in (a): |δsc| and π − |δsc|, respectively. Vertical dotted lines: positions of 2p to 6p resonances.
2.3. Hydrogen Atom
Let us now verify the above qualitative idea for the case of a hydrogen atom, for which an analytical expression of the Coulomb phase shift δsc,l for an azimuthal quantum number l is at hand as,
where Γ(z) denotes the gamma function, and k the wave number.
In principle, one could calculate cS and cD using the analytical expression for the dipole transition matrix elements in Equation (2), but it is not trivial to perform an integration over the continuum intermediate states, since the Dawson’s integral has a long tail (∼ 1/x). Instead, we take an approach in the time domain, namely, direct numerical solution of the time-dependent Schrödinger equation (TDSE) in the length gauge,
where we have assumed that the field is linearly polarized in the z direction. Equation (10) is numerically integrated using the alternating direction implicit (Peaceman–Rachford) method [9,65–73]. Sufficiently long (typically a few times the pulse width) after the pulse has ended, the ionized wave packet moving outward in time is spatially well separated and clearly distinguishable from the non-ionized part remaining around the origin. We calculate β2 and β4 by integrating the ionized part of |Φ(r)|2 over r and ϕ, from which one obtains W and δ by solving Equation (8). We have monitored the convergence of the results by calculating the PAD at different times. The calculation has been done for a Gaussian pulse envelope with a peak intensity of 1010 W/cm2, at which we have confirmed that the interaction is still in the perturbative regime.
The pulse-width dependence of δ and W for ħω = 10.2 eV corresponding to the 2p resonance is shown in Figure 2 (a). The calculations have been done at different values of full-width-at-half-maximum (FWHM) pulse width
between 1 and 21 fs. As expected, both δ and W substantially change with pulse width, especially when the pulse is shorter than 10 fs. δ approaches
for a larger pulse width. Accordingly, the PAD also varies as shown in Figure 3 (a). One finds that the distribution to the direction perpendicular to the laser polarization, i.e., θ ≈ 90°, 270° decreases as the pulse is shortened, which is more prominent for He as we will discuss later [Figure 3 (b)]. This can be understood as follows: roughly speaking, δ changes from
to ∼ π as T1/2 varies from 21 fs to 1 fs. Thus, cs/cd is approximately real and negative in the short-pulse limit, which leads to the cancellation between Y00(θ, φ) and Y20(θ, φ) around
.
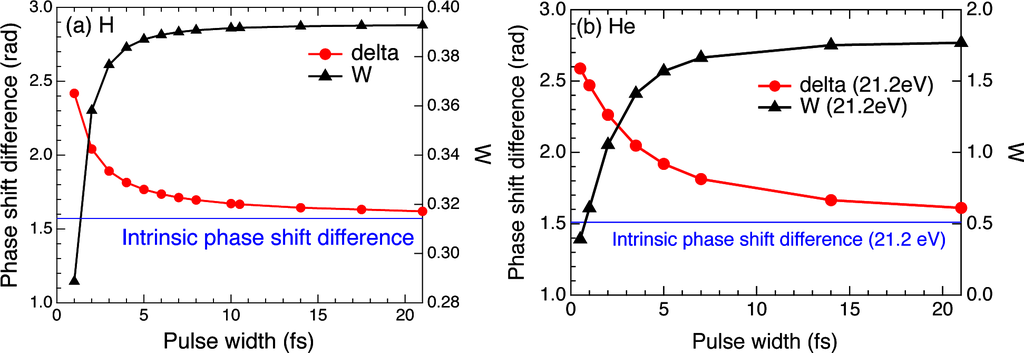
Figure 2.
Pulse-width dependence of the TDSE-derived apparent phase shift difference (relative phase) δ (left axis) and W = |cs/cd| (right axis). (a) The target atom is hydrogen, and ħω = 10.2 eV. The thin horizontal line denotes the value (= π/2)) of the Coulomb phase-shift difference; (b) The target atom is helium, and ħω = 21.2 eV. The thin horizontal line denotes the value (1.511 [63]) of the intrinsic scattering phase-shift difference δsc for ħω = 21.2 eV.
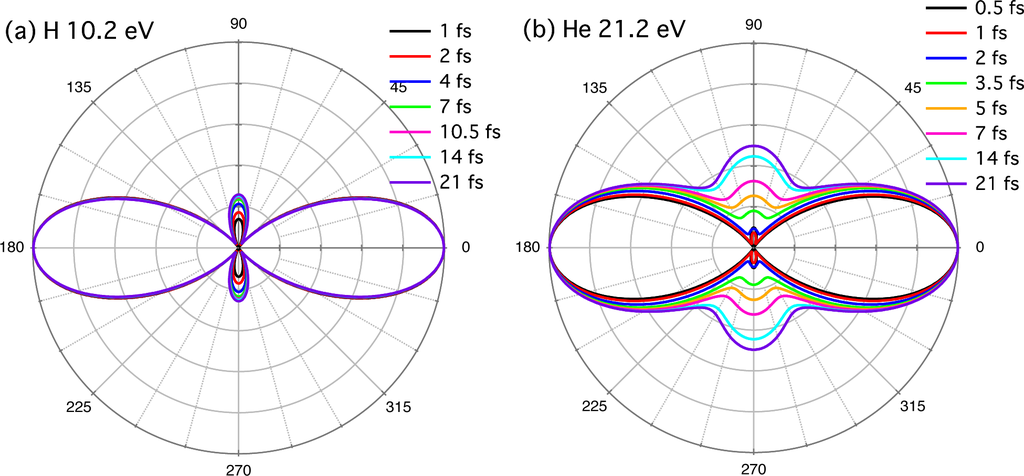
Figure 3.
Pulse-width dependence of the photoelectron angular distribution for (a) H and ħω = 10.2 eV; and (b) He and ħω = 21.2 eV.
In Figure 1, we plot the photon energy dependence of the phase difference δ and the amplitude ratio W for 7 fs and 14 fs pulse widths. By noting that the spectral width is 0.26 eV and 0.13 eV for each pulse width, respectively, we can identify several photon energy ranges.
First, if the pulse is not resonant with any level and the first term in Equation (3) is negligible, Equation (4) can be approximated as,
which is real. In our plots, we define the value of δ within the range [0, π]. Hence, the value of δ is either |δsc| [thin black line in Figure 1(a)] or π − |δsc| (thin dashed black line), depending on the sign of cS/cD. This situation corresponds to ħω ≲ 9.8 eV and 10.6 eV ≲ ħω ≲ 11.6 eV. The relative phase δ between the S and D partial waves does not depend on the pulse width [Figure 4(a)], except for the case of very short pulses where the broadened spectrum begins to be resonant with a 2p or 3p level, which belong to the second category. We can also see from Figure 1 that the sign of cS/cD changes, e.g., around ħω = 10.9 eV and ħω = 11.7 eV, where W sharply peaks or approaches to zero [Figure 1(b)]. The jump in δ is not completely step-function-like, since the contribution from the resonant path can be neglected no longer there.
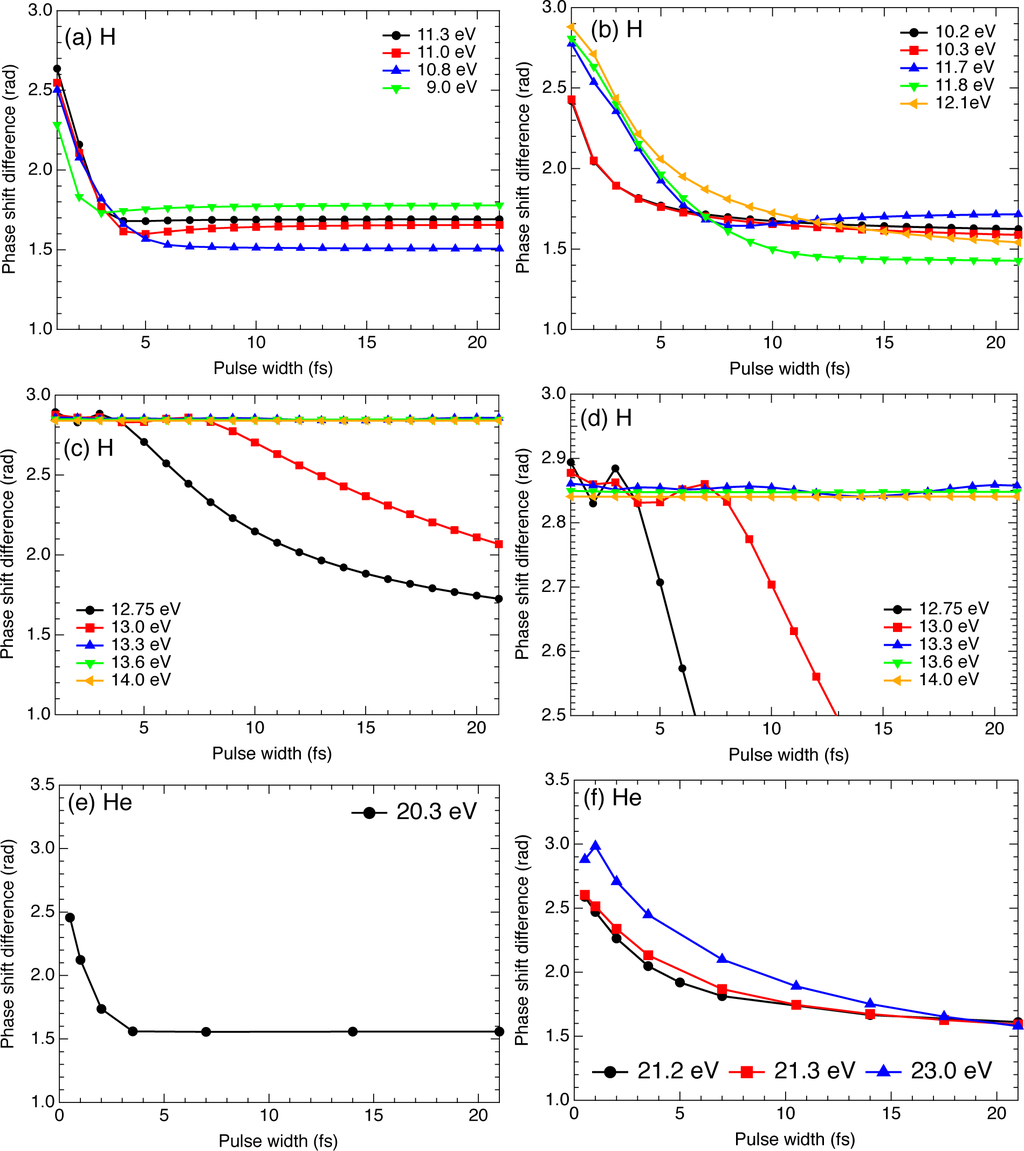
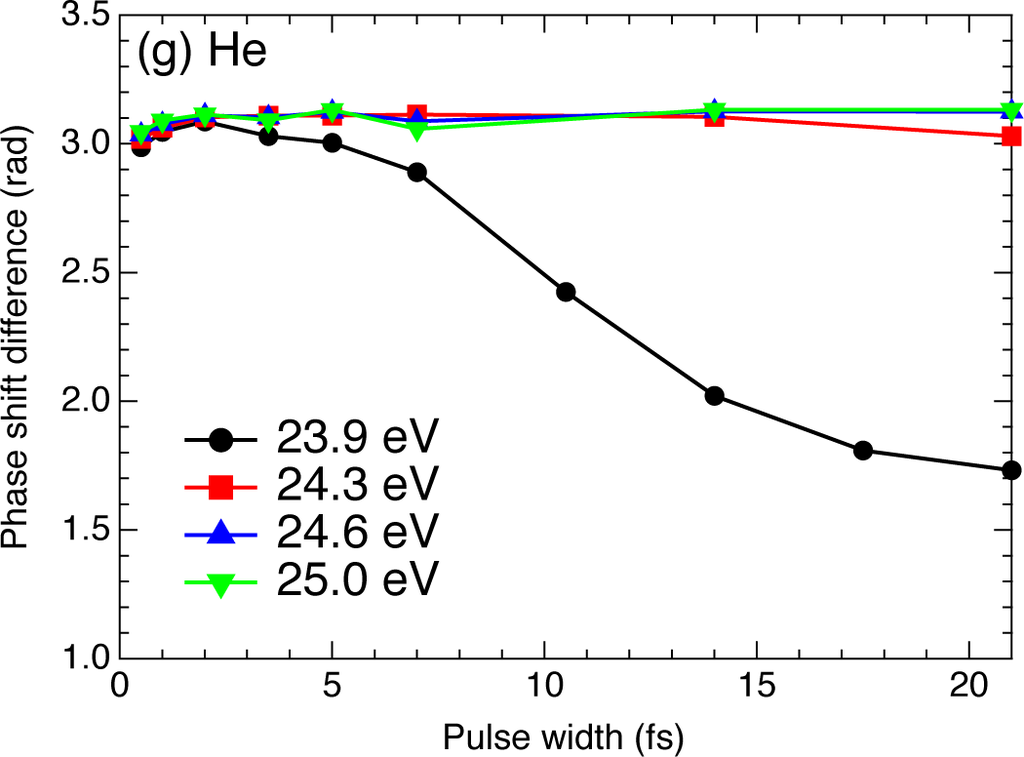
Figure 4.
Pulse-width dependence of the phase-shift difference δ for H [(a)–(d)] and He [(d)–(g)] for different values of photon energy. Panel (d) is the close-up of the vertical-axis range between 2.5 and 3.0 radians of panel (c). The pulse is nonresonant for (a) and (e), resonant with a single level for (b) and (f), and resonant with multiple levels for (c), (d), and (g). The resonant excitation energies for He 1s2p1P, 1s3p1P, 1s4p1P, 1s5p1P levels are 21.218, 23.087, 23.742, and 24.046 eV [48].
Second, if the pulse is resonant with a single excited level (near ħω = 10.2 eV and 12.1 eV for the 2p and 3p resonance, respectively), the competition between the resonant and nonresonant ionization paths leads to the value of δ that deviates from its intrinsic value (|δsc| or π −|δsc|) and varies with pulse width, as we have already seen above [Figure 2(a)] and can also see in Figure 4(b). It tends to either |δsc| or π − |δsc| for the longer pulse width. Interestingly, at ħω = 11.7 eV [blue line in Figure 4(b)], δ first decreases with increasing pulse width, approaching |δsc| = 1.40 (i.e., the resonant path is dominant), but then, for T1/2 ≳ 8 fs, increases again, tending to π − |δsc| = 1.74 (i.e., the nonresonant paths are dominant). Similar features can be observed for 9.0 and 11.0 eV in Figure 4(a) as well.
Then, above the 3p resonance, the pulse is always resonant with one or, more often, multiple levels. In this case, again, the value of δ deviates from its intrinsic value and varies with pulse width [see the lines for 12.75 and 13.0 eV in Figures 4(a) and 4(c)], while its photon-energy dependence is somewhat complicated. A new feature is that δ is roughly constant at T1/2 ≲ 4 fs and 7 fs for 12.75 and 13.0 eV, respectively, which we will discuss below.
Finally, when the pulse excites a Rydberg manifold (ħω ≳ 13.0 and 13.3 eV for 7 and 14 fs, respectively), δ varies smoothly with photon energy even across the ionization threshold (13.6 eV), indicating that the Rydberg manifold behaves similarly to the continuum for the case of an ultrashort pulse (note that a similar smooth transition can also be seen in the 2PI photoelectron spectrum [73]). Moreover, the relative phase is different from its intrinsic value, but surprisingly constant as a function of T1/2 within the pulse width range investigated here [Figure 4(c),(d)]. These features, seen also for He [Figure 4(g)] and presumably general for all the atoms, can be understood as follows. Let us assume that the spectral width of the pulse contains a sufficient number of levels that the sum in Equation (1) can be approximately replaced by an integral,
where s(∆m) denotes the density of states multiplied with
. By noting that F (∆T) ≈ (2∆T)−1, thus, F (∆T) ≈ F (∆)/T is a good approximation in most region of ∆T, Equation (12) can be rewritten as,
Since s(∆/T) in the first term in the integrand can usually be approximated as s(0) for the central frequency, the ratio cS/cD, and thus δ and W, becomes roughly independent of T. Also, due to the continuity of the oscillator strength distribution across the ionization threshold [74], one can see that cS/cD also changes smoothly as a function of ħω. It should be noticed that, for the case of two-photon above-threshold ionization [37] and in the long-pulse limit, the first (resonant path) and second (nonresonant path) terms of Equation (12) tend to, e.g., the second and first terms of Equation (3.2) of [37], respectively.
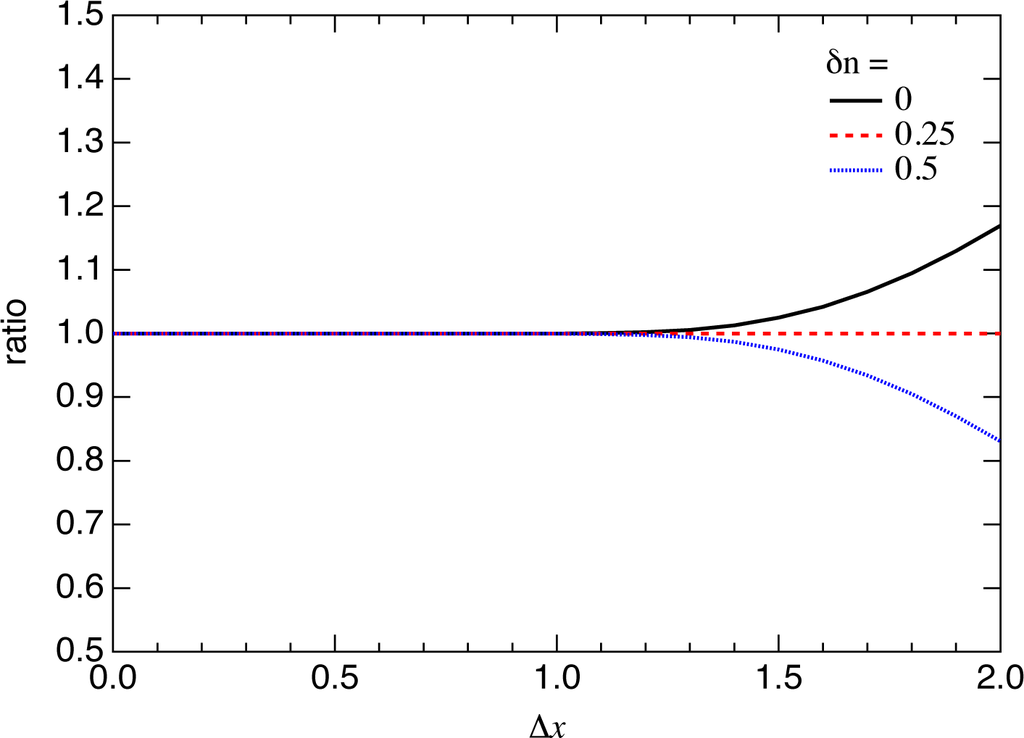
How dense should the levels be within the spectral width for the above discussion to be valid? One can estimate it by investigating how well the integral
can be approximated by the sum
of the values at discrete points, where xn = (n + δn)∆x, with ∆x(> 0) and δn being the increment of x and the offset of n, respectively. In Figure 5 we plot the ratio,
as a function of ∆x for
, and
, where θa(u, q) denotes the theta function [60]. The approximation is surprisingly good even with ∆x = 1, though the FWHM of
is 2 ln 2 (= 1.66511 ⋯). This explains why ∆ varies smoothly even in the range of ħω where the level spacing is not negligibly small compared with the spectral width in Figure 1.
2.4. Helium Atom
Let us now turn to a helium atom. As we have emphasized in Section 1, He is much more relevant to experiments than H, since it is much easier to handle experimentally, and its excitation energies lie well within the typical wavelength range of HHG and EUV FEL sources.
We use direct numerical solution of the full-dimensional two-electron TDSE in the length gauge [54]:
with the atomic and interaction Hamiltonian,
We solve Equation (15) using the time-dependent close-coupling method [50–54]. The numerically obtained excitation energies for the 1s2p 1P and 1s3p 1P states are 21.220 and 23.086 eV, respectively, in fair agreement with the experimental values (21.218 and 23.087 eV [48], respectively). Similarly to the case of a hydrogen atom, sufficiently long after the pulse has ended, we calculate β2 and β4 by integrating the ionized part of |Φ(r1, r2)|2 over r1, r2, θ2, ϕ1, ϕ2, from which one obtains W and δ by solving Equation (8). We use the values of δsc from [63] to calculate δex = δ − δsc. The calculation has been done for a Gaussian pulse envelope with a peak intensity of 1011 W/cm2, at which we have confirmed that the interaction is in the perturbative regime. Our preliminary investigation indicates that the interaction begins to deviate slightly from this regime around 1012 W/cm2 if we increase the intensity, but the correction is still small below 1013 W/cm2, which is the typical focal intensity of SCSS [40].
The pulse-width dependence of δ and W for ħω = 21.2 eV close to the 1s2p resonance (21.218 eV) is shown in Figure 2(b). The calculations have been done at different values of pulse width T1/2 between 500 as and 21 fs. As expected from the discussions in Sections 2.1 and 2.2, and similarly to the case of a hydrogen atom (Subsection 2.3), both δ and W substantially change with pulse width, especially when the pulse is shorter than 10 fs. Accordingly, the PAD also varies as shown in Figure 3(b). One finds that the distribution to the direction perpendicular to the laser polarization again decreases as the pulse is shortened. As stated earlier, strictly speaking, Equation (4) is applicable only to ωf = ωi + 2ω, and the actual PAD involves integration over ωf. Nevertheless, the results in Figure 2(b) can well be described by Equation (4) [44], except for δ in the ultrashort pulse regime T1/2 ≲ 1 fs, where the spectrum becomes broader than the level spacing. If we compare Figure 2(a) for H and (b) for He, both for the 2p resonance, the phase-shift difference δ has a similar pulse-width dependence. As for the amplitude ratio W = |cs/cd|, it is smaller than unity, i.e., |cd| > |cs| regardless of pulse width for H, while its variation is larger for He; |cd| > |cs| in the short-pulse limit, and |cd| < |cs| in the long-pulse limit. Accordingly, the variation in PAD is more prominent for He than for H (Figure 3).
It is interesting at this stage to examine some limiting cases. With increasing pulse duration, δ approaches the scattering phase shift difference δsc, and the PAD changes only slowly with T1/2 [Figure 3(b)]. When the pulse is resonant (∆rT ≪ 1) and sufficiently long (T ≫ aS, aD) at the same time, assuming that the resonant excitation is not saturated, one can approximate the extra phase shift as
hence, it is proportional to the spectral width, which can be confirmed in Figure 3 of [44].
On the other hand, if we plot δ as a function of spectral width, δ tends to an asymptotic value in the wide-spectrum, i.e., short-pulse limit. Correspondingly, the PAD does not change much with the pulse width for T1/2 ≲ 1 fs [Figures 3(b) and 6(b),(c)]. This is because the pulse becomes resonant with multiple levels; the spacing between the 1s2p and 1s3p is 1.9 eV. As we have shown in the previous subsection, when many neighboring states are resonantly excited by the pulse, the extra phase shift difference δex does not much depend on the pulse duration. Similarly to the case of the hydrogen atom, this especially applies when the photon energy lies in the Rydberg manifold, and exceeds the ionization potential (24.59 eV), i.e., in the case of above-threshold two-photon ionization.
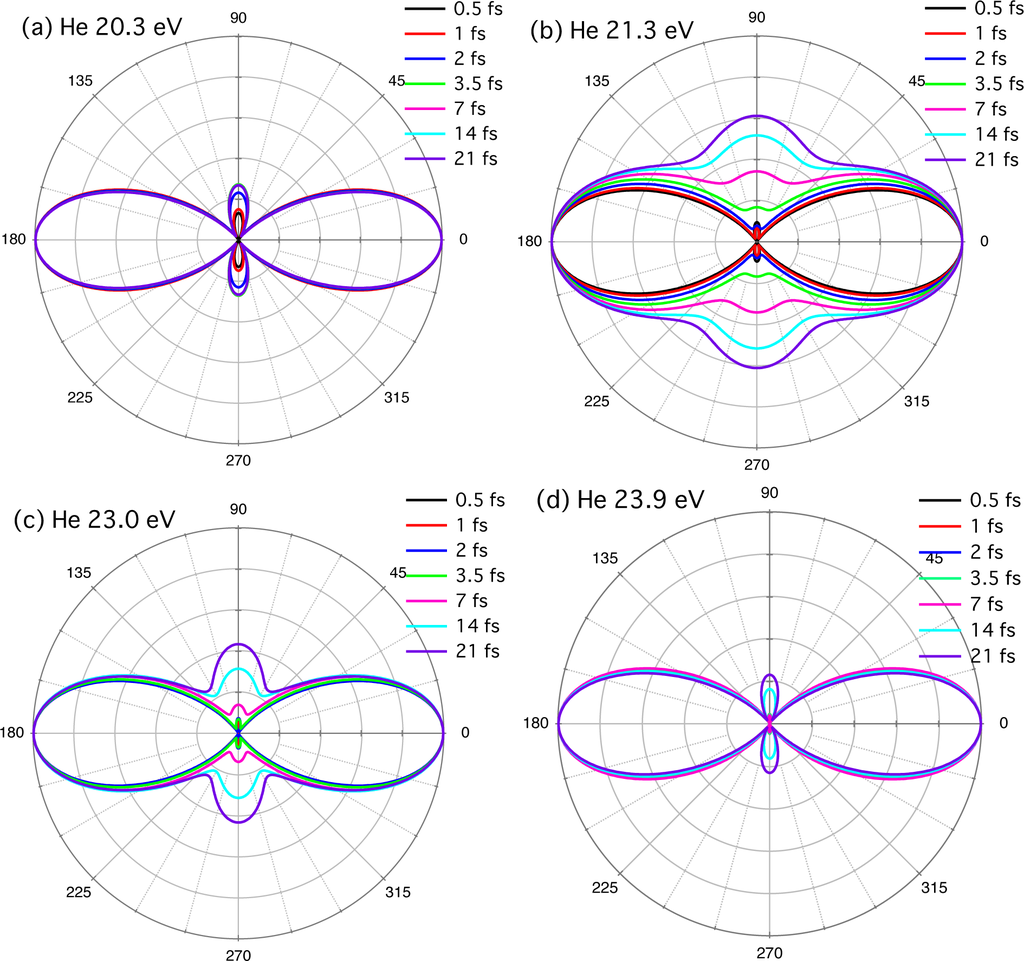
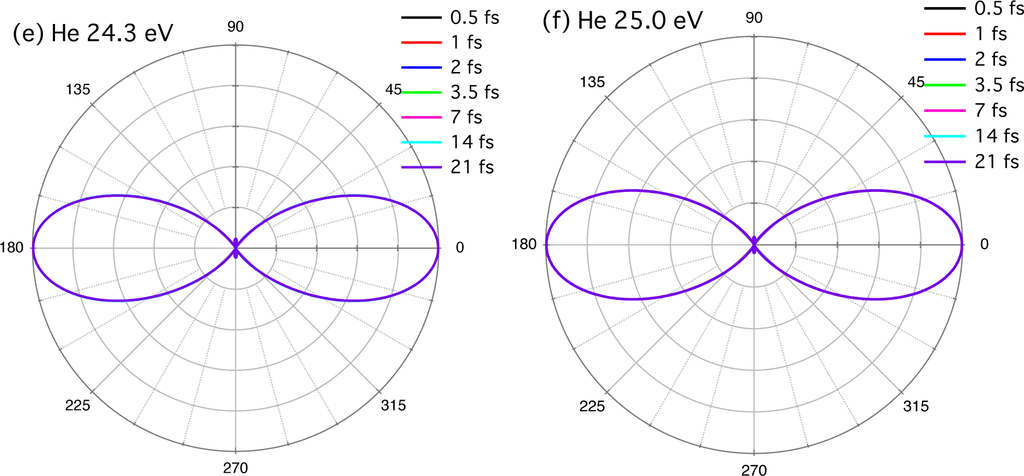
Figure 6.
Pulse-width dependence of the photoelectron angular distribution for (a) ħω = 20.3 eV; (b) ħω = 21.3 eV; (c) 23.0 eV; (d) 23.9 eV; (e) 24.3 eV; and (f) 25.0 eV. The target atom is helium.
In Figures 4(e)–(g) and 6 we compare the pulse-width dependence of δex and the PAD, respectively, for different values of ħω, where we find trends similar to the case of H. While δ ≈ δsc (δex ≈ 0) and the PAD are nearly independent of T1/2 for nonresonant pulses (ħω = 20.3 eV, T1/2 ≳ 3.5 fs), when the pulse is close to resonance with an excited level (ħω = 21.2, 21.3, and 23.0 eV), δex and PAD rapidly change with T1/2. On the contrary, δex is finite and nearly constant for ħω = 24.3, 24.6, and 25.0 eV [Figure 4(g)]; accordingly, the PAD hardly varies with pulse width. At T1/2 ≲ 1 fs, the spectrum is so broad that δex restarts to change slightly. One also sees that the transition across the ionization potential is smooth [Figure 4(g)], as has been seen for a hydrogen atom in Figures 1 and 4(c),(d). It should be pointed out that the extra phase shift difference due to free-free transitions plays a significant role in the recently observed time delay in photoemission by attosecond EUV pulses [75–79].
Figure 7 shows the photon energy dependence of the phase difference δ and the amplitude ratio W for a pulse width of 7 fs. Although the number of data points is limited, we can see features basically similar to those in Figure 1 for H.
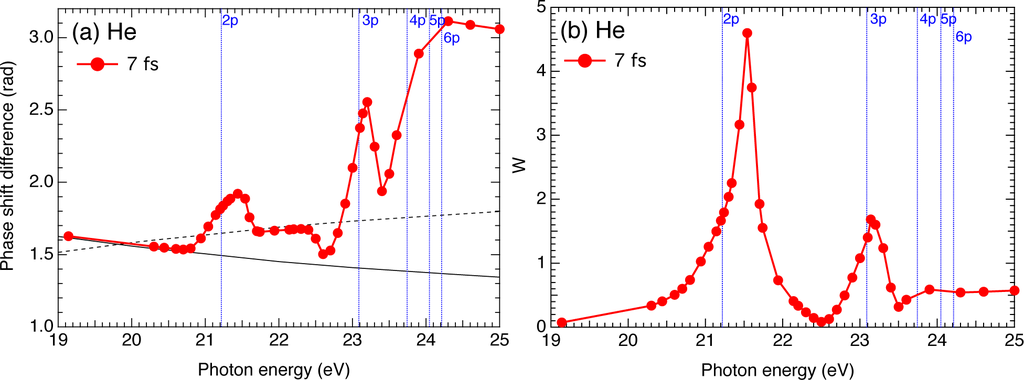
Figure 7.
Photon-energy dependence of (a) the relative phase (phase-shift difference) δ and (b) the amplitude ratio W between the S and D wave packets for a pulse width of 7 fs. The target atom is helium. Thin sold and dashed lines in (a): |δsc| and π − |δsc|, respectively. Vertical dotted lines: positions of 1s2p1P to 1s6p1P resonances.
3. Pulse Shapes Typical of Experiments
We have considered coherent Gaussian pulses so far. Such a pulse may be generated either by extracting a single harmonic order of HHG sources or by HHG-seeded FELs [80]. In practice, however, high-harmonic pulses are composed of several orders. Also, as is well known, the temporal pulse shapes of FEL operating in the self-amplified spontaneous emission (SASE) mode fluctuate from shot to shot [55–59]. In this section, we investigate the effects of these properties of practical pulses for the case of a He atom. While Gaussian pulses are characterized by a single time scale, i.e., the width of the (whole) pulse, both FEL and HHG pulses have two time scales: coherence time and mean pulse width for the former, and the width of each pulse in the pulse train and the overall pulse width for the latter. From the analysis of these pulses, we may also estimate to what extent the relative phase δ can be controlled by the pulse shape.
3.1. SASE-FEL Pulses
In order to investigate the effects of the chaotic nature of typical FEL pulses, we have performed numerical experiments for EUV pulses randomly generated by the partial-coherence method [81]. Typical pulse shapes for the case of a photon energy of 23.0 eV, coherence time (CT) of 2 fs, and mean pulse width (MPW) of 7 fs are presented in Figure 8. The pulse shape significantly fluctuates from shot to shot, and such pulses may be considered to be composed of many pulses that have a pulse width of 2 fs on average, random phases with each other, and a whole envelope corresponding to 7 fs pulse width on average.
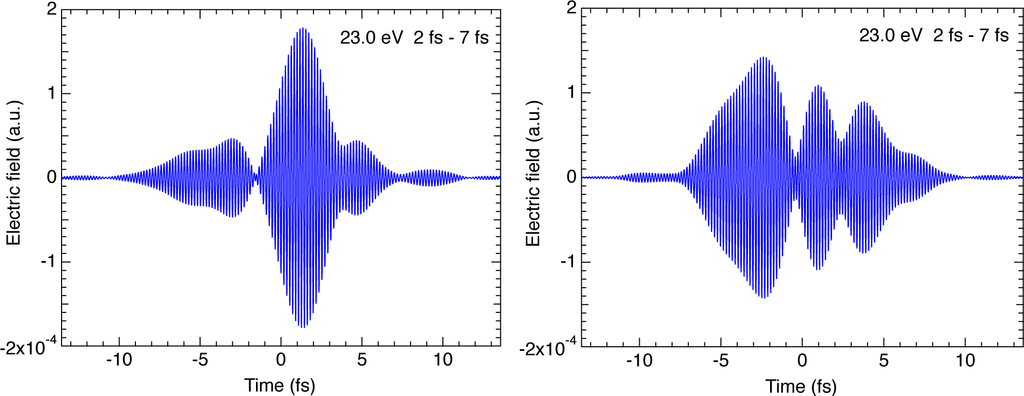
Figure 8.
Typical pulse shapes generated by the partial-coherence method [81] for the case of 23.0 eV photon energy, 2 fs coherence time, and 7 fs mean pulse width.
The obtained values of W and δ for several combinations of CT and MPW for ħω = 21.2, 21.3, and 23.0 eV, and some of the corresponding PAD are shown in Table 1 and Figure 9, respectively. The PADs for ħω = 20.3 and 24.3 eV are also shown in Figure 9. For ħω = 20.3 and 24.3 eV, for which the PAD hardly depends on pulse width, the PAD for a chaotic pulse is similar to that for a Gaussian pulse. For ħω = 21.2, 21.3, and 23.0 eV, we can see from the table that δ takes values between those corresponding to the CT and the MPW in most cases. Also, in general, the PAD is of a shape between those for the CT and the MPW (Figure 9). It is somewhat surprising that this simple empirical rule applies to most of the combinations of CT, MPW, and photon energy studied here. This may be because different constituent pulses have basically random phases from each other, smearing out the interference between different electron bursts.

Table 1.
W and δ calculated for chaotic pulses generated by the partial-coherence method for several pairs of coherence time (CT) and mean pulse width (MPW). The target atom is helium. The average values and standard deviation errors of W and δ by typically 48 runs are listed. The rows with the same CT and MPW values are for fully coherent Gaussian pulses.
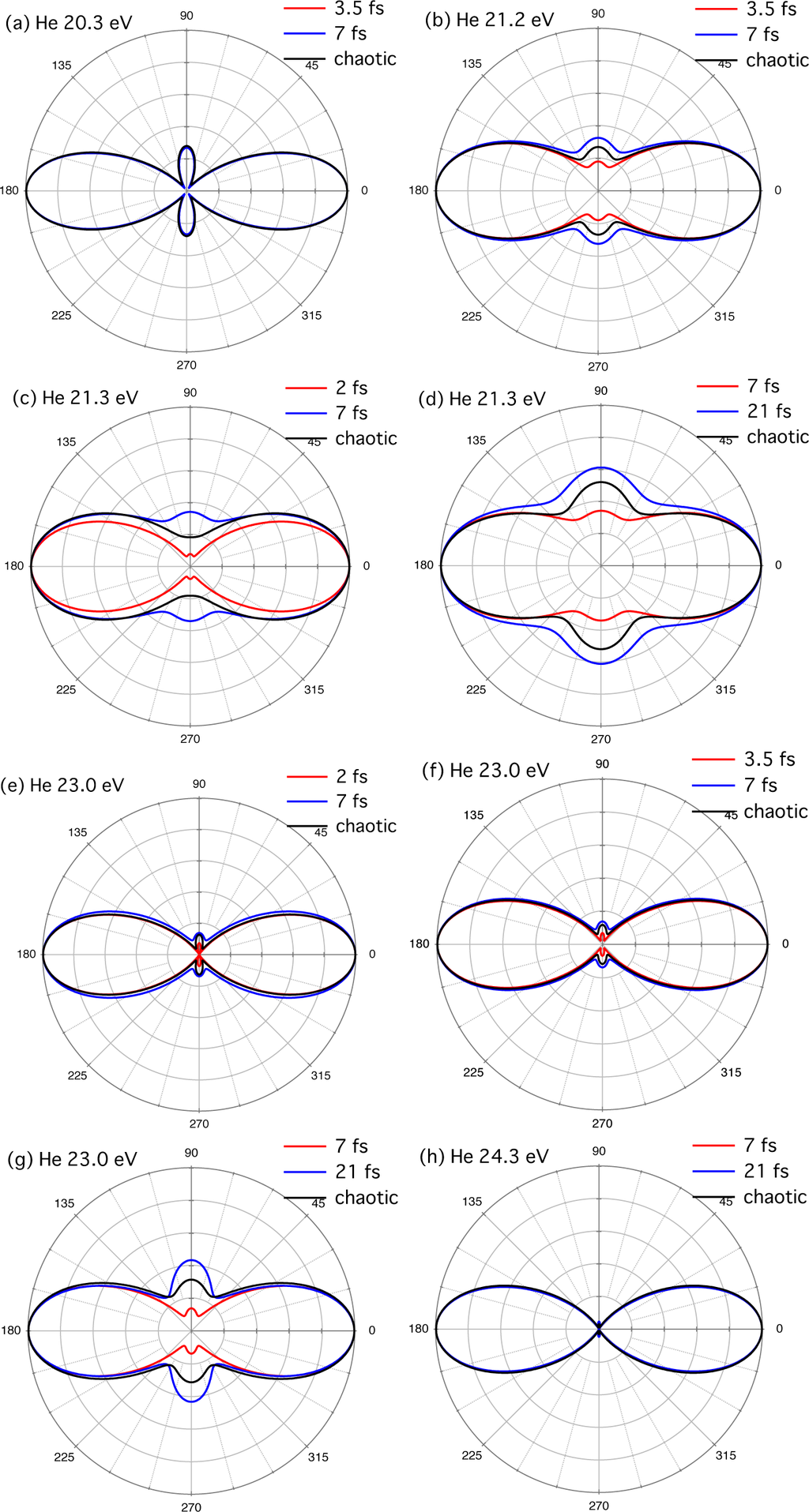
Figure 9.
Photoelectron angular distribution by a chaotic pulse for a photon energy, coherence time (CT), and mean pulse width (MPW) indicated in each panel. The target atom is helium. The red and blue curves are for Gaussian pulses whose widths are given by the CT and MPW, respectively of the chaotic pulse. For example, in panel (b), the photon energy, CT, and MPW, are 21.2 eV, 3.5 fs, and 7 fs, respectively.
The difference in PAD between the cases of Gaussian and SASE-FEL pulses is larger for ħω = 21.2 and 21.3 eV than for 23.0 eV, since the variation of PAD with T1/2 in the case of Gaussian pulses is already larger for the former, especially at T1/2 < 10 fs [Figures 3(b) and 6]. This suggests that the controllability of PAD by pulse shape can be roughly estimated by the results for Gaussian pulses.
3.2. High-Harmonic Pulses Containing Multiple Harmonic Orders
We simulate the 2PI of He by an attosecond pulse train composed of the ninth (H9) to the seventeenth (H17) harmonics of a fundamental wavelength of 808.7 nm, whose fifteenth harmonic (H15, 23.0 eV) is resonant with the 1s3p 1P state. We use the relative intensity of each harmonic component reported in Figure 1 of [82], neglecting inter- and intra-order chirps usually observed in experiments [83]. Each component is expressed as a Gaussian pulse with a common pulse width Tov, referred to as overall pulse width hereafter. We show the pulse shape and intensity spectrum for Tov = 7 fs in Figure 10. The whole pulse has a 7 fs envelope, while composed of many individual pulses with a pulse width ∼ 0.3 fs [Figure 10(a)]. The pulse spectrum, though composed of discrete harmonic peaks, is so broad as a whole that it spans from 13.8 eV (H9) to 26.1 (H17) [Figure 10(b)]. This latter manifests itself as a fact that each pulse in the pulse train [Figure 10(a)] has a sub-femtosecond duration, while the overall pulse width corresponds to the spectral width of each harmonic component.
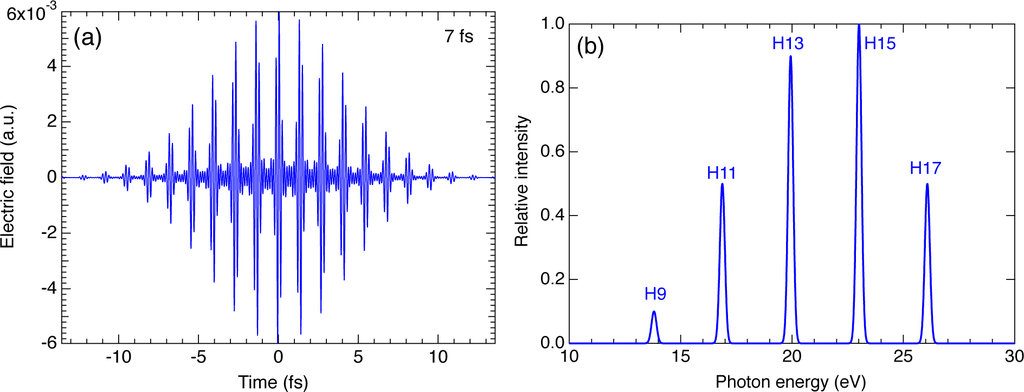
Figure 10.
(a) Pulse shape and (b) intensity spectrum of a 7 fs high-harmonic pulse (attosecond pulse train) composed of multiple harmonic orders used in the present study (see text).
The triangles in Figure 11 plot the calculated relative phase δ between the S and D partial waves for several values of Tov. Although δ changes with Tov especially at Tov < 4 fs, its variation is much smaller than for the case of a Gaussian pulse centered at 23.0 eV (squares in Figure 11). This is probably because the H9–H13 (nonresonant) and H17 (in the continuum) components would lead to a constant phase if alone, and that only resonant excitation by H15 contributes to the variation.
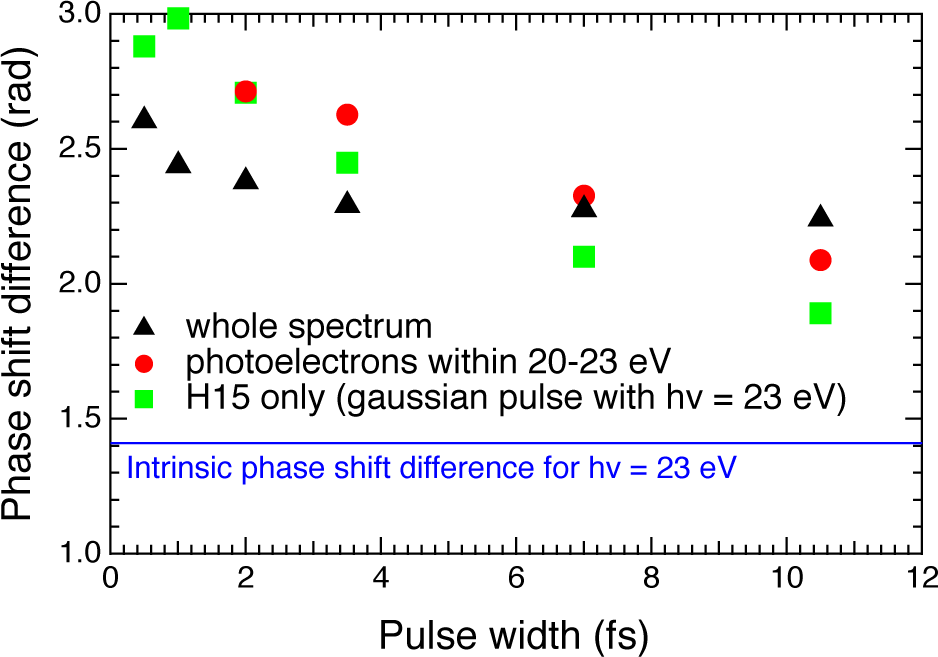
Figure 11.
Pulse-width dependence of the phase shift difference δ for high-harmonic pulses composed of multiple harmonic orders (see text). The target atom is helium. Black triangles: derived from the whole 2PI photoelectron wave packets. Red circles: derived from the 2PI photoelectron wave packets within the 20–23 eV energy range. Green squares: for Gaussian pulses with a photon energy of 23 eV. The thin horizontal line denotes the value (1.410 [63]) of the intrinsic scattering phase-shift difference δsc for ħω = 23.0 eV.
As can be seen from Figure 10(b), H15 is the most intense harmonic component in the spectrum, resonant with the 1s3p 1P state. The corresponding 2PI photoelectron energy is 21.4 eV, while the other photoelectron peaks are separated by 3.07 eV from each other. Then, in order to highlight the contribution from H15, let us focus ourselves on the wave packet between 20 and 23 eV, for which the values of δ are plotted as circles in Figure 11. Only the results at Tov ≥ 2 fs are plotted, since the pulse is so short at Tov < 2 fs that the photoelectron peaks are not well separated from each other anymore. As expected, we can see that δ now varies with Tov as rapidly as for the case of the Gaussian pulse, though its value is somewhat shifted due to an additional contribution from the H13+H17 and H17+H13 processes. The change in PAD corresponding to the wave packet between 20 and 23 eV, shown in Figure 12, is not so large as one might expect from the variation in δ, again probably due to the relatively small variation with pulse width below 10 fs even for the case of Gaussian pulses. Nevertheless, it is clearly different from what would be expected from the scattering phase shift difference [see the curve for 21 fs in Figure 6(c)], well indicating the presence of the competition between the resonant and nonresonant ionization paths.
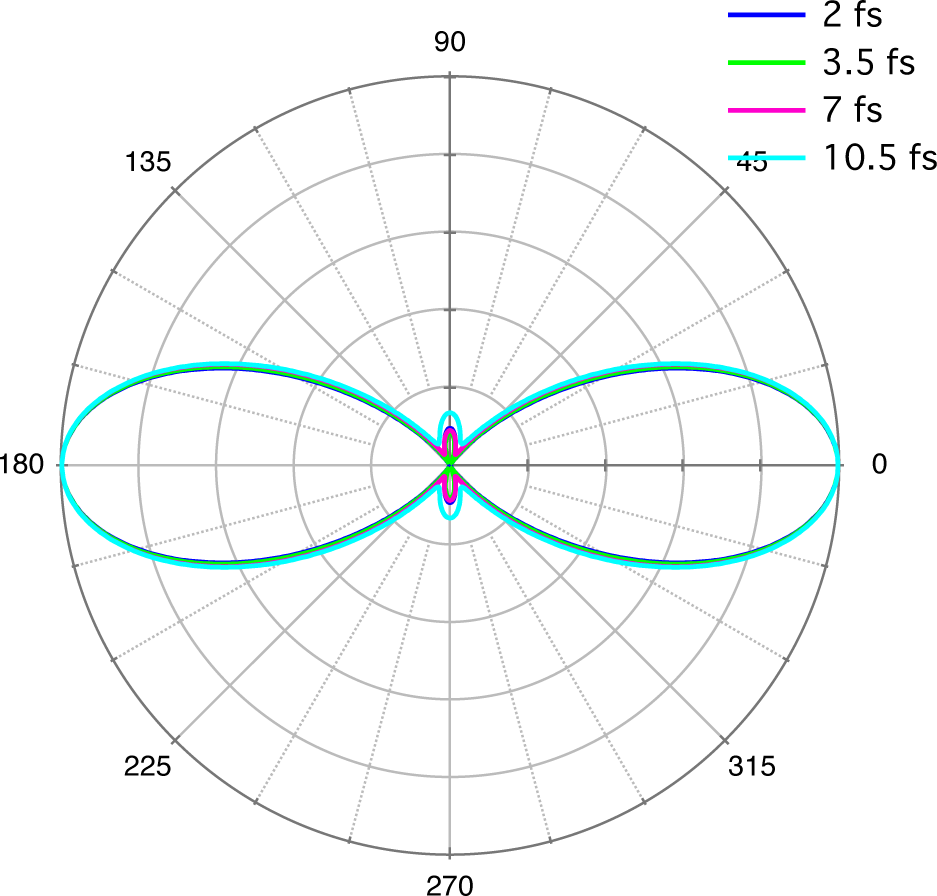
Figure 12.
Pulse-width dependence of the photoelectron angular distribution for high-harmonic pulses. The target atom is helium.
4. Conclusions
We have numerically studied the two-photon ionization of a hydrogen and helium atom by an ultrashort EUV pulse. Due to the competition between the resonant and nonresonant ionization paths, the relative phase δ between the S and D photoelectron wave packets from the resonance-enhanced two-photon ionization by fs EUV pulses is different from the scattering phase shift difference, |δsc| or π−|δsc| more precisely, which would be expected for single-photon ionization from an excited level [29] and nonresonant two-photon ionization, and rapidly changes with the pulse width when the pulse is resonant with an intermediate excited state and 2 fs ≲ T1/2 ≲ 10 fs. Accordingly, the photoelectron angular distribution varies with T1/2 as well. Hence, the control of the competition between the resonant and nonresonant paths in H and He by pulse width is a unique feature of a-few-fs EUV pulses.
Also, δ is different from |δsc| and π − |δsc| but nearly constant independent of T1/2 when the Rydberg manifold is excited and in the case of above-threshold two-photon ionization. The transition across the ionization threshold is smooth.
The PAD as well as W and δ is affected by the chaotic nature of SASE FEL pulses and by neighboring harmonic components typical of HHG. For the former case, the relative phase δ takes a value between those corresponding to the coherence time and the mean pulse width of the pulses. For the latter case, i.e., for the case of 2PI by high-harmonic pulses with multiple harmonic orders, δ does not depend much on the pulse width, similarly to the case of the Rydberg manifold excitation. On the other hand, by selecting an appropriate photoelectron energy range, one can recover the pulse-width dependence of δ originating from the competition of the resonant and nonresonant ionization paths.
The results of the present study stress the importance of the account of the nonresonant paths in the interpretation of resonant two-photon, single- or two-color, ionization experiments, including coherent control, by state-of-the-art ultrashort EUV sources.
Acknowledgments
We wish to thank N. Kabachnik for fruitful discussions. K.L.I. gratefully acknowledges support by the APSA Project (Japan), KAKENHI (No. 23656043 and No. 23104708), the Cooperative Research Program of “Network Joint Research Center for Materials and Devices,” (Japan) and the Project of Knowledge Innovation Program (PKIP) of Chinese Academy of Sciences (Project No. KJCX2.YW.W10). K.U. acknowledges support by the X-ray Free Electron Laser Utilization Research Project and the X-ray Free Electron Laser Priority Strategy Program of the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan, the Management Expenses Grants for National Universities Corporations from MEXT, and IMRAM research program.
References and Note
- Gontier, Y.; Trahin, M. Multiphoton processes in a hydrogen atom. Phys. Rev. A 1971, 4, 1896–1906. [Google Scholar]
- Beers, B.L.; Armstrong, L. Exact solution of a realistic model for two-photon ionization. Phys. Rev. A 1975, 12, 2447–2454. [Google Scholar]
- Crance, M.; Feneuiile, S. Resonant multiphoton ionization induced by pulsed excitation. Phys. Rev. A 1977, 16, 1587–1593. [Google Scholar]
- Andrews, D.L. Resonance two-photon ionisation with ultrashort laser pulses. J. Phys. B 1977, 10, L659–L662. [Google Scholar]
- McClean, W.A.; Swain, S. Theory of resonant two-photon ionisation. J. Phys. B 1978, 11, 1717–1732. [Google Scholar]
- McClean, W.A.; Swain, S. The time dependence of two-photon ionisation. J. Phys. B 1979, 12, 2291–2308. [Google Scholar]
- Jackson, R.I.; O’Brien, D.P.; Swain, S. The photoelectron energy distribution in two-photon ionisation. J. Phys. B 1982, 15, 3385–3403. [Google Scholar]
- Dixit, S.N.; Lambropoulos, P. Theory of photoelectron angular distributions in resonant multiphoton ionization. Phys. Rev. A 1983, 27, 861–874. [Google Scholar]
- Ishikawa, K.; Midorikawa, K. Two-photon ionization of He+ as a nonlinear optical effect in the soft-x-ray region. Phys. Rev. A 2002, 65. [Google Scholar] [CrossRef]
- Selstø, S.; Palacios, A.; Fernandez, J.; Martin, F. Electron angular distribution in resonance-enhanced two-photon ionization of H2+ by ultrashort laser pulses. Phys. Rev. A 2007, 75. [Google Scholar] [CrossRef]
- Varma, H.R.; Ciappina, M.F.; Rohringer, N.; Santra, R. Above-threshold ionization in the X-ray regime. Phys. Rev. A 2009, 80. [Google Scholar] [CrossRef]
- Smith, S.J.; Leuchs, G. Angular correlation in multiphoton ionization of atoms. Adv. At. Mol. Phys 1988, 24, 157–221. [Google Scholar]
- Lambropoulos, P.; xMaragikis, G.; Zhang, J. Two-electron atoms in strong fields. Phys. Rep 1998, 305, 203–293. [Google Scholar]
- Wang, Z.-M.; Elliott, D.S. Determination of the phase difference between even and odd continuum wave functions in atoms through quantum interference measurements. Phys. Rev. Lett 2001, 87. [Google Scholar] [CrossRef]
- Reid, K.L. Photoelectron angular distributions. Annu. Rev. Chem 2003, 54, 397–424. [Google Scholar]
- Kabachnik, N.M.; Fritzsche, S.; Grum-Grzhimailo, A.N.; Meyer, M.; Ueda, K. Coherence and correlations in photoinduced Auger and fluorescence cascades in atoms. Phys. Rep 2007, 451, 155–233. [Google Scholar]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bhr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photon 2007, 1, 336–342. [Google Scholar]
- Shintake, T.; Tanaka, H.; Hara, T.; Tanaka, T.; Togawa, K.; Yabashi, M.; Otake, Y.; Asano, Y.; Bizen, T.; Fukui, T.; et al. A compact free-electron laser for generating coherent radiation in the extreme ultraviolet region. Nat. Photon 2008, 2, 555–559. [Google Scholar]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photon 2010, 4, 641–647. [Google Scholar]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photon 2012, 6, 540–544. [Google Scholar]
- Nagasono, M.; Suljoti, E.; Pietzsch, A.; Hennies, F.; Wellhöfer, M.; Hoeft, J.-T.; Martins, M.; Wurth, W.; Treusch, R.; Feldhaus, J.; Schneider, J.R.; Föhlisch, A. Resonant two-photon absorption of extreme-ultraviolet free-electron-laser radiation in helium. Phys. Rev. A 2007, 75, 051406(R)-1–051406(R)-4. [Google Scholar]
- Santra, R.; Kryzhevoi, N. V.; Cederbaum, L. S. X-ray two-photon photoelectron spectroscopy: A theoretical study of inner-shell spectra of the organic para-aminophenol molecule. Phys. Rev. Lett 2009, 103, 013002-1–013002-4. [Google Scholar]
- Young, L.; Kanter, E. P.; Krässig, B.; Li, Y.; March, A. M.; Pratt, S. T.; Santra, R.; Southworth, S. H.; Rohringer, N.; DiMauro, L. F.; et al. Femtosecond electronic response of atoms to ultra-intense X-rays. Nat. (Lond.) 2010, 466, 56–61. [Google Scholar]
- Cryan, J.P.; Glownia, J. M.; Andreasson, J.; Belkacem, A.; Berrah, N.; Blaga, C. I.; Bostedt, C.; Bozek, J.; Buth, C.; DiMauro, L. F.; et al. Auger electron angular distribution of double core-hole states in the molecular reference frame. Phys. Rev. Lett 2010, 105, 083004-1–083004-5. [Google Scholar]
- Fang, L.; Hoener, M.; Gessner, O.; Tarantelli, F.; Pratt, S.T.; Kornilov, O.; Buth, C.; Gühr, M.; Kanter, E.P.; Bostedt, C.; et al. Double core-hole production in N2: Beating the Auger clock. Phys. Rev. Lett 2010, 105, 083005-1–083005-5. [Google Scholar]
- Berrah, N.; Fang, L.; Murphy, B.; Osipov, T.; Ueda, K.; Kukk, E.; Feifel, R.; van der Meulen, P.; Salen, P.; Schmidt, H.T.; et al. Double-core-hole spectroscopy for chemical analysis with an intense X-ray femtosecond laser. Proc. Nat. Acad. Sci. USA 2011, 108, 16912–16915. [Google Scholar]
- Doumy, G.; Roedig, C.; Son, S.-K.; Blaga, C. I.; DiChiara, A. D.; Santra, R.; Berrah, N.; Bostedt, C.; Bozek, J. D.; Bucksbaum, P. H.; et al. Nonlinear atomic response to intense ultrashort X rays. Phys. Rev. Lett 2011, 106, 083002-1–083002-4. [Google Scholar]
- Salén, P.; van der Meulen, P.; Schmidt, H. T.; Thomas, R. D.; Larsson, M.; Feifel, R.; Piancastelli, M. N.; Fang, L.; Murphy, B.; Osipov, T.; et al. Experimental verification of the chemical sensitivity of two-site double core-hole states formed by an X-ray free-electron laser. Phys. Rev. Lett 2012, 108, 153003-1–153003-5. [Google Scholar]
- Haber, L.H.; Doughty, B.; Leone, S.R. Continuum phase shifts and partial cross sections for photoionization from excited states of atomic helium measured by high-order harmonic optical pump-probe velocity map imaging. Phys. Rev. A 2009, 79, 031401(R)-1–031401(R)-4. [Google Scholar]
- Rouzée, A.; Johnsson, P.; Gryzlova, E.V.; Fukuzawa, H.; Yamada, A.; Siu, W.; Huismans, Y.; Louis, E.; Bijkerk, F.; Holland, D.M.P.; et al. Angle-resolved photoelectron spectroscopy of sequential three-photon triple ionization of neon at 90.5 eV photon energy. Phys. Rev. A 2011, 83, 031401(R)-1–031401(R)-4. [Google Scholar]
- Hasegawa, H.; Takahashi, E.J.; Nabekawa, Y.; Ishikawa, K.L.; Midorikawa, K. Multiphoton ionization of He by using intense high-order harmonics in the soft-X-ray region. Phys. Rev. A 2005, 71, 023407-1–023407-5. [Google Scholar]
- Kobayashi, Y.; Sekikawa, T.; Nabekawa, Y.; Watanabe, S. 27-fs extreme ultraviolet pulse generation by high-order harmonics. Opt. Lett 1998, 23, 64–66. [Google Scholar]
- Mitzner, R.; Sorokin, A.A.; Siemer, B.; Roling, S.; Rutkowski, M.; Zacharias, H.; Neeb, M.; Noll, T.; Siewert, F.; Eberhardt, W.; et al. Direct autocorrelation of soft-X-ray free-electron-laser pulses by time-resolved two-photon double ionization of He. Phys. Rev. A 2009, 80, 025402-1–025402-4. [Google Scholar]
- Sorgenfrei, F.; Schlotter, W.F.; Beeck, T.; Nagasono, M.; Gieschen, S.; Meyer, H.; Föhlisch, A.; Beye, M.; Wurth, W. The extreme ultraviolet split and femtosecond delay unit at the plane grating monochromator beamline PG2 at FLASH. Rev. Sci. Instrum 2010, 81, 043107-1–043107-7. [Google Scholar]
- Moshammer, R.; Pfeifer, Th.; Rudenko, A.; Jiang, Y.H.; Foucar, L.; Kurka, M.; Kühnel, K.U.; Schröter, C.D.; Ullrich, J.; Herrwerth, O.; et al. Second-order autocorrelation of XUV FEL pulses via time resolved two-photon single ionization of He. Opt. Exp 2011, 19, 21698–21706. [Google Scholar]
- Nabekawa, Y.; Shimizu, T.; Okino, T.; Furusawa, K.; Hasegawa, H.; Yamanouchi, K.; Midorikawa, K. Interferometric autocorrelation of an attosecond pulse train in the single-cycle regime. Phys. Rev. Lett 2006, 97, 153904-1–153904-4. [Google Scholar]
- Nikolopoulos, L.A.A.; Lambropoulos, P. Multichannel theory of two-photon single and double ionization of helium. J. Phys. B 2001, 34, 545–564. [Google Scholar]
- Van der Hart, H.W.; Bingham, P. Two- and three-photon ionization of He between 1013 and 1014 Wcm−2. J. Phys. B 2005, 38, 207–221. [Google Scholar]
- Sato, T.; Iwasaki, A.; Ishibashi, K.; Okino, T.; Yamanouchi, K.; Adachi, J.; Yagishita, A.; Yazawa, H.; Kannari, F.; Aoyama, M.; et al. Determination of the absolute two-photon ionization cross section of He by an XUV free electron laser. J. Phys. B 2011, 44, 161001-1–161001-5. [Google Scholar]
- Hishikawa, A.; Hishikawa, A.; Fushitani, M.; Hikosaka, Y.; Matsuda, A.; Liu, C.-N.; Morishita, T.; Shigemasa, E.; Nagasono, M.; Tono, K.; et al. Enhanced nonlinear double excitation of He in intense extreme ultraviolet laser fields. Phys. Rev. Lett 2011, 107, 243003-1–243003-5. [Google Scholar]
- Guyétand, O.; Gisselbrecht, M.; Huetz, A.; Agostini, P.; Taïeb, R.; Véniard, V.; Maquet, A.; Antonucci, L.; Boyko, O.; Valentin, C.; Douillet, D. Multicolour above-threshold ionization of helium: quantum interference effects in angular distributions. J. Phys. B 2005, 35, L357–L363. [Google Scholar]
- Haber, L.H.; Doughty, B.; Leone, S.R. Energy-dependent photoelectron angular distributions of two-color two-photon above threshold ionization of atomic helium. Phys. Rev. A 2011, 84, 013416-1–013416-9. [Google Scholar]
- O’Keeffe, P.; Bolognesi, P.; Richter, R.; Moise, A.; Ovcharenko, E.; Pravica, L.; Sergo, R.; Stebel, L.; Cautero, G.; Avaldi, L. Photoelectron imaging in pump-probe experiments combining synchrotron and laser radiation. J. Phys 2010, 235, 012006-1–012006-8. [Google Scholar]
- Ishikawa, K.L.; Ueda, K. Competition of resonant and nonresonant paths in resonance-enhanced two-photon single ionization of He by an ultrashort extreme-ultraviolet pulse. Phys. Rev. Lett 2012, 108. [Google Scholar] [CrossRef]
- Dudovich, N.; Dayan, B.; Gallagher Faeder, S.M.; Silberberg, Y. Transform-limited pulses are not optimal for resonant multiphoton transitions. Phys. Rev. Lett 2001, 86, 47–50. [Google Scholar]
- Wollenhapt, M.; Klug, M.; Köhler, J.; Bayer, T.; Sarpe-Tudoran, C.; Baumert, T. Photoelectron angular distributions from strong-field coherent electronic excitation. Appl. Phys. B 2009, 95, 245–259. [Google Scholar]
- Reid, K.L. Photoelectron angular distributions: Developments in applications to isolated molecular systems. Mol. Phys 2012, 110, 131–147. [Google Scholar]
- NIST: Atomic Spectra Database—Energy Levels Form. Available online: http://physics.nist.gov/PhysRefData/ASD/levels_form.html accessed on 28 February 2013.
- FERMI HomePage. Available online: http://www.elettra.trieste.it/FERMI/ accessed on 28 February 2013.
- Pindzola, M.S.; Robicheaux, F. Time-dependent close-coupling calculations of correlated photoionization processes in helium. Phys. Rev. A 1998, 57, 318–324. [Google Scholar]
- Pindzola, M.S.; Robicheaux, F. Two-photon double ionization of He and H−. J. Phys. B 1998, 31, L823–L831. [Google Scholar]
- Colgan, J.; Pindzola, M.S.; Robicheaux, F. Fully quantal (γ, 2e) calculations for absolute differential cross sections of helium. J. Phys. B 2001, 34, L457–L466. [Google Scholar]
- Parker, J.S.; Moore, L. R.; Meharg, K.J.; Dundas, D.; Taylor, K. T. Double-electron above threshold ionization of helium. J. Phys. B 2001, 34, L69–L78. [Google Scholar]
- Ishikawa, K.L.; Midorikawa, K. Above-threshold double ionization of helium with attosecond intense soft x-ray pulses. Phys. Rev. A 2005, 72, 013407-1–013407-8. [Google Scholar]
- Mitzner, R.; Siemer, B.; Neeb, M.; Noll, T.; Siewert, F.; Roling, S.; Rutkowski, M.; Sorokin, A. A.; Richter, M.; Juranic, P.; et al. Spatio-temporal coherence of free electron laser pulses in the soft X-ray regime. Opt. Exp 2008, 16, 19909–19919. [Google Scholar]
- Schlotter, W.F.; Sorgenfrei, F.; Beeck, T.; Beye, M.; Gieschen, S.; Meyer, H.; Nagasono, M.; Fohlisch, A.; Wurth, W. Longitudinal coherence measurements of an extreme-ultraviolet free-electron laser. Opt. Lett 2010, 35, 372–374. [Google Scholar]
- Bonifacio, R.; de Salvo, L.; Pierini, P.; Piovella, N.; Pellegrini, C. Longitudinal coherence measurements of an extreme-ultraviolet free-electron laser. Phys. Rev. Lett 1994, 73, 70–73. [Google Scholar]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Statistical properties of radiation from VUV and X-ray free electron laser. Opt. Commun 1998, 148, 383–403. [Google Scholar]
- Krinsky, S.; Gluckstern, R.L. Analysis of statistical correlations and intensity spiking in the self-amplified spontaneous-emission free-electron laser. Phys. Rev. ST Accel. Beams 2003, 6, 050701-1–050701-10. [Google Scholar]
- NIST Handbook of Mathematical Functions; Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) Cambridge: New York, NY, USA, 2010.
- Oza, D.H. Phase shifts and resonances for electron scattering by He+ below the N = 2 threshold. Phys. Rev. A 1986, 33, 824–838. [Google Scholar]
- Chang, T.N.; Fang,, T.K. Effect of positive-energy orbitals on the photoionization cross-sections and oscillator-strengths of He and divalent atoms. Phys. Rev. A 1995, 52, 2638–2644. [Google Scholar]
- Gien, T.T. Accurate calculation of phase shifts for electron-He+ collisions. J. Phys. B 2002, 35, 4475–4490. [Google Scholar]
- W and δ are related to X and ∆ in [29] as and δ = ∆.
- Kulander, K.C.; Schafer, K.J.; Krause, J.L. Time-Dependent Studies of Multiphoton Processes. In Atoms in Intense Laser Fields; Gavrila, M., Ed.; Academic: New York, NY, USA, 1992; Volume 247. [Google Scholar]
- Ishikawa, K.; Midorikawa, K. Coherent control of extreme uv absorption and photoemission by the simultaneous irradiation of ultrashort extreme uv and laser pulses. Phys. Rev. A 2002, 65, 031403(R)-1–031403(R)-4. [Google Scholar]
- Ishikawa, K. Photoemission and ionization of He+ under simultaneous irradiation of fundamental laser and high-order harmonic pulses. Phys. Rev. Lett 2003, 91, 043002-1–043002-4. [Google Scholar]
- Ishikawa, K.L. Temporal Young’s interference experiment by attosecond double and triple soft-x-ray pulses. Phys. Rev. A 2006, 74, 023806-1–023806-4. [Google Scholar]
- Ishikawa, K.L.; Takahashi, E.J.; Midorikawa, K. Single-attosecond pulse generation using a seed harmonic pulse train. Phys. Rev. A 2007, 75, 021801(R)-1–021801(R)-4. [Google Scholar]
- Schiessl, K.; Ishikawa, K.L.; Persson, E.; Burgdörfer, J. Quantum path interference in the wavelength dependence of high-harmonic generation. Phys. Rev. Lett 2007, 99, 253903-1–253903-4. [Google Scholar]
- Ishikawa, K.L.; Takahashi, E.J.; Midorikawa, K. Wavelength dependence of high-order harmonic generation with independently controlled ionization and ponderomotive energy. Phys. Rev. A 2009, 80, 011807(R)-1–011807(R)-4. [Google Scholar]
- Arbo, D.G.; Ishikawa, K.L.; Schiessl, K.; Persson, E.; Burgdörfer, J. Intracycle and intercycle interferences in above-threshold ionization: The time grating. Phys. Rev. A 2010, 81, 021403(R)-1–021403(R)-4. [Google Scholar]
- Ishikawa, K.L.; Kawazura, Y.; Ueda, K. Two-photon ionization of atoms by ultrashort laser pulses. J. Mod. Opt 2010, 57, 999–1007. [Google Scholar]
- Fano, U.; Cooper, J.W. Spectral distribution of atomic oscillator strengths. Rev. Mod. Phys 1968, 40, 441–507. [Google Scholar]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, Th.; et al. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar]
- Klünder, K.; Dahlström, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guénot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett 2011, 106, 143002-1–143002-4. [Google Scholar]
- Swoboda, M.; Fordell, T.; Klünder, K.; Dahlström, J.M.; Miranda, M.; Buth, C.; Schafer, K.J.; Mauritsson, J.; L’Huillier, A.; Gisselbrecht, M. Phase measurement of resonant two-photon ionization in helium. Phys. Rev. Lett 2010, 104, 103003-1–103003-4. [Google Scholar]
- Dahlström, J.M.; L’Huillier, A.; Maquet, A. Introduction to attosecond delays in photoionization. J. Phys. B 2012, 45, 183001-1–183001-32. [Google Scholar]
- Dahlström, J.M.; Guénot, D.; Klünder, K.; Gisselbrecht, M.; Mauritsson, J.; L’Huillier, A.; Maquet, A.; Taïeb, R. Theory of attosecond delays in laser-assisted photoionization. Chem. Phys 2012, in press. [Google Scholar]
- Togashi, T.; Takahashi, E.J.; Midorikawa, K.; Aoyama, M.; Yamakawa, K.; Sato, T.; Iwasaki, A.; Owada, S.; Okino, T.; Yamanouchi, K.; et al. Extreme ultraviolet free electron laser seeded with high-order harmonic of Ti:sapphire laser. Opt. Exp 2010, 19, 317–324. [Google Scholar]
- Pfeifer, T.; Jiang, Y.; Düsterer, S.; Moshammer, R.; Ullrich, J. Partial-coherence method to model experimental free-electron laser pulse statistics. Opt. Lett 2010, 35, 3441–3443. [Google Scholar]
- Okino, T.; Yamanouchi, K.; Shimizu, T.; Ma, R.; Nabekawa, Y.; Midorikawa, K. Attosecond nonlinear Fourier transformation spectroscopy of CO2 in extreme ultraviolet wavelength region. J. Chem. Phys 2008, 129, 161103-1–161103-4. [Google Scholar]
- Varjú, K.; Mairesse, Y.; Carré, B.; Gaarde, B.; Johnsson, P.; Kazamias, S.; López-Martens, R.; Mauritsson, J.; Schafer, K.J.; Balcou, Ph.; L’huillier, A.; Salières, P. Frequency chirp of harmonic and attosecond pulses. J. Mod. Opt 2005, 52, 379–394. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).