In Silico Methods for Assessing Cancer Immunogenicity—A Comparison Between Peptide and Protein Models
Abstract
1. Introduction
2. Materials and Methods
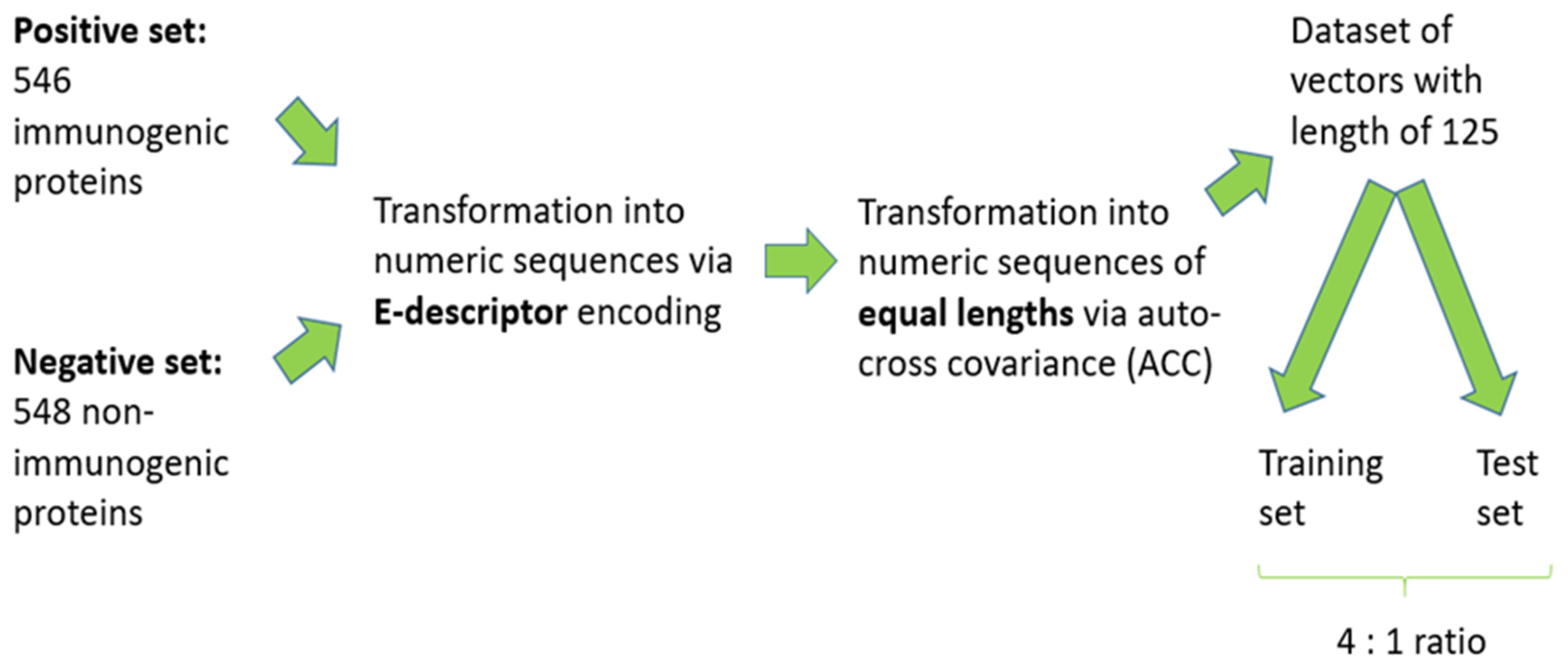
2.1. Datasets
2.2. Descriptors
2.3. Auto-Cross Covariance (ACC) Transformation
- E—E-descriptor value
- j, k (j ≠ k)—number of the E-descriptor (j, k = 1–5)
- i—position of amino acid in the peptide chain (i = 1, 2, 3…n)
- n—number of amino acids in the protein
- L—lag-value: the length of the frame of the contiguous amino acids
2.4. Machine Learning Methods
2.4.1. k-Nearest Neighbor (kNN)
2.4.2. Linear Discriminant Analysis (LDA)
2.4.3. Quadratic Discriminant Analysis (QDA)
2.4.4. Support Vector Machine (SVM)
2.4.5. Random Forest (RF)
2.4.6. Extreme Gradient Boosting (XGBoost)
2.5. Machine Learning Models Validation
- Sensitivity: The true positive rate, indicating the model’s capability to identify immunogenic proteins correctly.
- Specificity: The true negative rate, reflecting accurate detection of non-immunogenic proteins.
- Accuracy: The overall classification performance is calculated as the proportion of correct predictions across all samples.
- Area Under the ROC Curve (AUC): Ranging from 0.5 (random chance) to 1.0 (perfect discrimination), assessing overall predictive efficacy.
- Matthew’s Correlation Coefficient (MCC): A balanced measure particularly valuable for imbalanced datasets, where +1 represents perfect prediction, −1 indicates total disagreement, and 0 suggests random classification.
3. Results
3.1. Data Preprocessing
3.2. Development and Validation of ML Models
- kNN: k = 2 neighbors
- LDA: Singular Value Decomposition solver (svd)
- QDA: Regularization parameter (reg_param) = 0.0
- SVM: Radial basis function kernel (rbf) with C = 50 and γ = 100
- RF: 100 estimators with max_depth = 50 and max_features = 2
- XGBoost: learning_rate = 0.01, max_depth = 7, and 100 estimators
3.3. ML Models Robustness Assessment
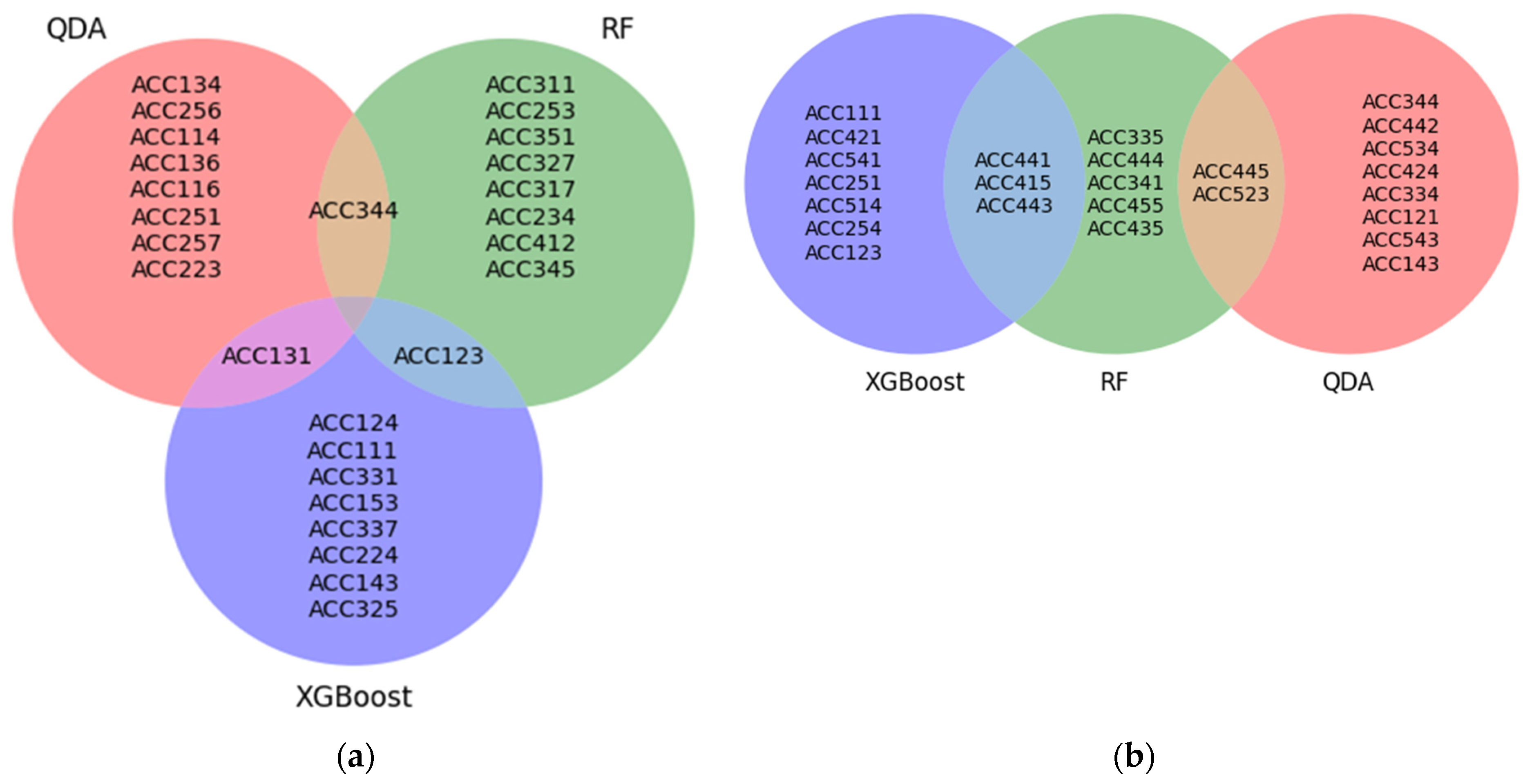
3.4. Attribute Importance Assessment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACC | Auto- and cross-covariance |
| AROC | The area under the ROC curve |
| FN | False negative |
| FP | False positive |
| kNN | k-Nearest neighbor |
| L | Lag value |
| LDA | Linear discriminant analysis |
| MCC | Matthes correlation coefficient |
| ML | Machine learning |
| PLS-DA | Partial least squares—discriminant analysis |
| QDA | Quadratic discriminant analysis |
| RF | Random forest |
| ROC | Receiver operating characteristic |
| SVM | Support vector machine |
| TN | True negative |
| TP | True positive |
| XGBoost | Extreme gradient boosting |
References
- Tsung, K.; Norton, J.A. In situ vaccine, immunological memory, and cancer cure. Hum. Vaccines Immunother. 2016, 12, 117–119. [Google Scholar] [CrossRef] [PubMed]
- Okada, M.; Shimizu, K.; Fujii, S.I. Identification of Neoantigens in Cancer Cells as Targets for Immunotherapy. Int. J. Mol. Sci. 2022, 23, 2594. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Soria-Guerra, R.E.; Nieto-Gomez, R.; Govea-Alonso, D.O.; Rosales-Mendoza, S. An overview of bioinformatics tools for epitope prediction: Implications on vaccine development. J. Biomed. Inform. 2015, 53, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Lissabet, J.F.B.; Belén, L.H.; Farias, J.G. TTAgP 1.0: A computational tool for the specific prediction of tumor T cell antigens. Comput. Biol. Chem. 2019, 83, 107103. [Google Scholar] [CrossRef]
- Charoenkwan, P.; Nantasenamat, C.; Hasan, M.M.; Shoombuatong, W. iTTCA-Hybrid: Improved and robust tumor T cell antigens identification by utilizing hybrid feature representation. Anal. Biochem. 2020, 599, 113747. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Zou, Q.; Guo, H.; Shi, L. iTTCA-RF: A random forest predictor for tumor T cell antigens. J. Transl. Med. 2021, 19, 449. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Herrera-Bravo, J.; Herrera Belén, L.; Farias, J.G.; Beltrán, J.F. TAP 1.0: A robust immunoinformatic tool for predicting tumor T-cell antigens based on AAindex properties. Comput. Biol. Chem. 2021, 91, 107452. [Google Scholar] [CrossRef] [PubMed]
- Sotirov, S.; Dimitrov, I. Application of Machine Learning Algorithms for Prediction of Tumor T-Cell Immunogens. Appl. Sci. 2024, 14, 4034. [Google Scholar] [CrossRef]
- Doytchinova, I.A.; Flower, D.R. VaxiJen: A server for predicting protective antigens, tumour antigens and subunit vaccines. BMC Bioinformatics 2007, 8, 4. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Hellberg, S.; Sjöström, M.; Skagerberg, B.; Wold, S. Peptide quantitative structure-activity relationships, a multivariate approach. J. Med. Chem. 1987, 30, 1126–1135. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Jonsson, J.; Sjöström, M.; Sandberg, M.; Rännar, S. DNA and peptide sequences and chemical processes multivariately modelled by principal component analysis and partial least squares projections to latent structures. Anal. Chim. Acta 1993, 277, 239–253. [Google Scholar] [CrossRef]
- Leardi, R.; Boggia, R.; Terrile, M. Genetic algorithms as a strategy for feature selection. J. Chemom. 1992, 6, 267–281. [Google Scholar] [CrossRef]
- Dad Ståhle, L.; Wold, S. Partial least squares analysis with cross-validation for the two-class problem: A Monte Carlo study. J. Chemom. 1987, 1, 185–196. [Google Scholar] [CrossRef]
- Venkatarajan, M.S.; Braun, W. New quantitative descriptors of amino acids based on multidimensional scaling of many physical-chemical properties. J. Mol. Model. 2001, 7, 445–453. [Google Scholar]
- Scikit-Learn Machine Learning in Python. Available online: https://scikit-learn.org (accessed on 5 May 2024).
- Sklearn.Model_Selection.GridSearchCV. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html (accessed on 5 May 2024).
- Goldberger, J.; Hinton, G.E.; Roweis, S.T.; Salakhutdinov, R.R. Neighbourhood components analysis. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 513–520. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2008; Section 4.3; pp. 106–119. [Google Scholar]
- Bhavsar, H.P.; Panchal, M. A Review on Support Vector Machine for Data Classification. IJARCET Int. J. Adv. Res. Comput. Eng. Technol. 2012, 1, 185–189. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ojala, M.; Garriga, G.C. Permutation tests for studying classifier performance. J. Mach. Learn. Res. 2010, 11, 1833–1863. [Google Scholar]
- Tharwat, A. Classification assessment methods. N. Engl. J. Entrepr. 2020, 17, 168–192. [Google Scholar] [CrossRef]
- Wold, S.; Eriksson, L. Statistical Validation of QSAR Results. In Chemometric Methods in Molecular Design; Weinheim van de Waterbeemd, H., Ed.; Wiley: Hoboken, NJ, USA, 1995; pp. 309–318. [Google Scholar]
| Algorithm | Sensitivity | Specificity | Accuracy | AROC | MCC |
|---|---|---|---|---|---|
| kNN | 0.73 | 0.46 | 0.60 | 0.60 | 0.20 |
| LDA | 0.71 | 0.53 | 0.62 | 0.63 | 0.22 |
| QDA | 0.67 | 0.81 | 0.74 | 0.83 | 0.49 |
| SVM | 0.80 | 0.66 | 0.73 | 0.80 | 0.46 |
| RF | 0.71 | 0.79 | 0.75 | 0.82 | 0.51 |
| XGBoost | 0.75 | 0.75 | 0.75 | 0.81 | 0.50 |
| Algorithm | Sensitivity | Specificity | Accuracy | AROC | MCC |
|---|---|---|---|---|---|
| Proteins | |||||
| QDA | 0.63 | 0.81 | 0.72 | 0.82 | 0.44 |
| RF | 0.71 | 0.79 | 0.75 | 0.81 | 0.50 |
| XGBoost | 0.74 | 0.77 | 0.75 | 0.80 | 0.51 |
| Peptides | |||||
| SVM | 0.79 | 0.86 | 0.82 | 0.83 | 0.64 |
| RF | 0.76 | 0.93 | 0.85 | 0.80 | 0.70 |
| XGBoost | 0.79 | 0.76 | 0.77 | 0.83 | 0.55 |
| Algorithm | Accuracy |
|---|---|
| Proteins | |
| QDA | 0.4986 |
| RF | 0.4906 |
| XGBoost | 0.4975 |
| Peptides | |
| SVM | 0.5075 |
| RF | 0.5182 |
| XGBoost | 0.4987 |
| Model | Top 10 Features |
|---|---|
| QDA | |
| Permutation feature importance | ACC251, ACC223, ACC344, ACC257, ACC114, ACC134, ACC131, ACC116, ACC256, ACC136 |
| Drop-column feature importance | ACC445, ACC334, ACC143, ACC121, ACC543, ACC534, ACC523, ACC442, ACC424, ACC344 |
| RF | |
| Permutation feature importance | ACC234, ACC327, ACC344, ACC351, ACC412, ACC253, ACC123, ACC345, ACC317, ACC311 |
| Drop-column feature importance | ACC445, ACC443, ACC341, ACC523, ACC455, ACC444, ACC441, ACC435, ACC415, ACC335 |
| XGBoost | |
| Permutation feature importance | ACC111, ACC331, ACC131, ACC123, ACC337, ACC224, ACC143, ACC124, ACC153, ACC325 |
| Drop-column feature importance | ACC514, ACC441, ACC254, ACC251, ACC123, ACC111, ACC541, ACC443, ACC421, ACC415 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotirov, S.; Dimitrov, I. In Silico Methods for Assessing Cancer Immunogenicity—A Comparison Between Peptide and Protein Models. Appl. Sci. 2025, 15, 4123. https://doi.org/10.3390/app15084123
Sotirov S, Dimitrov I. In Silico Methods for Assessing Cancer Immunogenicity—A Comparison Between Peptide and Protein Models. Applied Sciences. 2025; 15(8):4123. https://doi.org/10.3390/app15084123
Chicago/Turabian StyleSotirov, Stanislav, and Ivan Dimitrov. 2025. "In Silico Methods for Assessing Cancer Immunogenicity—A Comparison Between Peptide and Protein Models" Applied Sciences 15, no. 8: 4123. https://doi.org/10.3390/app15084123
APA StyleSotirov, S., & Dimitrov, I. (2025). In Silico Methods for Assessing Cancer Immunogenicity—A Comparison Between Peptide and Protein Models. Applied Sciences, 15(8), 4123. https://doi.org/10.3390/app15084123





