Employing Fuzzy Adaptive and Event-Triggered Approaches to Achieve Formation Control of Nonholonomic Mobile Robots Under Complete State Constraints

Abstract

This article delves into the problem of fuzzy adaptive event-triggered (ET) formation control for nonholonomic mobile robots (NMRs) subject to full-state constraints. Fuzzy logic systems (FLSs) are employed to identify the unknown nonlinear functions within the system. To guarantee that all system states remain within their constraint boundaries, barrier Lyapunov functions (BLFs) are meticulously constructed. Subsequently, within the framework of the backstepping control design algorithm, we propose a novel fuzzy adaptive ET formation controller. Our ET mechanism can achieve an overall resource-saving rate of 88.17% for the four robots. Rigorous theoretical analysis demonstrates that the designed strategy not only ensures the stability of the controlled NMRs but also enables the formation tracking errors to converge to a small neighborhood around zero. Notably, the BLFs-based control approach presented herein endows the system with the capacity to avoid collisions to a certain degree, enhancing the overall safety and reliability of the robot formation. Finally, a simulation example is provided. The results vividly illustrate the effectiveness and practicality of the proposed theory, validating its potential for real-world applications in the field of nonholonomic mobile robot formation control.

1. Introduction

In recent years, the advantages of multi-agent systems (MASs) over individual agents [1] have become increasingly prominent. MASs are characterized by significantly higher working efficiency and enhanced compatibility, which have attracted extensive attention from researchers in various fields. In the realm of practical engineering, with the exponential growth of network information and the increasing complexity of missions, the coordination control of multiple mobile robots [2] multiple unmanned aerial vehicles [3] and multiple marine surface vehicles [4] has emerged as a crucial research area. These multi-agent systems play a vital role in modern engineering applications, such as industrial automation, intelligent transportation, and marine exploration. For multi-agent formation tracking control, the core goal is to enable multiple agents to collaboratively track a target while moving in a coordinated manner to maintain a predefined formation geometry. This not only requires precise motion control of each agent but also effective communication and cooperation among them. In this process, maintaining connectivity and avoiding collisions are not only challenging aspects but also fundamental requirements for the stable operation of the multi-agent system. Ensuring seamless communication between robots to maintain connectivity is essential for coordinated movement, while collision-avoidance mechanisms are crucial to prevent potential accidents and ensure the safety and efficiency of the entire system. In the field of multi-agent formation control, a diverse array of strategies has been developed, each with its own unique characteristics and applications. Prominent among these are the leader–follower strategy [5], behavior-based strategy [6], and virtual structure strategy [7]. The leader–follower strategy stands out as one of the most widely adopted and fundamental approaches. Its popularity can be attributed to its simplicity and efficiency. In a leader–follower system, each follower robot only needs to focus on perceiving the information transmitted by its adjacent leader. This significantly reduces the computational burden on individual robots, as they are not required to process a vast amount of data related to the entire external environment.

NMRs’ formation control has become a hot research topic due to its important applications in all aspects, such as target searching, environmental monitoring, resource exploring, and area data acquiring. Therefore, a large number of consensus control issues have been reported [8,9,10,11,12,13,14,15,16]. In [9], the trajectory tracking problem in the formation control of robots was studied. The authors in [10] proposed the angle-constrained-based adaptive formation shape and maneuvering control for NMRs, respectively. The result in [11] suggested a solution for the formation problem using full consensus in torque-controlled NMRs, accounting for the absence of velocity measurements and time-varying communication delays. In earlier studies, most scholars did not consider the internal dynamics of robots. To solve this problem, the use of fuzzy logic systems (FLSs) is a very effective method [17,18,19,20]. Hence, for unicycle-type mobile robots, a leader–follower (L-F) formation control protocol was proposed in [16]. In [17], the formation control problem of NMRs with unknown dead zones was studied. The results in [18] show the feasibility of the finite-time neural network adaptive control scheme based on dynamic surface technique. For high-order nonlinear systems, [19] proposed a robust fuzzy adaptive finite-time control scheme.

In practice, the limitations of the speed and position of the NMRs are often overlooked. The running speed and distance between NMRs should be kept within a certain range. The constraints of the robot velocity variables are just as important as the constraints of the output variables, and it makes sense to consider the full-state constraints when designing the controller. In order to ensure all state variables are within constraints, studying the full-state constraint problem in NMR control is important. For example, the Ln-type barrier function is used to constrain the boundaries of the specified performance function in [20]. In [21], the authors used a tan-type barrier function to realize the collision avoidance and connectivity maintenance of the robot. In [22], the formation and collision avoidance problem of NMRs based on the artificial potential field method is proposed. To suppress the violation of tracking error constraints, a barrier Lyapunov function-based control method was proposed to realize the tracking control of incomplete mobile robots under specified performance conditions in [21].

Note that the above control schemes do not effectively control NMRs with unknown dynamics. FLSs are often used to identify unknown functions due to their strong fitting and approximation ability. In [9], a compensator and data-driven control scheme based on FLSs are designed to solve the NMRs’ formation control. In [23], the formation control issue of the networked non-complete mobile robot based on the L-F framework was studied. In [24], not only the NMR’s adaptive output feedback formation tracking control problem was solved but the connectivity maintenance and collision avoidance were also realized. In [25], an integrated L-F consensus formation framework using an optimized NN-based distributed model predictive control strategy was presented. Note that the formation control methods in [9,16,17,18,19,20,21,22,23,24,25] cannot possibly guarantee full-state constraints and save communication resources at the same time. To the best of our knowledge, there are no results on fuzzy adaptive event-triggered formation controllers for NMRs with full-state constraints. Therefore, designing an adaptive event-triggered formation controller for NMRs under full-state constraints is a challenging and important topic.

Inspired by the above analysis, this paper investigates the fuzzy adaptive formation control of NMRs with nonlinear uncertainty and full-state constraints. Our main contributions are summarized below:

(1)

By utilizing FLSs to estimate the unknown nonlinear functions, and constructing the barrier Lyapunov functions, this paper develops a fuzzy adaptive formation control approach within the adaptive backstepping control design framework. Although the work in [9,21,22] investigated the fuzzy adaptive formation control problems of NMRSs, their methods do not consider full-state constraints. Such formation control methods do not constrain the state of the robot within a reasonable range.

(2)

In [24,25,26], authors investigated the fuzzy adaptive formation control problems of NMRs. These methods cannot decrease the unnecessary waste of resources resulting from the update of the controller signal when considering complete state constraints. Therefore, this paper designs an event-triggering mechanism to avoid unnecessary waste of resources. In Table 1, a comparison of different control algorithms is presented.

Table 1. The comparison results of control algorithm.

Controlled Nonlinear NMRs	Event-Triggered Mechanism	State Constraints	First-Order Filter	Unknown Nonlinear Function
The proposed control method	√	√	√	√
The control method in [17]	√	✕	√	√
The control method in [21]	✕	✕	✕	√
The control method in [22]	✕	✕	✕	√

where √ indicates that the situation presented was considered in the corresponding article in Table 1.

The rest of this paper is structured as follows. The problem description for this work is the main content in Section 2. Section 3 describes the process of design controller and stability analysis. The proposed event-triggering protocol with numerical examples and summarizes the conclusions is verified in Section 4.

Notations: $\left|•\right|$ indicates the absolute value. $‖•‖$ denotes the Euclidean norm for vectors or induced 2-norm for matrices.

2. Problem Formulation

2.1. System Descriptions

Consider a group of NMRs with one passive wheel and two actuated wheels in Figure 1, the mathematical model of the $i$th $(i=1,\dots ,n)$ robot is given by [21]

$$\left\{\begin{array}{l}{\dot{\eta }}_i=J_i({\eta }_i){\overline{\omega }}_i\\ M_i{\dot{\overline{\omega }}}_i=-C_i({\dot{\eta }}_i){\overline{\omega }}_i-D_i{\overline{\omega }}_i+{\tau }_i\end{array}\right.$$

where ${\eta }_i={[x_i,y_i,{\psi }_i]}^T$ is the $i$th robot’s posture consisting of the position $(x_i,y_i)$ and heading angle (orientation) (${\psi }_i$) of the robot coordinated. ${\overline{\omega }}_i={[{\overline{\omega }}_{1i},{\overline{\omega }}_{2i}]}^T$ are the angular velocities of the two wheels, ${\tau }_i={[{\tau }_{i,1},{\tau }_{i,2}]}^T$ is the control input. $M_i$, $C_i({\dot{\eta }}_i)$, and $D_i$ are the inertia matrix, the centripetal and Coriolis matrix, and the damping matrix, respectively. The matrices $J_i({\eta }_i)$, $M_i$, $C_i({\dot{\eta }}_i)$, and $D_i$ in system (1) are given by

$$\begin{gathered} J_i({\eta }_i)={\displaystyle \frac{r_i}{2}}\left[\begin{array}{c}\begin{array}{cc}\cos {\psi }_i& \cos {\psi }_i\end{array}\\ \begin{array}{cc}\sin {\psi }_i& \sin {\psi }_i\end{array}\\ \begin{array}{cc}{b_i}^{-1}& -{b_i}^{-1}\end{array}\end{array}\right]M_i=\left[\begin{array}{cc}{m}_{11i}& m_{12i}\\ m_{12i}& m_{11i}\end{array}\right] \\ {C}_i({\dot{\eta }}_i)=\left[\begin{array}{cc}0& c_i{\dot{\psi }}_i\\ -c_i{\dot{\psi }}_i& 0\end{array}\right]D_i=\left[\begin{array}{cc}{d}_{11i}& 0\\ 0& d_{22i}\end{array}\right] \end{gathered}$$

where $r_i$ and $b_i$ shown in Figure 1 are the wheel radius and half-width of the $i$th mobile robot, respectively. We consider that the NMR model (1), the robot parameters $m_{11i}$, $m_{12i}$, $b_i$, and $r_i$, the centripetal and Coriolis coefficient $c_i$, and the damping coefficients $d_{11i}$ and $d_{22i}$ are uncertain constants.

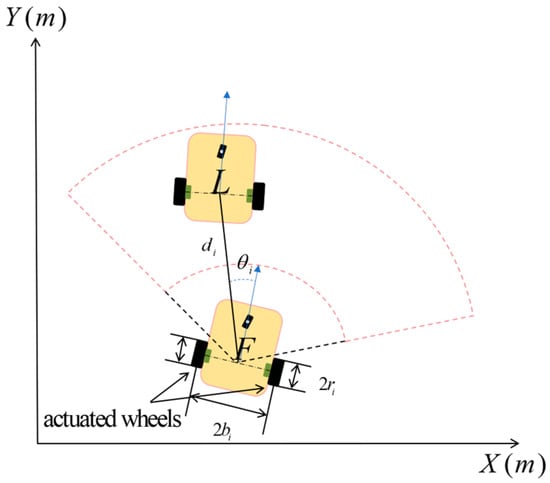
Figure 1. The structure of the L-F model.

To facilitate control development, we can convert the wheel angular velocities $({\overline{\omega }}_{1i},{\overline{\omega }}_{2i})$ to the robot’s linear velocity $v_i$ and angular velocity ${\omega }_i$ by the following equation:

$${\overline{v}}_i=B_i^{-1}{\overline{\omega }}_i$$

with ${\overline{v}}_i={[v_i,{\omega }_i]}^T$ and $B_i={\displaystyle \frac{1}{r_i}}\left[\begin{array}{cc}1& b_i\\ 1& -b_i\end{array}\right]$, where the matrix $B_i$ is invertible, since the determination of matrix $B_i$ is $\det (B_i)=-2b_i/r_i$. After the above description, we can obtain the following dynamic equations:

$$\left\{\begin{array}{l}{\dot{x}}_i=v_i\cos ({\psi }_i)\\ {\dot{y}}_i=v_i\sin ({\psi }_i)\\ {\dot{\psi }}_i={\omega }_i\\ M_i{\dot{\overline{\omega }}}_i=-C_i({\dot{\eta }}_i){\overline{\omega }}_i-D_i{\overline{\omega }}_i+{\tau }_i\end{array}\right.$$

(1)

The inertia matrix parameters are given by $m_{11i}=0.25{b_i}^{-2}{r_i}^2(m_i{b_i}^2+I_i)+I_{\omega i}$, $m_{12i}=0.25{b_i}^{-2}{r_i}^2(m_i{b_i}^2-I_i)$, $m_i=m_{ci}+2m_{\omega i}$, $I_i=m_{ci}{a_i}^2+2m_{\omega i}{b_i}^2+I_{ci}+2I_{mi}$ and $c_i=0.5{b_i}^{-1}{r_i}^2{m}_{ci}{a}_i$, where $m_{ci}$ and $m_{\omega i}$ are the body and wheel (with motor) masses; $a_i$ is the distance between the wheel axis center and robot mass center; and $I_{ci}$, $I_{\omega i}$, and $I_{mi}$ are the moment of inertia about the vertical axis, the wheel about the wheel axis, and the wheel about the wheel diameter, respectively.

From system (1), the dynamic equations can be defined by

$$\left\{\begin{array}{l}{\dot{v}}_i=f_{vi}(v_i)+{\overline{m}}_{1i}{\tau }_{vi}\\ {\dot{\omega }}_i=f_{\omega i}({\omega }_i)+{\overline{m}}_{2i}{\tau }_{\omega i}\end{array}\right.$$

(2)

where $f_{vi}$ and $f_{\omega i}$ are unknown nonlinear functions associated with $v_i$ and ${\omega }_i$, ${\overline{m}}_{1i}={\displaystyle \frac{r_i}{2(m_{11i}+m_{12i})}}$, and ${\overline{m}}_{2i}={\displaystyle \frac{r_i}{2b_i(m_{11i}-m_{12i})}}$. ${\overline{m}}_{1i}$ and ${\overline{m}}_{2i}$ are positive parameters.

The dynamic of the leader NMR is given by [27]

$$\left\{\begin{array}{l}{\dot{x}}_0=v_0\cos ({\psi }_0)\\ {\dot{y}}_0=v_0\sin ({\psi }_0)\\ {\dot{\psi }}_0={\omega }_0\end{array}\right.$$

where $(x_0,y_0)$ denotes the position of leader NMR, and ${\psi }_0$ is the heading angle. $v_0$ and ${\omega }_0$ represent linear velocity and angular velocity, respectively.

Assumption 1

([21]). The acceleration ${\dot{v}}_0$ is bounded such that $\left|{\dot{v}}_0\right|\le v_0^{*}$, with $v_0^{*}$ being constant.

From (1), we have

$${\dot{x}}_i\sin {\psi }_i-{\dot{y}}_i\cos {\psi }_i=0$$

which means the angle between the driving wheel’s axis and the robot’s speed direction is 90 degrees. In other words, the robot’s axle-direction speed is always zero, thus it is also called nonholonomic constraint. The nonholonomic constraint ensures the robot’s wheels roll without slipping.

2.2. Graph Theory

This subsection will introduce the definitions about the communication network topology.

The expression $\widehat{G}\triangleq (\widehat{S},\widehat{K})$ represents the transmission relationship between robot information, in which $\widehat{S}\triangleq \{1,\dots ,N\}$. $\widehat{K}\subseteq \widehat{S}\times \widehat{S}$ indicates the edge set, and $(i,j)\in \widehat{K}$ indicates that the $i$th robot obtains information from the $j$th robot in one direction. $d_{ij}$ is the distance between $i$th and $j$th robot, and $d_{Mi}$ is $i$th robot’s maximum information transmission range. If $d_{ij}<d_{Mi}$, an L-F model can be formed. $L_i(t)=\left\{j\right|d_{ij}<d_{Mi}\}$ means the $i$th robot’s leader set. In the L-F structure, the relationship between them can form a tree, thus forming the required L-F structure.

2.3. FLSs

The FLSs used to approximate uncertain model dynamics $f_{vi}$ are $f_{\omega i}$ in (1), and the properties of FLSs can be seen in Lemma 1.

Lemma 1

([26]). Let $f(x)$ be a continuous function on a compact set $\mathsf{\Lambda }$. For any constant $\epsilon$, there always exists a FLS $\widehat{f}(x|\widehat{\Theta })={\widehat{\Theta }}^T\varsigma (x)$ satisfying

$$\underset{x\in \mathsf{\Lambda }}{\sup }|f(x)-{\Theta }^T\varpi (x)|\le \epsilon$$

(3)

where $\varpi (x)={[{\varpi }_1(x),{\varpi }_2(x),\dots ,{\varpi }_N(x)]}^T/{\displaystyle \sum _{i=1}^N{\varpi }_i(x)}$ is the fuzzy basic function vector and satisfies ${\varpi }^T(\cdot )\varpi (\cdot )\le 1$. $\Theta ={[{\Theta }_1,{\Theta }_2,\dots ,{\Theta }_N]}^T$ is the ideal weight vector and $N$ is the fuzzy rule number.

Remark 1.

In this paper, we use a FLS to approximate the unknown continuous functions in (2). Note that neural networks and type-2 FLSs have also the approximation property of Lemma 1. Therefore, the FLSs used in this paper can be replaced by other approximators.

Control objective: For NMRs (1) with full-state constraints, this paper develops a fuzzy adaptive ET formation control method such that the following hold:

(1)

All the closed-loop signals are semi-globally uniformly ultimately bounded (SGUUB).

(2)

All robots will follow the leader by keeping a desired formation pattern, i.e., the angle and relative distance errors converge asymptotically to zero without violating the angle and relative distance constraints.

3. Fuzzy Adaptive Formation Control Design

In this section, a fuzzy adaptive ET formation controller is constructed under the backstepping control design. With the help of log-type barrier Lyapunov functions, it is proven that the system (1) is stable under full-state constraints and does not collide.

3.1. ET Formation Controller Design

The backstepping control design is a recursive method. For NMRs (1), it contains a two-step design procedure. In Step 1, we first select a Lyapunov function for each subsystem, and based on the Lyapunov function, we design the virtual controllers to stabilize each subsystem, respectively, and design the weight updating laws. In the same way, in Step 2, we select a Lyapunov function for the subsystem, and based on the Lyapunov function, we design the formation controller to stabilize the whole system and design the weight updating law.

To achieve the formation control design, we define the angle and relative distance between $i$th and $j$th robot as

$$d_{ij}(t)=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}$$

(4)

$${\phi }_{ij}(t)=\mathrm{atan}2({\tilde{y}}_i,{\tilde{x}}_i)$$

(5)

$$\left[\begin{array}{c}{\tilde{x}}_i\\ {\tilde{y}}_i\end{array}\right]=\left[\begin{array}{cc}\cos {\psi }_i& \sin {\psi }_i\\ -\sin {\psi }_i& \cos {\psi }_i\end{array}\right]\left[\begin{array}{c}{x}_j-x_i\\ y_j-y_i\end{array}\right]$$

(6)

where $\mathrm{atan}2({\tilde{y}}_i,{\tilde{x}}_i)\in (-\pi ,\pi ]$ is the arctangent function of the two arguments $(x,y)$ and returns the appropriate quadrant of the angle of point $(x,y)$.

In actual formation control, collision avoidance and field of view limitations among robots are crucial issues to consider. Therefore, to fulfill above range constraints, the constraints of distance and angle are described as

$$0<d_{mi}<d_{ij}(t)<d_{Mi},\forall t\ge 0$$

(7)

$$-{\displaystyle \frac{\pi }{2}}<-{\phi }_{Mi}<{\phi }_{ij}(t)<{\phi }_{Mi}<{\displaystyle \frac{\pi }{2}},\forall t\ge 0$$

(8)

where $d_{Mi}$ and $d_{mi}$ represent the maximum distance at which connectivity is maintained and the minimum distance at which a collision can be avoided, respectively. ${\phi }_{Mi}$ indicates the maximum angle that ensures continuous information transmission.

Define the coordinate transformation as

$$\left\{\begin{array}{l}{z}_{id}=d_{ij}-d_{ij,d}\\ z_{i\psi }={\psi }_{ij}-{\psi }_{ij,d}\\ z_{iv}=v_i-{\hslash }_{i,1}\\ z_{i\omega }={\omega }_i-{\hslash }_{i,2}\\ {\chi }_{i,1}={\hslash }_{i,1}-{\alpha }_{i,1}\\ {\chi }_{i,2}={\hslash }_{i,2}-{\alpha }_{i,2}\end{array}\right.$$

(9)

where $d_{ij,d}$ is the desired distance, which is a constant. ${\psi }_{ij,d}$ is the desired angle. ${\alpha }_{i,s}$, ${\chi }_{i,s}$ and ${\hslash }_{i,s}$, respectively, are virtual design control functions, first-order filter output errors, and variables ($s=1,2$). ${\hslash }_{i,s}$ are obtained through a first-order filter on intermediate virtual controls ${\alpha }_{i,1}$ and ${\alpha }_{i,2}$. We introduce the following first-order filter:

$${\delta }_{i,1}{\dot{\hslash }}_{i,1}+{\hslash }_{i,1}={\alpha }_{i,1}, {\hslash }_{i,1}(0)={\alpha }_{i,1}$$

(10)

$${\delta }_{i,2}{\dot{\hslash }}_{i,2}+{\hslash }_{i,2}={\alpha }_{i,2}, {\hslash }_{i,2}(0)={\alpha }_{i,2}$$

(11)

where ${\delta }_{i,1}>0$ and ${\delta }_{i,2}>0$ are design parameters.

Step 1: From (9), we have the following equations:

$${\dot{z}}_{id}=-v_i\cos {\phi }_i+v_{i-1}\cos {\gamma }_i$$

(12)

$${\dot{z}}_{i\psi }=-{\omega }_i+{\displaystyle \frac{v_i}{d_i}}\sin {\phi }_i-{\displaystyle \frac{v_{i-1}}{d_i}}\sin {\gamma }_i$$

(13)

where $v_{i-1}$ and ${\psi }_{i-1}$ are the linear velocity and orientation of robot $R_{i-1}$, respectively.${\gamma }_i={\phi }_i+{\psi }_i-{\psi }_{i-1}$.

We select log-type barrier Lyapunov functions:

$$V_{11i}={\displaystyle \frac{1}{2}}\log {\displaystyle \frac{{k_{d1}}^2}{{k_{d1}}^2-{z_{i,d}}^2}}$$

(14)

$$V_{12i}={\displaystyle \frac{1}{2}}\log {\displaystyle \frac{{k_{\phi 1}}^2}{{k_{\phi 1}}^2-{z_{i\psi }}^2}}$$

(15)

where $k_{d1}$ and $k_{\phi 1}$ are design parameters.

We construct the virtual control signals ${\alpha }_{vi}$ and ${\alpha }_{\omega i}$ as

$${\alpha }_{vi}={\displaystyle \frac{1}{\cos {\phi }_i}}(v_{i-1}\cos {\gamma }_i+k_{d1}{z}_{id})$$

(16)

$${\alpha }_{\omega i}={\displaystyle \frac{v_i}{d_i}}\sin {\phi }_i-{\displaystyle \frac{v_{i-1}}{d_i}}\sin {\gamma }_i+k_{\phi 1}{z}_{i\psi }$$

(17)

with $k_{d1}>0$ and $k_{\phi 1}>0$ being design constants. (Equation (16) defines the virtual control signals designed to stabilize the formation tracking errors. $k_{d1}$ and $k_{\phi 1}$ are positive control gains, while the logarithmic barrier function ensures the relative azimuth remains within the predefined constraints, thereby avoiding singularity issues.)

Remark 2.

If ${\phi }_i={\displaystyle \frac{\pi }{2}}$, then there will be singularity problem. We predefine constraints on the relative azimuth. The formation tracking controller is designed by using the barrier Lyapunov synthesis method, ensuring that the relative azimuth remains within a predetermined range.

Step 2: From (9), we have

$${\dot{z}}_{iv}=f_{vi}(v_i)+m_{1i}{\tau }_{vi}-{\dot{\hslash }}_{i,1}$$

(18)

$${\dot{z}}_{i\omega }=f_{\omega i}({\omega }_i)+m_{2i}{\tau }_{\omega i}-{\dot{\hslash }}_{i,2}$$

(19)

From (9), one has

$${\dot{\chi }}_{i,s}={\dot{\hslash }}_{i,s}-{\dot{\alpha }}_{i,s}=N_{i,s}(\cdot )-{\displaystyle \frac{{\chi }_{i,s}}{{\delta }_{i,s}}}$$

(20)

where $N_{i,s}(\cdot )$ is a continuous function.

Since $f_{\omega i}({\omega }_i)$ and $f_{vi}(v_i)$ are uncertain, the FLSs are utilized for approximating them. Assume that

$$f_{vi}(v_i)=G_{i,1}^{*T}{\varphi }_{i,1}(v_i)+{\epsilon }_{i,1}$$

(21)

$$f_{\omega i}({\omega }_i)=G_{i,2}^{*T}{\varphi }_{i,2}({\omega }_i)+{\epsilon }_{i,2}$$

(22)

where $G_{i,1}\in R^n$ and $G_{i,2}\in R^n$ are the ideal weights, ${\varphi }_{i,1}\in R^n$ and ${\varphi }_{i,2}\in R^n$ are the fuzzy basic functions. ${\epsilon }_{i,1}$ and ${\epsilon }_{i,2}$ are the approximated errors, and they satisfy $\left|{\epsilon }_{i,1}\right|\le {\epsilon }_{i,1}^{\ast }$ and $\left|{\epsilon }_{i,2}\right|\le {\epsilon }_{i,2}^{\ast }$, with ${\epsilon }_{i,1}^{\ast }$ and ${\epsilon }_{i,2}^{\ast }$ being unknown constants.

Thus, (18) and (19) can be rewritten as

$${\dot{z}}_{iv}=G_{i,1}^{*T}{\varphi }_{i,1}(v_i)+{\epsilon }_{i,1}+m_{1i}{\tau }_{vi}-{\dot{\hslash }}_{i,1}$$

(23)

$${\dot{z}}_{i\omega }=G_{i,2}^{*T}{\varphi }_{i,2}({\omega }_i)+{\epsilon }_{i,2}+m_{2i}{\tau }_{\omega i}-{\dot{\hslash }}_{i,2}$$

(24)

Consider the log-type barrier Lyapunov function

$$V_{2i}=V_{11i}+V_{12i}+{\displaystyle \frac{1}{2}}{z}_{iv}^2+{\displaystyle \frac{1}{2}}{z}_{i\omega }^2+{\displaystyle \frac{1}{2}}{\tilde{G}}_{i,1}^T{\tilde{G}}_{i,1}+{\displaystyle \frac{1}{2}}{\tilde{G}}_{i,2}^T{\tilde{G}}_{i,2}+{\displaystyle \frac{1}{2}}{\chi }_{i,1}^2+{\displaystyle \frac{1}{2}}{\chi }_{i,2}^2$$

(25)

In order to decrease the unnecessary waste of resources resulting from the update of the controller signal, we design the following event-triggered mechanism:

$${\tau }_{vi}(t)={\vartheta }_{vi}(t_{vik}),t\in [t_{vik},t_{vi(k+1)})$$

(26)

$${\tau }_{\omega i}(t)={\vartheta }_{\omega i}(t_{\omega ik}),t\in [t_{\omega ik},t_{\omega i(k+1)})$$

(27)

$$t_{vi(k+1)}=\inf \{t\in R||z_{vi}(t)|\ge {\lambda }_{1v}\left|{\tau }_{vi}\right|+{\lambda }_{2v}\}$$

(28)

$$t_{\omega i(k+1)}=\inf \{t\in R||z_{\omega i}(t)|\ge {\lambda }_{1\omega }\left|{\tau }_{\omega i}\right|+{\lambda }_{2\omega }\}$$

(29)

with $z_{\kappa i}(t)={\tau }_{\kappa i}(t)-{\vartheta }_{\kappa i}(t_{\kappa ik})$ representing the event-triggered error during time interval $[t_{\kappa ik},t_{\kappa i(k+1)})$, where $\kappa =v,\omega$. $0\le {\lambda }_{1\kappa }\le 1$ and ${\lambda }_{2\kappa }>0$ are constants. ${\vartheta }_{\kappa i}(t_{\kappa ik})$ are trigger control signals.

The virtual controllers, trigger controllers, adaptive formation controllers and adaptive laws are given as

$${\rho }_{vi}={\overline{m}}_{iv}^{-1}(-c_{iv}{z}_{iv}-{\widehat{G}}_{i,1}^T{\varphi }_{i,1}(v_i)+{\dot{\hslash }}_{i,1}+{\displaystyle \frac{z_{id}\cos {\phi }_i}{{k_{d1}}^2-{z_{id}}^2}}-{\displaystyle \frac{1}{2}}{z}_{iv}-{({\displaystyle \frac{{\overline{m}}_{1i}{\overline{\lambda }}_{iv}{\delta }_{iv2}}{1+{\lambda }_{iv}{\delta }_{iv1}}})}^2{z}_{iv})$$

(30)

$${\rho }_{\omega i}={\overline{m}}_{i\omega }^{-1}(-c_{i\omega }{z}_{i\omega }-{\widehat{G}}_{i,2}^T{\varphi }_{i,2}({\omega }_i)+{\dot{\hslash }}_{i,2}+{\displaystyle \frac{z_{i\psi }}{{k_{\phi 1}}^2-{z_{i\psi }}^2}}-{\displaystyle \frac{1}{2}}{z}_{i\omega }-{({\displaystyle \frac{{\overline{m}}_{i\omega }{\overline{\lambda }}_{i\omega }{\delta }_{i\omega 2}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}})}^2{z}_{i\omega })$$

(31)

$${\vartheta }_{vi}=-(1+{\lambda }_{iv})({\rho }_{vi}\tanh {\displaystyle \frac{z_{iv}{\rho }_{vi}}{\epsilon }}+{\overline{\lambda }}_{iv}\tanh {\displaystyle \frac{z_{iv}{\overline{\lambda }}_{iv}}{\epsilon }})$$

(32)

$${\vartheta }_{\omega i}=-(1+{\lambda }_{i\omega })({\rho }_{\omega i}\tanh {\displaystyle \frac{z_{i\omega }{\rho }_{\omega i}}{\epsilon }}+{\overline{\lambda }}_{i\omega }\tanh {\displaystyle \frac{z_{i\omega }{\overline{\lambda }}_{i\omega }}{\epsilon }})$$

(33)

$${\tau }_{vi}={\displaystyle \frac{{\vartheta }_{vi}}{1+{\lambda }_{iv}{\delta }_{iv1}}}-{\displaystyle \frac{{\overline{\lambda }}_{iv}{\delta }_{iv2}}{1+{\lambda }_{iv}{\delta }_{iv1}}}$$

(34)

$${\tau }_{\omega i}={\displaystyle \frac{{\vartheta }_{\omega i}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}-{\displaystyle \frac{{\overline{\lambda }}_{i\omega }{\delta }_{i\omega 2}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}$$

(35)

$${\dot{\widehat{G}}}_{i,1}=z_{i,v}^T{\varphi }_{i,1}(v_i)+{\sigma }_{i,1}{\widehat{G}}_{i,1}$$

(36)

$${\dot{\widehat{G}}}_{i,2}=z_{i,\omega }^T{\varphi }_{i,2}({\omega }_i)+{\sigma }_{i,2}{\widehat{G}}_{i,2}$$

(37)

where $c_{i,v}>0$, $c_{i,\omega }>0$, ${\sigma }_{i,1}>0$, and ${\sigma }_{i,2}>0$ are design parameters. ${\overline{\lambda }}_{iv}\ge {\displaystyle \frac{{\lambda }_{2v}}{1-{\lambda }_{1v}}}$ and ${\overline{\lambda }}_{i\omega }\ge {\displaystyle \frac{{\lambda }_{2\omega }}{1-{\lambda }_{1\omega }}}$ are design parameters. $\epsilon >0$ are design constants.

3.2. Stability Analysis

The properties of the above control scheme are provided in the following theorem.

Theorem 1.

For the NMRs (1), under above assumption 1, if the virtual controllers are adopted by (16) and (17), the trigger controllers are adopted by (32) and (33), the actual controller are adopted by (34) and (35), and the parameter updating laws are adopted by (36) and (34), and then the whole fuzzy adaptive ET formation control scheme can ensure the following:

(1)

The multiple underactuated NMRs are stable.

(2)

Each follower NMR can track the leader NMR.

(3)

The Zeno behavior can be excluded.

Proof. 

Differentiating (14) and (15) yields

$${\dot{V}}_{11i}={\displaystyle \frac{z_{id}{\dot{z}}_{id}}{{k_{d1}}^2-{z_{id}}^2}}={\displaystyle \frac{z_{id}}{{k_{d1}}^2-{z_{id}}^2}}[-(z_{iv}+{\alpha }_{vi})\cos {\phi }_i+v_{i-1}\cos {\gamma }_i]$$

(38)

$${\dot{V}}_{12i}={\displaystyle \frac{z_{i\psi }{\dot{z}}_{i\psi }}{{k_{\phi 1}}^2-{z_{i\psi }}^2}}={\displaystyle \frac{z_{i\psi }}{{k_{\phi 1}}^2-{z_{i\psi }}^2}}[-(z_{i\omega }+{\alpha }_{\omega i})+{\displaystyle \frac{v_i}{d_i}}\sin {\phi }_i-{\displaystyle \frac{v_{i-1}}{d_i}}\sin {\gamma }_i]$$

(39)

In the intervals $\left|z_{i\mathsf{\partial }}\right|\le k_{\mathsf{\partial }1},\mathsf{\partial }=d,\phi$, we have

$$\log {\displaystyle \frac{{k_{\mathsf{\partial }1}}^2}{{k_{\mathsf{\partial }1}}^2-{z_{i\mathsf{\partial }}}^2}}\le {\displaystyle \frac{{z_{i\mathsf{\partial }}}^2}{k_{\mathsf{\partial }1}^2-z_{i\mathsf{\partial }}^2}}$$

(40)

Substituting the virtual control laws (16), (17), and (40) into (38) and (39), we obtain

$${\dot{V}}_{11i}=-{\displaystyle \frac{z_{id}{z}_{iv}\cos {\phi }_i}{k_{d1}^2-z_{id}^2}}-{\displaystyle \frac{k_{d1}{z}_{id}^2}{k_{d1}^2-z_{id}^2}}\le -k_{d1}{V}_{11i}-{\displaystyle \frac{z_{id}{z}_{iv}\cos {\phi }_i}{k_{d1}^2-e_{di}^2}}$$

(41)

$${\dot{V}}_{12i}=-{\displaystyle \frac{z_{i\psi }{z}_{i\omega }}{k_{\phi 1}^2-z_{i\psi }^2}}-{\displaystyle \frac{k_{\phi 1}{z}_{i\psi }^2}{k_{\phi 1}^2-z_{i\psi }^2}}\le -k_{\phi 1}{V}_{12i}-{\displaystyle \frac{z_{i\psi }{z}_{i\omega }}{k_{\phi 1}^2-z_{i\psi }^2}}$$

(42)

Differentiating (25) yields

$$\begin{array}{cc}\hfill {\dot{V}}_{2i}& ={\dot{V}}_{11i}+{\dot{V}}_{12i}+z_{iv}{\dot{z}}_{iv}+z_{i\omega }{\dot{z}}_{i\omega }-{\tilde{G}}_{i,1}^T{\dot{\widehat{G}}}_{i,1}-{\tilde{G}}_{i,2}^T{\dot{\widehat{G}}}_{i,2}+{\chi }_{i,1}{\dot{\chi }}_{i,1}+{\chi }_{i,2}{\dot{\chi }}_{i,2}\hfill \\ & ={\dot{V}}_{11i}+{\dot{V}}_{12i}+z_{iv}({\widehat{G}}_{i,1}^T{\varphi }_{i,1}(v_i)+{\epsilon }_{i,1}+m_{1i}{\tau }_{vi}-{\dot{\hslash }}_{i,1})\hfill \\ & +z_{i\omega }({\widehat{G}}_{i,2}^T{\varphi }_{i,2}({\omega }_i)+{\epsilon }_{i,2}+m_{2i}{\tau }_{\omega i}-{\dot{\hslash }}_{i,2})\hfill \\ & +{\chi }_{i,1}(N_{i,1}(\cdot )-{\displaystyle \frac{{\chi }_{i,1}}{{\delta }_{i,1}}})+{\chi }_{i,2}(N_{i,2}(\cdot )-{\displaystyle \frac{{\chi }_{i,2}}{{\delta }_{i,2}}})\hfill \\ & +{\tilde{G}}_{i,1}^T(z_{iv}{\varphi }_{i,1}(v_i)-{\dot{\widehat{G}}}_{i,1})+{\tilde{G}}_{i,2}^T(z_{i\omega }{\varphi }_{i,2}({\omega }_i)-{\dot{\widehat{G}}}_{i,2})\hfill \end{array}$$

(43)

According to [27], define the set ${\Omega }_{i,s}=\{{\displaystyle \sum _{i=1}^N(z_{i\kappa }^2}+{\tilde{G}}_{i,s}^T{\tilde{G}}_{i,s}+{\chi }_{i,s}^2)\le 2\xi \}$, where $\kappa =v,\omega$, $s=1,2$, ξ > 0 is a constant and $V(0)<\xi$. Since ${\Omega }_i$ is compact in $R^{\dim ({\Omega }_i)}$, there exists a constant ${\overline{N}}_{i,s}$ with $\left|N_{i,s}(\cdot )\right|\le {\overline{N}}_{i,s}$ on ${\Omega }_{i,s}$. ($\dim ({\Omega }_i)$ denotes the dimension of ${\Omega }_i$.)

Invoke the fact that $0\le \left|\theta \right|-\theta \tanh (\theta /\mathcal{l})\le 0.2785\mathcal{l}$. According to (43), and event-triggered mechanism (26)–(29), we have

$$\begin{array}{cc}\hfill {\overline{m}}_{1i}{z}_{iv}{\tau }_{vi}-{\overline{m}}_{1i}{z}_{iv}{\rho }_{vi}& ={\overline{m}}_{1i}{z}_{iv}({\displaystyle \frac{{\vartheta }_{vi}}{1+{\lambda }_{iv}{\delta }_{iv1}}}-{\displaystyle \frac{{\overline{\lambda }}_{iv}{\delta }_{iv2}}{1+{\lambda }_{iv}{\delta }_{iv1}}}-{\rho }_{vi})\hfill \\ & \le {\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{v1})}{1+{\lambda }_{iv}{\delta }_{iv1}}}(\left|z_{iv}{\rho }_{vi}\right|-z_{iv}{\rho }_{vi}\tanh ({\displaystyle \frac{z_{iv}{\rho }_{vi}}{\epsilon }})+\left|z_{iv}{\overline{\lambda }}_{vi}\right|\hfill \\ & -z_{iv}{\overline{\lambda }}_{vi}\tanh ({\displaystyle \frac{z_{iv}{\overline{\lambda }}_{vi}}{\epsilon }}))-{\displaystyle \frac{{\overline{m}}_{1i}{z}_{iv}{\overline{\lambda }}_{iv}{\delta }_{iv2}}{1+{\lambda }_{iv}{\delta }_{iv1}}}\hfill \\ & \le 0.557\mathcal{l}{\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{v1})}{1+{\lambda }_{iv}{\delta }_{iv1}}}+({\displaystyle \frac{{\overline{m}}_{1i}{z}_{iv}{\overline{\lambda }}_{iv}{\delta }_{iv2}}{1+{\lambda }_{iv}{\delta }_{iv1}}}{)}^2+{\displaystyle \frac{1}{4}}\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\overline{m}}_{1i}{z}_{i\omega }{\tau }_{\omega i}-{\overline{m}}_{1i}{z}_{i\omega }{\rho }_{\omega i}& ={\overline{m}}_{1i}{z}_{i\omega }({\displaystyle \frac{{\vartheta }_{\omega i}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}-{\displaystyle \frac{{\overline{\lambda }}_{i\omega }{\delta }_{i\omega 2}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}-{\rho }_{\omega i})\hfill \\ & \le {\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{\omega 1})}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}(\left|z_{i\omega }{\rho }_{\omega i}\right|-z_{i\omega }{\rho }_{\omega i}\tanh ({\displaystyle \frac{z_{\omega i}{\rho }_{\omega i}}{\epsilon }})+\left|z_{i\omega }{\overline{\lambda }}_{\omega i}\right|\hfill \\ & -z_{i\omega }{\overline{\lambda }}_{\omega i}\tanh ({\displaystyle \frac{z_{\omega i}{\overline{\lambda }}_{\omega i}}{\epsilon }}))-{\displaystyle \frac{{\overline{m}}_{1i}{z}_{i\omega }{\overline{\lambda }}_{i\omega }{\delta }_{i\omega 2}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}\hfill \\ & \le 0.557\mathcal{l}{\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{\omega 1})}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}+{\overline{m}}_{1i}({\displaystyle \frac{z_{i\omega }{\overline{\lambda }}_{i\omega }{\delta }_{i\omega 2}}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}{)}^2+{\displaystyle \frac{1}{4}}\hfill \end{array}$$

(45)

According to Young’s inequality $a^2+b^2\le 2ab$, it is available

$$\begin{array}{l}{z}_{iv}{\epsilon }_{i,1}+z_{i\omega }{\epsilon }_{i,2}+{\chi }_{i,1}(N_{i,1}(\cdot )-{\displaystyle \frac{{\chi }_{i,1}}{{\delta }_{i,1}}})+{\chi }_{i,2}(N_{i,2}(\cdot )-{\displaystyle \frac{{\chi }_{i,2}}{{\delta }_{i,2}}})\\ \le {\displaystyle \frac{1}{2}}{z}_{iv}^2+{\displaystyle \frac{1}{2}}{z}_{i\omega }^2+{\displaystyle \frac{1}{2}}{\epsilon }_{i,1}^2+{\displaystyle \frac{1}{2}}{\epsilon }_{i,2}^2+({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{{\delta }_{i,1}}}){\chi }_{i,1}^2+{\displaystyle \frac{1}{2}}{N}_{i,1}^2\\ +({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{{\delta }_{i,2}}}){\chi }_{i,2}^2+{\displaystyle \frac{1}{2}}{N}_{i,2}^2\end{array}$$

(46)

$${\tilde{G}}_{i,s}^T{\widehat{G}}_{i,s}\le {\displaystyle \frac{1}{2}}({‖G_{i,s}^{*}‖}^2-{‖{\tilde{G}}_{i,s}‖}^2)$$

(47)

where $p_1$ and $p_2$ are positive design parameters.

From (30)–(37) and (43)–(47), we have

$$\begin{array}{cc}\hfill {\dot{V}}_2& \le ({\displaystyle \frac{1}{2}}+c_{i,d})z_{id}^2+({\displaystyle \frac{1}{2}}-c_{i,\psi })z_{i\psi }^2+(1-c_{i,v})z_{iv}^2+(1-c_{i,\omega })z_{i\omega }^2\hfill \\ & -{\displaystyle \frac{{\sigma }_{i,1}}{2}}{‖{\tilde{G}}_{i,1}‖}^2-{\displaystyle \frac{{\sigma }_{i,2}}{2}}{‖{\tilde{G}}_{i,2}‖}^2+({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{{\delta }_{i,1}}}){\chi }_{i,1}^2+({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{{\delta }_{i,2}}}){\chi }_{i,2}^2\hfill \\ & +{\displaystyle \frac{1}{2}}{N}_{i,1}^2+{\displaystyle \frac{1}{2}}{N}_{i,2}^2+{\displaystyle \frac{1}{2}}{\epsilon }_{i,1}^2+{\displaystyle \frac{1}{2}}{\epsilon }_{i,2}^2+{\displaystyle \frac{{\sigma }_{i,1}}{2}}{‖G_{i,1}^{*}‖}^2+{\displaystyle \frac{{\sigma }_{i,2}}{2}}{‖G_{i,2}^{*}‖}^2\hfill \\ & +0.557\mathcal{l}{\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{v1})}{1+{\lambda }_{iv}{\delta }_{iv1}}}+0.557\mathcal{l}{\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{\omega 1})}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}+{\displaystyle \frac{1}{2}}\hfill \end{array}$$

(48)

Let

$$\begin{array}{c}\overline{\Pi }={\displaystyle \frac{1}{2}}{N}_{i,1}^2+{\displaystyle \frac{1}{2}}{N}_{i,2}^2+{\displaystyle \frac{1}{2}}{\epsilon }_{i,1}^2+{\displaystyle \frac{1}{2}}{\epsilon }_{i,2}^2+{\displaystyle \frac{{\sigma }_{i,1}}{2}}{‖G_{i,1}^{*}‖}^2+{\displaystyle \frac{{\sigma }_{i,2}}{2}}{‖G_{i,2}^{*}‖}^2\\ +0.557\mathcal{l}{\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{v1})}{1+{\lambda }_{iv}{\delta }_{iv1}}}+0.557\mathcal{l}{\displaystyle \frac{{\overline{m}}_{1i}(1+{\lambda }_{\omega 1})}{1+{\lambda }_{i\omega }{\delta }_{i\omega 1}}}+{\displaystyle \frac{1}{2}}\end{array}$$

(49)

Denote $V={\displaystyle \sum _{i=1}^N{V}_{i,2}}$; according to (48) and (49), it yields that

$$\dot{V}\le -\overline{\psi }V+\overline{\Pi }$$

(50)

where $\overline{\psi }=\min \{({\displaystyle \frac{1}{2}}+c_{i,d},{\displaystyle \frac{1}{2}}-c_{i,\psi },1-c_{i,v},1-c_{i,\omega },{\displaystyle \frac{{\sigma }_{i,s}}{2}},{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{{\delta }_{i,s}}}\}$.

Integrating (50) over $[0,t]$, it shows

$$0\le V(0)e^{-\overline{\psi }t}+{\displaystyle \frac{\overline{\Pi }}{\overline{\psi }}}$$

(51)

From (51), it is shown that all the system’s closed-loop signals are bounded. Then, the fuzzy adaptive ET formation control errors based on ${(2V(0)e^{-\overline{\psi }t}+\overline{\Pi }/\overline{\psi })}^{1/2}$ for the union upper bound are given, and it is concluded that the event-triggered formation control error converges to the neighborhood of the origin. □

3.3. The Exclusion of Zeno Phenomenon

In this part, the main content is to explain that there is no Zeno phenomenon in the fuzzy adaptive ET formation control method.

According to [17], the event-triggered (ET) mechanism (26)–(29) dynamically determines when control signals are updated based on predefined thresholds. To ensure practicality, we must prove that the time between consecutive triggering events $\tau =t_{i(k+1)}-t_{ik}$ is strictly positive and bounded below by a minimum interval $\tau >0$, thereby excluding Zeno behavior.

According to the error $z_{i\tau m}(t)={\tau }_{im}(t)-{\alpha }_{im\tau }(t_{ik})$, one has

$${\displaystyle \frac{d}{dt}}\left|z_{i\tau m}\right|={\dot{z}}_{i\tau m}sign(z_{i\tau m})<\left|{\dot{\tau }}_{im}(t)\right|, m=v,\omega$$

All the signals are bounded in the NMRs and the actuators signals ${\tau }_{iv}$ and ${\tau }_{i\omega }$ are differentiable. Then, existing $\mathsf{\partial }$ can ensure $\left|{\dot{\tau }}_{im}(t)\right|\le \mathsf{\partial }$ is valid, where $\mathsf{\partial }$ is a constant.

By integrating, one has

$${\displaystyle {\int }_{t_{ik}}^{t_{i(k+1)}}\left|{\dot{z}}_{i\tau m}\right|}dt\le {\displaystyle {\int }_{t_{ik}}^{t_{i(k+1)}}\mathsf{\partial }}dt, m=v,\omega$$

It means that $t_{i(k+1)}-t_{ik}\ge ({\lambda }_{\tau 1}\left|{\tau }_{im}(t)\right|+{\lambda }_{\tau 2})/\sigma =\gamma >0$ for $\forall t\in [t_{ik},t_{i(k+1)})$. So there is no Zeno phenomenon in the fuzzy adaptive ET formation control method.

4. Simulation Studies

This section verifies the feasibility of the proposed fuzzy adaptive ET formation control method. We choose the robot parameters and give the values in Table 2 from the work in [28].

Table 2. Robot parameters.

Parameter	Value	Unit	Parameter	Value	Unit
$a_i$	0.75	m	$I_{ib}$	15.625	$\mathrm{kg}\cdot {\mathrm{m}}^2$
$c_i$	0.3	m	$I_{i\omega }$	0.005	$\mathrm{kg}\cdot {\mathrm{m}}^2$
$r_i$	0.15	m	$I_{im}$	0.0025	$\mathrm{kg}\cdot {\mathrm{m}}^2$
$m_{ib}$	30	kg	$d_{i11}$	5	$\mathrm{kg}\cdot {\mathrm{m}}^2/\mathrm{s}$
$m_{io}$	1	kg	$d_{i12}$	5	$\mathrm{kg}\cdot {\mathrm{m}}^2/\mathrm{s}$

4.1. Simulation Verification

The leader’s signal is $x_0=y_0=\sin t$. The robots’ initial positions are given as $p_0={\left[0,0,0\right]}^T$ $p_1={\left[0.1,0,\pi /9\right]}^T$ $p_2={\left[-0.1,0,\pi /9\right]}^T$ $p_3={\left[0.5,1,\pi /4\right]}^T$ $p_4={\left[0.1,0,\pi /4\right]}^T$.

The initial function is as follows:

$$\begin{gathered} f_{vi}={\displaystyle \frac{2b_i{c}_i{\omega }_i^2-v_i(d_{11i}+d_{22i})-b_i{\omega }_i(d_{11i}-d_{22i})}{2(m_{11i}+m_{12i})}} \\ {f}_{\omega i}=-{\displaystyle \frac{2c_i{v}_i{\omega }_i+v_i(d_{11i}-d_{22i})+b_i{\omega }_i(d_{11i}+d_{22i})}{2c_i(m_{11i}-m_{12i})}} \end{gathered}$$

To estimate the unknown nonlinear functions $f_{vi}$ and $f_{\omega i}$, assume that the universes of discourse for variables ${\kappa }_i$ are $[-4,4]$. Define If–Then fuzzy rules as

$L^j$: if ${\kappa }_i$ is $f_{\kappa i}$, then $y_i$ is $P$ $(\kappa =v,\omega ;i=1,2,3,4;j=1,2,3,4,5)$.

The fuzzy membership functions are given by ${\mu }_{f_{{\kappa }_1}}=1/(1+e^{[5(3+{\kappa }_1)/2]})$, ${\mu }_{f_{\kappa 2}}=e^{[-{(2+{\kappa }_2)}^2/2]}$, ${\mu }_{f_{\kappa 3}}=e^{[-{({\kappa }_3)}^2/2]}$, ${\mu }_{f_{\kappa 4}}=e^{[-{(-2+{\kappa }_4)}^2/2]}$, ${\mu }_{f_{\kappa 5}}=1/(1+e^{[-5(-3+{\kappa }_5)/2]})$, $\kappa =v,\omega$. Consequently, the fuzzy membership functions are presented in Figure 2. The FLS ${\widehat{f}}_{vi}(v_i)=G_{i,1}^T{\mathsf{\Psi }}_{i,1}(v_i)$ and ${\widehat{f}}_{\omega i}({\omega }_i)=G_{i,2}^T{\mathsf{\Psi }}_{i,2}({\omega }_i)$ are employed to estimate $f_{vi}(v_i)$ and $f_{\omega i}({\omega }_i)$.

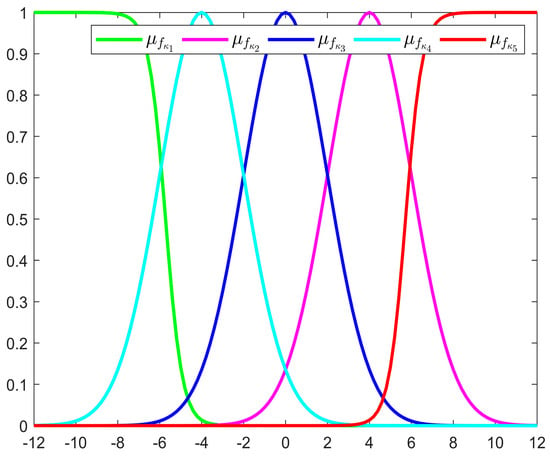
Figure 2. The fuzzy membership functions.

Remark 3.

It is also worth pointing out that according to Lemma 1, an FLS can approximate an unknown nonlinear function when the number of If–Then rules is larger, and for every input variable in the FLS, its fuzzy membership functions are chosen as Gaussian types  $\mu f_i({\kappa }_i)=\exp [{\displaystyle \frac{-{(\kappa -{\mu }_i)}^T(\kappa -{\mu }_i)}{{\gamma }_i^2}}],i=1,\dots ,n$, where the center points ${\mu }_i$ belong to the universe of discourse of the variable, and the width  ${\gamma }_i>0$. Moreover, the defined fuzzy membership functions should satisfy the following conditions.

(1)

Each pair of  $(\mu f_k({\kappa }_i),\mu f_j({\kappa }_i))$ is required to be overlapped.

(2)

The whole sequence of fuzzy membership functions $\mu f_1({\kappa }_i),\dots ,\mu f_n({\kappa }_i)$ is required to cover the universe of discourse of the variable x (the universe of discourse usually chosen as a symmetrical interval about zero).

The distance and angle of ensuring connectivity, collision avoidance, and the idealize are chosen as $d_{con,i}=5 \mathrm{m}$, $d_{col,i}=3 \mathrm{m}$, ${\phi }_{con,i}=1 \mathrm{rad}$, $d_{des,i}=4 \mathrm{m}$, and ${\phi }_{des,i}=0 \mathrm{rad}$, respectively. The parameters of the virtual controllers in expressions (16) and (17), along with the adaptive laws stated in (49) and (50), are given as $k_{d1}=k_{\phi 1}=9$ and ${\sigma }_{i,1}={\sigma }_{i,2}=1$ for robots 1–4, $i=1,2,3,4$. The parameters of trigger controllers (32) and (33) are given as ${\lambda }_{iv}=0.01$, ${\overline{\lambda }}_{iv}=0.05$, and $\epsilon =0.9$.

The simulation results are exhibited in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Figure 3 depicts the curves of NMRs. From Figure 3, it can be seen that Robot 1, Robot 2, Robot 3, and Robot 4 are stable and able to track Robot 0 to maintain the desired formation pattern. In the whole formation control process, there will be no collision between the robots, and the formation can be maintained within the scope of constraints. Figure 4 and Figure 5 show the tracking error of the four robots in terms of distance and angle, respectively. It can be observed from Figure 4 and Figure 5 that by adopting the formulated formation control approach, the tracking error of each NMR converges to a small neighborhood around zero even under full-state constraints. Figure 6 exhibits the trajectories of controllers. It can be observed from Figure 4 and Figure 5 that by adopting the formulated formation control approach, the tracking error of each NMR converges to a small neighborhood around zero even under full-state constraints. Figure 7 and Figure 8 display the triggering sequences of the four NMRs. Table 3 shows the specific number of triggers and the proportion of resource savings. It can be seen from them that the ET mechanism proposed in this study is capable of decreasing the unnecessary waste of resources resulting from the update of the controller signal. The above shows that the fuzzy formation control scheme presented in this article can achieve the control objective.

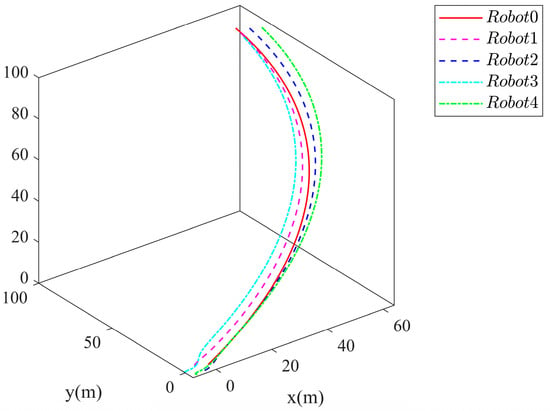
Figure 3. The trajectories of four NMRs.

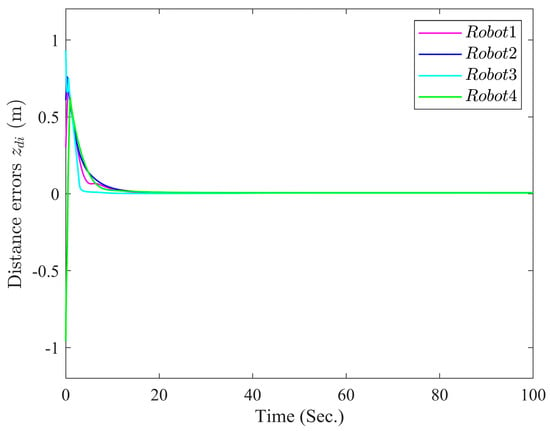
Figure 4. Curves of tracking errors $z_{di}(\mathrm{m})$.

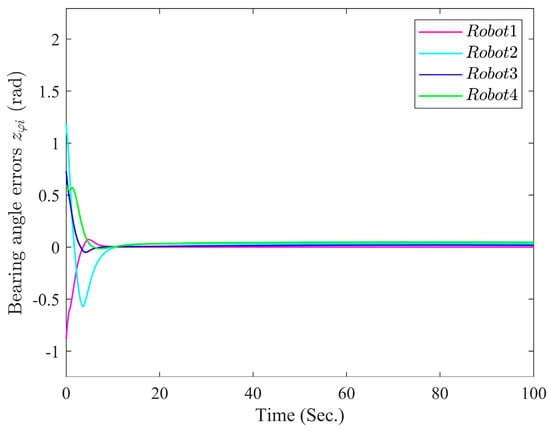
Figure 5. Curves of formation tracking errors $z_{\phi i}(\mathrm{rad})$.

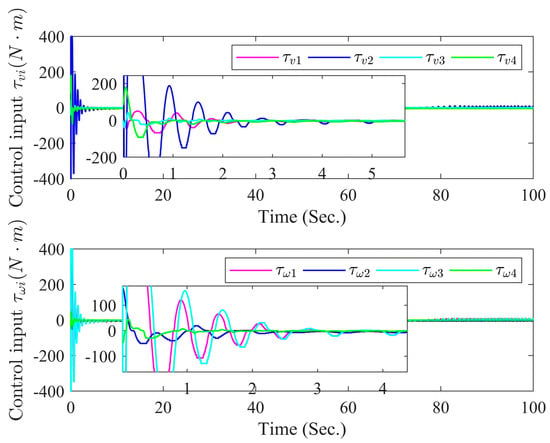
Figure 6. Curves of control inputs ${\tau }_{vi}$ and ${\tau }_{\omega i}(\mathrm{N}\cdot \mathrm{m})$.

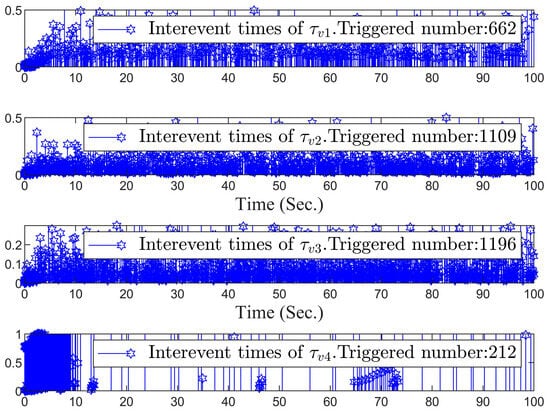
Figure 7. Triggering sequences of ${\tau }_{v1}$, ${\tau }_{v2}$, ${\tau }_{v3}$, and ${\tau }_{v4}$.

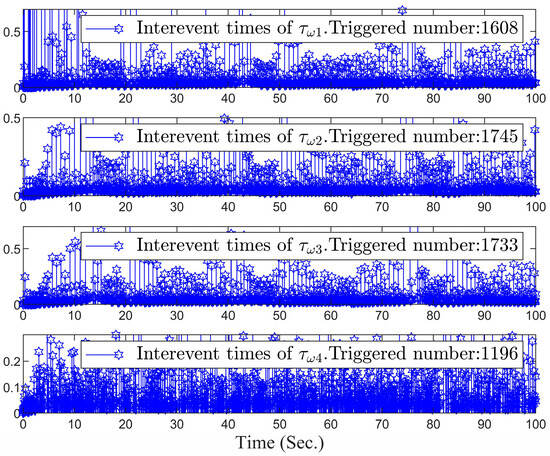
Figure 8. Triggering sequences of ${\tau }_{\omega 1}$, ${\tau }_{\omega 2}$, ${\tau }_{\omega 3}$, and ${\tau }_{\omega 4}$.

Table 3. Triggered times.

	$\mathbf{Triggered} \mathbf{Times} \mathbf{of} {\mathit{\tau }}_{\mathit{v}\mathit{i}}$ in the Paper	$\mathbf{Triggered} \mathbf{Times} \mathbf{of} {\mathit{\tau }}_{\mathit{\omega }\mathit{i}}$ in the Paper	Event Triggering Mechanisms Are Not Considered	Resource Saving Ratio
Robot 1	662	1608	20,000	88.65%
Robot 1	1109	1745	20,000	85.75%
Robot 1	1196	1733	20,000	85.36%
Robot 1	212	1196	20,000	92.96%
Total times	3179	6282	80,000	88.17%

4.2. Discussions

• Case 1. The Effect of Design Parameters.

To explain the effect of the design parameters in virtual controllers (16) and (17) and controllers (34) and (35), we select different design parameters for simulation. For ease of comparison, define the sum of the absolute values of the formation tracking errors as ${\overline{z}}_{di}={\displaystyle \sum _{i=1}^4\left|z_{di}\right|}$. Then, the responses to the tracking error ${\overline{z}}_{di}$ under different design parameters are shown in Figure 9.

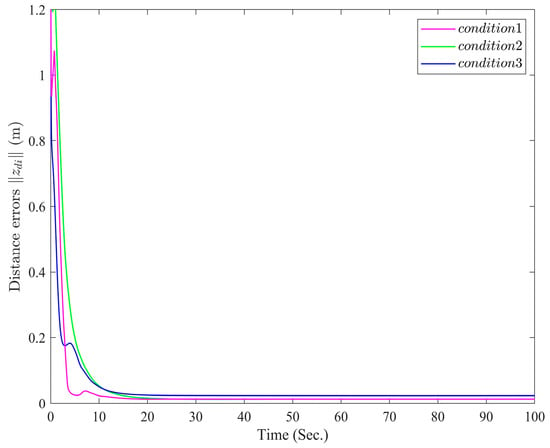
Figure 9. The responses of the tracking error ${\overline{z}}_{di}(\mathrm{m})$.

From Figure 9, we can see that selecting different parameters will affect the control performance of the system. Therefore, the formation tracking errors can be reduced by increasing the main design parameter. However, increasing the design parameters results in larger control energy. In practice, a tradeoff between improved control performance and the energy cost of control actions must be carefully considered.

• Case 2. The Effect of external interference.

In the simulation, we considered the influence of time-varying external interference on each robot. Figure 9 shows that the distance formation error of the robot will become larger under external interference. Similarly, Figure 10 and Figure 11 show that the robot’s formation errors will also be affected by external interference. The simulation results show that the time-varying external interference affects the control performance of the system.

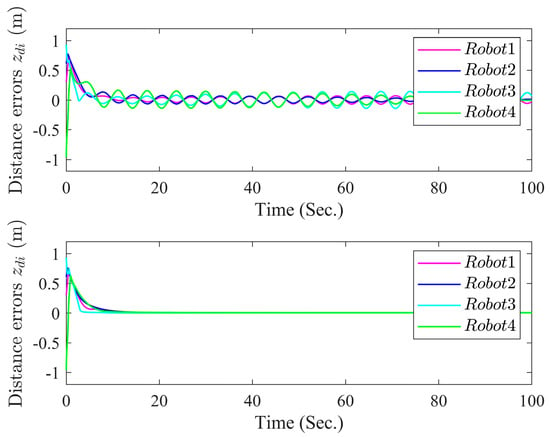
Figure 10. Curves of tracking errors $z_{di}(\mathrm{m})$.

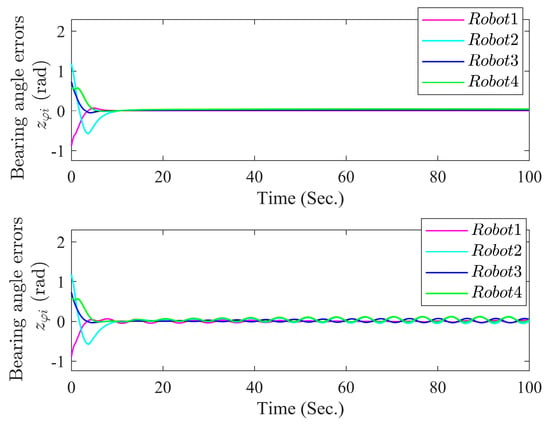
Figure 11. Curves of formation tracking errors $z_{\phi i}(\mathrm{rad})$.

The adaptive fuzzy formation control method proposed in this paper is robust and can deal with some small external disturbances, but the formation error will be larger when there are external disturbances or when there are external disturbances.

5. Conclusions

We proposed a fuzzy adaptive ET formation control design method for NMRs with full-state constants. The event-triggered mechanism can effectively reduce the number of unnecessary updates of control signals. Then, a fuzzy adaptive ET formation control strategy for NMRs was presented via backstepping control technology. Our results demonstrate that all signals of the controlled NMRs are SGUUB, and the tracking errors even converge to a small neighborhood around zero. It should be noted that the proposed fuzzy ET formation control algorithm cannot handle the consensus control problem when there are communication delays and the system is under sensor or other network attacks. It is also uncertain whether such a formation control method is applicable to heterogeneous multi-agent robots. Therefore, extending the results of this study to the case of communication time delays is a meaningful future research direction.