The Effect of Lightweight Wearable Resistance on the Squat and Countermovement Jumps: Does Load Dampen the Performance-Enhancing Effect of the Stretch-Shortening Cycle?

Abstract

This study investigated the effects of lightweight wearable resistance on the kinetics and kinematics of squat jumps (SJ) and countermovement jumps (CMJ) with 2%, 4%, and 6% body mass (BM). Twenty male athletes (age: 18.05 ± 0.6 years; weight: 76.4 ± 7.6 kg; height: 182.4 ± 5 cm) were assessed on a force plate. Key variables included jump height (JH), concentric (ConT) and eccentric (EccT) phase durations, concentric impulse (CI), mean force (CMF), mean velocity (CMV), mean power (CMP), and relative metrics. Elastic utilization ratios (EUR) were calculated to quantify stretch-shortening cycle enhancement. Load led to decrements in both jumps but with varying sensitivity. With 2% BM the CMJ significantly reduced JH (−8.6%), EccT (−7%), CMV (−4.1%), rCI (−4.1%), rPP (−4.4%), and velocity at PP (−4.8%), whereas variables in the SJ were non-significant until 4–6% BM. EURs observed the greatest differences with 2% BM with JH, CMV, rCMP, and VPP all significantly decreasing (p < 0.05). The varying sensitivity to load across variables observed in the two jumps supports the hypothesis that SJ and CMJ offer distinct diagnostic insights due to varying MTU contraction dynamics and neural factors. This has implications for WR use in training. Further, absolute metrics showed limited load sensitivity. However, when accounting for body mass, relative metrics revealed substantial declines. This indicates absolute values can misrepresent the effects of WR loading.

1. Introduction

The stretch-shortening cycle (SSC) is a naturally occurring muscle function process essential for powerful athletic movements. SSC-involved movements feature an initial eccentric contraction, a brief amortization phase, and a potentiated concentric contraction. This eccentric phase, exemplified by a countermovement, lengthens the muscle–tendon unit (MTU), enhancing subsequent concentric velocity, force, and/or power output [1,2,3,4,5,6].

Mechanical (elastic energy storage and reutilization) and neural factors (stretch reflexes and pre-activation) enhance SSC performance [7], though their relative contributions remain debated and task-dependent [7,8,9]. Regardless, performance enhancement observed with SSC movements can partly be attributed to the ability of the structural elements of the MTU to store energy during the eccentric phase and reutilize this stored energy during the concentric phase [2].

The theoretical framework provided by Hill’s three-component model (TCM) [10] provides valuable insights into the mechanical force transmission of the muscle–tendon unit (MTU) in the SSC. The TCM consists of three elements: the contractile component (CC) which generates active force; the series elastic component (SEC) which transmits force through elastic tissues such as tendons; and the parallel elastic component (PEC) which is made up of connective tissues such as the endomysium, perimysium and epimysium. Although the CC, SEC and PEC cannot be isolated, their contribution and interaction are influenced by the specific characteristics of the athletic movement [11,12,13].

Two movements commonly utilized to assess the SSC are the squat jump (SJ) and countermovement jump (CMJ). The CMJ has been shown to lead to greater jump height (JH), force, and power when compared with SJ [1,3,6,7,14,15,16]. This performance enhancement of the CMJ when compared to the SJ is due to how these two jumps are performed. The SJ is characterized by a pause for 3–4 s following an athlete’s descent into the squat position before executing the jump, dissipating stored elastic energy as heat [17]. As no eccentric contraction precedes the jump, the SJ serves as a baseline measure of an athlete’s capacity to concentrically produce force utilizing the CC. In contrast, the CMJ is characterized by its countermovement with a total contraction time varying from 350 to 1300 ms [7,15,18], therefore the CMJ is commonly classified as a slow SSC movement [7,19,20] and theoretically involve elastic tissues in the SEC and PEC to varying degrees, depending on the depth and velocity of the movement.

Various training strategies have been utilized to improve lower body SSC capabilities. One common method to improve the vertical jump (VJ) is through the addition of load. An important consideration when loading VJs is that any additional load needs to be sufficient to enable a training effect, without being too great that it effects the elastic potential of the SSC [21]. However, with the addition of load the entire power-, force-, and velocity-time curves are affected [22]. It has been observed that loaded VJs are executed at slower velocities when compared to VJs without additional load [23]. Further, load can affect the VJ technique as evidenced by a smaller countermovement and attenuated eccentric phase [24]. Despite this decreased countermovement depth, the duration of the concentric phase has been shown to increase with load [24].

The interaction of the TCM during a VJ is task and load dependent [25]. There is, however, a lack of understanding of the effects of load on the SJ and CMJ through the lens of Hill’s TCM. Earp et al. [25] observed in vivo that tendon strain decreases significantly during the SSC as loading increases. It is thought that the SEC acts as a power amplifier at lighter loads, whereas at heavier loads the tendon becomes a more rigid force transducer. Due to this, the contribution of the SSC to power output decreases with heavy loading [8]. Utilizing lighter loads has been shown to lead to faster concentric/eccentric phases and shorter amortization time [8] which may provide a training effect without impairing the SSC. As the performance of the SJ and CMJ rely on different mechanisms and have varying MTU contraction dynamics, the effects of load on these two jumps are likely to vary.

The application of external load in VJ has previously been achieved through various methods, such as barbells on the shoulders [26,27], elastic resistance [28], handheld weights [29], or wearable resistance (WR) [30]. WR, utilizing micro-loads attached to the body via compressive garments, allows sport-specific movements with enhanced training specificity [30]. Researchers have highlighted WR’s potential in diverse athletic contexts, including improved sprint performance in track sprinters [31], change of direction in soccer players [32], and throwing velocity in handball players [33]. These findings underscore WR’s ability to support high-velocity movements. Further, Macadam et al. [30] reported significant reductions in CMJ performance (12–17% reduction in jump height, p < 0.05) with 3% and 6% BM WR loads. This large reduction suggests that even lighter loads, such as 2% BM, may also affect the CMJ. However, there is a lack of investigation into the effects of light weight WR on the SJ and CMJ with their various contraction dynamics, differing reliance on the various components of the TCM, and neural factors.

Given the distinct nature of each jump, the primary aim of this study is to further understand how light external load affects the kinetics and kinematics of the SJ and CMJ at 2%, 4%, and 6% BM. These loads were selected to investigate thresholds for acute adaptations. Notably, the 2% BM load extends below the 3% BM examined by Macadam et al. [30], whereas the 6% BM load represented the heaviest practical option with our lower-limb loading setup (Lila™ Exogen™ suits), balancing feasibility with progressive increments. It is hypothesized that due to the varying movement requirements of these two jumps, the load dependent responses may differ between these jumps. It is further hypothesized that with increasing load there is a detrimental effect on SSC performance and therefore the CMJ will decrease at a greater rate than the SJ.

2. Materials and Methods

2.1. Experimental Approach

Experimental approach: An experimental cross-sectional design was used to investigate the effect of additional load (0%, 2%, 4%, and 6% BM) on the kinematics and kinetics of the SJ and CMJ.

2.2. Participants

Twenty male athletes from various sports (age: 18.05 ± 0.6 years; weight: 76.4 ± 7.6; height: 182.4 ± 5 cm) volunteered to participate in this study. All participants were free of any medical issues or injuries that could have compromised their performance. Participants were informed of the protocol and procedures prior to their involvement, and written consent to participate was obtained. The Institutional Ethics Committee of Auckland University of Technology provided approval for this study. The study was conducted in accordance with the Declaration of Helsinki and approved by the Auckland University of Technology Ethics Committee (AUTEC 20/105).

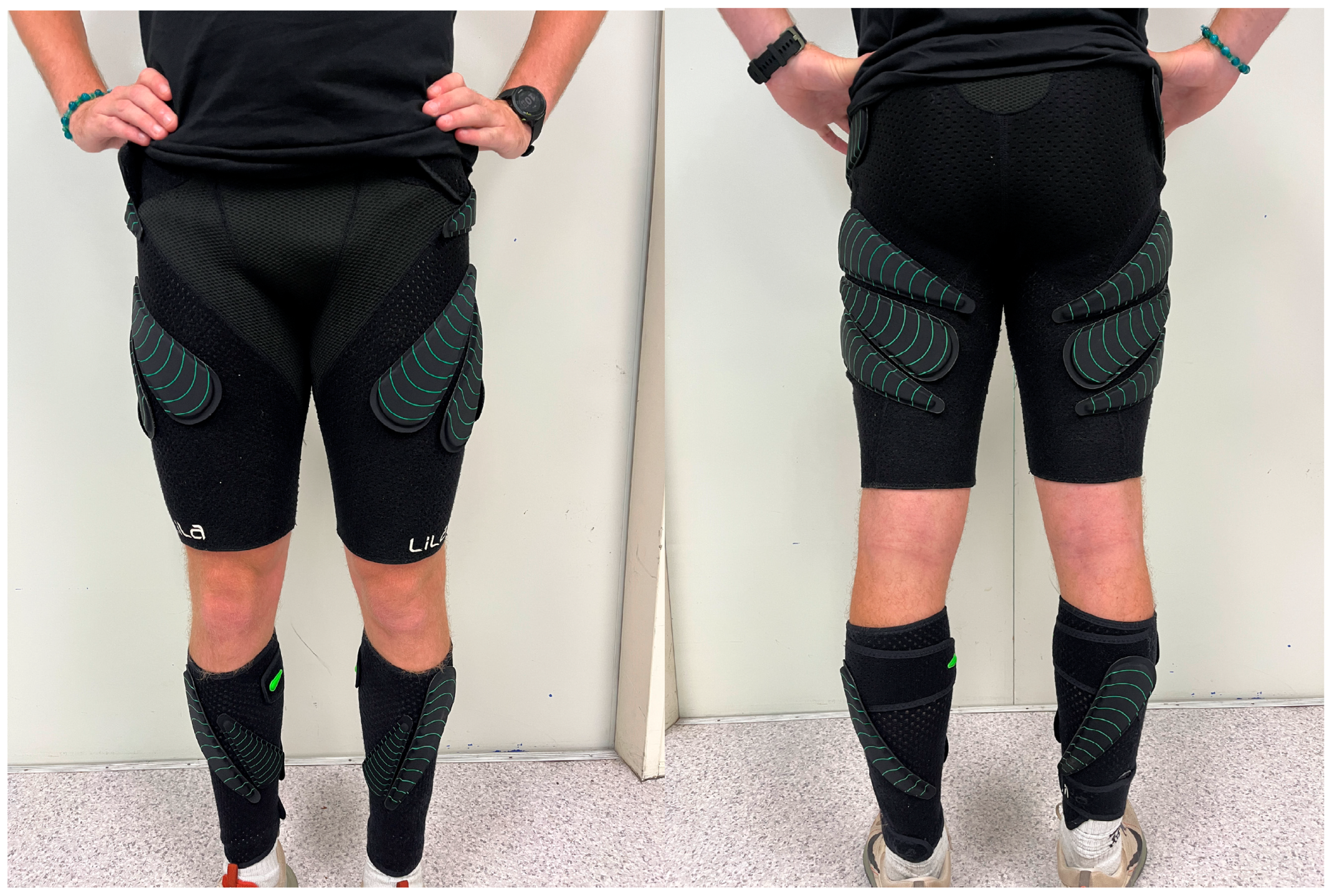
2.3. Equipment

Participants were loaded using Lila™ Exogen™ exoskeleton suits (Sportboleh Sdh Bhd, Kuala Lumpur, Malaysia). The Exogen™ exoskeleton suit allows load to be attached in multiple positions through the addition of fusiform shaped loads of 100 g and 200 g. Load was attached to the lower body using compression shorts and a pair of calf sleeves (Figure 1). Two thirds of the load was distributed evenly around the thigh and the remaining 1/3 distributed on the anterior and posterior surfaces of the shank of the leg [30]. The total mass of added load was 2%, 4%, or 6% of each participant’s body mass (BM) calculated to the closest 100 g. These loads were selected to investigate thresholds for acute adaptations. Notably, the 2% BM load extends below the 3% BM examined by Macadam et al. [30], whereas the 6% BM load represented the heaviest practical option with our lower-limb loading setup (Lila™ Exogen™ suits), balancing feasibility with progressive increments.

Figure 1. Lila^TM Exogen^TM wearable resistance.

2.4. Vertical Jump Testing

All vertical jump testing took place during a single session. Participants were required to avoid stressful physical activity for 24 h beforehand. Prior to testing, subject information [age, BM (scales), and height (stadiometer)] was collected. Participants were informed of the procedures and familiarized with each vertical jump test until technique was verified as correct by the researcher. Following a 10 min standardized warm-up, each subject was required to complete a total of 24 jumps (4 loading conditions × 2 jump conditions × 3 jumps). All unloaded trials were performed prior to the loaded trials to ensure that the unloaded trials were not influenced by the loaded trials. Participants performed either the SJ or CMJ trials in a randomized order. Thereafter, participants performed three consecutive trials for each jump/load condition in a randomized order. Each consecutive trial was separated by at least 30 s and each jump condition by at least a 2 min rest period [34]. Of the trials, the best two were averaged and used for analysis.

To improve the reliability of the data, participants were instructed to jump with the knees and ankles extended and land in a similarly extended position [14]. To limit the impact of instructions on performance, consistent instructions were provided to all participants during each VJ trial [20]. All participants were instructed to “jump as high and fast as possible off the force plate” for each jump variation. All jumps were performed with hands on hips to prevent the use of arms and attain true measures of leg force-time variables [20]. If the subject removed their hands from hips, displayed excessive knee flexion whilst airborne or landed in an incorrect position the jump was declared invalid and repeated after adequate rest.

Prior to both jump conditions, participants started in a standing position, with feet hip width apart on the force plate and stood still for 2–3 s to determine system weight which was used for analysis. To perform the SJ, participants were instructed to lower themselves into a squat to approximately a 90° knee angle (as determined visually by an experienced investigator), hold for four seconds [17], then jump as high as possible, attempting to eliminate any countermovement. If a countermovement was observed, the SJ was repeated. To perform the CMJ, the participants initiated the jump with a countermovement consisting approximately of a 90° knee angle (as determined visually by the investigator), instantly followed by a maximal effort vertical jump. Participants were instructed to jump for maximum height and ensure there was no pause between the eccentric and concentric phases.

2.5. Data Collection

All vertical jump data was collected with a portable force plate (AMTI, ACP, Watertown, MA, USA) using a sampling rate of 1000 Hz. Raw vertical ground reaction force (vGRF) data was analyzed using ForceDecks software V2.0.9064 (VALD, Brisbane, Australia) to calculate the variables of interest. The initiation of the concentric phase of the SJ was when vGRF exceeded 20 N above system weight [35]. Initiation of the CMJ was defined as the point when total vGRF deviated −20 N from system weight. All take-offs were identified as the instant when vGRF fell below 10 N. The impulse–momentum relationship was used to calculate JH. Where appropriate, contraction time was divided into an eccentric phase (EccT) and a concentric phase (ConT). The start of ConT was determined when velocity of the center of mass became positive. The concentric force index (CFI) was calculated as concentric mean force relative to bodyweight (CMF/kg) divided by ConT. Further, the elastic utilization ratio (EUR) was calculated to compare the SJ and CMJ from the following formula.

$$EUR={\displaystyle \frac{CMJVariable}{SJVariable}}$$

2.6. Statistical Analysis

Means and standard deviations were used as measures of centrality and spread of data. Normality and outlier analysis were undertaken on these means. Normal distribution of the data was checked using the Shapiro–Wilk test. If sphericity assumptions were violated according to Mauchly’s test, then Greenhouse-Geisser adjusted values were utilized. A repeated measures ANOVA with Bonferroni post hoc contrasts was used to determine significant differences between loads (Unloaded, 2%, 4%, and 6%). Statistical significance criterion was set at an alpha level of p < 0.05. Effect sizes are reported using Cohen’s d. Cohen’s d was calculated by dividing the mean difference between groups by the pooled standard deviation. The effect size is described as trivial (<0.2), small (0.21–0.5), moderate (0.51–0.79), and large (>0.8) [36].

3. Results

3.1. Squat Jump

Means and standard deviations for the SJ are presented in Table 1. Although there was a 3.5% decrease in JH with 2% load, this was non-significant. However, with the addition of 4% (−6.6%) and 6% (−11.7%) JH decreased significantly (ES = 0.63 and 1.12, respectively). No statistical significance was observed for any variables when comparing the 2% and 4% loads.

Table 1. Kinematic and kinetic variables during the SJ for all loading conditions.

Variable	0%	2%	4%	6%
JH (cm)	34.3 ± 4.1 cd	33.1 ± 3.4 d	32.1 ± 2.6 ad	30.5 ± 2.6 abc
ConT (ms)	412 ± 50	389. ± 43	399 ± 46	421 ± 62
CMV (m/s)	1.14 + 0.1 d	1.14 + 0.08 d	1.11 + 0.1	1.06 + 0.1 ab
CI (Ns)	197 ± 20	197 ± 21	198 ± 21	197 ± 19
rCI (Ns/kg)	2.59 ± 0.15 d	2.54 ± 0.13 d	2.51 ± 0.10 d	2.44 ± 0.11 abc
CMF (N)	1233 ± 150 bc	1272 ± 144 a	1277 ± 157 a	1274 ± 145
rCMF (N/kg)	16.2 ± 0.8	16.4 ± 0.7 d	16.2 ± 0.8	15.8 ± 0.9 b
CFI	3.99 ± 0.69	4.28 ± 0.66	4.14 ± 0.69	3.86 ± 0.82
CMP (W)	1410 ± 231	1450 ± 212	1421 ± 259	1359 ± 238
rCMP (W/kg)	18.5 ± 2.1 d	18.7 ± 1.9 d	18 ± 2.3	16.8 ± 2.4 ab
PP (W)	3994 ± 455	4002 ± 457	4004 ± 395	3943 ± 439
rPP (W/kg)	52.5 ± 4.5 d	51.7 ± 3.8 d	50.9 ± 2.8 d	48.8 ± 3.6 abc
FPP (N)	1672 ± 202 cd	1707 ± 191	1730 ± 178 a	1747 ± 201 a
VPP (m/s)	2.39 ± 0.15 d	2.35 ± 0.14 d	2.32 ± 0.11 d	2.26 ± 0.10 abc

Note. Abbreviations: CFI = concentric force index; CI = concentric impulse; CMF = concentric mean force; CMP = concentric mean power; CMV = concentric mean velocity; ConT = concentric duration; FPP = force at peak power; JH = jump height; PP = peak power; rCI = relative concentric impulse; rCMF = relative concentric mean force; rCMP = relative concentric mean power; rPP = relative peak power; VPP = velocity at peak power. Subscript letters indicate significant differences between loading conditions (p < 0.05): ‘a’ corresponds to 0%, ‘b’ to 2%, ‘c’ to 4%, and ‘d’ to 6%.

The effect of load on ConT was more variable, however, none of these changes were statistically significant.

Concentric impulse (CI) remained consistent across all loading conditions, with mean values of 197–198 Ns. However, relative CI (rCI) decreased with a significant 6% reduction with 6% BM (ES = 1.25). Absolute concentric mean force (CMF) increased significantly from unloaded to 2% BM (3.1%, ES = 0.27) and 4% BM (3.5%, ES = 0.28); however, minimal changes were observed in rCMF with increased load. With 2% BM there was an initial non-significant increase of 1.2%. However, there was a significant decrease of 3.7% (ES = 0.80) in rCMF when comparing 2% BM with 6% BM. The CFI showed no significant differences but trended upward at lighter loads (7% increase at 2% BM) before declining with 6% BM (−3.3%).

Concentric mean velocity (CMV) remained stable at 2–4% BM but decreased significantly by 7.3% (ES = 0.84) with 6% BM, while velocity at peak power (VPP) followed a similar pattern, with a 5.6% (ES = 1.01) reduction at 6% BM.

Concentric mean power (CMP) and peak power (PP) remained stable across all loads. In contrast, relative concentric mean power (rCMP) decreased significantly by 9.6% at 6% BM (ES = 0.72) and relative peak power (rPP) declined by 7.3% at 6% BM (ES = 0.96). Force at peak power (FPP) increased progressively, with significant gains at 4% (3.4%, ES = 0.31) and 6% BM (4.4%, ES = 0.37) compared to unloaded.

3.2. Countermovement Jump

Means and standard deviations for the CMJ are presented in Table 2. A significant reduction in JH (p < 0.05) across all loads (8.6–14%) compared to the unloaded condition with ES of 0.89, 1.04, and 1.51 was observed for 2%, 4%, and 6%, respectively. However, as with the SJ, when comparing the 2% and 4% loads there was no statistical change in JH. This was found repeatedly across all variables investigated in the CMJ.

Table 2. Kinematic and kinetic variables during the CMJ for all loading conditions.

Variable	0%	2%	4%	6%
JH (cm)	37.6 ± 3.4 bcd	34.5 ± 3.6 ad	34 ± 3.6 ad	32.7 ± 3.2 abc
TCT (ms)	833 ± 74 b	788 + 95 ad	810 ± 72	830 ± 100 b
CMD (cm)	34.2 ± 3.6 bcd	31.6 ± 4.9 a	31.5 ± 4.2 a	31.8 ± 4.7 a
EccT (ms)	561 ± 57 b	523 ± 71 ad	542 ± 56	556 ± 80 b
ConT (ms)	271 ± 22	265 ± 29	269 ± 29	274 ± 28
CMV (m/s)	1.47 + 0.07 bcd	1.41 + 0.08 ad	1.40 + 0.08 a	1.38 + 0.07 ab
CI (Ns)	207 ± 22 bd	202 ± 22 a	204 ± 22	204 ± 23 a
rCI (Ns/kg)	2.71 ± 0.12 bcd	2.60 ± 0.13 ad	2.58 ± 0.13 ad	2.53 ± 0.12 abc
CMF (N)	1516 ± 191	1534 ± 199	1546 ± 213	1538 ± 195
rCMF (N/kg)	19.8 ± 0.9 d	19.7 ± 1.1 d	19.5 ± 1.1	19.1 ± 1 ab
CFI	7.36 ± 0.92	7.56 ± 1.33 d	7.37 ± 1.2	7.07 ± 1.13 b
CMP (W)	2229 ± 330 d	2171 ± 334	2168 ± 347	2122 ± 328 a
rCMP (W/kg)	29.1 ± 2.4 cd	27.9 ± 2.6 d	27.3 ± 2.6 a	26.3 ± 2.2 ab
PP (W)	4089 ± 449 d	3985 ± 436	4009 ± 480	3952 ± 416 a
rPP (W/kg)	53.6 ± 3.7 bcd	51.3 ± 3.5 ad	50.7 ± 3.8 ad	49.2 ± 3.1 abc
FPP (N)	1611 ± 162 cd	1647 ± 166	1668 ± 193 a	1669 ± 151 a
VPP (m/s)	2.54 ± 0.11 bcd	2.42 ± 0.13 ad	2.4 ± 0.13 a	2.37 ± 0.12 ab

Note. Abbreviations: CFI = concentric force index; CI = concentric impulse; CMD = countermovement depth; CMF = concentric mean force; CMP = concentric mean power; CMV = concentric mean velocity; ConT = concentric phase time; EccT = eccentric phase time; FPP = force at peak power; JH = jump height; PP = peak power; rCI = relative concentric impulse; rCMF = relative concentric mean force; rCMP = relative concentric mean power; rPP = relative peak power; TCT = total contraction time; VPP = velocity at peak power. Subscript letters indicate significant differences between loading conditions (p < 0.05): ‘a’ corresponds to 0%, ‘b’ to 2%, ‘c’ to 4%, and ‘d’ to 6%.

Total contraction time (TCT) decreased 5.4% (ES = 0.54) with 2% BM; however, there was no statistical difference with either 4% or 6% when compared to the unloaded condition. There was no change (p > 0.05) in ConT across all loads, with all the change in TCT due to changes in the eccentric phase. Specifically, the 2% load resulted in the greatest decrease in EccT of 7% (p < 0.05, ES = 0.60). Further, countermovement depth decreased 7.2–8.2% under all loading conditions in comparison to the unloaded jumps (p < 0.05, ES = 0.56–0.69), with no significant differences in depth between the 2%, 4%, and 6% loads.

CMV decreased significantly across all loads (−4.1% to −6.3%, ES = 1.23–2.32), and VPP followed suit (−4.8% to −6.9%, ES = 0.95–1.48). CI showed minor non-significant reductions (−1.4% to −2.4%), but rCI declined significantly across loads (−4.1% to −6.9%, ES = 1.36–2.91). Absolute CMF increased slightly (1.2–2.0%, non-significant), while rCMF decreased, reaching significance at 6% BM (−3.6%, ES = 0.82). The CFI varied without significance, peaking at 2% BM (2.7%) before declining at 6% (−4.0%). FPP increased (3.5–3.6%), with significance at 4% and 6% BM (ES = 0.32–0.37)

CMP decreased non-significantly and PP showed similar stability with significant decreases only observed with 6% BM. However, rCMP declined significantly at 4% and 6% BM (−6.4% to −10.1%, ES = 1.03–1.56) and rPP decreased across all loads (−4.4% to −8.6%, ES = 0.87–2.30).

3.3. Elastic Utilization Ratios

The greatest difference in EURs with load was between the unloaded and 2% BM conditions, with JH, CMV, rCMP, and VPP all significantly different (see Table 3). Jump heights in the CMJ were observed to be higher than the SJ by 4.6–10.7%, with the greatest EUR value being in the unloaded condition and the lowest in the 2% load condition. This trend was consistent across all variables examined. Further, the CMJ led decrease in ConT (31.4–33.4%) and Force at PP (3–4%), whereas rCI (2.6–5.8%), CMV (25–29%), rCMF (20.1–22.8%) and CFI (78.9–90.7%), rCMP (50–59.3%), and VPP (3.2–6.2%) all observed increases whilst relative peak power (rPP) ranged from −0.2% to 3%.

Table 3. Elastic utilization ratios.

Variable	0%	2%	4%	6%
JH (cm)	1.11 ± 0.11	1.05 ± 0.07 a	1.06 ± 0.06	1.07 ± 0.06
ConT (ms)	0.67 ± 0.07	0.69 ± 0.09	0.68 ± 0.1	0.67 ± 0.11
CMV (m/s)	1.29 ± 0.1	1.25 ± 0.08 a	1.27 ± 0.1	1.3 ± 0.11
rCI (Ns/kg)	1.06 ± 0.13	1.03 ± 0.03	1.03 ± 0.03	1.03 ± 0.05
rCMF (N/kg)	1.23 ± 0.1	1.20 ± 0.07	1.21 ± 0.07	1.22 ± 0.09
CFI	1.87 ± 0.27	1.79 ± 0.32	1.82 ± 0.35	1.91 ± 0.49
rCMP (W/kg)	1.59 ± 0.17	1.5 ± 0.17 a	1.54 ± 0.19	1.59 ± 0.24
rPP (W/kg)	1.03 ± 0.08	0.99 ± 0.06	1.00 ± 0.06	1.01 ± 0.06
FPP (N)	0.97 ± 0.1	0.97 ± 0.05	0.96 ± 0.06	0.96 ± 0.07
VPP (m/s)	1.06 + 0.06	1.03 + 0.04 a	1.04 + 0.04 a	1.05 + 0.03

Note. Abbreviations: CFI = concentric force index; ConT = concentric phase time; CMV = concentric mean velocity; FPP = force at peak power; JH = jump height; rCI = relative concentric impulse; rCMF = relative concentric mean force; rCMP = relative concentric mean power; rPP = relative peak power; VPP = velocity at peak power. Subscript a indicates significant differences between loading condition and unloaded condition (p < 0.05).

4. Discussion

This study focused on the effects of lightweight WR on the kinematics and kinetics of SJ and CMJ, particularly how loads of 2%, 4%, and 6% BM influenced jump performance and load-dependent responses. Key findings included: (1) differing acute adaptations in SJ and CMJ relative to load; (2) the magnitude of these acute adaptations differed if expressed in absolute or relative terms; (3) load had little effect on the EUR of most variables; and (4) variable-specific differences in EUR enhancement magnitude.

4.1. SJ and CMJ Acute Adaptations

The acute adaptations observed in the SJ and CMJ differed in relation to the WR load applied. With the addition of 2% BM, notable differences emerged between the two jumps. No significant decreases were observed for any SJ variable compared to unloaded, whereas CMJ JH reduced significantly by 8.6% (p < 0.05). This finding represents the lowest loading condition to lead to significant decreases in JH for the CMJ and was practically significant with a large effect size (ES = 0.89), although Macadam et al. [30] did report a more substantial 12% decrease utilizing 3% BM. This observed decline in CMJ height was accompanied by a moderate reduction in countermovement depth (7.9%, ES = 0.56), shorter EccT (7%, ES = 0.60), and decreased CMV (4.1%, ES = 1.23). Notably, the shorter eccentric phase was attributed to a decreased countermovement depth rather than an increase in velocity. These contrasting effects of 2% BM on the CMJ and SJ highlight the sensitivity of the CMJ to light weight loading.

Significant decreases in SJ JH were only observed when the loading increased to 4% BM, resulting in a moderate reduction (6.6%). Interestingly, no other variables measured in the SJ decreased at 4% BM. Additionally, no significant differences were noted between the 2% and 4% loading conditions for either the SJ or CMJ.

When the load was increased to 6% BM, SJ height decreased further (p < 0.05) by 11.7%, which was accompanied by reductions in rCMP (9.6%) and rPP (7.3%). This decline was primarily due to a reduction in velocity, while rCMF remained relatively stable. A similar finding was observed in the CMJ. The large 8.6% decrease in rPP with 6% loading for the CMJ was similar to Macadam et al. [30] who reported a decrease of 8–17% with loads of 3–6% WR. However, this was also accompanied by a decrease in rCMF, which decreased 3.6% with 6%BM (p < 0.05).

Further, even at the 6% BM load, where statistical significance was evident for both jump types (p < 0.05), the practical implications differed markedly. The varying load-dependent responses observed between the SJ and CMJ could provide insights into the underlying mechanisms responsible. These include the contribution of the components of the TCM. As the SJ is purely concentric, the CC is, in theory, the dominant component in force production. From these findings, it could be extrapolated that these loading ranges provide limited overload for the CC and loads greater than 6% could be required.

In contrast, the performance of the CMJ relies on the passive elastic components SEC and PEC in addition to the CC. It seems that loads as light as 2% BM may limit elastic energy storage and reutilization mechanisms of the SEC and PEC within the MTU, as evidenced by the pronounced decrements in CMJ performance and EURs (Table 2 and Table 3). It could be concluded that while greater loads are necessary to provide adequate resistance to overload the force-generating capacity of the CC, lighter loads have greater effects on the SEC and PEC.

Interestingly, no significant changes in ConT occurred across loading conditions for either the SJ or CMJ. This may be attributed to the influence of load on joint angles and countermovement depth. SJ depth was visually inspected and therefore may have been altered throughout the loading conditions. Further, load reduced countermovement depth by 7.2–8.2% (p < 0.05) compared to the unloaded CMJ across all conditions. Although reduced depth partly explains CMJ performance changes, the stability of countermovement depth between 2% BM and 6% BM suggests that the effects of load in these loading conditions can be evaluated independently of countermovement depth. Notably, EccT increased 6.1% (p < 0.05) from 2% to 6% BM, extending eccentric duration despite consistent countermovement depth, resulting in reduced velocity heading into the concentric phase. Consequently, this had a significant effect on CMV decreasing 2.1% (p < 0.05) from 2% BM to 6% BM.

CI remained relatively unchanged across loads for both jumps. SJ values ranged from 197 Ns to 198 Ns, whilst minor decreases of 1–2% were observed in the CMJ. These findings align with Gutiérrez-Dávila et al. [37], who reported no significant differences in vertical impulse in the CMJ with 0–7.5% BM.

Similarly, light WR loading barely changed PP outputs in either jump. No significant differences were detected across the SJ loads, whilst only 6% BM was found significantly different to the unloaded CMJ. Previous researchers have reported varied findings regarding the effects of external loading on PP during the CMJ. Harrison et al. [38] reported a 6% increase in PP among males with vest loading of 20.6% BM. In contrast, Gutiérrez-Dávila et al. [37] found no significant changes with vest loading across 0–7.5% BM.

In the current study, accounting for BM changed the results of these metrics considerably. Notably rCI decreased 6%, whilst a 7.3% decrease was observed for the rPP with 6% BM for the SJ, whereas the CMJ rCI and rPP decreased across the loading spectrum. When compared to the unloaded CMJ, the observed 8.6% decrease in rPP with 6% loading aligns with Macadam et al. [30] who reported an 8–17% decrease with loads of 3–6% WR. Further, across both SJ and CMJ when comparing unloaded to 6%BM conditions, effect sizes for relative metrics (rPP, rCMP, rCI, rCMF) were moderate-to-large (ES = 0.72–2.91), whereas those for absolute metrics (PP, CMP, CI, CMF) were uniformly small (ES = 0.27–0.28).

It would seem using absolute metrics can be misleading when using additional load. These metrics incorporate added mass, potentially masking underlying performance decrements by inflating values due to the increased system weight. For example, absolute power may appear stable or even increase slightly as the increase in load force compensates for velocity reductions. However, this does not reflect the true biomechanical consideration for the athlete. In contrast, relative metrics showcase these decrements more accurately. This is clear from the substantial declines in rPP and rCMP across loads in the CMJ. In applied settings, coaches and practitioners should prioritize relative metrics when using lightweight WR and loaded jumps. This helps detect load-induced changes and avoids overestimating athlete capabilities.

4.2. Eccentric Utilization Ratios

The EUR was utilized in this study to compare the CMJ and SJ to determine if there was any enhancement of the concentric phase given the preceding eccentric contraction. Previously, Loturco et al. [39] reported that the potentiating effect of the CMJ diminished with increasing load, so it was thought that any enhancement would decrease with greater loading. Our findings, however, did not support this. The most significant differences (2.8–5.4%) were observed between the unloaded condition and 2% BM, in JH, CMV, rCMP, and VPP.

These changes, however, were not progressive or linear. With 4% and 6% BM, the EURs returned towards baseline levels. This finding is likely because the CMJ had greater sensitivity to the lower loads than the SJ. Specifically, whilst the SJ was found to have minimal changes at 2% loading, significant effects were seen in the CMJ. Loturco et al. [39] observed a linear reduction in the CMJ’s potentiating effect with increasing load, reporting an 8% difference in the unloaded condition, which decreased to 2.4% with 100% BM. The results of this study provide evidence that this linear reduction may not apply with light loads, where the SJ is minimally affected.

The significant CMJ decrements at 2% BM can be interpreted through various models. While this study interprets these findings primarily through the mechanical lens of lengthening and shortening of the TCM components (CC, SEC, and PEC), the authors acknowledge that neural factors provide a complementary perspective that could also influence the observed differences [40].

Mechanically, the additional mass may disrupt optimal elastic energy storage and reutilization in the SEC and PEC, leading to reduced SSC potentiation [25]. This disruption could arise from alterations in timing, velocity, and amplitude during the eccentric phase, resulting in lower energy reutilization during the concentric contraction [37,40]. For example, the observed reduction in CMD alongside shortened EccT suggests an attenuated eccentric phase that limits SEC and PEC lengthening.

Further, the effect of load on neural factors, such as stretch reflexes and pre-activation, may lead to altered neuromuscular coordination under load, with subtle changes potentially inhibiting the stretch reflex and/or pre-activation and thereby diminishing neuromuscular coordination while amplifying mechanical disruptions [7]. It is plausible that the addition of WR could modulate these neural factors in several ways, affecting both facilitatory and inhibitory processes. For example, the increased load and reduced eccentric velocity during the CMJ’s countermovement phase could lower stretch reflex sensitivity [7], resulting in diminished reflexive potentiation, reduced neural drive to the CC, and exacerbated performance decrements at lighter loads in the CMJ compared to the SJ, where no eccentric phase exists to trigger such reflexes. Additionally, the load might necessitate greater pre-activation or co-activation of muscles to stabilize joints and manage the added mass, altering the timing of muscle activation. This could be accompanied by prolonged coupling time during the amortization phase of the SSC, dissipating stored elastic energy. Further additional load could also engage protective inhibitory mechanisms. Increased tensile forces on the MTU could potentially activate Golgi tendon organs. These proprioceptors sense changes to force and provide inhibitory feedback to prevent overload [41]. This force feedback mechanism could lead to inhibition, reducing neural drive and exacerbating performance decrements in the CMJ’s SSC.

In the SJ, which relies on voluntary concentric activation without prior eccentric loading, these neural adjustments could be less pronounced until higher loads are used. This likely contributes to the CMJ’s greater sensitivity compared to the SJ, where neural SSC facilitation is non-existent and reliance is placed on voluntary concentric drive.

Furthermore, EUR magnitude varied by variable. Consequently, the interpretation varies greatly depending on which variables are examined. As shown in Table 3, four variables (JH, CI, VPP, and rPP) exhibited limited enhancement (3–11%), while ConT, CMV, rCMF, CFI, and rCMP all were found to have a 23–87% enhancement. The difference between these groups of metrics is that the former are either outcome variables or are quantified via a single data point, whereas the variables with the greater EURs are calculated over the entire concentric phase and/or are normalized to body weight. Elastic enhancement from the countermovement has a number of flow-on effects into the concentric phase in terms of contraction dynamics. It has been previously shown that the enhancement of the eccentric phase does not necessarily lead to greater magnitude of peak values but rather changes the timing of when these peaks occur in the concentric phase [42]. Therefore, when comparing the SJ and CMJ it may be beneficial to consider variables that account for the entire concentric phase rather than those quantified by a single data point later in the jump.

4.3. Practical Applications

Acute adaptations to the CMJ can occur with as little as 2% body mass (BM), whereas the SJ requires greater loading of at least 6% BM. Although there are many theories as to why the SJ and CMJ differ, it can be partly attributed to the active and passive lengthening and shortening of the components of the TCM involved in mechanical force transmission. Utilizing this model, it would suggest that aiming to increase active force-generating capacity of the contractile component CC requires greater loading, whereas the elastic enhancement of the series elastic component SEC and PEC is impaired even with lighter loading.

When translating these results, practitioners should interpret statistical significance/non-significance alongside the effect size (practical significance). For example, the ES provides insight into the magnitude of the loading effects on the variables of interest, and hence shapes decision-making on whether to use WR, even if effects are statistically non-significant. The greatest effects of load were observed in the CMJ. In particular JH, CMV, rPP and rCMP were all affected across the loading spectrum of the CMJ with large effect sizes and could be key variables to further understand the implications of loading on the CMJ in practice.

For practical implementation, coaches should consider the athlete’s sport-specific demands and training goals when selecting WR loads. In sports that are heavily reliant on the SSC and therefore the SEC and PEC, such as basketball (rebounding or blocking) or volleyball (spiking or blocking at the net), performing the CMJ with lighter loads such as 2% BM may be recommended during training phases to enhance elastic utilization. This could be ideal for in-season maintenance or speed-focused sessions where preserving jump height and velocity is key. Conversely, for activities emphasizing concentric force production through the CC, such as strength-oriented phases in weightlifting or sports with more static starts, heavier loads like 6% BM in SJ protocols may be appropriate to overload the CC, provided they do not exceed practical equipment limits or cause technique breakdown. Loads could be progressed gradually (e.g., from 2% to 6% BM over sessions) to monitor adaptations via relative metrics, ensuring training specificity aligns with competition demands.

4.4. Limitations

This study has several limitations that the reader should be cognizant of. Firstly, the sample was limited to 20 young males, which limits the generalizability of the findings to broader populations. Sex and age-related differences such as variations in tendon compliance or neuromuscular control could influence WR effects on jump performance, and our young male cohort may over or underestimate SSC sensitivity in other cohorts. A larger and more diverse cohort could enhance external validity and allow for subgroup analyses, such as sport and/or sex-based differences in responses to WR.

Secondly, the SJ knee angle was determined through visual inspection by the investigator, which may introduce measurement error or variability in jump depth across trials and participants. Although this method was consistently applied, it lacks the precision of objective tools like video analysis or goniometry, which could improve reliability in future studies.

Thirdly, the testing protocol involved performing all unloaded trials prior to loaded trials to establish a clean baseline and minimize fatigue from additional loading. However, this non-randomized sequence may introduce order effects, such as learning improvements or cumulative fatigue, potentially biasing comparisons between conditions. Counterbalancing trial order in future designs would help mitigate this issue.

Additionally, the absence of direct physiological measures limits mechanistic insights into load effects; future studies incorporating EMG or ultrasound imaging could elucidate underlying factors, such as mechanical tendon alterations or neural inhibition.

Finally, while this study focused on acute adaptations, it does not provide insights into the chronic effects of lightweight wearable resistance on squat and countermovement jump performance. Long-term training interventions are needed to understand the adaptations associated with repeated exposure to WR loading.

5. Conclusions

In conclusion, this study quantified the effects of light weight WR on SJ and CMJs. There was a clear effect of load on JH for both the CMJ and SJ; however, the CMJ was more sensitive to the effects of WR. This was also observed when comparing the jumps utilizing the EUR. Surprisingly, the greatest reduction in the EUR was with 2% BM. Acute adaptations to load with the CMJ can occur with as little as 2% BM, whereas the SJ requires greater loading of at least 6% BM. Although there are many theories as to why the SJ and CMJ differ, it can be partly attributed to the active and passive lengthening and shortening of the components of the TCM involved in mechanical force transmission. Utilizing this model, these findings suggest that aiming to increase active force generating capacity of the CC requires greater loading, whereas the elastic enhancement of the SEC and PEC is impaired by lighter loading. This sensitivity of the CMJ to lighter loads highlights the importance of considering the specific mechanical properties and underlying physiological mechanisms when designing loading vertical jump training programs. Furthermore, when interpreting metrics with light weight WR, it is recommended to use relative measures that account for BM. Additionally, since the potentiating effect of the eccentric phase has a greater impact over the entire concentric phase rather than just peak values, metrics that analyze the entire concentric phase should be utilized.