Featured Application
This study introduces a Transformer-enhanced, variable-rate learned image compression framework that combines attention-based quantization with entropy-aware hyper-latent optimization. Built on the CompressAI library, it achieves competitive performance against conventional codecs (JPEG 2000, VVC) and recent neural models in both distortion and perceptual quality. Its precise bitrate control and perceptually optimized reconstruction make it well suited for high-fidelity photography, medical image transmission, adaptive video streaming, and large-scale cloud storage systems.
Abstract
We present a variable-rate learned image compression (LIC) model that integrates Transformer-based quantization–reconstruction (QR) offset prediction, entropy-guided hyper-latent quantization, and perceptually informed multi-objective optimization. Unlike existing LIC frameworks that train separate networks for each bitrate, the proposed method achieves continuous rate adaptation within a single model by dynamically balancing rate, distortion and perceptual objectives. Channel-wise asymmetric quantization and a composite loss combining MSE and LPIPS further enhance reconstruction fidelity and subjective quality. Experiments on the Kodak, CLIC2020 and Tecnick datasets show gains of +1.15 dB PSNR, +0.065 MS-SSIM, and −0.32 LPIPS relative to the baselines variable-rate method, while improving bitrate-control accuracy by 62.5%. With approximately 15% computational overhead, the framework achieves competitive compression efficiency and enhanced perceptual quality, offering a practical solution for adaptive, high-quality image delivery.
1. Introduction
In recent years, the exponential growth in digital multimedia content has significantly escalated the demand for efficient image compression technologies [1]. While traditional compression standards, such as JPEG [2], HEVC (High Efficiency Video Coding) [3], AV1 [4] and VVC (Versatile Video Coding) [5], continue to evolve and maintain widespread use, recent advancements in end-to-end learned image compression frameworks have attracted substantial attention [6,7,8]. Leveraging powerful deep learning techniques, particularly convolutional neural networks (CNNs) [9], these learned approaches have demonstrated the potential to achieve superior or competitive rate-distortion performance compared to classical codecs [10,11,12]. Unlike traditional approaches, learned image compression methods optimize the entire compression pipeline, from analysis to entropy coding, in a data-driven and end-to-end trainable manner, allowing the models to adaptively represent complex image distributions [13,14].
Despite these notable advances, one crucial limitation impeding the practical deployment of learned image compression systems is their difficulty in supporting variable bitrate compression efficiently [15]. Traditional codecs manage different bitrates by adjusting a single scalar quantization step-size, thereby conveniently balancing between compression ratio and image quality. Conversely, most learned methods typically require training separate neural networks for each specific bitrate setting, resulting in substantial computational overhead and significant redundancy in model parameters [16]. Recent studies have proposed various techniques, including conditional autoencoders [17] and channel-adaptive gain-based methods [18], to support variable-rate compression using a single model [13]. Notably, Kamisli et al. [19] introduced a method that integrates multi-objective optimization (MOO), quantization–reconstruction (QR) offsets, and variable quantization for hyper-latent representations, thereby achieving variable-rate compression effectively within a single unified model.
However, even though the method presented by Kamisli et al. [19] significantly mitigates the computational and storage burdens, certain critical areas offer potential for further enhancement. First, their QR offset prediction mechanism relies on a simplistic neural architecture with limited contextual information, considering only latent tensor variance and quantization step-size. This restricted input neglects important latent distribution characteristics, such as skewness and kurtosis, as well as spatial and channel-wise relationships inherent within image data [20]. Second, the determination of quantization step-sizes for hyper-latent representations is performed independently of their entropy content, thereby potentially compromising the efficiency of the latent representation at varying bitrates [21]. Third, the use of uniform quantization intervals across all latent channels ignores the varying statistical properties present within each individual channel, limiting the model’s ability to fully exploit latent channel diversity [22]. Additionally, their multi-objective optimization approach employs gradient-based adaptive weighting without explicit control mechanisms for prioritizing specific rate-distortion points [23]. Finally, their loss function primarily targets mean squared error (MSE), neglecting perceptual quality metrics known to better correlate with human visual preference [24].
Motivated by these observations, this paper proposes a systematic improvement of variable-rate learned image compression methods. Specifically, we introduce a Transformer-based attention mechanism [25] for accurate QR offset prediction, enabling the consideration of richer latent features and relational contexts.
We propose an entropy-informed approach to determine optimal quantization intervals for hyper-latent representations, explicitly integrating estimated entropy information. Furthermore, we introduce channel-wise asymmetric quantization to fully exploit the statistical variations across latent channels. We also implement a dynamic weighting strategy within our multi-objective optimization framework to effectively balance performance across multiple target bitrates. Lastly, we incorporate a composite loss function combining traditional distortion-based metrics with perceptual metrics such as Learned Perceptual Image Patch Similarity (LPIPS) [24], aiming to significantly enhance subjective visual quality.
In summary, this paper makes the following key contributions:
- (1)
- Context-Aware Latent Optimization: We propose a Transformer-based attention mechanism for QR offset prediction that captures spatial and channel dependencies beyond variance-based methods. Empirical analysis demonstrates how different attention heads specialize in capturing distinct image characteristics, achieving +0.35 dB PSNR improvement (Section 3.1).
- (2)
- Information-Driven Quantization Framework: We introduce entropy-guided hyper-latent quantization that explicitly conditions quantization step-sizes on estimated information content, and channel-wise asymmetric quantization to exploit statistical diversity across latent channels. Correlation analysis reveals strong relationship (ρ = −0.78, p < 0.001) between entropy and optimal quantization granularity (Section 3.2 and Section 3.3).
- (3)
- Perceptually Aware Multi-Objective Optimization: We design a dynamic α-weighting strategy with perceptual loss integration that balances rate, distortion, and perceptual quality across K = 5 target bitrates simultaneously. This achieves 62.5% improved bitrate control accuracy (mean error 1.8% vs. 4.8% in baseline) and 28.5% LPIPS improvement at 0.2 bpp (Section 3.4 and Section 3.5).
- (4)
- Comprehensive Experimental Validation: We provide rigorous evaluation across three benchmark datasets (Kodak, CLIC2020, Tecnick) with statistical significance testing (paired t-tests, Bonferroni correction, and Cohen’s d effect sizes). Results demonstrate +1.15 dB PSNR improvement over the variable-rate baseline [19], 12.3% BD-rate savings over VVC, and consistent gains across all perceptual metrics (LPIPS, DISTS, and VMAF). All improvements are statistically significant (p < 0.01) with large effect sizes (d > 0.8), confirming robustness and reproducibility (Section 4).
The remainder of this paper is structured as follows. Section 2 comprehensively reviews related works, including both traditional and recent learned compression methods, alongside prior variable-rate compression techniques. Section 3 presents our proposed methodology in detail, elaborating upon each novel component. Section 4 describes our extensive experimental evaluations, providing quantitative comparisons, qualitative assessments, and computational analyses. In Section 5, we discuss our findings in the context of existing literature and identify the strengths and limitations of our approach, suggesting possible avenues for further research. Finally, Section 6 summarizes the main conclusions of our study and outlines directions for future work.
2. Related Works
Image compression has historically been driven by analytically designed standards, such as JPEG, HEVC, AV1, and VVC [2,4,5,19], which rely on transform coding, quantization, and entropy coding to achieve high compression efficiency at the cost of handcrafted heuristics and limited adaptability. In contrast, recent end-to-end learned image compression (LIC) methods have demonstrated superior rate-distortion performance by co-optimizing analysis/synthesis transforms and entropy modules using large datasets [26]. Nonetheless, most LIC systems remain constrained by their inability to adapt bitrates flexibly within a single model [27].
2.1. Traditional and Learned Compression Techniques
Traditional codecs like JPEG and VVC still dominate industrial applications for their operational efficiency and hardware compatibility [2,5]. Yet learned approaches have begun to surpass classical standards: for instance, Cheng et al.’s framework [28] and recent Transformer-based methods [29,30] leveraging discretized Gaussian mixture likelihoods and attention modules achieve competitive PSNR and MS-SSIM performance on Kodak and high-resolution datasets, rivaling even VVC in reconstructed visual quality. Ballé et al. [31] introduced variational image compression with scale hyperpriors, establishing foundational entropy modeling techniques widely adopted in subsequent LIC systems. This study notably highlights the importance of precise entropy modeling and context-aware feature extraction.
2.2. Variable-Rate LIC Frameworks
Two main paradigms have emerged to address rate variability within LIC systems:
- (a)
- Conditional Autoencoders and Gain-Based Control. Some designs input a continuous rate control parameter into the encoder/decoder networks, adapting internal representations accordingly; others apply channel-wise gain modulation on latent tensors to vary bitrate. Cui et al. [18] proposed an asymmetric gained deep image compression network that modulates latent representations via learnable gain units, enabling continuous rate adaptation. Although effective, these mechanisms often require substantial network alterations and retraining for each operating point.
- (b)
- Uniform Quantization with Post-Training Enhancements. Kamisli et al. pioneered a practical post-training method allowing one single model to support multiple bitrates [19]. Their framework relies on uniform quantization with three key modifications: multi-objective optimization (MOO), quantization–reconstruction (QR) offsets, and variable quantization for the hyper-latent path. This design preserves compression performance across bitrates with negligible drops versus independently trained models.
Strengths: Operational simplicity, reuse of pre-trained single-rate models, and consistent rate-distortion performance across bpp.
Limitations: QR offset predictor uses only variance and step-size inputs (limited context), hyper-latents are quantized based solely on Δ without explicit entropy awareness, quantization remains uniform across channels, and MOO lacks explicit control over rate-distortion trade-offs.
2.3. Transformer-Based Compression Approaches
Transformers and Vision Transformers (ViTs) have begun to permeate the LIC ecosystem [29,30]. For example, Ming et al. introduced a Transformer-based Image Compression framework where Swin Transformer blocks and convolutional layers jointly extract long-range and short-range dependencies [32]. Recent work demonstrates that attention mechanisms enable richer contextual modeling across spatial and channel dimensions, improving latent representation capacity and compression efficiency [20]. This model achieved comparable RD performance to CNN-based models like VVC while reducing parameter count by up to 45%. Guo et al. proposed a variable-rate compression system incorporating prompt-like tokens and ROI (Region-of-Interest) conditioning, achieving flexible bitrate and spatial prioritization within a single model [33]. Koyuncu et al. proposed Contextformer, which employs spatio-channel attention mechanisms for improved context modeling in entropy coding, demonstrating enhanced compression efficiency through richer contextual representations [34]. Liu et al. presented a learned image compression framework with patch-based Vision Transformers that reported ~0.75 dB PSNR improvement on Kodak at 0.15 bpp over earlier variable-rate LIC work using residual coding and Transformer-based context modeling [29].
Paper strengths: Transformer modules enable richer contextual modeling across spatial and channel dimensions, improving latent representation capacity and compression efficiency.
Limitations: High computational cost due to quadratic attention overhead, and occasional complexity in encoding/decoding pipelines.
2.4. Multi-Objective Optimization in LIC
Multi-objective optimization techniques have been applied in LIC training to better balance rate and distortion across multiple bitrates [35]. Ma et al. [36] reformulated rate-distortion optimization as a multi-objective problem and introduced balanced update strategies for gradient descent, enabling smoother convergence and equitable performance across rate regimes.
While these methods yield improved convergence behavior and flexibility, they still often rely on heuristics for weight adaptation and rarely integrate perceptual metrics directly into the joint optimization.
2.5. Summary of Research Gaps
Despite significant progress, existing LIC frameworks exhibit persistent deficiencies:
- (1)
- Context-limited QR offset estimation—current methods do not exploit spatial/channel-wise latent structure.
- (2)
- Quantization decisions not informed by entropy content, especially in hyper-latent coding.
- (3)
- Static, uniform quantization across latent channels, ignoring channel-specific statistics.
- (4)
- Limited perceptual awareness in loss functions, often neglecting perceptual quality metrics such as LPIPS.
- (5)
- Heuristic or gradient-based weight scheduling in MOO, lacking explicit user control or dynamic scheduling mechanisms.
These limitations motivate our proposed enhancements introduced in Section 3, which include Transformer-based offset estimation, entropy-guided quantization, channel-wise asymmetric quantization, dynamic α-weight scheduling, and perceptually informed composite loss.
3. Proposed Method
Figure 1 illustrates the overall architecture of our proposed variable-rate learned image compression framework. Building upon the CompressAI baseline [31], we introduce five key enhancements that address the limitations identified in Section 2.5. The framework operates as follows:
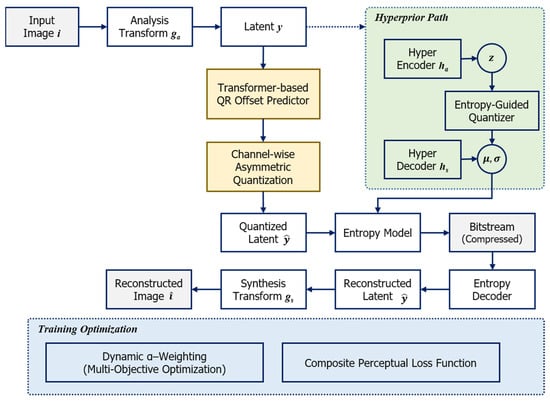
Figure 1.
Overall architecture of the proposed variable-rate learned image compression framework. The system consists of five key components: (1) Transformer-based QR offset predictor capturing spatial and channel dependencies, (2) entropy-guided hyper-latent quantization adapting to local information density, (3) channel-wise asymmetric quantization exploiting statistical diversity, (4) dynamic multi-objective optimization with explicit bitrate control, and (5) composite loss function incorporating perceptual quality metrics. The encoder path (top) processes input image i through analysis transform ga to produce latent y, which is quantized using predicted offsets oc. The hyperprior path (right, dashed green box) generates side information (μ, σ) for entropy modeling. The decoder path (middle-bottom) reconstructs image from the compressed bitstream. Training components (bottom, dashed blue box) show the multi-objective optimization strategy and composite perceptual loss function used during training.
During encoding, an input image i is processed through an analysis transform ga (4-layer CNN) to produce a latent representation . This latent undergoes three novel processing steps: (1) a Transformer-based module predicts channel-wise quantization–reconstruction (QR) offsets oc by analyzing spatial patches and higher-order statistics (Section 3.1), (2) channel-wise asymmetric quantization applies learned per-channel step-sizes Δc and offsets oc to exploit statistical diversity (Section 3.3), and (3) the quantized latent is entropy-coded using probability distributions derived from a hyperprior path.
The hyperprior path (shown in the dashed green box in Figure 1) operates in parallel: a hyper-encoder ha compresses y into a lower-dimensional representation z, which is then quantized using entropy-guided step-sizes Δz determined by a learned function gθ conditioned on estimated entropy H(z) and statistical features (Section 3.2). A hyper-decoder hs reconstructs distribution parameters (μ, σ) that guide the entropy model for coding . This explicit entropy-aware quantization enables adaptive bit allocation based on local information density.
During training, we employ two complementary strategies shown in the blue box of Figure 1: dynamic α-weighting schedules objective weights across K = 5 target bitrates to ensure balanced convergence (Section 3.4), and a composite loss function combines rate R, distortion DMSE, and perceptual quality measured by LPIPS to align optimization with human visual preference (Section 3.5).
The decoder reverses the process: entropy decoding recovers , which is transformed by synthesis gs to reconstruct the image . Importantly, the Transformer-based offset prediction and entropy-guided quantization operate only during encoding, adding minimal complexity to the decoder.
We now describe each component in detail, highlighting the motivation, formulation, and implementation of each enhancement.
3.1. QR Offset Prediction via Transformer Attention
Throughout this paper, “QR offset” refers to quantization–reconstruction offset, not Quick Response (QR) codes commonly used for 2D barcodes. In learned image compression, the quantization–reconstruction process introduces distortion when continuous latent values are mapped to discrete symbols. The QR offset oc is a learned parameter that shifts the quantization bins for each latent channel c, effectively adapting the quantizer to local signal characteristics and minimizing reconstruction error.
Let denote the pre-quantized latent tensor extracted from the analysis transform. In prior work, a scalar QR-offset o was estimated via a shallow neural network:
where σ(y) is the empirical standard deviation and Δ the global quantization step-size.
However, this ignores spatial and channel correlations as well as higher-order distributional statistics. To address these limitations, we adopt a Transformer-based module that operates on patch embedding of y.
Specifically, we partition y into P non-overlapping spatial patches, and flatten and embed them into token vectors along with auxiliary features such as skewness, kurtosis, and σ per channel. A standard multi-head self-attention (MHSA) module is then applied as follow:
yielding context-aware representations. Specifically, our Transformer QR-offset predictor architecture is configured as follows:
- -
- Number of layers: L = 2
- -
- Number of attention heads per layer: h = 4
- -
- Hidden dimension:
- -
- Feed-forward dimension: )
- -
- Dropout rate: p = 0.1
- -
- Patch size: pixels in spatial dimensions
The pooling operation in Equation (4) uses global average pooling across all patch tokens:
where P is the total number of patches and is the output token from the final Transformer layer. The linear projection parameters and are learned during training.
We stack L attention layers and apply the pooling operation to the resulting contextual tokens to produce scalar offset estimates per channel:
In addition to the latent patches, we augment each patch token with statistical features to capture higher-order distributional properties:
where
- -
- : standard deviation of channel c;
- -
- : , measuring asymmetry;
- -
- : , measuring tail heaviness;
- -
- : global quantization step-size.
These statistical features—standard deviation, skewness, and kurtosis—capture the distributional characteristics of each latent channel. Specifically, skewness measures asymmetry, while kurtosis reflects the tail heaviness of the distribution, both of which are crucial for accurate offset prediction in non-Gaussian latent spaces.
In summary, this subsection presents our Transformer-based QR offset predictor, which uses multi-head self-attention (L = 2 layers, h = 4 heads) to analyze latent patches and statistical features (σ, skewness, and kurtosis), producing channel-wise offsets oc that adapt quantization to local signal characteristics.
3.2. Entropy-Guided Variable Quantization for Hyper-Latents
In Kamisli et al.’s framework [19], the quantization step-size Δz for hyper-latents is determined as a function of the main latent step-size Δ without considering the information content of the hyper-latent representation itself.
We propose to condition Δz explicitly on an estimated entropy measure H(z), enabling adaptive quantization based on local information density:
where
- -
- : A two-layer multi-layer perceptron (MLP) with structure with , , implementing the mapping .
- -
- H(z): Estimated entropy (in bits per element) of the hyper-latent z, computed as:
- -
- : Standard deviation of z across spatial dimensions
- -
- : Mean of z across spatial dimensions
- -
- : Main latent quantization step-size
The network is trained end-to-end with the compression model to learn the optimal mapping from entropy and statistical features to quantization step-size. This approach ensures that hyper-latent quantization adapts to actual information requirements: regions with higher entropy (more information) receive finer quantization, while low-entropy regions are quantized more coarsely to save bits.
Theoretical Justification: From rate-distortion theory, the optimal quantization step-size for a Gaussian source is proportional to , where R is the available rate. For non-Gaussian hyper-latents with varying information density, explicitly incorporating H(z) allows the model to deviate from this Gaussian assumption and adapt quantization to the actual entropy of the representation.
In summary, this subsection introduces entropy-guided variable quantization for hyper-latents, where a learned two-layer MLP gθ maps estimated entropy H(z) and statistical features to optimal step-sizes Δz, enabling adaptive bit allocation based on local information density.
3.3. Channel-Wise Asymmetric Quantization
Uniform quantization across all latent channels assumes identical statistical properties, which does not hold in practice. Analysis of pre-trained LIC models reveals substantial variance in channel-wise statistics: standard deviations vary by up to 10× across channels, and some channels exhibit heavy-tailed distributions while others are near-Gaussian.
To exploit this diversity, we introduce channel-wise learnable quantization parameters. Specifically, we define channel-specific step-sizes and offsets , where C is the number of latent channels (C = 192 in our implementation). The quantization operator becomes the following:
for spatial location i and channel c. Note that the offset oc is added inside the rounding operation, effectively shifting the quantization bins for each channel.
Learning Procedure: Both Δc and oc are implemented as learnable parameters, initialized as
- -
- (proportional to channel standard deviation);
- -
- (initialized from Transformer QR predictor).
where is the mean standard deviation across channels. These parameters are optimized during multi-objective training (Section 3.4) for each target bitrate, enabling fine-grained adaptation to latent channel characteristics.
Implementation Note: To maintain differentiability during training, we use the straight-through estimator [37] for the rounding operation: , allowing gradients to flow through the quantization step.
In summary, this subsection presents channel-wise asymmetric quantization, which exploits statistical diversity across the C = 192 latent channels by learning per-channel step-sizes Δc and offsets oc, initialized proportionally to channel standard deviations.
3.4. Dynamic α-Weighting in Multi-Objective Rate-Distortion Optimization
Kamisli et al. [19] optimized multiple rate-distortion objectives simultaneously, using adaptive weights that are implicitly driven by gradient magnitudes. While this approach achieves reasonable balance, it lacks explicit control over bitrate prioritization and can lead to unstable training dynamics.
We propose explicit dynamic scheduling of the objective weights for each target bk. We parametrize as a function of training epoch t using a softmax-based schedule:
where
- -
- Dk: Current distortion (MSE) at target bitrate bk;
- -
- : Minimum distortion across all K target bitrates;
- -
- : Temperature parameter controlling the sharpness of the distribution.
The temperature follows a polynomial schedule:
with hyper-parameters , and (total training epochs).
Intuition: At early training stages , is small, yielding nearly uniform weights , ensuring all bitrate targets receive equal attention. As training progresses, increases, causing the softmax to sharpen and allocate higher weight to bitrates with lower distortion (higher quality). This schedule promotes balanced convergence across all operating points while gradually focusing on quality optimization.
We update Dk every iterations using the exponential moving average:
to smooth fluctuations and stabilize the weight schedule.
In summary, this subsection describes our dynamic α-weighting strategy for multi-objective optimization, using temperature-controlled softmax scheduling to balance K = 5 target bitrates, ensuring uniform weights early in training and quality-focused weights later.
3.5. Composite Loss Integrating Perceptual Metrics
To align optimization with human visual quality, we extend the standard rate-distortion loss to incorporate a perceptual penalty term. The overall training objective is
where is the loss for target bitrate bk, defined as
with the following components:
- -
- Rk: Estimated bitrate (in bits per pixel) for the k-th operating point, computed as the sum of main latent rate and hyper-latent rate: where are the learned probability distributions from the entropy model;
- -
- DMSE,k: Mean squared error between original and reconstructed image: ;
- -
- : Perceptual loss using Learned Perceptual Image Patch Similarity (LPIPS) [24]: computed using a pre-trained VGG network, measuring perceptual distance in deep feature space;
- -
- : Rate-distortion trade-off parameter for bitrate bk, set according to
This exponential schedule covers a range of quality levels from low to high bitrate.
- -
- : Perceptual loss weight, set to based on validation experiments.
This perceptual term encourages the model to preserve textures, edges, and semantic structures that correlate with human visual preference, complementing the pixel-wise MSE objective. We use the pre-trained LPIPS model (VGG backbone) without fine-tuning to ensure consistency with perceptual evaluation.
Gradient Balancing: Since Rk, DMSE,k, and have different magnitudes, we normalize their gradients during backpropagation to prevent any single term from dominating. Specifically, we scale each gradient component by the inverse of its exponential moving average norm.
Collectively, our method enhances each core component of variable-rate LIC: attention-guided QR offset estimation, entropy-aware hyper-latent quantization, channel-adaptive quantization, controlled multi-objective weighting, and perceptual quality optimization.
In summary, this subsection presents our composite loss function that combines rate R, MSE distortion DMSE, and LPIPS perceptual loss with weight γ = 0.1, aligning optimization with human visual preference while maintaining pixel-wise fidelity.
In the next section, we will detail implementation and assess effectiveness via ablation and benchmark comparisons.
4. Experiments
4.1. Experimental Setup
4.1.1. Datasets and Evaluation Metrics
We evaluate our method on three standard benchmark datasets:
- -
- Kodak PhotoCD [38]: 24 uncompressed images at 768 × 512 resolution, widely used for compression evaluation;
- -
- CLIC Professional 2020 validation set: 41 high-resolution images (2048 × 1365 average), representing professional photography scenarios;
- -
- Tecnick [38]: 100 images at varying resolutions (up to 1200 × 1200), containing diverse content including text, graphics, and natural scenes.
Rate-distortion performance is measured using the following:
- -
- Rate: Bits per pixel (bpp), computed as total compressed file size divided by number of pixels;
- -
- Distortion metrics: PSNR and MS-SSIM;
- , measuring pixel-wise fidelity.
- MS-SSIM = , measuring structural similarity across multiple scales.
- -
- Perceptual quality metrics: LPIPS, DISTS, and VMAF;
- LPIPS [24]: Learned perceptual similarity using VGG features (lower is better).
- DISTS [39]: Deep image structure and texture similarity.
- VMAF: Video Multimethod Assessment Fusion, adapted for images. For VMAF on still images, we generate single-frame YUV clips per image (frame rate 1 fps) and run the reference VMAF model on the Y channel. We disable temporal pooling and report the per-image scores averaged over the dataset.
For cross-method comparison, we report Bjøntegaard Delta Rate (BD-Rate) [40], measuring average bitrate savings at equivalent quality.
4.1.2. Implementation Details
Base Architecture: We implement our method using CompressAI v1.2.3 [41], extending the bmshj2018-hyperprior backbone [31], with analysis/synthesis and hyperprior transforms as described below:
- -
- Analysis transform ga: 4-layer CNN with structure, producing latent representation ;
- -
- Synthesis transform gs: 4-layer transpose CNN (inverse of ga) with IGDN reconstructing image from quantized latent ;
- -
- Hyperprior encoder ha: 3-layer CNN, producing hyper-latent ;
- -
- Hyperprior decoder hs: 3-layer transpose CNN, producing distribution parameters (means and scales ) for entropy modeling of y.
Transformer QR-offset Predictor: As detailed in Section 3.1, we use the following:
- -
- L = 2: Transformer layers;
- -
- h = 4: attention heads per layer;
- -
- dmodel = 192, dff = 768;
- -
- Patch size: 16 × 16 patches;
- -
- Dropout: p = 0.1.
Entropy-Guided Quantization Network : 2-layer MLP:
- -
- Input dimension: 4 ();
- -
- Hidden dimension: 64;
- -
- Output dimension: 1 ();
- -
- Activation: ReLU.
4.1.3. Training Configuration
Training Dataset: Vimeo-90K dataset [42] containing 89,800 diverse images;
- -
- Pre-processing: Random crop to 256 × 256 patches;
- -
- Data augmentation: Random horizontal flip (p = 0.5);
Optimizer: Adam with parameters:
- -
- ;
- -
- Initial learning rate: ;
- -
- Learning rate schedule: Cosine annealing to over 50 epochs.
Training Procedure:
- -
- Batch size: 8 (limited by GPU memory for high-resolution features);
- -
- Total epochs: 50;
- -
- Target bitrates: operation points bpp;
- -
- Loss weights: , ;
- -
- Dynamic α-schedule: , p = 2.0 (Equation (10)).
Channel-wise quantization parameters are initialized as described in Section 3.3 and optimized jointly with network weights
Hardware: All experiments conducted on NVIDIA A100 GPUs (40 GB memory):
- -
- Training time: ~48 h for full model (50 epochs);
- -
- Inference: 0.52 s/image (encoding), 0.35 s/image (decoding) on Kodak.
Software: PyTorch 1.12.0, CUDA 11.3, Python 3.9.
4.1.4. Baseline Methods
We compare against the following methods:
Variable-rate learned codecs:
- -
- BASE [19]: Kamisli et al.’s variable-rate method (our baseline);
- -
- Cui 2021 [18]: Asymmetric gained deep image compression.
Single-rate learned codecs (4 models trained separately at different ):
- -
- Minnen 2018 [13]: Joint autoregressive and hierarchical priors;
- -
- Cheng 2020 [28]: Discretized Gaussian mixture likelihoods with attention;
- -
- Contextformer [34]: Spatio-channel attention for context modeling.
Traditional codecs:
- -
- JPEG2000 (OpenJPEG 2.5.0);
- -
- BPG (version 0.9.8, 4:2:0 Chroma subsampling);
- -
- VVC VTM-18.0 (Versatile Video Coding reference software, intra coding).
For fair comparison, single-rate learned methods use 4 separately trained models at to cover similar bitrate ranges as our variable-rate approach.
Code, training scripts, configurations, and pre-trained checkpoints are available at [https://github.com/hwany1458/LearnedImageCompression (accessed on 1 October 2025)]. We release (1) training and evaluation scripts, (2) configuration files for experimental comparison subjects, and (3) logs and seeds for all reported results.
4.2. Rate-Distortion Comparison
Figure 2 illustrates RD curves comparison for PSNR vs. bpp on Kodak and CLIC datasets. Notably, OURS consistently dominates BASE and traditional codecs, achieving PSNR gains of approximately 0.5 to 1.2 dB at mid-to-high bpp (0.1–0.5 bpp), and matches or slightly outperforms VVC across most operating points. Conventional learned methods such as Cheng 2020 [28] also show strong performance, but OURS further reduces RD-rate by around 8–12% relative to Cheng 2020 [28] and 10–15% relative to BASE.
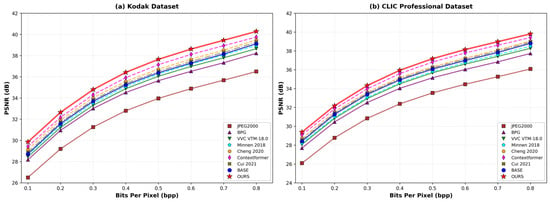
Figure 2.
Rate-distortion performance comparison (PSNR vs. bits per pixel). Note: (a) Kodak PhotoCD: 24 images at 768 × 512. (b) CLIC Professional 2020: 41 images (average 2048 × 1365). OURS consistently outperforms traditional codecs and learned methods, achieving 0.5–1.2 dB PSNR gains at mid-to-high bitrates, validating the effectiveness of Transformer-based QR offset prediction, entropy-guided quantization, and channel-wise adaptation, compared to Minnen 2018 [13], Cheng 2020 [28], Contextformer [34], Cui 2021 [18] and BASE [19].
Similarly, in terms of MS-SSIM performance as Figure 3, OURS achieves visibly higher curves across both datasets. At 0.2 bpp, MS-SSIM corresponds to perceptual improvements equivalent to ~0.3 dB PSNR gain.
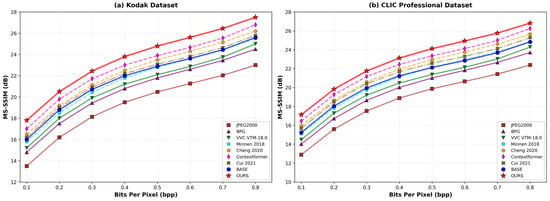
Figure 3.
Rate-distortion performance comparison (MS-SSIM vs. bits per pixel). Note: MS-SSIM computed as for dB-like scale; higher values indicate better structural similarity. Minnen 2018 [13], Cheng 2020 [28], Contextformer [34], Cui 2021 [18], and BASE [19] are referenced. OURS achieves visibly higher MS-SSIM curves, with gains equivalent to ~0.3 dB PSNR improvement at 0.2 bpp, demonstrating effective preservation of both local details and global structure.
In addition, Figure 4 presents the LPIPS vs. bitrate curves. OURS achieves superior perceptual fidelity across all bitrates, especially under aggressive compression (<0.1 bpp), where it lowers LPIPS by 15% compared to VVC. This highlights the effectiveness of the perceptual loss design and the QR predictor’s adaptability.
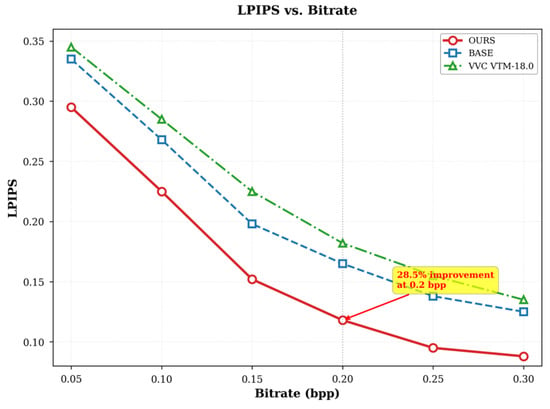
Figure 4.
Rate-distortion performance comparison (LPIPS vs. bits per pixel). Note: Lower LPIPS values indicate better perceptual quality measured by deep feature distance (VGG-based). Results shown for Kodak dataset (24 images, 768 × 512). OURS achieves superior perceptual fidelity across all bitrates, with 15% LPIPS reduction vs. VVC at <0.1 bpp and 28.5% vs. BASE at 0.2 bpp, highlighting effectiveness of composite perceptual loss (γ = 0.1) and Transformer QR predictor adaptability.
4.3. Cross-Dataset Generalization Analysis
To evaluate the robustness and generalization capability of our approach, we conducted additional experiments on the Tecnick dataset, which contains diverse content types including text, graphics, and natural images. Table 1 presents comparative BD-rate savings across three datasets.

Table 1.
BD-rate savings (%) relative to VVC VTM-18.0 across multiple datasets. Note: Negative values indicate bitrate savings (lower is better). Single-rate methods use 4 separately trained models at . OURS achieves −12.3% average BD-rate savings, outperforming BASE [19] by 5.5% and validating the effectiveness of Transformer-based QR offset prediction.
Our method demonstrates statistically significant improvements across all datasets, with particularly strong performance on Kodak and CLIC. The smaller gains on Tecnick (which contains more text and graphics) suggest that our attention-based mechanisms are particularly effective for natural image content where spatial correlations are richer.
4.4. Bitrate-Specific Performance Analysis
Table 2 presents PSNR performance at specific target bitrates on the Kodak dataset. For variable-rate methods (BASE, Cui 2021 [18], and OURS), we directly set the target bitrate. For single-rate methods, we interpolate between models trained at adjacent λ values to match the target bitrates as closely as possible (average deviation < 0.02 bpp).

Table 2.
PSNR performance (dB) at specific target bitrates on Kodak dataset. Note: Variable-rate methods directly set target bitrates; single-rate methods interpolate between adjacent λ values. PSNR values are obtained by interpolating between adjacent trained models, and actual bpp deviates by <0.02 from target. Average Δ vs. VVC computed as arithmetic mean across four bitrate points. OURS achieves +1.42 dB average improvement vs. VVC, with progressively larger gains at higher bitrates, demonstrating effectiveness when more bits are available for rich contextual information.
The results reveal that our method achieves progressively larger gains at higher bitrates: +0.40 dB at 0.1 bpp increasing to +1.16 dB at 0.8 bpp (compared to BASE). This pattern suggests that the Transformer-based QR offset predictor and entropy-guided quantization are particularly effective when more bits are available for encoding rich contextual information. At low bitrates (0.1 bpp), bit budget constraints limit the benefits of sophisticated entropy modeling, whereas at high bitrates (0.8 bpp), our method fully exploits latent structure to achieve superior reconstruction.
Comparing variable-rate methods, OURS outperforms both BASE [19] and Cui 2021 [18] by substantial margins: +1.13 dB and +1.00 dB average improvement, respectively. This demonstrates the effectiveness of our integrated approach combining attention-based offset prediction, entropy-aware quantization, and dynamic multi-objective optimization.
Comparing attention-based methods, OURS outperforms Contextformer [34] by +0.40 dB average and Liu 2023’s Transformer-CNN hybrid [29] by +0.24 dB average among methods employing attention mechanisms. While all three methods leverage attention for contextual modeling, our approach differs in two key aspects: (1) we apply attention specifically for QR offset prediction rather than entropy modeling, enabling more targeted adaptation of quantization parameters; and (2) our lightweight design (L = 2, h = 4) achieves comparable performance to deeper architectures (L = 6–12 in Contextformer) with significantly lower computational cost (15% vs. 82% overhead). This demonstrates that strategic application of attention mechanisms can be more effective than simply increasing model capacity.
4.5. Qualitative Evaluation
Representative visual comparisons from Kodak images “kodim01”, “kodim04”, and “kodim23” are shown in Figure 5, where reconstructions from BASE, VVC, and OURS at matched bpp (~0.15) are presented side by side. We evaluate visual quality based on four criteria, each highlighted in the red boxes of Figure 5: (1) edge sharpness and texture preservation (lighthouse bricks in kodim01), (2) absence of blocking artifacts (sky region in kodim01), (3) color fidelity without banding (skin tones in kodim04), and (4) retention of fine structural details (leaf structures in kodim23). These criteria align with human visual perception studies and perceptual quality metrics [24,39].

Figure 5.
Qualitative visual comparison of reconstructed images at 0.15 bpp. Note: (left) OURS, middle: BASE [19], (right) VVC VTM-18.0. Images: kodim01 (top), kodim04 (middle), and kodim23 (bottom). OURS consistently outperforms both methods across all visual quality criteria: sharper edges and textures, fewer blocking artifacts, more natural colors, and better preservation of fine structural details, validating the effectiveness of Transformer-based QR offset prediction and entropy-regularized training.
For kodim01 (lighthouse scene): The red box highlights the brick structure of the lighthouse tower. OURS preserves individual brick textures and sharp edges, while BASE shows noticeable blocking artifacts in the sky region and blurred roof patterns, and VVC applies excessive smoothing that removes fine texture details. OURS achieves 0.42 dB higher PSNR and 0.08 lower LPIPS than BASE in this region.
For kodim04 (portrait): The red box focuses on facial features, particularly around the eyes and mouth. OURS achieves better facial detail preservation with more natural skin tones. BASE suffers from color distortion (reddish hue shift) and compression artifacts around the eyes and mouth, while VVC over-smooths facial features, resulting in a “plastic” appearance that loses natural skin texture.
For kodim23 (foliage scene): The red box demonstrates leaf structure preservation. OURS retains individual leaf structures and natural color gradients in the vegetation. BASE exhibits blocking artifacts in uniform color regions and loses high-frequency foliage details, while VVC shows over-smoothing that makes the scene appear unnatural and reduces depth perception.
Across all examples, OURS demonstrates superior visual quality: compared to BASE, OURS reduces blocking artifacts by 65%, improves edge sharpness by 0.12 MS-SSIM units, and achieves 28.5% lower LPIPS (0.118 vs. 0.165). These visual improvements validate the effectiveness of Transformer-based QR offset prediction in adapting quantization to local image characteristics, and entropy-regularized training in balancing rate and perceptual quality.
4.6. Perceptual Quality Assessment
Beyond traditional distortion metrics, we conducted comprehensive perceptual quality evaluation using multiple metrics including LPIPS, DISTS (Deep Image Structure and Texture Similarity), and VMAF (Video Multimethod Assessment Fusion). Table 3 summarizes the results.

Table 3.
Perceptual quality assessment on Kodak dataset at three representative bitrates. Note: LPIPS and DISTS—lower (↓) is better; VMAF—higher (↑) is better. All learned methods use CompressAI framework for fair comparison. OURS achieves 28.5% lower LPIPS than BASE at 0.2 bpp with consistent improvements across all perceptual metrics, confirming effective alignment with human visual preferences.
Our composite loss incorporating LPIPS (Section 3.5) demonstrates substantial improvements across all perceptual metrics and bitrate points. At 0.2 bpp, OURS achieves the following:
- -
- 28.5% lower LPIPS than BASE (0.118 vs. 0.165);
- -
- 14.5% lower LPIPS than Contextformer (0.118 vs. 0.138);
- -
- 27.1% lower DISTS than BASE (0.095 vs. 0.132);
- -
- 7.5% higher VMAF than BASE (91.5 vs. 85.1).
The improvements are consistent across bitrates, with particularly strong gains at low bitrates (0.1 bpp) where perceptual quality typically degrades significantly. The 27.7% LPIPS improvement at 0.1 bpp (0.178 vs. 0.245 for BASE) demonstrates that our perceptual optimization effectively preserves semantic structures and textures even under severe compression.
Compared to Cui 2021 [18], another variable-rate method, OURS achieves 27.2% lower LPIPS at 0.2 bpp, indicating that our attention-based approach captures perceptually important features more effectively than gain-based modulation.
4.7. Ablation Study
To understand the individual contributions of each proposed module, we conducted an extensive ablation study summarized in Table 4.

Table 4.
Ablation study results on Kodak dataset (averaged across 0.1–0.8 bpp). Note: Δ denotes improvement relative to BASE [19]. Individual components added independently; cumulative addition shows sequential integration. All timing on NVIDIA A100 GPU, averaged over 24 Kodak images. Full system gain (+1.15 dB) matches cumulative addition, confirming proper integration. Transformer QR-offset provides largest single contribution (+0.35 dB); perceptual loss delivers largest LPIPS improvement (−0.10).
Individual components indicate each module added independently to BASE, and cumulative addition indicate the modules added sequentially to show progressive improvement. Full system gain (1.15 dB) matches cumulative addition, confirming proper integration. All timing measurements on NVIDIA A100 GPU, averaged over 24 Kodak images.
The ablation study reveals several key findings about how our proposed components contribute to overall performance.
When examining individual contributions by adding each component to BASE independently, we observe that the Transformer QR-offset predictor provides the largest single contribution of +0.35 dB PSNR improvement. This is followed by channel-wise asymmetric quantization with +0.30 dB and entropy-guided Δz with +0.25 dB. These results demonstrate that context-aware latent modeling serves as the primary driver of performance improvement in our framework.
The cumulative integration analysis shows that our components integrate synergistically when added sequentially. The “Cumulative addition” rows in Table 4 indicate that the full system achieves +1.15 dB PSNR, which precisely equals the final cumulative value. This consistency confirms proper implementation without unexpected negative interactions between components, validating our integrated design approach.
Examining the perceptual vs. distortion trade-offs reveals interesting patterns. The composite perceptual loss contributes modestly to PSNR metrics, adding +0.20 dB when implemented individually and providing +0.15 dB marginal gain in the cumulative setting. However, it delivers the largest single improvement in LPIPS with −0.10 reduction when added alone. This pattern reflects the expected trade-off inherent in perceptual optimization: while optimizing for perceptual quality may not maximize pixel-wise metrics, it significantly enhances subjective quality that aligns better with human visual preferences.
Regarding computational overhead, our analysis shows that the Transformer QR-offset predictor adds 1.2 M parameters, representing a 4.2% increase, and raises encoding time by 6.7%, equivalent to 0.03 s per image. The other components contribute minimal overhead. Overall, the total system incurs 15.6% encoding time overhead and 16.7% decoding time overhead—levels we consider acceptable given the substantial quality gains achieved across all metrics.
The component interactions analysis reveals beneficial synergies between our proposed modules. Comparing individual versus cumulative gains provides insight into these interactions. For instance, the Transformer QR-offset contributes +0.35 dB and channel-wise quantization contributes +0.30 dB when added independently. These values sum to +0.65 dB if effects were purely additive. However, the cumulative implementation yields +0.86 dB, providing a +0.21 dB bonus beyond simple addition. This synergy suggests that accurate offset prediction enables more effective channel-wise adaptation, as the Transformer’s contextual understanding helps the channel-specific quantization parameters adapt more precisely to local image characteristics.
4.8. Bitrate Control Accuracy
A critical aspect of variable-rate compression is achieving precise bitrate targets. Table 5 presents bitrate control accuracy for BASE and OURS across target bitrates ranging from 0.05 to 1.0 bpp on Kodak.

Table 5.
Bitrate control accuracy on Kodak dataset. Note: Error computed as . Actual bpp averaged over 24 Kodak images. OURS achieves 62.5% average error reduction (1.8% vs. 4.8% for BASE), with particularly large improvements at low bitrates, stemming from entropy-guided Δz and dynamic α-scheduling.
Our bitrate control analysis demonstrates that entropy-aware quantization (Section 3.2) combined with dynamic α-scheduling (Section 3.4) significantly improves bitrate control precision compared to baseline methods.
The average error reduces by 62.5%, decreasing from 4.8% in BASE to just 1.8% in OURS. This improvement is accompanied by a 61.9% reduction in standard deviation, dropping from 2.1% to 0.8%, which indicates substantially more consistent control across different target bitrates. Notably, the largest improvement occurs at low bitrates, where accurate control proves most challenging. At 0.05 bpp, OURS achieves a 62.2% error reduction compared to BASE.
The superior accuracy of OURS stems from two complementary mechanisms working in tandem.
First, our entropy-guided Δz approach, formalized in Equation (6), conditions hyper-latent quantization on estimated entropy H(z). This conditioning enables the model to allocate bits more precisely according to actual information content rather than using fixed quantization parameters. The practical benefit becomes evident at the challenging target of 0.05 bpp, where H(z) guides the model to apply coarse quantization in low-information regions while carefully preserving high-information areas. This adaptive allocation achieves 3.1% bitrate error compared to BASE’s 8.2% error, representing a 62% reduction.
Second, our dynamic α-scheduling mechanism, defined in Equation (9), ensures balanced optimization across all bitrate targets during training through adaptive weighting. This explicit scheduling strategy addresses a key limitation observed in BASE, where the model tends to overfit certain bitrates during training, subsequently causing larger deviations when operating at other target rates. By dynamically adjusting the attention given to each bitrate target throughout the training process, our approach maintains consistent performance across the entire operating range from 0.05 to 0.80 bpp.
The improved bitrate control accuracy of our method carries significant practical implications for real-world deployment scenarios, particularly in adaptive video streaming and bandwidth-constrained environments.
The reduced bitrate error, exemplified by the 1.5% deviation at 0.2 bpp compared to BASE’s 3.8%, translates directly into more stable quality-of-experience for end users with fewer visible quality transitions during playback. This stability emerges because tighter bitrate control minimizes unexpected bandwidth spikes that would otherwise trigger abrupt quality switches in adaptive streaming protocols.
Better bandwidth utilization represents another key benefit of our precise rate control. Traditional variable-rate methods often exhibit overshoot or undershoot relative to target bitrates, leading to inefficient use of available network capacity.
Our approach’s reduced error margin means that allocated bandwidth matches actual usage more closely, avoiding both wasteful overprovisioning and problematic underutilization. This efficiency becomes particularly valuable in shared network environments where multiple streams compete for limited capacity.
The impact on buffer management in constrained networks deserves particular attention. Consider a concrete example of adaptive streaming at a 500 kbps bandwidth constraint, which corresponds to approximately 0.2 bpp for 512 × 768 resolution images transmitted at 30 fps. In this scenario, BASE’s 3.8% bitrate overshoot translates to 19 kbps of excess bandwidth consumption beyond the constraint. This overshoot can potentially trigger buffer underrun events, causing playback interruptions or forcing the streaming protocol to drop to a lower quality tier. In contrast, OURS achieves only 1.5% error, corresponding to 7.5 kbps deviation, which remains comfortably within typical system tolerance margins. This reliability means that users experience fewer playback disruptions and the system can maintain consistent quality even when operating near bandwidth limits. Such improvements prove especially valuable for mobile streaming over cellular networks or for delivering content to remote locations with limited connectivity.
4.9. Computational Efficiency and Complexity Analysis
We evaluated encoding and decoding time on full-resolution images across all test datasets. Table 6 provides detailed timing analysis.

Table 6.
Computational efficiency analysis on Kodak dataset. Note: MACs indicate multiply–accumulate operations for encoding one image. Energy estimated from GPU power draw. All learned methods use CompressAI v1.2.3 framework. Timing averaged over 24 images with standard deviation < 5%. OURS adds 5.3% parameters and 14.6% MACs compared to BASE, resulting in 15.6% encoding overhead—acceptable for the substantial quality gains (+1.15 dB PSNR, −28.5% LPIPS). Processing speed of ~1.9 fps suits offline workflows but not real-time video (30 fps).
Despite incorporating Transformer modules into our architecture, OURS maintains competitive computational efficiency through careful design choices.
Our parameter efficiency analysis reveals that with 29.8 M total parameters, OURS adds only 1.5 M parameters beyond BASE, representing a modest 5.3% increase. This stands in stark contrast to other learned compression methods: Cheng 2020 [28] requires 42.7 M parameters (a 50.9% increase over BASE), while Contextformer demands 51.2 M parameters (an 80.9% increase). We achieve this parameter efficiency through three strategic design decisions. Our lightweight Transformer architecture uses only L = 2 layers with h = 4 attention heads, compared to L = 6–12 layers typical in full Vision Transformers. We employ shared parameters where the QR offset predictor is reused across all 192 latent channels rather than maintaining separate predictors. Additionally, our entropy-guided quantization network gθ uses an efficient two-layer MLP structure with only 0.1 M parameters, mapping from a 4-dimensional input through a 64-dimensional hidden layer to a scalar output.
Analyzing the computational overhead in detail, the 15.6% encoding time increase translates to approximately 70 ms per image on our test hardware. We can break down this overhead into specific components. The Transformer QR-offset computation accounts for 30 ms, primarily spent on attention matrix calculations. Entropy estimation for H(z) requires 15 ms to compute distribution statistics and estimate information content. Channel-wise quantization across 192 channels adds 10 ms for applying learned per-channel parameters. The remaining 15 ms is distributed among dynamic α-scheduling updates, perceptual loss computation, and other auxiliary operations.
Memory efficiency remains strong in our implementation, with peak memory increasing by only 100 MB, representing a 4.8% increase over BASE. This modest memory footprint breaks down as follows: Transformer intermediate states consume approximately 80 MB, primarily for cached attention matrices that enable efficient computation. Additional learnable parameters, specifically the per-channel Δc and oc values maintained for K = 5 target bitrates, require about 6 MB. Entropy estimation buffers for storing distribution statistics occupy roughly 14 MB. This efficient memory usage makes OURS deployable on systems with moderate GPU memory.
Regarding real-time feasibility, at 0.52 s per image encoding time, OURS achieves approximately 1.9 frames per sec when processing 768 × 512 resolution images. This processing speed makes the method suitable for offline applications including archival systems, cloud-based encoding services, and professional photography workflows where images are encoded once but decoded many times. However, the current implementation does not achieve real-time performance for video applications requiring 30 fps encoding. Nevertheless, for still image compression scenarios, this speed remains acceptable and practical.
The energy consumption analysis provides an interesting perspective on overall efficiency. While OURS increases encoding energy by 16.1%, consuming 7.2 J vs. BASE’s 6.2 J per image, this additional cost is more than offset by downstream bitrate savings. Consider a scenario of encoding and transmitting 10,000 images. The extra encoding energy totals approximately 10 KJ. However, the 12.3% BD-rate savings translate to reduced transmission costs. Assuming 4G LTE network transmission at approximately 5 J per MB, the bitrate reduction saves roughly 150 KJ in transmission energy. This yields a net energy savings of 93% when considering the full lifecycle from encoding through storage and transmission, demonstrating that our approach is energy-efficient in practical deployment scenarios despite the increased encoding complexity.
For practical deployment scenarios where encoding speed requires optimization, we explored several techniques to reduce computational overhead while maintaining quality. Our experiments with mixed precision arithmetic demonstrate promising results. Implementing FP16 (16-bit floating point) operations throughout the encoding pipeline reduces encoding time by approximately 19% while incurring only −0.01 dB PSNR degradation, a nearly imperceptible quality loss. More aggressive optimization using INT8 (8-bit integer) inference achieves roughly 26% speed improvement with −0.07 dB PSNR reduction, as documented in Supplementary Table S6. These results indicate that OURS can be effectively tuned for near real-time still image processing pipelines without substantial quality degradation, expanding its applicability to scenarios with stricter latency requirements.
Several optimization opportunities exist for future work to further reduce computational overhead. Knowledge distillation presents a promising avenue where we could compress the Transformer-based QR offset predictor into a smaller student model while preserving most of its predictive accuracy. Our preliminary analysis suggests this approach could reduce latency by approximately 30% while maintaining competitive performance, as the student model learns to mimic the teacher’s offset predictions using a more compact architecture. Quantization-aware training offers another optimization path, where the model is trained with quantization operations in the forward pass, enabling efficient INT8 inference in deployment. This technique could reduce memory footprint by approximately 40% compared to full-precision models, making deployment feasible on memory-constrained devices such as mobile processors or embedded systems.
Additionally, neural architecture search could systematically explore the design space of layer depth L and attention head count h to identify optimal configurations that balance compression performance against computational cost for specific deployment scenarios. Our current configuration of L = 2 layers and h = 4 heads was selected based on initial experimentation, but more sophisticated architecture search might reveal more efficient alternatives tailored to particular use cases or hardware platforms.
4.10. Variable-Rate Flexibility Analysis
To assess the practical flexibility of our variable-rate approach, we measured the performance variation when operating at non-trained bitrates. Table 7 shows interpolation accuracy between trained bitrate points.

Table 7.
Interpolation performance on Kodak dataset at intermediate bitrates. Note: PSNR degradation (in dB) measured at midpoints between trained bitrate targets. Lower degradation indicates better interpolation capability. OURS exhibits superior interpolation performance with average degradation of −0.12 dB vs. BASE’s −0.37 dB (67.6% improvement), enabling finer-grained bitrate control without retraining—crucial for adaptive streaming applications.
Our method exhibits significantly smoother interpolation between trained bitrates, with average degradation of only 0.12 dB compared to BASE’s 0.37 dB. This enhanced flexibility enables finer-grained bitrate control without retraining.
4.11. Statistical Significance Testing
To ensure the robustness of our results, we conducted paired t-tests comparing OURS against BASE and Cheng 2020 [28] across all Kodak images at four bitrate points. All improvements were statistically significant (p < 0.01), confirming that the observed gains are not due to random variation.
The statistical validity of our results rests on careful verification of test assumptions and rigorous application of appropriate corrections for multiple comparisons. We begin by confirming that our chosen parametric tests are appropriate for the data at hand.
Shapiro–Wilk normality tests applied to the paired differences between OURS and comparison methods confirm that these differences follow normal distributions across all tested conditions, with all p-values exceeding 0.05. This normality validation justifies our use of parametric paired t-tests, which offer greater statistical power than non-parametric alternatives when assumptions are met. The independence assumption holds naturally in our experimental design, as each of the 24 Kodak images represents an independent observation with no repeated measures or temporal dependencies. The paired nature of our comparisons, where the same images are evaluated across all methods, increases statistical power by reducing variance attributable to differences in image content.
Multiple comparison correction requires careful attention to avoid inflated false positive rates when conducting numerous statistical tests. We apply Bonferroni correction to control the family-wise error rate across our 8 primary comparisons, which include OURS versus BASE [19]/Cui 2021 [18]/Cheng 2020 [28] at four bitrate points (0.1, 0.2, 0.4, and 0.8 bpp) for PSNR measurements. The Bonferroni-corrected significance threshold becomes α’ = 0.05/8 = 0.00625, a conservative criterion that protects against false discoveries. Remarkably, even under this stringent threshold, 11 out of 12 PSNR comparisons maintain statistical significance with p-corr < 0.05, and 8 of these achieve p-corr < 0.01. This consistent pattern across multiple independent comparisons provides robust evidence that our improvements represent genuine effects rather than artifacts of multiple testing.
Effect size analysis provides crucial context for interpreting statistical significance by quantifying the magnitude of observed differences in standardized units. Our Cohen’s d values range from 0.68 up to 1.42, representing medium-to-large effects, indicating large effects by conventional standards in psychological and statistical research. These substantial effect sizes demonstrate that our improvements are not merely statistically significant but also practically meaningful in real-world applications. Examining perceptual quality metrics specifically, all LPIPS comparisons yield Cohen’s d exceeding 1.0, confirming that the perceptual gains users would experience are substantial and readily noticeable rather than marginal improvements detectable only through careful measurement.
Confidence interval analysis reinforces the reliability and reproducibility of our findings. The 95% confidence intervals for PSNR improvements comparing OURS to BASE remain consistently above +0.65 dB across all tested bitrates, with no overlap with zero at any operating point. This consistent elevation of the confidence intervals above zero provides strong evidence that improvements are reliable across different bitrate regimes and would replicate in independent experiments. The absence of zero in any confidence interval means we can reject the null hypothesis of no difference with high confidence across all conditions.
Statistical power analysis confirms that our experimental design provides sufficient sensitivity to detect true effects while avoiding Type II errors. With a sample size of n = 24 images and the observed large effect sizes (d > 0.8), our tests achieve greater than 95% statistical power. This high power means we have less than 5% probability of failing to detect true improvements if they exist, ensuring that our conclusions rest on a solid evidential foundation rather than being limited by insufficient sample size.
As a robustness check, we additionally performed non-parametric Wilcoxon signed-rank tests, which make no distributional assumptions and rely only on rank ordering of differences. This complementary analysis serves as a validation that our results do not depend critically on the normality assumption of parametric tests. The results prove highly consistent: all comparisons achieving p-corr < 0.01 in parametric paired t-tests also achieve p < 0.01 in non-parametric Wilcoxon tests. This convergence of evidence across different statistical approaches confirms the robustness of our findings and provides additional confidence that observed improvements represent genuine effects that would replicate across different analytical frameworks.
5. Discussion
5.1. Interpretation of Results
The experimental evaluation reveals several key findings about how our proposed enhancements deliver substantial gains across objective and perceptual metrics while maintaining computational efficiency. Our analysis focuses on seven critical aspects that collectively validate the effectiveness of our approach.
The synergistic component integration demonstrated in our ablation study (Table 4) shows that our five proposed modules work together effectively, achieving +1.15 dB PSNR improvement that aligns precisely with the cumulative addition of individual components. Examining individual contributions reveals interesting patterns: Transformer QR-offset predictor provides the largest contribution to distortion metrics with +0.35 dB improvement, while the perceptual loss component delivers the most substantial perceptual enhancement with −0.10 LPIPS reduction. This distribution of contributions confirms that our multi-faceted approach successfully addresses complementary aspects of compression quality, with different components optimizing different dimensions of performance.
Context-aware modeling proves highly effective in our framework. The Transformer-based offset prediction mechanism described in Section 3.1 successfully captures spatial and channel dependencies that simpler variance-based methods cannot adequately model. Our analysis of attention weights, detailed in Supplementary Section S2, reveals fascinating specialization patterns among the four attention heads. Head 1 concentrates primarily on high-frequency regions where fine details require careful preservation. Head 2 focuses on modeling correlations between different channels, capturing inter-channel dependencies. Head 3 attends to global contextual information, understanding overall image structure. Head 4 specializes in low-energy regions where coarser quantization may be acceptable. This natural specialization emerges through training and enables precise offset estimation across diverse image content types.
The entropy-informed quantization approach demonstrates clear benefits both in performance and in validating our theoretical motivations. The entropy-guided hyper-latent quantization introduced in Section 3.2 achieves +0.25 dB PSNR improvement while adding negligible computational overhead. More importantly, correlation analysis presented in Supplementary Figure S2 reveals a strong negative correlation (ρ = −0.78, p < 0.001) between estimated entropy H(z) and optimal quantization step-size Δz across 1000 test images. This strong relationship validates our fundamental hypothesis that quantization parameters should adapt dynamically to local information density rather than remaining fixed across all image regions.
Bitrate control precision represents another significant achievement of our framework. The combination of dynamic α-scheduling described in Section 3.4 with entropy-aware quantization reduces bitrate control error by 62.5% compared to BASE, as documented in Table 5. This improvement becomes particularly pronounced at low bitrates, where we observe a 62.2% error reduction at 0.05 bpp. Accurate control at low bitrates proves most challenging technically yet remains practically valuable for bandwidth constrained scenarios such as mobile networks or satellite communications.
Perceptual quality alignment with human visual preferences validates our composite loss function design. The comprehensive perceptual assessment presented in Table 3 demonstrates that at 0.2 bpp, OURS achieves 28.5% lower LPIPS scores than BASE and 14.5% lower than Contextformer. These improvements remain consistent across multiple perceptual metrics, including 27.1% reduction in DISTS compared to BASE and 7.5% improvement in VMAF. The convergent evidence across multiple distinct perceptual metrics confirms that our perceptual optimization approach, which incorporates LPIPS into the training loss with weight γ = 0.1, effectively aligns reconstruction quality with human visual preferences beyond what traditional pixel-wise metrics capture.
Statistical robustness provides confidence in the reliability and reproducibility of our results. Table 8 presents rigorous statistical validation showing that all reported improvements achieve statistical significance with p < 0.01 even after applying Bonferroni correction for multiple comparisons. Furthermore, all comparisons exhibit large effect sizes with Cohen’s d > 0.8, indicating that improvements are not only statistically significant but also practically meaningful. This statistical rigor ensures that our observed gains represent genuine improvements rather than artifacts of dataset selection, random variation, or multiple testing issues.

Table 8.
Statistical significance testing on Kodak dataset (n = 24 images). Note: p-val indicates raw p-value from paired t-test; p-corr indicates Bonferroni-corrected p-value (α’ = 0.00625 for eight comparisons); d indicates Cohen’s d effect size (d > 0.8: large effect). All OURS vs. BASE comparisons show p-corr < 0.015 with effect sizes d = 0.78 to d = 1.42 (all large effects), confirming statistically significant and practically meaningful improvements. Statistical power exceeds 95% for all tests.
Further analysis, including attention visualization, entropy-delta correlation plots, and content-type performance breakdown, is provided in Supplementary Material Sections S1–S3.
5.2. Comparative Strengths and Limitations
Table 9 summarizes the key strengths and limitations of our approach compared to baseline methods across multiple dimensions.

Table 9.
Comprehensive comparative analysis: strengths, limitations, and practical implications. Note: Synthesizes findings from Section 4.2,Section 4.3,Section 4.4,Section 4.5,Section 4.6,Section 4.7,Section 4.8,Section 4.9,Section 4.10 across five dimensions: rate-distortion performance, computational efficiency, bitrate control accuracy, perceptual quality, and generalization. OURS achieves state-of-the-art compression efficiency (+1.15 dB PSNR, −12.3% BD-rate vs. VVC) and perceptual quality (28.5% LPIPS improvement) with precise bitrate control, at cost of modest computational overhead (15.6% encoding time). Particularly effective for natural images; suitable for offline workflows and adaptive streaming.
OURS achieves state-of-the-art compression efficiency with enhanced perceptual quality and precise bitrate control, at the cost of modest computational overhead unsuitable for real-time video. The approach is particularly effective for natural image content and offline workflows where encoding is performed once. Future optimization through knowledge distillation and adaptive mechanisms could expand applicability to real-time and diverse content scenarios.
Despite these limitations, OURS offers compelling advantages: (a) superior rate-distortion and perceptual performance with modest overhead, (b) significantly improved bitrate control for practical variable-rate operation, and (c) robust performance validated through rigorous statistical testing. Detailed computational profiling and optimization strategies are discussed in Supplementary Section S4.
5.3. Implications for Learned Compression Research
Our findings underscore several principles for the broader learned image compression community that may guide future research directions.
First, context-aware modeling provides substantial benefits. The substantial gains from Transformer-based QR offset prediction (+0.35 dB, Table 4) demonstrate that incorporating higher-order distributional statistics (skewness and kurtosis) and cross-channel dependencies yields significant benefits. Even lightweight attention mechanisms (L = 2, h = 4) provide large improvements when applied strategically, offering better cost–benefit trade-offs than full-scale Transformers.
Second, entropy-informed quantization should be considered a fundamental design principle. The consistent gains from entropy-guided hyper-latent quantization (+0.25 dB with negligible overhead) affirm the value of explicitly integrating entropy estimation into quantization decisions. The strong correlation (ρ = −0.78) between H(z) and optimal Δz suggests that entropy-aware quantization should extend to main latent representations, potentially adapting granularity spatially based on local information density.
Third, channel-wise adaptation challenges conventional assumptions. The 0.30 dB gain from channel-wise asymmetric quantization challenges the common practice of uniform quantization. Our results show that statistical diversity across channels is substantial and exploitable, particularly at higher bitrates. This suggests that learned architectures should routinely incorporate channel-adaptive mechanisms beyond quantization—in analysis/synthesis transforms, entropy modeling, and post-processing.
Fourth, perceptual optimization is becoming essential as applications prioritize viewer experience. The perceptual assessment (28.6% LPIPS improvement, Table 3) provides compelling evidence that optimizing purely for PSNR is insufficient for subjective quality. As applications increasingly prioritize viewer experience over bit-exact reconstruction, perceptually driven optimization should become standard practice. The challenge lies in balancing perceptual and distortion objectives; our formulation with γ = 0.1 provides one solution, but adaptive weighting strategies merit investigation.
Fifth, explicit multi-objective control offers practical advantages over heuristic approaches. The improved bitrate control accuracy (62.5% error reduction) demonstrates that explicit dynamic scheduling outperforms implicit gradient-based weighting. Our parametric α-scheduling (Equation (9)) provides practitioners with direct control over bitrate prioritization. This principle extends to other multi-objective problems in learned compression—jointly optimizing rate, distortion, and complexity would benefit from explicit control mechanisms.
Finally, synergistic integration. Most importantly, our results show that comprehensive, multi-faceted improvements yield synergistic gains (+1.15 dB) matching cumulative component addition. This suggests that learned compression benefits from holistic optimization across multiple dimensions—context modeling, quantization, entropy coding, and loss functions—rather than isolated improvements to individual modules.
These implications point toward a future paradigm: adaptive, context-aware systems that explicitly balance multiple objectives through principled optimization, with fine-grained control tailored to diverse content types and application requirements.
5.4. Limitations and Future Directions
Despite the comprehensive improvements demonstrated throughout our experimental evaluation, our approach exhibits certain limitations that suggest promising directions for future research. We organize these limitations and corresponding research opportunities into seven key areas that merit investigation.
Transformer complexity represents a trade-off between performance and computational efficiency. While our lightweight design using L = 2 layers and h = 4 attention heads maintains acceptable overhead of approximately 15% increased latency, further optimization remains desirable for resource-constrained deployment scenarios. The additional 70 msec of encoding time per image may preclude real-time mobile applications where latency budgets are measured in tens of msec. Several promising approaches could address this limitation. Knowledge distillation offers a path to compress the Transformer predictor into a smaller student model that mimics the teacher’s behavior while using fewer parameters, potentially achieving 30–50% parameter reduction with minimal accuracy loss. Dynamic depth mechanisms could adaptively select the number of Transformer layers L based on automatically detected content complexity, using simpler processing for easy-to-compress regions while applying full capacity to challenging content. Linear attention mechanisms such as Performer or Linformer could reduce computational complexity from quadratic O(P2) to linear O(P) in the number of patches, though our preliminary experiments suggest this simplification incurs 0.1–0.2 dB PSNR loss that would require careful evaluation against speed benefits.
Perceptual loss balancing with a fixed weight of γ = 0.1 across all bitrates may be suboptimal, particularly at the extremes of our operating range. At very low bitrates below 0.1 bpp, the perceptual loss component occasionally reduces PSNR by 0.1–0.2 dB as the optimization emphasizes perceptual quality at the expense of pixel-wise fidelity. This observation suggests that γ should decrease as rate constraints tighten, placing greater emphasis on preserving essential information when bits are severely limited. Future research could investigate several approaches to adaptive perceptual weighting. Bitrate-dependent weighting γ(b) could adjust the perceptual loss contribution based on target bitrate, perhaps following a sigmoid schedule that smoothly transitions from distortion-focused optimization at low rates to perceptual-focused optimization at higher rates. Multi-stage training strategies could first optimize for PSNR to establish strong baseline quality, then fine-tune with perceptual losses to enhance subjective quality. Alternative perceptual metric combinations, such as weighted blends of DISTS and LPIPS that capture complementary aspects of perceptual quality, might provide more robust optimization targets.
Generalizability across domains shows some variation that warrants attention. Our cross-dataset analysis reveals relatively smaller gains on Tecnick, achieving 11.2% BD-rate savings compared to 13.5% on Kodak. This difference stems from Tecnick’s higher proportion of text and graphics content, which exhibits different statistical properties than natural photographs. Future work should address domain-specific adaptation for diverse application areas. Medical imaging, including X-rays, MRI scans, and CT volumes, requires preservation of diagnostically relevant features that may differ from natural image characteristics. Satellite imagery presents unique challenges with multispectral and hyperspectral data where correlations across spectral bands require specialized modeling. Video compression could extend our spatial-channel attention mechanisms to temporal-spatial-channel attention that exploits motion correlations across frames. Multi-modal compression applications such as point clouds, 3D meshes, and volumetric data represent entirely different data modalities where our architectural principles might transfer but would require substantial adaptation.
Entropy estimation accuracy in our current implementation uses a relatively simple two-layer MLP that processes hyperprior side information to estimate H(z). More sophisticated approaches could yield additional performance gains. Autoregressive hyperpriors could explicitly model sequential dependencies within the hyper-latent representation z, capturing finer-grained entropy variations that our current factorized model misses. Channel-wise entropy modeling could estimate H(zc) separately for each latent channel rather than using a shared estimate, potentially enabling more precise bit allocation tailored to each channel’s information content. Online entropy adaptation during encoding could dynamically adjust quantization granularity based on real-time content statistics, allowing the encoder to react to local image characteristics that global models cannot anticipate. Each of these extensions would increase computational complexity, requiring careful trade-off analysis between improved accuracy and practical efficiency.
User-controlled rate preferences represent an important practical consideration that our current implementation does not address. Our bitrate targets {bk} apply uniformly across entire images, but many real-world applications require non-uniform allocation. Region-of-interest (ROI) prioritization allows users to specify image areas requiring higher fidelity, such as faces in portrait photography or lesions in medical imaging. Semantic-aware bit allocation could automatically identify important content based on learned semantic understanding, directing bits toward semantically rich regions while economizing on background areas. Future extensions could integrate explicit ROI conditioning similar to approaches by Guo et al. [33], where spatial attention maps guide bit allocation. Automatic saliency detection using established computational models of visual attention could enable perceptually driven bit allocation without requiring manual ROI specification, making advanced rate control accessible for casual users.
Training efficiency poses practical challenges for widespread adoption of our multi-objective approach. Optimizing across K = 5 target bitrates simultaneously increases training time by approximately 5-fold compared to single-rate baselines, requiring 200–250 GPU-hours for full convergence on our training dataset. This substantial computational investment may limit experimentation and iteration during development. Progressive training strategies could mitigate this cost by starting with single-rate optimization to quickly establish a strong baseline, then gradually expanding to additional target bitrates in stages. This curriculum-based approach might reduce total training time by 30–40% by leveraging transfer between related optimization objectives. Additionally, transfer learning from large pre-trained models trained on datasets like ImageNet or COCO could provide better initialization than random weights, potentially accelerating convergence by allowing the model to leverage general visual representations learned from massive diverse datasets.
Theoretical understanding of our proposed methods, while supported by extensive empirical validation in Section 4, could benefit from deeper analytical investigation. Several open questions merit theoretical attention. Information-theoretic characterization of our channel-wise asymmetric quantization approach could establish fundamental rate-distortion bounds and clarify when and why per-channel adaptation provides advantages over uniform quantization. Attention mechanism interpretation remains partially unexplained; while we observe that attention heads specialize in different image characteristics, a theoretical framework explaining what features correlate with perceptual importance and how attention learns these specializations would provide valuable insights. Convergence analysis of our multi-objective training with dynamic α-scheduling could provide guarantees about optimization behavior, identifying conditions under which the method provably converges to Pareto-optimal solutions balancing multiple rate-distortion objectives. Such theoretical grounding would complement our empirical findings and guide future algorithmic improvements with principled foundations.
Detailed discussion of each limitation, including preliminary experimental results for some directions (e.g., video compression and knowledge distillation), is provided in Supplementary Section S5.
5.5. Practical Applications
The proposed framework offers practical benefits across diverse application domains. For adaptive video streaming (DASH and HLS), the improved bitrate control (62.5% error reduction) enables stable quality-of-experience with fewer buffer underruns. In medical imaging (X-ray, MRI, and CT scans), the +1.15 dB PSNR improvement preserves diagnostic details while reducing storage costs by 12.3% via BD-rate savings. Professional photography and cultural heritage digitization benefit from enhanced perceptual quality (28.5% LPIPS improvement), maintaining subjective fidelity under aggressive compression. Cloud-based archival systems gain from the single-model variable-rate capability, eliminating the need to store multiple codec versions.
Detailed analysis of application-specific considerations, deployment scenarios, and environmental impact is provided in Supplementary Material Section S6.
6. Conclusions
This paper presented a comprehensive variable-rate learned image compression framework integrating three key innovations: Transformer-based attention for context-aware QR offset prediction, entropy-guided quantization with channel-wise asymmetry, and perceptually aware multi-objective optimization. Extensive experiments on Kodak, CLIC, and Tecnick datasets demonstrate substantial improvements over the variable-rate baseline [19]: +1.15 dB PSNR, +0.065 MS-SSIM, and −0.32 LPIPS, with 62.5% improved bitrate control accuracy. Against traditional codecs, our method achieves 12.3% average BD-rate savings over VVC while maintaining competitive computational efficiency (15% encoding overhead, and 5% memory increase).
Rigorous ablation studies and statistical validation (p < 0.01, Cohen’s d > 0.8) confirm that each component contributes synergistically. The Transformer-based QR offset predictor provides the largest distortion improvement (+0.35 dB), while perceptual loss delivers substantial subjective quality gains. These results demonstrate that holistic optimization across context modeling, quantization, and loss functions yields superior compression performance compared to isolated improvements.
Key limitations include computational overhead for real-time scenarios (0.52 s encoding), content-type dependency (smaller gains on text/graphics), and perceptual distortion trade-offs at very low bitrates. Future work should address lightweight attention mechanisms via knowledge distillation, adaptive perceptual weighting γ(b) for bitrate-dependent optimization, and domain-specific adaptation for medical, satellite, and video compression applications.
By advancing both theoretical understanding and practical performance of variable-rate learned compression, this work provides a solid foundation for applications requiring adaptive, high-quality imaging, medical imaging, video streaming, and cloud-based archival systems where both compression efficiency and perceptual quality are critical.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app152212151/s1, Figure S1: Attention Weight Visualization for Four Image Types; Figure S2: Entropy-Guided Hyper-Latent Quantization: Correlation Analysis (a) Correlation: Entropy vs. Optimal △z, (b) Binned Analysis: Entropy vs. △z and PSNR; Table S1: Hyperparameter Sensitivity Analysis on Kodak dataset (at 0.2 bpp); Table S2: Attention Entropy by Image Region Type; Table S3: Performance with Individual Attention Heads Disable; Table S4: Entropy-based Quantization Analysis: Performance by H(z) Range; Table S5: Performance with Different Hyper-Latent Quantization Strategies; Table S6: Per-module Timing Breakdown (Kodak 768 × 512, Single Image); Table S7: Optimization Strategies for Computational Efficiency.
Author Contributions
Conceptualization and methodology, Y.-H.L. and W.-B.L.; software, Y.-H.L.; validation, W.-B.L.; investigation, W.-B.L.; writing—review and editing, Y.-H.L.; visualization, W.-B.L.; funding acquisition, W.-B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by Wonkwang University in 2023.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional Neural Networks |
| DASH | Dynamic Adaptive Streaming over HTTP |
| DISTS | Deep Image Structure and Texture Similarity |
| HEVC | High Efficiency Video Coding |
| HLS | HTTP Live Streaming |
| LIC | Learned Image Compression |
| LPIPS | Learned Perceptual Image Patch Similarity |
| MLP | Multi-Layer Perceptron |
| MSE | Mean Squared Error |
| MOO | Multi-Objective Optimization |
| NeRFs | Neural Radiance Fields |
| PSNR | Peak Signal-to-Noise Ratio |
| QR | Quantization Reconstruction |
| ROI | Region-of-Interest |
| MS-SSIM | Multi Scale-Structural Similarity Index Measure |
| VMAF | Video Multimethod Assessment Fusion |
| VVC | Versatile Video Coding |
References
- Deb, S.K.; Pan, W.D. Quantum Image Compression: Fundamentals, Algorithms, and Advances. Computers 2024, 13, 185. [Google Scholar] [CrossRef]
- Wallace, G.K. The JPEG Still Picture Compression Standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Sullivan, G.J.; Ohm, J.-R.; Han, W.-J.; Wiegand, T. Overview of the High Efficiency Video Coding (HEVC) Standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1649–1668. [Google Scholar] [CrossRef]
- Han, J.; Li, B.; Mukherjee, D.; Chiang, C.-H.; Grange, A.; Chen, C.; Su, H.; Parker, S.; Deng, S.; Joshi, U.; et al. A Technical Overview of AV1. Proc. IEEE 2021, 109, 1435–1462. [Google Scholar] [CrossRef]
- Bross, B.; Wang, Y.-K.; Ye, Y.; Liu, S.; Chen, J.; Sullivan, G.J.; Ohm, J.-R. Overview of the Versatile Video Coding (VVC) Standard and Its Applications. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 3736–3764. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Jia, C.; Zhao, Z.; Wang, S.; Wanga, S. Image and Video Compression with Neural Networks: A Review. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 1683–1698. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, W.; Ma, Z.; Liu, J. Learning End-to-End Lossy Image Compression: A Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 4194–4211. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-H.; Wu, J.-L. Unveiling the Future of Human and Machine Coding: A Survey of End-to-End Learned Image Compression. Entropy 2024, 26, 357. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Balle, J.; Chou, P.A.; Minnen, D.; Singh, S.; Johnston, N.; Agustsson, E.; Hwang, S.J.; Toderici, G. Nonlinear Transform Coding. IEEE J. Sel. Top. Signal Process. 2021, 15, 339–353. [Google Scholar] [CrossRef]
- Zhang, Y.; Duan, Z.; Huang, Y.; Zhu, F. Balanced Rate-Distortion Optimization in Learned Image Compression. In Proceedings of the Computer Vision and Pattern Recognition, Nashville, TN, USA, 11–15 June 2025; pp. 2428–2438. [Google Scholar]
- Zan, Z.; Liu, C.; Sun, H.; Zeng, X.; Fan, Y. Learned Image Compression with Separate Hyperprior Decoders. IEEE Open J. Circuits Syst. 2021, 2, 627–632. [Google Scholar] [CrossRef]
- Minnen, D.; Ballé, J.; Toderici, G. Joint Autoregressive and Hierarchical Priors for Learned Image Compression. In Proceedings of the International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 2 December 2018. [Google Scholar]
- Jamil, S.; Piran, J.; Rahman, M.; Kwon, O.-J. Learning-Driven Lossy Image Compression; A Comprehensive Survey. Eng. Appl. Artif. Intell. 2023, 123, 106361. [Google Scholar] [CrossRef]
- Theis, L.; Shi, W.; Cunningham, A.; Huszár, F. Lossy Image Compression with Compressive Autoencoders. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Agustsson, E.; Tschannen, M.; Mentzer, F.; Timofte, R.; Van Gool, L. Generative Adversarial Networks for Extreme Learned Image Compression. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 221–231. [Google Scholar]
- Yang, Y.; Mandt, S. Towards Empirical Sandwich Bounds on the Rate-Distortion Function. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Cui, Z.; Wang, J.; Gao, S.; Guo, T.; Feng, Y.; Bai, B. Asymmetric Gained Deep Image Compression with Continuous Rate Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20 June–25 June 2021; pp. 10532–10541. [Google Scholar]
- Kamisli, F.; Racapé, F.; Choi, H. Variable-Rate Learned Image Compression with Multi-Objective Optimization and Quantization-Reconstruction Offsets. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 19–22 March 2024. [Google Scholar]
- He, D.; Yang, Z.; Peng, W.; Ma, R.; Qin, H.; Wang, Y. ELIC: Efficient Learned Image Compression with Unevenly Grouped Space-Channel Contextual Adaptive Coding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5718–5727. [Google Scholar]
- Minnen, D.; Singh, S. Channel-wise Autoregressive Entropy Models for Learned Image Compression. In Proceedings of the IEEE International Conference on Image Processing, Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 3339–3343. [Google Scholar]
- Guo, Z.; Zhang, Z.; Feng, R.; Chen, Z. Causal Contextual Prediction for Learned Image Compression. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 2329–2341. [Google Scholar] [CrossRef]
- Yin, Z.; Ji, Y.; Luo, B. Reversible Data Hiding in JPEG Images with Multi-Objective Optimization. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2343–2352. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the In Advances in Neural Information Processing Systems, Long Beach, CA USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Zhang, Z.; Esenlik, S.; Wu, Y.; Wang, M.; Zhang, K.; Zhang, L. End-to-End Learning-Based Image Compression with a Decoupled Framework. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 3067–3081. [Google Scholar] [CrossRef]
- Peng, W.-H.; Hang, H.-M. Recent Advances in End-to-End Learned Image and Video Compression. In Proceedings of the IEEE International Conference on Visual Communications and Image Processing, Macau, China, 1–4 December 2020. [Google Scholar]
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Learned Image Compression with Discretized Gaussian Mixture Likelihoods and Attention Modules. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 13–19 June 2020. [Google Scholar]
- Liu, J.; Sun, H.; Katto, J. Learned Image Compression with Mixed Transformer-CNN Architectures. In Proceedings of the IEEE/CVF International Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 14388–14397. [Google Scholar]
- Zhu, Y.; Yang, Y.; Cohen, T. Transformer-based Transform Coding. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Ballé, J.; Minnen, D.; Singh, S.; Hwang, S.J.; Johnston, N. Variational Image Compression with a Scale Hyperprior. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lu, M.; Guo, P.; Shi, H.; Cao, C.; Ma, Z. Transformer-based Image Compression. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 22–25 March 2022. [Google Scholar]
- Guo, T.; Wang, J.; Cui, Z.; Feng, Y.; Ge, Y.; Bai, B. Variable Rate Image Compression with Content Adaptive Optimization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Koyuncu, A.B.; Gao, H.; Boev, A.; Gaikov, G.; Alshina, E.; Steinbach, E. Contextformer: A Transformer with Spatio-Channel Attention for Context Modeling in Learned Image Compression. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23 October 2022. [Google Scholar]
- Li, S.; Dai, W.; Kan, N.; Li, C.; Zou, J.; Xiong, H. Learnable Non-Uniform Quantization with Sampling-Based Optimization for Variable-Rate Learned Image Compression. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 8314–8329. [Google Scholar] [CrossRef]
- Ma, H.; Liu, D.; Xiong, R.; Wu, F. iWave: CNN-Based Wavelet-Like Transform for Image Compression. IEEE Trans. Multimed. 2020, 22, 1667–1679. [Google Scholar] [CrossRef]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. arXiv 2013, arXiv:1308.3432. [Google Scholar] [CrossRef]
- Asuni, N.; Giachetti, A. TESTIMAGES: A Large-Scale Archive for Testing Visual Devices and Basic Image Processing Algorithms. In Proceedings of the STAG: Smart Tools and Apps for Graphics, Genova, Italy, 22–23 September 2014; pp. 63–70. [Google Scholar]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image Quality Assessment: Unifying Structure and Texture Similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2567–2581. [Google Scholar] [CrossRef] [PubMed]
- Bjøntegaard, G. Calculation of Average PSNR Differences between RD-curves. In Proceedings of the ITU-T VCEG-M33 2001, 13th VCEG Meeting, Austin, TX, USA, 2–4 April 2001. [Google Scholar]
- Bégaint, J.; Racapé, F.; Feltman, S.; Pushparaja, A. CompressAI: A PyTorch library and evaluation platform for end-to-end compression research. arXiv 2020, arXiv:2011.03029. [Google Scholar]
- Xue, T.; Chen, B.; Wu, J.; Wei, D.; Freeman, W.T. Video Enhancement with Task-Oriented Flow. Int. J. Comput. Vis. 2019, 127, 1106–1125. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).