Mechanisms and Mitigation of Injection-Induced Microseismicity: The Critical Role of Fracture Orientation in Shear Reactivation
Abstract
1. Introduction
2. Numerical Methods
2.1. Governing Equations for Hydraulic Stimulation
2.1.1. Hydromechanical Coupled Model
- (1)
- Fracture Fluid Flow
- (2)
- Fracture Deformation
2.1.2. Microseismic Analysis Model
2.1.3. Numerical Implementation of Microseismic Model
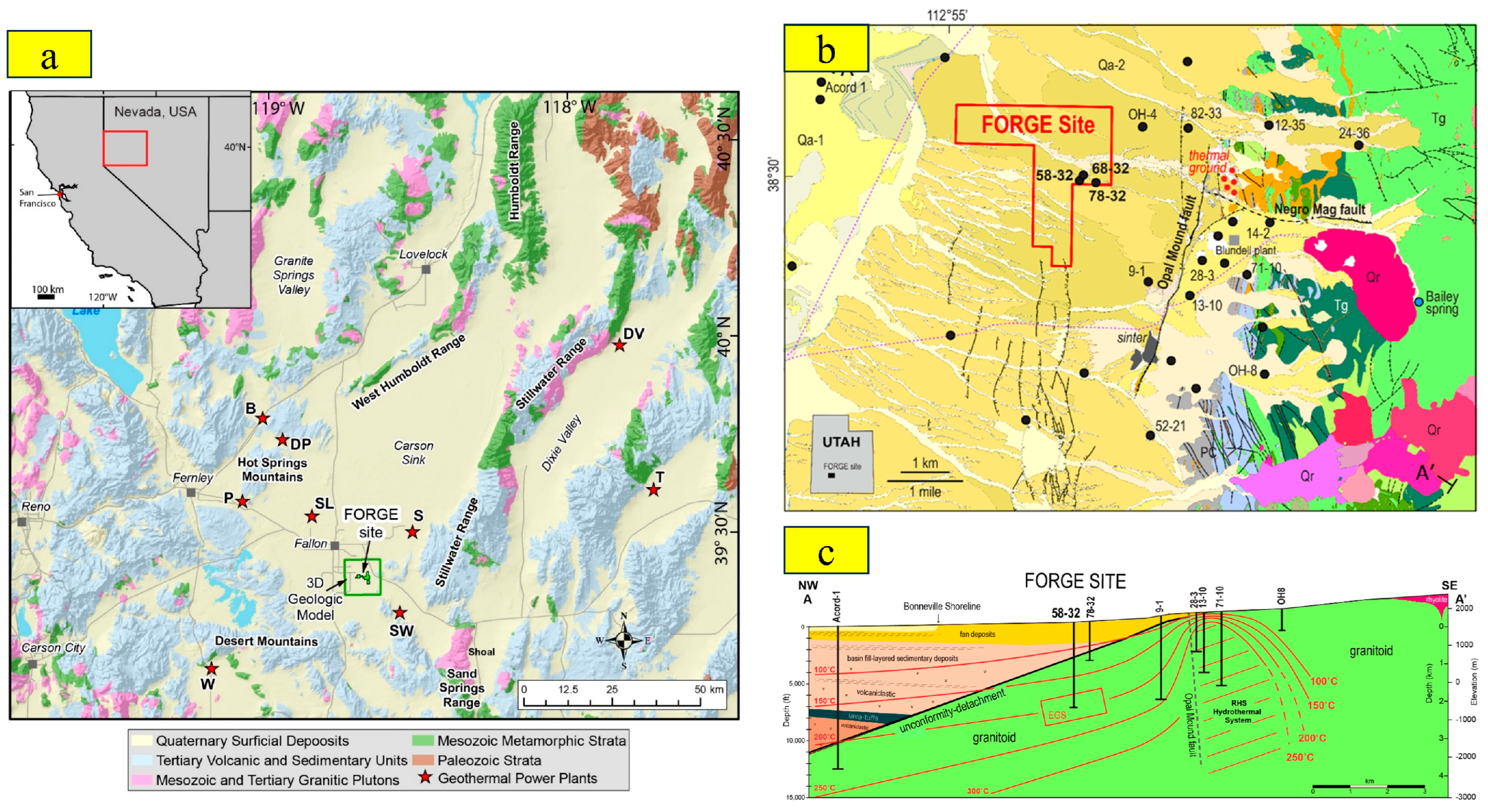
2.2. Site Natural Fractures Distribution and DFN Construction
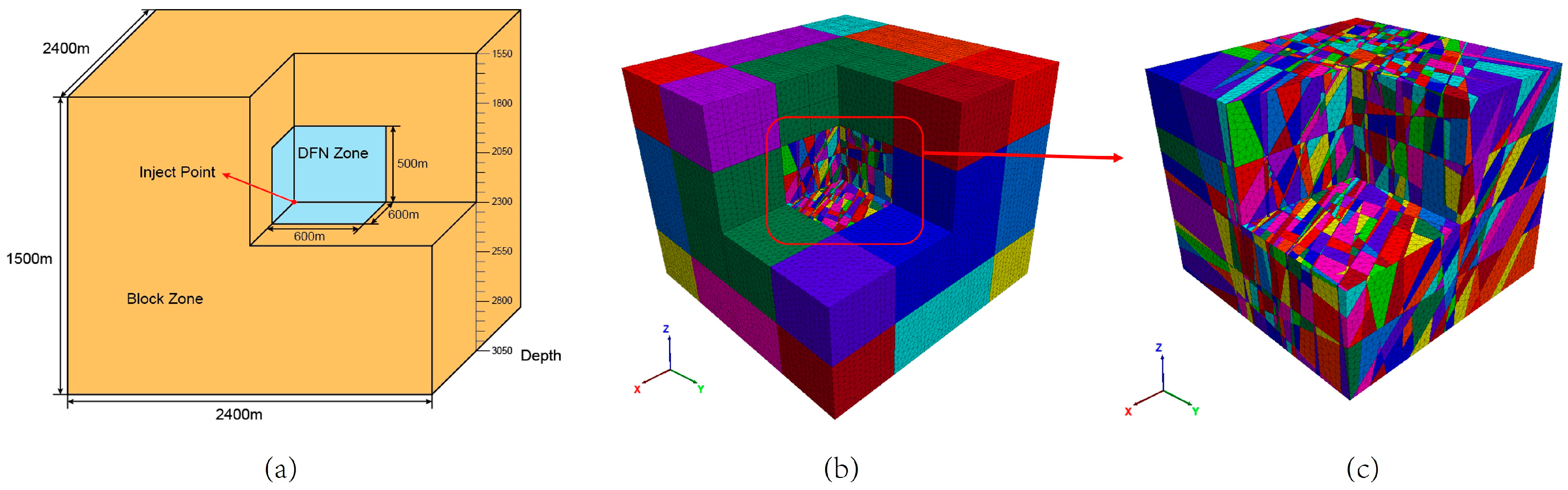
2.3. Reservoir Model Setup
2.4. Model Parameters
3. Simulation Results
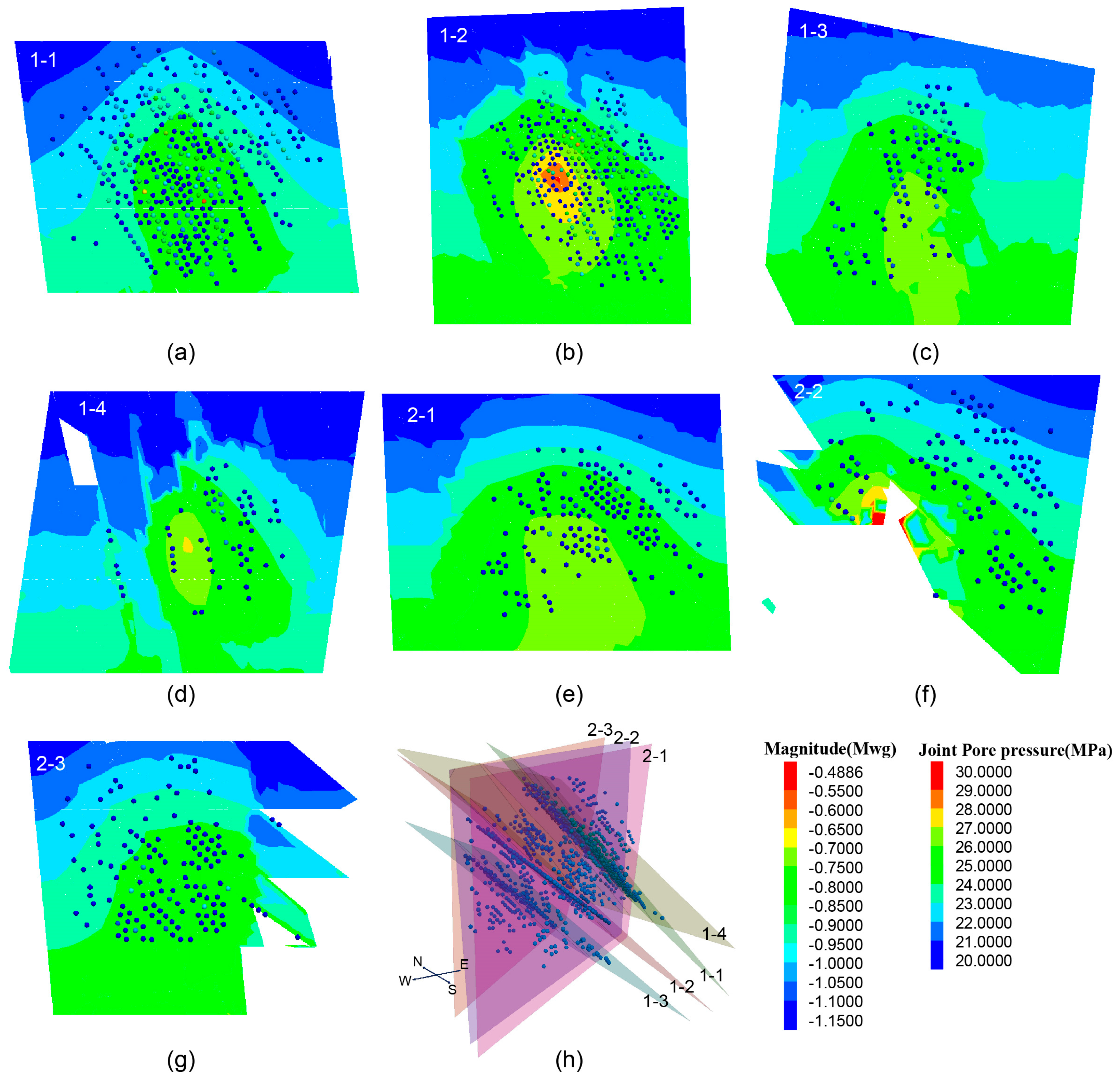
3.1. Spatial Distribution of Microseismic Events
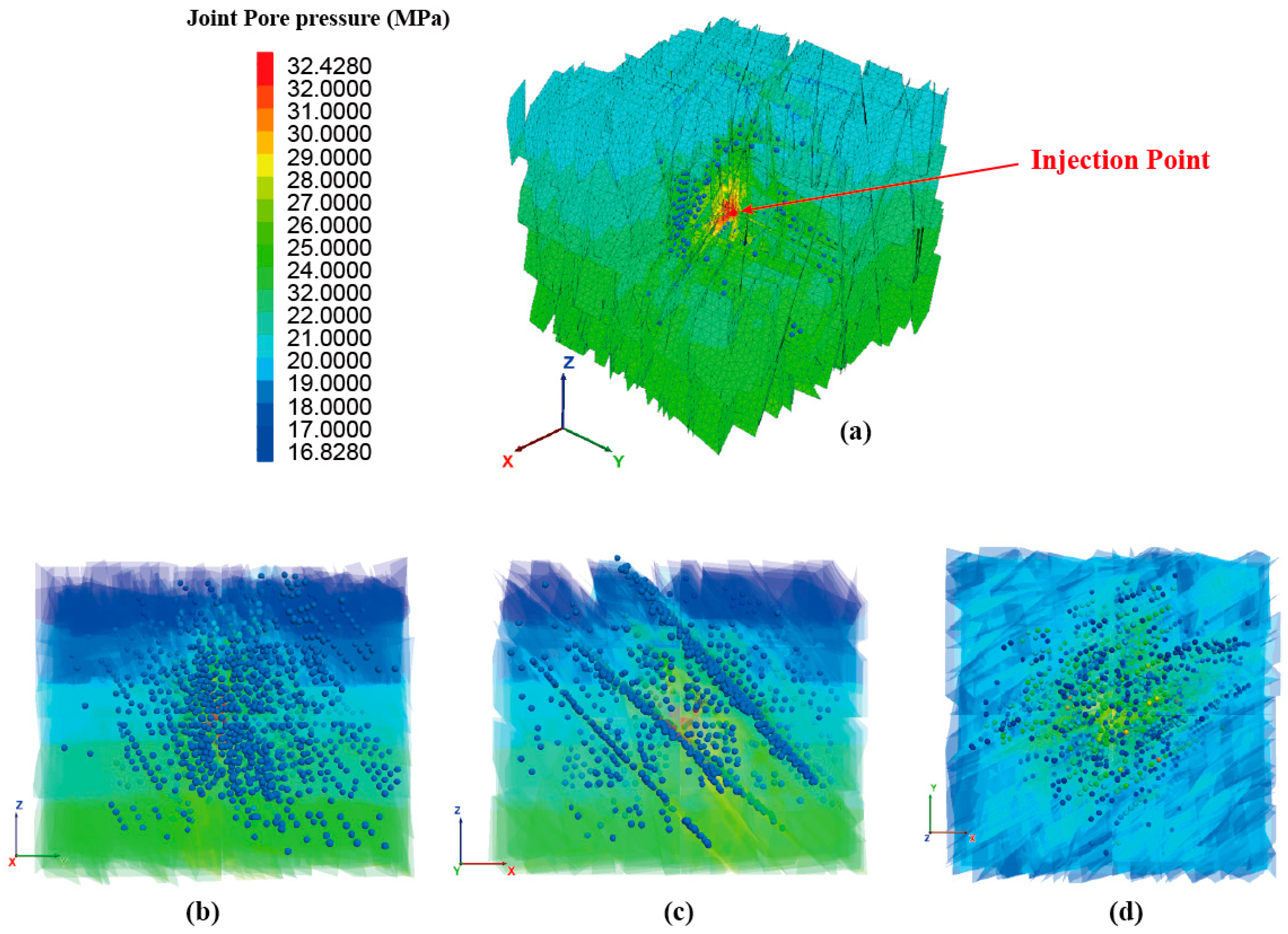
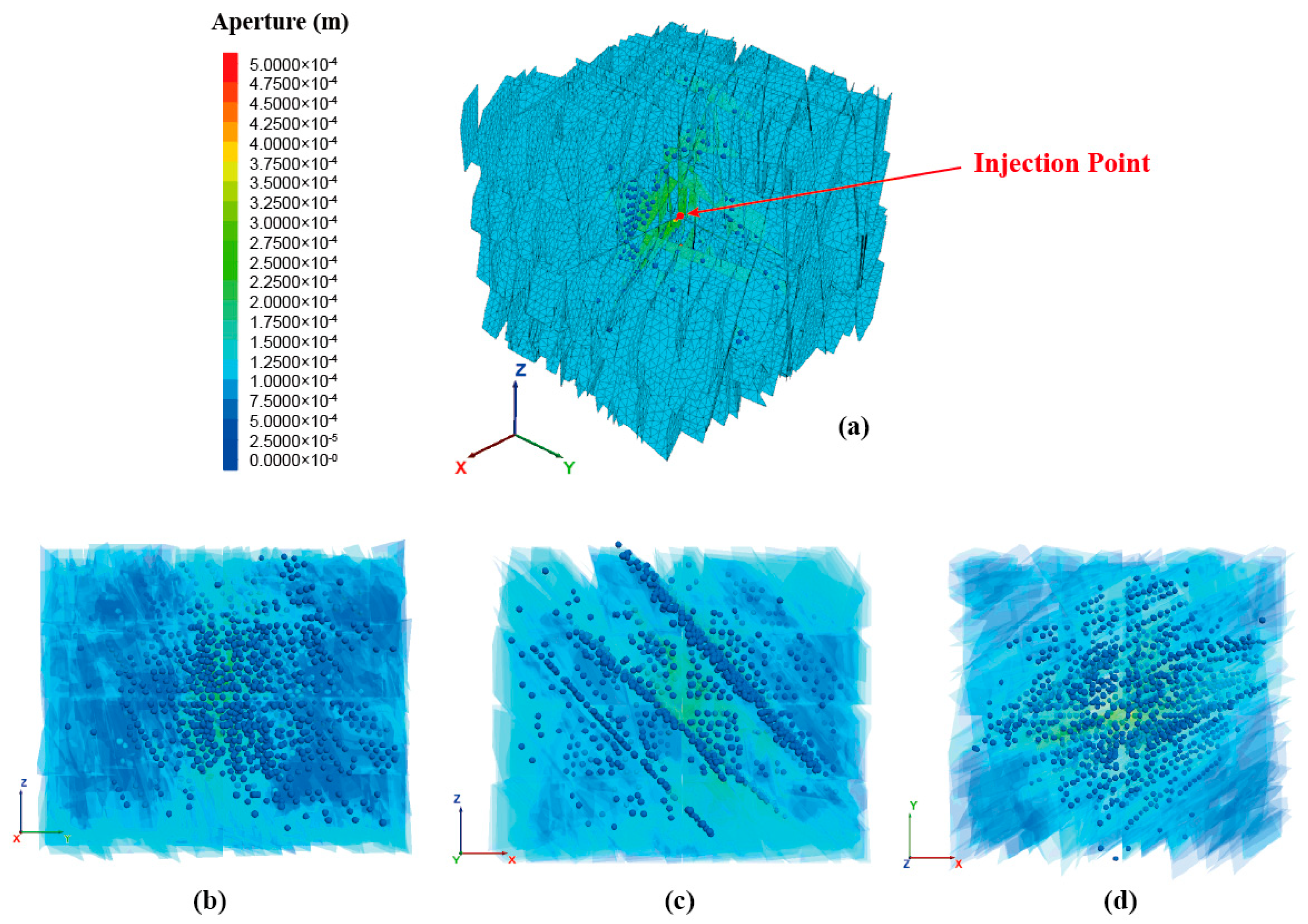
3.1.1. The Relationship Between Fluid Migration and Fracture Opening
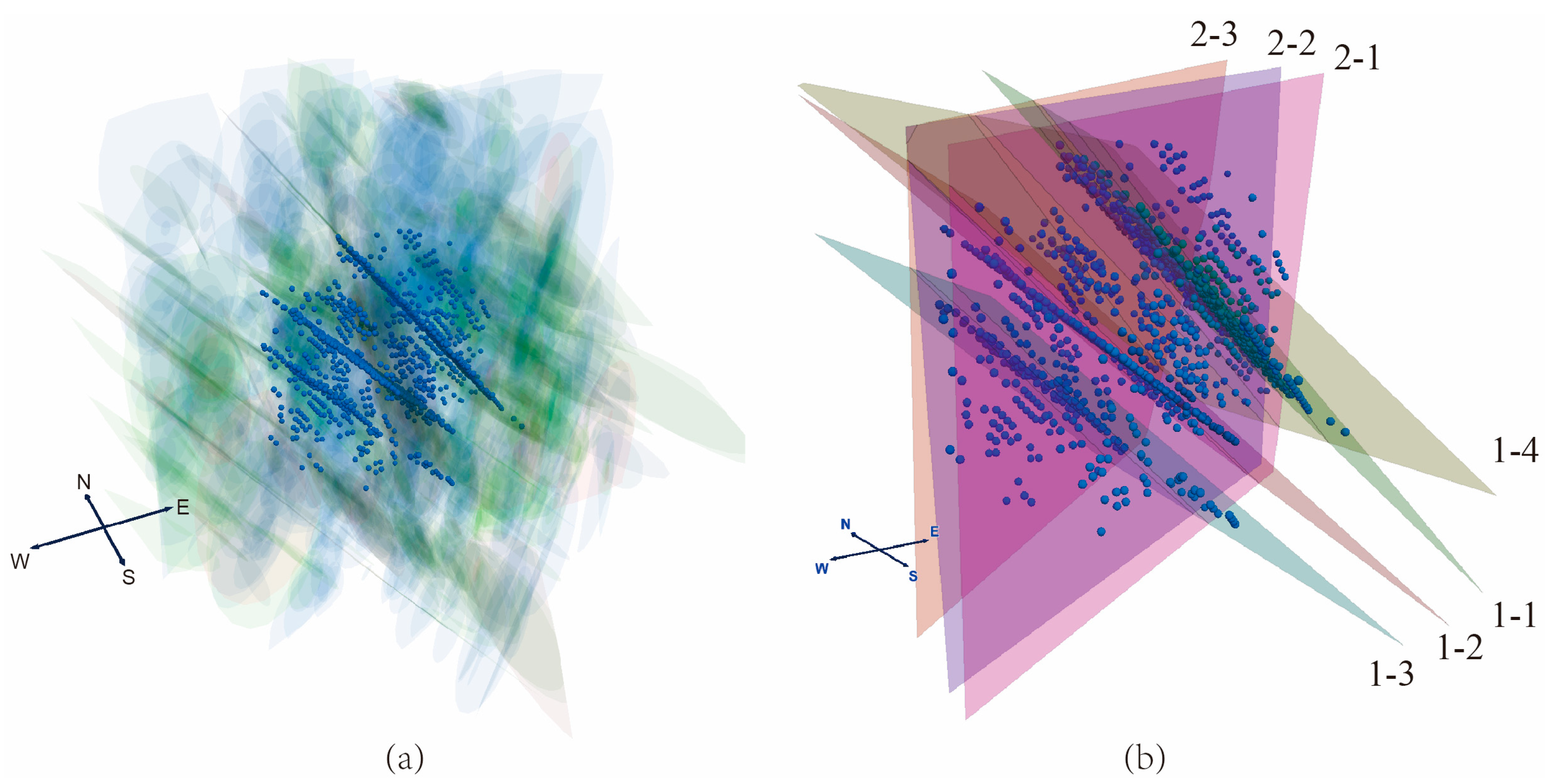
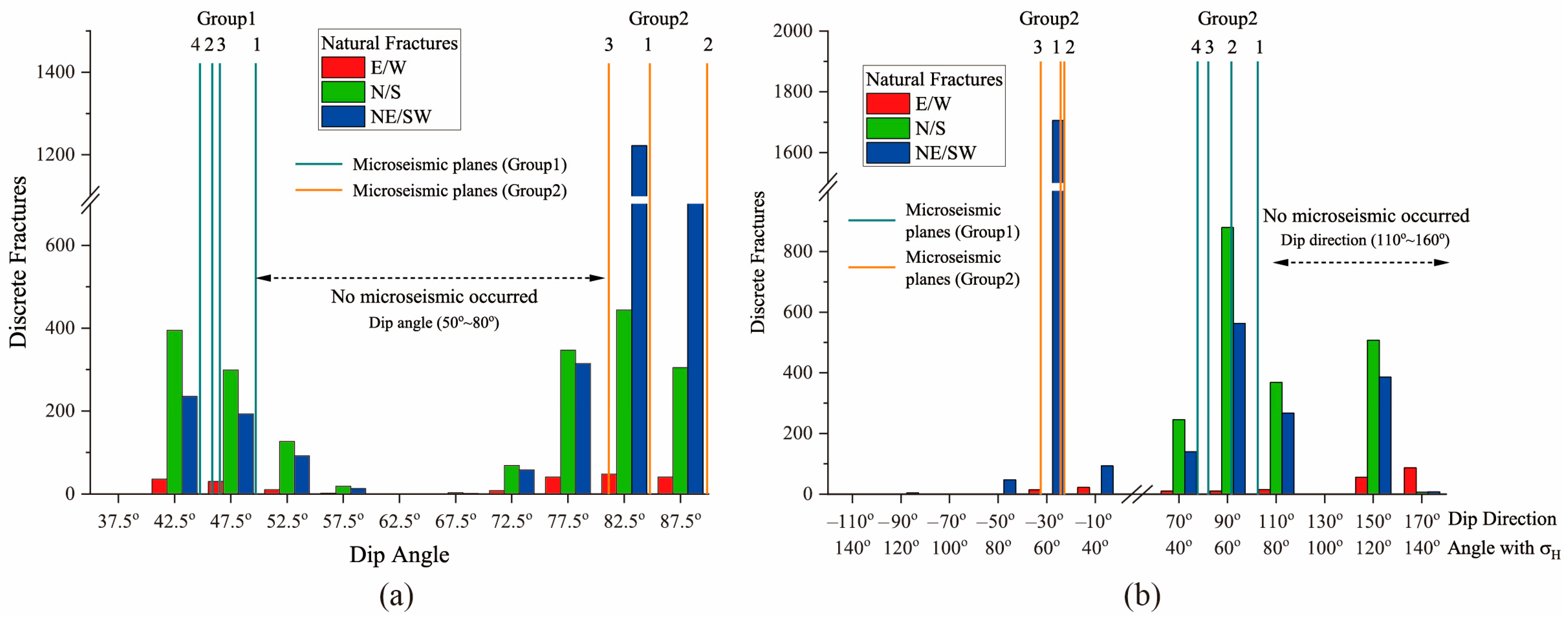
3.1.2. The Relationship with the Azimuth of Natural Fractures
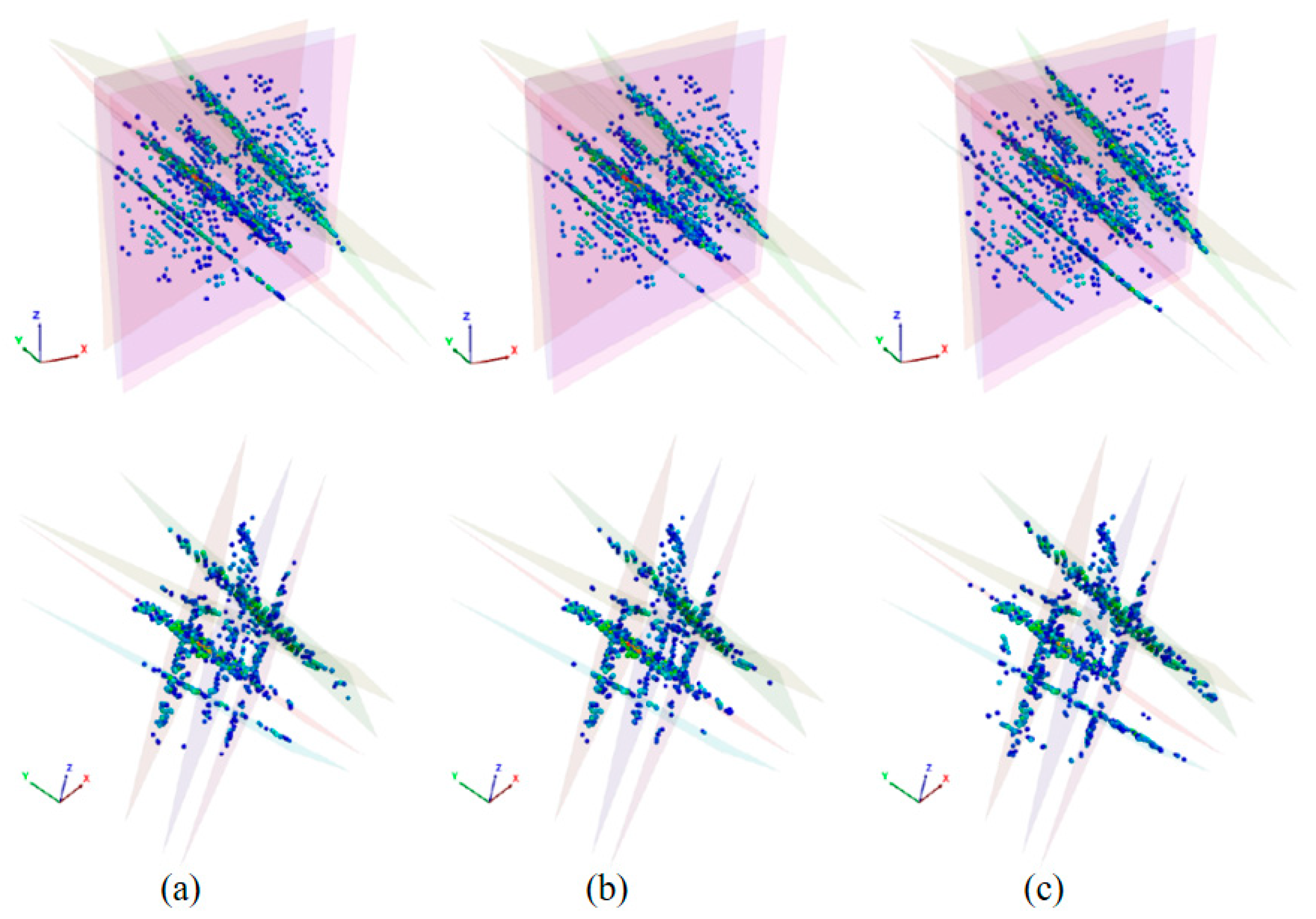
3.2. Evolution of Microseismic Events with Time
3.2.1. Microseismic Magnitude
3.2.2. Microseismic Distribution
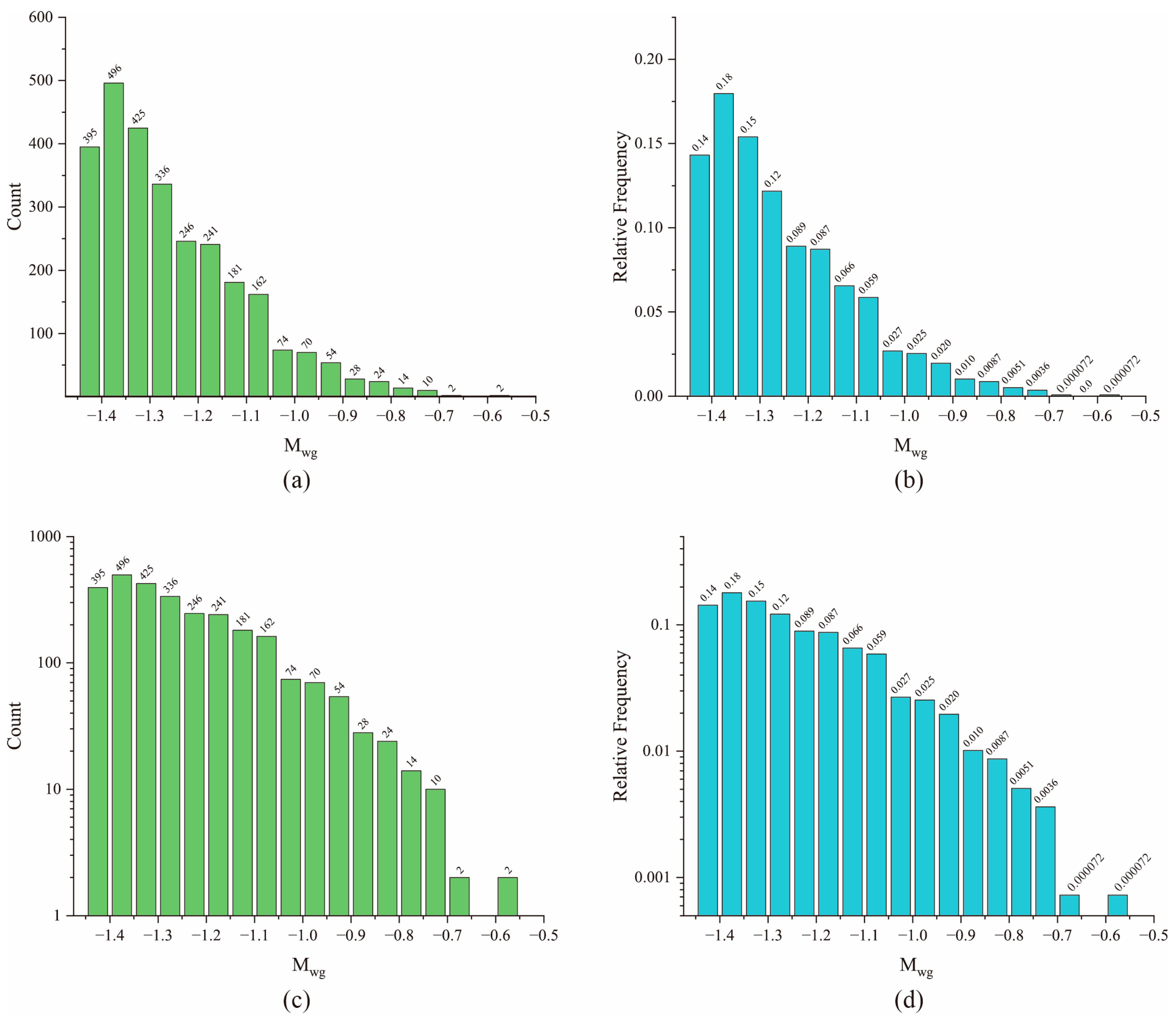
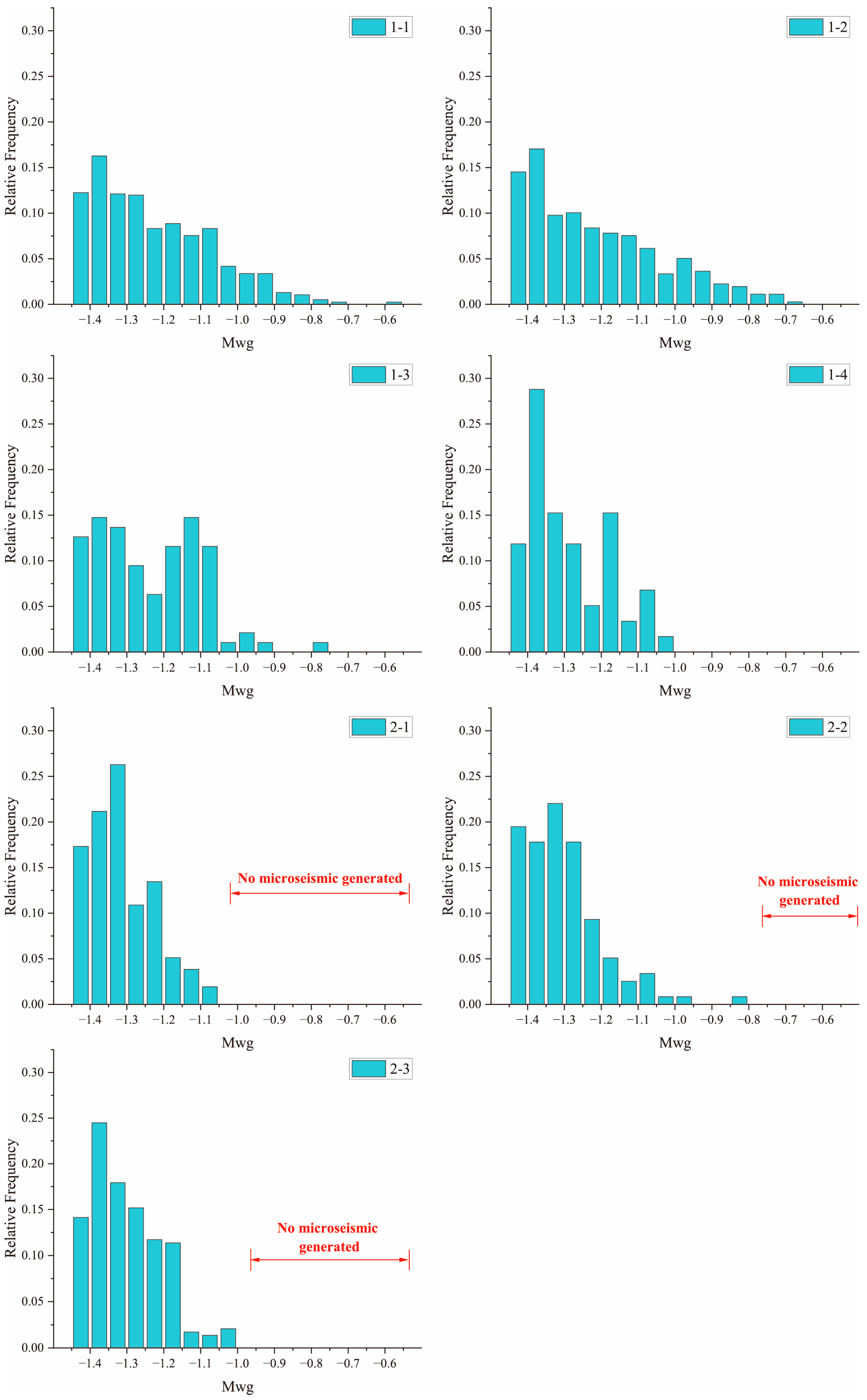
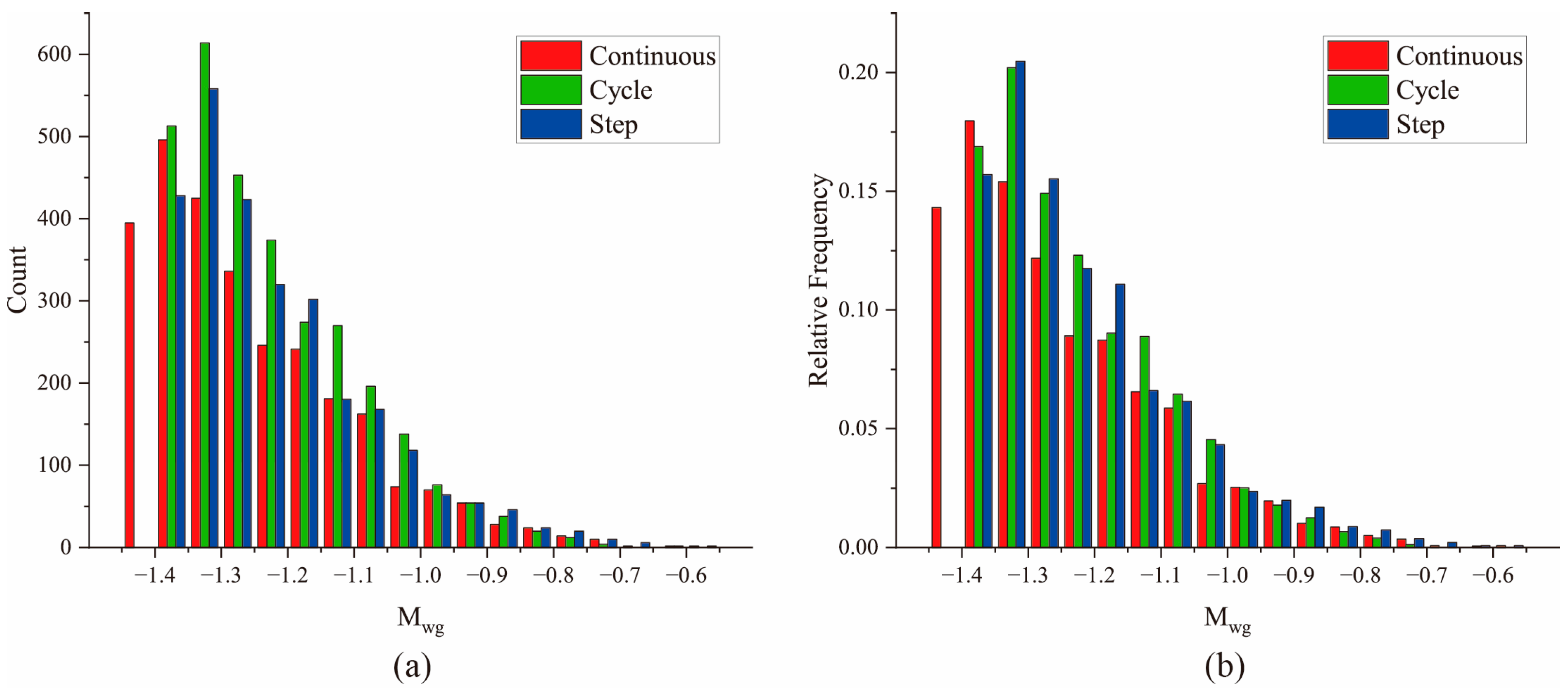
3.3. Distribution of Microseismic Events Magnitude
4. Discussion
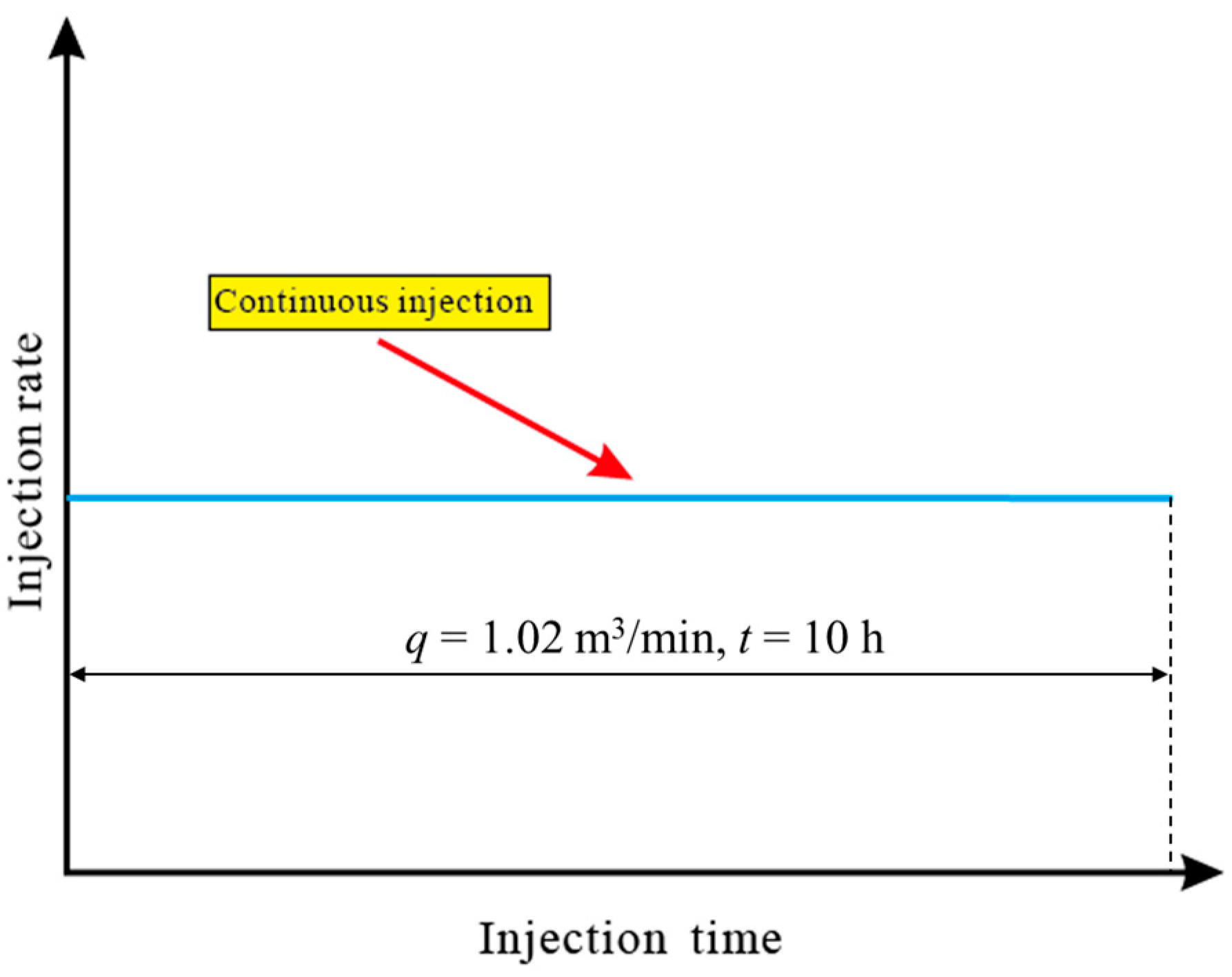
4.1. Effects of Injection Method on Spatial Distribution
4.2. Effects of Injection Method on Frequency and Magnitude
5. Conclusions
- (1)
- The microseismic event distribution exhibited an incomplete correlation with the fluid pressure fields. Proximal to the injection point, where the fluid pressure exceeds the stress on the fracture plane, tensile fracturing dominates, with negligible microseismicity. Conversely, in distal regions, where the fluid pressure remains insufficient to overcome fracture closure stress and significantly reduce frictional resistance, the shear failure potential increases proportionally with the fluid pressure elevation. This produces a strong spatial correlation between the fluid pressure distribution and concentrated microseismic activity because elevated fluid pressure directly enhances the effective shear stress along critically oriented fractures.
- (2)
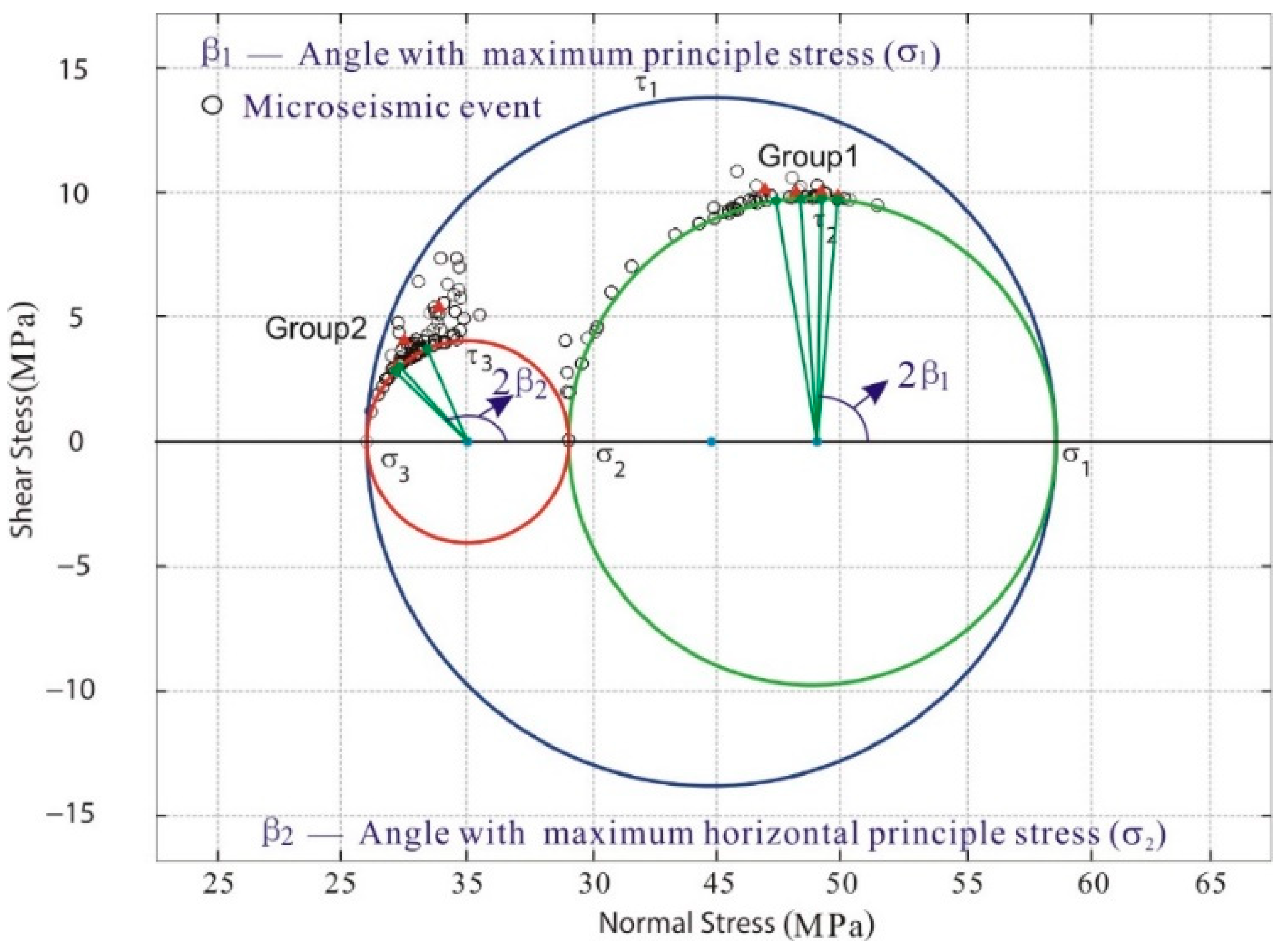
- Hydraulic fracturing induced microseismicity localizes preferentially to discrete fracture subsets rather than being distributed uniformly across all fractures. The fractures that were distributed at 45° from the direction of the maximum principal stress or at 45° from the principal stress were more likely to produce a concentration of microseismic events. The closer the fractures are to such features, the more likely a large number of microseismic events will occur during the hydraulic fracturing.
- (3)
- The maximum magnitude of the induced seismicity occurs only on specific fractures. The magnitude of the induced seismicity depends mainly on the fracture orientation and intra-fracture fluid pressure. When the angle between the fracture and maximum principal stress was 45°, the shear stress on the fracture was larger, and the induced microseismic events were stronger. Additionally, fractures near the injection point usually have a higher fluid pressure, which can also induce stronger microseismic events. Consequently, mitigation strategies should focus on preventing the development of critically high fluid pressures within the natural fractures near the injection well, particularly those oriented near 45° to the maximum principal stress. This necessitates the maintenance of fluid pressures below the local normal stress acting on the fracture plane.
- (4)
- Cyclic injection promotes shearing across a greater population of natural fractures while potentially reducing induced microseismic magnitudes through pressure relaxation during each injection hiatus. However, regardless of the specific injection protocol employed, surpassing a critical volumetric threshold may enable the development of critically elevated fluid pressures within fractures susceptible to large seismic events. Consequently, such pressures can trigger high-magnitude seismicity. Therefore, for cyclic hydraulic fracturing operations to enhance earthquake risk mitigation, it is recommended to implement measures within these susceptible fractures to prevent fracturing fluid from flowing into high-risk fractures (such as using packers, segmented fracturing, and temporary plugging techniques).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| DFM | Discrete Fracture Model |
| DFN | Discrete Fracture Network |
| EGS | Enhanced Geothermal System |
| FMI | Formation Micro-Imager |
| HDR | Hot Dry Rock |
| HF | Hydraulic Fracturing |
| MP | Microseismic Plane |
References
- Xie, L.; Min, K.-B.; Song, Y. Observations of hydraulic stimulations in seven enhanced geothermal system projects. Renew. Energy 2015, 79, 56–65. [Google Scholar] [CrossRef]
- Ma, W.; Wang, Y.; Wu, X.; Liu, G. Hot dry rock (HDR) hydraulic fracturing propagation and impact factors assessment via sensitivity indicator. Renew. Energy 2020, 146, 2716–2723. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, Y.; Hu, Z.; Lei, H.; Bai, L.; Lei, Z.; Zhang, Q. An experimental investigation into the characteristics of hydraulic fracturing and fracture permeability after hydraulic fracturing in granite. Renew. Energy 2019, 140, 615–624. [Google Scholar] [CrossRef]
- Zhou, Z.; Jin, Y.; Zeng, Y.; Zhang, X.; Zhou, J.; Zhuang, L.; Xin, S. Investigation on fracture creation in hot dry rock geothermal formations of China during hydraulic fracturing. Renew. Energy 2020, 153, 301–313. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, H.; Tao, S. Opportunity and challenges in large-scale geothermal energy exploitation in China. Crit. Rev. Environ. Sci. Technol. 2022, 52, 3813–3834. [Google Scholar] [CrossRef]
- Shu, B.; Zhu, R.; Zhang, S.; Dick, J. A qualitative prediction method of new crack-initiation direction during hydraulic fracturing of pre-cracks based on hyperbolic failure envelope. Appl. Energy 2019, 248, 185–195. [Google Scholar] [CrossRef]
- Song, X.; Shi, Y.; Li, G.; Yang, R.; Wang, G.; Zheng, R.; Li, J.; Lyu, Z. Numerical simulation of heat extraction performance in enhanced geothermal system with multilateral wells. Appl. Energy 2018, 218, 325–337. [Google Scholar] [CrossRef]
- Moska, R.; Labus, K.; Kasza, P. Hydraulic Fracturing in Enhanced Geothermal Systems—Field, Tectonic and Rock Mechanics Conditions—A Review. Energies 2021, 14, 5725. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, J.; Lei, Y. The Propagation Behavior of Hydraulic Fracture in Rock Mass with Cemented Joints. Geofluids 2019, 1, 5406870. [Google Scholar] [CrossRef]
- Li, N.; Xie, H.; Gao, Z.; Li, C. Study on the Hydraulic Fracturing Failure Behaviour of Granite and Its Comparison with Gas Fracturing. Sustainability 2022, 14, 14593. [Google Scholar] [CrossRef]
- Li, S.; Wang, S.; Tang, H. Stimulation mechanism and design of enhanced geothermal systems: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 155, 111914. [Google Scholar] [CrossRef]
- Liu, K.; Taleghani, A.D.; Gao, D. Calculation of hydraulic fracture induced stress and corresponding fault slippage in shale formation. Fuel 2019, 254, 115525. [Google Scholar] [CrossRef]
- McClure, M.W.; Horne, R.N. An investigation of stimulation mechanisms in Enhanced Geothermal Systems. Int. J. Rock Mech. Min. Sci. 2014, 72, 242–260. [Google Scholar] [CrossRef]
- Zang, A.; Oye, V.; Jousset, P.; Deichmann, N.; Gritto, R.; McGarr, A.; Majer, E.; Bruhn, D. Analysis of induced seismicity in geothermal reservoirs—An overview. Geothermics 2014, 52, 6–21. [Google Scholar] [CrossRef]
- Haering, M.O.; Schanz, U.; Ladner, F.; Dyer, B.C. Characterisation of the Basel 1 enhanced geothermal system. Geothermics 2008, 37, 469–495. [Google Scholar] [CrossRef]
- Baisch, S.; Voeroes, R.; Weidler, R.; Wyborn, D. Investigation of Fault Mechanisms during Geothermal Reservoir Stimulation Experiments in the Cooper Basin, Australia. Bull. Seismol. Soc. Am. 2009, 99, 148–158. [Google Scholar] [CrossRef]
- Baisch, S.; Voeroes, R.; Rothert, E.; Stang, H.; Jung, R.; Schellschmidt, R. A numerical model for fluid injection induced seismicity at Soultz-sous-Forets. Int. J. Rock Mech. Min. Sci. 2010, 47, 405–413. [Google Scholar] [CrossRef]
- Calo, M.; Dorbath, C.; Frogneux, M. Injection tests at the EGS reservoir of Soultz-sous-Forets. Seismic response of the GPK4 stimulations. Geothermics 2014, 52, 50–58. [Google Scholar] [CrossRef]
- Dorbath, L.; Evans, K.; Cuenot, N.; Valley, B.; Charlety, J.; Frogneux, M. The stress field at Soultz-sous-Forets from focal mechanisms of induced seismic events: Cases of the wells GPK2 and GPK3. Comptes Rendus Geosci. 2010, 342, 600–606. [Google Scholar] [CrossRef]
- Ellsworth, W.L.; Giardini, D.; Townend, J.; Ge, S.; Shimamoto, T. Triggering of the Pohang, Korea, Earthquake (Mw 5.5) by Enhanced Geothermal System Stimulation. Seismol. Res. Lett. 2019, 90, 1844–1858. [Google Scholar] [CrossRef]
- Kim, K.-H.; Ree, J.-H.; Kim, Y.; Kim, S.; Kang, S.Y.; Seo, W. Assessing whether the 2017 Mw 5.4 Pohang earthquake in South Korea was an induced event. Science 2018, 360, 1007–1009. [Google Scholar] [CrossRef]
- Lyakhovsky, V.; Shalev, E. Runaway Versus Stable Fracturing During Hydraulic Stimulation: Insights from the Damage Rheology Modeling. Rock Mech. Rock Eng. 2021, 54, 5449–5464. [Google Scholar] [CrossRef]
- Schwartzkopff, A.K.; Sainoki, A.; Elsworth, D. Numerical Simulation of An In-situ Fluid Injection Experiment into a Fault Using Coupled X-FEM Analysis. Rock Mech. Rock Eng. 2021, 54, 1027–1053. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.L.; Wason, H.R.; Choudhury, D.; Gonzalez, G. A Seismic Moment Magnitude Scale. Bull. Seismol. Soc. Am. 2019, 109, 1542–1555. [Google Scholar] [CrossRef]
- Izadi, G.; Elsworth, D. Reservoir stimulation and induced seismicity: Roles of fluid pressure and thermal transients on reactivated fractured networks. Geothermics 2014, 51, 368–379. [Google Scholar] [CrossRef]
- Yaghoubi, A.; Dusseault, M.B.; Leonenko, Y. Injection-induced fault slip assessment in Montney Formation in Western Canada. Sci. Rep. 2022, 12, 11551. [Google Scholar] [CrossRef]
- Zoback, M.D.; Gorelick, S.M. Earthquake triggering and large-scale geologic storage of carbon dioxide. Proc. Natl. Acad. Sci. USA 2012, 109, 10164–10168. [Google Scholar] [CrossRef]
- Chong, Z.; Yao, Q.; Li, X.; Liu, J. Investigations of seismicity induced by hydraulic fracturing in naturally fractured reservoirs based on moment tensors. J. Nat. Gas Sci. Eng. 2020, 81, 103448. [Google Scholar] [CrossRef]
- Alghannam, M.; Juanes, R. Understanding rate effects in injection-induced earthquakes. Nat. Commun. 2020, 11, 3053. [Google Scholar] [CrossRef] [PubMed]
- Izadi, G.; Elsworth, D. The effects of thermal stress and fluid pressure on induced seismicity during stimulation to production within fractured reservoirs. Terra Nova 2013, 25, 374–380. [Google Scholar] [CrossRef]
- Park, S.; Kim, K.-I.; Yoo, H.; Yim, J.; Min, K.-B. Comprehensive in-situ stress estimation in a fractured geothermal reservoir in Pohang, South Korea using drilling data, hydraulic stimulations, and induced seismicity. Int. J. Rock Mech. Min. Sci. 2025, 186, 105978. [Google Scholar] [CrossRef]
- Diaz, M.B.; Kim, K.Y.; Jung, S.G. Effect of frequency during cyclic hydraulic fracturing and the process of fracture development in laboratory experiments. Int. J. Rock Mech. Min. Sci. 2020, 134, 105978. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; Chen, Z.; Gu, F. An integrated approach to characterize hydraulic fracturing-induced seismicity in shale reservoirs. J. Pet. Sci. Eng. 2021, 196, 107624. [Google Scholar] [CrossRef]
- Zang, A.; Zimmermann, G.; Hofmann, H.; Stephansson, O.; Min, K.-B.; Kim, K.Y. How to Reduce Fluid-Injection-Induced Seismicity. Rock Mech. Rock Eng. 2019, 52, 475–493. [Google Scholar] [CrossRef]
- Zhou, W.; Lanza, F.; Grigoratos, I.; Schultz, R.; Cousse, J.; Trutnevyte, E.; Muntendam-Bos, A.; Wiemer, S. Managing Induced Seismicity Risks from Enhanced Geothermal Systems: A Good Practice Guideline. Rev. Geophys. 2024, 62, 2024RG000849. [Google Scholar] [CrossRef]
- Kwiatek, G.; Saarno, T.; Ader, T.; Bluemle, F.; Bohnhoff, M.; Chendorain, M.; Dresen, G.; Heikkinen, P.; Kukkonen, I.; Leary, P.; et al. Controlling fluid-induced seismicity during a 6.1-km-deep geothermal stimulation in Finland. Sci. Adv. 2019, 5, eaav7224. [Google Scholar] [CrossRef]
- Majer, E.L.; Baria, R.; Stark, M.; Oates, S.; Bommer, J.; Smith, B.; Asanuma, H. Induced seismicity associated with enhanced geothermal systems. Geothermics 2007, 36, 185–222. [Google Scholar] [CrossRef]
- Cheng, Y.; Xu, T.; Zhang, Y.; Shangguan, S.; Feng, B. An laboratorial investigation of induced seismicity characteristics in EGS hydraulic fracturing. Geothermics 2022, 105, 102482. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, T.; Yuan, Y.; Feng, B.; Tang, X.; Liu, X.; Cui, Z. A laboratory study on fracture initiation and propagation of granite under cyclic-injection hydraulic fracturing. J. Pet. Sci. Eng. 2022, 212, 110278. [Google Scholar] [CrossRef]
- Walsh, F.R., III; Zoback, M.D. Oklahoma’s recent earthquakes and saltwater disposal. Sci. Adv. 2015, 1, e1500195. [Google Scholar] [CrossRef]
- Kolawole, F.; Johnston, C.S.; Morgan, C.B.; Chang, J.C.; Marfurt, K.J.; Lockner, D.A.; Reches, Z.; Carpenter, B.M. The susceptibility of Oklahoma’s basement to seismic reactivation. Nat. Geosci. 2019, 12, 839–844. [Google Scholar] [CrossRef]
- Kivi, I.R.; Vilarrasa, V.; Kim, K.-I.; Yoo, H.; Min, K.-B. On the role of poroelastic stressing and pore pressure diffusion in discrete fracture and fault system in triggering post-injection seismicity in enhanced geothermal systems. Int. J. Rock Mech. Min. Sci. 2024, 175, 105673. [Google Scholar] [CrossRef]
- Rathnaweera, T.D.; Wu, W.; Ji, Y.; Gamage, R.P. Understanding injection-induced seismicity in enhanced geothermal systems: From the coupled thermo-hydro-mechanical-chemical process to anthropogenic earthquake prediction. Earth-Sci. Rev. 2020, 205, 103182. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, Z.; Xu, T.; Feng, B.; Yuan, Y.; Xing, P. Discrete element modeling for the multistage hydraulic stimulation of a horizontal well in hot dry rock. Comput. Geotech. 2023, 156, 105274. [Google Scholar] [CrossRef]
- McGarr, A. Seismic moments and volume changes. J. Geophys. Res. 1976, 81, 1487–1494. [Google Scholar] [CrossRef]
- Nadimi, S.; Forbes, B.; Moore, J.; McLennan, J.D. Effect of natural fractures on determining closure pressure. J. Pet. Explor. Prod. Technol. 2020, 10, 711–728. [Google Scholar] [CrossRef]
- Xing, P.; McLennan, J.; Moore, J. In-Situ Stress Measurements at the Utah Frontier Observatory for Research in Geothermal Energy (FORGE) Site. Energies 2020, 13, 5842. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, T.; Moore, J.; Feng, B.; Liu, Y.; McLennan, J.; Yang, Y. Investigation of the effect of different injection schemes on fracture network patterns in hot dry rocks—A numerical case study of the FORGE EGS site in Utah. J. Nat. Gas Sci. Eng. 2022, 97, 104346. [Google Scholar] [CrossRef]
- Riahi, A.; Pettitt, W.; Damjanac, B.; Varun; Blanksma, D. Numerical Modeling of Discrete Fractures in a Field-Scale FORGE EGS Reservoir. Rock Mech. Rock Eng. 2019, 52, 5245–5258. [Google Scholar] [CrossRef]
- Niemz, P.; McLennan, J.; Pankow, K.L.; Rutledge, J.; England, K. Circulation experiments at Utah FORGE: Near-surface seismic monitoring reveals fracture growth after shut-in. Geothermics 2024, 119, 102947. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Z.; Wu, Y.; Yu, B.; Wang, D.; Wang, Y. Study on the migration characteristics of temporary plugging agents in hot dry rock fractures considering ambient temperature field variations. Phys. Fluids 2024, 36, 093320. [Google Scholar] [CrossRef]
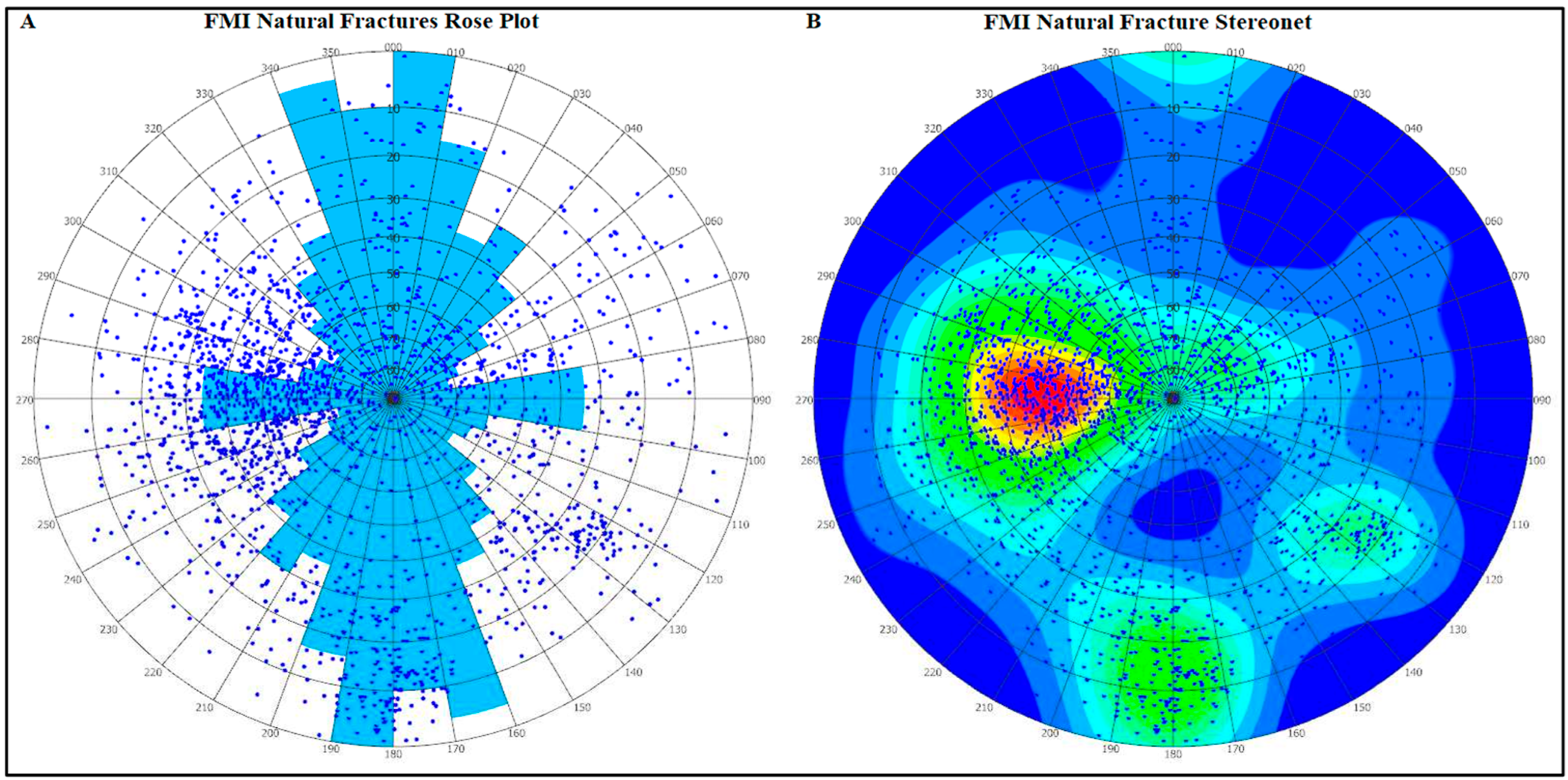
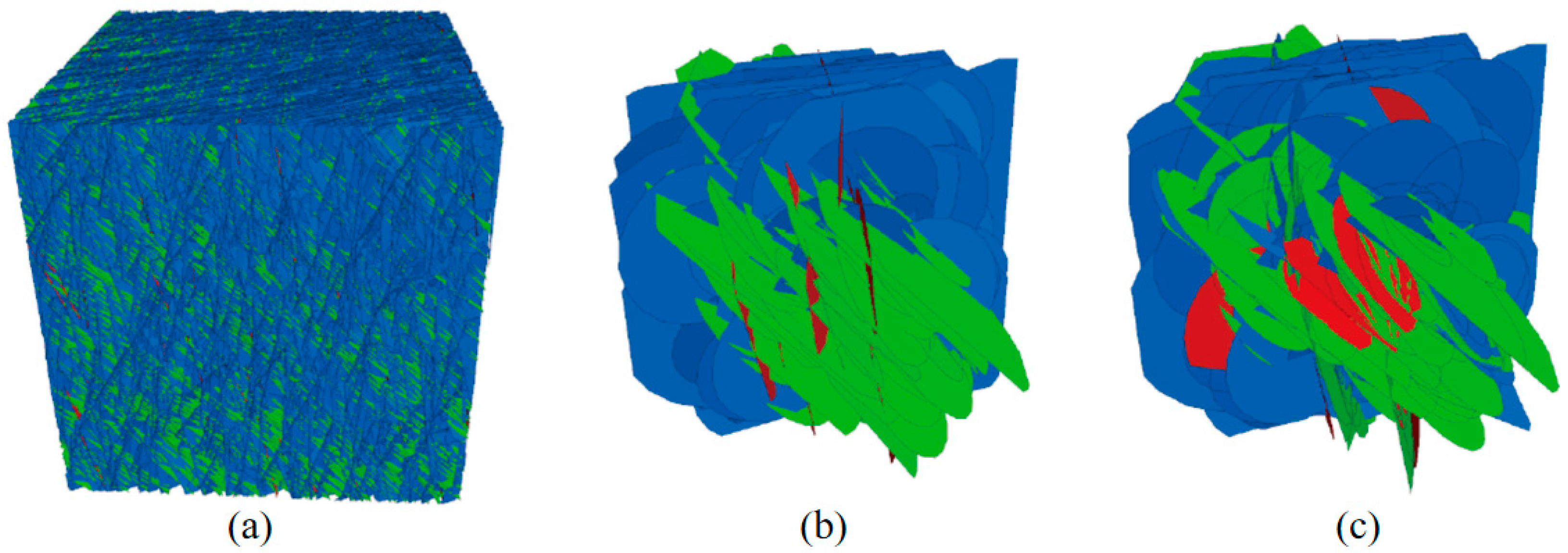




| Three Set Fractures | Orientation | Fracture Radius (m) | |||
|---|---|---|---|---|---|
| Fisher Distribution | Log Normal Distribution | ||||
| Fracture Density (Fractures/m) | Mean Dip (°) | Mean Dip Angle (°) | Mean (m) | Standard Deviation (m) | |
| NE/SW | 0.95 | 331 | 0.975 | 35 | 28.9 |
| N/S | 0.36 | 87 | 41.806 | 35 | 28.9 |
| E/W | 0.1 | 3 | 10.82 | 35 | 28.9 |
| Category | Parameter | Value | Unit |
|---|---|---|---|
| Mechanical parameters | Density (D) | 2650 | kg/m3 |
| Young’s modulus (E) | 50 | Gpa | |
| Poisson’s ratio | 0.25 | ||
| Fracture Properties | Tangential Stiffness under Compression (Ksc) | 75 | GPa |
| Normal Stiffness under Compression (Knc) | 90 | GPa | |
| Tangential Stiffness under Tension (Kst) | 70 | GPa | |
| Normal Stiffness under Tension (Knt) | 80 | GPa | |
| Fracture Tensile Strength (c) | 2 | MPa | |
| Fracture Friction (μ) | 0.35 | ||
| Fracture Dilatation Angle (φ) | 15 | ° | |
| Fracture Initial Aperture | 0.0001 | m | |
| Fluid Properties | Fluid bulk modulus (Kfluid) | 2 | GPa |
| Fluid density (ρfluid) | 1000 | kg/m3 | |
| Fluid viscosity (μfluid) | 0.0015 | Pa·s |
| Group 1 | ||||
| 1-1 | Unit Normal Vector | 0.744701 | −0.165379 | 0.646584 |
| Origin Point (m) | 67.2344 | −7.04769 | 71.2743 | |
| Dip∠Dip angle | 102.521∠49.7155 | |||
| 1-2 | Unit Normal Vector | 0.666871 | −0.0184136 | 0.744946 |
| Origin Point (m) | −16.6728 | 0.27786 | −17.8617 | |
| Dip∠Dip angle | 91.5816∠45.8455 | |||
| 1-3 | Unit Normal Vector | 0.718736 | 0.0998621 | 0.688074 |
| Origin Point (m) | −91.2317 | −16.2377 | −61.7154 | |
| Dip∠Dip angle | 82.0899∠46.5222 | |||
| 1-4 | Unit Normal Vector | 0.671779 | 0.146019 | 0.726218 |
| Origin Point (m) | 26.1889 | 47.5912 | 42.3995 | |
| Dip∠Dip angle | 77.7368∠45.4298 | |||
| Group 2 | ||||
| 2-1 | Unit Normal Vector | 0.407599 | −0.908598 | −0.0911685 |
| Origin Point (m) | −5.33765 | −61.5151 | 4.19486 | |
| Dip∠Dip angle | −24.1610∠84.7692 | |||
| 2-2 | Unit Normal Vector | 0.386651 | −0.922224 | −0.0020648 |
| Origin Point (m) | −54.1827 | −13.5785 | 35.3269 | |
| Dip∠Dip angle | −22.7462∠89.8817 | |||
| 2-3 | Unit Normal Vector | 0.529514 | −0.834164 | −0.154224 |
| Origin Point (m) | −96.2324 | 63.7412 | 6.21733 | |
| Dip∠Dip angle | −32.4070∠81.1282 | |||
| Time (h) | Magnitude (Mw) | Magnitude (Mwg) | x-Position | y-Position | z-Position |
|---|---|---|---|---|---|
| 1 | −0.148 | −1.04324 | −23.963 | 43.8798 | −10.1159 |
| 2 | −0.00569 | −0.88627 | −69.3056 | 44.0793 | 30.7332 |
| 3 | 0.06834 | −0.95533 | −69.3056 | 44.0793 | 30.7332 |
| 4 | 0.118628 | −0.74915 | −69.3056 | 44.0793 | 30.7332 |
| 5 | 0.1468 | −0.71803 | −69.3056 | 44.0793 | 30.7332 |
| 6 | 0.162716 | −0.70052 | 125.691 | 24.2346 | 10.7918 |
| 7 | 0.203844 | −0.617 | 125.691 | 24.2346 | 10.7918 |
| 8 | 0.23469 | −0.62114 | 125.691 | 24.2346 | 10.7918 |
| 9 | 0.259733 | −0.59351 | 125.691 | 24.2346 | 10.7918 |
| 10 | 0.277563 | −0.57385 | 125.691 | 24.2346 | 10.7918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Wang, W.; Tang, J.; Hu, Z. Mechanisms and Mitigation of Injection-Induced Microseismicity: The Critical Role of Fracture Orientation in Shear Reactivation. Appl. Sci. 2025, 15, 11919. https://doi.org/10.3390/app152211919
Yuan Y, Wang W, Tang J, Hu Z. Mechanisms and Mitigation of Injection-Induced Microseismicity: The Critical Role of Fracture Orientation in Shear Reactivation. Applied Sciences. 2025; 15(22):11919. https://doi.org/10.3390/app152211919
Chicago/Turabian StyleYuan, Yilong, Wei Wang, Jiawei Tang, and Zixu Hu. 2025. "Mechanisms and Mitigation of Injection-Induced Microseismicity: The Critical Role of Fracture Orientation in Shear Reactivation" Applied Sciences 15, no. 22: 11919. https://doi.org/10.3390/app152211919
APA StyleYuan, Y., Wang, W., Tang, J., & Hu, Z. (2025). Mechanisms and Mitigation of Injection-Induced Microseismicity: The Critical Role of Fracture Orientation in Shear Reactivation. Applied Sciences, 15(22), 11919. https://doi.org/10.3390/app152211919







