Coded Caching Optimization in Dual Time-Scale Wireless Networks: An Advantage Actor–Critic Learning Approach

Abstract

The rapid growth of mobile data traffic poses significant challenges to ensuring high-quality service in wireless networks. Although the caching technique is capable of alleviating network congestion, most existing schemes depend on uncoded caching with prior knowledge of content popularity and ignore the time-scale mismatch between content dynamics and user mobility. To address these challenges, we first formulate a dynamic coded caching optimization framework under a dual time-scale model that simultaneously captures long-term content popularity evolution and short-term user mobility patterns. Then, we model the optimization problem as a Markov decision process and design a novel advantage actor–critic (A2C) based coded caching algorithm. By introducing the advantage function, the proposed approach can mitigate variance in policy updates and accelerate convergence under the caching capacity constraint. Finally, extensive simulations are conducted to demonstrate that our proposed algorithm significantly outperforms baseline caching schemes in terms of average delay cost.

1. Introduction

With the proliferation of smart mobile devices and the rise of data-intensive applications such as ultra-high definition video and online interactive games, mobile data traffic has experienced explosive growth, which imposes tremendous pressure on the backhaul links of wireless cellular networks and results in severe network congestion. Consequently, mobile users (MUs) frequently suffer from a degraded Quality of Service (QoS), manifested in increased transmission delays and service interruptions. To address these issues, network operators deploy small cell base stations (SBSs) alongside conventional macro base stations (MBSs), forming the heterogeneous cellular networks to improve spectral efficiency and decrease the transmission latency [1,2]. Furthermore, by equipping SBSs with caching capabilities and proactively storing popular contents at the network edge, MUs’ content requests can be served by nearby SBSs without delivering to the wireless backhaul network [3]. This approach can significantly improve MUs’ QoS and alleviate the backhaul traffic.

However, designing an effective caching strategy is critical for determining which content to store and where to place it. Typically, content popularity is considered a key factor in formulating such strategies. Traditional studies typically assume that content popularity is known a priori and model it using a Zipf distribution [4,5]. In practice, content popularity is not time-invariant but evolves dynamically over time. For instance, a newly released movie may experience a surge in requests shortly after its release, but this demand rapidly declines within a few days. To cope with the dynamic content popularity, the authors in [6] developed a Bayesian dynamical model to predict the popularity and then designed a cooperative caching policy to minimize the network cost. In [7], inspired by recommendation algorithms, the authors employed collaborative filtering to predict user preferences, which serves as the basis for caching placement. Recently, deep learning methods have been applied to assist in making caching decisions in dynamic environments. In [8], the authors model the caching problem as a multi-agent multi-armed bandit problem and use Q-learning to make caching decisions. In [9], the problem of joint caching and resource allocation was investigated and solved by hierarchical reinforcement learning. Ref. [10] investigated the caching decisions and offloading on deep deterministic policy gradient in the highly dynamic vehicular environment.

All the aforementioned studies [4,5,6,7,8,9,10] assume that a given content item is either fully cached or not cached at all, which is referred to as uncoded caching. This approach has two main drawbacks: First, the uncoded caching strategy limits the diversity of cached contents, which is unfavorable for satisfying the diverse content demands of MUs. Second, due to the rapid mobility, MUs may not have enough time to completely download the entire requested content from the connected SBS. In this case, MUs will be forced to re-initiate a request for the unfinished portion of the content upon entering the coverage area of the next SBS, which increases the transmission delay and significantly degrades the quality of service for MUs. To further enhance caching efficiency, Maddah-Ali et al. [11] proposed the coded caching strategy, in which each requested content is encoded into multiple data packets of arbitrary size. The original content can be successfully decoded by MUs once the total size of the received coded packets is no less than that of the requested content. Refs. [12,13] studied the mobility-aware coded caching strategy to improve the performance of the wireless mobile network. Nevertheless, prior works [12,13] typically assume perfect knowledge of content popularity and fail to account for the temporal mismatch between content popularity evolution and user mobility.

To solve the aforementioned problems, we propose a novel dynamic coded caching algorithm based on deep reinforcement learning. Due to the time-varying nature of content popularity and the mobility of MUs, we first establish a dual time-scale model and subsequently formulate an optimization framework aimed at minimizing the average content request delay of MUs. Motivated by the continuous nature of coded caching decisions and the challenges of traditional deep learning methods, such as the curse of dimensionality and slow convergence, we propose the advantage actor–critic (A2C) based coded caching algorithm to accelerate convergence and significantly enhance caching efficiency. The contributions of this paper are summarized as follows:

• Under a dual-time-scale network model, we formulate the dynamic coded caching optimization problem to jointly consider long-term content demand changes and short-term MU movement patterns, thereby providing a more realistic and tractable basis for designing efficient caching strategies.
• We model the coded caching optimization problem as a Markov decision process and design an A2C-based coded caching algorithm with a caching capacity constraint. By incorporating an advantage function, the proposed algorithm reduces variance in gradient estimation and accelerates convergence, which ensures more efficient caching decisions.
• Through extensive simulations, we evaluate the convergence of the proposed A2C-based caching algorithm and compare its performance with several benchmark caching schemes. The results demonstrate that our algorithm significantly outperforms baseline caching schemes.

2. Related Work

In recent years, a large number of studies have focused on caching techniques as a promising solution to improve the quality of service of users and alleviate network congestion. In [14], the authors employed a hierarchical primal-dual decomposition method to provide a global optimal caching strategy with a priori knowledge of content popularity. In [15], with the aim of minimizing the delay and energy consumption, the authors proposed an enhanced binary particle swarm optimization algorithm to find the optimal caching strategy. The authors in [16] formulated a game-theoretic caching approach to jointly optimize the total utility of users and the cost of the base station. Ref. [17] introduced a service-oriented content caching framework that maximizes resource utilization and revenue while guaranteeing users’ QoS. Caching decisions in [14,15,16,17] were binary variables, indicating whether to store the entire content or not at all, which is known as uncoded caching. Although these caching methods are easy to implement, they face two key limitations: the lack of content diversity under limited caching storage and the inability to guarantee seamless content delivery for MUs who only have short contact durations with base stations.

To address the above two limitations, ref. [11] proposed a novel coded caching, which can achieve a global caching gain by cumulative global caching capacity. The work in [18] investigated the coded caching placement scheme by maximizing the average fractional offloaded traffic and average ergodic rate. In [19], the authors investigated the fronthaul load minimization problem by leveraging maximum-distance separable (MDS) codes and a weighted graph. By considering MDS-coded caching, the study [20] employed an alternating-iteration framework to jointly optimize caching and resource allocation in the space-air-ground integrated networks. A common problem of the research [14,15,16,17,18,19,20] is that their caching strategies all rely on static or perfectly known content popularity, which do not adequately capture the time-varying nature of content request demands.

With the recent advances in machine learning, deep reinforcement learning (DRL) has been introduced to a dynamical caching environment. In [21], the authors proposed a content importance-based caching scheme by leveraging dueling double deep Q networks to improve the caching hit ratio. By leveraging MDS coding, ref. [22] designed a novel multi-agent deep reinforcement learning algorithm by embedding homotopy optimization to intelligently make caching decisions. The studies in [23,24] both investigated coded caching and resource optimization in unmanned aerial vehicle (UAV)-assisted dynamical networks.

Despite the progress made by existing works, several key challenges remain unsolved. First, there is a lack of frameworks that jointly consider the long-term dynamics of content popularity and the short-term dynamics of MUs’ mobility. Second, how to efficiently solve high-dimensional, time-varying coded caching decision problems to achieve continuous optimization control? Our work proposes a novel dual time-scale dynamic model that integrates coded caching with an A2C-based algorithm. This approach continuously optimizes caching proportions to minimize the average delay cost for MUs, effectively bridging the gaps identified in the literature.

3. System Models

3.1. Network Model

As shown in Figure 1, we consider a wireless heterogeneous cellular network consisting of one macro base station (MBS) and N small cell base stations (SBSs) with caching capacities. Let $\mathcal{N}=\{0,1,2,\dots ,N\}$ denote the set of all base stations, where the index 0 denotes the MBS and the index $1,2,\dots ,N$ denotes the SBSs. There are K mobile users (MUs) with different content demands, denoted by the set $\mathcal{K}=\{1,2,\dots ,K\}$. It is assumed that each MU pre-plans its movement path using its own navigation system, such as the global positioning system [25], or a high-definition map [26], where the movement path in our work is represented as the sequential order of the small cell base stations that each MU passes through. Note that all MUs can communicate with the MBS at any time during their movement, implying that MUs are always within the coverage area of the MBS. We assume MU k is scheduled to pass through $N_k$ base stations along its predetermined movement path, where $1\le N_k\le \left|\mathcal{N}\right|,N_k\in {\mathbf{N}}^{+},\forall k\in \mathcal{K}$. Particularly, when $N_k=1$, it indicates that MU k only communicates with MBS and does not pass through the coverage area of any SBSs. When $N_k=\left|\mathcal{N}\right|$, it means that MU k not only communicates with the MBS but also passes through the coverage areas of all SBSs within the set $\mathcal{N}$. For the sake of generality, we assume that $N_k\ge 2$ in the following analysis. Table 1 presents the main symbols and their definitions.

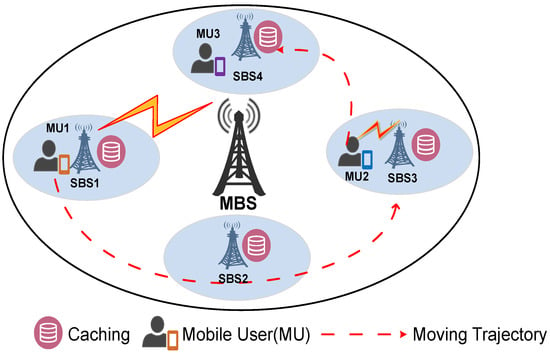
Figure 1. The illustration of the wireless heterogeneous cellular network.

Table 1. Main notations and descriptions.

Notation	Description
$\mathcal{N}$	Set of all base stations
$\mathcal{K}$	Set of MUs
$\mathcal{F}$	Set of contents
$N_k$	Number of base stations traversed by MU k
$\mathcal{T}$	Set of large time-scale slots
$t_i$	The i-th small time-scale slot within the t-th large time-scale slot
$\Delta t$	Duration of a small time-scale slot
$G_n$	Caching capacity of SBS n
B	Size of each content
M	Total number of small time-scale slots in each large time-scale slot
$R_{k,n}$	Transmission rate between MU k and base station n
${\eta }_{k,n}$	Unit transmission delay cost between MU k and base station n
$x_{n,f}\left(t\right)$	Proportion of content f cached by base station n in the t-th large time-scale slot

3.2. Dual Time-Scale Model

In practical scenarios, the popularity of content typically exhibits dynamic changes over time. For instance, the popularity of a newly released film tends to decline after a 2–3 week period, while that of headline news often subsides within 1–2 days. Consequently, to capture such temporal variations, the popularity of content can be quantified using a large time interval (e.g., days or weeks) as the measurement unit. In contrast, the movement duration of MUs in a cellular network is generally measured on the scale of minutes or hours. By comparing these two time measurement scales, it is evident that the temporal variation rate of content popularity is significantly slower than that of MU movement, and the two time scales are not of the same order of magnitude. Therefore, considering the mismatch between the time-varying characteristics of content popularity and MU mobility, we adopt the dual time-scale model to analyze the following two aspects: First, the caching decisions of SBSs tailored to the time-varying content popularity. Second, the delay costs incurred by MUs when requesting contents from base stations.

The dual time-scale model consists of a large time-scale slot and a small time-scale slot. Content popularity evolves over a large time scale, and it is assumed that there are T large time-scale time slots, denoted by $\mathcal{T}=\{1,2,\dots ,T\}$. Each large time-scale slot is further partitioned into M small time-scale slots of equal duration. Let $t_i$ represent the i-th small time-scale slot within the t-th large time-scale slot, where the duration of each small time-scale slot is defined as $\Delta t$. The mobility of MUs is characterized based on the designed small time scale.

3.3. Content Caching Model

There are F distinct contents in the network, denoted by $\mathcal{F}=\{1,2,\dots ,F\}$. For analytical simplicity, we assume that each content has an identical size of B bits. It is worth noting that this assumption of uniform content size can be extended to the scenario of heterogeneous content sizes. Specifically, we can split each content into multiple segments, where all segments are designed to have the same size [27]. We assume that MBS is capable of caching all the contents. Each SBS has a limited caching capacity, and the total size of contents it can cache does not exceed $G_n$ bits. Considering the mobility of MUs, if SBSs adopt uncoded caching, MUs may not have sufficient time to fully download the requested content when passing through the coverage area of SBSs. Therefore, a coded caching strategy is adopted in our work. By leveraging the MDS coding method, each content can be encoded into a set of coded data packets of different sizes. When an MU requests specific content according to its demand, it only needs to obtain the coded data packets of the content from multiple base stations. Once the total number of bits of the acquired coded data packets reaches or exceeds B bits, the MU can decode the data packets to retrieve the complete original content. In the t-th large time-scale slot, it is assumed that the proportion of content f cached by SBS n is $x_{n,f}\left(t\right)\in [0,1]$, and the caching proportion of content f remains unchanged during this large time-scale slot. Let $X_n\left(t\right)=[x_{n,1}\left(t\right),\dots ,x_{n,F}\left(t\right)]$ denote the caching decision of SBS n in the t-th large time-scale slot. Considering the caching capacity constraint of SBS n, the total number of bits of coded contents cached by SBS n in the t-th large time-scale slot must satisfy the following constraint:

$$\sum _{f=1}^F{x}_{n,f}\left(t\right)B\le G_n,\forall n\in \mathcal{N}\setminus \left\{0\right\},\forall t\in T.$$

(1)

3.4. Average Delay Cost Model

In accordance with its pre-planned movement path, MU k is scheduled to traverse $N_k$ base stations. For the purpose of the analysis, we assume that each MU requests a single content at the beginning of its journey, and this request remains active until the content is fully acquired along its pre-planned path. Handling multiple content requests during one traversal will be investigated in a future study. If MU k has not acquired all the data packets needed to decode the requested content by the time it reaches the last SBS in its path, it will then request the remaining data packets from the MBS. Due to the different caching strategies of SBSs, MU k may not need to traverse all the base stations along its pre-planned path to acquire all the coded data packets required for decoding the requested content. We assume that MU k acquires all data packets required for content decoding when passing through the $J_k$-th base station, $1\le J_k\le N_k,J_k\in N^{+}$. In particular, when $1\le J_k<N_k$, it indicates that MU k has acquired all the required coded data packets solely from the SBSs along its pre-planned path, i.e., it does not need to request data from the MBS. When $J_k=N_k=\left|\mathcal{N}\right|$, it means that MU k must send content requests to both SBSs along its pre-planned path and the MBS before it can acquire all the coded data packets for decoding the requested content.

In the t-th large time-scale slot, it is assumed that MU k resides within the coverage area of SBS n for $S_{k,n}\left(t\right)$ small time-scale slots. Let the content transmission rate between MU k and SBS n be $R_{k,n}$ bits/s, and the unit transmission delay cost be ${\eta }_{k,n}$. Specifically, we assume that the unit transmission delay cost is identical across all SBSs, and the transmission delay cost between any SBS and MBS is higher than that between any two SBSs, i.e., ${\eta }_{k,0}>{\eta }_{k,n}$. When MU k acquires all the coded data packets for the requested content f by traversing the first $J_k$ base stations along its pre-planned movement path, the transmission delay cost $C_{k,f}\left(t\right)$ can be expressed as follows:

$$C_{k,f}\left(t\right)=\sum _{n=1}^{J_k-1}min\left({\displaystyle \frac{x_{n,f}\left(t\right)B}{R_{k,n}}},S_{k,n}\left(t\right)\Delta t\right){\eta }_{k,n}+{\displaystyle \frac{B-{\sum }_{n=1}^{J_k-1}{B}_{k,n}}{R_{k,n_{J_k}}}}{\eta }_{k,n_{J_k}},$$

(2)

where $B_{k,n}=min(X_{n,f}\left(t\right)B,S_{k,n}\left(t\right)\Delta t{R}_{k,n})$ and denotes the actual bits of the requested content acquired by MU k within the coverage area of SBS n. In Equation (2), $n_{J_k}$ denotes the index of the base station that MU k traverses the $J_k$-th base station along its pre-planned movement path. $min\left({\displaystyle \frac{x_{n,f}\left(t\right)B}{R_{k,n}}},S_{k,n}\left(t\right)\Delta t\right)$ represents the actual delay incurred by MU k when requesting the content f within the coverage area of SBS n, which is determined by the minimum value between the time required for the SBS n to transmit cached content to the MU k and the time MU k spends traveling within the coverage area of the SBS n. Particularly, when $J_k=N_k=\left|\mathcal{N}\right|$, it indicates that MU k fails to obtain all data packets from the first $(J_k-1)$ SBSs, and thus must request the remaining coded data packets from the MBS. In this case, $n_{J_k}=0$.

Then, in the t-th large time-scale slot, the total delay cost $C\left(t\right)$ for all MUs in the network to request contents can be expressed as follows:

$$C\left(t\right)=\sum _{k=1}^K\sum _{f=1}^F\left(\sum _{n=1}^{J_k-1}min\left({\displaystyle \frac{x_{n,f}\left(t\right)B}{R_{k,n}}},S_{k,n}\left(t\right)\Delta t\right){\eta }_{k,n}+{\displaystyle \frac{B-{\sum }_{n=1}^{J_k-1}{B}_{k,n}}{R_{k,n_{J_k}}}}{\eta }_{k,n_{J_k}}\right).$$

(3)

3.5. Problem Formulation

We aim to minimize the average delay cost $C_{\left|\mathcal{T}\right|}$ of content requests from all MUs in the network over $\left|\mathcal{T}\right|$ large time-scale slots, given the coded caching decision vector $X\left(t\right)$. Thus, the dual time-scale time-varying coded caching optimization problem can be mathematically formulated as

$$\begin{array}{cc}\underset{X\left(t\right)}{min}\hfill & C_{\left|\mathcal{T}\right|}={\displaystyle \frac{1}{\left|\mathcal{T}\right|}}\sum _{t=1}^{\left|\mathcal{T}\right|}\sum _{k=1}^K\sum _{f=1}^F\left(\sum _{n=1}^{J_k-1}min\left({\displaystyle \frac{x_{n,f}\left(t\right)B}{R_{k,n}}},S_{k,n}\left(t\right)\Delta t\right){\eta }_{k,n}+{\displaystyle \frac{B-{\sum }_{n=1}^{J_k-1}{B}_{k,n}}{R_{k,n_{J_k}}}}{\eta }_{k,n_{J_k}}\right),\hfill \end{array}$$

(4)

$$\begin{array}{cc}s.t.\hfill & \sum _{f=1}^F{x}_{n,f}\left(t\right)B\le G_n,\forall n\in \mathcal{N}\setminus \left\{0\right\},\forall t\in \mathcal{T},\hfill \end{array}$$

(5)

$$\begin{array}{cc}& \sum _{n=1}^{N_k}{S}_{k,n}\left(t\right)\le M,\forall k\in \mathcal{K},\hfill \end{array}$$

(6)

$$\begin{array}{cc}& x_{n,f}\left(t\right)\in [0,1],\forall n\in \mathcal{N}\setminus \left\{0\right\},\forall f\in F,\forall t\in \mathcal{T}.\hfill \end{array}$$

(7)

The constraint (5) denotes the caching capacity constraint of SBS n. The constraint (6) indicates that the number of small time-scale slots required for MU k to traverse its planned path within the t-th large time-scale slot does not exceed the total number of small time-scale slots in that large time-scale slot. The constraint (7) represents the coded caching decision variable of SBS n.

In the aforementioned optimization problem, it is difficult to derive the exact analytical expression of content popularity due to the time-varying characteristic, which makes it challenging for SBSs to determine caching strategies in each large time-scale slot. Moreover, since the proportion of content cached at SBSs is a continuous decision variable, the caching decision problem becomes increasingly complex as the content catalog size grows. Subsequently, we design a dynamic coded caching algorithm based on deep reinforcement learning. By training the neural network associated with this algorithm, we achieve continuous optimal control over caching decisions while achieving the goal of minimizing the average delay cost of MUs’ content requests.

4. Coded Caching Algorithm Design

In this section, we first transform the above optimization problem into a Markov decision process model $<S,A,P,r>$, where S denotes the caching state space of all SBSs, A denotes the joint caching action space of all SBSs, P denotes the caching state transition probability matrix, and r denotes the real-time reward after SBSs implementing the caching action. Due to the adoption of the coded caching strategy, the caching states evolve continuously, which renders it challenging to derive a complete state transition probability matrix. To solve this problem, we integrate neural networks with a model-free learning approach to design a dynamic caching algorithm for solving the delay cost optimization problem.

4.1. Markov Decision Process

The caching states of all SBSs are transmitted to the MBS via the wireless backhaul network at the end of the last large time-scale slot. Subsequently, the MBS makes caching decisions based on the upload joint caching states and then transmits the data packets of contents to each SBS at the start of the current large time-scale slot. As MUs move, they request and receive contents from base stations, where the transmission of coded data packets for a given content may require multiple small time-scale slots. Figure 2 shows the caching decision and content transmission process under the dual time-scale model.

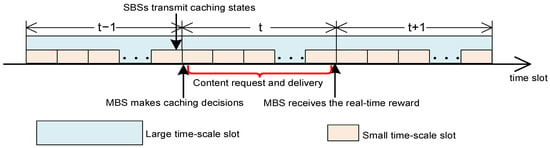
Figure 2. The caching decision and content transmission process under the dual time-scale model.

In the t-th large time-scale slot, the caching states received by MBS comprise two key features: the number of requests for each content and the caching states of SBSs, which are both observed during the $(t-1)$-th large time-scale slot. The vector composed of these two features is defined as the caching state space $S\left(t\right)$, which is expressed as

$$S\left(t\right)=[R(t-1),s_c(t-1)].$$

(8)

In Equation (8), $R(t-1)=[R_1(t-1),\dots ,R_F(t-1)]$ represents the vector composed of the number of requests for each content from all SBSs during the $(t-1)$-th large time-scale slot. $s_c(t-1)=[s_1(t-1),\dots ,s_N(t-1)]$ is the vector composed of the caching state of each SBS during the $(t-1)$-th large time-scale slot, and $s_n(t-1)=[s_{n,1}(t-1),\dots ,s_{n,F}(t-1)]$ denotes the caching proportion of each content by SBS n. The caching state space is represented as a one-dimensional vector of size $1\times (N+1)F$.

Based on the state space obtained in the t-th large time-scale slot, the MBS makes corresponding caching decisions, and the action space can be defined as

$$X\left(t\right)=[X_1\left(t\right),\dots ,X_n\left(t\right),\dots ,X_N\left(t\right)],$$

(9)

where $X_n\left(t\right)=[x_{n,1}\left(t\right),\dots ,x_{n,F}\left(t\right)]$ represents the caching proportion of each content by SBS n in the t-th large time-scale slot. This action space is a one-dimensional vector with a dimension of $1\times NF$.

At the start of the t-th large time-scale slot, the MBS transmits the coded data packets of each content to all SBSs based on the current caching states. Concurrently, each SBS begins to receive content requests from MUs and checks whether the requested content is in its local cache. If the requested content exists in the SBS’s local cache, the SBS directly sends the corresponding coded data packets to the requesting MU. At the end of the t-th large time-scale slot, the MBS will obtain a real-time reward $r_t$, which reflects the performance quality of the caching decision made in this time slot. Specifically, we define the real-time reward as the negative value of the total delay cost $C\left(t\right)$ incurred by all MUs for their content requests. Maximizing this real-time reward is equivalent to minimizing the total content request delay cost in this time slot, which aligns with the optimization objective in Equation (4). The real-time reward $r_t$ can be defined as

$$r_t=-\sum _{k=1}^K\sum _{f=1}^F\left(\sum _{n=1}^{J_k-1}min\left({\displaystyle \frac{X_{n,f}\left(t\right)B}{R_{k,n}}},S_{k,n}\left(t\right)\Delta t\right){\eta }_{k,n}+{\displaystyle \frac{B-{\sum }_{n=1}^{J_k-1}{B}_{k,n}}{R_{k,n_{J_k}}}}{\eta }_{k,n_{J_k}}\right).$$

(10)

The real-time reward defined in Equation (10) only reflects the quality of the caching decision in the current large time-scale slot. It fails to capture the impact of caching decisions across all large time-scale slots on the average delay cost incurred by all MUs for their content requests from a global optimization perspective. Thus, we define a discounted return (also called cumulative reward) $U_t$ based on the real-time reward as the optimization objective in the Markov decision process [28]. $U_t$ can be defined as

$$U_t=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\dots =\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k},$$

(11)

where $\gamma \in [0,1]$ denotes the reward discount factor, which reflects the weight of the current real-time reward and future rewards. When the discount factor $\gamma =0$, it indicates that the coded caching decision focuses exclusively on the current real-time reward. When $\gamma =1$, it means that future rewards are assigned equal importance to the current reward.

The purpose of formulating the average delay cost optimization problem as a Markov decision process is to determine the optimal coded caching strategy function $\pi \left(S\right(t\left)\right)$, whereby the MBS makes the optimal caching decision space $X\left(t\right)$ for each state $S\left(t\right)$ so as to maximize the expected discounted return, indicating the discounted return $U_t$ is determined by the current state $S\left(t\right)$ and the caching action $X\left(t\right)$. However, due to the time-varying nature of content popularity, both the state and the caching action are subject to uncertainty. To address this issue, we define the action-value function $Q_{\pi }(S\left(t\right),X\left(t\right))$ and the state value function $V_{\pi }\left(S\left(t\right)\right)$ based on the discounted return $U_t$ and Bellman equation [28].

$$Q_{\pi }(S\left(t\right),X\left(t\right))=E_{S(t+1),X(t+1)}\left[r_t+\gamma Q_{\pi }(S(t+1),X(t+1))|S\left(t\right),X\left(t\right)\right].$$

(12)

The action-value function $Q_{\pi }(S\left(t\right),X\left(t\right))$ in Equation (12) denotes the expected cumulative discounted reward by executing caching action $X\left(t\right)$ in state space $S\left(t\right)$ according to caching policy $\pi \left(S\right(t\left)\right)$.

$$V_{\pi }\left(S\left(t\right)\right)=E_{X\left(t\right),S(t+1)}\left[r_t+\gamma V_{\pi }\left(S(t+1)\right)|S\left(t\right)\right].$$

(13)

The state value function $V_{\pi }\left(S\left(t\right)\right)$ in Equation (13) represents the expected cumulative discounted reward that can be obtained under the caching state $S\left(t\right)$ according to the caching policy $\pi \left(S\right(t\left)\right)$.

In practice, computing the above two functions poses significant challenges. On one hand, both the action-value function and the state-value function depend on the state transition probabilities, which cannot be explicitly derived due to the continuous nature of the state space, thereby limiting the application of model-based computation methods. On the other hand, when the number of cached contents is large, the dimensions of the state and action spaces increase drastically, making it difficult for traditional reinforcement learning algorithms, such as Q-learning [29] and SARSA [30], to accurately estimate the value functions, which will trigger the curse of dimensionality. To address the continuous time-varying caching decision problem, we propose an improved actor–critic algorithm. Specifically, we employ the Monte Carlo approximation method to estimate the action values and state values, and then leverage the temporal-difference (TD) learning method to train the neural network, aiming to find the optimal coded caching policy.

4.2. Advantage Actor–Critic-Based Coded Caching Algorithm

The actor–critic algorithm consists of two components: an actor network (policy network) and a critic network (value network). The actor network is responsible for action selection, i.e., making the caching decisions based on the obtained state space $S\left(t\right)$. The critic network evaluates the quality of caching actions selected by the actor network, where higher evaluation scores indicate more optimal actions. This evaluation, approximated by the action-value function $Q_{\pi }(S\left(t\right),X\left(t\right))$, is then fed back to the actor network to guide the refinement of caching decisions. The traditional actor–critic algorithm tends to exhibit high variance and slow convergence. To address these limitations, we propose an advantage actor–critic (A2C)-based coded caching algorithm, which leverages an appropriate advantage function to mitigate variance and accelerate convergence. The advantage actor–critic architecture is illustrated in Figure 3.

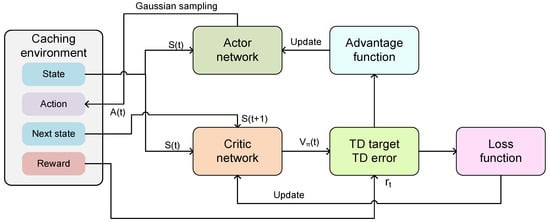
Figure 3. The illustration of the advantage actor–critic architecture.

Based on the above analysis, the minimization of the average delay cost can be reformulated as maximizing either the action-value function or the state-value function under a given caching policy. Consequently, we first construct a caching policy function and then optimize it to obtain the optimal state-value function. The caching policy function can be defined as

$$J\left(\pi \right)=E_{S\left(t\right)}\left[V_{\pi }\left(S\left(t\right)\right)\right].$$

(14)

The update of the caching policy is determined by the parameter $\theta$ of the actor network, which aims to increase the objective function $J\left(\pi \right)$, thereby improving the caching policy over time. The caching policy function in Equation (14) can be formulated as the following optimization problem with respect to the parameter $\theta$:

$$\underset{\theta }{max}J\left(\pi \left(X\left(t\right)\right|S\left(t\right);\theta )\right).$$

(15)

To maximize the state value, the parameter $\theta$ of the actor network can be updated using the gradient ascent method, i.e.,

$${\theta }^{\prime }\leftarrow \theta +{\alpha }_a{\nabla }_{\theta }J\left(\pi \left(X\left(t\right)\right|S\left(t\right);\theta )\right),$$

(16)

where ${\alpha }_a$ is the learning rate of the actor network. We can leverage the Monte Carlo approximation method to derive the approximate policy gradient $g\left(S\right(t),X(t\left)\right|\theta )$ [28],

$$g(S\left(t\right),X\left(t\right)|\theta )=Q_{\pi }(S\left(t\right),X\left(t\right))·{\nabla }_{\theta }ln\pi \left(X\left(t\right)\right|S\left(t\right);\theta ).$$

(17)

This approximate policy gradient in Equation (17) is an unbiased estimate of ${\nabla }_{\theta }J\left(\pi \left(X\left(t\right)\right|S\left(t\right);\theta )\right)$. Although $g\left(S\right(t),X(t\left)\right|\theta )$ is an unbiased estimation, it exhibits high variance and slow convergence during the algorithm training process. Therefore, we introduce the advantage function, defined as $Q_{\pi }(S\left(t\right),X\left(t\right))-V_{\pi }\left(S\left(t\right)\right)$, to derive a new unbiased estimate of ${\nabla }_{\theta }J\left(\pi \left(X\left(t\right)\right|S\left(t\right);\theta )\right)$ given by

$$g(S\left(t\right),X\left(t\right)|\theta )=\left[Q_{\pi }(S\left(t\right),X\left(t\right))-V_{\pi }\left(S\left(t\right)\right)\right]·{\nabla }_{\theta }ln\pi \left(X\left(t\right)\right|S\left(t\right);\theta ).$$

(18)

On the basis of the above analysis, the A2C-based coded caching algorithm is detailed as follows.

Actor network: The actor network uses policy function $\pi \left(X\right(t\left)\right|S\left(t\right);\theta )$ to guide the MBS making caching decisions. Since the caching decision variable $x_{n,f}\left(t\right)$ is continuous, we model the policy function using a Gaussian distribution, i.e.,

$$\pi \left(X\left(t\right)\right|S\left(t\right);\theta )={\displaystyle \frac{1}{\sqrt{2\pi exp\left({\sigma }^2\left(S\left(t\right)\right|\theta )\right)}}}·exp\left(-{\displaystyle \frac{{[X\left(t\right)-\mu \left(S\left(t\right)\right|\theta )]}^2}{2{\sigma }^2\left(S\left(t\right)\right|\theta )}}\right),$$

(19)

where $\mu \left(S\right(t\left)\right|\theta )$ and ${\sigma }^2\left(S\left(t\right)\right|\theta )$ denote the mean and variance of the Gaussian distribution, respectively. The caching decision is obtained by sampling from the Gaussian distribution to determine the action $X\left(t\right)$ for the current slot. After each SBS executes this action, the current caching state transitions to the next state $S(t+1)$ and the MBS computes the real-time reward $r_t$. Note that, when each SBS executes the caching action, the cached contents should satisfy ${\sum }_{f=1}^F{x}_{n,f}\left(t\right)B\le G_n,\forall n\in \mathcal{N}$. To meet the caching capacity constraint, the sampled continuous caching actions are mapped onto the feasible action space by a sorting-and-filling rule. This projection technique is widely adopted in the constrained deep reinforcement learning method [31], and it preserves the convergence behavior of the proposed algorithm. Specifically, the sampled caching proportions by the actor network are sorted in descending order. Then, the SBS caches the corresponding content ratio in this order until the maximum caching capacity is reached. Any remaining contents that would exceed the capacity are not cached.

Critic network: The critic network takes the caching states $S\left(t\right)$ and $S(t+1)$ as inputs and outputs the corresponding state values $V_{\pi }\left(S\left(t\right)\right|\omega )$ and $V_{\pi }\left(S(t+1)\right|\omega )$, where $\omega$ denotes the parameter of the critic network. The parameter $\omega$ of the critic network is updated using the temporal-difference (TD) method. The TD target is defined as ${\widehat{V}}_{\pi }\left(t\right)=r_t+\gamma V_{\pi }\left(S(t+1)\right|\omega )$ and the TD error is ${\delta }_t=V_{\pi }\left(S\left(t\right)\right|\omega )-{\widehat{V}}_{\pi }\left(t\right)$. A least-squares loss function is then constructed based on the TD error, and the gradient descent algorithm is used to update $\omega$.

Neural network update: First, the parameters $\theta$ of the actor network are updated. Since the critic network only outputs the state value, we can use the Monte Carlo approximation to reformulate Equation (18) as follows:

$$g(S\left(t\right),X\left(t\right)|\theta )=\left[r_t+\gamma V_{\pi }\left(S(t+1)\right|\omega )-V_{\pi }\left(S\left(t\right)\right|\omega )\right]·{\nabla }_{\theta }ln\pi \left(X\left(t\right)\right|S\left(t\right);\theta ).$$

(20)

We then leverage the gradient ascent method to update $\theta$, i.e.,

$${\theta }^{\prime }\leftarrow \theta +{\alpha }_{a}g(S\left(t\right),X\left(t\right)|\theta ).$$

(21)

Next, the parameters $\omega$ of the critic network are updated. Based on the least squares, the loss function is defined as follows:

$$L\left(\omega \right)={\displaystyle \frac{1}{2}}{\left[V_{\pi }\left(S\left(t\right)\right|\omega )-{\widehat{V}}_{\pi }\left(t\right)\right]}^2.$$

(22)

Then, the gradient of the loss function with respect to $\omega$ can be expressed as

$${\nabla }_{\omega }L\left(\omega \right)=\left(V_{\pi }\left(S\left(t\right)\right|\omega )-{\widehat{V}}_{\pi }\left(t\right)\right){\nabla }_{\omega }{V}_{\pi }\left(S\left(t\right)\right|\omega ).$$

(23)

The gradient descent algorithm is used to update the value network parameter $\omega$, i.e.,

$${\omega }^{\prime }\leftarrow \omega -{\alpha }_c{\nabla }_{\omega }L\left(\omega \right),$$

(24)

where ${\alpha }_c$ is the learning rate of the critic network. The proposed advantage actor–critic-based coded caching algorithm is summarized in Algorithm 1.

Algorithm 1 Advantage Actor–Critic (A2C) based Coded Caching Algorithm

Initialization: Randomly initialize the actor network parameter $\theta$ and critic network parameter $\omega$, caching state space $S\left(0\right)$, learning rates ${\alpha }_a$ and ${\alpha }_c$, reward discount factor $\gamma$ Loop for each episode $L=1,2,\dots ,L_{max}$ 1: for $t=1,2,3,\dots$ 2:       Input the state space $S\left(t\right)$ into the actor network, calculate $\mu \left(S\right(t\left)\right|\theta )$ and ${\sigma }^2\left(S\left(t\right)\right|\theta )$ 3:       Obtain the caching action $X\left(t\right)$ through random sampling from the Gaussian distribution $Normal(\mu \left(S\left(t\right)\right|\theta ),{\sigma }^2\left(S\left(t\right)\right|\theta ))$ 4:       All SBSs implement $X\left(t\right)$ and check the caching capacity constraint, acquire the real-time reward $r_t$ and the next caching state space $S(t+1)$ 5:       Input the state spaces $S\left(t\right)$ and $S(t+1)$ into the critic network, calculate the TD target ${\widehat{V}}_{\pi }\left(t\right)=r_t+\gamma V_{\pi }\left(S(t+1)\right|\omega )$ and TD error ${\delta }_t=V_{\pi }\left(S\left(t\right)\right|\omega )-{\widehat{V}}_{\pi }\left(t\right)$ 6:       Update the actor network parameter $\theta$ based on Equations (20) and (21) 7:       Update the critic network parameter $\omega$ based on Equations (23) and (24) 8:       $t=t+1$ 9: end for $L=L+1$ End Loop

4.3. Convergence and Complexity Analysis

The convergence of the proposed A2C-based coded caching algorithm can be guaranteed by selecting appropriate learning rates ${\alpha }_a$ and ${\alpha }_c$. According to [32], if the learning rate ${\alpha }_a$ satisfies ${\sum }_{t=0}^{\infty }{\alpha }_a=\infty$ and ${\sum }_{t=0}^{\infty }{\alpha }_a^2<\infty$, and the learning rate ${\alpha }_c$ also satisfies ${\sum }_{t=0}^{\infty }{\alpha }_c=\infty$ and ${\sum }_{t=0}^{\infty }{\alpha }_c^2<\infty$, then the convergence of the A2C-based coded caching algorithm can be guaranteed.

Next, the complexity of the proposed A2C-based coded caching algorithm is analyzed. During each episode of the training process, the time complexity of the actor network is $O\left(\right(N+1)F·d+d·NF)$, where d denotes the size of the hidden layer. The time complexity of the critic network is $O\left(\right(N+1)F·d+d)$. We assume that the size of the hidden layer in the critic network is the same as that in the actor network. Hence, the time complexity of the proposed algorithm is $O(L_{max}·|\mathcal{T}|·((N+1)F·d+d·NF))$.

5. Performance Evaluation

In this section, numerical simulations are conducted to verify the convergence and effectiveness of the proposed A2C-based coded caching algorithm. In addition, we compare the performance of the A2C-based coded caching algorithm with several benchmark caching schemes under different simulation parameters to further demonstrate the superiority of our algorithm.

5.1. Experimental Setups

We consider that the heterogeneous cellular network consists of one MBS and $N=6$ SBSs. There are 100 different types of content in the network, and each content has the same size of 100 MB. We assume the total number of large time-scale slots is $\left|\mathcal{T}\right|=50$. Within each large time-scale slot t, there are 100 small time-scale slots, each of duration $\Delta t=10$ s. The number of small time-scale slots required for MU k to pass through SBS n satisfies $3\le S_{k,n}\left(t\right)\le 9$, $S_{k,n}\left(t\right)\in {\mathbf{N}}^{+}$. The content transmission rate between MU k and SBS n is $R_{k,n}=2$ MB/s, and the unit transmission delay cost is ${\eta }_{k,n}=0.2$. The content transmission rate between node MU k and the macro base station is $R_{k,0}=0.5$ MB/s, and the unit transmission delay cost is ${\eta }_{k,0}=1$. All the experimental evaluations are performed on a Windows 11 64-bit desktop machine with the following hardware configuration: Intel Core i7, 32 GB of RAM, and RTX 4060 Ti GPU.

The advantage actor–critic neural network architecture is defined as follows: both the actor and critic networks are implemented as fully connected neural networks with one hidden layer. To balance learning performance and computational efficiency, the hidden layer size is set to 80 neurons, which provides sufficient representation capacity while maintaining stable training. The Rectified Linear Unit (ReLU) is used as the activation function for the hidden layer. For the actor network, a Sigmoid activation is applied to the output layer to ensure that the predicted caching proportions remain within $[0,1]$. In contrast, the critic network employs a Linear activation in the output layer to estimate the state value. Both networks are optimized using the Adam optimizer.

5.2. Benchmark Caching Schemes

We compare our proposed A2C-based coded caching algorithm with the following five baseline caching schemes.

(1)

A2C-based Uncoded Caching Algorithm: When content popularity remains unknown within each large time-scale slot, caching decisions are made leveraging the A2C algorithm framework, with each content being either fully cached or not cached at all.

(2)

Proximal Policy Optimization (PPO)-based Coded Caching Algorithm: This caching algorithm is based on an actor–critic model and utilizes the exact same problem formulation as our proposed method. The key difference is that PPO trains its actor network using a clipped surrogate objective function to optimize the caching policy.

(3)

Informed Greedy Caching (IGC) Algorithm: When the exact content requests of MUs are known a priori for the upcoming large time-scale slot, SBSs jointly determine a caching solution by greedily maximizing the amount of requesting content using coded caching. Although not a globally optimal solution, IGC provides a strong, information-assisted benchmark and effectively approximates a practical upper-bound performance for comparison.

(4)

Most Popular Caching (MPC) Algorithm [33]: At the start of each large time-scale slot, the macro base station makes caching decisions based on the historical popularity of the content. That is, each SBS n caches contents in descending order of the content popularity until the caching capacity of $G_n$ bits is reached.

(5)

Random Caching (RC) Algorithm: In each large time-scale slot, each SBS n randomly caches $G_n$ bits of contents.

5.3. Results and Discussion

We first investigate the impact of learning rates ${\alpha }_a$ and ${\alpha }_c$ on the convergence of our proposed A2C-based coded caching algorithm when it is assumed that the caching capacity of each SBS is 5000 MB and the reward discount factor $\gamma =0.9$. All the learning curves are plotted using a moving average with a window size of 50.

As shown in Figure 4a, we set the learning rate ${\alpha }_a$ to 0.0001, 0.0003, and 0.0005 to evaluate the convergence of the episode reward. It can be observed that all reward values increase with the number of training episodes for all learning rates. When ${\alpha }_a=0.0001$, this curve stabilizes after about 300 episodes and achieves the highest final reward among the three cases. When ${\alpha }_a=0.0005$, this curve converges relatively quickly initially, but exhibits significant fluctuations after 300 episodes. In Figure 4b, we set the critic learning rate to 0.0005, 0.001, and 0.003. We find that as the learning rate increases, the curves exhibit greater fluctuations after 200 episodes. For ${\alpha }_c=0.0005$, the corresponding curve remains stable after approximately 300 episodes and achieves the highest final reward. Therefore, in our simulations, we set the ${\alpha }_a$ as $0.0001$ and ${\alpha }_c$ as $0.0005$.

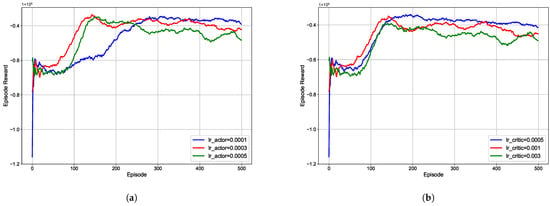
Figure 4. The impact of different learning rates ${\alpha }_a$ and ${\alpha }_c$ on the convergence of A2C-based coded caching algorithm. (a) learning rate ${\alpha }_a$; (b) learning rate ${\alpha }_c$.

Figure 5 illustrates the effect of different reward discount factors $\gamma$ on the episode reward per iteration. The figure shows that as $\gamma$ increases, the episode reward per iteration steadily rises, reaching its maximum at $\gamma =0.9$. A larger $\gamma$ indicates that the learning process places greater emphasis on the impact of current caching decisions on the future rewards, thereby facilitating the global reward optimization. Consequently, we can conclude that increasing the weight assigned to large time-scale rewards during the caching strategy learning process is beneficial.

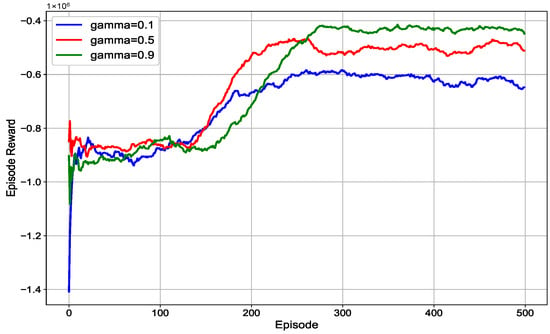
Figure 5. The impact of different discount reward factors on the convergence of A2C-based coded caching algorithm.

In Figure 6, we compare the convergence of A2C-based coded caching and A2C-based uncoded caching. We observe that both algorithms can converge when the number of iterations is sufficiently large. However, the A2C-based uncoded caching algorithm converges more quickly, as its caching decisions are discrete and the corresponding state and action spaces are relatively simple. In contrast, the A2C-based coded caching algorithm involves continuous decisions and requires sampling through a Gaussian policy, which increases the complexity of the state and action spaces. Nevertheless, once the coded caching algorithm converges, it exhibits significantly better performance than its uncoded counterpart.

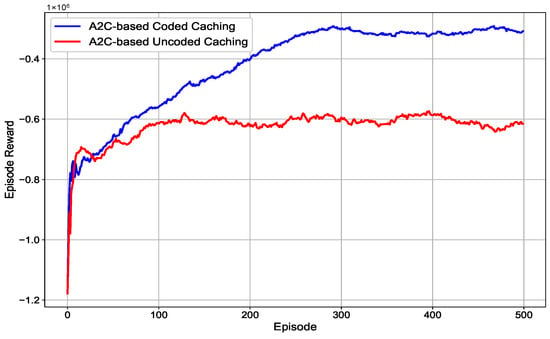
Figure 6. The convergence comparison of A2C-based coded caching and A2C-based uncoded caching.

In Table 2, we present a comparison of the computational cost for the A2C-based coded and uncoded caching algorithms, based on the results in Figure 6. We can find that the A2C-based coded caching algorithm requires approximately 31% more training time than the uncoded caching scenario, due to its continuous action space and more complex policy optimization. Energy consumption exhibits a similar trend, with the A2C-based coded caching consuming more energy during the training phase. Although the computational cost of our proposed A2C-based coded caching algorithm is slightly higher than that of the uncoded caching scenario, the performance gain once the algorithm converges reaches approximately 49.93%.

Table 2. The comparison of the computational costs between the A2C-based coded and uncoded caching algorithms.

Algorithm	Training Time (Seconds)	Energy Consumption (Wh)	Convergence Iterations	Average Reward
A2C-based Uncoded Caching	76.88	1.5374	300+	−615,189.06
A2C-based Coded Caching	100.78	2.0909	200+	−308,052.9

Figure 7 illustrates the trend of the average delay cost with caching capacity in different caching algorithms. It is observed that as the caching capacity of SBSs increases, the average delay cost of all caching algorithms decreases. This is because a larger caching capacity allows SBSs to store more content, increasing the probability that the content requested by MUs can be directly served from local caches. Consequently, the need for MUs to request contents from the macro base station is reduced, leading to lower average network delay costs. Note that the IGC serves as a lower bound on the average delay cost performance of all the caching algorithms. However, since MUs’ content demand is typically unknown in practice, achieving this lower bound is impossible.

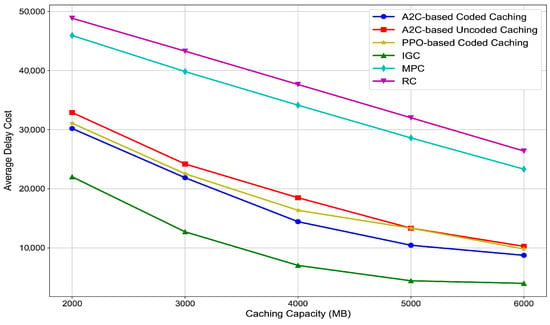
Figure 7. The comparison of the network average delay cost with caching capacity in different caching algorithms.

Among the other caching algorithms, we find that the performance of the deep reinforcement learning approaches (A2C-based coded, PPO-based coded, and A2C-based uncoded) significantly outperforms the MPC and RC algorithms. This is because the A2C and PPO-based algorithms make caching decisions by learning from the historical content requests of MUs, whereas MPC and RC do not take this adaptive historical request information into account. Furthermore, both the A2C-based coded and PPO-based coded algorithms yield a significantly lower average delay cost than the A2C-based uncoded caching algorithm. This is due to the uncoded caching strategy storing the entire content, which fundamentally reduces the diversity of cacheable contents under the limited caching space. Hence, some MUs’ content requests cannot be satisfied by SBSs, increasing the delay cost associated with requesting content from the MBS. Finally, when comparing the two coded algorithms, our A2C-based coded caching consistently outperforms the PPO-based counterpart. This indicates that A2C’s advantage-based update mechanism provides more effective and flexible policy adaptation to continuous caching decisions and dynamic environments than PPO’s clipped objective.

Figure 8 shows the impact of increasing the number of contents in the network on the scalability of the considered caching algorithms. As shown in the figure, the average delay costs of all algorithms increase with the number of contents due to the limited caching capacity of SBSs. However, the A2C-based coded caching algorithm proposed in our work consistently outperforms the other four caching algorithms. This demonstrates that the proposed A2C-based coded caching algorithm maintains good scalability as the number of contents in the network increases.

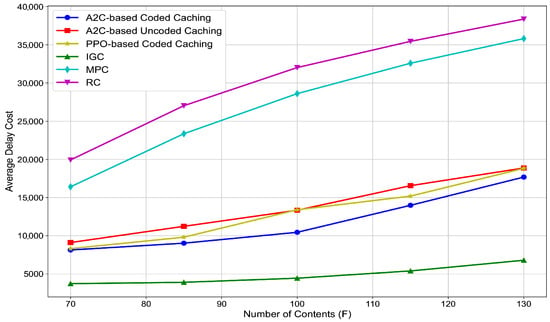
Figure 8. The comparison of the network average delay cost with the number of contents in different caching algorithms.

We further investigate the impact of the number of SBSs on the performance of all caching algorithms. As shown in Figure 9, as the number of SBSs increases, the average delay cost of all caching algorithms decreases. This is due to a larger number of SBSs increasing the total amount of content that can be cached across the network, thereby reducing the need for MUs to request content from the macro base station. Particularly, when the number of the SBSs is up to 9, our proposed algorithm outperforms the PPO-based coded caching, A2C-based uncoded caching, MPC, and RC algorithms with the improvement on the average delay cost of approximately 5%, 24%, 72%, and 75%, respectively. Moreover, the rate at which the average delay cost decreases slows as the number of SBSs increases. This suggests that once the number of SBSs along a MU’s planned path exceeds the minimum required to satisfy the MU’s content request, the MU can obtain all necessary coded packets for decoding without visiting all base stations in the path. At this point, further increasing the number of small base stations has diminishing returns on reducing the average delay cost of content requests.

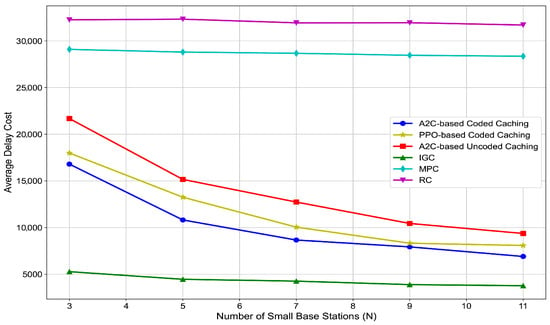
Figure 9. The comparison of the network average delay cost with the number of SBSs in different caching algorithms.

6. Conclusions

In this paper, we investigated the dynamic coded caching optimization problem in heterogeneous cellular networks under a dual time-scale model. By jointly considering long-term content popularity evolution and short-term user mobility, we formulated a realistic framework for minimizing the average content request delay cost of MUs. To effectively address the challenges of continuous caching decisions in time-varying environments, we proposed an advantage actor–critic (A2C)-based coded caching algorithm, which leverages an advantage function to reduce variance, accelerate convergence, and improve caching efficiency. Extensive simulations demonstrated that the proposed algorithm outperforms benchmark caching schemes, thereby validating its effectiveness and practicality. The proposed optimization framework and algorithm provide new insights into intelligent coded caching in future wireless cellular networks.