Deep Residual Learning for Hyperspectral Imaging Camouflage Detection with SPXY-Optimized Feature Fusion Framework

Abstract

Camouflage detection in hyperspectral imaging is hindered by the spectral similarity between artificial materials and natural vegetation. This study proposes a non-destructive classification framework integrating optimized sample partitioning, spectral preprocessing, and residual deep learning to address this challenge. Hyperspectral data of camouflage fabrics and natural grass (389.06–1005.10 nm) were acquired and preprocessed using principal component analysis, standard normal variate (SNV) transformation, Savitzky–Golay (SG) filtering, and derivative-based enhancement. The Sample set Partitioning based on joint X–Y distance (SPXY) algorithm was applied to improve representativeness of training subsets, and several classifiers were constructed, including support vector machine (SVM), random forest (RF), k-nearest neighbors (KNN), convolutional neural network (CNN), and residual network (ResNet). Comparative evaluation demonstrated that the SPXY-ResNet model achieved the best performance, with 99.17% accuracy, 98.89% precision, and 98.82% recall, while maintaining low training time. Statistical analysis using Kullback–Leibler divergence and similarity measures confirmed that SPXY improved distributional consistency between training and testing sets, thereby enhancing generalization. The confusion matrix and convergence curves further validated stable learning with minimal misclassifications and no overfitting. These findings indicate that the proposed SPXY-ResNet framework provides a robust, efficient, and accurate solution for hyperspectral camouflage detection, with promising applicability to defense, ecological monitoring, and agricultural inspection.

1. Introduction

Camouflage detection plays a crucial role in remote sensing and military surveillance, particularly in addressing the growing sophistication of artificial materials. These materials often exhibit spectral characteristics that closely resemble natural vegetation, presenting significant challenges for traditional imaging technologies [1,2]. Hyperspectral imaging (HSI), which captures detailed reflectance information across hundreds of contiguous narrow bands, is widely regarded as a powerful tool for identifying subtle material differences [3]. However, effectively utilizing such high-dimensional data remains a technical challenge.

Early studies on camouflage detection often relied on rule-based or thresholding techniques applied to spectral reflectance. Kamble and Rajarajeswari [1] adopted fixed spectral thresholds to identify artificial targets, but their method performed poorly under variable illumination and complex backgrounds. To improve robustness, Esin et al. [2] introduced SVMs, which achieved better performance in small-sample, high-dimensional scenarios. However, classifiers such as SVM and RF rely on handcrafted features and struggle to handle complex nonlinear boundaries [4,5].

To address these limitations, more advanced feature extraction approaches have been introduced. Jing and Hou [6] proposed a PCA–SVM pipeline to reduce redundancy while preserving informative variance. Li et al. [7] enhanced preprocessing using wavelet-based denoising and least squares filtering, effectively suppressing high-frequency noise but failing to maintain spatial continuity. Other strategies, including PCA–KNN and ICA-based pipelines, have also been explored to enhance classification robustness [8,9].

With the advent of deep learning, CNNs have gained prominence for their ability to automatically extract hierarchical spectral–spatial features [3,10,11]. Chen et al. [12] applied CNNs to camouflage detection, achieving significantly improved accuracy. Hybrid 3D–2D CNN architectures further strengthened the model’s ability to learn both local and global spectral patterns [10]. ResNets, which introduce shortcut connections to alleviate vanishing gradient issues, have also demonstrated strong performance in hyperspectral classification tasks [13,14,15]. Furthermore, residual models integrated with attention mechanisms and spatial–spectral regularization have been shown to improve class discrimination [11,16]. Recent reviews have emphasized that continuous methodological benchmarking and transparent reporting are critical for reproducibility and cross-study comparability in deep hyperspectral learning [17,18].

Recently, attention mechanisms have emerged as a key direction in hyperspectral classification, enabling dynamic modeling of contextual relationships across spectral and spatial dimensions. Li et al. [19] proposed a wide-area attention-based architecture for real-time object search using UAVs, effectively integrating spectral–spatial feature fusion for rapid camouflage detection. Qing and Liu [20] designed a multi-scale residual network with attention modules, capable of preserving both global structure and local textures in complex backgrounds. Sarker et al. [11] developed a spectral–spatial residual attention network (SS-RAN) that introduced both channel and spatial attention blocks to enhance sensitivity to fine-grained features. Zhu et al. [21] further extended this direction by proposing a Residual Spectral–Spatial Attention Network, which embedded attention modules within residual blocks to enhance class separability and spectral–spatial feature representation in complex scenes. Despite their high accuracy, these attention-based models often require deep architectures and introduce considerable computational overhead, making them unsuitable for deployment on resource-constrained platforms. To address this, Hupel and Stütz [22] introduced a lightweight hyperspectral anomaly detection strategy adapted for multispectral data, enabling near real-time camouflage detection under limited hardware conditions. In parallel, AI-driven automation of systematic literature reviews has been proposed to accelerate methodological synthesis in remote sensing and hyperspectral imaging [23,24].

While classification has been the dominant paradigm, recent research has also begun to address hyperspectral object detection, expanding the scope of spectral analysis to include spatial object-level interpretation. He et al. [25] proposed a unified spectral–spatial feature aggregation network that bridges the gap between pixel-wise classification and object detection, demonstrating promising performance on complex scenes. Moreover, modern review methodologies such as Rapid Literature Review (RLR) have been advocated for to ensure efficient synthesis of such diverse algorithmic developments [26].

To capture sequential dependencies across spectral dimensions, researchers have also incorporated temporal modeling techniques such as LSTM and Bi-GRU into hyperspectral classification. Dash et al. [27] proposed a deep learning framework combining PCA with LSTM to retain key principal components while modeling band-wise temporal patterns, improving robustness in dynamic environments. However, LSTM-based models typically suffer from long training times and poor scalability due to their sequential nature, particularly when applied to high-bandwidth hyperspectral cubes [11,19,20,28].

Beyond network design, training sample partitioning significantly affects model generalization. The commonly used Kennard–Stone (K-S) algorithm selects samples based solely on spectral distance, often resulting in sparse sampling of central data regions [9,11]. In contrast, the SPXY algorithm incorporates both spectral variance and label distribution, yielding more representative training subsets [8,12,16,29]. Zhao et al. [29] showed that SPXY significantly reduces KL divergence and improves spectral similarity between training and testing sets, enhancing generalization.

Data preprocessing also remains essential in hyperspectral classification workflows. SNV normalization and SG filtering have been widely adopted to correct baseline drift and suppress noise [14,30]. Spatial–spectral denoising strategies have further improved signal consistency in complex environments [7]. Abbasi and He [8] proposed a hybrid ICA–PCA–DCT preprocessing framework that exhibited greater spectral stability under varying illumination. However, these techniques are often applied in isolation and are not specifically optimized for camouflage detection, which requires heightened sensitivity to subtle spectral differences between artificial and natural targets.

Although significant progress has been made in attention models [11,19,20,28], recurrent architectures, and residual frameworks, few studies have integrated optimized sampling strategies, residual deep networks, and comprehensive preprocessing into a unified solution for camouflage detection. In this context, a more systematic framework that balances data representativeness, model efficiency, and generalization is still needed for practical hyperspectral camouflage detection. Moreover, most existing models are computationally expensive and complex, making them difficult to deploy in real-time or embedded environments. The integration of large language models (LLMs) into scientific review and analysis pipelines has recently enhanced reproducibility and evidence aggregation in data-intensive research [31].

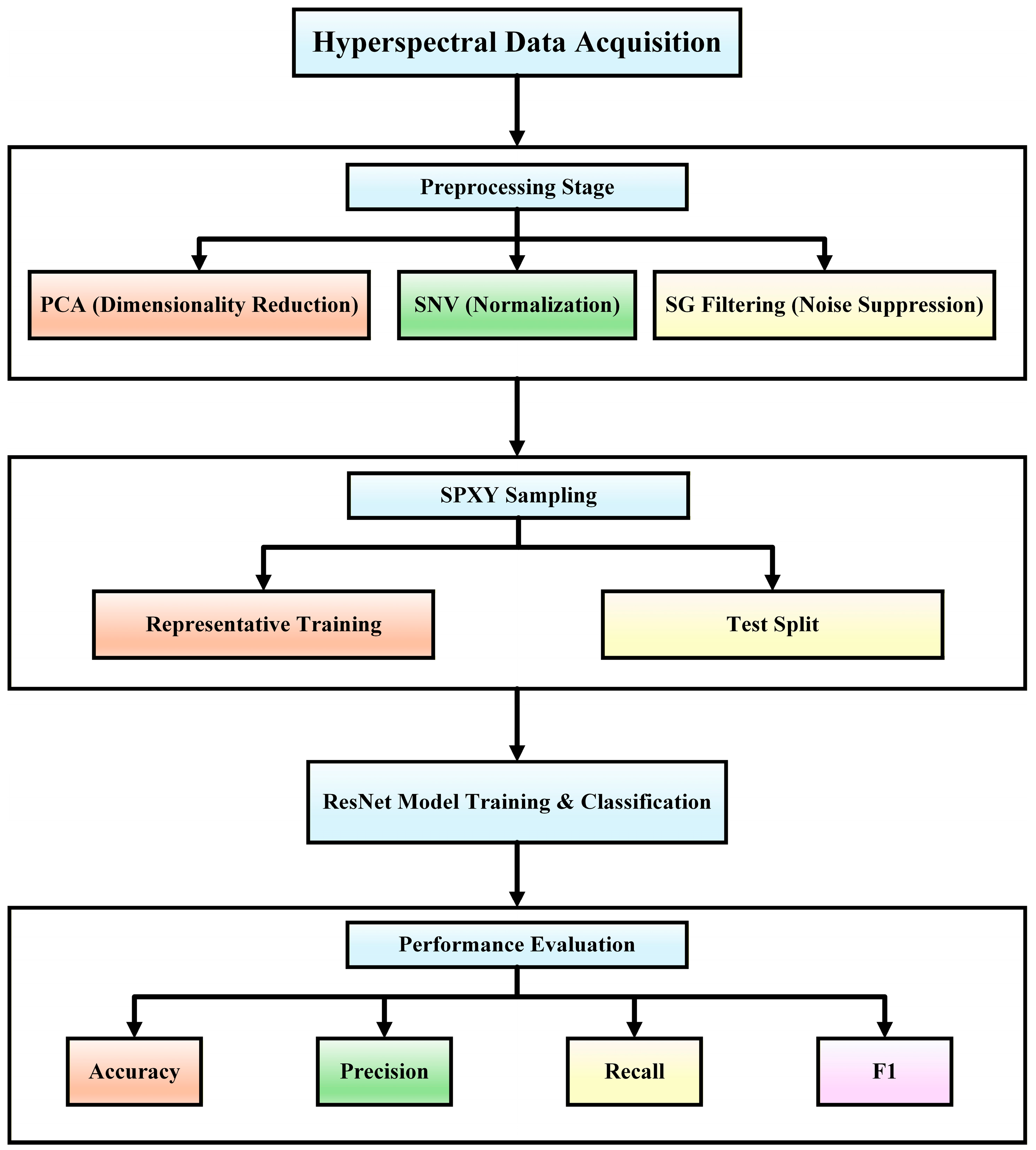
To address these challenges, this study proposes an integrated hyperspectral classification framework tailored for camouflage detection. The framework unifies SPXY-based sample partitioning, a multi-step preprocessing pipeline, and a lightweight residual CNN (ResNet18) architecture. Unlike prior studies that focus on isolated enhancements, our unified approach is designed to maximize class separability and generalization under spectral similarity and environmental variability. Experimental results demonstrate that this end-to-end framework not only achieves state-of-the-art accuracy but also maintains low computational overhead, making it practical for real-time and field-deployable applications in defense, agriculture, and environmental monitoring.

In Section 1, an overview of the background and challenges in hyperspectral camouflage detection is presented, stressing the need for advanced techniques to differentiate artificial materials from natural vegetation. The main components of the proposed framework are introduced, highlighting its potential advantages over existing methods. In Section 2, the materials, experimental setup, and methods for hyperspectral data acquisition, preprocessing, and classification are described, along with the algorithms used to improve classification accuracy. In Section 3, experimental results are presented, including an evaluation of preprocessing techniques, dataset partitioning strategies, and the performance of various classification models. The proposed SPXY-ResNet model is compared with other approaches, demonstrating its superior accuracy and efficiency. In Section 4, the findings are discussed, comparing the proposed framework to other methods in terms of performance and computational efficiency. Challenges and future improvements are also addressed. In Section 5, the study’s conclusions are summarized, and the practical applications of the proposed framework in camouflage detection, agriculture, and environmental monitoring are highlighted.

2. Materials and Methods

2.1. Experimental Materials and Environment

Camouflage uniforms and natural grass were sampled on the lawn of the South Campus of Changchun University of Science and Technology (43.82° N, 125.42° E) in September 2024. The grass species in the scene is Poa pratensis L. (Kentucky bluegrass), which is widely used across northern China as a standard lawn plant due to its cold tolerance and durability, ensuring that the collected samples realistically represent typical operational backgrounds. Figure 1 presents real-scene images of the data acquisition environment: Figure 1a shows a wide-area view of the natural outdoor environment, capturing the overall landscape and illumination conditions; Figure 1b presents a close-range view of the camouflage target within the grass, highlighting its blending effect, which poses a challenge to human visual detection; and Figure 1c displays a representative scene within ENVI 5.6 (64-bit) used for hyperspectral experiments. These visualizations emphasize the limitations of human visual perception and demonstrate the necessity of hyperspectral features for accurate and effective camouflage detection. All experiments were repeated under identical illumination and geometry to ensure data reliability and reproducibility.

2.2. Spectral Data Acquisition

Hyperspectral data were acquired using a FigSpec^® FS23 hyperspectral camera (Hangzhou Caipu Technology Co., Ltd., Hangzhou, China). The system operates within the 389.06–1005.10 nm spectral range and employs high-performance transmission grating dispersion to achieve a spectral resolution of 2.5 nm, supporting up to 1200 channels. The device features a high spatial resolution of 1920 × 1920 pixels, enabling rapid capture of both microscopic and macroscopic target details. The FS23 is a portable hyperspectral camera suitable for outdoor field measurements.

ENVI 5.6 software was employed for spectral data acquisition and analysis. It enables spectral extraction based on regions of interest (ROIs) from hyperspectral images and computes the mean reflectance spectrum for each selected area. Figure 2 illustrates ROIs selected from the hyperspectral images used in this study. The colored rhomboids visible in Figure 2 were manually defined in ENVI software to indicate the ROI boundaries for spectral extraction. Different colors are used solely to distinguish individual ROIs belonging to each material type (grass or camouflage fabric) and do not represent any physical or spectral differences. Figure 2a shows a representative ROI selected from the measured hyperspectral images of natural grass, encompassing a typical mixture of leaf and substrate structures and exhibiting relatively uniform green reflectance and pronounced red-edge amplitude variations in the spectral range between 680 nm and 750 nm, where vegetation reflectance increases sharply due to chlorophyll absorption, which are critical for distinguishing vegetation from fabric materials. ROIs were annotated in ENVI using a multi-point, multi-region approach to mitigate single-point noise effects. The prominent spatial details and red-edge features indicate that this ROI effectively captures the spectral heterogeneity of natural grass, providing reliable samples for SPXY sampling and model training. Figure 2b shows the corresponding ROI extracted from the camouflage fabric using ENVI software. Unlike the natural grass ROI, the camouflage area exhibits a more uniform texture distribution and weaker red-edge reflectance, reflecting the absence of chlorophyll absorption. This ROI provides clearer spatial boundaries and improved material contrast, serving as the basis for reliable spectral extraction and subsequent classification analysis.

All spectral preprocessing and model development were performed using MATLAB R2024a. To enhance the signal-to-noise ratio while preserving key spectral features, wavelet thresholding and SG filtering were applied for denoising and baseline correction. A spatial–spectral denoising method based on wavelet transforms and least squares filtering was also considered to further improve robustness in high-dimensional data [6]. Additionally, PCA was used to reduce dimensionality while retaining essential variance for classification tasks [7].

2.3. Spectral Data Extraction and Processing

Spectral profiles for both natural grass and camouflage fabrics were derived using ENVI 5.6 software, a commonly used platform for hyperspectral analysis. Data were collected across 600 continuous spectral bands (389.06–1005.10 nm), with five mixed-class images randomly chosen and 40 ROIs per class annotated, yielding 200 spectra per material type.

All samples were standardized and resampled to a common wavelength grid to ensure spectral consistency. Each was represented as a 600-dimensional reflectance vector covering the visible to near-infrared range. This high-resolution spectral encoding facilitates fine discrimination between materials with similar spectral characteristics [32].

Due to the high dimensionality and redundancy inherent in hyperspectral images, effective dimensionality reduction is essential before image analysis to highlight key features and improve processing efficiency. To reduce dimensionality, PCA was applied to the spectral dataset, producing a set of uncorrelated principal components ordered according to the amount of variance each explains.

Before ROI extraction, PCA was applied to the original hyperspectral images using ENVI’s built-in PCA module. The ENVI module calculates the covariance matrix and extracts principal components through eigenvalue decomposition, providing both the component scores and their respective cumulative variance ratios. To suppress noise, only the leading principal components (PCs) that collectively account for up to 99.95% of the total variance were retained. The preprocessing steps are illustrated in Figure 3, where each block corresponds to a specific operation, including PCA, SNV normalization, and SG filtering.

The PCA transformation can be mathematically expressed as follows:

$$\begin{array}{c}\mathrm{Z}=\mathrm{X}\mathrm{W}={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{B}}}{\mathrm{x}}_{\mathrm{i}}{\mathrm{w}}_{\mathrm{i}}\end{array}$$

(1)

$$\begin{array}{c}\mathrm{W}=\mathrm{e}\mathrm{i}\mathrm{g}\left.\left({\mathsf{\Sigma }}_{\left\{\mathrm{X}\right\}}\right.\right)\end{array}$$

(2)

where X is the original hyperspectral image matrix, W is the eigenvector matrix of the covariance matrix Σ_X, and Z represents the transformed principal component scores obtained by projecting the input spectra onto the eigenvector space. The number of retained principal components N is determined such that the cumulative variance satisfies:

$$\begin{array}{c}{\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathsf{\lambda }}_{\mathrm{i}}}{{\sum }_{\mathrm{j}=1}^{\mathrm{B}}{\mathsf{\lambda }}_{\mathrm{j}}}}\le 99.95\%\end{array}$$

(3)

where λ_i denotes the eigenvalue of the i-th principal component, and B = 600 is the total number of bands. This procedure preserved 36 components, striking a balance between dimensionality reduction and spectral integrity, thereby enhancing the discrimination between classes. As shown in Figure 4a, the PCA-processed grass region exhibits clearer boundaries and reduced background interference. In Figure 4b, the camouflage area becomes more distinguishable from surrounding features, indicating that dimensionality reduction improved class separability and visual clarity in both cases.

Hyperspectral data acquisition is influenced by sensor noise, ambient illumination variation, and surface scattering, particularly for materials with complex microstructures such as vegetation and textiles. These factors lead to baseline drift, signal attenuation, and spectral distortion, which degrade classification performance [16,30]. To mitigate scattering-related variability and improve spectral comparability, SNV transformation was applied, centering each spectrum to zero mean and unit variance [17,30]. Subsequently, Z-score normalization was used to standardize feature magnitudes across bands, enhancing model stability and convergence during training [14].

The SNV transformation is defined as:

$$\begin{array}{c}{\mathrm{x}}_{\mathrm{i}}^{\prime }={\displaystyle \frac{{\mathrm{x}}_{\mathrm{i}}-\stackrel{\mathrm{-}}{\mathrm{x}}}{\mathrm{s}}}\end{array}$$

(4)

where x_i is the reflectance value at the i-th wavelength, $\stackrel{\mathrm{-}}{\mathrm{x}}$ is the mean reflectance, and s denotes the standard deviation of the spectral vector. This transformation removes multiplicative scatter effects and offsets, ensuring consistent reflectance scaling across samples.

2.4. Classification Model

Dataset partitioning is a key step in organizing high-dimensional hyperspectral data, helping reduce redundancy and noise to improve classification model accuracy and robustness. Two dataset partitioning algorithms were employed: the SPXY algorithm and the K-S algorithm. These were integrated with a ResNet deep learning model to construct a classification framework for distinguishing between natural grass and camouflage fabric based on spectral data.

Representative training samples were selected using the SPXY algorithm [17], which jointly considers spectral variation and class label distribution to ensure balanced and diverse training sets. The SPXY algorithm selects representative samples by considering both the spectral similarity in the feature space and the label distance in the response space. The joint distance between two samples i and j is defined as:

$$\begin{array}{c}{\mathrm{D}}_{\mathrm{ij}}=\mathsf{\alpha }{\mathrm{d}}_{\mathrm{x}}\left(\mathrm{i},\mathrm{j}\right)+\left(1-\mathsf{\alpha }\right){\mathrm{d}}_{\mathrm{y}}\left(\mathrm{i},\mathrm{j}\right)\end{array}$$

(5)

where ${\mathrm{d}}_{\mathrm{x}}(\mathrm{i},\mathrm{j})={‖{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}‖}_2$ represents the Euclidean distance in spectral space and ${\mathrm{d}}_{\mathrm{y}}\left(\mathrm{i},\mathrm{j}\right)=\left|{\mathrm{y}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{j}}\right|$ denotes the distance in response space. The parameter α ∈ [0, 1] controls the relative weighting between spectral and response information. The pair of samples with the maximum D_ij value is selected iteratively to form a representative and well-distributed training subset. Zhao et al. [29] demonstrated that SPXY significantly improves classification accuracy in camouflage detection tasks by reducing distributional mismatch between training and testing sets. In contrast, the K-S algorithm selects samples based solely on spectral distance by iteratively choosing the most distant points in the feature space [9]. While K-S offers computational simplicity and helps reduce multicollinearity, it often results in underrepresentation of central classes and may impair generalization.

Dimensionality reduction was performed using PCA, which transforms correlated spectral variables into orthogonal components with maximal variance retention [6]. For classification, several models were implemented: RF, which builds an ensemble of decision trees through bootstrap sampling and feature randomness to enhance robustness [4]; SVM, which constructs optimal separating hyperplanes with maximum margin using kernel functions for nonlinear data [3]; and KNN, which assigns class labels based on local proximity in the feature space [5]. Deep CNNs were also employed to automatically extract hierarchical spectral–spatial features through convolutional filters and shared weights, offering strong noise resistance and scalability to high-dimensional inputs [10,11]. Traditional CNN-based approaches typically use 2D convolutions, treating each spectral band independently and ignoring inter-band correlations. To overcome this limitation, 3D convolutional neural networks (3D-CNNs) have been proposed to jointly extract spectral–spatial features in a volumetric fashion. Li et al. [28] demonstrated that 3D-CNNs significantly improve hyperspectral classification performance by maintaining spectral continuity and capturing spatial structures simultaneously. However, the high computational cost and model complexity of 3D-CNNs make them less suitable for real-time deployment, especially on resource-constrained platforms.

To balance performance and efficiency, a residual CNN architecture (ResNet18) was selected as the backbone for this study. ResNet is designed to mitigate vanishing gradients and performance degradation in deep neural networks by incorporating identity shortcut connections, enabling stable and efficient training. The core unit is the residual block, where shortcut connections allow direct information flow between layers, preserving low-level features and improving convergence speed and model stability. Mathematically, each residual unit in the ResNet architecture can be expressed as:

$$\begin{array}{c}{\mathrm{y}}_{\mathrm{l}}=\mathrm{F}\left({\mathrm{x}}_{\mathrm{l}},{\mathrm{W}}_{\mathrm{l}}\right)+{\mathrm{x}}_{\mathrm{l}}\end{array}$$

(6)

$$\begin{array}{c}{\mathrm{x}}_{\mathrm{l}+1}=\mathrm{f}\left({\mathrm{y}}_{\mathrm{l}}\right)\end{array}$$

(7)

where x_l and x_l+1 denote the input and output feature maps of the l-th residual block, respectively, F(x_l, W_l) represents the residual mapping composed of convolutional, batch normalization, and ReLU layers, and f(⋅) is a nonlinear activation function. The identity shortcut connection x_l enables direct gradient flow, preventing vanishing gradients and improving the stability of deep network training. This formulation allows the ResNet model to extract fine-grained spectral–spatial features while maintaining efficient convergence.

Spectral data preprocessed via SNV were reshaped into pseudo-images and input into the model. Within residual units, identity mappings allow information to bypass multiple convolutional layers, enhancing the model’s capacity to capture subtle spectral features in camouflage patterns [17]. During training, batch normalization and Rectified Linear Unit (ReLU) activation functions were applied to improve generalization, and global average pooling was used to compress spatial dimensions, which also reduces the number of trainable parameters and enhances computational efficiency. To ensure stable convergence and fair comparison, the key hyperparameters of all models were tuned empirically rather than using default values. For the ResNet classifier, the learning rate was initially set to 0.001 and decayed by a factor of 0.5 every 25 epochs. The batch size was adjusted between 8 and 32, depending on the dataset size, and the network depth was determined based on pilot experiments. Dropout was applied with a rate between 0.25 and 0.5, and batch normalization was incorporated to prevent overfitting. For traditional models, including SVM, KNN, RF, and PCA, core parameters were also optimized through grid-based selection to achieve the best validation accuracy. Specifically, the penalty factor C of SVM ranged from 0.1 to 10, the number of neighbors k in KNN varied from 1 to 5, the number of trees in RF was adjusted between 10 and 100, and the retained variance ratio in PCA was kept at or above 90%.

To evaluate the effectiveness of the SPXY and K-S sample partitioning algorithms in distinguishing natural grass from camouflage fabric, three statistical metrics were employed: KL divergence, mean similarity, and standard deviation similarity. These metrics quantify the distributional consistency between training and testing sets. A lower KL divergence indicates minimal spectral distribution shift, while higher mean and standard deviation similarities reflect alignment in central tendency and variability. Based on the optimal partitioning strategy, multiple classification models were developed by integrating it with CNN, SVM, KNN, PCA, and RF algorithms to assess their performance on hyperspectral data classification. Model construction constitutes a critical step in spectral analysis, facilitating accurate material identification. Using training samples partitioned by the SPXY algorithm and selected spectral bands, six models were developed: SPXY-RF, SPXY-SVM, SPXY-KNN, SPXY-CNN, SPXY-PCA, and SPXY-ResNet [17]. Their performance was evaluated using standard metrics, including accuracy, precision, recall, and F1-score.

Among the six models, SPXY-ResNet exhibited the highest overall performance. The residual learning mechanism of ResNet effectively mitigates vanishing gradient issues, enabling deeper architectures to capture fine-grained spectral–spatial features. Figure 5 presents the system workflow of the classification pipeline, illustrating the sequential steps involved in hyperspectral data processing, model training, and evaluation. The workflow begins with the acquisition of hyperspectral data, followed by preprocessing steps such as dimensionality reduction using PCA, normalization, and noise suppression techniques. These preprocessing steps are crucial in enhancing the quality of the spectral data by reducing redundancy and improving the separability of material classes. The dataset is then partitioned using the SPXY algorithm, ensuring representative sampling for training and testing, which is essential for improving the generalization performance of the model by mitigating potential biases introduced by non-representative training subsets. Several classification models, including SPXY-RF, SPXY-SVM, SPXY-CNN, and SPXY-ResNet, are applied to the preprocessed data, with each model evaluated based on standard performance metrics such as accuracy, precision, recall, and F1-score.

To ensure fair comparison and stable performance, all classifiers were trained using the same hyperparameter tuning strategy and validated under repeated SPXY-based sampling.

3. Results

3.1. Preprocessing

To enhance spectral data quality and suppress redundancy, PCA was performed on the original hyperspectral images before selecting regions of interest.

After PCA processing using the ENVI software module, thirty-six principal components were selected, ensuring that their cumulative variance explained remained below the 99.95% threshold. The raw hyperspectral image with evident spectral noise and low contrast is shown in Figure 6a, whereas the denoised and PCA-processed image, exhibiting improved boundary clarity and spectral separability, is shown in Figure 6b.

Preprocessing significantly enhanced spectral quality by suppressing noise and correcting baseline shifts. Figure 7a illustrates the smoothed reflectance profile of camouflage fabric, while Figure 7b shows the enhanced spectral curve of natural grass, with clear feature separation around the red-edge region. Based on the ICA–PCA–DCT framework proposed by Abbasi and He [8], key spectral characteristics in the 680–750 nm red-edge and near-infrared regions became more distinct after preprocessing. This improvement in signal clarity and spectral contrast contributes to better class separability and enhances the reliability of downstream classification.

3.2. Division of Training and Test Spectral Data

The dataset was randomly divided into training (70%) and testing (30%) subsets to support model calibration and performance evaluation. A total of 400 spectral samples were used in this experiment, each subjected to spectral analysis and chemical verification to ensure data reliability. Specifically, 280 samples were allocated for training and 120 for testing. To investigate the impact of sample selection strategies on classification performance, two commonly used partitioning algorithms, K-S and SPXY, were employed to divide the hyperspectral dataset [17]. Both algorithms were applied independently under identical class distribution conditions, and their effectiveness was evaluated using a combination of qualitative and quantitative methods. The analysis focused on sample distribution within the spectral feature space, histogram consistency of spectral values, and statistical similarity between training and testing sets. These evaluations aimed to determine how well each method preserved the dataset’s representativeness and diversity, which are essential for improving model generalization in camouflage detection. To further avoid relying on a single 70/30 split and statistically validate the reliability of SPXY-based sampling, a robustness experiment was conducted using repeated resampling. Specifically, 1000 independent SPXY partitions were generated, and each training subset was evaluated using 5-fold cross-validation. The resulting performance remained highly stable, with a mean Root Mean Square Error (RMSE) of 2.8231 and a standard deviation of only 0.1264, confirming that model generalization is minimally affected by changes in data division. Figure 8 illustrates the PCA distribution of all partitions, demonstrating consistent coverage of the feature space for both training and test samples across repeated trials. This comprehensive validation verifies that SPXY not only improves sample representativeness but also maintains strong robustness under stochastic resampling conditions.

The corresponding results are presented in Figure 8, Figure 9 and Figure 10. These figures illustrate the differences in spatial sampling uniformity, distributional consistency, and statistical alignment achieved by each algorithm, providing an empirical basis for selecting the optimal data partitioning strategy.

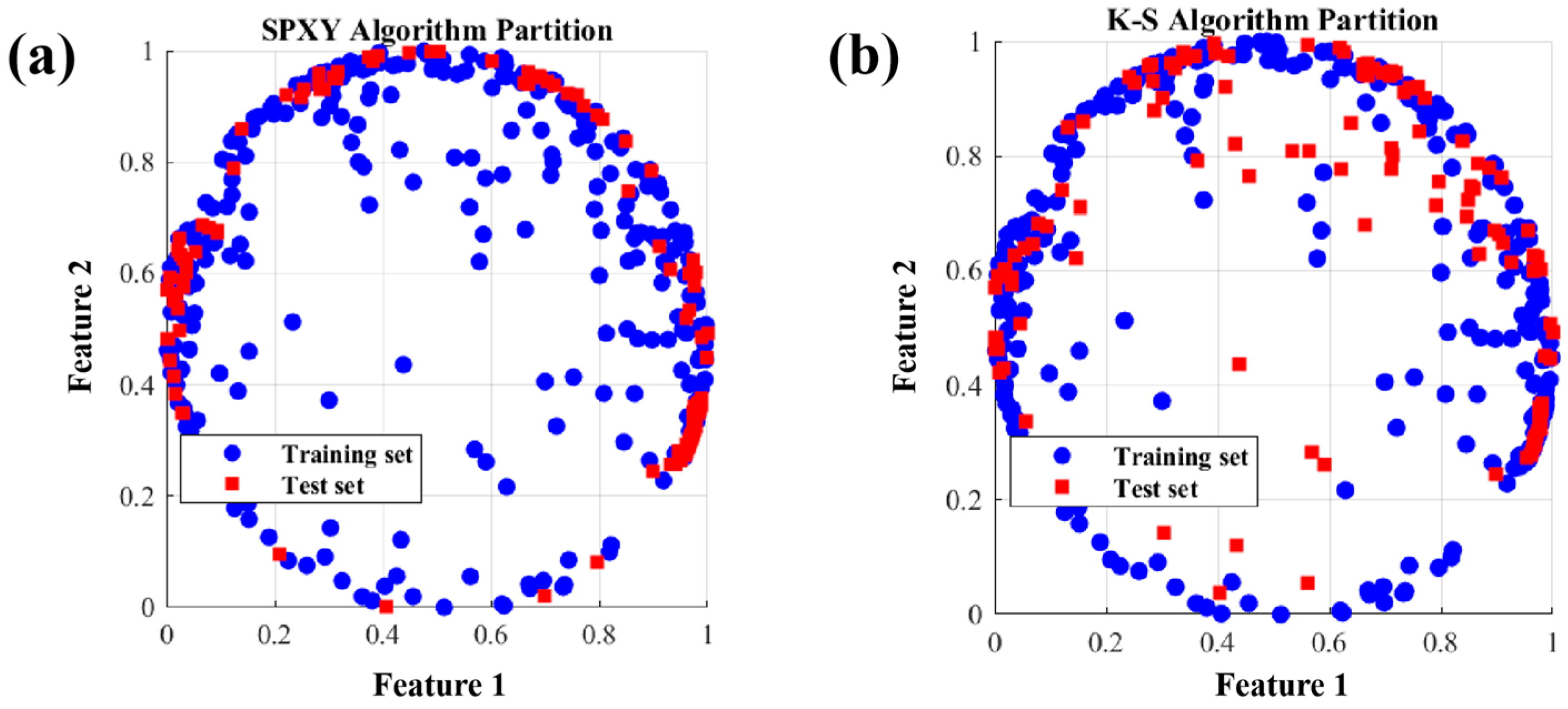
As illustrated in Figure 9a, the SPXY algorithm achieves a more uniform and representative distribution across the feature space, with samples densely covering both central and peripheral regions. This comprehensive coverage ensures that both typical and marginal spectral patterns are well represented in the training data. In contrast, Figure 9b reveals that the K-S algorithm tends to oversample spectral extremes while underrepresenting the central distribution, which may result in biased model learning and reduced generalization performance.

Figure 10a further demonstrates the superior statistical alignment between the SPXY-based training and test sets, particularly in the high-frequency spectral regions. This alignment is crucial for hyperspectral camouflage detection, where fine spectral features such as vegetation absorption dips and textile reflectance plateaus serve as key discriminative cues. In comparison, Figure 10b shows that the K-S partitioning leads to noticeable mismatches across several spectral intervals, indicating potential risk of model overfitting or reduced sensitivity to subtle class differences.

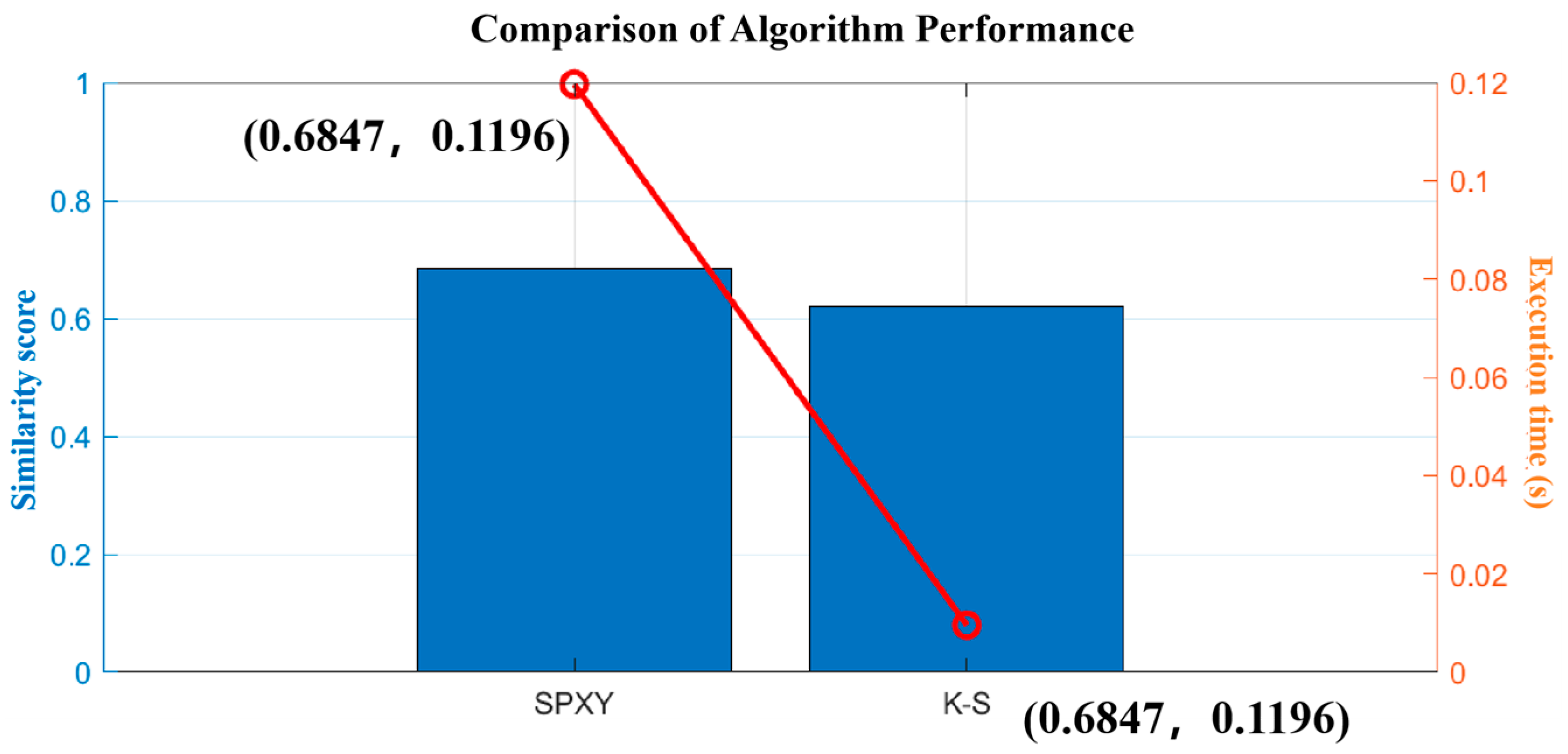
Figure 11 quantitatively confirms the advantage of SPXY in maintaining statistical consistency between training and testing subsets. The SPXY algorithm achieved a KL divergence of 0.1593, which is significantly lower than the 0.2485 recorded for the K-S algorithm, indicating a smaller spectral distribution shift. For mean spectral similarity, SPXY reached 0.6847 compared to 0.6217 for K-S, suggesting better alignment in average spectral characteristics. In terms of the standard deviation of similarity, SPXY achieved 0.1041 while K-S recorded 0.1382, reflecting a tighter match in spectral variability. Although the execution time for SPXY (0.1196 s) was slightly longer than that of K-S (0.0096 s), the improved distributional fidelity provided by SPXY offers clear benefits for subsequent model training and evaluation.

Overall, SPXY demonstrates superior performance in constructing representative and balanced training sets, a factor that directly contributes to improved model robustness in the presence of spectral variability and distributional shift. The observed improvements in similarity metrics and classification outcomes further confirm the effectiveness of SPXY in supporting high-performance hyperspectral modeling.

3.3. Classification Result

Six models were built to thoroughly assess the classification performance of several models based on the SPXY sample selection strategy: SPXY-PCA, SPXY-SVM, SPXY-RF, SPXY-CNN, SPXY-KNN, and SPXY-ResNet. To assess both performance and efficiency, all models were evaluated using accuracy, precision, recall, and F1-score as standard benchmarks. Additionally, training time was also used.

Table 1. Classification performance of SPXY-based models. The Mean Accuracy (%) and ±SD (%) are computed over 100 independent runs. Precision, Recall, F1-score, and Training time correspond to the best single-run results. Bold values in Table 1 indicate the highest performance among all compared models.

Model	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	Training Time (s)	SD (%)
SPXY-PCA	84.17	83.37	81.87	81.70	0.07	0.75
SPXY-SVM	97.50	96.64	97.25	96.87	1.80	0.87
SPXY-RF	96.67	95.72	96.25	95.83	0.37	0.85
SPXY-CNN	95.83	94.82	95.07	94.63	0.07	0.88
SPXY-KNN	95.00	95.38	93.75	94.35	0.17	0.89
SPXY-ResNet	99.17	98.89	98.82	98.82	0.14	0.79

summarizes the classification performance of all SPXY-based models. The Mean Accuracy % column reports the average accuracy obtained over 100 independent runs with randomly partitioned datasets, while the standard deviation (SD) of these runs indicates the stability and robustness of each model. The remaining metrics, Precision, Recall, F1-score, and Training time correspond to the best single-run results to facilitate direct comparison.

Among all evaluated methods, SPXY-ResNet outperformed all other models, achieving the highest mean accuracy of 99.17% with a small standard deviation of 0.79%, along with top scores in Precision (98.89%), Recall (98.82%), and F1-score (98.82%). This indicates its strong capability in extracting and generalizing complex spectral-spatial features while maintaining a competitive training time of 0.14 s, demonstrating that the residual structure facilitates efficient convergence without introducing significant computational overhead.

SPXY-SVM and SPXY-RF also delivered high mean accuracies of 97.5% and 96.67%, respectively. SPXY-SVM showed slightly better recall, while SPXY-RF was more balanced across metrics and required less training time (0.37 s). SPXY-CNN and SPXY-KNN offered solid performance (95–96% accuracy), with CNN showing faster training (0.07 s), yet slightly lower F1-score compared to ResNet and SVM. Error analysis demonstrates that all models exhibit small variations in accuracy, with standard deviations below 1%, indicating high repeatability and robust generalization. The superior performance and low fluctuation of SPXY-ResNet confirm that the proposed deep residual feature fusion framework is capable of learning fine-grained spectral-spatial representations and delivering stable classification outcomes across repeated experiments. These results collectively highlight the advantage of deep learning architectures, particularly ResNet-based models, in capturing nuanced hyperspectral patterns for camouflage detection.

3.4. Validation of a ResNet-Based Model for Discriminating Natural Grass and Camouflage Fabrics

To validate the ResNet model, unseen samples across five spectral categories were randomly selected for testing. The resulting confusion matrix, showing only two misclassifications and confirming high classification accuracy, is shown in Figure 12a. The training and validation accuracy over iterations, indicating stable learning behavior, is shown in Figure 12b, while the corresponding loss curves demonstrating effective convergence without overfitting are shown in Figure 12c.

The ResNet model was trained for a total of 800 iterations (100 epochs). The model’s validation accuracy remained consistently above 85%, with a final accuracy of 99.17%, demonstrating excellent predictive performance. At the same time, the validation loss converged and remained stable below 0.4, indicating good model generalization.

The performance of six classifiers in identifying spectral differences between natural grass and camouflage fabrics was compared, with SPXY-ResNet demonstrating the best overall accuracy and consistency across all categories. Its ability to integrate spatial and spectral features contributed to better generalization on the validation set.

4. Discussion

The proposed SPXY-ResNet framework achieved a classification accuracy of 99.17% using limited training data, indicating strong generalization capability and robustness. Compared with existing deep residual or attention-based models that rely on large datasets and complex architectures [19,20], comparable performance was attained with substantially reduced computational overhead. This improvement is primarily attributed to the integration of SPXY-based sample partitioning, which enhances representativeness in both spectral and label space [29], and a multi-step preprocessing pipeline that improves class separability.

Although attention-based networks such as SS-RAN and wide-field attention models have demonstrated high classification accuracy in hyperspectral imaging tasks [11,19], their reliance on multiple attention modules and deeper architectures leads to high computational cost, limiting their applicability to real-time or embedded systems. Similarly, sequential architectures like Bi-GRU effectively capture spectral dependencies [28], but their long training times and poor scalability reduce their practicality in high-dimensional applications. In contrast, the SPXY-ResNet framework avoids explicit sequence modeling while preserving spectral continuity through spatial–spectral preprocessing and residual connections, enabling a more lightweight and deployable solution.

Recent advances in multibranch 3D–2D convolutional neural networks have shown excellent performance by capturing both local and global spectral–spatial features [13]. However, such architectures often involve high model complexity and resource consumption, posing challenges for training and deployment in hardware-constrained environments. In comparison, the 2D ResNet-based approach, combined with efficient preprocessing and optimized sampling, delivers similar accuracy with significantly lower computational demand, making it better suited for real-world applications requiring fast and portable solutions.

Previous residual network designs have focused primarily on spectral denoising [33], often neglecting the integration of spatial context. By combining residual learning with spatial–spectral preprocessing, enhanced feature representation is achieved, particularly under conditions of high spectral similarity between camouflage materials and natural vegetation. The model also enhances reflectance contrast in the red-edge region (680–750 nm), which is critical for vegetation-related material discrimination [34].

Consistent improvements were observed across all evaluation metrics, including accuracy, precision, recall, and F1-score, when compared with baseline classifiers such as PCA, SVM, RF, KNN, and conventional CNNs. Minimal overfitting and stable convergence further confirm the robustness of the proposed approach. The repeated SPXY + 5-fold cross-validation experiments further demonstrated consistent model performance under 1000 stochastic resampling trials, eliminating the potential selection bias associated with a standalone 70/30 split. By jointly optimizing data partitioning, spectral preprocessing, and network architecture, the framework provides an efficient and scalable solution for hyperspectral camouflage detection.

Although the SPXY–ResNet framework achieved high accuracy in distinguishing camouflage fabric from natural vegetation, it should be noted that the model was trained and evaluated solely on a self-collected hyperspectral dataset. No publicly available camouflage or benchmark hyperspectral datasets were used in this study. Consequently, the generalizability and external validity of the proposed approach may be limited.

Future work will focus on extending the model evaluation to publicly available datasets and cross-scene validation to further verify its robustness and transferability. In addition, exploring the integration of transformer-based architectures or lightweight 3D CNN modules could enhance spatial–spectral modeling capabilities in more complex scenarios. Large-scale annotated datasets, such as BihoT [35], also provide opportunities to extend static classification frameworks toward spatiotemporal object detection and tracking.

5. Conclusions

This study developed a hyperspectral classification framework for distinguishing natural grass from camouflage fabrics. Among the tested models, SPXY-ResNet achieved the best performance, with an accuracy of 99.17%, benefiting from its deep residual structure and ability to capture subtle spectral–spatial features. The SPXY algorithm outperformed the traditional Kennard-Stone method by providing more representative training sets, improving model generalization. Applying SNV normalization, SG filtering, and derivative-based enhancements successfully minimized spectral noise and improved the representation of informative features. The proposed method offers a fast, accurate, and non-destructive solution for camouflage detection based on hyperspectral data, with potential applications in agriculture, ecology, and defense.

In addition to its low computational overhead, the framework incorporates several methodological innovations. The integration of SPXY-based sampling with residual deep learning establishes a joint optimization chain that maintains spectral label balance and strengthens model generalization under distributional variations. The sequential preprocessing pipeline maximizes informative variance while suppressing redundant noise, which is crucial for hyperspectral camouflage detection. As illustrated in Figure 4, the stepwise architecture unifies data acquisition, preprocessing, and classification into a lightweight and reproducible workflow. Validation across multiple acquisition distances (3 m, 5 m, and 10 m) demonstrates the model’s robustness and adaptability for real-world deployment.

Despite its high performance, the framework has certain limitations. Experiments were conducted only in a single grassland environment, and the camouflage materials consisted of a single fabric type under controlled illumination. These conditions may not fully capture the spectral and textural complexity of real-world camouflage targets.

Future work will address these limitations while further improving the framework’s interpretability and scalability. Planned efforts include expanding the dataset to cover forested and mixed-vegetation environments, incorporating multiple camouflage fabric types with distinct spectral characteristics, and conducting outdoor measurements under varying illumination and weather conditions to evaluate model robustness and transferability. Concurrently, Explainable AI techniques such as SHAP and Grad-CAM will be applied to visualize the contribution of individual spectral bands and enhance model interpretability. Additionally, large-scale deployment, automated hyperparameter optimization, and implementation on portable hyperspectral devices will be explored to improve operational efficiency and practical adaptability. Collectively, these developments aim to extend the robustness, transparency, and real-time applicability of the SPXY–ResNet framework across diverse environmental and operational conditions.