Uncertainty-Driven Reliability Analysis Using Importance Measures and Risk Priority Numbers

Featured Application

The framework was applied to Solid Waste Collection and Compaction Trucks, using real failure data to identify critical components and improve maintenance planning under uncertainty. Beyond this case, it can be extended to other complex systems such as heavy vehicles, industrial machinery, and energy infrastructure.

Abstract

Uncertainty is a key factor in the reliability assessment of complex engineering systems, especially when they operate under variable conditions that affect component degradation. This study presents a framework for the systematic and uncertainty-based prioritization of critical components and failure modes. The method combines Reliability Block Diagrams, Fault Tree Analysis, and Importance Measures with Failure Mode and Effects Analysis. This two-level approach links component failures with their effect on system reliability. Uncertainty is introduced through the statistical parameters of component reliability distributions and the resulting impact on system behavior is examined. Components with the highest importance are then examined through Failure Mode and Effects Analysis to identify main failure modes and calculate their Risk Priority Numbers. The framework is applied to a fleet of Solid Waste Collection and Compaction Trucks used by a waste management company in a Colombian city. This system operates under high-load variability, mechanical shocks, and environmental stress. The combined Importance Measures and Risk Priority Number analysis provides a probabilistic basis for identifying critical components and their dominant failure modes, linking reliability uncertainty with maintenance prioritization. The results show that combining Importance Measures and Risk Priority Number improves the identification of critical components and dominant failure modes, supporting maintenance prioritization based on reliability impact. The framework offers a practical approach for reliability assessment and maintenance planning under uncertainty, linking component-level uncertainty with system performance to guide decision-making in complex systems.

1. Introduction

Reliability analysis is fundamental to the design, operation, and maintenance of complex engineered systems [1,2,3]. Across energy production, transportation, and healthcare sectors, anticipating failures and quantifying risks are essential to ensure safety, performance, and sustainability [4,5,6,7,8,9,10]. However, traditional reliability approaches often assume deterministic component behavior, overlooking the pervasive influence of uncertainty [11,12]. Uncertainty may stem from incomplete knowledge, stochastic variability, or operational complexity, and inadequate treatment can compromise decision quality [9,13]. Consequently, reliability engineering is shifting toward probabilistic frameworks that explicitly quantify and propagate uncertainty in both component and system analyses [3,12,14,15].

Among reliability tools, combining Failure Mode and Effects Analysis (FMEA) with Fault Tree Analysis (FTA) or Reliability Block Diagrams (RBD) has proven effective. FMEA identifies and prioritizes potential failure modes, while FTA and RBD introduce probabilistic modeling at the system level, allowing interactions and dependencies to be represented more realistically.

A persistent challenge is the accurate assessment of component criticality, which directly influences maintenance planning, safety protocols, and resource allocation [3,12,16,17,18]. Critical analysis forms the bridge between reliability modeling and operational decision-making. Achieving informative rankings under deterministic and uncertain conditions requires methods that are analytically rigorous yet operationally practical [19,20]. Within this paradigm, two established instruments are Importance Measures (IMs) and the Risk Priority Number (RPN).

IMs quantify how changes in component reliability affect overall system performance [11,21,22,23]. They provide a mathematically grounded way to identify critical components, support redundancy allocation, and analyze uncertainty propagation across a system [13,15,24,25]. By contrast, the RPN, derived from FMEA, offers a semi-quantitative and highly interpretable index for prioritizing risk in industrial contexts. Its simplicity has made it widely used for decades, though it often lacks the probabilistic depth needed to represent uncertainty [26,27,28].

A comparison of these two strands highlights complementary strengths and limitations. IMs offer analytical rigor but can be challenging for practitioners to interpret, while RPNs are intuitive but rely on heuristic scoring. Although conceptual links exist—such as multi-factor RPN refinements resembling composite IMs or simulation-based IMs aligning with probabilistic FMEA—comprehensive frameworks that unify both perspectives remain uncommon [3,12,29]. This gap means that few approaches jointly address uncertainty quantification, interpretability and practical implementation in reliability-based prioritization.

Several recent studies illustrate the practical importance of integrating structured reliability tools into real-world systems. Applications in sectors such as medical waste management, transport logistics, and power generation demonstrate how probabilistic modeling can support maintenance and safety planning under uncertainty [30]. However, the literature remains fragmented, with IMs advancing in academic rigor and RPN remaining dominant in industrial practice, without sufficient integration between the two [4,22,23,31,32].

Despite these advances, most studies rely on deterministic parameter assumptions. They treat time-to-failure (TTF) parameters as fixed, disregarding the statistical uncertainty inherent in estimation. This simplification can lead to overconfident reliability predictions and unstable component rankings, limiting decision value in data-limited settings. Few works explicitly quantify how parameter-estimation uncertainty affects component prioritization metrics.

This study presents a statistics-based framework integrating parameter inference with uncertainty-informed prioritization, validated using operational data. The framework incorporates parametric uncertainty based on maximum-likelihood estimation and the observed information matrix, followed by Monte-Carlo propagation of uncertainties through FTA or RBD formulations. It defines IMs under parametric uncertainty, providing probabilistic intervals for classical reliability indices, and introduces a rank stability summary that quantifies the consistency of component prioritization under uncertainty. These tools are integrated into a single workflow linking parameter inference, uncertainty propagation and decision relevance. Specifically, the work advances reliability assessment by (i) combining inductive and deductive reliability perspectives to represent uncertainty propagation from components to the system; (ii) interpreting classical IMs as sensitivity indicators under parametric uncertainty; and (iii) incorporating these results into an RPN-based prioritization structure to support decision-making under variable conditions.

The approach is validated using field failure data from Solid Waste Collection and Compaction Trucks (SWCCTs). These systems operate under variable conditions where mechanical degradation and environmental stress amplify uncertainty effects, providing a relevant setting for evaluation. Results show that combining the probabilistic structure of IMs with the practical interpretability of RPN improves the identification of critical components and supports reliability-based maintenance decisions.

This paper is organized as follows: Section 2 reviews the theoretical background. Section 3 presents the methodological framework for parametric uncertainty modeling and propagation. Section 4 describes the case study, including data preparation and model construction. Section 5 reports the main results. Section 6 discusses implications for reliability and maintenance planning and concludes with directions for future research.

2. Theoretical Background

2.1. Importance Measures in Reliability Analysis

IMs have been explored in diverse contexts, with applications expanding from structural analyses to data-driven and cost-oriented frameworks [13,33,34,35,36]. Early work focused on binary systems, using IMs as sensitivity indices to quantify how component reliability affects system performance. Several authors advanced this line by applying Monte-Carlo methods to estimate differential IMs in nuclear reactor protection systems, demonstrating the value of stochastic simulation in capturing uncertainty. Differential importance has also been used for comparative statics beyond reliability (e.g., inventory settings). For multi-state systems, composite IMs address the limits of binary formulations and integrated generalizations have been used in aviation applications. Simulation-based analyses in offshore oil and gas have introduced measures tailored to repairable systems [11,15,24,37].

IMs are commonly classified as structural, reliability, lifetime, or cost-based [24]. The appropriate category depends on the available information and data quality [38]. For instance, structural IMs are used when only the system design is known, whereas reliability IMs are used when failure probability data is available. Lifetime IMs consider operational factors, such as age, usage, and environment. Cost-based IMs account for the financial impact of maintenance or improvements. Some of these measures also integrate uncertainty directly into the criticality assessment. However, the present study concentrates on Structural IMs and Reliability IMs, as they are the most widely used in reliability-centered decision-making. We use Birnbaum ($I_i^B\left(t\right)$), Risk Reduction Worth—RRW ($I_i^{RRW}\left(t\right)$), Risk Achievement Worth—RAW ($I_i^{RAW}\left(t\right)$), Fussell–Vesely ($I_i^{FV}\left(t\right)$), and Criticality ($I_i^{CR}\left(t\right)$), which together span structural sensitivity, failure contribution, and operational consequence.

Theoretical IMs clarify how reliability propagates through engineering systems (Table 1). Each measure captures a specific aspect of system behavior: $I_i^B\left(t\right)$ defines structural dependency, $I_i^{RRW}\left(t\right)$ and $I_i^{RAW}\left(t\right)$ quantify system improvement or degradation limits, $I_i^{FV}\left(t\right)$ measures the contribution of each component to overall risk, and $I_i^{CR}\left(t\right)$ combines structural sensitivity with operational reliability. Together, these indices form a diagnostic that helps engineers understand how and why system reliability changes under different configurations and operational conditions.

Table 1. Mathematical definitions of selected IMs.

Classification	IM	Used for Identify	Equation	Characteristics
Structural	Birnbaum	Components whose marginal reliability variation exerts disproportionate influence on overall system reliability.	$I_i^B\left(t\right)={\displaystyle \frac{{\partial R}_s\left(t\right)}{{\partial R}_i\left(t\right)}}$	Quantifies the sensitivity of system reliability to changes in the reliability of an individual component	[21,22,39,40]
Structural	RRW	Best candidates for reliability improvement	$I_i^{RRW}\left(t\right)={\displaystyle \frac{F_s\left(t\right)}{\left[F_s\left(t\right)|F_i\left(t\right)=0\right]}}$	Measures system unreliability change when a component is assumed perfect	[22,38,39]
Structural	RAW	Components where abrupt failure-probability escalation maximally degrades system performance	$I_i^{RAW}\left(t\right)={\displaystyle \frac{\left[F_s\left(t\right)|F_i\left(t\right)=1\right]}{F_s\left(t\right)}}$	Identifies the system components that are essential to rendering the system unreliable	[22,38,39]
Reliability	Fussell-Vesely	Allowed performance degradation	$I_i^{FV}\left(t\right)={\displaystyle \frac{F_i\left(t\right)}{F_s\left(t\right)}}$ $I_i^{FV}\left(t\right)=F_s\left(t\right)-{\displaystyle \frac{\left[F_s\left(t\right)|F_i\left(t\right)=0\right]}{F_s\left(t\right)}}$	A low probability of failure is not always the most suitable candidate for change	[41,42]
Reliability	Criticality	Relative contribution of component reliability to overall system reliability.	$I_i^{CR}\left(t\right)=\left[{\displaystyle \frac{\partial R_s\left(t\right)}{\partial R_i\left(t\right)}}\right]·\left[{\displaystyle \frac{R_i\left(t\right)}{R_s\left(t\right)}}\right]$ $I_i^{CR}\left(t\right)=I_i^B\left(t\right)·\left[{\displaystyle \frac{R_i\left(t\right)}{R_s\left(t\right)}}\right]$	Assesses component suitability beyond just failure probability	[24]

$I_i^B\left(t\right)$ quantifies the sensitivity of system reliability to variations in a component’s reliability. It identifies components for which small reliability changes produce larger effects on overall performance. In practice, it informs maintenance prioritization, inspection schedules and redundancy allocation. Components with high $I_i^B\left(t\right)$ are those whose failure leads to a significant loss of functionality.

$I_i^{RRW}\left(t\right)$ and $I_i^{RAW}\left(t\right)$ complement Birnbaum’s measure by expressing practical limits on improvement and degradation. $I_i^{RRW}\left(t\right)$ quantifies the gain if a component were perfect; $I_i^{RAW}\left(t\right)$ quantifies the loss if it were failed. High $I_i^{RRW}\left(t\right)$ indicated where upgrades yield the largest benefit, while high $I_i^{RAW}\left(t\right)$ flag elements that warrant close monitoring or redundancy. These measures are used in nuclear, aerospace, and industrial applications to support maintenance planning, redundancy design, and resource allocation. Taken together, they show how extreme component conditions influence overall system behavior, guiding risk-informed decisions.

$I_i^{CR}\left(t\right)$ evaluates a component’s contribution relative to system reliability. It is defined as the product of $I_i^B\left(t\right)$ and the ratio between component and system reliability, linking structural sensitivity with probabilistic significance. Whereas $I_i^B\left(t\right)$ measures absolute influence, $I_i^{CR}\left(t\right)$ expresses influence in proportional terms, indicating where a unit increase in component reliability most effectively increases system reliability. It is useful when resources are constrained, prioritizing components that are both influential and at reliability levels where improvements are most effective. It is often discussed alongside $I_i^{FV}\left(t\right)$ because both describe proportional system effects rather than purely structural dependence.

In applied reliability analysis, the measures provide complementary views: $I_i^B\left(t\right)$ identifies where the system is most structurally sensitive; $I_i^{RRW}\left(t\right)$ and $I_i^{RAW}\left(t\right)$ quantify the best and worst operational cases; $I_i^{FV}\left(t\right)$ shows current unreliability contributions; and $I_i^{CR}\left(t\right)$ highlights where proportional reliability improvements are most effective. Using them together allows engineers to balance structural significance, practical improvement potential, and probabilistic impact, providing a complete view of system reliability. This integrated approach supports maintenance prioritization, redundancy planning, and design optimization in complex engineering systems.

2.2. Uncertainty Modeling

Uncertainty in reliability modeling arises from the limited information available to estimate the statistical parameters of component lifetime models. For a component $i$, let the random variable $t_i=(t_{i1},t_{i2},\dots ,t_{in},)$ represent its TTF, characterized by a parametric probability density function (PDF) $f_i(t\mid {\theta }_i)$ and corresponding reliability function. For component $i$, let ${\theta }_i$ denote the parameters of the selected lifetime model [2,31]. The parameters ${\theta }_i$ are estimated from observed failure data $t_i$ using Maximum Likelihood Estimation (MLE):

$$\begin{array}{cccc}& \widehat{{\theta }_i}=\mathrm{a}\mathrm{r}\mathrm{g} \underset{{\theta }_i}{\mathrm{m}\mathrm{a}\mathrm{x}}{\displaystyle \prod _{j=1}^{n_i}}{f}_i(t_{ij}\mid {\theta }_i)& & \end{array}$$

Since these estimates are subject to sampling variability, they are treated as random variables. Under standard regularity conditions, the MLE is asymptotically normal,

$${\theta }_i~\mathcal{N}\left({\widehat{\theta }}_i,{\widehat{V}}_i\right)$$

where ${\widehat{V}}_i={\mathit{I}}_i^{-1}\left({\widehat{\theta }}_i\right)$ is the inverse observed information matrix and $I_i\left({\widehat{\theta }}_i\right)$ is the observed Fisher information. This provides a probabilistic representation of epistemic uncertainty in the parameter estimates.

$$\begin{array}{cccc}& I_i\left({\widehat{\theta }}_i\right)={-\left.{\displaystyle \frac{{\partial }^2\log L_i\left({\widehat{\theta }}_i\right)}{\partial {\theta }_i\partial {\theta }_i^T}}\right|}_{{\theta }_i={\widehat{\theta }}_i}& & \end{array}$$

This formulation enables the propagation of parameter uncertainty through the reliability structure function $\varphi (\cdot )$, which defines the system reliability as follows:

$$\begin{array}{cccc}& R_{sys}\left(t\right)=\varphi \left(R_1\right(t\mid {\theta }_1),R_2(t\mid {\theta }_2),\dots ,R_n(t\mid {\theta }_i\left)\right)& & \end{array}$$

As a result, $R_{sys}\left(t\right)$ becomes a random variable, and its distribution captures the uncertainty propagation from component-level parameters to the system level.

This parametric uncertainty affects the estimation of component reliability and, consequently, the derived IMs. By treating parameters as random variables, the variability in the data is reflected in the estimated reliability functions $R_i\left(t\right)$, the system reliability $R_{sys}\left(t\right)$, and the associated measures [2]. Accordingly, the analysis reports interval estimates of reliability and importance rather than single deterministic values, offering a more realistic basis for decision-making.

2.3. Risk Priority Numbers in Failure Mode and Effect Analysis

The RPNs a classical metric derived from Failure Mode and Effects Analysis (FMEA), used to identify and prioritize risk in engineering systems [41]. It guides maintenance decisions by ranking failure modes that need preventive or corrective actions and supports the definition of maintenance priorities [27,43,44]. The RPN is computed from three factors: occurrence (O), severity (S), and detectability (D). Which reflect how often a failure occurs, the impact of its effects and how easily it can be detected before it occurs [19,29,41,45]. The product of these three values provides a single numerical indicator that allows maintenance teams to focus on the most critical issues. Its simplicity and clarity make it widely used in industrial environments, where fast decisions are often required. Table 2 summarizes common RPN formulations, including the traditional multiplicative model and several adapted versions that consider different relations between failure causes, effects, and modes.

Table 2. Formulations of RPN.

Expression	Description
${RPN}_j^i=S_j^i·D_j^i·O_j^i$	Classical RPN definition for the j-th failure mode of the i-th component	[19,41,45]
${RPN}_j^i=(D_{jk}^i·O_{jk}^i)·\left(S_j^i\right)$	Adjusted RPN when severity is assigned to jth failure mode, and occurrence/detectability are assigned to kth causes.	[29]

Although the RPN is widely used in sectors such as automotive manufacturing, process industries, and aerospace, it has known limitations [17,26,43]. Because it uses ordinal scales, it depends strongly on expert judgment and assumes linear relationships between factors that may not be independent [19,29]. The lack of a probabilistic basis limits the description of how uncertainty propagates across related failure modes. To address these issues, studies propose variants that incorporate probabilistic reasoning, fuzzy logic [29,46], or cost-based weighting, aiming to improve consistency while retaining simplicity for practical use [27,46,47,48].

From a practical point of view, the main challenge is to keep the method easy to apply while improving its accuracy and reliability. Maintenance engineers often prefer tools that are simple, transparent, and adaptable to real data limitations. Probabilistic versions of the RPN can include confidence intervals or uncertainty ranges, making the results more consistent with the actual operating conditions. When used together with Importance Measures, the RPN supports not only the ranking of failure modes but also the evaluation of how stable those rankings remain when data or parameters vary. This connection helps link reliability analysis with maintenance planning, providing clear guidance for decisions in complex systems.

Despite its limitations, the RPN is a valuable tool for identifying and prioritizing risks early in the design phase and throughout the asset lifecycle. Its persistence in industrial practice underscores the importance of frameworks that build upon its strengths rather than discarding them.

The theoretical framework presented the basis for identifying critical components using IMs and RPN. The approach does not propose new reliability indices but extends classical IMs to a probabilistic context that considers parameter uncertainty. Using reliability estimates obtained from FT or RBD models allows the evaluation of how uncertainty in each component affects the overall system reliability. This helps to describe reliability sensitivities under changing operating conditions. The combination of IMs with the FMEA structure component-reliability assessment and failure-mode prioritization. IMs indicate how much each component contributes to system reliability, while RPN identifies the most critical failure modes by combining severity, occurrence, and detection. Comparing both results provides a complete view of system behavior and supports maintenance planning.

From a practical point of view, this theoretical foundation helps maintenance teams to focus their resources on components and failure modes that have the greatest effect on system reliability. Considering uncertainty in IMs reflects the natural variability of real operating conditions and the limitations of available data. The methodology serves as a tool to reduce maintenance costs and improve planning by concentrating efforts on the failures that most affect system performance. The integration of IMs and RPN converts reliability analysis into useful guidance for maintenance planning and decision-making under real operational uncertainty.

3. Methodology

The objective of this methodology is to enable a systematic prioritization of critical components and failure modes in complex engineering systems that account for uncertainty. The framework integrates quantitative reliability techniques, such as RBD, FTA, and IMs, with qualitative failure analysis via FMEA. This two-level approach evaluates failure mode impact and assesses each component’s effects on system reliability. The method traces failure propagation through critical components and identifies the failure modes with the highest impact on system performance. By linking the identification of critical failures with their quantified effects on reliability, the framework indicates which components should be prioritized, while facilitating the development of actionable mitigations.

Integrating these techniques provides a stronger basis for maintenance planning and risk management by accounting for epistemic uncertainty. The methodology follows a conditional workflow that adapts based on the level of available system knowledge. Figure 1 presents a workflow that combines deterministic, probabilistic and qualitative reliability tools for decision-making, showing the progression from structural definition to decisions under uncertainty in the reliability assessment process.

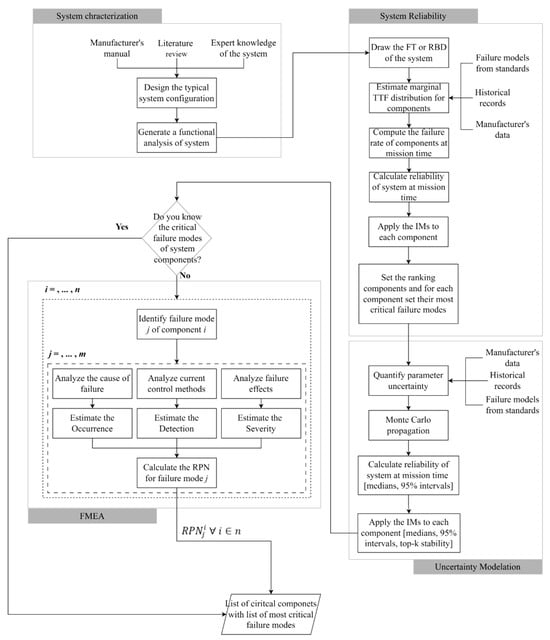
Figure 1. Proposed Methodology.

Numerically, the workflow after qualitative assessment proceeds as follows: estimate lifetime parameters for each component ($i\in n$) ${\widehat{\theta }}_i\to$ compute reliabilities $R_i\left(t\right)\forall i\in n\to$ evaluate system reliability $R_{sys}\left(t\right)=\varphi \left(R_1\left(t\right),R_2\left(t\right),\dots ,R_n\left(t\right)\right)$ via FTA or RBD$\to$ compute IMs $\left\{I_i^B,I_i^{RRW},I_i^{RAW},I_i^{FV},I_i^C\right\}\forall i\in n\to$ synthesize with FMEA by pairing each prioritized component with its top failure modes and RPNs.

The integration of these four analytical blocks establishes a closed-loop reliability framework in which each stage reinforces the subsequent stage. System Characterization defines the structural basis that constrains probabilistic modeling; System Reliability quantifies these relationships and reveals component dependencies; Uncertainty Modeling evaluates the robustness of these dependencies under parameter variability; and FMEA validates and complements quantitative findings by linking them to observable failure behavior and performable mitigations. Their interaction enables consistency between structural logic, probabilistic evidence, and operational experience, improving the traceability and reliability of maintenance decisions.

3.1. System Characterization

The first methodological block establishes the functional analysis through information from technical manuals, the literature, and expert knowledge. This stage is not merely descriptive; it serves as the source of conditions for the subsequent quantitative modeling. Defining system configuration and performing functional analysis enables a clear mapping between physical subsystems and their logical representation in reliability models. Based on this description, the method takes a systematic approach to identifying failure modes (j) for each component (i) of the system ($f_i^j$). A failure mode is the distinct mechanism by which a failure presents itself, resulting in a functional failure [49,50,51].

3.2. System Reliability

The second block converts the qualitative system representation into a quantitative structure using FTA or RBD. At this point, it is used to model system behavior and compute component and system failure probabilities [13,51,52]. This stage shifts the analysis from descriptive modeling to data-based evaluation. The estimation of TTF and failure rates connects historical records and manufacturer data with the probabilistic behavior of each component.

Let $\mathcal{F}=\left\{{\mathcal{F}}_p\left(·|{\theta }_{i,p}\right)\right\}$ denote a candidate set of lifetime distributions (e.g., Exponential, Weibull, Gamma). Given observed TTF data for component $i$, ${TTF}^i=\left\{t_1^i,t_2^i,\dots ,t_l^i\right\}$, the parameters ${\theta }_{i,p}$ are estimated by maximum likelihood.

$${\widehat{\theta }}_{i,p}=arg \underset{\theta }{\max } \mathcal{L}\left({TTF}^i|{\mathcal{F}}_{p,}\theta \right)$$

The preferred model for the $i$-th component is selected using goodness-of-fit diagnostics (e.g., Kolmogorov–Smirnov) and information criteria (the Akaike Information Criterion—AIC or the Bayesian Information Criterion—BIC). The resulting reliability function $R_i\left(t\right)$ follows from the chosen family, for instance,

$$R_i\left(t\right)=\left\{\begin{array}{c}exp\left(-{\theta }_{i}t\right)exponential\\ exp\left[-{\left({\displaystyle \frac{t}{{\theta }_{i,1}}}\right)}^{{\theta }_{i,2}}\right]weibull\end{array}\right.$$

The procedure for estimating the parameters of these distributions and using them to support reliability assessment and asset management follows the approach previously proposed [53].

If TTF data are unavailable, parameter estimates may be elicited from expert judgment, sectoral standards or analogous systems, ensuring methodological adaptability.

Subsequently, once $R_i\left(t\right)$ has been specified for $i=1,\dots ,n$, the overall system reliability is obtained from the structure function $\varphi \left(·\right)$ defined by the FT or RBD:

$$R_{sys}\left(t\right)=\varphi \left(R_1\left(t\right),R_2\left(t\right),\dots ,R_n\left(t\right)\right)$$

where series, parallel, or k-out-of-n relationships capture how component failure propagates within the system.

Once system reliability $R_{sys}\left(t\right)$ is obtained, the application of IMs extends the evaluation beyond failure probability to include the structural contribution of each element. Through this process, the influence of each component on the overall system reliability is quantified. The resulting hierarchy of component criticality provides a clear basis for prioritizing maintenance and risk mitigation actions.

Consistent with the concepts reviewed in Section 2.2 and the definitions in Table 1, we quantify component criticality from the system reliability function $R_{sys}\left(t\right)$ obtained via FTA/RBD. The goal is to translate system structure and behavior into operational indices that rank the $n$ components by their marginal influence on overall performance, while retaining the structural vs. reliability-based categories introduced earlier.

For each component $i$, IMs are evaluated by re-computing $R_{sys}\left(t\right)$ under targeted perturbations of $R_i\left(t\right)$, or under ideal/worst assumptions. Evaluating these metrics over the mission time of interest yields a quantitative ranking of components. In the synthesis step, this IM-based ranking is linked to the qualitative input of FMEA: for each prioritized component $i$, we report its IM values and rank together with its top failure modes and RPNs. This preserves the complementary roles of methodologies: interpretability of failure modes from FMEA, and probabilistic rigor plus systemic perspective from FTA/RBD and IMs, supporting risk-informed maintenance planning and resource allocation.

3.3. Propagation of Uncertainty

Acknowledging that, in practice, it is impractical to assume fixed parameters for the TTF of each component, we explicitly treat parametric uncertainty in the TTF models introduced in Section 3.2 and propagate its effect to the system reliability and IMs of Section 3.3, following our previous approach [7].

For component $i$, let ${\theta }_i$ denote the parameters of the selected lifetime model (e.g., $\theta$ for Exponential, $\left({\theta }_1,{\theta }_2\right)$ for Weibull).

Uncertainty propagation is performed via Monte-Carlo. For $b=1,\dots ,B$ (e.g., $B=\mathrm{10,000}$) and all components $i=1,\dots ,n$.

• Draw ${\theta }_i^b~\mathcal{N}\left({\widehat{\theta }}_i,{\widehat{V}}_i\right)$;
• Compute $R_i^b\left(t\right)$ from the chosen lifetime model;
• Evaluate $R_{sys}^b\left(t\right)=\varphi \left(R_1^b\left(t\right),R_2^b\left(t\right),\dots ,R_n^b\left(t\right)\right)$ via FTA or RBD;
• Compute IMs $\left\{I_i^{B\left(b\right)},I_i^{RRW\left(b\right)},I_i^{RAW\left(b\right)},I_i^{FV\left(b\right)},I_i^{C\left(b\right)}\right\}$.

After all iterations, we summarize $R_{sys}\left(t\right)$, subsystems failure probabilities and IMs by medians and 95% uncertainty intervals (Monte-Carlo percentiles). We also report rank stability, i.e., the proportion of iterations in which each element appears at the top-$k$ by a given IM, to indicate prioritization robustness.

This procedure quantifies how uncertainty in lifetime-model parameters propagates to system-level reliability and IMs, providing interval-based evidence rather than point estimates alone.

General assumptions: Unless stated otherwise, component failures are treated as statistically independent (dependences are represented by the FTA/RBD structure function); lifetime parameters are time-homogeneous over the analysis horizon; operating conditions are stationary within the mission window; repairs are not modeled (focus on reliability rather than availability). Candidates’ lifetimes, families, and parameter estimation follow Section 3.2; IM are computed as shown in Section 3.3; and parametric uncertainty is quantified and propagated as shown in Section 3.4. Dataset-specific assumptions (e.g., mission time, data sources) are detailed in the case study.

3.4. Closing the Loop: IMs, FMEA and Prioritization

The fourth methodological block introduces a conditional mechanism for knowledge completion. If the critical failure modes of system components are unknown, the process transitions toward the qualitative domain. Here, FMEA acts as an inference tool that decomposes uncertainty about specific failure mechanisms into measurable indices: occurrence, detection, and severity. The derived RPNs close the inferential loop by generating a criticality list that complements and validates the ranking obtained through IMs.

FMEA provides a structured list of components, their potential failure modes, and the corresponding risk rankings (${RPN}_j^i\forall i\in n$). These qualitative outputs are retained to support the interpretation of quantitative results at a later stage.

Each component $iϵ\left\{1,2,\dots ,n\right\}$ is decomposed into potential failure modes $f_i^j$with $j=1,2,\dots ,m_i$. A failure mode is the distinct mechanism by which a failure presents itself, resulting in a functional failure.

For each mode, three evaluation criteria are defined: occurrence $O_i^j$, severity $S_i^j$, and detection $D_i^j$; the RPN is computed as shown in Table 2.

Conceptually, this block closes the inferential loop: uncertainty about the system’s behavior is reduced by aligning deductive reliability results with inductive field evidence. The resulting criticality ranking not only identifies where failures are most probable but also where they are most consequential, guiding maintenance decisions that balance analytical rigor and empirical knowledge. The following sections demonstrate the practical value of this framework by presenting its application to SWCCT within a solid waste management company.

4. Case Study

For empirical validation, the proposed methodology was implemented in a real-world case study involving a fleet of SWCCT operated by a solid waste management company in a Colombian city, thereby providing a relevant testbed to assess its applicability and effectiveness under operational uncertainty.

In this section, the case study is introduced by presenting its operational context, the functional understanding of the SWCCT, and the scope of the analyses conducted at both qualitative and quantitative levels. Rather than focusing on results, which are developed in Section 5, the emphasis here is placed on explaining the system configuration, outlining the operational challenges faced by the fleet, and clarifying the procedures followed in each stage of the analysis. This structure ensures that the reader gains a clear overview of the system and its environment before addressing the findings of the methodology’s application.

The company operates a fleet that serves 248 urban routes dedicated to domestic and recyclable waste collection, exposing the trucks to highly demanding operational conditions such as steep terrain, long-distance travel to landfills, continuous loading and unloading cycles, and frequent stops. These challenges make SWCCT an appropriate testbed for assessing how reliability strategies that account for uncertainty can support engineering decision-making, enhance resource allocation, and improve system resilience in real-world environments.

4.1. Functional Analysis of System

SWCCT is the core unit of the vehicle, enabling reception, compaction, and temporary storage of solid waste prior to its final transport. From a methodological perspective, the decomposition of the system into hierarchical levels (system, subsystems, and components) is a prerequisite for implementing reliability-based assessment frameworks. Structurally, the SWCCT integrates two major subsystems: (i) the compaction system (CS) associated with electric and control units responsible for waste compression and operational control; and (ii) the heavy-duty truck system (HDTS), which collectively ensure vehicular mobility, load-bearing capacity and reliable operation under demanding service

The structured breakdown not only allows the identification of functional interdependencies but also facilitates the quantification of failure probabilities at different aggregation levels, which is fundamental for integrating uncertainty into risk evaluation. In summary, the primary function of the SWCCT: the collection and transportation of municipal solid waste to treatment facilities.

Building upon this system-level perspective, the subdivision into the compaction-box structure (CBS) and the hydraulic subsystem (HS) provides a more detailed view for analyzing reliability and risk propagation. CBS directly governs the mechanical integrity of waste containment, while the HS determines the performance and operational continuity of compaction (Figure 2).

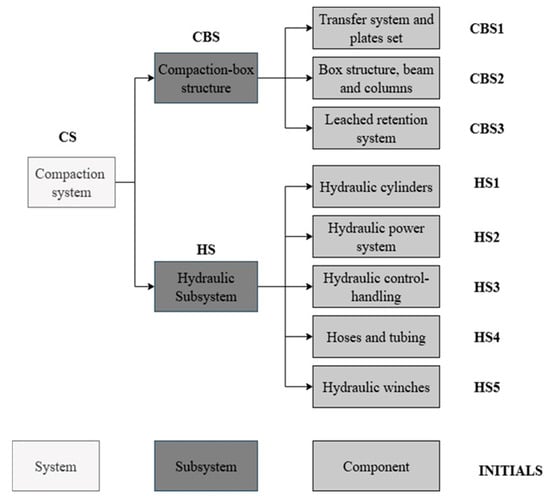
Figure 2. Compaction system of waste collection vehicles.

Uncertainty in these subsystems arises from heterogeneous loading conditions, hydraulic pressure fluctuations, and wear mechanisms, all of which may trigger cascading effects across the system. Therefore, emphasizing subsystems in the reliability framework ensures a more detailed understanding of failure propagation, enabling a probabilistic treatment that accounts for both epistemic and aleatory uncertainties inherent in waste collection operations.

Extending this system-level integration, the subdivision of the HDTS into critical subsystems—such as the engine, brakes and pneumatic subsystem, suspension, steering, power transmission, and electric and control—introduces a finer resolution for analyzing risk propagation (Figure 3).

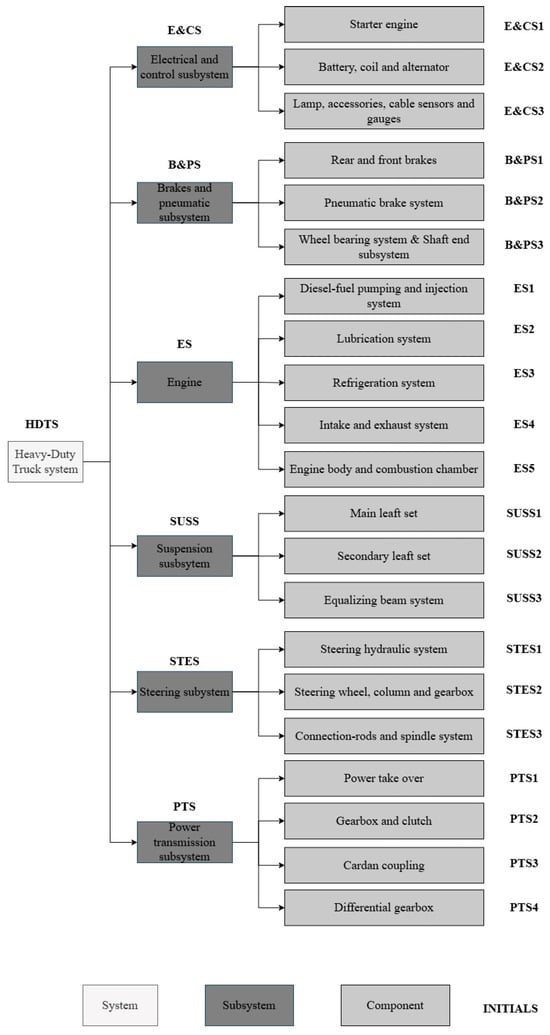
Figure 3. Heavy-Duty Truck System of waste collection vehicles.

These subsystems represent diverse physical domains, and their interactions are inherently nonlinear, making them key determinants of overall reliability. From a reliability perspective, this interconnectedness highlights the importance of capturing both aleatory uncertainties (stemming from variable loads, environmental stresses, and wear) and epistemic uncertainties (derived from limited knowledge of degradation mechanisms).

4.2. Critical Components Analysis of SWCCT

Using failure records from December 2015 to January 2020 (hours), Exponential, Weibull, and Lognormal TTF models were fitted using maximum likelihood for each component, selected the best family by AIC (BIC as tiebreaker), and assessed absolute fit with the Cramér–von Mises statistic (KS bootstrap p-values in Appendix A). Figure 4 summarizes both the empirical support (number of records) and the selected marginal family—panel (a) for the compaction system and panel (b) for the heavy-duty truck system. In line with mechanical wear mechanisms, Weibull predominates, while Exponential and Lognormal appear where memoryless or multiplicative effects are plausible. Full parameter estimates (with SEs) and diagnostics are reported in Appendix A. These fitted marginals feed directly into the system-level computation described next.

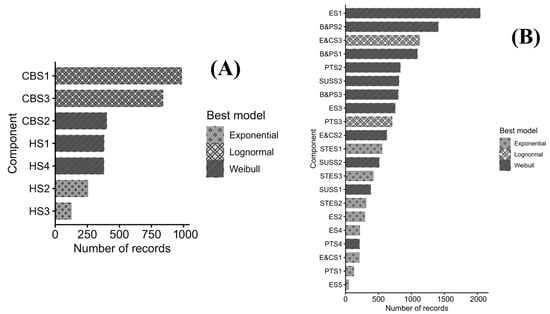
Figure 4. Selected marginal TTF model by component: (A) compaction system; (B) Heavy-Duty Truck System.

Given the complexity of the SWCCT and the uncertainty regarding which subsystems contribute most critically to overall reliability, the quantitative stage of the case study was structured around an FTA (Figure 5). This approach was chosen because it provides a direct representation of how specific component or subsystem failures propagate to total system loss, aligning with the operational realities of the fleet. The FTA, when applied to the failure data collected from the trucks, revealed that the HS5 showed no record failures; the compaction system and truck-level subsystems—including power transmission, brakes, and hydraulics—were the main contributors to system risks.

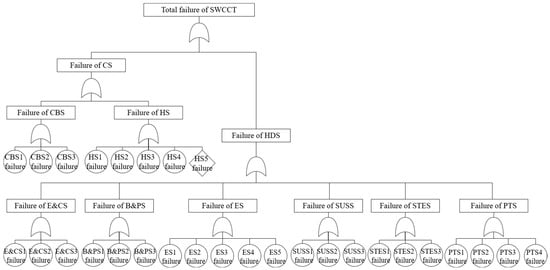
Figure 5. Fault Tree Analysis of waste collection vehicles.

By mapping these interdependencies, the FTA demonstrated that the overall reliability of the SWCCT is particularly vulnerable to failures in the compaction box and its hydraulics, or in any major truck subsystem such as the engine, electrical, or control systems. The detailed examination of the power transmission subsystem illustrated how single-component failures can escalate into total subsystem collapse, underscoring the systemic fragility created by tightly coupled elements. This practical insight provided by the FTA enabled the identification of high-impact failure pathways, supporting targeted maintenance actions and risk-informed decision-making for the fleet’s operation. The estimated reliability of the SWCCT was derived from the FTA and component failure rates. The FTA included 28 basic events, resulting in 28 minimum cut sets due to the use of OR gates. Based on these quantifications and failure rates, IMs were applied, and the results are discussed in the next section.

4.3. Uncertainty Quantification of SWCCT

In accordance with what is described in Section 3.3, parametric uncertainty was quantified under the marginal lifetime models and propagated to the SWCCT reliability and IMs. For each basic event (failure of component), the fitted distribution parameters (Appendix A) were treated as random: Exponential rates, Weibull and Lognormal were sampled from their asymptotic MLE normal centered at with standard errors taken from Appendix A. Positivity-constrained (rates, shapes, scales) were sampled from truncated normal to enforce physical bounds. Then, for mission time, each draw yields the failure probability of the component, i.e., the probability of a basic event. These probabilities are then mapped through the FTA to obtain the top-event probability (complete failure of the SWCCT) and, by complement, system reliability.

A Monte-Carlo simulation was run with parameter drawings. For each draw, we computed component failure probabilities, propagated them through the FTA, and then evaluated the IMs. We summarize medians and 90% uncertainty intervals (5th and 95th percentiles) for all IMs across the iterations. To support maintenance planning, we also provide an uncertainty-informed ranking (top five of SWCCT components per IM) and discuss their failure modes identified in the qualitative analysis.

4.4. Critical Modes Failures of SWCCT

Once critical components were identified, the subsequent FMEA revealed 322 potential failure modes across systems and subsystems. This evaluation integrated both static sources, such as manufacturer catalogs, troubleshooting guides, operations manuals, and dynamic sources, including failure records and maintenance work orders collected over a four-year period. Severity and occurrence rankings were assigned using standardized scales from the literature [54,55], ensuring methodological consistency and comparability. However, given the specific complexity of the SWCCT architecture, control design mechanisms and maintenance execution dynamics for the SWCCT fleet, it was necessary to develop tailored detectability criteria to better reflect diagnostic challenges faced in practice. These criteria account not only for the technical difficulty of identifying a failure but also for the expertise and personnel required to perform effective monitoring. As a result, the detectability index captured dimensions not addressed by conventional scales, thereby unifying the ranking procedure across all subsystems. This adaptation guaranteed a consistent and system-specific evaluation of failure modes, as summarized in Table 3.

Table 3. FMEA detectability criteria.

Detection	Likelihood of Detection	Personal (Mechanic/Engineer)	Ranking
Absolute Uncertainty	Design control (DC) cannot or will not detect a potential cause, mechanism, or failure mode	NA	10
Very Remote	Extremely unlikely that DC will detect a potential cause, mechanism, or failure mode	NA	9
Remote	Low likelihood that DC will detect a potential cause, mechanism, or failure mode	Diagnosis of the cause/mechanism requires disassembling multiple components	8
Very Low	Very small chance that DC will detect a potential cause, mechanism, or failure mode	Diagnosis of the cause/mechanism requires disassembling the component.	7
Low	Limited chance that DC will detect a potential cause, mechanism, or failure mode	Diagnosis of the cause/mechanism requires disassembling the sub-system	6
Moderate	Reasonable chance that DC will detect a potential cause, mechanism, or failure mode	Diagnosis of the cause/mechanism is possible without disassembling the sub-system	5
Moderately high	Fairly good chance that DC will detect a potential cause, mechanism, or failure mode	The operator can diagnose the cause/mechanism by disassembling the component	4
High	High likelihood that DC will detect a potential cause, mechanism, or failure mode.	Available sensors allow diagnosis of the cause/mechanism	3
Very High	Very strong chance that DC will detect a potential cause, mechanism, or failure mode.	An external observer can diagnose the cause/mechanism	2
Almost Certain	DC will almost certainly detect a potential cause, mechanism, or failure mode	The subsystem/component can self-diagnose the cause/mechanism	1

In practice, detectability was further refined to reflect the real-world constraints of maintenance operations, including the level of expertise and personnel required to diagnose specific failures. This final adjustment ensured that subsystem-specific design variations and operational realities were fully captured, reinforcing the robustness and applicability of the evaluation framework.

5. Results

The critical evaluation of the components in the SWCCT is presented, using the discussed methodology. Building on the functional analysis overview provided in Figure 2 and Figure 3, critical components of the SWCCT were identified by evaluating each item using importance measures. For each item, measures of importance such as $I_i^B\left(t\right)$, $I_i^{RRW}\left(t\right)$, $I_i^{RAW}\left(t\right)$, $I_i^{FV}\left(t\right)$, and $I_i^{CR}\left(t\right)$ were applied (see Figure 6).

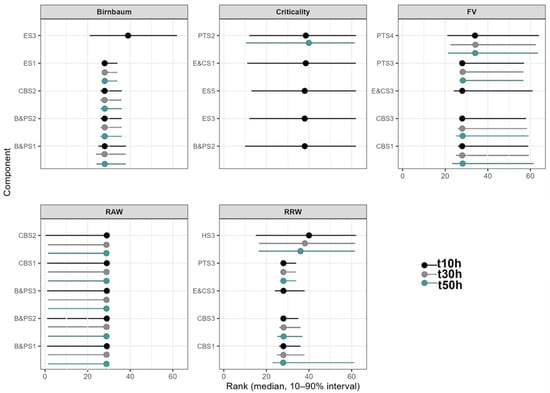
Figure 6. Top 5 Components—Rank Stability for critical components for waste collection vehicles.

Consequently, Figure 6 presents the computation of the four IMs obtained from the FTA of SWCCT. The Heavy-Duty Truck subsystems, particularly the Brakes and Pneumatic System (B&PS), the Electrical and Control Subsystem (E&CS), and the Power Transmission System (PTS), show the highest Importance Measure (IM) values, indicating the strongest influence on the overall reliability of the SWCCT. In contrast, the Compaction Box Structure (CBS) and Hydraulic System (HS) exhibit moderate IM values, suggesting that although they are relevant for operational performance, they are not the dominant contributors to system reliability.

Higher values of $I_i^{\left(B\right)}$indicate components whose reliability variations produce significant effects on the system-level reliability. In this case, B&PS1, E&CS3, and B&PS2 exhibit the largest $I_i^{\left(B\right)}$ values, confirming that they belong to minimal cut sets directly associated with the top event. Components in SUSS and STES show intermediate influence, whereas HS and ES components display low marginal contributions, indicating a degree of redundancy in those subsystems.

$I_i^{\left(FV\right)}$ values lie between 0.03 and 0.08, maintaining a consistent ranking pattern with $I_i^{\left(B\right)}$. The dominance of the B&PS and E&CS subsystems indicates that they act as failure-propagation paths. The reduced dispersion across components within HS and ES confirms that these subsystems act as reliability buffers under stochastic load conditions.

$I_i^{\left(RRW\right)}$ represents the relative improvement in system reliability if components B&PS1, E&CS3, and B&PS2 were made perfectly reliable, indicating the largest potential gain from maintenance or design improvement. Conversely, components from HS and ES present $I_i^{\left(RRW\right)}\approx 1.00$, confirming minimal potential for reliability enhancement through local interventions.

For $I_i^{CR}\left(t\right)$, it is observed that all components contribute proportionally to the overall system reliability. The values range between 0.93 and 0.99, indicating a narrow dispersion and suggesting that reliability improvements would benefit the entire system in a nearly uniform manner. This pattern implies that proportional enhancements in component reliability translate directly into global reliability gains. Such behavior is consistent with the series-dominant configuration of the SWCCT, where overall performance depends on the correct functioning of every subsystem.

For this case, $I_i^{CR}\left(t\right)$ and $I_i^{RAW}\left(t\right)$ are less meaningful because they become identical when the unreliability of any component reaches one, indicating that system unreliability is maximal.

In systems with series topology, the system reliability $R_{sys}$ can be approximated as the product of individual component reliability. Under this structure, even small variations in the reliability of any component have a noticeable influence on $R_{sys}$, which explains the relatively uniform criticality ($I_i^{CR}$) across components. Consequently, maintenance or design actions that target general reliability improvement—rather than focusing solely on isolated elements—will yield system-level benefits.

Figure 7 complements the deterministic (point) estimates of SWCCT reliability reported in Table 4 by displaying the median trajectory and the 90% uncertainty bands, obtained by propagating parametric uncertainty through the FTA.

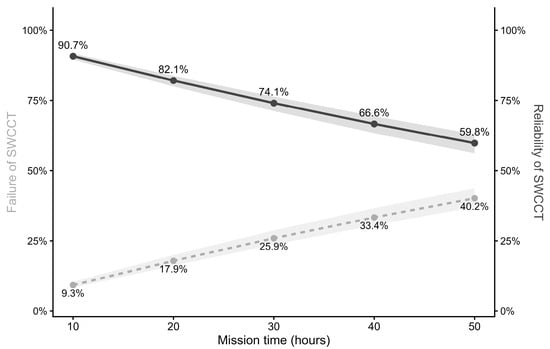
Figure 7. Uncertainty Analysis.

Table 4. Failure and Reliability under uncertainty of SWCCT.

	Operational Time (Hours)
	10	20	30	40	50
Reliability of SWCCT (5th percentile)	89.54%	80.01%	71.26%	63.34%	56.20%
Reliability of SWCCT (median)	90.74%	82.10%	74.06%	66.64%	59.83%
Reliability of SWCCT (95th percentile)	91.70%	83.79%	76.37%	69.42%	62.96%
Failure of SWCCT (5th percentile)	8.30%	16.21%	23.63%	30.58%	37.04%
Failure of SWCCT (median)	9.26%	17.90%	25.94%	33.36%	40.17%
Failure of SWCCT (95th percentile)	10.46%	19.99%	28.74%	36.66%	43.80%

Regarding the reliability of the vehicles, Figure 7 presents the results obtained when quantifying the main systems of the SWCCT for different periods of operation (10, 20, 30, 40, and 50 h), in accordance with the operators’ interest in evaluating fleet reliability at the beginning and at the end of the week (the SWCCT analyzed operates 10.44 h/day).

As outlined during methodology description (Section 3.3), once a baseline for system reliability was established, continuing with uncertainty analysis provides a more realistic view of prediction confidence over time. Figure 7 complements the deterministic estimates of SWCCT reliability reported in Table 4 by displaying the median trajectory and the 90% uncertainty bands, obtained by propagating parametric uncertainty through the FTA.

The reliability profile decreases monotonically with time, and the uncertainty bands widen at longer horizons, indicating the accumulation of parameter uncertainty in the system-level prediction. Relative to the deterministic curve, the uncertainty-aware median is slightly lower at all horizons, which signals that point estimates are mildly optimistic when parameter variability is acknowledged.

The IMs derived from the Fault Tree Analysis indicated that the Brakes and Pneumatic System (B&PS), Electrical and Control Subsystem (E&CS), and Power Transmission System (PTS) are the most critical contributors to the overall reliability of the SWCCT. Components within these subsystems exhibited the highest Birnbaum and Fussell–Vesely importance values, confirming that small variations in their reliability have significant effects at the system level. Conversely, the Compaction Box Structure (CBS) and Hydraulic System (HS) showed moderate IM values, while the Electrical Supply (ES) and Structural Subsystem (SUSS) presented the lowest ones, indicating lower marginal effects on the top event probability.

Maintenance prioritization was further supported by failure modes ranked using Risk Priority Numbers (RPNs), as described in the methodology (Figure 1). RPNs were evaluated across components and grouped by subsystem, reinforcing the relevance of B&PS, E&CS, and PTS—already identified as critical through IMs. Figure 8 presents NPR values, highlighting failure modes concentrated in these subsystems.

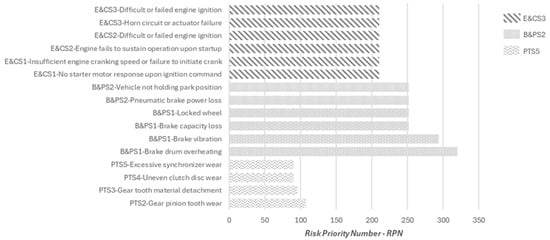
Figure 8. RPN summary for critical components for Systems according to IM prioritization.

The pneumatic braking subsystems require attention because two of their components show the highest RPN values and have safety implications. Brake drum overheating is a significant failure mode for braking subsystems, potentially caused by excessive braking without engine assistance. These results align with the IM analysis, confirming that the B&PS subsystem represents the main reliability bottleneck of the vehicle. The high NPR concentration in a limited set of modes implies that corrective actions focused on these faults can significantly reduce the overall operational risk.

Actions include inspection of braking assemblies, adjustment and replacement of linings and drums, verification of air compressor operation, and calibration of pressure regulators and governors. The intermediate group of modes, mainly related to compressor cycling, pedal response, and minor leaks, can be addressed through scheduled preventive maintenance. Low-ranked modes require only periodic monitoring, since their individual contribution to total risk is limited.

The distribution of NPR values supports a tiered maintenance strategy. The highest-ranked modes, which represent roughly 20% of the total number of modes, account for most of the aggregated NPR. These should receive immediate preventive and corrective attention. Actions include inspection of braking assemblies, adjustment and replacement of linings and drums, verification of air compressor operation, and calibration of pressure regulators and governors. The intermediate group of modes, mainly related to compressor cycling, pedal response, and minor leaks, can be addressed through scheduled preventive maintenance. Low-ranked modes require only periodic monitoring, since their individual contribution to total risk is limited.

The following section presents the discussion of findings, examining their technical implications, the relationship between system architecture and observed reliability patterns, and the practical relevance of the proposed framework for maintenance management and design improvement.

6. Discussion

The consistency between IM’s FMEA results demonstrates the internal validity of the proposed reliability framework. Both methods identified the same dominant subsystems within SWCCT, particularly the Brakes and Pneumatic System, Electrical and Control Subsystem, and Power Transmission System. This alignment confirms that the IM-based structural reliability model and the FMEA-based operational assessment converge in identifying the most critical components. The result validates that the methodology consistently links system-level reliability with component-level failure behavior.

The IMs provide a quantitative basis for determining which components have the highest structural influence on system reliability. In contrast, the NPR index obtained from the FMEA specifies which failure mechanisms should be prioritized within those components. When analyzed together, the IMs define where design or maintenance interventions produce the greatest effect, while the FMEA clarifies what failure modes must be addressed. This complementarity ensures that system-level reliability analysis is translated into concrete maintenance actions. Discrepancies between IM and NPR rankings arise mainly because IMs reflect structural sensitivity, whereas NPR combines severity, occurrence, and detection—factors that describe the operational impact of failures. The partial correlation observed between both approaches confirms that they are not redundant but complementary in nature.

The uncertainty analysis confirms the stability of the framework. Variations in component reliability parameters produced measurable changes in the system-level reliability indices, confirming that uncertainty propagation has a direct effect on prioritization outcomes. Subsystems that contain a higher number of components in series exhibit greater sensitivity and therefore account for a higher proportion of overall system failures. This structural characteristic explains why the heavy-duty truck section contributes to approximately 80% of total failures. Conversely, subsystems with partial redundancy, such as the Hydraulic System and Electrical System, show reduced sensitivity and act as reliability buffers under stochastic operating conditions.

The findings discussed above confirm that the integration of Importance Measures and FMEA provides a consistent and operationally relevant framework for reliability assessment and maintenance planning of SWCCTs. The combined approach ensures that structural reliability analysis and failure mode prioritization converge toward practical decision-making criteria. By incorporating uncertainty into both system-level and component-level evaluations, the methodology establishes a quantitative basis for prioritization that reflects real operating conditions. The following section presents the main conclusions derived from this study, emphasizing the methodological contributions, the implications for maintenance strategy design, and the potential extensions for future research.

7. Conclusions

This paper presents a methodology for identifying critical components in complex systems by integrating FMEA with IMs. This approach combines the qualitative risk assessment provided by FMEA, which evaluates potential failure modes based on their effects, causes and occurrence, with IMs, which use historical reliability data to identify critical components. This dual approach adds structure to the analysis and provides an understanding of system vulnerabilities, supporting the prioritization of maintenance efforts.

The application to SWCCT demonstrated that combining IMs and FMEA clarifies the interpretation of reliability behavior. IMs determine which components most affect system reliability, while FMEA identifies the specific failure modes that require attention. Together, they enable more accurate maintenance prioritization and resource allocation under uncertain operating conditions. The results obtained provide a consistent and quantifiable overview of the reliability behavior of the SWCCT. The integration of IMs and FMEA allowed the identification of subsystems and specific failure modes with the highest impact on overall system performance, as well as establishing clear priorities for maintenance planning and resource allocation. The coherence between both analytical approaches supports the consistency of the proposed methodology for diagnosing reliability structures in complex mechanical systems.

From a maintenance perspective, the integration of IMs and FMEA provides a systematic approach for reliability-based decision-making. The IMs identify the most reliability-sensitive components, while the NPR refines maintenance priorities by ranking failure modes within those components. The resulting prioritization map supports maintenance scheduling, spare-part management, and inspection planning. Furthermore, by quantifying uncertainty, the framework allows preventive maintenance intervals to be set that are both risk-informed and operationally feasible. Overall, the integrated analysis transforms system reliability results into a decision-support tool for maintenance planning, ensuring that efforts and resources are directed toward the components and failure mechanisms with the highest impact on SWCCT reliability.

Future work should focus on extending the methodology toward dynamic reliability updating using stochastic or Bayesian inference, integrating real-time condition monitoring, and applying data-driven models to improve predictive maintenance and decision support in uncertain operational environments.