A Correlation Between Earthquake Magnitude and Pre-Seismic Gravity Field Variations over Its Epicenter

Abstract

Earthquakes are the result of complex interactions between tectonic plates, the mantle, and the lithosphere. Complex geodynamic conditions contribute to the occurrence of seismic phenomena. Tectonic plates can collide, move apart, or slide past each other. Mantle convection by internal heat drives plate motions that deform the lithosphere. Rocks deform elastically as stress accumulates and pore fluid pressure changes. Rupture occurs when stress exceeds frictional resistance. The connection between variations in gravity and the magnitude of earthquakes remains unclear. This work aims to examine aspects of this correlation. Three sets of earthquakes, one with events from all over the world, one from broader Greece, and one from the Hellenic Trench in Greece, aiming to cover all cases of geodynamics, from very different to very similar, were employed. Time series of gravity measurements at earthquake epicenters were extracted from GRACE satellite data. Time derivatives of the gravity field, as well as magnitude-dependent variations—reflecting changes relative to earthquake strength—were computed. Multiple linear regression (MLR), partial least squares (PLS) regression, and neural networks (NN) were used to model the relationship between gravity or its derivatives and earthquake magnitude. A correlation between the earthquake magnitude and magnitude derivatives was found. By using the global and Greek datasets, the best accuracy was obtained with MLR, reporting a mean squared error (MSE) of 0.069 with an R² of 0.979, and MSE was 0.011 with R² score of 0.997, respectively. By using the Hellenic Trench set, PLS regression derived the best correlation results, reporting an MSE of 0.004 and an R² of 0.977. Experimental results suggest that gravity, and therefore crustal density, is related to the magnitude of the impending earthquake, but not to its timing.

1. Introduction

Earthquakes are among the most devastating natural disasters. Predicting the occurrence and magnitude of earthquakes has long been a subject of scientific research [1,2]. Prediction of earthquake occurrence or magnitude is based on the detection and monitoring of certain seismic precursor geophysical events occurring at various distances around the epicenter of the earthquake [3,4,5]. These seismic precursor signs include electromagnetic perturbations of ultra-low frequency (ULF) and very low frequency (VLF) [6,7,8,9], gravity changes [10,11,12,13], vertical and lateral ground movements [14,15,16,17], alterations in groundwater level, its chemical composition, and its temperature [18,19,20,21], emission of hydrogen, carbon dioxide, and radon gases [22,23,24], the occurrence of swarms of lower magnitude earthquakes before the main one [25,26], and changes in characteristics of the atmosphere over the imminent earthquake epicenter, such as atmospheric heat and density, ionosphere electron content, and atmospheric cation (H⁺, O⁺ and He⁺) content.

The study of gravity perturbations as potential seismic precursors has a long history in earthquake research. Pre-seismic gravity fluctuations have been recorded around the site of an imminent earthquake in many cases [11,13,27,28,29,30,31,32,33,34]. Early observations date back to the 1960s. Barnes (1966) [35] documented gravity variations associated with the 27 March 1964, Alaska earthquake, while Fujii (1966) [36] reported both pre-seismic and post-seismic gravity anomalies related to the Niigata earthquake of 16 June 1964, in Japan. Between 1967 and 1971, similar gravity changes were also recorded related to other earthquakes [37,38,39]. Various mechanisms were proposed to explain these phenomena: Kisslinger (1975) [38] attributed gravity changes to horizontal dilatancy of subsurface layers and inflow of groundwater into fractures; Barnes (1966) [35] suggested mass displacements, whereas Oliver et al. (1975) [39] argued that both crustal deformation and surface movements could account for the observed gravity disturbances.

Research on pre-seismic gravity variations continued over the following three decades. Chen Yun-Tai et al. (1979) [40] found that gravity decreased in areas surrounding the 4 February 1975, Haicheng earthquake but increased before the 28 July 1976, Tangshan earthquake, both in China. Their analysis outlined mass redistribution as the most plausible explanation. Similarly, Hagiwara (1979) [41] reported pre-seismic gravity anomalies preceding three Chinese earthquakes between 1975 and 1976. During that period, significant efforts were directed toward modeling the relationship between gravity changes and seismic activity, with approaches incorporating dilatancy, deep fluid migration, and dip-slip faulting models of crustal deformation [42,43,44,45,46]. Until recently, these studies relied mainly on terrestrial gravimeters; however, since 2020, satellite-based gravity measurements have also been employed [11,12,27,47].

In addition to precursor studies, it has been shown that rapid mass redistribution during large earthquake ruptures produces so-called Prompt Elasto-Gravity Signals (PEGS) [48,49]. These signals propagate at the speed of light and can be detected seconds before seismic waves arrive at distant locations. While PEGS may provide useful constraints on the magnitude of very large earthquakes, they are not considered true precursor signals, since they are generated concurrently with the rupture process.

There is still no agreement regarding the underlying reasons for the local disturbances detected in gravity. Most of the related theories are cited by Liu et al. [50] and Zhu et al. [34]. According to the proposed models, the rocks are expanding under the stress imposed on them before the earthquake, and cracks are created in the lithosphere, causing changes in the average crustal mass density, with or without aqueous fluid insurgence from deep crustal sources, and therefore changes in the local gravity are observed. According to the lithospheric plate dislocation model, it is the release of stress at the points of contact of the continuously moving plates that causes the cracks. There is evidence that the change in the weight of ice masses over polar regions, as the ice melts, could trigger earthquakes [51]. But there is also evidence of magma movements as the causal factor of earthquake generation, at least in regions close to volcanoes [29,32,52,53]. Whatever the causes of gravity changes, there is undisputable published evidence that they constitute pre-seismic signals of incoming earthquakes [13,28,29,30,31,32,33,34]. In only a few cases, the gravity changes were measured by satellites [12,27,47,53]. In the majority of the published work, the gravity was recorded using ground-based gravimeters [12,27,47]. Prediction of earthquake occurrence or magnitude using gravity data is still far from satisfactory. In one of the most successful efforts, Zhu et al. [34] used an extensive network of terrestrial gravimeters all over China to predict the epicenter and year of occurrence of 13 earthquakes of surface wave magnitude (M_s) only between 6 and 7 degrees M_s. They measured the gravity change intensity in a time series and its variation trend. Note that the M_s scale is logarithmic, like the Richter scale, and is designed to give similar numerical results, especially towards the middle values. The authors attribute the limitations in the prediction range to restrictions in the accuracy of the gravity meters and their coordination in the network, the unforeseen underground water and mass movements, and the fluctuating nature of the gravity magnitudes over time.

To this end, the objective of this work is to investigate and establish a more comprehensive relation between the gravity change intensities and the magnitudes of various earthquakes selected from all over the world, covering a broad range of geodynamics, from very different to very similar. The fluctuating nature of the gravity readings indicates either wave-like up and down movements of solid and semi-solid masses under the lithosphere or cyclical opening and resealing of lithospheric cracks. A way was sought to relate these cyclical changes, rather than the absolute gravity reading, to the earthquake magnitudes. Satellite-recorded gravity data over the epicenter of a list of worldwide earthquakes were used for this study. The gravity data were used by Python 3.11.13 algorithms run in the Jupiter Notebook environment of the Anaconda graphical user interface. Multiple linear regression (MLR) and partial least squares (PLS) regression methods were used as described before [54] to correlate earthquake magnitudes with the gravity values or their derivatives. A neural network (NN) algorithm was also implemented. It was found that a close relation exists between the derivatives of pre-existing gravity values over the epicenter of the earthquakes and the earthquake magnitude. This information holds a promising potential for integration into feature fusion techniques; by combining gravity derivatives with other relevant predictors, we can enhance the accuracy and robustness of artificial intelligence (AI) earthquake magnitude prediction models as a warning for natural disaster prevention, leveraging the complementary strengths of multiple data sources.

The rest of the paper is structured as follows: Section 2 presents materials and proposed methods. Results are summarized in Section 3, while discussions and conclusions are included in Section 4 and Section 5, respectively.

2. Materials and Methods

2.1. Proposed Methodology

A block diagram of the steps followed for the examination of the correlation of an earthquake’s magnitude to gravity is given in Figure 1. Three earthquake datasets were constructed, one including earthquakes from all over the world, one including earthquakes from Greece and its close neighborhood, and one targeted on the Hellenic Trench in Greece. The global dataset consisted of 25 earthquakes with magnitudes between 1.0 and 7.3, the Greek dataset consisted of 26 earthquakes with magnitudes between 2.7 and 7.0, while the Hellenic Trench dataset consisted of 12 earthquakes of magnitudes 5.0 to 6.5.

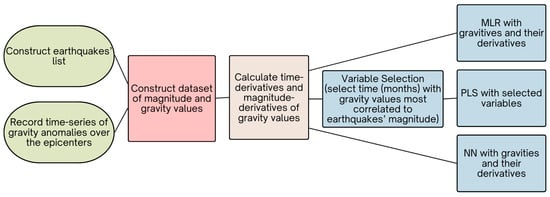
Figure 1. Proposed methodology.

The Greek dataset was employed due to the fact that the particular geodynamics of distant localities on Earth can vary to a large extent, and this might theoretically affect the association of gravity anomaly values with the earthquake magnitude. The Greek dataset refers to a much more confined geographic area, and, therefore, it is expected to have more homogeneous geodynamics. Towards the same direction, the Hellenic Trench dataset aims to test earthquakes of an even higher geodynamic homogeneity. The Hellenic Trench, also referred to as the Hellenic Arc or Hellenic Conduction Zone area, is a convergent plate boundary where the African Plate is sliding beneath the Aegean microplate. This boundary is a narrow arc starting from the Ionian Sea in the west, passing south of the island of Crete and rising again towards the Dodecanese Islands in the east. The earthquakes occurring at this boundary are interplate thrust Earthquakes [55,56,57,58].

For the global dataset, a time series of gravity anomaly values at their epicenter was also recorded for the day closest to the earthquake and for each of the nine consecutive months before this measurement. For the Greek dataset, the gravity anomaly values were recorded for five 10-day intervals, starting nine months before the earthquake and ending with a final measurement as close as possible to the earthquake date.

It should be noted here that, since in this work we are analyzing the derivatives of the gravity values G with respect to the earthquake magnitudes M, the latter implies that G is a continuous function of M. Therefore, it is considered necessary that M consistently refers to the same physical quantity. For this reason, in case of magnitude values less than 5, referring to the global and the Greek datasets, which were recorded in the mb, ml, md, or mwr scales, these values were converted to the mww scale, which is the scale used in case of magnitudes over 5.0, by employing widely accepted conversion formulas [59,60].

Since the dataset of global earthquakes is formed from earthquakes from all over the world, it is important to examine whether the local geodynamics would influence the correlation between the magnitude of the earthquakes and the gravity anomaly values or their derivatives. A more confined geographic area would answer the argument that different geodynamics of the earthquakes make them unsuitable for comparison. In addition, the time span of gravity measurements was shortened in the Greek dataset to only 50 days, five measurements at 10-day intervals, ending on a day as close as possible to the day of the earthquake. This limits the possibility of large changes in geodynamics in Greece during the 50-day interval of gravity measurements. In the Hellenic Trench dataset, the similarity of earthquake types is ensured to an even more significant degree, not only due to the limited geographic extent but primarily because of the uniform geodynamic characteristics.

Based on these data, the final datasets were then constructed, containing the earthquake magnitudes and the recorded gravity values. The derivatives along months were calculated and are referred to in this text as time derivatives. Magnitude derivatives, showing the change in gravity as the earthquake magnitude changes, were also calculated.

Finally, gravity values and their derivatives were separately fed into MLR, PLS, and NN algorithms to infer any connection between magnitude and gravity from the magnitude prediction accuracy of the prediction models. For improved prediction of the PLS model, variable selection was applied by selecting the months of the dataset whose gravity and derivative values produced the lowest mean squared error (MSE).

2.2. Construction of Earthquake Datasets

In this work, earthquakes were selected from all over the world and in Greece using the United States Geological Survey Search Comprehensive Earthquake Catalogue (USGS Earthquake Hazards Program) [61,62]. It should be noted here that the aim of this work is not to examine the geodynamic details of earthquakes but to look for a common factor among many earthquakes that have different geodynamic substrates. In the case of the global dataset, the earthquakes are purposely selected from widespread areas so as to minimize the influence of local geodynamic conditions. The latter approach is an effort to investigate the common gravity-related denominator related to their magnitude, irrespective of the local geological peculiarities. The mechanism of earthquake induction could be different, yet the accompanying gravity conditions still exist. Moreover, a close time window was selected to neutralize as far as possible the external factors, such as lunar and solar gravity effects.

Thus, the following datasets of earthquakes were constructed: the global dataset, which comprised 25 earthquakes that occurred in May of 2021; the Greek dataset comprised 26 earthquakes that occurred during the year 2020; and the Hellenic Trench dataset, which comprised 12 earthquakes of the same geodynamics. For this work, gravity anomaly is defined as the deviation (in μGal) of the mean monthly gravity value at the earthquake (epicenter) from the long-term mean gravity value, calculated over the six-year reference period between January 2004 and December 2009. More details on both datasets are provided in Table A1 and Table A2 in the Appendix A section.

This research relies on gravity observations from the GRACE mission, a joint initiative between NASA and the German Aerospace Center (DLR), implemented through its twin satellites GRACE-1 and GRACE-2, available at https://earthquake.usgs.gov/earthquakes/search/ (assessed on 11 September 2025). The datasets are archived within the GFZ Data Services Sample catalog, maintained by the Helmholtz Center for Geosciences in Brandenburg [63]. For the purposes of this study, processed gravity solutions were obtained via the COST-G Plotter [64]. COST-G, operating under the International Combination Service for Time-Variable Gravity Fields and linked to the International Gravity Field Service (IFS), combines individual monthly gravity field solutions into an internally consistent global model. Time series of gravity anomalies (reported in mGAL) at the central locations of the selected earthquakes were extracted from the GFZ repository [63]. For monthly data visualization, the RL06.1 DDK5 product of COST-G was employed, which represents gravity field variations using GPS-based coordinates of the earthquake epicenters, while for 10-day intervals, the collection CNES RLO5 TSVD (10-day) was used.

It should be noted here that GRACE satellite gravity sensors suffer from attenuation or leakage bias of the gravity signal, meaning that the induced filtering smooths out the noise but also may weaken the actual gravity signal. The latter issue is avoided by employing spatial filtering of the gravity data. Our data come from the GFZ RL06.1 DDK5 dataset in the COST-G Plotter, which employs spatial filtering to reduce noise and leakage bias. The DDK filters (decorrelation and smoothing filters) are performing exactly this; they have various ratios of noise suppression to preserve spatial details. The DDK5 is a compromise-level filter.

2.3. Data Processing and Machine Learning

The earthquake dataset was saved in the Jupyter Notebook v6.3 as an .xlsx file. A summary of the data processing and the algorithm characteristics is given in Table 1. The column containing the magnitudes of the earthquakes was separated and transformed into a one-dimensional array. The gravity values were formulated into a two-dimensional array and were standardized by scaling to unit variance. The Savitzky–Golay filter was implemented to calculate the first- and second-order derivatives of the gravity values. The first-order time derivatives show the speed of gravity changes as the time of the earthquake occurrence is approached. The second derivatives are the accelerations; the rate of change in the speed of gravity changes as the time of the earthquake is approached. Magnitude derivatives, showing the rate and acceleration of gravity changes as we move along the earthquake magnitudes, were also estimated. Their physical meaning is the correlation between the magnitude of the earthquake and any pre-existing geophysical factors determining the gravity magnitude at the site of the earthquake, irrespective of time-related gravity changes. For MLR, the magnitude and gravity sets were split into training and test sets, with thirty percent of the earthquakes used for testing the regression model performance. For NN, the best prediction results were produced with a test set size of twenty percent.

Table 1. Data processing and algorithm characteristics.

Data Processing	MLR	PLS Regression	Neural Network
Data scaling by using the Standard scaler () function of the Scikit-learn 1.7.1 library. Calculation of derivatives by using the SavgolFilter () function of the Scipy 1.16.1 library. Calculation of the slope of gravity values through the months, by using the LinearRegression.fit () function of the Scikit-learn 1.7.1 library.	Used as callable function. Regression: linear. Test size: 0.3 Performance metrics: MSE, R2 score. Plotting predicted against actual magnitudes.	Used as callable function Number of components: The optimal determined by variable selection. Model regression function: PLS regression Metrics for evaluation of model performance and prediction: MSE, R2 score Plotting predicted against actual magnitudes	Used as callable function. Keras 3.10.0 model: sequential, regression. Test size: 0.2 Input shape: 10 Input layer: 10 nodes, activation: relu Hidden layers: one layer of three nodes, activation: relu Output layer: one node, activation: linear 200 epochs, batch size: 3 Performance metrics: MSE, R2 score Plotting predicted against actual magnitudes

Variable selection refers to the selection of those columns (variables) from the gravity or gravity derivative datasets that produce the least MSE of magnitude prediction using PLS regression. A Python algorithm was formulated for variable selection, described in Chariskou et al. [54].

The neural network was a Keras 3.10.0 regression net. The input layer of the neural network model had as input shape the number of columns of the tested gravity data and also ten neural nodes. One hidden layer of three nodes and activation ‘relu’ followed. The output layer had one node and activation ‘linear’, as suggested for regression models. Two hundred passes (epochs) of the entire set of rows were used, and weights were recalculated after every three-row pass (batch size). The algorithm is splitting the gravity and earthquake magnitude sets into train and test sets (80–20%), calculating the MSE and R² score between the actual and predicted magnitudes, and plotting them.

3. Results

3.1. Results on the Global Dataset

In Table 2, the gravity anomaly values for the set of global earthquakes are presented, consisting of 25 earthquakes. The monthly gravity anomaly values at a variable time (last column, depending on the available data in the COST-G Plotter) from the days before the occurrence of the earthquake up to nine months before this last measurement were recorded. The magnitude spans a range of earthquake magnitudes from 1.0 to 7.3.

Table 2. The magnitude (mag) and gravity anomaly values over the earthquake epicenter on the first day closest to the day of the earthquake (‘last measurement’) and for each of the nine months before that last measurement. The time lag between the day of the earthquake and the last measurement of gravity anomaly is given in the column ‘days after last measurement’ and depends on the available data in the COST-G Plotter gravity database.

Mag	Gravity Anomaly (µGal) Before the Earthquake Occurrence										Days After Last Measurement
	9 Months	8 Months	7 Months	6 Months	5 Months	4 Months	3 Months	2 Months	1 Month	Last Measurement
1.57	−3.487	−5.937	−4.278	−4.369	−1.289	−3.520	−1.749	−4.532	−5.786	−2.765	4
2.24	−4.138	−4.108	−2.820	−3.337	−0.600	−4.086	−3.067	−1.144	−1.055	−1.535	15
3.15	−1.034	−0.426	0.364	0.614	−1.279	1.061	1.197	−0.086	−1.932	0.854	25
3.81	0.056	3.094	2.305	−0.931	−1.231	1.719	3.018	1.632	2.674	0.022	8
3.92	2.037	0.632	2.405	1.711	4.630	1.980	2.967	0.818	−0.591	3.452	11
4.38	−5.344	−5.530	−6.569	−3.466	−3.616	0.480	−1.455	−2.676	−2.694	1.791	15
4.49	2.777	1.443	2.865	2.702	2.388	−0.754	1.278	−0.077	2.233	1.667	15
4.60	−1.349	0.794	1.304	0.276	1.835	−2.168	3.664	2.941	3.101	0.715	29
4.71	−0.035	3.146	2.384	−0.854	−1.071	1.737	3.107	1.705	2.794	0.102	11
4.82	6.548	5.996	4.717	3.617	4.899	4.233	4.752	4.362	7.393	5.855	4
4.93	−5.026	−5.050	−4.505	−5.224	−1.393	−4.778	−1.554	0.512	4.305	−1.561	11
5.10	−4.883	−0.989	−2.268	−1.282	−0.539	−1.495	0.799	−0.655	0.856	−0.549	15
5.20	−0.739	−1.745	−0.400	−1.701	−3.591	−4.291	−3.604	−0.037	−3.262	−0.828	4
5.30	0.181	−3.431	−0.853	0.221	−1.784	−1.306	0.347	−0.111	−0.933	−0.341	18
5.40	1.187	−0.334	1.644	1.786	1.259	0.978	0.387	2.953	1.942	1.578	4
5.50	10.093	10.243	9.949	10.278	13.981	9.739	9.423	8.840	9.917	6.484	14
5.60	3.130	−0.102	0.223	1.814	−0.386	0.390	0.583	0.014	−0.552	−1.204	15
5.70	−0.159	−0.092	2.888	0.080	0.945	2.912	1.728	1.169	1.571	1.153	8
5.80	1.452	1.319	−1.649	−1.760	−1.215	0.774	−1.389	2.153	1.243	−0.059	4
5.90	−1.462	−1.574	−0.793	1.784	4.895	1.487	1.953	2.877	−0.031	1.044	15
6.10	4.072	4.061	1.557	−0.345	−0.356	−3.801	−0.013	−4.869	−5.458	−5.185	4
6.50	0.320	−2.159	0.689	−0.731	0.544	−0.226	−0.375	0.524	−0.554	0.413	4
6.70	2.542	−0.193	−0.378	−1.175	−1.334	−1.365	2.048	−0.372	−0.829	−0.673	25
6.90	2.360	1.813	3.379	3.316	3.046	7.530	4.223	2.591	2.588	2.585	14
7.30	5.915	5.242	4.546	3.199	4.956	3.133	3.633	4.263	7.501	4.647	4

During data processing, indications of a trend in gravity change over time, as the time of the earthquake approached, were observed by visual inspection of the plots. Figure 2 presents indicative, randomly selected plots of gravity values and their time derivatives against earthquake magnitudes. Recall that magnitude (mag) measurements are all in the mww scale. To verify and accurately measure them, the slopes of the gravity values over time, as the time of the earthquake was approached, were calculated from the earthquake time-series data for each earthquake. Plots of earthquake magnitudes against their pre-seismic time-series gravity slopes and their time derivatives were constructed. In a pilot investigation step, earthquake magnitude prediction was also attempted by applying multiple linear regression on their magnitude derivatives.

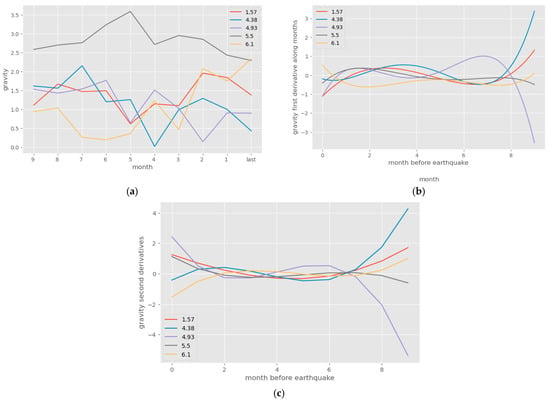
Figure 2. Plots of (a) gravities; (b) first derivatives; (c) second derivatives, against time before an earthquake. Randomly selected earthquakes are shown to avoid plot overcrowding. They are shown by their magnitude in the legend. Gravity values fluctuate unpredictably over time, in a way unrelated to the earthquake magnitude. The gravity rate of change (first derivative over time) and its acceleration (second derivative) also do not show any pattern associated with the earthquake magnitude.

Figure 3 shows the MLR results of attempts to predict earthquake magnitudes from the time series of gravity and its derivatives. It is clear from the results presented in Figure 3 that there is no connection between gravity time series and magnitudes; gravities over the epicenter fluctuate unpredictably over time. Wave-like patterns are observed for the first and second time derivatives, but with phases, wavelengths, or amplitudes unrelated to the earthquake magnitudes. In accordance with that, negative R² values were produced by the attempted prediction models, indicating no correlation between the gravities or their time derivatives to the earthquake magnitudes. Also, large mean-squared errors were produced.

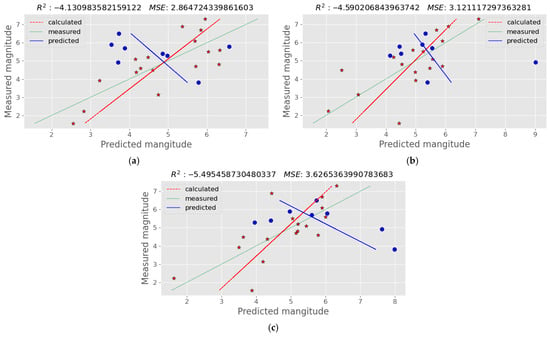
Figure 3. Plots of actual earthquake magnitudes against the values predicted by multiple linear regression using (a) the gravity values of the dataset; (b) their first-order time derivatives; (c) their second-order time derivatives. Neither the time series of gravity values over the earthquake epicenters, nor their time derivatives, are correlated to the earthquake magnitude. Blue dots indicate the generated values, while blue trend line indicates how well this predictions align with the actual measurements; red stars are the calculated data, while the red trend line shows the relationship between calculated and measured values. Green dotted trend line shows the internal consistency of measured data.

The first-order magnitude derivatives of gravity show the amount by which the gravity changes for an infinitesimally small, but always the same, change in earthquake magnitude. In Figure 4, it can be seen that this relates to the earthquake magnitude. Progressively larger gravity values are associated with larger magnitudes (Figure 4a), although a fluctuation is evident, curiously more intense in the range of 4.5 to 6.5. The first-order magnitude derivative plot (Figure 4b) reveals an interesting phenomenon. For small magnitudes, up to 4.5, the derivative is positive but with a negative slope. The second-order magnitude derivative for the same magnitude interval is negative with a positive slope (Figure 4c). A possible explanation and conclusion could be that as the lithosphere becomes denser and ‘tighter’, increasingly resisting large changes in its density, earthquakes that occur would be of a larger magnitude. In the interval of 5.8 to 7.3, the first derivative is again positive, but with a positive slope, while the second derivative is becoming increasingly positive (positive slope). Once again, larger earthquakes are associated with a denser lithosphere, but there is no resistance to further densening. The intriguing range is between 4.5 and 5.8, where a drop in the first and second derivative values is observed. Both the rate of gravity changes and the acceleration of this change decline to reach negative values. The lithosphere is at first still resistant to further densening. But as this resistance is weakening, as indicated by the negative derivatives, larger earthquakes occur. No increase in gravity is observed in this magnitude range, but an oscillatory fluctuation and a negative first derivative are. This indicates a negative ‘speed’ of gravity change. Decreases in gravity values occur for each unit of change in magnitude to achieve earthquakes of these magnitudes. The curves of second-order derivatives are in agreement with those of the first derivatives. Notably, the curve patterns are similar for almost all months before the earthquake.

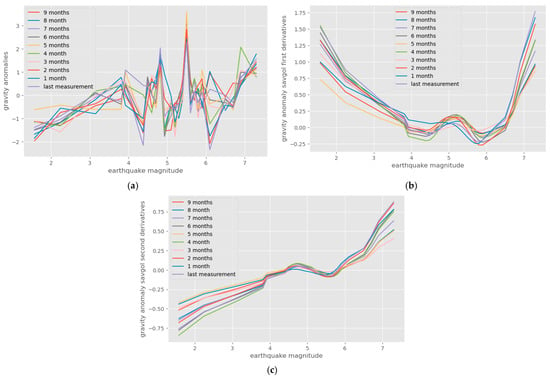
Figure 4. (a) Plots of gravity values; (b) their first-order magnitude derivatives; (c) second-order magnitude derivatives, against earthquake magnitudes and for various time periods in months before the earthquake occurrence, using the global dataset. Similar patterns were observed for all months. Gravity values are higher at all months for earthquakes of greater magnitudes, although they oscillate widely in the range of 4 to 6.5. The first derivatives are negative in magnitude in the range of 5.5 to 6.5 for most months. They gradually decrease to approach zero in the region of almost zero to four and increase precipitously for magnitudes above six. These alterations are correspondingly reflected in the shapes of the second-order derivatives.

Figure 5 illustrates the plots of actual earthquake magnitudes against the values predicted by MLR using the first-order and the second-order magnitude derivatives of the gravity values, whereas Figure 6 and Figure 7 show the results of PLS regression and neural network, respectively. All three methods indicate a correlation of the earthquake magnitude to the first- and second-order magnitude derivatives, with MLR slightly better, followed by the neural network, but with the PLS regression not falling significantly behind in predictive efficiency. The first-order magnitude derivatives are a comparatively better predictor dataset than the second-order derivatives.

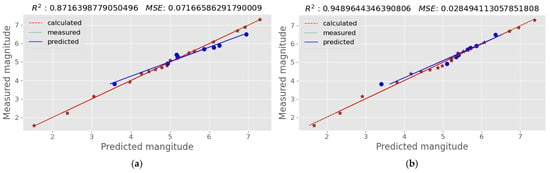
Figure 5. Plots of actual earthquake magnitudes against the values predicted by MLR using (a) the first-order magnitude derivative; (b) the second-order magnitude derivative of gravity values. The correlation between the earthquake magnitude and the rate of gravity change for each infinitely small change in the magnitude of the earthquake (first derivative-over-magnitudes) allows a very accurate prediction of the earthquake magnitude. Better predictions can be made using the second-order derivatives. Blue dots indicate the generated values, while blue trend line indicates how well this predictions align with the actual measurements; red stars are the calculated data, while the red trend line shows the relationship between calculated and measured values. Green dotted trend line shows the internal consistency of measured data.

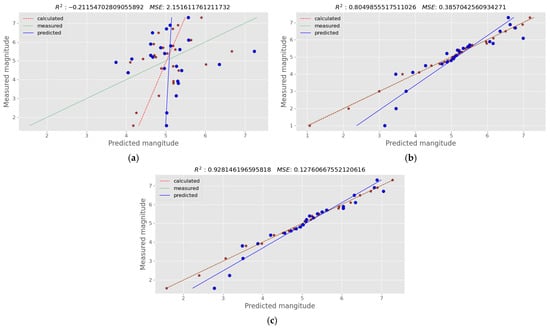
Figure 6. Plots of actual earthquake magnitudes against the values predicted by PLS using (a) the gravity data; (b) their first-order magnitude derivatives; (c) their second-order magnitude derivatives. The best correlation of the earthquake magnitude, as inferred by the R² score, is with the first-order magnitude derivatives of the gravity values. Blue dots indicate the generated values, while blue trend line indicates how well this predictions align with the actual measurements; red stars are the calculated data, while the red trend line shows the relationship between calculated and measured values. Green dotted trend line shows the internal consistency of measured data.

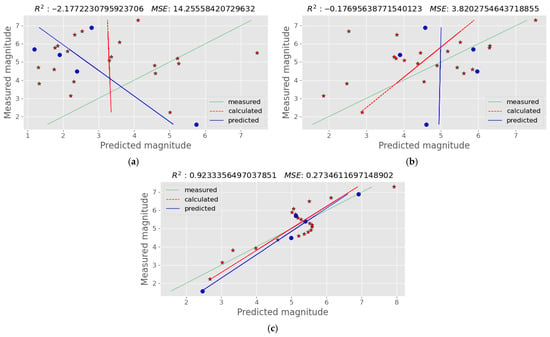
Figure 7. Plots of actual earthquake magnitudes against the values predicted by NN using (a) the gravity anomaly values; (b) the first-order magnitude derivative; (c) the second-order magnitude derivative of the gravity values. The best correlation of the earthquake magnitude, as inferred by the R² score and MSE value, is with the second-order magnitude derivatives of the gravity values. Blue dots indicate the generated values, while blue trend line indicates how well this predictions align with the actual measurements; red stars are the calculated data, while the red trend line shows the relationship between calculated and measured values. Green dotted trend line shows the internal consistency of measured data.

A summary of the prediction performance of the three machine learning algorithms on the gravity values and their derivatives is given in Table 3. The first- and second-order magnitude derivatives are very well correlated to the earthquake magnitudes with any of the three machine learning methods used. Good correlation was also observed when the third-order magnitude derivatives of the gravity time slopes were used. Large MSEs and negative R² scores were obtained when the gravity values themselves or their time derivatives were used. Negative R² values signify a correlation even worse than if the average values of the gravities or their derivatives were used.

Table 3. MSE and R² (coefficient of determination) regression score for the correlation of earthquake magnitude from their gravity values and their derivatives over their epicenter, using various machine learning methods, on the global dataset.

	MLR		PLS		NN
	MSE	R2 Score	MSE	R2 Score	MSE	R2 Score
Gravity values	2.864	−4.130	2.151	−0.211	11.860	−1.545
1st magnitude derivative	0.071	0.871	0.127	0.928	0.191	0.940
1st time derivative	3.121	−4.590	2.116	−0.192	4.291	−0.182
2nd magnitude derivative	0.028	0.948	0.131	0.926	0.273	0.923
2nd time derivative	3.626	−5.495	1.978	−0.114	7.553	−1.030
Slope 3rd magnitude derivative	2.864	−4.130	2.151	−0.211	11.860	−1.545

3.2. Results on the Greek Dataset

The characteristics of the Greek earthquake dataset are provided in Table A2 in the Appendix A section. Table 4 includes the gravity anomaly values at their epicenters as five measurements 10 days apart, while the last measurement is taken as close to the day of the earthquake as possible. Recall that magnitude (mag) measurements are all in the mww scale.

Table 4. The magnitude (mag) and gravity anomaly value over the earthquake epicenter on the first day closest to the day of the earthquake (‘last measurement’) and for each of the five 10-day intervals before that last measurement. The time lag between the day of the earthquake and the last measurement of gravity anomaly is given in the column ‘days after last measurement’ and depends on the available data in the COST-G Plotter gravity database.

Mag	Days After Last Measurement	Last Measurement	10 Days	20 Days	30 Days	40 Days	50 Days
2.71	7	−0.665	−0.386	−0.503	0.238	−0.438	0.052
2.91	6	0.817	1.031	0.517	0.728	−0.660	−1.309
2.98	2	−1.483	−0.964	−1.787	−0.573	−1.319	−2.641
3.05	5	0.439	−0.586	0.164	1.085	1.670	1.638
3.12	8	−0.022	3.567	0.120	2.772	5.024	0.111
3.37	15	2.155	4.949	3.695	2.672	3.271	2.827
3.81	5	−3.674	−2.813	−2.314	−3.629	−2.234	−2.255
3.92	3	0.962	0.408	2.035	0.966	1.041	0.533
4.03	2	1.892	2.155	2.863	3.689	4.217	3.337
4.30	2	1.552	2.646	2.042	1.738	2.334	3.304
4.38	9	1.248	1.552	1.050	1.180	1.161	1.099
4.49	9	−0.583	1.290	−2.100	−2.683	−2.627	−4.802
4.25	5	3.745	3.237	3.858	2.852	1.635	2.059
4.70	1	3.966	5.240	3.552	2.874	2.715	1.944
4.71	13	−0.280	−0.442	1.513	−1.728	−2.296	−2.171
4.90	8	4.907	0.536	4.569	4.866	3.655	1.786
5.00	2	4.779	3.889	3.028	4.914	3.689	4.271
5.10	7	0.748	−0.082	−0.064	0.200	0.148	−2.086
5.20	7	2.771	1.793	1.597	2.318	1.574	1.103
5.30	5	−3.235	−2.493	−2.009	−3.333	−1.940	−1.945
5.40	1	−0.950	0.526	0.808	0.394	1.118	0.587
5.50	3	−0.994	1.306	−2.422	0.198	0.441	0.643
5.60	7	1.457	−1.820	−2.383	−2.275	−4.461	−5.903
5.70	5	−0.248	−1.054	−1.715	0.706	−0.062	0.368
5.90	3	1.744	2.939	1.980	1.220	1.351	0.532
7.00	5	−3.205	−2.497	−2.036	−3.357	−1.949	−1.975

A correlation of the magnitudes of the earthquakes that occurred in Greece to the gravity anomaly values over their epicenters and the derivatives of these values was implemented. Figure 8 includes the plots of gravity values and their first-order derivatives, as well as the second-order magnitude derivatives, against earthquake magnitudes and for various time periods in days before the earthquake occurrence. Similar patterns are observed for all measurements. Derivative values are higher for earthquakes of greater magnitudes, although they oscillate in the range of 4 to 6.0. The shapes of the first- and second-order derivatives are similar to those of the corresponding plots for the set of global earthquakes for the same magnitude range, with negative derivatives in approximately the same magnitudes between 4.5 and 6.0. The first derivatives are negative in magnitude in the range between 4.8 and 5.8, while they increase rapidly for magnitudes above six. These alterations are correspondingly reflected in the shapes of the second-order derivatives, as observed from the figure.

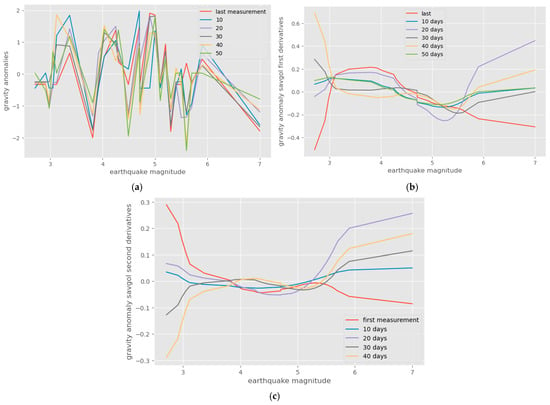
Figure 8. (a) Plots of gravity values; (b) their first-order derivatives; (c) second-order magnitude derivatives, against earthquake magnitudes and for various time periods in days before the earthquake occurrence, using the Greek dataset.

Figure 9 illustrates the results of MLR and PLS regression on the Greek dataset, by using the first-order and the second-order magnitude derivatives. Except for MLR using the first-order derivatives, the rest of the results exhibit excellent correlation between the magnitude derivatives and the earthquake magnitude. The best performance is achieved with MLR on the second-order derivatives, showing an MSE of 0.011 and a correlation score R² of 0.977. The combined results for all three machine learning methods are shown in Table 5. Once again, the magnitude derivatives are ones better associated with the earthquake magnitudes, while the raw gravity anomaly values and their time derivatives show no relation to the magnitudes.

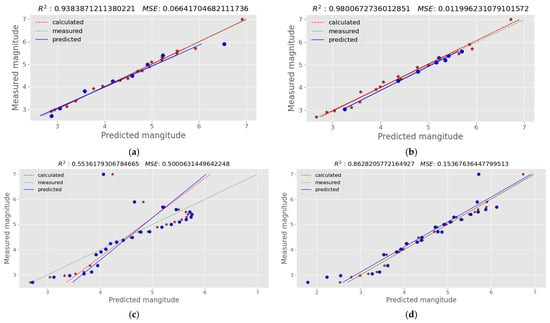
Figure 9. Plots of actual earthquake magnitudes against the values predicted by MLR and PLS regression for the Greek dataset: (a) MLR with the first-order magnitude derivatives; (b) MLR with the second-order magnitude derivatives; (c) PLS regression with the first-order magnitude derivatives; (d) PLS regression with the second-order magnitude derivatives. Blue dots indicate the generated values, while blue trend line indicates how well this predictions align with the actual measurements; red stars are the calculated data, while the red trend line shows the relationship between calculated and measured values. Green dotted trend line shows the internal consistency of measured data.

Table 5. MSE and R² (coefficient of determination) regression score for the correlation of earthquake magnitude from their gravity values and their derivatives over their epicenter, using various machine learning methods, on the Greek dataset.

	MLR		PLS		NN
	MSE	R2 Score	MSE	R2 Score	MSE	R2 Score
Gravity values	2.072	−0.923	1.303	−0.163	2.056	−0.986
1st magnitude derivative	0.066	0.932	0.500	0.553	0.436	−0.603
1st time-derivative	0.562	0.065	1.086	0.029	1.671	−0.449
2nd magnitude derivative	0.011	0.980	0.153	0.862	0.685	0.456
2nd time-derivative	1.886	−0.750	1.216	−0.086	2.199	−0.953

3.3. Results on the Hellenic Trench Dataset

The characteristics for the Hellenic Trench dataset are provided in Table A3 in the Appendix A section. The gravity anomaly values for the dataset of the earthquakes that occurred in the Hellenic Trench region are presented in Table 6. The dataset contains earthquakes of magnitude over 5.0 mww. In this case, no conversion of the magnitude scale was necessary. The first-order and the second-order magnitude derivative plots against the earthquake magnitudes are shown in Figure 10. In agreement with the first-order magnitude derivative shapes on the other two earthquake datasets (Figure 4 and Figure 8), negative values are observed in the approximate region of 5.0 to 6.0 mww. The exact areas of negative values vary somewhat, since quite different datasets are used. Very good correlations of the earthquake magnitudes to the magnitude derivatives were obtained with both MLR and PLS regression, especially with the second-order derivatives. Figure 11 illustrates the results of MLR and PLS regression on the Hellenic Trench dataset, by using the first-order and the second-order magnitude derivatives. A summary of the results obtained by all three ML methods is given in Table 7. It should be noted that the results lead to the same assumptions as in all previous experimental cases.

Table 6. The magnitude (mag) and gravity anomaly value over the earthquake epicenter on the first day closest to the day of the earthquake (‘last measurement’) and for each of the five 10-day intervals before that last measurement, for the Hellenic trench dataset. The time lag between the day of the earthquake and the last measurement of gravity anomaly is given in the column ‘days after last measurement’ and depends on the available data in the COST-G Plotter gravity database.

Mag	Days After Last Measurement	Last Measurement	10 Days	20 Days	30 Days	40 Days	50 Days
5.00	3.6	0.636	−0.295	−0.323	0.191	0.403	−1.514
5.10	4.4	−1.615	−1.544	−0.118	0.604	−0.320	−0.301
5.20	3.6	0.688	−0.223	−0.260	0.202	0.341	−1.644
5.30	8.0	0.423	0.835	1.844	0.242	2.119	2.656
5.40	8.0	0.305	0.800	−0.043	−0.080	0.220	0.159
5.50	1.5	0.799	0.810	−0.223	0.127	−0.906	0.091
5.60	6.9	2.807	2.447	4.805	1.373	1.564	0.232
5.70	3.7	0.622	−0.308	−0.319	0.186	0.403	−1.524
5.90	3.3	1.744	2.939	1.980	1.221	1.352	0.533
6.00	6.9	3.786	2.515	3.083	3.846	3.931	3.982
6.40	2.6	0.996	2.296	0.914	0.485	1.366	0.274
6.50	7.3	−0.207	0.213	0.285	−1.760	−2.037	−2.490

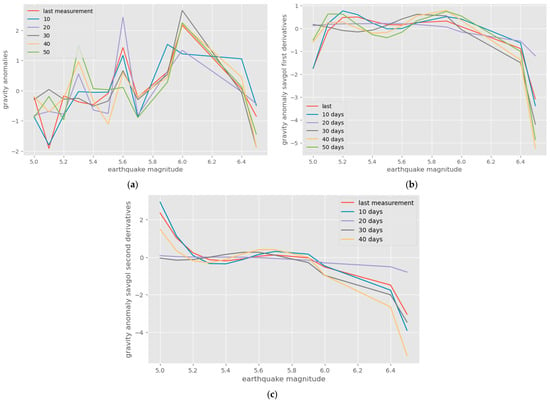
Figure 10. (a) Plots of gravity values; (b) their first-order magnitude derivatives; (c) second-order magnitude derivatives, against earthquake magnitudes and for various time periods in days before the earthquake occurrence, using the Hellenic Trench dataset.

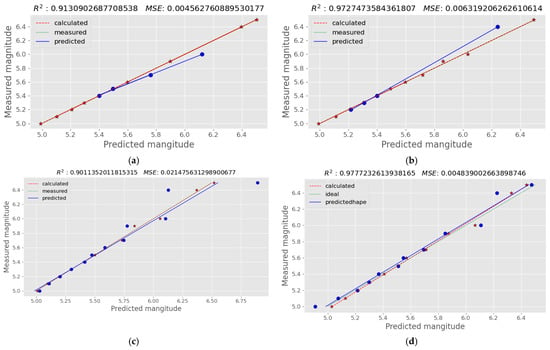
Figure 11. Plots of actual earthquake magnitudes against the values predicted by MLR and PLS regression for the Hellenic Trench Dataset: (a) MLR with the first-order magnitude derivatives; (b) MLR with the second-order magnitude derivatives; (c) PLS regression with the first-order magnitude derivatives; (d) PLS regression with the second-order magnitude derivatives. Blue dots indicate the generated values, while blue trend line indicates how well this predictions align with the actual measurements; red stars are the calculated data, while the red trend line shows the relationship between calculated and measured values. Green dotted trend line shows the internal consistency of measured data.

Table 7. MSE and R² (coefficient of determination) regression score for the correlation of earthquake magnitude to their gravity values and their derivatives over their epicenter, using various machine learning methods, on the Hellenic Trench dataset.

	MLR		PLS		NN
	MSE	R2 Score	MSE	R2 Score	MSE	R2 Score
Gravity values	4.861	−91.600	0.238	−0.095	9.479	−100.03
1st magnitude derivative	0.004	0.913	0.021	0.901	1.064	−2.549
1st time-derivative	1.722	−6.428	0.283	−0.306	2.352	−32.933
2nd magnitude derivative	0.006	0.972	0.004	0.977	9.113	−48.970
2nd time-derivative	0.687	−12.103	0.269	−0.241	12.818	−40.710

4. Discussion

Despite the intense efforts by many researchers to predict earthquake occurrence and magnitude from gravity changes, the results are still far from satisfactory. This work shows that time series of gravity changes are not associated with earthquake magnitudes. Their first-order time derivatives represent the speed with which gravity changes take place, and the second-order derivatives are the accelerations in the gravity changes. Gravity changes are supposed to be the result of lithospheric-level pressures and relaxations created by plate contacts or by convection currents of flowing masses under the plates. Since the gravity first-order time derivatives are not related to earthquake magnitude, it is not the speed of convectional mass flows, and in extension, their momentum, responsible for the magnitudes.

However, it is shown that the gravity magnitude derivatives are associated with earthquake magnitude. Since this first derivative is negative in the magnitude range between 4.5 and 6.5, we conclude that earthquakes of those magnitudes are associated with a looser crustal mass net and its lower density or with downwards positioning of magma masses. In contrast, larger magnitudes are associated with a denser crustal mass, perhaps the result of pressure between the plates or with magma masses positioned close to the surface. It must be emphasized that these are not time derivatives but magnitude derivatives. The meaning of this is that the changes in crustal density or magma positioning do not occur timewise before the earthquake but are already in place. Whatever the reason for triggering the earthquake, the magnitude is related to the already existing crustal density or magma positioning. The negative slopes of the first derivatives in the magnitude range of almost zero to 4 degrees indicate that looser masses or deeper magma positions help to cause earthquakes of gradually increasing magnitudes.

There is plenty of evidence that gravity alterations, caused by interaction with celestial bodies, such as the sun or moon, are contributing to earthquake occurrence [65,66,67,68,69]. In this work, we examined the gravity field vector perpendicular to the Earth’s surface. Gravity field vectors exercised by celestial bodies horizontally to the Earth’s surface are possible. Their pulling-pushing effect on lithospheric plates could be a cause of earthquakes. Due to the Earth’s rotation, the perpendicular or horizontal effect of celestial gravity fields would last only a few hours, unlikely to be detected by the monthly or weekly recordings of the satellites. To our knowledge, no daily, let alone multiple daily, gravity recording exists yet.

It must be noted that the atmospheric pressure can affect the ground gravity [70,71,72]. The same applies to hydrology factors, including groundwater movements [73,74,75,76,77]. Regardless of the cause, it is ultimately changes in gravity that play a role in triggering earthquakes. Although the effect of groundwater could also be attributed to crust extension or contraction [78], no such explanation is possible for the atmospheric pressure. In conclusion, it is not only the underground pressures that stress the lithosphere, but the overground or surface forces also have a significant role in earthquakes’ induction. In both cases, it is the crustal plates that receive both pressures, and this is recorded as changes in gravity.

A possible limitation of this work is the consideration of low-magnitude earthquakes in the methodology. Future work will consider extending the dataset by including high-magnitude earthquakes from Mw = 5.0 to Mw = 9.0. Yet, it should be noted that the latter is not always feasible, since most of the time, for most regions, there is a lack of actual acceleration time-history records, especially of high intensity, due to the absence of nearby seismic stations or due to low seismic variations.

This work does not intend to predict the occurrence or the magnitude of earthquakes; it aims to elucidate some of the relations of gravity to the magnitudes of the earthquakes. There are significant problems in attempting to predict earthquake magnitudes using derivatives. Since it is the magnitude derivatives that are related to earthquake magnitude, these derivatives must be calculated for any earthquake of unknown magnitude to be predicted. Yet, derivative calculations require the gravity values of the unknown-magnitude earthquake to be intercalated between the rows of a dataset of known-magnitude earthquakes. The exact intercalation position is not known since the new earthquake is of unknown magnitude. Also, the constructed MLR, PLS, or NN prediction model will be different after the intercalation of the new earthquake. Preliminary prediction attempts were, however, made in this work; the results were not satisfactory, confirming our concerns, and therefore were not included.

5. Conclusions

This work aims to investigate the potential relationship between gravity field variations and earthquake magnitude using GRACE satellite data and advanced AI-based modeling techniques.

Three different earthquake datasets, one with large differences in the geodynamics of the epicenters and long time series of gravity data, one with more limited geodynamic differences and short time series data, and one with similar geodynamics, were used, resulting in the same shape of curves in the plots of magnitude derivative against earthquake magnitude. In both cases, there are negative first-order magnitude derivative values in approximately the same magnitude range between 4.5 and 6.0. While no direct correlation was found between gravity or its temporal derivatives and earthquake magnitude, strong predictive performance was achieved using magnitude derivatives. The derivatives of both datasets show very good correlation to the earthquake magnitudes, while the best results were obtained with MLR and poorer with the NN.

Our experimental findings indicate that, despite the fact that gravity changes do not determine the timing of seismic events, they are indicative of the underlying crustal density and magma dynamics that influence earthquake strength. Results emphasize that pre-existing geophysical conditions play a critical role in shaping the magnitude of an earthquake, offering valuable insight for future seismic risk assessment and modeling efforts.