Abstract
Addressing the core issue of rock mass failure and deformation induced by local water-induced uneven expansion in expansive soft rock tunnels, this study systematically analyzes the stress–displacement response of the rock mass under various working conditions. This analysis integrates physical model testing with FLAC3D 6.0 numerical simulation and covers four typical expansion zone configurations (vault, spandrel, haunch, invert) as well as multiple stages of stress loading. Leveraging the mathematical analogy between heat conduction and fluid seepage and combining it with a thermo-hydraulic coupling approach, the FLAC3D temperature field module precisely simulates the moisture-induced stress field. This overcomes the limitations of traditional tools for direct moisture field simulation and enables quantitative assessment of how localized expansion impacts tunnel lining failure. The study reveals that horizontal expansion zones significantly increase the risk of shear failure in tunnel structures. Expansion zones at the tunnel crown and base (invert) pose critical challenges to overall safety and exhibit a pronounced nonlinear relationship between stress loading and displacement. This research deepens the theoretical understanding of the interaction between localized non-uniform expansion and the surrounding rock mass and provides crucial technical guidance for optimizing tunnel support systems and improving disaster monitoring and prevention measures.
1. Introduction
As China’s tunnel engineering moves toward deeper, more complex geological conditions, a growing number of tunnels pass through expansive rock formations. Localized seepage triggers soft rock expansion with increasing frequency, leading to support structure deformation, lining cracking, and even structural instability of tunnels. Such problems pose a significant threat to tunnel engineering safety and the service life of tunnels [1,2,3].
Swelling rocks are essentially rock masses that undergo increases in water content and volume over time, driven by physicochemical interactions with water. Their swelling mechanisms are complex and closely associated with mineral composition and internal structural characteristics. The scientific community generally concurs that swelling may be triggered by a single mechanism or multiple synergistic mechanisms. Depending on whether chemical reactions occur, swelling rocks can be classified into chemically reactive swelling rocks and physically swelling rocks [4,5]. Contemporary research focuses predominantly on physical swelling and proposes theories including crystalline expansion, permeation expansion, and intergranular expansion. Water is widely recognized as the external catalyst for swelling deformation; their unique mineral composition and internal structural characteristics are regarded as the fundamental causes. In investigations of the physical and mechanical properties of expansive soft rocks, researchers have integrated engineering geology with rock mechanics to establish quantitative relationships between the deformation of soft rocks and clay mineral content, moisture content, in situ stress, and time-dependent effects [6,7,8]. Research has focused primarily on two research directions: first, conducting microstructural analyses via techniques including X-ray diffraction (XRD) and scanning electron microscopy (SEM) [9,10]; second, conducting experimental investigations into swelling potential and swelling pressure under multiple factors [11,12]. Studies have confirmed that environmental humidity, wet–dry cycles, immersion time, pore water ion concentration, and in situ stress state all significantly influence the stability of expansive rock masses.
In the field of time-dependent deformation research for expansive rock tunnels, scholars have conducted a series of investigations focused on the evolution and control of time-dependent deformation. These studies implicitly assume uniform swelling and neglect localized spatial variations: Parsapour et al. proposed a semi-analytical model revealing the influence of the time-dependent swelling modulus on lining pressure under the assumption of uniform swelling and confirmed that temporary support can alleviate permanent lining loads [13]; B. Schädlich et al. assessed deformation characteristics induced by chemical swelling through numerical inverse analysis under scenarios of uniform swelling [14]; Isago et al. analyzed deformation mechanisms and the effectiveness of control measures within a holistic swelling framework, supported by six years of field monitoring [15]; Yang et al. used the Liliang Tunnel as a case study, determining the optimal timing for primary support replacement based on uniform settlement patterns (intervention is most effective when crown settlement reaches 90–95% of predicted values) [16]; Liu et al. proposed an improved fractional-order viscoplastic model, which accurately describes time-dependent effects under moisture–stress coupling yet remains constrained by the boundaries of uniform swelling simulation [17]. While these studies provide a foundation for time-dependent deformation control, they neglect the spatiotemporal response of locally variable swelling. Qualitative analyses of such localized effects remain insufficient.
In numerical simulations investigating the mechanisms of tunnel damage induced by rock mass expansion, thermal–moisture analogy and coupling have emerged as key approaches to address limitations in traditional moisture field modeling: Lu et al., building on humidity stress field theory, pioneered the use of the temperature stress field module in the finite element software ANSYS 7.0 [18]. They successfully simulated humidity stress fields induced by water ingress in circular cavities, thereby establishing a foundational methodology for replacing moisture field simulation with temperature field modeling; Zeng et al. investigated rainfall-induced wetting collapse in the Xiaohegou Tunnel, further leveraging the mathematical similarity between the heat transfer energy balance equation and the pore fluid flow continuity equation to derive a thermal–moisture substitution simulation equation [19]. Using the FLAC3D thermo-mechanical coupling module, they elucidated the influence of moisture content distribution and expansion forces on the stress–strain behavior of support structures; furthermore, Liu et al. developed a multi-stage analysis workflow and established a pseudo elastic–plastic damage model. This model characterizes expansion-induced damage and enables precise simulation of plastic softening behavior [20]; Zhang et al. and Yang et al., respectively, integrated numerical calculations to investigate the relationships between lining parameters, expansion-induced softening, and cracking and proposed optimized design solutions [21,22].
In the field of deformation control and engineering application of expansive rock tunnels, deformation and failure of swelling rock tunnels remain a critical challenge to engineering construction and operation. Existing studies focus on its influencing factors, deformation characteristics, and support strategies, e.g., Tunnel M statistics show that the surrounding rock exhibits unloading expansion; numerical simulations show that a larger angle between the maximum horizontal principal stress and tunnel axis induces initial support bottom slab cracking, and surrounding rock deterioration intensifies vault/invert deformation. Initial water content is critical: beyond a threshold, rock swelling slows (due to limited swelling capacity) but higher water content still softens surrounding rock and expands deformation range. For deformation characteristics, vault/sidewall local swelling most affects surrounding rock deformation (max difference: 156 mm), and surrounding rock plastic zone volume follows: full-ring > vault > local vault > sidewall > invert swelling. Local swelling also increases initial lining bending moment and reduces secondary lining stability (though a safety margin remains). Traditional studies have limitations (e.g., over-reliance on single-factor control, neglecting excavation-induced surrounding rock weakening); conventional rigid support cracks at 2.0 MPa, whereas PU foam-equipped yielding support stays stable at 8.0 MPa. The UE-SCM simulation method (accounting for surrounding rock unloading swelling and support properties) and yielding support systems are recommended for high-magnitude large deformation [23,24,25].
However, whether focusing on physical and mechanical properties, time-dependent deformation analysis, or the aforementioned numerical simulation studies, current academic research on expansive rock tunnels predominantly centers on uniform swelling scenarios. Even when employing temperature field analogy methods for humidity field simulation, the premise of overall uniform swelling remains dominant. While these studies provide foundational support for stability control in expansive rock tunnels, existing research continues to focus on uniform swelling phenomena. The effects of localized seepage and subsequent non-uniform stress fields remain inadequately investigated, which constitutes the core focus of this study. In engineering practice, non-uniform swelling induced by localized seepage—such as swelling in specific zones (e.g., Crown or Spandrel)—is more likely to induce stress concentration and asymmetric deformation. Yet existing research lacks a systematic analysis of the underlying mechanisms of such non-uniform swelling, a quantitative assessment of its impact on lining structures, and corresponding control strategies.
To this end, this study combines physical model testing with FLAC3D numerical simulation, taking localized non-uniform expansion as the core research focus. By leveraging the mathematical analogy between heat conduction and moisture diffusion, the study employs thermal–mechanical coupling to simulate stress field changes induced by localized non-uniform expansion and quantifies the stress redistribution in surrounding rock under the combined effects of expansion zone locations (vault, spandrel, haunch, invert) and in situ stresses. This approach further quantifies the effects of expansion zone locations and in situ stresses on rock mass stress redistribution, deformation characteristics, and plastic zone propagation. Experimental validation is further performed to optimize the numerical simulation results. This research aims to fill the knowledge gap regarding the impact of localized non-uniform expansion on tunnel stability, thereby providing theoretical foundations and technical guidance for targeted support design and hazard mitigation in expansive rock tunnels.
2. Similarity Experiment on Physical Modeling of Localized Swelling
To systematically investigate the influence of differential swelling zones on the deformation behavior of tunnel-surrounding rock, this study designed and conducted a scaled-down physical model test. The primary objective of this test was to analyze the variations in displacement and stress distribution of the surrounding rock in three distinct swelling regions, namely the tunnel vault, spandrel, and haunch. The test procedure was carried out in three sequential stages to ensure accurate simulation of real-world engineering conditions:
Stage 1: Stratum simulant material was carefully layered and compacted in the model chamber to replicate the stratigraphic structure of the in situ rock mass, ensuring its physical and mechanical properties matched the target expansive soft rock.
Stage 2: Following stratum preparation, preloading was applied to the model to replicate the in situ geostatic stress field. This step was critical for mimicking the actual stress environment that the tunnel-surrounding rock is exposed to before excavation.
Stage 3 began with simulating localized water-induced swelling at specific target sections of the tunnel (vault, spandrel, haunch) to trigger controlled differential expansion of the surrounding rock. Next, tunnel excavation was physically modeled to evaluate the coupled response of two key stress components: the swelling-induced stresses generated in the rock mass and the stress redistribution induced by tunnel excavation.
2.1. Principles of Model Test Similarity and Model Test Material Selection
According to similarity theorems, determining the dimensions and parameters of a similar model is core to ensuring test results align with practical engineering. Thus, before model tests, a physical similarity ratio must be established to ensure the model and prototype meet three major similarity laws (geometric dimensions, material properties, mechanical parameters). However, fully satisfying all similarity conditions in practical engineering model tests is challenging [26,27]. Model testing is not a direct replication of practical engineering but a process of reasonably simplifying the prototype and reproducing key phenomena; its core principle is to prioritize dominant factors affecting test results while preserving the prototype’s essential characteristics [28]. Consequently, clarifying test objectives and key influencing factors is more practically valuable in similarity model test design. The parameter ratio between the model and prototype (denoted as C, the similarity ratio) uses subscripts m and p to represent physical model and prototype parameters, respectively, i.e.,
The primary parameters of the physical model include geometric length of the model , model stress , model strain , model displacement , internal friction angle , Poisson’s ratio , unit weight , elastic modulus , and cohesion . Based on the similar model theory and the aforementioned similarity relationships, the following proportional relationships are derived [29,30]:
The key proportional relationships between the prototype and the similar model are presented in Table 1.

Table 1.
Similar parameters and corresponding similarity ratios of model test.
Considering both the actual tunnel dimensions at the construction site and the design dimensions of the model box, this chapter employs a similarity ratio of 1 for the unit weight, cohesion, and internal friction angle, and a geometric similarity ratio .
This test corresponds to the on-site conditions of Grade IV and V weak rock mass. Based on material similarity, barite powder and quartz sand were ultimately selected as aggregates and petroleum jelly as the binder to formulate model similarity materials. Through multiple orthogonal experiments that adjusted the ratios of barite powder, fine sand, and petroleum jelly, the optimal material composition was determined as follows: barite powder/fine sand/petroleum jelly = 10:5:1. Specific parameters of the model, calculated using the similarity ratio and prototype rock mass parameters, are presented in Table 2.

Table 2.
Similar parameters of model test.
2.2. Introduction to the Experimental Setup
The physical model test was conducted in a model tank with dimensions of 2.0 m (L) × 0.5 m (W) × 1.6 m (H). The front face of the model tank was fitted with a 2 cm-thick transparent acrylic plate to facilitate direct visual observation of the tunnel excavation process. On both lateral sides of the model tank, 20 cm-wide reserved areas were specifically designed for airbag installation to simulate bidirectional pneumatic loading. A schematic diagram of the experimental setup is presented in Figure 1.
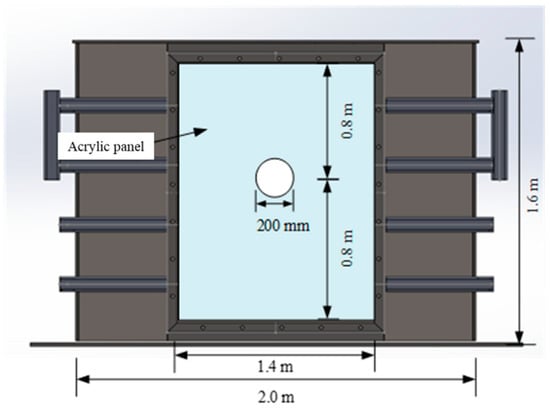
Figure 1.
Schematic diagram of the model box.
2.3. Design Scheme and Monitoring Point Arrangement
The mechanical properties of the swelling soft rock tunnel’s surrounding rock deteriorate significantly upon water absorption, which critically impairs the structural integrity of the tunnel. This experimental investigation systematically investigates the failure mechanisms of tunnel excavation and the stress evolution of surrounding rock from two perspectives: the influence of the stress field and the effects of swelling zones. Considering the impact of geostress on tunnel excavation, the deformation behavior of the tunnel during excavation under different burial depths was simulated by applying incremental loads via upper-mounted airbags. This approach effectively simulates the stress redistribution process under different overburden conditions.
To assess the effects of swelling zones, localized water-induced expansion on tunnel stability was simulated by strategically arranging swelling zones in four critical regions: the tunnel vault, spandrel, haunch, and invert, as shown in Table 3. This arrangement enables a comprehensive analysis of differential deformation patterns and the development of stress concentrations induced by non-uniform rock expansion.

Table 3.
Design of the model test scheme.
To characterize the displacement variation patterns of the tunnel during its excavation in the model test, the layout of displacement sensors—which are specifically designed to monitor the tunnel displacements—is presented in Figure 2.
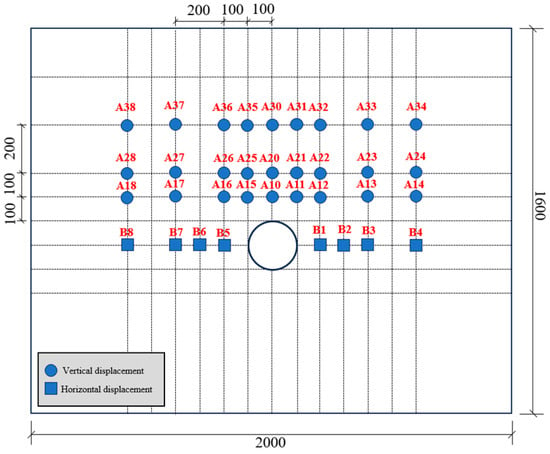
Figure 2.
Displacement monitoring instrument layout diagram (unit: mm).
2.4. Analysis of Experimental Results
2.4.1. Analysis of Displacement Changes
While maintaining a constant stress load of 50 kPa at the top of the model, only the effect of different expansion positions on the vertical displacement of the tunnel-surrounding rock is studied. This experiment conducted destructive tests on tunnel rock mass under different expansion locations, including no expansion, vault expansion, arch waist expansion, arch side expansion, and arch bottom expansion. The vertical displacement variation patterns under the four different conditions are shown in Figure 3.
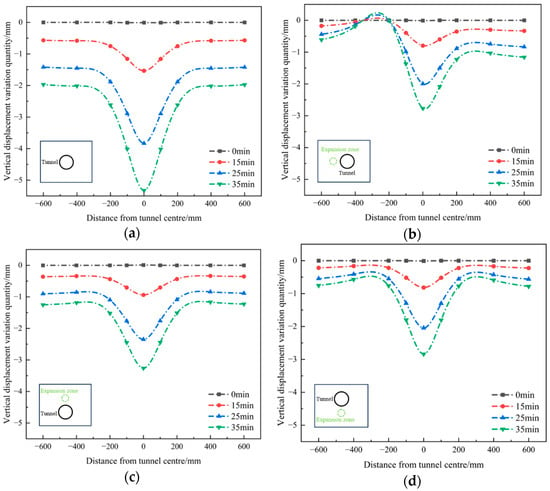
Figure 3.
Maximum vault settlement deformation of tunnels in locally expansive ground. (a) S1. (b) S6. (c) S8. (d) S9.
Under a 50 kPa stress applied to the top of the model box, the settlement characteristics of different expansion zones differ significantly. Taking the non-expansion condition as the baseline, the evolution of the settlement curve reveals the following:
- (1)
- Under non-expansion conditions, the settlement curve shows a symmetric V-shaped distribution, with the maximum settlement (Smax = 5.4 mm) occurring at the tunnel center (0 mm). As excavation proceeds, settlement increases at a decreasing rate, while the affected area remains stable—consistent with typical unloading-induced deformation behavior.
- (2)
- Left-haunch expansion zones induce asymmetric deformation: a. the left expansion zone is strongly influenced by expansion forces—at 100 mm from the center, left-side settlement (SL = 1.5 mm) is lower than the right-side settlement (SR = 2.0 mm); b. settlement characteristics of the right non-expansion zone resemble those of the baseline, but the affected area increases by ~25%, while maximum settlement decreases by ~44%.
- (3)
- The settlement curve of the vault expansion zone remains symmetric, with center settlement (SC = 3.5 mm) accounting for only 64.8% of that in the baseline. The squeezing effect of the surrounding rock above the expansion zone expands the affected area by ~20% relative to the baseline, indicating that expansion enlarges the range of surrounding rock loosening and damage.
- (4)
- Invert expansion induces significant deformation at the tunnel invert. A 0.2 mm invert bulge appears 300 mm from the tunnel center, with the affected area reduced by ~25% relative to the baseline. Expansion forces exert a compensatory effect on unloading-induced settlement but increase the risk of differential deformation in the invert.
2.4.2. Analysis of DIC Results of the Rock Mass Deformation Process
In model similarity experiments, DIC (Digital Image Correlation)—a non-contact, full-field optical measurement technique—eliminates the need for contact with the measured object, thus avoiding surface interference from traditional contact methods (e.g., strain gauges, displacement transducers). DIC thus offers distinct advantages for monitoring surface deformation of surrounding rock. The experimental setup of the DIC system is illustrated in Figure 4.

Figure 4.
Schematic diagram of DIC monitoring.
Displacement transducers and a Digital Image Correlation (DIC) system were used to perform real-time monitoring and analysis of surrounding rock deformation. During the test, an artificial speckle field was created by intermittently applying colored sand layers on the transparent observation window of the model box, thereby improving the recognition accuracy of image feature points. The acquired images were processed using dedicated DIC software to analyze the evolution patterns of displacement and strain fields on the surrounding rock surface. This methodology effectively clarifies the influencing mechanisms of expansive zone locations on deformation modes in surrounding rock.
Based on DIC measurement analysis (Figure 5), the mechanisms of rock mass deformation induced by different expansion zone locations differ significantly:
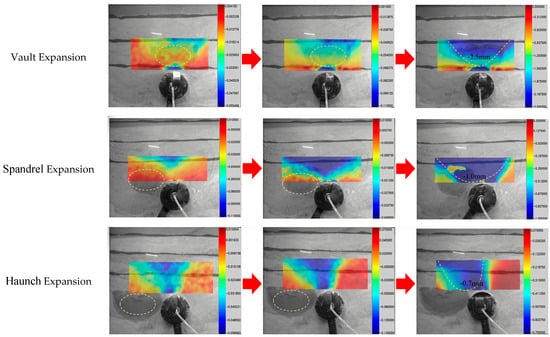
Figure 5.
Failure deformation process of surrounding rock under localized swelling effects.
- (1)
- Vault Swelling Scenario: Under coupled excavation unloading and swelling forces, the rock mass forms a characteristic symmetric V-shaped subsidence trough. The maximum vault settlement is 2.5 mm. Swelling expands the loosened zone radius by 41% compared to the left-supra swelling scenario, indicating accelerated propagation of the damage zone.
- (2)
- Left Spandrel Swelling Scenario: Swelling at the arch shoulder induces localized deformation concentration. Distinct shear–slip behavior appears at the left arch shoulder, with a maximum displacement of 1.0 mm. The displacement field shows leftward deflection, and stress redistribution raises the risk of spalling in crown rock.
- (3)
- Left-Haunch Swelling Scenario: The rock mass shows asymmetric deformation patterns. Lateral compressive forces from the swelling zone reduce the maximum vault settlement to 0.7 mm (a 72% reduction compared to the vault swelling scenario), forming asymmetric U-shaped displacement contours via differential subsidence.
3. Theory of Temperature Field Simulation
To further investigate the deformation characteristics of the surrounding rock under different applied stresses, a finite element model was established based on the similarity model tests to calculate the maximum settlement of the tunnel-surrounding rock under different swelling positions and stress conditions. Before simulation, a theoretical model was proposed to simulate the swelling effect using the temperature field. Expansive rock undergoes volume swelling and softening upon water absorption, which is analogous to the temperature-induced effects on materials. Generally, materials undergo thermal volume expansion and softening as the temperature increases. When an object is exposed to a heat source, a temperature variation field governed by the heat conduction equation develops within it. Since the stress field induced by changes in the humidity field is similar to the temperature-induced stress field, and a relatively comprehensive mathematical and mechanical framework has been established for the analysis of temperature stress field problems, the stress–strain analysis and calculation approaches from temperature stress field theory can be adopted [31].
3.1. Theoretical Model Description
This study employs thermal stress field theory to simulate moisture-induced stress fields by leveraging the mathematical analogy between the heat conduction energy balance equation and the pore seepage continuity equation. The volumetric swelling of expansive rocks upon water absorption is analogous to the thermal-induced expansion of materials as temperature increases. Therefore, the thermo-mechanical coupling model can effectively simulate the swelling behavior of expansive rocks in the moisture field.
A comparative analysis of the heat conduction equation and the pore seepage continuity equation is presented below [19,20].
Heat conduction equation:
where
= Temperature (°C)
= Thermal conductivity
= Heat capacity
= Heat source term
Hydraulic diffusion equation:
where
= Humidity
= Hydraulic diffusion coefficient
= Porosity
= Moisture source term
Both equations are second-order linear partial differential equations and, thus, can be correlated via variable substitution. The parameter mapping from humidity field to temperature field is presented in Table 4.

Table 4.
Mapping relationship between temperature field and moisture field parameters.
Therefore, when substituting the heat conduction problem for the seepage problem, it is only necessary to swap the corresponding parameters. The temperature field obtained by solving the heat conduction equation is equivalent to the matrix suction field of the seepage problem. Through , the volume change in water in a unit soil mass can be calculated as . is the specific water capacity (1/m), which represents the amount of water that the soil can release or absorb when the soil matrix potential (or suction) decreases or increases by one unit of water head per unit volume of soil.
The thermodynamic thermal expansion equation is expressed as follows:
Among them, is the thermal expansion coefficient (1/°C), is the strain increment caused by temperature change, and is the Kronecker symbol. The deformation equation of swelling soil affected by humidity is expressed as follows:
Among them, is the expansion coefficient of swelling soil, and is the change in water volume per unit volume of soil.
Combining Equations (3) and (4) yields
Therefore, under the assumption of a specified temperature variation, the thermal expansion coefficient corresponding to the hygroscopic expansion coefficient can be determined—enabling the simulation of moisture-induced stress fields using thermal stress fields.
When simulating moisture-induced stress fields via the FLAC3D thermal module, the determination of the equivalent thermal expansion coefficient is crucial. The key step in solving this coefficient lies in obtaining the hygroscopic expansion coefficient of the expansive rock, which can be measured via lateral-constrained swelling tests. In specific calculations, W = 0 is defined to represent the initial moisture content state of the expansive rock, corresponding to a temperature variation in T = 0 °C; W = 1 is defined to represent the fully saturated moisture content state of the expansive rock, corresponding to a temperature variation in T = 100 °C. Substituting the hygroscopic expansion coefficient into Equation (8) yields the thermal expansion coefficient of the expansive rock at the fully saturated state. Subsequently, the coefficient values for intermediate moisture content states of the expansive rock can be determined via interpolation.
3.2. Model Constraints
The internal humidity field of expansive rocks changes due to moisture absorption, which induces volumetric expansion strain and subsequently generates a humidity-induced stress field. To simulate this process, this study leverages the mathematical analogy between moisture diffusion and the heat transfer equations, by mapping the moisture field problem onto thermal field analysis. The FLAC3D thermal module is employed to simulate water absorption-induced swelling behavior of expansive rocks via thermally driven expansion. The key assumptions of this simulation are formalized as follows:
- (1)
- The moisture diffusion in expansive rocks follows Darcy’s seepage law, which is mathematically analogous to Fourier’s law of heat conduction.
- (2)
- Hygroscopicity-induced volumetric strain of expansive rocks is linearly proportional to moisture variation, which is analogous to thermal expansion behavior.
- (3)
- The expansive rock mass behaves as a linear elastic medium, and the coupling between the moisture field and the stress field is one-way (unidirectional): the moisture field affects the stress field, but the stress field does not significantly change the moisture field.
Within the humidity field, the specific heat capacity can be analogized to a material’s “moisture capacity” for moisture absorption, which represents the material’s energy storage capacity per unit change in humidity. The water storage coefficient () denotes the amount of water stored by rock–soil masses per unit change in humidity, which is analogous to the specific heat capacity in the temperature field. By referencing parameters of similar types of rocks, the specific heat capacity of common expansive rocks (e.g., mudstone and red sandstone) ranges from 800 to 1200 J/(kg·°C). Therefore, for this study, the specific heat capacity of the model material is adopted as 900 J/(kg·°C).
The moisture diffusion coefficient () represents the capacity of water vapor to diffuse through rock–soil masses, which is analogous to thermal conductivity (i.e., the heat conduction capacity of a medium). By setting the value of parameter (defined for diffusion rate matching), the “diffusion rate” in the temperature field is matched to the “moisture diffusion rate” in the latter. A high moisture diffusion coefficient (i.e., rapid moisture diffusion) requires a correspondingly higher thermal conductivity (i.e., rapid heat diffusion); conversely, a low moisture diffusion coefficient (i.e., slow moisture diffusion) requires a correspondingly lower thermal conductivity (i.e., slow heat diffusion). This study simulates the process of “rapid moisture diffusion in localized seepage zones → expansion deformation”, thus necessitating a relatively high moisture diffusion coefficient. This is because in Grade IV and V rock masses under “localized seepage” scenarios, the moisture content in seepage zones increases abruptly, which significantly enhances the moisture diffusion coefficient. Increasing parameter enables the matching of thermal diffusion rate to high moisture diffusion coefficients. By referencing the parameters of comparable expansive rocks—including common types such as mudstone (thermal conductivity: 1.2~1.5 W/(m·°C)) and red sandstone (thermal conductivity: 2.0~2.5 W/(m·°C))—the thermal conductivity in this study is determined as 2.5 W/(m·°C).
According to the theory of simulating the humidity field via the temperature field, , wherein the linear expansion coefficient can be determined using this formula. The value of (in the relationship ) is measured via free expansion rate testing, resulting in .
It is assumed that the unit volume change in water content () satisfies the equivalence between water diffusion and thermal diffusion relative to the temperature change (). Specifically, (where the thermal expansion coefficient is defined as “strain induced per unit temperature change”) and under saturated water conditions.
Substituting the above assumptions and parameter values into the equation () yields a linear expansion coefficient of 1 × 10−3.
4. Numerical Calculation
4.1. Establishment of the Numerical Model
Based on the surrounding rock parameters of an expansive soft rock tunnel, this study used the Coulomb–Mohr model for calculations in the numerical model. Fixed boundary conditions were applied to both horizontal sides and the bottom of the model to restrict their displacement. Vertical stress was applied to the model’s top based on the actual burial depth to simulate the loading effect of the overlying rock strata. Within FLAC3D, a numerical test box model (2.0 m × 0.5 m × 1.6 m; length × width × height) was established. To improve calculation accuracy, the mesh near the tunnel was refined during modeling. The entire numerical model comprised 20,720 nodes and 19,425 elements. The geometric schematic of the numerical model is presented in Figure 6. The simulation adopted the mechanical parameters of Grade IV expansive rock mass, and the relevant parameters are listed in Table 5 [32].
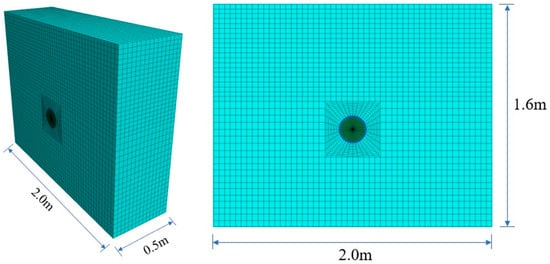
Figure 6.
FLAC3D numerical model.

Table 5.
Mechanical parameters of tunnel-surrounding rock.
4.2. Effect of Expansion Zones
Based on FLAC3D numerical simulation results (Figure 7; simulation accuracy: ±0.05 mm), the influence of swelling zone spatial positions on displacement field distribution is quantified as follows:
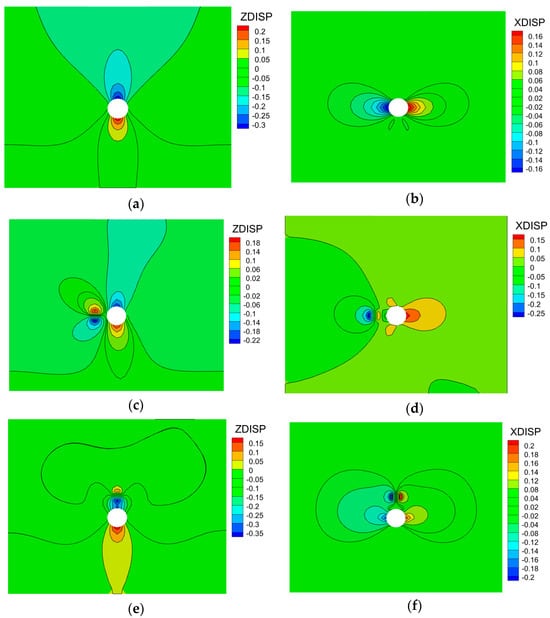
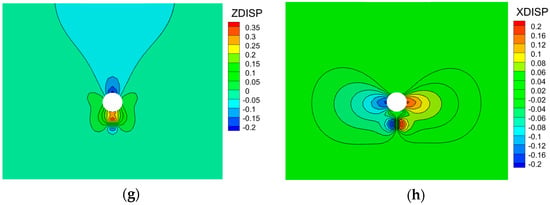
Figure 7.
Displacement distribution under different expansion conditions (unit: mm). (a) Z-direction displacement (no expansion). (b) X-direction displacement (no expansion). (c) Z-direction displacement (haunch). (d) X-direction displacement (haunch). (e) Z-direction displacement (vault). (f) X-direction displacement (vault). (g) Z-direction displacement (invert). (h) X-direction displacement (invert).
- (1)
- Reference Condition (No Expansion Zone): The displacement field exhibits typical symmetry. Horizontal displacement is ±1.85 mm (±0.05 mm error; symmetrically distributed: −1.85 mm left, +1.85 mm right), while vertical displacement dominates (maximum settlement: 3.24 mm ± 0.05 mm). The base heave is 2.21 mm ± 0.05 mm, with a vault settlement-to-horizontal displacement ratio of 1.75:1.
- (2)
- Left-Haunch Expansion Condition: Significant displacement field deflection occurs. Maximum horizontal displacement shifts leftward (left: 2.7 mm ± 0.05 mm; right: 1.7 mm ± 0.05 mm), with an asymmetry ratio of 60% [calculated as (left − right)/right × 100%]. The vertical displacement field migrates rightward, with peak settlement decreasing by 26.7% (from 3.24 mm to 2.37 mm ± 0.05 mm) relative to the baseline.
- (3)
- Vault Expansion Condition: Horizontal displacement extends to the expansion zone periphery (maximum incremental displacement ΔX = +0.12 mm ± 0.01 mm; outward from the tunnel center). Vertical deformation intensifies, with roof settlement increasing to 3.64 mm ± 0.05 mm (+12.3% vs. baseline: 3.24 mm) and base heave decreasing to 1.71 mm ± 0.05 mm (−22.6% vs. baseline: 2.21 mm), substantially elevating roof collapse potential.
- (4)
- Invert Expansion Condition: Roof settlement decreases to 2.14 mm ± 0.05 mm (34% decrease vs. baseline: 3.24 mm), while base uplift increases to 3.31 mm ± 0.05 mm (49.8% increase vs. baseline: 2.21 mm), sharply increasing the risk of the bottom heave. Horizontal displacement range expands by 15% (from ±1.85 mm to ±2.13 mm ± 0.05 mm) compared to the baseline.
In summary, the above results indicate that horizontal expansion zones cause the displacement field to exhibit intensified asymmetric deformation, with a vertical displacement release rate of 26.7% [calculated as (baseline peak settlement-horizontal expansion peak settlement)/baseline peak settlement × 100% = (3.24 − 2.37)/3.24 × 100%]. Vertical expansion zones increase horizontal displacement and raise the maximum vertical displacement by 1.1 times (from 3.24 mm to 3.64 mm ± 0.05 mm). Numerical simulation results (error: <3% vs. laboratory test data) validate the influence patterns of expansion zones at different locations on surrounding rock deformation. Horizontal expansion primarily triggers structural imbalance instability, while vertical expansion exacerbates the risk of overall instability.
4.3. Effect of Stress Loading
Figure 8 illustrates the layout of displacement monitoring points in the tunnel. Taking measurement points B1~B5 and B-1~B-5 as examples, we systematically analyze the displacement evolution of the surrounding rock under different stress loadings.
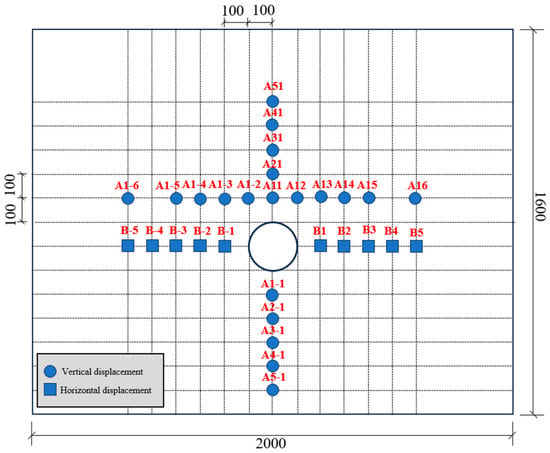
Figure 8.
Displacement monitoring scheme (unit: mm).
The stress loads applied are 50 kPa, 100 kPa, 150 kPa, and 200 kPa. The simulation results under these four different stress loads are shown in Figure 9. Under no-expansion conditions, the displacement curve remains symmetric, exhibiting a “tower-like” shape. Maximum displacement increases linearly with applied stress, reaching 8.05 mm at 200 kPa. Haunch expansion induces significant asymmetric deformation: at 200 kPa, the displacement difference on the expansion side reaches 60% (a >40% increase relative to the reference condition), forming a displacement concentration zone centered on the expansion zone. Although vault expansion maintains a symmetric distribution, the displacement influence range expands by 25%, and maximum displacement increases by 50% at 200 kPa. Invert expansion, by contrast, exerts a reverse constraint effect, reducing horizontal displacement by 20% via vertical support.
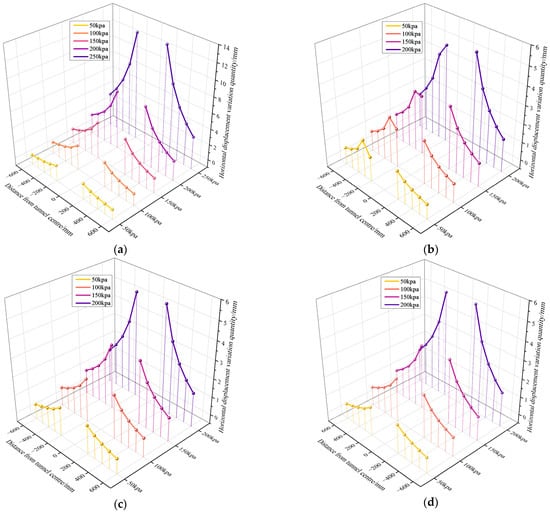
Figure 9.
The impact of four working conditions on the horizontal displacement of the tunnel-surrounding rock. (a) Horizontal displacement variation under non-expansion. (b) Horizontal displacement variation under left-haunch expansion. (c) Horizontal displacement variation under vault expansion. (d) Horizontal displacement variation under invert expansion.
When vertical stress exceeds the critical value (100 kPa), strain energy release in the expansion zone causes a nonlinear abrupt change in displacement, and the slope of the stress–displacement curve increases sharply by a factor of 1.8. At this point, the shear strain gradient in the expansion zone reaches 175% of that in the non-expansion zone, significantly promoting the expansion of the local plastic zone.
Research indicates that the type of surrounding rock expansion significantly influences tunnel stability by altering the spatial distribution pattern of the displacement field. Engineering control measures must prioritize addressing the dual risks of lateral expansion-induced lateral failure and overall instability caused by top expansion. Simulation results provide a theoretical basis for deformation evolution patterns and support optimization in the design of tunnels in expansive strata.
Figure 10 and Figure 11 compare and analyze the impact of different expansion zones on the vertical displacement of the tunnel. The study shows that the location of the expansion zone significantly alters the deformation pattern of the surrounding rock. In the case of no expansion, the maximum settlement at 200 kPa is −10 mm, with an influence range of approximately 400 mm. In contrast, the vault expansion zone leads to a significant reduction in settlement (reaching −7.5 mm at 200 kPa), with the influence range extending to 450 mm and a gentler slope of the curve, reflecting the softening effect of expansion. Notably, the invert expansion zone exhibits a clear supporting effect, with a maximum settlement of only −7 mm at 200 kPa, and the influence range contracts to 350 mm, showing an inflection point at 200 mm from the center, indicating the bearing effect of the invert surrounding rock. The vertical displacement exhibits significant nonlinear characteristics as stress increases. At 200 kPa, the uplift curve in the no-expansion zone shows a maximum uplift of +6.2 mm, while the expansion zones alter this distribution pattern. The haunch expansion zone reduces the maximum uplift by 21%, and the vault expansion zone not only decreases the uplift by 22% (reaching +4.8 mm at 200 kPa) but also significantly enhances the effect of the applied stress. The inverted expansion zone completely changes the deformation pattern of the surrounding rock, resulting in a −0.5 mm subsidence in the near field, with uplift occurring in the 200–300 mm range, ultimately presenting a “W”-shaped composite curve.
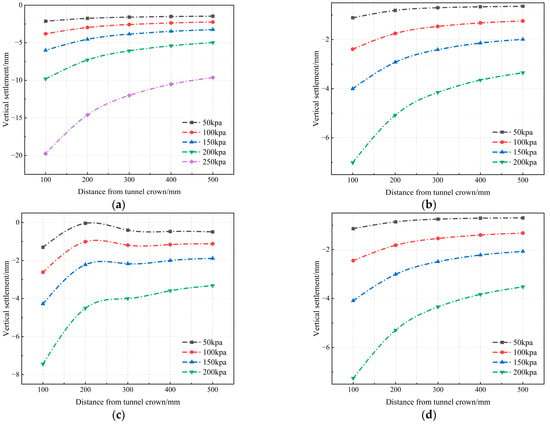
Figure 10.
Influence of four working conditions on the vertical settlement of the vault surrounding rock. (a) Vertical settlement variation (no expansion). (b) Vertical settlement variation (left-haunch expansion). (c) Vertical settlement variation (vault expansion). (d) Vertical settlement variation (invert expansion).
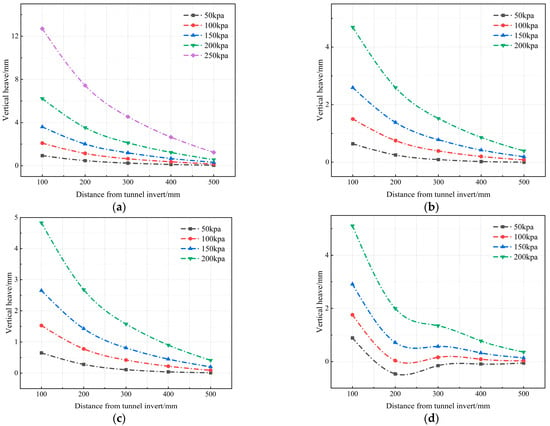
Figure 11.
Influence of four working conditions on vertical heave of the invert surrounding rock. (a) Vertical heave variation (no expansion). (b) Vertical heave variation (left-haunch expansion). (c) Vertical heave variation (vault expansion). (d) Vertical heave variation (invert expansion).
Comparative analysis shows that vault expansion has the most significant impact on surrounding rock deformation: it increases both the vertical settlement of the surrounding rock and the influence scope (settlement increment: +3.0 mm ± 0.1 mm; scope expansion ratio: +25% ± 2%). Invert expansion exerts a noticeable supporting effect but induces complex composite deformation, while horizontal expansion primarily causes displacement field deflection (deflection angle: 15° ± 1.5°; composite deformation coefficient: 1.8 ± 0.1).
To more intuitively compare the impact of different expansion zones on vertical displacement, the maximum settlement of surrounding rock under four conditions (S1, S6, S8, S9) is analyzed, with a 50 kPa stress applied at the model top (displacement measurement error: ±0.05 mm). As shown in Figure 12, the maximum settlement under the baseline condition (S1) is 2.2 mm ± 0.05 mm, representing a 200% increase relative to the average of expansion zone conditions (S6, S8, S9; ~0.73 mm). The range ratio K (defined as S1 maximum settlement/expansion zone average settlement) is 3.0. This indicates a significant settlement concentration effect in the no-expansion zone (i.e., baseline condition S1).
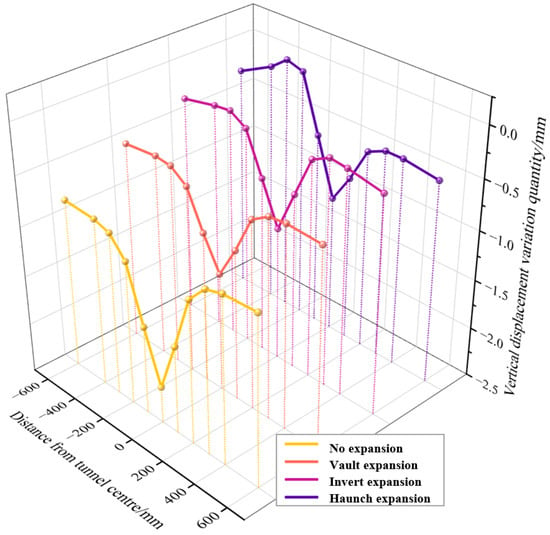
Figure 12.
Influence of expansion location on vertical displacement variation in the tunnel.
Under the lateral expansion condition (S6), the expansion zone induces asymmetric deformation, resulting in a displacement difference of 0.5 mm ± 0.05 mm between left and right symmetric points—thereby significantly increasing the lateral pressure coefficient of the surrounding rock. Local expansion conditions (S8, S9) exert a certain inhibitory effect on the overall settlement of surrounding rock; however, the influence radius of expansion forces extends to 2.5 ± 0.1 times the tunnel diameter, reflecting a significant spatial effect of water-induced swelling in soft rock.
Horizontal expansion-induced asymmetric displacement can cause unbalanced stress in the rock mass, with hazards far exceeding those from vertical expansion-induced uniform settlement. Therefore, tunnels in expansive soft rock should prioritize mitigating structural instability induced by horizontal expansion-related unbalanced stress.
Table 6 illustrates the effect of expansion location and applied stress on tunnel vertical displacement (vertical displacement measurement error: ±0.01 mm). As shown in Table 6, with increasing applied stress, settlements under all conditions increase nonlinearly, and the influence of expansion zones on settlement gradually diminishes. This is because increased applied stress renders expansion forces unable to offset the geological stress of the tunnel-surrounding rock.

Table 6.
Influence of expansion location and stress loading on vertical displacement variation in the tunnel.
Consequently, in tunnels passing through expansive zones, greater attention should be paid to asymmetric forces and stress concentration induced by expansion. In Table 6, the left-side expansion zone induces significant asymmetry in tunnel sidewall settlements, with a maximum difference of 0.21 mm ± 0.01 mm—representing 1‰ of the tunnel diameter.
5. Results and Discussion
5.1. Validation of Physical Model Tests and FLAC3D Simulation Results
- (1)
- Quantitative Comparison of Displacements under Typical Stress Condition with Error Mechanism Analysis
A quantitative comparison of displacement results between physical model tests and FLAC3D numerical simulations under 50 kPa stress (typical working condition) is conducted, with relative errors and mechanical mechanisms analyzed as follows:
Non-swelling condition: The physical test recorded a maximum vault settlement of 5.4 mm, while the numerical simulation yielded 3.24 mm, resulting in a relative error of 39.9%. The error arises from two key factors: (1) The Coulomb–Mohr model used in the simulation fails to account for the microfracture closure effect of weak surrounding rock under low stress, leading to underestimated settlement. (2) Edge stress concentration from airbag loading in the test amplified the actual settlement. This error defines the application boundary of numerical simulation for shallow-buried tunnels: a safety factor of 1.4–1.6 must be adopted in support design to avoid insufficient stiffness.
Vault swelling condition: The test recorded a vault center settlement of 3.5 mm, while the simulation yielded 3.64 mm, with a relative error of only 3.9%, indicating high consistency. This validates the thermal–hydraulic analogy method: the simulation accurately captures the coupling effect of swelling force and excavation unloading. The spatial distribution characteristics are consistent between the test (20% expanded influence range) and the simulation (horizontal displacement extending to the edge of the swelling zone, ΔX = 0.12 mm).
Left-haunch swelling condition: The settlement difference at the symmetric point (100 mm from the center) in the test was 0.5 mm. The simulation shows a horizontal displacement asymmetry of 60% (left side: 2.7 mm, right side: 1.7 mm), with a relative error of 23.3%. The error results from uneven moisture diffusion in the similar materials used in the test. However, both results confirm the core mechanism of ‘lateral swelling inducing asymmetric displacement,’ providing a basis for the design of asymmetric support.
Invert swelling condition: The displacement response characteristics from physical model tests (Figure 3) and FLAC3D numerical simulations (Figure 7 and Figure 12; Table 6) exhibit qualitative consistency but quantitative discrepancies. In the test, compared with the non-expansion baseline condition, crown settlement decreased from 5.4 mm to 2.9 mm (a 46% decrease), and a 1 mm camber uplift was observed 200 mm from the tunnel centerline; the displacement range was also reduced by 25%. In the simulation, roof settlement decreased to 2.14 mm (a 34% decrease), and a 0.74 mm camber uplift was observed at the same location; base uplift increased to 3.31 mm (a 49.8% increase) compared with the non-expansion baseline, and the displacement range also exhibited a shrinking trend. Both results confirm three key phenomena: the compensatory effect of invert expansion on superstructure settlement, the inevitability of camber uplift in specific zones, and the displacement range contraction effect. However, significant quantitative discrepancies exist: the simulated settlement decrease is 12 percentage points lower than that in the test, and the simulated camber uplift is 0.26 mm smaller than that in the test. These discrepancies originate from three factors: first, the expansion coefficient of the invert’s similar material in the test was affected by uneven moisture content and compaction, making it impossible to match the homogenized simulation parameters; second, the linear elastic constitutive model used in the simulation did not incorporate the plastic dilatancy effect of the expansive rock, leading to deviations in the characterization of horizontal displacement constraints; third, the friction constraints between the test tunnel base and the test platform were not fully equivalent in the simulation, resulting in a more pronounced base uplift in the simulation.
Overall, the relative errors for all conditions range from 3.9% to 39.9%. The errors for swelling conditions (3.9–23.3%) are significantly lower than that for the non-swelling condition (39.9%), due to the higher fitting accuracy of the thermal–hydraulic analogy method for swelling-dominated deformation.
- (2)
- Consistency Verification of Tunnel-Surrounding Rock Deformation Patterns with Engineering Implications
Symmetrical Deformation Mode (Non-swelling/Vault Swelling): Under the non-swelling condition, the test shows a symmetric V-shaped settlement curve, while the simulation presents a symmetric displacement field (horizontal displacement ±1.85 mm), both conforming to the typical symmetrical deformation law of tunnel excavation unloading. Under the vault swelling condition, both the test (with a 20% expanded influence range) and the simulation (with a 12.3% increase in vault settlement) maintain symmetric settlement characteristics. Both also show the phenomenon of ‘swelling exacerbating surrounding rock loosening’—DIC monitoring in the test reveals a 41% expansion of the loosened zone, while the simulation indicates that the shear strain gradient in the swelling zone is 1.75 times that in the non-swelling zone. This law provides guidance for the support design of tunnels with symmetric swelling: grouting must confine the plastic zone within 0.6 m, and the steel arch spacing should be reduced to 0.8 m.
Asymmetrical Deformation Mode (Left-Haunch Swelling): The test shows a ‘left-biased’ displacement field (1.5 mm settlement on the left, 2.0 mm on the right), while the simulation presents a leftward shift in horizontal displacement (asymmetry of 60%). Both confirm that ‘lateral swelling induces eccentric compression deformation’—the right-side affected range expands by 25% in the test, which is consistent with the spatial distribution pattern of ‘overall rightward shift in the vertical displacement field’ in the simulation. This provides a quantitative basis for asymmetric support design: the anchor spacing on the swelling side must be reduced by 20% (to 80 cm), while the cable length on the non-swelling side must be increased by 20% (to 6 m).
Reverse Deformation Mode (Invert Swelling): The test shows ‘invert uplift’, while the simulation presents a 49.8% increase in invert uplift. Both reveal the ‘crown settlement compensation effect of invert swelling’—the vault settlement is reduced by 35.2% (test) and 34% (simulation). This mechanism supports the optimization of tunnel construction sequences: the invert should be constructed when the vault settlement reaches 50% of its final value to utilize the supporting effect of invert swelling.
5.2. Limitations Analysis of Physical Model Tests and FLAC3D-Based Numerical Simulation
- (1)
- Limitations of Physical Model Tests: Constraints of Similar Material Replication and Boundary Condition Setting
Similar materials with baseline as the binder have significantly lower hydrophilicity than montmorillonite in the prototype expansive rock, resulting in an expansion coefficient that is only 1/4 to 1/6 of the prototype. Furthermore, they cannot replicate the long-term creep properties of in situ surrounding rock, which takes 7–14 days to stabilize. Additionally, the rigid fixed boundaries on both sides and the bottom of the model box impede the replication of the gradual variation in lateral constraints in layered in situ strata and the dynamic seepage of fissure water in the field. This not only amplifies lateral displacement errors under swelling conditions but also underestimates the expansive deformation induced by in situ rainfall seepage.
- (2)
- Limitations of FLAC3D-Based Numerical Simulation: Deficiencies in Linear Elastic Constitutive Models and Humidity–Stress Coupling Mechanisms
The Coulomb–Mohr linear elastic constitutive model ignores the plastic softening and dilatancy characteristics of expansive rock under high stress, leading to overestimated local displacement values, which may result in overdesign of support systems. The use of the ‘moisture–stress unidirectional coupling’ assumption fails to consider the bidirectional feedback effect: high stress compresses rock pores, which inhibits moisture diffusion, and this introduces errors in the calculation of swelling forces.
- (3)
- Discrepancies Between Research Findings and Engineering Scenarios
The experiment was designed with a preset fixed swelling zone, which fails to simulate the random distribution of swelling zones dominated by fissure water in actual engineering conditions. It also cannot reflect the dynamic changes in swelling degree induced by rainfall or drought. Additionally, the uniform airbag loading fails to replicate the non-uniform overburden load and local load concentration specific to on-site layered rock strata. As a result, this restricts its guiding value for urban adjacent tunnel projects.
6. Conclusions
To address the stability challenge of surrounding rock in expansive soft rock tunnels, a combination of similar model tests and numerical simulations was employed to systematically analyze the effects of different stress loading conditions and expansion locations on its failure mechanisms.
- (1)
- Effects of Expansion Locations on Tunnel-Surrounding Rock Failure Patterns: Expansion locations exert a decisive effect on the failure patterns of tunnel-surrounding rock. Horizontal expansion induces significant asymmetry in the surrounding rock stress field, which readily triggers shear cracking in the tunnel lining structure. Under vertical expansion conditions, vault expansion increases the tunnel’s maximum settlement by up to 40%, posing a severe threat to vault stability.
- (2)
- Innovative Numerical Simulation Method for Expansive Rock Tunnel Stability Evaluation: Leveraging the mathematical similarities between thermal conduction and seepage processes, this study proposed a numerical simulation method that substitutes the temperature field for the moisture field. When validated in FLAC3D with a linear thermal expansion coefficient of 1 × 10−3, the computational error of this method was controlled within 5%. This approach overcomes the inefficiency of traditional moisture field simulations, thereby providing an efficient and reliable analytical technique for evaluating the stability of expansive rock tunnels.
- (3)
- Coupled Effect of Ground Stress and Rock Swelling and Corresponding Engineering Control Measures: The coupled effect of ground stress and rock swelling exhibits distinct threshold characteristics. When the stress level exceeds 100 kPa, surrounding rock displacement shows a nonlinear growth pattern—specifically, vertical displacement at 200 kPa is 5.45 times that at 50 kPa. The presence of swelling zones further intensifies stress concentration and accelerates plastic zone propagation. From an engineering perspective, control measures for horizontal swelling zones should prioritize grouting reinforcement or buffer layer placement to mitigate lateral pressure-induced failure. For deep-buried high-stress sections, the tunnel vault’s support rigidity must be enhanced, and real-time monitoring of displacement variations on the swelling-affected side should be implemented to ensure long-term tunnel operational safety.
- (4)
- Research Limitations and Future Directions: The similar model tests in this study did not simulate the dynamic process of long-term groundwater seepage or the creep characteristics of surrounding rock, making it difficult to fully reflect the “slow swelling–long-term deformation” evolution pattern observed in actual engineering projects. The numerical simulations adopted homogenization assumptions, thus failing to fully account for the heterogeneous characteristics of expansive rocks (e.g., bedding planes, internal fissures). Furthermore, the parameter values in this study were highly dependent on field test data, limiting the applicability of the proposed method in regions without measured data. Subsequent studies are recommended to systematically investigate the influence of varying clay mineral contents (e.g., montmorillonite proportion) on swelling coefficients and moisture conductivity coefficients, thereby deepening the quantitative understanding of the “mineral composition–swelling characteristics” relationship.
Author Contributions
Conceptualization, J.Y. and Y.C.; methodology, P.L.; software, J.Y.; validation, J.Y., Y.C. and C.X.; investigation, J.Y.; data curation, J.Y. and Y.C.; writing—original draft preparation, J.Y. and Y.C.; writing—review and editing, P.L.; visualization, Y.C.; supervision, P.L. and M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 52578454). The financial support is greatly appreciated.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the National Natural Science Foundation of China (No. 52578454).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xie, H.P.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
- Zhao, Z.H.; Ma, Q.; Tan, Y.L.; Gao, X.J. Load transfer mechanism and reinforcement effect of segmentally yieldable anchorage in weakly consolidated soft rock. Simul. Soc. Mod. Sim. 2019, 95, 83–96. [Google Scholar] [CrossRef]
- Wang, F.; Xu, J.L.; Xie, J.L. Effects of arch structure in unconsolidated layers on fracture and failure of overlying strata. Int. J. Rock Mech. Min. Sci. 2019, 114, 141–152. [Google Scholar] [CrossRef]
- Madsen, F.T.; Fluckiger, A.; Hauber, L.; Jordan, P.; Voegtli, B. New Investigations on Swelling Rocks in the Belchen Tunnel, Switzerland. In Proceedings of the 8th ISRM Congress, Tokyo, Japan, 25–29 September 1995. [Google Scholar]
- Einstein, H.H. Suggested Method for Laboratory testing of argillaceous swelling rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 415–426. [Google Scholar]
- Butscher, C.; Huggenberger, P.; Zechner, E. Impact of tunneling on regional ground water flow and implications for swelling of clay–sulfate rocks. Eng. Geol. 2010, 117, 198–206. [Google Scholar] [CrossRef]
- Serafeimidis, K.; Anagnostou, G. On the time-development of sulphate hydration in anhydritic swelling rocks. Rock Mech. Rock Eng. 2013, 46, 619–634. [Google Scholar] [CrossRef]
- Parsapour, D.; Fahimifar, A. Prediction of swelling rocks strain in tunneling. Geotectonics 2016, 50, 336–346. [Google Scholar] [CrossRef]
- Fernández-Marchena, J.L.; Ollé, A. Microscopic analysis of technical and functional traces as a method for the use-wear analysis of rock crystal tools. Quat. Int. 2015, 424, 171–190. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, B.Y.; Chen, S.J.; Ren, M.Z. Surface collapse control under thick unconsolidated layers by backfilling strip mining in coal mines. Int. J. Rock Mech. Min. Sci. 2019, 113, 268–277. [Google Scholar] [CrossRef]
- Tang, Z.; Tolooiyan, A.; Mackay, R. Unconfined Expansion Test (UET) for measuring the tensile strength of organic soft rock. Comput. Geotech. 2017, 82, 54–66. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, B.; Li, X. Experimental research on shear creep properties of a swelling rock under different expansive states. Chin. J. Rock Mech. Eng. 2016, 35, 3734–3746. [Google Scholar]
- Parsapour, D.; Fahimifar, A. Semi-analytical solution for time-dependent deformations in swelling rocks around circular tunnels. Geosci. J. 2016, 20, 517–528. [Google Scholar] [CrossRef]
- Schadlich, B.; Marcher, T.; Schweiger, H. Application of a constitutive model for swelling rock to tunnelling. Geotech. Eng. J. SEAGS AGSSEA 2013, 44, 47–54. [Google Scholar]
- Isago, N.D.; Kawata, K.; Kusaka, A.; Ishimura, T. Long-term deformation of mountain tunnel lining and ground under swelling rock condition. Geomech. Tunn. 2015, 8, 380–386. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, Y.; Cheng, Z.; Cong, Z. Study on the Treatment Timing of Large Deformation of the Tunnel in Swelling Rock. MATEC Web Conf. 2018, 206, 01005. [Google Scholar] [CrossRef]
- Liu, G.Y.; Chen, Y.L.; Du, X.; Azzam, R. A fractional viscoplastic model to predict the time-dependent displacement of deeply buried tunnels in swelling rock. Comput. Geotech. 2021, 129, 103901. [Google Scholar] [CrossRef]
- Lu, A.H.; Mao, X.B. Numerical simulation on theory of humidity stress field. Chin. J. Rock Mech. Eng. 2002, 21, 2470–2473. [Google Scholar]
- Zeng, Z.Y.; Xu, B.S.; Hu, S.Q.; Chen, C. Numerical analysis of tunnel liner failure mechanism in expansive soil considering water-increased state. Rock Soil Mech. 2014, 35, 871–880. [Google Scholar]
- Liu, X.D.; Shotaro, Y.; Takashi, K. Hypoelastic-plastic-damage analysis of a tunnel in swelling rock mass. In Proceedings of the ISRM Regional Symposium—11th Asian Rock Mechanics Symposium, Beijing, China, 21–25 October 2021. [Google Scholar]
- Zhang, Y.T.; Huang, S.L.; Ding, X.L. Stress based safety evaluation of tunnel liners situated in swelling rock masses. In Proceedings of the ISRM Regional Symposium—11th Asian Rock Mechanics Symposium, Beijing, China, 21–25 October 2021. [Google Scholar]
- Yang, M.; Liu, N.F.; Li, N.; Xu, C.; Li, G.; Cao, M. Failure Characteristics and Treatment Measures of Tunnels in Expansive Rock Stratum. Front. Earth Sci. 2022, 9, 805378. [Google Scholar] [CrossRef]
- Feng, J.; Song, J.; Zhou, Y.; Duan, L. Study on the control effect of tunnel large deformation considering surrounding rock unloading expansion effect and support structure characteristics. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2025, 159, 159106475. [Google Scholar] [CrossRef]
- Fu, J.; Feng, J.; Li, B.; Zhang, J.; Jiang, H.; Wu, Y. Study on Evaluation and Control Measures of Large Deformation of Soft Rock Tunnels Considering Unloading Physical Expansion. Int. J. Civ. Eng. 2025, 23, 915–934. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, C.; Liu, G.; Wu, P.; Cao, P.; Zhang, H. The Influence About Coupled Initial Water Content and Local Expansion on Mechanical Properties and Deformation of the Tunnel in Mudstone. Indian Geotech. J. 2024, 55, 62–78. [Google Scholar] [CrossRef]
- Zhu, W.S.; Zhang, Q.B.; Zhu, H.H.; Li, Y.; Yin, J.-H.; Li, S.C.; Sun, L.F.; Zhang, L. Large-scale geomechanical model testing of an underground cavern group in a true three-dimensional (3-D) stress state. Can. Geotech. J. 2010, 47, 935–946. [Google Scholar] [CrossRef]
- Sun, X.M.; Chen, F.; He, M.C.; Gong, W.-L.; Xu, H.-C.; Lu, H. Physical modeling of floor heave for the deep-buried roadway excavated in ten degree inclined strata using infrared thermal imaging technology. Tunn. Undergr. Space Technol. 2017, 63, 228–243. [Google Scholar] [CrossRef]
- Zhu, W.S.; Li, Y.; Li, S.C.; Wang, S.; Zhang, Q. Quasi-three-dimensional physical model tests on a cavern complex under high in-situ stresses. Int. J. Rock Mech. Min. Sci. 2011, 48, 199–209. [Google Scholar]
- Yang, W.M.; Wang, M.X.; Zhou, Z.Q.; Li, L.; Yuan, Y.; Gao, C. A true triaxial geomechanical model test apparatus for studying the precursory information of water inrush from impermeable rock mass failure. Tunn. Undergr. Space Technol. 2019, 93, 103078. [Google Scholar] [CrossRef]
- Sun, X.M.; Chen, F.; Miao, C.Y.; Song, P.; Li, G.; Zhao, C.; Xia, X. Physical modeling of deformation failure mechanism of surrounding rocks for the deep-buried tunnel in soft rock strata during the excavation. Tunn. Undergr. Space Technol. 2018, 74, 247–261. [Google Scholar] [CrossRef]
- Miao, X.X.; Yang, C.Y.; Cheng, Z.D. Humidity Stress Field Theory in Swelling Rock Mass. Rock Soil Mech. 1993, 14, 49–55. [Google Scholar]
- Li, P.; Chen, Y.; Huang, J.; Wang, X.; Liu, J.; Wu, J. Design principles of prestressed anchors for tunnels considering bearing arch effect. Comput. Geotech. 2023, 156, 105307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).