Abstract
Objectives: This study aimed to compare the biomechanical effects of Ballista Spring and Elastic Thread systems on impacted maxillary canines using three-dimensional finite element analysis (FEA). Materials and Methods: Finite element models were constructed from CBCT images of a human maxilla, incorporating cortical bone, spongy bone, teeth, and periodontal ligament. Two orthodontic force application methods were simulated: Ballista Spring (0.016-inch stainless steel) and Elastic Thread (0.25 mm medical-grade latex). Both systems delivered a force of 150 g to the impacted canine. Stress distribution and initial displacement patterns were analyzed using ANSYS Workbench. Results: The Ballista Spring generated a more uniform stress distribution across the periodontal ligament and cortical bone, with a maximum von Mises stress of 0.0042 MPa. The impacted canine exhibited an initial displacement of 0.015 μm, primarily in the vertical and distal directions, indicating a controlled movement path. In contrast, the Elastic Thread showed a more concentrated stress pattern with a maximum von Mises stress of 0.0035 MPa, and the impacted canine experienced 0.013 μm of displacement, accompanied by greater lateral deviation and buccal tipping of the adjacent teeth. The Ballista Spring induced higher stress levels on anchorage teeth—particularly the first molars and premolars—while the Elastic Thread exerted more localized stress around the impacted canine and adjacent structures. All observed stress values remained within physiological thresholds, indicating no immediate risk of tissue damage. Conclusions: Both systems were effective in facilitating the eruption of the impacted canines. However, the Ballista Spring provided more favorable stress distribution and controlled displacement, making it suitable for complex cases requiring anchorage preservation. The Elastic Thread, while less biomechanically efficient, remained a practical and cost-effective alternative in patients with adequate periodontal support.
1. Introduction
Maxillary canines are among the most strategically significant teeth in the human dentition due to their roles in both esthetics and function. Positioned at the junction of the anterior and posterior segments of the dental arch, they contribute to the maintenance of arch integrity, distribution of occlusal forces during mastication, and guidance during lateral mandibular movements. Additionally, their prominent location in the smile line makes them crucial for facial harmony and midfacial aesthetics [1,2,3].
Despite their importance, the eruption pathway of maxillary canines is anatomically complex and prolonged. These teeth follow the longest and most tortuous eruption trajectory, often navigating around the roots of adjacent lateral incisors and first premolars before reaching their final position in the arch [4,5]. Consequently, they are the second most frequently impacted teeth after third molars, with a reported prevalence ranging from 0.9% to 2.2% in the general population—occurring more frequently in females than in males [6,7,8].
Etiological factors contributing to canine impaction include genetic predisposition, tooth size–arch length discrepancies, the presence of supernumerary teeth, premature loss, or prolonged retention of deciduous canines and systemic conditions such as cleft lip and palate [9]. Impactions may occur labially or palatially, with the latter being more common in populations of European descent. While labial impactions are often associated with space deficiency, palatal impactions may occur even when space is adequate, suggesting a genetic component [10,11].
If left untreated, impacted canines can cause a variety of complications, including root resorption of adjacent teeth, displacement of adjacent teeth, cyst formation, infection, and functional malocclusion. Therefore, timely diagnosis and effective intervention are critical for preserving dental and periodontal health [12].
Surgical exposure followed by orthodontic traction remains the standard approach for managing impacted maxillary canines. Various force delivery systems have been developed to facilitate their eruption, including the Ballista Spring and Elastic Thread techniques—each offering distinct biomechanical characteristics and clinical advantages [13,14].
The Ballista Spring is a custom-bent 0.016-inch stainless steel spring anchored on posterior teeth and designed to deliver light, continuous, and directional forces to the impacted canine. It enables precise control over the force vector, promoting gradual and controlled tooth movement with minimal damage to surrounding structures. However, this method may increase stress on posterior anchorage units, potentially necessitating the use of additional stabilization such as temporary anchorage devices (TADs) [15].
In contrast, the Elastic Thread method employs a medical-grade latex elastic attached between the impacted canine and a rigid arch wire. Its simplicity and cost-effectiveness have made it widely used in clinical practice. Nevertheless, the forces generated by elastic threads are less controlled and more variable, potentially leading to excessive stress on the periodontal ligament (PDL) and undesired movements of adjacent teeth [16,17].
Finite element analysis (FEA) has emerged as a valuable computational tool in orthodontics, allowing detailed evaluation of stress distribution and tooth displacement in complex clinical scenarios. FEA provides a non-invasive method to simulate orthodontic mechanics and assess their effects on hard and soft tissues under various loading conditions [18].
This study aimed to compare the biomechanical performance of the Ballista Spring and Elastic Thread techniques in the traction of impacted maxillary canines using three-dimensional finite element analysis. The Ballista Spring was chosen as it represents a spring-based system capable of delivering controlled and directional forces, while the Elastic Thread was included as a commonly used, simple, and cost-effective elastic-based system in clinical orthodontic practice. By contrasting these two biomechanically distinct yet widely applied methods, the study seeks to provide clinicians with evidence-based guidance, inform clinical decision-making, and optimize treatment strategies for canine impaction.
2. Materials and Methods
2.1. Model Construction
Three-dimensional finite element (FE) models of the maxilla, teeth, periodontal ligament (PDL), cortical bone, and spongy bone were constructed based on cone-beam computed tomography (CBCT) data from a clinically representative human subject. The impacted canine was modeled in a palatal position at an angle of 25° to the midline, reflecting the most common clinical presentation of impaction. Anatomical segmentation was performed using Mimics software, version 24.0, and meshing was completed using tetrahedral elements in ANSYS 2025 R2 (version 25.2) Workbench (Figure 1).
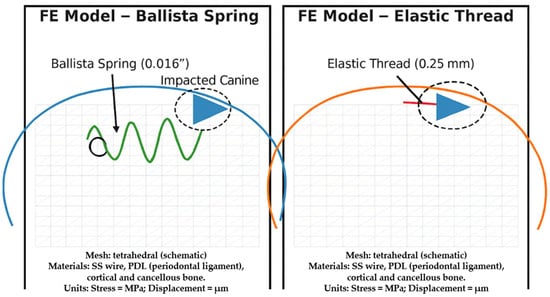
Figure 1.
Finite element (FE) models of the maxilla with an impacted canine, comparing two orthodontic traction methods: Ballista Spring (0.016″) and Elastic Thread (0.25 mm). The geometry, mesh schematic, and appliance positioning are shown. Both models used tetrahedral meshes (schematic illustration). Materials included stainless steel (SS) wire, periodontal ligament (PDL), cortical bone, and cancellous bone. Results are expressed as stress (MPa) and displacement (μm).
2.2. Appliance Design and Force Application
Two orthodontic force systems were simulated:
- Ballista Spring: Constructed from 0.016-inch stainless steel wire and designed with an occlusal loop to apply a controlled vertical and distal force. The spring extended from the first molar region, engaging the impacted canine via a bonded button.
- Elastic Thread: A 0.25-mm medical-grade latex elastic thread was tied between the canine button and the stainless-steel arch wire. For the elastic thread, hyperelastic properties were modeled using a Mooney–Rivlin formulation to replicate its non-linear stress–strain behavior. The initial force of 150 g was applied by pre-stretching the elastic element to the corresponding elongation, which was verified experimentally with a calibrated force gauge. This approach allowed the model to simulate realistic initial force delivery, while the hyperelastic material model accounted for force decay with deformation, which is consistent with the clinical behavior of elastic threads.
The Ballista Spring was constructed using 0.016-inch stainless steel wire. This dimension was chosen as it offers a favorable compromise between flexibility and stiffness, allowing controlled and continuous force application on the impacted canine. A thinner 0.014-inch wire, while more flexible, may provide insufficient control over force vectors, whereas a thicker 0.018-inch wire increases stiffness, potentially generating excessive force and stress on the anchorage teeth. The 0.016-inch dimension has been widely recommended in the literature and is commonly used in clinical practice for Ballista Spring construction, thereby ensuring both biomechanical accuracy and clinical applicability of the simulation model [13,19,20].
Both systems applied an orthodontic force of 150 g. All teeth were bonded with MBT prescription brackets (0.022 × 0.028-inch slot) and engaged with a 0.019 × 0.025-inch stainless steel arch wire. A transpalatal arch (TPA) constructed from 0.9-mm stainless steel wire connected the first molars bilaterally to enhance anchorage stability. A visual overview of the methodological steps was shown in Figure 2.
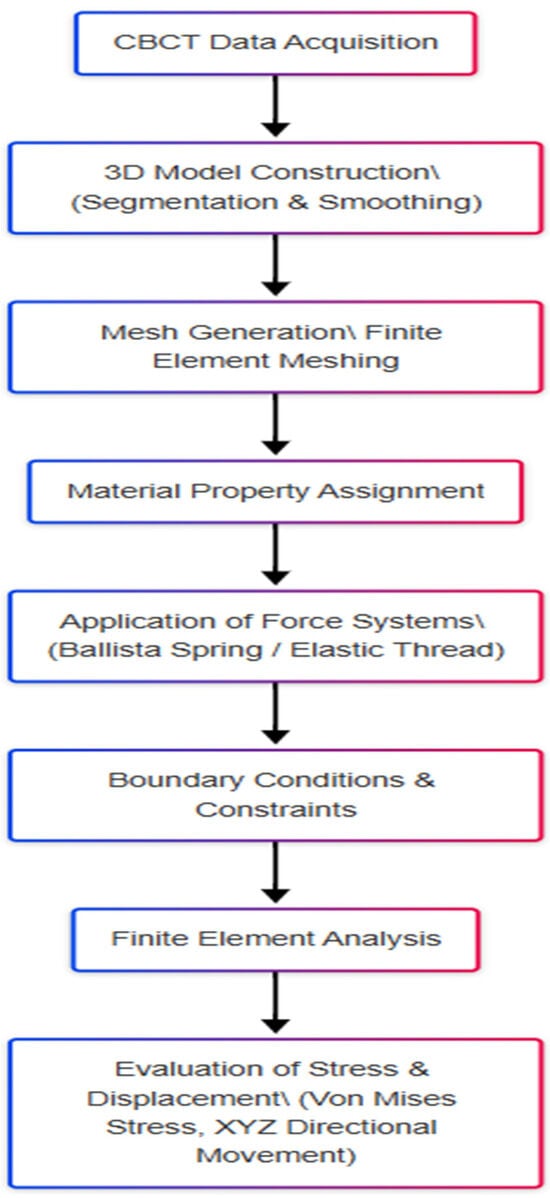
Figure 2.
Flowchart of the study design and finite element analysis workflow.
2.3. Finite Element Modeling and Mesh Generation
The geometric structures of bone and teeth were reconstructed based on the Sobotta Human Anatomy Atlas and refined with data from a Steinbichler 3D optical scanner (Steinbichler Optotechnik GmbH, Neubeuern, Germany). Point cloud data were processed in CATIA V5 (Dassault Systèmes, France) software to generate precise boundary meshes. The PDL was modeled as a 0.2-mm offset layer around the root surfaces. Boolean operations were used to simulate the tooth sockets within the bone.
Each component was meshed using 4-node tetrahedral elements to capture stress gradients and displacement patterns accurately. The final mesh included both cortical and cancellous bone layers, as well as bracket, wire, TPA, elastic thread, and button components.
Contact interactions in the model were defined as follows: bonded contacts were established between the tooth root and PDL, as well as between the PDL and alveolar bone, to simulate physiological continuity. Between the brackets, arch wire, and auxiliary components, frictionless sliding contacts were applied to replicate clinical conditions. In addition, a mesh convergence test was conducted by progressively refining the element size until changes in maximum von Mises stress were less than 5%. This procedure confirmed that the final mesh was sufficiently fine to ensure stable and accurate stress and displacement results.
2.4. Material Properties
All structures were modeled as linearly elastic, homogeneous, and isotropic materials, except for the latex elastic, which was modeled with hyperelastic properties. The mechanical properties were defined in Table 1. Cortical and spongy bone were modeled with Young’s moduli of 13.7 GPa and 1.37 GPa, respectively, and a Poisson’s ratio of 0.30. The periodontal ligament (PDL) was assigned a modulus of 0.068 GPa and a Poisson’s ratio of 0.45 to replicate its viscoelastic cushioning effect. Stainless-steel components (arch wire and Ballista Spring) were modeled with a modulus of 200 GPa and a Poisson’s ratio of 0.29 (Table 1).

Table 1.
Mechanical properties of materials used in finite element modeling.
2.5. Boundary Conditions and Load Application
The base of the maxilla was fixed in all directions to simulate anatomical stability. A vertical and distal-directed force vector was applied to the bracket attached to the impacted canine. To simulate physiological tooth mobility, shared displacement constraints were assigned to the nodes at the PDL–root interface, allowing controlled displacement of the root within the alveolar socket under applied forces. This setup reproduced the natural cushioning effect of the PDL and ensured realistic load transfer to the alveolar bone. The initial displacement and von Mises stress distributions were calculated for: (1) the impacted maxillary canine and its surrounding tissues, (2) the anchorage teeth (first molars and premolars) and adjacent periodontal structures, and (3) the directional displacement of teeth in the X (transversal), Y (sagittal), and Z (vertical) axes.
2.6. Statistical Analysis
Since the finite element analysis was based on a single 3D model without repeated simulations or patient-derived datasets, statistical analysis was not applicable. Instead, a descriptive comparative evaluation of the stress and displacement values was performed between the two systems. All finite element simulations were performed on a workstation equipped with an Intel i7 processor (2.8 GHz), 32 GB RAM, and 1 TB hard drive, using the ANSYS Mechanical APDL environment under Windows 7 Pro.
3. Results
All descriptive stress and displacement values are presented in Table 2. In addition, a linear graph was created to compare von Mises stress values at cortical bone and periodontal ligament sites between the Ballista Spring and Elastic Thread models (Figure 3).

Table 2.
Descriptive comparison of Ballista Spring and Elastic Thread models (von Mises stress and displacement values).
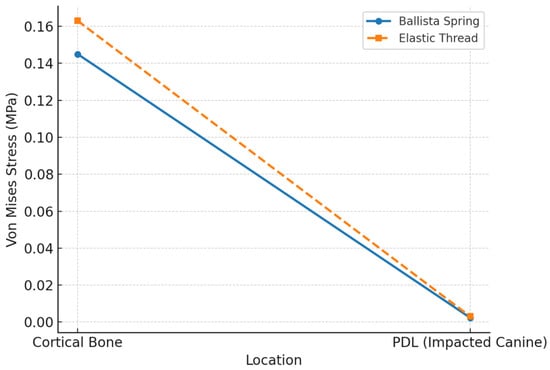
Figure 3.
Von Mises stress (MPa) at different locations.
Baseline movements observed in the X (transverse), Y (vertical), and Z (sagittal) planes in the impacted canine and anchorage teeth were evaluated, alongside the stress and strain distribution in the impacted canine, anchorage teeth, and surrounding periodontal structures following the activation of the applied mechanics. In the Ballista Spring model, the highest von Mises stress in the maxillary cortical bone was measured at 0.145 MPa, localized in the mesiopalatal region of the left first premolar. Additional elevated stress levels were recorded around the second premolar and molar teeth, with values ranging between 0.081 MPa and 0.113 MPa (Figure 4).
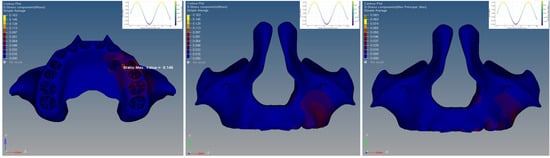
Figure 4.
Von Mises stress distribution in the cortical bone in the Ballista Spring model.
In the periodontal ligament (PDL), the peak von Mises stress was 0.036 MPa in the buccal cervical region of the left first premolar. Stress levels initially decreased toward the second premolar, then increased again near the first molar. The highest stress in the PDL of the impacted canine was 0.0024 MPa, recorded at the distobuccal root surface (Figure 5).
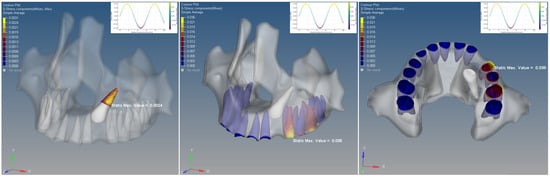
Figure 5.
Von Mises values of the periodontal ligament in the Ballista Spring model.
In terms of displacement, distinct patterns were observed across all three spatial planes in the Ballista Spring model. On the X plane (transverse), the greatest displacement occurred at the crown of the left first premolar, which moved 43 × 10−5 mm in the palatal direction. Posterior to this tooth, the displacement direction reversed toward the buccal side, with the second premolar displacing 5 × 10−5 mm and the first molar 29 × 10−5 mm. The impacted canine tooth exhibited a buccal displacement of 96 × 10−6 mm at the crown, with diminishing displacement toward the root. On the Y plane (vertical), the left first premolar demonstrated a combination of buccal extrusion (32 × 10−5 mm) and palatal intrusion (17 × 10−5 mm). The impacted canine exhibited 18 × 10−5 mm of mesial crown extrusion, with the crown displaying greater mobility than the root, a pattern consistent with orthodontic force application mechanics. On the Z plane (sagittal), the largest displacement was observed at the mesiopalatal aspect of the first premolar, measuring 34 × 10−5 mm, and shifted posteriorly in direction. While displacement gradually decreased from the first to the second premolar, it increased again in the first molar. The impacted canine crown exhibited mesial displacement of 95 × 10−6 mm, with reduced movement observed at the apical level (Figure 6).
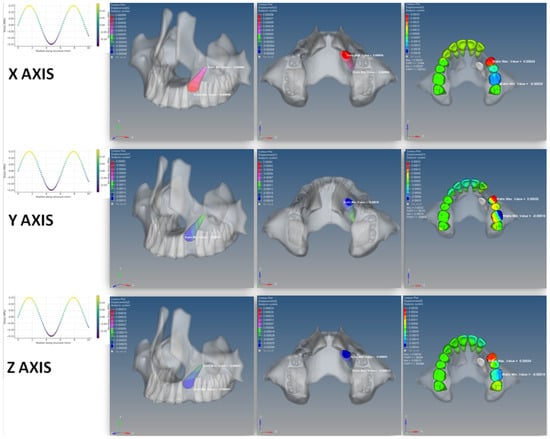
Figure 6.
Initial displacement vectors of the impacted canine and anchorage teeth in the Ballista Spring model.
In the Elastic Thread model, the highest von Mises stress in the cortical bone was 0.163 MPa, observed in the palatal region of the left first premolar. Significant stress was also noted around the left central and lateral incisors, the first and second premolars, and especially in the crestal area adjacent to the impacted canine. Stress gradually decreased toward the zygomatic process buccally and sutura palatina media palatially (Figure 7).

Figure 7.
Von Mises stress distribution in the cortical bone in the Elastic Thread model.
The PDL stress peaked at 0.021 MPa on the mesial surface of the left first premolar. Stress values declined gradually from the left lateral incisor to the right canine anteriorly, and from the first premolar distally. The highest PDL stress in the impacted canine was 0.0031 MPa, localized at the apex of the root (Figure 8).
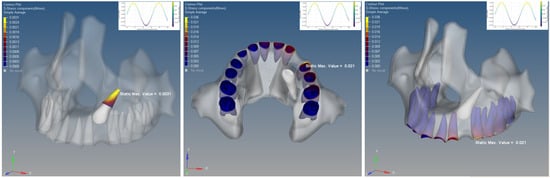
Figure 8.
Von Mises stress distribution in the periodontal ligament in the Elastic Thread model.
Regarding displacement in the Elastic Thread model, distinct movement patterns were observed across all three spatial planes. On the X plane (transverse), the greatest displacement was noted at the crown of the left lateral incisor, which shifted 35 × 10−5 mm distally. Most maxillary anterior and left posterior teeth exhibited medial movement toward the impacted canine. The impacted canine crown displayed a buccal displacement of 57 × 10−6 mm, which progressively decreased toward the root. On the Y plane (vertical), the left central incisor demonstrated 17 × 10−5 mm of mesial extrusion and 3 × 10−5 mm of distal intrusion. In general, anterior teeth showed intrusion on distal surfaces and extrusion on mesial surfaces, while posterior teeth exhibited the opposite pattern—mesial intrusion and distal extrusion. The impacted canine showed 11 × 10−5 mm of mesial crown extrusion, consistent with the direction of force application. On the Z plane (sagittal), the distoincisal edge of the left central incisor displaced 35 × 10−5 mm palatially. The anterior teeth moved palatially, while the posterior teeth shifted mesially. The crown of the impacted canine exhibited anterior displacement of 17 × 10−6 mm, while the root showed movement in the opposite direction, suggesting rotational stress around the tooth’s long axis (Figure 9).
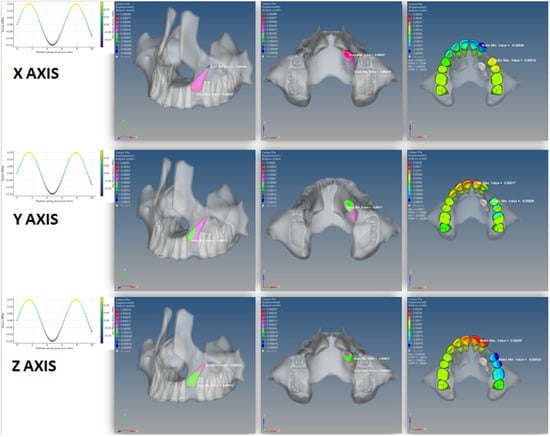
Figure 9.
Initial displacement vectors of the impacted canine and adjacent teeth in the Elastic Thread model.
4. Discussion
In this study, we compared the biomechanical effects of two commonly used traction methods—Ballista Spring and Elastic Thread—on impacted maxillary canines using three-dimensional finite element analysis (FEA). The stress distribution and displacement patterns observed in each model provided critical insights into the mechanical behavior of surrounding periodontal structures and anchorage teeth during initial force application. The findings demonstrated that while both methods were effective in generating sufficient forces for tooth movement, they differed significantly in terms of stress concentration, displacement direction, and effect on anchorage units. The Ballista Spring model exhibited more controlled and directional movement of the impacted canine, with greater extrusion and mesial displacement, particularly along the vertical and sagittal planes. In contrast, the Elastic Thread model resulted in more diffuse and less controlled movement, along with higher stress concentrations around the anterior segment, suggesting a greater potential for undesired tipping or deformation of the arch form.
The Ballista Spring system demonstrated superior control over the directionality and magnitude of force, particularly favoring extrusion and mesiodistal movement of the impacted canine in a predictable trajectory. This is consistent with its segmental design, which enables localized force delivery without involving the full arch [13,14,19]. In addition, the Ballista Spring was considered more relevant than NiTi coil springs, as NiTi coils—although capable of producing light continuous forces—provide less adaptability in vector control and typically require integration with full-arch mechanics, which can transmit undesirable side effects to anchorage teeth. In contrast, the Ballista Spring allows clinicians to customize the force direction and magnitude in a segmental approach, offering superior biomechanical versatility in impacted canine traction. The greater displacement values on all three planes in the Ballista Spring model—especially the vertical (Y) and sagittal (Z) planes—suggest a more efficient initial activation phase [20]. However, this method also concentrated higher stress on the anchorage teeth, notably in the mesiopalatal regions of the premolars and molars, raising concerns about potential root resorption or anchorage loss if auxiliary support such as TADs or reinforced TPAs are not utilized [21,22]. To address this, preventive reinforcement strategies such as the use of transpalatal arches (TPAs), reinforced stainless steel arch wires, or temporary anchorage devices (TADs) are strongly recommended to preserve anchorage and minimize unwanted posterior tooth movement during impacted canine traction.
In contrast, the Elastic Thread model produced lower displacement values in the impacted canine but resulted in greater displacement in the anterior segment, indicating force diffusion through the arch wire. The broader stress distribution in the cortical bone and periodontal ligament, particularly in the anterior teeth, may reflect the continuous and less focused nature of force application via elastic materials [23,24]. Although the peak von Mises values were higher in the cortical bone for the Elastic Thread model, the pattern of stress was more scattered. This diffuse loading is associated with increased tipping forces and potential deformation of the dental arch, especially in cases where the anterior teeth serve as anchorage units [25,26]. These findings align with previous studies indicating that elastic-based systems, while easy to apply and cost-effective, may compromise biomechanical efficiency and anchorage integrity in complex cases [23,27].
From a clinical standpoint, the selection between Ballista Spring and Elastic Thread should be guided by multiple factors, including periodontal health, anchorage capacity, tooth position, and the degree of control required during canine traction [28,29]. The Ballista Spring appears more suitable in scenarios that demand precise tooth movement, especially in patients with complex impactions, thin biotypes, or limited anchorage options [14]. Its segmental design minimizes the involvement of anterior teeth, preserving incisor inclination and maintaining arch integrity [30]. However, clinicians should be cautious of the elevated stress levels on molars and premolars, which may necessitate the reinforcement of anchorage via transpalatal arches or temporary anchorage devices (TADs) to prevent unwanted tipping or extrusion of posterior teeth [20,31].
In contrast, the Elastic Thread may be advantageous in simpler cases, where anchorage is abundant and precision is not as critical. Its ease of use, flexibility, and lower cost make it an attractive option in routine orthodontic practice [27,32]. Nevertheless, the broader distribution of forces and increased stress on anterior structures observed in this study raise concerns about loss of arch form, uncontrolled tipping, and iatrogenic effects on the periodontal ligament, particularly if force magnitude is not meticulously calibrated [23]. Preventive strategies—such as the use of thicker arch wires, open coil springs, or limiting the involvement of the anterior segment—may help reduce these adverse effects [24].
The use of finite element analysis (FEA) in this study offered a significant advantage by allowing a non-invasive, three-dimensional, and quantifiable comparison of stress and displacement patterns under identical loading conditions [33,34]. Unlike clinical trials, where biological variability and patient factors introduce confounders, FEA provides a controlled computational environment to analyze mechanical behavior with high precision. Although the assumptions of linearity, isotropy, and material homogeneity may slightly diverge from in vivo conditions, the method remains invaluable for preclinical evaluation, especially when comparing treatment modalities or appliance designs [35].
The findings of this study are consistent with prior research investigating the biomechanical implications of orthodontic force application on impacted canines. For instance, Yadav et al. demonstrated that segmental mechanics such as Kilroy springs provided more consistent and controlled forces compared to elastic chains or ligature wires, minimizing adverse effects on anchorage teeth [20]. Nakandakari et al. reported favorable outcomes using segmental TMA arches, highlighting the importance of force vector directionality and control in reducing unnecessary tipping forces [30]. The present study supports these observations, showing that the Ballista Spring—by offering focused and segmental force delivery—achieved more desirable displacement trajectories with less disruption to the overall arch form, albeit at the cost of increased posterior stress.
On the other hand, the stress values recorded in the Elastic Thread model were in line with those reported by Spuntarelli et al., who noted that although elastic threads provide sufficient force for eruption, they often result in greater tipping moments and undesirable anterior tooth movement if anchorage is not adequately reinforced [24]. These comparisons further validate the clinical relevance of the finite element results observed in the current study.
Compared to previously published studies that investigated the biomechanics of canine traction, the present study offers several distinctive contributions. While earlier works—such as those by Yadav et al. and Silva et al.—focused on the mechanical behavior of a single traction method or assessed force systems in simplified two-dimensional models [20,23], our study is among the few that perform a direct three-dimensional finite element comparison between Ballista Spring and Elastic Thread systems under identical anatomical and loading conditions. Furthermore, unlike prior simulations that primarily reported stress values without correlating them with displacement directionality, this study integrates both von Mises stress distribution and three-dimensional tooth displacement vectors across the cortical bone, periodontal ligament, and impacted canine structures, offering a more comprehensive biomechanical interpretation. In addition, the use of two different force systems on a model simulating a unilateral canine impaction with full-arch dentition, including anchorage effects, provides clinically realistic insights that go beyond the simplified models or in vitro extrapolations often found in the earlier literature [24,36]. As such, this study not only confirms some of the biomechanical trends previously reported but also extends the current understanding by demonstrating how force delivery method can alter the stress–displacement balance in both the target and anchorage teeth.
Limitations of the Study
This study also had some limitations. The FEA models used in this study assumed that all materials—bone, PDL, and teeth—were homogeneous, isotropic, and linearly elastic, which may not fully replicate biological variability in vivo. Furthermore, most materials in this study—including bone, teeth, and PDL—were modeled as homogeneous, isotropic, and linearly elastic, which simplifies but does not fully replicate their complex anisotropic and viscoelastic nature. In addition, the simulations were conducted on a single anatomical model, without reflecting patient-specific variability in bone density, root morphology, or arch size. Additionally, time-dependent behavior such as viscoelasticity of the PDL and biological responses (e.g., bone remodeling, root resorption) could not be simulated. While these assumptions improve computational feasibility, they inevitably limit the direct clinical translation of the findings. As such, while the trends observed offer meaningful biomechanical guidance, they must be interpreted within the limits of computational modeling. Future studies should aim to expand on these findings by incorporating patient-specific CBCT-based models, conducting parametric variations (e.g., different force magnitudes or angles), and exploring longitudinal simulations that mimic the sequence of tooth movement over time. Moreover, validation of the FEA predictions with clinical trials or in vitro studies could bridge the gap between simulation and real-world outcomes, thereby enhancing clinical decision-making in the management of impacted canines.
It should also be noted that the results of this study are based on a unilateral palatal impaction at a 25° angulation. Different impaction positions (e.g., labial vs. palatal) or angulations (mild vs. severe) could significantly alter stress distribution and displacement vectors, as well as anchorage requirements. Therefore, the findings presented here should be interpreted within this context, and future simulations incorporating varying impaction scenarios would provide more generalizable insights.
5. Conclusions
In conclusion, this finite element analysis revealed that the Ballista Spring and Elastic Thread systems exhibit distinct biomechanical behaviors in the traction of impacted maxillary canines. The Ballista Spring provided more focused force delivery, resulting in greater and more controlled displacement of the impacted canine along all three spatial planes, particularly in the vertical and sagittal axes. However, this came at the expense of higher stress accumulation in the anchorage teeth, necessitating careful planning and reinforcement in clinical application. In contrast, the Elastic Thread induced diffuse stress patterns and less predictable tooth movement, especially in the anterior region, raising concerns about anchorage loss and unintended arch deformation.
From a clinical perspective, the Ballista Spring may be better suited for cases requiring high precision and segmental control, particularly in complex impactions or patients with limited anchorage. Meanwhile, the Elastic Thread may be appropriate in low-risk cases with favorable anatomy and sufficient anchorage. This study emphasizes the importance of biomechanical customization in orthodontic treatment planning and supports the use of finite element modeling as a valuable tool for preclinical evaluation of force systems.
Author Contributions
Conceptualization, A.F.K. and A.G.; methodology, A.F.K.; software, A.F.K.; validation, A.F.K., A.G. and O.D.O.; formal analysis, A.F.K.; investigation, A.F.K.; resources, A.G.; data curation, A.F.K.; writing—original draft preparation, A.F.K.; writing—review and editing, A.G. and O.D.O.; visualization, A.F.K.; supervision, A.G.; project administration, A.F.K.; funding acquisition, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Gaziantep University Research Projects (Grant number DHF.UT.17.04) and was produced from the thesis of Ali Furkan Karakoyunlu.
Institutional Review Board Statement
This study involved a computer-based finite element simulation using digital anatomical data and did not include any procedures involving human participants or animals. Therefore, approval by an Institutional Review Board (IRB) and informed consent were not required in accordance with local and international ethical guidelines. The study was conducted in compliance with the principles of the Declaration of Helsinki.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Oliveira, T.C.P.; Copello, F.M.; Paes-Souza, S.A.; Castro, A.C.R.; Nojima, L.I.; Goncalves Nojima, M.D.C. Influence of the maxillary dimensions and lateral incisor anatomy on the palatal impaction of maxillary permanent canines: A three-dimensional case-control study. Int. Orthod. 2023, 21, 100804. [Google Scholar] [CrossRef]
- Sokmen, T.; Bagci, N.; Balos Tuncer, B. Buccolingual inclination of posterior dentition in maxillary impacted canine patients using quadrant analysis—A cone-beam computed tomographic study. BMC Oral Health 2024, 24, 1012. [Google Scholar] [CrossRef]
- Gudeleviciute, I.; Spaicyte, N.; Smailiene, D. Skeletal and dental maxillary morphological characteristics in patients with impacted canines: Systematic review and meta-analysis. Eur. J. Orthod. 2023, 45, 832–841. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Bi, M.; Yang, H.; He, X.; Wang, X.; Chen, Z.; Ji, F. Epidemiological and imaging characteristics of impacted maxillary incisors and effect on root development. Sci. Rep. 2025, 15, 13049. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.K.; Kim, S.H.; Kim, Y.I.; Kim, S.S.; Park, S.B.; Choi, D.S.; Kim, H.J.; Kim, K.A.; Lee, M.H.; Choi, S.H.; et al. Prevalence and characteristics of impacted teeth in Korean orthodontic patients at ten university dental hospitals. Korean J. Orthod. 2025, 55, 234–241. [Google Scholar] [CrossRef]
- Dekel, E.; Nucci, L.; Weill, T.; Flores-Mir, C.; Becker, A.; Perillo, L.; Chaushu, S. Impaction of maxillary canines and its effect on the position of adjacent teeth and canine development: A cone-beam computed tomography study. Am. J. Orthod. Dentofac. Orthop. 2021, 159, e135–e147. [Google Scholar] [CrossRef]
- Pineda-Mendez, A.; Aliaga-Del Castillo, A.; Rodriguez-Cardenas, Y.A.; Ruiz-Mora, G.A.; Dutra, V.; Arriola-Guillen, L.E. Frequency of odontogenic lesions in patients with impacted maxillary canines and the association with impaction characteristics. Dent. Med. Probl. 2025, 62, 479–485. [Google Scholar] [CrossRef]
- Al-Salmany, L.H.A.; Hussein, L.K.; Altaee, Z.H. Impacted canine prevalence, localization, and related etiological factors among orthodontic sample of Fallujah city. J. Orthod. Sci. 2025, 14, 15. [Google Scholar] [CrossRef]
- Papageorgiou, S.N.; Seehra, J.; Cobourne, M.T.; Kanavakis, G. Does Current Evidence Support the Discussion Around the Guidance Theory? A Systematic Review and Meta-Analysis on the Association Between Maxillary Lateral Incisor Agenesis and Displacement or Impaction of the Permanent Canine. Orthod. Craniofac. Res. 2025, 28, 312–323. [Google Scholar] [CrossRef]
- Philip-Alliez, C.; Le Gall, M. Prophylaxis of impacted canines: Prevention, diagnosis, and early management. L’Orthodontie Française 2025, 96, 79–104. [Google Scholar] [CrossRef]
- Araujo, V.Z.; Heckmann, S.; Araujo, F.B.; Casagrande, L.; Ziegelmann, P.K.; Araujo, E.A.; Marques, L.S.; Lenzi, T.L. Is there a better interceptive treatment for unerupted palatally displaced canines? A network meta-analysis. Braz. Oral Res. 2023, 36, e119. [Google Scholar] [CrossRef]
- Schroder, A.G.D.; Guariza-Filho, O.; de Araujo, C.M.; Ruellas, A.C.; Tanaka, O.M.; Porporatti, A.L. To what extent are impacted canines associated with root resorption of the adjacent tooth?: A systematic review with meta-analysis. J. Am. Dent. Assoc. 2018, 149, 765–777.e8. [Google Scholar] [CrossRef] [PubMed]
- Baser, E.N.; Akar, N.K.; Sayar, G. Effects of Ballista and Kilroy Springs on Palatally Impacted Canines: A Finite Element Model Analysis. Turk. J. Orthod. 2023, 36, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Zogakis, I.P.; Anagnostou, C.; Ioannidou, I.; Chaushu, S.; Papadopoulos, M.A. A Comparison of Different Biomechanical Systems for the Orthodontic Treatment of Palatally Impacted Canines. Bioengineering 2025, 12, 267. [Google Scholar] [CrossRef]
- Marinelli, G.; Inchingolo, A.M.; Inchingolo, A.D.; Ferrante, L.; Avantario, P.; Campanelli, M.; Palermo, A.; Inchingolo, F.; Dipalma, G. Temporary Anchorage Devices in Clear Aligner Therapy: A Systematic Review. Bioengineering 2025, 12, 531. [Google Scholar] [CrossRef]
- Waremani, A.S.; Ahmed, N. Effects of Mandibular Canine Intrusion Obtained Using Cantilever Versus Bone Anchorage: A Comparative Finite Element Study. Cureus 2022, 14, e27548. [Google Scholar] [CrossRef]
- Pinho, L.C.; Santos, C.; Fernandes, M.H.; Colaco, B. Canine periodontal ligament stem cells as a tool for periodontal regeneration. Res. Vet. Sci. 2025, 193, 105787. [Google Scholar] [CrossRef]
- Nazeri, A.; Castillo, J.A., Jr.; Ghaffari-Rafi, A. Impact of Molar Distalization with Clear Aligners on Periodontal Ligament Stress and Root Resorption Risk: A Systematic Review of 3D Finite Element Analysis Studies. Dent. J. 2025, 13, 65. [Google Scholar] [CrossRef]
- Verma, S.; Singh, S.P.; Verma, R.K.; Kumar, V.; Singh, S.; Bhupali, N.R. Success rate, treatment duration, and pain perception in the management of palatally impacted canines using the K9 and Ballista spring: A randomized clinical trial. Angle Orthod. 2023, 93, 33–40. [Google Scholar] [CrossRef]
- Yadav, S.; Chen, J.; Upadhyay, M.; Jiang, F.; Roberts, W.E. Comparison of the force systems of 3 appliances on palatally impacted canines. Am. J. Orthod. Dentofac. Orthop. 2011, 139, 206–213. [Google Scholar] [CrossRef]
- Inchingolo, F.; Inchingolo, A.; Cardarelli, F.; Settanni, V.; Piras, F.; Riccaldo, L.; Carpentiere, V.; Ceci, S.; Ferrante, L.; Palermo, A. Impacted Teeth and Temporary Anchorage Devices, A Modern Approach: Systematic Review and Clinical Cases. Eur. J. Musculoskelet. Dis. 2024, 13, 65–82. [Google Scholar]
- Oğuz, F.; Özden, S.; Cicek, O. Distalization Methods for Maxillary Molars Utilizing Temporary Anchorage Devices (TADs): A Narrative Review. Appl. Sci. 2024, 14, 1333. [Google Scholar] [CrossRef]
- Silva, A.C.; Capistrano, A.; Almeida-Pedrin, R.R.; Cardoso, M.A.; Conti, A.C.; Capelozza, L.F. Root length and alveolar bone level of impacted canines and adjacent teeth after orthodontic traction: A long-term evaluation. J. Appl. Oral Sci. 2017, 25, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Spuntarelli, M.; Cecchetti, F.; Arcuri, L.; Testi, D.; Melone, P.; Bigelli, E.; Germano, F. Combined orthodontic-surgical approach in the treatment of impacted maxillary canines: Three clinical cases. Oral Implantol. 2015, 8, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Mosavar, A.; Ziaei, A.; Kadkhodaei, M. The effect of implant thread design on stress distribution in anisotropic bone with different osseointegration conditions: A finite element analysis. Int. J. Oral Maxillofac. Implant. 2015, 30, 1317–1326. [Google Scholar] [CrossRef] [PubMed]
- Alemayehu, D.B.; Jeng, Y.R. Three-Dimensional Finite Element Investigation into Effects of Implant Thread Design and Loading Rate on Stress Distribution in Dental Implants and Anisotropic Bone. Materials 2021, 14, 6974. [Google Scholar] [CrossRef]
- Buchmann, N.; Senn, C.; Ball, J.; Brauchli, L. Influence of initial strain on the force decay of currently available elastic chains over time. Angle Orthod. 2012, 82, 529–535. [Google Scholar] [CrossRef]
- Raghav, P.; Singh, K.; Munish Reddy, C.; Joshi, D.; Jain, S. Treatment of Maxillary Impacted Canine using Ballista Spring and Orthodontic Wire Traction. Int. J. Clin. Pediatr. Dent. 2017, 10, 313–317. [Google Scholar] [CrossRef]
- Chung-Leng, I.; Beltri Orta, P.; De la Hoz Calvo, A. Radiographic assessment of unerupted permanent maxillary canines and their relationship to the phases of dentition in mixed dentition Spanish children: A retrospective cross-sectional study. Eur. Arch. Paediatr. Dent. 2023, 24, 711–718. [Google Scholar] [CrossRef]
- Nakandakari, C.; Goncalves, J.R.; Cassano, D.S.; Raveli, T.B.; Bianchi, J.; Raveli, D.B. Orthodontic Traction of Impacted Canine Using Cantilever. Case Rep. Dent. 2016, 2016, 4386464. [Google Scholar] [CrossRef]
- Shastri, D.; Nagar, A.; Tandon, P. Alignment of palatally impacted canine with open window technique and modified K-9 spring. Contemp. Clin. Dent. 2014, 5, 272–274. [Google Scholar] [CrossRef]
- Elkolaly, M.A.; Hasan, H.S. MH cortical screws, a revolutionary orthodontic TADs design. J. Orthod. Sci. 2022, 11, 53. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Zeng, A.; Yan, P. Finite Element Analysis and Polarization Test of IDEs Piezoelectric Actuator. Micromachines 2022, 13, 154. [Google Scholar] [CrossRef] [PubMed]
- Field, C.; Ichim, I.; Swain, M.V.; Chan, E.; Darendeliler, M.A.; Li, W.; Li, Q. Mechanical responses to orthodontic loading: A 3-dimensional finite element multi-tooth model. Am. J. Orthod. Dentofac. Orthop. 2009, 135, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Gautam, P.; Valiathan, A.; Adhikari, R. Skeletal response to maxillary protraction with and without maxillary expansion: A finite element study. Am. J. Orthod. Dentofac. Orthop. 2009, 135, 723–728. [Google Scholar] [CrossRef] [PubMed]
- Jacoby, H. The ‘ballista spring” system for impacted teeth. Am. J. Orthod. 1979, 75, 143–151. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).