Abstract
As global energy systems shift to low-carbon models, microgrid systems play an increasingly vital role in decentralized energy management. This study proposes a collaborative scheduling strategy, incorporating both power and carbon contribution for multi-microgrid systems. Through the utilization of a cooperative Stackelberg game and a Nash bargaining model, a bi-level game framework is established between grid operators and microgrid alliances, enabling efficient resource sharing and equitable benefit distribution. To accurately assess each microgrid’s impacts, a VCG (Vickrey–Clarke–Groves)-based mechanism is introduced to quantify its marginal contribution to both power supply and carbon mitigation. The contribution factors are then embedded into the bargaining process, guiding incentive-compatible allocation. Furthermore, to improve computational efficiency and enable distributed problem-solving, an enhanced analytical target cascading (ATC) algorithm is applied. Experimental results reveal that this approach improves both economic and environmental performance, effectively reducing carbon emissions and dependence on the main grid.
1. Introduction
As global energy systems evolve and low-carbon economies progress, many countries have enacted stringent carbon reduction policies to combat climate change []. These policies challenge traditional power systems, driving a shift toward renewable energy-based production and consumption models []. Microgrids, as a flexible and controllable distributed energy solution, have attracted growing attention. However, individual microgrids are often constrained by equipment capacity and environmental conditions, limiting optimal resource utilization [,]. Therefore, promoting collaboration and resource sharing between multiple microgrids can achieve coordinated energy and carbon emission optimization, enhancing economic and environmental outcomes while advancing low-carbon energy systems.
Multi-source energy systems, which integrate diverse generation technologies including renewable sources (solar PV, wind), conventional units (gas turbines), and energy storage systems, have become the foundation of modern microgrid design []. These systems are characterized by the heterogeneous nature of their energy sources, each with distinct operational characteristics, output patterns, and environmental impacts. Renewable sources such as solar and wind provide clean energy but exhibit inherent variability due to weather conditions and seasonal fluctuations []. Conventional generation units like gas turbines offer controllable and dispatchable power but contribute to carbon emissions. Energy storage systems serve as crucial components for temporal energy shifting, load balancing, and grid stabilization services. The integration of these diverse energy technologies within multi-microgrid frameworks creates complex interdependencies that require careful consideration of both individual source characteristics and their collective system-wide impacts.
In addition to the integration of multiple energy sources, the physical structure of microgrids has also evolved to meet the increasingly complex demands of smart energy systems []. Hybrid AC/DC microgrid architectures have emerged as a promising solution due to their ability to reduce power conversion losses, improve energy efficiency, and enhance compatibility with renewable energy sources and energy storage systems []. These hybrid systems facilitate more flexible scheduling and resilient operation, particularly in urban environments where diverse types of loads and distributed resources coexist. Reference [] identified the grid of hybrid AC/DC microgrids as a new paradigm for future smart cities, enabling seamless interconnection and advanced coordinated control across heterogeneous microgrids.
Driven by low-carbon policies, multi-microgrid systems play a pivotal role in distributed energy management []. Compared to single microgrids, they enable regional resource sharing and coordinated scheduling, promoting efficient use of renewable energy resources []. This enhances energy supply stability and reduces carbon emissions. However, realizing these benefits requires seamless collaboration among microgrids and strong coordination with grid operators to manage electricity and carbon trading []. Through such cooperation, multi-microgrids can obtain grid support during peak demand and supply excess energy during surpluses, maintaining supply–demand balance [,]. Additionally, peer-to-peer (P2P) trading allows flexible allocation of electricity and carbon quotas, boosting system efficiency and adaptability []. These collaborative mechanisms support clean energy integration and the development of low-carbon, efficient power systems. Nonetheless, ensuring fair and effective coordination among multiple microgrids remains a key challenge.
Despite efforts to optimize resource allocation and utilization in multi-microgrid collaborations, current solutions still face certain limitations []. One prominent challenge arises from the differing objectives regarding supply, demand, and resource allocation, which complicates direct resource sharing and cost distribution []. Yang et al. [] introduced an asymmetric Nash bargaining-based approach for integrated energy systems (IES), leveraging P2P trading to enhance coordination and ensure equitable benefit distribution. Similarly, Wu et al. [] developed an energy management model based on a Stackelberg–Nash game to regulate electricity trading among photovoltaic (PV) prosumers, incorporating demand response (DR) and carbon emission considerations. While these studies offer valuable insights, they largely address isolated components of a complex optimization problem, leaving several critical issues unresolved.
At the same time, carbon trading mechanisms have become the collaborative optimization of multi-microgrid systems and grid operators []. As carbon reduction targets intensify, their influence on power system operations grows, complicating trading dynamics. Carbon trading impacts microgrid operating costs, grid operators’ emission goals, and system scheduling strategies. By engaging in carbon markets, microgrids can balance electricity use with emissions, improving both economic and environmental performance []. However, challenges persist in quota allocation, fair trading, and cost management. Han et al. [] applied a nonlinear energy mapping function to quantify microgrid contributions and allocate benefits, but they focused mainly on electricity, overlooking carbon reduction. Similarly, Liu et al. [] proposed a blockchain-based model for secure electricity trading, yet failed to capture the interdependence of power and carbon contributions. Wu et al. [] introduced a VCG-based method to promote truthful demand response, but they did not address cooperative optimization or benefit sharing. The aforementioned approaches highlight the pressing need for holistic solutions that not only coordinate power and carbon but also ensure fair and incentive benefit distribution.
Furthermore, in the collaborative optimization of multi-microgrid systems and grid operators, the increasing complexity of electricity and carbon trading presents challenges in ensuring efficient resource allocation and equitable benefit distribution [,]. Traditional centralized optimization methods often struggle with the large-scale data and multi-dimensional constraints involved. For instance, Karush–Kuhn–Tucker (KKT)-based reformulations and heuristic algorithms have been used to simplify such problems, but their scalability and applicability remain limited []. Although suitable for specific cases, these methods often fall short in dynamic, multi-agent environments. Feng et al. [] proposed a decentralized P2P trading model incorporating network constraints, using an event-driven mechanism and a fast dual ascent algorithm to enable efficient local trading while ensuring system safety. Chen et al. [] developed a distributed optimization framework for multi-energy microgrids (MEMGs), integrating electricity, heat, and carbon emission rights (CER) trading, and they employed an adaptive consensus ADMM algorithm to enhance privacy and transparency. While these approaches mark meaningful progress, challenges in convergence speed, computational efficiency, and real-time responsiveness remain.
Existing research indicates that the collaborative optimization between multi-microgrid systems and grid operators still has room for improvement, particularly in carbon trading mechanisms, multi-agent resource coordination, and equitable benefit distribution. This study presents a collaborative optimization strategy for power and carbon marginal contributions in multi-microgrid systems, developed within a cooperative Stackelberg game framework. To achieve both system efficiency and fairness, the strategy combines cooperative game theory with an asymmetric Nash bargaining model and incorporates a VCG-based contribution evaluation mechanism. The VCG mechanism is used to quantify the marginal impact of each microgrid on system performance, serving as the basis for fair and incentive-compatible benefit allocation. Furthermore, to adapt to dynamic demand fluctuations, an improved ATC algorithm is employed for distributed optimization, facilitating progressive coordination between hierarchical decision levels while ensuring computational tractability and fairness. The main contributions of this study are as follows:
(1) A bi-level energy trading framework for multi-microgrid systems is developed based on a cooperative Stackelberg game. The upper level represents the grid operator, responsible for the overall scheduling and adjustment, while the lower level encompasses the microgrid alliance. Within this alliance, energy trading and sharing are facilitated through cooperative game theory, alongside collaborative trading with the grid operator.
(2) An asymmetric Nash bargaining model is developed for benefit distribution, using a VCG-based power and carbon contribution factor to evaluate each microgrid’s marginal impact on system performance. It ensures incentive compatibility and fair allocation. A nonlinear energy mapping function captures interactions among microgrids, while the Jain index assesses distributional equity.
(3) To effectively implement the bi-level collaborative scheduling framework and accurately quantify the marginal contributions proposed in this study, an improved ATC algorithm combined with Anderson acceleration is developed. This methodological enhancement improves convergence efficiency and computational speed, enabling distributed problem-solving in dynamic, multi-agent environments and thus addressing the computational complexity inherent in the proposed model.
The remainder of this manuscript is structured as follows. Section 2 introduces the multi-microgrid system model, detailing the hierarchical structure and interaction mechanisms between the microgrid alliance and the grid operator. Section 3 outlines the optimization strategy for power and carbon contribution based on a cooperative Stackelberg game with VCG-based contribution evaluation. Section 4 presents the improved ATC algorithm for distributed problem-solving. Section 5 evaluates the proposed strategy through numerical results. Finally, Section 6 outlines the conclusion of this study.
2. System Models
The multi-microgrid system comprises a grid operator, a microgrid alliance, and individual microgrids, as depicted in Figure 1. The grid operator acting as the upper-level authority oversees power supply adjustments and manages energy and carbon quota interactions. The microgrid alliance serves as an intermediary, facilitating coordination between the grid operator and individual microgrids. Based on its own energy needs and carbon targets, a microgrid can trade energy and carbon quotas with the grid operator or other microgrids, enhancing overall system performance.
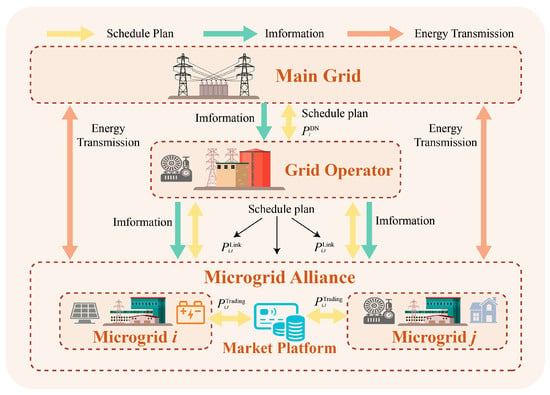
Figure 1.
Framework of the multi-microgrid system.
The grid operator and microgrid alliance interact through power coordination, information exchange, and dynamic carbon trading. If emissions exceed limits, the alliance can buy additional quotas. It shares power demand and emissions data with the operator to support scheduling, while microgrids conduct P2P energy trading and adjust carbon quotas within the alliance.
Effective coordination among multiple energy sources within each microgrid is essential for optimal system performance. Each microgrid integrates gas turbines, PV systems, wind power, and energy storage, requiring sophisticated coordination to balance renewable intermittency with load demands. The coordination strategy follows the following hierarchical approach: local source optimization within each microgrid, alliance-level resource sharing through P2P trading, and system-level coordination via the grid operator. This multi-source management framework ensures reliable operation while maximizing renewable energy utilization and minimizing carbon emissions.
2.1. Grid Operator Model
The grid operator maintains supply–demand balance and optimizes operations by coordinating with the microgrid alliance. It allocates resources and uses controllable generation and energy storage to support peak demand or emergencies.
The grid operator primarily utilizes diesel generators as its generation units, modeled as follows []:
where is the output of generation unit m at time t; is the fuel-to-electricity conversion efficiency; is the fuel power input to the generator.
The output of the generation units must satisfy the following conditions:
where and denote the lower and upper output limits of generation unit m; and signify the minimum on-time and minimum off-time for generation unit m, respectively; represents the binary variable indicating the startup and shutdown status of the unit m.
2.2. Microgrid Alliance Model
The microgrid alliance coordinated dispatch by aggregating data from individual microgrids, enabling internal energy sharing and unified grid transactions []. Each microgrid manages local operations with gas turbines, renewables, and storage and collaborates through the alliance when needed.
The power generation from renewable sources, such as PV and wind units, is inherently influenced by environmental parameters. For PV systems, solar irradiance determines the amount of electricity produced, while ambient temperature affects the conversion efficiency of photovoltaic panels. In the case of wind power, generation depends on both wind speed and wind direction—where higher wind speeds increase output, and favorable wind direction improves turbine alignment and energy capture. These factors introduce uncertainty and volatility into renewable generation, thereby affecting energy management strategies, scheduling decisions, and the need for coordinated resource sharing in multi-microgrid systems.
2.2.1. Gas Turbine Unit Model
The gas turbine unit operated by burning natural gas is necessary to generate electricity efficiently []. The relationship between the electricity produced by the gas turbine unit in microgrid i and natural gas consumption is expressed as follows:
where and denote the power output and power generation of the gas turbine unit, respectively; signifies the calorific value of natural gas; and refers to the amount of natural gas consumed by the unit.
The gas turbine unit’s output must follow the minimum and maximum constraints, as follows:
2.2.2. Photovoltaic Model
The PV system’s output power is calculated as follows:
where refers to the efficiency of the PV panel, is the actual working temperature of the PV cell, is the PV cell temperature under standard test conditions, generally 25 °C, represents the surface area of the PV panel, and denotes the solar irradiance intensity.
2.2.3. Wind Power Model
The output power of a wind turbine is primarily influenced by wind speed, which typically follows a Weibull distribution. Based on this, the wind turbine units’ output power model can be expressed as follows:
where is the rated power of the wind turbine, is the cut-in wind speed, is the cut-out wind speed, and is the rated wind speed.
2.2.4. Energy Storage System Model
The ESS stores surplus power from generation units and releases it during peak demand to balance supply and demand. Its charging and discharging behavior is modeled as follows:
where and are the charging and discharging power of energy storage unit i at time t, respectively; and denote the charging and discharging efficiencies, respectively. The state of charge (SOC) is subject to upper and lower limits, as well as constraints on charging and discharging power:
The soc is constrained by the following:
2.2.5. Demand Response Model
This study examines the adjustable and transferable DR loads. The electricity demand of microgrids is divided into fixed loads and controllable loads . Controllable loads are further classified into transferable loads and reducible loads , as outlined below:
Controllable loads can be reformulated as follows:
Transferable loads can be shifted to other time periods to reduce costs or gain compensation. Their constraints are shown as follows:
where represents the proportion of transferable loads in the total electricity load; signifies the total time; denotes the pre-demand-response electricity load; and corresponds to the transferable load.
Reducible loads allow users to cut power use in response to demand signals or price changes, with constraints as follows:
where refers to the proportion of reducible loads in the total electricity load, and denotes the reducible load.
2.3. Carbon Emission Model
This study adopts a carbon trading mechanism to manage the microgrid alliance’s emissions. Microgrids exceeding their quotas must purchase allowances, while those with surplus can sell them.
The carbon quota of the grid operator is mainly allocated based on fossil fuel generation units, calculated as follows:
The associated carbon emission is expressed as follows:
The carbon emission model for the microgrid alliance framed in this study includes the following two key components: (1) allocation of emissions for gas turbine units, and (2) allocation of emissions for renewable energy units. The corresponding calculation is as follows:
where and denote the emission allocation per unit of power output for conventional and renewable generation units, respectively.
The actual carbon emissions are given by the following:
where denotes the emission factors for the gas turbine unit.
3. Mechanism Design
This section builds on the previous models by introducing a bi-level game framework and benefit allocation mechanism. A Stackelberg game is formed between the grid operator and the microgrid alliance, where the operator sets prices as the leader, and the alliance responds to maximize overall benefit. Within the alliance, microgrids engage in a cooperative game, optimizing internal scheduling and trading to minimize costs before submitting a unified strategy to the operator.
3.1. Cooperative Stackelberg Game Framework
In the Stackelberg game, the grid operator manages the supply–demand balance by controlling power distribution to microgrids []. When electricity prices are low, microgrids prefer purchasing from the grid; at higher prices, they turn to ESS or peer trading.
The grid operator’s scheduling model aims to minimize the total operational cost of both the grid and the microgrid system, with the objective function defined as follows:
where indicates the operating and startup/shutdown costs of the grid operator’s generation units; refers to the operational cost of fuel; denotes the generation unit parameters; and signify the startup and shutdown costs, respectively; represents the cost of distribution transactions; indicates the distribution price; corresponds to the transaction cost between the grid operator and the microgrid alliance; and signify the transaction and carbon trading prices, respectively; and refers to the carbon trading cost.
Microgrids interact with the grid operator to regulate interconnection power. The grid operator manages this exchange to balance system load and ensure overall optimization. The following constraints must be met:
(1) Power Balance Constraint: At each time step t, the power exchange between the grid operator, generation units, loads, and microgrids must be balanced, as follows:
where refers to the power transfer between the grid operator and the upper-level grid; corresponds to the power output of generation unit i; indicates the load demand of the n-th load; and denotes the power exchanged between the microgrid alliance and the grid operator.
(2) Interchange Power Constraint: The power exchanged between the microgrid alliance and grid operator must stay within interconnection and transmission capacity limits, as follows:
where and signify the minimum and maximum power exchange limits between the grid operator and the upper-level grid, respectively; and denote the minimum and maximum power exchange limits between the grid operator and the microgrid alliance, respectively.
Each microgrid within the alliance aims to minimize costs through a shared energy optimization model. The specific formulation is outlined as follows:
In Equations (20) and (21), denotes the total operating cost of microgrid i; denotes the electricity-related operating cost of microgrid i, including costs associated with power generation, energy storage, demand response, grid interaction, and electricity trading; denotes the carbon emission costs of microgrid i; signifies the carbon trading prices; refers to the cost of the microgrid’s gas turbine unit; , , and signify the cost coefficients for gas turbines; denotes the depreciation coefficient for the ESS; represents the depreciation coefficient of ESS; refers to the interaction cost between the microgrid and the grid operator; signifies the electricity trading prices, respectively; denotes the DR costs; refers to the compensation for controlled loads; corresponds to the cost of power trading between microgrids; and represents the trading price.
In addition to the gas turbine unit constraints, microgrids must adhere to the power balance requirement, as follows:
The upper and lower bounds on the linking power between the microgrids and the grid operator, along with the power exchanged between the microgrids, are outlined as follows:
The power transfer between microgrids must adhere to the following conditions:
Microgrids can also trade with each other to reduce the alliance’s overall costs, which are then allocated based on individual contributions to encourage participation. This study assumes full cooperation to minimize total electricity and carbon trading costs. Internal transactions are modeled using Nash bargaining, as defined in Equation (26), ensuring that no microgrid can improve its benefit without reducing overall efficiency [].
where refers to the independent operational cost of microgrid i when it is not involved in the alliance, serving as the breakdown point in the Nash bargaining; at this juncture, ; represents the total operational cost of microgrid i within the alliance; and indicates the revenue generated by microgrid i through cooperation.
Due to the model’s non-convexity and nonlinearity, it is reformulated into two subproblems for tractability. Framed as a cost-minimization problem, cooperative cost savings define microgrid revenues. The total cost equals the sum of individual energy expenditures, leading to the following Nash bargaining-based energy-sharing model:
3.2. VCG-Based Contribution Factors for Revenue Allocation
After minimizing the alliance’s total cost, the main challenge is fair revenue allocation that encourages participation. Since microgrids contribute differently to power supply and carbon reduction, allocations must reflect their impact on overall system performance.
This study introduces a power and carbon contribution factor to quantify each microgrid’s role in trading and emission reduction, linking earnings to actual contribution. To improve fairness and accuracy, the VCG mechanism [,,] is integrated by calculating each microgrid’s marginal impact as the difference in system performance with and without its participation. This ensures incentive compatibility, prevents manipulation, and aligns local decisions with global optimization. The calculation is as follows:
where refers to the power contribution factor of microgrid i, which represents its marginal contribution to reducing system-wide electricity costs. denotes the electricity-related cost of microgrid j. The numerator reflects the total cost without microgrid i, minus the cost with its inclusion, thus capturing its VCG-based marginal benefit. A higher value of indicates a greater contribution of microgrid i to system efficiency, reflecting the marginal benefit principle at the core of the VCG mechanism.
The carbon emission contribution factor, based on the VCG mechanism, measures each microgrid’s marginal impact on total emission reduction by comparing system performance with and without its participation. This ensures incentive compatibility, rewards greater contributors, and encourages low-carbon involvement. The calculation is shown as follows:
where and refer to the carbon emissions of microgrid i before and after cooperation, and is the corresponding reduction for microgrid i. The contribution factor is calculated via the VCG mechanism, reflecting the marginal change in system-wide emission reduction due to microgrid i’s participation. It captures the difference in total emissions with and without microgrid i, reflecting its actual impact.
To assess microgrid contributions to power supply and carbon reduction, a Sigmoid-based function maps values between 0 and 1 []. This nonlinear approach avoids extreme allocations, rewards high contributors, and encourages improvement from others. Adjustable parameters ensure flexibility across scenarios, balancing efficiency and fairness. The corresponding formula is as follows:
where and refer to the weights for power and carbon emission contributions, satisfying .
Based on power and carbon contribution factors, revenue is allocated using a Nash bargaining model that maximizes the Nash product. At its maximum, no microgrid can increase its benefit without reducing overall system efficiency. This ensures fair, optimal, and stable allocation, with revenues reflecting each microgrid’s contribution to power trading and carbon reduction, and this is shown as follows:
The natural logarithm is a monotonically increasing convex function; thus, applying it to Equation (30) converts the maximization into the following equivalent minimization problem:
The Nash bargaining model ensures equitable revenue distribution by accounting for differences in power and carbon contributions. A microgrid’s revenue is proportional to its contribution, with higher contributions resulting in greater revenue.
This study also assesses the fairness of benefit distribution improvements using the Jain fairness index [], which is calculated as follows:
where denotes the benefit improvements of microgrid i.
4. Model Solution Based on the Improved ATC Algorithm
The ATC algorithm is a hierarchical optimization method that decomposes a global objective into layered sub-problems coordinated via coupling variables. This study refines ATC by introducing decoupling variables, transforming the bi-level Stackelberg model into two independent single-level problems.
Figure 2 provides a detailed overview of the proposed hierarchical optimization process. The left section presents the structure of the improved ATC algorithm, where the upper-level scheduling problem coordinates the operation of individual microgrids through iterative information exchange. The lower-level problems, representing local microgrid decision-making, are solved in parallel, and their feedback guides the upper-level adjustments.
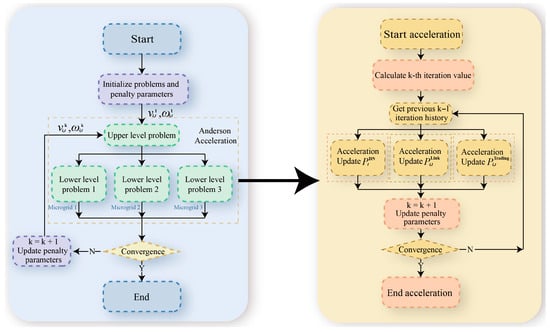
Figure 2.
Improved ATC optimization.
The right section illustrates the integration of Anderson acceleration, which enhances the convergence of the iterative process. It leverages the iteration history to adjust key variables more effectively, avoiding oscillation and reducing the number of iterations required. During each acceleration step, adjustments are made to the main coordination parameters based on past iteration data, and the penalty parameters are updated adaptively until convergence is achieved.
To resolve the coupling between the upper and lower levels, this study introduces an augmented Lagrangian penalty function.
In the lower level, due to power exchanges between microgrids, the penalty term must account for iterative updates of exchanged power between microgrids, as follows:
where and signify the objective functions of the grid operator and microgrids; and denote the decision variables of Equations (33) and (34); and denote the feedback values exchanged between upper and lower levels; and and are the first- and second-order penalty coefficients used to constrain microgrid transaction behaviors.
To expedite optimization process convergence, this study applies the Anderson acceleration algorithm to update power rates []:
- (1)
- Microgrid Power Update:
- (2)
- Linking Power Update:
- (3)
- Determination of Anderson Acceleration Coefficients:
- (4)
- Solution of Coefficients:
- (5)
- Convergence Criterion:
The updated rules for the first- and second-order penalty multipliers are as follows:
where and are the first- and second-order penalty multipliers in the k-th iteration, typically initialized as small constants; is the expansion factor for penalty adjustment, and is the threshold for updating ; and represent the linking variables in the k-th iteration for the upper- and lower-level problems.
The convergence criteria are defined as follows:
where and are convergence tolerances. controls the precision of linking variable optimization, while ensures overall system efficiency and coordination.
5. Case Study
This study investigates energy transactions between a grid operator and a microgrid alliance consisting of three microgrids, each equipped with renewable energy sources and adjustable loads. The grid operator operates three diesel generators with capacities of 350 kW, 300 kW, and 250 kW. Microgrid 1 includes a 200 kW gas turbine, a 150 kW PV unit, and a 150 kW ESS. Microgrid 2 is equipped with a 200 kW PV unit, a 130 kW wind power unit, and a 200 kW ESS. Microgrid 3 contains a 400 kW gas turbine, a 100 kW wind unit, a 130 kW PV unit, and a 150 kW ESS. The configuration of each microgrid is shown in Table 1.

Table 1.
Configuration of each microgrid.
In the implementation, the first- and second-order penalty multipliers and were initialized to 0.01. The expansion factor for penalty adjustment was set to 1.05, and the threshold for the multiplier update was defined as 10−3. The convergence tolerances and were both set to 10−3, and the maximum iteration count was limited to 20. In addition, Anderson acceleration was incorporated to improve convergence speed during the iterative coordination process.
The proposed bi-level optimization model and the improved ATC algorithm were implemented in MATLAB R2020b, with Gurobi 10.0 serving as the optimization solver through the YALMIP R20230622 interface. Numerical simulations were conducted on a PC equipped with an Intel Core i7-12700H CPU (Intel Corporation, Santa Clara, CA, USA) and 32 GB RAM (Samsung Electronics Co., Ltd., Suwon, Republic of Korea). The upper- and lower-level problems were solved using an iterative coordination framework based on augmented Lagrangian decomposition. The Anderson acceleration technique was embedded into the solution process to enhance convergence speed and stability.
5.1. Revenue and Cost Analysis
Table 2 presents the changes in operational costs before and after cooperation. The alliance’s total revenue increased by CNY 1956.55, with individual gains of 4.5%, 8.79%, and 1.85%. These results show that internal electricity trading improved microgrid benefits, while the grid operator’s revenue declined due to reduced dependence from the alliance.

Table 2.
Cost and benefit analysis before and after cooperation.
Table 3 and Table 4 compare the effects of asymmetric and standard Nash bargaining on revenue distribution. In standard Nash bargaining (Table 3), Microgrid 3 gains the most due to its larger capacity and higher generation. However, this method overlooks the renewable energy contributions of Microgrids 1 and 2, offering limited incentives for clean energy and carbon reduction, leading to suboptimal results.

Table 3.
Benefit distribution of the standard model.

Table 4.
Benefit distribution of the asymmetric bargaining model.
By applying asymmetric Nash bargaining with a Sigmoid-based contribution model, greater benefits are allocated to microgrids with higher contributions. Adjusting power and carbon factors emphasizes emission reductions, ensuring fairer revenue distribution and encouraging further low-carbon efforts.
Table 4 shows that increasing carbon contribution weights and applying exponential scaling raised the revenues of smaller microgrids like Microgrids 1 and 2. However, due to their lower renewable output and higher reliance on imported electricity, their contribution factors remain low, limiting revenue gains. As a result, Microgrid 3 retains the largest share.
5.2. Fairness Analysis
Table 5 presents the Jain fairness index for different bargaining models, where higher values indicate fairer benefit distribution. Incorporating power and carbon contribution factors and asymmetric Nash bargaining improves fairness. Adding the VCG mechanism further increases the index, from 0.735 to 0.763 in the standard model and from 0.856 to 0.874 in the asymmetric model, confirming the effectiveness of the VCG-based approach.

Table 5.
Jain fairness index.
5.3. Microgrid Electricity Trading Analysis
Figure 3 shows power distribution among microgrids after implementation. Microgrids 1 and 2, equipped with higher shares of photovoltaic and wind power generation, export excess electricity to Microgrid 3 during periods of low load or renewable generation peaks. In contrast, during high-demand periods, Microgrid 3 utilizes its gas turbine units to supply electricity to the other two microgrids. The power exchange is dynamic and varies with time, reflecting the fluctuations in renewable output and demand levels. During off-peak hours, Microgrid 3 reduces its own generation and purchases more low-carbon electricity from Microgrids 1 and 2 to optimize operational costs and improve efficiency.
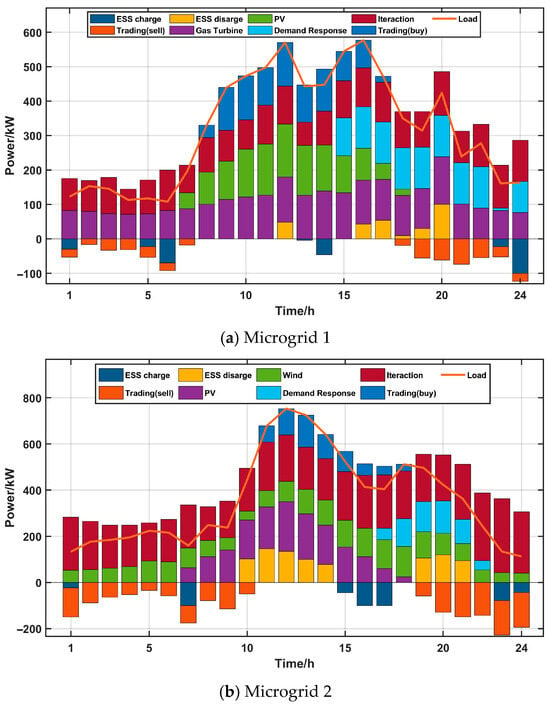
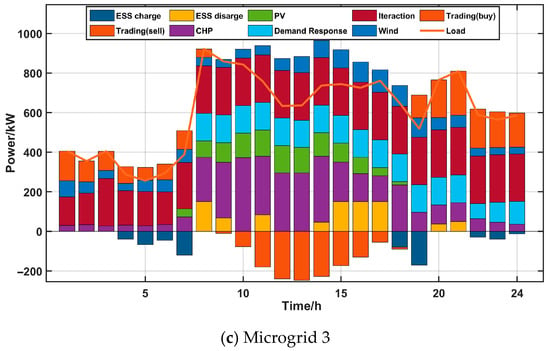
Figure 3.
Power optimization of microgrids.
Figure 4 illustrates the power distribution and trading among microgrids. During 06:00–14:00, Microgrid 3 mainly purchases electricity from Microgrids 1 and 2, which act as sellers due to higher renewable output. After 16:00, Microgrid 3 becomes a power supplier. Although most trading still involves the grid operator, inter-microgrid exchanges occur regularly and reflect dynamic load and generation conditions.
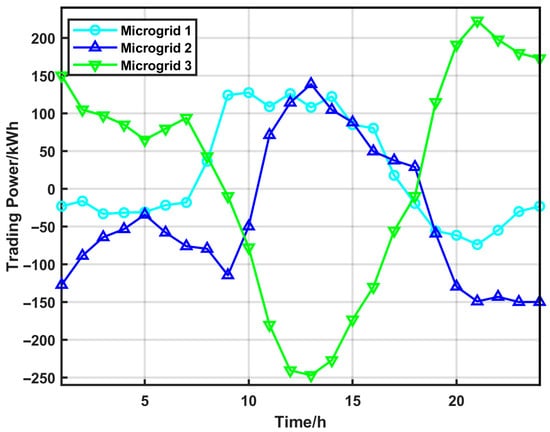
Figure 4.
Power trading among microgrids.
5.4. Carbon Emission Analysis
Table 6 compares carbon emissions and trading revenues for each microgrid before and after electricity trading. After integration, Microgrids 1 and 3 reduced emissions by 15.5% and 19.78%. Microgrid 2, which has no carbon-emitting units, is excluded. Overall, the alliance saw lower carbon emissions, reduced trading costs, and increased revenues.

Table 6.
Carbon emission analysis.
Figure 5 illustrates the impact of different power and carbon contribution weightings on revenue allocation among microgrids. When carbon weighting increases, Microgrids 1 and 2 receive higher revenues due to their greater renewable generation. Conversely, higher power weighting shifts more revenue to Microgrid 3, which has a larger generation capacity. The allocation pattern changes gradually with the weighting, showing a clear trade-off between power and carbon contributions.
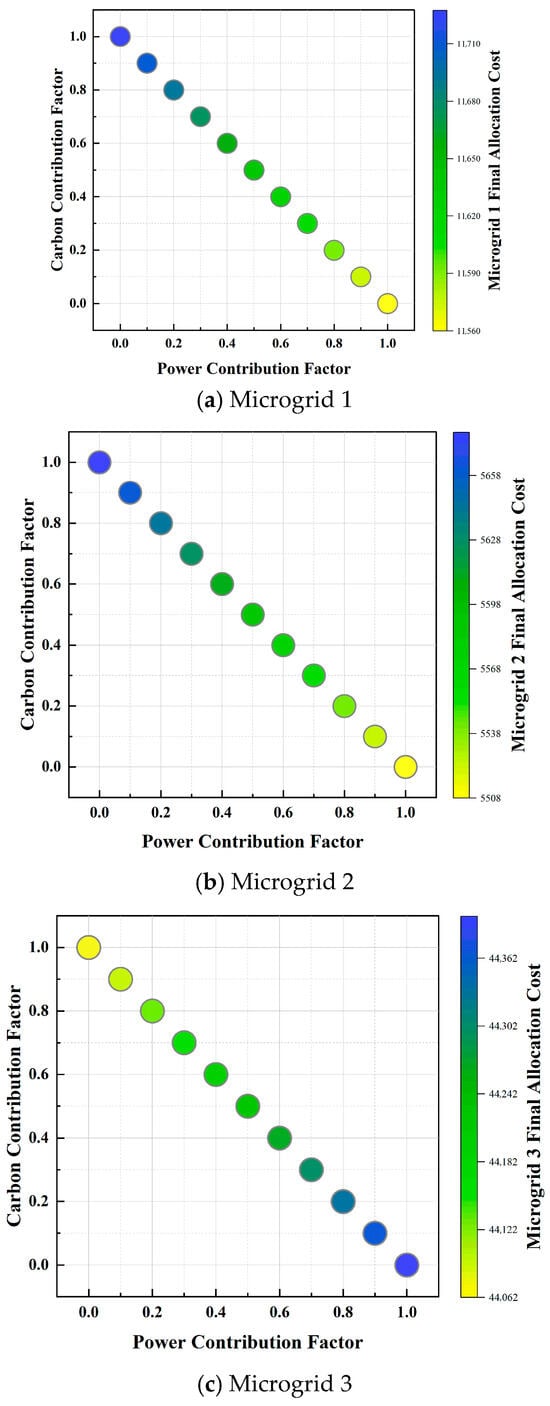
Figure 5.
Power and carbon contribution factor.
5.5. Convergence Analysis
This study applies the ATC algorithm to solve Subproblems 1 and 2 through distributed iterative processes, as illustrated in the following figures.
Figure 6 illustrates the iterative convergence results for Problems 1 and 2 using the improved ATC algorithm. Problem 1, which involves the coordination between the grid operator and the microgrid alliance, converges in seven iterations. Problem 2, incorporating more complex inter-microgrid trading behavior, requires nine iterations to reach convergence. Both problems exhibit stable decline in residuals and ultimately meet the set convergence threshold of 10−3.
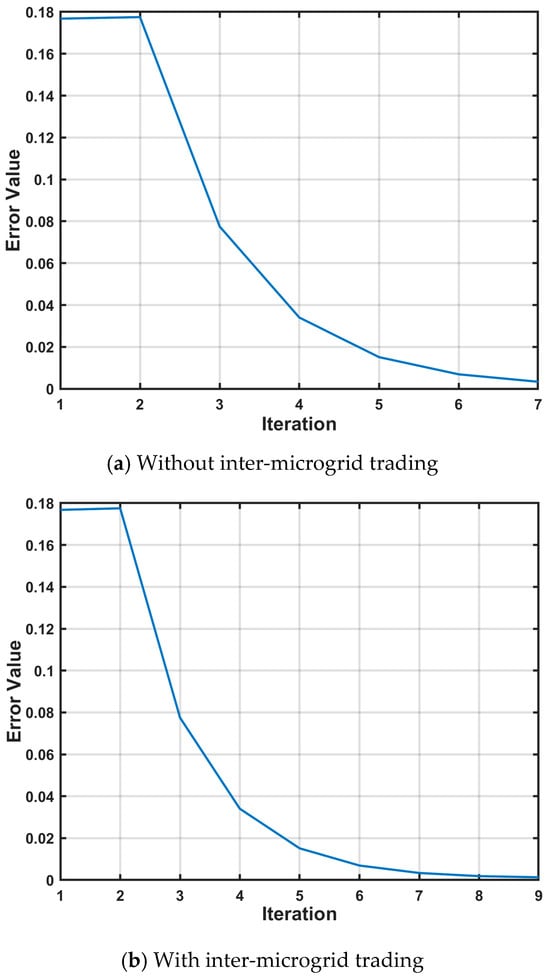
Figure 6.
Iterative convergence results.
Figure 7 shows the iterative process of linking power between the microgrids and the grid operator under two scenarios. In the case without inter-microgrid trading, the linking power values gradually stabilize and converge within seven iterations. When inter-microgrid trading is enabled, the presence of additional coupling relationships leads to a slightly longer convergence process, reaching stability after nine iterations. In both cases, the linking power values from different microgrids align to a common value as the iterations progress.
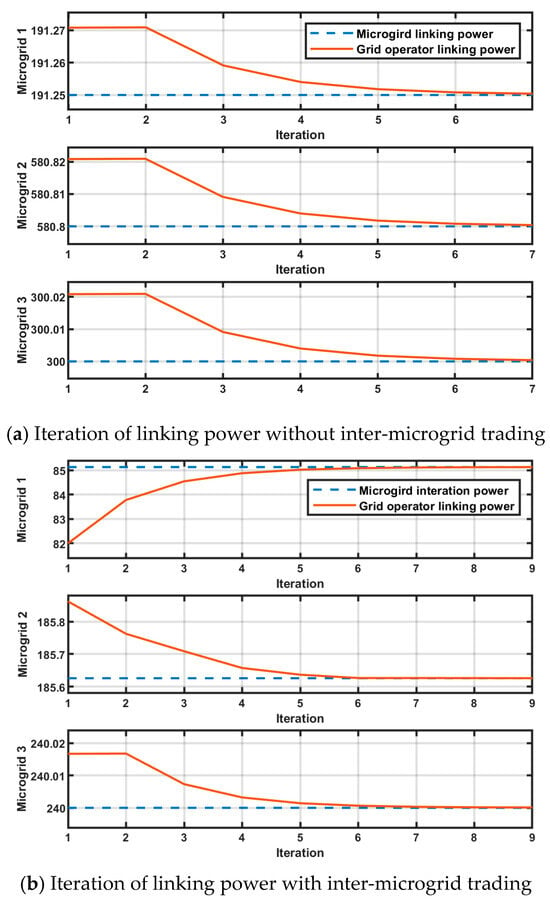
Figure 7.
Iteration of linking power: (a) without inter-microgrid trading; (b) with inter-microgrid trading.
6. Conclusions
This study proposes a collaborative scheduling strategy for multi-microgrid systems that optimizes power and carbon marginal contributions based on a cooperative Stackelberg game framework. The approach balances power and carbon efficiency while enabling equitable revenue distribution and global optimization. A power and carbon contribution factor is proposed to evaluate each microgrid’s role, ensuring fair resource sharing and benefit allocation. To enhance incentive compatibility and fairness, the VCG mechanism is integrated into the revenue distribution process. Additionally, a refined ATC algorithm with Anderson acceleration is adopted for faster convergence. The case study yields the following conclusions:
(1) In the cooperative Stackelberg game model, the upper-level grid operator directs overall scheduling and revenue distribution for the microgrid alliance. The lower-level microgrid alliance facilitates resource sharing and cooperation, boosting economic and environmental outcomes, promoting renewable energy development, and encouraging microgrid collaboration.
(2) By incorporating power and carbon impact factors into the revenue model, this approach ensures fair benefit allocation among microgrids, promoting clean energy and carbon reduction. The VCG mechanism is introduced to enhance fairness and incentive compatibility. Distribution equity is measured using the Jain fairness index. This strategy can foster microgrid collaboration and enhance low-carbon operation.
(3) The improved ATC algorithm is utilized for decentralized optimization. By applying hierarchical optimization across upper and lower levels and integrating Anderson acceleration, the algorithm substantially boosts convergence rate, enhances computational efficiency, enables real-time scheduling in multi-microgrid systems, and improves result accuracy and effectiveness.
The framework developed in this work may provide useful insights for stakeholders in the energy sector. Grid operators could potentially utilize the coordination mechanisms to improve multi-microgrid management, while microgrid developers might apply the cooperative strategies in designing collaborative energy systems. The carbon contribution evaluation methods could serve as a reference for energy policy makers developing carbon trading policies, and the VCG-based allocation mechanism might be adopted by energy market designers for creating fair trading platforms.
Although this study focuses on collaborative scheduling and fair benefit allocation from economic and environmental perspectives, the proposed framework provides a solid foundation for the future integration of advanced intelligent functionalities. The hierarchical Stackelberg–Nash architecture and the distributed optimization approach are inherently adaptable and can be extended to incorporate modules such as self-healing control, real-time fault diagnostics, and resilience-oriented dispatch. These enhancements would significantly improve the autonomy, robustness, and adaptability of multi-microgrid systems operating under uncertain and dynamic conditions. Future research will explore these directions to broaden the model’s applicability toward more intelligent and resilient energy systems.
Author Contributions
Conceptualization, H.H.; writing-original draft, X.J. and S.Z.; methodology, X.J.; writing—review and editing, X.J. and Z.Y.; data curation, S.Z. and Z.L.; visualization, C.W.; resources, C.W.; funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No. 52307090).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sang, M.; Shen, L.; Du, X.; Yang, Y. Is There a Joint Force between Academic Literature and Policy Measure in Promoting Low-Carbon City. Renew. Sustain. Energy Rev. 2025, 210, 115163. [Google Scholar] [CrossRef]
- Han, H.; Zhang, Y.; Wei, T.; Zang, H.; Sun, G.; Wu, C.; Wei, Z. A Flexible Demand Response Dispatch Strategy Considering Multiple Response Modes and Wind Power Uncertainty. Appl. Sci. 2021, 11, 10165. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, P.; Sun, X.; Ni, G. Disparities in Energy Efficiency and Its Determinants in Chinese Cities: From the Perspective of Heterogeneity. Energy 2024, 289, 129959. [Google Scholar] [CrossRef]
- Gul, E.; Baldinelli, G.; Bartocci, P.; Shamim, T.; Domenighini, P.; Cotana, F.; Wang, J.; Fantozzi, F.; Bianchi, F. Transition toward Net Zero Emissions—Integration and Optimization of Renewable Energy Sources: Solar, Hydro, and Biomass with the Local Grid Station in Central Italy. Renew. Energy 2023, 207, 672–686. [Google Scholar] [CrossRef]
- Tehrani, K.; Simde, D.; Fozing, J.; Jamshidi, M. A 3D Design of Small Hybrid Farm for Microgrids. In Proceedings of the 2022 World Automation Congress (WAC), San Antonio, TX, USA, 11 October 2022; pp. 1–6. [Google Scholar]
- Castano-Solis, S.; Fernandez-Muñoz, D.; Ardanuy, J.F.; Gutierrez, A.; Conti, G.; Jimenez-Bermejo, D.; Perez Diaz, J.I. Management of a Local Multi-Source Energy System in a Research Centre Based on Self-PV Generation and Electric Vehicles. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6 June 2023; pp. 1–6. [Google Scholar]
- Wu, C.; Zhou, Y.; Gan, W.; Wu, J. Robust Scheduling of a Pulp and Paper Mill Considering Flexibility Provision from Steam Power Generation. Appl. Energy 2025, 377, 124595. [Google Scholar] [CrossRef]
- Yu, D.; Gao, S.; Han, H.; Zhao, X.; Wu, C.; Liu, Y.; Song, T.E. Intraday Two-Stage Hierarchical Optimal Scheduling Model for Multiarea AC/DC Systems with Wind Power Integration. Appl. Energy 2024, 364, 123079. [Google Scholar] [CrossRef]
- Kazerani, M.; Tehrani, K. Grid of Hybrid AC/DC Microgrids: A New Paradigm for Smart City of Tomorrow. In Proceedings of the 2020 IEEE 15th International Conference of System of Systems Engineering (SoSE), Budapest, Hungary, 2–4 June 2020; pp. 175–180. [Google Scholar]
- Merabet, A.; Al-Durra, A.; El-Saadany, E.F. Energy Management System for Optimal Cost and Storage Utilization of Renewable Hybrid Energy Microgrid. Energy Convers. Manag. 2022, 252, 115116. [Google Scholar] [CrossRef]
- Wang, J.; Zhong, H.; Yang, Z.; Lai, X.; Xia, Q.; Kang, C. Incentive Mechanism for Clearing Energy and Reserve Markets in Multi-Area Power Systems. IEEE Trans. Sustain. Energy 2020, 11, 2470–2482. [Google Scholar] [CrossRef]
- Huang, H.; Sun, G.; Chen, S.; Wei, Z.; Zang, H. Peer-to-Peer Energy Trading of Hydrogen-Producing Prosumers in Power Distribution Network. Sustain. Energy Technol. Assess. 2025, 75, 104221. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, X.; Xie, H.; Tang, L.; Bie, Z. Bi-Level Coordinated Restoration for the Distribution System and Multi-Microgrids. Int. J. Electr. Power Energy Syst. 2025, 164, 110371. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Yang, Y.; Parisio, A.; Li, Y.; Amjady, N.; Islam, S.; Cheng, K.W.; Guerrero, J.M.; Rodríguez, J. Economic Model Predictive Control for Microgrid Optimization: A Review. IEEE Trans. Smart Grid 2024, 15, 472–484. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, Y.; Cao, Y. Collaborative Optimization for Energy Hub and Load Aggregator Considering the Carbon Intensity-Driven and Uncertainty-Aware. Energy 2024, 312, 133546. [Google Scholar] [CrossRef]
- Zhang, B.; Dou, C.; Yuan, D.; Zhang, Z. Interval Forecasting Strategy of Photovoltaic Generation Considering Multi-Factor Self-Fluctuation. Electr. Power Syst. Res. 2024, 234, 110495. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, H.; Chen, S.; Sun, G.; Zhou, Y. Learning-Aided Distributionally Robust Optimization of DC Distribution Network with Buildings to the Grid. Sustain. Cities Soc. 2024, 113, 105649. [Google Scholar] [CrossRef]
- Yang, M.; Liu, Y.; Kobashi, T. Asymmetric Nash Bargaining Model for Operation Optimization of Multi-Integrated Energy Systems Considering Peer-to-Peer Energy Trading. Sustain. Cities Soc. 2024, 114, 105791. [Google Scholar] [CrossRef]
- Wu, Y.; Tian, X.; Gai, L.; Lim, B.-H.; Wu, T.; Xu, D.; Zhang, Y. Energy Management for PV Prosumers inside Microgrids Based on Stackelberg–Nash Game Considering Demand Response. Sustain. Energy Technol. Assess. 2024, 68, 103856. [Google Scholar] [CrossRef]
- Zhang, Z.; Fedorovich, K.S. Optimal Operation of Multi-Integrated Energy System Based on Multi-Level Nash Multi-Stage Robust. Appl. Energy 2024, 358, 122557. [Google Scholar] [CrossRef]
- Li, G.; Li, Q.; Liu, Y.; Liu, H.; Song, W.; Ding, R. A Cooperative Stackelberg Game Based Energy Management Considering Price Discrimination and Risk Assessment. Int. J. Electr. Power Energy Syst. 2022, 135, 107461. [Google Scholar] [CrossRef]
- Han, H.; Xu, Y.; Wu, C.; Jiang, X.; Cao, S.; Zang, H.; Chen, S.; Wei, Z. Nash Equilibrium-Based Two-Stage Cooperative Operation Strategy for Multi-Microgrids Considering Uncertainty. Prot. Control Mod. Power Syst. 2024, 9, 42–57. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, B.; Li, Y.; Sun, Q.; Pedersen, T.B.; Gao, D.W. Pricing Game and Blockchain for Electricity Data Trading in Low-Carbon Smart Energy Systems. IEEE Trans. Ind. Inform. 2024, 20, 6446–6456. [Google Scholar] [CrossRef]
- Wu, Y.; Lin, Z.; Chen, Z.; Chen, R.; Chen, Y. Vickrey-Clark-Groves-Based Method for Eradicating Deceptive Behaviors in Demand Response Transactions. J. Mod. Power Syst. Clean Energy 2024, 12, 1260–1271. [Google Scholar] [CrossRef]
- Qi, X.; Ju, L.; Yang, S.; Gan, W.; Li, G.; Bai, X. A Bi-Level Peer-to-Peer Interactive Trading Optimization Model and Distributed Solution Algorithm for Rural Distributed Energy System Group Based on Stackelberg-Nash Game Strategy. Energy 2025, 318, 134767. [Google Scholar] [CrossRef]
- Liu, L.; Yao, X.; Qi, X.; Han, Y. Low-Carbon Economy Configuration Strategy of Electro-Thermal Hybrid Shared Energy Storage in Multiple Multi-Energy Microgrids Considering Power to Gas and Carbon Capture System. J. Clean. Prod. 2023, 428, 139366. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, Y.; Wu, J. Two-Layer Data-Driven Robust Scheduling for Industrial Heat Loads. J. Mod. Power Syst. Clean Energy 2024, 13, 265–275. [Google Scholar] [CrossRef]
- Feng, C.; Liang, B.; Li, Z.; Liu, W.; Wen, F. Peer-to-Peer Energy Trading under Network Constraints Based on Generalized Fast Dual Ascent. IEEE Trans. Smart Grid 2023, 14, 1441–1453. [Google Scholar] [CrossRef]
- Chen, P.; Ye, Y.; Wang, H.; Bu, S.; Tang, Y.; Strbac, G. Holistic Coordination of Transactive Energy and Carbon Emission Right Trading for Heterogenous Networked Multi-Energy Microgrids: A Fully Distributed Adaptive Consensus ADMM Approach. Sustain. Energy Technol. Assess. 2024, 64, 103729. [Google Scholar] [CrossRef]
- Luo, N.; Dou, B.; Zhang, H.; Yang, T.; Wu, K.; Wu, C.; Chen, H.; Xu, Y.; Li, W. Process Design and Energy Analysis on Synthesis of Liquid Fuels in an Integrated CCUS System. Appl. Energy 2023, 351, 121903. [Google Scholar] [CrossRef]
- Liu, B.; Wang, D.; Zhu, J.; Gu, B.; Mao, C. A Rule-Based Bionic Energy Management System for Grid-Connected Community Microgrid Using Peer-to-Peer Trading with Rapid Settlement. IEEE Trans. Sustain. Energy 2024, 15, 215–235. [Google Scholar] [CrossRef]
- Babagheibi, M.; Sahebi, A.; Jadid, S.; Kazemi, A. An Integrated Design of Heat and Power Market for Energy Hubs Considering the Security Constraints of the System. Sustain. Cities Soc. 2023, 96, 104616. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Ji, X.; Ye, P.; Yu, D.; Zhang, B. Optimal Dispatching of Electric-heat-hydrogen Integrated Energy System Based on Stackelberg Game. Energy Convers. Econ. 2023, 4, 267–275. [Google Scholar] [CrossRef]
- Vickrey, W. Counterspeculation, Auctions, and Competitive Sealed Tenders. J. Financ. 1961, 16, 8–37. [Google Scholar] [CrossRef]
- Groves, T. Incentives in Teams. Econometrica 1973, 41, 617. [Google Scholar] [CrossRef]
- Clarke, E.H. Multipart Pricing of Public Goods. Public Choice 1971, 1, 17–33. [Google Scholar] [CrossRef]
- Wu, C.; Han, H.; Gao, S. Feedback-Driven Real-Time Forecasting Method for the Arrival Times of Electric Vehicles. Electr. Power Syst. Res. 2024, 228, 110077. [Google Scholar] [CrossRef]
- Jain, R.; Chiu, D.; Hawe, W. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems. arXiv 1998, arXiv:9809099. [Google Scholar]
- Chen, K.; Vuik, C. Non-Stationary Anderson Acceleration with Optimized Damping. J. Comput. Appl. Math. 2024, 451, 116077. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).