Few-Shot Intelligent Anti-Jamming Access with Fast Convergence: A GAN-Enhanced Deep Reinforcement Learning Approach

Abstract

To address the small-sample training bottleneck and inadequate convergence efficiency of Deep Reinforcement Learning (DRL)-based communication anti-jamming methods in complex electromagnetic environments, this paper proposes a Generative Adversarial Network-enhanced Deep Q-Network (GA-DQN) anti-jamming method. The method constructs a Generative Adversarial Network (GAN) to learn the time–frequency distribution characteristics of short-period jamming and to generate high-fidelity mixed samples. Furthermore, it screens qualified samples using the Pearson correlation coefficient to form a sample set, which is input into the DQN network model for pre-training to expand the experience replay buffer, effectively improving the convergence speed and decision accuracy of DQN. Our simulation results show that under periodic jamming, compared with the DQN algorithm, this algorithm significantly reduces the number of interference occurrences in the early communication stage and improves the convergence speed, to a certain extent. Under dynamic jamming and intelligent jamming, the algorithm significantly outperforms the DQN, Proximal Policy Optimization (PPO), and Q-learning (QL) algorithms.

1. Introduction

With rapid development in economies and societies, wireless communication applications have become increasingly widespread. However, due to the openness of wireless channels, wireless communication is vulnerable to unintentional and malicious human-made jamming. Therefore, wireless communication anti-jamming technology has been subject to long-term research and extensive application, with a history of more than 50 years so far [1]. Traditional communication anti-jamming technologies, such as spread spectrum anti-jamming technology, have fixed anti-jamming strategies that cannot effectively ensure the reliability and effectiveness of information transmission in the face of complex and diverse jamming.

Early spread spectrum technologies improved anti-jamming capabilities through spectrum expansion, but essentially belonged to a “blind anti-jamming” mechanism without environmental perception, failing when the jamming band exceeded 1/3 [2]. Subsequently, spread spectrum technologies evolved from conventional spread spectrum to adaptive spread spectrum, including technologies such as frequency/power-adaptive frequency hopping and direct-sequence spread spectrum based on narrowband jamming adaptive suppression/power adaptation [3]. Although these adaptive anti-jamming technologies introduce closed-loop parameter adjustment, they are still limited by the fixed strategies of pre-set rule bases and have difficulty coping with rapidly time-varying jamming threats. This limitation has prompted researchers to explore higher-level anti-jamming intelligent technologies.

In recent years, with the rapid development of artificial intelligence and machine learning, intelligent communication anti-jamming has become a current research hotspot. Artificial intelligence algorithms represented by DRL provide new methods for intelligent anti-jamming technologies by virtue of their iterative learning ability of “perception–decision optimization”. At present, DRL-based communication anti-jamming technologies widely adopt the DQN and its improved methods to solve complex communication anti-jamming problems.

Bailin et al. [4] proposed a dynamic $\epsilon$-DQN intelligent decision algorithm that can optimally select $\epsilon$ values according to the state of the decision network, significantly improving the convergence speed and decision success rate. Liang et al. [5] presented a cross-domain anti-jamming algorithm based on the DQN, enabling mobile nodes to learn optimal position adjustment and power control strategies in unknown dynamic-jamming environments to achieve reliable transmission. Boyu et al. [6] proposed a joint frequency–power domain anti-jamming algorithm based on the Prioritized Experience Replay Deep Q-Network, which combines the DQN method with the prioritized replay strategy to realize channel selection and power control in wireless communication systems, improve the fault tolerance of wireless communication systems, and effectively enhance their transmission success rate. Feng et al. [7] modeled the communication anti-jamming process in a limited channel state as a partially observable Markov process and proposed a deep recurrent Q-network algorithm suitable for this scenario, whose convergence performance is significantly better than that of the ordinary DQN algorithm. Yangyang et al. [8] proposed a practical and fast-converging DRL anti-jamming algorithm that uses soft labels instead of rewards to obtain more information entropy, and which does not require random exploration, significantly accelerating the algorithm convergence speed. Yangyang et al. [9] proposed a parallel DRL method, which decomposes complex action spaces through a parallel network architecture, significantly improving the convergence speed and the effectiveness of anti-jamming strategies. Gang et al. [10] proposed a sample information entropy-assisted DRL anti-jamming method, which uses information entropy to predict and finely select training samples for the anti-jamming strategy network so as to improve the quality of training samples and enhance the online decision-making ability and generalization performance of anti-jamming strategies.

In summary, although AI algorithms markedly enhance anti-jamming efficacy by constructing a three-tier “environmental cognition–decision reasoning–waveform reconstruction” architecture, the existing DRL approaches are still confronted by three fundamental challenges in contested communications:

(1)

Small-sample training bottleneck: In complex electromagnetic environments, jamming patterns are typically unknown and scarce, causing conventional DQN to suffer from insufficient samples and slow convergence during training [1].

(2)

Limited convergence efficiency: In high-dimensional action–state spaces, the exploration–exploitation trade-off is easily destabilized and traditional policies require lengthy exploration steps before discovering optimal strategies. This latency risks rendering anti-jamming decisions obsolete before adapting to rapidly evolving jamming.

(3)

Poor transferability: Methods leveraging transfer learning or knowledge graphs perform better when confronting identical or similar jamming styles, whereas the traditional DQN still demands extensive retraining.

To address the above challenges, this paper investigates how Generative Adversarial Networks (GANs) can enhance the convergence speed of DQN anti-jamming algorithms based on the traditional DQN framework. As a generative model, GANs can solve the problem of insufficient samples by generating similar samples with the same distribution as real samples, as has been widely applied in fields such as image processing [11,12], target detection [13,14], and audio generation [15,16,17]. This paper applies GANs to the field of communication anti-jamming and proposes a small-sample anti-jamming decision method based on a GAN-enhanced Deep Q-Network (GA-DQN). The method uses a GAN to independently learn from collected jamming signals, capture the latent distribution of jamming signals, and generate training samples that approximate the jamming signals distribution to construct a mixed experience replay buffer. Then, a stochastic gradient descent method is adopted to train the policy network, which significantly improves the number and diversity of samples obtained in each algorithm iteration and accelerates the training process of the policy network.

2. Related Work

2.1. The Principle of GANs

GANs were proposed by Goodfellow et al. [18], as a generative model for unsupervised learning. The birth of the GAN idea was inspired by the two-person zero-sum game in game theory, in which two participants fight against each other and improve each other. Compared with traditional generative models, such as autoencoders and variational autoencoders, there are two models in a GAN: the generative model G and the discriminant model D. The generator G aims to generate samples $G\left(\mathrm{z}\right)$ that follow the real data distribution $P_{\mathrm{data}}$ as closely as possible, based on the input noise sequence z, so as to deceive the discriminator D. On the other hand, the discriminator D is used to determine whether the input sample is a real sample x or a generated sample $G\left(\mathrm{z}\right)$. G and D confront and promote each other. During the continuous confrontation, both will reach a Nash equilibrium. Eventually, G can capture the distribution of x and generate a $G\left(\mathrm{z}\right)$ that can pass for real, while D, due to its inability to correctly distinguish between x and $G\left(\mathrm{z}\right)$, will output a value approaching a fixed constant.

The loss functions of the discriminator and the generator are as follows:

$$\underset{D}{max}V(D,G)=E_{x\sim P_{data}\left(x\right)}[log\left(D\left(x\right)\right)]+E_{z\sim P_z\left(z\right)}[log(1-D\left(G\left(z\right)\right))]$$

(1)

$$\underset{G}{max}V(D,G)=E_{z\sim P_z\left(z\right)}[log\left(D\left(G\left(z\right)\right)\right)],$$

(2)

where $D\left(x\right)$ is the probability that D judges the input x as a real sample; $D\left(G\right(z\left)\right)$ is the probability that the generated sample is judged as a real sample after passing through the discriminator.

2.2. GAN Applied to Data Augmentation

Data augmentation (DA) is an effective method for expanding a dataset scale, enabling models to learn the original data distribution to generate new data with consistent distribution. In recent years, GANs have been extensively applied in data augmentation. By learning real sample distributions from random noise inputs, GANs generate novel sample data, serving as an effective solution for few-sample data augmentation. GANs have been utilized for data augmentation across numerous domains. Zhang et al. [19] proposed a Dual-Attention Deep Convolutional Generative Adversarial Network (DADCGAN), which incorporates efficient channel attention and external attention mechanisms to capture fundamental feature information from channel and spatial dimensions of images, respectively. Additionally, spectral normalization and dual-timescale update rule strategies are integrated to stabilize the training process. Ye et al. [20] constructed a cycle-consistent GAN for domain transformation, using prior-knowledge-based attention modules, leveraging self-attention and channel attention mechanisms to facilitate conversion, thereby achieving targeted generation of defective insulator samples. Seon et al. [21] introduced a novel GAN-based method for augmenting time series data to address dataset imbalance in IoT applications. Embedding, restoration, and supervised networks are adopted to encapsulate temporal dynamics in the time series data. Furthermore, incorporating mutual information and MSE terms into the loss function while implementing spectral normalization enhances GAN training stability. These diverse improved GAN variants provide a solid theoretical foundation for few-sample data augmentation.

2.3. Methods of Combining GAN with DRL

The performance of Deep Reinforcement Learning (DRL) relies on extensive, high-quality, and diverse interaction data. However, acquiring such data in real-world scenarios often proves costly, inefficient, or even infeasible. For instance, in communication anti-jamming problems, obtaining specific jamming information before encountering jamming is challenging, and DRL exhibits prolonged convergence times in complex jamming environments. The core functionality of a GAN lies in learning from data distributions to generate realistic samples, effectively alleviating data scarcity bottlenecks. Han et al. [22] designed a GAN-based spectrum completion network to reconstruct missing spectral data, which was subsequently used to train DRL-based channel networks, effectively addressing spectrum access issues caused by incomplete sensing information. Strickland et al. [23] employed a GAN to generate synthetic network traffic data, integrating synthetic and real data into DRL models to enhance the overall performance of intrusion detection systems. Wang et al. [24] proposed a GAN-based algorithm to recover traffic data from adjacent intersections, addressing the problem of insufficient traffic data caused by limited communication bandwidth, and they introduced a value-decomposition-based multi-agent DRL algorithm for cooperative traffic-light control; the proposed method significantly improved traffic efficiency. Shi et al. [25] developed a DRL approach that integrates a GAN with DDPG, constructing a DDPG model together with an environment-predictive GAN module to facilitate efficient agent–environment interaction; compared with conventional DRL algorithms, the method achieved substantial performance gains in dormitory environment scenarios. Guo et al. [26] introduced a GAN-augmented Meta-DRL intelligent routing framework for dynamic network environments, employing a learnable GAN feature encoder to generate high-quality rare traffic features that markedly accelerate convergence and improved reward performance. Huang et al. [27] presented a DRL-based risk-averse stochastic dynamic scheduling method to enhance both the robustness and economic efficiency of power system operation in critical risk scenarios. They further proposed KEG-GAN to synthesize additional critical scenario samples, which not only elevated the economic efficiency of power system operation but also reduced the potential high costs associated with critical scenarios.

In summary, GAN-enhanced DRL approaches have been widely adopted across diverse domains, leveraging synthetic data to boost the performance of DRL algorithms. Our work follows this paradigm by integrating GANs into a DQN-based anti-jamming decision framework for communications: we employ the GAN to generate a richer variety of jamming samples for pre-training the DQN, thereby substantially accelerating and improving the learning process of the agent.

3. System Model

3.1. Communication Model

As shown in Figure 1, the communication scenario consists of a pair of transceivers and an active jammer, where the transmitter and receiver continuously communicate. The intelligent agent at the receiver end perceives the electromagnetic environment in real time to acquire the features of the jamming signals, and the transmitter dynamically selects anti-jamming strategies. When the transmitter sends signals to the receiver, the jammer performs electromagnetic jamming on the receiver’s channel access, blocking legitimate communications between the two parties.

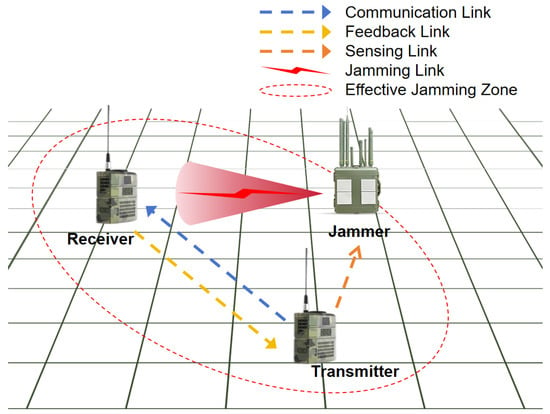
Figure 1. The schematic diagram of the communication confrontation model.

The system uniformly divides the communication frequency band into N continuous non-overlapping channels with a bandwidth of b, and the channel set is $f\in \{0,1,2,\cdots ,N-1\}$. In the discrete time model, the communication time is divided into multiple time slots with a length of T. A time slot is the minimum time unit for continuous data transmission, and the system can communicate within the given wireless communication frequency band by changing the communication channel in the time slot. The receiver determines the jamming degree of this communication according to the Signal-to-Jamming-plus-Noise Ratio (SJNR) of the received signal and evaluates the communication effect, which can be represented by

$${\theta }_t=10lg{\displaystyle \frac{P_S}{P_S+P_J+P_N}}.$$

(3)

where $P_S$ is the transmission power of the signal transmitter, $P_J$ is the transmission power of the jammer, and $P_N$ is the radio frequency environmental noise. The SJNR in the communication system needs to satisfy ${\theta }_t\ge {\theta }_{th}$ in any time slot T of the time period to ensure successful signal transmission. Here, ${\theta }_{t}h$ represents the SJNR threshold.

3.2. Problem Formulation

In this study, we modeled the anti-jamming problem using a Markov Decision Process (MDP). The MDP model involves a set of interacting entities, namely, an agent and an environment. Within a time slot t, the agent observes the current state ${\mathbf{s}}_{\mathbf{t}}$ from the environment, derives an action ${\mathbf{a}}_{\mathbf{t}}$ based on this current state, and inputs the action into the environment. The environment then determines the next state according to ${\mathbf{s}}_{\mathbf{t}}$, and ${\mathbf{a}}_{\mathbf{t}}$ yields a corresponding reward r based on the state value function. The following are the five key elements of the MDP model for solving decision-making problems:

• State space $\mathbf{S}$ represents the set of all channel jamming states; ${\mathbf{s}}_t\in \mathbf{S}$ is an element of the environmental state space, denoting the set of jamming states of all channels at time slot t. The actual state of the entire target frequency band can be expressed as ${\mathbf{s}}_t=[s_t^1,s_t^2,\cdots ,s_t^N]$.
• Action space $\mathbf{A}$ is the set of all executable anti-jamming actions ${\mathbf{a}}_t\in \mathbf{A}$ of the wireless communication system. The transmission power of the communication transmitter is constant. At time slot t, the action of the system is to select one channel from N channels for communication; ${\mathbf{a}}_t{=[\mathrm{a}}_t^1{,\mathrm{a}}_t^2,\cdots {,\mathrm{a}}_t^N]$ represents the transmission channel selected by the transmitter at time slot t.
• Reward function r represents the return obtained from the environment after the wireless communication system selects and executes the anti-jamming action ${\mathbf{a}}_t$. This reward function r is used to calculate the immediate reward. The immediate reward is measured by the normalized throughput and is defined as

  $$r({\mathbf{s}}_t,{\mathbf{a}}_t)=\delta ({\theta }_t\ge {\theta }_{th}),$$

  (4)

  where ${\theta }_t$ is the average SJNR received by the receiver; $\delta \left(\right)$ is an indicator function. The average normalized throughput is used to evaluate the performance of the decision-making algorithm from time slot $t_1$ to $t_2$:

  $$r_{t_1,t_2}={\sum }_{t_1}^{t_2}r({\mathbf{s}}_t,{\mathbf{a}}_t)/(t_2-t_1).$$

  (5)
• The state transition probability p is the probability $\mathbf{P}\left({\mathbf{s}}_{t+1}\right|{\mathbf{s}}_t,{\mathbf{a}}_t)\to [0,1]$ that the intelligent anti-jamming communication system transitions to ${\mathbf{s}}_{t+1}$ after selecting and executing the action ${\mathbf{a}}_t$ in the jamming environment state ${\mathbf{s}}_t$.
• Policy $\pi ({\mathbf{a}}_t,{\mathbf{s}}_t)$ represents the conditional probability distribution of selecting different anti-jamming actions ${\mathbf{a}}_t$ in the current jamming state ${\mathbf{s}}_t$.

4. Experimental Principles

4.1. LACGAN-Based Small-Sample Data-Augmentation Method

4.1.1. Auxiliary-Classifier Generative Adversarial Networks

To address the issue of potential multi-type communication jamming in complex electromagnetic environments, this paper proposes a jamming data-augmentation method using a Layer-normalized Auxiliary-Classifier Generative Adversarial Network (LACGAN) to supplement samples that follow the same distribution as real samples. A traditional GAN is unsupervised learning and cannot generate interference samples of specific categories. The LACGAN is a multi-task learning method based on conditional Generative Adversarial Networks. It can utilize the auxiliary classifier in the discriminator to achieve precise control over the category attributes of generated samples. By combining adversarial loss and classification loss, the generator can synthesize realistic samples with specified features.

The LACGAN inputs both the jamming signal x and the label l into G simultaneously. In D, while determining whether the input sample is a real sample through the auxiliary classifier, it also accomplishes the classification task. When a single sample is input into the LACGAN, the discriminator will output two values: one is the adversarial loss $L_{\mathrm{adv}}$ that measures the distribution difference between the generated sample and the real sample; the other is the classification loss $L_D$ that distinguishes the category label of the generated sample from the target jamming type. Similarly, the loss function of the LACGAN consists of the discriminative loss $L_{\mathrm{adv}}$ and the classification loss $L_D$.

The overall loss after summarization is as follows:

$$L_{\mathrm{adv}}=E_{x\sim P_{data}\left(x\right)}[log\left(D_{ac}\left(x\right)\right)]+E_{z\sim P_z\left(z\right)}[log(1-D_{ac}\left(G(z,l)\right))]$$

(6)

$$L_{cls}=E_{x\sim P_{data}\left(x\right)}[log\left(L_{cls}\left(l_x\right|x)\right)]+E_{z\sim P_z\left(z\right)}[log{L}_{cls}\left(l\right|G(z,l)))],$$

(7)

where $D_{ac}\left(x\right)$ is the probability that D judges the input x as a real sample; $D_{ac}\left(G(z,y)\right)$ is the probability that the generated sample is judged as a real sample after passing through the discriminator; $L_{cls}\left(l_x\right|x)$ represents the classification loss of D for x, and $l_x$ is the real label of x; and $L_{cls}\left(y\right|G(z,l))$ represents the classification loss for the generated sample.

The overall loss after summarization is as follows:

$$\underset{D}{max}V(D,G)=L_{adv}+L_D$$

(8)

$$\underset{G}{max}V(D,G)=-L_{adv}+L_D.$$

(9)

4.1.2. Network Architecture Design

The specific design of the LACGAN network is shown in Figure 2. Based on a traditional GAN, mainly the following improvements have been made:

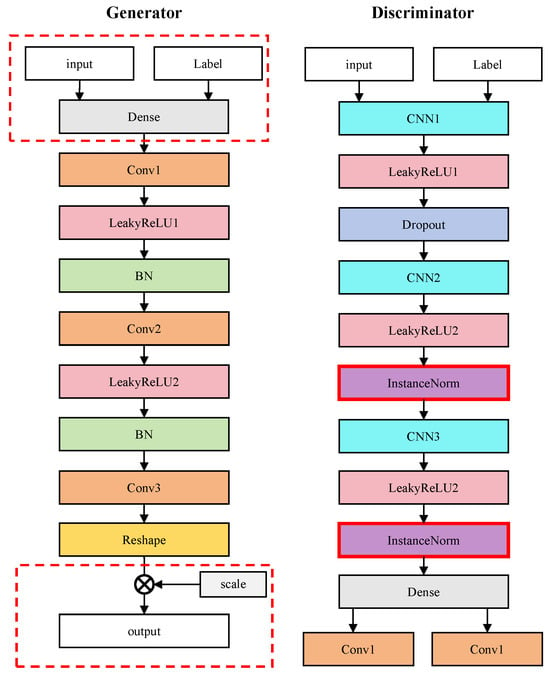
Figure 2. The network architectures of the generator and discriminator in a LACGAN (the red border is the improvement).

• A label-embedding layer is added to the input of the generator. It maps discrete category labels into continuous vectors, which are then concatenated with jamming vectors to form combined inputs. This enables the generator to clearly distinguish the feature distributions of different jamming types in the latent space, achieving precise control over jamming types.
• Instance normalization (InstanceNorm) is adopted in the discriminator. The discriminator of a traditional GAN only outputs the authenticity probability and uses batch normalization (BatchNorm), which leads to instability in small-batch training. Instance normalization performs normalization on the feature dimension of each sample and does not depend on the batch size, improving the fine-grained classification of samples.
• The LACGAN introduces learnable scaling factors at the output layer of the generator by setting learnable intensity parameters. It can automatically learn the optimal intensity range for different jamming types through backpropagation, dynamically adjusting the jamming intensity. This enhances the adaptability of the generator in different Signal-to-Jamming-plus-Noise Ratio (SJNR) conditions.

4.1.3. Sample Evaluation of Sample Evaluation Metrics

This paper evaluated and screened the jamming samples generated by a LACGAN using the Pearson correlation coefficient. In the process of improving the success rate of DQN anti-jamming decision-making through data augmentation, if the similarity between the generated signal and the real signal is extremely high and the added training data fails to bring diversity to the recognition model then the augmentation effect exerted by the generated signal will be limited. Conversely, if the similarity between the generated signal and the real signal is too low then it will mislead the DQN model. Not only will it fail to achieve an augmentation effect but it will also reduce the decision-making accuracy of the DQN.

This paper applied the Pearson correlation coefficient [28] to evaluate the linear correlation between the original samples and the generated jamming samples. Its value range is $\left[0,1\right]$, where the closer the absolute value is to 1 the higher the similarity between the two. The calculation formula is as follows:

$$r(x_l,y_l)={\displaystyle \frac{{\displaystyle \sum _{i=1}^N}(x_{l_i}-\overline{x_l})(y_{l_i}-\overline{y_l})}{\sqrt{{\displaystyle \sum _{i=1}^N}{(x_{l_i}-\overline{x_l})}^2{\displaystyle \sum _{i=1}^N}{(y_{l_i}-\overline{y_l})}^2}}}.$$

(10)

where r represents the Pearson correlation coefficient; $x_{l_i}$ and $y_{l_i}$ are the original sample of category l; and $\overline{x_l}$ and $\overline{y_l}$ are the mean values of the generated samples of category l.

Finally, according to the calculation results of the Pearson correlation coefficient, the signals in the generated sample set $S_{coarse-grained}$ are sorted in descending order. The five samples with the highest similarity and the five samples with the lowest similarity are selected, and the final generated jamming sample result $S_{fine-grained}$ is obtained.

4.2. GA-DQN Anti-Jamming Decision-Making Method

4.2.1. DQN Algorithm

In the MDP, the goal of the intelligent anti-jamming communication system is to find an optimal policy ${\pi }^{*}$, such that in any given state the selected action can maximize the long-term cumulative reward. To achieve this goal, a neural network is used to approximate the state-action value function $Q\left(\mathbf{s},\mathbf{a};\theta \right)$, where $\theta$ represents the network parameters. Thus, it can be expressed using the optimal Q-function as

$$Q^{*}(s,\mathrm{a})={\mathrm{E}}^{\pi }\left[\sum _{\tau =0}^{\infty }{\gamma }^{\tau }r(s_{t+\tau },{\mathrm{a}}_{t+\tau })|s_t=s,{\mathrm{a}}_t=\mathrm{a}\right],$$

(11)

where ${\mathrm{E}}^{\pi }\left[\right]$ is the mathematical expectation operator and $\tau$ denotes the subsequent steps starting from time slot t.

To enhance training stability, an independent target Q-network is employed to compute the target Q-value. The parameters ${\theta }^{-}$ of the target network are periodically copied from the main network, with the update frequency controlled by hyperparameters. The loss function of the DQN is defined as the Mean Squared Error (MSE):

$$L\left(\theta \right)=\mathrm{E}\left[{(r_t+\gamma maxQ({\mathbf{s}}_{t+1},{\mathbf{a}}^{\prime };{\theta }^{-})-Q({\mathbf{s}}_t,{\mathbf{a}}_t;\theta ))}^2\right].$$

(12)

During the algorithm training phase, the $\epsilon$-greedy policy is adopted for training updates. The optimal policy ${\pi }^{*}\left(a|\mathbf{s}\right)$ can then be inferred as follows:

$${\pi }^{*}\left(a|\mathbf{s}\right)=\left\{\begin{array}{c}\underset{a\in A}{\mathrm{argmax}}{Q}^{*}(\mathbf{s},\mathbf{a}),0\le x\le 1-\epsilon \hfill \\ random,1-\epsilon \le x\le 1\hfill \end{array}\right..$$

(13)

4.2.2. DQN Algorithm

For the anti-jamming decision-making problem in small-sample conditions, firstly, LACGAN is used to complete the data augmentation and concatenation of the small-sample jamming signals. Then, the augmented samples are input into the DQN model as training samples. The entire training process for generating jamming samples is shown in Algorithm 1.

Algorithm 1 GAN Algorithm for Synthetic Sample Generation

1: Initialize G, D with random weights; 2: Initialize Adam optimizers for G and D; 3: Initialize learning rate, epochs N, batch size B; 4: for  $epoch\leftarrow 1$ to N do 5:     for $batch\leftarrow 1$ to B do 6:         Sample real jamming batch $x_{\mathrm{real}}$; sample noise batch z; 7:         Generate fake data $x_{\mathrm{fake}}\leftarrow G\left(z\right)$; 8:         Train Discriminator D: 9:         Update D parameters via Adam to minimize ${\mathcal{L}}_D$; 10:       Sample new noise batch $z^{\prime }$; generate new fake data $x_{\mathrm{fake}}^{\prime }$; 11:       Train Generator G: 12:       Update G parameters via Adam to minimize ${\mathcal{L}}_G$; 13:     end for 14:     Compute Pearson correlation coefficients r; concatenate selected samples to form augmented dataset; 15: end for 16: return Augmented dataset.

To accelerate the convergence speed and enhance the decision-making accuracy of the DQN anti-jamming algorithm, this paper proposes a fast anti-jamming algorithm based on a Generative Adversarial DQN. The DQN model in this algorithm adopts the classical conventional architecture [29], as shown in Figure 3, and it incorporates Algorithm 1, enabling the GAN to generate additional experience samples every K time slots. This approach improves the efficiency of sample collection during the training phase of the algorithm, thereby accelerating the learning process. The specific procedure is detailed in Algorithm 2.

Algorithm 2 DQN Anti-Jamming Decision-Making Algorithm

Input: Environmental state ${\mathit{s}}_t$. Output: Anti-jamming transmission policy $\pi$. 1: Initialization: Q, $\widehat{Q}$ (set $Q=\widehat{Q}$), and parameter K. 2: for $T=1,2,\cdots ,\infty$ do 3:     The transmitter executes the transmission action ${\mathit{a}}_{T+1}$ according to the action instruction. 4:     Calculate the transmission action reward $r({\mathit{s}}_T,{\mathit{a}}_{T+1})$. 5:     Obtain the channel state set ${\mathit{s}}^{T+1}$ of the next time slot and collect channel states. 6:     if $T\%K=0$ then 7:         Execute Algorithm 1, generate additional experience samples. After pre-training by the DQN, store them in the experience pool $\mathcal{E}$. 8:     end if 9:     Batch sample from the experience pool $\mathcal{E}$. 10:   Input samples into the target network and the policy network. The former outputs $max\widehat{Q}({\mathit{s}}^{\prime },{\mathit{a}}^{\prime };\theta )$, and the latter outputs $Q(\mathit{s},\mathit{a};\theta )$. 11:   Use stochastic gradient descent + backpropagation to update the network parameters $\theta$. 12:   At the end of the time slot, sense the spectrum to obtain the state ${\mathit{s}}_{T+1}$ of the next time slot. 13:   Continue to execute the policy according to the previous time slot. 14: end for

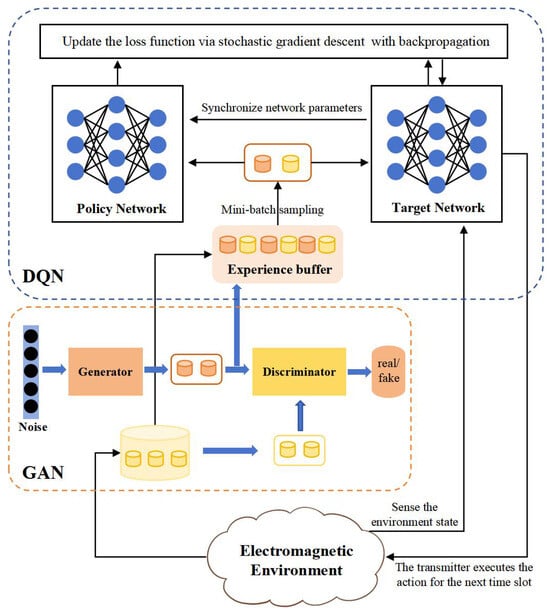
Figure 3. Algorithm architecture.

5. Experimental Results and Analysis

The analysis of our experimental results is mainly divided into two parts. The first part focuses on the performance analysis of jamming sample signals generated by the LACGAN network, verifying whether a GAN can learn the time–frequency features of jamming signals when applied in communication environments. The second part aims to verify the anti-jamming decision-making effect of a GA-DQN, testing whether the DQN model can improve its decision-making accuracy and convergence speed after pre-training with experience sample signals generated by a GAN.

5.1. Simulation Setup

To support the performance analysis and comparison of small-sample jamming signal data augmentation in this paper, four types of jamming signals were provided for sample generation by a GAN: Multi-Tone Jamming (MTJ), Frequency-Hopping Jamming (FH), Comb-shaped Sweeping Jamming (CSJ), and Linear Sweeping Jamming (LSJ). The specific parameters are shown in Table 1. In the dataset, the jamming signals are transmitted through a random noise channel. The JNR can be selected within the range of −4 dB to 16 dB (with a step size of 2). The shape is set as 12 × 100, where the number of channels is 12 and the jamming time slots number 100.

Table 1. GAN-enhanced DRL models.

Ref	Application	Method	Key Feature
[22]	Dynamic spectrum access	SWGAN	Simulates the spectrum environment for offline training.
[23]	Network intrusion detection	CTGAN	Generates datasets via a GAN to pre-train DRL.
[24]	Traffic signal control	GAN	Reconstructs neighboring traffic data, using traffic statistics.
[25]	Dormitory environment design	GAN	Rapidly predicts indoor performance with a GAN.
[26]	Network routing optimization	GAN	Produces rare traffic features; optimizes the discriminator boundary.
[27]	Power system scheduling	KEG-GAN	Synthesizes additional critical scenario samples.

• Multi-Tone Jamming: The energy of this jamming is evenly concentrated on multiple fixed channels. The interval between the jamming channels is 4 channels, and the initial jamming position is channel 2. It continuously acts on multiple fixed channels within 100 time slots.
• Frequency-Hopping Jamming: This type of jamming adopts a pseudo-random hopping mode, performing time-varying frequency point switching within 12 channels. Only 1 channel is activated in each time slot, and the activation position is determined cyclically by the frequency-hopping pattern map.
• Comb-shaped Sweeping Jamming: This type of jamming presents a dynamically changing comb-tooth shape in the time–frequency domain. The interference channels are spaced 4 channels apart, starting from channel 2, and the sweep is at a rate of 1 channel per time slot.
• Linear Sweeping Jamming: This jamming exhibits continuous frequency sweeping characteristics. The jamming starts from a random channel number and scans at a constant rate of 1 channel per time slot. It reflects at the spectrum boundary, forming a saw-toothed jamming path.

In the experiment, firstly, the jamming signals are input into the LACGAN for data augmentation. Then, the generated jamming samples are subjected to time-stitching data expansion, input into the DQN model for pre-training, and stored in the experience pool, so as to improve the anti-jamming capability of the DQN.

5.2. Experiment on the Generalization of Network Application

Intelligent anti-jamming methods based on Deep Reinforcement Learning (DRL) determine optimal communication anti-jamming strategies autonomously by learning the patterns and characteristics of detected jamming signals, thus evading jamming signals emitted by jammers. However, a distinctive feature of such methods is that they require acquiring jamming information over sufficient time slots for strategy exploration. In contrast, the intelligent anti-jamming decision-making method based on the GA-DQN proposed in this paper directly leverages a GAN to learn the time–frequency characteristics of sudden jamming signals from short-term attacks. It then generates samples with similar characteristics as the jamming signals. When facing unfamiliar and unknown jamming, this enables the DQN to converge more rapidly. Compared with traditional intelligent anti-jamming methods, it exhibits stronger generalization. The following presents an experimental investigation into the application effects of GANs under different jamming signals, different JNRs, and different iteration counts, to verify its generalization.

Figure 4 shows the process of the simultaneous convergence of the loss functions of the generator and the discriminator. Due to the mutual antagonism between the two networks, in the initial stage of training the oscillation of the generator loss is relatively obvious, reflecting that the learning of the time–frequency characteristics of the jamming samples by the generator of the GAN network is still unstable. From the overall trend, the loss function of the discriminator network shows a decreasing trend, while the loss function of the generator shows an increasing trend, indicating that the discrimination ability of the discriminator is improving. When the number of iterations exceeds 250, both the generator loss and the discriminator loss function tend to be stable, and the network can converge.

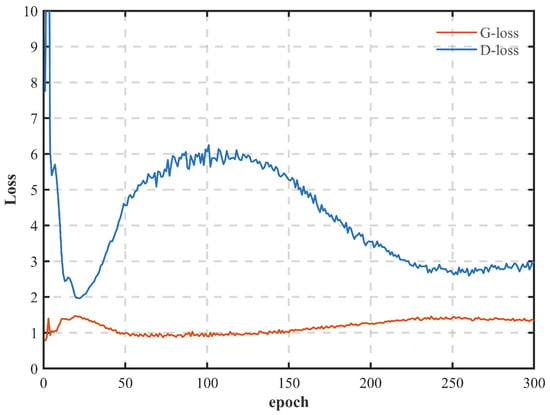
Figure 4. Generator and discriminator loss function variations during GAN training.

In experiment 1, time–frequency feature learning was performed on the CSJ signal, and the signal was input into the GAN network for training. To illustrate that a GAN also has a good generation effect on different types of jamming signals, MTJ, FH, and LSJ were, respectively, selected as the target jamming signals. All the signals were normalized, and the JNR was set to 10 and then input into the GAN for adversarial training.

As can be seen from Figure 5, for different types of jamming signals the network learned their time–frequency features. Among these, the jamming samples generated from the MTI and CSJ signals had the greatest similarity and almost overlapped with the original samples. The jamming samples generated from the LSJ signal possessed the time–frequency characteristics of the original jamming, but the start time slot of the attack was delayed by 50 time slots. The jamming samples generated from the FH signal had relatively large differences from the original samples, but they conformed to the signal characteristics of Frequency-Hopping Jamming with fast carrier-frequency switching. The GAN could not only generate jamming samples with very high similarity to the original samples, meeting the subsequent needs of improving the decision-making accuracy and convergence speed of the DQN, but it could also generate jamming samples with relatively low similarity but similar jamming strategies. The added training data can bring diversity to the decision-making model and exert a better enhancement effect.

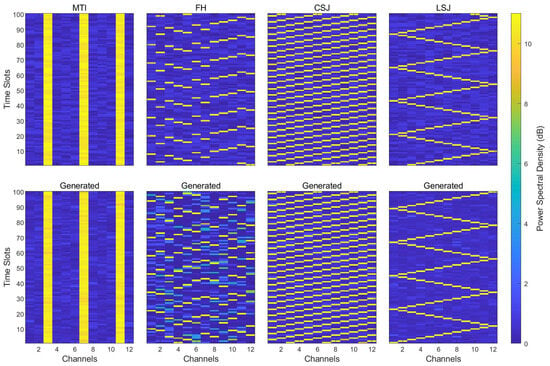
Figure 5. Comparison between generated samples and original samples.

Figure 6 presents the Pearson correlation coefficients between the samples generated under the JNR and iteration counts and the original jamming samples, demonstrating the generalization ability of the LACGAN. It can be seen from the figure that the Pearson correlation coefficient was basically positively correlated with the iteration count and JNR. As the iteration count or the JNR increased, the Pearson correlation coefficient also increased. In subsequent experiments, the JNR was set to 10, and when the iteration count reached 90 the Pearson correlation coefficient had exceeded 0.99. Therefore, the iteration count of the GAN was set to 90 in the subsequent experiments.

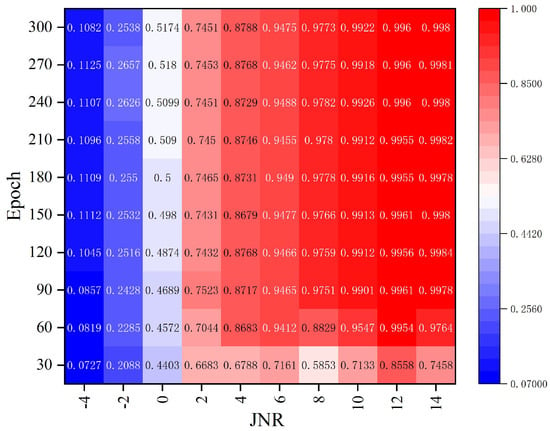
Figure 6. Heatmap of Pearson correlation coefficients.

5.3. Simulation Analysis of GA-DQN

To verify the anti-jamming decision-making capability of the GA-DQN algorithm, this paper compares the GA-DQN algorithm with the conventional DQN algorithm [29], the Proximal Policy Optimization algorithm (PPO) [30], and the Q-learning algorithm [31]. For an objective analysis of the performance of the proposed algorithm, the parameters of the algorithms involved in the comparison were all set to the same values as those of the proposed algorithm. The maximum capacity of the experience replay buffer was 10,000, and the batch processing size was 64. The other simulation parameters were set as shown in Table 2. In addition, the normalized throughput of rewards was adopted as the evaluation index for the anti-jamming decision-making capability of the intelligent algorithm, and the sliding average method (with a window length of 50) was used for curve plotting to obtain smooth curves.

Table 2. Simulation parameter settings.

Parameter	Value
Length of communication time slot $T_s$	350
Number of channels M	12
Threshold of JSR ${\theta }_{th}$	8
Discount rate $\gamma$	0.3
Communication power $p_L/dBm$	10
Jamming power $p_L^{\prime }/dBm$	10

In the performance comparison simulation, four distinct jamming environments were configured to analyze the anti-jamming performance and robustness of the proposed algorithm, as can be seen from Figure 7:

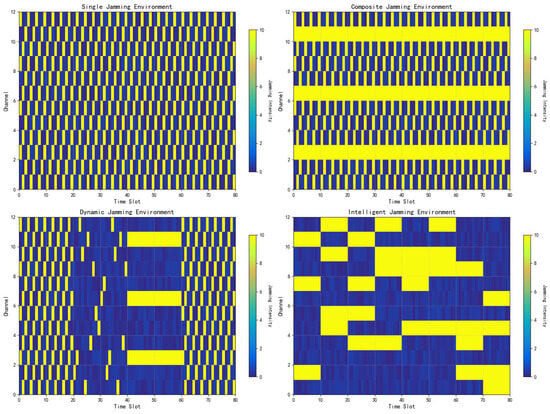
Figure 7. Time–frequency schematic diagram of jamming environment.

• Single-jamming environment: The jammer employs only single comb-shaped sweeping jamming to disrupt the receiver;
• Composite-jamming environment: The jammer simultaneously deploys comb-shaped sweeping jamming and multi-channel jamming to challenge the receiver;
• Dynamic-jamming environment: The jammer switches jamming types every 100 time slots in the sequence of $\mathrm{CSJ}\to \mathrm{FH}\to \mathrm{MTJ}\to \mathrm{LSJ}$. This dynamic pattern prevents the DQN from fully exploring and adapting to any single jamming type;
• Intelligent-jamming environment: The jammer updates its target channels every 10 time slots, selecting the channels occupied by the communication signals in the previous 10 slots plus 4 adjacent channels. This adaptive strategy mimics intelligent adversarial behavior.

In neural network training, the learning rate is of great importance to the performance of the neural network. To set appropriate learning rate parameters, this paper analyzed the performance of the DQN algorithm at different learning rates in a single-jamming environment. Figure 8 compares the normalized throughput performance of the algorithm proposed in this paper when the learning rates were 0.01, 0.001, and 0.0001, respectively. It can be seen from the figure that when the learning rate was 0.01, due to the too-fast convergence of the neural network parameters, the DQN calculation was unstable and problems such as gradient explosion occurred; when the learning rate was 0.0001, the convergence speed of the DQN network was slow and the ideal performance was not achieved; when the learning rate was set to 0.001, the DQN converged well and could achieve the ideal performance. Therefore, this learning rate was used in the subsequent simulations.

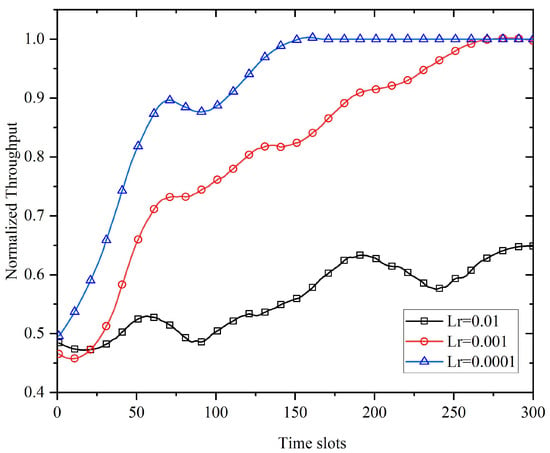
Figure 8. Comparison of DQN algorithm at different learning rates.

In this paper, the experience sample generation cycle of the GA-DQN algorithm was set to k time slots. To achieve optimal performance, it was necessary to validate the impact of different generation cycles K on the algorithm’s performance. Figure 9 compares the normalized performance of the proposed algorithm in different generation cycles ($k\in \left\{0,10,20,30,40,50\right\}$) in a single-jamming environment. When $k=0$, it corresponded to the traditional DQN algorithm; when $k=10$, the GAN could not effectively learn the jamming signal characteristics, due to the excessively short generation cycle, which affected the algorithm’s convergence; when $k=30,40,50$, the longer generation cycles failed to achieve the optimal performance; when $k=20$, the GAN could both learn the jamming signal characteristics and effectively improve the convergence speed, achieving the ideal effect. Therefore, the experience sample generation cycle was set to 20 in the subsequent experiments.

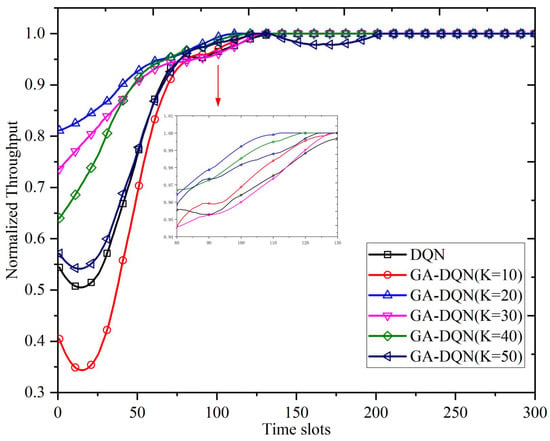
Figure 9. Comparison of the proposed algorithm in different generation cycles.

Figure 10 shows the performance comparison between the GA-DQN algorithm and the three other comparative algorithms in the four types of jamming environments. It can be seen from the figure that the GA-DQN algorithm had the fastest convergence speed and the highest convergence value. In single- and composite-jamming environments, the GA-DQN algorithm outperformed the traditional Deep Reinforcement Learning algorithms such as the DQN and PPO in convergence, with significantly reduced jamming times in the early communication stage; the DQN algorithm converged slightly slower than the GA-DQN but could reach around 1; the PPO algorithm performed slightly worse than the DQN and needed about 275 time slots to converge, while the QL algorithm showed the worst performance and could only converge to about 0.65. In the dynamic-jamming environment, the GA-DQN algorithm could converge at 170 time slots and resist the last fixed multi-channel jamming; the DQN algorithm could only converge to about 0.94, and the PPO and QL algorithms had poor convergence with severe jamming. In the intelligent-jamming environment, the normalized throughput performance of the GA-DQN algorithm decreased at the beginning of communication, started to rise at 100 time slots, and converged to about 0.95 at 130 time slots; due to the intelligent jamming changing every 10 time slots, the other three algorithms did not achieve convergence within 300 time slots. Table 3 aggregates the anti-jamming performance metrics (convergence slots and throughput performance) of our proposed algorithm alongside the three benchmark algorithms across the four distinct jamming environments. The comparative analysis visually demonstrates our algorithm’s superior convergence speed and enhanced throughput efficiency relative to the alternatives.

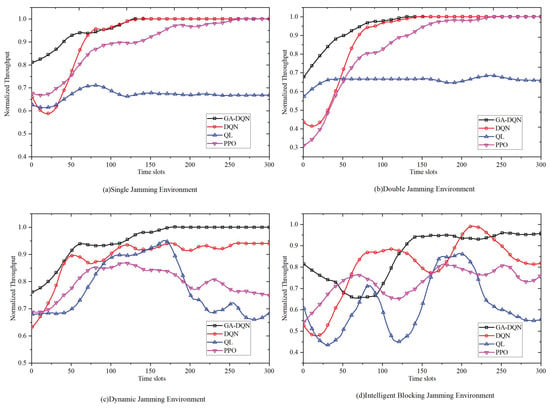
Figure 10. Comparison of multiple algorithms in different jamming environments.

Table 3. The performance index of the anti-jamming algorithm based on comparing the convergence slot (CS) and the throughput performance (TP) of the four types of algorithms.

Model	Single Jamming		Double Jamming		Dynamic Jamming		Intelligent Jamming
	C S	T P	C S	T P	C S	T P	C S	T P
GA-DQN	126	1	131	1	185	1	245	0.95
DQN	147	1	156	1	256	0.94	280	0.82
PPO	263	1	252	1	280	0.75	300	0.75
QL	149	0.67	211	0.67	300	0.68	300	0.55

6. Conclusions

In this paper, we addressed the convergence speed issue of DRL algorithms in complex jamming environments by proposing a GAN-enhanced DQN fast anti-jamming algorithm. The algorithm leverages a GAN to learn the time–frequency characteristics of jamming signals, generate additional experience samples, and input them into the DQN model for pre-training, thereby accelerating the algorithm’s learning process and convergence speed. Furthermore, this paper simulated and compared three other anti-jamming algorithms. The proposed algorithm demonstrated faster convergence, higher convergence values, and more stable communication across diverse jamming environments. The algorithm also holds the potential to be applied to more complex jamming scenarios, effectively improving communication reliability.