Discrete Element Analysis of Grouting Reinforcement and Slurry Diffusion in Overburden Strata
Abstract
1. Introduction
2. Fundamental Principles of Mechanics
2.1. Wall Servo Loading Mechanism
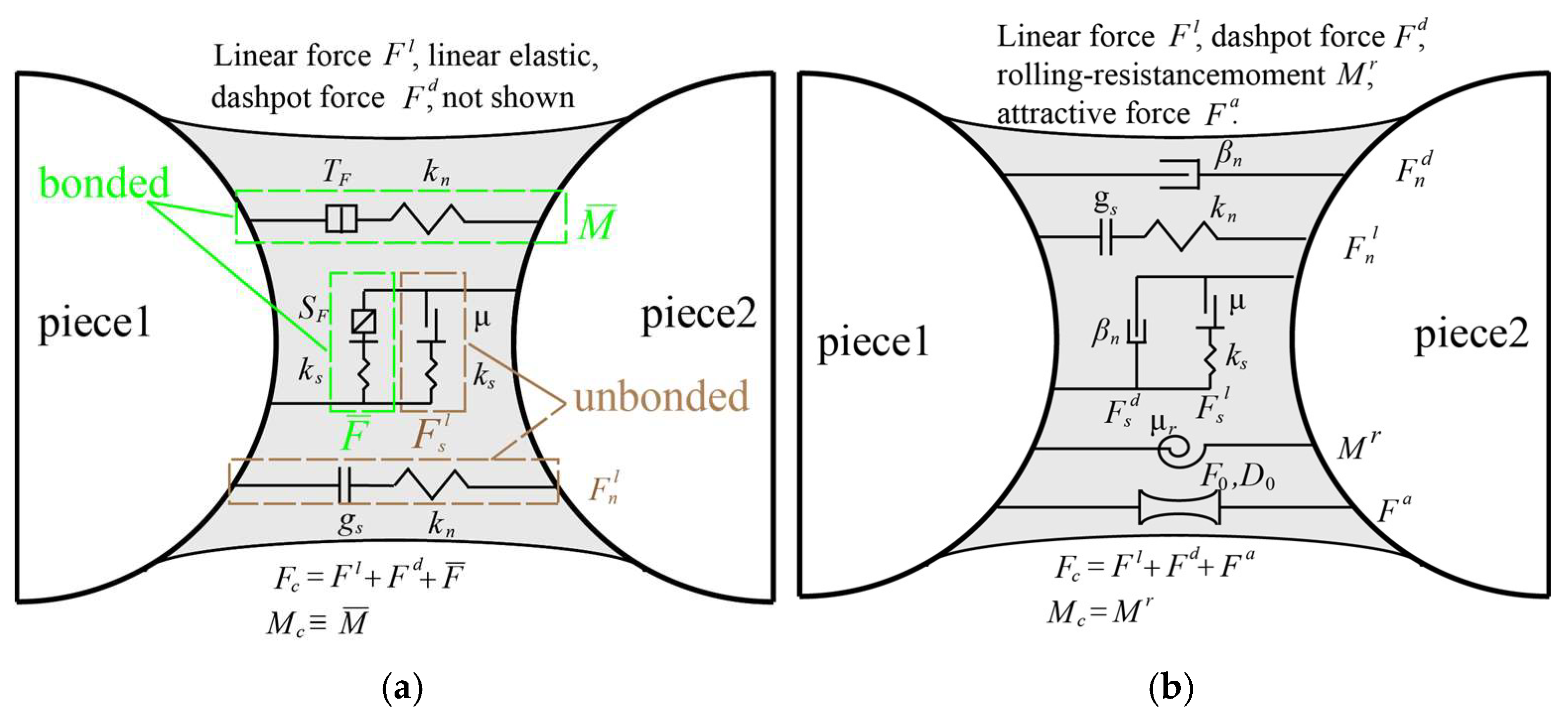
2.2. Particle Contact Contact Model
2.3. Numerical Calculation Assumptions
3. Model Establishment and Parameter Calibration
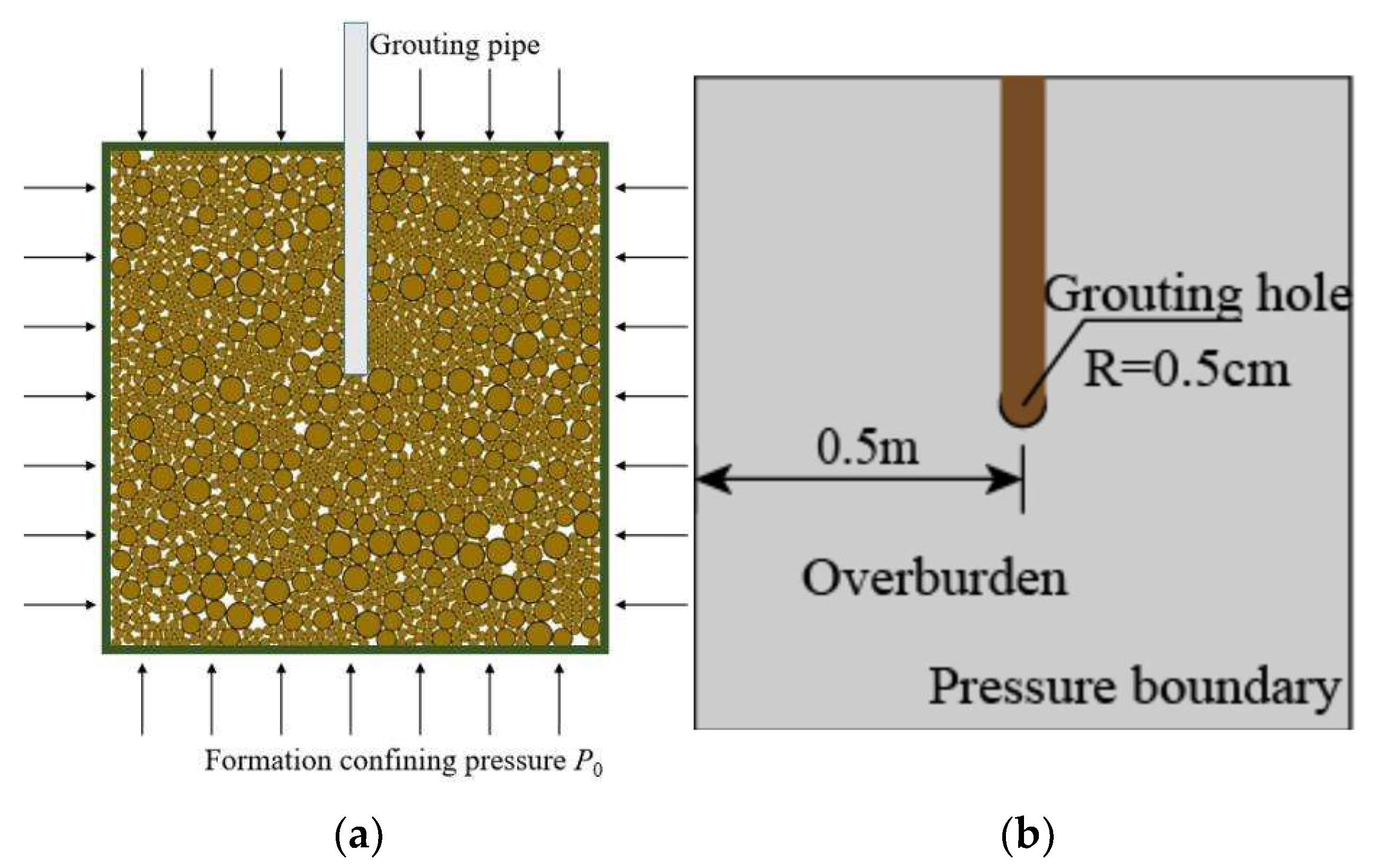
3.1. Geometric Model and Particle Generation
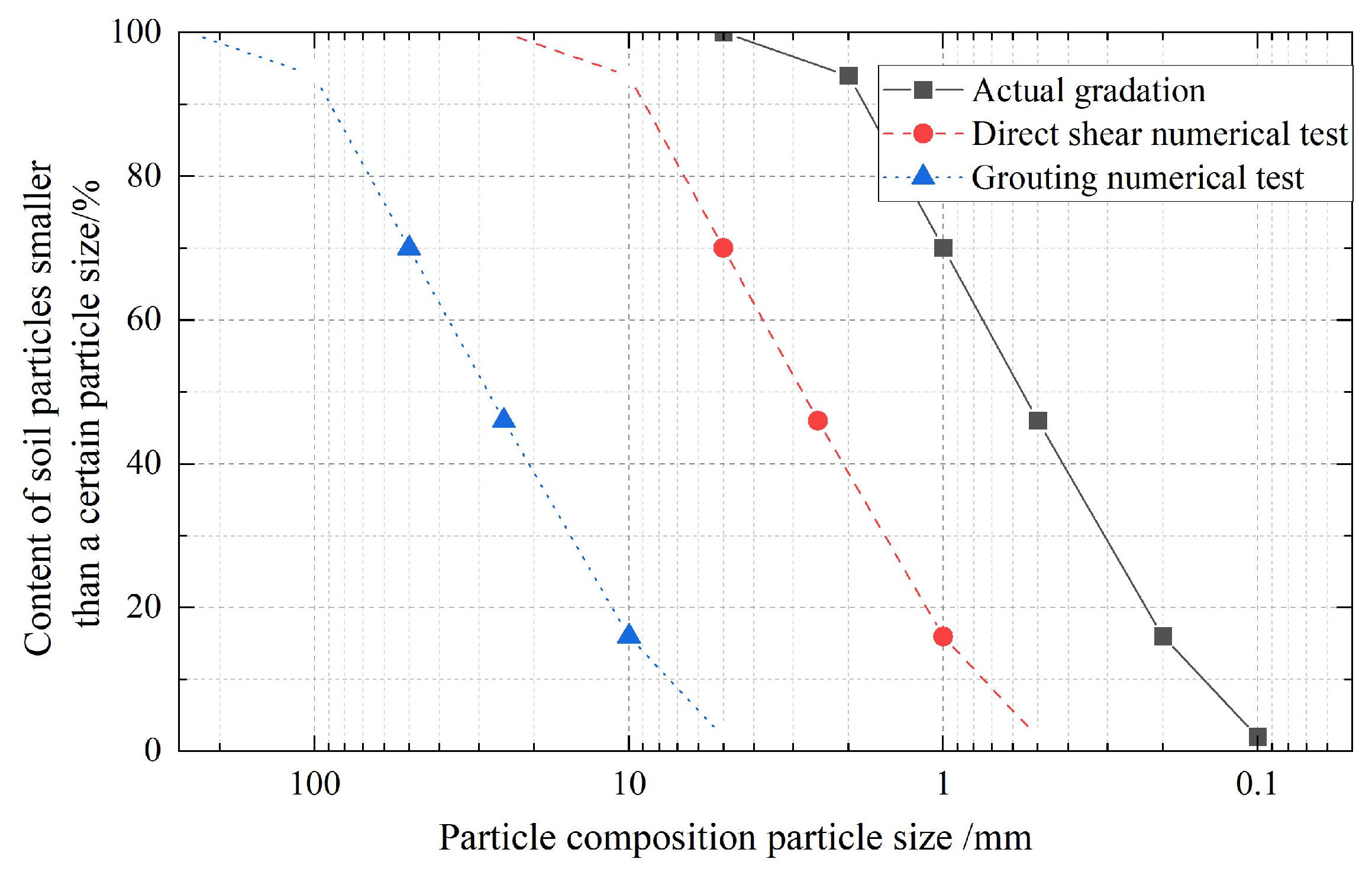
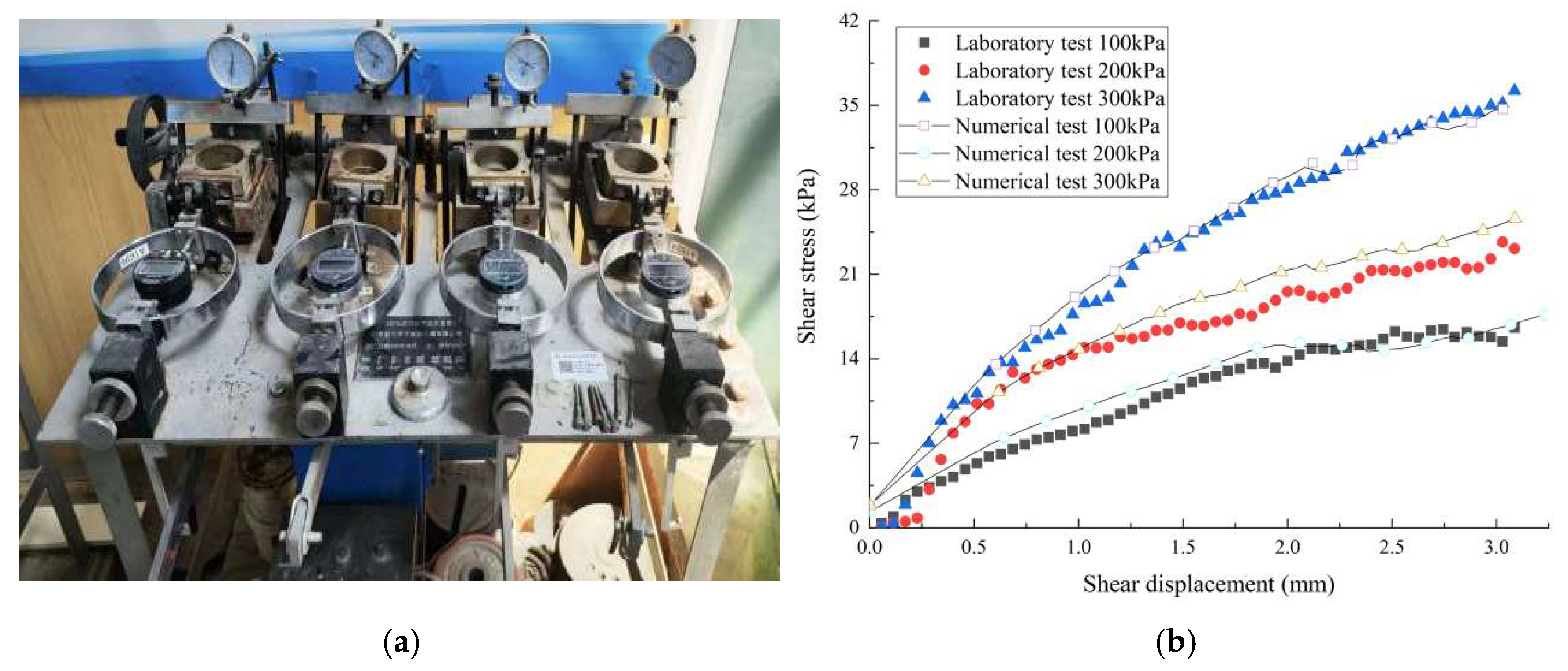
3.2. Overburden Strength Parameter Calibration (Direct Shear Test)
3.3. Calibration of Cement Slurry Flow Parameters (Marsh Funnel Test)
3.4. Calculation of Particle Coarsening Treatment Method
4. Discrete Element Grouting Diffusion Results
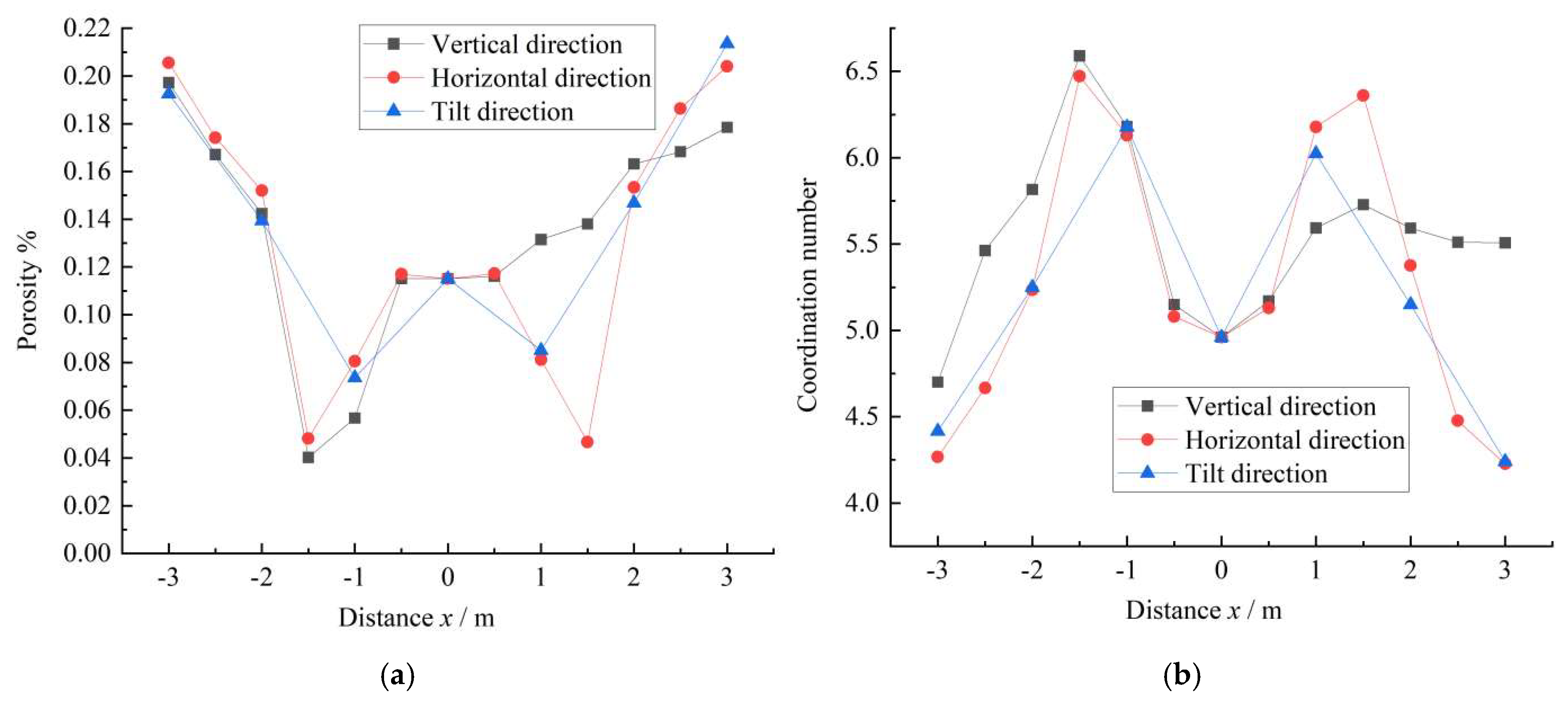
4.1. Analysis of Grouting Reinforcement Form
4.2. Grouting Reinforcement Mechanism Analysis
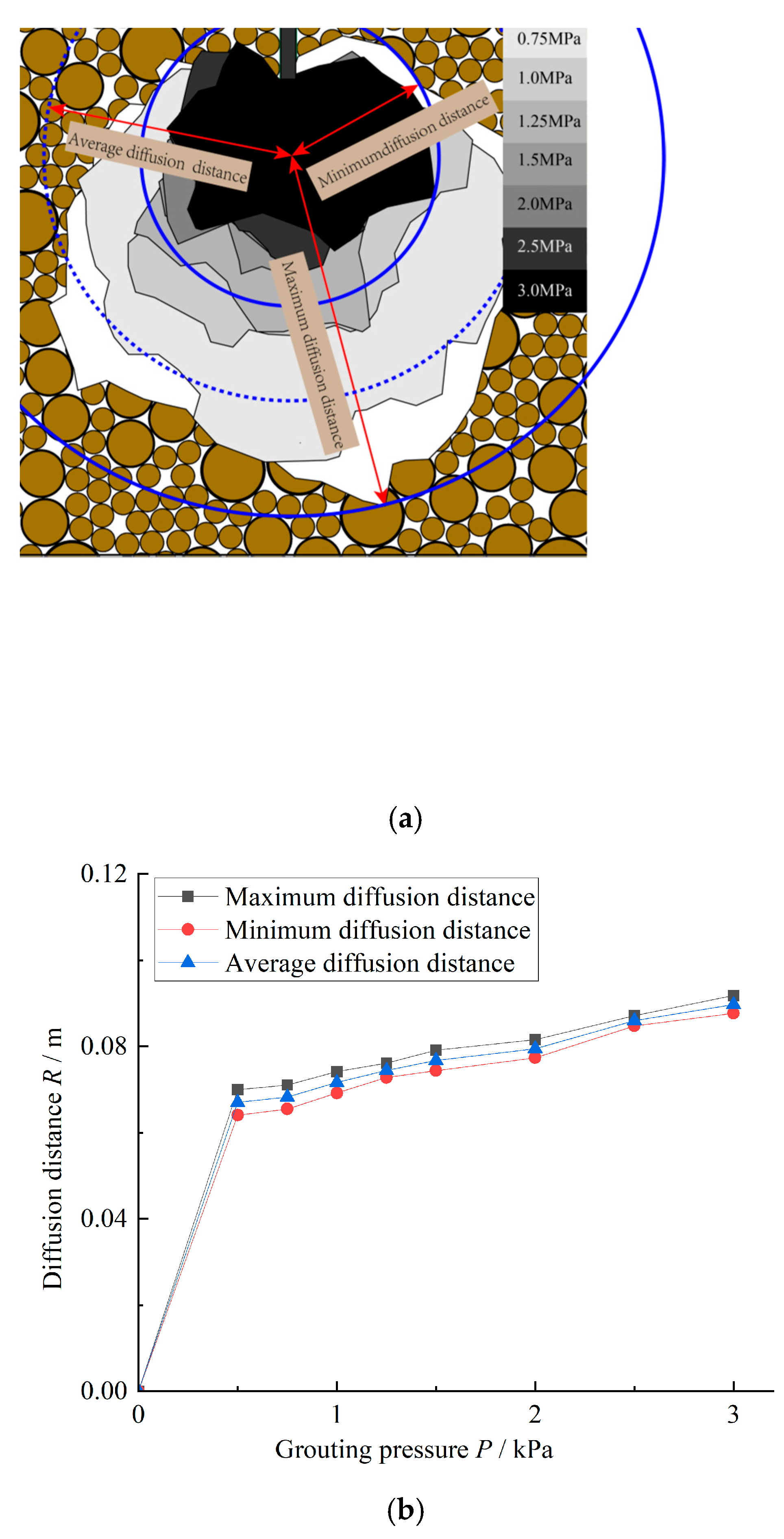
4.3. Influence of Formation Confining Pressure on Slurry Diffusion Radius
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Z.J.; Jiang, Y.Y.; Wang, X.D.; Yu, X.M.; Wang, D.Z. Numerical simulation method of grouting diffusion for foundation with overburden and its application. Chin. J. Undergr. Space Eng. 2017, 13, 646–650. (In Chinese) [Google Scholar]
- Deng, S.H.; Wang, X.L.; Ao, X.F.; Ren, B.Y.; Li, R.J. Three-dimensional numerical simulation of curtain grouting in the dam bedrock based on binghamian grouts. J. Hydraul. Eng. 2016, 47, 165–172. (In Chinese) [Google Scholar]
- Cheng, S.Z.; Chen, T.L.; Guo, W.Q.; Zhang, Y. Numerical simulation of fracture grouting and influencing factors for morphology of grout veins. Chin. J. Geotech. Eng. 2019, 41, 484–491. (In Chinese) [Google Scholar]
- Li, X.L.; Chen, C.; Wang, Y.S.; Zhang, B.; Zhong, Y.H. Simulation method for fracture grouting of expansible polymer in soil. China Civ. Eng. J. 2023, 56, 156–165. (In Chinese) [Google Scholar]
- Shi, G.C.; Yang, L.Q.; Dai, G.Z. A porous grouting theory based on natural boundary element method. China Rural. Water Hydropower 2013, 135–138. (In Chinese) [Google Scholar]
- Hou, X.P.; Chen, S.H. Simulation of variably-saturated flow in fractured porous media using composite element method. Rock Soil Mech. 2020, 41, 1437–1446. (In Chinese) [Google Scholar]
- Bouchelaghem, F.; Vulliet, L. Mathematical and numerical filtration–advection–dispersion model of miscible grout propagation in saturated porous media. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 1195–1227. [Google Scholar] [CrossRef]
- Papanastasiou, T.C.; Boudouvis, A.G. Flows of viscoplastic materials: Models and computations. Comput. Struct. 1997, 64, 677–694. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Zang, H.Z.; Wang, S.Y.; Du, X.M.; Ma, D.; Zhang, J. Filtration behaviour of cement-based grout in porous media. Transp. Porous Media 2018, 125, 435–463. [Google Scholar] [CrossRef]
- Wang, D.L.; Hao, B.Y.; Liang, X.M. Slurry diffusion of single fracture based on fluid-solid coupling. J. Min. Strat. Control Eng. 2021, 3, 104–112. (In Chinese) [Google Scholar]
- Ao, X.F.; Wang, X.L.; Zhu, X.B.; Zhou, Z.Y.; Zhang, X.X. Grouting simulation and stability analysis of coal mine goaf considering hydromechanical coupling. J. Comput. Civ. Eng. 2017, 31, 4016069. [Google Scholar] [CrossRef]
- Min, H.J.; Chen, X.; Lu, X.C.; Tian, X.C.; Wei, K.X. Laboratory experimental study on seepage erosion in wide-graded soils considering saturated permeability coefficient. Water Resour. Hydropower Eng. 2023, 54, 183–192. (In Chinese) [Google Scholar]
- Geng, P.; Lu, Z.K.; Ding, T.; Quan, Z.L.; Yan, Q.X. Research on the dynamic process simulation of rock grouting based on particle flow. J. Railw. Eng. Soc. 2017, 34, 34–40. (In Chinese) [Google Scholar]
- Lin, T.; Zhao, Z.H.; Zhou, S.M. Block-based DEM modeling on grout penetration in fractured rock masses. Chin. J. Undergr. Space Eng. 2021, 17, 1080–1090. (In Chinese) [Google Scholar]
- Zhou, Z.; Zhao, Y.; Chen, Z.; Du, X.M.; Wu, Z.B. Meso-mechanism of compaction grouting in soil based on particle flow method. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 465–472. (In Chinese) [Google Scholar]
- Liu, X.L.; Wang, F.; Huang, J.; Wang, S.J.; Zhang, Z.Z.; Nawnit, K. Grout diffusion in silty fine sand stratum with high groundwater level for tunnel construction. Tunn. Undergr. Space Technol. 2019, 93, 103051. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Shao, Z.S.; Fang, X.B.; Liang, X.J. Research on the fracture grouting mechanism and PFC numerical simulation in loess. Adv. Mater. Sci. Eng. 2018, 2018, 4784762. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, S.; Liu, R. Analysis on structural characteristics of grout and rock distribution in complex geological mixtures after grouting reinforcement and its mechanical strength. Rock Mech. Rock Eng. 2021, 54, 3757–3782. [Google Scholar] [CrossRef]
- Yu, H.; Jia, H.S.; Liu, S.W.; Liu, Z.H.; Li, B.Y. Macro and micro grouting process and the influence mechanism of cracks in soft coal seam. Int. J. Coal Sci. Technol. 2021, 8, 969–982. [Google Scholar] [CrossRef]
- Yang, S.; Li, X.Q. Shear simulation and macro meso analysis of sand based on PFC3D. Chin. J. Comput. Mech. 2019, 36, 777–783. (In Chinese) [Google Scholar]
- Gao, Z.G.; Dong, P.K.; Zhang, Y.J.; Sun, H.Z.; Di, Y. A novel discrete element rolling resistance model based on hysteresis spring energy dissipation. Chin. J. Theor. Appl. Mech. 2021, 53, 2384–2394. (In Chinese) [Google Scholar]
- Guo, P.; Hou, T.S.; Liu, Q.; Luo, Y.S. Study on the influence of direct shear test methods on shear strength of lightweight soil. Water Resour. Hydropower Eng. 2023, 54, 161–170. (In Chinese) [Google Scholar]
- Peng, C.; Liu, W.; Wang, Z. Parameter checking method of large scale particle model. Geotech. Geol. Eng. 2021, 39, 1533–1540. [Google Scholar] [CrossRef]
- Yang, P.; Tang, Y.Q.; Peng, Z.B.; Chen, A. Study on grouting simulation experiment in sandy gravels. Chin. J. Geotech. Eng. 2006, 28, 2134–2138. (In Chinese) [Google Scholar]
- Xu, H.F.; Wang, C.; Li, C.F.; Jiang, M.; Geng, H.S.; Chen, F. Estimating diffusion radius grouting into broken rock mass. Appl. Mech. Mater. 2013, 353–356, 44–49. [Google Scholar] [CrossRef]
- Fan, K. Study on the Diffusion Mechanism of Solidified Grouting Slurry in Surface Moraine at Pulang Copper Mine. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2024. [Google Scholar]
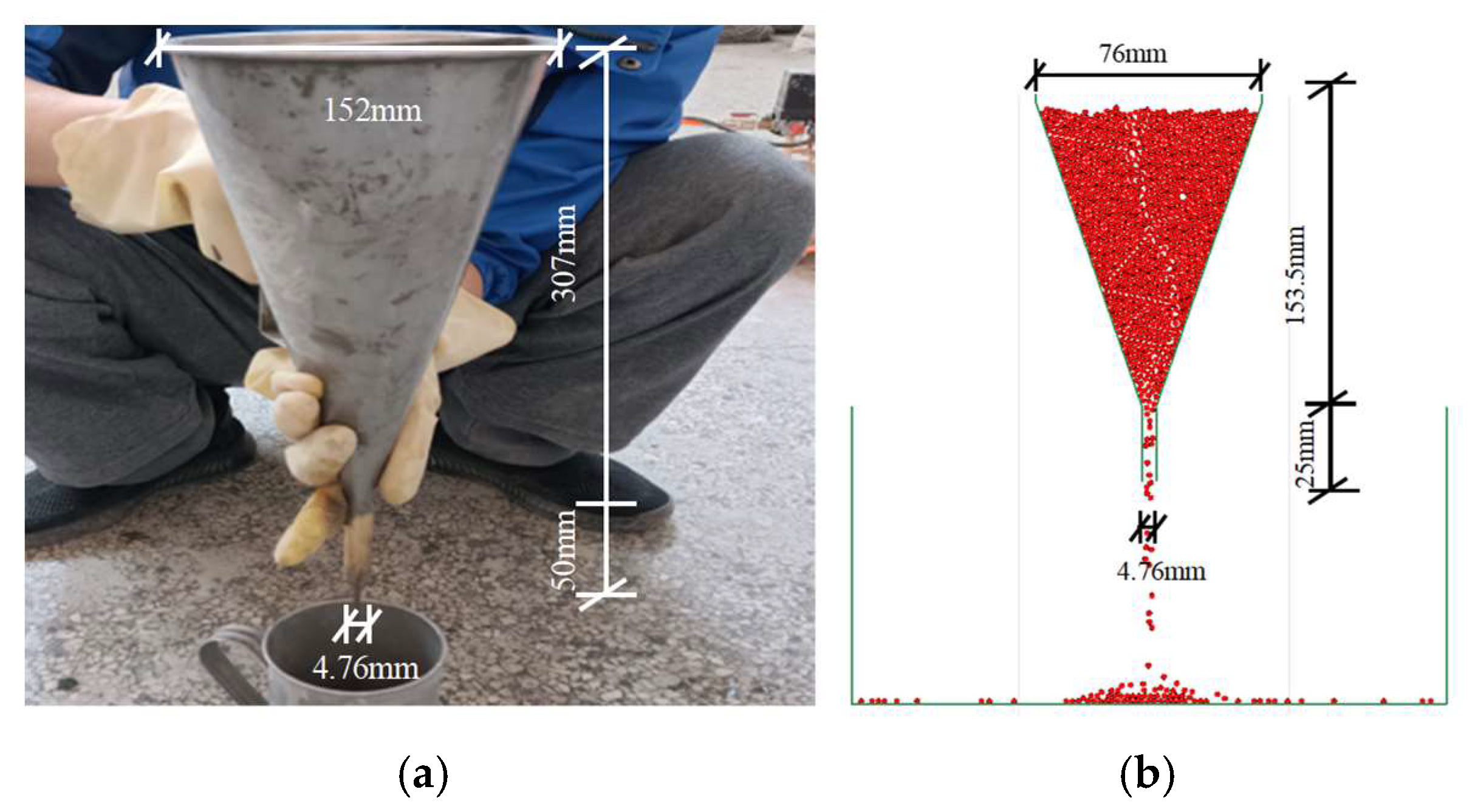
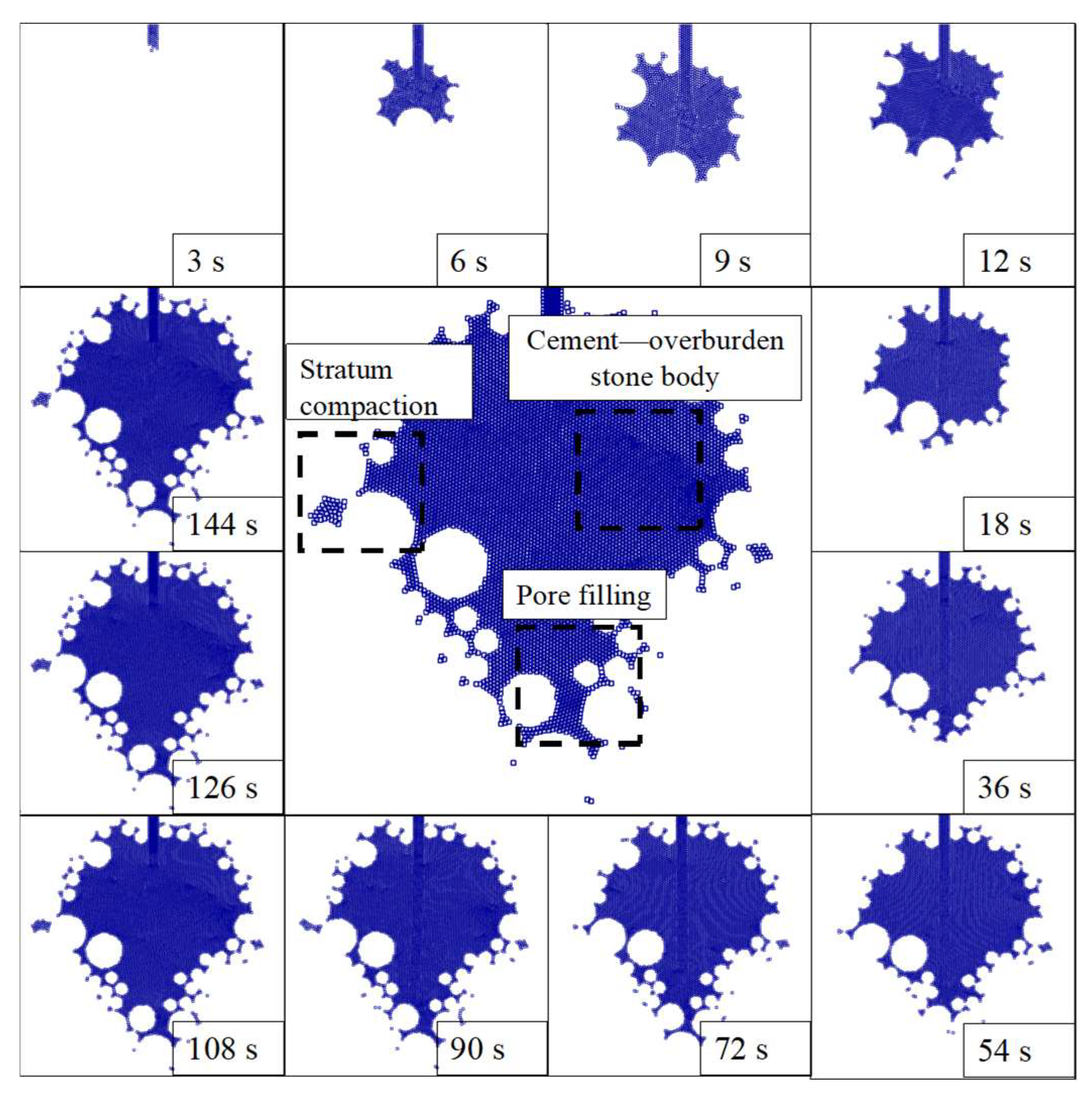

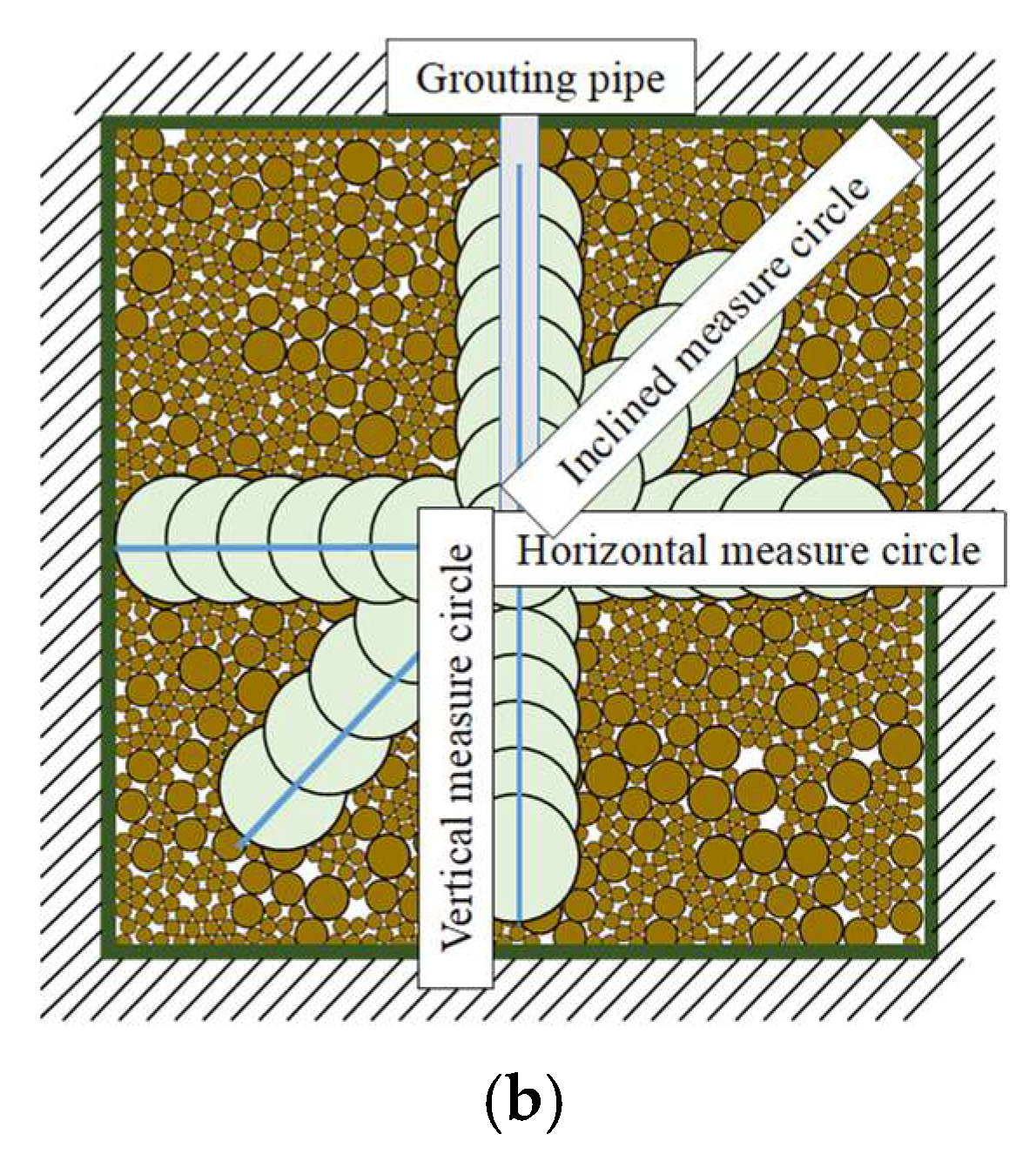
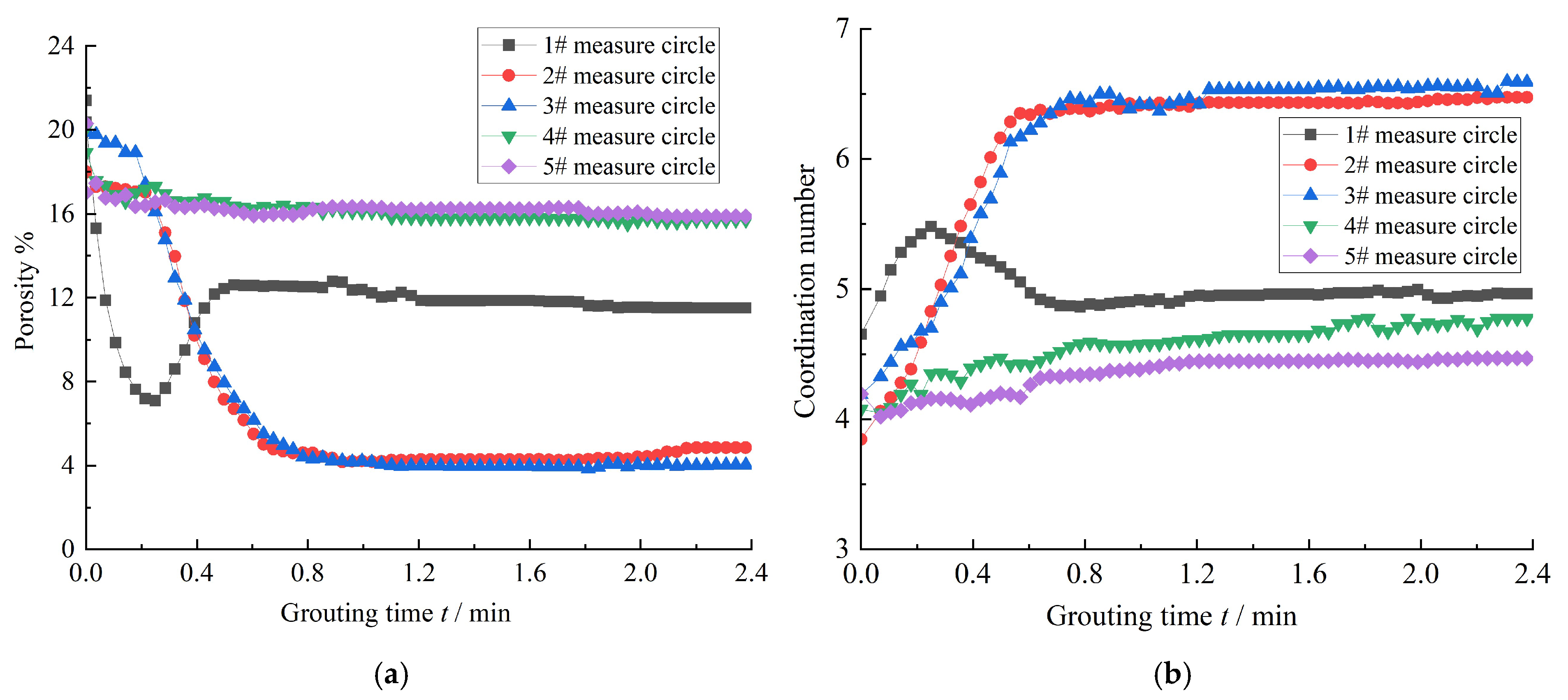
| Lithological Name | Density ρ/g/m3 | Void Ratio e | Permeability Coefficient K/cm/s (×10−4) | |||
|---|---|---|---|---|---|---|
| Moraine soil | 1.84 | 0.73 | 28.14 | 1 | 0.5 | 0.2 |
| Overburden Particles | LCBM Model | Contact Modulus /kPa | Stiffness Ratio | Normal Critical Damping Ratio | Shear Critical Damping Ratio | Tensile Strength/N | Shear Strength/N | Friction Coefficient |
| Parameter Value | 1.2 × 106 | 1.5 | 0.8 | 0 | 1 × 104 | 1 × 104 | 0.3 | |
| Cement | ARRLM model | Contact modulus /kPa | Stiffness ratio | Normal critical damping ratio | Shear critical damping ratio | Rolling friction coefficient | Attraction range/m | Friction coefficient |
| Parameter value | 8 × 104 | 2 | 0.1 | 0.05 | 0.01 | 0.001 | 0.1 |
| Grouting Pressure/MPa | Numerical Test Value/cm | Theoretical Calculation Value/cm | The Calculated Value of This Formula/cm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Diffusion Distance rmin | Maag Formula Equation (5) | Error | Cylindrical Diffusion Formula Equation (6) | Error | Polynomial Formula Equation (7) | Error | Rmin Fitting Formula Equation (4) | Error | |
| 0.5 | 6.41 | 3.99 | −37.73% | 4.95 | −22.75% | 10.79 | 68.38% | 6.21 | −3.09% |
| 0.75 | 6.55 | 4.56 | −30.38% | 6.06 | −7.48% | 13.11 | 100.15% | 6.70 | 2.29% |
| 1 | 6.92 | 5.02 | −27.43% | 7.01 | 1.34% | 15.05 | 117.58% | 7.06 | 2.07% |
| 1.25 | 7.28 | 5.41 | −25.69% | 7.83 | 7.55% | 16.76 | 130.22% | 7.37 | 1.24% |
| 1.5 | 7.44 | 5.75 | −22.72% | 8.58 | 15.32% | 18.29 | 145.83% | 7.62 | 2.42% |
| 2 | 7.74 | 6.32 | −18.37% | 9.9 | 27.87% | 21.01 | 171.38% | 8.04 | 3.85% |
| 2.5 | 8.48 | 6.82 | −19.58% | 11.08 | 30.66% | 23.39 | 175.83% | 8.38 | −1.18% |
| 3 | 8.77 | 7.24 | −17.45% | 12.13 | 38.31% | 25.53 | 191.11% | 8.67 | −1.14% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, P.; Zhao, W.; Ma, Y.; Gen, H. Discrete Element Analysis of Grouting Reinforcement and Slurry Diffusion in Overburden Strata. Appl. Sci. 2025, 15, 8464. https://doi.org/10.3390/app15158464
Guo P, Zhao W, Ma Y, Gen H. Discrete Element Analysis of Grouting Reinforcement and Slurry Diffusion in Overburden Strata. Applied Sciences. 2025; 15(15):8464. https://doi.org/10.3390/app15158464
Chicago/Turabian StyleGuo, Pengfei, Weiquan Zhao, Yahui Ma, and Huiling Gen. 2025. "Discrete Element Analysis of Grouting Reinforcement and Slurry Diffusion in Overburden Strata" Applied Sciences 15, no. 15: 8464. https://doi.org/10.3390/app15158464
APA StyleGuo, P., Zhao, W., Ma, Y., & Gen, H. (2025). Discrete Element Analysis of Grouting Reinforcement and Slurry Diffusion in Overburden Strata. Applied Sciences, 15(15), 8464. https://doi.org/10.3390/app15158464






