Abstract
The problem of the conversion of diesel buses to electric ones in connection with the inevitable introduction of the EURO 7 emission standards entails an automatic requirement to follow several additional United Nations Economic Commission for Europe rules, like R100 regulations. They regulate the preservation of battery units at longitudinal 12 g and transverse 10 g accelerations without penetrating into the elements of the bus body. Three models (12 modes in total) of battery units with frames made of S235 steel were analysed. The maximum stress value varies between 364.89 MPa and 439.08 MPa in 10 g and 12 g modes, respectively, which is beyond the tensile strength (360 MPa) and provokes plastic deformations. The max deformations were recorded in the models with the highest average stress: 63.04 mm in the 12 g mode with an average stress of 83.18 MPa. The minimum deformations of 6.95 and 7.95 mm were found in the 10 g modes (left and right acceleration direction, respectively), which meet the manufacturer’s requirements (45–50 mm maximum). The study’s primary contribution lies in developing a practical method for assessing battery unit integrity and structural behaviour during the conversion of diesel buses to electric propulsion, fully compliant with R100 regulations. By combining transient structural simulation, mathematical centre modelling of acceleration propagation, and centre of gravity prediction, the proposed approach enables engineers to evaluate electric conversions’ safety and certification feasibility without modifying the existing bus body.
1. Introduction
Cities are racing against time to clean the air, cut emissions, and electrify their transport systems. Diesel buses, once the workhorses of public mobility, have become symbols of pollution and outdated technology. Yet, replacing the entire fleet with new electric models is neither fast nor affordable. This creates a pressing need for transitional solutions that bridge the gap between current limitations and long-term sustainability goals. A promising alternative emerges: what if humanity could transform the old into new by electrifying diesel buses already on the road? Buses are not just a mode of transport—they are the circulatory system of modern cities, influencing air quality, energy consumption, and public health.
To appreciate the scale of this transition, it is essential to understand the composition of the current bus fleet. According to the Coöperatieve Rabobank U.A. research and ACEA (European Automobile Manufacturers Association) statistics, in 2023, there were around 750,000 buses in total, with 535,000 designated for intercity routes and 215,000 serving urban areas, making buses a crucial component of the transportation infrastructure. Most of these buses are diesel-powered, but the adoption of electric ones has been on the rise. The momentum is shifting, albeit gradually, as policy, innovation, and public awareness converge. This trend is particularly evident in the fleet segment utilising alternative fuels, where the number of electric models increased by 11,000 last year, nearly doubling the previous count. Only 2% (18,000) of the entire bus fleet consists of battery electric vehicles (BEVs), plug-in hybrid electric vehicles (PHEVs), and hydrogen-powered vehicles (H2). This underlines a critical gap between climate policy goals and the current technical reality. As predicted, electric city buses have surpassed diesel in new registrations within the EU (European Union), achieving a 41% share of all new city models in 2023. This marks a significant milestone, especially considering that BEVs accounted for only about 10% of new city bus registrations. Such a shift signals a transformative moment for urban transport, where electric models are no longer niche but a growing norm. The trend is evident—the EURO 7 will be applied to cars and vans from July 2030, and buses and trucks (M2, M3, and N2, N3 categories according to UNECE classification) in the next 12 months. The tightening of emission standards will likely serve as a catalyst, accelerating the need for practical electrification strategies, including the conversion of existing fleets.
The observed sharp contrast between new registrations and the legacy fleet raises an urgent question: What will happen to the existing fleet of around 215,000 diesel buses mentioned earlier, the engines of which will not be able to meet the limits of NOx (nitrogen oxides) and other emissions? Meeting the tighter NOx limits requires advanced and expensive after-treatment systems, such as selective catalytic reduction (SCR) and more effective diesel particulate filters (DPFs), which add to the complexity and cost of diesel vehicles (according to the aforementioned AECC association). These technologies, while effective, push the boundaries of economic feasibility, especially for older buses nearing the end of their life cycles. As a result, it is economically more profitable to convert diesel buses to electric ones. Several additional UNECE (United Nations Economic Commission for Europe) certification requirements are imposed in this case. This introduces a new layer of complexity: transforming legacy vehicles is not just a technical challenge, but a regulatory one.
Among the key hurdles in diesel-to-electric conversion are the international safety certifications, initially designed for factory-built electric vehicles, not retrofits. For example, the UNECE R100 (uniform provisions concerning the approval of vehicles about specific requirements for the electric power train) [1] is the safety requirements concerning the electric drive of road vehicles of categories M and N1, the maximum design speed of which exceeds 25 km/h and which are equipped with an electric drive, except vehicles with a permanent connection to the network. Retrofitted buses, though mechanically sound, must now be evaluated through the same lens as newly manufactured electric vehicles. The development of an applicable simulation methodology in accordance with R100 is the subject of the current research. Establishing such methodologies is a vital step in streamlining certification, reducing development time, and accelerating fleet-wide transformation.
While electric vehicle safety has been broadly studied, the unique challenges posed by retrofitting diesel buses to electric powertrains remain underexplored. While numerous studies address frontal crash behaviour in electric vehicles, few tackle the nuanced structural risks introduced by converting existing diesel platforms. The UNECE R100 regulations are related to the impulse impact and foresee the transverse 10 g and longitudinal 12 g (frontal impact) accelerations. This focus on specific acceleration parameters highlights the strict safety standards that converted buses must meet to be viable on the road. It is evident that the re-equipment of diesel buses with electric ones is just beginning its trend; therefore, there is a lack of scientific research on the impacts of R100. On the other hand, the exact nature of the frontal impact of buses is particularly presented in relevant scientific publications dedicated to the UNECE R29 and NCAPs (New Car Assessment Programs) regulations (in the case of R100, the analysis of the results is performed mostly locally—on the battery blocks). These studies provide valuable insights but do not fully address the structural complexities of retrofitted vehicles as a whole. Thus, in works presented by Holenko et al. [2], the validation of frontal crashworthiness simulation for low-entry type buses is investigated according to UNECE R29 requirements. Key findings include the observation that city buses, unlike suburban and intercity models, have lower stiffness in frontal collisions. This necessitates the inclusion of deformation zones in new models, which are currently lacking in most city buses, and signalise that low-entry and low-floor buses have a significantly lighter front end compared to traditional designs. Yang et al. [3] evaluated the structural safety of a newly developed hydrogen fuel cell city bus body frame using finite element analysis under four conditions: horizontal bending, ultimate torsion, emergency cornering, and braking. While the initial design met the stiffness and vibration criteria, stress levels exceeded the material’s yield strength under torsion and cornering. Size optimisation of frame components reduced peak stresses by up to 20.13%, ensuring compliance with strength requirements and achieving a 106 kg weight reduction. This demonstrates the importance of structural optimisation to balance safety and efficiency in next-generation bus designs. Frontal impact on the bus superstructure, as per UNECE R29 and NCAP, is a subject of [4]. The study [5] investigates the crashworthiness of crash box components using finite element models sourced from NHTSA (National Highway Traffic Safety Administration) vehicle data. Key parameters—energy absorption, crush force efficiency, and specific energy absorption—were analysed and optimised through RSM (Response Surface Methodology) design of experiments. Reduced-order models using the sPGD (sparse Proper Generalised Decomposition) method achieved 90% accuracy in capturing nonlinear behaviour. Results showed a 34.33% improvement in energy absorption and an 18.91% mass reduction in heavier variants without compromising performance. These advances illustrate how sophisticated computational methods can lead to safer and lighter bus components.
Building upon this progress, further studies are exploring how these methods can be applied to improve passive safety technologies in specific bus configurations. The study [6] aims to develop new passive safety technologies for coaches, focusing on driver safety during frontal collisions, using UNECE R29 regulations to guide experimental and numerical simulations, which compare strain, acceleration, and displacement data to determine if current designs meet safety criteria or need improvements. The LSDYNA finite element analysis of the school bus frame structure as per the AIS029 (Automotive Industry Standards used in India) pendulum impact test, which is also used in the R29 regulations, is presented by Lashkari et al. [7]. The paper [8] aims to compare existing NCAPs with BNVSAP (Bharat New Vehicle Safety Assessment Program) and suggest improvements by analysing the experiences of older NCAPs and real-world accident data in India and other countries. In [9], the stress analysis simulations of the welded and bolted joints method for the chassis structure of an electric low-floor medium bus are investigated. Joint integrity is critical for maintaining structural performance under impact. A robust optimisation scheme considering uncertainties and tolerance design is proposed to optimise the electric bus body frame for frontal crashes [10]. A triple-objective robust optimisation model is created and solved with a double-loop nested algorithm combining NSGA-III (Non-dominated Sorting Genetic Algorithm III) and SQP (Sequential Quadratic Programming) methods. The results demonstrate enhanced crashworthiness and robustness under practical manufacturing conditions. Such multi-objective optimisation approaches pave the way for safer, more reliable electric buses that can meet regulatory and operational demands.
The work [11] highlights the balance between minimising weight and ensuring occupant protection in critical collision scenarios. Yang et al. investigated the design optimisation of a lightweight electric bus body frame, orienting the static performance and side-impact safety. Deulgaonkar et al. [12] have used FEA (Finite Element Analysis) for various crash conditions (front, side, rear) in Ansys Workbench, estimating stresses, deflections, and energy distribution of the bus body structure. The effect of electric battery mass distribution on electric vehicle movement safety is investigated in [13]—this problem remains a very important influence factor of the shock energy distribution. Proper battery placement not only affects vehicle dynamics but also plays a crucial role in crash energy management. Weight optimisation and structural analysis of an electric bus chassis frame are other topics of consideration [14].
Having studied the nature of the impact (acceleration, boundary conditions, plastic deformations, etc.) based on the above publications, it is appropriate to proceed to existing research on the structure and strength of bus bodies in non-impact conditions. Understanding the structural integrity of bus frames under everyday static and dynamic loads complements impact safety research by ensuring overall durability and passenger comfort. Bagus et al. [15] conducted a structural strength analysis of a medium bus’s floor frame, which supports static loading from the interior and passengers, comparing materials ASTM (American Society for Testing and Materials) A514, AISI (American Iron and Steel Institute) 1020, and Aluminium 2014-T4. The rise in car ownership in China has increased air pollution, making electric vehicles more attractive despite battery endurance challenges. The paper [16] uses FEA to optimise the lightweight design of an electric bus frame using structural steel and aluminium alloy. The redesigned frame reduces weight and enhances performance by considering four driving conditions (full load bending, torsional, emergency braking, and steering). This multidisciplinary approach ensures that structural improvements translate into tangible operational benefits across a range of real-world scenarios.
While structural performance under operational loads is critical, occupant safety during collision events remains equally important. The study [17] investigates head injury risk in bus frontal collisions, focusing on the influence of structural configuration. Finite element sledge test simulations were conducted using acceleration data to analyse how interior components and body layout affect dummy kinematics and Head Injury Criterion—HIC15, which was reduced by approximately 5.6%. This underscores the importance of internal design in mitigating occupant injury beyond external crashworthiness. The authors of [18] used FEA to compare the current EN10025 S355JR-type battery carrier frame material with alternatives like aluminium 6061-T6, aluminium 7075-T6, and carbon fibre-reinforced PEEK (Polyether Ether Ketone), achieving weight reductions of 65.54% and 73.07% with aluminium 6061-T6 and carbon fibre-reinforced PEEK, respectively. Hjelkrem et al. [19] investigated a battery electric bus energy consumption model for strategic purposes and proceeded with the validation of a proposed model structure with data from bus fleets in China and Norway. Such models are essential for optimising operational efficiency and supporting broader electrification strategies. Elhussieny et al. [20] evaluated the crash performance of a bus front structure during a frontal impact. A finite element model was simulated in ANSYS/Explicit Dynamics using two impact velocities to assess deformation and deceleration. Energy absorption was validated using the Lag rangian function. A lumped mass model in MATLAB/Simulink helped estimate design parameters, and a Genetic Algorithm was applied for multi-objective optimisation. Experimental tests on four samples confirmed the findings. Results showed that beyond the first crash zone, safety limits were exceeded. To improve crashworthiness, extending the front deformation zone is recommended. Lopes et al. [21] presented a numerical dynamic analysis of a multi-body bus. Optimisation of bus body frame structure for weight minimising with the constraint of natural frequency using an adaptive single-objective method is a topic of [22]. These studies collectively contribute to the growing body of knowledge aimed at improving bus safety, efficiency, and performance through advanced simulation and optimisation techniques. However, simulation-based advancements must be evaluated in the context of long-term structural performance and real-world ageing effects. Ruban et al. [23] examined the ageing of bus bodies on frame chassis, finding durability ranges from 5 to 11 years depending on factors like occupancy, road conditions, speed, and corrosion. Such real-world factors significantly influence the lifespan and safety of bus structures, underscoring the importance of material choice and design in extending operational life. A frame made of alloy steel with closed profiles lasts 1.5–1.8 times longer than a body frame with open sections, affecting the bus’s safety. Traditional bus body frame optimisation focuses on part thickness, but the study [24] optimises the sectional shape of tube beams using mesh morphing technology.
While these studies focus on durability and structural enhancement, crash performance remains a critical dimension in evaluating modern electric bus safety. Holenko et al. [25] investigated the frontal crash behaviour of a low-entry electric bus frame under NCAP-like conditions at 32 and 56 km/h, using LS-DYNA software simulations to assess deformation zones influenced by added battery mass. The results show reduced body deviations and a safer deceleration profile at lower speeds, supporting a recommendation to lower NCAP test speeds for city buses, highlighting greater passenger risk compared to UNECE R29 due to deeper structural deformations. These findings emphasise the need for safety testing protocols tailored to the unique structural characteristics of city buses. The study [26] presents a detailed analysis of a lightweight sandwich composite microbus body under full-frontal crash conditions, using LS-DYNA simulations and Chang–Chang failure criteria. Results show that structural reinforcements can significantly reduce passenger injury risks, despite initial high intrusion values, while adding only 35.6 kg to the vehicle’s weight, demonstrating a viable balance between crashworthiness and lightweight design. The average decelerations of the original and modified microbus are 11.2 g and 14.8 g, respectively. This approach illustrates how innovative materials and reinforcement strategies can improve safety without compromising efficiency.
It is also advisable to cite publications that effectively demonstrate the so-called reverse engineering-style research framework, for example [27], where Gattamelata et al. provided an applicable research step-by-step scheme based on increasing the safety of using agricultural tractors. The framework consists of the following stages: 1. preliminary analysis; 2. concrete experience; 3. modelling (functional analysis, geometrical compatibility, dynamical compatibility); and 4. validation. This structured methodology offers a replicable model that can be adapted to bus safety research, enhancing systematic development and validation of safer vehicle designs.
There is a particular shortage of scientific publications devoted to transforming diesel city buses into electric ones with the appropriate certification according to the UNECE R100 regulations. Most of the analysed publications investigate the impact loads on the body in the conditions of NCAP and R29 regulations, but there are fundamental differences in the boundary conditions. For example, the acceleration module (10 and 12 g) and its application vector (locally to the battery units), criteria for their penetration into the body elements, checking the strength of bolted connections of battery units, etc. The problem is also complicated by the direct ban on making structural changes to the body frame, because any modifications invalidate the results according to other already passed UNECE certification tests of the diesel modification, i.e., R80, R66, R107, R118, etc.
This study bridges a methodological gap between crash safety certification, structural simulation, and practical retrofitting constraints, ensuring that the shift to electric mobility is safe and scalable. The broader aim is to develop a methodology for safely converting diesel buses to electric power without altering certified body structures. To achieve this, the research focuses on simulating battery unit behaviour under UNECE R100 impact loads and modelling the effect on stress distribution, deformation, and centre behaviour under UNECE R100 impact loads and modelling the effect on stress distribution, deformation, and centre of gravity. These objectives are crucial for minimising the need for structural modifications, thereby avoiding costly re-certification under other UNECE regulations already passed by the vehicle in its diesel configuration.
2. Materials and Methods
2.1. Reverse Engineering-Style Research Framework
To improve methodological transparency and academic robustness, as well as practical applicability and alignment with best engineering redesign practices in our study, it is recommended to clearly define the following research stages, which engineers or scientists can adopt:
- -
- Preliminary Analysis: an initial assessment to identify the key design constraints (R100 acceleration limits, manufacturer displacement caps, etc.) and performance requirements for the battery pack housings;
- -
- Parameter Identification: analysis of vehicle dynamics and technical specifications to determine critical geometrical and dynamic parameters influencing the structural configuration (battery unit mass, bracket geometry, damping coefficient, steel specs, and OEM (Original Equipment Manufacturer) guidelines, etc.);
- -
- Modelling and Design Implementation: use of CAD (Computer-Aided Design) tools to develop and refine battery housing models (Ansys solid-modelling) that meet both structural and functional requirements;
- -
- Validation via Virtual Prototyping: simulation-based evaluation of the modelled systems under realistic loading and dynamic conditions to verify design performance and compliance (execute transient structural simulations under R100-specified pulses (10 g transverse, 12 g longitudinal), extract max and average stress and deformations (/, ) SF (Safety Factors) maps, and reaction forces; compare outcomes against yield, allowed displacement, and fastener capacity limits, etc.)
Such an approach is consistent with current practices in machinery redesign, as discussed in several studies [27] and can be attributed to the so-called “best practices” for organising design processes for compliance with safety certification requirements (UNECE R17, 29, 52, 66, 80, 107, etc.).
2.2. Practical Framework Application
When switching from a diesel power unit (together with a gearbox) to an electric one (three battery units of 500 kg each according to the customer’s technical documentation—Figure 1a), the position of the bus centre of gravity (CoG) must be preserved; otherwise, braking, handling, active, and passive safety will be affected. For the long-range BEVs, the number of battery units can be increased to four (Figure 1b), though the new CoG should be minimally changed—this is a conceptual challenge to distribute the masses evenly.
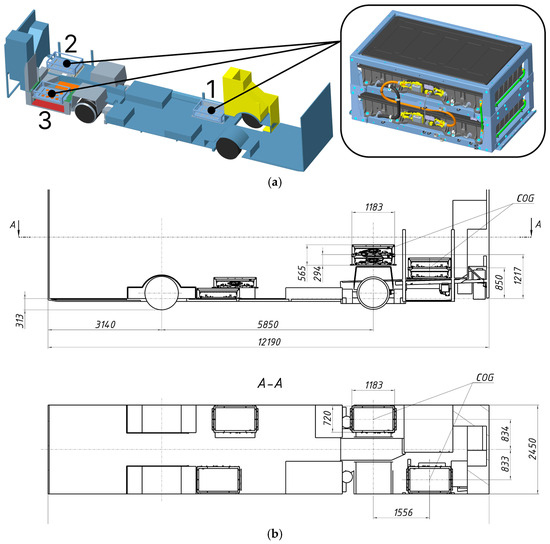
Figure 1.
Layout of a 12 m long low-floor bus when switching from a diesel to an electric powertrain: (a) 3D model of the battery unit location; (b) drawing fragment (side and top view).
A balance equation that ensures the total new mass and CoG remain consistent or within acceptable limits relative to the initial total mass can be written in the following form:
where mit, mnt—initial and new total mass of the bus accordingly; , —linear mass density function along the longitudinal x axis of the bus, kg/m; —bus length, m.
where xi, xn—initial and new CoG position, m.
A similar modelling approach should be used for other coordinates (y, z), a possible direction for further research.
According to R100, the test pulse applied to the battery unit shall be between the “max curve” and “min curve”—an example of a graph of longitudinal acceleration is shown in Figure 2. The corresponding values of acceleration in the intermediate points (moments of impact time) are listed in Table 1.
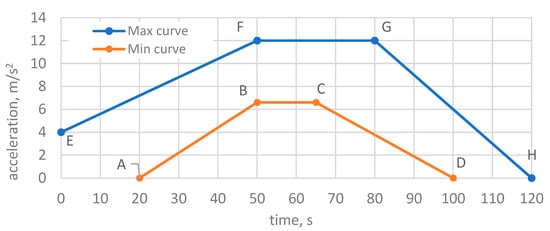
Figure 2.
Longitudinal acceleration according to R100, points A, B, C, etc., form the limits of permissible minimum and maximum pulse values acting on battery units.

Table 1.
Acceleration for M3 and N3 vehicles according to R100.
In reality, for heavy buses (M3 category), typical acceleration values during frontal crash tests range between 15 and 20 g [6,25,26] (measured at the impact point near the wall at the front of the bus). The energy transfer from a frontal impact will result in different acceleration values for the frontal and rear battery units due to the following concepts: (a) wave propagation: the shock wave generated by a frontal impact will travel through the bus structure, causing the front part to experience higher accelerations compared to the rear part; (b) damping and absorption: as the shock wave travels through the bus, its intensity diminishes due to damping and absorption by the structure and components; (c) distance from impact point: the farther a component is from the point of impact, the lower the peak acceleration it will experience.
It is proposed to describe the difference in acceleration experienced by the frontal and rear battery units using the next mathematical model, considering such parameters k = 0.05 m−1; df = 3 m; dr = 9 m (which were determined together with the customer based on technical documentation):
- Frontal battery unit:
- Rear battery unit:
The model of the acceleration pulse, preserving the character of the line segments (graph in Figure 2), can be described as follows for the case of peak acceleration A:
where ao(t)—function which describes the acceleration as a function of time during a frontal crash test for an M3 category bus; t—variable which represents time, s; —frontal or rear battery unit acceleration coefficient ( or accordingly).
In the context of the provided Equation (5), the symbol { is not a mathematical operator but a notation used to define a piecewise function. A piecewise function is a function that is characterised by different expressions based on different intervals of the input variable t (time).
Taking into account the typical acceleration for the M3 category mentioned above ( g), the values of the front and rear battery unit accelerations (3, 4) are calculated as follows:
- Frontal battery unit:
- Rear battery unit:
Thus, the peak acceleration during t = 50–80 ms remains stable according to the horizontal line segment F-G (Figure 2) and is: af(50) = 12.91 g and ar(50) = 9.56 g. Intermediate values in characteristic moments of time t are as follows: af(30) = 4.30 g and ar(30) = 3.19 g; af(100) = 6.46 g and ar(100) = 4.78 g. These results show energy absorption during the frontal impact at = 15 g.
Bus manufacturers and engineering design teams can create their mathematical models that are an alternative to Equations (3) and (4). Still, the approach proposed in the current work already demonstrates that the acceleration in battery units depends on the location relative to the front of the bus and can be simulated.
The mode index “2-10g-L” (Figure 1) means that unit #2 under a transverse acceleration of 10 g is directed to the left (L) side along the bus. Other designations are: 1/2/3—the unit number according to the mounting scheme (Figure 1a); 10 g/12 g—acceleration value (98.06/117.67 m/s2); L/R/F/B—acceleration direction relative to the longitudinal axis of the bus (left/right/front/back accordingly). Each of the three models has its constraints with M10 or M12 thread bolt joints and the brackets mounted to the original bus body frame, which cannot be modified due to the number of UNECE certification tests already passed by the bus originally equipped with a diesel engine.
The following Ansys transient structural boundary conditions are explored using battery pack #2 (Figure 1) as an example of their application (Figure 3):
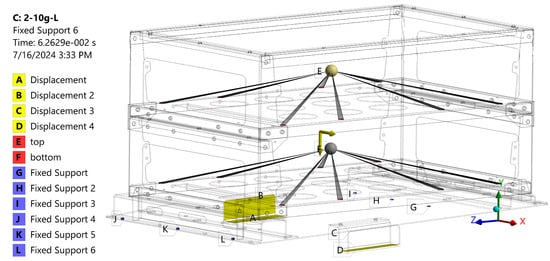
Figure 3.
Parametric Ansys model of the “2-10g-L” mode boundary conditions: A–D are the vertical displacement constraints; E, F are masses of batteries; G–F are the bolted joints.
- -
- A, B, C, D—restriction of displacement in the direction perpendicular to the surface of the brackets (dimensionless);
- -
- E, F—distributed masses of batteries (two blocks of 250 kg each according to the technical documentation);
- -
- G, H, I, J, K, L—fixed support constraints in places of bolted joints (dimensionless); standard Earth gravity (9806.6 mm/s2).
Acceleration (98,060 mm/s2) along the X axis according to the graph (Figure 2): first step of linear acceleration growth to the max value 0–50 ms; keeping the acceleration stable during 50–70 ms; acceleration decay to zero at 100 ms (according to the graph in Figure 2).
The models are made of S235 steel, which has the following parameters: Young’s modulus = 205 × 109–215 × 109 Pa; yield strength (σy) = 235 × 106–274 × 106 Pa; tensile strength = 360 × 106–510 × 106 Pa; tangent modulus = 1.185 × 109 Pa; nonlinear stress–strain curve. Data was taken from Ansys Granta EduPack 2023 R1 version.
The study is based on a set of engineering assumptions, including: (a) the battery mounting brackets do not change the dynamic behaviour of the battery except according to the Ansys boundary conditions according to R100 (i.e., extraneous factors that may additionally manifest themselves in real operating conditions are not taken into account), and the bolted joints are modelled as perfectly fixed Ansys supports; (b) the battery blocks are rigid and unchanging with a continuous linear mass distribution (represented as distributed masses in Ansys); (c) constant damping properties throughout the structure with a coefficient k (3, 4); (d) the frame materials are homogeneous throughout the model volume, i.e., they do not model possible defects that may arise during the technological process of manufacturing.
3. Results and Discussion
It should be noted that the practical results presented above were obtained through the sequential passage of the evaluation stages indicated in the “Materials and Methods” section, starting with the “Reverse Engineering-Style Research Framework” where the algorithm for solving a typical problem is described as given, and ending directly “Practical Framework Application”. It is recommended that the results be presented by the key objectives of the research and that the strength and safety parameters of the model be consistently investigated in accordance with R100 and the requirements of the customer (bus manufacturer).
Objective 1: to evaluate stress concentration and plastic deformation behaviour of battery mounting structures under R100 loading conditions. When analysing stresses, there is no question whether they will remain within the material linearity according to Hooke’s law. Unambiguously, there will be zones of plastic deformation, where : for example, max von Mises stress is 376.7 MPa in transverse 10 g mode (“2-10g-L” in Figure 4a) and 426.85 MPa in longitudinal 12 g mode (“2-12g-F” in Figure 4b).
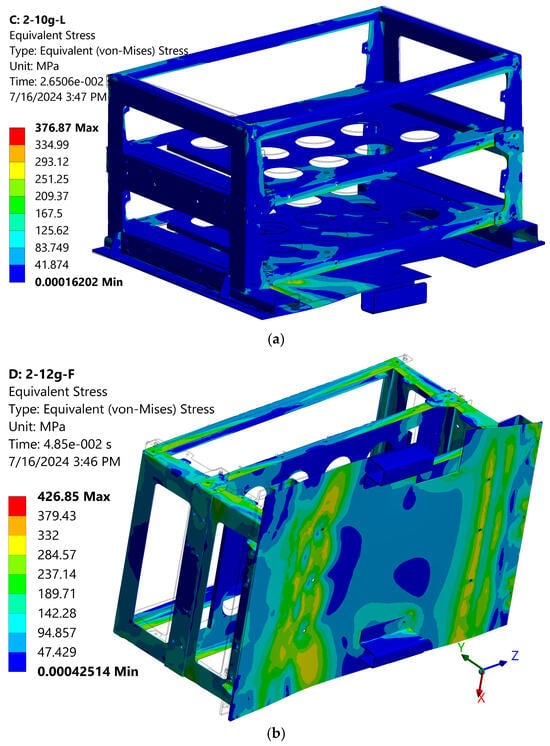
Figure 4.
Von Mises stress maps of the battery unit #2 in the following modes: (a) “2-10g-L” (left pulse direction); (b) “2-12g-F” (front pulse direction).
The mode with the highest local stress is “3-12g-B” with 12 g acceleration applied in the back longitudinal direction. It has received σmax = 439.08 MPa at tσmax = 0.1 s (Table 2), although the average stress σave = 56.29 MPa, which is not the highest among the studied modes: the maximum σave is obtained in the “2-12g-B” mode—83.18 MPa. It should be noted that none of the σmax results reached the tensile strength of S235 steel (360 MPa). Element-by-element analysis of the model allows for selecting the optimal steel grades, for example, S275 for increased stresses (over 275 MPa) and reducing the cost, since the structure is collapsible (bolted).

Table 2.
Results of the simulation of battery units in Ansys transient structural simulation according to UNECE R100.
In addition to the stress values in the unit model itself (Figure 4), the reactions in the places of the bolt fasteners (Table 3) are a question of interest—they determine what forces will be transmitted to the original bus body (whether they are permissible) and what grades of bolts are recommended.

Table 3.
Total reactions in the fixed supports.
The pre-calculated maximum shear load on an M10 bolt from a hardware guide is 1494 kg (14,651 N), considering the 5.6 grade. Thus, increasing the number of bolt holes and using M12 (max shear load is 20,947 N) with a higher grade (at least 8.8–10.9) is suggested.
The graphs (Figure 5a–c) show dense fluctuations of σmax during the period of 0–0.05 s, which corresponds to the zone of acceleration growth according to the graph of Figure 2. There are at least two reasons for such behaviour: the transients cause the σmax locations to migrate during the experiment; plastic deformations change the model at each of the 300 substeps (threshold applied in Ansys). The processes stabilise from 0.05 s, since the acceleration does not change, and after 0.07 s it drops to zero. However, in some modes, this did not cause stress. This indicates the presence of residual stresses, which also turned out to be maximum during the experiment at some modes: “1-10g-L”, “3-12g-F”, and “3-12g-B” showed σmax exactly at 0.1 s. The average stress σave behaviour is similar for all modes; therefore, it is enough to demonstrate a typical graph based on model #1 (Figure 5d) as an example—it echoes the regulative graph of acceleration according to R100 (Figure 2).
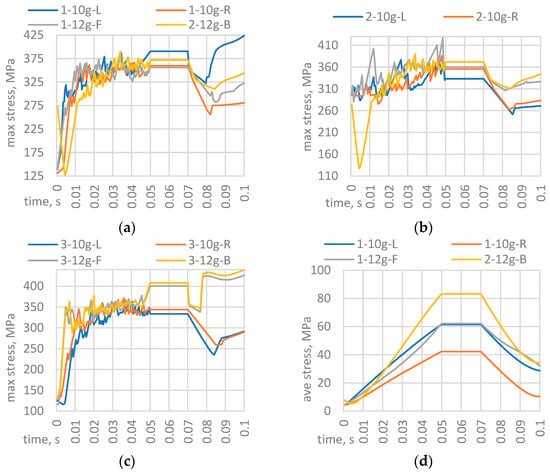
Figure 5.
Graphs of the dynamics of stress changes during the loading process: (a–c) max von Mises stress of battery units #1,2,3, respectively; (d) average stress of unit #1.
Objective 2: to analyse Safety Factor (SF) along with the level of deformations and validate whether the model remains within safe limits defined by the manufacturer and regulatory criteria. To establish a comprehensive assessment of the stress state, it is recommended to refer to the Safety Factor (SF), which is a ratio of σmax to σy. A zero value means no safety margin in red spots (model #3 in Figure 6). Their locations and surface area determine the final deformations of the model (Table 2 and Figure 7), for example, 58.13 and 58.77 mm, which are almost the same for both longitudinal and transverse modes (“1-10g-L” and “1-12g-F” in Figure 7). Interestingly, this is a positive coincidence because it indicates the equal strength of the structure in both load directions.
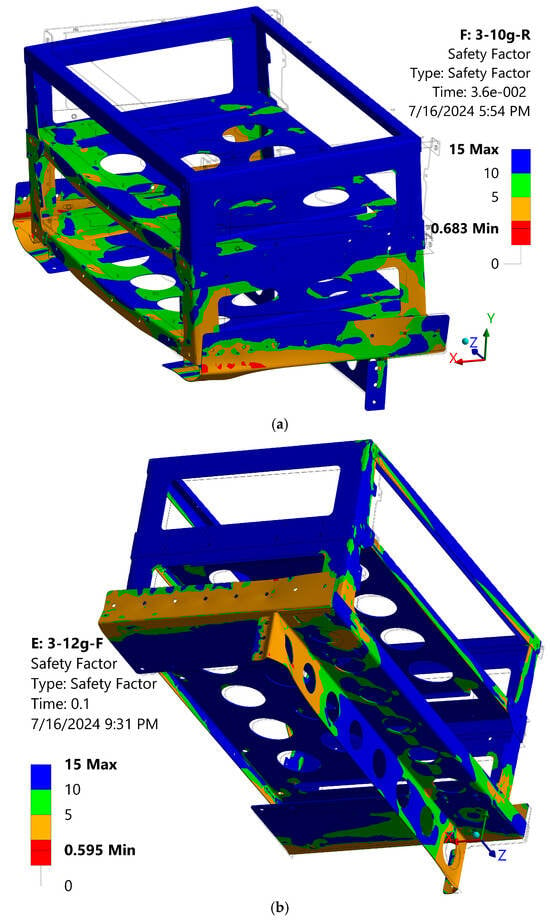
Figure 6.
Safety Factor (SF) maps in different modes: (a) “3-10g-R”; (b) “3-12g-F”.
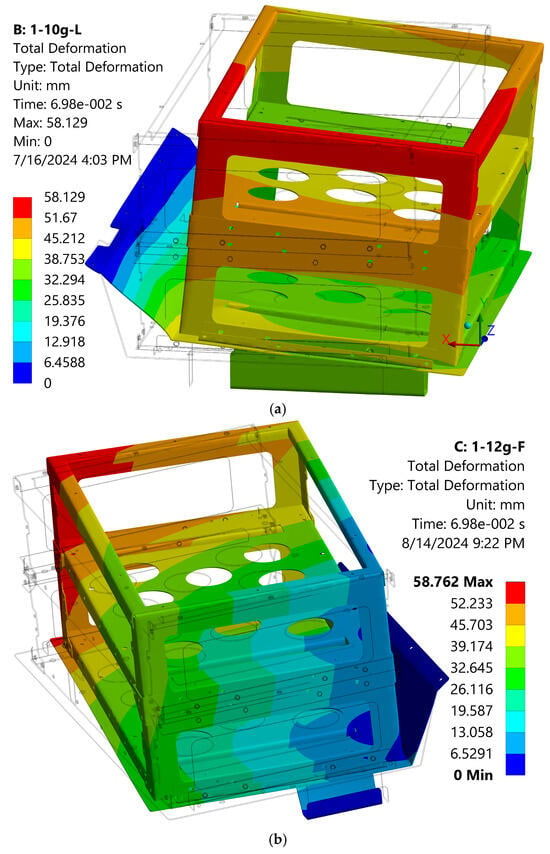
Figure 7.
Total deformation in different modes: (a) “1-10g-L”; (b) “1-12g-F”.
The maximum deformations during the experiment are 63.04 mm—they were recorded in the “2-12g-B” mode, where the highest average stress σave = 83.18 MPa was found. At the same time, the value of σmax was even lower than in other modes (390.23 MPa). This confirms the theory that it is practically more important to check the average rather than the maximum stresses of the model to establish its safety. The minimal deformations (6.95 and 7.95 mm) were recorded in the “3-10g-L” and “3-10g-R” modes. Accordingly, the stresses σmax are minimal precisely in them: 40.90 and 43.02 MPa, respectively. Two criteria determine the upper limit of permissible deformation: (a) requirements of the battery manufacturer regarding the relative displacement of the units, considering their power supply and mounting; (b) lack of contact with elements of the body and interior (inner lining, etc.). In this case, deformations higher than 45–50 mm are not recommended (according to the customer’s requirements and the specifics of the interior equipment), so those modes that showed higher values should be locally investigated and reinforced, which is the subject of further research. In cases of deformations exceeding the recommended ones, it is advisable to conduct full-scale tests, the results of which may lead to recommendations such as equipping structures with dampers to absorb impact energy. The graphs (Figure 5) demonstrate the change in stresses over time, which indirectly hints at the need to assess the accelerations that can act on batteries. This is a possible future study to compare the acceleration results with those permissible according to the battery manufacturer’s data.
Objective 3: to consolidate the findings into a practical methodology that ensures R100 compliance during diesel-to-electric bus conversion, without altering certified structures. The problem of converting Europe’s huge diesel bus fleet (around 215,000 vehicles in 2023) to electric traction turns out to be quite difficult: changes to the body frame are inadmissible, otherwise the bus will have to be recertified following UNECE R17, 29, 52, 66, 80, 107, etc. In each case, it is necessary to check the indicators of σmax, σave, and especially δ of the battery units on the one hand and transmission reactions from bolted connections to the body on the other. Accounting for approximately 40–50% of the cost of the bus, the body is its most expensive part, which is why an individual approach is often used in manufacturing the body in each individual order; there are many modifications with varying complexity. Each such modification must be certified for compliance with R100, because, for example, the allowable δ values may differ from other modifications, etc. The global scope of the problem of adaptation and certification considered in the work is dramatic.
Speaking about the novelty of this study, a comparison should be made with the reviewed academic literature. Thus, the problem of local R100-oriented battery-mount analysis for retro-fits is not sufficiently covered: Most prior works (e.g., Holenko et al. [2], Yang et al. [3], Deulgaonkar et al. [12]) examine the entire bus frame or full-vehicle crashworthiness under NCAP or R29 conditions. In contrast, the current study isolates battery mounting frames and simulates them locally under UNECE R100 accelerations, while maintaining the constraint of no structural modification to the certified diesel bus body. Another problem is a mathematical attenuation model of acceleration propagation. Unlike studies that apply constant 10 g/12 g loads (e.g., [3,26]), the current study proposes an exponential decay model of acceleration based on battery location and damping coefficient k = 0.05 m−1, further used to calculate the coefficients in the final Equations (6) and (7). This more realistically represents how actual acceleration differs between front and rear battery units (12.91 g vs. 9.56 g) due to structural damping and wave dissipation. Another problem is UNECE R100 certification for bolt-on electric conversion: Prior studies (e.g., [4,5]) do not address the specific challenge of retrofitting existing diesel buses with electric powertrains while complying with UNECE R100. The current study is focused on battery mounting designs that meet R100 g-load requirements without triggering re-certification under R66, R80, etc. This is a key step for practical large-scale implementation. In conclusion, it can be noted that, unfortunately, among the analysed modern literary sources that touch on the topic of bus certification UNECE tests, there are no studies on the transformation of buses from diesel to electric traction. This area of engineering and scientific work is only beginning to gain popularity as Europe approaches 2030, when the problem will become relevant.
The primary contribution of the study lies in the development of a practical methodology for assessing battery unit integrity and structural behaviour during the conversion of diesel buses to electric propulsion, fully compliant with UNECE R100 regulations. By combining transient structural simulation, mathematical centre modelling of acceleration propagation, and centre of gravity (CoG) prediction, the proposed approach enables engineers to evaluate electric conversions’ safety and certification feasibility without modifying the existing bus body. Readers—particularly transport engineers, fleet operators, and vehicle retrofitting professionals—can benefit from these findings by applying the outlined models and boundary condition strategies to streamline electric bus conversion projects while avoiding costly recertifications.
Regarding future research directions and system-level integration: as a foundation for future research, several directions are recommended: (1) experimental validation of simulation results using physical crash and vibration tests; (2) exploration of scalability to other bus types and bracket geometries; (3) integration of this method into vehicle-level system optimisation, including thermal management, energy distribution, and structural weight reduction for full-system efficiency; and (4) comparing acceleration results with those permissible according to the battery manufacturer’s data and considering the possibility of equipping structures with shock absorbers to dissipate impact energy.
4. Conclusions
The following points have been stated based on extensive discussions:
- Regulatory constraints: The transition from diesel to electric propulsion in the context of the EURO 7 standards requires compliance with UNECE regulations, particularly R100. Since modifications to the certified bus body would trigger re-certification under R66, R80, R107, etc., battery units must be integrated without altering the frame. This presents a structural challenge, as the bus must now withstand longitudinal and transverse accelerations of 12 g and 10 g, respectively.
- Feasibility of battery integration: The results confirm that battery systems can be safely integrated into existing diesel bus frames while meeting UNECE R100 acceleration thresholds, without requiring structural changes. This enables regulatory-compliant electrification of older buses using bolt-on designs.
- Stress and plastic deformation: it is evident that keeping the battery units within the material elasticity (Hooke’s law) is impossible and makes no sense (otherwise the material capacity and mass will be inadequate), so it is essential to control the amount of stress (must be within the limits of tensile strength—360 MPa) and σmax locations (effective zones of plastic deformation). The value of σmax varies between 364.89 MPa (“3-10g-L” mode) and 439.08 MPa (“3-12g-B” mode).
- Deformation and Safety Factor: the maximum deformations are recorded in the models with the highest σave: δ = 63.04 mm in the “2-12g-B” mode with σave = 83.18 MPa. The minimal δ of 6.95 and 7.95 mm are in the “3-10g-L” and “3-10g-R” modes with σave of 40.90 and 43.02 MPa, respectively. Therefore, it is necessary to focus primarily on σave, but not on σmax, while evaluating the stress-deformed state of the battery unit. In addition, it is mandatory to comply with the manufacturer’s requirements regarding the relative displacement (in this case, it should not exceed 45–50 mm).
- CoG preservation: when switching from a diesel power unit (together with a gearbox) to an electric one, the position of the bus CoG must be preserved; otherwise, braking, handling, active, and passive safety will be affected. That is why mathematical modelling was proposed to determine CoG based on the linear mass density function. Consequently, it is an effective model that was proposed to determine CoG based on the linear mass density function.
- Acceleration modelling: despite the regulatory requirements of R100 are the longitudinal 12 g and transverse 10 g accelerations, in reality, for heavy buses (M3 category), typical values during frontal crash tests range between 15 and 20 g and depend on the distance from impact point: the farther a component is, the lower the peak acceleration it will experience. At the same time, the indicated acceleration values do not correlate with the real ones, which may arise as a result of the problem of the mathematical attenuation model of acceleration propagation: an exponential decay model of acceleration based on battery CoG location and damping coefficient (like k = 0.05 m−1) was used. The proposed mathematical modelling is an effective way of predicting the acceleration that will act on a specific battery unit, like: af = 12.91 m/s2 for the front battery unit and ar = 9.56 m/s2 for the back unit due to structural damping and wave dissipation.
Author Contributions
Conceptualisation, K.H. and E.K.; methodology, K.H.; software, K.H.; validation, O.H.; formal analysis, I.K., O.D., R.H., S.B. and Y.S.; investigation, Y.R., V.R., R.H., S.B. and Y.S.; resources, O.D.; writing—original draft preparation, K.H. and O.D.; writing—review and editing, K.H., T.W. and A.M.; visualisation, O.D., I.K. and Y.R.; supervision, K.H., E.K., I.K., T.W. and A.M.; project administration, O.H.; funding acquisition, E.K., T.W. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Uniform Provisions Concerning the Approval of Vehicles to Specific Requirements for the Electric Power Train. Regulation No. 100. Available online: https://unece.org/transport/documents/2022/03/standards/regulation-no-100-rev3 (accessed on 10 June 2025).
- Holenko, K.; Dykha, O.; Koda, E.; Kernytskyy, I.; Royko, Y.; Horbay, O.; Berezovetska, O.; Rys, V.; Humenuyk, R.; Berezovetskyi, S.; et al. Validation of Frontal Crashworthiness Simulation for Low-Entry Type Bus Body According to UNECE R29 Requirements. Appl. Sci. 2024, 14, 5595. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, W.; Li, S.; Xu, M.; Huang, W.; Qin, Z. Finite Element Analysis and Optimization of Hydrogen Fuel Cell City Bus Body Frame Structure. Appl. Sci. 2023, 13, 10964. [Google Scholar] [CrossRef]
- Afripin, A.; Zainudin, A.; Sahar, M.; Yusof, M. Frontal Impact on Bus Superstructure as per UNECE R29 and NCAP. IOP Conf. Ser. Mater. Sci. Eng. 2019, 670, 012014. [Google Scholar] [CrossRef]
- Prabhaharan, S.A.; Balaji, G.; Annamalai, K.; Gobinath, V.M. Robust design assessment of automotive crash box structures through model order reduction. Int. J. Crashworthiness 2022, 28, 256–269. [Google Scholar] [CrossRef]
- Lopes, R.; Viriato, N.; Cunha, R.; Maia, R.; Rodrigues, R.; Parente, M.; Moreira, P. Passive Safety Solutions on Coach according ECE R29: Experimental and Numerical Analyses. Procedia Struct. Integr. 2023, 42, 1159–1168. [Google Scholar] [CrossRef]
- Lashkari, A.; Aslamjaved, K.; Manjunath, V.S.; Ahuja, P. Finite Element Analysis of School Bus Frame Structure as per AIS029 Pendulum Impact Test Using LSDYNA. Int. J. Recent Eng. Sci. 2022, 9, 1–4. [Google Scholar] [CrossRef]
- Salhan, P.; Jain, P. A Comparative Study Between Different NCAPs and The Future of BNVSAP. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1168, 012001. [Google Scholar] [CrossRef]
- Sudirja, S.; Hapid, A.; Amin, A.; Kaleg, S.; Budiman, A.C. Stress Analysis Simulations of Welded and Bolted Joints Method for Full Steel and Composite-Steel Chassis Structure of Electric Low Floor Medium Bus. Eureka Phys. Eng. 2020, 6, 61–70. [Google Scholar] [CrossRef]
- Yang, X.; Liu, B. Frontal Crash Oriented Robust Optimization of the Electric Bus Body Frame Considering Tolerance Design. SAE Int. J. Mater. Manuf. 2024; submitted. [Google Scholar]
- Yang, X.; Tian, D. Design Optimization of a Lightweight Electric Bus Body Frame Orienting the Static Performance and Side-Impact Safety. SAE Int. J. Mater. Manuf. 2024; in press. [Google Scholar]
- Deulgaonkar, V.; Kulkarni, M.S.; Khedkar, S.S.; Kharosekar, S.; Sadavarte, V.U. Crash Analysis of Bus Body Structure Using Finite Element Analysis. Int. J. Veh. Struct. Syst. 2020, 12, 312–316. [Google Scholar] [CrossRef]
- Wang, P. Effect of Electric Battery Mass Distribution on Electric Vehicle Movement Safety. Vibroeng. PROCEDIA 2020, 33, 78–83. [Google Scholar] [CrossRef]
- Nandhakumar, S.; Seenivasan, S.; Saalih, A.; Saifudheen, M. Weight Optimization and Structural Analysis of an Electric Bus Chassis Frame. Mater. Today Proc. 2020, 37, 3894–3898. [Google Scholar] [CrossRef]
- Bagus, C.; Sholeh, M.; Sari, E.; Wahid, M.; Fiveriati, A. Numerical Analysis of Static Structure on the Floor Frame of the Medium Bus. J. Keselamatan Transp. Jalan 2024, 11, 71–82. [Google Scholar]
- Yang, Z.; Deng, B.; Deng, M.; Sun, G. A Study on Finite Element Analysis of Electric Bus Frame for Lightweight Design. MATEC Web Conf. 2018, 175, 03049. [Google Scholar] [CrossRef]
- Mihradi, S.; Setiawan, J.; Mahyuddin, A.; Wicaksono, S.; Haq, M. Analysis of the effect of seat foam on passenger head injuries in bus front crash accidents. ASEAN Eng. J. 2025, 15, 133–139. [Google Scholar] [CrossRef]
- Kılınç, S.; Özlü, Ö.; İmren, R.; Şimşir, Ö. Optimum Material Selection for Battery Carrier System in Electric Buses. Eur. J. Res. Dev. 2023, 3, 205–217. [Google Scholar] [CrossRef]
- Hjelkrem, O.; Lervåg, K.Y.; Babri, S.; Lu, C.; Södersten, C.-J. A Battery Electric Bus Energy Consumption Model for Strategic Purposes: Validation of a Proposed Model Structure with Data from Bus Fleets in China and Norway. Transp. Res. Part D Transp. Environ. 2021, 94, 102804. [Google Scholar] [CrossRef]
- Elhussieny, S.; Oraby, W.; Elkady, M.; Abdelhamid, A.; El-Demerdash, S. Optimization of crash dynamics for bus cabin structure based on attained intrusion and deceleration during a frontal collision. Int. J. Crashworthiness 2020, 26, 501–514. [Google Scholar] [CrossRef]
- Lopes, R.; Farahani, B.V.; Melo, F.Q.; Ramos, N.V.; Moreira, P.M.G.P. A Numerical Dynamic Analysis of a Multi-Body Bus. Procedia Struct. Integr. 2022, 37, 81–88. [Google Scholar] [CrossRef]
- Haryanto, I.; Raharjo, F.; Kurdi, O.; Haryadi, G.; Santosa, S. Optimization of Bus Body Frame Structure for Weight Minimizing with Constraint of Natural Frequency Using Adaptive Single-Objective Method. Int. J. Sustain. Transp. Technol. 2018, 1, 9–14. [Google Scholar] [CrossRef][Green Version]
- Ruban, D.; Kraynyk, L.; Ruban, H.; Zakharova, M.; Metelap, V.; Khotunov, V.; Mykhaylyuta, S. Devising an Approach to Assessing the Durability of Bus Body on a Frame Chassis. East.-Eur. J. Enterp. Technol. 2023, 2, 32–39. [Google Scholar]
- Fan, D.; Yang, X.; Song, Y.; Zhang, S. Robust Optimization of an Electric Bus Body Frame Based on the Mesh Morphing Technology. SAE Int. J. Mater. Manuf. 2023; accepted. [Google Scholar]
- Holenko, K.; Dykha, A.; Koda, E.; Kernytskyy, I.; Royko, Y.; Horbay, O.; Berezovetska, O.; Rys, V.; Humeniuk, R.; Berezovetskyi, S.; et al. A Low-Entry Bus Body Structure Performance under the Conditions of the New Car Assessment Program Frontal Crash Tests. SAE Int. J. Trans. Safety 2025, 13, 2. [Google Scholar] [CrossRef]
- Jongpradist, P.; Saingam, N.; Tangthamsathit, P.; Chanpaibool, P.; Sirichantra, J.; Aimmanee, S. Crashworthiness analysis and design of a sandwich composite electric bus structure under full frontal impact. Heliyon 2022, 8, e11999. [Google Scholar] [CrossRef] [PubMed]
- Gattamelata, D.; Vita, L.; Fargnoli, M. Machinery Safety and Ergonomics: A Case Study Research to Augment Agricultural Tracklaying Tractors’ Safety and Usability. Int. J. Environ. Res. Public Health 2021, 18, 8643. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).