Abstract
Underwater inspection images of hydraulic structures often suffer from haze, severe color distortion, low contrast, and blurred textures, impairing the accuracy of automated crack, spalling, and corrosion detection. However, many existing enhancement methods fail to preserve structural details and suppress noise in turbid environments. To address these limitations, we propose a compact image enhancement framework called Wavelet Fusion with Sobel-based Weighting (WWSF). This method first corrects global color and luminance distributions using multiscale Retinex and gamma mapping, followed by local contrast enhancement via CLAHE in the L channel of the CIELAB color space. Two preliminarily corrected images are decomposed using discrete wavelet transform (DWT); low-frequency bands are fused based on maximum energy, while high-frequency bands are adaptively weighted by Sobel edge energy to highlight structural features and suppress background noise. The enhanced image is reconstructed via inverse DWT. Experiments on real-world sluice gate datasets demonstrate that WWSF outperforms six state-of-the-art methods, achieving the highest scores on UIQM and AG while remaining competitive on entropy (EN). Moreover, the method retains strong robustness under high turbidity conditions (T ≥ 35 NTU), producing sharper edges, more faithful color representation, and improved texture clarity. These results indicate that WWSF is an effective preprocessing tool for downstream tasks such as segmentation, defect classification, and condition assessment of hydraulic infrastructure in complex underwater environments.
1. Introduction
The global development of hydraulic infrastructure is on the rise. The 2024 release of the International Commission on Large Dams (ICOLD) World Register of Dams lists more than 62,000 large dams [1,2], a figure that has grown steadily over the past decade. Regular inspection, therefore, represents an increasingly important element of global water-safety governance [3].
Long-serving underwater components—piers, stilling basins, draft-tube linings—are exposed to continuous immersion, chemical corrosion, abrasive sediment transport, and cyclic hydrodynamic loading [4]. These mechanisms accelerate surface scaling, reinforcement exposure, and ultimately the loss of structural capacity, escalating the risk of service failures or catastrophic collapse. Targeted, high-resolution visual assessment is thus indispensable for validating stability and informing maintenance programs.
Remotely operated vehicles (ROVs) equipped with optical cameras currently provide the primary data stream for apparent damage detection [5,6,7]. Unfortunately, raw underwater images suffer from backscatter veiling, wavelength-dependent absorption, severe scattering, and non-uniform ambient illumination, leading to color casts, low contrast, and blurred details. Such degradations impede human interpretation and automated defect recognition [8,9]. Backscatter, scattering, and blur obscure key details like cracks and exposed reinforcements, making human inspection unreliable. Color distortion can hide signs of corrosion, while low contrast reduces visibility. For automated detection, these degradations confuse features and lower model accuracy. Deep learning models rely on clear textures and edges—poor image quality results in suboptimal detection performance. Thus, image enhancement is essential for both human and machine-based underwater inspections. Meniconi et al. [10] noted that poor underwater visibility limited the visual verification of detected faults during underwater pipeline inspection. Image enhancement methods can effectively address this issue by improving the clarity of underwater imagery and supporting both manual and model-based diagnosis.
This paper introduces a wavelet fusion algorithm with Sobel-based weighting (WWSF), tailored for the underwater inspection of hydraulic structures. The WWSF algorithm performs wavelet fusion with weights derived from the edge response intensity. The pipeline comprises (1) color correction using multiscale Retinex with color restoration (MSRCR) [11]; (2) gamma-guided luminance compensation in the CIELAB color space, with CLAHE applied to the L channel [12]; (3) the multilevel discrete wavelet decomposition of both pre-enhanced outputs; and (4) the Sobel-guided weighting of high-frequency sub-bands, followed by inverse fusion to yield the final image.
The remainder of the paper is organized as follows. Section 2 presents a review of the relevant literature. Section 3 details the WWSF algorithm and its implementation. Section 4 reports the experimental settings and results. Section 5 discusses the comparative performance and outlines future research directions, including physics-informed deep priors for real-time inspection. Section 6 summarizes the main conclusions.
2. Literature Review
Recent studies have shown that applying deep learning models following initial image enhancement preprocessing can significantly improve the accuracy of target detection tasks. In underwater inspection scenarios, image quality is often degraded by factors such as wavelength-dependent light absorption, scattering, and non-uniform illumination, making image enhancement a critical prerequisite for restoring key structural information. For example, Wang et al. demonstrated that traditional image augmentation techniques—such as brightness adjustment, scaling, and simulated weather effects—can effectively enrich image datasets and improve window state recognition performance using Faster R-CNN [13]. Similarly, Park et al. found that image enhancement significantly improves the robustness and accuracy of non-protective equipment detection based on YOLOv8 under visually degraded conditions [14]. However, their experiments also revealed that not all enhancement strategies are universally effective; the improvement in model performance depends on the specific detection task. Therefore, enhancement strategies should be tailored to the characteristics and types of the target objects. In other words, to improve the defect detection performance of hydraulic structures in underwater imagery using deep learning models, it is necessary to develop image enhancement methods suited to the specific types of structural defects. These findings further emphasize the importance of image enhancement in underwater inspection tasks, not only for optimizing datasets but also for enhancing the performance of subsequent target recognition.
Existing enhancement algorithms can be grouped into three broad families: (i) Non-model-based adjustment methods—for example, global or adaptive histogram equalization [15], contrast-limited adaptive histogram equalization (CLAHE) [16], white-balance heuristics [17], and Retinex-type operators [18]—redistribute pixel intensities without explicit regard for underwater optics; their performance deteriorates in turbid or unevenly lit scenes [19,20]. (ii) Physics-model-based restoration methods estimate the parameters of an underwater imaging model—typified by the underwater dark channel prior (UDCP) [21] and the Sea-thru framework [22]—but depend heavily on accurate scene assumptions and depth priors. (iii) Fusion-based strategies combine complementary pre-enhancements via multiscale pyramids [23] or wavelet decomposition [24] to exploit their respective advantages. The concept of wavelet decomposition was first introduced in the early 1980s [25], and has become a cornerstone in the fields of signal and image processing. However, many fusion strategies still fail to preserve fine structural features in these specific applications.
To address these limitations, our WWSF algorithm is proposed. The principal contributions are the following:
- Parallel a priori enhancement paths are designed, and a structure-guided fusion mechanism is embedded to accentuate crack edges and scour boundaries.
- A Sobel-energy weighting scheme is introduced that assigns higher fusion weights to regions rich in gradient energy, thereby preserving high-detail content.
- Quantitative metrics and qualitative evaluations are conducted on real-world datasets of hydraulic infrastructure, demonstrating superior enhancement quality and structural fidelity compared to state-of-the-art methods.
3. Weighted Wavelet Fusion Approach
Underwater images acquired for hydraulic infrastructure inspection typically suffer from haze, color casts, low contrast, and blurred textures. To address these issues, we propose an enhancement pipeline based on weighted wavelet fusion. The enhancement process, as illustrated in Figure 1, comprises four stages:
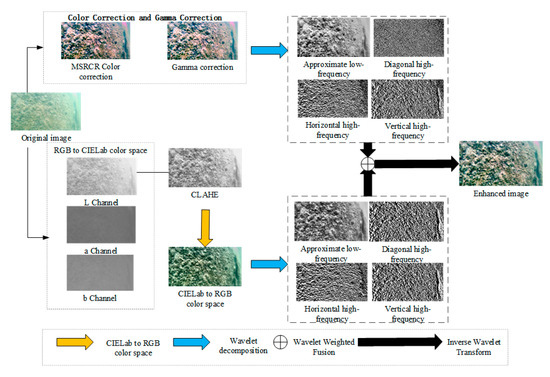
Figure 1.
The complete processing pipeline of the proposed WWSF algorithm.
- Color correction: The raw RGB image is processed with MSRCR, followed by γ-correction, producing a brightness-balanced reference image .
- Contrast enhancement: The RGB image is also transformed to the CIELAB color space; the luminance channel is enhanced with CLAHE and then recombined with the original and channels to form the contrast-enhanced image .
- Wavelet decomposition and weighting: Both and undergo discrete wavelet decomposition to separate low- and high-frequency sub-bands. The Laplacian energy of each sub-band is used as a saliency measure to compute spatially varying fusion weights.
- Wavelet fusion and reconstruction: The weighted sub-bands are fused and inverted via wavelet synthesis, yielding the final enhanced image.
3.1. Color and Brightness Correction
Underwater imaging follows markedly different optical principles from terrestrial photography [26]. On land, light travels mainly through air; underwater, it is repeatedly reflected, refracted, scattered, and absorbed by the water column. Absorption is wavelength-dependent: the longer the wavelength, the faster the attenuation. Consequently, red light is lost within a few meters, while blue-green components persist, giving raw underwater photographs a characteristic cyan tint and severely distorting color fidelity.
Color compensation schemes for underwater scenes fall into two broad classes: (i) white-balance algorithms, grounded in the gray-world assumption, scale the RGB channels so that their means converge to a neutral gray. In shallow, turbid rivers and reservoirs, this assumption rarely holds, because illumination is highly non-uniform and the average scene brightness is well below that of open-ocean imagery; white balance therefore overcompensates or undercompensates individual channels. (ii) Retinex-based methods, inspired by human visual adaptation, decompose an image into illumination and reflectance components and then restore color by normalizing the former. MSRCR is especially suitable for hydraulic infrastructure inspection: it tolerates spatially varying lighting, suppresses the blue–green cast, and simultaneously boosts local contrast.
The formula for the MSRCR color correction method is as follows:
where is the image after color correction, is the weight of the th scale, is the number of scales, denotes the original image, is a Gaussian filter used to simulate the lighting components at different scales, and is the color recovery factor.
Nevertheless, MSRCR processing can over-sharpen an image, causing edge regions to appear either excessively bright or unnaturally dark. To mitigate this artifact, we apply nonlinear gamma correction to rebalance the image brightness. The transformation is defined as follows:
where is the input image, is the output image, and is the correction exponent. Setting < 1 expands low-intensity values and therefore brightens the image, whereas > 1 compresses them and makes the image darker. In this study, was set to 0.8, based on empirical analysis of the luminance histogram. This value enhances midtone details while avoiding overexposure in bright regions.
To verify that the color bias is removed, we analyze the cumulative distribution functions (CDFs) of the RGB channels before and after enhancement (Figure 2). In the raw frame (Figure 2a), the three CDFs (Figure 2b) rise steeply as the normalized gray level goes from 0.6 to 0.9 and almost overlap, indicating low global contrast and a narrow tonal range. The right-shifted green curve reveals a marked green cast. After MSRCR, followed by γ-correction, the CDFs (Figure 2d) become smoother, extend across the full 0–1 range, and separate from one another, showing that the pixel intensities have been redistributed and the chromatic balance improved. The corrected image (Figure 2c) consequently exhibits higher contrast, suppressed overexposure, and clearer structural details, confirming the effectiveness of the proposed workflow.
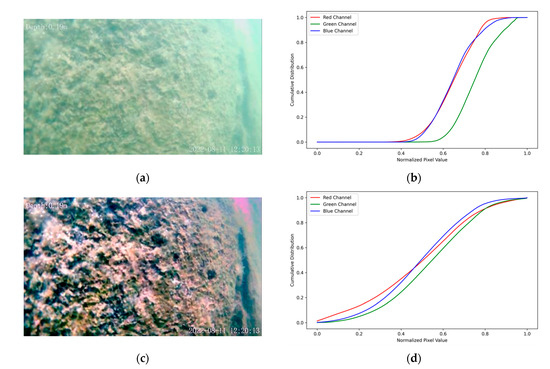
Figure 2.
Distribution of RGB channel CDF curves for the original and MSRCR color-corrected images: (a) Original image; (b) CDF curves of original image; (c) MSRCR color correction image; (d) CDF curves of color correction image.
3.2. Contrast Enhancement Based on CIELAB Color Space
After color correction, the image still exhibits low contrast, a limitation rooted in the physics of underwater imaging. Consequently, additional contrast-enhancement techniques are required. Huang et al.’s imaging model expresses the total irradiance received by the camera as follows [27]:
where is the directly transmitted signal, is the forward-scattering component, and is the back-scattering component. Forward scattering occurs when light reflected from the scene is deflected by suspended particles yet continues roughly toward the sensor. The resulting blur softens edges and depresses local contrast. Backward scattering arises when illumination strikes particles and is redirected toward the camera. This veiling light elevates background brightness, lowers global contrast, and obscures the true color and shape of distant objects.
Global histogram equalization (HE) is the simplest means of enhancing the contrast of underwater photographs; yet, by stretching the dominant gray-level range, it often overemphasizes specific regions, accentuates sensor noise, and introduces chromatic artifacts. Adaptive histogram equalization (AHE) improves on HE by computing histograms in sliding windows, but it still amplifies noise when local variance is low. CLAHE addresses this drawback by (i) partitioning the image into small, non-overlapping tiles and (ii) clipping each local histogram at a predefined threshold before redistribution. In our implementation, the clip limit was set to 2.0, which provided a good balance between local contrast enhancement and noise suppression in underwater scenes. The clip limit prevents excessive amplification and makes CLAHE the de facto standard for localized contrast enhancement in underwater imaging [28].
To decouple luminance manipulation from chromatic information, the RGB frame is first mapped to the device-independent CIELAB color space defined by the International Commission on Illumination in 1976 [12]. In this perceptually motivated space, encodes lightness, whereas the opponent axes (green ↔ red) and (blue ↔ yellow) describe chromaticity. Because the channels are decorrelated, applying CLAHE solely to the component enhances the image contrast without altering the color balance established during the preceding correction stage.
3.3. Weighted Wavelet Fusion Based on Structure-Aware Sobel Operator
Color correction and contrast enhancement solve complementary parts of the visual-quality problem, so the final stage combines their strengths through image fusion. Early work by Ancuti et al. employed a Laplacian pyramid scheme that blends two preprocessed versions of the same frame in the spatial domain [23]. Although it is effective for global appearance, the method relies on fixed weight maps and therefore recovers fine textures only weakly.
Weighted wavelet fusion, introduced by Zhang et al., first decomposes each input into one low-frequency band and three directional high-frequency bands (horizontal, vertical, diagonal) and then assigns an independent weight to every band [24]. Direction-specific weighting enhances edges and micro-textures more selectively than pyramid fusion. Building on this idea, we fuse the color-corrected and contrast-enhanced images after a three-level discrete wavelet transform. Following Zhang et al.’s practice, the weights for the high-frequency coefficients are proportional to the average gradient, because a larger gradient indicates richer local detail and thus a sharper contribution. For the low-frequency bands, we complement the gradient cue with the sum-modified Laplacian energy, which quantifies the spatial distribution of high-frequency content and helps to suppress low-contrast haze. Experiments show that this hybrid weighting produces a fused image that is simultaneously color-balanced, high-contrast, and rich in structural detail.
The MSRCR-enhanced images first undergo a two-dimensional discrete wavelet transform (2D DWT) to perform single-level decomposition. This decomposition yields approximation coefficients representing the low-frequency component, which encodes the structural profile and intensity distribution of underwater infrastructure elements (e.g., piles, columns), alongside detail coefficients capturing high-frequency components that preserve critical edge features and surface texture details essential for defect identification. An adaptive weighting scheme, dynamically derived from the average gradient magnitude within the high-frequency sub-bands, is then applied to optimize detail preservation under varying turbidity conditions. The inverse discrete wavelet transform (IDWT) subsequently reconstructs the fused image, integrating enhanced structural clarity with amplified defect signatures for improved inspection efficacy [29]. The procedure is formally described through the following algorithmic steps:
where is the low-frequency component of the image; represent the horizontal, vertical, and diagonal high-frequency components, respectively; denotes the low-pass filter; is the high-pass filter; and is the original image. The Sobel operator calculates the intensity of edge responses by detecting the gradient of the image [30], which is computed using the following formula:
where and denote the number of rows and columns of the image, respectively; and are the row and column indices of the pixel, respectively; and and denote the gradient magnitude maps of the pixel in the horizontal and vertical directions, i.e., the product of the gradient map and the Sobel convolution kernel. In order to fully fuse the high-frequency components, the Sobel operator is computed for each image and used as a weight factor for the detail intensity. To obtain the weights of the high-frequency components, they are calculated using the following equation:
where denote the Sobel operator for the vertical high-frequency component, the Sobel operator for the horizontal high-frequency component, and the Sobel operator for the diagonal component, respectively. denote the weight coefficients of the horizontal, vertical, and diagonal high-frequency components, respectively. The weighting coefficients for the high-frequency sub-bands (detail coefficients) are calculated to enable frequency-adaptive fusion. These coefficients simultaneously govern the integration of both high-frequency texture details and low-frequency structural information during reconstruction. For the low-frequency sub-band (approximation coefficients), weights are assigned proportional to the regional energy content , ensuring the preferential retention of illumination-stable structural profiles critical for underwater infrastructure assessment.
The energy metric for an image region is defined as follows:
where is the pixel value of the image in the column of the row, and and are the height and width of the image, respectively.
The fusion weights of the low-frequency components are denoted as follows:
where denotes the fusion weights of the low-frequency components of the image, and and are the energy values of the image computed by Equation (8). The fused low-frequency component is denoted as follows:
where , and are the low-frequency components obtained from the wavelet decomposition of the two input images, respectively.
The horizontal, vertical, and diagonal high-frequency components of the fusion, , are denoted as follows:
where denote the horizontal, vertical, and diagonal high-frequency components, respectively; and denote the horizontal, vertical, and diagonal high-frequency component weighting coefficients, respectively.
Finally, the high- and low-frequency component images obtained above are wavelet-inverted to reconstruct the final fused image :
where is the wavelet inversion function, which is used to fuse the high- and low-frequency components of the image. The low-frequency sub-bands are fused with the maximum-energy rule. For every location, the coefficient whose energy is larger is retained, because a higher low-band energy more completely conveys the scene’s overall luminance distribution and dominant contours. For the high-frequency sub-bands, fusion weights are derived from the Sobel gradient magnitude. The Sobel operator estimates the local edge strength; a larger response implies richer detail and texture, so its normalized value is used as the weight assigned to that coefficient set. Consequently, sub-bands with stronger Sobel responses contribute more to the final reconstruction.
4. Underwater Image-Enhancement Experiments and Result Analysis
This section details the experimental design. We conducted quantitative and qualitative evaluations on the acquired underwater building-inspection images and compared our weighted wavelet fusion method with several widely used conventional enhancement algorithms to assess its performance.
4.1. Experimental Setup and Assessment Indicators
To validate the proposed algorithm for underwater-image enhancement, we performed experiments on real underwater structural-inspection photographs and evaluated the performance with several complementary metrics.
(1) Comparison methods. The WWSF approach developed in this study was benchmarked against six widely used enhancement techniques: UDCP, CLAHE, relative global histogram stretching (RGHS), unsupervised color correction method (UCM), minimal color loss and locally adaptive contrast enhancement (MLLE), and weighted wavelet visual perception fusion (WWPF) [24,27,31,32,33].
(2) Image data. High-quality inspection imagery of hydraulic structures is scarce because acquiring it requires extensive time and specialized equipment [34,35]. We therefore used an underwater inspection dataset recorded at a controlling sluice gate in Anhui Province, China.
(3) Evaluation metrics. Guided by the review of Saad Saoud et al., three objective indices were selected: the average gradient (AG), information entropy (EN), and underwater image quality measure (UIQM) [36,37,38,39]. The AG quantifies image sharpness—the larger the AG, the clearer the image—and is calculated as follows:
where and represent the gradient components of the image in the horizontal and vertical directions, respectively, and represent the number of rows and the number of columns in the image.
EN measures the randomness of the gray-level distribution. A larger EN value indicates a more heterogeneous histogram—useful for judging quality improvements in scenarios such as complex-texture enhancement. It is defined as follows:
where denotes the probability of occurrence of each gray value, and is the level of gray level division of the image.
The UIQM is a reference-free index designed specifically for evaluating the visual quality of underwater photographs. The UIQM blends three perceptual attributes—color fidelity (UICM), sharpness (UISM), and contrast (UIConM)—and produces a single score via a weighted sum:
where are the weighting factors. Commonly used general values of these factors are = 0.0282, = 0.2953, and = 0.3753.
(4) Experimental environment. All experiments were executed on Windows 11 with Python 3.10 and accelerated by an NVIDIA RTX 3050 Ti GPU.
4.2. Qualitative Evaluation
This study focuses on image clarity and texture rendition, which are both critical for underwater structural inspection. To test the proposed WWSF algorithm, eight inspection images—showing concrete spalling, cracking, corrosion, and voids—were enhanced, and the results were compared against six established methods (CLAHE, UDCP, RGHS, UCM, MLLE, and WWPF).
In terms of color fidelity, the CLAHE, WWPF, RGHS, and WWSF methods demonstrate relatively accurate color restoration. In contrast, the UDCP method, based on image restoration principles, causes severe color distortion, while the UCM method introduces an excessive reddish tone. These distortions can be attributed to the high turbidity and strong optical variability in lake water, which hinder accurate modeling of underwater light attenuation. Furthermore, in shallow waters where red light absorption is not yet significant, forcibly applying red-channel compensation may lead to unnatural reddish hues.
Regarding contrast performance, CLAHE and WWSF show superior contrast enhancement. Conversely, RGHS performs poorly in this aspect due to its global histogram stretching strategy, which lacks the ability to enhance local contrast, a critical factor in emphasizing fine structures. The WWSF method, which incorporates CLAHE for contrast enhancement, effectively improves the local contrast of structural details, making it well-suited for underwater hydraulic imagery.
As for detail preservation, the WWPF, MLLE, and WWSF methods achieve better visual recovery of fine features, such as cracks and surface textures, while other approaches fail to adequately reveal these structural cues. These three methods belong to the fusion-based enhancement category, which excels in detail preservation. Specifically, both WWSF and WWPF utilize wavelet transform-based fusion to highlight edge and texture features, while the MLLE method enhances details and color by adopting a minimum color-loss principle and maximum attenuation-guided fusion strategy.
In terms of structural integrity, our WWSF method demonstrates excellent performance. It substantially reduces shadowing across the image, and avoids overexposed edges or false contours. In contrast, WWPF tends to produce overexposed boundaries and more noticeable artifacts. This difference stems from WWSF’s incorporation of gamma correction, which effectively adjusts global brightness and suppresses structural distortions, thereby preserving the visual coherence of the enhanced image.
4.3. Quantitative Evaluation
Reference-free objective metrics were used to eliminate subjective bias in assessing the enhancement quality. Three indices—the UIQM, AG, and EN—were chosen to measure color fidelity, sharpness, and contrast, respectively. Table 1 lists the scores obtained by the seven algorithms for the eight test images in Figure 3; the highest value for each metric is shown in the background shading.

Table 1.
Evaluation of multiple underwater-image-enhancement algorithms.

Figure 3.
Comparison of the original image and images enhanced by different algorithms.
The results show that the WWSF method achieves the best performance in both UIQM and AG, indicating its significant advantages in color restoration, edge sharpness, and detail preservation. This can be attributed to its wavelet-based fusion strategy combined with Sobel-weighted enhancement, which effectively strengthens structural features while suppressing noise and redundant textures.
In contrast, the WWPF method achieves the highest EN score, reflecting its effectiveness in increasing the overall information entropy of the image. However, it is worth noting that an excessively high EN value may introduce redundant textures and noise, which can compromise the structural clarity and consistency. By comparison, WWSF deliberately moderates EN to prioritize structural integrity and visual purity, especially beneficial in underwater structural imagery.
Figure 4a–c further visualize the metric trends. It is evident that WWSF significantly outperforms competing methods in both UIQM and AG, while maintaining competitive EN values—demonstrating a well-balanced trade-off between enhancement and structural coherence.
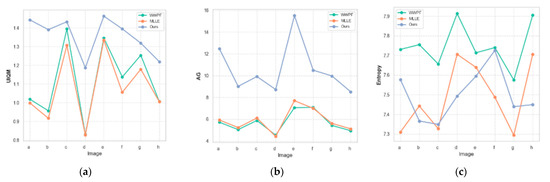
Figure 4.
Line graphs of metrics for experimental comparison results: (a) UIQM; (b) AG; (c) Entropy.
In summary, WWSF not only excels across multiple objective metrics but also aligns well with qualitative visual assessments, confirming its effectiveness and practical value for underwater structural inspection tasks. Beyond visual improvement, the method provides clearer and more consistent image inputs for both manual interpretation and automated detection models, making it a promising choice for real-world engineering applications.
In addition to visual and quantitative quality, runtime performance was evaluated to assess the practical feasibility of the WWSF algorithm. On images with a resolution of 946 × 512, the average processing time was 0.1973 s per image, corresponding to approximately 5.07 FPS. These results suggest that the proposed method is computationally efficient and suitable for offline enhancement in practical underwater inspection tasks.
4.4. Ablation Studies
To quantify the contribution of each component, we ran an ablation study that yielded four simplified versions of the WWSF pipeline: one without the multiscale Retinex with color restoration module (No-MSRCR), one without the gamma-correction step (No-γ), one without the CLAHE-based contrast enhancer (No-CLAHE), and one that substitutes ordinary, unweighted wavelet fusion for the weighted stage (Plain-WF). Each variant, together with the complete WWSF model, was scored with the objective image-quality metrics, the UIQM, AG, and EN (Table 2); the visual output of the model variants is shown in Figure 5a–f.

Table 2.
Quantitative assessment of ablation studies.

Figure 5.
Images of different ablation studies: (a) Original image; (b) Image without MSRCR method; (c) Image without gamma-correction method; (d) Image without CLAHE method; (e) Image using normal fusion; (f) WWSF (full model).
A visual comparison of the ablated outputs in Figure 5 reveals distinct impacts of each component. The No-MSRCR variant enhances edge sharpness to some extent; however, due to the absence of the multiscale Retinex with color restoration module, the overall tone appears grayish and the local contrast is subdued. This highlights the essential role of the MSRCR module in suppressing underwater color casts (e.g., bluish–green bias) and restoring the intrinsic color of submerged objects. The No-γ version improves color saturation, yet fails to appropriately compress the overall luminance, leading to overexposed regions. This emphasizes the compensatory effect of gamma correction in adjusting the dynamic range and suppressing localized glare.
In the No-CLAHE version, while the colors are vivid, the fine structural textures appear less prominent. This indicates that the CLAHE module is critical for enhancing local contrast and edge definition, particularly under uneven illumination and turbid water conditions where hydraulic structural details may otherwise remain obscured. The Plain-WF result approximates the output of the complete model but lacks significant texture reinforcement, suggesting that the introduction of a weighted fusion mechanism effectively strengthens scale-specific texture cues—beneficial for highlighting microstructural features such as concrete spalling and cracks.
By contrast, the complete WWSF model achieves a well-balanced enhancement across color, brightness, and texture domains. The MSRCR module provides global illumination compensation and color fidelity; gamma correction suppresses local overexposure; CLAHE enhances local detail and clarity; and the weighted wavelet fusion aggregates multiscale information to preserve structural integrity. This collaborative effect among modules is particularly advantageous in underwater environments with complex lighting and significant scattering, delivering visually reliable inputs for downstream hydraulic defect identification tasks.
Table 2 confirms these observations: the full model attains the highest or second-highest scores for nearly every metric, demonstrating that each module makes a positive, measurable contribution to the overall performance.
5. Discussion
The proposed algorithm excels in both subjective and objective assessments, demonstrating marked improvements in overall clarity, as well as in fine-texture rendering for hydraulic infrastructure inspection images. Its success stems from a structure-aware, WWSF framework that highlights defect edges while suppressing noise. The preceding steps—MSRCR color correction, γ-adjustment, and CLAHE-based contrast enhancement—provide balanced luminance and chromatic information, which the fusion stage can then exploit.
Unlike most current enhancement studies—which center on de-hazing, global clarity, color restitution, or contrast—this work targets the texture detail essential for recognizing cracks, corrosion, spalling, and voids in hydraulic facilities. Conventional underwater algorithms often perform poorly under artificial lighting: dark-channel priors (e.g., GDCP, UDCP) misestimate tones and introduce color shifts [31,40]; CLAHE boosts contrast but leaves textures muted; and classic gray-world white balance fails on near-monochrome concrete and metal surfaces. In contrast, MSRCR, grounded in Retinex theory, operates on local reflectance differences, recovering both color constancy and structural cues vital to condition assessment.
Texture enhancement is crucial because subsequent tasks—segmentation and defect recognition—depend on accurate structural cues. Physical-model approaches cannot resolve this, and standard fusion rules (averaging, max-selection) ignore the complexity of underwater scenes. Decomposing images with the discrete wavelet transform and weighting sub-bands using the Sobel structure energy preserves orientation-specific edges while attenuating background noise, outperforming average-gradient weights in both detail fidelity and artifact control. Experiments confirm that Sobel-weighted fusion not only heightens clarity and contrast but also reduces noise and color error, delivering reliable inputs for downstream analysis.
WWSF surpasses pyramid-based and unweighted fusion in visual sharpness and structural detail, yet its EN scores lag behind those of WWPF and RGHS. This drop suggests that some high-frequency coefficients were intentionally suppressed to maintain structural consistency and visual purity. Future work should aim to strike a better balance between detail richness and noise control—potentially through deep learning-driven adaptive weighting schemes—to improve information density without compromising clarity. We also plan to conduct comparative experiments with representative deep learning-based enhancement models such as WaterNet and UIE-CNN, which have demonstrated strong capabilities in addressing non-uniform illumination and severe scattering through data-driven learning. Benchmarking the proposed WWSF framework against these approaches will not only further validate its performance but may also inspire future hybrid enhancement strategies that combine traditional fusion mechanisms with deep neural networks.
6. Conclusions
This study proposes a WWSF algorithm to resolve color, contrast, and texture deficiencies in optical images collected during underwater inspections of hydraulic structures. Extensive qualitative and quantitative experiments on dam-inspection imagery confirm its effectiveness. The principal findings are the following:
(1) WWSF consistently achieves the highest or near-highest scores across three reference-free evaluation metrics—UIQM, AG, and EN—outperforming existing state-of-the-art methods. This confirms its effectiveness in enhancing underwater imagery for real-world engineering applications.
(2) By applying Sobel edge energy weighting to high-frequency wavelet sub-bands, WWSF enhances fine-scale defect features such as cracks, spalling, and corrosion more effectively than traditional average-gradient-based approaches. Simultaneously, it suppresses background noise and irrelevant textures.
(3) The algorithm maintains strong performance in terms of contrast and color fidelity even in highly turbid waters. However, partial loss of micro-texture is still observed under severe scattering conditions, indicating a limitation in extreme environments.
(4) This study indicates that future research should focus on integrating turbidity-aware light transmission models and designing dynamically adaptive wavelet decomposition frameworks, in order to further enhance the preservation of fine textures and structural consistency under complex underwater conditions.
Author Contributions
Conceptualization, M.Z. and J.X.; methodology, M.Z.; software, M.Z.; validation, M.Z., J.Z. and J.X.; formal analysis, M.Z.; investigation, M.Z.; resources, J.L.; data curation, M.Z.; writing—original draft preparation, M.Z.; writing—review and editing, J.Z., J.L., J.H., X.Z. and J.X.; visualization, M.Z.; supervision, J.X.; project administration, J.X.; funding acquisition, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was made possible thanks to the generous financial support provided by various organizations. Specifically, we would like to acknowledge the Anhui Province Natural Science Foundation of China under grant number 2208085US02.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the corresponding author on request.
Acknowledgments
The authors are grateful to the three anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- International Commission on Large Dams (ICOLD). World Register of Dams 2024. Available online: https://www.icold-cigb.org/GB/world_register/world_register_of_dams.asp (accessed on 16 July 2025).
- Zhang, A.T.; Gu, V.X. Global Dam Tracker: A Database of More Than 35,000 Dams with Location, Catchment, and Attribute Information. Sci. Data. 2023, 10, 111. [Google Scholar] [CrossRef]
- Gao, J.; Chen, B.; Tang, S.-K. Water Quality Monitoring: A Water Quality Dataset from an On-Site Study in Macao. Appl. Sci. 2025, 15, 4130. [Google Scholar] [CrossRef]
- Rasheed, P.A.; Nayar, S.K.; Barsoum, I.; Alfantazi, A. Degradation of Concrete Structures in Nuclear Power Plants: A Review of the Major Causes and Possible Preventive Measures. Energies 2022, 15, 8011. [Google Scholar] [CrossRef]
- Xu, P.; Chen, M.; Yan, K.; Wang, Z.; Li, X.; Wang, G.; Wang, Y. Research progress on remotely operated vehicle technology for underwater inspection of large hydropower dams. J. Tsinghua Univ. (Sci. Technol.) 2023, 63, 1032–1040. [Google Scholar] [CrossRef]
- Hao, Z.; Wang, Q. Research Review on Underwater Target Detection Using Sonar Imagery. J. Unmanned Undersea Syst. 2023, 31, 339–348. [Google Scholar] [CrossRef]
- Li, Z.; Liu, A.; Chen, B.; Wang, J.; Lan, T.; Wang, B. Bridge Underwater Structural Defects Detection Based on Fusion Image Enhancement and Improved YOLOv7. Eng. Mech. 2024, 42, 276–282. [Google Scholar] [CrossRef]
- Wei, G.; Chen, S.; Liu, Y.; Li, X. Survey of underwater image enhancement and restoration algorithms. Appl. Res. Comput. 2021, 38, 2561–2569. [Google Scholar] [CrossRef]
- Xu, J.; Yu, X. Detection of Concrete Structural Defects Using Impact Echo Based on Deep Network. J. Test. Eval. 2021, 49, 109–120. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient tests for checking the Trieste subsea pipeline: Diving into fault detection. J. Mar. Sci. Eng. 2024, 12, 391. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Nagdy, A.S.; Hashem, K.M.; Mohamed, D.S. A Computational Technique for Solving Three-Dimensional Mixed Volterra–Fredholm Integral Equations. Fractal. Fract. 2023, 7, 196. [Google Scholar] [CrossRef]
- Robertson, A.R. Historical Development of CIE Recommended Color Difference Equations. Color. Res. Appl. 1990, 15, 167–170. [Google Scholar] [CrossRef]
- Wang, S.; Korolija, I.; Rovas, D. Impact of Traditional Augmentation Methods on Window State Detection. CLIMA 2022, 1–8. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.; Wang, S.; Kim, J. Effectiveness of Image Augmentation Techniques on Non-Protective Personal Equipment Detection Using YOLOv8. Appl. Sci. 2025, 15, 2631. [Google Scholar] [CrossRef]
- Stark, J.A. Adaptive Image Contrast Enhancement Using Generalizations of Histogram Equalization. IEEE Trans. Image Process. 2000, 9, 889–896. [Google Scholar] [CrossRef] [PubMed]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; Romeny, T.H.; Zimmerman, J.B.; Zuiderveld, K. Adaptive Histogram Equalization and Its Variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Ancuti, C.O.; Ancuti, C.; De Vleeschouwer, C.; Bekaert, P. Color Balance and Fusion for Underwater Image Enhancement. IEEE Trans. Image Process. 2018, 27, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Dong, L.; Xu, W. Retinex-Inspired Color Correction and Detail Preserved Fusion for Underwater Image Enhancement. Comput. Electron. Agric. 2022, 192, 106585. [Google Scholar] [CrossRef]
- Ou, Y.; Fan, J.; Zhou, C.; Zhang, P.; Shen, Z.; Fu, Y.; Liu, X.; Hou, Z. An Underwater, Fault-Tolerant, Laser-Aided Robotic Multi-Modal Dense SLAM System for Continuous Underwater In-Situ Observation 2025. arXiv 2025, arXiv:2504.21826. [Google Scholar]
- Li, X.; Hou, G.; Li, K.; Pan, Z. Enhancing Underwater Image via Adaptive Color and Contrast Enhancement, and Denoising. Eng. Appl. Artif. Intell. 2022, 111, 104759. [Google Scholar] [CrossRef]
- Sathya, R.; Bharathi, M.; Dhivyasri, G. Underwater Image Enhancement by Dark Channel Prior. In Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; IEEE: Coimbatore, India, 2015; pp. 1119–1123. [Google Scholar]
- Akkaynak, D.; Treibitz, T. Sea-Thru: A Method for Removing Water from Underwater Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1682–1691. [Google Scholar]
- Ancuti, C.; Ancuti, C.O.; Haber, T.; Bekaert, P. Enhancing Underwater Images and Videos by Fusion. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: Providence, RI, USA, 2012; pp. 81–88. [Google Scholar]
- Zhang, W.; Zhou, L.; Zhuang, P.; Li, G.; Pan, X.; Zhao, W.; Li, C. Underwater Image Enhancement via Weighted Wavelet Visual Perception Fusion. IEEE Trans. Circuits. Syst. Video. Technol. 2024, 34, 2469–2483. [Google Scholar] [CrossRef]
- Morlet, J. Sampling Theory and Wave Propagation. In Issues in Acoustic Signal—Image Processing and Recognition. NATO ASI Series; Chen, C.H., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; Volume 1. [Google Scholar] [CrossRef]
- Quan, X.; Wei, Y.; Li, B.; Liu, K.; Li, C.; Zhang, B.; Yang, J. The Color Improvement of Underwater Images Based on Light Source and Detector. Sensors 2022, 22, 692. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Wang, Y.; Song, W.; Sequeira, J.; Mavromatis, S. Shallow-Water Image Enhancement Using Relative Global Histogram Stretching Based on Adaptive Parameter Acquisition. In MultiMedia Modeling; Schoeffmann, K., Chalidabhongse, T.H., Ngo, C.W., Aramvith, S., O’Connor, N.E., Ho, Y.-S., Gabbouj, M., Elgammal, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 10704, pp. 453–465. [Google Scholar]
- Pizer, S.M.; Johnston, R.E.; Ericksen, J.P.; Yankaskas, B.C.; Muller, K.E. Contrast-Limited Adaptive Histogram Equalization: Speed and Effectiveness. In Proceedings of the [1990] Proceedings of the First Conference on Visualization in Biomedical Computing, Atlanta, GA, USA, 22–25 May 1990; IEEE Computer Society: Atlanta, GA, USA, 1990; pp. 337–345. [Google Scholar]
- Xu, J.; Wei, H. Ultrasonic Testing Analysis of Concrete Structure Based on S Transform. Shock. Vib. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Math, M.; Halse, S.V.; Jagadale, B.N. Underwater Image Enhancement Using Edge Detection Filter and Histogram Equalization. Int. J. Mod. Trends. Sci. Technol. 2023, 9, 32–38. [Google Scholar] [CrossRef]
- Liang, Z.; Ding, X.; Wang, Y.; Yan, X.; Fu, X. GUDCP: Generalization of Underwater Dark Channel Prior for Underwater Image Restoration. IEEE Trans. Circuits. Syst. Video. Technol. 2022, 32, 4879–4884. [Google Scholar] [CrossRef]
- Iqbal, K.; Odetayo, M.; James, A. others Enhancing the Low Quality Images Using Unsupervised Colour Correction Method. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; pp. 1703–1709. [Google Scholar]
- Zhang, W.; Zhuang, P.; Sun, H.-H.; Li, G.; Kwong, S.; Li, C. Underwater Image Enhancement via Minimal Color Loss and Locally Adaptive Contrast Enhancement. IEEE Trans. Image Process. 2022, 31, 3997–4010. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Huang, B.; Kang, F. A Review of Detection Technologies for Underwater Cracks on Concrete Dam Surfaces. Appl. Sci. 2023, 13, 3564. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Huang, X.; Chen, H.; Xu, B.; Shu, X.; Zhou, Y.; Cao, Q.; Tu, J.; Wang, R.; et al. Underwater Crack Pixel-Wise Identification and Quantification for Dams via Lightweight Semantic Segmentation and Transfer Learning. Autom. Constr. 2022, 144, 104600. [Google Scholar] [CrossRef]
- Saad Saoud, L.; Elmezain, M.; Sultan, A.; Heshmat, M.; Seneviratne, L.; Hussain, I. Seeing Through the Haze: A Comprehensive Review of Underwater Image Enhancement Techniques. IEEE Access. 2024, 12, 145206–145233. [Google Scholar] [CrossRef]
- Mohd Azmi, K.Z.; Abdul Ghani, A.S.; Md Yusof, Z.; Ibrahim, Z. Natural-Based Underwater Image Color Enhancement through Fusion of Swarm-Intelligence Algorithm. Appl. Soft Comput. 2019, 85, 105810. [Google Scholar] [CrossRef]
- Chan, R.; Rottmann, M.; Gottschalk, H. Entropy Maximization and Meta Classification for Out-of-Distribution Detection in Semantic Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5128–5137. [Google Scholar]
- Panetta, K.; Gao, C.; Agaian, S. Human-Visual-System-Inspired Underwater Image Quality Measures. IEEE J. Ocean. Eng. 2016, 41, 541–551. [Google Scholar] [CrossRef]
- Peng, Y.T.; Cao, K.; Cosman, P.C. Generalization of the Dark Channel Prior for Single Image Restoration. IEEE Trans. Image Process. 2018, 27, 2856–2868. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).