Uncertainty-Aware Deep Learning for Robust and Interpretable MI EEG Using Channel Dropout and LayerCAM Integration
Abstract
1. Introduction
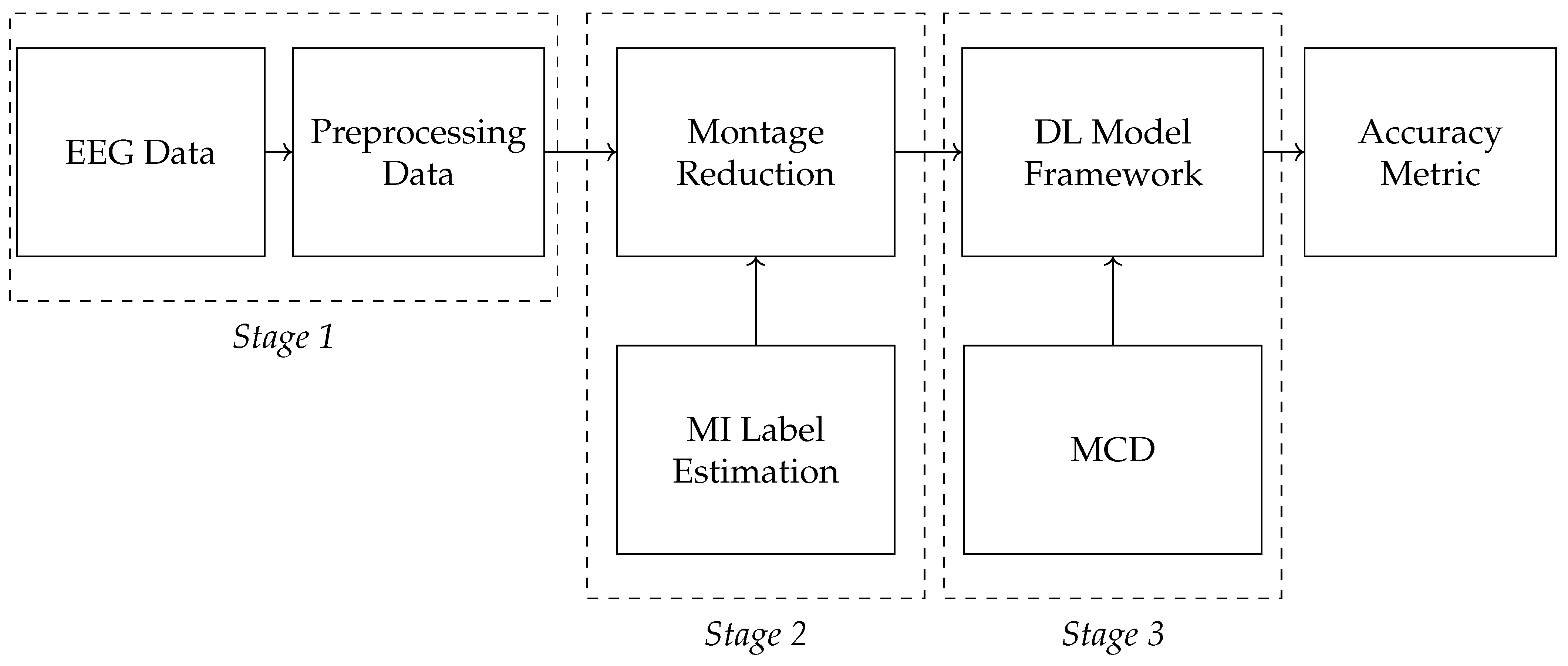
- A framework for robust and interpretable MI classification: We propose and validate a novel framework that, for the first time, integrates channel-wise Monte Carlo dropout (MCD) for uncertainty-aware robustness with LayerCAM for neurophysiologically relevant interpretability, addressing two critical challenges in BCI simultaneously.
- Comprehensive evaluation across multiple architectures and conditions: We conduct a rigorous evaluation of our framework on a 52-subject dataset, testing its efficacy across three distinct deep learning architectures (ShallowConvNet, EEGNet, TCNet Fusion) and under varying channel montage densities (8, 16, 32, and 64 channels).
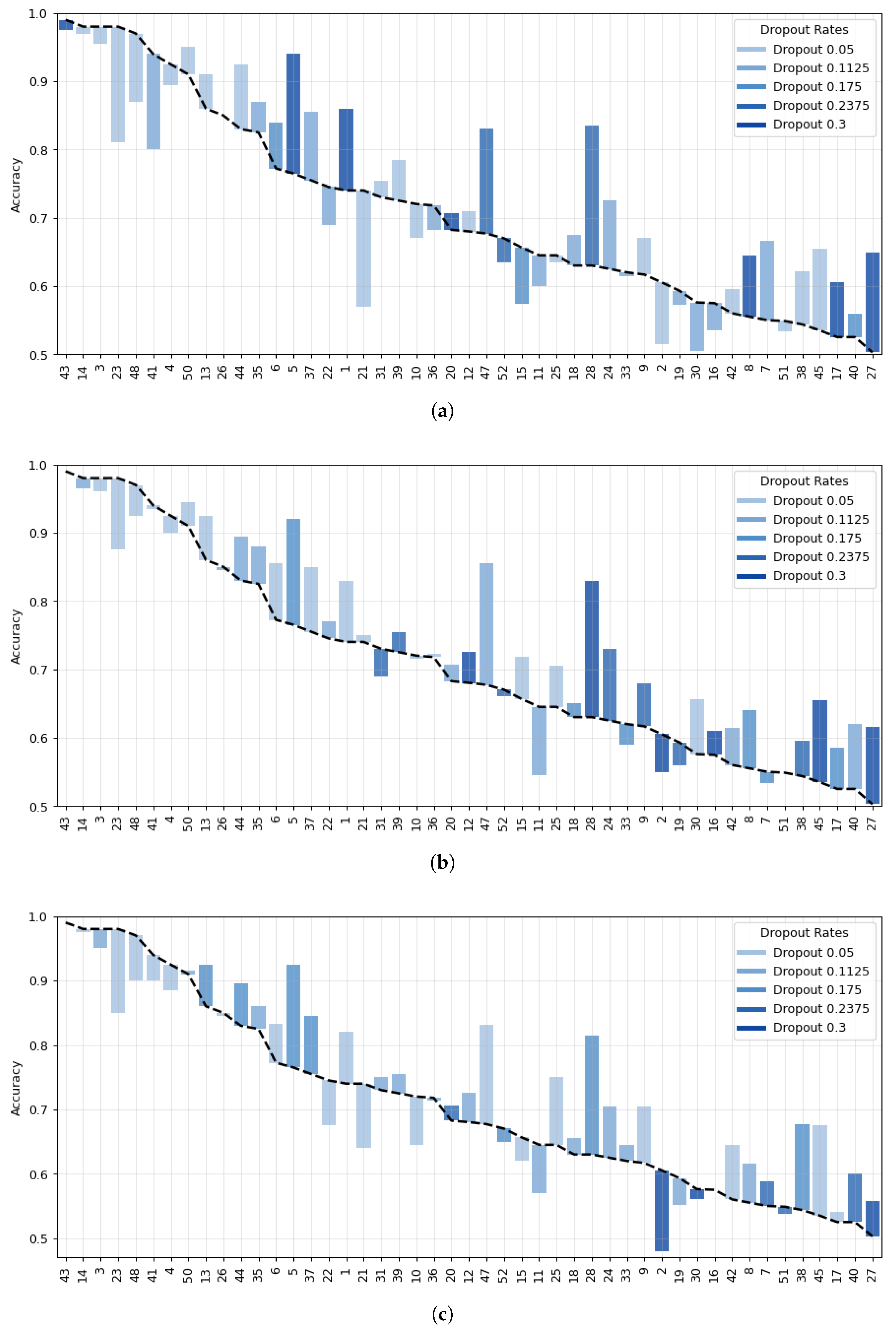
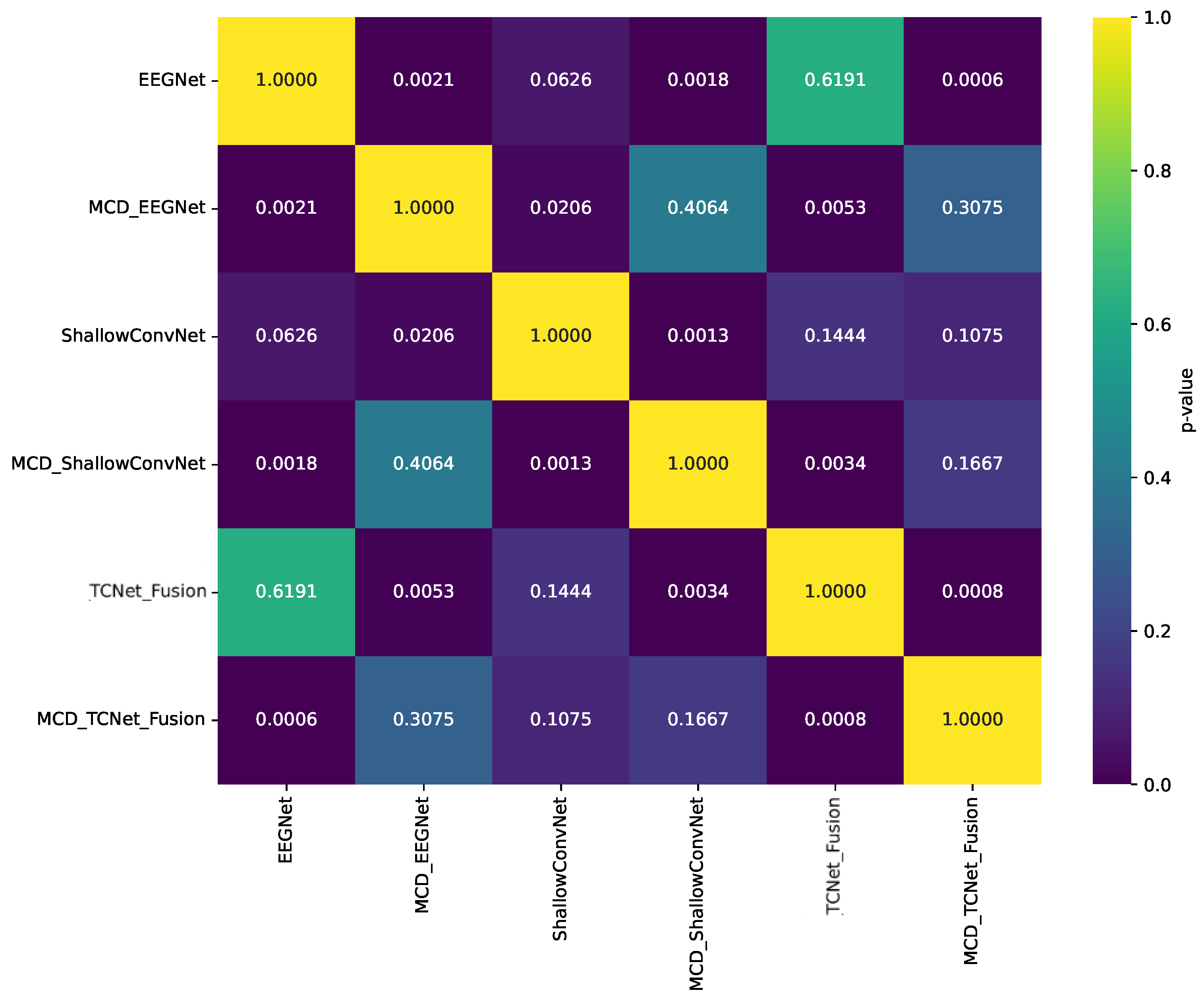
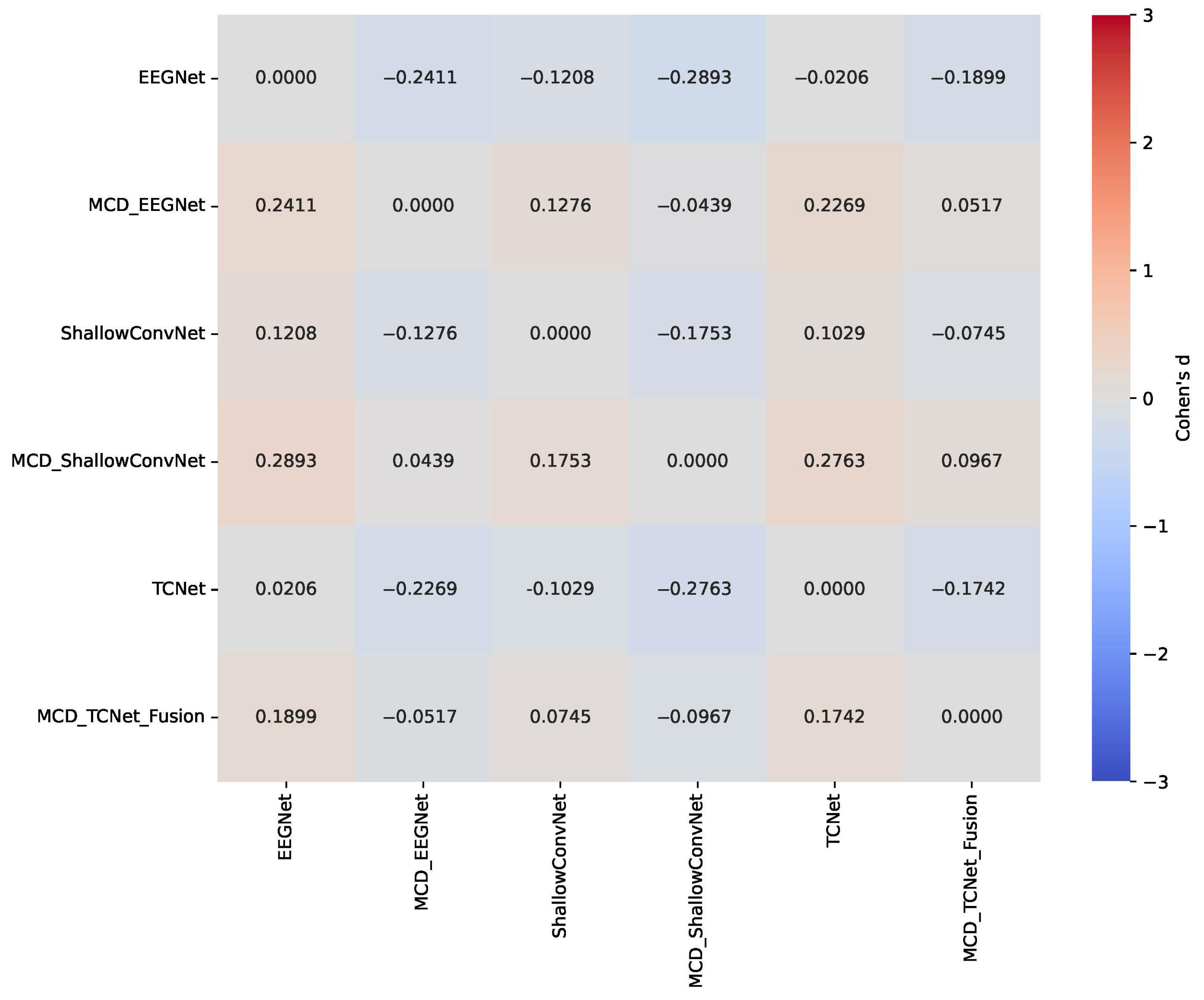
- Statistically validated performance improvement: We provide statistically significant evidence (p < 0.05) that our MCD-enhanced models consistently outperform their baseline counterparts, with particularly notable gains for low-performing subjects, thereby enhancing both accuracy and inter-subject consistency.
- Enhanced interpretability through CAMs: We demonstrate through LayerCAM visualizations that our uncertainty-aware approach transforms diffuse, difficult-to-interpret spatial attention maps into focused, neurophysiologically plausible topograms, significantly improving model transparency and clinical trust.
2. Related Work
2.1. Deep Learning for MI-EEG Classification
2.2. Sparse Electrode Configurations
2.3. Explainable AI in EEG-Based BCI Systems
2.4. Uncertainty Estimation in Neural Models
3. Materials and Methods
3.1. Baseline Feature Extraction of Spatiotemporal Characteristics
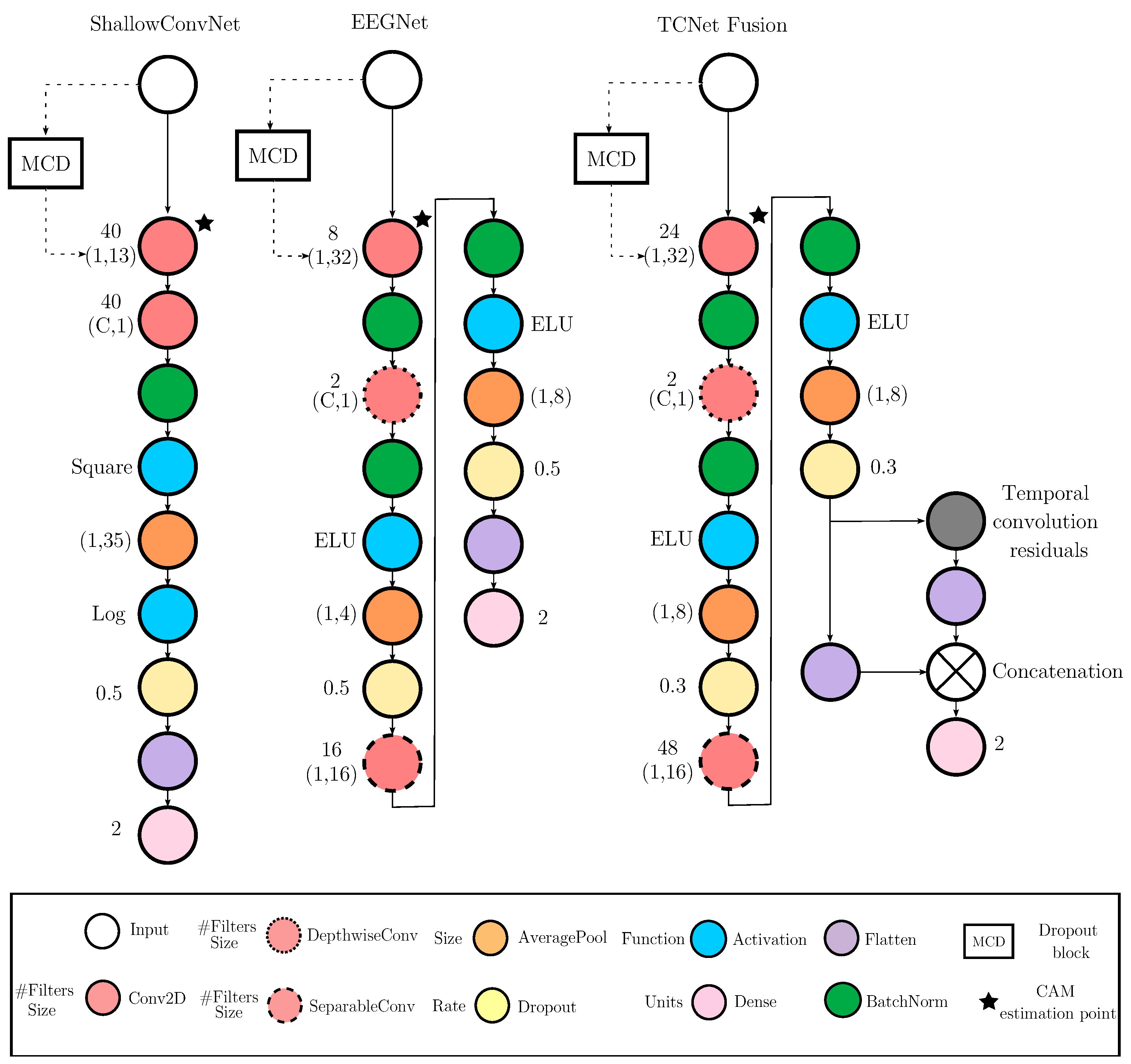
3.2. Deep Learning Frameworks for Feature Extraction of MI Responses
- ∗
- ∗
- EEGNet Framework. In this architecture, feature extraction is carried out through a sequence of convolutional blocks , structured as [38]:where and denote the number of temporal and separable filters, respectively; and are the kernel sizes for the temporal and depthwise convolutions; and is the number of spatial filters. Each block is followed by batch normalization and non-linear activation.
- ∗
- TCNet (Temporal Convolutional Network) Framework. TCNet extends the prior architectures by integrating temporal convolutional modules with residual connections [66,67]. The model combines filter bank design with deep temporal processing through the sequential application of blocks , as follows:where and are the kernel sizes for the initial and filter bank convolutions, is the number of feature maps, L is the number of residual blocks, , and denotes a temporal convolutional block with dilated convolutions. The dilation factor increases with l, enabling exponential growth in the receptive field while preserving temporal resolution.
3.3. Monte Carlo Dropout with CAM Integration for MI Classification
4. Experimental Set-Up
4.1. Evaluating Framework
- ∗
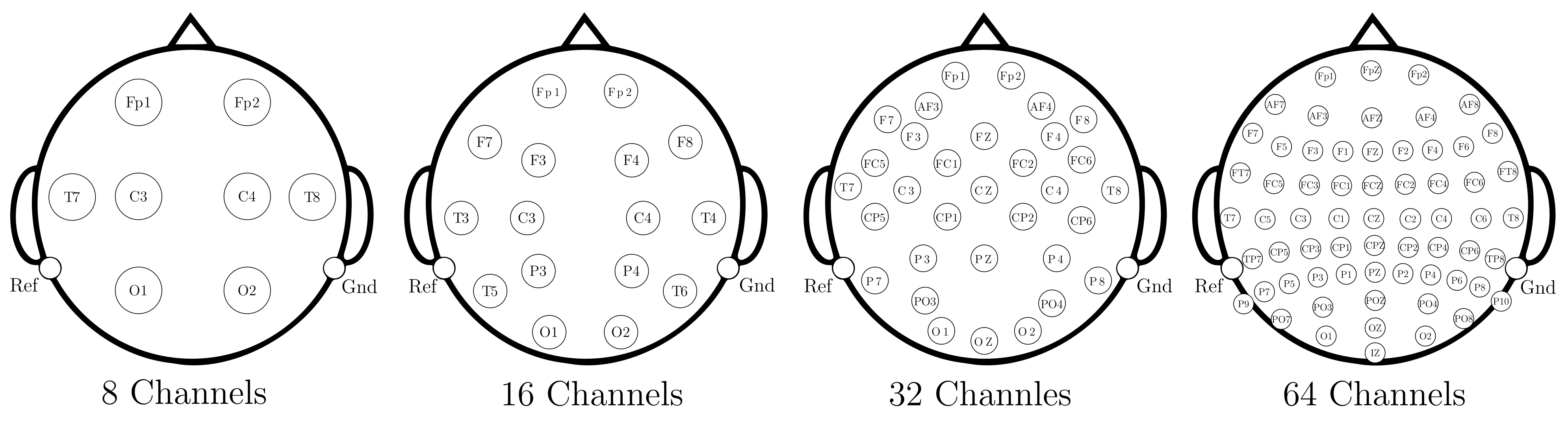
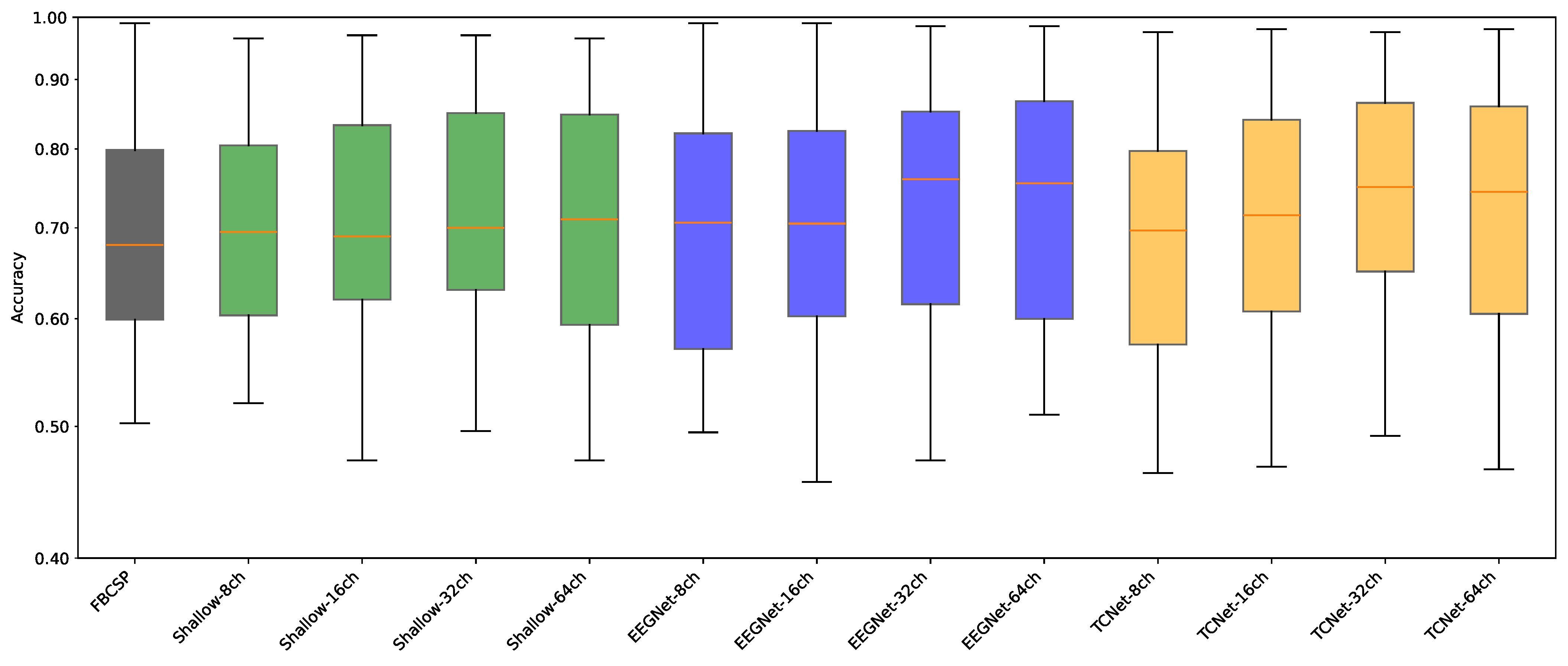
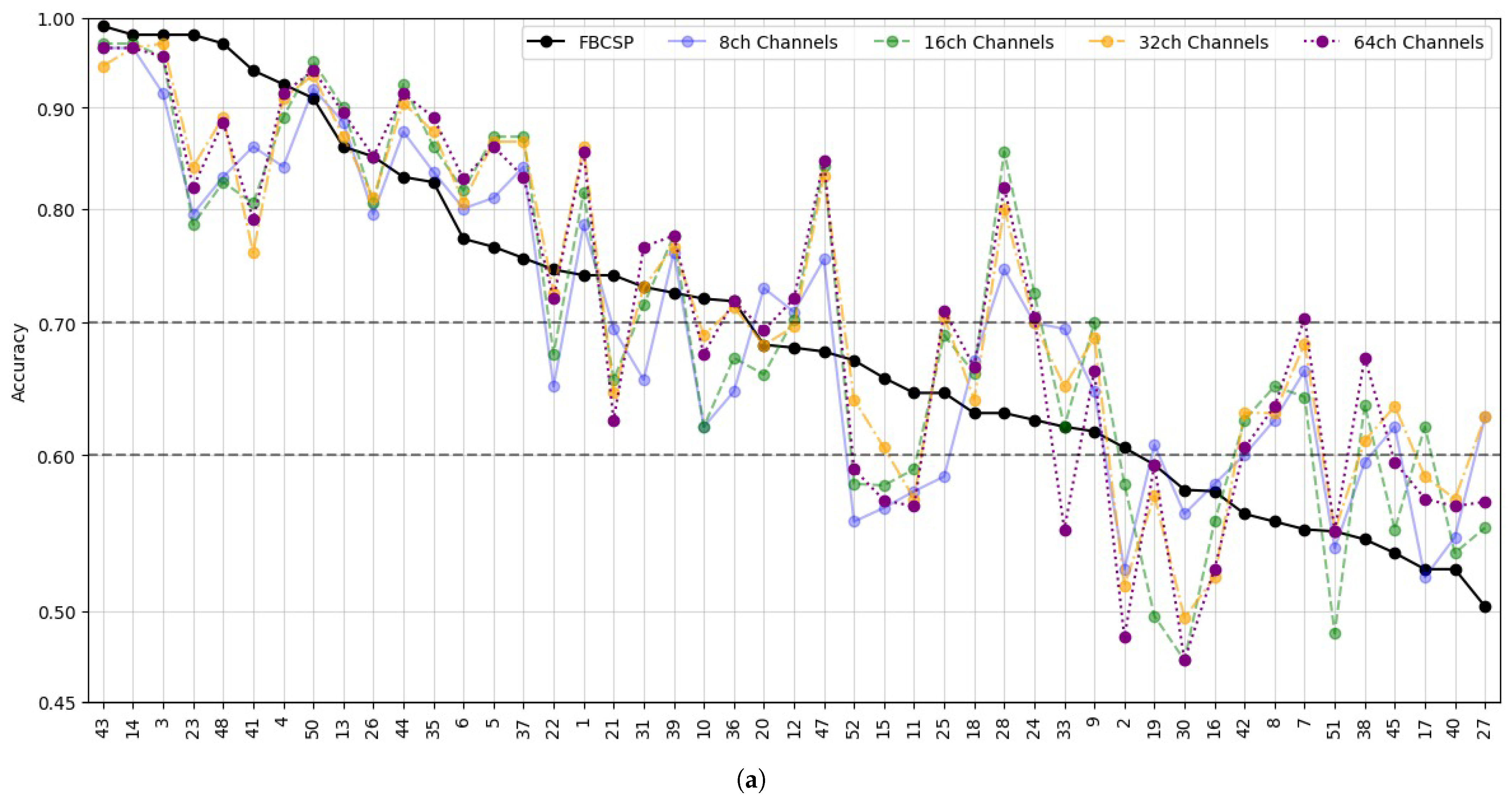
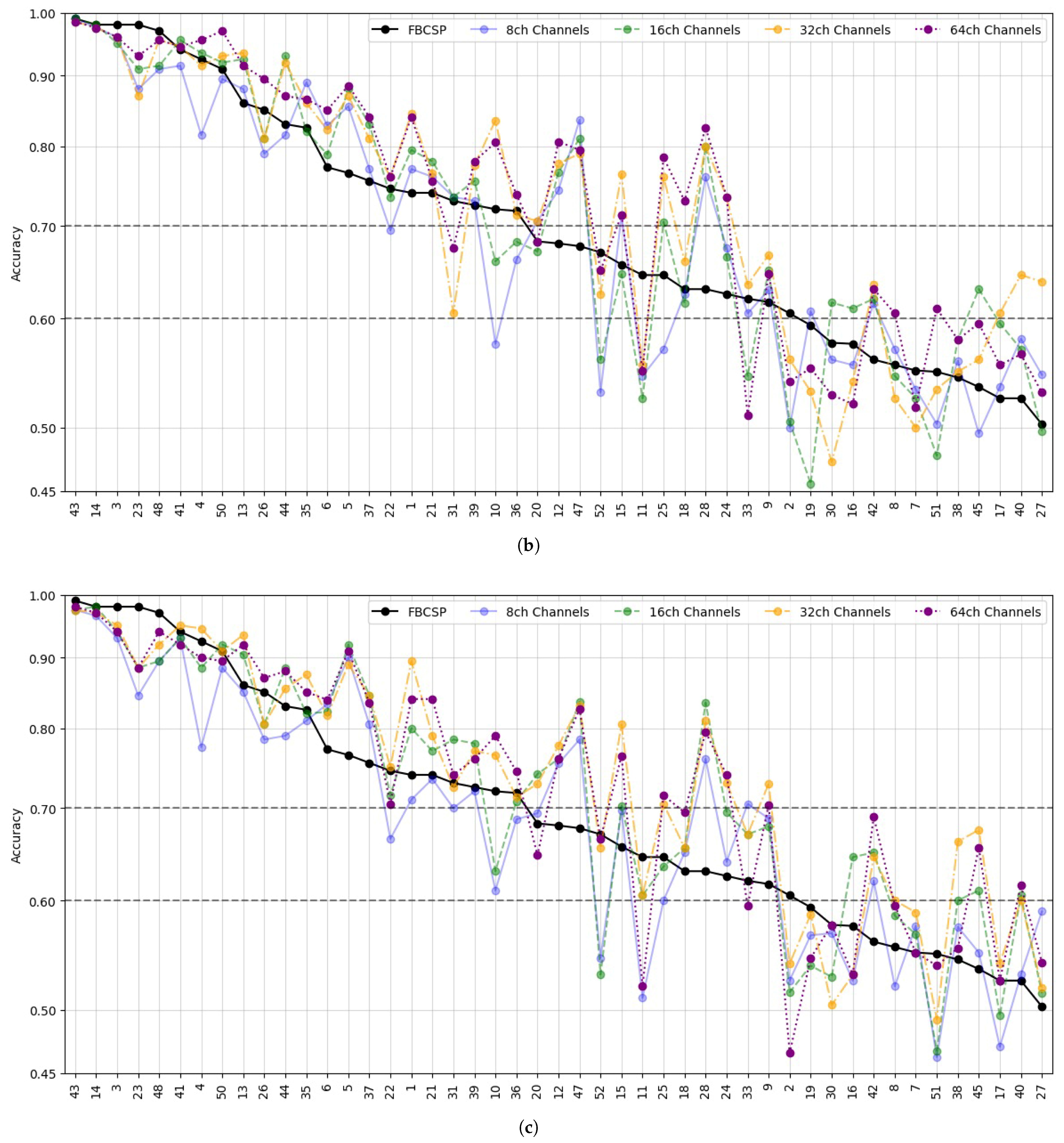
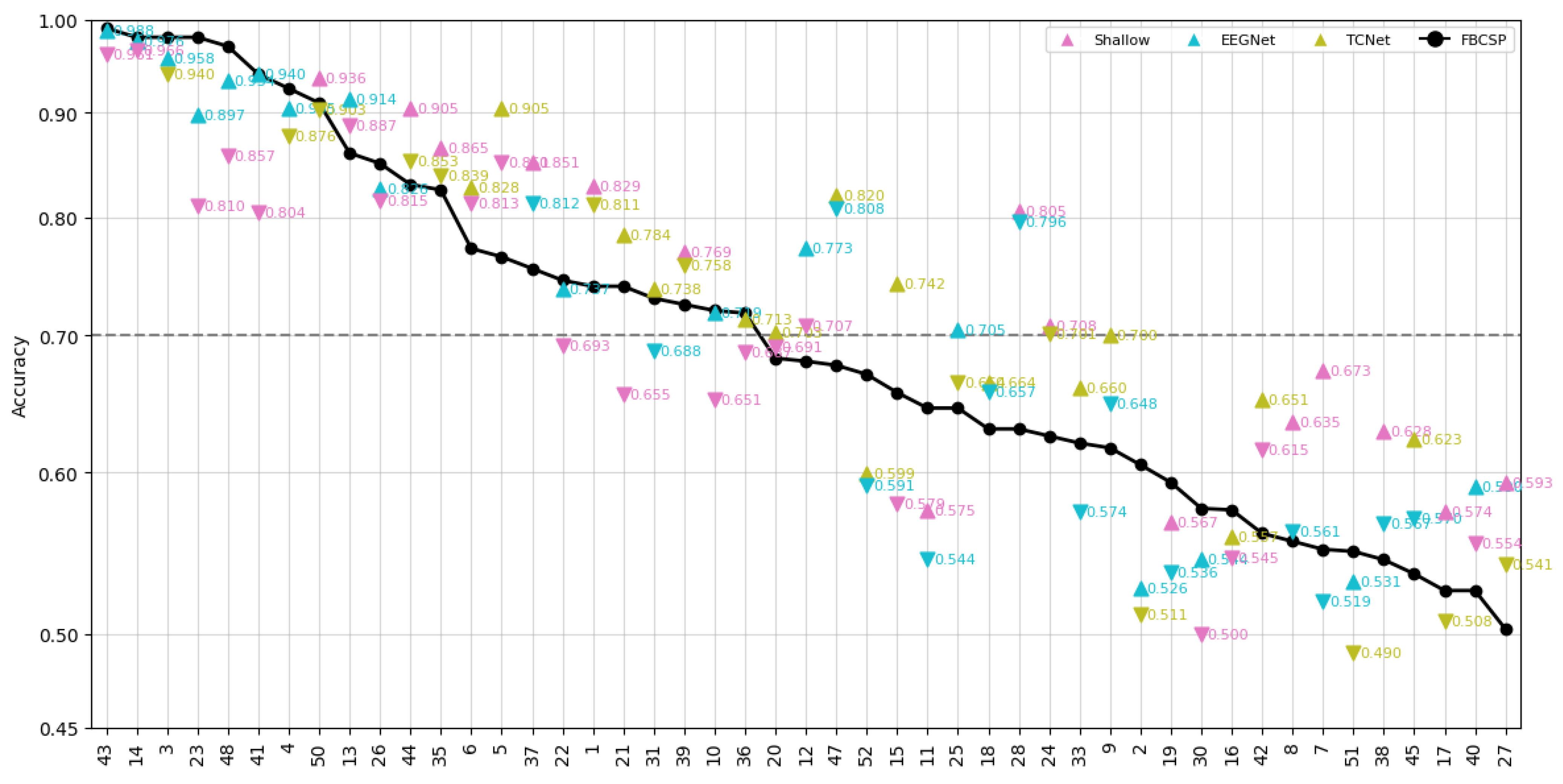
- Data Preprocessing and Montage Reduction. We evaluate the impact of EEG montage size on model generalizability, hypothesizing that excessive channels promote overfitting on spatially correlated artifacts rather than task-specific MI neural dynamics. Montage sizes are tested separately for the best- and worst-performing subjects. Subjects are stratified into high (best)- and low (worst)-performance cohorts based on evaluated trial accuracy (<70% or ≥70%). This serves as a conventional reference for evaluating the benefits of DL-based frameworks in ranking subjects based on their trial-level classification accuracy.
- ∗
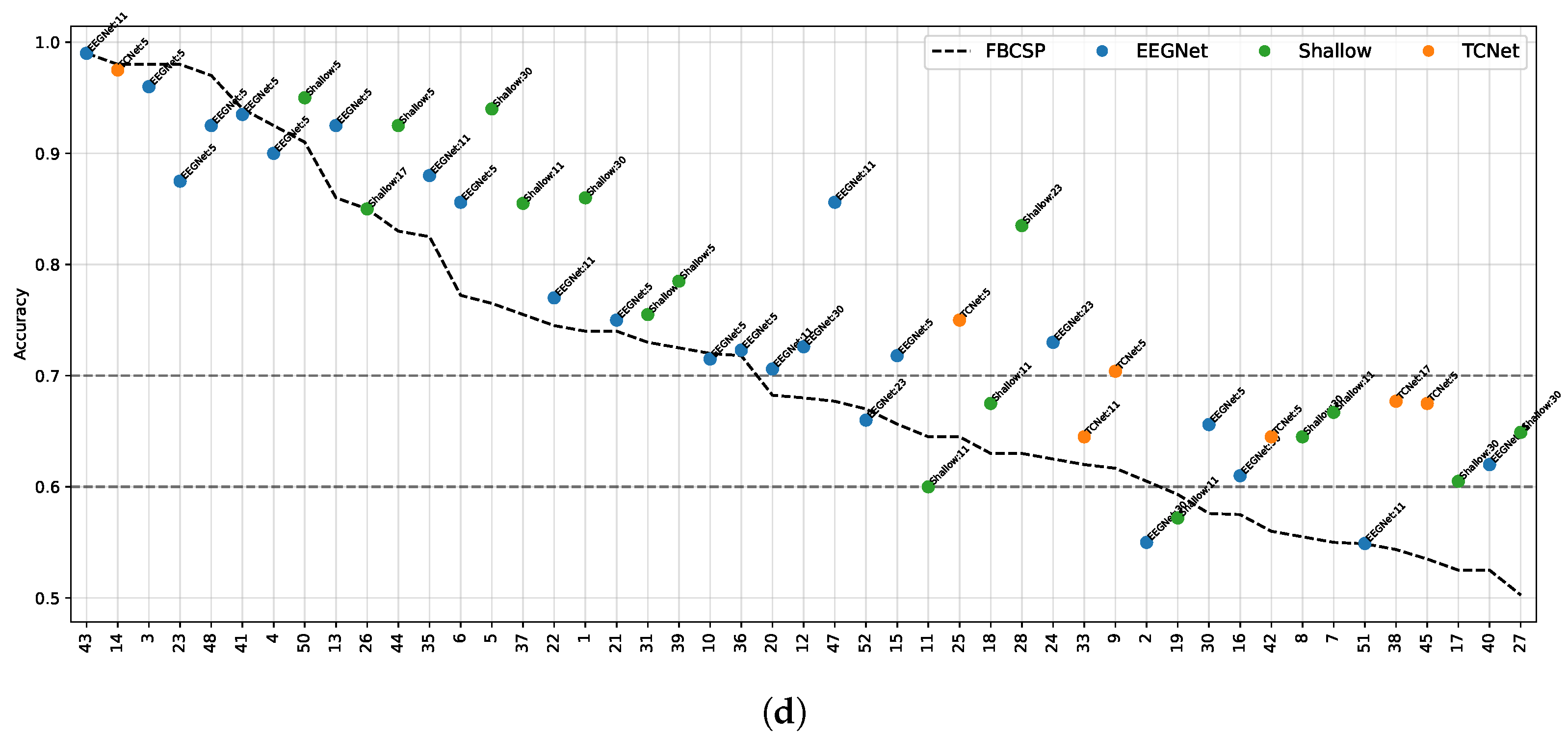
- Subject Grouping Based on the Classification Accuracy of MI Responses. We evaluate three Neural network models for EEG-based classification, EEGNet and ShallowConvNet, for their real-time applicability, alongside the advanced TCNet Fusion architecture for enhanced performance. As stated above, we use FBCSP as a classical baseline for extracting subject-specific spatio-spectral features. This provides a conventional reference to assess the benefits of deep learning-based approaches.
- ∗
- Spatio-temporal uncertainty estimation. MCD is applied to assess each model’s ability to learn robust, channel-independent features, thereby reducing overfitting and improving generalization. Furthermore, MCD is combined with CAMs to estimate spatiotemporal uncertainty and enhance model interpretability. Specifically, the variance computed across CAMs is overlaid onto the original CAM representation, highlighting regions where the model exhibits reduced certainty in its interpretation of MI responses.
4.2. Motor Imagery EEG Data Collection
4.3. EEG Preprocessing and Reduction of EEG-Channel Montage Set-Up
4.4. Evaluated Deep Learning Models for EEG-Based Classification
- ∗
- ShallowConvNet [77]: A low-complexity architecture that emphasizes early-stage feature extraction through sequential convolutional layers, square and logarithmic nonlinearities, and pooling operations. It effectively emulates the principles of the classical FBCSP pipeline within an end-to-end trainable deep learning framework, offering robust performance in MI classification tasks.
- ∗
- EEGNet [38]: A compact, parameter-efficient model that utilizes depthwise and separable convolutions to disentangle spatial and temporal features. Designed for cross-subject generalization and computational efficiency, EEGNet maintains competitive accuracy across a wide range of EEG-based paradigms.
- ∗
- TCNet Fusion [39]: A high-capacity architecture that incorporates residual connections, dilated convolutions, and convolutions to construct a multi-pathway fusion network. Its hierarchical design captures long-range temporal dependencies and enhances feature integration across time, improving classification performance in complex MI scenarios.
4.5. Subject Grouping Based on the Classification Accuracy of MI Responses
- ∗
- Group I: Well-performing subjects with binary classification accuracy above 70%, as proposed in [32].
- ∗
- Group II: Poor-performing subjects with accuracy below this threshold.
4.6. Enhanced CAM-Based Spatial Interpretability
4.7. Implementation and Reproducibility for DL Models
5. Results and Discussion
5.1. Tuning of Validated DL Models
5.2. Accuracy of MI Responses: Results of Subject Grouping
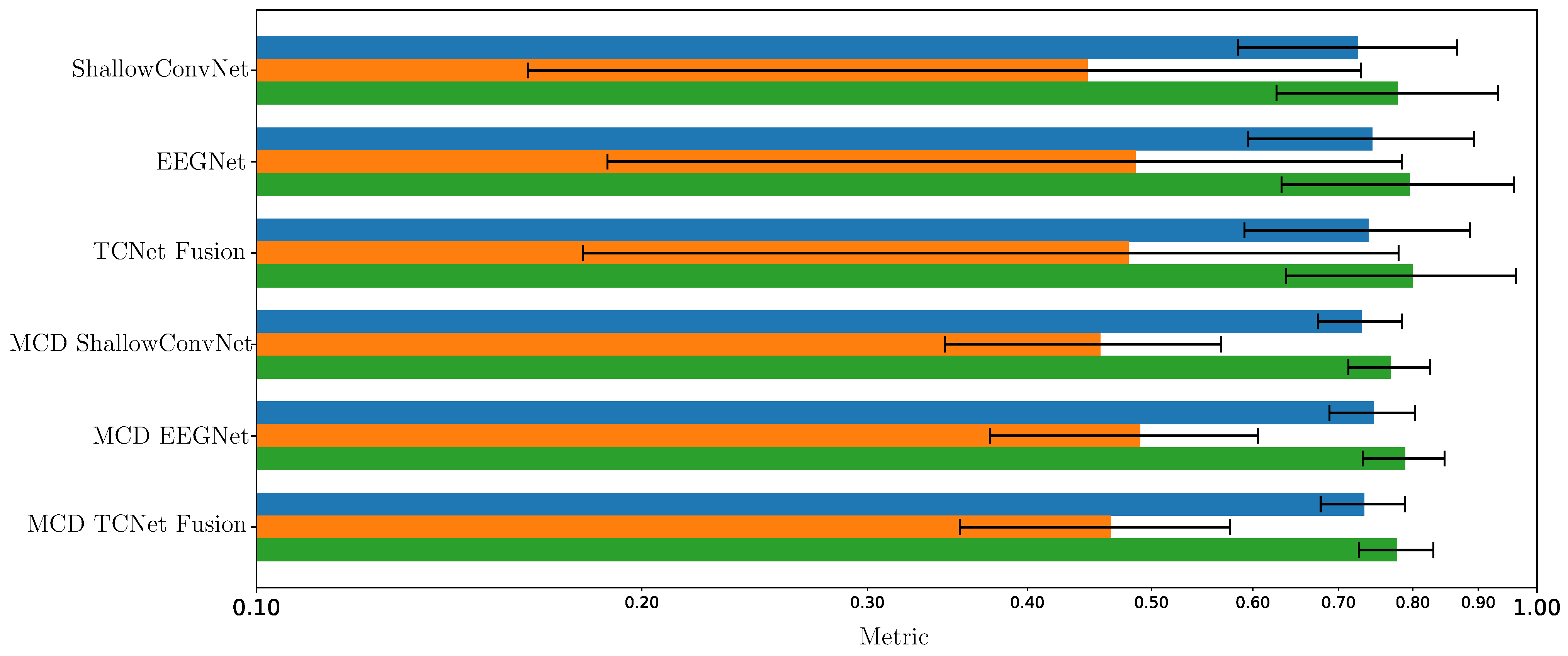
5.3. Enhanced Consistency of DL Model Performance Using Monte Carlo Dropout
5.4. CAM-Based Interpretability of Spatial Patterns
5.5. Practical Implications: Dropout Rate Selection and Prediction Safety
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santhanam, G.; Ryu, S.I.; Yu, B.M.; Afshar, A.; Shenoy, K.V. A high-performance brain–computer interface. Nature 2006, 442, 195–198. [Google Scholar] [CrossRef]
- Machado, S.; Araújo, F.; Paes, F.; Velasques, B.; Cunha, M.; Budde, H.; Basile, L.F.; Anghinah, R.; Arias-Carrión, O.; Cagy, M.; et al. EEG-based Brain-Computer Interfaces: An Overview of Basic Concepts and Clinical Applications in Neurorehabilitation. Rev. Neurosci. 2010, 21, 451–468. [Google Scholar] [CrossRef]
- Serruya, M.D.; Hatsopoulos, N.G.; Paninski, L.; Fellows, M.R.; Donoghue, J.P. Instant neural control of a movement signal. Nature 2002, 416, 141–142. [Google Scholar] [CrossRef]
- Carmena, J.M.; Lebedev, M.A.; Crist, R.E.; O’Doherty, J.E.; Santucci, D.M.; Dimitrov, D.F.; Patil, P.G.; Henriquez, C.S.; Nicolelis, M.A.L. Learning to Control a Brain–Machine Interface for Reaching and Grasping by Primates. PLoS Biol. 2003, 1, 42. [Google Scholar] [CrossRef]
- Hatsopoulos, N.; Joshi, J.; O’Leary, J.G. Decoding Continuous and Discrete Motor Behaviors Using Motor and Premotor Cortical Ensembles. J. Neurophysiol. 2004, 92, 1165–1174. [Google Scholar] [CrossRef] [PubMed]
- Collinger, J.L.; Gaunt, R.A.; Schwartz, A.B. Progress towards restoring upper limb movement and sensation through intracortical brain-computer interfaces. Curr. Opin. Biomed. Eng. 2018, 8, 84–92. [Google Scholar] [CrossRef]
- Padfield, N.; Zabalza, J.; Zhao, H.; Masero, V.; Ren, J. EEG-Based Brain-Computer Interfaces Using Motor-Imagery: Techniques and Challenges. Sensors 2019, 19, 1423. [Google Scholar] [CrossRef] [PubMed]
- Glaser, J.I.; Benjamin, A.S.; Chowdhury, R.H.; Perich, M.G.; Miller, L.E.; Kording, K.P. Machine Learning for Neural Decoding. eNeuro 2020, 7, 0506-19. [Google Scholar] [CrossRef] [PubMed]
- Pichiorri, F.; Morone, G.; Petti, M.; Toppi, J.; Pisotta, I.; Molinari, M.; Paolucci, S.; Inghilleri, M.; Astolfi, L.; Cincotti, F.; et al. Brain–computer interface boosts motor imagery practice during stroke recovery. Ann. Neurol. 2015, 77, 851–865. [Google Scholar] [CrossRef] [PubMed]
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain Computer Interfaces, a Review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef]
- Cervera, M.A.; Soekadar, S.R.; Ushiba, J.; Millán, J.d.R.; Liu, M.; Birbaumer, N.; Garipelli, G. Brain-computer interfaces for post-stroke motor rehabilitation: A meta-analysis. Ann. Clin. Transl. Neurol. 2018, 5, 651–663. [Google Scholar] [CrossRef]
- Shen, Y.W.; Lin, Y.P. Challenge for Affective Brain-Computer Interfaces: Non-stationary Spatio-spectral EEG Oscillations of Emotional Responses. Front. Hum. Neurosci. 2019, 13, e00366. [Google Scholar] [CrossRef] [PubMed]
- Borra, D.; Filippini, M.; Ursino, M.; Fattori, P.; Magosso, E. Motor decoding from the posterior parietal cortex using deep neural networks. J. Neural Eng. 2023, 20, 036016. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Meamardoost, S.; Gunawan, R.; Komiyama, T.; Mewes, C.; Zhang, Y.; Hwang, E.; Wang, L. Deep learning for neural decoding in motor cortex. J. Neural Eng. 2022, 19, 056021. [Google Scholar] [CrossRef]
- Al-Qaysi, Z.; Suzani, M.; bin Abdul Rashid, N.; Ismail, R.D.; Ahmed, M.; Sulaiman, W.A.W.; Aljanabi, R.A. A frequency-domain pattern recognition model for motor imagery-based brain-computer interface. Appl. Data Sci. Anal. 2024, 2024, 82–100. [Google Scholar] [CrossRef]
- de Melo, G.C.; Castellano, G.; Forner-Cordero, A. A procedure to minimize EEG variability for BCI applications. Biomed. Signal Process. Control 2024, 89, 105745. [Google Scholar] [CrossRef]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M.; Amin, S.U.; Altuwaijri, G.A.; Abdul, W.; Bencherif, M.A.; Faisal, M. Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: A review. Neural Comput. Appl. 2023, 35, 14681–14722. [Google Scholar] [CrossRef]
- Zhou, S.; Geng, S.; Li, J.; Zhang, D.; Xie, Z.; Cheng, C.; Hong, S. Less is More: Reducing Overfitting in Deep Learning for EEG Classification. In Proceedings of the 2023 Computing in Cardiology (CinC), Atlanta, GA, USA, 1–4 October 2023; Volume 50, pp. 1–4. [Google Scholar] [CrossRef]
- Rithwik, P.; Benzy, V.; Vinod, A. High accuracy decoding of motor imagery directions from EEG-based brain computer interface using filter bank spatially regularised common spatial pattern method. Biomed. Signal Process. Control 2022, 72, 103241. [Google Scholar] [CrossRef]
- Le, T.; Shlizerman, E. STNDT: Modeling Neural Population Activity with Spatiotemporal Transformers. In Proceedings of the Advances in Neural Information Processing Systems; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Sydney, Australia, 2022; Volume 35, pp. 17926–17939. [Google Scholar]
- Candelori, B.; Bardella, G.; Spinelli, I.; Ramawat, S.; Pani, P.; Ferraina, S.; Scardapane, S. Spatio-temporal transformers for decoding neural movement control. J. Neural Eng. 2025, 22, 016023. [Google Scholar] [CrossRef]
- Vafaei, E.; Hosseini, M. Transformers in EEG Analysis: A Review of Architectures and Applications in Motor Imagery, Seizure, and Emotion Classification. Sensors 2025, 25, 1293. [Google Scholar] [CrossRef]
- Milanés-Hermosilla, D.; Trujillo Codorniú, R.; López-Baracaldo, R.; Sagaró-Zamora, R.; Delisle-Rodriguez, D.; Villarejo-Mayor, J.J.; Núñez-Álvarez, J.R. Monte Carlo Dropout for Uncertainty Estimation and Motor Imagery Classification. Sensors 2021, 21, 7241. [Google Scholar] [CrossRef]
- Mattioli, F.; Porcaro, C.; Baldassarre, G. A 1D CNN for high accuracy classification and transfer learning in motor imagery EEG-based brain-computer interface. J. Neural Eng. 2022, 18, 066053. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Shi, Y.; Chen, J. Towards Better Evaluations of Class Activation Mapping and Interpretability of CNNs. In Proceedings of the Neural Information Processing, Singapore, 2–7 December 2024; pp. 352–369. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, D.; Yu, T.; Duan, Y.; Daly, I.; He, S. Editorial: Explainable and advanced intelligent processing in the brain-machine interaction. Front. Hum. Neurosci. 2023, 17, 1280281. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Cui, W.; Li, Y. Temporal-Spectral Generative Adversarial Network based Multi-Level Consistency Learning for Epileptic Seizure Prediction. In Proceedings of the 2024 4th International Conference on Industrial Automation, Robotics and Control Engineering (IARCE), Chengdu, China, 15–17 November 2024; pp. 349–354. [Google Scholar] [CrossRef]
- Bian, S.; Kang, P.; Moosmann, J.; Liu, M.; Bonazzi, P.; Rosipal, R.; Magno, M. On-device Learning of EEGNet-based Network For Wearable Motor Imagery Brain-Computer Interface. In Proceedings of the ISWC ’24 2024 ACM International Symposium on Wearable Computers, New York, NY, USA, 5–9 October 2024; pp. 9–16. [Google Scholar] [CrossRef]
- Jiang, P.T.; Zhang, C.B.; Hou, Q.; Cheng, M.M.; Wei, Y. LayerCAM: Exploring Hierarchical Class Activation Maps for Localization. IEEE Trans. Image Process. 2021, 30, 5875–5888. [Google Scholar] [CrossRef]
- Kabir, M.H.; Mahmood, S.; Al Shiam, A.; Musa Miah, A.S.; Shin, J.; Molla, M.K.I. Investigating Feature Selection Techniques to Enhance the Performance of EEG-Based Motor Imagery Tasks Classification. Mathematics 2023, 11, 1921. [Google Scholar] [CrossRef]
- Astrand, E.; Plantin, J.; Palmcrantz, S.; Tidare, J. EEG non-stationarity across multiple sessions during a Motor Imagery-BCI intervention: Two post stroke case series. In Proceedings of the 2021 10th International IEEE/EMBS Conference on Neural Engineering (NER), IEEE, Virtual Event, 4–6 May 2021; pp. 817–821. [Google Scholar]
- Hooda, N.; Kumar, N. Cognitive Imagery Classification of EEG Signals using CSP-based Feature Selection Method. IETE Tech. Rev. 2020, 37, 315–326. [Google Scholar] [CrossRef]
- Pérez-Velasco, S.; Marcos-Martínez, D.; Santamaría-Vázquez, E.; Martínez-Cagigal, V.; Moreno-Calderón, S.; Hornero, R. Unraveling motor imagery brain patterns using explainable artificial intelligence based on Shapley values. Comput. Methods Programs Biomed. 2024, 246, 108048. [Google Scholar] [CrossRef]
- Liman, M.D.; Osanga, S.I.; Alu, E.S.; Zakariya, S. Regularization effects in deep learning architecture. J. Niger. Soc. Phys. Sci. 2024, 6, 1911. [Google Scholar] [CrossRef]
- Lotte, F.; Bougrain, L.; Cichocki, A.; Clerc, M.; Congedo, M.; Rakotomamonjy, A.; Yger, F. A review of classification algorithms for EEG-based brain–computer interfaces: A 10 year update. J. Neural Eng. 2018, 15, 031005. [Google Scholar] [CrossRef]
- Saibene, A.; Ghaemi, H.; Dagdevir, E. Deep learning in motor imagery EEG signal decoding: A Systematic Review. Neurocomputing 2024, 610, 128577. [Google Scholar] [CrossRef]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Musallam, Y.K.; AlFassam, N.I.; Muhammad, G.; Amin, S.U.; Alsulaiman, M.; Abdul, W.; Altaheri, H.; Bencherif, M.A.; Algabri, M. Electroencephalography-based motor imagery classification using temporal convolutional network fusion. Biomed. Signal Process. Control 2021, 69, 102826. [Google Scholar] [CrossRef]
- Tayeb, Z.; Fedjaev, J.; Ghaboosi, N.; Richter, C.; Everding, L.; Qu, X.; Wu, Y.; Cheng, G.; Conradt, J. Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals. Sensors 2019, 19, 210. [Google Scholar] [CrossRef] [PubMed]
- Rammy, S.A.; Abbas, W.; Mahmood, S.S.; Riaz, H.; Rehman, H.U.; Abideen, R.Z.U.; Aqeel, M.; Zhang, W. Sequence-to-sequence deep neural network with spatio-spectro and temporal features for motor imagery classification. Biocybern. Biomed. Eng. 2021, 41, 97–110. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, K.; Jian, D.; Yao, L. Motor Imagery Classification via Temporal Attention Cues of Graph Embedded EEG Signals. IEEE J. Biomed. Health Inform. 2020, 24, 2570–2579. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, X.; Zhang, B.; Xiao, S.; Weng, S. CTNet: A convolutional transformer network for EEG-based motor imagery classification. Sci. Rep. 2024, 14, 20237. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, M.; Liu, K.; Deng, X. Enhancing EEG Motor Imagery Decoding Performance via Deep Temporal-domain Information Extraction. In Proceedings of the 2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS), Chengdu, China, 3–5 August 2022; pp. 420–424. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, J.; Sun, J.; Ma, Z.; Qin, L.; Li, G.; Zhou, H.; Zhan, Y. A Transformer-Based Approach Combining Deep Learning Network and Spatial-Temporal Information for Raw EEG Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2126–2136. [Google Scholar] [CrossRef]
- de Menezes, J.A.A.; Gomes, J.C.; de Carvalho Hazin, V.; Dantas, J.C.S.; Rodrigues, M.C.A.; dos Santos, W.P. Classification based on sparse representations of attributes derived from empirical mode decomposition in a multiclass problem of motor imagery in EEG signals. Health Technol. 2023, 13, 747–767. [Google Scholar] [CrossRef]
- Rao, Z.; Zhu, J.; Lu, Z.; Zhang, R.; Li, K.; Guan, Z.; Li, Y. A Wearable Brain-Computer Interface With Fewer EEG Channels for Online Motor Imagery Detection. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 4143–4154. [Google Scholar] [CrossRef]
- Shiam, A.A.; Hassan, K.M.; Islam, M.R.; Almassri, A.M.M.; Wagatsuma, H.; Molla, M.K.I. Motor Imagery Classification Using Effective Channel Selection of Multichannel EEG. Brain Sci. 2024, 14, 462. [Google Scholar] [CrossRef] [PubMed]
- Raoof, I.; Gupta, M.K. CLCC-FS (OBWOA): An efficient hybrid evolutionary algorithm for motor imagery electroencephalograph classification. Multimed. Tools Appl. 2024, 83, 74973–75006. [Google Scholar] [CrossRef]
- Arif, M.; ur Rehman, F.; Sekanina, L.; Malik, A.S. A comprehensive survey of evolutionary algorithms and metaheuristics in brain EEG-based applications. J. Neural Eng. 2024, 21, 051002. [Google Scholar] [CrossRef]
- Soler, A.; Giraldo, E.; Molinas, M. EEG source imaging of hand movement-related areas: An evaluation of the reconstruction and classification accuracy with optimized channels. Brain Inform. 2024, 11, 11. [Google Scholar] [CrossRef]
- Tjoa, E.; Guan, C. A Survey on Explainable Artificial Intelligence (XAI): Toward Medical XAI. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 4793–4813. [Google Scholar] [CrossRef]
- Rajpura, P.; Cecotti, H.; Kumar Meena, Y. Explainable artificial intelligence approaches for brain–computer interfaces: A review and design space. J. Neural Eng. 2024, 21, 041003. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, New York, NY, USA, 13–16 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations From Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Haufe, S.; Meinecke, F.; Görgen, K.; Dähne, S.; Haynes, J.D.; Blankertz, B.; Bießmann, F. On the interpretation of weight vectors of linear models in multivariate neuroimaging. NeuroImage 2014, 87, 96–110. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Sydney, Australia, 2017; Volume 30. [Google Scholar]
- Jiahao, H.; Ur Rahman, M.M.; Al-Naffouri, T.; Laleg-Kirati, T.M. Uncertainty Estimation and Model Calibration in EEG Signal Classification for Epileptic Seizures Detection. In Proceedings of the 2024 46th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 15–19 July 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Balcan, M.F., Weinberger, K.Q., Eds.; Volume 48—Proceedings of Machine Learning Research, 2016; Eds. PMLR: New York, NY, USA; pp. 1050–1059. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Sydney, Australia, 2017; Volume 30. [Google Scholar]
- Tveter, M.; Tveitstøl, T.; Hatlestad-Hall, C.; Pérez T, A.S.; Taubøll, E.; Yazidi, A.; Hammer, H.L.; Haraldsen, I.R.H. Advancing EEG prediction with deep learning and uncertainty estimation. Brain Inform. 2024, 11, 27. [Google Scholar] [CrossRef]
- Ramoser, H.; Muller-Gerking, J.; Pfurtscheller, G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabil. Eng. 2000, 8, 441–446. [Google Scholar] [CrossRef]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Muller, K.R. Optimizing Spatial filters for Robust EEG Single-Trial Analysis. IEEE Signal Process. Mag. 2008, 25, 41–56. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter Bank Common Spatial Pattern (FBCSP) in Brain-Computer Interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 2390–2397. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Amin, S.U.; Alsulaiman, M.; Muhammad, G.; Mekhtiche, M.A.; Shamim Hossain, M. Deep Learning for EEG motor imagery classification based on multi-layer CNNs feature fusion. Future Gener. Comput. Syst. 2019, 101, 542–554. [Google Scholar] [CrossRef]
- Proverbio, A.M.; Pischedda, F. Measuring brain potentials of imagination linked to physiological needs and motivational states. Front. Hum. Neurosci. 2023, 17, 1146789. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.K.; Lee, T.; Reyes, R.D.D.; Hong, J.; Tran, H.H.; Lee, D.; Jung, J.; Yoon, I.Y. Confidence-Based Framework Using Deep Learning for Automated Sleep Stage Scoring. Nat. Sci. Sleep 2021, 13, 2239–2250. [Google Scholar] [CrossRef] [PubMed]
- Wong, S.; Simmons, A.; Villicana, J.R.; Barnett, S. Estimating Patient-Level Uncertainty in Seizure Detection Using Group-Specific Out-of-Distribution Detection Technique. Sensors 2023, 23, 8375. [Google Scholar] [CrossRef]
- Cho, H.; Ahn, M.; Ahn, S.; Kwon, M.; Jun, S.C. Supporting Data for “EEG Datasets for Motor Imagery Brain Computer Interface”. 2017. Available online: https://gigadb.org/dataset/100295 (accessed on 1 December 2024).
- Kim, H.; Luo, J.; Chu, S.; Cannard, C.; Hoffmann, S.; Miyakoshi, M. ICA’s bug: How ghost ICs emerge from effective rank deficiency caused by EEG electrode interpolation and incorrect re-referencing. Front. Signal Process. 2023, 3, 1064138. [Google Scholar] [CrossRef]
- Li, C.; Qin, C.; Fang, J. Motor-imagery classification model for brain-computer interface: A sparse group filter bank representation model. arXiv 2021, arXiv:2108.12295. [Google Scholar]
- Vempati, R.; Sharma, L.D. EEG rhythm based emotion recognition using multivariate decomposition and ensemble machine learning classifier. J. Neurosci. Methods 2023, 393, 109879. [Google Scholar] [CrossRef]
- Demir, F.; Sobahi, N.; Siuly, S.; Sengur, A. Exploring Deep Learning Features for Automatic Classification of Human Emotion Using EEG Rhythms. IEEE Sensors J. 2021, 21, 14923–14930. [Google Scholar] [CrossRef]
- García-Murillo, D.G.; Álvarez Meza, A.M.; Castellanos-Dominguez, C.G. KCS-FCnet: Kernel Cross-Spectral Functional Connectivity Network for EEG-Based Motor Imagery Classification. Diagnostics 2023, 13, 1122. [Google Scholar] [CrossRef]
- Kim, S.J.; Lee, D.H.; Lee, S.W. Rethinking CNN Architecture for Enhancing Decoding Performance of Motor Imagery-Based EEG Signals. IEEE Access 2022, 10, 96984–96996. [Google Scholar] [CrossRef]
- Edelman, B.J.; Zhang, S.; Schalk, G.; Brunner, P.; Müller-Putz, G.; Guan, C.; He, B. Non-Invasive Brain-Computer Interfaces: State of the Art and Trends. IEEE Rev. Biomed. Eng. 2025, 18, 26–49. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Yuan, L.; Wang, Z.; Li, R.; Jiang, T. Towards best practice of interpreting deep learning models for EEG-based brain computer interfaces. Front. Comput. Neurosci. 2023, 17, 1232925. [Google Scholar] [CrossRef]
- Sedi Nzakuna, P.; Gallo, V.; Paciello, V.; Lay-Ekuakille, A.; Kuti Lusala, A. Monte Carlo-Based Strategy for Assessing the Impact of EEG Data Uncertainty on Confidence in Convolutional Neural Network Classification. IEEE Access 2025, 13, 85342–85362. [Google Scholar] [CrossRef]
- Ye, N.; Zeng, Z.; Zhou, J.; Zhu, L.; Duan, Y.; Wu, Y.; Wu, J.; Zeng, H.; Gu, Q.; Wang, X.; et al. OoD-Control: Generalizing Control in Unseen Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 7421–7433. [Google Scholar] [CrossRef]
- Ye, N.; Li, K.; Bai, H.; Yu, R.; Hong, L.; Zhou, F.; Li, Z.; Zhu, J. OoD-Bench: Quantifying and Understanding Two Dimensions of Out-of-Distribution Generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 7947–7958. [Google Scholar]
- He, H.; Wu, D. Transfer Learning for Brain–Computer Interfaces: A Euclidean Space Data Alignment Approach. IEEE Trans. Biomed. Eng. 2020, 67, 399–410. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Zhou, G.; Jin, J.; Wang, B.; Wang, X.; Cichocki, A. Multi-kernel extreme learning machine for EEG classification in brain-computer interfaces. Expert Syst. Appl. 2018, 96, 302–310. [Google Scholar] [CrossRef]


| Model | 8 Channels | 16 Channels | 32 Channels | 64 Channels |
|---|---|---|---|---|
| ShallowConvNet | 0.708 ± 0.015 | 0.718 ± 0.012 | 0.727 ± 0.010 | 0.725 ± 0.011 |
| EEGNet | 0.706 ± 0.014 | 0.720 ± 0.013 | 0.737 ± 0.009 | 0.733 ± 0.010 |
| TCNet Fusion | 0.700 ± 0.016 | 0.729 ± 0.011 | 0.744 ± 0.008 | 0.740 ± 0.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Morales, Ó.W.; Escalante-Escobar, S.; Collazos-Huertas, D.F.; Álvarez-Meza, A.M.; Castellanos-Dominguez, G. Uncertainty-Aware Deep Learning for Robust and Interpretable MI EEG Using Channel Dropout and LayerCAM Integration. Appl. Sci. 2025, 15, 8036. https://doi.org/10.3390/app15148036
Gómez-Morales ÓW, Escalante-Escobar S, Collazos-Huertas DF, Álvarez-Meza AM, Castellanos-Dominguez G. Uncertainty-Aware Deep Learning for Robust and Interpretable MI EEG Using Channel Dropout and LayerCAM Integration. Applied Sciences. 2025; 15(14):8036. https://doi.org/10.3390/app15148036
Chicago/Turabian StyleGómez-Morales, Óscar Wladimir, Sofia Escalante-Escobar, Diego Fabian Collazos-Huertas, Andrés Marino Álvarez-Meza, and German Castellanos-Dominguez. 2025. "Uncertainty-Aware Deep Learning for Robust and Interpretable MI EEG Using Channel Dropout and LayerCAM Integration" Applied Sciences 15, no. 14: 8036. https://doi.org/10.3390/app15148036
APA StyleGómez-Morales, Ó. W., Escalante-Escobar, S., Collazos-Huertas, D. F., Álvarez-Meza, A. M., & Castellanos-Dominguez, G. (2025). Uncertainty-Aware Deep Learning for Robust and Interpretable MI EEG Using Channel Dropout and LayerCAM Integration. Applied Sciences, 15(14), 8036. https://doi.org/10.3390/app15148036






