A Fast Algorithm for Three-Way Object-Oriented Concept Acquisition

Abstract

Three-way rules can be extracted from three-way object-oriented concepts, which describe the necessary attributes of object sets based on the formal context as well as the necessary attributes not possessed by them based on the complement formal context. Thus, acquiring these three-way object-oriented concepts is important but difficult because of computing’s high time complexity. This study proposes a novel algorithm, called $3WOC$, which can be used to directly and quickly acquire all three-way object-oriented concepts from a given formal context $(U,V,R)$. Moreover, it has a time complexity of $\mathcal{O}((\left|U\right|+2\left|V\right|)\times {\left|OEOL(U,V,R)\right|}^2)$. We theoretically and experimentally proved the completeness of the generated concepts. Moreover, the results of comparative experiments showed that it outperforms the QM algorithm on a variety of datasets.

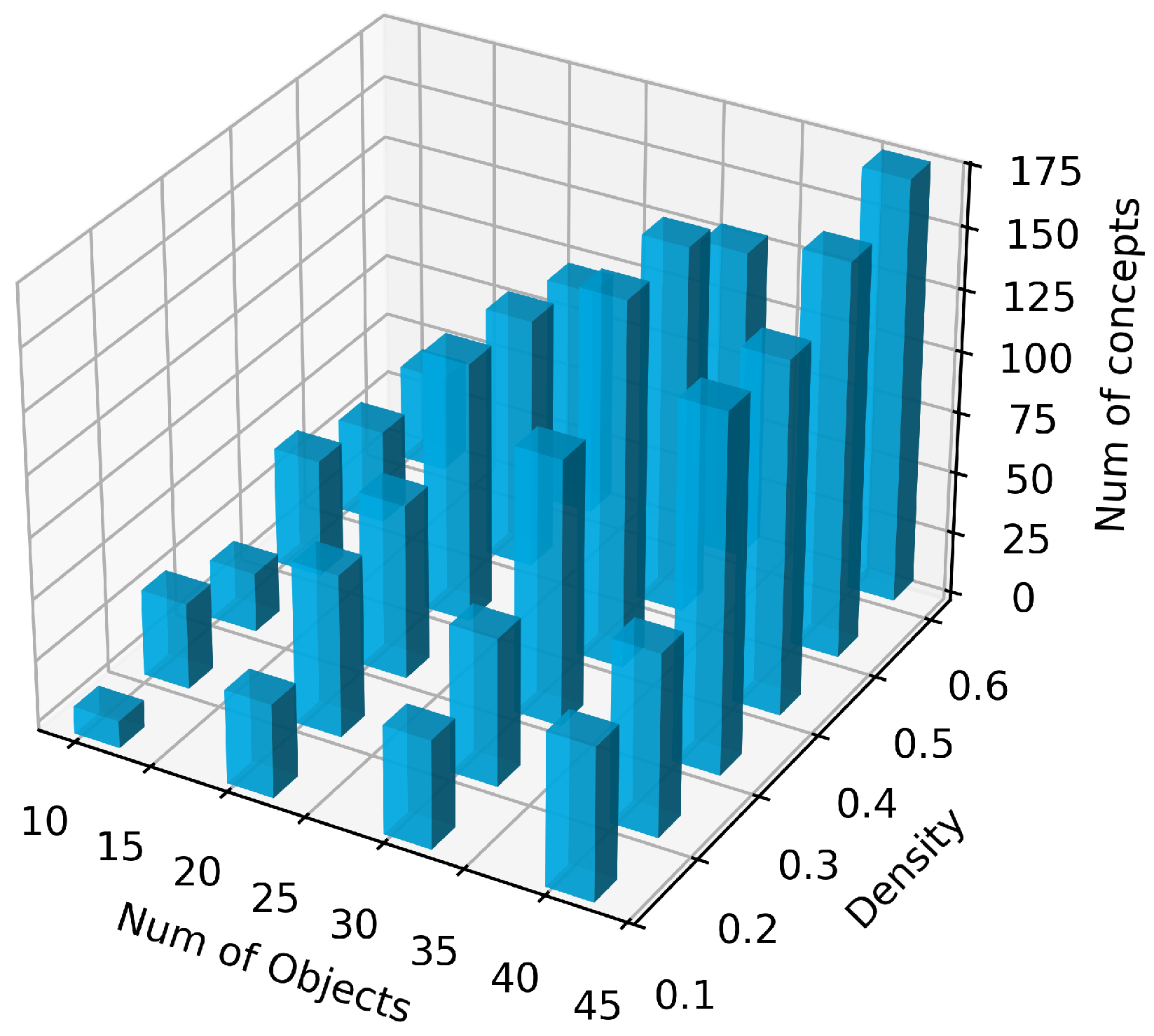
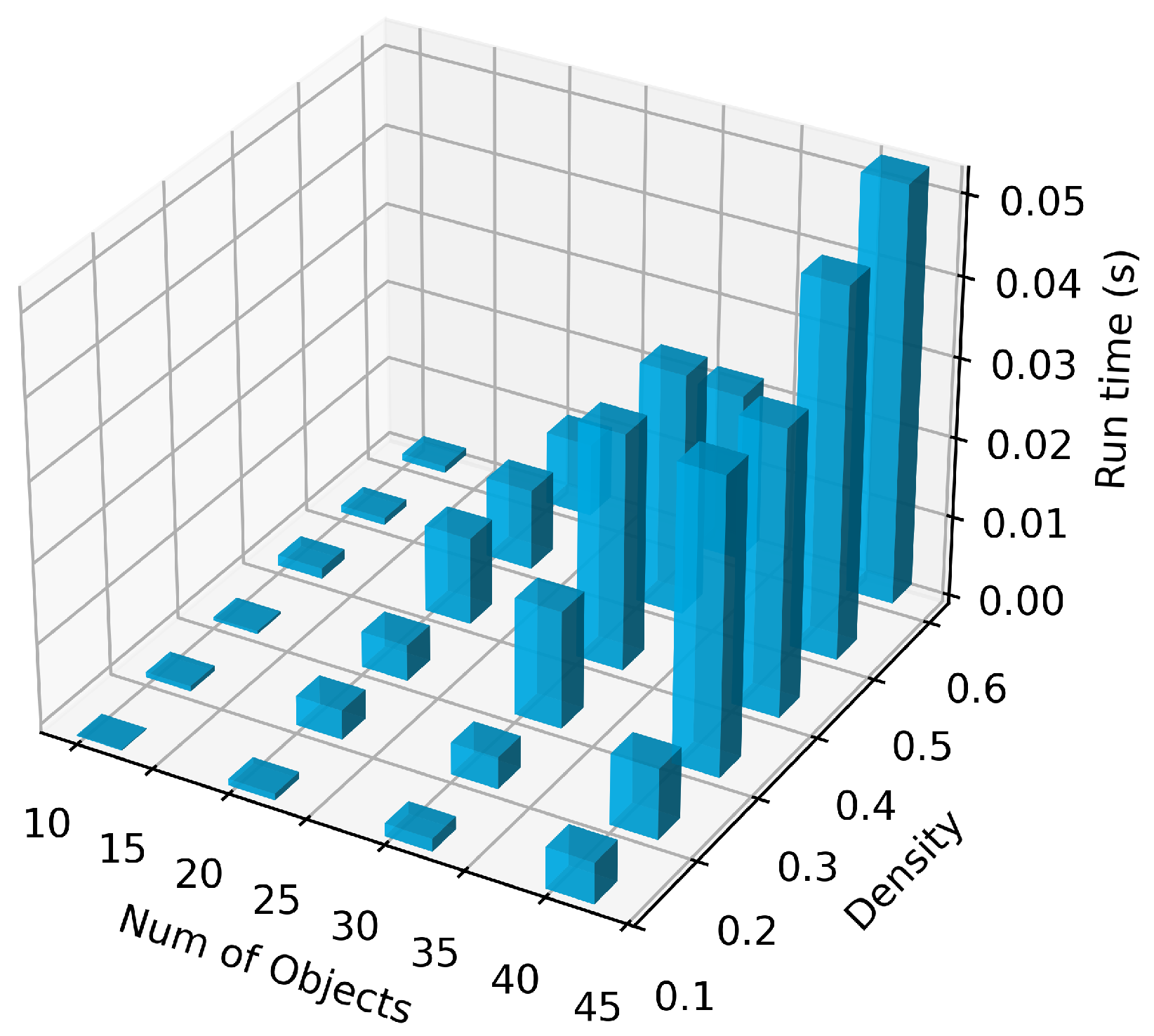
1. Introduction

The theory of formal concept analysis (FCA), proposed by Rudolf Wille in 1982 [1,2], describes entities or abstract concepts in a formal manner and establishes their corresponding hierarchical structures. Regarding the core data structures and tools for formal concept analysis in the context of data analysis and processing, the concept lattice has been widely used in many fields. Many studies have extensively explored the diversity of knowledge representation and reasoning based on the theory of the concept lattice [3]. Examples include knowledge exploration [4,5,6], concept learning [7,8,9,10,11], data extraction [12], and path planning [13].

Significant progress has been made in research on the formal concept lattice and its extended structure in recent years. Rough set (RS) theory is a useful mathematical tool that was proposed by Pawlak [14]. Given that FCA and the RS are highly complementary, it is useful to combine them for knowledge discovery. Duntsch and Gediga [15] defined model-style operators based on a binary relation. Inspired by this, Yao [16,17] proposed the object-oriented concept lattice based on necessary and possible operators. A number of studies on the subject have been published following the proposal of the three-way decision [18]. Three-way concept analysis is the product of combining the three-way decision with FCA [19,20]. The three-way concept lattice is the minimal closure system that contains both the concept lattice and complementary concept lattice [21]; thus, it can describe more information. Wei et al. [22] extended the three-way concept lattice to the three-way object-oriented concept lattice. They described the necessary attributes of object sets based on the formal context as well as the necessary attributes not possessed by them based on the complement formal context. Thus, the three-way object-oriented concept contains both positive and negative parts. However, in contrast to the three-way concept, these two parts can be used to simultaneously describe the attributes that are necessarily possessed and not possessed by the object sets. Moreover, three-way rules can be extracted from these concepts [23,24,25].

In addition, most applications based on FCA require first acquiring a concept lattice or its extended structure. Obtaining all the relevant concepts is important but difficult because of their high time complexity. Many studies have been devoted to acquiring object-oriented concept lattices and three-way concept lattices. Wang et al. [26] proposed a method to construct object-oriented concept lattices based on approximation operators. Ma et al. [27] put forward an approach to acquire all object-oriented concepts based on layered extent sets. She et al. [28] presented a theoretical study on object-oriented concept lattices and property-oriented concept lattices in multi-scale formal contexts. Shao et al. [29] proposed the zoom algorithm, which is composed of the zoom-in and zoom-out algorithms. It can be used to transform object-oriented concept lattices with different combinations of attribute granularity. Qian et al. [30,31,32] proposed a method for generating three-way object-oriented concepts. It first generates the apposition of a given formal context and its complementary context, and then applies an algorithm of constructing the object-oriented concepts to obtain all three-way object-oriented concepts based on the isomorphic relationship between the object-oriented concept lattice and the three-way object-oriented concept lattice. Long et al. [33] and Hu et al. [34] developed a method to update attribute-induced and object-induced three-way concepts, respectively. Hao et al. [35] proposed a method to incrementally construct the three-way concept lattice.

However, to the best of our knowledge, little effort has been dedicated in research for three-way object-oriented concept acquisition. Inspired by past work in the field [26,30,31,32], this study develops an algorithm that can completely and directly acquire all three-way object-oriented concepts from a given formal context $(U,V,R)$. We call it the $3WOC$ algorithm. It is a structured algorithm with a time complexity of $\mathcal{O}\left(\right(\left|U\right|+2\left|V\right|)\times {\left|OEOL(U,V,R)\right|}^2)$. It not only avoids traversing the power set of the attribute set V but also uses bitwise operations on hash values instead of union operations on object sets to enhance the efficiency of acquisition. The results of comparative experiments demonstrated that it can be used to acquire all three-way object-oriented concepts more quickly than the prevalent algorithm in the field on various datasets. Our work can serve as a basic algorithm for three-way rule acquisition from three-way object-oriented concepts.

The remainder of this paper is organized as follows: Section 2 reviews some basic notions that are relevant to three-way object-oriented concept lattices. To clearly and accurately illustrate concept acquisition process of the $3WOC$ algorithm, we provide its theoretical foundation in Section 3. Section 4 presents the pseudo-code of the $3WOC$ algorithm and analyses its time complexity, while Section 5 provides its experimental verification. Finally, Section 6 summarizes our contributions and future research in the area.

2. Preliminaries

In this section, we briefly review some basic notions and relevant properties of three-way object-oriented concepts in order to clearly describe the acquisition process of these concepts in next section.

Definition 1 

(Formal context [1,2]). A formal context $(U,V,R)$ consists of two sets U and V and a relation R between U and V. The elements of set U are called objects, while those of set V are called attributes of the context. For $x\in U$ and $y\in V,(x,y)\in R$ can be written as $xRy$, which means that object x has attribute y, or that attribute y belongs to object x.

For a formal context $(U,V,R)$, let $R^c=(U\times V)\setminus R$. $(U,V,R^c)$ is then the complement context of $(U,V,R)$. For $x\in U$ and $y\in V$, if $(x,y)\in R^c$, this can be written as $x{R}^{c}y$. This means that object x does not possess attribute y, or that attribute y does not belong to object x.

For any $X\subseteq U$ and any $Y\subseteq V$ on a formal context $(U,V,R)$, Wille and Ganter also defined two operators, f and g [1,2]:

$$\begin{array}{c}f\left(X\right)=\{y\in V|\forall x\in X,xRy\}\end{array}$$

(1)

$$\begin{array}{c}g\left(Y\right)=\{x\in U|\forall y\in Y,xRy\}\end{array}$$

(2)

The f and g operators are also called positive operators, while the two corresponding operators, $\overline{f}$ and $\overline{g}$, on the complement context $(U,V,R^c)$ are called negative operators in three-way concept analysis [19]. The $\overline{f}$ and $\overline{g}$ operators are defined as follows:

$$\begin{array}{c}\overline{f}\left(X\right)=\{y\in V|\forall x\in X,x{R}^{c}y\}\end{array}$$

(3)

$$\begin{array}{c}\overline{g}\left(Y\right)=\{x\in U|\forall y\in Y,x{R}^{c}y\}\end{array}$$

(4)

Example 1. 

Table 1. The formal context $(U_1,V_1,R_1)$.

	a	b	c	d	e
1	1	0	1	1	1
2	1	0	1	0	0
3	0	1	0	0	1
4	1	0	0	0	0
5	1	1	0	0	1

shows a formal context $(U_1,V_1,R_1)$, while

Table 2. The complement context $(U_1,V_1,R_1^c)$.

	a	b	c	d	e
1	0	1	0	0	0
2	0	1	0	1	1
3	1	0	1	1	0
4	0	1	1	1	1
5	0	0	1	1	0

shows the complement context $(U_1,V_1,R_1^c)$. $U_1=\{1,2,3,4,5\}$ is the object set, and $V_1=\{a,b,c,d,e\}$ is the attribute set. Each row represents an object and each column represents an attribute.

Usually, □ is called the necessity operator and ⋄ the possibility operator. For a formal context $(U,V,R)$, $X\subseteq U$ and $Y\subseteq V$, $X^{\square }$ is the set consisting of all necessary attributes of X, while $Y^{\diamond }$ is the object set that possesses at least one attribute in Y. They are defined as follows [16,17]:

$$\begin{array}{cc}\hfill X^{\square }& =\{y\in V|\forall x\in U(xRy\Rightarrow x\in X)\}\hfill \\ \hfill & =\{y\in V|Ry\subseteq X\}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill Y^{\diamond }& =\{x\in U|\exists y\in V(xRy\wedge y\in Y)\}\hfill \\ \hfill & =\{x\in U|xR\cap Y\ne ⌀\}\hfill \\ \hfill & =\bigcup _{y\in Y}Ry\hfill \\ \hfill & =RY\hfill \end{array}$$

(6)

Furthermore, □ and ⋄ have the following properties [16,17]:

$$\begin{array}{cc}\hfill & X_1\subseteq X_2\Rightarrow X_1^{\square }\subseteq X_2^{\square }\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & A_1\subseteq A_2\Rightarrow A_1^{\diamond }\subseteq A_2^{\diamond }\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & X^{\square \diamond }\subseteq X,A\subseteq A^{\diamond \square }\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & X^{\square \diamond \square }=X^{\square },A^{\diamond \square \diamond }=A^{\diamond }\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & {(X_1\cap X_2)}^{\square }=X_1^{\square }\cap X_2^{\square },{(A_1\cup A_2)}^{\diamond }=A_1^{\diamond }\cup A_2^{\diamond }\hfill \end{array}$$

(11)

For the complement context $(U,V,R^c)$, operators □ and ⋄ are called negative approximation operators as a pair. To refer to them explicitly, they are denoted by $\overline{\square }$ and $\overline{\diamond }$, respectively. $\overline{\square }$ and $\overline{\diamond }$ have the same properties as □ and ⋄; thus, we do not list them here again. By combining the operators □, ⋄, $\overline{\square }$, and $\overline{\diamond }$, a pair of object-induced three-way object-oriented operators (OEO operators), “⊳:” $\mathcal{P}\left(U\right)\to \mathcal{DP}\left(V\right)$ and “⊲:” $\mathcal{DP}\left(V\right)\to \mathcal{P}\left(U\right)$, can be defined as follows [22,30]:

$$\begin{array}{cc}\hfill X^{⊳}& =(X^{\square },X^{\overline{\square }})\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {(Y,Z)}^{⊲}& =Y^{\diamond }\cup Z^{\overline{\diamond }}\hfill \end{array}$$

(13)

where $X\subseteq U$ and $Y,Z\subseteq V$. If and only if $X={(Y,Z)}^{⊲}$ and $X^{⊳}=(Y,Z)$, the pair $(X,(Y,Z\left)\right)$ is called an object-induced three-way object-oriented concept, i.e., an OEO-concept [22,30]. X and $(Y,Z)$ are called the extent and the intent of the OEO-concept $(X,(Y,Z\left)\right)$, respectively. The set of all OEO-concepts of $(U,V,R)$ is denoted by $OEOL(U,V,R)$. For any $(X,(Y,Z\left)\right)$ and $(A,(B,C\left)\right)$$\in OEOL(U,V,R)$,

$$\begin{array}{c}\hfill (X,(Y,Z\left)\right)\le (A,(B,C\left)\right)\iff X\subseteq A\iff (Y,Z)\subseteq (B,C)\end{array}$$

(14)

The relation ≤ defined above is a partial-order relation on $OEOL(U,V,R)$ [22,30]. For any $(X_1,(Y_1,Z_1)),(X_2,(Y_2,Z_2))\in OEOL(U,V,R)$,

$$\begin{array}{c}\hfill (X_1,(Y_1,Z_1))\bigwedge (X_2,(Y_2,Z_2))=({(X_1\cup X_2)}^{⊳⊲},(Y_1,Z_1)\cap (Y_2,Z_2))\end{array}$$

(15)

$$\begin{array}{c}\hfill (X_1,(Y_1,Z_1))\bigvee (X_2,(Y_2,Z_2))=(X_1\cup X_2,{((Y_1,Z_1)\cup (Y_2,Z_2))}^{⊲⊳})\end{array}$$

(16)

Thus, $\left(OEOL\right(U,V,R),\le )$ forms a complete lattice, which is called the three-way object-oriented concept lattice.

3. Theoretical Foundation

In this section, we describe the theoretical principles of the $3WOC$ algorithm to acquire all three-way object-oriented concepts, i.e., OEO-concepts, from a given formal context $(U,V,R)$. The related definitions and propositions are as follows.

Definition 2 

(Single-attribute concept). For a formal context $(U,V,R)$, a pair $(X_i,a_i)$, with $X_i\subset U$, $a_i\in V$ and $g\left(a_i\right)=X_i$, is called a single-attribute concept. Similarly, for the complement context $(U,V,R^c)$, a pair $(X_h,a_h)$, with $X_h\subset U$, $a_h\in U$ and $\overline{g}\left(a_h\right)=X_h$, is also called a single-attribute concept.

For the formal context $(U,V,R)$, the set of all single-attribute concepts is denoted by $C_s$. Similarly, for the complement context $(U,V,R^c)$, the set of all single-attribute concepts is denoted by $C_s^c$. Single-attribute concepts are directly obtained by mapping individual attributes to objects, with the operators g and $\overline{g}$, i.e., Equations (2) and (4), in the formal context and the complement context, respectively. Therefore, these single-attribute concepts are not formal concepts. However, we can obtain OEO-concepts through single-attribute concepts. This procedure is defined by using the following $\lambda$ function:

Definition 3 

(Function $\lambda$). Given a formal context $(U,V,R)$, the λ function is a mapping $C_s\cup C_s^c$ to $OEOL(U,V,R)$. The definition is as follows:

$$\begin{array}{c}\hfill \lambda ((X,a_i)=(X,(Y,Z))\end{array}$$

(17)

$$\begin{array}{c}\hfill Y=\bigcup a_j,\forall (X_j,a_j)\in C_a,X_j\subseteq X\end{array}$$

(18)

$$\begin{array}{c}\hfill Z=\bigcup a_h,\forall (X_h,a_h)\in C_a^c,X_h\subseteq X\end{array}$$

(19)

where $(X,a_i)\in C_s\cup C_s^c$.

In order to prove that $\lambda \left((X,a_i)\right)$ is an OEO-concept, Propositions 1 and 2 are presented separately.

Proposition 1. 

For a formal context $(U,V,R)$ and its complement context $(U,V,R^c)$, if $X\subseteq U$, then $(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }}$, $(X^{\square },X^{\overline{\square }}))$ is an OEO-concept.

Proof. 

According to the definition of the OEO-concept [22,30], we need to only prove that $\forall X\subseteq U$, ${(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})}^{⊳}$ = $(X^{\square },X^{\overline{\square }})$.

First, we can obtain $X^{\square \diamond }\subseteq (X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})$. It follows from the property (Equation (7)) that $X^{\square \diamond \square }\subseteq {(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})}^{\square }$. Further, we can deduce from the property in Equation (10) that $X^{\square }\subseteq {(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})}^{\square }$. Second, we know from the property in Equation (9) that $X^{\square \diamond }\subseteq X$ and $X^{\overline{\square }\overline{\diamond }}\subseteq X$. Consequently, we obtain $(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})\subseteq X\cup X$. This implies $(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})\subseteq X$. Thus, we can conclude that ${(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})}^{\square }=X^{\square }$.

Similarly, ${(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }})}^{\overline{\square }}=X^{\overline{\square }}$. Hence, based on the definition of the OEO concept, $(X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }},(X^{\square },X^{\overline{\square }}))$ is an OEO-concept.    □

For any given object set $X\in U$, an OEO-concept can be obtained based on Proposition 1. It can subsequently be used in the proof of Proposition 2.

Proposition 2. 

For a formal context $(U,V,R)$ and its complement context $(U,V,R^c)$, any $(X,a_i)\in C_s\cup C_s^c$, $\lambda \left((X,a_i)\right)$ is an OEO-concept.

Proof. 

Based on the function $\lambda$ (Definition 3), let $\lambda \left((X,a_i)\right)$ = $(X,(Y,Z\left)\right)$. We need to prove that $(X,(Y,Z\left)\right)$ satisfies such conditions that $Y=X^{\square },Z=X^{\overline{\square }}$ and $X=Y^{\square }\cup Z^{\overline{\diamond }}$. According to Proposition 1, it is an OEO-concept.

(1)

First, we prove that $Y=X^{\square }$. According to Definition 3, we can obtain $Y=\cup a_j$, where $\forall a_j\in V,g\left(a_j\right)\subseteq X$. Therefore, Y satisfies the definition of $X^{\square }$ in the formal context $(U,V,R)$, i.e., Equation (5). Thus, $Y=X^{\square }$.

(2)

Second, we prove that $Z=X^{\overline{\square }}$. We know that $Z=\cup a_h$, where $\forall a_h\in V,\overline{g}\left(a_h\right)\subseteq X$. Thus, $Z=X^{\overline{\square }}$ satisfies the definition of $X^{\overline{\square }}$ in the complement context $(U,V,R^c)$. Hence, $Z=X^{\overline{\square }}$.

(3)

Finally, we prove $X=Y^{\diamond }\cup X^{\overline{\diamond }}$. Based on (1), (2), and the property in Equation (9), we obtain $Y^{\diamond }\cup Z^{\overline{\diamond }}=X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }}\subseteq X$. Assuming that $X^{\square \diamond }\cup X^{\overline{\square }\overline{\diamond }}\subset X$, we have $X^{\square \diamond }\subset X$ and $X^{\overline{\square }\overline{\diamond }}\subset X$. As $(X,a_j)\in C_s$, this means that $g\left(a_j\right)=X$ and $a_j\in X^{\square }$. Thus, we obtain $X^{\square \diamond }\supseteq X$. This leads to a contradiction with the assumption. Thus, we obtain $X=Y^{\diamond }\cup Z^{\overline{\diamond }}$.

Based on (1), (2) and (3), the proposition has been proven.    □

According to Proposition 2, we can obtain OEO-concepts with the function $\lambda$ for a formal context $(U,V,R)$. Furthermore, these OEO-concepts that are derived by the function $\lambda$ can be used to obtain the other remaining OEO-concepts by using the steps below. For convenience of expression, we provide the following definitions:

Definition 4 

(Basic OEO-concept). For a formal context $(U,V,R)$, the concept derived from $\lambda \left((X,a_i)\right)$, where $X\subset U$ and $(X,a_i)\in C_s\cup C_s^c$, is called a basic OEO-concept. The set of all basic OEO-concepts is denoted by $B_{OEO}$.

Definition 5 

(k-granularity OEO-concept). Given an OEO-concept c of a formal context $(U,V,R)$, if the cardinality of the extent of c is equal to k, i.e., $\left|Ext\right(c\left)\right|$ = k, then the concept c is called a k-granularity OEO-concept, and it is denoted by $c_{OEO}^k$.

For a formal context $(U,V,R)$, the set of all k-granularity OEO-concepts is denoted by $C_{OEO}^k$, while the set of all k-granularity basic OEO-concepts is denoted by $B_{OEO}^k$. Moreover, all OEO-concepts can be categorized into $C_{OEO}^0,C_{OEO}^1,\dots ,C_{OEO}^{\left|U\right|}$ by their k-granularity. Thus, we can get the following equation:

$$\begin{array}{c}\hfill OEOL(U,V,R)=\bigcup _{k=0}^{\left|U\right|}{C}_{OEO}^k\end{array}$$

(20)

Proposition 3. 

Any 1-granularity OEO-concept $c_{OEO}^1\in C_{OEO}^1$ can be obtained from the basic OEO-concepts, i.e., $C_{OEO}^1=B_{OEO}^1$.

Proof. 

For a 1-granularity OEO-concept $c_{OEO}^1$$=(X,(Y,Z\left)\right)$, we can obtain $\left|X\right|=1$. $\forall a_i\in Y,g\left(a_i\right)=X$ and $\forall a_h\in Z,\overline{g}\left(a_h\right)=X$. Thus, $(X,a_i)$ and $(X,a_h)$ are single-attribute concepts based on Definition 2. Furthermore, according to Definition 4, we can obtain $\lambda (X,a_i)$ = $c_{OEO}^1$, which is a basic OEO-concept. Thus, any 1-granularity OEO-concept can be obtained from basic OEO-concepts, i.e., $C_{OEO}^1=B_{OEO}^1$.    □

Now, we can obtain $C_{OEO}^0$ by Proposition 1, i.e., $(\varnothing ,({\varnothing }^{\square },{\varnothing }^{\overline{\square }}))$, and can obtain $C_{OEO}^1$ based on Proposition 3. In order to obtain the remaining OEO-concepts, i.e., $C_{OEO}^2,\dots ,C_{OEO}^{\left|U\right|}$, it is necessary to perform merge operations on the generated OEO-concepts.

Definition 6 

(Concept merging). For a formal context $(U,V,R)$, if $c_1=(X_1,(Y_1,Z_1))$ and $c_2=(X_2,(Y_2,Z_2))$ are OEO-concepts, then the merge operation of $c_1$ and $c_2$ is defined as follows:

$$\begin{array}{c}\hfill M(c_1,c_2)=(X_1\cup X_2,(Y_1\cup Y_2,Z_1\cup Z_2)).\end{array}$$

(21)

where $X_1,X_2\subseteq U$, $Y_1,Y_2\subseteq V$, and $Z_1,Z_2\subseteq V$,

For any two OEO-concepts $c_1$ and $c_2$, a new pair can be obtained by using $M(c_1,c_2)$. However, the new pair derived from the merge operation may be not an OEO-concept. Thus, we introduced the definitions of the candidate k-granularity OEO-concept.

Definition 7 

(Candidate k-granularity OEO-concept). For a formal context (U, V, R), $c_1$ and $c_2$ are any two OEO-concepts, and the pair obtained by $M(c_1,c_2)$ is called the candidate OEO-concept. If $\left|Ext\right(M(c_1,c_2)\left)\right|=k$, the pair can be called the candidate k-granularity OEO-concept and is denoted by $c_{Candi}^k$.

For a formal context (U, V, R), the set of all candidate k-granularity concepts is denoted by $C_{Candi}^k$, i.e.,

$$\begin{array}{cc}\hfill C_{Candi}^k=& \left\{M(c_{OEO}^i,c_{OEO}^j)\right|\forall c_{OEO}^i\in C_{OEO}^i,\forall c_{OEO}^j\in C_{OEO}^j,\hfill \\ & i<k,j<k,\left|Ext\right(M(c_{OEO}^i,c_{OEO}^j)\left)\right|=k\}\hfill \end{array}$$

(22)

For any $c\in C_{Candi}^k$, regardless of whether c is an OEO-concept or not, its extent part, i.e., $Ext\left(c\right)$, must be the extent of a certain OEO-concept based on the definition of the supremum of two OEO-concepts (Equation (16)) and merge operation (Definition 6). Does the set of all candidate k-granularity concepts $C_{Candi}^k$ include all extents of all k-granularity OEO-concepts $C_{OEO}^k$, i.e., $Ext\left(C_{Candi}^k\right)=Ext\left(C_{OEO}^k\right)$? We answer this question by following proposition.

Proposition 4. 

For a formal context (U, V, R), $c_1$ and $c_2$ are OEO-concepts. If $c_2$ is an immediate sub-concept of $c_1$, i.e., $c_2<c_1$, then there must exist an OEO-concept $c_3$ such that $c_3\le c_1$ and $Ext\left(M(c_2,c_3)\right)=Ext\left(c_1\right)$.

Proof. 

Assume that $c_1=(X_1,(Y_1,Z_1))$ and $c_2=(X_2,(Y_2,Z_2))$. Because $c_2<c_1$, there must at least exist an object $x\in X_1\setminus X_2$.

(1)

If $X_1^{\square }\cap f\left(x\right)\ne \varnothing$, we obtain $g(X_1^{\square }\cap f\left(x\right))\subseteq X_1$. Thus, let $X_3=g(X_1^{\square }\cap f\left(x\right))$. Based on Proposition 1, let $c_3$ = $(X_3^{\square \diamond }\cup X_3^{\overline{\square }\overline{\diamond }},(X_3^{\square },X_3^{\overline{\square }}))$; thus, it is an OEO-concept. According to the properties of □ and ⋄ (Equation (9)), $X_3^{\square \diamond }\cup X_3^{\overline{\square }\overline{\diamond }}\subseteq X_3\cup X_3\subseteq X_1$. Thus, $c_3\le c_1$. Furthermore, according to the properties of OEO-concept lattices and the definition of supremum (Equation (16)), we obtain $c_2\bigvee c_3$ = $c_1$. Hence, $Ext\left(M(c_2,c_3)\right)=Ext\left(c_1\right)$.

(2)

If $X_1^{\square }\cap f\left(x\right)=\varnothing$, we get $x\notin X_1^{\square \diamond }$. Thus, $X_1^{\overline{\square }}\cap \overline{f}\left(x\right)\ne \varnothing$. We thus let $X_3=\overline{g}(X_1^{\overline{\square }}\cap \overline{f}\left(x\right))$. Similarly, we can get $c_3$ and $Ext\left(M(c_2,c_3)\right)=Ext\left(c_1\right)$.

Based on (1) and (2), the proposition has been proven.    □

According to Proposition 4, if $c_3<c_1$, we can get $|Ext\left(c_3\right)|<|Ext\left(c_1\right)|$ and $M(c_2,c_3)\in C_{Candi}^{\left|Ext\right(c_1\left)\right|}$. However, if $c_3=c_1$, $M(c_2,c_3)\notin C_{Candi}^{\left|Ext\right(c_1\left)\right|}$ owing to the definition of $C_{Candi}^k$ (Equation (22)). However, if $c_3=c_1$, we can obtain a further conclusion based on Proposition 4. We state it as the following proposition:

Proposition 5. 

For a formal context (U, V, R), $c_1=(X_1,(Y_1,Z_1))$ and $c_2=(X_2,(Y_2,Z_2))$ are OEO-concepts, such that $c_2<c_1$ and $x\in X_1\setminus X_2$. If $g(X_1^{\square }\cap f\left(x\right))=X_1$ or $\overline{g}(X_1^{\overline{\square }}\cap \overline{f}\left(x\right))=X_1$, then $c_1\in B_{OEO}$.

Proof. 

If $g(X_1^{\square }\cap f\left(x\right))=X_1$ and $\forall a\in X_1^{\square }\cap f\left(x\right)$, we can get $g\left(a\right)\supseteq X_1$ based on the properties of operator g. On the contrary, because a is a necessary attribute, we get $g\left(a\right)\subseteq X_1$. Thus, it can be concluded that $g\left(a\right)=X_1$. Furthermore, according to Definitions 2 and 4, we get $(X_1,a)\in C_s$ and $c_1\in B_{OEO}$.

The same conclusion can be obtained for the case where $\overline{g}(X_1^{\overline{\square }}\cap \overline{f}\left(x\right))=X_1$. We omit its proof.    □

Based on Propositions 4 and 5, it can be concluded that $Ext\left(C_{OEO}^k\right)=Ext(C_{Candi}^k\cup B_{OEO}^k)$. Therefore, we can group the candidate k-granularity OEO-concepts $C_{Candi}^k$ and the k-granularity basic OEO-concepts $B_{OEO}^k$ with the same extent. And, then, the corresponding intents of these extents are confirmed as follows:

Definition 8 

(Equivalence class of extent). Given a formal context (U, V, R), if $c\in C_{Candi}^k\cup B_{OEO}^k$ and the set ${\left[c\right]}_{Ext}$ meets the condition

$$\begin{array}{cc}\hfill {\left[c\right]}_{Ext}=& \left\{(X,(Y,Z))\right|\forall (X,(Y,Z))\in C_{Candi}^k\cup B_{OEO}^k,\hfill \\ & Ext(X,(Y,Z\left)\right)=Ext\left(c\right)\}\hfill \end{array}$$

(23)

then the set ${\left[c\right]}_{Ext}$ is called the equivalence class of the extent of c.

The equivalence class of the extent of c is used to obtain the intents of a new OEO-concept through the union operations of the intents of all concepts in the equivalence class. The process is defined as the function $\phi$.

Definition 9 

(Function $\phi$). Given a formal context (U, V, R), the φ function is a mapping $C_{Candi}^k$ to $C_{OEO}^k$. The definition is as follows:

$$\begin{array}{cc}\hfill \phi \left(c\right)& =(X,(Y_{max},Z_{max})),\hfill \\ \hfill \forall (X_i,(Y_i,Z_i))& \in {\left[c\right]}_{Ext},Y_{max}=\cup Y_i,Z_{max}=\cup Z_i\hfill \end{array}$$

(24)

where $c=(X,(Y,Z))\in C_{Candi}^k$.

As $B_{OEO}^k\subseteq B_{OEO}$ has been already generated by $\lambda$ (Definition 3), $\phi$ needs to only map each concept $c\in C_{Candi}^k$ to an OEO-concept in $C_{OEO}^k$. Now, Proposition 6 is provided to prove that $\phi \left(c\right)$ is an OEO-concept.

Proposition 6. 

For a formal context (U, V, R), if $c_1=(X_1,Y_1,Z_1)\in C_{Candi}^k$, then $\phi \left(c_1\right)=(X_1,(Y_{max},Z_{max}))$ is an OEO-concept.

Proof. 

If we want to prove that $\phi \left(c_1\right)$ is an OEO-concept, it needs to satisfy $Y_{\max }=X_1^{\square },Z_{\max }=X_1^{\overline{\square }}$ and $X_1=Y_{\max }^{\diamond }\cup Z_{\max }^{\overline{\diamond }}$ based on the definition of OEO-concepts.

(1)

First, we prove that $Y_{\max }=X_1^{\square }$.

• $\forall b\in Y_{\max }$, if $g(b)\subseteq X_1$; then, by the definition of the necessary operator, $b\in X_1^{\square }$. Given the arbitrariness of b, it follows that $Y_{\max }\subseteq X_1^{\square }$.
• Assume that $\exists b\in X_1^{\square }$ but $b\notin Y_{\max }$, i.e., $b\in X_1^{\square }\setminus Y_{\max }$; then, let $c_2$ = $(g{(b)}^{\square \diamond }\cup g{(b)}^{\overline{\square }\overline{\diamond }},(g{(b)}^{\square },g{(b)}^{\overline{\square }}))$. $c_2$ is then an OEO-concept based on Proposition 1. Because $g(b)\subseteq X_1$, $g{(b)}^{\square \diamond }\cup g{(b)}^{\overline{\square }\overline{\diamond }}\subseteq X_1$. If $g{(b)}^{\square \diamond }\cup g{(b)}^{\overline{\square }\overline{\diamond }}=X_1$, then we get $c_2\in {\left[c_1\right]}_{\mathrm{Ext}}$. This implies that $b\in Y_{\max }$. Therefore, given the arbitrariness of b, we conclude that $X_1^{\square }\subseteq Y_{\max }$.
  In the case $g{(b)}^{\square \diamond }\cup g{(b)}^{\overline{\square }\overline{\diamond }}\subset X_1$, let $c_3=(X_1,(X_1^{\square },X_1^{\overline{\square }}))$. Because $c_1\in C_{Candi}^k$ and $X_1$ is the extent of an OEO-concept, $c_3$ is an OEO-concept and $c_2<c_3$. According to Proposition 4, there must exist an OEO-concept $c_4\le c_3$ such that $M(c_2,c_4)\in {\left[c_1\right]}_{Ext}$. This means that $b\in Y_{Max}$. Given the arbitrariness of b, we get $X_1^{\square }\subseteq Y_{\max }$ as well.
• According to above 1. and 2., we get $Y_{\max }=X_1^{\square }$.

(2)

Second, it can similarly be proved that $Z_{\max }=X_1^{\overline{\square }}$.

(3)

Third, $Y_{\max }^{\diamond }\cup Z_{\max }^{\overline{\diamond }}=X_1^{\square \diamond }\cup X_1^{\overline{\square }\overline{\diamond }}\subseteq X_1$. Moreover, $(X_1,(X_1^{\square },X_1^{\overline{\square }}))$ is an OEO-concept. Therefore, $X_1=X_1^{\square \diamond }\cup X_1^{\overline{\square }\overline{\diamond }}$. Thus, $Y_{\max }^{\diamond }\cup Z_{\max }^{\overline{\diamond }}=X_1$.

From the above proofs, the proposition has been proven.    □

For the formal context $(U,V,R)$, all OEO-concepts can be categorized into $C_{OEO}^0$, $C_{OEO}^1$, $\dots ,C_{OEO}^{\left|U\right|}$ by their k-granularity. Thus, we can obtain $C_{OEO}^0,C_{OEO}^1$ from the basic OEO-concepts, and we can then apply function $\phi$ to iteratively obtain the others based on the k-granularity. Consequently, all OEO-concepts of the formal context $(U,V,R)$ can be obtained. Proposition 7 proves that the OEO-concepts generated by this method are complete.

Proposition 7. 

All OEO-concepts of the formal context $(U,V,R)$ can be obtained by iteratively applying function φ based on the basic OEO-concepts.

Proof. 

We use mathematical induction to prove the proposition. For convenience, all OEO-concepts are categorized into $C_{OEO}^0,C_{OEO}^1,\dots$, $C_{OEO}^{\left|U\right|}$ by their k-granularity.

(1)

Inductive Foundation: Based on Propositions 1 and 3, $C_{OEO}^0$ and $C_{OEO}^1$ can be obtained from basic OEO-concepts.

(2)

Inductive Hypothesis: Assume that the k-granularities of all OEO-concepts with granularity less than k are known, i.e., $C_{OEO}^0,C_{OEO}^1,\dots$, and $C_{OEO}^k$ are already known.

(3)

Inductive Step: Based on the inductive hypothesis and the partial-order relationship among OEO-concepts, all of the sub-concepts of each k + 1 granularity OEO-concept are known. The candidate set for k + 1 granularity OEO-concepts, $C_{Candi}^{k+1}$, can be obtained by Definition 7. Furthermore, according to Propositions 4 and 5, and Definition 8, the equivalence class of the extent of each k + 1 granularity OEO-concept can be obtained. Thus, all k + 1 granularity OEO-concepts can be obtained by using the function $\phi$ based on Proposition 6. Finally, $C_{OEO}^{k+1}$ can be obtained.

(4)

Conclusion: $C_{OEO}^0,C_{OEO}^1,\dots ,C_{OEO}^{\left|U\right|}$ can all be obtained.

   □

Based on Proposition 7, we designed a structural algorithm to construct all OEO-concepts from a formal context. The details are provided in the next section.

4. Algorithm Description and Time Complexity

The main idea underlying the 3WOC algorithm is as follows: First, $C_{OEO}^0$ is obtained by Proposition 1, and then the set of single-attribute concepts (Definition 2) is built from the formal context $(U,V,R)$ and its complementary context $(U,V,R^c)$. Second, the set of all basic OEO-concepts, i.e., $B_{OEO}$, is obtained from function $\lambda$ (Definition 3), and $C_{OEO}^1$ is obtained based on Propostion 3. Third, the candidate k-granularity OEO-concepts $C_{Candi}^k$ (k = 2 when beginning) are obtained according to Propositions 4 and 5. The function $\phi$ is then used to obtain all new k-granularity OEO-concepts in $C_{OEO}^k$ based on Proposition 6. By iteratively repeating this procedure, all concepts in $C_{OEO}^{k+1}$, $\dots ,C_{OEO}^{\left|U\right|}$ can be constructed. Finally, all OEO-concepts of the formal context $(U,V,R)$, i.e., $C_{OEO}^0,C_{OEO}^1,\dots ,C_{OEO}^{\left|U\right|}$, are constructed based on Proposition 7.

4.1. Algorithm Description

The pseudo-code description of our proposed $3WOC$ algorithm is as follows:

Algorithm 1 is a structured algorithm. Lines 2 to 5 are used to generate the basic OEO-concepts, i.e., $B_{OEO}$ (Definition 4). By Proposition 3, $C_{OEO}^1$ was constructed. Lines 6 to 16 are then used to iteratively construct $C_{OEO}^2,C_{OEO}^3,\dots ,C_{OEO}^{\left|U\right|}$. Lines 7 to 16 implement the function $\phi$ (Definition 9). Finally, all OEO-concepts are constructed and collected (line 17). The computational process of the 3WOC algorithm involves a large number of search and union operations, i.e., the functions find() and M(). The hash key is not only used to improve the efficiency of searching for a concept in L but also to improve the efficiency of union operations by directly performing bitwise operations with their hash values in place of the union operations on the set. The hash function $h\left(\right)$, which maps the extent of an OEO-concept to a unique value, is defined as follows:

Definition 10 

(Function h). Given a formal context $(U,V,R)$, we can provide a linear order on the object set U, i.e., $U=\{x_1,x_2,x_3,\dots ,x_{\left|U\right|}\}$. Then, each object $x_i\in U$, $1\le i\le \left|U\right|$, has its ordered position i in U. The function h is a mapping from an object set to a natural number, i.e., $\mathcal{P}\left(U\right)\to N$:

$$\begin{array}{c}\hfill h\left(X\right)=\sum _{x_i\in X}{2}^{i-1}\end{array}$$

(25)

where X = $\{x_i,x_m,\dots ,x_j\}\subseteq U$, $1\le i\le m\le \dots \le j\le \left|U\right|$.

Algorithm 1: 3WOC

Due to the correspondence relationship between the hash value and the extent of a concept, the time complexity of $Find\left(key\right)$ in line 12 is $\mathcal{O}\left(1\right)$. Furthermore, we can obtain the extent that is composed of objects from the hash value by using the function $h^{\prime }$:

Definition 11 

(Function $h^{\prime }$). Function $h^{\prime }$: $N\to P\left(U\right)$

$$\begin{array}{c}\hfill h^{\prime }\left(key\right)=\left\{x_i\right|x_i\in U,2^{i-1}\mathrm{AND}key\ne 0\}\end{array}$$

(26)

where AND is the bitwise AND operation on the binary representation of two natural numbers.

For a given formal context $(U,V,R)$, each $X\subseteq U$ corresponds to a hash key $h\left(X\right)$ based on the above functions, h and $h^{\prime }$. Let $KEY$ represent all hash values from $P\left(U\right)$, i.e., $KEY=\left\{h\right(X\left)\right|\forall X\in \mathcal{P}\left(U\right)\}$. Thus, $\left|KEY\right|$ = $2^{\left|U\right|}$. We can consider $<\mathcal{P}\left(U\right),\cup >$ and $<KEY,OR>$ as two algebraic systems, where OR is the bitwise OR operation on the binary representation of two natural numbers. They are isomorphic. Moreover, the proof is given in Proposition 8.

Proposition 8. 

The algebraic systems $<\mathcal{P}\left(U\right),\cup >$ and $<KEY,\mathit{OR}>$ are isomorphic.

Proof. 

(1)

$KEY$ is the non-empty set of natural numbers ranging from 0 to $2^{\left|U\right|}-1$. Thus, $\left|KEY\right|$ = $\left|\mathcal{P}\right(U\left)\right|$.

(2)

For any $X\in \mathcal{P}\left(U\right)$, there is an $n\in KEY$ such that $h\left(X\right)=n$. Thus, the function h is an injection. Furthermore, for any $X,Y\in \mathcal{P}\left(U\right)$, if $X\ne Y$, then $h\left(X\right)\ne h\left(Y\right)$. Thus, the function h is a surjection. Consequently, the function h is a bijection.

$$\begin{array}{cc}\hfill h(X\cup Y)& =\sum _{\forall x_i\in X\cup Y}{2}^{i-1}=\sum _{\forall x_i\in X}{2}^{i-1}\mathit{OR}\sum _{\forall y_j\in Y}{2}^{j-1}=h\left(X\right)\mathit{OR}h\left(Y\right)\hfill \end{array}$$

(27)

(3)

For any $a\in KEY$, there exists $X\in \mathcal{P}\left(U\right)$ such that $h^{\prime }\left(a\right)=X$. Thus, the function $h^{\prime }$ is an injection. For any $a,b\in KEY$, if $a\ne b$, then there must be at least one bit that is different between the binary representations of a and b, i.e., $h^{\prime }\left(a\right)\ne h^{\prime }\left(b\right)$. Thus, the function $h^{\prime }$ is a surjection. Consequently, the function $h^{\prime }$ is a bijection.

$$\begin{array}{cc}\hfill h^{\prime }\left(a\mathit{OR}b\right)=& \left\{x_i\right|x_i\in U,2^{i-1}\mathit{AND}\left(a\mathit{OR}b\right)\ne 0\}\hfill \\ \hfill =& \left\{x_i\right|x_i\in U,(2^{i-1}\mathit{AND}a\ne 0)\mathrm{or}(2^{i-1}\mathit{AND}b\ne 0)\}\hfill \\ \hfill =& \left\{x_i\right|x_i\in U,2^{i-1}\mathit{AND}a\ne 0\}\cup \left\{x_i\right|x_i\in U,2^{i-1}\mathit{AND}b\ne 0\}\hfill \\ \hfill =& h^{\prime }\left(a\right)\cup h^{\prime }\left(b\right)\hfill \end{array}$$

(28)

Based on the above, (1), (2), (3), the proposition has been proven. □

According to Proposition 8, we can directly perform the bitwise OR operations with their hash values in place of union operations on object sets in the $3WOC$ algorithm. However, the time complexity of function h, which converts the extent of concepts into a natural number, is $\mathcal{O}\left(\right|U\left|\right)$.

4.2. Time Complexity

The time complexity of Algorithm 1 is analyzed as follows: According to Equations (2) and (4), executing Steps 2–3 takes $\mathcal{O}\left(2\right|U|\times |V\left|\right)$ to obtain all single-attribute concepts (Definition 2) from the formal context $(U,V,R)$ and its complement context $(U,V,R^c)$. According to Definition 3 and Proposition 8, the time complexity of function $\lambda$ is $\mathcal{O}\left(\right|U|+|C_a|+|C_a^c\left|\right)$, and it is $\mathcal{O}\left(\right|U|+2|V\left|\right)$ in the worst case. Thus, Steps 4–5 take at most $\mathcal{O}\left(2\right|U|\times |V|+4|V{|}^2)$ to obtain all basic OEO concepts, $B_{OEO}$ (Definition 4). Steps 6–16 take at most $\mathcal{O}(\sum _{k=2}^{\left|U\right|}\left(\right|C_{OEO}^{k-1}|\times \sum _{j=1}^{k-1}|C_{OEO}^j\left|\right)\times \left(\right|U|+2\left|V\right|\left)\right)$. Based on Equation (20), letting $\left|OEOL(U,V,R)\right|=\sum _{k=0}^{\left|U\right|}\left(\right|C_{OEO}^k\left|\right)$, we can obtain the total time complexity of Algorithm 1 as $\mathcal{O}\left(4\right|U|\times \left|V\right|+{4\left|V\right|}^2+\left(\right|U|+2\left|V\right|)\times {\left|OEOL(U,V,R)\right|}^2)$. As $\left|OEOL\right(U,V,R\left)\right|$ is significantly larger than $\left|V\right|$, the time complexity of Algorithm 1 is $\mathcal{O}\left(\right(\left|U\right|+2\left|V\right|)\times {\left|OEOL(U,V,R)\right|}^2)$.

Example 2 illustrates the process of constructing OEO-concepts for the 3WOC algorithm. The details are as follows:

Example 2. 

The formal context $(U_1,V_1,R_1)$ is shown in Table 1 while the complement context is shown in Table 2. The object set is $U_1$ = 1, 2, 3, 4, 5 and the attribute set is $V_1$ = a, b, c, d, e. For the sake of clarity, the extents of the concepts considered in this example are still represented in the form of object sets. Additionally, the hash key of the extent of each concept is also provided.

By using g and $\overline{g}$ (Equations (2) and (4)), we can obtain sets of single-attribute concepts $C_s$ and $C_s^c$ (Definition 2), as shown in

Table 3. $C_s\cup C_s^c$.

Attribute	${\mathit{C}}_{\mathit{s}}$	${\mathit{C}}_{\mathit{s}}^{\mathit{c}}$
a	[key: 27, (1245,a)]	[key: 4, (3,a)]
b	[key: 20, (35,b)]	[key: 11, (124,b)]
c	[key: 3, (12,c)]	[key: 28, (345,c)]
d	[key: 1, (1,d)]	[key: 30, (2345,d)]
e	[key: 21, (135,e)]	[key: 10, (24,e)]

. The hash key can be obtained by using the above function h (Definition 10) on the extent of each concept. For instance, the object set {1,2,4,5} is the extent of the single-attribute concept $(1245,a)$. Thus, its hash key is $h\left(\{1,2,4,5\}\right)=2^0+2^1+2^3+2^4=27$.

Then, $B_{OEO}$ (Definition 4) is generated from $C_s$ and $C_s^c$, as shown in

Table 4. $B_{OEO}$.

k-Granularity	OEO-Concepts
1	[key: 1, (1,(d, ⌀))], [key: 4, (3,(⌀,a))]
2	[key: 3, (12,(cd, ⌀))], [key: 10, (24,(⌀,e))], [key: 20, (35,(b,a))]
3	[key: 21, (135,(bde,a))], [key: 11, (124,(cd,be))], [key: 28, (345,(b,ac))]
4	[key: 27, (1245,(acd,be))], [key: 30, (2345,(b,acde))]

.

According to line 1 in Algorithm 1, $C_{OEO}^0$ is $[key:0,(\varnothing ,(\varnothing ,\varnothing )\left)\right]$. Based on Proposition 3, all 1-granularity OEO-concepts have been constructed. In this example, $C_{OEO}^1$ = $\left\{\right[key:1,(1,(d,⌀\left)\right)],[key:4,(3,(⌀,a\left)\right)\left]\right\}$. In order to obtain all 2-granularity OEO-concepts except for $B_{OEO}^2$, we need to perform $M(c_1,c_2)$, such that $\forall c_1\in C_{OEO}^1$ and $\forall c_2\in C_{OEO}^0\cup C_{OEO}^1$. Thus, key: 1 OR key: 4 = key: 5 = $h\left(\right\{1\}\cup \{3\left\}\right)$ based on Proposition 8. Thus we get $C_{Candi}^2$: $[key:5,(13,(d,a)\left)\right]$. When the loop (lines 7 to 16 in Algorithm 1) is completed, we obtain $(13,(d,a\left)\right)$ as a new OEO-concept according to Proposition 6, i.e., $\phi \left(\right(13,(d,a)\left)\right)=(13,(d,a\left)\right)$. Consequently, $[key:5,(13,(d,a)\left)\right]$ is added to $C_{OEO}^2$. The updated $C_{OEO}^2$ is shown in

Table 5. $B_{OEO}$ ∪ $C_{OEO}^0$ ∪ $C_{OEO}^2$.

k-Granularity	OEO-Concepts
0	[key: 0, $(\varnothing ,(\varnothing ,\varnothing \left)\right)$]
1	[key: 1, (1,(d, ⌀))], [key: 4, (3,(⌀,a))]
2	[key: 3, (12,(cd, ⌀))], [key: 10, (24,(⌀,e))], [key:20, (35,(b,a))], [key: 5, (13,(d,a))]
3	[key: 21, (135,(bde,a))], [key: 11, (124,(cd,be))], [key:28, (345,(b,ac))]
4	[key: 27, (1245,(acd,be))], [key:30, (2345,(b,acde))]

.

We now construct $C_{OEO}^3$, i.e., $k=3$. $\forall c_1\in C_{OEO}^2$ and $\forall c_2\in C_{OEO}^1\cup C_{OEO}^2$, $M(c_1,c_2)$ are computed. This yields the following candidate OEO-concepts: $[key:11,(124,(d,e)\left)\right]$, $[key:7,(123,(cd,a)\left)\right]$, $[key:21,(135,(bd,a)\left)\right]$, $[key:14,(234,(\varnothing ,ae)\left)\right]$, $[key:23,(1235,(bcd,a)\left)\right]$, $[key:30,(2345,(b,ae)\left)\right]$, and $[key:15,(1234,(d,ae)\left)\right]$. Similarly, we can obtain $[key:7,(123,(cd,a)\left)\right]$ and $[key:14,(234,(\varnothing ,ae)\left)\right]$ as new OEO-concepts according to Proposition 6, and we add them to $C_{OEO}^3$. $[key:23,(1235,(bcd,a)\left)\right]$, $[key:30,(2345,(b,ae)\left)\right]$, and $[key:15,(1234,(d,ae)\left)\right]$ are 4-granularity candidate OEO-concepts now. We can obtain $C_{OEO}^4$ when k = 4. Finally, all OEO-concepts are obtained as shown in

Table 6. $OEOL(U_1,V_1,R_1)$.

k-Granularity	OEO-Concepts
0	[key: 0, (⌀,(⌀,⌀))]
1	[key: 1, (1,(d, ⌀))], [key: 4, (3,(⌀,a))]
2	[key: 3, (12,(cd, ⌀))], [key: 10, (24,(⌀,e))], [key: 20, (35,(b,a))], [key: 5, (13,(d,a))]
3	[key: 21, (135,(bde,a))], [key: 11, (124,(cd,be))], [key: 28, (345,(b,ac))], [key: 7, (123,(cd,a))], [key: 14, (234,(⌀,ae))]
4	[key: 27, (1245,(acd,be))], [key: 30, (2345,(b,acde))], [key: 29, (1345,(bde,ac))], [key: 15, (1234,(cd,abe))], [key: 23, (1235,(bcde,a))]
5	[key: 31, (U,(V,V))]

.

Furthermore, the three-way object-oriented concept lattice $(OEOL(U_1,V_1,R_1),\le )$ can be built based on the partial relationship between the concepts (Equation (14)). The lattice is shown in Figure 1, in which the concepts marked with a box are basic OEO-concepts.

For any two formal contexts, $(U,V,R)$ and $(U,T,J)$, V is the set of condition attributes, T is the set of decision attributes, and $V\cap T=\varnothing$. They form a formal decision context $(U,V,R,T,J)$. We can obtain two three-way object-oriented concept lattices, $OEOL(U,V,R)$ and $OEOL(U,T,J)$, using Algorithm 1. Assume that the formal decision context $(U,V,R,T,J)$ is OEO-consistence. Then, for any $(X,(A,B\left)\right)\in OEOL(U,V,R)$ and $(Y,(C,D\left)\right)\in OEO(U,T,J)$, if $X\subset Y$, and $X,Y,A,B,C,D$ are not ∅, we can obtain a positive three-way rule $A\to C$ and a negative three-way rule $\neg B\to \neg D$ [25]. Thus, Algorithm 1 can serve as a basic algorithm for three-way rule acquisition from OEO-concepts.

5. Experimental Evaluation

In this section, we evaluate the completeness and performance of our proposed $3WOC$ algorithm. We compared it with Qian’s method—the generation of three-way object-oriented concepts [30]—for which we used Ma’s algorithm to acquire object-oriented concepts [27]. We call it the QM algorithm for the sake of convenience. All algorithms were implemented in Python 3.8, and all experiments were run on an otherwise idle Windows system.

The data consisted of artificial datasets and real-world datasets. For a formal context $(U,V,R)$, there are three factors, the number of objects $\left|U\right|$, the number of attributes $\left|V\right|$, and the dense of non-zero entries, which can influence the number of OEO-concepts $\left|OEOL\right(U,V,R\left)\right|$. Thus, we used different arguments of these three factors to randomly generate a series of datasets. It is not necessary to separately illustrate them, and we represent the characteristics of each dataset by a naming rule whereby a randomly generated data table with m objects, n attributes, and average non-zero entries of $d\%$ is called Data_OmAnDd. $m\in \{10,20,30,40\}$, $n\in \{5,10\}$, and $d\%\in \{10\%$, $20\%$, $30\%$, $40\%$, $50\%$, $60\%\}$. Furthermore, any group of datasets can be simply expressed. For instance, the datasets Data_OmA5Dd, in which $m=10,\dots ,40$ and $d=10,\dots ,50,60$, can be simply denoted by Data_A5. The real-world datasets came from the UCI Machine Learning Repository (https://archive.ics.uci.edu/datasets/, accessed on 17 February 2025), including Balloons, Lenses, COVID-19 surveillance. All of the datasets were prepared as formal contexts without noisy and incomplete data in our experiments.

5.1. Completeness Experiment

To verify the completeness of OEO-concepts generated by our Algorithm 1, we compared them with the concepts generated by the QM algorithm. We executed the experiments on several datasets, including the formal context listed in Table 1, the UCI dataset (Balloons, Lenses, and COVID-19 surveillance), and random datasets (Data_A5, Data_A10). The extent and intent of each of the OEO-concepts derived from the above datasets were separately checked. We confirmed that the OEO-concepts generated by Algorithm 1 were complete.

The number of concepts derived from the UCI datasets is shown in

Table 7. Number of concepts, run times and memory usage on the UCI datasets.

Dataset	$\left|\mathit{U}\right|$	$\left|\mathit{V}\right|$	Num. of Concepts	Run Time of 3WOC	Mem. Usage of 3WOC	Run Time of QM	Mem. Usage of QM
Balloons	20	10	91	0.0108 s	4696 bytes	5.5065 s	904 bytes
Lenses	24	12	229	0.0964 s	9312 bytes	64.3453 s	1920 bytes
COVID-19 Surveillance	14	17	139	0.0178 s	4696 bytes	86.4654 s	1240 bytes

, while those derived from the random datasets are shown in Figure 2 and Figure 3. Furthermore, the concepts obtained by Algorithm 1 from Table 1 are listed in Table 6.

5.2. Performance Evaluation

To evaluate the efficiency of Algorithm 1, we measured its run time and memory usage when constructing three-way object-oriented concepts from scratch in comparison with those of the QM algorithm. We used both the UCI datasets and randomly generated datasets for these experiments.

Table 7 lists the run times and memory usage of both algorithms on the UCI datasets (Balloons, Lenses, COVID-19 surveillance). It shows that Algorithm 1 was significantly more efficient than the QM algorithm on each dataset. However, Algorithm 1 used more memory than the QM algorithm on each dataset. This is because Algorithm 1 not only stored the hash key of each OEO-concept but also was implemented with the dictionary and list data structure in Python 3.8, whereas the QM algorithm was implemented with the list data structure in Python 3.8. On the other hand, Table 7 shows that Algorithm 1 used the same size of memory on both datasets, Balloons and COVID-19 surveillance, due to the memory preallocation mechanism of Python 3.8.

The QM algorithm requires computing the power set of attribute sets and obtaining the corresponding extent of object-oriented concepts based on the size of the power set. The more attributes there are, the greater the number of power sets of attributes that needs to be calculated. By contrast, Algorithm 1 derives OEO-concepts directly from single-attribute concepts. By iteratively merging these concepts, all OEO-concepts are obtained while avoiding the exhaustive calculation of the power sets of the attribute sets. Furthermore, it uses bitwise operations with the hash values, in place of union operations on extents of concepts, to improve its efficiency.

Figure 4 and Figure 5 show the run times of Algorithm 1 on datasets Data_A5 and Data_A10, respectively. These results reflect the inherent property of the proposed algorithm for constructing formal concepts: its time complexity increased exponentially with the number of objects and attributes, and the density of the datasets. Figure 6 and Figure 7 show the run times of the QM algorithm on Data_A5 and Data_A10, respectively. It is clear that Algorithm 1 delivered better performance than the QM algorithm on each dataset.

In addition, a comparison between Figure 2 and Figure 4 shows that the run time of Algorithm 1 exhibited a similar trend of change with the number of concepts. This phenomenon is also shown in Figure 3 and Figure 5. Given that the time complexity of Algorithm 1 (in Section 4.2) is $\mathcal{O}\left(\right(\left|U\right|+2\left|V\right|)\times {\left|OEOL(U,V,R)\right|}^2)$, its run time was mainly influenced by the number of OEO-concepts.

6. Conclusions

In this study, we proposed an algorithm for quickly and completely acquiring all OEO-concepts from a formal context $(U,V,R)$. We also theoretically and experimentally proved that the OEO-concepts generated by our proposed algorithm are complete. Its time complexity is $\mathcal{O}\left(\right(\left|U\right|+2\left|V\right|)\times {\left|OEOL(U,V,R)\right|}^2)$. Moreover, it not only avoids traversing the power set of the attribute set V but also uses use the bitwise operations on hash values in place of union operations on object sets to improve the efficiency of acquisition. Furthermore, it delivered better performance than the QM algorithm on various datasets in comparative experiments. Our work in this paper can serve as a basic algorithm for the three-way rule acquisition from OEO-concepts.

There remains considerable room for further research in the area, including ways to quickly and simultaneously acquire three-way object-oriented concepts and their lattice structures, as well as techniques to design parallel construction algorithms, and so on.