Abstract
Cricket is a dynamic sport, making the selection of key performance indicators (KPIs) challenging. Objective: The study aims to identify KPIs in Twenty-20 (T20) cricket affecting match outcomes. Methods: Cricket performance data was analysed from three seasons of male T20 matches, identifying 136 performance indicators (PIs). The random forest algorithm and lasso logistic regression were used to develop a model to predict match outcomes. Results: The hybrid model achieved 85.9% accuracy with leave-one-out cross-validation statistical analyses. Sixteen KPIs were identified and ranked by importance including wickets lost in the last six overs, two or more wickets in the second innings, run rate in the last six overs, wickets by seam and spin bowling, batting strike rate, singles percentage in the second innings, sixes in the first innings, overs bowled by seam, runs in last six overs, sixes in middle overs, total catches in second innings, dot ball percentage, opening partnership runs, dot balls in the opening six, and singles in the last six. Conclusions: Cricket match performance in the final overs, especially bowling strike rate and scoring runs, were crucial for successful match outcomes. These KPIs offer insights into team strategy, player selection, and match performance evaluation in T20 cricket.
1. Introduction
Cricket, with its rich history and global fan base [1], has evolved into a multifaceted sport with various components that affect player and team performance [2]. Performance analysis is an essential component in evaluating players, teams, and match strategies, thereby facilitating evidence-based decision making to predict and enhance performance tactically [3,4,5].
Performance analysis is the process of recording and analysing players’ performances during practices and competitions [6,7]. It focuses on recording discrete categories of cricket information, such as important biomechanical characteristics, match statistics, and tactical and technical decision-making features [6]. All of this data is used to inform and support the coaching process and, ultimately, to enhance match performance [8,9]. The methods employed in match analysis usually involve performance data about the batters’ run-scoring capabilities and the bowlers’ wicket-taking abilities [10]. Several studies explored the factors that influenced performance in T20 cricket, such as batting, bowling, and fielding [11,12,13,14,15,16,17]. These factors are generally known as performance indicators (PIs) [8]. These performance indicators (PIs) refer to metrics that provide broad aspects of matches, which are used to evaluate and gain useful information on the players’ and teams’ performances [3,8,17]. Key performance indicators (KPIs) are a subset of PIs and are considered critical for assessing the team’s performances and successes [8,18]. These metrics are significantly associated with successful performance and winning a match [8,18].
To date, there are few studies which determine the KPIs that predict successful performance in professional T20 cricket matches [11,12,13,14,15,16,17]. Current research highlighted that the KPIs, specifically for batting, were scoring more boundaries, scoring more runs in the middle eight overs (7th–14th), and achieving a higher run rate during the middle and final overs, namely, 7th–16th and 17th–20th overs [11,12,13,14,15,16,17]. Furthermore, individual and partnership scores of 50 or more runs had a significant effect on winning a match [12,13,15].
Furthermore, the KPIs, specifically for bowling, were taking more wickets during a match [13,14,16], how quickly the first three to five wickets were taken [11], losing fewer wickets in both the powerplay phase [12,15] and between the 7th–10th overs of a match [15], taking wickets in the last six overs (15th–20th) [14,16], and bowling more dot balls in a match [12,13]. Scholes and Shafizadeh [17] also indicated that fielding run outs and taking catches were also essential KPIs.
A total of seven articles were identified that investigated KPIs in cricket, of which five compared match statistics between winning and losing teams [12,13,14,15,16]. All five studies ranked the KPIs based on effect size. These five studies analysed a range of domestic and international T20 matches, with sample sizes varying from seven to fifty-six matches. The statistical analyses applied in these studies were appropriate but lacked clarity and sufficient detail [12,13,14,15,16]. Specifically, while comparative statistical tests, such as T-tests, have been used to determine differences in PIs between winning and losing matches [12,13,14,15,16], conducting multiple T-tests on a large number of PIs significantly increases the likelihood of Type 1 error (i.e., incorrectly rejecting a null hypothesis) due to an inflated proportion of false positive results [19]. The use of T-tests in these studies presents a significant limitation, as it may overlook the potential negative effects resulting from interactions or correlations between various PIs, thus limiting their predictive capabilities [20].
This contrasts with the existing literature focusing on a few pre-selected KPIs in T20 cricket matches [12,13,14,15]. Since cricket is a complex and dynamic sport, selecting KPIs can be challenging [8,11]. The sport is multidimensional with various performance aspects, such as batting, bowling, fielding, and wicket-keeping. However, there is no consensus on which specific PIs should be used to measure the success or effectiveness of a cricketer [21]. By pre-selecting PIs, there is the risk of overlooking important aspects of the game and focusing on variables that may not accurately reflect success in cricket [11]. Therefore, the aim of this study is to utilise a hybrid approach to develop a model that predicts match outcomes, which combines the strengths of both statistical and machine learning methods and enables a larger number of potential KPIs to be employed in the model [22]. While some of the previous studies employed machine learning techniques, the studies were constrained by the limited number of PIs identified [11,17].
The existing literature on performance analysis in cricket research often suffers from limitations that constrain a comprehensive assessment of the players’ and teams’ abilities [11]. Some limitations are the predominant focus on batting and bowling while neglecting the importance of fielding [17]. Current studies that focus on PIs, without specifying the significance of a particular innings, make it challenging to draw meaningful conclusions about the impact of the KPIs on match outcomes [15]. Another limitation is that the authors draw questionable conclusions based on limited sample sizes [14,17]. Relying on a small number of matches or innings can lead to unreliable or skewed results, as these may not be representative of a player’s true abilities or a team’s overall performance [23,24]. Furthermore, the use of magnitude-based inference has been criticised for lacking statistical rigour and failing to control adequately for Type I and Type II errors, thus producing potentially unreliable results [25,26]. Relying solely on effect sizes without considering the broader statistical context presents a significant limitation. This approach can be misleading, as it may not account for the variability or practical significance of the observed effects, potentially leading to inaccurate interpretations [25].
Efforts to address these limitations in current research on performance analysis are essential for fostering a comprehensive and accurate understanding of the match performances of players and teams, as well as for assessing their overall impact on determining the outcome of cricket matches [11]. Therefore, the appropriate use of statistical analysis is crucial in performance analysis [11]. By incorporating fielding metrics, larger datasets, and robust statistical and machine learning techniques, researchers can more accurately evaluate the validity and reliability of their findings and, thereby, yield more meaningful insights for the benefit of players, teams, and sports analysts [27]. In order to address some of these challenges in performance analysis, the current study developed a model to predict match outcomes. The model employed a novel strategy using a hybrid method that leveraged a broad range of KPIs in both innings of T20 cricket matches. Therefore, the aim of the study is to analyse the KPIs in T20 cricket matches and develop a predictive model that enhances the ability to predict match outcomes.
2. Materials and Methods
2.1. Research Design
This study adopts a quantitative, non-experimental predictive research design [28]. The design facilitates robust pattern recognition and predictive modelling without manipulating variables, making it well-suited for performance analytics in sports contexts.
2.2. Data Description
This study analysed the match performance data of 80 cricket matches from three cricket seasons (2018, 2019, and 2022) of professional men’s T20 cricket in South Africa. Match statistics for 2020 and 2021 were excluded due to COVID-19. The cricket data was obtained from an online open-access site, www.ESPNcricinfo.com [29]. Two matches were excluded because they were shortened due to inclement weather and did not meet the study’s inclusion criteria. Therefore, a total of 78 matches were included in the final analyses. The data from ESPN Cricinfo was verified for accuracy using another website, https://cricsheet.org [30].
Reliability tests for intra-observer and inter-observer reliability were conducted on the 78 matches. Inter-observer reliability was assessed by two investigators who coded the same 78 matches, while intra-observer reliability was determined by the same investigator coding the matches twice. The coding sessions were separated by a period of 2 weeks. Cohen’s kappa coefficient was employed to calculate both the intra-observer and inter-observer reliability. Specifically, the values ≤0.20, 0.21–0.40, 0.41–0.60, 0.61–0.80, and ≥0.81 indicated poor, fair, moderate, good, and very good levels of agreement ([31]). The intra-observer and inter-observer reliability ratings were 0.96 and 0.92, respectively.
All the research procedures received approval from the Humanities and Social Sciences Research Ethics Committee at the University of the Western Cape (Institutional ethics reference code: HS21/2/2).
2.3. Data Processing
Ball-by-ball data from www.ESPNcricinfo.com included the number of overs, balls bowled, bowling style (spin vs. seam), partnership scores, match venues (home vs. away), and coin toss outcomes (winning vs. losing the coin toss). The data was checked for errors and missing values, and then cleaned and restructured using R Studio software (RStudio) version 4.4.1. The key packages used within R were dplyr and tidyr, which were applied to clean and structure the raw dataset [32].
Pre-recorded data may contain noise or random variations that distort the accuracy of information. Due to error(s) in recording, sometimes there may be missing values for different columns [33]. This results in improper data classification [33]. Hence, columns with missing values were removed from the final dataset in this study.
With regard to data processing, the data was initially aggregated into a set of PIs that represented various aspects of a team’s performance in each innings of a match. Thereafter, the data was divided into specific play intervals to examine match dynamics and identify KPIs. The following match divisions or play intervals were commonly used: (1) the opening six overs (1st–6th)—this interval is known as the powerplay overs, where only two fielders are allowed outside the 27 m (30-yard) circle, and the focus during this phase is on aggressive batting to maximise the run rate; (2) the lower middle overs (7th–10th)—these overs are when captains and batsmen strategise to consolidate their innings, rotate the strike or batsmen and build a solid batting foundation for the latter part of the match—(3) the upper middle overs (11th–14th)—this interval is sometimes called the acceleration phase, when batsmen aim to increase the run rate, take calculated risks and build momentum leading into the final overs; and, lastly, (4) the last six overs (15th–20th)—this is the final stage of the innings, also known as the “death-overs”, when batsmen typically target a higher run rate and, often, play more aggressively to maximise the total score. This interval is crucial for determining the team’s overall score and setting competitive targets for the opposition. Therefore, the focus during this interval is on hitting boundaries and scoring runs quickly [11,13,14,15].
This study examined 136 PIs, including some PIs drawn from the existing literature [13,15], and also introduced some novel PIs that had not been evaluated previously. Notably, the innovative approach used in the current study involved 68 PIs for each team per innings. Due to the COVID-19 pandemic, some contextual features (such as the match venue) were excluded from the data analyses because the pandemic affected the travel of players and the scheduling of matches; consequently, many matches were moved to neutral venues or played without spectators. A summary of these PIs and their definitions is listed in Table 1.

Table 1.
The features of the performance indicators (PIs) used in the current study.
2.4. Data Analysis
The data analysis aimed to identify KPIs for developing a predictive model for determining match outcomes. It utilised non-parametric regression methods, fitting a non-linear model, with match outcome as the response variable and PIs as the features. A dynamic programming formula analysed the match performance of both teams. For clarity, the first-batting team is referred to as “Team A” in the “first innings”, and the second-batting team as “Team B” in the “second innings”.
On the one hand, the response variable Y assumed a value of 1 if Team A won the match (i.e., Team B lost), and a value of 0 if Team A lost the match. On the other hand, the symbol X was used to denote the matrix of feature values. Each row of the data matrix [Y, X] contained all the information for one match. Furthermore, the features in the data matrix X were divided into five groups of PIs: (1) general match performance, (2) team performance, (3) batting performance, (4) bowling performance, and (5) fielding performance. The primary tool for performance analysis in the current study was the random forest algorithm. Subsequently, lasso logistic regression was applied to enhance the predictive model, enabling it to utilise fewer predictors while achieving high prediction accuracy [34]. A brief summary of the process is shown in Figure 1.
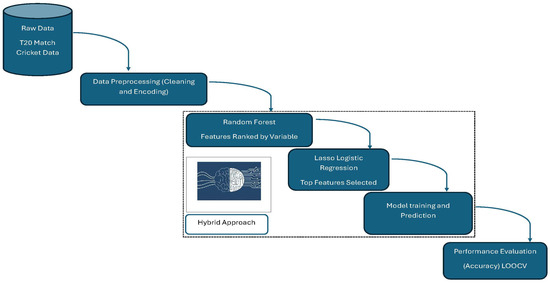
Figure 1.
A summary of the process of statistical data analyses.
The random forest algorithm is an ensemble method that amalgamates several individual classification trees, with each tree being trained on a distinct bootstrapping sample [35]. The individual trees generate their predictions for a new input point, and the random forest subsequently employs a majority vote on these predictions to arrive at a final prediction [35]. This technique can significantly enhance prediction accuracy compared to using a single classification tree, as the ensemble method compensates for the instability of the individual trees [34]. The random forest model captures higher-order and non-linear interactions among PIs, as well as the influence of these interactions in making predictions [36]. While some individual KPIs may not contribute to accurate predictions when considered separately, aggregating them together could considerably improve their overall prediction accuracy [37].
An important property of the random forest algorithm is that in addition to making predictions, it can also be used to evaluate the importance of the features in the model when making the final predictions [38]. There are two standard ways of measuring variable importance in the algorithm [38]. The method used in the current analysis is based on the random permutation method [38]. To obtain an importance score for a feature using this method, the algorithm first calculates the out-of-bag errors for making predictions with the original dataset. It then modifies the dataset by randomly permuting the values of that feature and calculates the out-of-bag prediction errors again. The mean squared difference between the two sets of errors provides the importance score [34].
The importance score in the random forest measures the differences in prediction accuracy with and without a feature [38], providing a quantitative rating of the feature’s usefulness in the model. To determine the KPIs, importance scores were calculated for each feature in the random forest model, and the top-rated features were selected. A common issue in using the random forest for feature selection is that it often picks more features than necessary, especially when several highly correlated features exist, with only one being sufficient for the prediction model.
In order to reduce the potential for selecting unnecessary features, when using the random forest model, lasso logistic regression was used to fine-tune the feature selection [34]. Lasso logistic regression is a penalising logistic regression that estimates the regression coefficients by maximising the log-likelihood function (or the sum of squared residuals) plus a penalty term, which penalises when more features are added to a model. A critical property of this algorithm is that the estimates of the regression coefficients are sparse, which means that many coefficients are exactly 0; i.e., it automatically deletes less important covariates in the model [37].
The overall analysis in the current study adopted a hybrid approach that combined rankings of the features, based on variable importance, from the random forest model with lasso logistic regression. More specifically, the final features selected were those that had both the highest importance rankings and were selected via lasso logistic regression, i.e., features with non-zero regression coefficients. These features were identified as the KPIs that could be used to fit a new random forest model for future prediction.
In the current study, the random forest algorithm was run using the R function ranger, wherein the parameters were num.trees = 1000, importance = permutation, and oob.error = True. The lasso logistic regression was run using the R function glmnet, with lambda = lambda.min, which was obtained via cross-validation using the R function cv.glmnet. All the other parameters in both R functions took the default values. The prediction accuracy of the model, based on the KPIs obtained, was estimated using leave-one-out cross-validation (LOOCV). Since there were 78 data points in the dataset, there were also 78 cross-validation runs in LOOCV. The hybrid approach outperforms single-method models. It first uses random forest to capture complex, non-linear and higher-order interactions among PIs and rank them in order of importance. Then, lasso logistic regression prunes irrelevant variables by shrinking weak predictors to zero. Finally, a new random forest is trained on the refined set, and strong predictive accuracy is achieved with fewer, but more meaningful, KPIs. The hybrid model provided a balance between model complexity and performance. It remained relatively interpretable while still delivering robust results, as observed in a pseudo-code in Figure 2.

Figure 2.
Data analysis pseudo-code.
3. Results
The data analysis encompassed a diverse set of variables (PIs), necessitating the prioritisation of their significance in predicting match outcomes (win/loss). This prioritisation aimed to determine the most important variables in designing the model, as well as ensure their relevance and impact. The initial random forest model was trained on 136 PIs using 1000 trees with permutation-based importance scoring. This process identified a wide set of PIs influencing match outcomes, with greater importance indicated by higher increases in out-of-bag error upon permutation (Table A1). Lasso logistic regression was applied to the same feature set, shrinking the coefficient of redundant variables to zero. This allows a reduction in the list to a reduced subset of potential KPIs, although Lasso logistic regression alone cannot identify non-linear interactions (Table A2). The hybrid approach was constructed by retraining random forest on the KPIs retrained through lasso logistic regression. Following the approach outlined above, from the 136 PIs in the data (Table A3), 16 PIs were identified through the prediction model and called KPIs.
A hybrid model, consisting of the random forest and lasso logistic regression, was formulated to illustrate the relationship between the KPIs and the outcomes of the match. The model constructed, using the 16 KPIs, has a classification accuracy of 85.9%, as assessed through LOOCV. The KPIs variable importance scores are listed in Table 2. Eight KPIs were related to bowling and fielding, and eight to batting.

Table 2.
The ranking of the sixteen key performance indicators (KPIs) in order of importance with respect to successful match outcomes.
The results indicated in Table 2 revealed the relative importance of each KPI in predicting successful match outcomes. It was evident that the KPIs in the second innings, particularly wicket-taking performance and run rate in the final overs, hold significant importance in determining the outcome of cricket matches, as indicated by their high variable importance scores.
At the pinnacle of the model lies the significance of wickets taken in the last six overs (15th–20th) of the second innings. The ability of the bowling side to secure wickets during this crucial match phase emerged as the single most influential factor in determining match outcomes. This variable has the highest importance score, indicating that the closing phase of a match, particularly defending totals or restricting runs, plays a critical role in determining the match outcome. The run rate in the last six overs (15th–20th) of the second innings emerged as another pivotal determinant of match success. This KPI reflects a more distributed bowling performance, where multiple bowlers contribute to maintaining pressure. Such pressure often forces batsmen to take more risks, which can lead to lower run rates or more frequent dismissals, thereby enhancing the accuracy of match outcome predictions. Furthermore, the batting strike rate in the final six overs of the second innings emerged as an influential KPI. It reflected the capacity of batters to score swiftly, when it mattered most, and demonstrated a trait that could tip the balance of power in favour of the batting side. Similarly to wicket-taking, maintaining a high run rate in the death overs, especially when the team is chasing a target, is a strong indicator of successful performance. It indicates both batting pressure and bowling effectiveness, as reliable predictors. Furthermore, additional KPIs, such as the percentage of singles (1’s) scored in the second innings, wickets taken by spin bowlers, the number of sixes scored in the first innings, and the number of overs bowled by seam bowlers in the last six overs (15th–20th) of the second innings, all held notable importance in predicting match outcomes. The results also revealed that the number of runs scored in the final six overs (15th–20th) of the first innings, and the number of sixes hit in the 11th-14th overs of the first innings could influence a match. The following are the lower-ranked variable importance KPIs. Notably, the total number of catches taken in the second innings. While catching is crucial in cricket, the number of catches alone may not capture the broader dynamics of the match, thereby limiting its predictive strength. The dot ball percentage in the first innings, although dot balls reduce run rate, may not be sufficient in isolation to accurately predict match outcomes. The number of runs scored by the opening partnership in the first innings is valuable, but it does not always correlate strongly with match results in T20 cricket, where the middle and death overs often determine the match outcome. The number of dot balls in the first six overs in the first innings can hinder momentum, but it may be offset by strong performances in the middle or later stages of a match, thereby reducing its predictive value. Lastly, the number of ones in the last six overs of the second innings has been identified as a contributor to match outcomes, but has limited impact during the high-pressure final overs of T20 matches, albeit with slightly lower variable importance scores.
LOOCV was employed to evaluate the predictive strength of various performance indicators. The LOOCV results generated feature counts, reflecting how often each PI was selected across validation rounds. A higher count indicates that the feature was consistently selected as being influential in predicting match outcomes. The top three KPIs, appearing in at least 77 out of 78 folds, were predominantly related to second innings performance, particularly in the death overs (Figure 3), and are listed as The number of wickets lost in the last six overs (n = 78); the number of bowlers taking two or more wickets (n = 78); and the run rate for 15 to 20 overs (n = 78). These KPIs suggest that bowling effectiveness and scoring efficiency during the death overs of the second innings are crucial to match outcomes, reinforcing the strategic importance of performance in the death overs of T20 cricket. Several first-inning KPIs featured prominently, viz., the number of sixes in overs 11–14 (n = 77), the total number of sixes (n = 77), and the number of runs in the last six overs (15th–20th overs) (n = 77). This highlights that boundary-hitting capacity and acceleration before the death overs in the first innings were key to setting a good target. Specifically, the KPIs, such as the number of wickets from spin bowlers in the second innings (n = 76) and the single percentage in the second innings (n = 72), demonstrate the influence of containment and strike rotation, alongside wicket-taking and power hitting during the match. Alternatively, the KPIs with variable importance scores included the number of runs in overs 11–14 in the second innings (n = 7) and dot balls in the 11th–14th overs of the second innings (n = 1), and these indicators were selected infrequently across validation tuns, suggesting they had limited influence match outcomes.
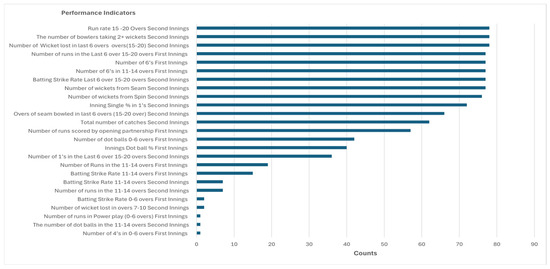
Figure 3.
Distribution of KPI feature counts based on LOOCV.
4. Discussion
Prediction forecasting of cricket match outcomes is crucial in the field of machine learning [39]. Researchers have explored the various techniques in the field of machine learning and artificial intelligence to address the challenges of predictive outcomes in cricket [40]. The aim of the study was to analyse the KPIs in T20 cricket matches and develop a predictive model that enhances the ability to predict match outcomes. A hybrid model, developed by combining variable importance and features ranking from the random forest algorithm with lasso logistic regression, was used to predict match outcome and player performance. This hybrid model was found to be adequate with an accuracy power of 85.9%. Sixteen KPIs were found to be most relevant in predicting cricket match outcomes. The following sections will discuss the sixteen KPIs identified in the present study under the subheadings of batting, bowling, and fielding. In comparison to traditional statistical methods such as effect analysis (e.g., Cohen’s d) to distinguish the performance difference between winning and losing teams [12,13,14,15,16], the statistical analyses applied in these studies were appropriate but lacked clarity [12,13,14,15,16]. The current model used in the study provides greater predictive accuracy of 85.9% and accounts for non-linear interactions. Previous studies illustrate the limitations of single-method approaches. Ahamad and Nazir [41] obtained 80% accuracy with a logistic model in One-Day Internationals (ODIs); yet its assumptions reflect the nature of 50-over play, reducing transferability to T20 [41]. Within the Indian Premier League (IPL), Tripathi et al. [42] applied a random forest and reported 60% accuracy, while Kapadia et al. [43] used k-nearest neighbours and achieved 62% accuracy. Both results display how a single algorithm struggles to accommodate the diverse nature of T20 [42,43]. Rahman et al. analysed ODI innings by innings; the accuracy increased from 63.6% during pre-match to 81.8% during the second innings, but the sequential design ignored the simultaneous influence of batting, bowling, and fielding variables that characterise T20 cricket [44]. The present study surpasses those benchmarks and offers flexibility for the dynamic format of T20.
4.1. Batting
The present study suggests that batting, as a KPI for T20 Cricket, is especially important at the end of an innings, and specifically the team’s ability to bat well and accelerate the run rate towards the end of the innings. A high run rate and strike rate in the last overs are crucial, as they significantly impact a team’s ability to efficiently chase down the opposing team’s score [45]. If more runs are scored, specifically in this shorter period (end of an innings), it increases the chances of a team winning a match [45,46]. It is, therefore, understandable that the results of the present study indicated that the number of sixes scored in the last six overs was a critical KPI.
In addition, the number of singles scored in the last six overs in the second innings was also a KPI. The reason for this is presumably that in the last six overs of the second innings, there is a need to score as many runs as possible to achieve the target [46]. Scoring a single run allows for the continuous rotation of strike, reduces the number of dot balls, maintains pressure on the bowlers, and provides ample time for a set batter to face more deliveries [47].
The number of runs scored by the opening partnership in the first innings was another KPI in the present study. At the start of a match, building a solid foundation and a high score during the powerplay and the middle overs are crucial for settng a formidable target for the opposing team [48,49]. A strong opening partnership not only establishes a potentially unassailable target but also allows the subsequent batters to play more aggressively and further increase the score [48,49]. The number of sixes during the middle overs (11th–14th) in the first innings was a KPI, which further emphasises the importance of hitting boundaries and maximising the scoring of runs despite the risks associated with hitting the ball in the air [14]. In contrast, previous research reported that the number of sixes scored during the middle overs (11th–14th) had a small impact on match outcome [15].
4.2. Bowling
Several bowling KPIs are also related to the team’s performance at the end of an innings and match outcome [12,14,16]. The number of wickets taken in the last six overs in the second innings was the most important KPI identified in this study, which is similar to previous studies [12,14,16]. In contrast, Irvine and Kennedy [13] reported that the wickets taken in the last six overs had less of an impact on the outcome of a match. Furthermore, losing wickets in the last six overs of an innings was found to be less important [15].
Taking wickets in the last six overs disrupts the momentum of the game for three possible reasons. Firstly, the dismissal of a batter towards the end of an innings generally indicates that one of the better batters is removed and replaced by a less skilled batter. The less skilled batter might not be able to score runs as quickly as the previous batter. Secondly, a new batter often needs time to familiarise themself with the playing conditions and, usually, plays less aggressively early in the innings and, consequently, scores fewer runs. Finally, the partner of a non-dismissed batter often plays cautiously, at least for the first few balls of a new batting partnership, to prevent more wickets from falling in a relatively short time-period [46]. All these tactics would slow the run rate and increase the bowling team’s chances of winning [50].
Other KPIs identified in the current study that related to bowling and fielding included the number of wickets taken by seam and spin bowling in the second innings, and the number of bowlers taking two or more wickets in the second innings. This reiterates the importance of taking wickets in T20 cricket and is supported by previous research [13,15]. Bowlers are limited to a maximum of four overs. Therefore, when they take more than two wickets, it often means that those wickets are taken in a short period of time, which puts pressure on the batting team. Therefore, the batting team with a new batting pair often plays more cautiously at the beginning of the batting partnership to prevent further collapse of the batting partnership and the team overall [46].
4.3. Fielding
The fielding KPI in the present study was the number of catches taken, similar to the results reported by Irvine and Kennedy [13] and Najdan et al. [15]. Fielding plays a crucial role in supporting bowlers [51]. The number of catches taken is a clear indicator of a fielding team’s strength and tactics [17,51]. Strong fielding support often converts chances into wickets taken, thereby, supporting the bowling effort and maintaining pressure on the opposing team, as well as serving to further uplift the morale of a team [17,51].
While some of the KPIs in the current study have been used in previous research, the novel KPIs included in this study were batting strike rate and the number of overs bowled by seam bowlers in different phases of the game, especially in the last six overs of the second innings. Furthermore, batting strike rate partnerships indicated the scoring abilities of the batsmen, which could be particularly useful in phase-specific strategies in T20 matches [52]. Also, the number of overs bowled by seam bowlers in the last six overs can reveal team strategies and preferences, depending on the pressure dynamics of the game [45].
Most noteworthy, this study analyses the KPIs in both innings, in consideration of the dynamic nature of cricket, and brings this novel perspective to performance analysis in predicting match outcomes. Another novel feature of this study is that it provides context-specific analysis, which assists in understanding the situational relevance of each KPI.
The hybrid model proposed in this study supports the concept of multiple factors and techniques for properly predicting cricket match outcomes [53]. The results of this study are in line with previous studies, where important KPIs have been identified that have a significant effect on cricket match outcomes [54]. This study also reiterates the importance of aggressive batting in the second innings when chasing down formidable target scores [54]. This means that the batting aggressiveness in the second innings may vary for different target scores since the target score achieved in the first innings affects the quality of batting in the second innings [48,49].
4.4. Strengths of the Study
This study contributes to the existing literature on sports analytics and hybrid models, especially in T20 cricket by providing clear definitions for a wide range of performance indicators, including general match indicators, batting, bowling, and fielding. This study is particularly relevant, as it includes novel KPIs, such as batting strike rate and the number of overs bowled by seam bowlers in the different phases of the game, especially in the last six overs of the second innings, which have not been identified in the previous literature. These KPIs provide unique insights into the game, particularly in phase-specific strategies of T20 matches. The study also analyses the KPIs in both innings, considering the dynamic nature of cricket, and brings this novel perspective to performance analysis in predicting match outcomes. Another unique feature of this study is that it provides context-specific analysis, which assists in understanding the situational relevance of each KPI.
4.5. Limitations of the Study
Despite the valuable insights provided by this study, it is not without limitations. Firstly, the number of performance indicators (PIs) exceeds the number of observations (78 matches), which can negatively impact the analysis. Secondly, the dataset is confined specifically to the T20 cricket competition, potentially limiting its applicability to other competitions or women’s cricket, due to differences in playing conditions and strategies. Moreover, the matches used in the study occurred without spectators, during the COVID-19 pandemic, which can influence a home team’s advantage and overall match performance. Finally, the dataset used in the study lacks detailed contextual features, such as pitch conditions, weather conditions, and specific information on deliveries and shots played on the field. Future research should consider incorporating these contextual features to enhance the understanding of field placement strategies against different types of batters to improve prediction accuracy. Furthermore, future research should contemplate including data from diverse T20 leagues, enriching models with context, employing more robust validation strategies, and utilising alternative feature selection methods. Furthermore, Emphasis on interpretability and data integrity will further enhance model utility and practical relevance.
5. Conclusions
In conclusion, the hybrid random forest–lasso logistic regression model developed in the present study to predict cricket match outcomes was found to be robust and identified the significant features that predict cricket match outcomes based on the dynamic nature of the game. This model, therefore, can be used to assist players, teams, and cricket analysts to better understand, visualise, and improve their decision making when preparing for matches. The results of this study can help cricket teams and coaches to better understand the importance of KPIs, which they can utilise for improved decision making and to enhance the likelihood of successful performances. The combined approach in developing the predictive model in this study can also be beneficial in other sports domains, where accurate prediction is needed. Sports analysts, coaches and researchers can use the predicted probabilities of outcome variables to make more accurate predictions in future matches. Furthermore, the model’s predictive accuracy of 85.9% surpasses that of previous approaches using single-model methods, such as logistic regression, random forest, and k-nearest neighbours. This reinforces the model’s comparative strength and suggests that a hybrid approach may offer more reliable insights into T20 match dynamics than single-model methods.
Author Contributions
Conceptualization, R.V.N. and H.C.; methodology, R.V.N., H.C. and C.N.; software, R.V.N. and H.C.; validation, R.V.N., H.C. and M.S.T.; formal analysis, R.V.N. and H.C.; investigation, R.V.N.; resources, R.V.N.; data curation, R.V.N.; writing—original draft preparation, R.V.N.; writing—review and editing, R.V.N., H.C., M.S.T., C.N. and L.L.L.; visualisation, R.V.N.; supervision, L.L.L., H.C., M.S.T. and C.N.; project administration, R.V.N., H.C., M.S.T., C.N. and L.L.L.; funding acquisition, R.V.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Council for Scientific and Industrial Research (CSIR).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Random forest output as a single model.
Table A1.
Random forest output as a single model.
| Performance Indicators | Variable Importance |
|---|---|
| Wicket lost in last six overs (15th–20th) Second Innings | 1.3125 |
| Bowlers taking 2+ wickets Second Innings | 0.9712 |
| Run rate 15th–20th overs Second Innings | 0.8193 |
| Wickets from Seam Second Innings | 0.8120 |
| Strike Rate last six overs 15th–20th overs Second Innings | 0.6538 |
| Inning Single % in ones Second Innings | 0.4848 |
| Wickets from Spin Second Innings | 0.4796 |
| Inning Boundary % in sixes First Innings | 0.4130 |
| Number of sixes First Innings | 0.4100 |
| Overs of seam bowled in last six overs (15th–20th) Second Innings | 0.3167 |
| Run rate 15th–20th overs First Innings | 0.2991 |
| Runs in the last six overs 15th–20th overs First Innings | 0.2911 |
| Sixes in 11th–14th overs First Innings | 0.2821 |
| Strike Rate last six overs 15th–20th overs First Innings | 0.2748 |
| Inning Single % in ones First Innings | 0.2742 |
| Strike Rate 11th–14th overs Second Innings | 0.2685 |
| Runs in the 11th–14th overs Second Innings | 0.2654 |
| Number of fours First Innings | 0.2535 |
| Dot balls in the 11th–14th overs Second Innings | 0.2492 |
| Runs in the 11th–14th overs First Innings | 0.2467 |
| Strike Rate 11th–14th overs First Innings | 0.2291 |
| Partnerships of 50+ runs Second Innings | 0.2186 |
| Inning Boundary % in sixes Second Innings | 0.2170 |
| Total number of catches Second Innings | 0.2157 |
| Dot ball First Innings | 0.2147 |
| Innings Dot ball % First Innings | 0.2098 |
| Dot ball Second Innings | 0.2086 |
| Runs scored by opening partnership First Innings | 0.2048 |
| Power play runs 0th–6th overs First Innings | 0.2047 |
| Total overs of seam bowled Second Innings | 0.1901 |
| Ones in the last six overs 15th–20th overs Second Innings | 0.1858 |
| Wicket lost in overs 7–10 Second Innings | 0.1559 |
| Strike Rate 0th–6th overs First Innings | 0.1550 |
| Dot balls 0th–6th overs First Innings | 0.1502 |
| Number of fours Second Innings | 0.1390 |
| Runs scored by opening partnership Second Innings | 0.1373 |
| Fours in 0th–6th overs First Innings | 0.1323 |
| Number of sixes Second Innings | 0.1298 |
| Number of twos First Innings | 0.1245 |
| Dot balls in the last six overs 15th–20th overs Second Innings | 0.1230 |
| Wickets lost in powerplay First Innings | 0.1228 |
| Dot balls 0th–6th overs Second Innings | 0.1223 |
| Sixes in the last six overs 15th–20th overs First Innings | 0.1202 |
| Ones in 0th–6th overs Second Innings | 0.1196 |
| Runs in the 7th–10th overs Second Innings | 0.1184 |
| Total number of catches First Innings | 0.1146 |
| Strike Rate 7th–10th overs Second Innings | 0.1113 |
| Power play runs 0th–6th overs Second Innings | 0.1087 |
| Number of ones Second Innings | 0.1085 |
| Total number of run outs Second Innings | 0.1036 |
| No Balls First Innings | 0.1013 |
| Sixes in 11th–14th overs Second Innings | 0.0925 |
| Fours in the last six overs 15th–20th overs First Innings | 0.0913 |
| Batsmen scoring 75 + runs Second Innings | 0.0892 |
| Strike Rate 0th–6th overs Second Innings | 0.0881 |
| Fours in 0th–6th overs Second Innings | 0.0857 |
| Wickets lost in powerplay Second Innings | 0.0837 |
| Ones in 7th–10th overs Second Innings | 0.0823 |
| 59 Wickets from Seam First Innings | 0.0816 |
| Total overs of spin bowled Second Innings | 0.0809 |
| Ones in 7th–10th overs First Innings | 0.0765 |
| Partnerships of 25–49 runs Second Innings | 0.0749 |
| Wickets from Spin First Innings | 0.0717 |
| Sixes in the last six overs 15th–20th overs Second Innings | 0.0716 |
| Number of threes Second Innings | 0.0707 |
| Runs in the last six overs 15th–20th overs Second Innings | 0.0696 |
| Batsmen scoring 50–74 runs First Innings | 0.0695 |
| Wicket lost in overs 7–10 First Innings | 0.0676 |
| Ones in 0th–6th overs First Innings | 0.0675 |
| Batsmen scoring 50–74 runs Second Innings | 0.0673 |
| Wicket lost in overs 11–14 Second Innings | 0.0670 |
| Bowlers taking 2+ wickets First Innings | 0.0651 |
| Partnerships of 50+ runs First Innings | 0.0639 |
| Number of fives First Innings | 0.0615 |
| Number of fives Second Innings | 0.0608 |
| LegByes Second Innings | 0.0599 |
| Partnerships of 25–49 runs First Innings | 0.0595 |
| Total number of run outs First Innings | 0.0595 |
| Overs of spin bowled in last six overs (15th–20th) Second Innings | 0.0581 |
| Fours in 7th–10th overs Second Innings | 0.0579 |
| Fours in the last six overs 15th–20th overs Second Innings | 0.0564 |
| Batsmen scoring 75+ runs First Innings | 0.0563 |
| Wicket lost in last six overs (15th–20th) First Innings | 0.0549 |
| Byes Second Innings | 0.0541 |
| Overs of seam bowled in overs 7–10 Second Innings | 0.0519 |
| Dot balls in the 7th–10th overs Second Innings | 0.0515 |
| Innings Dot ball % Second Innings | 0.0508 |
| LegByes First Innings | 0.0482 |
| Batsmen scoring 25–49 runs Second Innings | 0.0468 |
| Number of threes First Innings | 0.0465 |
| Sixes in 7th–10th overs First Innings | 0.0453 |
| Ones in the last six overs 15th–20th overs First Innings | 0.0451 |
| Wicket lost in overs 11–14 First Innings | 0.0442 |
| Overs of seam bowled in powerplay Second Innings | 0.0427 |
| Fours in 11th–14th overs Second Innings | 0.0423 |
| Dot balls in the 7th–10th overs First Innings | 0.0416 |
| Sixes in 0th–6th overs Second Innings | 0.0405 |
| Number of ones First Innings | 0.0387 |
| Overs of spin bowled in powerplay First Innings | 0.0380 |
| Byes First Innings | 0.0377 |
| No Balls Second Innings | 0.0360 |
| Batsmen scoring 25–49 runs First Innings | 0.0356 |
| Sixes in 7th–10th overs Second Innings | 0.0343 |
| Overs of spin bowled in overs 7–10 Second Innings | 0.0342 |
| Sixes in 0th–6th overs First Innings | 0.0339 |
| Overs of seam bowled in last six overs (15th–20th) First Innings | 0.0332 |
| Overs of seam bowled in powerplay First Innings | 0.0328 |
| Overs of seam bowled in overs 7–10 First Innings | 0.0318 |
| Overs of spin bowled in overs 7–10 First Innings | 0.0312 |
| Fours in 11th–14th overs First Innings | 0.0306 |
| Overs of seam bowled in overs 11–14 Second Innings | 0.0290 |
| Overs of spin bowled in last six overs (15th–20th) First Innings | 0.0287 |
| Overs of spin bowled in overs 11–14 First Innings | 0.0283 |
| Total overs of seam bowled First Innings | 0.0279 |
| Innings boundary % in fours Second Innings | 0.0266 |
| Overs of seam bowled in overs 11–14 First Innings | 0.0265 |
| Overs of spin bowled in powerplay Second Innings | 0.0263 |
| Extras Second Innings | 0.0258 |
| Strike Rate 7th–10th overs First Innings | 0.0245 |
| Dot balls in the last six overs 15th–20th overs First Innings | 0.0237 |
| Fours in 7th–10th overs First Innings | 0.0233 |
| Overs of spin bowled in overs 11–14 Second Innings | 0.0233 |
| Dot balls in the 11th–14th overs First Innings | 0.0231 |
| Extras First Innings | 0.0227 |
| Total overs of spin bowled First Innings | 0.0226 |
| Wides Second Innings | 0.0183 |
| Ones in 11th–14th overs Second Innings | 0.0178 |
| Innings boundary % in fours First Innings | 0.0159 |
| Ones in 11th–14th overs First Innings | 0.0109 |
| Runs in the 7th–10th overs First Innings | 0.0053 |
| Number of twos Second Innings | 0.0020 |
| Wides First Innings | 0.0020 |

Table A2.
Lasso logistic regression.
Table A2.
Lasso logistic regression.
| Performance Indicators | Feature Coefficient |
|---|---|
| Wicket lost in last six overs (15th–20th) Second Innings | 0.50114 |
| Bowlers taking 2+ wickets Second Innings | 0.25384 |
| Run rate 15th–20th overs Second Innings | 0.15770 |
| Wickets from Seam Second Innings | 0.12563 |
| Inning Single % in ones Second Innings | 0.11829 |
| Sixes in 11th–14th overs First Innings | 0.11057 |
| Wickets from Spin Second Innings | 0.07084 |
| Batting Strike Rate last six overs 15th–20th overs Second Innings | 0.01158 |
| Inning Boundary % in sixes First Innings | –0.01141 |
| Overs of seam bowled in last six overs (15th–20th) Second Innings | –0.01299 |
| Strike Rate last six overs 15th–20th overs First Innings | –0.02058 |
| Runs in the last six overs 15th–20th overs First Innings | –0.05339 |
| Total number of catches in Second Innings | –0.06194 |
| Number of sixes First Innings | –0.08274 |
| Run rate 15th–20th overs First Innings | –0.09664 |
| Partnerships of 50+ runs in the Second Innings | –0.13322 |
| Strike Rate 0th–6th overs First Innings | –0.14433 |
| Power play runs 0th–6th overs First Innings | –0.19465 |

Table A3.
Hybrid model approach retrained output.
Table A3.
Hybrid model approach retrained output.
| Performance Indicators | Importance |
|---|---|
| Wicket lost in last six overs (15th–20th) Second Innings | 0.02613 |
| Bowlers taking 2+ wickets Second Innings | 0.01957 |
| Run rate 15th–20th Overs Second Innings | 0.01302 |
| Wickets from Seam Second Innings | 0.01216 |
| Strike Rate last six overs 15th–20th overs Second Innings | 0.00916 |
| Inning Single % in ones Second Innings | 0.00729 |
| Wickets from Spin Second Innings | 0.00542 |
| Inning Boundary % in sixes First Innings | 0.00469 |
| Number of sixes First Innings | 0.00392 |
| Overs of seam bowled in last six overs (15th–20th) Second Innings | 0.00355 |
| Runs in the last six overs 15th–20th overs First Innings | 0.00344 |
| Strike Rate last six overs 15th–20th overs First Innings | 0.00341 |
| Sixes in 11th–14th overs First Innings | 0.00262 |
| Inning Single % in ones First Innings | 0.00260 |
| Number of fours First Innings | 0.00244 |
| Run rate 15th–20th overs First Innings | 0.00230 |
| Total number of catches Second Innings | 0.00221 |
| Strike Rate 11th–14th overs First Innings | 0.00205 |
| Dot balls in the 11th–14th overs Second Innings | 0.00191 |
| Strike Rate 11th–14th overs Second Innings | 0.00179 |
| Runs in the 11th–14th overs First Innings | 0.00178 |
| Runs in the 11th–14th overs Second Innings | 0.00170 |
| Dot ball Second Innings | 0.00143 |
| Partnerships of 50+ runs Second Innings | 0.00141 |
| Strike Rate 0th–6th overs First Innings | 0.00140 |
| Innings Dot ball % First Innings | 0.00139 |
| Runs scored by opening partnership First Innings | 0.00137 |
| Dot balls 0th–6th overs First Innings | 0.00128 |
| Dot ball First Innings | 0.00117 |
| Ones in the last six overs 15th–20th overs Second Innings | 0.00109 |
| Inning Boundary % in sixes Second Innings | 0.00101 |
| Power play runs 0th–6th overs First Innings | 0.00096 |
| Wicket lost in overs 7–10 Second Innings | 0.00088 |
| Number of twos First Innings | 0.00085 |
| Number of fours Second Innings | 0.00082 |
| Dot balls 0th–6th overs Second Innings | 0.00075 |
| Total overs of seam bowled Second Innings | 0.00072 |
| Ones in 0th–6th overs Second Innings | 0.00067 |
| Fours in 0th–6th overs First Innings | 0.00065 |
| wickets lost in powerplay First Innings | 0.00058 |
| Number of sixes Second Innings | 0.00048 |
| Dot balls in the last six overs 15th–20th overs Second Innings | 0.00042 |
| Runs scored by opening partnership Second Innings | 0.00042 |
| Sixes in the last six overs 15th–20th overs First Innings | 0.00036 |
| Ones in 7th–10th overs Second Innings | 0.00036 |
| Strike Rate 7th–10th overs Second Innings | 0.00030 |
| Fours in 0th–6th overs Second Innings | 0.00029 |
| Total number of run outs Second Innings | 0.00027 |
| Ones in 0th–6th overs First Innings | 0.00027 |
| No Balls First Innings | 0.00027 |
| Total overs of spin bowled Second Innings | 0.00021 |
| Number of threes Second Innings | 0.00020 |
| wickets lost in powerplay Second Innings | 0.00020 |
| Runs in the 7th–10th overs Second Innings | 0.00020 |
| Sixes in 11th–14th overs Second Innings | 0.00019 |
| Innings Dot ball % Second Innings | 0.00019 |
| Number of ones Second Innings | 0.00018 |
| Partnerships of 25–49 runs Second Innings | 0.00017 |
| Strike Rate 0th–6th overs Second Innings | 0.00017 |
| Batsmen scoring 50–74 runs First Innings | 0.00014 |
| Power play runs 0th–6th overs Second Innings | 0.00013 |
| Batsmen scoring 75+ runs Second Innings | 0.00012 |
| Sixes in the last six overs 15th–20th overs Second Innings | 0.00009 |
| Batsmen scoring 25–49 runs Second Innings | 0.00009 |
| Total number of catches First Innings | 0.00007 |
| Ones in 7th–10th overs First Innings | 0.00004 |
| Batsmen scoring 50–74 runs Second Innings | 0.00004 |
| Bowlers taking 2+ wickets First Innings | 0.00004 |
| Wickets from Spin First Innings | 0.00003 |
| Fours in the last six overs 15th–20th overs First Innings | 0.00002 |
| LegByes Second Innings | 0.00002 |
| Wickets from Seam First Innings | 0.00002 |
| Overs of seam bowled in powerplay Second Innings | 0.00001 |
| Partnerships of 50+ runs First Innings | 0.00000 |
| Number of fives First Innings | 0.00000 |
| Number of fives Second Innings | 0.00000 |
| Wicket lost in overs 7–10 First Innings | −0.00001 |
| Overs of spin bowled in overs 7–10 Second Innings | −0.00001 |
| Ones in the last six overs 15th–20th overs First Innings | −0.00001 |
| Partnerships of 25–49 runs First Innings | −0.00001 |
| Fours in 7th–10th overs First Innings | −0.00001 |
| Batsmen scoring 75+ runs First Innings | −0.00002 |
| Wicket lost in overs 11–14 Second Innings | −0.00004 |
| Number of ones First Innings | −0.00005 |
| Fours in 7th–10th overs Second Innings | −0.00005 |
| Overs of seam bowled in last six overs (15th–20th) First Innings | −0.00005 |
| Overs of spin bowled in overs 11–14 First Innings | −0.00005 |
| Dot balls in the last six overs 15th–20th overs First Innings | −0.00005 |
| Sixes in 7th–10th overs First Innings | −0.00007 |
| Wicket lost in last six overs (15tht–20h) First Innings | −0.00007 |
| Wicket lost in overs 11–14 First Innings | −0.00007 |
| Dot balls in the 7th–10th overs Second Innings | −0.00008 |
| Overs of spin bowled in last six overs (15th–20th) Second Innings | −0.00008 |
| Sixes in 0th–6th overs Second Innings | −0.00009 |
| Total number of run outs First Innings | −0.00009 |
| Number of twos Second Innings | −0.00009 |
| Fours in 11th–14th overs Second Innings | −0.00009 |
| Number of threes First Innings | −0.00010 |
| LegByes First Innings | −0.00010 |
| Byes Second Innings | −0.00010 |
| Overs of spin bowled in overs 11–14 Second Innings | −0.00011 |
| Overs of seam bowled in powerplay First Innings | −0.00011 |
| Overs of seam bowled in overs 7–10 Second Innings | −0.00013 |
| Overs of seam bowled in overs 11–14 Second Innings | −0.00013 |
| Overs of spin bowled in overs 7–10 First Innings | −0.00014 |
| Sixes in 7th–10th overs Second Innings | −0.00014 |
| Ones in 11th–14th overs First Innings | −0.00014 |
| Fours in the last six overs 15th–20th overs Second Innings | −0.00014 |
| Dot balls in the 7th–10th overs First Innings | −0.00015 |
| Overs of seam bowled in overs 7–10 First Innings | −0.00015 |
| Overs of spin bowled in powerplay Second Innings | −0.00015 |
| Wides Second Innings | −0.00016 |
| Runs in the 7th–10th overs First Innings | −0.00016 |
| Overs of spin bowled in powerplay First Innings | −0.00017 |
| Innings boundary % in fours Second Innings | −0.00017 |
| Sixes in 0th–6th overs First Innings | −0.00019 |
| Byes First Innings | −0.00019 |
| Overs of seam bowled in overs 11–14 First Innings | −0.00019 |
| No Balls Second Innings | −0.00020 |
| Total overs of spin bowled First Innings | −0.00020 |
| Overs of spin bowled in last six overs (15th–20th) First Innings | −0.00021 |
| Batsmen scoring 25–49 runs First Innings | −0.00023 |
| Wides First Innings | −0.00024 |
| Runs in the last six overs 15th–20th overs Second Innings | −0.00024 |
| Total overs of seam bowled First Innings | −0.00024 |
| Extras First Innings | −0.00024 |
| Strike Rate 7th–10th overs First Innings | −0.00026 |
| Dot balls in the 11th–14th overs First Innings | −0.00028 |
| Extras Second Innings | −0.00028 |
| Ones in 11th–14th overs Second Innings | −0.00029 |
| Fours in 11th–14th overs First Innings | −0.00033 |
| Innings boundary % in fours First Innings | −0.00035 |
References
- Anuraj, A.; Boparai, G.S.; Leung, C.K.; Madill, E.W.; Pandhi, D.A.; Patel, A.D.; Vyas, R.K. Sports data mining for cricket match prediction. In Advanced Information Networking and Applications; Barolli, L., Ed.; Springer: Cham, Switzerland, 2023; pp. 668–680. [Google Scholar] [CrossRef]
- Noorbhai, H. Cricket coaching and batting in the 21st century through a 4IR lens: A narrative review. BMJ Open Sport Exerc. Med. 2022, 8, e001435. [Google Scholar] [CrossRef] [PubMed]
- Colomer, C.M.; Pyne, D.B.; Mooney, M.; McKune, A.; Serpell, B.G. Performance analysis in rugby union: A critical systematic review. Sports Med.-Open 2020, 6, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Lord, F.; Pyne, D.B.; Welvaert, M.; Mara, J.K. Field hockey from the performance analyst’s perspective: A systematic review. Int. J. Sports Sci. Coach. 2022, 17, 220–232. [Google Scholar] [CrossRef]
- Vella, A.; Clarke, A.C.; Kempton, T.; Ryan, S.; Coutts, A.J. Assessment of physical, technical, and tactical analysis in the Australian football league: A systematic review. Sports Med.-Open 2022, 8, 124. [Google Scholar] [CrossRef]
- Hughes, M.; Franks, I.; Franks, I.M.; Dancs, H. (Eds.) Essentials of Performance Analysis in Sport; Routledge: London, UK, 2019. [Google Scholar] [CrossRef]
- Lees, A. Science and the major racket sports: A review. J. Sports Sci. 2003, 21, 707–732. [Google Scholar] [CrossRef]
- Hughes, M.D.; Bartlett, R.M. The use of performance indicators in performance analysis. J. Sports Sci. 2002, 20, 739–754. [Google Scholar] [CrossRef]
- Wright, C.; Atkins, S.; Jones, B. An analysis of elite coaches’ engagement with performance analysis services. Int. J. Perform. Anal. Sport 2012, 12, 436–451. [Google Scholar] [CrossRef]
- Mittal, H.; Rikhari, D.; Kumar, J.; Singh, A.K. A study on machine learning approaches for player performance and match results prediction. arXiv 2021, arXiv:2108.10125.2021. [Google Scholar]
- Bhardwaj, D.; Dwyer, D.B. Team technical performance in elite men’s and women’s T20 cricket–determinants of performance within a match and across a season. Int. J. Perform. Anal. Sport 2022, 22, 277–290. [Google Scholar] [CrossRef]
- Douglas, M.J.; Tam, N. Analysis of team performances at the ICC World Twenty20 Cup 2009. Int. J. Perform. Anal. Sport 2010, 10, 47–53. [Google Scholar] [CrossRef]
- Irvine, S.; Kennedy, R. Analysis of performance indicators that most significantly affect International Twenty20 cricket. Int. J. Perform. Anal. Sport 2017, 17, 350–359. [Google Scholar] [CrossRef]
- Moore, A.; Turner, J.D.; Johnstone, A.J. A preliminary analysis of team performance in English first-class Twenty-Twenty (T20) cricket. Int. J. Perform. Anal. Sport 2012, 12, 188–207. [Google Scholar] [CrossRef]
- Najdan, J.M.; Robins, T.M.; Glazier, S.P. Determinants of success in English domestic Twenty20 cricket. Int. J. Perform. Anal. Sport 2014, 14, 276–295. [Google Scholar] [CrossRef]
- Petersen, C.; Pyne, D.B.; Portus, M.J.; Dawson, B. Analysis of Twenty/20 Cricket performance during the 2008 Indian Premier League. Int. J. Perform. Anal. Sport 2008, 8, 63–69. [Google Scholar] [CrossRef]
- Scholes, R.; Shafizadeh, M. Prediction of successful performance from fielding indicators in cricket: Champions League T20 tournament. Sports Technol. 2014, 7, 62–68. [Google Scholar] [CrossRef]
- Parmar, N.; James, N.; Hughes, M.; Jones, H.; Hearne, G. Team performance indicators that predict match outcome and points difference in professional rugby league. Int. J. Perform. Anal. Sport 2017, 17, 1044–1056. [Google Scholar] [CrossRef]
- Rouam, S. False Discovery Rate (FDR). In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.H., Yokota, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 731–736. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 6th ed.; Pearson: Boston, MA, USA, 2013; pp. 481–498. [Google Scholar]
- Saikia, H.; Bhattacharjee, D.; Radhakrishnan, U.K. A new model for player selection in cricket. Int. J. Perform. Anal. Sport 2016, 16, 373–388. [Google Scholar] [CrossRef]
- Zhou, F.; Fan, H.; Liu, Y.; Zhang, H.; Ji, R. Hybrid model of machine learning method and empirical method for rate of penetration prediction based on data similarity. Appl. Sci. 2023, 13, 5870. [Google Scholar] [CrossRef]
- Lewis, A.J. Towards fairer measures of player performance in one-day cricket. J. Oper. Res. Soc. 2005, 56, 804–815. [Google Scholar] [CrossRef]
- Shah, P.; Shah, M. Pressure Index in Cricket. IOSR J. Sports Phys. Educ. 2014, 1, 9–11. [Google Scholar] [CrossRef]
- Lohse, K.R.; Sainani, K.L.; Taylor, J.A.; Butson, M.L.; Knight, E.J.; Vickers, A.J. Systematic review of the use of “magnitude-based inference” in sports science and medicine. PLoS ONE 2020, 15, e0235318. [Google Scholar] [CrossRef] [PubMed]
- McLean, S.; Kerhervé, H.A.; Stevens, N.; Salmon, P.M. A systems analysis critique of sport-science research. Int. J. Sports Physiol. Perform. 2021, 16, 1385–1392. [Google Scholar] [CrossRef] [PubMed]
- Saikia, H.; Bhattacharjee, D.; Mukherjee, D. Cricket Performance Management: Mathematical Formulation and Analytics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 37–94. [Google Scholar] [CrossRef]
- Starbuck, C. Research Design. In The Fundamentals of People Analytics: With Applications in R; Springer International Publishing: Cham, Switzerland, 2023; pp. 51–57. [Google Scholar] [CrossRef]
- ESPNcricinfo 2021. Available online: https://www.espncricinfo.com/ (accessed on 28 April 2024).
- Cricsheet. T20 Cricket. Available online: https://cricsheet.org/ (accessed on 1 July 2021).
- Kordzadeh, N.; Ghasemaghaei, M. Algorithmic bias: Review, synthesis, and future research directions. Eur. J. Inf. Syst. 2022, 31, 388–409. [Google Scholar] [CrossRef]
- RStudio Open Source & Professional Software for Data Science Teams. Available online: https://www.rstudio.com/ (accessed on 1 September 2022).
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining (Intelligent Systems Reference Library); Springer: Berlin/Heidelberg, Germany, 2015; pp. 36–55. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Rokach, L. Decision forest: Twenty years of research. Inf. Fusion 2016, 27, 111–125. [Google Scholar] [CrossRef]
- Van Witteloostuijn, A.; Kolkman, D. Is firm growth random? A machine learning perspective. J. Bus. Ventur. Insights 2019, 11, e00107. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 337–387. Available online: https://www.sas.upenn.edu/~fdiebold/NoHesitations/BookAdvanced.pdf (accessed on 29 April 2024).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Raju, V.S.; Sethi, N.; Rajender, R. A Review of Data Analytic Schemes for Prediction of Vivid Aspects in International Cricket Matches. In Proceedings of the 2019 5th International Conference on Computing, Communication, Control and Automation (ICCUBEA), Pune, India, 19–21 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Wickramasinghe, I. Applications of Machine Learning in cricket: A systematic review. Mach. Learn. Appl. 2022, 10, 100435. [Google Scholar] [CrossRef]
- Ahmed, W. A Multivariate Data Mining Approach to Predict Match Outcome in One-Day International Cricket. Master’s Dissertation, Karachi Institute of Economics and Technology, Karachi, Pakistan, 2015. [Google Scholar]
- Tripathi, A.; Islam, R.; Khandor, V.; Murugan, V. Prediction of IPL matches using Machine Learning while tackling ambiguity in results. Indian J. Sci. Technol. 2020, 13, 4013–4035. [Google Scholar] [CrossRef]
- Kapadia, K.; Abdel-Jaber, H.; Thabtah, F.; Hadi, W. Sport analytics for cricket game results using machine learning: An experimental study. Appl. Comput. Inform. 2022, 18, 256–266. [Google Scholar] [CrossRef]
- Rahman, M.M.; Shamim, M.O.; Ismail, S. An analysis of Bangladesh one day international cricket data: A machine learning approach. In Proceedings of the 2018 International Conference on Innovations in Science, Engineering and Technology (ICISET), Kuala Lumpur, Malaysia, 27–28 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 190–194. [Google Scholar]
- Petersen, C.J. Comparison of performance at the 2007 and 2015 Cricket World Cups. Int. J. Sports Sci. Coach. 2017, 12, 404–410. [Google Scholar] [CrossRef]
- Jamil, M.; Kerruish, S.; Mehta, S.; Phatak, A.; Memmert, D.; McRobert, A. Identifying which factors impact bowling and batting performances during the “death” phase of an innings in international men’s 50-over cricket. Int. J. Perform. Anal. Sport 2023, 23, 111–124. [Google Scholar] [CrossRef]
- Modekurti, D.P. Setting final target score in T-20 cricket match by the team batting first. J. Sports Anal. 2020, 17, 205–213. [Google Scholar] [CrossRef]
- Ahmed, S. Game Theory in Cricket [Honours Thesis]. Colby University, USA. 2019. Available online: https://digitalcommons.colby.edu/honorstheses/918 (accessed on 28 April 2024).
- Talukdar, P. Investigating the Role of Opening Partners While Chasing on the Outcome of Twenty 20 Cricket Matches. Manag. Labour Stud. 2020, 45, 222–232. [Google Scholar] [CrossRef]
- Brown, P. Optimising Batting Partnership Strategy in the First Innings of a Limited Overs Cricket Match. Doctoral Dissertation, Victoria University of Wellington, Wellington, New Zealand, 2017. [Google Scholar]
- MacDonald, D.C.; Cronin, J.; Mills, J.; McGuigan, M.; Stretch, R. A review of cricket fielding requirements. S. Afr. J. Sports Med. 2013, 25, 87. [Google Scholar] [CrossRef]
- Norman, J.M.; Clarke, S.R. Dynamic programming in cricket: Optimizing batting order for a sticky wicket. J. Oper. Res Soc. 2007, 58, 1678–1682. [Google Scholar] [CrossRef]
- Davis, J.; Perera, H.; Swartz, T.B. A simulator for Twenty20 cricket. Aust. N. Z. J. Stat. 2015, 57, 55–71. [Google Scholar] [CrossRef]
- Perera, H.; Gill, P.S.; Swartz, T.B. Declaration guidelines in test cricket. J. Quant. Anal. Sports. 2014, 10, 15–26. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).