Abstract
Bicycle riding requires a high standard width and continuity of lanes, as an appropriate width directly improves the service level of the lanes. Therefore, the width of bicycle lanes should be designed considering the characteristics of the bicycle traffic flow and the actual conditions of an area. In order to explore the relationship between bicycle traffic flow characteristics and lane width, this study references the vehicle traffic flow model and introduces the concept of bicycle traffic flow width, defined as the average width of bicycle traffic flow over a certain distance in a unit of time. Based on measured data, this study analyzes the relationships among bicycle traffic flow, lane width, and other parameters. The research results show that when the bicycle lane width is between 2.0 and 3.4 m, there is a clear linear relationship between the speed of bicycle traffic flow and the traffic flow width, with bicycle traffic flow width increasing as speed increases. Furthermore, overly wide bicycle lanes can result in more instances of bicycle over-speeding. These findings will guide the design of bicycle lanes.
1. Introduction
As a general rule, the width of a bicycle lane depends on the standard specification of road construction. For vehicles, the width of a lane is decided based on vehicle traffic flow characteristics. But for a bicycle lane, bicycle flow characteristics are completely neglected. Even the standard specifications of road construction are not uniform [1]. Therefore, this paper focuses on the characteristics of bicycle traffic flow and their relationship with bicycle traffic flow width.
Many studies have focused on modeling vehicle traffic flow, which motivates us to develop a bicycle traffic flow model based on the same principle. We also need to consider a mixed bicycle traffic flow, which refers to a traffic flow composed of both mechanical and electric bicycles. Traffic flow models can generally be divided into macroscopic and microscopic models [2]. Macroscopic traffic flow is the study of the relationships among density, flow, and speed under different conditions. Microscopic traffic flow models are employed to characterize the interactions between individual vehicles. For instance, the car-following model—a typical example of microscopic traffic flow models—describes the microscopic movements of adjacent vehicles operating within the same lane. In contrast, this paper focuses on macroscopic traffic flow models. Currently, there are numerous studies on macroscopic traffic flow models for bicycles. Smith Jr. [3] investigated the relationships among the flow, density, and speed of bicycles. Navin [4] experimentally studied the speed–flow relationship of bicycles. In the research realm of bicycle traffic in China, Peng and Yang [5] established the first bicycle traffic flow model. Zhu and Chi [6] defined the density of vehicles in a lane of unit area as the density of mixed bicycle traffic flow. This definition played a crucial role in subsequent studies on bicycle traffic flow in China. Hui et al. [7] conducted statistical analysis on vehicle speeds on actual road segments, and constructed a traffic flow model. Dan [8] used mathematical and statistical methods to study the speed–flow relationship of mechanical bicycles, electric bicycles, and mixed bicycles on physically separated road sections, with varying proportions of mixed electric bicycles. Based on the characteristics of mixed bicycle traffic flow, Zhou et al. [9] introduced a logistic model and established mathematical models for describing the flow–density relationship of mixed bicycle traffic. Liu et al. [10] used video analysis systems to analyze the characteristics of mixed bicycle traffic in bicycle lanes in peak periods. These studies enriched the theory of macroscopic bicycle traffic flow.
However, the above studies rarely described any variation in the width of bicycle traffic flow under different conditions. In vehicle traffic flow, the three primary variables, also known as the three macroscopic parameters, are flow, speed, and density. Through observation, it was found that under high bicycle traffic flow density, cyclists do not exhibit distinct queuing behavior as motor vehicles do. Instead, when encountering slower-moving vehicles ahead, some cyclists deviate from the designated non-motor-vehicle lane by crossing the isolation line to utilize motor vehicle lanes for overtaking, thereby inducing lateral variations in traffic flow patterns. Therefore, it is necessary to consider the width of the bicycle traffic flow. This parameter is crucial for analyzing the relationship between bicycle traffic flow and bicycle lane width. Maria J. Wierbos investigated the relationship between capacity and path width through a controlled bottleneck experiment in Delft in the Netherlands. A key finding of their study was the positive linear correlation between bicycle lane capacity and lane width. Specifically, within the width range of 0.50 to 1.50 m, each additional meter of bicycle lane width corresponds to a capacity increase of 1.11 bicycles per second [11]. Sebastian Seriani [12] also identified a linear correlation between bicycle flow and bicycle lane width in his research. Additionally, bicycle traffic flow is influenced by many other factors, such as the performance differences between bicycles, and subjective and objective differences among riders [13,14,15]. These factors not only affect the longitudinal flow, but also cause variations in the lateral width of the traffic flow. Therefore, the establishment of a model to describe the variations in the width of bicycle traffic flow will not only enhance our understanding about the operational mechanisms of bicycle traffic flow, but also lay a foundation for the design of urban bicycle lanes.
In summary, this paper proposes a research methodology based on the macroscopic bicycle traffic flow model to investigate the relationships between the three parameters of bicycle traffic flow—speed, density, and flow—and the width of bicycle traffic flow. The objective is to provide theoretical support for the width design of urban non-motor-vehicle lanes. The established bicycle traffic speed–width model enables the analysis of maximum and minimum traffic flow width variations under peak-hour conditions based on bicycle flow characteristics across different urban road segments. This facilitates the design of optimal bicycle lane widths that meet practical non-motorized travel demands for various road sections. This research provides technical support for optimizing bicycle lane dimensions in aging urban areas or roads where widening is not feasible. Since no work could be found in the specialized literature considering the width of bicycle traffic flow as a parameter, this paper introduces a definition of the width of bicycle traffic flow as the average lateral extent of bicycle traffic flow passing through a given distance within a unit of time.
2. Data Collection
Based on related research [16,17], the selection of sampling survey locations in this paper follows the following principles: (1) the selected road segments should exhibit significant variation in bicycle lane width; (2) segments with facilities that may interfere with bicycle traffic, such as bus stops, were excluded; (3) the separation method of bicycle lanes must be soft isolation (e.g., by road markings), rather than physical barriers such as curbs or fences, as hard isolation would prevent lateral variation in bicycle traffic flow. Sampling was conducted during peak hours to capture the typical characteristics of bicycle traffic flow.
Most bicycle lanes are separated using marking lines. In this study, we focus on bicycle lanes that utilize isolating line markings. There are two key reasons for this choice. Firstly, most urban roads employ isolating line markings for bicycle lanes; lanes separated by green plants or footpaths are less prevalent and often involve higher maintenance costs. Secondly, isolating line markings do not rigidly separate bicycle traffic flow from vehicle traffic flow. Under certain conditions, bicycles may be allowed to cross the line and enter motor vehicle lanes, thereby introducing more lateral variability to bicycle traffic flow.
Based on these considerations, six road sections were ultimately selected for this study, as presented in Table 1. The surveys were conducted on Tuesday, Wednesday, and Thursday mornings from 7:30 to 8:30 a.m., under clear weather conditions.

Table 1.
Road section information.
3. Data Extraction
The traffic flow data collected for this study included the speed, flow rate, density, and traffic flow width of bicycles, and the counts of bicycles crossing the lane and entering motor vehicle lanes. The variable “the counts of bicycles crossing the lane and entering motor vehicle lanes” refers to situations where non-motorized vehicles temporarily leave their designated lanes to overtake slower-moving vehicles or respond to special circumstances. Typically, these vehicles return to non-motorized lanes after completing overtaking maneuvers (though some faster electric bicycles may persistently occupy motor vehicle lanes, a behavior that visibly reflects their speed relative to the width of non-motorized traffic flow). Specifically, while we recorded the furthest and closest lateral positions of bicycles to the curb within 30 s intervals, we also noted instances when bicycles crossed into the adjacent motor vehicle lane. By quantifying this variable, we can not only determine when non-motorized traffic flow reaches its maximum width, but also analyze how lane-crossing behavior correlates with traffic speed, density, and flow under varying conditions. This analysis provides theoretical reference for improving the management of cycling behaviors.
In order to obtain bicycle speeds, this research employed the simulation coil method, which extracts relevant data from roadside video recordings. Specifically, the simulation coil method involves placing two white adhesive tapes on the ground perpendicular to the travel direction at each survey section, serving as the survey reference lines. The distance between these two reference lines was set at 10 m, and the survey area was confined to the space within these reference lines, as depicted in Figure 1.

Figure 1.
Schematic diagram of simulation coil method.
- Speed of bicycle
In this work, the potplayer software (version 1.7) was used to play the video frame-by-frame to extract bicycle speed. The rate of movement of the frames at which the front wheel of a bicycle reached the first white tape was recorded as f1, and the rate at which it reached the second white tape was recorded as f2. Accordingly, the speed of the bicycle can be calculated using Equation (1).
where s is the distance traveled by the bicycle through the test segment, which is 10 m, and f is the frame rate of the video.
- 2.
- Bicycle traffic flow rate
The bicycle flow rate is obtained by dividing the number of standard bicycles passing through a certain section by the width of the lane within a unit time interval. There are studies which indicate that different sampling time intervals have a significant impact on the results. If the statistical interval is too short, the volatility of traffic flow will increase, resulting in poor stability of traffic flow. However, if the statistical interval is too long, the density level will be “averaged” out, masking changes in vehicle concentration states, which is not conducive to studying the characteristics of traffic flow under different congestion conditions [18]. Therefore, combining the findings reported in the literature with the actual situation, this article sets the sampling time interval to 30 s. Considering that n1 mechanical bicycles and n2 electric bicycles passed during this period, the bicycle flow rate can be calculated using Equation (2).
where BE is the conversion coefficient for electric bicycles [19] and w is the width of the lane (m).
- 3.
- Bicycle traffic flow density
Due to the lack of strict lane division for bicycles, surface density is used to represent the bicycle traffic flow density, which is defined as the number of bicycles per unit area at a certain moment, with a sampling time interval of 30 s. Within each sampling interval, the number of mechanical and electric bicycles is recorded every 5 s. The average of six such records is taken as the density for that period, which is represented by k and expressed as in Equation (3).
where n is the number of bicycles within the observation range at a certain moment, and w is the width of the lane (m).
- 4.
- Width of bicycle lane
In order to satisfy the sampling requirements for calculating the speed, flow, and density of bicycle traffic, this article adopted a sampling time interval of 30 s. Furthermore, the original bicycle lane was segmented into lanes with a width interval of 1 m using previously calibrated reference objects on the sections of the bicycle lane. Taking a 3.3 m wide bicycle lane as an example, the lane was divided into three 1 m wide bicycle lanes (denoted as L1, L2, and L3) and one 0.3 m wide L-boundary lane (denoted as LB) starting from the curb. If the width of the lane can be divided evenly into integer lanes, an L-boundary lane need not be created. This approach was applied to other roads also, as shown in Figure 2. Additionally, the scenario where bicycles cross into other lanes is denoted as CL (crossing the lane).

Figure 2.
Lane division diagram.
Then, the distribution of the positions of the bicycle flow within each sampling interval was observed and measured. The average width of the bicycle flow in a sampling interval is calculated using Equation (4).
where wt is the average width of the bicycle flow in the t-th time interval, Lik is the width of the k-th subdivided lane occupied by the i-th bicycle, and n is the total number of bicycles passing through in that time interval.
This study defines the width of bicycle flow as the average width of the bicycle traffic flow passing through a certain distance within a unit of time. It is measured from the curb to the position of the outermost bicycle in the observation section. This study first categorizes common mixed bicycle flow widths based on whether they exceed the width of the designated bicycle lane. Specifically, the common mixed bicycle flow is classified into four states based on the positions of the bicycles on the road: unsaturated state, saturated state, supersaturated state, and random riding state, as shown in Figure 3.

Figure 3.
Four states of mixed traffic flow.
The unsaturated state refers to the ideal condition where the width of the mixed bicycle flow on a road segment during peak hours is less than the width of the bicycle lane, and few instances of bicycles crossing the lane and entering the motor vehicle lane are observed. The saturated state occurs when the width of mixed bicycle flow on a road segment during peak hours is less than or slightly greater than the width of the bicycle lane, with a small number of bicycles entering the motor vehicle lane. The supersaturated state is characterized by frequent occurrences of bicycles crossing the lane and entering the motor vehicle lane during peak hours, indicating that the width of the mixed bicycle flow exceeds the width of the bicycle lane. The random riding state describes a situation where the position of bicycle riding exhibits no fixed pattern during peak hours, but is determined solely by the rider’s own habits, which may negatively impact traffic safety and efficiency.
Through video analysis, it can be observed that when the bicycle traffic flow during peak hours exhibits a saturated or unsaturated state, this indicates that the width design of the bicycle lane in this road segment meets the actual travel demand of the bicycle traffic flow. When an unsaturated state occurs, this indicates that the designed width of the lane exceeds the actual riding demand. Conversely, the supersaturated state reveals that the width of the bicycle lane on the segment is relatively narrow and does not adequately meet the actual riding demand. Furthermore, this paper also finds that when the traffic volume in a bicycle lane is relatively low, the bicycle traffic flow is basically in a state of random riding. At this point, the riding position of bicycles in the lane is related to their speed, with faster bicycles tending to ride closer to the outer side of the lane and slower bicycles closer to the inner side of the road.
4. Data Analysis
This survey did not exclude the impact of retrograded vehicles, and endeavored to capture real alterations in the width of bicycle traffic flow. A total of 2948 non-motorized vehicles were observed, comprising 1078 mechanical bicycles and 1870 electric bicycles. The average proportion of electric bicycles across various road sections stood at 63.43%, with over 70% in two distinct sections, as detailed in Table 2.

Table 2.
Statistics of road traffic volume.
The riding speeds of the bicycles observed on diverse road sections are summarized in Table 3, where it can be seen that the average riding speed of the mechanical bicycles was 12.35 km/h, with a standard deviation of 2.80 km/h. In contrast, the average riding speed of electric bicycles was 18.79 km/h, with a standard deviation of 5.078 km/h. Given the influence of objective factors, slight variations in the speed of mechanical bicycles on certain roads are inevitable. Nevertheless, the speeds of electric bicycles prevailed over those of mechanical bicycles. The greater standard deviation in the speed of electric bicycles suggests a more flexible speed adjustment, thereby leading to more significant speed dispersion. This finding aligns with the existing research findings [20,21].

Table 3.
Summary of speed statistics for different types of bicycles.
In China, definitive regulations exist pertaining to the maximum speed limit for electric bicycles. According to the mandatory national standard, the maximum designated speed for electric bicycles should not exceed 25 km/h [22]. Table 4 presents the comprehensive data for each road section, encompassing the number of bicycles exceeding the speed limit, bicycles crossing lanes, and the status of traffic flow. The over-speed rate is defined as the proportion of over-speeding bicycles to the total bicycle traffic flow on a specific road section. The rate of bicycles entering motor vehicle lanes, which includes instances of overtaking and other lane-crossing behaviors, is calculated as the ratio of such occurrences to the total bicycle traffic flow on the respective road section.

Table 4.
Traffic flow characteristics on each road section.
From Table 4, it is clear that as the width of the bicycle lane increases, the proportion of over-speeding behaviors among cyclists also increases, while the number of instances of bicycles entering motor vehicle lanes decreases. The width of the bicycle lane has a significant relationship with traffic speed. Using the average elasticity formula, it is found that for every 1% increase in lane width, the incidence of over-speeding increases by 2.875%.
Additionally, from the traffic flow state, it can be observed that at the bicycle lane of width of 1.5 m, the bicycle traffic flow showed a clear supersaturated state, indicating that this lane width does not meet the actual demand for bicycle riding. However, in bicycle lanes with a width between 2 and 3 m, the bicycle traffic flow appeared to be in a saturated state, indicating that this lane width meets the actual demand for bicycle riding. When the bicycle lane reached a width of 4.2 m, the road condition exhibited an undersaturated state, implying that this lane width exceeds the actual demand for bicycle riding.
This study further analyzes the speed of mixed bicycle traffic per meter of lane width, as shown in Figure 4.

Figure 4.
Box plots of bicycle speed against width of bicycle lane.
From Figure 4, it can be seen that as the width of the bicycle lane increased, the speed of the mixed traffic flow gradually increased. Specifically, at the bicycle lane width of 2.5 m or less, the average speed of the bicycles CL was 20 km/h. For the bicycle lane of width of 2.5 m or less, the average speed of the bicycles did not change significantly. However, when the lane width exceeded 3 m, the speed of bicycles CL approached 35 km/h, and there were more noticeable changes in the speeds of bicycles in the L1, L2, L3, and LB lanes. Figure 5 shows the average speed and distribution ratio of the bicycles in each subdivided lane according to the road width.
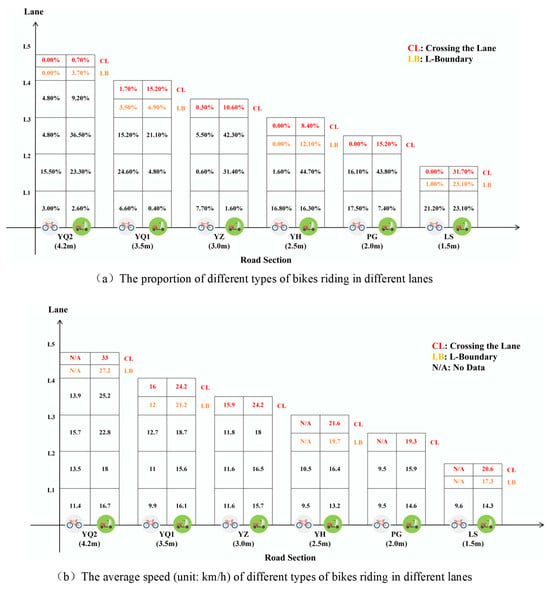
Figure 5.
Statistical parameters of different bicycles riding in different lanes.
From Figure 5, it can be seen that in lanes with a width of 3 m or more, about 5% of mechanical bicycles traveled in the L1 lane at speeds ranging from 9 to 11 km/h. A higher proportion of mechanical bicycles, over 15%, traveled in the L2 lane, at speeds around 11–13 km/h. Fewer mechanical bicycles traveled in lanes beyond the L2 lane, leading to a reduced proportion of incidents where mechanical bicycles entered the motor vehicle lanes. In the case of electric bicycles, only around 1% of electric bicycles traveled in lanes with a width of 3 m or more, at speeds of 15–16 km/h. A large number of electric bicycles, around 20–30% of the total traffic flow, traveled in the L2 lane, at speeds of 15–18 km/h. Around 40–50% of electric bicycles traveled in the L3 lane and other lanes beyond it, at speeds over 18 km/h. Electric bicycles that traveled in lanes with a width of 4.2 m rarely entered the motor vehicle lane. For other lanes, the proportion of electric bicycles entering the motor vehicle lane was about 10%, with traffic speeds exceeding 25 km/h.
In lanes with a width of 2.5 m or less, about 15% of mechanical bicycles traveled in the L1 lane at speeds of 9–10 km/h. Fewer mechanical bicycles, about 20%, traveled in the lanes beyond the L2 lane, at speeds of around 10–11 km/h, and almost no mechanical bicycles entered the motor vehicle lane. In the case of electric bicycles, there was an increase in the number of bicycles traveling in lanes with a width of 2.5 m or less (e.g., lane L1), making up more than 15%, traveling at speeds of 13–14 km/h. The lanes beyond L2 carried a large number of electric bicycles, exceeding 40%, traveling at speeds of 15–17 km/h. In cases of lane segments with a width of 2.5 m—where electric bicycles rarely entered the motor vehicle lane—the PG and LS segments had a high proportion of bicycles entering the motor vehicle lane due to the narrow lane width.
5. Characteristics of Bicycle Traffic Flow
Before exploring the relationship between the macroscopic bicycle traffic flow model and bicycle flow width, this section first analyzes the former for each road section. By comparing the results with previous findings, we verify the usability of the collected traffic flow data. Subsequently, we study the relationship between the macroscopic bicycle traffic flow model and bicycle flow width.
5.1. Macroscopic Bicycle Traffic Flow Model
- (1)
- Speed and Density
In the macroscopic bicycle traffic flow model, the speed–density relationship is relatively straightforward. It can be visualized most intuitively in the form of a scatter plot, as shown in Figure 6. The speed of the bicycle traffic flow decreases with increasing traffic density. This principle is similar to that of the motor vehicle speed–density model, which states that as the number of vehicles on a road section increases, the vehicle density also increases, leading to a congested state. The traffic flow in a lane slows down the adaptability to the road conditions.
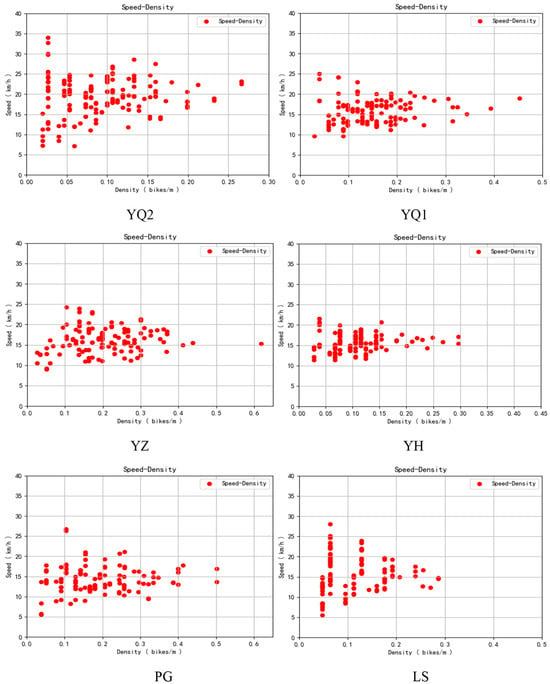
Figure 6.
Scatter plots considering speed against the density of bicycle traffic flow.
- (2)
- Speed and Flow
In the macroscopic bicycle traffic flow model, the relationship between speed and flow is similar to that between speed and density. As the number of bicycles on a road section increases, the bicycle flow per unit of time also increases. This results in a decrease in bicycle speed as the flow rate increases, as shown in Figure 7.

Figure 7.
Scatter plots considering speed against the flow of bicycle traffic.
- (3)
- Flow and Density
In the macroscopic bicycle traffic flow model, the relationship between the flow and density of bicycle traffic indicates that the flow of mixed bicycle traffic increases as the traffic density increases. The flow and density exhibit a monotonically increasing relationship, as shown in Figure 8.

Figure 8.
Scatter plots considering flow against the density of bicycle traffic.
By comparing the characteristics of bicycle traffic flow observed in this study with the classical conclusions of macroscopic bicycle traffic flow models, we found that our obtained results are similar to those in the references, thus validating the reliability of our data. Therefore, this paper continues to explore the relationship between the macroscopic bicycle traffic flow model and bicycle traffic flow width.
5.2. Relationship Between Macroscopic Bicycle Traffic Flow Model and Bicycle Traffic Flow Width
This study conducts a Pearson correlation analysis to examine the relationships among different parameters related to bicycle traffic flow, including width, speed, density, and flow under different traffic conditions across various road sections. The obtained results are presented in Table 5, where it can be seen that the width of the bicycle traffic flow on each road section is primarily related to speed in that section, but not related to flow and density.

Table 5.
Results of Pearson correlation analysis.
- (1)
- Speed and Width
From Figure 9, it can be observed that, except for the insignificant relationship between traffic speed and width in the YQ2 and LS sections, there is a relatively clear linear relationship between them in the remaining road sections. Therefore, this paper adopts a linear regression model to construct a speed–width fitting function for these four road sections. The obtained results are presented in Table 6.
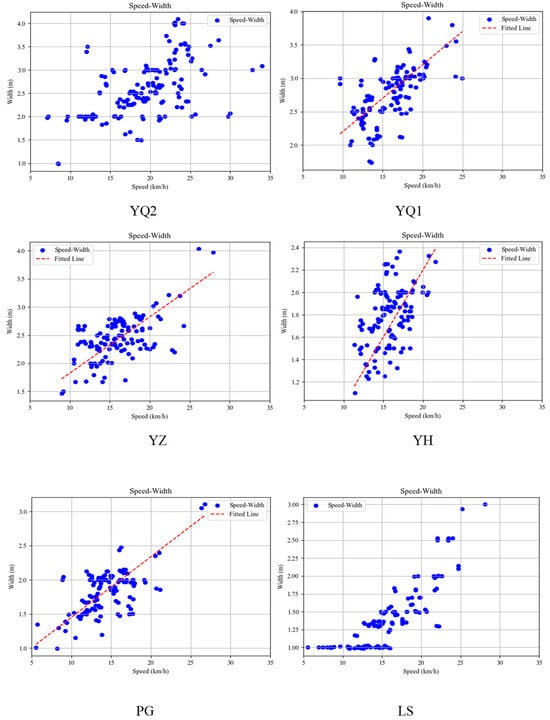
Figure 9.
Scatter plots considering speed against the width of bicycle traffic flow.

Table 6.
Model obtained by fitting width and speed of mixed bicycle flow.
Based on the analysis results, the significant p-value for the speed–width fitting model of bicycle traffic flow is found to be 0.000 ***, which indicates the significance of the results. Therefore, the model basically meets the requirements. It can be seen that, when the width of the bicycle lane is between 2.0 and 3.4 m, the width of the flow increases with increasing flow speed. However, the fitting effects of the models are not satisfactory for all the road sections. The analysis results also indicate that there are still other variables influencing the width of bicycle flow. Further research can be conducted in this direction.
- (2)
- Density and Width
As Figure 10 illustrates, the width of bicycle traffic flow usually correlates with its density. At low flow densities, the width distribution of bicycles is dispersed, spanning various lanes. This dispersion is influenced by the speed and density of the traffic flow. Based on Figure 6, the scatter plot of speed versus density of bicycle traffic flow, it can be observed that when the density of bicycle traffic is low, the corresponding speeds of the bicycle traffic flow vary, depending on differences in bicycle performance and the subjective consciousness of riders. For riders, when their own speed is excessively high, they will instinctively move away from the roadside for safety reasons, to prevent accidents. This also helps us understand why there is a linear relationship between the speed and width of bicycle traffic flow. Conversely, at a high density of bicycle flow, the width of the traffic flow becomes more congested. This is attributed to the speed factor: as the roadway traffic density increases, most vehicles maintain a similar speed, resulting in a more congested width of traffic flow.

Figure 10.
Scatter plots considering density against the width of bicycle traffic flow.
- (3)
- Flow and Width
From Figure 11, it can be seen that, when the bicycle traffic flow on the road segment is low, the distribution of the width of the bicycle traffic flow is relatively scattered. However, when the traffic flow is high, the width becomes more congested. The reason for this phenomenon is similar to the previously mentioned relationship between the density and width of the bicycle traffic flow. The conclusions derived from this experiment are corroborated by and consistent with findings from relevant existing studies [11,12].

Figure 11.
Scatter plots considering flow against the width of bicycle traffic flow.
The above analysis reveals that while the speed, density, and flow of bicycle traffic flow contribute to the overall variation in its width, a particular significant linear correlation exists between speed and width. Therefore, the width of the bicycle traffic flow can be inferred from its speed, thereby determining a suitable width for bicycle lanes. This also suggests that wider bicycle lanes are not always better. Overly wide bicycle lanes may lead to inefficient use of the lane space and a wastage of road space.
6. Conclusions
Based on the research methodology of macroscopic bicycle traffic flow models, this paper defines the concept of bicycle traffic flow width and proposes a model for investigating the relationship between bicycle traffic flow speed and width, aiming to provide improved guidance for the design of urban non-motor-vehicle lanes. By analyzing the relationship between macroscopic bicycle traffic flow characteristics and lane width, the following conclusions are drawn:
1. In terms of the width settings for bicycle lanes, the distribution of bicycles in mixed bicycle traffic flow is most ideal when the lane width is between 2.0 and 3.0 m. Compared to bicycle lanes with widths of 3.0–4.2 m, lanes with widths of 2.0–3.0 m exhibit higher space utilization efficiency within the 0–2 m range: approximately 16% of mechanical bicycles travel in the 0–1 m range, and about 40% of electric bicycles travel in the 1–2 m range. Additionally, within this width range, the incidence of bicycles crossing lane boundaries decreases as the width increases.
2. Regarding vehicle speed, when the lane width is below 3.0 m, the speed of mixed bicycle traffic within the bicycle lane space is relatively reasonable. Specifically, the overall speed of bicycles ranges between 9 and 11 km/h, while the overall speed of electric bicycles ranges between 14 and 18 km/h; even if an electric bicycle crosses lane boundaries, its speed remains below the regulated speed of 25 km/h. When the lane width exceeds 3.0 m, while the speed of mixed bicycle traffic within the 0–2 m range remains within a reasonable interval, the incidence of electric bicycles exceeding the speed limit of 25 km/h gradually increases beyond the 2 m range.
3. There is a linear correlation between the width of mixed bicycle traffic and the speed of bicycle flow. When the width of the bicycle lane is between 2.0 m and 3.4 m, the width of mixed bicycle traffic increases with increasing speed, allowing for the construction of a model relating mixed bicycle traffic width to speed using a simple linear equation.
4. The width of the bicycle lane also has a certain impact on the speed of mixed bicycle traffic flow. As the width of the bicycle lane gradually increases, the speed of mixed bicycle traffic on the outermost part of the road increases. Using the average elasticity formula, it can be calculated that for every 1% increase in bicycle lane width, the number of speed violations in mixed bicycle traffic increases by 2.875%.
5. In cases where the width of non-motor-vehicle lanes in Chinese urban roads does not meet the requirements of relevant design specifications, urban road management authorities may design lane widths based on actual bicycle traffic flow characteristics to address practical travel demands. This approach prioritizes contextual adaptation over the rigid application of fixed standards of assessment or reconstruction, particularly in historical urban areas and sections where reconstruction is challenging.
The established bicycle traffic speed–width model enables the analysis of maximum and minimum traffic flow width variations under peak-hour conditions based on bicycle flow characteristics across different urban road segments. This facilitates the design of optimal bicycle lane widths that meet practical non-motorized travel demands for various road sections. This research provides technical support for optimizing bicycle lane dimensions in aging urban areas or on roads where widening is not feasible.
7. Limitations
Since this study exclusively analyzes bicycle flow characteristics under conditions of lane-marking-separated bicycle lanes without traffic accidents, motor vehicles, or pedestrian interference, the proposed model currently applies only to scenarios with identical operational conditions. Furthermore, regarding the relationship between the three parameters of bicycle traffic flow (speed, density, and flow) and lane width, the research methodology for analyzing traffic flow width in this study has room for improvement. Specifically, the inability to precisely track the exact distance traveled by each bicycle resulted in relatively coarse width data. At the same time, bicycle traffic flow width is influenced by multiple factors beyond the three parameters, including cyclist demographics (e.g., age, gender) and psychological factors, which were not incorporated in this analysis. Future studies could explore these dimensions further. Future research will incorporate variations in bicycle traffic speed, width, and density under special conditions to develop a more universally applicable model for optimizing practical urban bicycle lane widths.
Author Contributions
Q.Z.: study conception and design; L.W.: data collection; W.X. and Z.W.: analysis and interpretation of results; Z.W.: writing—original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by the Yuxiu Innovation Project of NCUT (Project No.2024NCUTYXCX108).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, Y.; Liu, J. A Study on the Width of Non Motorized Vehicle Lanes on Urban Roads. Road Traffic Manag. 2019, 34–35. Available online: https://kns.cnki.net/kcms2/article/abstract?v=qQX4xeHgc6vomyEeBbneYk2wi2KsvoxFIVmvSxIpFJcmClmDdT9PUz8foRbjnNLAKSEKAUwhi9SXg_KIz9ACnzu02kmjii_P9nFK_SP2mUnB6Dwt3dlj6wll3AaEBR0xkRMBx32-aoS8FjIuQs8E3xjAFERB2fCVnAumvyxbHVg&uniplatform=NZKPT&captchaId=dfc3cbef-ea6d-41c8-afa9-59e56e749aa7 (accessed on 22 May 2025).
- Zhou, D. Study on Characteristic of Mixed Bicycle Traffic Flow in Basic Sections of Urban Road. Master’s Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Smith, T.D., Jr. Safety and Location Criteria for Bicycle Facilities Users Manual. In Bicycle Facility Location Criteria; National Technical Information Service: Alexandria, VA, USA, 1976; Volume 2. [Google Scholar]
- Navin, F. Bicycle traffic flow characteristics: Experimental results and comparisons. ITE J. 1994, 64, 31–36. [Google Scholar]
- Peng, R.; Yang, P. The basic model of bicycle traffic flow. J. Tongji Univ. Nat. Sci. 1993, 463–468. [Google Scholar]
- Zhu, C.; Chi, Y. Relationship between speed and density in mixed non-motorized vehicle. J. Univ. Sci. Technol. Suzhou Eng. Technol. 2009, 22, 26–29. [Google Scholar] [CrossRef]
- Hui, H. Research on characteristics of the mixed non-motorized traffic flow. Mod. Transp. Technol. 2015, 12, 79–82. [Google Scholar] [CrossRef]
- Dan, W. Research on Speed-Flow Relation of Non-Motor Vehicle Based on Mixed Traffic Flow on Road Section. Traffic Transp. 2015, 22–26. Available online: https://d.wanfangdata.com.cn/periodical/Ch9QZXJpb2RpY2FsQ0hJTmV3UzIwMjUwMTE2MTYzNjE0Eg5qdHl5czIwMTV6MjAwNxoIcjQxZTIzeG0%253D (accessed on 22 May 2025).
- Zhou, D.; Ma, X.; Jin, S.; Wang, D. Flow-density relationship of mixed bicycles based on Logistic model. J. Traffic Transp. Eng. 2016, 16, 133–141. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Q.; Rong, J.; Liu, X. Mixed traffic flow characteristic of the crosswalk of the signal control crossing. Comput. Comun. 2008, 26, 42–44. [Google Scholar] [CrossRef]
- Wierbos, M.J.; Knoop, V.L.; Hänseler, F.S.; Hoogendoorn, S.P.; Affiliations, V.A.A.A. Capacity, Capacity Drop, and Relation of Capacity to the Path Width in Bicycle Traffic. Transp. Res. Rec. 2019, 2673, 693–702. [Google Scholar] [CrossRef]
- Seriani, S.; Fernandez, R.; Hermosilla, E. Experimental Study for Estimating Capacity of Cycle Lanes. Transp. Res. Procedia Online 2015, 8, 192–203. [Google Scholar] [CrossRef][Green Version]
- Zhu, S.; Wang, Y.; Wu, J.; Chen, Q.; Wang, W. Design of basic demand width for non-motorized vehicle lanes under mixed flows. J. Chongqing Jiaotong Univ. Nat. Sci. 2024, 43, 73–83. [Google Scholar] [CrossRef]
- Zhonghua, W.; Wenjia, H.; Fangzhou, L.I.; Liang, C.; Songpo, Y. Micro modeling and simulation of mixed bicycle traffic flow considering retrograde behavior. J. Chongqing Jiaotong Univ. Nat. Sci. 2023, 42, 116–123. [Google Scholar] [CrossRef]
- Ni, Y.; Li, Y.; Li, X.; Sun, J. Modeling and simulation of the non-motorized traffic flow on physically separated bicycle roadways. J. Tongji Univ. Nat. Sci. 2019, 47, 778–786. [Google Scholar]
- Hu, W.; Nan, S.; Cheng, H.; Zhou, W. Blend of mixed non-motorized traffic flow of crossed road. J. Zhongyuan Univ. Technol. 2017, 28, 5. [Google Scholar]
- Chen, X.; Han, H.; Lin, B. Developing bicycle equivalents for mopeds in Shanghai, China. Transp. Res. Rec. J. Transp. Res. Board 2012, 2317, 60–67. [Google Scholar] [CrossRef]
- Li, N. Research on Level of Service Evaluation System for Urban Non-Motorized Lanes. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Xu, C.; Qu, Z.; Tao, P. Estimation of bicycle path capacity under mixed bicycle traffic flow. J. Jilin Univ. Eng. Technol. Ed. 2016, 46, 63–69. [Google Scholar] [CrossRef]
- Zeng, M. The Research on Traffic Safety of Mixed Non-Motor Vehicle Flow Based on Conflict. Master’s Thesis, Chang’an University, Xi’an, China, 2018. [Google Scholar]
- Yang, H.; Dillon, T.S.; Chen, Y.P. Optimized structure of the traffic flow forecasting model with a deep learning approach. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2371–2381. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q. Interpretation of GB 17761-2018 “Safety Technical Specification for Electric Bicycles”. China Qual. Superv. 2019, 61–63. Available online: https://kns.cnki.net/kcms2/article/abstract?v=8t0HcLKTPb31JLtBHY3I3kXVFqMeKKf1mzt79lOYbUajJz4FC6BteO5-59wg1RGEpJiI4paVQZByipkVt9R1eMKnk0AcnPp0bYBMHimyIrsHBjoMfxUJBkGsX83yVRM8yNuyqeSmW3cTJLdCwA4CHonTFj9urKcP7nuW1tts_18=&uniplatform=NZKPT (accessed on 22 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).