Abstract
Today, power electronic-based converters are at the core of many modern systems, such as smart grids and electric vehicles. In this context, the Dual Two-Level Inverter (DTLI) supplying an open-end winding machine offers an innovative and promising solution for marine propulsion, aeronautics, and electric vehicles. This configuration provides several advantages, including a reduced DC bus voltage, enhanced fault tolerance, and improved overall system performance. However, ensuring optimal energy efficiency and high-power quality remains a major challenge given the increasing demands for performance and sustainability. This paper presents a state-of-the-art review of the main DTLI configurations and their impact on system performance. Three architectures are analyzed, highlighting their benefits and limitations. This study aims to demonstrate the influence of the DC bus voltage ratio and pulse width modulation strategies on power quality and energy efficiency. The objective is to enhance the understanding of the DTLI’s potential and to guide its integration into other electrical systems.
1. Introduction
Over the past century, industrial development has significantly contributed to climate change, primarily by increasing greenhouse gas emissions (see Figure 1) [1]. In response to this reality, a global transition towards more environmentally friendly energy sources and less polluting industries has become imperative [2]. In this context, enhancing the quality and energy efficiency of electric drive systems is a crucial factor in the shift towards greener industries. Technological advancements in this field aim to develop more efficient systems that minimize energy consumption and losses while ensuring high levels of performance, reliability, and durability [3]. In recent years, extensive research has been conducted to overcome this technological challenge.
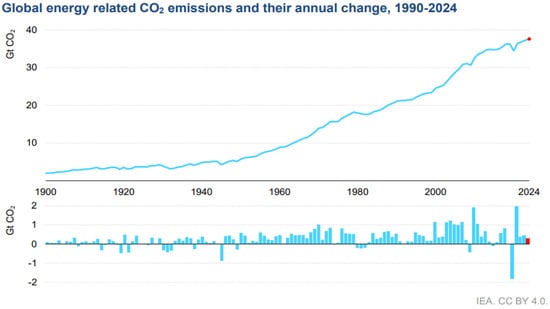
Figure 1.
Worldwide greenhouse gas emissions [1].
Several studies have focused exclusively on improving power quality. For instance, research in [4] has demonstrated that integrating FACTS devices, such as the Unified Power Quality Conditioner and the Static Synchronous Compensator, can reduce total harmonic distortion (THD) and enhance the stability of modern power distribution grids. Similarly, the study in [5] investigated the implementation of a Dynamic Voltage Restorer to mitigate voltage sags and ensure a stable supply to sensitive loads. Additionally, the authors of [6,7] analyzed the impact of multilevel inverters on the power quality of wind and photovoltaic systems. The study in [8] examined converter topologies dedicated to high-power electrolysis and their influence on the quality of power injected into AC grids. Furthermore, research in [9,10,11,12] proposes a robust control strategy based on sliding mode and fuzzy logic, applied to power electronic converters. This approach aims to enhance the integration of wind turbines and photovoltaic power plants into the grid, enabling them to provide ancillary services while ensuring compliance with grid codes. In addition, studies in [13,14,15] propose advanced fixed-time sliding mode control strategies combined with nonlinear observers to enhance power quality in microgrid applications. These approaches improve disturbance rejection, ensure fast and robust regulation of the DC-link and output voltages, and enhance the dynamic performance of converters operating within renewable-based hybrid networks. Moreover, studies in [16,17,18] focus on detecting and diagnosing faulty current sensors to improve power quality by ensuring the stable and reliable control of wind power systems. Finally, research in [19,20] explores high-frequency modeling of electrical machines to design high-performance filters, ultimately improving power quality in the grid.
In the context of improving energy efficiency, several researchers have focused on reducing losses and optimizing energy management to enhance the overall performance of electrical systems. For example, the authors of [21] analyzed asymmetric bidirectional DC-DC converters for power electronic transformers. Their findings demonstrated that these converters reduce peak current and enhance switch safety, thereby optimizing energy efficiency. And the study by [22] proposed the use of a multi-port converter with a high-frequency link for interfacing clean power sources, improving system flexibility and overall efficiency. In addition, the research in [23] introduced a multi-objective approach based on Pareto analysis for Volt/Var control of photovoltaic inverters, enabling the optimized management of reactive power injected into the grid. Other works, such as those in [24,25,26,27,28], have explored advanced power maximization techniques for photovoltaic and wind power systems. These approaches allow for a more efficient utilization of solar and wind resources while minimizing energy losses.
In the pursuit of simultaneously improving power quality and energy efficiency, research aims to address a major challenge in modern power systems: reconciling performance, reliability, and energy optimization. Studies in [6,29,30,31] have explored innovative converter configurations to reduce losses, enhance the integration of renewable energy sources, and ensure a high-quality power supply. The integration of NPC multilevel inverters, as investigated in [32], has led to a reduction in THD and power losses, thereby contributing to overall efficiency improvements. Other studies, such as those in [33,34], have introduced advanced inverter architectures designed to optimize both power quality and efficiency in photovoltaic and electric traction systems. Regarding power electronic interfaces, the authors of [35,36] have proposed integrated solutions for electric and plug-in hybrid vehicles, combining an on-board charger and a traction inverter within a unified system. Further research in [37,38] has focused on optimizing multilevel inverters and power electronic converters to enhance the energy efficiency and modularity of electric vehicle charging systems. Additionally, studies in [39,40] have explored the use of cascaded H-bridge inverters and Z-source inverters to optimize electric vehicle performance, extending driving range and improving energy efficiency. Finally, the study in [41] introduces a novel high-performance switched active Z-source inverter topology, demonstrating significant improvements in the lifespan and autonomy of hybrid energy storage systems.
These recent advancements highlight the crucial role of electrical engineering research in enhancing both power quality and energy efficiency while addressing the evolving constraints and demands of modern electrical systems. In this context, increasing attention is being given to a new DC/AC power electronic configuration. Originally proposed by H. Stemmler and P. Guggenbach [42], this topology differs from conventional approaches by isolating the neutral point from the stator windings and arranging two inverters in series, either as two-level or multilevel structures. This design enables independent control of the machine windings through two separate inverters, one for each phase set, leading to what is known as an open-end winding machine driven by a Dual Two-Level Inverter (OEWM-DTLI). The literature identifies three primary power supply configurations for this topology: (i) common DC bus supply (C-DCB) [43,44], (ii) two isolated DC bus sources (TI-DCB) [45,46], and (iii) common DC bus supply with a floating capacitor (DCB-FC) [47,48]. The increasing interest in the DTLI structure is driven by its growing adoption in diverse applications, including electric vehicles [49,50,51,52], aerospace [53], and marine propulsion systems [54]. The widespread adoption of this configuration is due to its numerous benefits, including the following:
- -
- The simplicity of the power circuit [55,56].
- -
- The absence of fluctuations in the neutral point [57].
- -
- Enhanced fault tolerance [58].
- -
- Lower DC bus voltage [51].
- -
- A wider operating speed range [59,60,61].
- -
- The ability to independently control the stator current of each phase [62].
- -
- The potential to achieve a switching frequency that is effectively double, depending on the modulation strategy employed [63].
- -
- The generation of a voltage space vector similar to that of a three-level inverter [64].
- -
- The flexibility to incorporate various energy storage systems on the DC bus of each inverter [65,66].
Nevertheless, it is crucial to recognize that this configuration also comes with certain challenges, such as the following:
- -
- The risk of capacitor overcharging due to unequal DCB voltages in TI-DCB power supplies [67]: this can result in capacitor damage and unwanted harmonics in the motor phase voltage [68].
- -
- The occurrence of zero-sequence voltage (ZSV) caused by the direct coupling of two inverters [69]: this leads to homopolar currents, which generate triple current harmonics [62], adversely affecting motor windings, increasing copper losses, and contributing to circuit saturation [62].
- -
- The presence of common-mode voltage (CMV) resulting from the high-frequency switching of inverter devices [70,71,72]: CMV creates common-mode currents between the stator phase windings and ground, which can lead to accelerated bearing wear, reducing their service life [73]. Additionally, these currents do not contribute to electromechanical energy conversion and add to the motor’s heat losses [74].
- -
- An increase in power losses, due to the greater number of power switches when compared to two-level converters.
It should be noted that each DTLI configuration has a direct influence on performance, complexity, and field of application. Table 1 summarizes the main applications, along with the advantages and disadvantages associated with each type of configuration. In order to fully exploit the potential of these structures and optimize their design, this paper proposes an in-depth state-of-the-art review of the three DTLI configurations and analyzes their impact on system quality and efficiency. To this end, this paper is organized as follows: Section 2 presents the principle of operation of the system under study; Section 3 explores in detail the three DTLI configurations and their specific features; Section 4 analyzes the effect of the DC bus voltage ratio on DTLI performance; Section 5 deals with the control principles applied to this structure; Section 6 discusses the evaluation criteria in terms of quality and efficiency; and, finally, Section 8 summarizes the conclusions of this study.

Table 1.
Three different DTLI configurations with their applications, advantages, and drawbacks.
2. Study System Definition and Operating Principle
The basic principle of the DTLI configuration is to supply the stator using two separate inverters instead of coupling it in a star or delta configuration [92,93] (see Figure 2). In this configuration, each side of the stator is powered by a dedicated inverter (see Figure 3). This approach has gained popularity in various modern applications due to its advantages [49,50,51,53,54].
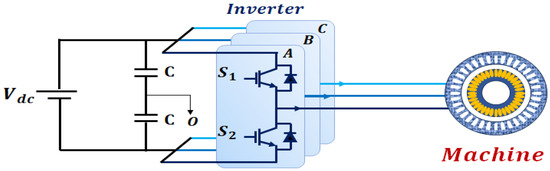
Figure 2.
Typical configurations of a star- or delta-connected AC machine.
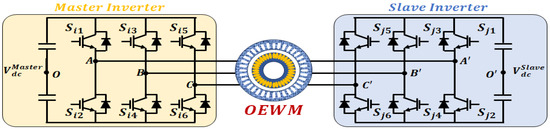
Figure 3.
Schematic diagram of machine control with DTLI.
This structure consists of two two-level inverters, referred to as inverter i (Master inverter) and inverter j (Slave inverter), respectively. The voltage vectors in an reference frame for each inverter ( and ) can be calculated as follows [94]:
where , is the DC bus voltage, and and represent the switching states of inverters i and j, respectively.
As highlighted in the study of [95], the operating principle of the DTLI structure relies on the coordinated synthesis of voltage vectors from both inverters to generate the rotating magnetic field required for motor operation. In a symmetric configuration, when the Master and Slave inverters apply identical voltage vectors simultaneously, their resulting magnetic fields tend to cancel each other out. This cancelation disrupts the formation of the rotating field, potentially causing the motor to stop. To overcome this limitation, asymmetric control strategies are employed. These strategies introduce a phase shift between the voltage vectors generated by the Slave inverter relative to those of the Master inverter, ensuring constructive vector interaction, effective field generation, and sustained motor operation.
Figure 4 illustrates the hexagon formed by the eight voltage vectors generated by Equations (1) and (2). Within this hexagon, each inverter generates six active vectors and two zero vectors. The values “1” and “0” correspond to the on and off states of the inverter switches, respectively.
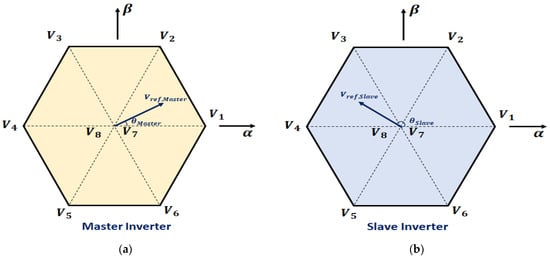
Figure 4.
Vectorial diagram of the voltage space of each inverter: (a) Master inverter. (b) Slave inverter.
Considering the circuits , , and in Figure 3, the three-phase voltages , and can be expressed using Kirchhoff’s law, as shown in Equation (3):
where , , and , , represent the three-phase pole voltages of the master inverter and the slave inverter, respectively.
Assuming that the three-phase loads are symmetrical, the sum of the load phase voltages must be zero, as expressed in Equation (3).
Thus, can be obtained by summing the three equations in (3), leading to Equation (5).
By substituting Equation (5) into Equation (3), the phase voltage expression is updated as follows:
From Equation (6), it can be observed that the phase voltage applied by the DTLI to the OEWM in Figure 2 corresponds to the voltage difference between the two inverters, and . Thus, can be expressed by Equation (7) [96].
In the power circuit configuration of the three-phase inverters shown in Figure 3, the two switches in each inverter leg operate in a complementary manner, meaning that, when one switch is turned on, the other is turned off. By utilizing this switching behavior, the phase output voltages of each inverter, referenced to the negative terminal of the DCB, can be expressed in matrix form as follows:
As presented in Equation (7), the phase voltages applied by the DTLI to the OEWM are obtained by computing the difference between the output voltages of the two inverters. This relationship can therefore be modeled by the following equation, which yield
Based on this principle, the space vector diagram of a DTLI can be represented in Figure 5, where the hexagonal space vector set generated by the slave inverter ‘orbits’ around the hexagon of the master inverter.
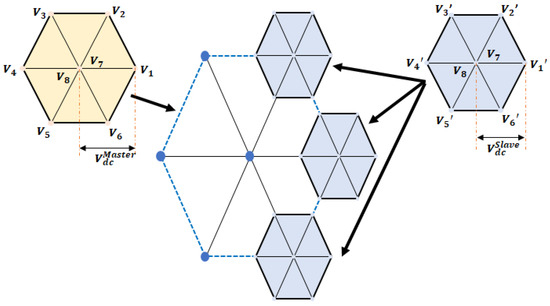
Figure 5.
The principle of a space vector diagram resulting from a DTLI.
3. Various System Configurations Studied
In the literature, three different types of system configurations powered by two inverters are identified (see Figure 6): (i) a single common DCB source, (ii) two isolated DCB sources, and (iii) a single DCB source with a floating capacitor.
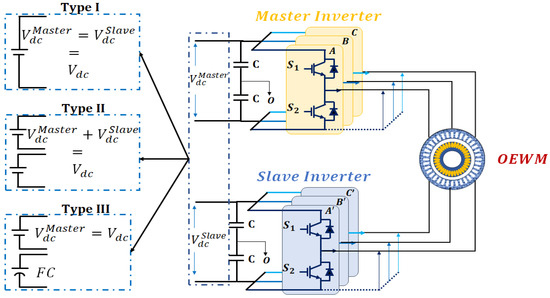
Figure 6.
Three types of DTLI configurations for an OEWM.
3.1. Configuration Type I: A Single Common DCB Source
The DTLI drive circuit configuration powered by a single common DCB source (Type I) is shown in Figure 7, where a two-level voltage inverter is connected to each side of the OEWM.
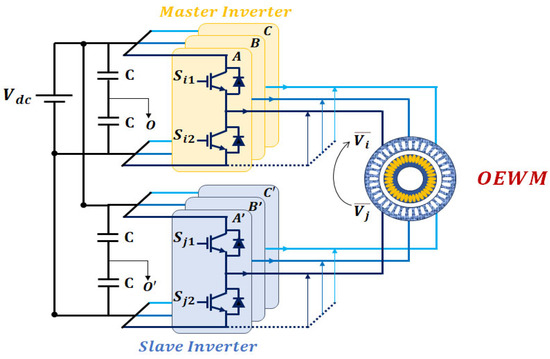
Figure 7.
Configuration of a DTLI powered by a common DCB.
Consequently, the DTLI configuration uses twelve semiconductor switching devices (typically IGBTs or MOSFETs) and twelve antiparallel diodes. This configuration relies on the combination of the space vectors from both inverters, resulting in 64 () possible switching combinations distributed across 19 distinct spatial locations. In this configuration, the set of space vector hexagons generated by the slave inverter ‘orbits’ around the space vector hexagon of the master inverter. This DTLI configuration is similar to that of a three-level inverter, as shown in Figure 8. It consists of three hexagons with vertices of different lengths: a vertex of length (hexagon ABCDEF), a vertex of length (hexagon HJLNQS), and a vertex of length (hexagon GIKMPR). Table 2 summarizes the classification of these three hexagons into different vector groups.
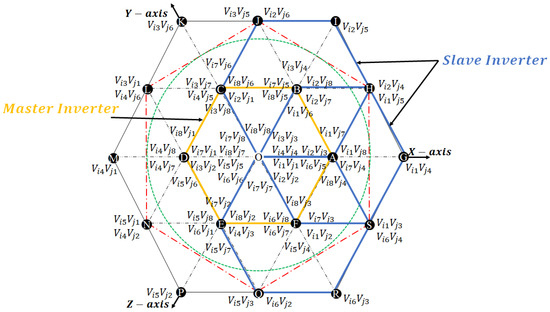
Figure 8.
Vector diagram of the space of a DTLI.

Table 2.
Voltage vector groups for DTLIs with a common DCB.
However, the DTLI configuration powered by a single DC bus source inherently leads to the presence of ZSV, resulting in excessive current and voltage THD. This phenomenon results in high losses, increased temperature, and undesirable vibrations within the machine [97]. Additionally, this configuration is also affected by the presence of CMV.
3.2. Configuration Type II: Two Isolated DCB Sources
This topology is the same as that described in Section 3.1. However, it is based on the use of two isolated DCB sources (Type II), as shown in Figure 9.
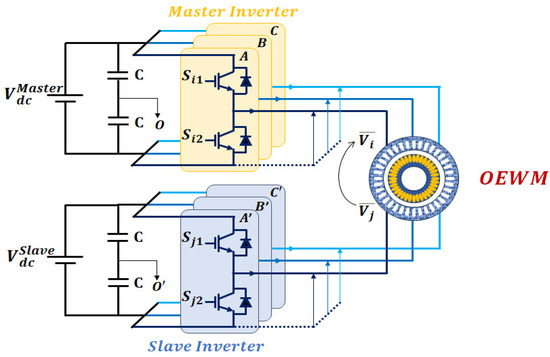
Figure 9.
Configuration of a DTLI powered by a two isolated DCB.
This configuration can be divided into two categories: DTLI configurations with symmetrical and asymmetrical voltage sources.
As shown in Figure 9, this configuration features two separate DC buses, which are mutually isolated [55,57,91,96,98,99,100,101,102,103,104,105,106,107,108]. The isolation of the DC buses prevents the circulation of triple-harmonic currents.
The use of the DTLI system, with two DCB sources of unequal values (asymmetrical voltage source), leads to a significant change in the converter operation, compared to the scenario where both DCB sources have equal values (symmetrical voltage source). Figure 10 illustrates the voltage vector generation diagrams for these two cases: one with equal voltage sources and the other with unequal voltage sources .
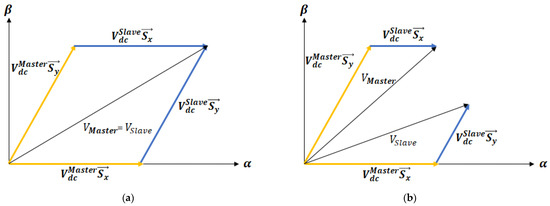
Figure 10.
Voltage vector compositions: (a) symmetrical voltage source and (b) asymmetrical source ratio of (2:1).
The vector voltage diagrams are derived by considering the complex switching sequences and . These sequences are defined for the master inverter and for the Slave inverter , as shown in Figure 3. The output voltages are given by Equation (11), and the corresponding diagrams are provided in Figure 10.
The complex vectors resulting from various switching combinations are used to indicate the direction of the complex voltage vectors’ positions. In this context, there are two voltage vectors: one aligned with the “” axis and the other 60 degrees out of phase with the “” axis. The amplitude of the voltage vectors is determined by the electrical source value. If the two voltage sources are of equal intensity, the corresponding voltage vectors will have the same magnitude and orientation. However, if the voltages are unequal, such as in a voltage ratio, additional vectors are generated. These extra vectors can be observed in Figure 10. Further analysis shows that some of these additional vectors may be redundant. By employing asymmetrical voltage sources, these redundant vectors can be isolated, increasing the number of available output voltage vectors. This provides a broader range of options for generating distinct output voltages.
Figure 11a illustrates a spatial vector scheme for a two-level DTLI, utilizing voltage sources with an unequal voltage ratio of . This converter system, with a voltage ratio, generates 37 voltage vectors, which are uniformly and symmetrically distributed in the plane.
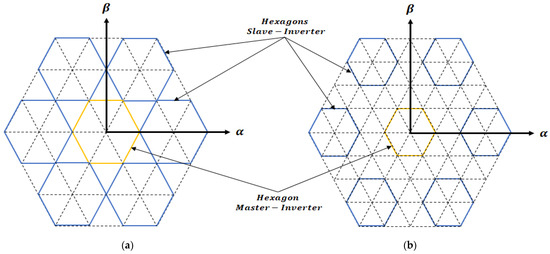
Figure 11.
Spatial vector diagram of a DTLI with asymmetrical sources: (a) source ratio and (b) source ratio .
On the other hand, the vector diagram shown in Figure 11b is constructed considering the use of asymmetrical sources with a voltage ratio of . In this converter configuration, 48 voltage vectors can be generated. However, these vectors are distributed asymmetrically in the plane. It should be noted that, in this arrangement, certain areas present challenges regarding the selection of the three closest vectors. This complexity may introduce additional harmonics into the output waveform. Furthermore, in this configuration, the number of redundant states is minimized. As a result, at lower modulation levels, the inverter may cause the overcharging of low-voltage capacitors in specific regions.
The main drawback of this configuration with two iso-linked DC bus sources is the risk of overcharging the DC buses. To prevent this issue, additional components must be integrated.
3.3. Configuration Type III: A Single DCB Source with an FC
This configuration is similar to the one described in Section 3.1. However, a key difference is that, in this structure, the slave inverter is supplied by a floating capacitor (Type III) instead of a DCB source. This distinction is illustrated in Figure 12.
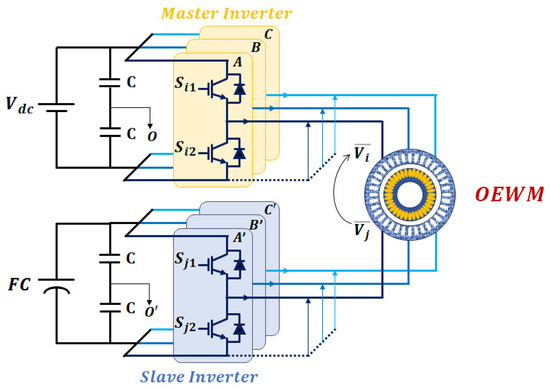
Figure 12.
Configuration of a DTLI powered by a single DCB source with an FC.
In the DTLI with an FC, as illustrated in Figure 12, the voltage ratio between the DCB sources is defined as , where is a constant coefficient. In this setup, the master inverter is supplied with a fixed DCB voltage , while the Slave inverter is powered by a floating capacitor that provides a voltage of . The capacitor is connected without a fixed reference point, and its voltage is naturally self-balanced based on the system configuration and the applied control strategy.
During the modulation process, the phase currents can flow through the FC, resulting in voltage fluctuations across it. By convention, a current flowing into the Slave inverter is considered positive, and the switching states of the Slave inverter directly influence the current through the capacitor.
Since a single modulation vector can be synthesized from multiple switching states, these vectors can be categorized based on their impact on the current flowing through the FC as follows:
- -
- Type 1 vectors: These vectors induce two opposite current flows within the same phase, such as positive and negative currents in phase , depending on the specific switching states.
- -
- Type 2 vectors: These vectors result in current flow in only one direction within a given phase, for example, only a positive current in phase .
- -
- Type 3 vectors: These vectors produce no current flow through the FC, regardless of the switching states.
- -
- Type 4 vectors: These vectors generate current flow in different phases, such as a positive current in phase in one state and a negative current in phase in another.
This classification offers valuable insight into the interaction between modulation vectors and the dynamic behavior of the FC. A more detailed example of the application of these principles is provided in Section 5.
This configuration combines the advantages of the other two setups, offering multilevel output voltage and voltage amplification capabilities, thanks to the elimination of ZSV circulation. Additionally, it eliminates the need for an isolation circuit, as one of the inverters is floating.
In this DTLI configuration with an FC, the main challenge is regulating the FC voltage to the desired value. Likewise, in DTLI systems with isolated asymmetrical power supplies, a potential concern is that the capacitor on the low-voltage side may be overcharged due to energy flow from the high-voltage side.
In summary, each of the three DTLI configurations presents distinct characteristics in terms of performance, complexity, and implementation requirements. The Type I configuration stands out for its structural simplicity and ease of implementation. However, it is affected by the generation of CMV and ZSV, which can degrade the output voltage quality and increase the overall system losses. The Type II configuration eliminates these undesirable effects and enhances modulation flexibility, especially when asymmetric voltage sources are used. On the other hand, the need for galvanic isolation adds to the cost and increases the risk of capacitor overcharging on the lower voltage side. The Type III configuration offers a good compromise by combining the benefits of the two previous structures while eliminating the need for isolation. Nonetheless, it introduces a challenge in regulating the voltage across the floating capacitor, particularly in transient operating conditions. Therefore, the selection of the most appropriate configuration should be guided by the specific requirements of the application, including cost constraints, control complexity, and desired output voltage quality.
4. DCB Voltage Factor and Ratio
4.1. DCB Voltage Factor
The DCB voltage factor essentially defines the area of the space vector diagram, the inverter’s output level characteristics, and the distribution of switching vectors. The area of the space vector diagram limits the maximum utilization of the DC bus voltage, while the level characteristics determine the output quality. It is calculated by dividing the maximum output voltage of a DTLI by the DC bus voltage in the linear modulation region, as expressed in Equation (12) [48].
4.2. DCB Voltage Ratio
The diagram in Figure 3 shows that the output voltage of a DTLI is essentially the difference between the output voltages generated by the master and slave inverters. Consequently, the ratio between these voltages plays a critical role in shaping the distribution of space vectors in a DTLI. This voltage ratio variation directly affects two key aspects: the area of the space vector diagram and the number of output voltage levels produced by the inverter.
To better illustrate these effects, Figure 13 presents the space vector diagrams of DTLIs for different voltage ratios. As shown, the voltage ratios of , , and allow the generation of three, four, and five distinct output levels, respectively. In other words, the selected voltage ratio determines the number of achievable output levels, which directly influences the DTLI’s performance characteristics.
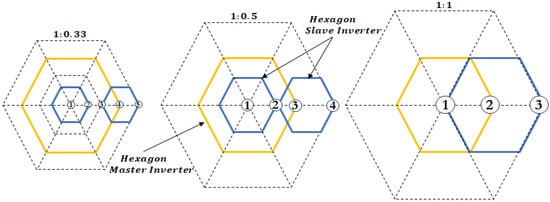
Figure 13.
Space vector diagram of DTLIs with different voltage ratios.
5. DTLI Control Features
A review of the existing literature highlights two main modulation strategies applicable to DTLIs: coupled and decoupled schemes [95,105]. These two strategies propose distinct approaches to inverter control and significantly influence the performance of OEWM.
5.1. Coupled Modulation Control
In the case of coupled modulation, a DTLI can be treated as a single multilevel converter. To minimize switching activity, an alternating sub-hexagonal center (SHC) modulation strategy can be implemented, whereby one inverter operates while the other remains in a steady state during a switching period [104,109,110].
Figure 14 illustrates the operation of this alternating SHC modulation technique. The entire space vector diagram is segmented into six regions, each associated with a central SHC point marked by green circles labeled A through F. For each SHC, one inverter performs the switching while the other remains fixed, and then their roles alternate for the subsequent SHC.
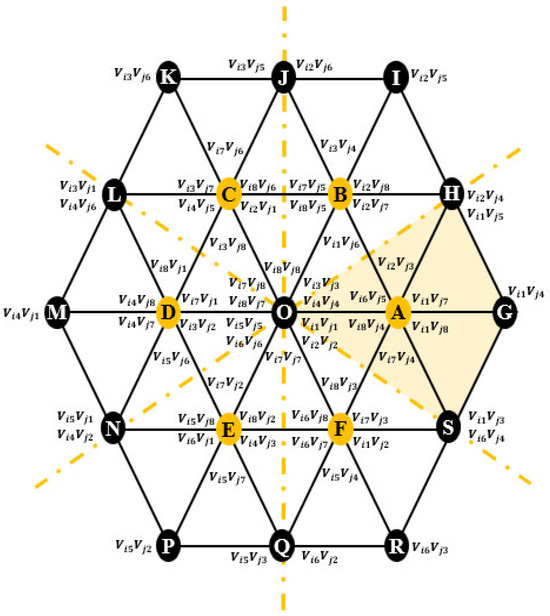
Figure 14.
Sub-hexagonal center alternative modulation scheme principle for DTLI.
For instance, point A corresponds to the SHC of the light-green OSGH quadrilateral in Figure 14. Within this region, the switching states can either involve keeping the master inverter fixed at while switching the slave inverter across and , or vice versa, holding the Slave inverter constant at and switching the master inverter among states such as and .
The authors in [109] conducted a thermal loss analysis of this alternating SHC scheme, demonstrating its impact on system efficiency. Additionally, the authors in [110] showed that this modulation strategy leads to an equal distribution of power losses between the two inverters.
A power-sharing strategy is also defined in [111], taking into account unbalanced power distribution and modulation index values. Moreover, several studies [68,99,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128] have focused on capacitor voltage regulation for TI-DCB configuration and DCB-FC configuration of DTLIs, respectively.
5.2. Decoupled Modulation Control
As previously mentioned, the output voltage of a DTLI is obtained as the difference between the voltages generated by the two individual inverters.
Under decoupled modulation, the reference voltage is decomposed into two components, namely, and , which are individually supplied to the master and slave inverters, respectively.
This decomposition process is mathematically represented by Equation (13).
The reference vector synthesis diagram is illustrated in Figure 15. Based on Equation (13) and the diagram, it is evident that there are four user-defined parameters, which provide substantial control flexibility that can be strategically exploited.
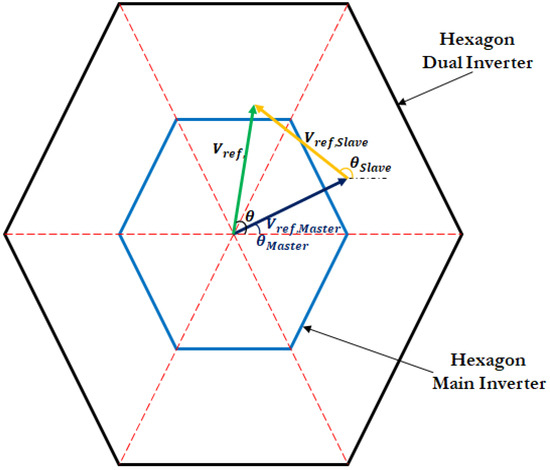
Figure 15.
DTLI decoupled modulation principle.
For instance, the authors in [69] adjusted the parameters and to enhance the output voltage profile of DTLIs.
To minimize output current fluctuations, the authors of [96] conducted an analytical study and subsequently proposed a control strategy grounded in decoupled modulation.
Researchers in [67,111,119,120,121,122,123,124,125,126,128,129,130,131] focused on capacitor voltage regulation for TI-DCB configuration and the DCB-FC configuration of DTLIs, respectively.
Nevertheless, despite its high flexibility, decoupled modulation introduces undesired voltage steps at the inverter output [119], which can deteriorate the inverter’s output performance.
6. Various Criteria for Assessing the Power Quality and Efficiency of the Studied System
The deployment of DTLI configurations offers promising prospects across a wide spectrum of power electronic applications. Nevertheless, each configuration presents a unique set of technical challenges that must be addressed to ensure optimal operation and achieve the desired performance.
In this context, we examine the challenges associated with three distinct DTLI architectures, whose difficulties stem from their specific characteristics, ranging from complex voltage modulation to the management of asymmetrical power sources.
A comprehensive understanding of these constraints is crucial to fully harness the benefits provided by the various DTLI topologies. These challenges can broadly be classified into two categories: those related to power quality and those concerning energy efficiency.
6.1. Power Quality
Electrical power quality has become a critical factor in the design and operation of power systems and electrical machines. This subject has garnered considerable interest from both academic researchers and industrial practitioners, leading to the publication of numerous works in this dynamic and relatively recent field [132].
Power quality encompasses several key issues, such as voltage dips, outages, harmonics (notably THD), over-voltages, unbalances, and voltage fluctuations, among others.
With the introduction of new converter configurations, two additional quality concerns arise: common-mode voltage and zero-sequence voltage.
This study addresses a range of quality-related challenges, including harmonic distortion, common-mode voltage, zero-sequence voltage, DC bus overcharging, and the regulation of floating capacitor voltages.
6.1.1. THD
In systems associated with power converters, output voltage/current quality is closely linked to THD. The IEEE Std 519-1992 standard recommends harmonic control requirements for electrical systems [133].
By definition, THD characterizes the effects of harmonics on power system voltage and can be applied to low-, medium-, and high-voltage systems [133]. The THD is defined by Equation (14).
where is the harmonic order, is the amplitude of the harmonic component, and is the amplitude of the fundamental component.
The IEEE Std 519-1992 standard defines voltage distortion limits at the Point of Common Coupling (PCC) and requires that customers do not introduce excessive current harmonics [133]. For systems where the bus voltage at the PCC is less than or equal to 69 kV, individual voltage distortion must remain below 3%, and the THD must not exceed 5%. The Fast Fourier Transform (FFT) can be used to perform a spectral analysis of electrical signals and thus serves as an effective tool for THD evaluation [134].
6.1.2. Common-Mode Voltage (CMV)
In three-phase sinusoidal power systems, balance and symmetry are fundamental under normal operating conditions. The phase voltages naturally compensate each other, and grounding the source’s neutral point reinforces this symmetry.
However, when a three-phase pulse width modulation (PWM) inverter is employed, the switching of asymmetrical voltages introduces a DC voltage () across the load phases. This deviates from the ideal sinusoidal behavior, as the instantaneous sum of the load terminal voltages is no longer zero. This deviation leads to the emergence of CMV between the load and ground [135].
CMV results from the high-frequency switching of inverter devices. The common-mode currents induced between the stator windings and ground can have serious consequences, such as premature bearing degradation, increased thermal losses, and an overall decline in motor performance [73].
The CMV generated by the inverter can be expressed by the following equation [136]:
In DTLI systems, like the one shown in Figure 5, the CMV for each inverter can be calculated using the formulas provided in the study of [58]:
Consequently, the CMV of DTLIs can be calculated as follows [137]:
In the context of DTLI systems, CMV-related issues become more critical due to the frequent high-frequency switching of the inverters’ switches. This rapid switching can shorten motor life and increase the risk of inverter failure. Moreover, the impact of these issues is amplified by factors such as shaft voltages, bearing currents, and electromagnetic disturbances caused by common-mode leakage currents [138].
The effects of CMV on the system are primarily influenced by the parasitic parameters between the motor and ground. Among these, parasitic capacitance and parasitic resistance are crucial in the generation of bearing current, an undesirable component that can negatively affect the system’s performance. A schematic diagram (Figure 16) effectively illustrates how these parasitic parameters contribute to bearing current generation in response to CMV.
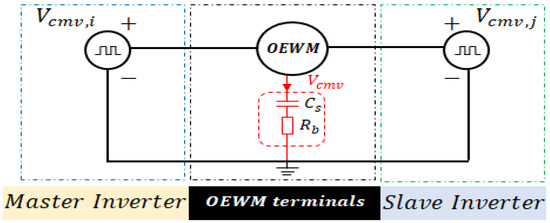
Figure 16.
CMV equivalent circuit of an OEWM.
One of the key advantages of a DTLI connection is its ability to attenuate CMV, thereby mitigating the problems associated with it. The combination of spatial vectors resulting from the use of DTLIs leads to a variety of CMV levels, as thoroughly demonstrated in Table 3. From this table, it is evident that large vectors (such as , , , , , ) and zero vectors (, , ) effectively eliminate CMV. On the other hand, zero vectors (, ) and intermediate vectors (, , , , , , , , , , , ) generate varying levels of CMV.

Table 3.
CMV switching vector variations.
- CMV Reduction
Various approaches have been developed to mitigate CMV, including the use of passive and active common-mode filters [139,140,141,142]. However, the implementation of these devices introduces additional costs and significant power losses. As a result, PWM methods have become the preferred solution for two-level inverters, though they do not fully eliminate CMVs [143,144].
In a previous study [145], an approach was presented that exclusively uses even or odd space vector combinations to reduce CMV from to , without relying on null vector states, within a conventional two-level inverter. Additional modulation-based strategies have been developed to eliminate common-mode voltages by using only a specific subset of the output space vectors [146,147]. However, these methods face a limitation regarding the maximum phase voltage, which restricts the optimal use of the DC bus voltage.
6.1.3. Zero-Sequence Voltage (ZSV)
It is widely recognized that unbalanced three-phase voltages can be decomposed into three distinct sets of voltage components [126]. These components, known as “symmetrical components,” are classified into positive sequence, negative sequence, and zero sequence. Their schematic representation is shown in Figure 17a. The positive and negative sequence components represent three-phase, rotationally balanced phases, while the zero sequence components correspond to a phase with a zero-phase angle. To provide a clearer understanding of this decomposition, Figure 17b illustrates how an unbalanced three-phase voltage breaks down into its symmetrical voltage components.
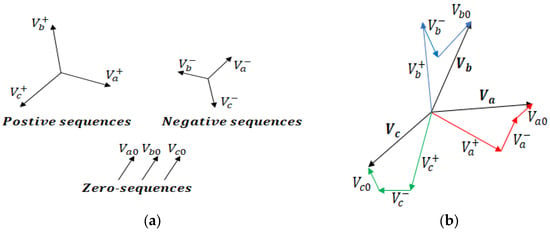
Figure 17.
(a) Symmetrical components. (b) Decomposition of an unbalanced three-phase voltage into symmetrical components.
Unlike positive and negative sequence currents, zero-sequence currents present a unique challenge. Unlike the former, which compensate for each other, zero-sequence currents add arithmetically at the neutral point of a three-phase, four-wire system. This accumulation can lead to the overloading of the neutral conductor or cause a higher voltage between neutral and earth. Additionally, harmonic currents of any sequence flowing through an AC drive can increase the RMS current, resulting in higher system losses, increased THD for current or voltage, and potential overheating and vibration issues in the machine [135].
In a DTLI-powered configuration with a single DCB source, zero-sequence currents (ZSCs) can occur due to ZSV. This voltage arises from the asymmetry of the instantaneous pulse width modulated phase voltages applied to the machine windings, which results from the use of spatial voltage vectors. The corresponding equivalent diagram of the zero-sequence loop is shown in Figure 18. In this diagram, represents the inductance of the homopolar sequence, is the resistance of the phase winding, and and are the CMVs generated by the two inverters in the system, respectively.
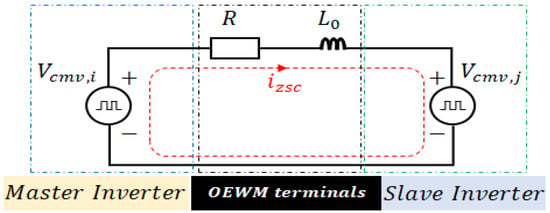
Figure 18.
ZSV equivalent circuit of an OEWM.
The ZSV can be expressed in terms of the CMV of each inverter as follows [62]:
In the DTLI configuration, the ZSV resulting from the 64 space vector combinations can be calculated using Equation (21), as shown in Table 4. From Table 3, it is clear that the zero vectors (, ) and the intermediate vectors (, , , , , , , , , , , ) eliminate the ZSV. Conversely, large vectors (, , , , , ) and zero vectors (, ) generate various levels of ZSV.

Table 4.
ZSV switching vector variations.
Table 3 and Table 4 demonstrate that vectors generating ZSV effectively eliminate CMV. In contrast, vectors designed to eliminate ZSV inevitably introduce CMV. These results highlight the complex interplay between the vectors responsible for both generating and reducing the CMV and ZSV components.
- ZSV reduction
The ZSV issue generates ZSCs, leading to the presence of triple current harmonics [137]. This current can be harmful to motor windings, resulting in increased copper losses and potential circuit saturation. Several methods have been proposed to eliminate this voltage in DTLI configurations. In [148], the solution involved integrating auxiliary switches, while, in [91], an approach was suggested where one side of the OEWM is fed by a three-level inverter, and the other side is fed by a two-level inverter. However, these solutions require additional hardware, which increases costs. Therefore, a more cost-effective solution would be to design appropriate control strategies to eliminate the ZSV. For instance, in [149], the authors proposed desynchronizing the control between the two inverters to create a 120° phase shift between the voltages of the first and second inverters. Similarly, the authors of [150,151] employed a 180° phase shift and introduced the use of even or odd synchronous vectors. In [152], two approaches were suggested that allow for free selection of DTLI switching states. However, these approaches not only eliminate the ZSV but also restrict the inverter switching. Finally, the authors of [48,153] developed a technique called Decoupled Sample-Averaged Zero-Sequence Elimination, which forces the ZSV to zero while minimizing switching losses. A new method tailored for low switching frequencies, called Synchronous Off-Line Optimum PWM, was presented in [154].
6.1.4. DCB Overcharging
DTLI configurations, supplied by two isolated and symmetrical voltage sources (with a voltage ratio of , i.e., both converters use the same voltage level), designed to improve output voltage quality by enabling three-level operation, represented a significant advance in terms of output voltage quality [155].
However, to further improve voltage quality, configurations with two isolated but asymmetrical voltage sources (with a voltage ratio of ) were introduced, allowing a four-level operation [67]. However, the use of these asymmetrical sources introduced a potential overcharging problem, particularly at the DC bus capacitor (DCB-C) (see Figure 19).
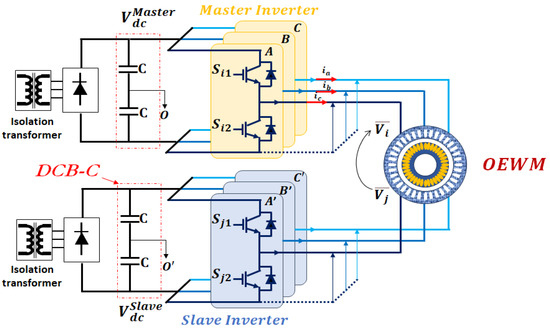
Figure 19.
DTLI structure (the overcharging effect).
The overcharging problem is related to the phase current flowing in the DCB-C during the modulation process. This current is made up of the components , , and , as shown in Figure 19. Depending on the specific switching states, these currents can cause the DCB-C to overcharge. To better understand these scenarios, Figure 20 shows different cases of current flow in the DCB-C, using colors to indicate the path of phase current flow. Green represents the current, red the current, and blue the current.
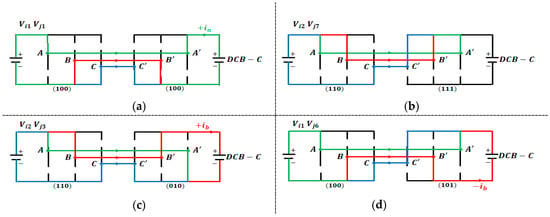
Figure 20.
Examples of currents affecting the DCB-C as a function of the switching vectors applied: (a) , (b) , (c) , (d) .
For example, in Figure 20a, current acts on the positive pole of the DCB-C for the switching state . However, for the switching state , shown in Figure 20b, no current flows through the DCB-C. Figure 20c,d show the current flows resulting from switching states and , respectively. In the case of the state, the current flows in the positive polarity of the DCB-C, while, for the switching state, it flows in the negative polarity of the DCB-C. These currents are referred to as and , respectively.
- Solving the overcharging problem
When addressing the issue of overcharging in DTLI systems, the literature typically presents two main approaches. The first approach involves adjusting modulation schemes [67,116,118,129,131,156], while the second involves the use of additional hardware [113,117,119,130].
In the first approach, switching states are selected by analyzing the current associated with these states to identify those that are likely to cause overcharging. These problematic states are then avoided during the modulation process. This method of voltage regulation, which assumes the direction of the load current, is referred to as the passive regulation method [157]. However, the disadvantage of this approach is that it reduces the number of vectors available for modulation, which can negatively impact the quality of the output voltage. A strategy to switch the master inverter while keeping the slave inverter engaged is presented in [118], but this approach involves a larger modulation area, which may result in higher harmonic distortion in the inverter output. To improve power quality, a coupled discontinuous carrier modulation technique is proposed in [129], but this can increase switching losses. A significant limitation of passive control is that it assumes the direction of current, which can be affected by the power factor of the load [157]. An enhanced version of passive control, called active control, was proposed in [156]. This approach actively selects the appropriate states based on control requirements and measured phase current values.
The second approach, which utilizes additional hardware, is based on the nested rectifier–inverter structure proposed in [117] (see Figure 21) and further refined in [158]. In this structure, the slave inverter with a lower DCB voltage is nested inside a higher-voltage DCB feeding the master inverter. This configuration enables the implementation of advanced modulation schemes to optimize voltage utilization for motors [119] or to suppress ZSCs in an averaged manner [130].
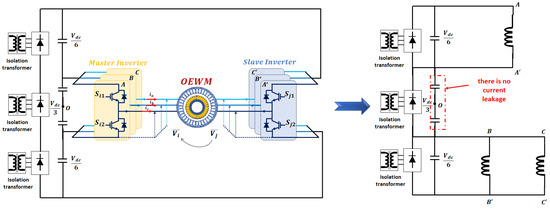
Figure 21.
DTLI with a nested rectifier–inverter with OEWM phase connection for the state reported in [117].
It should be noted that, while the nested rectifier–inverter configuration can address the overcharging problem, it requires an additional isolated DC power supply. This addition can lead to increased complexity, size, and cost of the motor drive system [118,129].
6.1.5. Floating-Capacitor (FC) Voltage
Compared to other DTLI configurations, whether with isolated or shared continuous buses, the structure based on a continuous bus and an FC has the notable advantage of minimizing the circulation of ZSVs (ZSCs), which is virtually nonexistent, and does not require additional isolation circuits. However, this approach is not without significant challenges. The main obstacle it faces lies in FC voltage management, which, due to its floating nature [119], generates undesirable voltage steps at the converter output.
As a result of the voltage control approach applied to both converters, the voltage across the load becomes unpredictable. These unwanted voltage steps have the potential to significantly degrade output performance, thereby reducing the attractiveness of this configuration [120]. For example, in the case where the voltage ratio is , Table 5 presents the 37 space vectors that will charge or discharge the FC and generate a voltage variation. These vectors can be classified into three types: Type 1 for vectors with redundancy states that cause the phase current to act on both the positive and negative polarities of the FC, Type 2 for vectors that have only one instance of current flow, and Type 3 for vectors that have no effect on the voltage variation in the FC.

Table 5.
Effects of the three types of vectors on current flow in the FC.
- Maintaining FC voltage
The authors in [121,125] addressed the issue of FC voltage regulation in a DTLI while maintaining multilevel operation. Several approaches were examined:
- Coupled Modulation [121,123,124,125,128,159]: This method treats the DTLI as a single unit for modulation, enabling analysis of the switching states’ impact on the capacitor voltage in steady-state operation. However, there is a risk of under-utilizing the capacitor voltage, which can reduce the output level.
- FC Voltage Regulation with Reference to Motor Power Factor [121]: This method involves feedback from the motor power factor angle for regulation, providing an active yet complex solution based on motor speed.
- Decoupled Modulation [65,122,160,161,162,163]: In this approach, the FC is treated as a reactive power capacitor, and active power regulation is applied to the FC. However, it may lead to undesirable voltage steps that affect output performance.
- Step Modulation for the Master Inverter and High-Frequency PWM for the Slave [164]: In this scheme, the master inverter operates at the fundamental frequency, while the slave inverter uses high-frequency modulation. The FC voltage is regulated by adjusting the trigger angle of the fundamental voltage. While this approach reduces switching losses, it may not be suitable for all situations and is relatively complex.
6.2. Energy Efficiency: Power Losses
Generally, there are two types of losses in PWM power electronics converters: conduction losses and switching losses , with switching losses occurring during the transitions from to switch-on and from to switch-off. These losses are expressed as follows [75]:
where is the instantaneous phase current, is the switch-off voltage, and are the switch-on and switch-off times, is the voltage drop, is the on-time, and is the switching frequency.
It is well established that, in power semiconductor devices, power losses due to switching are directly proportional to the switching frequency. These switching-related losses occur during the turn-on and turn-off phases of the device and are mainly influenced by the time over which the switching voltage and current rise and fall, respectively [165]. In other words, as the switching frequency increases, the power losses generated by switching also increase. These losses are primarily determined by the variations in voltage and current during these phases.
As an example, Figure 22 illustrates phase A of an inverter arm. In this diagram, components and represent the upper and lower switches of the arm, while and are the associated antiparallel diodes. Furthermore, Figure 23 shows the voltage across the switch and the antiparallel diode, as well as the current flowing through them and the resulting power losses, particularly when .
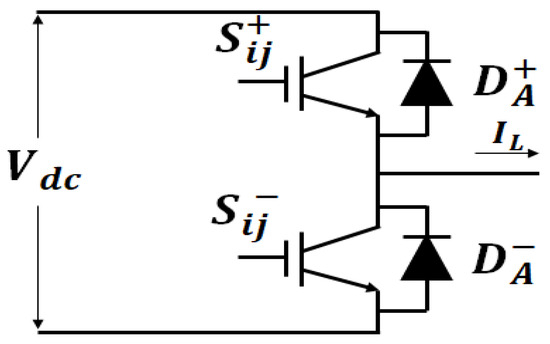
Figure 22.
Phase A of the inverter branch.
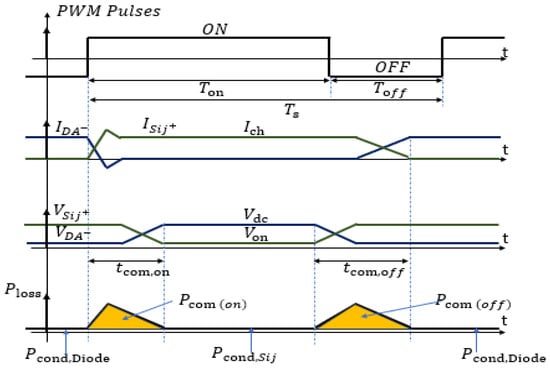
Figure 23.
Current through inverter switches and voltage drop between them in phase branch A.
However, the introduction of DTLIs into a system can negatively impact its overall efficiency, primarily due to the increased power losses they generate. In the context of our configuration, it is important to highlight that total switching losses are significantly higher, potentially reaching up to twice the levels observed in conventional systems [97].
- Power loss reduction
To increase the efficiency of DTLI systems, various modulation strategies have been explored in the literature. In references [91,151,152,166], the sub-hexagonal center PWM (SHCPWM) modulation scheme, based on PWM pulse shifting, has been developed to mitigate switching losses. This method involves sequential switching of the two inverters, effectively halving switching losses compared to conventional DTLI configurations. Additionally, SHCPWM avoids the generation of unwanted bearing currents [91]. However, it is limited by a restricted set of switching states and requires complex PWM pulse reordering, which can be computationally intensive [91,151,152,166].
Another approach to minimizing switching losses is discontinuous pulse width modulation (DPWM), as described in [118,167,168]. DPWM holds certain power semiconductors in the ON or OFF position over specific intervals. This technique is more efficient than space vector PWM (SVPWM) for high-power, high-frequency switching applications [59]. Furthermore, different DPWM variants, such as DPWM 30°, 60°, and 120°, have been developed, which reduce switching losses by an average of 33% by avoiding switching transitions near phase current peaks [169]. DPWM also accounts for the phase difference between current and voltage, even when the power factor is considered [170].
7. Impact of Control Strategies on OEWM-DTLI Performance
As previously mentioned, the OEWM system is powered by a DTLI, and its modeling is similar to that of a conventional AC machine. In terms of control, two complementary levels of strategies can be identified in the literature: high-level control techniques, which focus on the regulation of machine variables (such as scalar control, vector control, and direct torque control (DTC)), and low-level control techniques, which deal directly with the generation of the modulation and carrier signals, typically based on PWM.
Given our focus on voltage quality and energy efficiency, we concentrate on the PWM control of both inverters. Thus, the performance of the OEWM largely depends on how these two inverters are modulated to produce the appropriate output signals.
To provide an overview of the existing literature, Table 6 presents a summary of the three types of configurations studied, highlighting their key contributions and their significant effects on OEWM performance. These contributions are particularly notable for their substantial improvements in critical performance parameters, including overcharging of the capacity, CMV, ZSV, THD, and the efficiency of the DTLI system.

Table 6.
Summary of existing contributions on DTLI configurations and their impact on OEWM perfor-mance.
8. Conclusions
This paper presented a comprehensive technical analysis of Dual Two-Level Inverter (DTLI) topologies for motor drive applications. The investigation covered the fundamental operating principles of DTLI systems and examined three key structural configurations: the conventional Common DC Bus (C-DCB), the Two-Isolated DC Bus (TI-DCB), and the more recent Floating Capacitor-based DC Bus (DCB-FC). A detailed mathematical model of the DTLI system was developed to support this analysis, highlighting voltage distribution mechanisms and control strategies specific to each architecture.
To evaluate system performance, several critical criteria were considered, including total harmonic distortion (THD), common-mode voltage (CMV), zero-sequence voltage (ZSV), energy efficiency, floating capacitor voltage behavior, and the risk of DC bus overcharging. In addition, this study included a comparative summary (Table 6) of several PWM techniques, emphasizing their influence on waveform quality and overall system efficiency across the three configurations.
Among the architectures studied, the dual C-DCB configuration stood out for its simplicity and robustness, attributed to its symmetrical design and straightforward control implementation without the need for additional hardware. However, its limitations in suppressing ZSV, alongside the DC bus overcharging risks associated with the TI-DCB configuration, motivated further interest in the DCB-FC structure. The DCB-FC demonstrated superior performance thanks to its self-regulated floating capacitor voltage and the elimination of isolation requirements.
In conclusion, both the C-DCB and DCB-FC configurations exhibit strong potential for modern high-performance power conversion systems, offering practical trade-offs between simplicity, control complexity, and electromagnetic performance. These findings serve as a foundation for the development of more efficient and reliable inverter systems in future industrial and renewable energy applications.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DTLI | Dual Two-Level Inverter |
| DC | Direct Current |
| AC | Alternative Current |
| FACTS | Flexible AC Transmission System |
| THD | Total harmonic distortion |
| NPC | Neutral Point Clamped |
| OEWM | Open-end winding machine |
| FC | Floating capacitor |
| DCB | Direct Current Bus |
| C-DCB | Common-Direct Current Bus |
| TI-DCB | Two Isolated-Direct Current Bus |
| DCB-FC | Direct Current Bus–Floating Capacitor |
| ZSC | Zero-sequence current |
| ZSV | Zero-sequence voltage |
| CMV | Common-mode voltage |
| EV | Electrical Vehicle |
| HEV | Hybrid Electrical Vehicle |
| PV | Photovoltaic |
| IGBT | Insulated-Gate Bipolar Transistor |
| MOSFET | Metal-Oxide-Semiconductor Field-Effect Transistor |
| SHC | Sub-hexagonal center |
| PCC | Point of Common Coupling |
| RMS | Root Mean Square |
| DCB-C | Direct Current Bus Capacitor |
| PWM | Pulse width modulation |
| SVPWM | Space vector pulse width modulation |
| DPWM | Discontinuous pulse width modulation |
| SHCPWM | Sub-hexagonal center pulse width modulation |
References
- IEA—Global Energy Review 2025: CO2 Emissions. Available online: https://www.iea.org/reports/global-energy-review-2025/co2-emissions (accessed on 23 April 2025).
- Hassan, M.H.; Mohamed, E.M.; Kamel, S.; Ardjoun, S.A.E.M. Stochastic Optimal Power Flow Integrating with Renewable Energy Resources and V2G Uncertainty Considering Time-Varying Demand: Hybrid GTO-MRFO Algorithm. IEEE Access 2024, 12, 97893–97923. [Google Scholar] [CrossRef]
- Gonzalez-Abreu, A.-D.; Osornio-Rios, R.-A.; Jaen-Cuellar, A.-Y.; Delgado-Prieto, M.; Antonino-Daviu, J.-A.; Karlis, A. Advances in Power Quality Analysis Techniques for Electrical Machines and Drives: A Review. Energies 2022, 15, 1909. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Atia, B.S.; Esmail, Y.M.; Ardjoun, S.A.E.M.; Anwer, N.; Omar, A.I.; Mohamed, S.A. Application of whale optimization algorithm based FOPI controllers for STATCOM and UPQC to mitigate harmonics and voltage in-stability in modern distribution power grids. Axioms 2023, 12, 420. [Google Scholar] [CrossRef]
- Moghassemi, A.; Padmanaban, S. Dynamic Voltage Restorer (DVR): A Comprehensive Review of Topologies, Power Converters, Control Methods, and Modified Configurations. Energies 2020, 13, 4152. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Poorfakhraei, A.; Vahedi, H.; Guse, M.; Trabelsi, M.; Abdelrahem, M.; Ahmed, M.; Fahad, M.; Lin, C.H.; et al. Common DC-Link Multilevel Converters: Topologies, Control and Industrial Applications. IEEE Open J. Power Electron. 2023, 4, 512–538. [Google Scholar] [CrossRef]
- Qi, Z.; Hossain, M.B.; Islam, M.R.; Rahman, M.A.; Raad, R. Advancement in Converter Topology, Control, and Power Management: Magnetic Linked Power Converter for Emerging Applications. IEEE Access 2024, 12, 101228–101246. [Google Scholar] [CrossRef]
- Sánchez, L.; Reigosa, D.; Bilbao, A.; Peña-Gonzalez, I.; Briz, F. Comparative Analysis of Power Converter Topologies for Hydrogen Electrolyzers. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 4325–4341. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Abid, M. Fuzzy Sliding Mode Control Applied to a Doubly Fed Induction Generator for Wind Turbines. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 12. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Denai, M.; Abid, M. A Robust Power Control Strategy to Enhance LVRT Capability of Grid-Connected DFIG-Based Wind Energy Systems. Wind Energy 2019, 22, 834–847. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Denai, M.; Abid, M. Robustification du contrôle des éoliennes pour une meilleure intégration dans un réseau déséquilibré. In Proceedings of the 2019 Algerian Large Electrical Network Conference (CAGRE), Algiers, Algeria, 20–21 November 2019. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Denaï, M.; Chafouk, H. A Robust Control Approach for Frequency Support Capability of Grid-Tie Photovoltaic Systems. J. Sol. Energy Eng. 2023, 145, 021009. [Google Scholar] [CrossRef]
- Shen, X.; Liu, G.; Liu, J.; Gao, Y.; Leon, J.I.; Wu, L.; Franquelo, L.G. Fixed-Time Sliding Mode Control for NPC Converters with Improved Disturbance Rejection Performance. IEEE Trans. Ind. Inform. 2025. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, X.; Gao, Y.; Xu, R.; Wang, J.; Wang, Y.; Liu, J. Fixed-Time Sliding Mode Control for DC/DC Buck Converters with Mismatched Uncertainties. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 472–480. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Liu, G.; Zhang, J.; Leon, J.I.; Wu, L.; Franquelo, L.G. Finite-Time Sliding Mode Control for NPC Converters with Enhanced Disturbance Compensation. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 1822–1831. [Google Scholar] [CrossRef]
- Mohammed Abbas, H.; Chafouk, H.; Ardjoun, S.A.E.M. Current Sensor Fault Diagnosis of DFIG Wind Turbines Using an Extended Kalman Filter Observer: Experimental Validation. IFAC-Pap. OnLine 2024, 58, 610–615. [Google Scholar] [CrossRef]
- Abbas, M.; Ardjoun, S.A.E.M.; Chafouk, H. Current Sensor Fault Diagnosis in DFIG Wind Turbines: Kalman Filter-Based Dedicated Observer Scheme. In Proceedings of the 2024 3rd International Conference on Advanced Electrical Engineering (ICAEE), Sidi-Bel-Abbes, Algeria, 5–7 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Abbas, M.; Chafouk, H.; Ardjoun, S.A.E.M. Fault Diagnosis in Wind Turbine Current Sensors: Detecting Single and Multiple Faults with the Extended Kalman Filter Bank Approach. Sensors 2024, 24, 728. [Google Scholar] [CrossRef]
- Miloudi, H.; Miloudi, M.; Ardjoun, S.A.E.M.; Mahmoud, M.M.; Telba, A.A.; Denaï, M.; Khaled, U.; Ewais, A.M. Electromagnetic Compatibility Characterization of Start-Capacitor Single-Phase Induction Motor. IEEE Access 2024, 12, 2313–2326. [Google Scholar] [CrossRef]
- Miloudi, H.; Miloudi, M.; Ardjoun, S.A.E.M.; Nour, A.A.; Mahariq, I. Experimental Investigation of Conducted Electromagnetic Interference Differential-Mode Performance in Various Split-Phase Induction Motors Designs. Results Eng. 2025, 25, 103963. [Google Scholar] [CrossRef]
- Wang, K.; Wu, S.; Fan, C.; Yang, C.; Wu, W.; Liserre, M. Peak Current Reduction of Bidirectional-Asymmetrical-Power-Flow DC-DC Converters for Low-Penetration-Renewable-Energy Power Distribution Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 4342–4351. [Google Scholar] [CrossRef]
- Ibrahim, N.F.; Ardjoun, S.A.E.M.; Alharbi, M.; Alkuhayli, A.; Abuagreb, M.; Khaled, U.; Mahmoud, M.M. Multiport Converter Utility Interface with a High-Frequency Link for Interfacing Clean Energy Sources (PV\Wind\Fuel Cell) and Battery to the Power System: Application of the HHA Algorithm. Sustainability 2023, 15, 13716. [Google Scholar] [CrossRef]
- Chai, Q.; Zhang, C.; Xu, Y.; Dong, Z.Y.; Zhang, R. Pareto Front Analysis Method for Optimization of PV Inverter Based Volt/Var Control Considering Inverter Lifetime. CSEE J. Power Energy Syst. 2023, 9, 111–121. [Google Scholar] [CrossRef]
- Ibrahim, N.F.; Mahmoud, M.M.; Alnami, H.; Mbadjoun Wapet, D.E.; Ardjoun, S.A.E.M.; Mosaad, M.I.; Abdelfattah, H. A New Adaptive MPPT Technique Using an Improved INC Algorithm Supported by Fuzzy Self-Tuning Controller for a Grid-Linked Photovoltaic System. PLoS ONE 2023, 18, e0293613. [Google Scholar] [CrossRef]
- Boudjemai, H.; Ardjoun, S.A.E.M.; Chafouk, H.; Denai, M.; Elbarbary, Z.M.S.; Omar, A.I.; Mahmoud, M.M. Application of a Novel Synergetic Control for Optimal Power Extraction of a Small-Scale Wind Generation System with Variable Loads and Wind Speeds. Symmetry 2023, 15, 369. [Google Scholar] [CrossRef]
- Boudjemai, H.; Ardjoun, S.A.E.M.; Chafouk, H.; Denaï, M.; Alkuhayli, A.; Khaled, U.; Mahmoud, M.M. Experimental Analysis of a New Low Power Wind Turbine Emulator Using a DC Machine and Advanced Method for Maximum Wind Power Capture. IEEE Access 2023, 11, 92225–92241. [Google Scholar] [CrossRef]
- Boudjemai, H.; Ardjoun, S.A.E.M.; Chafouk, H.; Denai, M.; Aljohani, M.; Mosaad, M.I.; Mahmoud, M.M. Design, Simulation, and Experimental Validation of a New Fuzzy Logic-Based Maximal Power Point Tracking Strategy for Low Power Wind Turbines. Int. J. Fuzzy Syst. 2024, 26, 2567–2584. [Google Scholar] [CrossRef]
- Alnami, H.; Ardjoun, S.A.E.M.; Mahmoud, M.M. Design, Implementation, and Experimental Validation of a New Low-Cost Sensorless Wind Turbine Emulator: Applications for Small-Scale Turbines. Wind Eng. 2024, 48, 565–579. [Google Scholar] [CrossRef]
- Wang, J.; Sun, K.; Xue, C.; Liu, T.; Li, Y. Multi-Port DC-AC Converter with Differential Power Processing DC-DC Converter and Flexible Power Control for Battery ESS Integrated PV Systems. IEEE Trans. Ind. Electron. 2022, 69, 4879–4889. [Google Scholar] [CrossRef]
- Menzi, D.; Imperiali, L.; Bürgisser, E.; Ulmer, M.; Huber, J.; Kolar, J.W. Ultralightweight High-Efficiency Buck-Boost DC-DC Converters for Future eVTOL Aircraft with Hybrid Power Supply. IEEE Trans. Transp. Electrif. 2024, 10, 10297–10313. [Google Scholar] [CrossRef]
- Srivastava, A.; Seshadrinath, J. A New Nine-Level Highly Efficient Boost Inverter for Transformerless Grid-Connected PV Application. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2730–2741. [Google Scholar] [CrossRef]
- Fahim, R.A.; Biswas, S.P.; Hosain, M.K.; Hossain, S.; Mondal, S.; Islam, M.R.; Fekih, A. Improved Switching Technique to Mitigate THD and Power Loss of NPC Inverters. IEEE Trans. Appl. Supercond. 2024, 34, 5000505. [Google Scholar] [CrossRef]
- Liu, H.; Fang, T.; Lin, Z.; Wang, P.; Huang, X.; Li, Y. Droop Control Strategy Without Interconnection Lines for Input-Parallel Output-Series Grid-Connected Inverter System. IEEE Trans. Ind. Electron. 2024, 71, 15224–15228. [Google Scholar] [CrossRef]
- Ge, B.; Chen, L.; Yonak, S.H. A 240° Phase Voltage Clamped Inverter for Electric Drives. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 937–941. [Google Scholar] [CrossRef]
- Payarou, T.; Pillay, P. Integrated Multipurpose Power Electronics Interface for Electric Vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 2429–2443. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.A.; Sarebanzadeh, M.; Garcia, C.F.; Babaei, E.; Rodriguez, J.; Kennel, R. A New Generalized Multisource Inverter for Electric Vehicles Controlled by Model Predictive. IEEE Trans. Ind. Electron. 2024, 71, 10184–10197. [Google Scholar] [CrossRef]
- Jelodar, Y.J.; Salari, O.; Youssef, M.Z.; Ebrahimi, J.; Bakhshai, A. A Novel Control Scheme for Traction Inverters in Electric Vehicles with an Optimal Efficiency Across the Entire Speed Range. IEEE Access 2024, 12, 25906–25916. [Google Scholar] [CrossRef]
- Ali, A.; Mousa, H.H.H.; Shaaban, M.F.; Azzouz, M.A.; Awad, A.S.A. A Comprehensive Review on Charging Topologies and Power Electronic Converter Solutions for Electric Vehicles. J. Mod. Power Syst. Clean Energy 2024, 12, 675–694. [Google Scholar] [CrossRef]
- Pongnot, G.; Desreveaux, A.; Mayet, C.; Labrousse, D.; Roy, F. Comparative Analysis of a Low-Voltage CHB Inverter Without PWM and Two-Level IGBT/SiC Inverters for Electric Vehicles on Driving Cycles. IEEE Open J. Veh. Technol. 2025, 6, 542–553. [Google Scholar] [CrossRef]
- Do, T.V.; Kandidayeni, M.; Trovão, J.P.F.; Boulon, L. Multi-Criteria Ranking of Z-Source Inverter Topologies for a Three-Wheel Fuel Cell Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2025, 74, 2527–2537. [Google Scholar] [CrossRef]
- Do, T.V.; Kandidayeni, M.; Trovão, J.P.F.; Boulon, L. Dual-Source High-Performance Active Switched Quasi-Z-Source Inverter for Fuel Cell Hybrid Vehicles. IEEE Trans. Power Electron. 2023, 38, 12497–12507. [Google Scholar] [CrossRef]
- Stemmler, H.; Guggenbach, P. Configurations of high-power voltage source inverter drives. In Proceedings of the 1993 Fifth European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; Volume 5, pp. 7–14. Available online: https://ieeexplore.ieee.org/abstract/document/265146 (accessed on 4 February 2025).
- Djellouli, Y.; Ardjoun, S.A.E.M.; Zerdali, E.; Denai, M.; Chafouk, H. The Real-Time Observation of Electric Vehicle Operating Points Using an Extended Kalman Filter. Automation 2024, 5, 613–629. [Google Scholar] [CrossRef]
- Lee, K.; Kim, H. A Novel ZSC Suppression Strategy with Third-harmonic Back-EMF Estimation for OW-PMSM Fed by Dual Inverter with a Common DC-bus. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; pp. 6110–6115. [Google Scholar] [CrossRef]
- Lee, H.-W.; Jang, S.-J.; Lee, K.-B. Advanced DPWM Method for Switching Loss Reduction in Isolated DC Type Dual Inverter With Open-End Winding IPMSM. IEEE Access 2023, 11, 2700–2710. [Google Scholar] [CrossRef]
- Kim, T.-H.; Lee, J.-H.; Yoon, B.-R.; Lee, J.-S. Clamping Modulation Technique for Balancing Power Losses of Dual Inverter with Isolated DC Bus. IEEE Access 2023, 11, 41868–41879. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, T.; Giangrande, P.; Chowdhury, S.; Galea, M.; Wheeler, P. Enhanced Performance of Dual Inverter with a Floating Capacitor for Motor Drive Applications. IEEE Trans. Power Electron. 2021, 36, 6903–6916. [Google Scholar] [CrossRef]
- Riccio, J.; Testa, A.; Iannuzzo, F.; Zanchetta, P.; Andenna, G. Effects of the Floating Capacitor Voltage on the Torque-Speed Characteristic of an Open-End Winding Synchronous Reluctance Motor Drive. IEEE Trans. Ind. Appl. 2025, 61, 3269–3278. [Google Scholar] [CrossRef]
- Zerdani, M.; Ardjoun, S.E.; Chafouk, H.; Denai, M. Experimental Validation of a New Power Chain for Electric Vehicles. In Proceedings of the 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 23–24 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Subotic, I.; Bodo, N.; Levi, E.; Jones, M. Onboard integrated battery charger for EVs using an asymmetrical nine-phase machine. IEEE Trans. Ind. Electron. 2014, 62, 3285–3295. [Google Scholar] [CrossRef]
- Drissi, K.E.K.; Pasquier, C. Angular modulation of dual-inverter fed open-end motor for electrical vehicle applications. IEEE Trans. Power Electron. 2015, 31, 2980–2990. [Google Scholar] [CrossRef]
- Younes, D.; Ahmed El Mehdi, A.S.; Houcine, C.; Mouloud, D. Sensorless Torque Control of an Electric Vehicle Driven by an Open End Winding Induction Motor: An Experimental Study. In Proceedings of the 2023 Second International Conference on Energy Transition and Security (ICETS), Adrar, Algeria, 12–14 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Bojoi, R.; Cavagnino, A.; Tenconi, A.; Vaschetto, S. Control of shaft-line-embedded multiphase starter/generator for aero-engine. IEEE Trans. Ind. Electron. 2015, 63, 641–652. [Google Scholar] [CrossRef]
- Sun, C.; Ai, S.; Hu, L.; Chen, Y. The development of a 20MW PWM driver for advanced fifteen-phase propulsion induction motors. J. Power Electron. 2015, 15, 146–159. [Google Scholar] [CrossRef]
- Srinivas, S.; Sekhar, K.R. Theoretical and experimental analysis for current in a dual-inverter-fed open-end winding induction motor drive with reduced switching PWM. IEEE Trans. Ind. Electron. 2012, 60, 4318–4328. [Google Scholar] [CrossRef]
- Mohammed, Z.; Mehdi, S.A.S.A.E.; Houcine, C.; Mouloud, D. Experimental Analysis of the Decoupled PWM Influence on the Open-End Winding Induction Machine. In Proceedings of the 2022 2nd International Conference on Advanced Electrical Engineering (ICAEE), Constantine, Algeria, 29–31 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Somasekhar, V.T.; Srinivas, S.; Kumar, K.K. Effect of zero-vector placement in a dual-inverter fed open-end winding induction-motor drive with a decoupled space-vector PWM strategy. IEEE Trans. Ind. Electron. 2008, 55, 2497–2505. [Google Scholar] [CrossRef]
- Nguyen, N.K.; Meinguet, F.; Semail, E.; Kestelyn, X. Fault-tolerant operation of an open-end winding five-phase PMSM drive with short-circuit inverter fault. IEEE Trans. Ind. Electron. 2015, 63, 595–605. [Google Scholar] [CrossRef]
- An, Q.; Liu, J.; Peng, Z.; Sun, L.; Sun, L. Dual-space vector control of open-end winding permanent magnet synchronous motor drive fed by dual inverter. IEEE Trans. Power Electron. 2016, 31, 8329–8342. [Google Scholar] [CrossRef]
- Ewanchuk, J.; Salmon, J.; Chapelsky, C. A method for supply voltage boosting in an open-ended induction machine using a dual inverter system with a floating capacitor bridge. IEEE Trans. Power Electron. 2012, 28, 1348–1357. [Google Scholar] [CrossRef]
- Djellouli, Y.; El Mehdi Ardjoun, S.A.; Zerdali, E.; Denai, M.; Chafouk, H. Real Time Implementation of a Speed/Torque Sensorless Observer for Induction Motor Utilizing Extended Kalman Filtering Technique. In Proceedings of the 2024 3rd International Conference on Advanced Electrical Engineering (ICAEE), Sidi-Bel-Abbes, Algeria, 5–7 November 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Panda, D.; Lipo, T.A.; Pan, D. Open-winding power conversion systems fed by half-controlled converters. IEEE Trans. Power Electron. 2012, 28, 2427–2436. [Google Scholar] [CrossRef]
- Riedemann, J.; Clare, J.C.; Wheeler, P.W.; Blasco-Gimenez, R.; Rivera, M.; Pena, R. Open-end winding induction machine fed by a dual-output indirect matrix converter. IEEE Trans. Ind. Electron. 2016, 63, 4118–4128. [Google Scholar] [CrossRef]
- Naganathan, P.; Srinivas, S. Voltage-injected PWM variants for a dual two-level inverter-fed open-end winding induction motor drive. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1532–1540. [Google Scholar] [CrossRef]
- Lee, Y.; Ha, J.-I. Hybrid modulation of dual inverter for open-end permanent magnet synchronous motor. IEEE Trans. Power Electron. 2014, 30, 3286–3299. [Google Scholar] [CrossRef]
- Jia, Y.-F.; Xu, N.; Chu, L.; Zhang, L.F.; Zhao, D.; Li, Y.K.; Yang, Z.H. Power flow control strategy based on the voltage vector distribution for a dual power electric vehicle with an open-end winding motor drive system. IEEE Access 2018, 6, 54910–54926. [Google Scholar] [CrossRef]
- Reddy, B.V.; Somasekhar, V.T.; Kalyan, Y. Decoupled space-vector PWM strategies for a four-level asymmetrical open-end winding induction motor drive with waveform symmetries. IEEE Trans. Ind. Electron. 2011, 58, 5130–5141. [Google Scholar] [CrossRef]
- Somasekhar, V.; Shivakumar, E.; Gopakumar, K.; Pittet, A. Multi level voltage space phasor generation for an open-end winding induction motor drive using a dual inverter scheme with asymmetrical DC-link voltages. EPE J. 2002, 12, 59–77. [Google Scholar] [CrossRef]
- Kiadehi, A.D.; Drissi, K.E.K.; Pasquier, C. Voltage THD reduction for dual-inverter fed open-end load with isolated DC sources. IEEE Trans. Ind. Electron. 2016, 64, 2102–2111. [Google Scholar] [CrossRef]
- Chen, S.; Lipo, T.A.; Fitzgerald, D. Source of induction motor bearing currents caused by PWM inverters. IEEE Trans. Energy Convers. 1996, 11, 25–32. [Google Scholar] [CrossRef]
- Zhong, E.; Lipo, T.A. Improvements in EMC performance of inverter-fed motor drives. IEEE Trans. Ind. Appl. 1995, 31, 1247–1256. [Google Scholar] [CrossRef]
- Kalaiselvi, J.; Srinivas, S. Bearing currents and shaft voltage reduction in dual-inverter-fed open-end winding induction motor with reduced CMV PWM methods. IEEE Trans. Ind. Electron. 2014, 62, 144–152. [Google Scholar] [CrossRef]
- Datta, A.K.; Dubey, M.; Jain, S. Effect of static power supply in alternator used for short-circuit testing-observation of shaft voltage. IEEE Trans. Power Electron. 2014, 29, 6074–6080. [Google Scholar] [CrossRef]
- Akhtar, M.J.; Behera, R.K. Space vector modulation for distributed inverter-fed induction motor drive for electric vehicle application. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 379–389. [Google Scholar] [CrossRef]
- Zerdani, M.; Ardjoun, S.A.E.M.; Chafouk, H.; Denaï, M. Experimental investigation of decoupled discontinuous PWM strategies in open-end winding induction motor supplied by a common DC-link. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3087–3096. [Google Scholar] [CrossRef]
- Calzo, G.L.; Zanchetta, P.; Gerada, C.; Lidozzi, A.; Degano, M.; Crescimbini, F.; Solero, L. Performance evaluation of converter topologies for high speed starter/generator in aircraft applications. In Proceedings of the 2014 IECON 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1707–1712. [Google Scholar] [CrossRef]
- Rovere, L.; Formentini, A.; Calzo, G.L.; Zanchetta, P.; Cox, T. Zero-sequence voltage elimination for dual-fed common DC-link open-end winding PMSM high-speed starter–generator—Part I: Modulation. IEEE Trans. Ind. Appl. 2019, 55, 7804–7812. [Google Scholar] [CrossRef]
- Rovere, L.; Formentini, A.; Calzo, G.L.; Zanchetta, P.; Cox, T. Zero-sequence voltage elimination for dual-fed common DC-link open-end winding PMSM high-speed starter-generator—Part II: Deadtime hysteresis control of zero-sequence current. IEEE Trans. Ind. Appl. 2019, 55, 7813–7821. [Google Scholar] [CrossRef]
- Jia, Y.-F.; Xu, N.; Chu, L.; Zhang, Y.; Xu, Z.; Li, Y.K.; Yang, Z.H. Control strategy for an open-end winding induction motor drive system for dual-power electric vehicles. IEEE Access 2020, 8, 8844–8860. [Google Scholar] [CrossRef]
- Lee, K. Fault-Tolerant Control for One-Phase Current Sensor Fault in Open-End Winding PMSM fed by Dual Inverter with a Common DC Bus. IEEE Trans. Power Electron. 2025, 40, 124–128. [Google Scholar] [CrossRef]
- Raherimihaja, H.J.; Zhang, Q.; Na, T.; Shao, M.; Wang, J. A three-phase integrated battery charger for EVs based on six-phase open-end winding machine. IEEE Trans. Power Electron. 2020, 35, 12122–12132. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Lorenz, R.D.; Nied, A.; Cheng, M. Design and comparison of three-phase and five-phase FTFSCW-IPM motor open-end winding drive systems for electric vehicles applications. IEEE Trans. Veh. Technol. 2017, 67, 385–396. [Google Scholar] [CrossRef]
- Kim, J.; Jung, J.; Nam, K. Dual-inverter control strategy for high-speed operation of EV induction motors. IEEE Trans. Ind. Electron. 2004, 51, 312–320. [Google Scholar] [CrossRef]
- Matsumori, H.; Kosaka, T.; Matsui, N.; Saha, S. Inverter power device fault detection and fail safe action strategy for electric vehicle with a dual inverter fed open winding motor. IEEE Trans. Ind. Appl. 2023, 59, 3875–3888. [Google Scholar] [CrossRef]
- Kim, T.-H.; Lee, J.-H.; Kim, Y.-J.; Lee, J.-S. PWM technique of dual inverter with an isolated DC bus considering power factor to minimize and balance power loss. IEEE Trans. Power Electron. 2025, 40, 4303–4313. [Google Scholar] [CrossRef]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Pires, A.J.; Chen, H.; Martins, J.F.; Castro, R. A cascaded dual four-leg inverter for photovoltaic systems with capability to compensate unbalanced distribution networks. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 960–968. [Google Scholar] [CrossRef]
- Calzo, G.L.; Zanchetta, P.; Gerada, C.; Gaeta, A.; Crescimbini, F. Converter topologies comparison for more electric aircrafts high speed starter/generator application. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3659–3666. [Google Scholar] [CrossRef]
- Zhou, Y.; Nian, H. Zero-sequence current suppression strategy of open-winding PMSG system with common DC bus based on zero vector redistribution. IEEE Trans. Ind. Electron. 2014, 62, 3399–3408. [Google Scholar] [CrossRef]
- Vasuda, K.V.; Johny, L.K.; Mathew, J. Effective DC Link Utilization of Multilevel Dual Inverter with Single Source in the Maximal Distention Mode. IEEE Access 2024, 12, 26212–26221. [Google Scholar] [CrossRef]
- Wang, G.; Sun, X.; Liu, Z.; Jiang, D.; Wang, D.; Qu, R. Open-Circuit Fault-Tolerant Control of Dual Three-Phase Open-Winding Machine Drive with a Floating Capacitor. IEEE Trans. Transp. Electrific. 2025, 11, 6731–6741. [Google Scholar] [CrossRef]
- Baiju, M.R.; Mohapatra, K.K.; Kanchan, R.; Gopakumar, K. A dual two-level inverter scheme with common mode voltage elimination for an induction motor drive. IEEE Trans. Power Electron. 2004, 19, 794–805. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Abıd, M.; Aıssaouı, A.G.; Tahour, A. A Robust Sliding Mode Control Applied to the Double Fed Induction Machine. IU-J. Electr. Electron. Eng. 2013, 12, 1445–1451. Available online: https://dergipark.org.tr/en/pub/iujeee/issue/9356/117021 (accessed on 4 February 2025).
- Younes, D.; El Mehdi, S.A.A.S.A.; Mouloud, D.; Houcine, C. Real-Time Implementation of the Luenberger Torque Observer for an Induction Motor. In Proceedings of the 2023 2nd International Conference on Electronics, Energy and Measurement (IC2EM), Medea, Algeria, 28–30 November 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Khan, H.; Miliani, E.-H.; Drissi, K.E.K. Discontinuous Random Space Vector Modulation for Electric Drives: A Digital Approach. IEEE Trans. Power Electron. 2012, 27, 4944–4951. [Google Scholar] [CrossRef]
- Zerdani, M.; Chafouk, H.; Ardjoun, S.A.E.M. Performance Analysis of a Dual-Inverter-Fed Open-End Winding Induction Machine under Asymmetrical Control: Theoretical Approach and Experimental Validation. Symmetry 2024, 16, 395. [Google Scholar] [CrossRef]
- Sekhar, K.R.; Srinivas, S. Discontinuous Decoupled PWMs for Reduced Current Ripple in a Dual Two-Level Inverter Fed Open-End Winding Induction Motor Drive. IEEE Trans. Power Electron. 2012, 28, 2493–2502. [Google Scholar] [CrossRef]
- Lee, K.; Han, Y. Simple Discontinuous Pulse-Width Modulation Scheme for the Loss Reduction of a Dual Inverter Fed an Open-End Winding Induction Motor. IEEE Trans. Energy Convers. 2022, 38, 495–506. [Google Scholar] [CrossRef]
- Haque, R.U.; Kowal, A.; Ewanchuk, J.; Knight, A.; Salmon, J. PWM control of a dual inverter drive using an open-ended winding induction motor. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 150–156. [Google Scholar] [CrossRef]
- Corzine, K.; Sudhoff, S.; Whitcomb, C. Performance Characteristics of a Cascaded Two-Level Converter. IEEE Trans. Energy Convers. 1999, 14, 433–439. [Google Scholar] [CrossRef]
- Pradabane, S. A new SVPWM for dual-inverter fed three-level induction motor drive. In Proceedings of the 2013 International Conference on Green Computing, Communication and Conservation of Energy (ICGCE), Chennai, India, 12–14 December 2013; pp. 514–518. [Google Scholar] [CrossRef]
- Ramachandrasekhar, K.; Mohan, S.; Srinivas, S. An improved PWM for a dual two-level inverter fed open-end winding induction motor drive. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Kumar, A.; Fernandes, B.G.; Chatterjee, K. DTC of open-end winding induction motor drive using space vector modulation with reduced switching frequency. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; Volume 2, pp. 1214–1219. [Google Scholar] [CrossRef]
- Somasekhar, V.T.; Srinivas, S.; Kumar, K.K. Effect of zero-vector placement in a dual-inverter fed open-end winding induction motor drive with alternate sub-hexagonal center PWM switching scheme. IEEE Trans. Power Electron. 2008, 23, 1584–1591. [Google Scholar] [CrossRef]
- Baiju, M.R.; Mohapatra, K.K.; Gopakumar, K. PWM signal generation for dual inverter fed open-end winding induction motor drive using only the instantaneous reference phase amplitudes. In Proceedings of the Fifth International Conference on Power Electronics and Drive Systems, 2003—PEDS 2003, Singapore, 17–20 November 2003; Volume 1, pp. 450–455. [Google Scholar] [CrossRef]
- Chou, Y.; Nian, H. Sensorless control of PMSG based on dual two-level inverter open winding configuration for wind turbines. In Proceedings of the 2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012; pp. 1–6. Available online: https://ieeexplore.ieee.org/document/6401982 (accessed on 4 February 2025).
- George, D.S.; Baiju, M.R. Space vector based Random Pulse Width Modulation scheme for a 3-level inverter in open-end winding induction motor configuration. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 742–747. [Google Scholar] [CrossRef]
- Shivakumar, E.G.; Gopakumar, K.; Sinha, S.K.; Pittet, A.; Ranganathan, V.T. Space vector PWM control of dual inverter fed open-end winding induction motor drive. In Proceedings of the 2001 Sixteenth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 4–8 March 2001; Volume 1, pp. 399–405. [Google Scholar] [CrossRef]
- Satheesh, G.; Bramhananda Reddy, T.; Sai Babu, C. Space-vector based PWM switching strategy for a four-level dual inverter fed open-end winding induction motor drive. In Proceedings of the IEEE-International Conference on Advances in Engineering, Science and Management (ICAESM—2012), Nagapattinam, India, 30–31 March 2012; pp. 111–115. Available online: https://ieeexplore.ieee.org/document/6216101 (accessed on 4 February 2025).
- Srinivas, S.; Somasekhar, V. Space-vector-based PWM switching strategies for a three-level dual-inverter-fed open-end winding induction motor drive and their comparative evaluation. IET Electr. Power Appl. 2008, 2, 19–31. [Google Scholar] [CrossRef]
- Srinivasan, P.; Narasimharaju, B.L.; Srikanth, N.V. Space-vector pulse width modulation scheme for open-end winding induction motor drive configuration. IET Power Electron. 2015, 8, 1083–1094. [Google Scholar] [CrossRef]
- Casadei, D.; Grandi, G.; Lega, A.; Rossi, C. Multilevel operation and input power balancing for a dual two-level inverter with insulated DC sources. IEEE Trans. Ind. Appl. 2008, 44, 1815–1824. [Google Scholar] [CrossRef]
- Shivakumar, E.G.; Somasekhar, V.T.; Mohapatra, K.K.; Gopakumar, K.; Umanand, L.; Sinha, S.K. A multi level space phasor based PWM strategy for an open-end winding induction motor drive using two inverters with different DC link voltages. In Proceedings of the 4th IEEE International Conference on Power Electronics and Drive Systems (IEEE PEDS 2001), Denpasar, Indonesia, 25 October 2001; Volume 1, pp. 169–175. [Google Scholar] [CrossRef]
- Reddy, B.V.; Somasekhar, V.T. A dual inverter fed four-level open-end winding induction motor drive with a nested rectifier-inverter. IEEE Trans. Ind. Inform. 2013, 9, 938–946. [Google Scholar] [CrossRef]
- Darijevic, M.; Jones, M.; Levi, E. An open-end winding four-level five-phase drive. IEEE Trans. Ind. Electron. 2016, 63, 538–549. [Google Scholar] [CrossRef]
- Darijevic, M.; Bodo, N.; Jones, M. On the five-phase open-end winding drives performance. In Proceedings of the PCIM Europe 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 24–26 June 2015; pp. 1–8. Available online: https://ieeexplore.ieee.org/document/7149077 (accessed on 4 February 2025).
- Lakhimsetty, S.; Surulivel, N.; Somasekhar, V.T. Improvised SVPWM strategies for an enhanced performance for a four-level open-end winding induction motor drive. IEEE Trans. Ind. Electron. 2017, 64, 2750–2759. [Google Scholar] [CrossRef]
- Reddy, B.V.; Somasekhar, V.T. An SVPWM scheme for the suppression of zero-sequence current in a four-level open-end winding induction motor drive with nested rectifier–inverter. IEEE Trans. Ind. Electron. 2016, 63, 2803–2812. [Google Scholar] [CrossRef]
- Reddy, M.H.V.; Reddy, T.B.; Reddy, B.R.; Kalavathi, M.S. Discontinuous PWM technique for the asymmetrical dual inverter configuration to eliminate the overcharging of DC-link capacitor. IEEE Trans. Ind. Electron. 2018, 65, 156–166. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, T.; Giangrande, P.; Chowdhury, S.; Galea, M.; Wheeler, P. An active modulation scheme to boost voltage utilization of the dual converter with a floating bridge. IEEE Trans. Ind. Electron. 2019, 66, 5623–5633. [Google Scholar] [CrossRef]
- Chowdhury, S.; Wheeler, P.W.; Patel, C.; Gerada, C. A multilevel converter with a floating bridge for open-end winding motor drive applications. IEEE Trans. Ind. Electron. 2016, 63, 5366–5375. [Google Scholar] [CrossRef]
- Corzine, K.A.; Wielebski, M.W.; Peng, F.Z.; Wang, J. Control of cascaded multilevel inverters. IEEE Trans. Power Electron. 2004, 19, 732–738. [Google Scholar] [CrossRef]
- Pereda, J.; Dixon, J. Cascaded multilevel converters: Optimal asymmetries and floating capacitor control. IEEE Trans. Ind. Electron. 2013, 60, 4784–4793. [Google Scholar] [CrossRef]
- Lu, S.; Mariéthoz, S.; Corzine, K.A. Asymmetrical cascade multilevel converters with noninteger or dynamically changing DC voltage ratios: Concepts and modulation techniques. IEEE Trans. Ind. Electron. 2010, 57, 2411–2418. [Google Scholar] [CrossRef]
- Majumder, M.G.; Yadav, A.K.; Gopakumar, K.; Raj, K.R.; Loganathan, U.; Franquelo, L.G. A 5-level inverter scheme using single DC link with reduced number of floating capacitors and switches for open-end IM drives. IEEE Trans. Ind. Electron. 2020, 67, 960–968. [Google Scholar] [CrossRef]
- Oto, Y.; Noguchi, T.; Sasaya, T.; Yamada, T.; Kazaoka, R. Space vector modulation of dual-inverter system focusing on improvement of multilevel voltage waveforms. IEEE Trans. Ind. Electron. 2019, 66, 9139–9148. [Google Scholar] [CrossRef]
- Chowdhury, S.; Wheeler, P.W.; Gerada, C.; Patel, C. Model predictive control for a dual-active bridge inverter with a floating bridge. IEEE Trans. Ind. Electron. 2016, 63, 5558–5568. [Google Scholar] [CrossRef]
- Jayasinghe, S.D.G.; Vilathgamuwa, D.M.; Madawala, U.K. A dual inverter-based supercapacitor direct integration scheme for wind energy conversion systems. IEEE Trans. Ind. Appl. 2013, 49, 1023–1030. [Google Scholar] [CrossRef]
- Jayasinghe, S.D.G.; Vilathgamuwa, D.M.; Madawala, U.K. A novel dc-link voltage regulation method for single source hybrid multilevel inverters. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 740–745. [Google Scholar] [CrossRef]
- Jones, M.; Darijevic, M.; Levi, E. Decoupled modulation techniques for a four-level five-phase open-end winding drive. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 21–24 June 2014; pp. 178–186. [Google Scholar] [CrossRef]
- Somasekhar, V.T.; Venugopal Reddy, B.; Sivakumar, K. A four-level inversion scheme for a 6n-pole open-end winding induction motor drive for an improved DC-link utilization. IEEE Trans. Ind. Electron. 2014, 61, 4565–4572. [Google Scholar] [CrossRef]
- Darijevic, M.; Jones, M.; Dordevic, O.; Levi, E. Decoupled PWM control of a dual-inverter four-level five-phase drive. IEEE Trans. Power Electron. 2017, 32, 3719–3730. [Google Scholar] [CrossRef]
- Masoum, M.A.S.; Fuchs, E.F. (Eds.) Introduction to Power Quality. In Power Quality in Power Systems and Electrical Machines, 2nd ed.; Academic Press: Boston, MA, USA, 2015; pp. 1–104. [Google Scholar] [CrossRef]
- IEEE Std 519-1992; Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems. IEEE: Piscataway, NJ, USA, 1993; pp. 1–112. [CrossRef]
- Bateman, A.; Paterson-Stephens, I. The DSP Handbook: Algorithms, Applications and Design Techniques, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; pp. 1–250. [Google Scholar]
- Riedemann Aros, J.A. Control of Open-end Winding Induction Machine Based on Indirect Matrix Converter. Ph.D. Thesis, Doctor en Ciencias de la Ingeniería Mención Ingeniería Eléctrica, Universidad de Concepción, Concepción, Chile, April 2015. [Google Scholar]
- Lu, H.; Qu, W.; Cheng, X.; Fan, Y.; Zhang, X. A Novel PWM Technique With Two-Phase Modulation. IEEE Trans. Power Electron. 2007, 22, 2403–2409. [Google Scholar] [CrossRef]
- Somasekhar, V.; Gopakumar, K.; Pittet, A.; Ranganathan, V. PWM inverter switching strategy for a dual two-level inverter fed open-end winding induction motor drive with a switched neutral. IEE Proc.-Electr. Power Appl. 2002, 149, 152–160. [Google Scholar] [CrossRef]
- Srinivas, S. Elimination of dead time effects on common mode voltage in an open-end winding induction motor drive under low speed operation using a simplified model predictive control. IEEE J. Emerg. Sel. Topics Ind. Electron. 2022, 3, 1195–1204. [Google Scholar] [CrossRef]
- Murai, Y.; Kubota, T.; Kawase, Y. Leakage current reduction for a high-frequency carrier inverter feeding an induction motor. IEEE Trans. Ind. Appl. 1992, 28, 858–863. [Google Scholar] [CrossRef]
- Ogasawara, S.; Ayano, H.; Akagi, H. An active circuit for cancellation of common-mode voltage generated by a PWM inverter. IEEE Trans. Power Electron. 1998, 13, 835–841. [Google Scholar] [CrossRef]
- Akagi, H.; Tamura, S. A passive EMI filter for eliminating both bearing current and ground leakage current from an inverter-driven motor. IEEE Trans. Power Electron. 2006, 21, 1459–1469. [Google Scholar] [CrossRef]
- Akagi, H.; Doumoto, T. An approach to eliminating high-frequency shaft voltage and ground leakage current from an inverter-driven motor. IEEE Trans. Ind. Appl. 2004, 40, 1162–1169. [Google Scholar] [CrossRef]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Testa, A. Reduction of common-mode currents in PWM inverter motor drives. IEEE Trans. Ind. Appl. 1999, 35, 469–476. [Google Scholar] [CrossRef]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Scelba, G.; Testa, A. A Novel Space-Vector Modulation Technique for Common Node Emissions Reduction. In Proceedings of the 2007 International Aegean Conference on Electrical Machines and Power Electronics, Bodrum, Turkey, 10–12 September 2007; pp. 199–204. [Google Scholar] [CrossRef]
- Ratnayake, K.R.M.N.; Murai, Y. A novel PWM scheme to eliminate common-mode voltage in three-level voltage source inverter. In Proceedings of the 29th Annual IEEE Power Electronics Specialists Conference (PESC 98 Record), Fukuoka, Japan, 22 May 1998; Volume 1, pp. 269–274. [Google Scholar] [CrossRef]
- Ruderman, A.; Reznikov, B. Evaluation of motor PWM loss increase due to zero common-mode voltage modulation strategy of multilevel converter. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, North Macedonia, 6–8 September 2010; pp. T3-66–T3-72. [Google Scholar] [CrossRef]
- Costa, L.L.H.; Serni, P.J.A.; Marafão, F.P. An analysis of Generalized Symmetrical Components in non-sinusoidal three-phase systems. In Proceedings of the XI Brazilian Power Electronics Conference, Natal, Brazil, 11–15 September 2011; pp. 502–507. [Google Scholar] [CrossRef]
- Somasekhar, V.T.; Gopakumar, K.; Baiju, M.R.; Mohapatra, K.K.; Umanand, L. A multilevel inverter system for an induction motor with open-end windings. IEEE Trans. Ind. Electron. 2005, 52, 824–836. [Google Scholar] [CrossRef]
- Baranwal, R.; Basu, K.; Mohan, N. Dual two level inverter carrier SVPWM with zero common mode voltage. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 21–24 July 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Baranwal, R.; Basu, K.; Mohan, N. Carrier-Based Implementation of SVPWM for Dual Two-Level VSI and Dual Matrix Converter with Zero Common-Mode Voltage. IEEE Trans. Power Electron. 2015, 30, 1471–1487. [Google Scholar] [CrossRef]
- Kalaiselvi, J.; Rama Chandra Sekhar, K.; Srinivas, S. Common mode voltage elimination PWMs for a dual two-level VSI with single inverter switching. In Proceedings of the IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 234–239. [Google Scholar] [CrossRef]
- Somasekhar, V.; Srinivas, S.; Reddy, B.P.; Reddy, C.N.; Sivakumar, K. Pulse width-modulated switching strategy for the dynamic balancing of zero-sequence current for a dual-inverter fed open-end winding induction motor drive. IET Electr. Power Appl. 2007, 1, 591–600. [Google Scholar] [CrossRef]
- Boller, T.; Holtz, J.; Rathore, A.K. Optimal Pulsewidth Modulation of a Dual Three-Level Inverter System Operated From a Single DC Link. IEEE Trans. Ind. Appl. 2012, 48, 1610–1615. [Google Scholar] [CrossRef]
- Huangfu, Y.; Pang, S.; Nahid-Mobarakeh, B.; Guo, L.; Rathore, A.K.; Gao, F. Stability Analysis and Active Stabilization of On-Board DC Power Converter System with Input Filter. IEEE Trans. Ind. Electron. 2018, 65, 790–799. [Google Scholar] [CrossRef]
- Madonna, V.; Giangrande, P.; Galea, M. Electrical Power Generation in Aircraft: Review, Challenges, and Opportunities. IEEE Trans. Transp. Electr. 2018, 4, 646–659. [Google Scholar] [CrossRef]
- Lakhimsetty, S.; Somasekhar, V.T. A Four-Level Open-End Winding Induction Motor Drive with a Nested Rectifier–Inverter Combination with Two DC Power Supplies. IEEE Trans. Power Electron. 2019, 34, 8894–8904. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, T.; Giangrande, P.; Wheeler, P.; Galea, M. An active modulation scheme for avoiding overcharging in the dual converter with isolated asymmetric supplies. In Proceedings of the 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 2–5 September 2019; pp. P.1–P.9. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, T.; Giangrande, P.; Galea, M.; Wheeler, P. Technical Review of Dual Inverter Topologies for More Electric Aircraft Applications. IEEE Trans. Transp. Electrif. 2022, 8, 1966–1980. [Google Scholar] [CrossRef]
- Toulabi, M.S.; Salmon, J.; Knight, A.M. Design, Control, and Experimental Test of an Open-Winding IPM Synchronous Motor. IEEE Trans. Ind. Electron. 2017, 64, 2760–2769. [Google Scholar] [CrossRef]
- Mengoni, M.; Amerise, A.; Zarri, L.; Tani, A.; Serra, G.; Casadei, D. Control Scheme for Open-Ended Induction Motor Drives with a Floating Capacitor Bridge over a Wide Speed Range. IEEE Trans. Ind. Appl. 2017, 53, 4504–4514. [Google Scholar] [CrossRef]
- Sun, D.; Zheng, Z.; Lin, B.; Zhou, W.; Chen, M. A Hybrid PWM-Based Field Weakening Strategy for a Hybrid-Inverter-Driven Open-Winding PMSM System. IEEE Trans. Energy Convers. 2017, 32, 857–865. [Google Scholar] [CrossRef]
- Amerise, A.; Mengoni, M.; Zarri, L.; Tani, A.; Rubino, S.; Bojoi, R. Open-End Windings Induction Motor Drive with Floating Capacitor Bridge at Variable DC-Link Voltage. IEEE Trans. Ind. Appl. 2019, 55, 2741–2749. [Google Scholar] [CrossRef]
- Lu, S.; Corzine, K.A. Advanced Control and Analysis of Cascaded Multilevel Converters Based on P-Q Compensation. IEEE Trans. Power Electron. 2007, 22, 1242–1252. [Google Scholar] [CrossRef]
- Grandi, G.; Rossi, C.; Lega, A.; Casadei, D. Multilevel operation of a dual two-level inverter with power balancing capability. In Proceedings of the IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; pp. 603–610. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 1–750. [Google Scholar]
- Srinivas, S.; Kalaiselvi, J. Pulse width modulation schemes enabling single DC power source driven dual two-level voltage source inverter with single voltage source inverter switching. IET Power Electron. 2014, 7, 1181–1191. [Google Scholar] [CrossRef]
- Kim, S.-M.; Lee, E.-J.; Lee, J.-S.; Lee, K.-B. An improved phase-shifted DPWM method for reducing switching loss and thermal balancing in cascaded H-bridge multilevel inverter. IEEE Access 2020, 8, 187072–187083. [Google Scholar] [CrossRef]
- Giacomini, J.C.; Michels, L.; Cavalcanti, M.C.; Rech, C. Modified discontinuous PWM strategy for three-phase grid-connected PV inverters with hybrid active–passive damping scheme. IEEE Trans. Power Electron. 2020, 35, 8063–8073. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, C.; Xing, X.; Li, X.; Chen, Z. Novel three-layer discontinuous PWM method for mitigating resonant current and zero-crossing distortion in Vienna rectifier with an LCL filter. IEEE Trans. Power Electron. 2021, 36, 14478–14490. [Google Scholar] [CrossRef]
- Nguyen, N.-V.; Nguyen, B.-X.; Lee, H.-H. An optimized discontinuous PWM method to minimize switching loss for multilevel inverters. IEEE Trans. Ind. Electron. 2011, 58, 3958–3966. [Google Scholar] [CrossRef]
- Dong, Z.; Song, Z.; Wang, W.; Liu, C. Improved Zero-Sequence Current Hysteresis Control-Based Space Vector Modulation for Open-End Winding PMSM Drives with Common DC Bus. IEEE Trans. Ind. Electron. 2023, 70, 10755–10760. [Google Scholar] [CrossRef]
- Zhong, L.; Hu, S. Zero-Sequence-Current Suppression of Open-End Winding PMSM with Common DC Bus Based on Virtual Vector Control. IEEE Trans. Ind. Electron. 2024, 71, 2356–2364. [Google Scholar] [CrossRef]
- Reddy Chagam, V.S.; Devabhaktuni, S. An Isolation Transformer-less Single DC Source Fed Dual 5-Leg Inverter Controlled 5-Phase Induction Motor with Modified Direct Torque Control. IEEE Lat. Am. Trans. 2024, 22, 229–239. [Google Scholar] [CrossRef]
- Lee, K.; Han, Y. PWM Strategy in OVM and Six-Step Regions for Open-End Winding PMSM Fed by a Dual Inverter with a Common DC Bus. IEEE Trans. Power Electron. 2024, 39, 13696–13707. [Google Scholar] [CrossRef]
- Lakhimsetty, S.; Somasekhar, V.T. An Efficient Predictive Current Control Strategy for a Four-Level Open-End Winding Induction Motor Drive. IEEE Trans. Power Electron. 2020, 35, 6198–6207. [Google Scholar] [CrossRef]
- Matsumori, H.; Maeda, Y.; Kosaka, T.; Matsui, N.; Saha, S. Dual Inverter-Fed Open Winding IPMSM Drive System for High-Power Premium Class EV. IEEE Trans. Ind. Appl. 2023, 59, 2069–2080. [Google Scholar] [CrossRef]
- Nadh, G.; Rahul, S.A. Clamping Modulation Scheme for Low-Speed Operation of Three-Level Inverter Fed Induction Motor Drive with Reduced CMV. IEEE Trans. Ind. Appl. 2022, 58, 7336–7345. [Google Scholar] [CrossRef]
- Muduli, U.R.; Beig, A.R.; Behera, R.K.; Jaafari, K.A.; Alsawalhi, J.Y. Predictive Control with Battery Power Sharing Scheme for Dual Open-End-Winding Induction Motor Based Four-Wheel Drive Electric Vehicle. IEEE Trans. Ind. Electron. 2022, 69, 5557–5568. [Google Scholar] [CrossRef]
- Perera, C.; Kish, G.J.; Salmon, J. Decoupled Floating Capacitor Voltage Control of a Dual Inverter Drive for an Open-Ended Winding Induction Motor. IEEE Trans. Power Electron. 2020, 35, 7305–7316. [Google Scholar] [CrossRef]
- Mohan, L.; Pant, K.; Rajeevan, P.P. A Speed Range Extension Scheme for Scalar-Controlled Open-End Winding Induction Motor Drives. IEEE Trans. Ind. Appl. 2022, 58, 2055–2062. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).