Sample-Based Gradient Edge and Angular Prediction for VVC Lossless Intra-Coding

Abstract

Lossless coding is a compression method in the Versatile Video Coding (VVC) standard, which can compress video without distortion. Lossless coding has great application prospects in fields with high requirements for video quality. Since the current VVC standard is mainly designed for lossy coding, the compression efficiency of VVC lossless coding makes it hard to meet people’s needs. In order to improve the performance of VVC lossless coding, this paper proposes a sample-based intra-gradient edge detection and angular prediction (SGAP) method. SGAP utilizes the characteristics of lossless intra-coding to employ samples adjacent to the current sample as reference samples and performs prediction through sample iteration. SGAP aims to improve the prediction accuracy for edge regions, smooth regions and directional texture regions in images. Experimental results on the VVC Test Model (VTM) 12.3 reveal that SGAP achieves 7.31% bit-rate savings on average in VVC lossless intra-coding, while the encoding time is only increased by 5.4%. Compared with existing advanced sample-based intra-prediction methods, SGAP can provide significantly higher coding performance gain.

1. Introduction

With the development of video capture technology and information transmission technology, videos have gradually become the main way for people to obtain information in their daily lives. In order to meet the ever-growing need for improved video compression, the Joint Video Experts Team (JVET) of the International Telecommunication Union-Telecommunication Standardization Sector (ITU-T) Video Coding Experts Group (VCEG) and the International Organization for Standardization/International Electrotechnical Commission (ISO/IEC) Moving Picture Experts Group (MPEG) developed the most recent international video coding standard, Versatile Video Coding (VVC) [1]. Compared to its predecessor, the High-Efficiency Video Coding (HEVC) standard [2], VVC can decrease the coding bit rate by 50% while maintaining the same video quality. Compared to the most commonly used video coding standard at present, the Advanced Video Coding (AVC) standard [3], VVC can reduce the coding bit rate by 75% while maintaining the same video quality. Video coding can be divided into lossy coding and lossless coding based on whether distortion will be introduced. As a coding method of the VVC standard, lossless coding compresses videos without distortion at the cost of losing a portion of compression efficiency. Lossless coding is widely used in some fields that require high video quality, such as satellite remote sensing image processing, medical image transmission, fingerprint image storage, digital archiving [4], remote desktop sharing, and so on.

Figure 1 shows the encoding framework of VVC lossless coding. VVC achieves lossless coding by skipping transformation [5], quantization and other steps that will introduce distortion. Without transformation and quantization, the residual samples to be encoded have high energy, which may lead to low compression efficiency of lossless intra-coding. Although lossless coding can provide excellent reconstructed video quality, it is difficult to achieve satisfactory compression efficiency of lossless coding, which greatly limits its practical application. Since the coding tools of VVC are mainly designed for lossy coding, there is a large optimization space for lossless coding. In order to improve the practical application value of lossless coding, it is necessary to explore optimization methods for lossless coding.

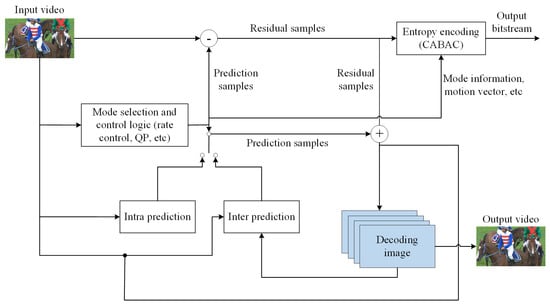
Figure 1. The encoding framework of VVC lossless coding.

The existing optimization methods improve lossless coding chiefly from block partition, prediction, transformation, and so on. Among them, improving the intra-prediction step is the most common method. In conventional intra-prediction, the reconstructed samples from the adjacent prediction blocks of the current prediction block serve as reference samples. These reference samples are located outside the current prediction block and are referred to as out-block reference samples. This prediction method uses prediction blocks as the basic prediction unit and is referred to as block-based intra-prediction. In lossless intra-coding, the reconstructed samples on the decoder side are the same as the original samples on the encoder side. Therefore, in-block samples can be employed as reference samples. This prediction method uses samples as the basic prediction unit and performs prediction in an iterative way. The main encoding and decoding framework of sample-based lossless intra-coding is shown in Figure 2. On the encoder side, the adjacent original samples of the current sample are employed as reference samples for prediction. The original samples are subtracted from the prediction samples to obtain residual samples. On the decoder side, the reconstructed samples adjacent to the current sample serve as reference samples for prediction. The residual samples are added to the prediction samples to obtain the reconstructed samples. The reconstructed samples participate in subsequent iterative prediction.

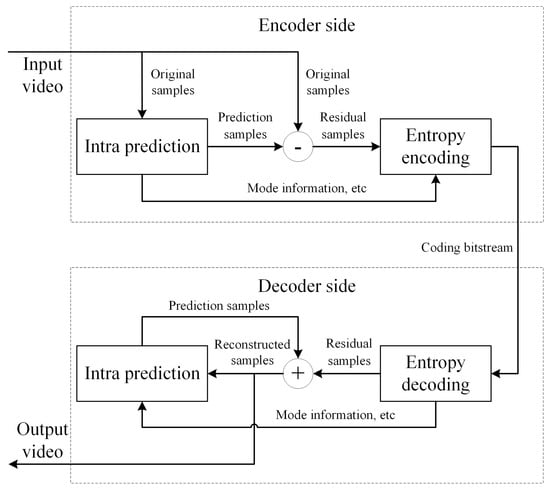
Figure 2. The main framework of sample-based lossless intra-coding.

In the VVC standard, Block Differential Pulse Code Modulation (BDPCM) [6] is a sample-based prediction tool that can provide performance gain of lossless coding. However, BDPCM only has two prediction modes: horizontal mode and vertical mode. The coding performance gain brought about by BDPCM is limited. Therefore, this paper analyzes the characteristics of different types of image regions and proposes a new sample-based intra-prediction method to replace the conventional intra-prediction method in VVC. The proposed prediction method is intended to perform accurate prediction on frequently occurring image regions to improve the performance of VVC lossless intra-coding.

The structure of this article is organized as follows. Section 2 reviews and introduces existing lossless coding optimization methods. Section 3 describes the proposed SGAP method in detail by presenting its principle and implementation processing. Section 4 provides the experimental comparison results with analysis and discussion. Finally, Section 5 draws the conclusions of this paper.

2. Related Works

In terms of the performance optimization of lossless coding, scholars in the field of video coding have conducted a series of studies. Lee et al. [7,8] proposed a Differential Pulse Code Modulation (DPCM) method within the framework of the AVC standard. Firstly, conventional horizontal or vertical predictions were performed on the current Prediction Unit (PU). Then, the residual samples were subtracted from adjacent residual samples to obtain secondary residual samples. This method was also known as Residual DPCM (RDPCM). In RDPCM coding, all samples within the current PU share the same prediction mode. References [9,10] proposed enhanced sample-based intra-prediction, which allows for selecting different prediction modes for each sample within the current PU. The HEVC standard continued to use the RDPCM method to improve the performance of lossless intra-coding by reprocessing residual samples [11,12]. Hong et al. [13] proposed cross-residual prediction (CRP), using DPCM for residual samples in both horizontal and vertical directions. References [14,15] utilized gradient information between adjacent reference samples of the current sample to improve the prediction accuracy of RDPCM. In the VVC standard, RDPCM served as a trigger for developing BDPCM coding tools [16]. Zhou et al. [17] extended DPCM to all angular intra-prediction modes and proposed a sample-based angular intra-prediction (SAP) method. SAP-Horizontal and Vertical (SAP-HV) [18] applied SAP only in the horizontal and vertical directions. SAP1 [19] adopted an equidistant prediction method for all angular prediction modes in SAP. In the case of short prediction distances, the equidistant prediction method is more suitable. On the basis of using adjacent reference samples for prediction, Sanchez et al. [20,21,22] introduced median edge detection (MED) [23] as the planar mode to enhance the prediction ability of the intra-prediction module for edge regions. References [24,25] analyzed the gradient information between adjacent reference samples to judge the edges around the current sample. Wige et al. [26,27] proposed a Sample-based Weighted Prediction (SWP) method with Directional Template Matching (DTM), which weighted the surrounding reference samples to predict the current sample. Sanchez et al. [28] proposed a Sample-based Edge and Angle Prediction (SEAP) method for lossless intra-coding of screen content. Weng et al. [29] proposed an L-shape-based Iterative Prediction (LIP) method and a Residual Median Edge Detection (RMED) method. LIP divided the current coding unit (CU) into adjacent one-dimensional sub-regions and allowed each sub-region to possess a separate prediction mode. RMED applied MED on residual blocks to remove edge spatial redundancy between residual samples.

Considering that the energy of residual values in lossless coding is relatively dispersed, some studies transformed residual samples to concentrate the energy of residual values. During the coding process, distortion should not be introduced. Chen et al. [30] designed reversible transforms for residual samples of different prediction modes. These transforms would not affect the quality of reconstructed videos. Cai et al. [31] performed transform and quantization in lossless coding. On the encoder side, quantized residual values and quantization error information were encoded together. On the decoder side, quantization error information was utilized to eliminate video distortion. Kamisli [32] proposed an integer-to-integer discrete sine transform, which performed a transform on residual samples without distortion and without increasing the dynamic range of values.

The above methods of transforming residual samples can improve the performance of lossless coding to some extent, but the performance gain is relatively limited. In addition, there are different complex types of regions in the image. The existing sample-based prediction methods make it difficult to perform accurate predictions for different image regions. Therefore, it is necessary to explore a method that can accurately predict frequently occurring image regions.

3. Proposed Method

The frequently occurring regions in images mainly include sharp edge regions, smooth regions with less noise and directional texture regions. The proposed SGAP contains three prediction algorithms that are suitable for these regions. This section analyzes the characteristics of the aforementioned image regions and introduces the three prediction algorithms in SGAP. In addition, the flowchart of SGAP in VVC lossless intra-coding is expounded.

3.1. Sample-Based Intra-Gradient Edge Detection and Angular Prediction

The following discussions and calculations are based on an $M\times N$ prediction block. Except for in-block reference samples, two rows and columns of out-block reference samples are employed for the prediction of top and left samples. The coordinate of the top-left-corner out-block reference sample is defined as $(0,0)$. The following intra-prediction is performed using sample iteration.

3.1.1. Edge Regions: Gradient Edge Detection

Edges are the intersection of different image attributes. The value differences between image samples located at both ends of edges are significant. Since images generally contain a large number of different attributes, the occurrence frequency of edges is very high. In conventional intra-prediction, all samples in a prediction block share the same predictor. However, in a prediction block, samples located at edges in different directions are suitable for different predictors. To improve this situation, a gradient edge detection (GED) algorithm is proposed. GED detects edges near the current sample by analyzing gradient information between adjacent reference samples. Then, GED selects the optimal predictor for the current sample based on the result of edge detection. The prediction process of GED and the positional relationship between the reference samples and the current sample are shown in Figure 3. In order to use reference sample d in the prediction process, the prediction has to be performed line-by-line. In the absence of reference sample d, the closest sample is used to populate it.

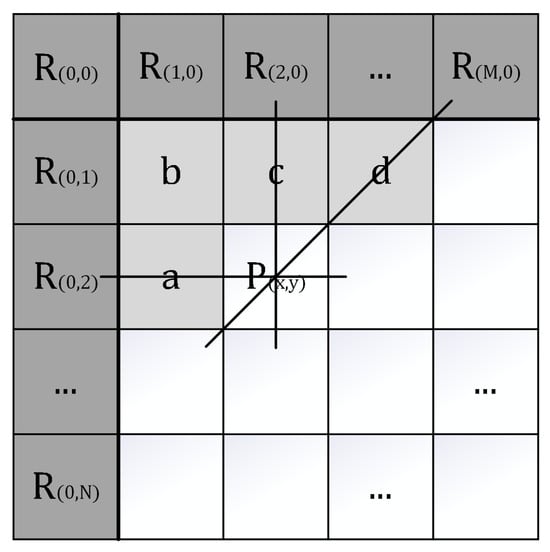
Figure 3. The prediction process of GED and the positional relationship between the reference samples and the current sample.

GED can detect edges in both horizontal and vertical directions, as well as the top-right diagonal direction. GED uses four reference samples—a, b, c and d—around the current sample for prediction. The prediction sample is calculated as:

$$P_{(x,y)}=\left\{\begin{array}{c}\begin{array}{c}max(2·m-b,d),\mathrm{if}b>2·m-n\mathrm{and}d<n\hfill \end{array}\hfill \\ \begin{array}{c}n,\mathrm{if}b>m\mathrm{and}(b<=2·m-n\mathrm{or}d>=n)\hfill \end{array}\hfill \\ \begin{array}{c}min(2·n-b,d),\mathrm{if}b<2·n-m\mathrm{and}d>m\hfill \end{array}\hfill \\ \begin{array}{c}m,\mathrm{if}b<n\mathrm{and}(b>=2·n-m\mathrm{or}d<=m)\hfill \end{array}\hfill \\ \begin{array}{c}m+n-b,\mathrm{otherwise}\hfill \end{array}\hfill \end{array}\right.$$

(1)

where m is the max value of a and c, n is the min value of a and c. When b is greater than m, a b-m-direction edge near the current sample is expected. Therefore, it is appropriate to take n as the value for the prediction sample $P_{(x,y)}$. In the above case, if the difference between b and m is greater than the difference between m and n ($b>2·m-n$), and d is less than n, the current sample will be expected to tend to approach d from n. $P_{(x,y)}$ is obtained by subtracting the difference between b and $2·m-n$ from n ($2·m-b$). When $2·m-b$ is less than d, a top-right diagonal edge near the current sample is expected. Thus, d is selected as the best value for $P_{(x,y)}$. If the condition that b is greater than $2·m-n$ and d is less than n, n is still taken to generate $P_{(x,y)}$. Furthermore, when b is less than n, the a b-n-direction edge near the current sample is expected. Therefore, it is appropriate to take m as the value for the prediction sample $P_{(x,y)}$. In this event, if the difference between n and b is greater than the difference between m and n ($b<2·n-m$), and d is greater than m, the current sample will be expected to tend to approach d from m. $P_{(x,y)}$ is obtained by adding the difference between $2·n-m$ and b to m ($2·n-b$). When $2·n-b$ is greater than d, a top-right diagonal edge near the current sample is expected. Similarly, d is selected as the best value for $P_{(x,y)}$. If the condition that b is less than $2·n-m$ and d is greater than n is not met, m is still taken to generate $P_{(x,y)}$. In other cases, according to the trend of changes between a, b, and c, $m+n-b$ ($a+c-b$) is selected as the optimal value for the prediction sample $P_{(x,y)}$.

3.1.2. Smooth Regions: Average Prediction

Smooth regions are the parts of images that contain less noise. The value fluctuations between image samples located at the smooth regions are relatively gentle. Within the same image attribute, the probability of sharp value fluctuations between samples is low, and the occurrence frequency of smooth regions is high. In this paper, an average predictor is used to deal with smooth regions. The process of average prediction and the positional relationship between the reference samples and the current sample are shown in Figure 4.

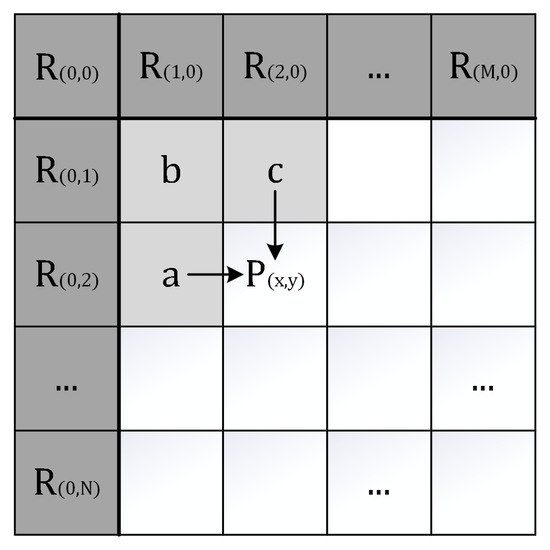
Figure 4. The process of average prediction and the positional relationship between the reference samples and the current sample.

The adjacent samples a and c are employed as reference samples for prediction. The prediction sample is obtained as an average value of two reference samples:

$$P_{(x,y)}=(a+c+1)>>1$$

(2)

where a is the left reference sample of the current sample, c is the top reference sample of the current sample. Since the regions to be handled are smooth, the values between adjacent samples are expected to be relatively close. In the sample-based prediction, the samples at positions a and c of the current sample are the closest reference samples that can be obtained. Therefore, the average value of the reference samples a and c is expected to be the optimal value for the prediction sample $P_{(x,y)}$.

3.1.3. Directional Texture Regions: Angular Prediction

The video images contain massive textures in different directions. The values between image samples on the same texture are typically close. In conventional VVC intra-prediction, angular modes are used to predict these directional texture regions. Considering that the spatial correlation between image samples is enhanced with the decrease in sample distances, reference [17] proposed SAP, which uses adjacent reference samples for angular prediction. SAP has been proven to bring significant performance gains for lossless coding. We Introduce an additional adjacent reference line to extend and improve SAP. The process of improved SAP and the positional relationship between the reference samples and the current sample are shown in Figure 5. The improved SAP projects the current sample onto two adjacent reference lines to obtain two projection points. The prediction sample is generated through these two projection points. In addition, the distance between projection points of adjacent angular modes on the same reference line is relatively short, and the projection points of adjacent prediction modes on the same reference line are spaced relatively small. Therefore, sample-based angular prediction does not need to use too many prediction modes. The improved SAP reduces the VVC angular modes by half and only retains 33 angular modes. In addition, an equidistant prediction method the same as SAP1 is adopted.

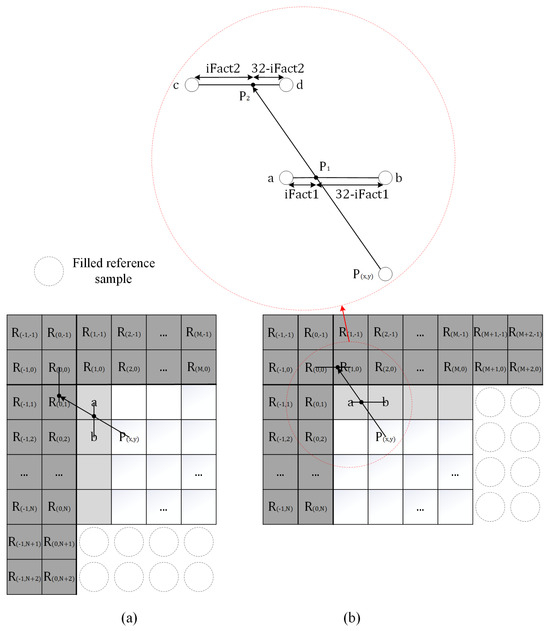
Figure 5. The process of improved SAP and the positional relationship between the reference samples and the current sample: (a) Prediction in the horizontal direction. (b) Prediction in the vertical direction.

The improved SAP uses the prediction values of two projection points to generate prediction samples according to a certain weight allocation. The projection point closer to the current sample is defined as $P1$. The projection point farther from the current sample is defined as $P2$. The prediction values of two projection points are obtained from:

$$P1=\left(\right(32-iFact1)·a+iFact1·b+16)>>5$$

(3)

$$P2=\left(\right(32-iFact2)·c+iFact2·d+16)>>5$$

(4)

where a and b are the two reference samples closest to the $P1$, and c and d are the two reference samples closest to the $P2$. The interpolation weight $iFact1$ is determined by the distances between the $P1$ and the two reference samples (when $P1$ is located at a, $iFact1$ is 0, and when $P1$ is located at b, $iFact1$ is 32). The interpolation weight $iFact2$ is determined by the distances between the $P2$ and the two reference samples (when $P2$ is located at c, $iFact2$ is 0, and when $P2$ is located at d, $iFact2$ is 32). The improved SAP has three types of weight allocations, respectively, named type 0, 1, and 2. Type 0 uses $P1$ to generate the prediction sample:

$$P_{(x,y)}=P1$$

(5)

Type 0 is consistent with the conventional SAP. Type 1 adds half of the difference between $P1$ and $P2$ to $P1$ to generate the prediction sample:

$$P_{(x,y)}=P1+(P1-P2)/2$$

(6)

The trend of changes between image samples has continuity. There is a correlation between the difference between the current sample and $P1$ and the difference between $P1$ and $P2$. Type 1 uses the difference between $P1$ and $P2$ to compensate for $P1$ to obtain the prediction sample, which expands the scope of application of angular prediction. Type 2 uses the average value of $P1$ and $P2$ to generate the prediction sample:

$$P_{(x,y)}=(P1+P2)/2$$

(7)

If there are significant fluctuations between adjacent samples on the same texture, type 2 is expected to increase the accuracy of prediction.

Different prediction types of a prediction direction share the same prediction mode. The encoder uses additional data information to represent the weight allocation types of angle modes and writes the information data into the bitstream. Since the use frequency of type 0 is high, type 0 of all angular modes is tested in angular prediction. The use frequencies of types 1 and 2 are low. In order to avoid a significant increase in coding complexity, only types 1 and 2 of specific angular modes are tested.

3.2. Intra-Prediction Flowchart

In the SGAP coding, the PLANAR mode and DC mode are not retained. The GED mode is set to mode 0. The average prediction mode is set to mode 1. The angle mode in SGAP is set to modes 2–34. Figure 6 shows the intra-prediction flowchart of SGAP.

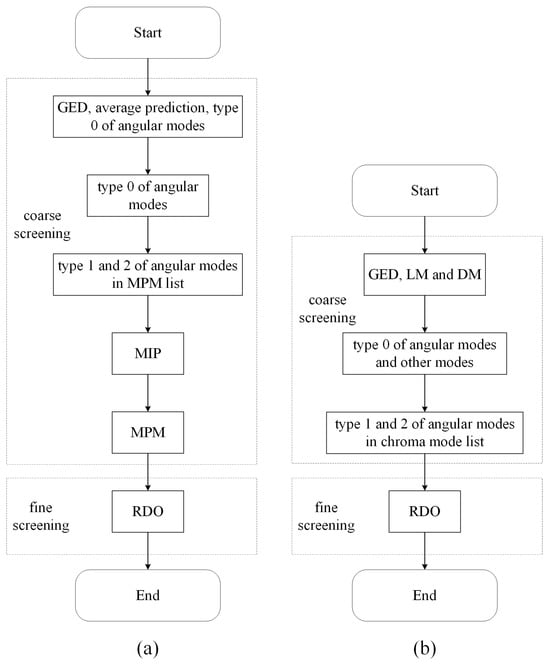
Figure 6. The flowchart of the proposed SGAP in VVC lossless intra-coding: (a) Luma component. (b) Chroma component.

The flowchart of the luma component is shown in Figure 6a. The optimal luma mode of the Current Coding Unit (CU) is determined through two steps: coarse screening and fine screening. In the first round of coarse screening, the Sum of Absolute Transformed Difference (SATD) of the prediction results of the GED mode, average prediction mode and type 0 of 17 even angular modes is calculated. A certain number of modes with the smallest SATD are selected to enter the mode candidate list. In the second round of coarse screening, the SATD of the prediction results of type 0 of the angular modes adjacent to the angular modes in the mode candidate list are calculated. Then, the candidate list is updated according to SATD. In the subsequent coarse screening steps, the SATD of the prediction results of type 1 and 2 of angular modes in the Most Probable Modes (MPM) list and modes in the Matrix-based Intra-Prediction (MIP) list and MPM list are calculated. Then, the candidate list is updated according to SATD. The fine screening is implemented by Rate-Distortion Optimization (RDO). In the RDO step, the Rate-Distortion Cost (RD cost) of all modes in the mode candidate list is calculated. The mode with the smallest RD cost is selected as the optimal luma mode.

The flowchart of the chroma component is shown in Figure 6b. The obtainment of the optimal chroma mode also goes through coarse screening and fine screening. In the coarse screening, the SATD of the prediction results of type 0 of the angular modes and other modes in the chroma mode list are calculated. Since the GED mode, Linear Model (LM) and Derived Mode (DM) must be tested, the SATD of the prediction results of GED mode, LM and DM are set to 0. A certain number of modes with the smallest SATD are selected to enter the mode candidate list. Then, the SATD of the prediction results of type 1 and 2 of angular modes in the mode candidate list are calculated. After completing the SATD calculation, the candidate list is updated. Finally, in the RDO step, the RD cost of all modes in the mode candidate list is calculated, and the mode with the smallest RD cost is selected as the optimal chroma mode.

4. Results and Analysis

In order to evaluate the performance of SGAP, we implemented it on the VTM12.3 platform and tested 26 video sequences (six natural scene classes and one screen content class) in the 4:2:0 format specified by the VVC standard. The parameter information of these sequences is shown in Table 1. The tests are run in a lossless All Intra (AI) configuration under the common test conditions [33]. In addition, performance tests for several existing lossless coding optimization methods on the VTM12.3 platform proceeded. In the coding schemes that do not retain block-based intra-prediction, the multiple reference lines (MRL) tool is not enabled. In the coding schemes that retain block-based intra-prediction and in which basic VVC coding is used for comparison, the MRL tool is enabled. Except for the MRL tool, other configurations for all coding schemes are identical. We compare and analyze the experimental results of the proposed SGAP and other optimization methods.

Table 1. The parameter information of VVC test sequences.

Class	Sequence	Resolution	Frames	Frame-Rate/fps
A1	Tango2	3840 × 2160	294	60
	FoodMarket4	3840 × 2160	300	60
	Campfire	3840 × 2160	300	30
A2	CatRobot	3840 × 2160	300	60
	DaylightRoad2	3840 × 2160	300	60
	ParkRunning3	3840 × 2160	300	50
B	MarketPlace	1920 × 1080	600	60
	RitualDance	1920 × 1080	600	60
	Cactus	1920 × 1080	500	50
	BasketballDrive	1920 × 1080	500	50
	BQTerrace	1920 × 1080	600	60
C	BasketballDrill	832 × 480	500	50
	BQMall	832 × 480	600	60
	PartyScene	832 × 480	500	50
	RaceHorses	832 × 480	300	30
D	BasketballPass	416 × 240	500	50
	BlowingBubbles	416 × 240	500	50
	BQSquare	416 × 240	600	60
	RaceHorses	416 × 240	300	30
E	FourPeople	1280 × 720	600	60
	Johnny	1280 × 720	600	60
	KristenAndSara	1280 × 720	600	60
F	BasketballDrillText	832 × 480	500	50
	ChinaSpeed	1024 × 768	500	30
	SlideEditing	1280 × 720	300	30
	SlideShow	1280 × 720	500	20

Table 2 shows the bit-rate differences of several coding schemes compared to basic VVC coding. Negative numbers indicate a decrease in the bit rate of the coding schemes compared to basic VVC encoding. It can be observed that BDPCM achieves the lowest average bit-rate savings. BDPCM only applies sample-based angular prediction in horizontal and vertical directions, resulting in limited coding performance gain. SAP and SAP1 both use sample-based angular prediction to replace all conventional angle predictions and achieve close average bit-rate savings. Due to adopting an equidistant prediction method, the average bit-rate savings achieved by SAP1 are slightly higher than that achieved by SAP. LIP-RMED and SAP-E introduce the edge detection method into coding. Compared to coding schemes that only apply sample-based prediction in angular modes, LIP-RMED and SAP-E achieve higher coding performance gains. Since the proposed SGAP can perform accurate prediction on frequently occurring image regions, SGAP saves 7.31% bit-rate, on average, in VVC lossless intra-coding, which is ahead of other experimental coding schemes. Moreover, SGAP provides the highest bit-rate savings for all video sequences except the Campfire sequence.

Table 2. Experimental results of bit-rate differences (%) of optimization coding schemes compared to basic VVC coding.

Class	Sequence	BDPCM	SAP	SAP1	SAP−E	LIP−RMED	SGAP
A1	Tango2	−1.12	−1.49	−1.50	−3.40	−2.80	−3.54
	FoodMarket4	−3.71	−4.76	−4.78	−8.76	−7.72	−9.37
	Campfire	−0.44	−0.43	−0.43	−0.54	−0.95	−0.78
A2	CatRobot	−0.73	−1.28	−1.28	−2.14	−1.52	−2.47
	DaylightRoad2	−0.94	−1.24	−1.24	−2.24	−1.63	−2.53
	ParkRunning3	−4.03	−6.01	−6.03	−9.91	−9.36	−11.59
B	MarketPlace	−2.95	−4.06	−4.07	−6.98	−5.64	−7.58
	RitualDance	−3.70	−5.55	−5.56	−7.55	−5.96	−8.72
	Cactus	−1.17	−1.68	−1.68	−2.43	−1.98	−2.74
	BasketballDrive	−1.51	−1.71	−1.72	−2.15	−2.00	−2.75
	BQTerrace	−1.70	−1.71	−1.71	−2.34	−2.56	−2.85
C	BasketballDrill	−1.11	−3.86	−3.86	−4.18	−2.27	−5.05
	BQMall	−3.09	−3.71	−3.72	−4.73	−3.53	−5.36
	PartyScene	−2.60	−3.40	−3.40	−4.36	−2.77	−4.70
	RaceHorses	−3.10	−4.36	− 4.37	−7.43	−5.65	−7.93
D	BasketballPass	−8.01	−9.45	−9.45	−12.04	−8.70	−13.08
	BlowingBubbles	−2.90	−4.89	−4.89	−5.60	−2.97	−5.95
	BQSquare	−2.01	−2.49	−2.49	−3.18	−2.31	−3.57
	RaceHorses	−4.39	−6.56	−6.56	−9.58	−7.13	−10.47
E	FourPeople	−6.29	−7.52	−7.52	−10.28	−8.09	−11.20
	Johnny	−4.92	−6.31	−6.31	−8.10	−6.22	−8.81
	KristenAndSara	−5.64	−6.86	−6.85	−8.80	−6.58	−9.56
F	BasketballDrillText	−1.93	−4.48	−4.48	−4.92	−2.78	−5.72
	ChinaSpeed	−11.42	−12.47	−12.48	−13.93	−9.22	−15.03
	SlideEditing	−10.47	−8.26	−8.28	−10.05	−9.88	−10.89
	SlideShow	−11.09	−11.24	−11.26	−16.42	−13.67	−17.82
Average of $\Delta$bit−rate		−3.88	−4.84	−4.84	−6.62	−5.15	−7.31

The bold represents the highest bit-rate savings.

The average encoding and decoding time of several coding schemes compared to basic VVC coding are shown in Table 3. The allocation proportion of the average encoding and decoding time for each sequence is the same. Since SAP, SAP1, SAP-E and SGAP use the introduced prediction modes to replace the conventional prediction modes in the intra-prediction step without increasing additional testing costs, their coding times are close to that of the basic VVC coding. BDPCM and LIP-RMED add additional tests for the introduced prediction modes while retaining the original tests for the conventional prediction mode. Therefore, compared to the basic VVC coding, their encoding time is significantly increased. On the decoder side, sample-based intra-prediction increases the accuracy of prediction, reduces the energy of prediction residuals, and accelerates the speed of entropy decoding. Compared to the basic VVC coding, the decoding time of the experimental coding schemes is decreased in varying degrees.

Table 3. Experimental results of average encoding and decoding time (%) of optimization coding schemes compared to basic VVC coding.

Scheme	Encoding Time	Decoding Time
BDPCM	124.1	94.6
SAP	98.9	75.0
SAP1	98.3	74.8
SAP-E	97.4	71.4
LIP-RMED	131.2	92.7
SGAP	105.4	74.2

Compared with several existing optimization methods for lossless coding, SGAP has a great advantage in terms of coding performance gain. The encoding time of SGAP is close to that of the basic VVC lossless intra-coding, as well as other coding schemes with short encoding times. This indicates that SGAP brings significant coding performance gain at the cost of increasing the less encoding time and has high practical application value.

5. Conclusions

Lossless coding has great application prospects in some fields that require high video quality. However, the low compression efficiency of current VVC lossless coding greatly limits the practical application of lossless coding. In order to improve the coding performance of VVC lossless coding, this paper analyzes the characteristics of several types of frequently occurring image regions and proposes an SGAP method under the framework of sample-based prediction. In lossless intra-coding, SGAP can perform accurate prediction for edge regions, smooth regions with less noise and directional texture regions and provide significant coding performance gain. The experimental results show that SGAP can save 7.31% coding bit rate on average at the cost of increasing the lossless encoding time in VVC lossless intra-coding. Compared with existing lossless coding optimization methods, SGAP has a significant advantage.