Path Planning of Obstacle-Crossing Robot Based on Golden Sine Grey Wolf Optimizer

Abstract

This paper proposes a golden sine grey wolf optimizer (GSGWO) that can be adapted to the obstacle-crossing function to solve the path planning problem of obstacle-crossable robot. GSGWO has been improved from the gray wolf optimizer (GWO), which provide slow convergence speed and easy to fall into local optimum, especially without obstacle-crossing function. Firstly, aiming at the defects of GWO, the chaotic map is introduced to enrich the initial population and improve the convergence factor curve. Then, the convergence strategy of the golden sine optimizer is introduced to improve the shortcomings of GWO, such as insufficient convergence speed in the later stage and the ease with which it falls into the local optimum. Finally, by adjusting the working environment model, path generation method and fitness function, the path-planning problem of the obstacle-crossing robot is adapted. In order to verify the feasibility of the algorithm, four standard test functions and three different scale environment models are selected for simulation experiments. The results show that in the performance test of the algorithm, the GSGWO has higher convergence speed and accuracy than the GWO under different test functions. In the path-planning experiment, the length, number and size of inflection points and stability of the path planned by the GSGWO are better than those of the GWO. The feasibility of the GSGWO is verified.

1. Introduction

Mobile robots with obstacle-crossing capabilities can perform wider and more efficient searches, so they are often used in complex work environments [1]. The movement mode of the obstacle-crossing robots is more complex and diverse than those that cannot cross the obstacles, which can open up new paths but also bring new challenges to path-planning technology [2].

Robot path planning refers to the mobile robot independently designing a safe and collision-free path with the shortest distance from the starting point to the end point, taking the least time. Algorithm is the core of robot path planning [3]. The path-planning algorithm can be roughly classified as (1) path-planning algorithms based on map search, such as the A-star algorithm [4,5,6], artificial potential field algorithm [7,8], etc., (2) sampling-based path-planning algorithms, such as the RRT algorithm [9,10,11], PRM algorithm [12], etc., and (3) swarm intelligence algorithms based on global optimization, such as the ant colony optimizer [13,14,15], artificial bee colony optimizer [16,17], algorithms based on deep learning [18,19,20], etc.

The GWO is a kind of swarm intelligence algorithm [21]. Because of its strong convergence performance and relatively simple algorithm structure, it has been applied to parameter optimization [22,23], fault diagnosis [24,25], path planning [26,27,28] and other fields. However, the GWO also has problems, such as a too singular initial population, slow convergence speed and the ease with which it falls into the local optimum. To solve these problems, Shitu Singh [29] proposed an improved grey wolf algorithm driven by mutation, which used the Levy flight model to perform mutation operation on the population and the greedy selection method to update the path. Amir Seyyedabbasi [30] proposed two grey wolf algorithms for position updating based on alpha wolves and all wolves, respectively, and analyzed the advantages and disadvantages of the two algorithms and their usage scenarios. Kazem Meidani [31] proposed a grey wolf algorithm with an adaptive convergence factor and convergence times, which calculates the next convergence factor and determines whether to end the program using historical optimization data. Dong Lin [32] proposed a multi-strategy integrated improved grey wolf algorithm, which improved the GWO in many aspects and formulated new leader election rules. Farzad Kiani [33] proposed two different strategies to improve the grey wolf algorithm and applied them to the 3D environmental path planning of agricultural robots. Huaiqin Liu [34] combined BPNN and ALGWO to enhance the unpredictable behavior and exploration ability of the grey wolf algorithm and applied it to the PID control model.

Although the performance of the GWO has been significantly improved by the efforts of many scholars, there are still problems such as a single initial population, slow convergence speed in the later stage and the ease with which it falls into the local optimum, and when it is used in the path planning of obstacle-crossing robots, because the path selection of the robot is more diversified, the shortcomings are more prominent. Aiming at this problem, this paper proposes an improved GWO based on the golden sine strategy. Firstly, a piecewise chaotic map is introduced to generate the distribution and initial population. Secondly, the nonlinear convergence factor and dynamic weight index are used to balance the global search and local search ability of the algorithm, so as to avoid falling into the local optimum and find the optimal solution as accurately as possible. Finally, the golden sine strategy is introduced to perform secondary convergence of the population, optimize the optimization method and enhance the search ability of the algorithm. At the same time, the feasibility of the application of the algorithm in the path planning of the obstacle-crossing robot is discussed. The grey obstacle-surmountable area is added to the traditional path-planning map and given a certain traffic cost. By quantifying the cost of the robot’s obstacle-crossing, the robot makes a better choice between obstacle crossing and obstacle avoidance and further optimizes the path while adapting to the obstacle-crossing function.

2. Grey Wolf Optimizer

The GWO is an algorithm that imitates the hunting mechanism of wolves to achieve the purpose of optimization. The algorithm divides the wolves into the head wolf $\alpha$ who guides the wolves to hunt, wolf $\beta$, assisting the head wolf in hunting, $\delta$, responsible for reconnaissance and sentry, and the other wolf $\omega$. The hunting behavior of wolves is mainly divided into three stages: encirclement, pursuit and attack. In the encirclement phase, the algorithm updates the position using the following equation:

$$X\left(t+1\right)=X_P\left(t\right)-A·\left|C·X_P\left(t\right)-X\left(t\right)\right|,$$

(1)

$$A=2a_1·r_1-a_1,$$

(2)

$$C=2r_2,$$

(3)

$$a_1=2-2t/t_{max},$$

(4)

where $X$ and $X_P$ are the position vectors of grey wolf and prey, respectively. $A$ and $C$ are coefficient vectors. The definition of $a_1$ is the convergence factor. $r_1$ and $r_2$ are random numbers between [0, 1]. $t$ and $t_{max}$ are the current number of iterations and the maximum number of iterations, respectively.

In the pursuit and attack phase, the algorithm updates the location through the following equation:

$$\left\{\begin{array}{c}{X}_1=X_{\alpha }-A_1·\left|C_1·X_{\alpha }-X\right|\\ X_2=X_{\beta }-A_2·\left|C_2·X_{\beta }-X\right|\\ X_3=X_{\delta }-A_3·\left|C_3·X_{\delta }-X\right|\end{array}\right.,$$

(5)

$$X\left(t+1\right)=\left(X_1+X_2+X_3\right)/3,$$

(6)

where $X_1$, $X_2$ and $X_3$ represent the location update influence factors of the $\alpha$, $\beta$ and $\delta$ wolves, respectively.

3. Golden Sine Grey Wolf Optimizer

In this section, aiming at the shortcomings of the grey wolf algorithm, it is improved in four aspects, and the operation logic of the algorithm is introduced at the end of the section.

3.1. Piecewise Linear Chaotic Map

The GWO uses a random method to generate the initial population, which makes it difficult to guarantee the ergodicity and diversity of the initial population. Aiming at the problem of the single initial population of the algorithm, a piecewise linear chaotic map is introduced to generate the initial population. The piecewise linear chaotic map (PWLCM) can generate chaotic sequences with good randomness and ergodicity for the initial population by using a simple mathematical model. The piecewise linear chaotic sequence is defined as follows:

$$x^k\left(n+1\right)=\left\{\begin{array}{l}\frac{x^k\left(n\right)}{p},0\le x^k\left(n\right)<p\\ \frac{x^k\left(n\right)-p}{0.5-p},p\le x^k\left(n\right)<0.5\\ \frac{1-p-x^k\left(n\right)}{0.5-p},0.5\le x^k\left(n\right)<1-p\\ \frac{1-x^k\left(n\right)}{p},1-p\le x^k\left(n\right)<1\end{array}\right.,$$

(7)

where $x\left(n\right)$ is the nth item in the sequence, $k$ is the number of individuals in the population and $p$ is a constant between [0, 0.5].

According to Equation (7), it is possible to generate a sequence of uniform distribution between [0, 1] of any length based on the randomly generated $x\left(1\right)$. The effect is shown in Figure 1.

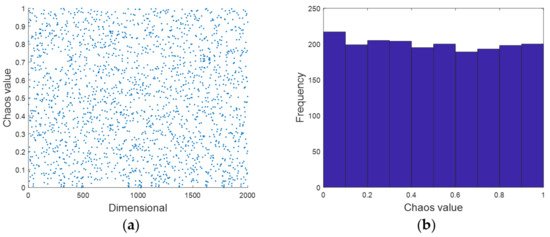
Figure 1. The effect of piecewise chaotic map: (a) profile; (b) spectrogram.

After generating a sequence, the number in the sequence is converted into the value in the search area of the algorithm by Equation (8):

$$X^k\left(0\right)=I_{min}+\left(I_{max}-I_{min}\right)x^k,$$

(8)

where $X^k\left(0\right)$ is the characteristic of the individual with sequence number $k$ in the initial population and $I_{max}$ and $I_{min}$ are the upper and lower bounds of the search region, respectively.

3.2. Nonlinear Convergence Factor

The convergence factor of the GWO is an important parameter of the convergence speed of the control algorithm. When the convergence factor is large, the algorithm tends to global search, and the convergence speed is faster, but it falls into the local optimum more easily. When the convergence factor is small, the algorithm tends to local search, and the convergence speed is slow, but there is a greater probability of jumping out of the local optimum. The convergence factor of the GWO shown in Equation (4) is linearly decreasing between 2 and 0. In order to more effectively balance the global search ability and local search ability of the algorithm, it is improved. The improved convergence factor is shown in Equation (9):

$$a_1=a_{min}+\left(a_{max}-a_{min}\right)·e^{-{\left(k_1·t/t_{max}\right)}^{k_2}},$$

(9)

where $a_{max}$ and $a_{min}$ are the upper and lower limits of the convergence factor, respectively. $k_1$ and $k_2$ are the constants of the control search interval and the curvature of the function, respectively. The larger $k_1$ is, the less the global search time is. The larger $k_2$ is, the higher the curvature of the function is. After testing, the appropriate parameters $k_1=1.5$ and $k_2=4$ are obtained.

The improved convergence factor change diagram is shown in Figure 2. Compared with the linear convergence factor, the improved nonlinear convergence factor has improved the global search ability in the early stage and the local search ability in the later stage. At the same time, the global search time is increased, the local search time is reduced to balance the two search capabilities of the algorithm and the efficiency of the algorithm is improved as much as possible under the same number of iterations.

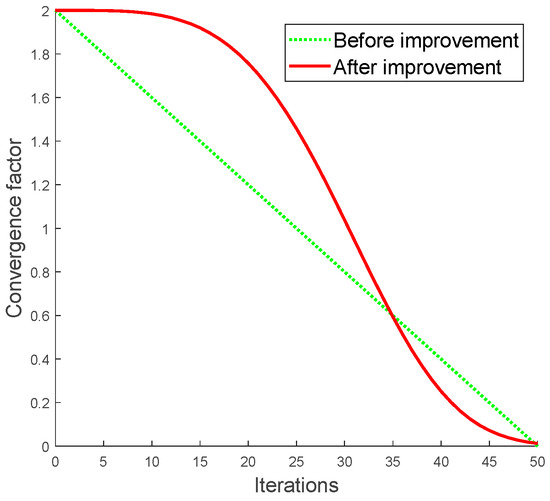
Figure 2. Comparison of convergence factor before and after improvement.

3.3. Dynamic Weight Coefficient

The weight coefficient of the GWO shown in Equation (6) is 1:1:1, which means that the three wolves of $\alpha$, $\beta$ and $\delta$ are equally important for the position guidance of $\omega$ wolves. However, in the practical application of the algorithm, the weight coefficient is not necessarily the ideal position update direction and may be far from the ideal direction.

In order to solve the above problems, a dynamic weight coefficient based on fitness function is proposed. The individuals with higher fitness in the three-headed wolves can obtain higher weights so that the population is more inclined to move in the direction of high fitness and improve the speed of the algorithm. The specific rules are as shown in Equations (10) and (11):

$$\left\{\begin{array}{c}{\theta }_1=V_f^{\alpha }/\left(V_f^{\alpha }-V_p\right)\\ {\theta }_2=V_f^{\beta }/\left(V_f^{\beta }-V_p\right)\\ {\theta }_3=V_f^{\omega }/\left(V_f^{\omega }-V_p\right)\end{array}\right.,$$

(10)

$$X\left(t+1\right)=\frac{{\theta }_1·X_1+{\theta }_2·X_2+{\theta }_3·X_3}{{\theta }_1+{\theta }_2+{\theta }_3},$$

(11)

where ${\theta }_1$, ${\theta }_2$ and ${\theta }_3$ represent the weight coefficients of the $\alpha$, $\beta$ and $\delta$ wolves, respectively. $V_f$ is the path cost of the corresponding wolf. The higher the path cost is, the lower the fitness is. $V_p$ is the theoretical minimum cost under unconstrained conditions, where is the Euclidean distance from the starting point to the end point of the path.

3.4. Golden Sine Strategy

The golden sine algorithm [35] is a mathematical model-based meta-heuristic algorithm proposed by Tanyildizi in 2017. It traverses all points on the circle through the sine function and reduces the search space through the golden section coefficient, so that the algorithm can have higher search efficiency without falling into the local optimum.

The position update equation of the golden sine algorithm is as follows:

$$X^{\prime }\left(t+1\right)=X\left(t+1\right)·\left|\sin r_1\right|-r_2·\sin r_1·\left|s_1·X_1-s_2·X\left(t+1\right)\right|,$$

(12)

$$\left\{\begin{array}{c}{s}_1=a·\tau +b·\left(1-\tau \right)\\ s_2=a·\left(1-\tau \right)+b·\tau \end{array}\right.,$$

(13)

where $X^{\prime }\left(t+1\right)$ is the convergence direction of the golden sine algorithm. $r_1$ and $r_2$ are random numbers between [0, 2π] and [0, π], respectively. $s_1$ and $s_2$ are the golden section coefficients. $\tau$ is the golden section number, take $\left(\sqrt{5}-1\right)/2$. The values of $a$ and $b$ are set to −π and π and then change with the target value.

The update rule after introducing the golden sine search strategy into the grey wolf algorithm is as follows: when $a_1<1$, the iteration enters the local search stage; after obtaining $X\left(t+1\right)$, it will converge twice. The golden sine convergence position is calculated by Equation (12), and then the cost between $X\left(t+1\right)$ and $X^{\prime }\left(t+1\right)$ is compared, and the better one is taken. Because of the ergodicity of the golden sine algorithm and the high efficiency of the search range, the grey wolf algorithm is quadratically convergent after the position update is completed. It can also jump out of the local optimum while ensuring the convergence speed in the later stage.

3.5. Logic and Process of Algorithm

The pseudo-code of the Algorithm 1 is as follows:

Algorithm 1: Golden Sine Grey Wolf Optimizer (GSGWO)

Input: $t_{max}$, $nu{m}_p$, $func\left(x\right)$, $I_{max}$, $I_{min}$, $dim$

Output: $ans=\mathsf{\alpha }$

1: Initialize $\alpha$, $\beta$ and $\delta$ wolf;

2: Initialize $X;$

3: for $t$ = 1 to $t_{max}$

4:   Calculate $a_1$ with Equation (9);

5:   for $num$ = 1 to $nu{m}_p$

6:   Update the location with Equations (10) and (11);

7:   if $a_1<1$

8:   Perform secondary convergence with Equations (12) and (13);

9:   end

10:  end

11:  Update α, β and δ wolf;

10:  end

11:  Return α;

4. Application of the GSGWO in Path Planning of Obstacle-Crossing Robot

This section adjusts the three aspects of working environment modeling, path generation and fitness function so that the algorithm can be applied to the path-planning problem of an obstacle-surmounting robot.

4.1. Working Environment Model

The working environment models of path planning include grid maps, vector maps, point cloud maps and so on. As the most widely used environmental model, a grid map has the advantages of simplicity and intuition, so a grid map is used as the environmental model of the obstacle-crossing robot.

The core idea of the general path-planning algorithm is obstacle avoidance, so the map is simply divided into accessible areas represented by white and non-accessible areas represented by black when establishing the environmental model. This division method is not applicable in the path planning of the obstacle-crossing robot. In this paper, an environmental model is proposed to add a grey obstacle-surmountable area between the two-color areas and give it a certain passage cost. The model can quantify the obstacle-crossing action cost of the obstacle-crossing robot so that the robot can make better choices in obstacle crossing and avoiding and achieve good cooperation with the obstacle-crossing function of the robot.

Taking the real map shown in Figure 3a as an example, the environment models without an obstacle-surmountable area and with an obstacle-surmountable area are shown in Figure 3b,c, respectively.

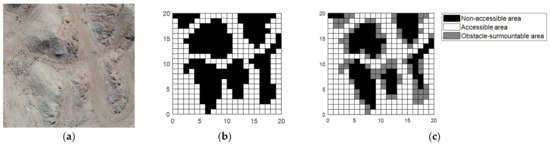
Figure 3. Environmental models and comparisons: (a) the map reality; (b) without obstacle-surmountable area; (c) with obstacle-surmountable area.

The map adopts a discrete node processing method. Each grid represents a node. The corresponding relationship between the node number and the coordinates is as follows:

$$p=\left(x+0.5\right)+\left(y-0.5\right)·n,$$

(14)

where $n$ is the number of rows or columns of the map.

4.2. Path Generation

The generation and optimization steps of the path are as follows: (1) At the beginning of the generated path, a random node is first generated by a chaotic sequence in each row between the starting point and the end point of the map, and all nodes are placed in the path in order as a grey wolf individual. (2) After generating the individual, the connection between the individuals may pass through the black impassable area, so the intermediate value is inserted in the middle of each two nodes through a specific interpolation program so that the path is continuous and does not pass through the obstacle. (3) Although the interpolated path can guide the robot to move from the starting point to the end point without obstacles, the path often has redundant inflection points and too large corners, so it is necessary to perform node optimization operations. The basic logic of the node optimization operation is when the connection between two points does not pass through any impassable area, and the path cost of the connection between two points is less than the original path cost, the original path is cleared and replaced by the connection between two points, as shown in Figure 4:

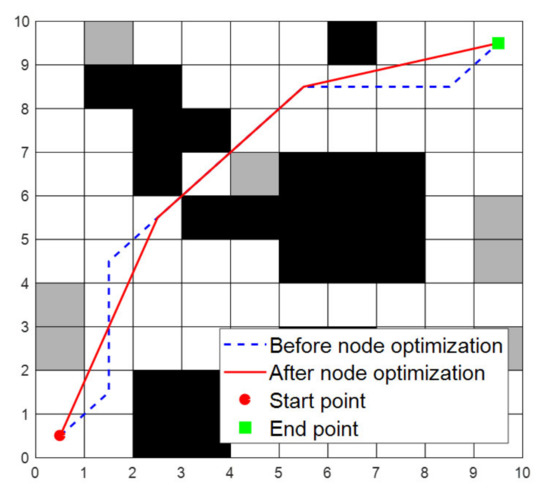
Figure 4. Node optimization.

The path before optimization is {1, 12, 22, 32, 42, 53, 64, 75, 86, 87, 88, 89, 100}, and the optimized path is {1, 53, 86, 100}. The detailed data are shown in Table 1. It can be seen that the optimized path length is shorter, the inflection point is less and the corner is smaller.

Table 1. Node optimization data comparison.

Parameter	Before Optimization	After Optimization
Path length	14.4853	13.7509
Number of inflection points	4	2

4.3. Fitness Function

The fitness function is a function that measures the pros and cons of candidate solutions in solving problems. A better fitness function can play an important role in guiding the convergence process of the algorithm. The general path-planning algorithm uses the path length equation as the fitness function, and some algorithms also introduce the influencing factors of the inflection point. In the path planning of an obstacle-crossing robot, the cost of obstacle-crossing action must be introduced as one of the evaluation criteria. Therefore, the fitness function used in this paper is as follows:

$$V_f=L+\lambda {{\displaystyle \sum }}_{i=1}^k{V}_{ti}+\mu {{\displaystyle \sum }}_{j=1}^l{V}_{pj},$$

(15)

where $V_f$ is the total cost of the path, and the greater the cost, the lower the fitness. $L$ is the total path length. $V_{ti}$ and $V_{pj}$ are the turning cost and obstacle-crossing cost of the path, respectively. $\lambda$ and $\mu$ are the weight coefficients of turning and obstacle crossing, respectively.

The evaluation of turning cost adopts the method of hierarchical processing. The larger the turning angle is, the larger the cost coefficient is. The specific rules are shown in Equation (16). The obstacle-crossing cost is classified: if the path passes through the center point of the obstacle area, it is regarded as a bilateral obstacle crossing, and the obstacle-crossing cost is 1. If the connection of the path passes through the obstacle area and does not pass through the center point of the area, it is regarded as a unilateral obstacle crossing, and the obstacle-crossing cost is 0.5.

$$V_t=\left\{\begin{array}{l}\phi ,\phi \le \pi /6\\ 3\phi ,\pi /6<\phi \le \pi /3\\ 9\phi ,\pi /3<\phi \le \pi /2\\ 100\phi ,\phi \ge \pi /2 \end{array}\right.,$$

(16)

where $\phi$ is the corner size, and the unit is the radian system.

5. Simulation Experiment and Analysis

5.1. Introduction to the Algorithm Selected for the Experiment

In order to better demonstrate the performance of the GSGWO, the other three algorithms are selected to experiment with GSGWO. The first algorithm is the original GWO introduced in ref. [8], and the principle of the algorithm is shown Section 2. The second algorithm is the TGWO based on the tent chaotic map to solve the problem of uneven distribution of initial population. It is a commonly used improved GWO algorithm at present. The third algorithm is the IGWO introduced in ref. [32].

5.2. Algorithm Performance Test

In order to verify the optimization performance of GSGWO shown in Algorithm 1, four test functions are selected to compare the GSGWO and the other three algorithms. The information of the functions is shown in Table 2. Before the experiment, the preset parameters of the function need to be set, and the detailed setting information is shown in Table 3. The other parameters of the GWO and TGWO are shown in ref. [8], and the other parameters of the IGWO are shown in ref. [32]. Each test function in the experiment runs 30 times. The average represents the optimization performance of the algorithm, and the standard deviation represents the stability of the test results; both are shown in Table 4. In order to clearly see the convergence process of the algorithm in the experiment, a certain convergence process curve in each group of experiments is selected to draw the graph shown in Figure 5.

Table 2. Test function information.

Function Name	Function Expressions	Region of Search	Solution
Sphere	$f\left(x\right)={{\displaystyle \sum }}_{i=1}^D{x}_i^2$	[100, −100]	0
Schwefel	$f\left(x\right)={{\displaystyle \sum }}_{i=1}^D\left|x_i\right|+{{\displaystyle \prod }}_{i=1}^D\left|x_i\right|$	[−10, 10]	0
Prem	$f\left(x\right)={{\displaystyle \sum }}_{i=1}^D{\left({{\displaystyle \sum }}_{j=1}^D\left(j+\beta \right)\left(x_j^i-\frac{1}{j^i}\right)\right)}^2$	[−30, 30]	0
Ellipsoid	$f\left(x\right)={{\displaystyle \sum }}_{i=1}^D{{\displaystyle \sum }}_{j=1}^D{x}_j^2$	[−65.536, 65.536]	0

Table 3. Algorithm parameters.

Parameter	Numerical Value
$t_{max}$	100
$nu{m}_p$	50
$func\left(x\right)$	Function Expressions in Table 2
$I_{max}$	Region of Search in Table 2
$I_{min}$
$dim$	30

Table 4. Test results.

Function Name	Performance	GWO	TGWO	IGWO	GSGWO
Sphere	average	2.35 × 10−14	2.41 × 10−25	3.61 × 10−57	6.18 × 10−81
	standard deviation	2.01 × 10−14	8.27 × 10−26	3.36 × 10−57	2.16 × 10−81
Schwefel	average	9.80 × 10−7	2.14 × 10−14	1.06 × 10−29	1.35 × 10−47
	standard deviation	4.13 × 10−7	6.52 × 10−15	8.15 × 10−30	7.21 × 10−48
Perm	average	6.57 × 100	2.60 × 10−1	3.54 × 10−3	5.58 × 10−5
	standard deviation	8.15 × 101	1.48 × 10−2	4.98 × 10−4	6.14 × 10−6
Ellipsoid	average	2.17 × 10−25	1.65 × 10−49	0	0
	standard deviation	1.85 × 10−25	7.56 × 10−50	0	0

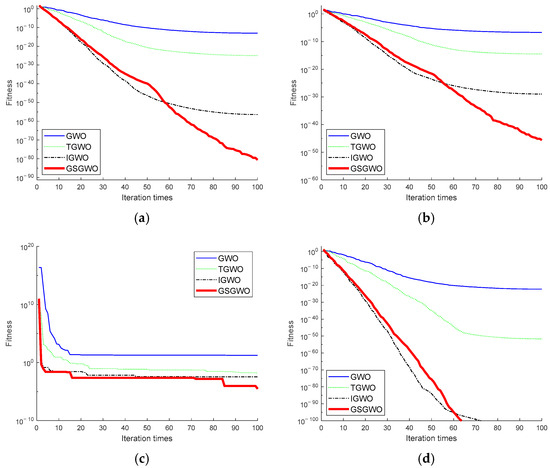
Figure 5. Convergence curve: (a) Sphere; (b) Schwefel; (c) Prem; (d) Ellipsoid.

It can be seen from the data in Table 4 that the average and standard deviation of the convergence results after 30 runs of the algorithm that the GSGWO was better than the GWO, TGWO and IGWO, and the performance of the algorithm was greatly improved. Through the comparison of the convergence curves in Figure 5, it can be seen that in the early global search, the convergence mode of the GSGWO is similar to that of the former three; it is faster than the GWO and TGWO but slower than the IGWO. In the later local search state, the convergence speed of the other algorithms gradually decreases, but due to the effect of the golden sine strategy, the GSGWO algorithm can still ensure a high convergence speed.

5.3. Path-Planning Simulation Experiment

5.3.1. Parameter Settings

Before the experiment, it is necessary to determine the weight coefficient in Equation (15), and the basic logic of setting is that when the angle of rotation is less than 30°, the two-sided obstacle crossing can be avoided as much as possible. Under the critical conditions, the cost of choosing the path to cross the obstacle and turn is the same, as shown in Equation (17):

$$\lambda V_t+\mathsf{\Delta }L=\mu V_p,$$

(17)

where $\mathsf{\Delta }L$ is the change in path length caused by turning.

Because $\mathsf{\Delta }L$ will change with the position of the starting and ending points and must be a positive number, as long as $\lambda V_t>\mu V_p$ is established, then $\lambda V_t+\mathsf{\Delta }L>\mu V_p$ is bound to hold, and by substituting the known number into the equation, we can obtain $\lambda /\mu >1.91$. So, here we take $\lambda /\mu =2$. The detailed path-planning parameter settings are shown in Table 5.

Table 5. Experimental parameters of path planning.

Parameter	Numerical Value
$t_{max}$	100
$nu{m}_p$	50
$func\left(x\right)$	Equation (15)
$I_{max}$	Map rows $n$
$I_{min}$	1
$dim$	$n-2$
$\lambda$	1.5
$\mu$	0.75

5.3.2. Path-Planning Experiment

In order to explore the feasibility of the GSGWO in the field of obstacle-crossing robot path planning, three different scale grid maps of 20 × 20, 30 × 30 and 40 × 40 were selected for simulation and comparison experiments. The starting point is set in the lower left corner of the map, and the end point is set in the upper right corner. The experimental results and convergence curves are shown in Figure 6.

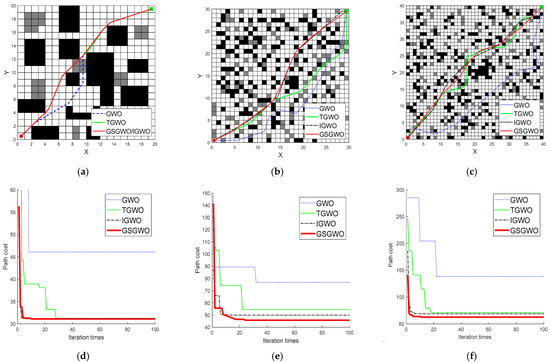
Figure 6. Experimental results of path planning: (a) path of 20 × 20; (b) path of 30 × 30; (c) path of 40 × 40; (d) convergence curve of 20 × 20; (e) convergence curve of 30 × 30; (f) convergence curve of 20 × 20.

By comparing the performance of the three algorithms, it can be found that the GWO has slow convergence speed, poor search ability and multiple local optimizations in the path planning of the obstacle-surmounting robot, which leads to search stagnation. The TGWO improves the convergence speed of the GWO and the probability of falling into the local optimum to a certain extent by improving the initial population through the chaotic sequence, but there is still a local optimum. The IGWO has a fast convergence speed and can plan the path at the fastest speed in simpler maps, but there will be premature convergence in complex maps. Compared with the former three, the GSGWO performs better. It can jump out of the local optimum faster while having a higher convergence speed. It has the shortest path length, fewer inflection points and the smallest corners and has better trafficability. By comparing the performance of the algorithm in different complex working environments, it can be found that with the increase in the complexity of the working environment, the overlap part of the paths planned by the four algorithms gradually decreases, and the advantages of the paths planned by the GSGWO are greater.

5.3.3. Stepped Simulation Experiment

In order to verify the influence of environmental model and path generation operation improvement on the path planning of obstacle-crossing robots, the GSGWO (GSGWO1) without obstacle-crossing function, the GSGWO (GSGWO2) without node optimization and the GSGWO are compared in the environment shown in Figure 6a. The experimental results are shown in Figure 7.

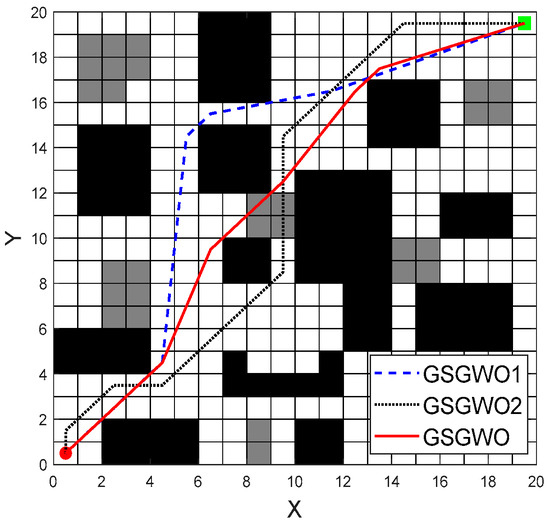
Figure 7. Stepped simulation experimental result.

The total path cost of the GSGWO1 algorithm in the figure is 39.8236. The total path cost of the GSGWO2 algorithm is 53.6763. The total path cost of the GSGWO algorithm is 31.1093. Through comparative analysis, it can be seen that the GSGWO1 algorithm has great limitations because it cannot cross the obstacle-surmountable passage area, so the final path has great limitations. The path obtained by the GSGWO2 algorithm can only walk in a limited direction, resulting in problems such as a too-long path, too many inflection points and too large corners. At the same time, because of the large number of nodes, the convergence speed of the algorithm is also affected to a certain extent. The GSGWO algorithm can effectively combine the advantages of the two, and the generated path is shorter while the inflection point is less, which has higher trafficability.

5.3.4. Stability Test

In order to verify the stability of the algorithm for obstacle-crossing robot path planning, the GWO, TGWO, IGWO and GSGWO were tested 30 times on different maps. The average and standard deviation of the test results are shown in Table 6. The data in the table are organized as shown in Figure 8. The comparison shows that the stability of the GSGWO in three map environments is better than the GWO and TGWO and is similar to the IGWO. As the environment becomes more and more complex, the stability of the four algorithms decreases, but the decrease in the GSGWO is the smallest.

Table 6. Stability test results.

Map Size	Performance	GWO	TGWO	IGWO	GSGWO
20 × 20	average	34.77	33.06	31.21	31.21
	standard deviation	3.10	2.31	0.27	0.13
30 × 30	average	84.94	58.34	51.87	49.77
	standard deviation	14.94	5.49	1.01	1.05
40 × 40	average	154.28	82.18	67.65	61.74
	standard deviation	25.51	9.71	3.23	2.13

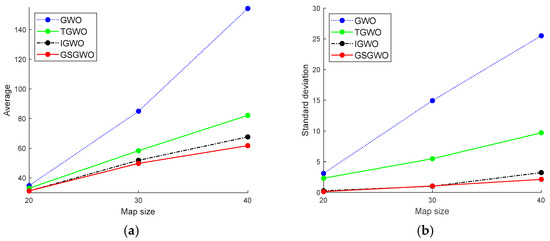
Figure 8. Stability change trend: (a) change trend of average; (b) change trend of standard deviation.

6. Conclusions and Future Work

In order to solve the problems of a single initial population, slow convergence speed in the later stage and the ease with which it falls into the local optimum when the GWO is used in the path planning of an obstacle-surmounting robot, an improved GWO with the golden sine strategy is proposed. The piecewise chaotic sequence, nonlinear convergence factor and golden sine strategy are introduced to improve the performance of the GWO, and the path-planning problem of the obstacle-crossing robot is adapted by improving the working environment, path generation mode and fitness function. According to the results of the simulation experiment, the comparison diagram shown in Figure 9 can be calculated. It can be seen that compared with the GWO, the path length planned by the GSGWO in 20 × 20, 30 × 30 and 40 × 40 maps is optimized by 3.45%, 11.2% and 15.6%, respectively, the number of inflection points is optimized by 28.57%, 22.22% and 57.14%, respectively, and the path cost is optimized by 32.5%, 40.32% and 54.69%, respectively. Although the randomness of the map environment has a certain influence on judging the change rule of the data, the overall optimization rate increases with the increase in the complexity of the map. At the same time, the rotation angle of the path planned by the GSGWO and the stability of the algorithm are also optimized to a certain extent. The feasibility of the path-planning field of the GSGWO obstacle-crossing robot is proved.

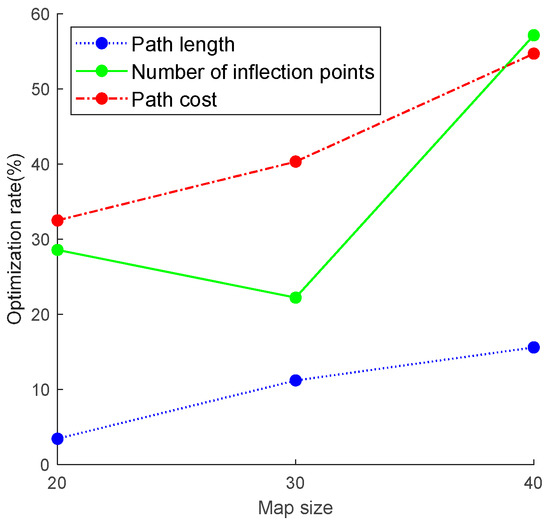
Figure 9. Optimization rate compared with GWO.

According to the content described above, some characteristics of the algorithm can be summarized: (1) The GSGWO is improved on the basis of the GWO and can be used to solve single-objective optimization problems. (2) Because the GSGWO adopts the golden sine strategy for secondary convergence, it has a larger amount of calculation and higher requirements for equipment than the GWO when the parameters are the same. (3) The appropriate interval of the weight coefficients $\lambda$ and $\mu$ in Equation (15) will change due to the different performance of the map and the obstacle-surmounting robot, so the GSGWO is suitable for robots that often perform tasks within a fixed range.

For the subsequent improvement and application expansion of the GSGWO, the following ideas are proposed: (1) Adaptive adjustment of $\lambda$ and $\mu$. The preliminary idea is to extract map features such as map size, number of obstacles, average obstacle size and starting and ending positions. The mathematical relationship between these features and $\lambda$ and $\mu$ is analyzed through experiments. Finally, the values of $\lambda$ and $\mu$ are calculated by establishing a mathematical equation between the features and $\lambda$ and $\mu$. If the adaptive adjustment of $\lambda$ and $\mu$ can be achieved, the GSGWO will be able to process new maps through a small map processing program, and robots equipped with the GSGWO will be able to perform tasks in areas that have never been explored. (2) Enrich the types of obstacle-surmountable passage areas. In the actual scene, there are many kinds of obstacle-crossing robots that can cross obstacles, and the ways and costs of obstacle-crossing are not the same. By classifying the obstacle-crossing areas into roadblocks, slopes, gullies, grasses, etc., it can make the GSGWO more intelligent in path selection and reduce the probability of accidents.