GMN+: A Binary Homologous Vulnerability Detection Method Based on Graph Matching Neural Network with Enhanced Attention

Abstract

The widespread reuse of code in the open-source community has led to the proliferation of homologous vulnerabilities, which are security flaws propagated across diverse software systems through the reuse of vulnerable code. Such vulnerabilities pose serious cybersecurity risks, as attackers can exploit the same weaknesses across multiple platforms. Deep learning has emerged as a promising approach for detecting homologous vulnerabilities in binary code due to their automated feature extraction and high efficiency. However, existing deep learning methods often struggle to capture deep semantic features in binary code, limiting their effectiveness. To address this limitation, this paper presents GMN+, which is a novel graph matching neural network with enhanced attention for detecting homologous vulnerabilities. This method comprehensively considers the information contained in instructions and incorporates types of input instruction. Masked Language Modeling and Instruction Type Prediction are developed as pre-training tasks to enhance the ability of GMN+ in extracting semantic information from basic blocks. GMN+ utilizes an attention mechanism to focus concurrently on the critical semantic information within functions and differences between them, generating robust function embeddings. Experimental results indicate that GMN+ outperforms state-of-the-art methods in various tasks and achieves notable performance in real-world vulnerability detection scenarios.

1. Introduction

With the continuous growth of the open-source community, software developers increasingly utilize open-source code to boost development efficiency. However, code reuse increases the risk of spreading homologous vulnerabilities [1,2]. According to the 2023 Open Source Security & Risk Analysis Report, 96% of audited code included open-source components with 84% containing at least one open-source related vulnerability [3]. Vulnerable open-source code, when compiled and deployed across diverse platforms and architectures, leads to a proliferation of homologous vulnerabilities, posing substantial risks to cybersecurity [4].

Remarkable advancements in deep learning technologies [5] have revealed enormous potential in natural language processing (NLP), speech recognition, and computer vision [6]. Researchers have successfully applied deep learning to the detection of binary homologous vulnerabilities, yielding significant research outcomes [7,8,9,10,11]. Among these, the graph matching network (GMN) model [9] utilizes both intra-function semantic information and inter-function differences to compute similarity scores, achieving notable detection accuracy. GMN employs attention mechanisms to extract pivotal information for assessing functional homology. However, this approach restricts the attention mechanism to inter-function matching, potentially overlooking critical semantic information during intra-function graph convolution. Moreover, current methods often treat the disassembled instructions as natural language, neglecting their unique characteristics and limiting the accuracy of vulnerability detection.

To address these challenges, we propose GMN+, which is an enhanced GMN for binary homologous vulnerability detection. GMN+ integrates NLP models with graph neural networks (GNN) to achieve high accuracy in homologous vulnerability detection. It consists of three modules: an Instruction Preprocessor, a Semantic Learner, and a Graph Learner. The Instruction Preprocessor normalizes disassembled instructions and extracts the type of the operator and operand. The Semantic Learner is a BERT model [12] trained with Masked Language Modeling (MLM) and Instruction Type Prediction (ITP), generating semantic embeddings for basic blocks in functions. In the Graph Learner, GMN+ uses a GMN with enhanced attention to extract robust function embeddings and compute similarity scores between the query and functions in the vulnerability database. We evaluate the performance of GMN+ relative to baseline methods across various tasks, including function similarity detection, homologous function search, and real-world vulnerability detection. We further analyze the contributions of different modules in GMN+. Experimental results indicate that GMN+ outperforms baseline methods in all these areas. However, GMN+ has specific limitations, such as limited effectiveness for certain types of vulnerabilities and computational overhead, which are discussed in detail in a later section. In addition, we have released the code of GMN+ at https://github.com/haidachenxing/GMN-plus (accessed on 16 November 2024).

2. Related Work

Deep learning-based vulnerability detection methods can be broadly classified into two categories: NLP-based and GNN-based methods.

2.1. NLP-Based Methods

Recent research has regarded code as natural language and leveraged natural language models to extract code representations for detecting software vulnerabilities. Ding et al. [13] developed Asm2vec, which employs PV-DM [14] to generate function embeddings specifically for vulnerability detection. This approach, however, is limited to a single instruction set architecture, constraining its application in cross-architecture vulnerability detection. To overcome this limitation, Massarelli et al. [7] introduced SAFE, which is a self-attention-based neural network model that generates instruction embeddings using word2vec [15]. These embeddings are further processed by a bi-directional recurrent neural network (RNN) with an attention mechanism used to derive function embeddings. However, this method is only feasible across ARM and AMD architectures. To address such issues, Xing et al. [4] proposed an innovative multi-architecture instruction embedding approach using Unsupervised Multilingual Word Embeddings (UMWE) [16]. This method maps codes from diverse architectures into a shared semantic space, enabling the extraction of common semantic information across ARM, MIPS, and X86 architectures.

The Transformer model [6], a neural network based on self-attention mechanisms, can globally model each token in a token sequence and has achieved notable success in NLP. Recently, researches have tried to apply the Transformer model to extract semantics from binary code for vulnerability detection. Jiang et al. [17] developed an adaptive binary code similarity analysis method for vulnerability discovery. This system integrates semantic and structural features of functions and utilizes the Transformer’s attention mechanism to maintain robustness across different compilation settings. BERT [12], recognized for its high-performance capabilities as a Transformer method with efficient semantic extraction, is extensively employed by researchers in vulnerability detection methods. For example, Yu et al. [18] developed pre-training tasks at both the basic block and function levels to train a BERT model, generating semantic embeddings for function basic blocks. Subsequently, they utilized the Control Flow Graph (CFG) of a function and a Message Passing Neural Network (MPNN) [19] to learn the structural features of functions and integrated these with sequence features to create comprehensive function embeddings. Luo et al. [2] utilized an intermediate language to mitigate the effects of architectural differences on code homogeneity assessments and introduced the novel Intermediate Representation Function Model (IRFM). This method transforms binary code into microcode [20] and establishes root operand prediction and adjacent block prediction tasks for training the RoBerta model [21]. This training enables the model to understand the relationships between operands and the data flow within basic blocks, facilitating the generation of semantic embeddings for basic blocks. Finally, a Graph Convolutional Network (GCN) [22] is employed to create function embeddings. Gu et al. [23] developed BinAIV, which is a method that utilizes SimBERT [24] to learn the representation of assembly code and incorporates function name information into function semantics, thus enhancing the accuracy of vulnerability detection. Concurrently, Li et al. [25] utilize BERT to extract semantic information from instructions and employ a graph encoder with a self-gating layer to capture both structural and semantic features within CFGs.

Large language models (LLMs) [26], known for their powerful analytical and reasoning capabilities, are increasingly employed to improve performance in vulnerability detection. Lu et al. [27] enhanced the capabilities of LLMs for vulnerability detection by integrating structural information with in-context learning [28]. This approach evaluates semantic, lexical, and syntactic similarities to accurately identify code examples that are most similar to the target code. Leveraging this method, they designed an effective example retrieval system that supplies optimized examples for the in-context learning of LLMs.

All of the above methods treat code as natural language and use natural language models to extract its semantic features, but they usually overlook unique characteristics of instructions, such as instruction types. This oversight can lead to code embeddings that fail to accurately reflect the true semantics of the code, thus hindering the effectiveness of vulnerability detection. Our method incorporates instruction type into token embeddings, enabling a more comprehensive extraction of code semantics.

2.2. GNN-Based Methods

In the field of vulnerability detection, researchers use graph structures to represent binary functions and employ GNNs to learn function semantics. GNNs are effective models for learning representations of unstructured data and solving graph prediction problems [9]. Xu et al. [29] first proposed a GNN-based vulnerability detection method, which combines the CFG of a binary function with statistical features of basic blocks to create an Attributed Control Flow Graph (ACFG). This method employs the Structure2vec model [30] to extract structural features from the ACFG of functions and generate their embeddings, which are then used to identify vulnerabilities. Zhang et al. [31] proposed a graph Transformer-based method for obfuscation-resilient code similarity detection to identify binary vulnerabilities. This approach utilizes multiple positional encodings to capture structural information from the function’s ACFG. These encodings are then incorporated as bias terms into the Transformer self-attention computation, ultimately generating graph embeddings. Li et al. [9] further extended GNN and introduced the GMN model, which processes pairs of ACFGs and employs a cross-graph attention-based matching mechanism to perceive their differences through the computation of node matching metrics between graphs.

While these methods utilize ACFGs to represent functions, ACFGs only encapsulate partial function information, thus inadequately describing function semantics and limiting detection accuracy. In response to this issue, researchers have utilized various novel graph structures to describe functions more comprehensively. Yang et al. [1] utilized Abstract Syntax Trees (ASTs) to represent binary functions and introduced a deep learning-based method for AST encoding. This method employs a Tree-LSTM network [32] to learn the semantic representations of functions from their ASTs and generate function embeddings. Gao et al. [33] introduced data flow information to the CFG to create a labeled semantic flow graph (LSFG) and applied the Structure2vec model to extract its structural features.

Liang et al. [10] integrated instruction, basic block, and function features to construct a 3-Level Attributed Control Flow Graph (3LACFG) and introduced the FIT method. This method initially uses the word2vec model to learn the contextual information from binary code for instruction embeddings and employs LSTM [34] to create embeddings for basic blocks. It then uses the Structure2vec model to generate function embeddings that incorporate features at the instruction, basic block, and function levels. Yu et al. [35] believed that function call relationships also encapsulate function semantics. Accordingly, they merged CFGs with function call graphs to create a Graph-of-Graphs (GOG) for binary codes, employing GNNs to extract structural features of GOGs and generate function embeddings. Wang et al. [36] argue that current GNN-based code similarity detection methods excessively depend on CFG features, potentially diminishing model performance. They employ existing explanation methods to assess the reliance of GNN-based models on CFG features and enhance performance by reducing this dependency.

Software vulnerabilities often necessitate slight alterations to produce patched versions. This results in minimal differences between vulnerable and patched versions, consequently elevating false positive rates in vulnerability detection. To mitigate this issue, Liu et al. [37] proposed PG-VulNet, which is a multi-model cross-architecture vulnerability detection method based on pseudocode and GMN. PG-VulNet extracts behavioral and structural features from pseudocode, constructs pseudocode feature graphs, and uses GMN to detect subtle differences between these graphs. Sun et al. [38] selected code segments related to typical vulnerabilities and used code-slicing strategies to create slice subgraphs for specific vulnerabilities, reducing redundant semantics and focusing the model on vulnerability-related code parts. This method utilizes the UniXcoder model [39] and the InfoGraph model [40] to encode the slice subgraphs and generate graph embeddings, effectively detecting vulnerabilities by minimizing distances between similar functions and maximizing those between vulnerable and patched functions.

Current methods leverage diverse graph structures to generate semantic embeddings, effectively representing the structural semantics of codes. However, different compilation configurations can cause significant structural differences in binary codes generated from the same source code, challenging vulnerability detection. Our method employs an attention mechanism to concurrently focus on important semantic information within functions and differences between functions, effectively mitigating the impact of different compilation configurations.

3. Method

GMN+ utilizes semantic comparison to identify code homology, revealing potential vulnerabilities within the code. The GMN+ primarily consists of three modules: the Instruction Preprocessor, Semantic Learner, and Graph Learner, as shown in Figure 1. The Instruction Preprocessor employs the advanced disassembly tool IDA Pro [41] to transform binary codes into disassembled instructions, normalizes these instructions, and extracts types of instruction opcodes and operands. Additionally, the CFGs of the binary functions are constructed during this step. The Semantic Learner generates semantic embeddings for function basic blocks using a BERT model, which is pre-trained using the Masked Language Modeling (MLM) and Instruction Type Prediction (ITP) tasks. The Graph Learner integrates these semantic embeddings with CFGs of functions to construct ACFGs. It utilizes intra-graph and inter-graph attention mechanisms to learn structural and matching information within and between functions, ultimately detecting function homology via semantic similarity.

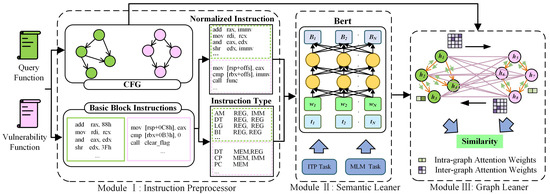
Figure 1. Architecture of the GMN+ model.

3.1. Instruction Preprocessor

3.1.1. Instruction Normalization

The process of disassembling binary codes inherently generates a diverse set of tokens due to the inclusion of numerous memory addresses, immediate values, and address offsets. This diversity significantly exacerbates the out-of-vocabulary (OOV) problem, complicating the model’s learning process. As shown in Figure 2a, the original assembly code contains a vast array of tokens that represent memory addresses (e.g., ‘loc_61C9’), immediate values (e.g., ‘0’), or address offsets (e.g., ‘0B8h’). The exact values of these tokens carry limited semantic information. But their roles are semantically rich. To mitigate this issue, our method implements instruction normalization rules, as detailed in Table 1. These specific rules are designed to reduce the complexity of the code and improve the learnability of the code semantics by the model:

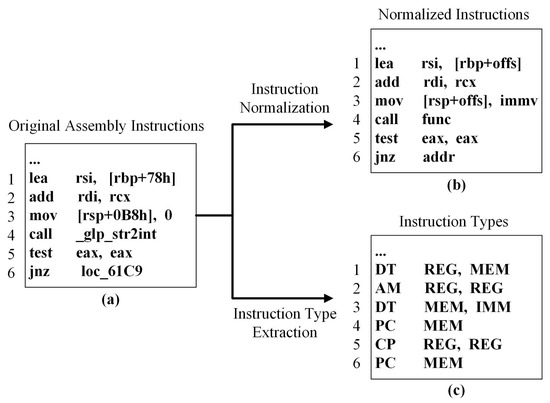
Figure 2. An example of instruction normalization and instruction type extraction. (a) Original assembly instructions; (b) Normalized instructions; (c) Instruction types.

Table 1. Instruction normalization rules.

Type	Token	Example
Immediate Value	immv	sub rbx, 0A0h → sub rbx, immv
Memory Address	addr	lea rax, qword 1B4770 → lea rax, addr
Address Offset	offs	mov rax, [rbp+80h] → mov rax, [rbp+offs]
Function Name	func	call _glp_str2in → call func

• Immediate values are replaced with the token ‘immv’.
• Memory addresses are replaced with the token ‘addr’.
• Address offsets are replaced with the token ‘offs’.
• Function names are replaced with the token ‘func’.

The above normalization process produces a normalized instruction corpus, as shown in Figure 2b. This normalization helps to homogenize the input data, reducing the number of unique tokens the model must handle and maximizing the retention of semantic information.

3.1.2. Instruction Type Extraction

The disassembled code consists of structured instructions that significantly differ from natural language text. Each instruction contains an opcode and multiple operands, each playing distinct roles and can be classified into various types. Specifically, instruction opcodes are classified into 10 types based on functionality, such as data transfer, arithmetic, and logical operations, as shown in Table 2. Operands are classified into three types based on their storage locations within a computer: immediate values, registers, and memory addresses, as outlined in Table 3. Each operand and opcode type is assigned a specific label. A sequence of labels from continuous instructions forms an instruction type sequence.

Table 2. Opcode types.

Opecode Type	Label	Example
Data transfer instruction	DT	mov, movq
Arithmetic instruction	AM	add, sub
Logical instruction	LG	and, or
Program control instruction	PC	jmp, call
Bit instruction	BI	shr, shl
Conditional move instruction	CM	cmova, cmovnb
Conditional set instruction	CS	setz, setle
Stack operation instruction	SO	push, pop
Data conversion instruction	DC	cvttsd2si, cvtsi2sd
Comparative instruction	CP	cmp, test

Table 3. Operand types.

Operand Type	Label	Example
Register	REG	r0, rbx
Memory address	MEM	[rbx+offset], [rax]
Immediate value	IMM	01Ch, 0FFh

Figure 2c illustrates the process of extracting instruction types from a sequence of original assembly instructions. In this process, opcodes and operands are identified and assigned corresponding type tokens. For instance, the first instruction is classified as a Data Transfer instruction (DT), involving a register (REG) and a memory address (MEM).

3.2. Semantic Learner

The BERT model [12], developed by Google, is an advanced pre-trained language model that significantly improves performance across a range of NLP tasks. Our study utilizes BERT to extract semantic information from code basic blocks. However, instructions, distinct from natural language, possess unique syntax and semantics with various opcode and operand types exhibiting notable semantic differences. This discrepancy affects the performance of BERT in semantic understanding. To address this issue, we incorporate opcode and operand type information into the model training process, enabling a more comprehensive capture of code semantics.

3.2.1. Input Embeddings

In GMN+, each opcode or operand from the normalized instruction corpus is uniquely represented as a token along with its associated type. The input to the BERT model consists of two sequences: a normalized instruction sequence with n tokens $w_1,w_2,\dots ,w_n$ and a corresponding instruction type sequence detailing the types of each token $t_1,t_2,\dots ,t_n$. Similar to the methodology of BERT, three types of embeddings are constructed for each token: token embedding, type embedding, and position embedding. These embeddings are summed to form a comprehensive input embedding $E_1,E_2,\dots ,E_n$ for input tokens. Figure 3 illustrates the construction of BERT input embeddings by summing the token, type, and position embeddings for each instruction code and operand in the normalized instruction sequence.

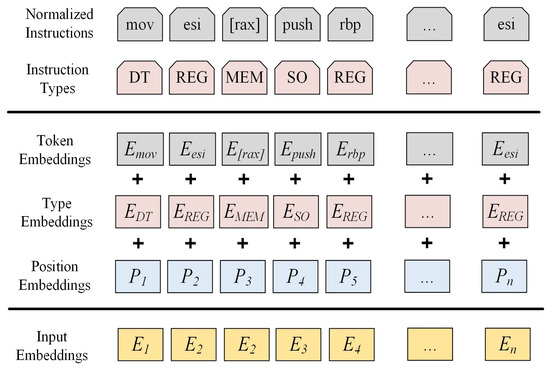
Figure 3. BERT input embedding.

3.2.2. BERT Model Training

BERT employs a Transformer architecture that enables the model to capture context from both directions in a sequence. To enhance the ability of BERT to learn code semantics, GMN+ utilizes two key pre-training tasks: Masked Language Modeling and Instruction Type Prediction tasks.

Masked Language Modeling (MLM): In this task, 15% of the tokens in the instruction sequence along with their corresponding instruction types are randomly masked. The model then predicts these masked tokens based on their surrounding context, which enables BERT to learn semantic relationships and interactions within the instruction sequences. This task helps the model develop a comprehensive understanding of binary function semantics. The MLM process is formalized as follows:

$$O=Transformer\left(E_{mask}\right)$$

(1)

$$p(w\mid E_{mask})=Softmax\left(ML{P}_{token}\left(O\right)\right)$$

(2)

where $E_{mask}$ represents input embedding after masking, and O represents the output from the Transformer encoder. The $ML{P}_{token}$ is a multilayer perceptron and w denotes the input token sequence of the model. The cross-entropy loss $L_{MLM}$ for the MLM task is computed by comparing the predicted probability distribution of the masked tokens with their ground truth, as shown below, where M represents the index set of the masked tokens.

$$L_{MLM}=-{\displaystyle \frac{1}{\left|M\right|}}\sum _{j\in M}log\left(p(w_j\mid E_{mask})\right)$$

(3)

Instruction Type Prediction (ITP): Similarly, 15% of the input tokens and their types are masked, and the model predicts the types based on the context. This task facilitates learning the semantics inherent to various instruction types and allows the model to develop deeper semantic representations of the code. The formalization of the ITP process is as follows:

$$p(t\mid E_{mask})=Softmax\left(ML{P}_{type}\left(O\right)\right)$$

(4)

where $ML{P}_{type}$ is a multilayer perceptron, and t is the type sequence of the input token sequence. The cross-entropy loss $L_{TYPE}$ for the ITP task is computed based on the predicted probability distribution of the masked token types compared to their ground truth, as shown below.

$$L_{ITP}=-{\displaystyle \frac{1}{\left|M\right|}}\sum _{j\in M}log\left(p(t_j\mid E_{mask})\right)$$

(5)

GMN+ employs the above two pre-training tasks to pre-train the BERT model. The pre-trained BERT model is subsequently utilized to generate semantic embeddings for basic blocks of binary functions. Specifically, the normalized instruction sequence and instruction type sequence of basic blocks in a function are fed into the BERT model. The semantic embedding of the basic block is obtained by averaging the outputs of the last four layers of the Transformer encoder.

3.3. Graph Learner

The ACFG for a binary function is defined as $G=<V,E,B>$, where V is the set of nodes (each representing a basic block), E is the set of edges, and B is the set of node features. For any node $i\in V$, its initial feature $b_i$ ($b_i\in B$) is derived from the Semantic Learner. The feature $l_{ij}$ for an edge $(i,j)\in E$ is the concatenation of $b_i$ and $b_j$. Given two functions’ ACFGs, $G_1=<V_1,E_1,B_1>$ and $G_2=<V_2,E_2,B_2>$, the Graph Learner uses GMN with enhanced attention to generate semantic embeddings of functions and computes their cosine similarity. The Graph Learner is divided into three parts: Encoder, Propagation Layers, and Aggregator, as shown in Figure 4.

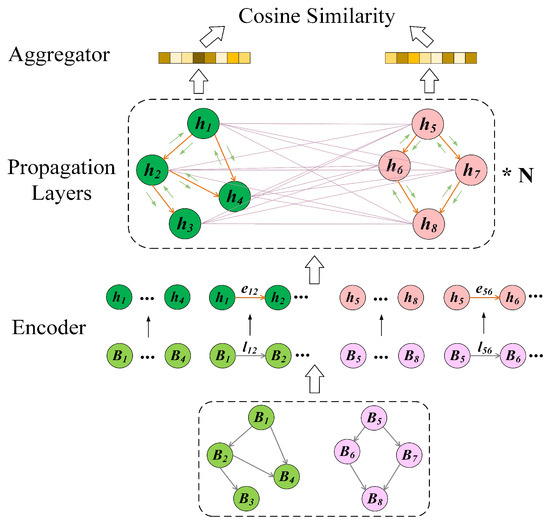
Figure 4. Graph Learner of GMN+.

The Encoder uses multilayer perceptrons, $ML{P}_{node}$ and $ML{P}_{edge}$, to encode node and edge features, respectively, generating initial embeddings for nodes and edges as shown in Equations (6) and (7), where $h_i^{\left(0\right)}$ represents the initial node embedding, and $e_{ij}$ represents the edge embedding.

$$h_i^{\left(0\right)}=ML{P}_{node}\left(b_i\right),\forall i\in V$$

(6)

$$e_{ij}=ML{P}_{edge}\left(l_{ij}\right),\forall (i,j)\in E$$

(7)

The Propagation Layer, based on ACFG, uses a GMN with enhanced dual-level attention to extract information within and between functions, ultimately generating robust function embeddings. Specifically, an intra-function attention mechanism is employed to focus on critical semantic details within each function. This mechanism allows the model to selectively emphasize information that reflects deeper semantic attributes of the function, enhancing its sensitivity to nuanced, function-specific patterns that may be indicative of vulnerabilities. The intra-function attention is shown in Equations (8)–(10).

$$m_{j\to i}=f_{message}(h_i^{\left(t\right)}\left|\right|h_j^{\left(t\right)}\left|\right|e_{ij}),\forall (i,j)\in E$$

(8)

$$a_{j\to i}={\displaystyle \frac{exp\left(s_c(h_i^{\left(t\right)},h_j^{\left(t\right)})\right)}{{\sum }_{j^{\prime }}exp\left(s_c(h_i^{\left(t\right)},h_{j^{\prime }}^{\left(t\right)})\right)}},j^{\prime }\in N_i$$

(9)

$${\gamma }_i=\sum _j{a}_{j\to i}{m}_{j\to i},j\in N_i$$

(10)

where $f_{message}$ is a multilayer perceptron taking concatenated inputs $h_i^{\left(t\right)}$, $h_j^{\left(t\right)}$ and $e_{ij}$, while $m_{j\to i}$ is the massage transmitted from node j to node i. $N_i$ is the set of neighbor nodes of node i. The term $s_c$ is a similarity function. We use cosine similarity. $a_{j\to i}$ is the attention weight for the information transmitted from node j to node i. ${\gamma }_i$ represents the aggregated information transmitted to node i from all its neighbor nodes.

On the other side, an inter-function attention mechanism, i.e., graph matching attention [9], is used to capture key semantic distinctions between functions, facilitating the model’s ability to detect homologous vulnerabilities across different but related functions. For the functions’ ACFGs $G_1$ and $G_2$, assume $\forall i\in V_1,\forall s\in V_2$. The graph matching attention mechanism is defined by Equations (11) and (12).

$$a_{s\to i}={\displaystyle \frac{exp\left(s_c(h_i^{\left(t\right)},h_s^{\left(t\right)})\right)}{{\sum }_{s^{\prime }\in V_2}exp\left(s_c(h_i^{\left(t\right)},h_{s^{\prime }}^{\left(t\right)})\right)}}$$

(11)

$${\mu }_{s\to i}=a_{s\to i}(h_i^{\left(t\right)}-h_s^{\left(t\right)})$$

(12)

where $a_{s\to i}$ represents the attention weight describing the proportion of information passed from note s of $G_2$ to note i of $G_1$, and ${\mu }_{s\to i}$ represents the corresponding matching information. The aggregate of ${\mu }_{s\to i}$, for each s in $V_2$, is calculated as shown in Equation (13), capturing the differential information between $h_i^{\left(t\right)}$ and the closest node in the graph for comparison.

$${\omega }_i=\sum _{s\in V_2}{\mu }_{s\to i}=\sum _{s\in V_2}{a}_{s\to i}(h_i^{\left(t\right)}-h_s^{\left(t\right)})=h_i^{\left(t\right)}-\sum _{s\in V_2}{a}_{s\to i}{h}_s^{\left(t\right)}$$

(13)

At last, node embeddings are updated using a Gated Recurrent Unit (GRU). The update function, denoted by $f_{update}$, is a GRU cell. The updating procedure, represented by Equation (14), uses $h_i^{\left(t\right)}$ as the input and concatenates ${\gamma }_i$ with ${\omega }_i$ to form the hidden state.

$$h_i^{(t+1)}=f_{update}(h_i^{\left(t\right)},{\gamma }_i\left|\right|{\omega }_i)$$

(14)

After T rounds of propagation, the Aggregator combines all node embeddings $h_i^{\left(T\right)}$ from the ACFG of the function into a single graph embedding $h_G$, using a gated vector weighting method [42], as described in Equation (15). This process selectively retains crucial information, resulting in a graph embedding that accurately embodies semantics of the function. Given graph embeddings $h_{G1}$ and $h_{G2}$ corresponding to $G_1$ and $G_2$, GMN+ computes their similarity using cosine similarity.

$$h_G=ML{P}_G\left(\sum _{i\in V}\sigma (ML{P}_{gate}\left(h_i^{\left(T\right)}\right)\odot MLP\left(h_i^{\left(T\right)}\right))\right)$$

(15)

The training of GMN+ employs a loss function as outlined in Equation (16), where $(G_1,G_2,G_3)$ are model inputs, consisting of homologous functions ($G_1$, $G_2$) and non-homologous functions ($G_1$, $G_3$). The objective of this loss function is to minimize the distance between homologous functions and maximize it between non-homologous functions, enhancing the discriminatory ability of the model.

$$L_G=log(1+e^{cos(h_{G_1},h_{G_3})}-e^{cos(h_{G_1},h_{G_2})})$$

(16)

Figure 4 provides an example that illustrates the process of Graph Learner, with which the similarity between functions based on the ACFG is calculated. In this process, the Encoder encodes each function’s nodes and edges. Then, Propagation Layers generate updated node embeddings using enhanced attention. Finally, the Aggregator aggregates these node embeddings to produce the graph embeddings used for computing function similarity.

4. Experiments and Analysis

To validate the effectiveness of GMN+, we pose the following three research questions (RQs) and answer them through experiments:

• RQ1: How does the performance of GMN+ compare to baseline methods?
• RQ2: What contributions do different modules of GMN+ make to its performance?
• RQ3: How does GMN+ perform in real-world vulnerability detection tasks?

4.1. Experimental Setup

4.1.1. Dataset and Experimental Platform

We collected three source codes from GNU software programs: Glpk (v4.65), Xml (v2.9.4), and Sqlite3 (v0.8.6). Each program was compiled into 12 binary versions using GCC (v11.3) across various architectures (ARM, MIPS, X86) and optimization levels (O0-O3). These binary codes were disassembled with IDA Pro (V7.3), yielding 87,488 functions, 1,802,028 basic blocks, and 10,269,352 instructions, as shown in Table 4. We constructed the experimental dataset by generating pairs of homologous and non-homologous function samples, dividing it into training (80%), validation (10%), and testing (10%) subsets.

Table 4. Summary of the dataset used in our study (FN, BB, IN representing the number of FuNctions, Basic Blocks, and INstructions, respectively).

Software	FNs	BBs	INs
Glpk(v4.65)	19,457	431,144	2,792,595
Xml(v2.9.4)	35,107	757,433	3,831,902
Sqlite3(v0.8.6)	32,924	613,451	3,644,855
All	87,488	1,802,028	10,269,352

We implemented the GMN+ using PyTorch (v1.8.1) and trained it on two 24 GB NVIDIA GeForce RTX 3090ti GPUs. The values of the key hyperparameters used in our experiments are detailed in Table 5. A batch size of 128 is used to optimize computational efficiency. Node and edge embedding dimensions are set at 256 to capture detailed graph structures effectively. A graph-embedding dimension of 128 is chosen to balance detail with computational efficiency, and a learning rate of 0.0001 ensures gradual optimization of the model.

Table 5. The hyperparameters used in the experiments.

Hyperparameters	Value
Batch size	128
Node embedding dimension	256
Edge embedding dimension	256
Graph embedding dimension	128
Learning rate	0.0001

4.1.2. Baselines

The baselines for our experiments include three state-of-the-art methods: one NLP-based method, SAFE [7], and two GNN-based methods, FIT [10] and GMN [9]. All baseline methods are implemented according to the original papers. The evaluation metrics used in the experiments are listed in Table 6. We define TP as the number of correctly detected similar pairs, TN as the number of correctly detected dissimilar pairs, FP as the number of dissimilar pairs incorrectly detected as similar, and FN as the number of similar pairs incorrectly detected as dissimilar.

Table 6. The evaluation metrics used in the experiments.

Metrics	Definition
Precision	TP/(TP + FP)
Recall	TP/(TP + FN)
F-measure (F1)	2 × Precision × Recall/(Precision + Recall)
Area Under ROC Curve (AUC)	Area under the ROC curve
HR-K	Hit rate of the top K candidate
NDCG-K [43]	Evaluate the quality of ranking

4.2. Model Performance Evaluation

To respond to RQ1, all models were trained using the designated training set and evaluated across various tasks. Two types of tasks were set up: one-to-one function similarity detection and one-to-many homologous function search. Furthermore, the detection efficiency of GMN+ and baseline methods, in terms of time cost, were assessed.

4.2.1. Function Similarity Detection

This experiment assessed GMN+ alongside baseline methods in detecting similar function pairs across various architectures with a balanced 1:1 ratio between positive and negative sample pairs, which were all optimized at level O1. These methods were evaluated on recall, precision, and F1 score with detailed results in Table 7. ARM-MIPS, ARM-X86, and MIPS-X86 represent function pairs involving only two architectures, while ARM-MIPS-X86 denotes function pairs that involve three architectures simultaneously. Since the SAFE lacks support for the MIPS architecture, its experimental results are limited to ARM-X86. The results indicate the superior performance of FIT, GMN, and GMN+ over SAFE, which was possibly because SAFE merely focuses on the semantic information of instructions without considering the structural information of functions, whereas the other methods incorporate structural insights. The FIT performs better than the GMN model, which is possibly due to its use of NLP techniques to extract significant semantic features from basic blocks, whereas GMN primarily utilizes rudimentary code statistics for basic block characterization. Among the models tested, GMN+ demonstrated superior performance, especially in the most challenging scenario (ARM-MIPS-X86), achieving the highest recall, precision, and F1 scores of 0.9835, 0.9321, and 0.9571, respectively. Figure 5 illustrates the ROC curves of the proposed GMN+ and baseline models. It can be seen that GMN+ (highlighted in red) consistently outperforms the baseline methods, achieving the highest area under the curve (AUC). These results demonstrate the superior efficacy of GMN+ across varied architectural conditions.

Table 7. Results of the similarity detection task across architectures.

Method	ARM-MIPS			ARM-X86			MIPS-X86			ARM-MIPS-X86
	Recall	Precision	F1	Recall	Precision	F1	Recall	Precision	F1	Recall	Precision	F1
FIT	0.9042	0.8479	0.8752	0.9160	0.9124	0.9142	0.9383	0.9012	0.9194	0.9186	0.8719	0.8946
GMN	0.8573	0.8636	0.8604	0.9122	0.8638	0.8873	0.8798	0.8984	0.8891	0.9161	0.8491	0.8813
SAFE	-	-	-	0.8854	0.8451	0.8647	-	-	-	-	-	-
GMN+(ours)	0.9943	0.9215	0.9565	0.9727	0.9549	0.9637	0.9822	0.9375	0.9594	0.9835	0.9321	0.9571

Note: Values in bold font are the optimal values for each column.

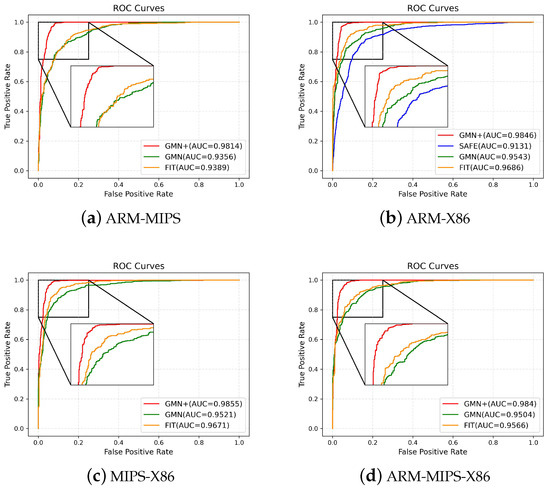
Figure 5. Comparison of ROC curves for different methods across architectures.

We further evaluated the performance of GMN+ and the baseline methods in detecting homologous functions across varied optimization levels, which are all compiled targeted to the ARM architecture. The dataset comprises 5592 sample pairs balanced between positive and negative sample pairs. The results are shown in Table 8 where O0-O1, O1-O2, and O0-O3 indicate the respective optimization levels of the test pairs; O0-O1-O2-O3 denotes that the test pairs are of any two of the four optimization levels. GMN+ consistently surpassed the baseline methods in the majority of scenarios. Notably, all methods experienced declines in performance for the O0-O3 scenario. This could be attributed to the pronounced structural difference between the highest (O3) and lowest (O0) optimization levels, complicating the identification of homologous functions. Figure 6 illustrates ROC curves across various scenarios. As can be seen, GMN+ consistently outperforms baseline methods, particularly in scenarios with significant optimization level differences, such as O0-O3.

Table 8. Results of the similarity detection task across optimization levels.

Method	O0-O1			O0-O3			O1-O2			O0-O1-O2-O3
	Recall	Precision	F1	Recall	Precision	F1	Recall	Precision	F1	Recall	Precision	F1
FIT	0.9379	0.8769	0.9074	0.7033	0.8469	0.7685	0.9224	0.9681	0.9446	0.8418	0.8605	0.8511
GMN	0.8221	0.8791	0.8696	0.8541	0.8623	0.8582	0.9192	0.9312	0.9252	0.8894	0.9161	0.9025
SAFE	0.8881	0.8185	0.8519	0.7973	0.7668	0.7818	0.8972	0.8988	0.8981	0.8603	0.8174	0.8383
GMN+(ours)	0.9601	0.9265	0.9431	0.9343	0.8888	0.9111	0.9468	0.9417	0.9442	0.9373	0.9004	0.9185

Note: Values in bold font are the optimal values for each column.

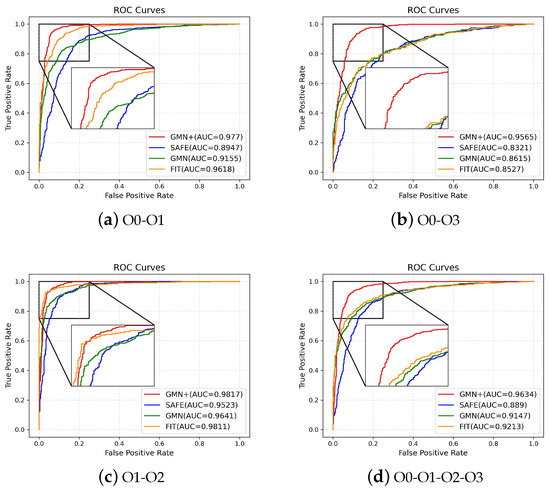
Figure 6. Comparison of ROC curves for different methods across optimization levels.

GMN+ achieved the best performance in the function similarity detection task, outperforming baseline methods across various architectures and optimization levels. The advantages of GMN+ over baselines are analyzed as follows: In contrast to SAFE, GMN+ incorporates not only the semantic information of the code but also its structural information, allowing the extraction of more comprehensive code semantics. Compared to GMN, GMN+ employs NLP techniques to extract deeper semantic content. Furthermore, it introduces attention mechanisms at both intra-function and inter-function levels rather than limiting to one. Lastly, GMN+ significantly enhances semantic extraction from binary code by integrating instruction type information into instruction embeddings, providing a marked improvement over the FIT method.

4.2.2. Homologous Function Search

A homologous function search involves identifying functions within a designated pool that share homology with a query function. The performance of GMN+ and the baseline methods was evaluated using HR-K and NDCG-K. For each function in the test set, we constructed a pool consisting of one randomly selected homologous function version and 100 non-homologous functions to assess the similarity rankings of the homologous function relative to the pool. The results are shown in Figure 7. The horizontal axes represent the number of top results evaluated, denoted as K, and the vertical axes give the Hit Rate (HR) and Normalized Discounted Cumulative Gain (NDCG), respectively. As can be seen from Figure 7, for K ≤ 40, the HR values for GMN+ surpassed those of the baseline methods, whereas for K > 40, the HR values for all methodologies converged toward 1. Similarly, GMN+ also achieved the highest NDCG-K. These results demonstrate the superior capability of GMN+ in homologous function search tasks compared to baseline methods. The distinct advantage of GMN+ over baseline methods arises from its advanced modeling of both structural and semantic aspects of code. GMN+ enhances homologous function search by effectively integrating various data modalities, such as the code structure and the semantic aspects of instructions, particularly by incorporating instruction type information into the model.

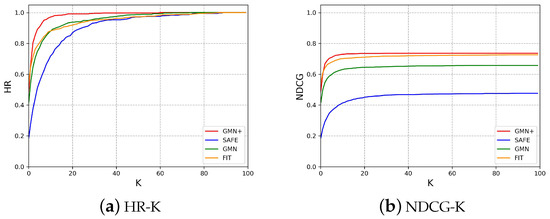
Figure 7. Comparative results of homologous function search using various methods.

4.2.3. Detection Efficiency

This experiment evaluated the time costs of function homology detection for GMN+ and baseline methods on different function sizes, i.e., the number of basic blocks. The primary time cost components involve generating function embeddings and calculating similarity scores. The results depicted in Figure 8 show the distinct time costs associated with different methods, where the horizontal axis represents the CFG size and the vertical axis represents the time cost of detection. The time costs of FIT are significantly higher than those of the other methods, escalating linearly with CFG size. The higher time costs for FIT stem from its use of LSTM to generate basic block embeddings, which are computationally intensive. The SAFE method, which uses a bidirectional RNN to aggregate instruction embeddings into function embeddings, incurs slightly higher time costs than the graph embedding method used by GMN+. GMN+ demonstrates marginally higher time costs than GMN due to its integration of an additional attention mechanism. Moreover, the application of NLP methods to automatically generate basic block embeddings, characterized by heightened dimensions, also increases the computation time of GMN+.

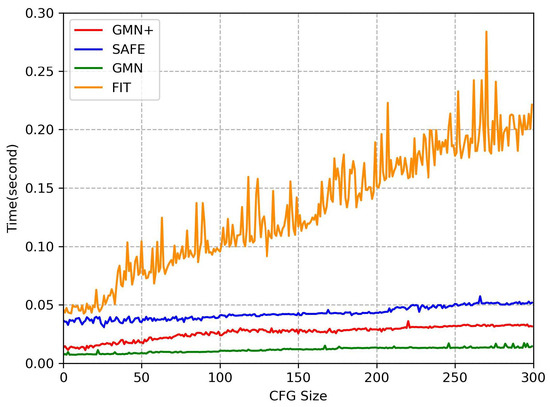
Figure 8. Comparison of time overhead for different methods.

4.3. Ablation Study

To answer RQ2, ablation studies were performed, focusing on two points: semantic learning of basic blocks and GMN with enhanced attention. The efficacy of our semantic learning for basic blocks was assessed by testing various versions of our model:

• (w/o) Type: The model excludes instruction type information.
• (w/o) ITP: The model omits the ITP task during pre-training.
• (w/o) Type & ITP: The model excludes instruction type information and omits the ITP task during pre-training.

These models were evaluated using three datasets constructed with functions from Sqlite3, Glqk and Xml software. The results are shown in Figure 9 where the vertical axis represents the average detection precision. GMN+, (w/o) Type, (w/o) ITP, and (w/o) Type & ITP achieved average precision values of 0.9367, 0.8780, 0.8687, and 0.8317, respectively, across different datasets. GMN+ consistently achieved the best performance in different datasets, demonstrating the significance of integrating instruction type and executing ITP during pre-training.

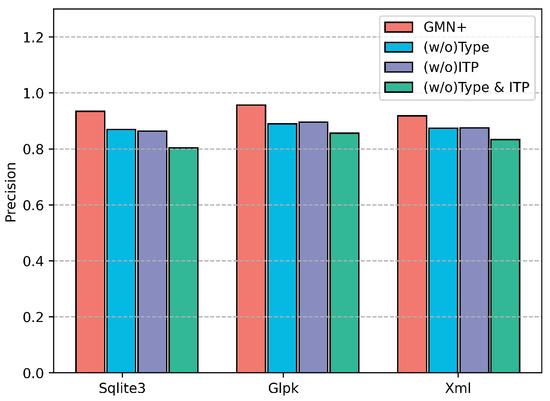
Figure 9. The performance of GMN+ variants with different blocks in the Semantic Learner.

We further evaluated two versions of our model, BERT-GNN and BERT-GMN, which substitute the GMN with enhanced attention with standard GNN and GMN, respectively. As illustrated in Figure 10, where the vertical axis represents average detection precision, BERT-GMN outperformed BERT-GNN. This improvement is attributed to the graph matching mechanism employed by GMN, which builds upon the foundational GNN structure to effectively perceive differences between nodes, enhancing similarity detection. Meanwhile, GMN+ outperformed the BERT-GMN model because GMN+ incorporates an additional graph attention mechanism to focus on nodes containing significant semantic information within the CFG.

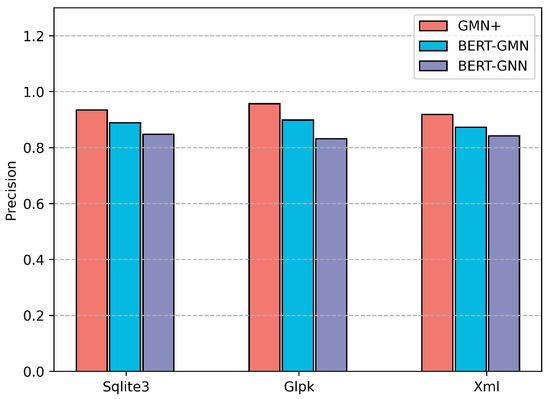
Figure 10. The performance of GMN+ variants with different blocks in the Graph Learner.

4.4. The Performance Evaluation on Real-World Vulnerability Detection

To address RQ3, we collected nine real CVE vulnerability functions from two software packages, as detailed in Table 9. Each software was compiled across three architectures (ARM, MIPS, X86) and four optimization levels (O0, O1, O2, O3), producing 12 versions that constituted a function pool of 27,714 functions. For each vulnerable function, a version for the X86 architecture at optimization level O1 was selected as the query function. Its similarity to other functions in the pool was assessed and ranked. The number of functions with homologous vulnerabilities within the top 10 highest similarities is illustrated in Figure 11, where the horizontal axis represents specific CVE identifiers. The experimental results reveal that GMN+ surpasses all baseline methods in detecting real-world vulnerabilities. Specifically, GMN+ identified 61 vulnerable functions (within the top 10) in total, in contrast to 32 by FIT, 35 by GMN, and 8 by SAFE. The reasons for superior performance of GMN+ in real-world vulnerability detection align with the benefits seen in the function similarity detection task, underscoring the efficacy of our method.

Table 9. The details of the CVE vulnerable function.

Software	CVE Number	Function Name	CFG Size
Curl(v7.29.0)	CVE-2013-2174	curl_easy_unescape	18
	CVE-2013-0249	Curl_sasl_create_digest_md5_message	47
	CVE-2014-3707	curl_easy_duphandle	21
	CVE-2016-7167	curl_easy_escape	19
	CVE-2016-8621	curl_getdate	89
Xml(v2.9.2)	CVE-2015-8317	xmlParseXMLDecl	67
	CVE-2015-8242	xmlSAX2TextNode	42
	CVE-2016-2073	htmlParseNameComplex	51
	CVE-2016-3627	xmlStringGetNodeList	68

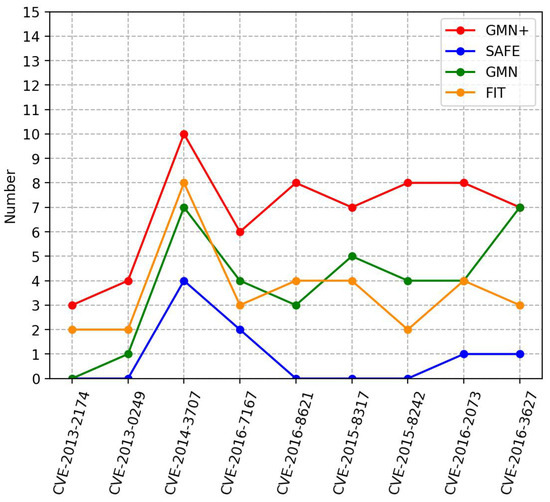
Figure 11. Comparison of detection results of different methods on real-world vulnerability detection tasks.

5. Discussion

GMN+ leverages an NLP model to extract semantic information within the basic blocks of binary functions and employs a GMN with enhanced attention to analyze the semantic similarity between functions, thus facilitating the detection of homologous vulnerabilities in binaries. Experimental results demonstrate that GMN+ outperforms baseline methods in function similarity detection, homologous function search tasks, and real-world vulnerability detection as well. The effectiveness of GMN+ can be attributed to several key aspects:

• An efficient instruction embedding method is utilized, which integrates operator and operand type information for a more comprehensive representation of instructions.
• An ITP pre-training task is used to pre-train BERT to enhance its capability in the semantic learning of functions.
• Enhanced attention is applied, focusing concurrently on crucial information for assessing homology within and between functions.

However, it still faces several challenges:

• Subtle Semantic Distinctions: GMN+ may fail to recognize subtle semantic distinctions between vulnerable functions and their patched versions, often resulting in high false positive rates. To address this limitation, incorporating fine-grained homology detection at the code slices level could provide a more nuanced understanding of code semantics and reduce false positives.
• Inter-function Vulnerability Detection: While GMN+ primarily analyzes individual functions for vulnerability detection, many real-world vulnerabilities emerge from interactions between multiple function [25]. Future studies should explore integrating function call relationships into the input of the model to enhance detection capabilities for inter-function vulnerabilities.
• Computational Overhead: GMN+ is computationally intensive, particularly during inference, where both the query function and functions in the vulnerability pool require processing, leading to substantial computational overhead. To mitigate this problem, a tiered detection approach could be employed, using initial quick filters based on function representations before conducting a detailed analysis with GMN+.
• Dependency on Disassembly Accuracy: The effectiveness of GMN+ heavily depends on the accuracy of the disassembly tool used to convert binaries into instructions. Errors in disassembly can lead to incomplete or inaccurate semantic representations, which may impair the detection accuracy of GMN+. Developing strategies to handle disassembly errors, such as using multiple disassembly tools for cross-validation, could enhance robustness.

6. Conclusions

This paper introduces a novel binary homologous vulnerability detection method, GMN+, which merges NLP techniques and GMN. By integrating instruction type information into the BERT model and designing a pre-training task for instruction type prediction, GMN+ effectively captures semantic features of basic blocks. It leverages a GMN with enhanced attention to concurrently focus on critical semantic information within functions and the differences information between functions. Extensive experiments validated the performance and efficiency of GMN+ with real-world vulnerability detection tasks illustrating its practical utility. GMN+ shows promise for application across various domains, including software vulnerability detection, clone detection, and malware detection.