Study on the Optimization of Site Selection for Emergency Supply Reserve Warehouses Based on Multi-Attribute Weighted Intelligent Gray Target Decision-Making Evaluation Model

Abstract

To reasonably allocate emergency supply reserve warehouses and enhance the utilization efficiency of emergency supply reserves, this paper proposes a new optimization method for the site selection of emergency supply reserve warehouses based on gray system theory—the multi-attribute weighted intelligent gray target decision-making evaluation model. This method innovatively incorporates the density of road networks, population density, economic density, and post-disaster response capability as key indicators. It then utilizes the multi-attribute weighted intelligent gray target decision-making evaluation model to evaluate the synthetic effect. Based on the evaluation results, optimization recommendations for the site selection of emergency supply reserve warehouses are provided. To validate the credibility of the proposed method, a comparative analysis is then conducted using the EEM-TOPSIS and TOPSIS–Gray Correlation Degree methods, resulting in largely consistent evaluation results. The study demonstrates that the multi-attribute weighted intelligent gray target decision-making evaluation model accounts for both hitting-the-target and missing-the-target scenarios for effect values and vectors of objectives. This approach effectively addresses the limitation of traditional multi-attribute evaluation methods, which can only rank evaluation schemes without effectively distinguishing between superior and inferior ones. This method also proves to be more user-friendly compared to others.

1. Introduction

In order to enhance the efficiency of rescue operations and improve the survival rates of disaster sufferers, it is essential to reserve emergency supplies [1]. Likewise, the reserve of supplies holds critical significance for a country’s military, economic, and social security [2]. How to achieve optimal resource allocation, enhance the efficiency of emergency supply reserve warehouses, scientifically evaluate existing emergency supply reserve warehouses, and optimize site selection are significant practical issues that require immediate resolution.

Extensive studies have been conducted by scholars both in China and abroad on the evaluation and optimization of site selection for emergency supply reserve warehouses. The optimization of emergency facilities is influenced by a multitude of complex factors. Some scholars utilized Data Envelopment Analysis (DEA) [3,4,5] to analyze various quantitative indicators that impact the input and output of site selection for emergency facilities. Most scholars employed multi-attribute decision-making techniques, such as fuzzy mathematics theory [6,7,8,9,10,11,12,13,14,15,16,17,18], Analytic Hierarchy Process (AHP) [14,16,18,19,20,21], and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [9,16,22,23,24,25,26].

Most scholars have considered the impact of economic, safety, service, and social factors on emergency supply reserve warehouses. While the aforementioned methods can rank alternative sites based on their superiority or inferiority, they do not offer a correct decision on the suitability of a site for establishing an emergency supply reserve warehouse. To uncover important information included in observational data of emergency systems, this study pioneers the application of the multi-attribute weighted intelligent gray target decision-making evaluation model to the optimization of site selection for emergency supply reserve warehouses. Deng [27] first introduced the concept of gray system theory. Building on the foundation of four types of uniform effect measure functions, Liu et al. [28] proposed the multi-attribute weighted gray target decision model. This model assists decision-makers in selecting the optimal decision from multiple objectives under conditions of limited information and sparse data. Currently, this model has been applied across various fields, yielding impressive outcomes. Examples include the selection of supply chain suppliers [29,30], maintenance decision for power transformers [31], selection of weapon procurement plans for artillery weaponry for a military unit [32], determination of the optimal mix ratio [33], selection of energy-saving service providers [34], synthetic effect measures of the leading industry objective system in the Kashgar urban agglomeration [35], fault localization [36], emergency plan selection after the outbreak of public health incidents [37], risk assessment for coal and gas outbursts [38], multi-attribute scheduling for mixed-flow production workshops of missile components [39], and the tendering process for civilian biogas energy projects [40]. Beyond theoretical discussions, the application of these methods is equally important. Some scholars have implemented these methods to optimize the allocation of emergency supply reserve warehouses at the national, municipal, and town levels [41,42,43,44].

This study utilizes the multi-attribute weighted intelligent gray target decision-making evaluation model for a comprehensive evaluation of the site selection for emergency supply reserve warehouses. Subsequently, the site selection is optimized based on the evaluation results. The innovations of this paper include the following:

(1)

It introduces a new evaluation method for the site selection of emergency supply reserve warehouses—the multi-attribute weighted intelligent gray target decision-making evaluation model. This model comprehensively accounts for both hitting-the-target and missing-the-target scenarios and effectively addresses the limitation of other multi-attribute decision-making methods that can only rank schemes without distinguishing between superior and inferior ones. By evaluating whether the target is hit, the model can effectively identify which emergency supply reserves are unnecessary to establish;

(2)

It constructs a new evaluation indicator system for the site selection of the emergency supply reserve warehouse. To objectively evaluate the level of transportation development, the efficiency of economic activities, the degree of population concentration, and the allocation of medical resources in various regions, the density of road networks, population density, economic density, and post-disaster response capability are innovatively incorporated as key indicators for optimizing the site selection of emergency supply reserve warehouses.

The remainder of this study is organized as follows. Section 2 introduces a multi-attribute weighted intelligent gray target decision-making evaluation model for optimizing the site selection of emergency supply reserve warehouses. Section 3 presents a case study to demonstrate the superiority of the proposed model. Section 4 concludes with a summary of the study’s findings and a discussion of future study directions.

2. Materials and Methods

2.1. Multi-Attribute Weighted Intelligent Gray Target Decision-Making Evaluation Model

The multi-attribute weighted intelligent gray target decision-making evaluation model is a method derived from gray system theory, specifically from its suite of gray decision-making methods. It synergizes multi-attribute decision-making with gray target decision-making, offering a significant and practical solution for decision-making issues that involve a multitude of indicators and strategies. It transforms decision objectives with varying meanings, dimensions, and natures into uniform effect measures. By designating the gray target’s critical value as the demarcation point for positive and negative values (i.e., the zero point) of the uniform effect measure function, it serves as the bullseye for gray target decision-making, which fully accounts for the degree to which decision objectives are met or deviated.

At the essence of gray target decision-making, the bullseye represents the zone of satisfactory effects within the context of relative optimization. In many instances, attaining absolute optimality is unfeasible, prompting a shift toward a more achievable, satisfactory result. This approach involves aiming for the situation’s objective effect vector to reside within a specified proximity to the bullseye, a concept typically described as “hitting the target”. Failure to meet this criterion is referred to as “missing the target”.

Definition 1.

(1) If $\underset{1\le j\le m}{\mathit{max}}\left\{r_{ij}\right\}=r_{i{j}_0}$, then $b_{j_0}$ is referred to as the optimal strategy for event $a_i$ ;

(2) If$\underset{1\le i\le n}{\mathit{max}}\left\{r_{ij}\right\}=r_{i_{0}j},$then$a_{i_0}$is referred to as the optimal event for strategy$b_j$;

(3) If$\underset{1\le i\le n}{\mathit{max}}\underset{1\le j\le m}{\mathit{max}}\left\{r_{ij}\right\}=r_{i_0{j}_0},$then$s_{i_0{j}_0}$is referred to as the optimal solution.

2.2. The Steps of the Multi-Attribute Weighted Intelligent Gray Target Decision-Making Algorithm

Step 1: The entirety of events within a given research scope is referred to as the event set within that research scope, denoted as $A=\left\{a_1,a_2,\dots ,a_n\right\}$, where $a_i\left(i=\mathrm{1,2},\dots ,n\right)$ represents the i-th event. Correspondingly, the complete set of possible strategies forms the strategy set, denoted as $B=\left\{b_1,b_2,\dots ,b_m\right\}$, where $b_j\left(j=\mathrm{1,2},\dots ,n\right)$ represents the j-th decision. Based on the event and strategy sets, the decision-making solution set, $S=\left\{s_{ij}=\left(a_i,b_j\right)|a_i\in A,b_j\in B\right\}$, is constructed;

Step 2: Determine the decision objectives $k=\mathrm{1,2},\dots ,s$ based on actual needs;

Step 3: Employ EEM to determine the indicator weights ${\eta }_1,{\eta }_1,\dots {,\eta }_s$;

Step 4: For objectives $k=\mathrm{1,2},\dots ,s$, compute the corresponding matrix of target effect samples.

$$U^k=\left(u_{ij}^{\left(k\right)}\right)=\left[\begin{array}{cccc}{u}_{11}^{\left(k\right)}& u_{12}^{\left(k\right)}& \dots & u_{1m}^{\left(k\right)}\\ u_{21}^{\left(k\right)}& u_{22}^{\left(k\right)}& \dots & u_{2m}^{\left(k\right)}\\ ⋮& ⋮& \ddots & ⋮\\ u_{n1}^{\left(k\right)}& u_{n2}^{\left(k\right)}& \dots & u_{nm}^{\left(k\right)}\end{array}\right];$$

(1)

Step 5: According to the different types of effect objectives (effect type objectives, cost type objectives, and moderate type objectives), set the critical value for the target effect, $u_{ij}^{\left(k\right)}$.

To ensure that the measures of various objective effects adhere to standardization, i.e., $r_{ij}^{\left(k\right)}\in \left[-\mathrm{1,1}\right]$, the following conditions are established:

For the benefit type objective, set the decision-making gray target $u_{ij}^{\left(k\right)}\ge 2u_{i_0{j}_0}^{\left(k\right)}-\underset{i}{\max }\underset{j}{\max }\left\{u_{ij}^{\left(k\right)}\right\}$ for the objective $k$;

For the cost type objective, set the decision-making gray target $u_{ij}^{\left(k\right)}\le 2u_{i_0{j}_0}^{\left(k\right)}-\underset{i}{\min }\underset{j}{\min }\left\{u_{ij}^{\left(k\right)}\right\}$ for the objective $k$;

For the moderate type objective with the effect value falling below the lower limit critical value $A-u_{i_0{j}_0}^{\left(k\right)}$, set the decision-making gray target $u_{ij}^{\left(k\right)}\ge A-2u_{i_0{j}_0}^{\left(k\right)}$ for the objective $k$;

For the moderate type objective with the effect value exceeding the upper limit critical value $A+u_{i_0{j}_0}^{\left(k\right)}$, set the decision-making gray target $u_{ij}^{\left(k\right)}\le A+2u_{i_0{j}_0}^{\left(k\right)}$ for the objective $k$.

Step 6: Compute the matrix of uniform effect measures for the objective $k$.

Due to the varying meanings, dimensions, and natures of the effect values for different objectives, direct comparison of these values is typically impractical. To facilitate the generation of comparable values, it is essential to convert the effect values of the objective samples, $u_{ij}^{\left(k\right)}$, into uniform effect measure values. This conversion forms the basis for establishing the matrix of uniform effect measures for the objective samples.

$$R^{\left(k\right)}=\left(r_{ij}^{\left(k\right)}\right)=\left[\begin{array}{cccc}{r}_{11}^{\left(k\right)}& r_{12}^{\left(k\right)}& \dots & r_{1m}^{\left(k\right)}\\ r_{21}^{\left(k\right)}& r_{22}^{\left(k\right)}& \dots & r_{2m}^{\left(k\right)}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}^{\left(k\right)}& r_{n2}^{\left(k\right)}& \dots & r_{nm}^{\left(k\right)}\end{array}\right]$$

(2)

Step 7: According to $r_{ij}^{\left(k\right)}=\sum _{k=1}^s{\eta }_k\ast r_{ij}^{\left(k\right)}$, the matrix of synthetic effect measures is computed as follows:

$$R=\left(r_{ij}\right)=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \dots & r_{1m}\\ r_{21}& r_{22}& \dots & r_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \dots & r_{nm}\end{array}\right]$$

(3)

Step 8: Determine whether the value of the synthetic effect measure hits the gray target. If $r_{ij}^{\left(k\right)}\in \left[\mathrm{0,1}\right]$, it indicates a hit on the gray target for the effect value of the objective $k$; conversely, if $r_{ij}^{\left(k\right)}\in [-\mathrm{1,0}]$, it denotes a miss from the target for the effect value of the objective $k$. Following this, the optimal strategy $b_{j_0}$ or the optimal solution $s_{i_0{j}_0}$ is identified in accordance with Definition 1.

3. Results

The subjects of this study include 96 county-level administrative divisions in Xinjiang. Each division, such as Tianshan District, Saybag District, High-tech Zone (Xinshi District), Shuimogou District, and Economic and Technological Development Zone (Toutunhe District), is represented by the number 1, 2, 3, 4, 5…, respectively, as shown in Figure 1. The figure illustrates the distribution of 14 regions, prefectures, and cities, including Urumqi City, Karamay City, Hami Region, and Turpan Region, along with the railway network, expressways, national highways, and provincial highways.

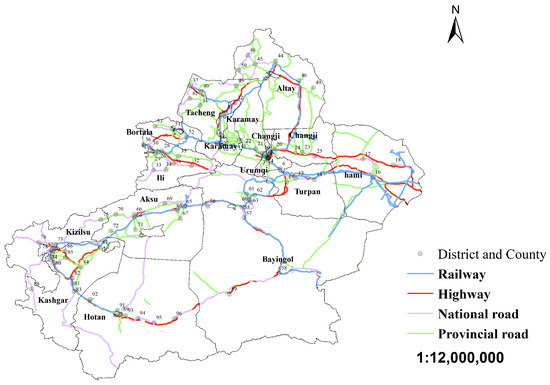
Figure 1. Distribution map of 14 regions, prefectures, cities, and 96 county-level administrative divisions in Xinjiang alongside situations of road networks.

3.1. Construction of Event and Decision Sets

The optimization issue of site selection for emergency supply reserve warehouses is defined as the event set, denoted as $A=\left\{a_i\right\}$. A decision set consisting of 96 districts and counties, including Tianshan District, Saybag District, High-tech Zone (Xinshi District), Shuimogou District, and Economic and Technological Development Zone (Toutunhe District), is denoted as $B=\left\{b_1,b_2,\dots ,96\right\}$. From the event set and the decision set, a decision scheme set is constructed, denoted as $S=\left\{s_{ij}=\left(a_i,b_j\right)|a_i\in A,b_j\in B,i=1;j=\mathrm{1,2},\dots 96\right\}$.

3.2. Determination of Decision Objectives

Given the sudden and unpredictable nature of sudden incidents, the optimization of emergency supply reserve warehouses is influenced by multiple factors. Current scholars typically take into account factors such as cost, transportation, population, economy, environment, and public infrastructure, as presented in Table 1. However, each type of disaster may present distinctly different risks and is related to specific regional characteristics [45]. The site selection for emergency supply reserve warehouses should satisfy the needs of both pre-disaster preparedness and post-disaster emergency response. Therefore, the density of road networks, population density, economic density, and post-disaster response capability are identified as decision objectives for the site selection of emergency supply reserve warehouses.

Table 1. Analysis of factors and objectives influencing site selection of emergency supply reserve warehouses.

Author	Factors and Objectives Influencing Site Selection of Emergency Supply Reserve Warehouses
[19]	Natural conditions, transportation conditions, public facilities, social benefits, costs, etc.
[46]	Adherence to convenient transportation and alignment with local socio-economic development
[9]	Safety factor, transportation factor, social environment factor, public facility factor, and economic factor
[47]	Population distribution, economic situation, transportation, etc.
[48]	Natural conditions, environmental conditions, cost factor, policy environment, and other factors
[49]	Level of regional economic development, natural geographical location, level of logistics development, extent of disaster impact, comprehensive transportation accessibility, infrastructure competitiveness, attention to emergency policies, etc.
[50]	Population distribution, economic conditions, and transportation situation
[51]	Potential disaster threats, population characteristics, economy, education, etc.
[18]	Accessibility, operating costs, land utilization, impact on surrounding residents, and development costs
[52]	Economy, transportation, logistics level, and disaster rate

3.2.1. Density of Road Networks

The road vector data utilized in this study are sourced from the 1:1,000,000 scale public edition of basic geographic information data (Edition 2021), available through the National Catalogue Service for Geographic Information. The highway mileage, railway mileage, and land area within the 96 county-level administrative divisions in Xinjiang are computed based on these data. The density of road networks is defined as the absolute ratio of a region’s length of road networks to its land area [53]. To precisely depict road density and investigate the varying impacts of highways and railways within an administrative division, the densities of highway networks and railway networks for each region are computed. The Entropy Evaluation Method (EEM) is then utilized to weigh the densities of highway networks and railway networks, resulting in the comprehensive network density for the region. The computational formula is as follows:

$$V_{i1}=L_i/A_i,i\in (1,2\dots 96)$$

(4)

$$V_{i2}=l_i/A_i,i\in (1,2\dots 96)$$

(5)

$$V_i=W_1\times V_{i1}+W_2\times V_{i2}$$

(6)

where $A_i$ represents the land area within the region $i$ (in ${\mathrm{k}\mathrm{m}}^2$); $L_i$ and $l_i$ represent the highway mileage (in $\mathrm{k}\mathrm{m}$) and railway mileage (in $\mathrm{k}\mathrm{m}$) within the region $i$, respectively; $V_{i1}$ and $V_{i2}$ represent the density of highway networks (in $\mathrm{k}\mathrm{m}/{\mathrm{k}\mathrm{m}}^2$) and the density of railway networks (in $\mathrm{k}\mathrm{m}/{\mathrm{k}\mathrm{m}}^2$) within the region $i$, respectively; $W_1$ and $W_2$ represent the weights for densities of highway network and railway network computed using the EEM, respectively; and $V_i$ represents the density of road networks within the region $i$.

3.2.2. Population Density

In this study, population density is utilized primarily to evaluate the vulnerability of bearers in natural disasters, specifically, the population vulnerability. Xi et al. [50] suggested that a higher population density indicator (population vulnerability) within a region is associated with increased vulnerability of local bearers to natural disasters, which amplifies the imperative for the establishment of emergency supply reserve warehouses within that region. This is represented by $P_i$.

$$P_i={POP}_i/A_i$$

(7)

where ${POP}_i$ represents the total population within the region $i$ (in persons); $A_i$ represents the land area within the region $i$ (in ${\mathrm{k}\mathrm{m}}^2$); and $P_i$ represents the population density within the region $i$ (in person/${\mathrm{k}\mathrm{m}}^2$).

3.2.3. Economic Density

The rapid growth of the economy not only fosters social advancement, augments human capacity to alter the natural environment, and elevates the standards of material and living conditions but also precipitates ongoing population increase and expansion, substantial depletion of resources, and environmental pollution. Within the context of this study, economic density serves as an indicator of regional economic development levels. It is believed that a higher economic density within a region is indicative of more substantial losses in areas affected by disasters, which amplifies the imperative for the establishment of emergency supply reserve warehouses within that region.

The computational formula for the economic density of a region is as follows:

$$D_i={GDP}_i/A_i,i\in (1,2,3\dots \mathrm{n})$$

(8)

where ${GDP}_i$ represents the total economic output of the region $i$ (in CNY 100 million); $A_i$ represents the land area within the region $i$ (in ${\mathrm{k}\mathrm{m}}^2$); and $D_i$ represents the economic density of the region $i$ (in CNY 100 million/${\mathrm{k}\mathrm{m}}^2$).

3.2.4. Post-Disaster Response Capability

In the event of sudden incidents, it is imperative to mobilize an array of medical resources to diminish and alleviate the consequences of disasters or incidents, illustrating that an augmentation in medical resources bolsters disaster response capabilities. Since the availability of beds reflects the reach of medical resources [54], this study measures the post-disaster response capability in terms of beds available per 1000 people at medical institutions.

$$B_i={\displaystyle \frac{{BED}_i}{{POP}_i}}\ast 1000,i\in (1,2,3\dots \mathrm{n})$$

(9)

where ${BED}_i$ represents the number of beds available at medical institutions within the region $i$ (in beds); ${POP}_i$ represents the total population within the region $i$ (in persons); and $B_i$ represents the post-disaster response capability of the region $i$ (in number of beds per 1000 people).

3.3. Determination of Decision-Making Power for Each Objective

Given the variations in work experience, professional knowledge, and understanding of the decision-making issue among experts, this study employs the EEM to determine the indicator weights in order to ensure the reasonableness and accuracy of the comprehensive evaluation results for emergency supply reserve warehouses. The specific computational steps are detailed in Appendix A. The basic data for the optimization scheme pertaining to the site selection of district- and county-level emergency supply reserve warehouses in Xinjiang are presented in Table 2. Utilizing Formulas (4)–(9), the values for various indicators in the optimization scheme for the site selection of these warehouses are computed, as shown in Table 3. The weights of the density of road networks, population density, economic density, and post-disaster response capability, computed using the EEM, are 0.1216, 0.2396, 0.5815, and 0.0573, respectively.

Table 2. The basic data for the optimization scheme pertaining to the site selection of district- and county-level emergency supply reserve warehouses in Xinjiang.

District and County	Length of Railways in Operation (km)	Total Length of Highways (km)	Land Area (km2)	Permanent Population (Person)	Gross Regional Product (CNY 100 Million)	Beds Available at Medical Institutions (Bed)
Tianshan District	27.77	119.47	171.40	652,792	376.32	10,735
Saybag District	46.79	208.14	420.17	799,539	416.00	6738
High-tech Zone (Xinshi District)	45.42	126.58	261.08	1,011,440	1330.00	10,608
Shuimogou District	12.71	127.57	279.06	549,576	380.66	2531
Economic and Technological Development Zone (Toutunhe District)	49.71	244.44	272.47	419,022	556.40	1053
Dabancheng District	159.66	851.53	4773.65	35,540	31.17	100
Midong District	72.08	513.86	3398.55	512,870	335.23	2313
Urumqi County	6.88	732.91	4218.62	73,590	28.23	215
Karamay District	103.02	677.66	3845.76	337,188	597.51	1231
Dushanzi District	12.06	92.85	403.60	84,395	191.28	470
Baijiantan District	47.09	108.16	1267.18	50,825	143.23	250
Urho District	51.55	290.43	2229.47	17,940	14.88	60
Gaochang District	254.48	1953.79	13,653.26	317,443	118.62	1921
Shanshan County	292.17	2755.46	39,646.63	242,310	152.28	1143
Toksun County	184.01	1746.15	16,566.66	134,235	102.51	634
Yizhou District	1477.78	7378.53	81,370.88	569,388	454.99	2732
Barkol Kazakh Autonomous County	0.00	4039.28	37,098.70	65,531	76.47	222
Yiwu County	241.21	2247.21	19,729.53	38,464	76.46	239
Changji City	25.25	1456.35	7976.84	607,441	420.17	2044
Fukang City	75.83	1191.71	8530.27	181,144	185.31	818
Hutubi County	44.09	1527.95	9524.22	192,638	139.38	923
Manas County	33.78	1258.55	9168.50	192,098	153.48	766
Qitai County	115.06	2287.26	16,664.93	219,811	177.62	1062
Jimsar County	133.10	1251.22	8148.16	153,197	262.57	812
Mulei Kazakh Autonomous County	0.00	1934.53	13,540.31	67,256	48.72	430
Yining City	28.00	300.79	639.01	778,047	295.87	6233
Kuytun City	93.60	418.43	1172.74	229,122	202.67	2228
Yining County	51.96	886.42	4492.40	365,307	94.66	1446
Qapqal Xibe Autonomous County	0.00	936.09	4143.77	157,764	69.96	763
Huocheng County	34.92	560.49	2949.01	243,303	99.63	1144
Gongliu County	0.00	784.99	4131.46	175,766	56.58	918
Xinyuan County	0.00	1252.32	7591.95	306,525	111.18	1235
Zhaosu County	0.00	1345.67	10,498.39	146,887	45.82	801
Tekes County	0.00	1357.77	8100.05	148,945	38.18	864
Nilka County	55.70	1602.08	10,161.28	155,737	57.55	788
Khorgos City	12.96	384.01	1883.34	71,466	193.89	378
Tacheng City	37.03	725.38	3997.67	158,098	106.60	1378
Wusu City	88.56	2197.10	14,399.19	262,906	214.18	1332
Shawan City	63.31	2030.96	12,464.11	301,046	204.90	859
Emin County	96.43	1777.88	9154.24	188,642	104.10	736
Toli County	79.14	2572.33	20,009.13	85,451	43.77	537
Yumin County	0.00	966.62	6095.77	50,819	19.57	260
Hoboksar Mongol Autonomous County	173.66	3221.85	28,806.16	61,785	44.51	560
Altay City	89.13	1779.40	10,799.55	221,454	101.38	1461
Burqin County	0.00	1337.12	10,381.16	72,894	30.99	496
Fuyun County	280.01	3509.75	32,306.45	99,748	57.53	557
Fuhai County	138.02	3451.71	32,516.76	75,537	51.70	352
Habahe County	0.00	1188.65	8178.37	82,524	50.06	550
Qinghe County	0.00	1781.39	15,750.78	61,680	26.73	249
Jeminay County	0.00	933.63	7130.04	34,336	17.92	169
Bole City	44.74	954.51	6662.60	246,706	174.10	1671
Jinghe County	184.28	1274.52	10,419.20	125,968	89.68	528
Wenquan County	0.00	619.95	5946.43	49,696	29.44	346
Alashankou City	33.38	157.69	1257.95	11,097	83.91	100
Korla City	131.64	1133.48	6881.04	779,352	654.93	4429
Bugur County	112.56	1400.66	14,191.42	137,327	62.12	901
Yuli County	195.02	2751.58	59,208.56	101,866	76.92	420
Ruoqiang County	528.02	6356.33	198,680.22	43,045	54.13	353
Qiemo County	0.00	4712.72	138,745.62	69,236	34.80	565
Yanqi Hui Autonomous County	51.09	572.02	2427.46	122,961	66.32	834
Hejing County	223.06	3655.08	34,985.08	147,859	92.39	766
Hoxud County	135.37	1444.46	12,763.44	59,299	38.88	332
Bohu County	0.00	415.56	3587.99	48,288	25.80	354
Aksu City	74.41	873.06	14,499.15	715,319	251.25	1797
Kuqa City	191.69	2031.91	14,551.47	530,328	288.88	2432
Wensu County	92.19	1829.87	14,419.26	266,002	84.98	878
Shaya County	0.00	1571.46	31,943.84	278,516	85.88	1183
Xinhe County	106.81	836.79	5848.78	194,473	60.89	1201
Baicheng County	5.76	1607.27	15,951.54	231,113	93.43	1290
Uqturpan County	0.00	1113.19	9143.81	205,571	51.48	760
Awat County	0.00	1103.71	13,119.44	242,481	62.88	927
Kalpin County	85.98	887.08	9013.91	50,619	14.68	380
Artush City	76.45	2367.56	15,795.05	290,936	69.75	2392
Akto County	29.79	1905.42	24,721.23	226,005	47.83	1211
Akqi County	0.00	1588.59	11,603.91	44,369	15.63	300
Ulugqat County	0.00	2425.59	19,238.92	60,912	36.03	561
Kashgar City	31.85	316.90	1020.72	782,662	238.27	5683
Shufu County	2.62	384.30	2777.00	263,014	50.08	1329
Shule County	15.32	494.12	2208.69	355,544	74.17	2688
Yengisar County	73.86	553.24	3496.09	276,641	47.05	1216
Poskam County	23.09	295.36	1024.20	214,543	47.70	1717
Yarkant County	66.44	1482.26	9104.91	860,800	137.81	2978
Kargilik County	55.59	2381.94	29,175.73	525,436	109.46	3579
Makit County	0.00	824.74	11,053.97	224,154	63.28	1566
Yopurga County	0.00	426.38	3186.01	162,675	35.76	800
Payzawat County	78.95	885.28	6642.52	424,821	70.72	1096
Maralbexi County	144.50	1789.25	18,598.97	366,141	75.11	1706
Tashkurgan Tajik Autonomous County	0.00	1483.73	24,202.35	39,946	17.79	206
Hotan City	7.53	180.50	470.03	501,028	114.28	2155
Hotan County	10.07	2318.17	41,584.54	342,603	46.36	1004
Karakax County	44.11	1365.30	25,841.94	571,648	78.94	3182
Pishan County	140.89	2367.32	39,954.05	281,573	41.46	1239
Lop County	0.00	743.59	14,220.47	286,900	42.65	1179
Qira County	0.00	1151.00	31,810.59	157,792	26.85	725
Keriya County	0.00	1597.93	39,228.52	257,038	40.63	1468
Niya County	0.00	1411.94	56,855.62	42,649	15.14	302

Table 3. The values of each indicator in the optimization scheme for site selection of district- and county-level emergency supply reserve warehouses in Xinjiang.

No.	District and County	Density of Road Networks (km/km2)	Population Density (Person/km2)	Economic Density (CNY 100 Million/km2)	Post-disaster Response Capability (Number of Beds per 1000 People)
1	Tianshan District	0.2826	3808.5881	2.1956	16.4447
2	Saybag District	0.1979	1902.8941	0.9901	8.4274
3	High-tech Zone (Xinshi District)	0.2441	3874.0616	5.0942	10.4880
4	Shuimogou District	0.1383	1969.3829	1.3641	4.6054
5	Economic and Technological Development Zone (Toutunhe District)	0.3435	1537.8647	2.0421	2.5130
6	Dabancheng District	0.0661	7.4450	0.0065	2.8137
7	Midong District	0.0505	150.9085	0.0986	4.5099
8	Urumqi County	0.0404	17.4441	0.0067	2.9216
9	Karamay District	0.0605	87.6779	0.1554	3.6508
10	Dushanzi District	0.0750	209.1056	0.4739	5.5691
11	Baijiantan District	0.0480	40.1087	0.1130	4.9188
12	Urho District	0.0473	8.0468	0.0067	3.3445
13	Gaochang District	0.0467	23.2503	0.0087	6.0515
14	Shanshan County	0.0214	6.1117	0.0038	4.7171
15	Toksun County	0.0324	8.1027	0.0062	4.7231
16	Yizhou District	0.0345	6.9974	0.0056	4.7981
17	Barkol Kazakh Autonomous County	0.0245	1.7664	0.0021	3.3877
18	Yiwu County	0.0351	1.9496	0.0039	6.2136
19	Changji City	0.0436	76.1506	0.0527	3.3649
20	Fukang City	0.0384	21.2354	0.0217	4.5157
21	Hutubi County	0.0397	20.2261	0.0146	4.7914
22	Manas County	0.0338	20.9520	0.0167	3.9875
23	Qitai County	0.0363	13.1900	0.0107	4.8314
24	Jimsar County	0.0473	18.8014	0.0322	5.3004
25	Mulei Kazakh Autonomous County	0.0322	4.9671	0.0036	6.3935
26	Yining City	0.1400	1217.5819	0.4630	8.0111
27	Kuytun City	0.1422	195.3732	0.1728	9.7241
28	Yining County	0.0534	81.3167	0.0211	3.9583
29	Qapqal Xibe Autonomous County	0.0509	38.0726	0.0169	4.8363
30	Huocheng County	0.0520	82.5033	0.0338	4.7020
31	Gongliu County	0.0428	42.5433	0.0137	5.2229
32	Xinyuan County	0.0372	40.3750	0.0146	4.0290
33	Zhaosu County	0.0289	13.9914	0.0044	5.4532
34	Tekes County	0.0378	18.3882	0.0047	5.8008
35	Nilka County	0.0398	15.3265	0.0057	5.0598
36	Khorgos City	0.0513	37.9464	0.1030	5.2892
37	Tacheng City	0.0481	39.5475	0.0267	8.7161
38	Wusu City	0.0392	18.2584	0.0149	5.0664
39	Shawan City	0.0407	24.1530	0.0164	2.8534
40	Emin County	0.0519	20.6071	0.0114	3.9016
41	Toli County	0.0320	4.2706	0.0022	6.2843
42	Yumin County	0.0357	8.3368	0.0032	5.1162
43	Hoboksar Mongol Autonomous County	0.0299	2.1449	0.0015	9.0637
44	Altay City	0.0435	20.5059	0.0094	6.5973
45	Burqin County	0.0290	7.0218	0.0030	6.8044
46	Fuyun County	0.0312	3.0876	0.0018	5.5841
47	Fuhai County	0.0272	2.3230	0.0016	4.6600
48	Habahe County	0.0328	10.0905	0.0061	6.6647
49	Qinghe County	0.0255	3.9160	0.0017	4.0370
50	Jeminay County	0.0295	4.8157	0.0025	4.9219
51	Bole City	0.0375	37.0285	0.0261	6.7732
52	Jinghe County	0.0413	12.0900	0.0086	4.1915
53	Wenquan County	0.0235	8.3573	0.0050	6.9623
54	Alashankou City	0.0488	8.8215	0.0667	9.0114
55	Korla City	0.0519	113.2608	0.0952	5.6829
56	Bugur County	0.0284	9.6768	0.0044	6.5610
57	Yuli County	0.0130	1.7205	0.0013	4.1231
58	Ruoqiang County	0.0093	0.2167	0.0003	8.2007
59	Qiemo County	0.0077	0.4990	0.0003	8.1605
60	Yanqi Hui Autonomous County	0.0694	50.6542	0.0273	6.7826
61	Hejing County	0.0285	4.2263	0.0026	5.1806
62	Hoxud County	0.0337	4.6460	0.0030	5.5987
63	Bohu County	0.0261	13.4582	0.0072	7.3310
64	Aksu City	0.0175	49.3352	0.0173	2.5122
65	Kuqa City	0.0417	36.4450	0.0199	4.5858
66	Wensu County	0.0336	18.4477	0.0059	3.3007
67	Shaya County	0.0111	8.7189	0.0027	4.2475
68	Xinhe County	0.0464	33.2502	0.0104	6.1757
69	Baicheng County	0.0230	14.4884	0.0059	5.5817
70	Uqturpan County	0.0274	22.4820	0.0056	3.6970
71	Awat County	0.0190	18.4826	0.0048	3.8230
72	Kalpin County	0.0296	5.6157	0.0016	7.5071
73	Artush City	0.0375	18.4194	0.0044	8.2217
74	Akto County	0.0183	9.1421	0.0019	5.3583
75	Akqi County	0.0309	3.8236	0.0013	6.7615
76	Ulugqat County	0.0284	3.1661	0.0019	9.2100
77	Kashgar City	0.0941	766.7744	0.2334	7.2611
78	Shufu County	0.0319	94.7116	0.0180	5.0530
79	Shule County	0.0558	160.9751	0.0336	7.5602
80	Yengisar County	0.0520	79.1287	0.0135	4.3956
81	Poskam County	0.0825	209.4737	0.0466	8.0031
82	Yarkant County	0.0423	94.5424	0.0151	3.4596
83	Kargilik County	0.0199	18.0094	0.0038	6.8115
84	Makit County	0.0168	20.2781	0.0057	6.9863
85	Yopurga County	0.0302	51.0592	0.0112	4.9178
86	Payzawat County	0.0392	63.9548	0.0106	2.5799
87	Maralbexi County	0.0277	19.6861	0.0040	4.6594
88	Tashkurgan Tajik Autonomous County	0.0138	1.6505	0.0007	5.1570
89	Hotan City	0.0990	1065.9490	0.2431	4.3012
90	Hotan County	0.0128	8.2387	0.0011	2.9305
91	Karakax County	0.0132	22.1209	0.0031	5.5664
92	Pishan County	0.0161	7.0474	0.0010	4.4003
93	Lop County	0.0118	20.1751	0.0030	4.1094
94	Qira County	0.0082	4.9604	0.0008	4.5947
95	Keriya County	0.0092	6.5523	0.0010	5.7112
96	Niya County	0.0056	0.7501	0.0003	7.0811

3.4. Computation of Effect Sample Vector for Each Objective

According to Table 3, the values of each indicator in the optimization scheme for site selection of district- and county-level emergency supply reserve warehouses in Xinjiang are determined. The matrix of effect sample vectors for each objective is as follows:

$$U^k=\left(u_{ij}^{\left(k\right)}\right)=\left[\begin{array}{cccc}0.2826& 3808.5881& \dots & 16.4447\\ 0.1979& 1902.8941& \dots & 8.4274\\ ⋮& ⋮& \ddots & ⋮\\ 0.0056& 0.7501& \dots & 7.0811\end{array}\right]$$

3.5. Definition of Critical Values for Objective Effects

The density of road networks, population density, economic density, and post-disaster response capability are all benefit type indicators, with higher values indicating better effects. According to Table 4, the basic data for the optimization scheme pertaining to the site selection of region- and city-level emergency supply reserve warehouses in Xinjiang are used to compute the density of road networks, economic density, population density, and post-disaster response capability across 14 regions, prefectures, and cities, as presented in Table 5. The minimum value of each indicator is selected as the critical value for objective effect in optimizing the site selection for 96 district- and county-level emergency supply reserve warehouses. Specifically, the density of road networks $u_{ij}^{\left(1\right)}=0.0145$, population density $u_{ij}^{\left(2\right)}=3.2011$, economic density $u_{ij}^{\left(3\right)}=0.0016$, and post-disaster response capability $u_{ij}^{\left(4\right)}=4.1012$.

Table 4. The basic data for the optimization scheme pertaining to the site selection of region- and city-level emergency supply reserve warehouses in Xinjiang.

No.	Region, Prefecture, and City	Length of Railways in Operation (km)	Total Length of Highways (km)	Land Area km2	Permanent Population (Person)	Gross Regional Product (CNY 100 Million)	Beds Available at Medical Institutions (Bed)
1	Urumqi	422.46	2903.70	13,794.98	4,054,369	3337.32	33,191
2	Karamay	215.40	1169.11	7746.00	490,348	886.90	2011
3	Turpan	728.41	6244.02	69,866.56	693,988	373.41	3772
4	Hami	1710.61	13,657.37	138,199.10	673,383	607.91	3195
5	Changji Hui Autonomous Prefecture	427.56	10,840.18	735,53.23	1,613,585	1387.25	9542
6	Ili Kazakh Autonomous Prefecture	277.91	9820.98	55,763.41	2,778,869	1266.01	19,298
7	Tacheng Prefecture	539.95	13,485.92	94,926.27	1,108,747	737.57	6115
8	Altay Prefecture	509.85	13,953.10	117,063.10	648,173	334.53	3740
9	Bortala Mongol Autonomous Prefecture	263.62	3001.98	24,286.17	433,467	377.14	2634
10	Bayingolin Mongol Autonomous Prefecture	1380.88	22,402.26	471,470.80	1,509,233	1106.29	9821
11	Aksu Prefecture	105.88	11,854.38	128,491.20	2,714,422	1315.05	15,409
12	Kizilsu Kyrgyz Autonomous Prefecture	556.03	8287.08	71,359.11	622,222	169.24	8053
13	Kashgar Prefecture	491.55	11,389.05	112,491.10	4,496,377	1130.22	28,953
14	Hotan Prefecture	200.87	11,121.46	249,965.80	2,441,231	406.32	17,732

Table 5. The values of each indicator in the optimization scheme for site selection of regions, prefectures, and city-level emergency supply reserve warehouses in Xinjiang.

Emergency Supply Reserve Warehouses	Density of Road Networks (km/km2)	Population Density (Person/km2)	Economic Density (CNY 100 Million/km2)	Post-Disaster Response Capability (Number of Beds per 1000 People)
Urumqi	0.0872	293.9018	0.2419	8.1865
Karamay	0.0665	63.3034	0.1145	4.1012
Turpan	0.0353	9.9330	0.0053	5.4353
Hami	0.0396	4.8726	0.0044	4.7447
Changji Hui Autonomous Prefecture	0.0503	21.9376	0.0189	5.9135
Ili Kazakh Autonomous Prefecture	0.0588	49.8332	0.0227	6.9446
Tacheng Prefecture	0.0486	11.6801	0.0078	5.5152
Altay Prefecture	0.0405	5.5370	0.0029	5.7701
Bortala Mongol Autonomous Prefecture	0.0463	17.8483	0.0155	6.0766
Bayingolin Mongol Autonomous Prefecture	0.0170	3.2011	0.0023	6.5073
Aksu Prefecture	0.0296	21.1254	0.0102	5.6767
Kizilsu Kyrgyz Autonomous Prefecture	0.0419	8.7196	0.0024	12.9423
Kashgar Prefecture	0.0348	39.9709	0.0100	6.4392
Hotan Prefecture	0.0145	9.7663	0.0016	7.2635

3.6. Computation of the Uniform Effect Measure Vector

The matrix of uniform effect measures for the $k$ objective is presented below.

$$\begin{gathered} R^1=[0.8148,0.5574,0.6976,0.3762,1.0000,0.1567,0.1093,0.0786,0.1396,0.1838,0.1018,0.0995, \\ 0.0977,0.0207,0.0541,0.0607,0.0304,0.0626,0.0883,0.0724,0.0766,0.0585,0.0661,0.0995,0.0537, \\ 0.3815,0.3882,0.1182,0.1106,0.1139,0.0860,0.0688,0.0436,0.0706,0.0767,0.1117,0.1019,0.0748, \\ 0.0794,0.1136,0.0532,0.0644,0.0466,0.0881,0.0440,0.0506,0.0385,0.0554,0.0333,0.0455,0.0697, \\ 0.0812,0.0272,0.1042,0.1137,0.0421,-0.0046,-0.0160,-0.0209,0.1668,0.0424,0.0583,0.0351, \\ 0.0091,0.0825,0.0578,-0.0105,0.0968,0.0257,0.0392,0.0134,0.0457,0.0699,0.0114,0.0496,0.0422, \\ 0.2420,0.0528,0.1254,0.1139,0.2065,0.0845,0.0162,0.0069,0.0475,0.0751,0.0400,-0.0022,0.2566, \\ -0.0055,-0.0040,0.0047,-0.0084,-0.0194,-0.0163,-0.0272] \\ {R}^2=[0.9831,0.4908,1.0000,0.5079,0.3965,0.0011,0.0382,0.0037,0.0218,0.0532,0.0095,0.0013, \\ 0.0052,0.0008,0.0013,0.0010,-0.0004,-0.0003,0.0188,0.0047,0.0044,0.0046,0.0026,0.0040, \\ 0.0005,0.3137,0.0496,0.0202,0.0090,0.0205,0.0102,0.0096,0.0028,0.0039,0.0031,0.0090,0.0094, \\ 0.0039,0.0054,0.0045,0.0003,0.0013,-0.0003,0.0045,0.0010,0.0000,-0.0002,0.0018,0.0002, \\ 0.0004,0.0087,0.0023,0.0013,0.0015,0.0284,0.0017,-0.0004,-0.0008,-0.0007,0.0123,0.0003, \\ 0.0004,0.0026,0.0119,0.0086,0.0039,0.0014,0.0078,0.0029,0.0050,0.0039,0.0006,0.0039,0.0015, \\ 0.0002,0.0000,0.1973,0.0236,0.0408,0.0196,0.0533,0.0236,0.0038,0.0044,0.0124,0.0157,0.0043, \\ -0.0004,0.2746,0.0013,0.0049,0.0010,0.0044,0.0005,0.0009,-0.0006] \\ {U}^3=[0.4308,0.1941,1.0000,0.2675,0.4007,0.0010,0.0190,0.0010,0.0302,0.0927,0.0219, \\ 0.0010,0.0014,0.0004,0.0009,0.0008,0.0001,0.0004,0.0100,0.0039,0.0026,0.0030,0.0018,0.0060, \\ 0.0004,0.0906,0.0336,0.0038,0.0030,0.0063,0.0024,0.0026,0.0005,0.0006,0.0008,0.0199,0.0049, \\ 0.0026,0.0029,0.0019,0.0001,0.0003,0.0000,0.0015,0.0003,0.0000,0.0000,0.0009,0.0000,0.0002, \\ 0.0048,0.0014,0.0007,0.0128,0.0184,0.0005,-0.0001,-0.0003,-0.0003,0.0050,0.0002,0.0003, \\ 0.0011,0.0031,0.0036,0.0008,0.0002,0.0017,0.0008,0.0008,0.0006,0.0000,0.0005,0.0001, \\ -0.0001,0.0000,0.0455,0.0032,0.0063,0.0023,0.0088,0.0027,0.0004,0.0008,0.0019,0.0018, \\ 0.0005,-0.0002,0.0474,-0.0001,0.0003,-0.0001,0.0003,-0.0002,-0.0001,-0.0003] \\ {R}^4=[1.0000,0.3505,0.5174,0.0408,-0.1287,-0.1043,0.0331,-0.0956,-0.0365,0.1189, \\ 0.0662,-0.0613,0.1580,0.0499,0.0504,0.0565,-0.0578,0.1711,-0.0596,0.0336,0.0559, \\ -0.0092,0.0592,0.0972,0.1857,0.3168,0.4555,-0.0116,0.0596,0.0487,0.0909,-0.0058,0.1095, \\ 0.1377,0.0777,0.0962,0.3739,0.0782,-0.1011,-0.0162,0.1769,0.0822,0.4020,0.2022,0.2190, \\ 0.1201,0.0453,0.2077,-0.0052,0.0665,0.2165,0.0073,0.2318,0.3978,0.1281,0.1993,0.0018,0.3321, \\ 0.3289,0.2172,0.0874,0.1213,0.2617,-0.1287,0.0393,-0.0648,0.0119,0.1681,0.1199,-0.0327, \\ -0.0225,0.2759,0.3338,0.1018,0.2155,0.4139,0.2560,0.0771,0.2802,0.0239,0.3161,-0.0520,0.2196, \\ 0.2337,0.0662,-0.1232,0.0452,0.0855,0.0162,-0.0948,0.1187,0.0242,0.0007,0.0400,0.1304,0.2414] \end{gathered}$$

3.7. Computation of the Matrix of Synthetic Effect Measures

The matrix of synthetic effect measures is derived from $r_{ij}^{\left(k\right)}=\sum _{k=1}^s{\eta }_k\ast r_{ij}^{\left(k\right)}$.

$$\begin{gathered} R=[0.6424,0.3183,0.9356,0.3254,0.4422,0.0139,0.0354,0.0055,0.0377, \\ 0.0958,0.0312,0.0095,0.0230,0.0058,0.0103,0.0113,0.0003,0.0176,0.0177, \\ 0.0141,0.0151,0.0094,0.0131,0.0221,0.0175,0.1924,0.1047,0.0208,0.0208, \\ 0.0252,0.0195,0.0118,0.0126,0.0178,0.0150,0.0328,0.0389,0.0160,0.0068, \\ 0.0151,0.0167,0.0130,0.0286,0.0243,0.0183,0.0130,0.0072,0.0196,0.0038, \\ 0.0095,0.0258,0.0116,0.0173,0.0432,0.0387,0.0172,-0.0006,0.0167, \\ 0.0160,0.0386,0.0103,0.0143,0.0205,-0.0016,0.0164,0.0047,0.0001, \\ 0.0243,0.0112,0.0045,0.0016,0.0215,0.0289,0.0076,0.0184,0.0289,0.1178, \\ 0.0184,0.0447,0.0213,0.0611,0.0145,0.0157,0.0158,0.0136,0.0069,0.0087, \\ 0.0044,0.1255,-0.0058,0.0076,0.0021,0.0002,-0.0001,0.0056,0.0102] \end{gathered}$$

3.8. Decision-Making

Since $r_{157},r_{164},r_{167},\mathrm{a}\mathrm{n}\mathrm{d}{r}_{190}$ are less than 0, the four administrative divisions of Yuli County, Aksu City, Shaya County, and Hotan County missed the target, suggesting they are currently unsuitable for establishing an emergency supply reserve warehouse. The remaining 92 districts and counties all hit the target. According to $\underset{1\le j\le m}{\max }\left\{r_{ij}\right\}=r_1=0.9356$, the High-tech Zone (Xinshi District) in Urumqi City demonstrated the best evaluation result.

4. Sensitivity Analysis

In this study, appropriate critical values for objectives were determined in order to optimize the site selection for emergency supply reserve warehouses. This was achieved by adjusting the minimum values of indicators such as the density of road networks, economic density, population density, and post-disaster response capability in 14 regions, prefectures, and cities, with reductions of 5%, increases of 5%, and increases of 10%, respectively. The new optimal evaluation results and cities that miss the target were then identified, as presented in Table 6.

Table 6. Effects of changes in critical values for objectives on optimal evaluation and missing-the-target situations.

Critical Value for Objective	$\mathbf{Density}\mathbf{of}\mathbf{Road}\mathbf{Networks}{\mathit{u}}_{\mathit{i}\mathit{j}}^{\left(1\right)}$	$\mathbf{Population}\mathbf{Density}{\mathit{u}}_{\mathit{i}\mathit{j}}^{\left(2\right)}$	$\mathbf{Economic}\mathbf{Density}{\mathit{u}}_{\mathit{i}\mathit{j}}^{\left(3\right)}$	$\mathbf{Post}-\mathbf{Disaster}\mathbf{Response}\mathbf{Capability}{\mathit{u}}_{\mathit{i}\mathit{j}}^{\left(4\right)}$	Optimal Site Based on Evaluation Result	Missing-the-Target and Ranking Situation
After a 5% reduction	0.0138	3.0410	0.0015	3.8961	High-tech Zone (Xinshi District)	Aksu City > Hotan County
Unchanged	0.0145	3.2011	0.0016	4.1012	High-tech Zone (Xinshi District)	Shaya County > Yuli County > Aksu City > Hotan County
After a 5% increase	0.0152	3.3612	0.0017	4.3063	High-tech Zone (Xinshi District)	Barkol Kazakh Autonomous County > Lop County > Qira County > Shaya County > Yuli County > Aksu City > Hotan County
After a 10% increase	0.0160	3.5212	0.0018	4.5113	High-tech Zone (Xinshi District)	Pishan County > Awat County > Barkol Kazakh Autonomous County > Lop County > Qira County > Shaya County > Yuli County > Aksu City > Hotan County

It was observed that as the critical values for objectives increase or decrease, the number of instances missing the target also rises or falls, but the final ranking remains unchanged. The changes in the critical values for objectives do not affect the optimal evaluation results for those hitting the target.

These results suggest that the multi-attribute weighted intelligent gray target decision-making evaluation model is both scientifically robust and effective, which contributes to enhanced stability in site selection decisions.

5. Discussion

Considering that the multi-attribute weighted intelligent gray target decision-making evaluation model is being applied for the first time to optimize the site selection for emergency supply reserve warehouses and that a new evaluation indicator system has been constructed, the reliability of the model’s evaluation results is verified using both EEM-TOPSIS and Gray Correlation Degree–TOPSIS methods. The study results indicate that evaluation results obtained through the multi-attribute weighted intelligent gray target decision-making evaluation model are largely consistent with those derived from the two commonly used evaluation methods (Table 7). The multi-attribute weighted intelligent gray target decision-making evaluation model identifies the High-tech Zone as the optimal decision, which is consistent with the results obtained using the EEM-TOPSIS method. Among the 96 district- and county-level administrative divisions, the four that missed the target are Shaya County, Yuli County, Aksu City, and Hotan County. Their respective EEM-TOPSIS comprehensive evaluation rankings are 95th (Shaya County), 94th (Yuli County), 88th (Aksu City), and 96th (Hotan County). Similarly, their Gray Correlation Degree–TOPSIS comprehensive evaluation rankings are 93rd (Shaya County), 94th (Yuli County), 89th (Aksu City), and 96th (Hotan County).

Table 7. Comparison of ranking results by different models and methods.

District and County	EEM-TOPSIS Closeness	EEM-TOPSIS Ranking	Gray Correlation Degree–TOPSIS Closeness	Gray Correlation Degree–TOPSIS Ranking	Synthetic Effect Measure for Multi-Attribute Weighted Intelligent Gray Target Decision-Making Evaluation Model	Decision Result of Multi-Attribute Weighted Intelligent Gray Target Decision-Making Evaluation Model
High-tech Zone (Xinshi District)	0.9651	1	0.5842	2	0.9356	Hit the target
Tianshan District	0.4824	2	0.5367	1	0.6425	Hit the target
Economic and Technological Development Zone (Toutunhe District)	0.4101	3	0.4975	3	0.4422	Hit the target
Shuimogou District	0.2929	4	0.4748	4	0.3254	Hit the target
Saybag District	0.2354	5	0.4745	5	0.3183	Hit the target
…	…	…	…	…	…	…
Qira County	0.0042	92	0.4144	95	0	Hit the target
Shaya County	0.0039	95	0.4056	93	−0.0001	Miss the target
Yuli County	0.0040	94	0.4056	94	−0.0006	Miss the target
Aksu City	0.0063	88	0.4062	89	−0.0016	Miss the target
Hotan County	0.0027	96	0.3318	96	−0.0058	Miss the target

Through comparison, it is found that the multi-attribute weighted intelligent gray target decision-making evaluation model not only ranks the target schemes but also effectively identifies the superiority or inferiority of schemes by distinguishing between hitting-the-target and missing-the-target scenarios. The computation process is simple, making it superior compared to other methods.

The analysis of the study results reveals an intriguing phenomenon. In Shaya County, despite all other indicators being above the critical value, the density of road networks falls below the critical value for the objective, resulting in the target being missed. Similarly, in Aksu City, although other indicators surpass the critical values, the post-disaster response capability is below the critical value for the objective, leading to the target being missed (Table 8). In this study, the density of road networks and post-disaster response capability significantly influence the comprehensive evaluation results. However, whether they can be considered key indicators affecting the evaluation of emergency supply reserve warehouses remains to be validated by further studies from other scholars.

Table 8. Comparison of various indicators with critical values in target-missing districts and counties.

District and County	Density of Road Networks (km/km2)	Population Density (Person/km2)	Economic Density (CNY 100 Million/km2)	Post-Disaster Response Capability (Number of Beds per 1000 People)	Synthetic Effect Measure
Critical Value for Objective	0.0145	3.2011	0.0016	4.1012	—
Shaya County	0.0111	8.7189	0.0027	4.2475	−0.0001
Yuli County	0.0130	1.7205	0.0013	4.1231	−0.0006
Aksu City	0.0175	49.3352	0.0173	2.5122	−0.0016
Hotan County	0.0128	8.2387	0.0011	2.9305	−0.0058

6. Contributions

The main contributions of this paper are as follows:

(1)

The optimization of site selection for emergency supply reserve warehouses based on the multi-attribute weighted intelligent gray target decision-making evaluation model accounts for both hitting-the-target and missing-the-target scenarios for effect values and vectors of objectives. It provides a definitive conclusion on the suitability of a site for establishing an emergency supply reserve warehouse and offers decision-makers a basis for their decision. It not only expands the application scope of gray system theory but also enriches the optimization method for the site selection of emergency supply reserve warehouses;

(2)

This paper effectively addresses the issue of determining the critical value of the objective effect during optimization using the multi-attribute weighted intelligent gray target model. Given that the critical value greatly influences the comprehensive evaluation results, it is essential to exercise great caution in its determination. It proposes a method that adopts the minimum value of each indicator from the higher-level emergency supply reserve warehouse as the critical value for the current level, thereby addressing the issue of determining the critical value of the objective effect. This study presents a new approach to determining the critical value of the objective effect and offers a reference for other scholars encountering similar challenges in their studies;

(3)

The density of road networks and post-disaster response capability are critical factors in evaluating the site selection for emergency supply reserve warehouses. Case studies reveal that they significantly impact the evaluation results for site selection of emergency supply reserve warehouses. However, it remains to be validated by further research whether they can become key indicators for optimizing site selection of emergency supply reserve warehouses and whether similar research results are applicable to other subjects of study.