A Method for Assisting GNSS/INS Integrated Navigation System during GNSS Outage Based on CNN-GRU and Factor Graph

Abstract

In complex urban road environments, vehicles inevitably experience frequent or sustained interruptions of the Global Navigation Satellite System (GNSS) signal when passing through overpasses, near tall buildings, and through tunnels. This results in the reduced accuracy and robustness of the GNSS/Inertial Navigation System (INS) integrated navigation systems. To improve the performance of GNSS and INS integrated navigation systems in complex environments, particularly during GNSS outages, we propose a convolutional neural network–gated recurrent unit (CNN-GRU)-assisted factor graph hybrid navigation method. This method effectively combines the spatial feature extraction capability of CNN, the temporal dynamic processing capability of GRU, and the data fusion strength of a factor graph, thereby better addressing the impact of GNSS outages on GNSS/INS integrated navigation. When GNSS signals are strong, the factor graph algorithm integrates GNSS/INS navigation information and trains the CNN-GRU assisted prediction model using INS velocity, acceleration, angular velocity, and GNSS position increment data. During GNSS outages, the trained CNN-GRU assisted prediction model forecasts pseudo GNSS observations, which are then integrated with INS calculations to achieve integrated navigation. To validate the performance and effectiveness of the proposed method, we conducted real road tests in environments with frequent and sustained GNSS interruptions. Experimental results demonstrate that the proposed method provides higher accuracy and continuous navigation outcomes in environments with frequent and sustained GNSS interruptions, compared to traditional GNSS/INS factor graph integrated navigation methods and long short-term memory (LSTM)-assisted GNSS/INS factor graph navigation methods.

1. Introduction

The integration of the Global Navigation Satellite System and the Inertial Navigation System has long provided a reliable solution for navigation in various dynamic environments [1,2]. GNSS offers high-precision location information [3], while the INS can maintain short-term navigation capabilities without external signals. However, the performance of this integrated system is limited by the availability of GNSS signals, especially in urban environments with high buildings, tunnels, and similar settings where GNSS signals are prone to interference or interruptions. Additionally, while the INS can provide location information without GNSS signals, its errors accumulate rapidly over time, leading to decreased accuracy with prolonged use. Thus, maintaining the continuity and accuracy of the navigation system in the absence of GNSS signals has become a focal point of navigation technology research.

In integrated navigation systems, data fusion algorithms play a central role, especially in synchronizing and merging data from different sensors. Traditionally, the Kalman Filter (KF) [4] and its derivatives, such as the Extended Kalman Filter (EKF) [5,6] and the Unscented Kalman Filter (UKF) [7,8], have been crucial for estimating system states. These algorithms significantly enhance the system’s positioning accuracy and robustness across various environments by effectively integrating positioning data from different navigation systems. However, as the application environments become increasingly complex, these filtering techniques show certain limitations in handling complex nonlinear dynamics, error accumulation, and global optimization needs. Traditional filtering methods tend to perform estimations in local regions, where errors may accumulate over long periods or during large-scale operations. To address these challenges, factor graph algorithms have recently attracted widespread attention from researchers [9]. Factor graphs offer a novel perspective and approach, integrating various sensor data through a globally optimized graph model to comprehensively update and optimize system states. Unlike traditional sequential update filtering methods, factor graphs use historical information to establish more complex constraints and significantly reduce error accumulation through iterative optimization processes, thereby enhancing long-term accuracy and stability [10]. This method not only performs excellently in highly nonlinear systems but also maintains high performance in complex navigation environments. Factor graphs can achieve more consistent global state estimates compared to KF, EKF, and UKF through global optimization. Wen et al. [11] conducted a performance comparison of factor graph-based and EKF-based integrated navigation. The factor graph, using multiple iterations for robust estimation, achieved better navigation performance than the EKF. Jiang et al. [12] integrated PDR step lengths and GNSS using a factor graph for pedestrian navigation. The relinearization and full utilization of time-correlated states and measurements in factor graphs contribute to achieving better estimates than KF. Yang et al. [13] conducted indoor integrated navigation experiments with drones to evaluate the performance of EKF and factor graphs in various environments. The factor graph utilizes more historical data to construct constraints and obtains the optimal state by solving nonlinear optimization. Zhang et al. [14] applied a factor graph for INS/USBL integration in underwater navigation and positioning. Due to multiple iterations and the application of large amounts of data, its performance is generally superior to that of KF. Studies [11,12,13,14] compared factor graphs with KF and its derivatives across various test scenarios, with experimental results showing that factor graphs provided superior positioning accuracy, confirming their potential for navigation and positioning applications in complex scenarios.

In GNSS/INS integrated navigation systems, several solutions have been provided to maintain continuous high-precision navigation capabilities during GNSS signal outages. One method is the zero-velocity update (ZUPT) [15,16], where the vehicle’s speed is zero when stationary, and the calculated speed from the vehicle’s inertial system is used as an observation of the system’s speed error to correct other error quantities. The application of zero-velocity correction is limited because the vehicle must periodically stop moving, which is challenging in high-dynamic or continuous motion scenarios. Another method is the non-holonomic constraint (NHC) [17,18], which enhances system performance by using the vehicle’s motion restrictions (e.g., the vehicle cannot move laterally), but this method relies on an accurate understanding of the vehicle’s dynamic model. In practice, the actual driving state of the vehicle may deviate from the model assumptions, especially in complex road conditions and extreme driving behaviors, making NHC’s restrictions and assumptions less effective and reducing the accuracy of the navigation system.

Recently, with the development of artificial intelligence and neural network technologies, neural networks have been proposed to address GNSS/INS integrated navigation issues during GNSS outages [19,20]. By training neural networks and predicting GNSS data, they can cope with various signal interruption scenarios, enhancing integrated navigation accuracy during GNSS outages [21]. Yao et al. [22] used a multilayer perceptron (MLP) to assist GPS/INS positioning, reducing the cumulative positioning error of the independent INS during GNSS interruptions. Dai et al. [23] used a recurrent neural network (RNN) to assist INS/GNSS integrated navigation in GNSS denial environments. However, MLP and RNN tend to overfit on training data and face issues of gradient vanishing or exploding. To overcome some of the shortcomings of MLP and RNN, Zhang et al. [24] and Wei et al. [25] used long short-term memory (LSTM) to predict pseudo GNSS positions during GNSS outages. LSTM reduces the risk of overfitting through regularization and introduces gating mechanisms to mitigate gradient vanishing or exploding. Gated recurrent unit (GRU) maintains LSTM’s ability to handle long-term dependencies while reducing model complexity and computational demands. Tang et al. used GRU to bridge GNSS outages [26], with GRU surpassing LSTM in prediction accuracy and training efficiency.

In response to the issues with traditional compensation methods, this paper proposes a CNN-GRU-assisted GNSS/INS factor graph integrated navigation method. This unique combination not only enhances the robustness of the integrated navigation system during signal interruptions but also improves the system’s adaptability to complex environments.

The proposed method demonstrates significant advantages in handling nonlinear dynamics, addressing GNSS signal interruptions, and mitigating error accumulation during long-term operations. Experimental validation shows that this method significantly improves navigation accuracy in special environments such as urban buildings and tunnels, demonstrating superior performance over traditional integrated navigation technologies.

The remainder of this paper is organized as follows: Section 2 introduces the integrated system solution and presents the implementation process of the proposed method. Section 3 discusses the model and information fusion theory of factor graph. Section 4 details the CNN-GRU network and the neural network prediction assistance model. Section 5 conducts road tests and result analysis under frequent and sustained GNSS interruptions, with conclusions presented in Section 6.

2. Integrated System Solution

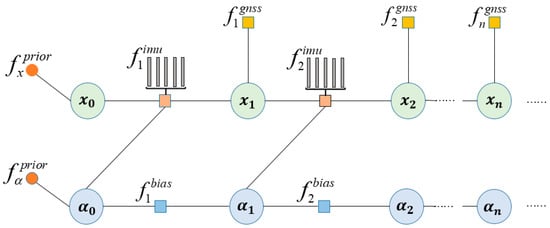
The system solution for the factor graph integrated navigation method assisted by the CNN-GRU neural network proposed in this paper is illustrated in Figure 1. When GNSS signals are strong, the factor graph is used to fuse GNSS and INS data and output navigation results, while simultaneously training the CNN-GRU prediction model. The training and prediction processes of the CNN-GRU model are detailed later in the text. If a GNSS signal interruption occurs, the CNN-GRU prediction model generates pseudo GNSS position information to supplement the missing information in the integrated navigation system. The basic idea of using the CNN-GRU prediction model to assist the integrated navigation system is to train the model using INS and GNSS measurement information when the GNSS reception signal quality is good, and to predict GNSS position data using the trained model when GNSS signals are unexpectedly interrupted. The INS and GNSS factors are connected via undirected edges to form the factor graph model. Additionally, it is necessary to continuously correct the INS using the integrated navigation information to eliminate the error accumulation in inertial navigation, thereby enhancing the accuracy and robustness of the integrated navigation system.

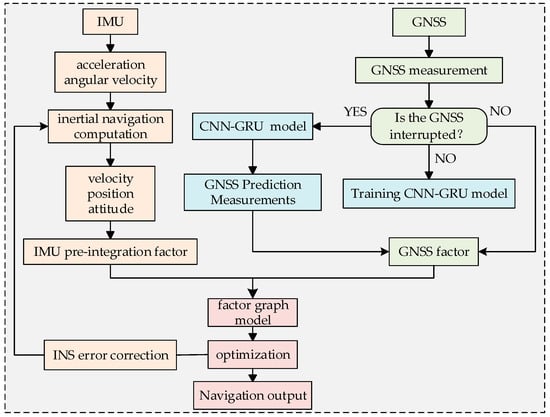
Figure 1. Programmatic framework for integrated navigation systems.

3. Factor Graph Integrated Navigation Framework

3.1. Factor Graph Information Fusion Theory

Considering the problems of occlusion and signal interference in the urban road environment, this paper constructs a GNSS/INS integrated navigation information fusion framework based on the factor graph to meet the needs of in-vehicle navigation systems for positioning accuracy and robustness. The integrated navigation information fusion factor graph framework is shown in Figure 2. In the figure, the IMU pre-integration factor node $f^{imu}$ is connected to the navigation state variable node $x$ and the system error variable node $\alpha$ in the neighboring moments, and the GNSS factor node is connected to the navigation state variable node in the corresponding moments. At the same time, the system error factor node $f^{bias}$ is connected to the system error variable node of the neighboring moment, and the factor graph model expands with the access of measurement information [27].

Figure 2. GNSS/INS integrated navigation information fusion factor graph framework.

A factor graph is a graph structure consisting of factor nodes and variable nodes used to represent a probabilistic model, which is able to visually describe the dependencies and conditional probabilities between random variables. In the factor graph framework, the system state variables $x={[\phi ,v,p]}^T$, where $\phi =[\psi ,\theta ,\gamma ]$ is the 3D attitude angle vector, $v=[v_N,v_E,v_D]$ is the velocity vector, and $p=[L,\lambda ,h]$ is the position vector. The system deviation variables $\alpha ={[b_{\omega },b_a]}^T$, $b_{\omega }$ and $b_a$ are the three-axis deviations of the gyroscope and accelerometer, respectively. The set of system state variables and system error variables from the initial moment $t_0$ to the current moment $t_k$ is defined as $X_k={\{x,\alpha \}}_{i=0}^k$. The set of measurement information of the system from the initial moment $t_0$ to the current moment $t_k$ is defined $Z_k={\{z_i^{imu},z_i^{gnss}\}}_{i=0}^k$, where $z_i^{imu},z_i^{gnss}$ are the IMU and GNSS measurement values, respectively. The optimal navigation solution corresponding to the navigation system is the maximum a posteriori estimate of the system state. According to Bayesian theory, the a posteriori probability $P\left(X_k|Z_k\right)$ based on the navigation system state variables $X$ can be factorized as:

$$\begin{array}{c}P\left(X_k|Z_k\right)={\displaystyle \frac{P(Z_k|X_k)P(X_k|X_{k-1})}{P(Z_k)}}P(X_{k-1}|Z_{k-1})\\ ={\displaystyle \prod _{i=1}^k}{\displaystyle \frac{P(z_i|x_i)P(x_i|x_{i-1})}{P(z_i)}}P(X_0)\end{array}$$

(1)

where $P(X_0)$ denotes the a priori information of the initial state, $P(Z_k)$ is the probability density of the sensor measurements, $P(Z_k|X_k)$ is the a priori probability density function of the navigation system’s state quantity and sensor quantity measurements. The Bayesian estimation process consists of two parts: prediction and updating. In the prediction process of the factor graph, the probability density $P(X_k|X_{k-1})$ is utilized to pass the state backward, providing a priori information about the state quantities at each moment in time. The updating process, on the other hand, corrects the prior probability density of the state quantities by using the most recent observations to obtain the posterior probability density $P\left(X_k|Z_k\right)$. Based on the maximum a posteriori probability estimation, the optimal estimation of the navigational state variables can be expressed as follows:

$$X^{map}=\arg \max P\left(X_k|Z_k\right)$$

(2)

It is functionally decomposed according to the principle of factor graph, and each probability density from the decomposition corresponds to the factor node in it, respectively. Therefore, the above equation can be rewritten as [28]:

$$X^{map}=\underset{X}{\arg \max }{\displaystyle \prod _i{f}_i(X_i)}$$

(3)

In the factor graph model, each factor node will correspond to an error function that characterizes the magnitude of the error between the predicted and actual measurements of the navigation system state quantities. The sensor factor $f_i(X_i)$ can be represented as:

$$f_i(X_i)=\exp (-{\displaystyle \frac{1}{2}}{‖(h_i(X_i)-z_i)‖}_{{\sum }_i}^2)$$

(4)

$$r(z_i,X_i)=h_i(X_i)-z_i$$

(5)

where $h(X)$ is the measurement function of the sensor, ${\sum }_i$ is the noise covariance matrix of the corresponding sensor, and $r(z_i,X_i)$ is the corresponding sensor measurement residual. The maximum a posteriori estimate $X^{map}$ needs to be obtained by minimizing ${\displaystyle \sum _i}{‖r(x_i,z_i)‖}_{{\sum }_i}^2$, which turns the maximum a posteriori estimation problem of the system state quantities in the navigation system into a nonlinear least squares problem:

$$\begin{array}{l}{X}^{map}=\underset{X}{\arg \min }\left\{-\log {\displaystyle \prod _i{f}_i(X_i)}\right\}\\ =\underset{X}{\arg \min }\left\{{\displaystyle \sum _i}{‖r(x_i,z_i)‖}_{{\sum }_i}^2\right\}\end{array}$$

(6)

Combining the sensor factors and the a priori information, the maximum a posteriori probabilistic solution of the navigation system state variables is derived, so as to realize the fusion of sensor information. For the GNSS/INS integrated navigation factor graph model proposed in this paper, the optimal estimate $X^{map}$ of the navigation system state can be expressed as:

$$X^{map}=\underset{X}{\arg \min }\left\{\begin{array}{l}{\displaystyle \sum _k^n}{‖r_{imu}(z_{b(k)}^{b(k-1)},X)‖}_{{\sum }_{k-1,k}^{imu}}^2\\ +{\displaystyle \sum _i^n}{‖r_{gnss}(z_i^{gnss},X)‖}_{{\sum }_i^{gnss}}^2\\ +{‖r_p-H_{p}X‖}_{{\sum }_p}^2\end{array}\right\}$$

(7)

Using unconstrained nonlinear least squares optimization theory to solve Equation (7) allows for obtaining the optimal values of the navigation state variables at each moment. In the equation, $r_{imu},{\sum }^{imu}$ represents the measurement residuals and noise covariance matrix of the IMU pre-integration factor, $r_{gnss},{\sum }^{gnss}$ represents the measurement residuals and covariance matrix of the GNSS factor, which will be detailed later in the text. $\left\{r_p,H_P\right\}$ stands for prior information, and ${\sum }_p$ is the noise covariance matrix of the prior information. Prior factors are used in navigation problems to introduce prior knowledge or measurement information about the state variables, helping the navigation system to more accurately estimate the states.

3.2. IMU Pre-Integration Factor Node

IMU typically output acceleration and angular velocity information at a high frequency. Constructing a factor node for each sampling point would result in a substantial amount of redundant information in the factor graph, leading to considerable computational load [29]. To address this issue, pre-integration is employed to preprocess IMU data. To obtain the current position, velocity, and attitude, the state variables from the previous moment are needed. However, when these state variables change, it is necessary to retransmit the IMU measurements for integration to obtain the current state variables. Each time an adjustment in pose is made, the IMU measurements must be retransmitted, which is a time-consuming and computationally intensive measurement strategy. Using IMU pre-integration ensures that the IMU integration values between two nodes are only related to the IMU errors at those two moments, thus avoiding repeated integrations caused by changes in the starting point of integration. This process involves integrating the raw IMU data to obtain the relative displacement and rotational changes in the carrier over a period of time, thereby reducing data processing volume and minimizing the risk of error accumulation.

In integrated navigation systems, the inertial measurement unit can reflect changes in the carrier’s motion state by measuring angular velocity ${\tilde{\omega }}_{ib}^b$ and acceleration (specific force) ${\tilde{f}}^b$. The measurement equation can be expressed as [30]:

$${\tilde{\omega }}_{ib}^b={\omega }_{ib}^b+b_{\omega }+{\epsilon }_{\omega },{\tilde{f}}^b=f^b+b_a+{\epsilon }_a$$

(8)

where ${\omega }_{ib}^b$ and $f^b$, respectively, represent the true values of the gyroscope and accelerometer, while $b_{\omega }$ and $b_a$, respectively, denote the biases of the gyroscope and accelerometer. ${\epsilon }_{\omega }$ and ${\epsilon }_a$ represent the noise associated with the gyroscope and accelerometer, respectively. Based on inertial devices, the navigation information of the carrier is calculated by first solving for the carrier’s attitude information, and then using the updated attitude information to compute the carrier’s velocity and position. Traditional inertial navigation gyro modeling outputs do not consider the effects of the Earth’s rotation rate ${\omega }_{ie}^n$ and the angular velocity of entrainment ${\omega }_{en}^n$ on the accuracy of gyro measurements. Therefore, considering these two types of rotational velocities, the differential equation for the carrier’s attitude is as follows:

$$\begin{array}{l}{\dot{q}}_b^n={\displaystyle \frac{1}{2}}{q}_b^n\otimes \left[\begin{array}{l}0\\ {\omega }_{nb}^b\end{array}\right],{\omega }_{nb}^b={\omega }_{ib}^b-C_n^b({\omega }_{ie}^n+{\omega }_{en}^n)\\ {\omega }_{ie}^n=[\begin{array}{ccc}{\omega }_e\cos L& 0& -{\omega }_e\sin L\end{array}]\\ {\omega }_{en}^n=[\begin{array}{ccc}{\displaystyle \frac{v_E}{(R_N+h)}}& -{\displaystyle \frac{v_N}{(R_M+h)}}& -{\displaystyle \frac{v_E\tan L}{(R_N+h)}}\end{array}]\end{array}$$

(9)

where $q_b^n$ is the attitude quaternion from the body coordinate system (b-frame) to the navigation coordinate system (n-frame), with the n-frame defined as (END). $C_n^b$ is the attitude rotation matrix from the b-frame to the n-frame. $L$ is the latitude of the carrier’s location. $h$ is the height of the carrier’s location relative to the horizontal plane. $R_M$ is the meridian radius of curvature, and $R_N$ is the prime vertical radius of curvature, with their respective calculation formulas as follows:

$$\begin{array}{l}{R}_M={\displaystyle \frac{R_e(1-{e_1}^2)}{{(1-{e_1}^2{\sin }^{2}L)}^{3/2}}}\\ R_N={\displaystyle \frac{R_e}{{(1-{e_1}^2{\sin }^{2}L)}^{1/2}}}\end{array}$$

(10)

where $R_e$ is the radius of the Earth and $e_1$ is the first eccentricity. When describing the carrier’s attitude using quaternions, the update of the carrier’s attitude between two adjacent IMU sampling times can be expressed as:

$$q_{b(k)}^n=q_{b(k-1)}^n\otimes q_{b(k-1)}^{n(k-1)}\otimes q_{b(k)}^{n(k-1)}$$

(11)

Updating the carrier’s attitude information using pre-integration for quaternions from $t_{k-1}$ to $t_k$ can be expressed as:

$$q_{b(k)}^{b(k-1)}={({(q_{b(k)}^{n(k)})}^{-1}\otimes q_{n(k-1)}^{n(k)}\otimes q_{b(k-1)}^{n(k-1)})}^{-1}$$

(12)

The velocity update equation for the carrier can be expressed as:

$$v_{b(k)}^n=v_{b(k-1)}^n+{\displaystyle {\int }_{t_{k-1}}^{t_k}{C}_{b(t)}^{n(t)}({\tilde{f}}^b-b_a-{\epsilon }_a)dt}+{\displaystyle {\int }_{t_{k-1}}^{t_k}(g^n-(2{\omega }_{ie}^n+{\omega }_{en}^n)\times v^n)dt}$$

(13)

where $g^n$ is the local gravity. The velocity pre-integration from $t_{k-1}$ to $t_k$ can be expressed as:

$$\begin{array}{c}△v_{b(k)}^{b(k-1)}=C_{n(t)}^{b(k-1)}(v_{b(k)}^n-v_{b(k-1)}^n-g^n△t_{k-1,k}+((2{\omega }_{ie}^n+{\omega }_{en}^n)\times v_{b(k-1)}^n△t_{k-1,k})\\ ={\displaystyle {\int }_{t_{k-1}}^{t_k}{C}_{b(t)}^{b(k-1)}({\tilde{f}}^b-b_a-{\epsilon }_a)dt}\end{array}$$

(14)

Integrating the velocity of the carrier yields the position increment of the carrier, which, when added to the previous position, provides the current pose measurement. Therefore, the position update equation for the carrier can be expressed as:

$$p_{b(k)}^n=p_{b(k-1)}^n+{\displaystyle {\int }_{t_{k-1}}^{t_k}{v}_{b(t)}^{n}dt}$$

(15)

The position pre-integration from $t_{k-1}$ to $t_k$ can be expressed as:

$$\begin{array}{c}△p_{b(k)}^{b(k-1)}=C_{n(t)}^{b(k-1)}(p_{b(k)}^n-p_{b(k-1)}^n-v_{b(k-1)}^n△t_{k-1,k}\\ +0.5((2{\omega }_{ie}^n+{\omega }_{en}^n)\times v_{b(k-1)}^n-g^n)△t_{k-1,k}^2)\\ ={\displaystyle \int {\displaystyle {\int }_{t_{k-1}}^{t_k}{C}_{b(t)}^{b(k-1)}({\tilde{f}}^b-b_a-{\epsilon }_a)d{t}^2}}\end{array}$$

(16)

During the position update process using the position pre-integration model, the influences of ${\omega }_{ie}^n$ and ${\omega }_{en}^n$ are considered, which improves the position solving accuracy compared to traditional inertial pre-integration methods. In factor graph optimization, a noise covariance matrix is needed to weight the IMU factors, and the error state vector is defined as follows:

$$\delta z_t={\left[\begin{array}{ccccc}\delta p_{b(k)}^{b(k-1)}& \delta v_{b(k)}^{b(k-1)}& \delta q_{b(k)}^{b(k-1)}& \delta b_{\omega }& \delta b_a\end{array}\right]}^T$$

(17)

In the formula, $\delta p_{b(k)}^{b(k-1)},\delta v_{b(k)}^{b(k-1)},\delta q_{b(k)}^{b(k-1)}$ represents the pre-integrated measurement errors for position, velocity, and attitude, while $\delta b_{\omega },\delta b_a$ represents the bias errors for the gyroscope and accelerometer. The continuous-time system’s error state equation is expressed as:

$$\delta {\dot{z}}_t=F_t\delta z_t+G_t{\epsilon }_t$$

(18)

where the system error state transition matrix $F_t$, the process noise transition matrix $G_t$, and the noise vector ${\epsilon }_t$ are represented as:

$$F_t=\left[\begin{array}{ccccc}0& I& 0& 0& 0\\ 0& 0& -{\widehat{C}}_{b(t)}^{b(k-1)}({\widehat{f}}^b-b_a)\times & 0& {\widehat{C}}_{b(t)}^{b(k-1)}\\ 0& 0& -({\widehat{\omega }}_{ib}^i-b_{\omega })\times & -I& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$

(19)

$$G_t=\left[\begin{array}{cc}0& 0\\ 0& {\widehat{C}}_{b(t)}^{b(k-1)}\\ -I& 0\\ 0& 0\\ 0& 0\end{array}\right],{\epsilon }_t=\left[\begin{array}{c}{\epsilon }_{\omega }\\ {\epsilon }_a\end{array}\right]$$

(20)

The pre-integration covariance matrix can be expressed as:

$${\sum }_{b(t)}^{imu}={\mathsf{\Phi }}_t{\sum }_{b(t-1)}^{imu}{{\mathsf{\Phi }}_t}^{\mathrm{T}}+{\displaystyle {\int }_{t-1}^t{\mathsf{\Phi }}_t{G}_{t}Q}{G_t}^{\mathrm{T}}{{\mathsf{\Phi }}_t}^{\mathrm{T}}dt$$

(21)

where ${\sum }_{b(t-1)}^{imu}=0$ is the initial covariance matrix, ${\mathsf{\Phi }}_t\approx {\rm I}+F_t$ is the transition matrix, and $Q=diag\left[{\sigma }_{\omega }^2,{\sigma }_a^2\right]$ is the discrete-time noise covariance matrix. The update equation for the Jacobian matrix of the system state variables with respect to the system error state variables, which calculates the first derivative, can be expressed as:

$$J_{k-1,t}={\mathsf{\Phi }}_t{J}_{k-1,t-1}$$

(22)

where $J_{k-1,t-1}$ is the initial Jacobian matrix and is an identity matrix. To avoid repeated integration, the pre-integrated measurements are approximated using a first-order expansion based on the Jacobian and covariance matrices. The updated pre-integrated measurement values are calculated as follows:

$$\left\{\begin{array}{l}△{\widehat{p}}_{b(k)}^{b(k-1)}\approx △p_{b(k)}^{b(k-1)}+J_{b\omega }^p\delta b_{\omega }+J_{ba}^p\delta b_a\\ △{\widehat{v}}_{b(k)}^{b(k-1)}\approx △v_{b(k)}^{b(k-1)}+J_{b\omega }^v\delta b_{\omega }+J_{ba}^v\delta b_a\\ {\widehat{q}}_{b(k)}^{b(k-1)}\approx q_{b(k)}^{b(k-1)}\otimes \left[\begin{array}{c}1\\ {\displaystyle \frac{1}{2}}{J}_{b\omega }^{\varphi }\delta b_{\omega }\end{array}\right]\end{array}\right.$$

(23)

where $J_{b\omega }^p,J_{ba}^p,J_{b\omega }^v,J_{ba}^v,J_{b\omega }^{\varphi }$ is a submatrix of $J_{k-1,k}$, representing the Jacobian matrix of the first derivative of the superscript with respect to the subscript. For example, $J_{b\omega }^p$ corresponds to the position of $\delta p_{b(k)}^{b(k-1)}/\delta b_{\omega }$. Based on the previous derivation, the IMU pre-integration factor residual can be expressed as:

$$r_{imu}(z_{b(k)}^{b(k-1)},X)=\left[\begin{array}{c}△p_{b(k)}^{b(k-1)}-△{\widehat{p}}_{b(k)}^{b(k-1)}\\ △v_{b(k)}^{b(k-1)}-△{\widehat{v}}_{b(k)}^{b(k-1)}\\ 2{(q_{b(k)}^{n(k)})}^{-1}\otimes q_{n(k-1)}^{n(k)}\otimes q_{b(k-1)}^{n(k-1)}\otimes {\widehat{q}}_{b(k)}^{b(k-1)}\\ b_{\omega (k)}-b_{\omega (k-1)}\\ b_{a(k)}-b_{a(k-1)}\end{array}\right]$$

(24)

3.3. GNSS Factor Nodes

GNSS factors are extremely valuable for providing absolute position information and long-term data, especially in open sky environments. However, in environments with obstructions such as urban high-rise buildings and tunnels, GNSS signal reception may be interrupted. Therefore, it is necessary to integrate GNSS data with other sensor data to improve navigation accuracy and robustness. The GNSS sensor measurement equation is given as [31]:

$$z_i^{gnss}=h^{gnss}(x_i)+n^{gnss}$$

(25)

where $n^{gnss}$ represents the measurement noise and $h^{gnss}(x_i)$ is the GNSS measurement function. GNSS positioning provides the coordinates of the antenna phase center, while INS mechanical arrangement provides the navigation results from the IMU measurement center. These two centers do not physically coincide, necessitating lever-arm effect correction during integrated navigation computation. The GNSS factor residual can be expressed as:

$$r_{gnss}(z_i^{gnss},X)=z_i^{gnss}-{\widehat{z}}_i^{gnss}+C_b^n{l}_{gnss}^b$$

(26)

where ${\widehat{z}}_i^{gnss}$ is the GNSS estimated value, and $l_{gnss}^b$ is the GNSS antenna lever arm.

4. CNN-GRU Neural Network Prediction-Assisted Positioning Method

4.1. CNN-GRU Model

CNN is a commonly used multilayer feedforward neural network model [32], with its basic structure shown in Figure 3. A typical CNN includes an input layer, multiple alternating convolutional and pooling layers, and a fully connected layer. CNNs extract hidden topological features from data through layer-by-layer convolution and pooling operations, capturing the spatial characteristics of the input data with fewer parameters. The convolution operation efficiently extracts data feature parameters and reduces matrix dimensions, while the pooling layer reduces network parameters and computational complexity. Finally, the fully connected layer combines all local features. After the convolutional and pooling layers, a flattening layer is used to convert the data from multidimensional to one-dimensional, preparing it for connection to the GRU layer.

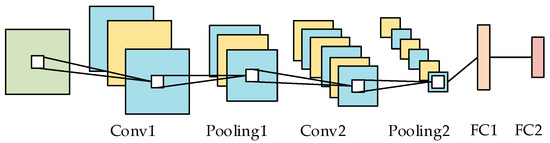
Figure 3. CNN basic structure.

The structure of a GRU is shown in Figure 4. The main variables include the hidden state information at the previous time step $h_{t-1}$, the input state $x_t$, and the current hidden state $h_t$. There are also two gates: vector $r_t$ corresponds to the reset gate, and vector $Z_t$ corresponds to the update gate. The update gate controls how much of the previous information should be retained in the current state and how much new information from the current candidate hidden state should be introduced. The reset gate determines how much past information should be included in the current state computation.

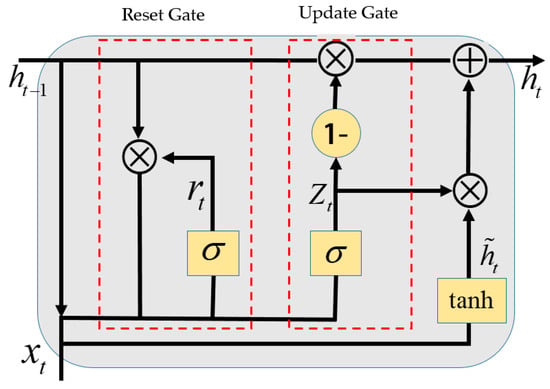
Figure 4. GRU basic structure.

The specific computation formulas for the GRU can be expressed as follows [33]:

$$Z_t=\sigma (W_z·[h_{t-1},x_t])$$

(27)

$$r_t=\sigma (W_r·[h_{t-1},x_t])$$

(28)

$${\tilde{h}}_t=\tanh (W_h·[r_t\odot h_{t-1},x_t])$$

(29)

$$h_t=(1-Z_t)\odot h_{t-1}+Z_t\odot {\tilde{h}}_t$$

(30)

In the formula, $W_r,W_z,W_h$ refers to the weight matrices for the reset gate, update gate, and candidate hidden state, $\sigma$ is the sigmoid function, and $\tanh$ is the activation function.

The CNN-GRU neural network model consists of a combination of CNN and GRU [34], as shown in Figure 5. Initially, a CNN layer is established to extract spatial features from motion sensor data. Following the CNN layer, a max pooling layer is added, which extracts primary features by selecting the maximum value within each pooling window, thereby reducing the spatial dimensions and size of the input feature map. This operation helps to reduce the number of model parameters and computational complexity, minimize the risk of overfitting, and enhance the model’s computational efficiency. After the CNN module, a GRU layer is connected, using Flatten to spread out the features into a flat array linked to a fully connected layer. The CNN-GRU-assisted prediction model is used to output pseudo GNSS data, compensating for the accuracy of the integrated positioning system during interruptions. This solves the problem of the integrated positioning system degrading to a pure INS during GNSS outages.

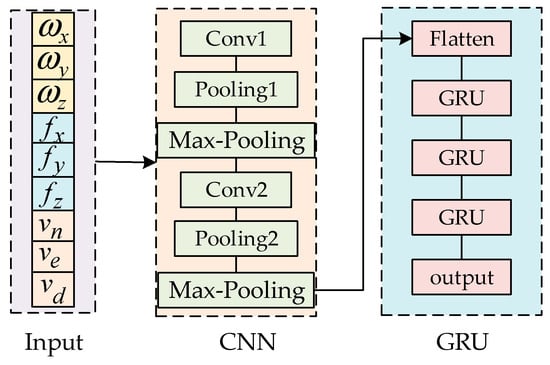
Figure 5. CNN-GRU model structure.

The training of the CNN-GRU combined neural network in this paper is primarily conducted in the following six steps:

Step 1: input acceleration, angular velocity, and velocity data into the convolutional neural network, perform convolution on the data separately, and then sum the data within each convolution channel to generate feature maps.

Step 2: Feed the feature maps into a pooling layer and perform max pooling on the convoluted features, selecting the maximum value to reduce the feature dimensions. Then, transform the dimensions of the pooling layer’s output and connect it to the GRU layer.

Step 3: solve for the propagation parameters of each neuron and compute the values of vector $Z_t,r_t,{\tilde{h}}_t,h_t$.

Step 4: compare the output values with the expected values, and if there is a discrepancy, calculate the error for the neurons and construct a loss function based on this.

Step 5: update the weight parameters according to the loss function.

Step 6: calculate the gradient for each weight and then update the weights using an optimization algorithm.

4.2. CNN-GRU-Based GNSS Outage Assisted Prediction

In GNSS/INS integrated systems, there are already many neural network-assisted models. The common approach is to establish a relationship between INS outputs (angular velocity, specific force, velocity, position, etc.) and certain GNSS information. When GNSS signals are available, these data are used to train the neural network. If GNSS signals are interrupted, the trained neural network is capable of generating pseudo GNSS data. Before beginning to construct the neural network model, it is necessary to establish a system model and select appropriate parameters as inputs and outputs, which helps to enhance the efficiency of model training and the accuracy of predictions. A commonly used model is model $O_{INS}-{\delta }_{GNSS,INS}$ [35], because ${\delta }_{GNSS,INS}$ represents the difference between INS and GNSS positions, and the constructed model is always affected by errors from both GNSS and INS. To avoid this problem, model $O_{INS}-\Delta P_{GNSS}$ is proposed, where the model output $(\Delta P_{GNSS})$ is only the GNSS position increment. The ideal scenario for neural networks is when training data and prediction data are in the same motion state. However, in practical applications, the motion state of vehicles always changes due to complex road environments. A single neural network may not effectively train with these mixed data. Therefore, CNN is used to extract the motion state of the vehicle. CNN has excellent feature extraction capabilities and can accurately capture changes in motion states from raw data in complex and dynamic motion states. Additionally, GRU is introduced to help the model better understand long-term dependencies in time series data. These mechanisms enable the model to more effectively filter and utilize historical information when processing navigation data with temporal dynamics, enhancing navigation and positioning performance in complex environments.

The specific structure of the CNN-GRU neural network-assisted model is shown in Figure 6. Here, $\omega ,f$ represents the angular velocity and specific force output by the IMU, $v_{INS},p_{INS}$ represents the velocity and position output by the inertial navigation system, $p_G$ is the GNSS output position, and $\delta p$ is the position error. The assisted prediction model includes a training phase and a prediction phase. In the training phase, the CNN-GRU model parameters are determined based on the acceleration, specific force, and velocity of the INS at the previous and current times, as well as the GNSS position increment $\Delta P_G$. In the prediction phase, the acceleration, specific force, and velocity of the INS at the current and next times are input to the CNN-GRU model to predict the GNSS position increment. Subsequently, the predicted position increment $\Delta P_G$ is added to the initial position information $P_{G0}$ to generate the pseudo GNSS position $P_G^{pse}$, thereby suppressing the divergence of the inertial navigation system errors.

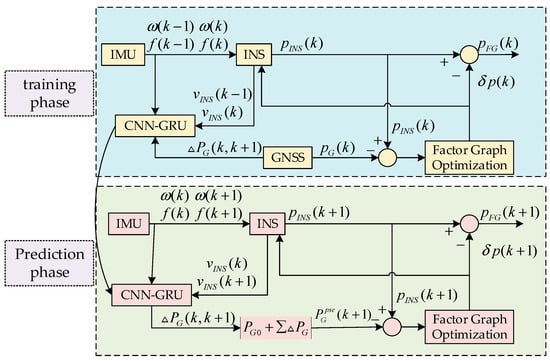
Figure 6. CNN-GRU-assisted model structure diagram.

5. Experiment

5.1. Experimental Setup and Data Acquisition

In order to verify the effectiveness of the proposed algorithm in this paper, we conducted in-vehicle experiments in a typical urban environment in Beijing, China. The sensors were provided by the Beijing Key Laboratory of High Dynamic Navigation Technology, and the sensor parameters are shown in Table 1.

Table 1. Sensor parameters.

Sensor	Parameters	Accuracy
IMU	Gyroscope Bias	20°/h
GNSS	Gyroscope Random Walk	$0.0667°/\sqrt{\mathrm{h}}$
	Accelerometer Bias	50 mg
	Sampling Frequency	100 Hz
	Position Accuracy	2 m
	Sampling Frequency	1 Hz

We conducted experiments with frequent and sustained interruptions of GNSS signals to evaluate the performance of the proposed algorithm. The experimental test trajectory is shown in Figure 7, which includes common occlusion environments such as overpasses and tunnels that the vehicle passed through. The total length of the experimental trajectory was 32.96 km. The light blue section, which is 18.99 km long, includes data collected for training the neural network prediction model and determining its parameters. The green trajectory, measuring 7.79 km, was used to assess the algorithm’s performance under conditions of frequent GNSS interruptions. The orange trajectory, extending for 6.18 km, was used to evaluate the algorithm’s performance during sustained GNSS interruptions. To highlight the superiority of the proposed algorithm, we compared three different integrated navigation methods.

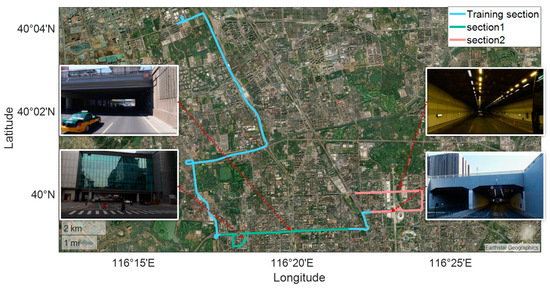
Figure 7. Test vehicle driving route.

(1)

FGO: factor graph-based integrated navigation method;

(2)

LSTM-FGO: factor graph-based integrated navigation method assisted by a long short-term memory (LSTM) network;

(3)

CNN-GRU-FGO: The proposed integrated navigation method, combining convolutional neural network (CNN) and gated recurrent unit (GRU) with factor graph assistance.

5.2. Experimental Verification and Analysis

5.2.1. Frequent Interruption Test

To validate the algorithm’s performance in common GNSS interruption environments, we designed a vehicle driving route that covers typical urban occlusion environments, including high-rise buildings, overpasses, and densely built areas. These environments frequently cause satellite signal interruptions, making it very challenging to achieve high-precision GNSS/INS integrated navigation. The test route is divided into sections with frequent GNSS interruptions, including winding roads and long straight roads. The total GNSS was interrupted 25 times during the journey. The winding road section is 2.97 km long and lasts 580 s (0–580 s), with GNSS being interrupted 16 times. The long straight road section is 4.82 km long and lasts 420 s (580–1000 s), with GNSS being interrupted 9 times. The GNSS interruption times are detailed in Table 2.

Table 2. GNSS interruption time statistics for Section 1.

Start Time (s)	Interruption Duration (s)	Start Time (s)	Interruption Duration (s)	Start Time (s)	Interruption Duration (s)
70	4	450	2	616	6
96	2	465	5	650	6
156	8	471	3	662	8
168	14	474	4	686	12
183	25	482	10	717	6
241	25	511	7	730	5
320	6	543	5	775	7
366	2	597	11
413	9	608	7

The trajectory calculations for the section with frequent interruptions on winding roads are shown in Figure 8, the long straight section with frequent interruptions, as shown in Figure 9. Regarding the the section with frequent interruptions on winding roads, when examining the eastward error curve in Figure 10 and the northward error curve in Figure 11 (0–580 s), it is clear that all three methods exhibit a notable increase in errors in this section, with frequent GNSS interruptions compared to the uninterrupted sections. However, the error increase is significantly smaller with LSTM-FGO and CNN-GRU-FGO, because these methods use neural network models for auxiliary prediction during GNSS interruptions. Specifically, LSTM-FGO utilizes long short-term memory networks for GNSS position prediction, while CNN-GRU-FGO employs a combination of convolutional neural networks and gated recurrent units for the same purpose. Both approaches maintain higher position accuracy during GNSS signal interruptions, offering a clear advantage over traditional factor graph optimization methods.

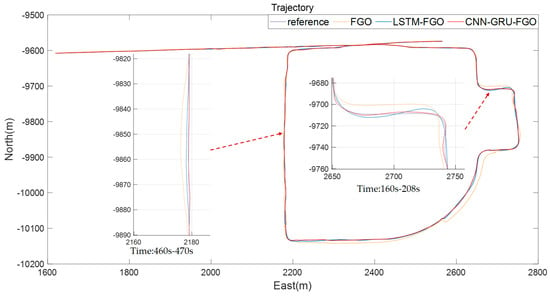
Figure 8. Trajectory calculation for Section 1 with frequent interruptions on winding roads.

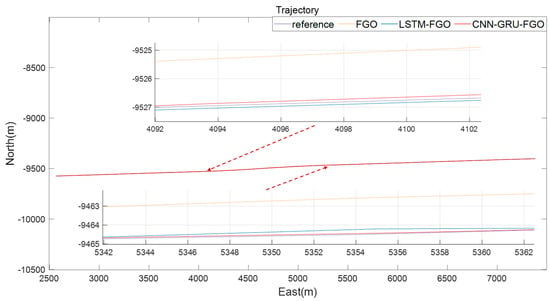
Figure 9. Trajectory calculation for Section 1 with frequent interruptions on long straight road.

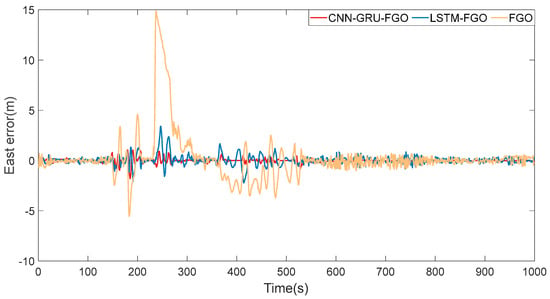
Figure 10. Section 1 east error.

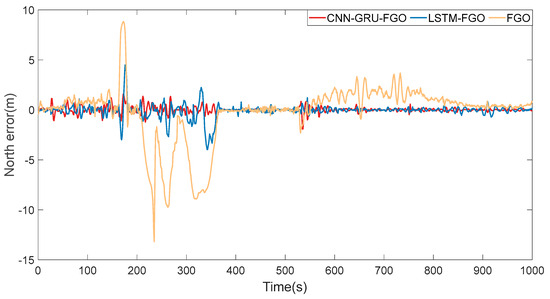
Figure 11. Section 1 north error.

Regarding the long straight section with frequent interruptions, considering the eastward error curve in Figure 10 and the northward error curve in Figure 11 (580–1000 s), the vehicle’s motion pattern on the straight road is relatively simple, as the vehicle moves in a straight line. This simplicity allows for more accurate and reliable position predictions based on historical data. Utilizing the LSTM and CNN-GRU neural network models enhances the precision of position predictions, thus reducing the possibility of positioning errors.

From the position error statistics in Table 3, it can be seen that CNN-GRU-FGO, compared to FGO and LSTM-FGO, has reduced the root mean square error of position by 89% and 56%, respectively. In environments with frequent GNSS interruptions, both LSTM-FGO and CNN-GRU-FGO significantly enhance position accuracy compared to the traditional FGO algorithm. CNN-GRU is capable of capturing long-term dependencies and dynamic changes in time series, better adapting to these complex dynamic environments. As a result, in settings with frequent GNSS interruptions, CNN-GRU-FGO is able to provide more accurate and stable vehicle positioning results.

Table 3. Position error statistics for Section 1.

Section 1	Algorithm	Orientation	RMSE (m)	Maximum Error (m)
winding road	FGO	east	3.06	14.91
		north	3.54	13.19
	LSTM-FGO	east	0.62	3.41
		north	0.90	4.48
	CNN-GRU-FGO	east	0.27	1.81
		north	0.40	1.92
long straight road	FGO	east	0.38	0.99
		north	1.35	3.67
	LSTM-FGO	east	0.26	0.85
		north	0.19	0.80
	CNN-GRU-FGO	east	0.05	0.19
		north	0.12	0.56
all road	FGO	east	2.34	14.91
		north	2.84	13.19
	LSTM-FGO	east	0.50	3.41
		north	0.70	4.48
	CNN-GRU-FGO	east	0.21	1.81
		north	0.31	1.92

5.2.2. Continuous Interruption Test

In urban environments, vehicles passing through tunnels often face continuous interruptions of GNSS signals, posing significant challenges to high-precision navigation. To evaluate the performance of the proposed algorithm in such continuously interrupted environments, we consider two types of road sections: continuously interrupted curved road sections and continuously interrupted long straight road sections. The continuously interrupted curved road section is 3.06 km long with a duration of 400 s (0–400 s), including a curved tunnel section of 1.5 km with continuous interruptions lasting 144 s. The continuously interrupted long straight road section is 3.12 km long with a duration of 400 s (400–800 s), including a straight tunnel section of 1.37 km with continuous interruptions lasting 108 s. Interruption times are detailed in Table 4.

Table 4. GNSS interruption time statistics for Section 2.

Start Time (s)	Interruption Duration (s)	Start Time (s)	Interruption Duration (s)	Start Time (s)	Interruption Duration (s)
44	144	432	6	789	4
285	4	469	5
310	8	534	108

From the solution trajectories of the three algorithms shown in Figure 12, in cases of continuous GNSS interruptions, the trajectory of FGO gradually deviates from the reference trajectory, and this deviation increases over time. According to the eastward error curve in Figure 13 and the northward error curve in Figure 14, we can clearly see that the error of FGO is significant. Although the errors of LSTM-FGO and CNN-GRU-FGO also increase, they are significantly smaller compared to FGO. This significant reduction in error is mainly attributed to the LSTM-FGO and CNN-GRU-FGO algorithms’ ability to more effectively utilize past data to predict GNSS positions, especially in the absence of real-time GNSS data, ensuring the robustness of the integrated navigation.

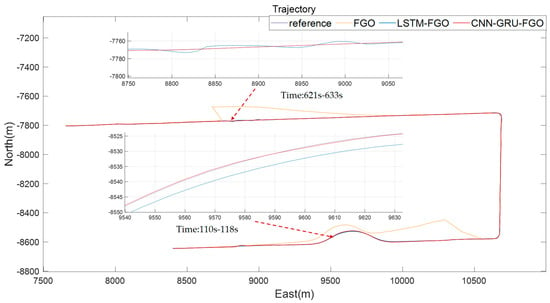
Figure 12. Continuously interrupted section solution trajectories.

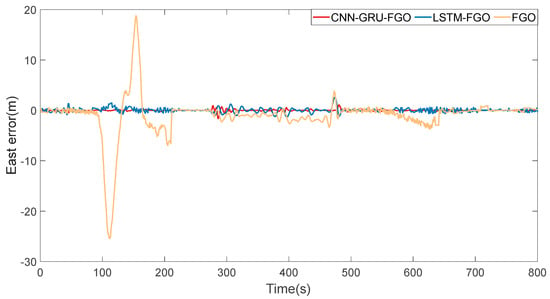
Figure 13. Section 2 east error.

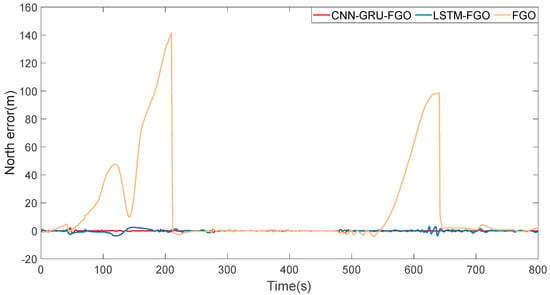
Figure 14. Section 2 north error.

In environments with continuous GNSS interruptions, according to the error statistics in Table 5, there is a significant difference in the precision performance of the three algorithms in handling positioning issues. Specifically, the CNN-GRU-FGO and LSTM-FGO algorithms show a substantial improvement in accuracy compared to the traditional FGO method. The eastward and northward RMSEs of FGO are as high as 4.16 m and 36.55 m, respectively, demonstrating the severe inadequacy of the traditional factor graph algorithm in positioning accuracy in complex environments with continuous GNSS interruptions. In contrast, the eastward and northward RMSEs of LSTM-FGO are reduced to 0.45 m and 0.88 m. CNN-GRU-FGO achieves even more remarkable precision improvements, with eastward and northward RMSEs of just 0.16 m and 0.26 m, reducing the position root mean square errors by 99% and 69% compared to FGO and LSTM-FGO, respectively. Overall, in environments with continuous GNSS interruptions, the combination of neural networks with traditional factor graph optimization methods significantly enhances the algorithm’s navigation and positioning performance in complex settings.

Table 5. Position error statistics for Section 2.

Section 2	Algorithm	Orientation	RMSE (m)	Maximum Error (m)
winding road	FGO	east	5.73	25.42
		north	41.48	141.69
	LSTM-FGO	east	0.48	1.66
		north	1.08	3.62
	CNN-GRU-FGO	east	0.19	1.49
		north	0.28	2.18
long straight road	FGO	east	1.33	3.81
		north	30.79	98.44
	LSTM-FGO	east	0.41	2.58
		north	0.62	3.54
	CNN-GRU-FGO	east	0.13	1.08
		north	0.24	1.60
all road	FGO	east	4.16	25.42
		north	36.55	141.69
	LSTM-FGO	east	0.45	2.58
		north	0.88	3.62
	CNN-GRU-FGO	east	0.16	1.49
		north	0.26	2.18

6. Conclusions

This study addresses the issue of GNSS signal interruptions in urban environments by proposing a CNN-GRU neural network-assisted factor graph integrated navigation method. Through vehicular experiments conducted in typical urban settings in Beijing, we have validated the effectiveness and superiority of this method in navigating complex road environments. The experimental design covered various typical urban driving scenarios, including areas with high-rise buildings, overpasses, tunnels, and other dense constructions that cause GNSS signal blockages. By comparing this method with traditional factor graph optimization methods and LSTM-assisted factor graph methods, we found that the CNN-GRU-FGO algorithm demonstrated significant performance improvements in all aspects. The application of the CNN-GRU neural network-assisted factor graph integrated navigation method in urban environments showcases its technical innovation and operational efficiency. This method not only provides a new direction for future smart transportation technologies but also offers robust technical support and a theoretical foundation for solving similar navigation and positioning challenges.