Fuzzy Comprehensive Evaluation of Collapse Risk in Mountain Tunnels Based on Game Theory

Abstract

In view of the problem that mountain tunnel construction is prone to collapse risk and disaster accidents, this paper proposes a fuzzy comprehensive evaluation method based on CRITIC and D-AHP combined weighting, which can effectively improve the accuracy of mountain tunnel collapse risk evaluation and reduce construction risks. This method combines the improved subjective weighting method D-number analytic hierarchy process and the more scientific and reasonable objective weighting method CRITIC method for combined weighting and uses game theory to optimize the weights, which improves its accuracy compared to traditional evaluation methods and makes up for the lack of subjective and objective weighting of a single evaluation method. The results show that the introduction of the D-number theory can reduce the impact of an uncertain environment on the evaluation results. The risk levels of the sample sections are all between three and four, which is consistent with the actual situation of the project, indicating that the evaluation model is feasible.

1. Introduction

In recent years, the construction mileage of highways in China has been steadily increasing. During the construction of mountainous highways, the incorporation of tunnels has proven to be highly advantageous. However, due to the challenging geological conditions and complexities associated with mountain tunnel construction, significant risks are involved. Wang et al. [1] conducted a statistical analysis of 97 geological disasters that occurred during tunnel construction in China from 2002 to 2018, resulting in a devastating toll of 393 fatalities, 467 injuries, and 51 missing persons along with substantial economic losses. Among these disasters, collapse emerged as the most prominent issue encountered during mountain tunnel construction, accounting for a staggering total of 61 incidents (62.89% of all cases). The mechanism of incitement for collapse disasters in mountain tunnel construction is intricate, encompassing geological conditions, construction technology, on-site management level, and other factors. The primary cause lies in the deficiency of the risk management mechanism system. Therefore, conducting an in-depth investigation into collapse risk assessment using an enhanced fuzzy theory [2] holds immense theoretical value and practical significance.

Zhang et al. [3] divided the evaluation indicators in the risk assessment process of mountain tunnels into qualitative and quantitative and proposed a static and dynamic risk assessment model by introducing the efficacy coefficient method and the multi-level weighted iteration method. Lv et al. [4] relied on engineering examples, used the fuzzy analytic hierarchy process to determine the judgment matrix of the evaluation indicators, and then calculated the membership degree, and combined with the consequence equivalent estimation method to construct a model for evaluating the possibility of mountain tunnel accidents, which is consistent with the excavation situation in engineering practice. In view of the problem that the evaluation of index weights overly relies on expert experience, resulting in low accuracy of the evaluation results, Chen et al. [5] based on the improvement of the rough set theory, introduced the information entropy theory in the index calculation process, and combined with the fuzzy comprehensive evaluation method, proposed a risk evaluation model that can reduce the evaluation factors, and conducted verification. Wu et al. [6] calculated the objective weight by using the entropy weight theory, introduced the extensible theory to calculate the correlation degree of each index, and analyzed the qualitative problems in a quantitative way to establish a risk assessment model. Zhang et al. [7] used the analytic hierarchy process combined with multi-level fuzzy comprehensive decision-making to calculate the probability of the occurrence of risk events and introduced the equivalent estimation method to propose an evaluation model that can also evaluate the consequences generated by risk events at the same time. Pérez et al. [8] introduced the viability analysis of tidal turbine installation using fuzzy logic.

To improve the accuracy of risk assessment of mountain tunnel collapse, this paper proposes a fuzzy comprehensive evaluation method based on CRITIC and D-AHP combined weighting. Relying on the Niulan’gang Tunnel project, firstly, a tunnel collapse risk assessment index system is established considering factors such as engineering geology, exploration and design, construction management, and the natural environment. Secondly, the D-number theory is introduced to improve the traditional analytic hierarchy process, the CRITIC method is used to objectively weight the evaluation indexes, and the game theory combined weighting is used to optimize the index weights. A normal distribution membership function is constructed, and the weighted average method is used to solve the evaluation matrices of quantitative and qualitative indexes, respectively. Finally, based on the fuzzy comprehensive evaluation method, the risk level can be obtained. The above research provides a useful reference for the collapse risk control of similar tunnel projects.

2. The Index System for Evaluating the Risk of Collapse in Highway Mountain Tunnel and the Standard for Classifying the Levels

2.1. Identification of Risk Assessment Factors of Mountain Tunnel Collapse

By studying the possible risk factors affecting the construction of highway and mountain tunnels, on the basis of consulting the relevant literature [9] and combining with the engineering practice, a tunnel collapse evaluation index system of eight quantitative and qualitative indicators was established, as shown in Figure 1.

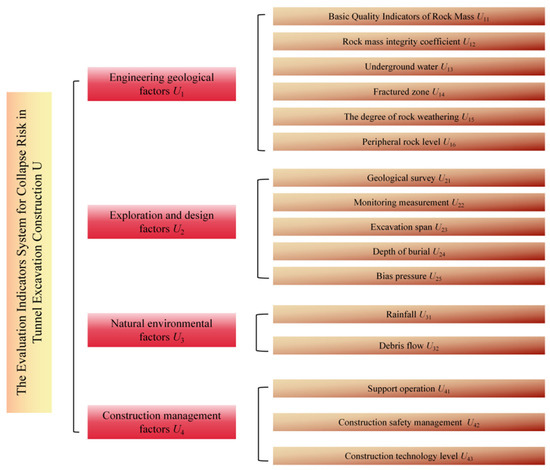
Figure 1. Evaluation index system of tunnel collapse.

2.2. Classification Standard for Risk Collapse of Mountain Tunnels

In order to comprehensively analyze the risk situation of mountain tunnels, this paper obtains categories [10,11,12,13,14] based on the relevant industry standards and the existing research results, as shown in Table 1.

Table 1. Classification criteria of construction collapse assessment index.

Category	Index	Indicator
		Rank 1	Rank 2	Rank 3	Rank 4	Rank 5
Geotechnical geology	Basic quality index of rock mass	>550	451–550	351–450	251–350	<250
	Rock mass integrity coefficient	>0.75	>0.55–0.75	>0.35–0.55	>0.15–0.35	<0.15
	Underground water (m3·d−1·m−1)	<0.15	0.15–0.3	0.3–0.45	0.45–0.6	>0.6
	Fault broken belt/m	<10	10–20	3	4	5
	The degree of rock weathering	1 (Unweathered)	2 (Slightly effloresced)	3 (Medium weathering)	4 (Strong weathering)	5 (Full weathering)
	Surrounding rock level	1, 2	3	4	5	6
Exploration and design	Geological survey	1 (Careful geological survey, data survey is fully complete	2 (The geological survey is more careful, and the data survey is more complete)	3 (Geological survey is general, and data survey is general)	4 (The geological survey is rough, and the data survey is incomplete)	5 (Geological survey is rough, but the data survey is incomplete)
	Monitoring measurement	1 (The measurement frequency is reasonable, the data collected is complete, and the information is timely feedback)	2 (The measurement frequency is reasonable, the data collection is complete, and some timely feedback)	3 (Measurement frequency is general, data collection is general, information feedback is general)	4 (The measurement frequency is low, the data collection intersection is poor, and the information feedback is poor)	5 (Low frequency of measurement, less data collection, and poor information feedback)
	Excavation span/m	<7	7–10	10–12	12–15	>15
	Buried depth/m	>60	40–60	20–40	10–20	<10
	Bias/°	<10	10–20	20–30	30–40	>40
Natural environment	Annual mean precipitation /mm	<400	400–800	800–1200	1200–1600	>1600
	Seismic intensity	<3	3–5	5–7	7–9	9–12
Construction and management	Support operation	1 (Support operation is timely and reasonable, and the parameters and quality meet the design requirements)	2 (The support operation is reasonable, and the parameter quality basically meets the design requirements)	3 (Support operation is general, parameters, quality)	4 (Support operation is unreasonable, and the parameter quality is poor)	5 (Support operation is unreasonable, poor parameter quality, does not meet the design requirements)
	Construction safety management	1 (Strong safety and quality awareness, strict compliance with the construction specifications, and reasonable construction operations)	2 (Strong safety, quality awareness, more compliance with the construction specifications, the construction work is more reasonable)	3 (Safety, quality awareness is general, and the construction operation is general)	4 (Safety and quality awareness is weak, and the construction operation is poor)	5 (Safety and quality awareness is weak, do not comply with the construction specifications, poor construction work)
	Construction technology level	1 (Rich construction experience and good technical level)	2 (Rich construction experience, good technical level)	3 (General construction experience, general technical level)	4 (Less construction experience and poor technical level)	5 (Less construction experience, poor technical level)

3. Theoretical Analysis

3.1. Subjective Empowerment Based on the Improved D-Number Hierarchy Analysis Method

3.1.1. D-Number Theory

Deng first proposed the D-number theory [15], which is extended and extended in DS evidence theory. It has a stronger ability to handle uncertain and incomplete information and has a larger application scope. Therefore, this paper cites the D-number theory in the risk assessment of mountain tunnel collapse.

Definition 1. 

Assume there is a non-empty and finite set Ω, D is its mapping, and D: Ω→[0,1]. This condition meets with having $\sum _{B\subseteq \Omega }D\left(B\right)\le 1$, D($\varnothing$) = 0. Where B is a subset of Ω and is an empty set. If there is $\sum _{B\subseteq \Omega }D\left(B\right)=1$, it means that the information contained in the number of D is complete. If it is not equal to 1, then the information is missing, because D = {($b_1$,$v_1$), ($b_2$,$v_2$),$\dots$, ($b_n$,$v_n$)}. Then the form of its fusion is shown in Formula (1):

$$I(D)={\displaystyle \sum _{i=1}^n}{b}_i{v}_i$$

(1)

Definition 2. 

Assume that the sample $G=\{G_1$, $G_2$,$\dots$, $G_n\}$ for evaluation is to be evaluated. The set of this sample belongs to the set of real numbers (R). The existence of G $\times$ G is manifested in a specific manner and has a relevant nature: ${\mu }_R$: G$\times$G$\to$[0,1]. R = ${\left[r_{ij}\right]}_{n\times n}$is shown in Formula (2):

$$\mathrm{R}=\left[\begin{array}{ccccc}& G_1& G_2& \dots & G_n\\ G_1& r_{11}& r_{12}& \dots & r_{1n}\\ G_2& r_{21}& r_{22}& \dots & r_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ G_n& r_{n1}& r_{n2}& \dots & r_{nn}\end{array}\right]$$

(2)

where $r_{ij}$ is the preference degree of expert $G_i$ compared to $G_j$.

$$R_D{{\mathrm{r}}_{\mathrm{i}\mathrm{j}}=\mathsf{\mu }}_{\mathrm{R}}\left({\mathrm{G}}_{\mathrm{i}},{\mathrm{G}}_{\mathrm{j}}\right)=\left\{\begin{array}{c}0,{\mathrm{G}}_{\mathrm{j}}\mathrm{is}\mathrm{decidedly}\mathrm{more}\mathrm{important}\mathrm{than}{\mathrm{G}}_{\mathrm{i}}\\ \in \left(0,0.5\right){\mathrm{G}}_{\mathrm{j}}\mathrm{is}a\mathrm{little}\mathrm{more}\mathrm{important}\mathrm{than}{\mathrm{G}}_{\mathrm{i}}\\ 0.5,{\mathrm{G}}_{\mathrm{j}}\mathrm{is}\mathrm{equally}\mathrm{important}\mathrm{than}{\mathrm{G}}_{\mathrm{i}}\\ \in \left(0.5,1\right),{\mathrm{G}}_{\mathrm{i}}\mathrm{is}a\mathrm{little}\mathrm{more}\mathrm{important}\mathrm{than}{\mathrm{G}}_{\mathrm{j}}\\ 1,{\mathrm{G}}_{\mathrm{i}}\mathrm{is}\mathrm{decidedly}\mathrm{more}\mathrm{important}\mathrm{than}{\mathrm{G}}_{\mathrm{j}}\end{array}\right.$$

(3)

Definition 3. 

Assume that the assess the set  $G=\{G_1$,$G_2$,$\dots$,$G_n\}$. The D-number preference relationship that exists among them is: $R_D:G\times G\to D$. In matrix form as presented in Formula (4).

$$R_D=\left[\begin{array}{ccccc}& G_1& G_2& \dots & G_n\\ G_1& D_{11}& D_{12}& \dots & D_{1n}\\ G_2& D_{21}& D_{22}& \dots & D_{2n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ G_n& D_{n1}& D_{n2}& \dots & D_{nn}\end{array}\right]$$

(4)

The matrix meets the conditions shown in Formulas (5)–(8):

$$D_{ij}=\left\{\left(b_1^{ij},v_1^{ij}\right),\left(b_2^{ij},v_2^{ij}\right),\cdots ,(b_m^{ij},v_m^{ij})\right\}$$

(5)

$$D_{ji}=\left\{\left(1-b_1^{ij},v_1^{ij}\right),\left(1-b_2^{ij},v_2^{ij}\right),\cdots ,({1-b}_m^{ij},v_m^{ij})\right\}$$

(6)

$$b_k^{ij}\in \left[0,1\right],\forall \mathrm{k}\in \left\{1,2,3,\cdots ,n\right\}$$

(7)

$$D_{ii}=\left\{(0.5,1.0)\right\},\forall i\left\{1,2,3,\cdots ,n\right\}$$

(8)

where  $\forall i,j\in \left\{1,2,3,\cdots ,n\right\}$;  $b_k^{ij}$  is the scoring of the importance level made by expert k regarding the plans i and j; $v_k^{ij}$  is the support degree.

3.1.2. D-AHP Theory

The analytic hierarchy process improved by the D-number theory has the ability to fuse the evaluation information given by each expert into group evaluation and can give full play to its advantages in the uncertainty evaluation environment [16]. The steps of using D-AHP method are as follows:

Step 1: Through expert evaluation, carry out pairwise comparison of the evaluation indicators according to the parameter requirements, construct the preference relation matrix $R_D$, and through fusion to determine the numerical value to obtain the real number matrix $R_C$;

Step 2: Computes the preference probability to obtain the matrix $R_P$;

Step 3: Available by triangulation process $R_P^T$;

Step 4 Transformed the real number matrix $R_C$ and obtained $R_C^T$;

Step 5: Triangulate matrix $R_C$ according to $R_P^T$ matrix, and obtain matrix $R_{c1}^T$;

Step 6: The index weights were calculated from the matrix $R_{c1}^T$.

Inconsistency coefficient test is performed by Formulas (9) and (10):

$${\displaystyle \sum _{i=1}^n}{R}_P^T(i,j)$$

(9)

$$I.D.=\frac{\mathrm{j}<\mathrm{i}}{n(n-1)/2}$$

(10)

where $R_P^T(i,j)$ is the $\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}\mathrm{i}\mathrm{n}$ $R_P^T$, n is the number of risk indicators being compared.

3.2. Objective Empowerment Based on the CRITIC Method

In this paper, considering the differences and correlations among each evaluation index in the text, and in order to improve the rationality of weighting and the accuracy of the decision result, a more scientifically reasonable CRITIC method [16,17] is selected for calculation. The calculation steps are as follows:

(1) Standardized processing. The calculation formula for benefit-type indicators is:

$$y_{ij}=\frac{x_{ij}-{min}_j\left(x_{ij}\right)}{{max}_j\left(x_{ij}\right)-{min}_j\left(x_{ij}\right)}$$

(11)

The calculation formula for the cost-type index is:

$$y_{ij}=\frac{{max}_j\left(x_{ij}\right)-x_{ij}}{{max}_j\left(x_{ij}\right)-{min}_j\left(x_{ij}\right)}$$

(12)

(2) Calculate the correlation coefficient:

$${\rho }_{XY}=\frac{{\displaystyle \sum _{i=1}^n}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\displaystyle \sum _{i=1}^n}{(X_i-\overline{X})}^2}\sqrt{{\displaystyle \sum _{i=1}^n}{(Y_i-\overline{Y})}^2}}$$

(13)

Standard deviation calculation:

$$\sigma =\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{(X_i-\overline{X})}^2}$$

(14)

where $\overline{X}$, $\overline{Y}$ is the average number; n is the number of evaluations of each index.

(3) The information contained in the measurement:

$$E_j={\sigma }_j{\displaystyle \sum _{i=1}^n}(1-{\rho }_{ij})(j=1,2\cdots \mathrm{n})$$

(15)

where ${\displaystyle \sum _{i=1}^n}(1-{\rho }_{ij})$ is the quantified value of the difference between the j index and the other n factors.

(4) Determine the objective weight:

$${\omega }_j=\frac{E_j}{{\displaystyle \sum _{j=1}^m}{E}_j}(j=1,2\cdots \mathrm{n})$$

(16)

3.3. Comprehensive Weight Calculation Based on Game Theory

The calculation method is as follows. Assuming that there is L species in the empowerment method used for the evaluation index, the set of weight vectors constructed is ${\omega }_l=\left\{e_{l1},e_{l2},\cdots e_{lL}\right\},(\mathrm{l}=1,2$,$\cdots \mathrm{L})$. The available linear combination is: $\omega ={\displaystyle \sum _{l=1}^L}{a}_l{\omega }_l^T(a_l>0,{\displaystyle \sum _{l=1}^L}{a}_l=1)$, and $a_l$ is the linear combination coefficient.

$${min‖{\displaystyle \sum _{l=1}^L}{a}_l{\omega }_l^T-{\omega }_l‖}_2(j=1,2\cdots \mathrm{n})$$

(17)

According to the differential properties, the linear equation corresponding to the optimal first derivative of the above equation is:

$$\left[\begin{array}{cccc}{e}_1·e_1^T& e_1·e_2^T& \cdots & e_1·e_L^T\\ e_2·e_1^T& e_2·e_2^T& \cdots & e_2·e_L^T\\ ⋮& ⋮& ⋮& ⋮\\ e_L·e_1^T& e_L·e_2^T& \cdots & e_L·e_L^T\end{array}\right]\times \left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_L\end{array}\right]=\left[\begin{array}{c}{e}_1·e_1^T\\ e_2·e_2^T\\ ⋮\\ e_L·e_L^T\end{array}\right](j=1,2\cdots \mathrm{n})$$

(18)

According to the above equation $(a_1,a_2,\cdots a_L)$, normalized to obtain:

$$a_l^{*}=\frac{\left|a_l\right|}{{\displaystyle \sum _{l=1}^L}\left|a_l\right|}(j=1,2\cdots \mathrm{n})$$

(19)

Finally, the comprehensive weight vector of the evaluation index is obtained:

$${\omega }^{*}={\displaystyle \sum _{l=1}^L}{a}_l^L{\omega }_l^T$$

(20)

3.4. Fuzzy Comprehensive Decision-Making

The fuzzy comprehensive evaluation method [18] refers to the assessment of a target that is influenced by multiple factors simultaneously. By incorporating membership theory, this approach effectively handles fuzzy events and enhances the comprehensiveness of the evaluation process. In particular, applying these methods in engineering practice can lead to significant progress [19]. The flow chart of fuzzy integrated decision-making is shown in Figure 2.

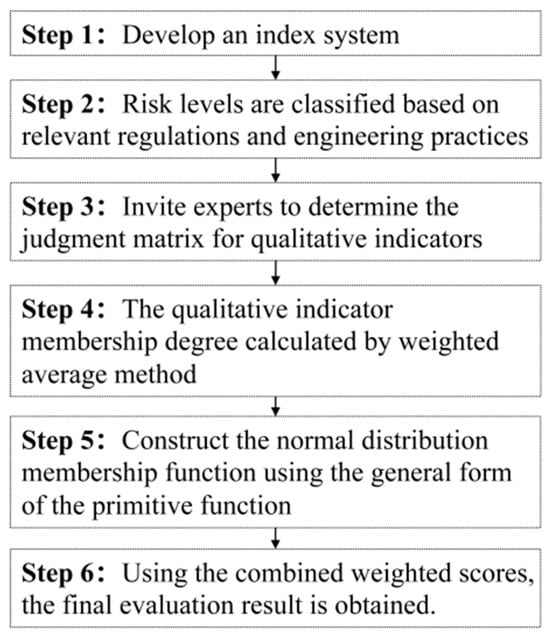
Figure 2. Flow chart of fuzzy integrated decision-making.

(1) Establish primary factor set from the index system: $U=\left\{U_1,U_2,U_3,U_4\right\}$; secondary factor set: $U_1=\left\{u_{11},u_{12},u_{13},u_{14},u_{15},u_{16}\right\}$, $U_2=\left\{u_{21},u_{22},u_{23}\right\}$, $U_3=\left\{u_{31},u_{32},u_{33},u_{34},u_{35}\right\}$, $U_4=\left\{u_{41},u_{42}\right\}$.

(2) According to the risk level classification standard and the supporting engineering examples, the risk is divided into five levels, namely $\mathrm{V}=(v_1,v_2,v_3,v_4,v_5)$, as shown in Table 2.

Table 2. Comments on risk grade.

Rank	Risk Comments
$v_1$	Low risk
$v_2$	Relatively low risk
$v_3$	Medium risk
$v_4$	Relatively high risk
$v_5$	High risk

(3) Invite experts to determine the evaluation matrix of qualitative indicators. The formula is as follows:

$$h_{ij}=(u_{ij}\left(v_1\right),u_{ij}\left(v_2\right),u_{ij}\left(v_3\right),u_{ij}\left(v_4\right),u_{ij}(v_5\left)\right)$$

(21)

where $u_{ij}$ is the evaluation of the index j by the expert i ($1\le \mathrm{i}\le 10$, $1\le \mathrm{j}\le 16$, $1\le \mathrm{s}\le 5$).

The qualitative index membership formula calculated by the weighted mean method is as follows:

$$u_j^{\prime }={\sum }_{i=1}^n{\phi }_i{u}_{ij}\left(v_s\right)/{\sum }_{i=1}^n{\phi }_i$$

(22)

$$h_j^{\prime }=(u_j^{\prime }\left(v_1\right),u_j^{\prime }\left(v_2\right),u_j^{\prime }\left(v_3\right),u_j^{\prime }\left(v_4\right),u_j^{\prime }\left(v_5\right),)$$

(23)

where $u_j^{\prime }\left(v_s\right)$ is the weighted affirmative membership of the s evaluation grade of the j index; ${\phi }_i$ is the weight coefficient of the expert i; n is the number of experts.

The normally distributed membership function is constructed by using the general form of the original function, and the parameter value calculation process is as follows:

$$\mathrm{u}(\mathrm{x})=e^{{-\left[\right(x-x_0)/c]}^2}$$

(24)

$$\mathrm{c}=(f_1-f_2)/1.66$$

(25)

where $x_0$ is the midpoint of the index interval, where a value is 1, u($x_0$) = 1; $f_1,f_2$ is the upper and lower limits of the indicator interval.

(4) Combined with the comprehensive weight of $w^{*}$, the final evaluation results can be obtained as follows:

$$B=w^{*}\times \mathrm{H}=(b_1,b_2,\cdots b_f)$$

(26)

where H is the set of qualitative and quantitative index membership; f is the number of comments.

4. Application Instances

4.1. Project Overview

The Niulan’gang Tunnel is located in the hilly area, and the outcrop of the hillside bedrock is poor. According to the results of field on-site mapping and drilling, the rock mass inside the tunnel is broken, and there are phenomena such as bias pressure and water gushing in the entrance and exit sections. The construction is difficult and is prone to geological disasters such as landslides. The evaluation process of the tunnel is shown in Figure 3.

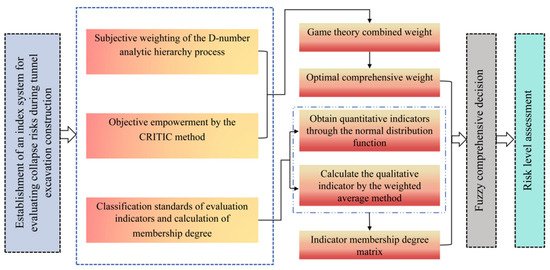
Figure 3. Flow chart of game theory.

4.2. Weight Calculation

Based on the data obtained from the on-site investigation of the project and the explanations provided by the project, this article selects the tunnel entrance section, exit section, and the section of the tunnel body from K242 + 815 to K242 + 875 as the evaluation samples, and the measured data of each evaluation index are shown in Table 3.

Table 3. Measured data of sample evaluation indicators.

Sample Section	Geological Factor ${\mathit{U}}_1$						Design Factors ${\mathit{U}}_2$					Natural Factor ${\mathit{U}}_3$		Construction Factors ${\mathit{U}}_4$
	Basic Quality Indica-tors of Rock Mass ${\mathit{u}}_{11}$	Rock Mass Integrity Coefficient ${\mathit{u}}_{12}$	Underground Water ${\mathit{u}}_{13}$	Fractured Zone ${\mathit{u}}_{14}$	The Degree of Rock Weathering ${\mathit{u}}_{15}$	Peripheral Rock Level ${\mathit{u}}_{16}$	Geological Survey ${\mathit{u}}_{21}$	Monitoring Measurement ${\mathit{u}}_{22}$	Excavation Span ${\mathit{u}}_{23}$	Depth of Burial ${\mathit{u}}_{24}$	Bias Pressure ${\mathit{u}}_{25}$	Rainfall ${\mathit{u}}_{31}$	Debris Flow ${\mathit{u}}_{32}$	Support Operation ${\mathit{u}}_{41}$	Construction Safety Management ${\mathit{u}}_{42}$	Construction Technology Level ${\mathit{u}}_{43}$
The value of the imported section	297	0.49	0.38	32	4	4	4	4	14.75	131	22	1450	3	3	3	2
Tunnel entrance section, exit part and main part of the tunnel (K242 + 815-K242 + 875)	316	0.51	0.37	31	3	4	4	3	14.55	182	23	1530	3	4	4	3
Take the value of the exit section	322	0.56	0.42	34	4	3	3	4	14.75	152	25	1470	4	4	3	4

4.2.1. Subjective Weight Calculation Based on D-AHP

(1) Weight calculation of the first-level indicators

Ten experts comprehensively considered the situation of the selected sample section tunnel, and scored the evaluation indicators and took the average value for calculation. Taking the scoring of the first-level index evaluation as an example, the D-number matrix $R_D$ is obtained as follows:

$$R_D=\left[\begin{array}{cccc}\left\{\right(0.5,1\left)\right\}& \left\{\right(0.7,1\left)\right\}& \left\{\right(0.8,1\left)\right\}& \left\{\right(0.8,0.9\left)\right(0.7,0.1\left)\right\}\\ \left\{\right(0.3,1\left)\right\}& \left\{\right(0.5,1\left)\right\}& \left\{\right(0.7,0.8\left)\right(0.8,0.2\left)\right\}& \left\{\right(0.7,0.8\left)\right\}\\ \left\{\right(0.2,1\left)\right\}& \left\{\right(0.3,0.8\left)\right(0.2,0.2\left)\right\}& \left\{\right(0.5,1\left)\right\}& \left\{\right(0.4,0.8\left)\right\}\\ \left\{\right(0.2,0.9\left)\right(0.3,0.1\left)\right\}& \left\{\right(0.3,0.8\left)\right\}& \left\{\right(0.6,0.8\left)\right\}& \left\{\right(0.5,1\left)\right\}\end{array}\right]$$

The real number matrix is obtained by the fusion matrix $R_C$:

$$R_C=\mathrm{I}\left(R_D\right)=\left[\begin{array}{cccc}0.5& 0.7& 0.8& 0.99\\ 0.3& 0.5& 0.72& 0.56\\ 0.2& 0.28& 0.5& 0.32\\ 0.21& 0.24& 0.48& 0.5\end{array}\right]$$

Transform the real number matrix $R_C$ to obtain the $R_C^T$:

$$R_C^T=\left[\begin{array}{cccc}0.5& 0.7& 0.79& 0.8\\ 0.3& 0.5& 0.56& 0.72\\ 0.21& 0.24& 0.5& 0.48\\ 0.2& 0.28& 0.32& 0.5\end{array}\right]$$

From $R_C^T$, the normalized matrix $R_{c1}^T$ is obtained:

$$R_{c1}^T=\left[\begin{array}{cccc}0.5& 0.7& 0.79& 0.8\\ 0.3& 0.5& 0.66& 0.72\\ 0.21& 0.34& 0.5& 0.58\\ 0.2& 0.28& 0.42& 0.5\end{array}\right]$$

Construction of the system of equations according to the normalized matrix $R_{c1}^T$:

$$\left\{\begin{array}{c}\lambda ({\omega }_1-{\omega }_2)=0.7-0.5\\ \lambda ({\omega }_2-{\omega }_4)=0.66-0.5\\ \lambda ({\omega }_4-{\omega }_3)=0.58-0.5\\ {\omega }_1+{\omega }_2{+\omega }_3+{\omega }_4=1\\ \lambda >0\\ {\omega }_i\ge 0,\forall i\in \{1,2,3,4\}\end{array}\right.$$

Because of the high expert credibility, take $\mathsf{\lambda }=2$ and obtain it by solving the system of equations:

$${\omega }_1=0.375,{\omega }_2=0.275,{\omega }_3=0.155,{\omega }_4=0.195$$

where ${\omega }_1$ is the index weight of geological factors is 0.375; ${\omega }_2$ is the weight of design factor index is 0.275; ${\omega }_2$ is the natural factor index is 0.155; ${\omega }_4$ is the construction factor index is 0.195.

(2) The weight calculation of the secondary evaluation indicators

Similarly, the relative weight of other indicators can be obtained, and the comprehensive weight is calculated, as shown in Table 4.

Table 4. Index weight coefficient.

Target Layer	Firstly Indicators	Weight	Secondary Indicators	Weight	Comprehensive Weight
The evaluation indicators system for collapse risk in tunnel excavation construction	Engineering geological factors $U_1$	0.375	Basic quality index of rock mass $u_{11}$	0.255	0.096
			Rock mass integrity coefficient $u_{12}$	0.045	0.017
			Underground water $u_{13}$	0.335	0.126
			Fractured zone $u_{14}$	0.155	0.058
			The degree of rock weathering $u_{15}$	0.015	0.006
			Peripheral rock level $u_{16}$	0.195	0.073
	Exploration and design factors $U_2$	0.275	Geological survey $u_{21}$	0.114	0.031
			Monitoring measurement $u_{22}$	0.104	0.029
			Excavation span $u_{23}$	0.335	0.092
			Depth of burial $u_{24}$	0.324	0.089
			Bias pressure $u_{25}$	0.123	0.034
	Natural environmental factors $U_3$	0.155	Rainfall $u_{31}$	0.56	0.087
			Debris flow $u_{32}$	0.44	0.068
	Construction management factors $U_4$	0.195	Support operation $u_{41}$	0.362	0.071
			Construction safety management $u_{42}$	0.274	0.053
			Construction technology level $u_{43}$	0.364	0.071

The subjective comprehensive weight of the second-level index is:

$$\begin{array}{cc}& w_1=(0.096,0.017,0.126,0.058,0.006,0.073,0.031,0.029,0.092,0.089,0.034,\\ & 0.087,0.068,0.071,0.053,0.071)\end{array}$$

4.2.2. Objective Weight Calculation Based on the CRITIC Method

(1) For the sample raw data in Table 2, the available normalized matrix P is calculated according to Equations (11) and (12).

$$P=\left(\begin{array}{cccccccccccccccc}0& 0& 0.8& 0.667& 0& 0& 1& 1& 1& 0& 0& 0.5& 0& 1& 1& 1\\ 0.76& 0.286& 1& 1& 1& 0& 0& 0& 0.5& 0& 1& 1& 1& 0.667& 0& 1\\ 1& 1& 0& 0& 0& 1& 0& 1& 0& 1& 0& 0& 0.412& 0& 0.75& 0\end{array}\right)$$

(2) According to Formula (13)–(16), the objective weight of the evaluation indicators can be calculated:

$$\begin{array}{cc}& w_2=\\ & (0.067,0.072,0.052,0.05,0.056,0.077,0.065,0.076,0.055,0.078,0.056,0.056,0.056,0.053,\\ & 0.07,0.062)\end{array}$$

4.2.3. Weight Optimization Using the Game Theory Combined Empowerment Method

According to the above sought subjective and objective weight set can be obtained:

$$\begin{array}{cc}& w_1{w}_1^{{\rm T}}=0.079,w_1{w}_2^{\mathsf{{\rm T}}}=w_2{w}_1^{\mathsf{{\rm T}}}=0.062,w_2{w}_2^{\mathsf{{\rm T}}}=0.064,\mathrm{Solution}\mathrm{by}\\ & \mathrm{formula}:{\mathsf{\alpha }}_1=0.898,{\mathsf{\alpha }}_2=0.13.\end{array}$$

After standardized treatment: ${\mathsf{\alpha }}_1^{*}=0.874,{\mathsf{\alpha }}_2^{*}=0.126$.

The optimal comprehensive weight can be obtained from Formula (20):

$$\begin{array}{cc}& w^{*}=\\ & (0.092,0.024,0.117,0.057,0.012,0.073,0.035,0.035,0.087,0.088,0.037,0.083,0.066,0.069,\\ & 0.055,0.070)\end{array}$$

4.3. Membership Function Determination

The value of the qualitative index mainly relies on the actual situation of the project and is determined by the experts based on the construction status of the Niulan’gang Tunnel, the surveyed data, engineering experience, etc., combined with the expert scoring method and the weighted average value method. From the Formulas (21)–(23), the value of the membership degree of the qualitative index is obtained as shown in Table 5.

Table 5. Summary of membership of qualitative indicators.

Qualitative Indicators	Comments Set
	1	2	3	4	5
The degree of rock weathering $u_{15}$	0	0.204	0.414	0.382	0
Peripheral rock level $u_{16}$	0	0.134	0.583	0.283	0
Geological survey $u_{21}$	0	0.012	0.512	0.476	0
Monitoring measurement $u_{22}$	0	0.133	0.311	0.556	0
Debris flow $u_{32}$	0.102	0.221	0.503	0.174	0
Support operation $u_{41}$	0	0.172	0.593	0.235	0
Construction safety management $u_{42}$	0	0.113	0.503	0.384	0
Construction technology level $u_{43}$	0	0.163	0.242	0.595	0

Quantitative indicators are mainly obtained by constructing the membership degree function. For the eight quantitative indicators such as the basic quality index of the rock mass, the integrity coefficient of the rock mass, groundwater, fractured zone, excavation span, buried depth, bias pressure, and annual average precipitation, the normal distribution function can be constructed to solve them. According to Formulas (24)–(25) and the classification standards, the parameter value $x_0$ and c can be obtained, as shown in Table 6:

Table 6. Parameter values of the membership function of the quantitative index interval.

Category	Basic Quality Index of Rock Mass ${\mathit{u}}_{11}$		Rock Mass Integrity Coefficient ${\mathit{u}}_{12}$		Underground Water ${\mathit{u}}_{13}$		Fractured Zone ${\mathit{u}}_{14}$		Excavation Span ${\mathit{u}}_{23}$		Depth of Burial ${\mathit{u}}_{24}$		Bias Pressure ${\mathit{u}}_{25}$		Rainfall ${\mathit{u}}_{31}$
	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c	${\mathit{x}}_0$	c
Rank 1	825	331.33	1.125	0.45	0.075	0.09	5	6.02	3.5	4.22	140	36.14	5	6.02	200	240.96
Rank 2	500	60.24	0.65	0.12	0.225	0.09	15	6.02	8.5	1.81	50	12.05	15	6.02	600	240.96
Rank 3	400	60.24	0.45	0.12	0.375	0.09	25	6.02	11	1.2	30	12.05	25	6.02	1000	240.96
Rank 4	300	60.24	0.25	0.12	0.525	0.09	35	6.02	13.5	1.81	15	6.02	35	6.02	1400	240.96
Rank 5	125	150.6	0.075	0.09	10.05	0.36	45	24.1	23	9.04	5	6.02	45	24.1	2000	963.86

Taking the sample inlet section as an example with the excavation span, by bringing in 14.75 m into the constructed membership degree function [20], the membership function is obtained as shown in the following formula:

$$u_{\left(1\right)}=\left\{\begin{array}{c}1,x\le 3.5\\ e^{{-\left[\right(x-3.5)/4.22]}^2},3.5\le x\le 7\\ {1-e}^{{-\left[\right(x-3.5)/4.22]}^2},7<x\le 8.5\end{array}\right.$$

(27)

$$u_{\left(2\right)}=\left\{\begin{array}{c}0,x\le 3.5orx\ge 11\\ {1-e}^{{-\left[\right(x-3.5)/4.22]}^2},3.5\le x\le 7\\ e^{{-\left[\right(x-8.5)/1.81]}^2},7\le x\le 10\\ {1-e}^{{-\left[\right(x-11)/1.2]}^2},10\le x\le 11\end{array}\right.$$

(28)

$$u_{\left(3\right)}=\left\{\begin{array}{c}0,x\le 8.5orx\ge 13.5\\ {1-e}^{{-\left[\right(x-8.5)/1.81]}^2},8.5\le x\le 10\\ e^{{-\left[\right(x-11)/1.2]}^2},10\le x\le 12\\ {1-e}^{{-\left[\right(x-13.5)/1.81]}^2},12\le x\le 13.5\end{array}\right.$$

(29)

$$u_{\left(4\right)}=\left\{\begin{array}{c}0,x\le 11orx\ge 23\\ {1-e}^{{-\left[\right(x-11)/1.2]}^2},11\le x\le 12\\ e^{{-\left[\right(x-13.5)/1.81]}^2},12\le x\le 15\\ {1-e}^{{-\left[\right(x-23)/9.04]}^2},15\le x\le 23\end{array}\right.$$

(30)

$$u_{\left(5\right)}=\left\{\begin{array}{c}0,x\le 13.5\\ {1-e}^{{-\left[\right(x-13.5)/1.81]}^2},13.5\le x\le 15\\ e^{{-\left[\right(x-23)/9.04]}^2},15\le x\le 23\\ 1,x>23\end{array}\right.$$

(31)

The available membership is (0,0,0,0.621,0.379), and the membership of the other quantitative indicators are shown in Table 7.

Table 7. Quantitative indicator membership.

Quantitative Indicators	Each Level of Membership
	1	2	3	4	5
Basic quality index of rock mass $u_{11}$	0	0	0	0.271	0.729
Rock mass integrity coefficient $u_{12}$	0	0	0.895	0.105	0
Underground water $u_{13}$	0	0	0.734	0.266	0
Fractured zone $u_{14}$	0	0	0.220	0.780	0
Depth of burial $u_{24}$	1	0	0	0	0
Bias pressure $u_{25}$	0	0.220	0.780	0	0
Rainfall $u_{31}$	0	0	0	0.958	0.042

4.4. Comprehensive Decision-Making

The evaluation matrix is constructed according to the index membership values of Table 5 and Table 7, and combined with the weight value of game theory, the comprehensive risk evaluation result of the tunnel inlet section obtained by Formula (26) is as follows: $W_1=(0.074,0.073,0.372,0.381,0.101)$. According to the principle of maximum membership, the risk level of collapse at the tunnel entrance can be determined to be level 4, that is, the relatively high risk. Similarly, the tunnel body can be calculated as K242 + 815-K242 + 875: $W_2=(0.074,0.063,0.418,0.416,0.030)$. It can be seen that its risk level is more inclined to 3, that is, medium risk.

The evaluation results of the tunnel exit section are as follows: $W_3=(0.074,0.071,0.382,0.438,0.036)$. The risk level is more inclined to level 4, that is, the relatively high risk.

Based on the actual project conditions, the geological complexities at the tunnel entrances and exits, including lateral pressure and water infiltration issues, contribute to a higher construction risk. In contrast, the K242 + 815-K242 + 875 section of the tunnel exhibits relatively simple geology with lower associated risks compared to other sections. Consequently, it can be inferred that the risk assessment results are reliable. The fuzzy comprehensive evaluation method, which combines CRITIC and D-AHP for weighting, offers enhanced convenience and practicality compared to the traditional AHP approach.

5. Discussion

Currently, the risk evaluation methods for mountain tunnels exhibit two main characteristics. Firstly, the traditional and singular approach used to determine the weight of risk evaluation indicators often leads to subjective randomness or unreasonable objective weight coefficients due to a lack of preference information from decision-makers’ experience backgrounds. Secondly, most established evaluation indicators incorporate both qualitative and quantitative aspects without clear differentiation during the evaluation process. The utilization of automated and intelligent machine learning-based evaluation methods is still limited in terms of research and application, while the concept of utilizing multi-source information for risk assessment has started to emerge. Furthermore, dynamic risk assessment heavily relies on real-time monitoring data updates but lacks foresight capabilities.

6. Limitations

At present, the risk assessment methods and theories of tunnel engineering are undergoing a transition stage to a combination of static and dynamic, as well as a combination of qualitative and quantitative; the risk assessment process still relies relatively on the participation of experts and subjective experience, and there is still much room for improvement in objectivity. Among them, the introduction of numerical simulation in risk assessment has great potential. The numerical simulation method is less used in the assessment process of tunnel collapse risk, and there is less research on the collapse risk assessment for specific construction behaviors.

The article did not employ numerical simulation methods in the assessment process of tunnel collapse risk, and no research has been conducted on the collapse risk assessment for specific construction activities. The selection and grading of collapse risk indicators still exhibit significant subjectivity and reliance on experiential characteristics. An in-depth investigation into the collapse mechanism of tunnels represents an effective approach to enhance the objective comprehension of collapses and the objectivity of collapse risk assessment.

7. Conclusions

(1)

Based on the actual construction conditions of the project, this paper comprehensively considers four aspects: engineering geology, exploration and design, construction management, and natural environment, and deeply analyzes the subjective and objective factors that may affect the risk of tunnel collapse. On the basis of fully considering the operability, comprehensiveness, and representativeness of the evaluation index, a scientific evaluation system including 16 secondary indexes for tunnel collapse risk assessment is constructed.

(2)

The subjective weighting by improving the traditional analytic hierarchy process based on the D-number theory can increase the accuracy of the evaluation and reduce the impact of the uncertainty environment on the evaluation result. The objective weighting of the indicators by the CRITIC method can comprehensively consider the correlation and difference between the indicators. Performing the weight combination optimization through the game theory avoids the singleness and absoluteness of the weight calculation method and can also strengthen the rationality of the weight distribution coefficient, making the evaluation result more accurate.

(3)

By combining with the actual data of the project, the risk indicators are distinguished and calculated by using both qualitative and quantitative methods, and the obtained evaluation results have higher accuracy. Through the analysis based on the process example, it can be known that the risk level of each section of the tunnel is between level 3 and level 4, and the overall risk of the tunnel is between medium and higher risk. The evaluation results are consistent with the actual situation of the tunnel, indicating that this evaluation model can be promoted and applied.

(4)

The findings presented in this article can contribute to the identification of potential collapse risks during the tunnel design phase. Moreover, the risk assessment framework employed in this study can effectively guide maintenance schedules and procedures, ensuring that areas with higher risks are subjected to more frequent review and reinforcement. By integrating fuzzy logic and game theory with other analytical methods, more comprehensive risk assessment models for diverse engineering challenges can be developed.

This paper presents novel ideas and methodologies for assessing and predicting the risk of tunnel collapse during construction. However, there is still a significant level of subjectivity and reliance on experience in the selection and grading of collapse risk indicators. Conducting in-depth research on the collapse mechanism of tunnels can enhance our objective understanding of collapses and improve the accuracy of risk assessment. Nevertheless, due to limited available cases for tunnel collapse risk assessment, establishing a comprehensive public database becomes challenging, thereby hindering accurate evaluation by intelligent models that consider various features. Therefore, future research should focus on developing dynamic collapse risk assessments based on intelligent algorithms.