Featured Application
Design and implementation of structural health monitoring systems for bridges.
Abstract
Currently, there is a growing concern about the conservation and maintenance of infrastructure. Within this context, bridges deserve special attention, given their technical complexity and strategic nature. To this end, modern technology provides the opportunity to implement systems for structural health monitoring (SHM), a field in which great advances have been made in recent years. In this sense, one of the fastest-growing lines of work in Civil Engineering is the early detection of incidents because of changes in the dynamic behaviour of structures. Throughout this paper, some of the most notable considerations that the authors have been appreciating in the latest structures studied are summarized. These may be of interest for the possible incorporation of dynamic parameters in SHM systems that could be implemented in other structures in the future. With this purpose, a review of the different issues that must be studied within the dynamic analysis of a structure is carried out, such as the structural typology, the type of instrumentation, the recorded accelerations, the analysis of the natural frequencies, the study of the modal damping ratio and the set of thresholds; issues that are also accompanied by examples observed in two real monitored structures.
1. Introduction
In most developed countries, there is a growing concern regarding the conservation and maintenance of already built and in-service infrastructures, which society needs to meet the increasing demands of transportation and which millions of citizens use every day. In the case of linear infrastructures, there is no doubt about the critical nature of bridges, whose technical complexity is accompanied by a clear strategic role within communications systems, on which territorial connectivity may depend and, hence, its importance. Two recent tragedies that have affected bridges in service serve as an example: the fall of the Morandi Bridge in Italy in 2018, which left 43 dead, and the collapse of line 12 of the Mexico City Metro in 2021, with 25 deaths [1,2].
Within the context of the United Nations Sustainable Development Goals [3] in the world community, which include the construction of resilient infrastructure, promoting sustainable industrialization, and fostering innovation, the changes that have occurred in recent years in technology, including the Internet of Things and big data, represent a true revolution in the field of structural health monitoring systems (hereinafter, SHM) of infrastructure.
Several publications have studied SHM systems in-depth, especially in recent years. Among the most relevant, these can be highlighted: Deraemaeker et al. on vibration-based SHM methodology using output-only measurements under changing environments [4]; Gomez et al. on the testing and long-term monitoring of a curved concrete box girder bridge in California (United States) [5]; Cross et al. on the long-term monitoring and data analysis of the Tamar Bridge (United Kingdom) [6]; and the comprehensive review about operational modal analysis in bridges conducted recently by Hasani and Freddi [7].
Regarding the introduction of new technologies in SHM systems, the current panorama is in continuous evolution and fields of work that until now were unthinkable are opening. Thus, for example, a number of recent publications may be mentioned: Han et al. about the introduction of nanosensors [8]; Dong, Bas, and Catbas or Bai et al. in relation to the use of systems based on computer vision to monitor the behaviour of bridges, even long spans [9,10]; Xu et al. on the methodology for identifying damage in spacecraft from measurements made on optical fibre [11]; Ramón–Zamora et al. in the field of evaluation of reinforcement corrosion in concrete structures by means of embedded sensors [12]; Jia and Li on the introduction of tools based on deep learning [13]; and Biondi et al. on the application of synthetic aperture radars [14].
Undoubtedly, the early detection of incidents because of changes in the dynamic behaviour of structures is an emerging line of study in civil engineering, as is also happening in other areas of technology. However, bridges are not repetitive constructions since each structure responds to the specific needs of the environment in which it is located, such as topography, geology, or the required functionality.
Furthermore, among the problems that we encounter today are the excess of data obtained in the instrumentation, which must be analysed, interpreted, and selected to have a true image of the situation of the monitored structure, the relative lack of academic studies on real monitored structures in service, and the uncertainty about both the influence of environmental variables and the calculation methodology used in the case of the modal damping factor to propose systems that monitor the status of the structures.
This paper highlights some considerations that the authors have appreciated in the latest structures studied that may be of interest for the possible incorporation of dynamic parameters in SHM systems that could be implemented in other structures in the future.
It must be noted that this paper is only focused on the incorporation and analysis of the dynamic parameters in SHM systems, so the appropriate design and implementation of the whole SHM system of bridges (devices, wiring, connections, etc.) is out of the scope.
2. Some References of Interest about the Dynamic Monitoring of Structures
This section presents the most relevant background information within the state-of-the-art related to the dynamic monitoring of structures that have been published in recent years and are the starting point for the preparation of this paper.
The addressed references have been extracted from papers focused on the dynamic behaviour of bridges, from which the knowledge has evolved over time and which has given rise to the current understanding of the phenomena, synthesising the main characteristics of the topic.
As an introductory summary of the issue, it can be said that there are several relevant references where the dynamic behaviour of real structures in terms of natural frequencies is analysed; a smaller group of studies take into account not only eigenfrequencies but also damping and just a few references where the dynamic behaviour of damaged structures is studied. In global terms, it must be noted that there is an important lack of academic studies about the dynamic behaviour of real structures, so any effort to increase the knowledge in this sense is welcomed by Civil Engineering.
In detail, the studies carried out on the monitoring of the Europe Bridge [15] in Austria should be cited, where a certain correlation was observed between the first natural frequency and the ambient temperature. Likewise, it was necessary to compensate for the additional moving masses. The introduction of both corrections allowed for obtaining reasonably stable values of the first natural frequency of the structure and, therefore, to establish thresholds that could be used in an SHM system.
In the same sense, Magalhães, Cunha, and Caetano carried out various studies on the dynamic monitoring of the Infante Don Enrique Bridge in Porto (Portugal) [16,17,18], where they studied the evolution over time of the modal parameters under the influence of environmental effects. In these papers, a model is proposed to correct the natural frequencies based on several variables, among which are the temperature and the recorded accelerations, which made it possible to establish a threshold to implement an SHM system, even despite the small variations detected.
The work carried out by Gentile and Saisi on the evolution over time of the dynamic behaviour of the Paderno Bridge in Italy [19], in this case, a historic bridge, should also be mentioned. The study showed that small variations over time in the natural frequencies occured, which were attributed to changes in excitation.
Along these same lines, Soria, Díaz, García-Palacios, and Ibán studied the dynamic behaviour of a pedestrian walkway in Valladolid (Spain) [20,21]. In this work, the great dependence of the modal parameters on temperature was confirmed and that, once corrected, they could be taken as a reference in an SHM system.
On the other hand, Astiz also studied the dynamic behaviour of the stay cables of the Waterford Bridge in Ireland. In that case, it was concluded that the maximum accelerations in the cables were not produced by traffic, but by wind, and that it was not a resonant phenomenon that occurred at a specific speed but that the accelerations were an increasing function of wind speed, so they seemed to be motivated by wind buffeting, although vortex shedding was also considered as a possible cause [22].
More recently, Tan et al. published their conclusions on the implementation of an SHM system on a cable-stayed bridge, in which they studied its dynamic behaviour and were able to establish thresholds after applying corrections for the effect of temperature [23].
More particularly, in relation to the possible identification of damage through changes in the dynamic behaviour of structures, the scale test carried out by Kölling, Resnik, and Sargsyan [24] is of great interest. In this test, new dominant natural frequencies appear in the damaged structure, as well as a reduction in the value of the main natural frequency (from 4.1 Hz to 4.0 Hz, 2.4% less). Likewise, as far as the damping factor is concerned, in forced vibration tests, there is a notable increase in damping, between 50 and 100% of its value. However, in environmental vibration tests, reductions between 10 and 20% were found.
Another interesting reference is the one cited by Wenzel in relation to the Regau Bridge in Austria [15]. In the analysis of the behaviour of the damaged structure, important variations were observed both in the frequency amplitude, which became 28% less, and in the damping, which increased by 85%.
Finally, in relation to the problems that arise in practice when calculating the modal damping ratio, the studies carried out on the Berlin Bridge in Halle can be cited [15]. They reveal the behaviour of cable-stayed bridges, in which a significant overlap can occur between the natural frequencies and, therefore, complicate these calculations. In addition, the disparity of the results can also be seen depending on the calculation method used, in this case, the logarithmic decrement, the theoretical curve adjustment, and the random decrement technique method (RDT).
Likewise, in the case of the Regau Bridge, previously referenced, discrepancies were evident in the calculations of the modal damping ratio when the bandwidth method was used on the signal spectrum and depending on the filter that was used over the recorded accelerogram.
3. Materials and Methods
This section includes the details of the two real structures that were studied, including the monitoring that was carried out after opening to traffic, and that serve to exemplify the analysed issues, as well as the general description of the parameters under study.
3.1. E-1 Structure
The first of the structures is the viaduct over the Tagus River called “Arcos de Alconétar”, which from now on will be designated as the E-1 structure (Figure 1). This viaduct is located within the itinerary of Highway A-66, belonging to the State Road Network in Spain [25,26,27].

Figure 1.
Viaduct “Arcos de Alconétar” (E-1 structure) (Mitma).
This structure is composed of two twin structures 400 m in length, whose main spans are metal arches (spans of 220 m and 42.5 m rise) with an upper deck. Each of the arches is formed by two longitudinal pieces with a box section braced together. The deck, formed from a continuous section of composite steel–concrete structure, is simply supported on the metal pillars that rest on the arch and the reinforced concrete piers belonging to the access sections. The length of the spans, 26 m, is identical both in the access sections and in the main section. The steel used in the whole structure (arches, deck beams, and pillars on arches) is a weathering steel with improved resistance to atmospheric corrosion.
The dynamic instrumentation of the structure was made up of 10 accelerometers (5 force feedback capacitive accelerometers, with a resolution of 1.3 × 10−6 g at frequencies lower than 10 Hz, installed on each road), 2 anemometers and 2 wind vanes (on the left road). These accelerometers were located on each roadway as follows: three vertical accelerometers in the haunches of the arch (two in the south haunch and one in the north haunch) and two accelerometers in the key of the arch, one of them vertical and the other transversal. In all cases, they were inside the arch box, on the lower side. The instrumentation was completed with a total of 37 thermometers and 2 laser distance meters to measure the movement of the expansion joints of the structure. The monitoring period in which there are dynamic records is between the months of March and September 2010. The range of ambient temperature recorded throughout this period was between 10 and 40 °C, which allowed us to detect its influence over dynamic parameters, as explained in the following sections.
The behaviour of the E-1 structure was studied in different technical papers due to the particularities of the construction system of the bridge and the technical incidents that occurred during its execution, especially regarding the vortex shedding phenomenon (von Karman vortices), which caused a resonance phenomenon [28,29,30,31,32].
3.2. E-2 Structure
The second of the structures is the viaduct “Arroyo del Valle” (Figure 2), which will be designated as the E-2 structure for the rest of the paper. This viaduct is part of the Madrid–Segovia–Valladolid/Medina del Campo high-speed railway line, also in Spain, which opened to traffic at the end of 2007 [33,34,35].

Figure 2.
Viaduct “Arroyo del Valle” (E-2 structure) (Adif-AV, Mitma).
The total length of the viaduct is 1755 m, divided into 2 extreme spans of 52.50 m and 25 intermediate spans of 66.00 m each. It is made up of a concrete box beam with a hollow trough-type cross-section with a lower and upper slab and a variable depth between 3.30 m in the centre of the span and 5.00 m in the pier support area. There are a total of 25 piers, with a hollow rectangular concrete box section. In addition, there is an ogival-type arch in the central area of the viaduct, formed by two semi-arches with a radius of curvature of 312.00 m and a hollow rectangular concrete box section so that the key of the arch materializes the fixed point of the structure, and both ends remain free.
The instrumentation that was implemented in the viaduct made it possible to control the following variables: pier movements, relative movements of pier/abutment–deck, accelerations due to centrifugal force and braking, vertical accelerations, wind speeds (gusts), train speeds, temperatures, and environmental conditions. For the study of dynamic behaviour, there were 15 accelerometers (accelerometers installed in structure E-2 were precision capacitive accelerometers, with a resolution of 30 × 10−6 g at frequencies lower than 100 Hz), 12 of which were vertical, 2 longitudinal, and 1 transversal. All these devices were inside the box section, either on the central axis or the lateral extremes, but in all cases, on the lower side. The structure was monitored between the months of June 2008 and December 2009 [36,37]. The range of temperatures recorded throughout this period was between 4 and 29 °C.
3.3. Parameters under Study
According to the general theory of Dynamics of Structures, as described by Chopra [38] or Clough and Penzien [39], the behaviour of these bridges has been analysed by means of the study of the following dynamic parameters:
- Accelerations, registered in the experimental accelerograms;
- Eigenfrequencies, obtained by the analysis of the accelerograms in the frequency domain and modes of vibration associated with these natural frequencies;
- Modal damping ratios calculated from the accelerograms after filtering in the neighbourhood of the eigenfrequencies.
These parameters were complemented with the records of environmental conditions, such as temperature and wind, for each dynamic event.
4. Results
During the period of time indicated previously, the monitoring of these structures provided, in the case of structure E-1, a total number of 541 registered events, which were selected in order to both be equally distributed along the research and include extreme values of measured accelerations and wind velocity, arising to 41 representative events (7.6%). In structure E-2, the monitoring was activated one day per month during the research period, providing 218 registered events. In this case, 16 events were selected (7.3%), one per each completed monitored day.
As it was mentioned in the previous subsection, from events information, accelerograms were studied in the frequency domain in order to obtain eigenfrequencies. Moreover, after filtering the signals around each natural frequency, values of the modal damping ratio were obtained using the logarithmic decrement method. All these numerical results were collected, together with the environmental conditions, into a database.
Nevertheless, this paper is intentionally focused on the qualitative aspects of the dynamic behaviour of these structures rather than the quantitative details, which are part of other previously referred publications.
5. Discussion
The qualitative study of the numerical results raises the discussion about the following aspects: structural typology, type of instrumentation, accelerations, natural frequencies and vibration modes, damping, and thresholds, which are detailed below.
5.1. About the Structural Typology
The first question that must be reflected on before considering the incorporation of dynamic parameters in an SHM system for bridges is whether the structural typology is appropriate for this or not.
This is because, to determine with certain precision the natural frequencies and modal damping ratios, accelerograms of a certain duration are required.
Regarding natural frequencies, according to the Nyquist-Shannon Sampling Theorem, a higher sampling rate allows a wider range of frequencies to be covered. However, in the case of bridges, their importance is relative since the values of their natural frequencies are usually low, so the areas of greatest interest for study are usually between 0 and 10 Hz. Therefore, attending strictly to this issue, a sampling frequency of 20 Hz (data every 0.05 s) could be enough. On the contrary, what is of greatest interest is that this frequency range is defined with the greatest possible precision, which is the result of having accelerograms of a certain length. For example, an accelerogram of 50 s duration would allow the study frequency range to be analysed with a discretization of 0.02 Hz; while one of 5 s duration would only achieve a discretization of 0.2 Hz.
In the case of the modal damping ratio, something similar happens. The most common situation is that available accelerograms correspond to specific events. In these circumstances, to determine the modal damping ratio, the free vibration sections must be located. Therefore, the longer the duration of the free vibration sections within the accelerogram, the greater certainty in the calculation of the modal damping ratio.
Therefore, if the modal damping ratio of the structure is lower, the recorded accelerograms will be more appropriate. In other words, a priori, compared to structures where concrete is the predominant construction material, metallic and composite structures would be more suitable for the implementation of SHM systems that incorporate dynamic parameters.
As an example, Figure 3a,b includes, respectively, two accelerograms corresponding to the E-1 and E-2 structures. As can be seen, the first accelerogram has a length in free vibration regime much greater than the second, practically its entire length, about 55 s in the first case compared to barely 2 s in the second case, between t = 40 and t = 42 s, which allows the dynamic parameters to be determined with much greater precision in the E-1 structure. Furthermore, all this, regardless of the fact that in absolute value, the accelerations recorded in the first structure are lower, of the order of a tenth (maxima of 0.010 g in E-1 compared to 0.10 g in E-2).
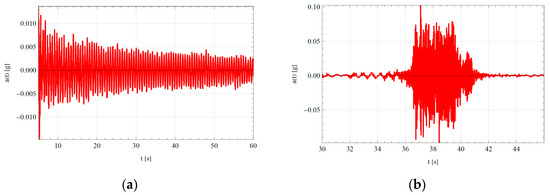
Figure 3.
Examples of real recorded accelerograms: (a) E-1 structure; (b) E-2 structure.
5.2. About the Type of Instrumentation
In order to have a greater knowledge of the structure to be studied and to allow the adequate implementation of an SHM system, the advantages of having continuous instrumentation compared to a discontinuous one are clear [4,5,6,7]. Furthermore, as indicated in the introduction, new technologies offer great possibilities that have yet to be explored [8,9,10,11,12,13,14].
However, excessive instrumentation, which generates a large amount of information but whose data have no practical interest in the installed bridge SHM system, should also be avoided. In that case, the investment made in the system would not be useful. Technical professionals with knowledge and experience must plan in advance which instrumentation is necessary for the desired objective.
Therefore, a balanced situation must be reached so that the instrumentation installed in the structures is truly useful for the projected SHM system at a reasonable cost.
5.3. About the Analysis of the Accelerations
It is also interesting to analyse the values of the recorded accelerations. It is desirable to be able to compare the experimental values both with the values obtained with the computational model and with those prescribed by the applicable structural code.
Regarding the comparison with the values of the computational model, for the excitations due to the passage of vehicles, in the case of railway viaducts, it may be simpler, given that the loads of each train and circulation speeds can be known very approximately. In the case of road bridges, this is more complicated since, a priori, the configuration of the vehicles that produces the excitation, their weight, or the speeds of circulation are not known, which has a great influence on the values.
As an example, Figure 4 shows the relationship between the maximum vertical accelerations in the different sections of the arch of the E-1 structure and the circulation speed under the hypothesis that the excitation is due exclusively to a heavy vehicle circulating with the maximum authorized mass (440 kN) and without concomitant wind. It must be emphasized that the monitoring range of accelerations must be wide enough to detect all possible cases. In this example, it can be seen that, even with small changes in speed, for example, between 60 and 70 km/h, the variation in accelerations can be very relevant, of the order of three times. However, these differences are higher if wider speed intervals are compared.
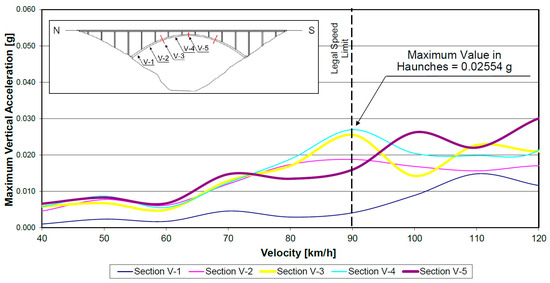
Figure 4.
Influence of the circulation speed on the maximum vertical accelerations obtained with the computational model of the E-1 structure.
5.4. About the Analysis of the Natural Frequencies and Vibration Modes
5.4.1. Study of the Available Background Information: Computational Models and Load Test
As a prior stage to carrying out the analysis of the vibration frequencies, a study of the available background information must be undertaken, particularly of the structure computational model and the load test.
The computational model of the structure provides very relevant information: the natural frequencies and vibration modes of the structure. Therefore, an attempt should be made to find the correspondence between each of the recorded events with the theoretical vibration frequencies and, if feasible, also with those obtained during the load test. Thus, for example, when the analysis of the E-1 structure was carried out, a very acceptable correspondence was observed.
However, on other occasions, this analysis is not so immediate, and a further step should be taken. This can happen in the case of concrete structures, where the moving load may not be enough to excite the structure as a whole or do so to a lesser extent. Therefore, the possibility of the spans being excited independently should not be ignored, even with the same frequency of passage of the moving load.
An example of this is indicated in Figure 5, corresponding to a dynamic event recorded in the E-2 structure (event recorded on 13 August 2008 at 2:46 p.m., selected channel AV011, vertical accelerometer installed in the centre of the first span of the viaduct). The spectrum shows its highest peak around 3.4 Hz. However, in this structure, the first vibration modes are between 1.36 and 1.77 Hz (from vibration mode number 1 to number 8, respectively), an area where several peaks of the spectrum would occur but very far from the highest peak. Indeed, a possible explanation would have to be sought in moving loads. The train that caused this event was, according to the information available, a type S-102 train traveling at 141.85 km/h. Taking into account the characteristics of the composition of this train, the dynamic load would have a frequency spectrum with a peak in the vicinity of 3.1 Hz. Likewise, based on the computational model, this first span of the viaduct vibrating independently would have a natural frequency between 2.8 Hz (supposed simple support at both ends, which obviously does not happen) and 4.2 Hz (supposed simple support at one end and perfect embedment at the other, which is the theoretical behaviour). However, with the information available, it is not feasible to specify at what point the span would behave as perfectly supported-embedded and how much mass would be really mobilized in the dynamic event so it can explain the displacement of the natural frequency from 4.2 Hz to the vicinity of 3.1 Hz.
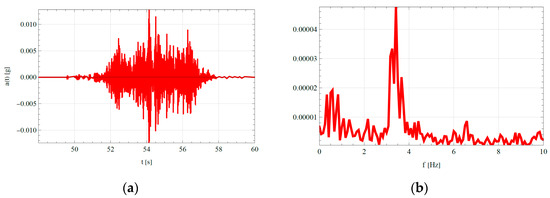
Figure 5.
Analysis of the natural frequencies in an event of the E-2 structure, accelerometer AV011: (a) Accelerogram; (b) Spectrum.
5.4.2. Possible Correction of Values
Another issue already noted by some authors, as indicated in Section 2, is the variation in the values obtained for the natural frequencies and, consequently, the possible need to correct them to implement an SHM system, given that the mentioned variations may not be negligible and would give rise to false positives.
Indeed, the referenced studies state that the values of the natural frequencies can be affected by temperature and that they can also be correlated with the maximum accelerations recorded since it is an indirect measure of the load that is supporting the structure and, therefore, of the internal mechanisms that are activated in the materials to resist such actions.
In the case of the E-1 structure, an in-depth study was carried out on the influence of several variables: the arch temperature, the ambient temperature, the average wind, and the maximum accelerations, both vertical and transversal. Regarding the role of temperature, the analysis of individual correlations showed a greater correlation in the case of ambient temperature and not for the arch temperature. In the case of the average wind, no correlation was observed, and in the case of maximum accelerations, it was seen that there was a certain correlation in both the vertical and transverse cases, although they were manifested to a greater or lesser extent depending on the vibration modes. These results were in coherence with the behaviour suggested by other authors in the case of various bridges [15,16,17,18,20,21,22,23].
Consequently, a model that took into consideration the ambient temperature and the maximum accelerations, both vertical and transverse, was proposed. It allowed achieving correlations with a coefficient of determination (R2) of up to a value of 0.90 in the case of the natural frequency fexp 6, as shown in Figure 6, where the relationship with the ambient temperature is represented, as it is the variable that, independently, had a greater correlation.

Figure 6.
Multiple correlation model for natural vibration frequencies.
5.5. About the Analysis of the Modal Damping Ratio
5.5.1. Study of the Modal Damping Ratio Values
In contrast to what was indicated in the previous section, the values of the modal damping ratio show greater variability between some events and others, as Wenzel suggested for other bridges [15]. Therefore, with few tests, it is difficult to specify this variable, recommending a study over time. Likewise, it is interesting to reference these values with those of other structures of similar typology.
5.5.2. Possible Correction of Values
If the results are precise, as happened in the E-1 structure, it is also advisable to study the possible correlation of the damping factor with other variables in an analogous manner to the case of natural frequencies. However, in this case, the conclusions are not so obvious or immediate.
As an example, the in-depth analysis of the case of the E-1 structure showed the following [28]:
- Although, a priori, the mechanical properties of the materials could vary depending on the temperature, in the E-1 structure, no relationship was observed between the variations recorded in the modal damping ratio neither with the ambient temperature nor the arch temperature.
- On the other hand, some correspondence was seen (coefficients of determination R2 of the order of 0.20 and 0.30) in the case of two of the natural frequencies and the average wind speed. The justification for this fact may be that the modal damping ratio has an aerodynamic component, although this contribution is usually very small.
- Finally, the relationship with the maximum vertical and transverse accelerations was also analysed since it is a measure of the degree of excitation of the structure. However, in this case, no clear relationships were obtained.
As can be seen, although the conclusions are not as clear as with the natural frequencies, the possibility that there may be relationships between the damping factor and environmental variables should not be ignored in order to implement SHM systems. Therefore, it would be desirable to study in each case if there is a relationship between damping and environmental parameters.
5.5.3. About the Calculation Method of the Modal Damping Ratio
Another relevant issue is knowing which calculation method is used to determine the modal damping ratio and maintaining the same criterion throughout the monitoring period.
As is well known, there are multiple calculation methods that can be classified according to whether they require controlling the excitation or not and, within the latter, whether they are applicable to specific events or to continuous records.
The methods of amplification at resonance, of the bandwidth on the amplitude-frequency curve, and of the energy loss per cycle at resonance are among the calculation methods that are required to control the excitation. However, these three methods are complex to apply on real structures because they require the performance of a test whose implementation is not easy on structures in service since they require stopping the traffic and precisely controlling the excitation source, and lastly, but possibly most important, exciting the structure with frequencies close to the resonance frequency, which poses the serious possibility of causing structural damage.
On the contrary, calculation methods that do not require controlling the excitation, that is, those that study ambient vibrations, avoid the problems indicated above. Within this set, among those that are applicable to records of specific dynamic events, we can mention the logarithmic decrement method, the bandwidth method over the signal spectrum with its two possible formulations (half-power and half-quadratic gain), and the adjustment to the theoretical curve. Likewise, among the methods that are applicable to continuous records, we can mention the random decrement technique (RDT) and the stochastic subspace identification (SSI).
However, for the same dynamic event, the results of the modal damping ratio obtained by applying the different calculation methods can be very different. As an example, Figure 7 shows an accelerogram corresponding to a specific dynamic event of the E-1 structure (event recorded on 20 August 2010 at 7:55 p.m., selected channel C-5, corresponding to the vertical accelerometer installed in the haunch of the arch, fexp 5 = 1.675 Hz), its study in the frequency domain, the filtered wave, and the values of the modal damping ratio obtained as a result of applying different calculation methods. As can be seen, there is an important variation in the results, which in this case ranges from the 0.18% value obtained through the methods of logarithmic decrement, adjustment to the theoretical curve, and the RDT combined with the logarithmic decrement, to the value of 0.30% obtained through the RDT method combined with curve fitting. Therefore, in SHM systems, it is essential to know which modal damping ratio calculation method has been used and to maintain the same criterion throughout the monitoring period.
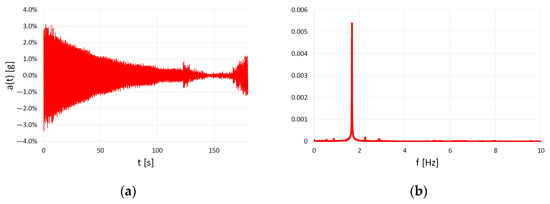
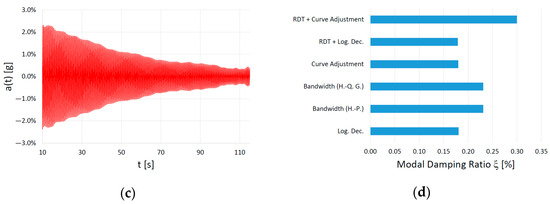
Figure 7.
Calculation of the modal damping ratio in a dynamic event of the E-1 structure: (a) Registered accelerogram; (b) Spectrum; (c) Filtered accelerogram; (d) Modal damping ratios obtained by applying different calculation methods.
In line with what is indicated in the preceding paragraphs, the authors are finalizing a specific study, both theoretical and experimental, where the possibility of introducing improvements in calculation methodologies is also assessed [40].
5.5.4. Relationship between Modal Damping Ratios and Natural Frequencies
To conclude this review of the issues related to the dynamic behaviour of the structures that should be studied, another relevant element is the analysis of the possible relationship between the recorded modal damping ratios and the natural frequencies.
In this sense, it is of interest to check whether the experimental data obtained fit the hypothesis proposed by Rayleigh or not [38,39]. If damping is supposed to be proportional to the mass and stiffness matrices of the structure, the following expression for the i-th modal damping ratio of the system can be derived:
where and are the proportionality parameters.
Based on the N experimental data of natural frequencies and associated modal damping ratios, the best possible adjustment would be the one that minimizes the sum of the squared differences between the estimated modal damping factors and those measured experimentally. This is equivalent to optimizing the following function:
The condition of the best adjustment to minimize the function G is that the partial derivatives with respect to each of the parameters are null. Thus, combining the two previous expressions, we have:
Solving the system of equations, we arrive at:
These expressions may be directly applied to the experimental data.
As an example, if this formulation is applied to the data obtained after the field tests of the E-1 structure, coefficients α0 = 0.02272472 and α1 = 0.00020197 result. The recorded modal damping factors (green points), their average values (blue points), and the adjustment obtained by applying the formulation indicated in this section (orange curve) have been represented in Figure 8. It can be seen how the values obtained with the instrumentation reasonably adjust in this case to the Rayleigh hypothesis.

Figure 8.
Example of the study of the relationship between natural frequencies and modal damping ratio under the Rayleigh hypothesis in structure E-1.
Since accelerograms in E-2 are extremely short, as mentioned above, the results for the modal damping ratio are not as clear as in E-1, so it was not possible to carry out a similar study.
5.6. About the Set of Thresholds
Last, but not least, some considerations must be indicated about the set of thresholds. Indeed, this is certainly the decisive issue if an SHM system is going to be installed, in other words, if it will be really capable of the early detection of damages.
In the opinion of the authors, as well as other cited references, natural frequencies, once corrected by ambient variables and statistically analysed, can be adopted for setting thresholds. However, it must be pointed out once more that in steel and composite structures, values can be more precisely calculated than in concrete structures. This is because of the fact that damping is higher in these last cases, so accelerograms have a shorter extension and, in consequence, frequencies have a lower resolution.
On the other hand, the set of thresholds based on damping values is a promising issue because it is a parameter that can reflect damage in structures in a more sensitive way, particularly in bridges. However, nowadays, two main aspects must be solved. First is the great dispersion in measurements, even under the same environmental conditions; therefore, further studies must be carried out, both in scale tests and in real structures. Second is the great dependence of these values on the calculation method. Therefore, it is important to clarify how these methods affect the results and if some improvements are possible.
6. Possible Future Lines of Research
As a consequence of the studies carried out by the authors, several possible future lines of research are proposed:
- Firstly, the extension of this type of study to other real bridges with more actual results, which analyse the dynamics of structures of different typologies, given that, although there are more and more studies in the field of SHM systems, there are relatively few that relate the behaviour of real structures.
- Likewise, due to the enormous influence that the calculation method adopted can have on the values of the modal damping ratio, an in-depth study must be carried out on this issue, both on a theoretical and experimental level, which also analyses the possibility of introducing improvements in the mentioned procedures.
- Thirdly, it is necessary to explore the physical modelling of the correlations observed during the experimental analysis, especially in the case of the variation of the natural frequencies as a function of the ambient temperature, as well as the damping factor for certain natural frequencies as a function of the average wind speed.
- Fourth and last, more studies should be carried out on the variation in dynamic parameters as a consequence of specific damage having occurred, both through computational models, which will allow analysing of the behaviour, especially in terms of frequencies, and in scale tests, which will make it possible to see the behaviour both in terms of frequencies and the modal damping ratio.
7. Conclusions
Throughout this paper, some of the most relevant considerations that the authors have found in the different studies that they are carrying out on the incorporation of dynamic parameters in SHM systems have been jointly revealed.
To this end, after a review of the main technical references, the main issues analysed are the structural typology, the type of instrumentation, the accelerations, the natural frequencies, with special attention to the possible correction of the registered values, and the modal damping ratio, including an important reflection on calculation methods.
Furthermore, this general overview of bridge monitoring has been accompanied by various practical examples corresponding to two real viaducts: one road, whose main span is a long-span metal arch, and a railway, corresponding to a continuous prestressed concrete girder.
As a consequence of all the above, as happens in other areas of engineering, the potential of incorporating dynamic parameters in SHM systems in the case of bridges has been confirmed.
Nevertheless, the suitability of the structure where the dynamic SHM system should be installed, the possibility of having continuous registers or not, the analysis of the accelerations and its comparison both with the computational model and those prescribed by structural codes, the study of natural frequencies and vibration modes and its high dependence on ambient variables, not only the ambient temperature, but also maximum accelerations, the analysis of modal damping ratios, whose values can considerably vary, in some cases related with ambient variables also, such wind and maximum accelerations, and which are enormously influenced by the applied calculation method, and the considerations about setting thresholds, are altogether essential issues that must be considered, as they have been addressed in this paper.
Finally, the article ends with the proposal of several possible lines of future research oriented toward expanding the typologies of structures studied, detailed analysis of modal damping ratio calculation methods, exploring the physical modelling of the observed correlations, and carrying out more studies on the dynamic behaviour of damaged structures.
Author Contributions
Conceptualization, J.-A.L.-A. and M.-Á.A.; Methodology, J.-A.L.-A. and M.-Á.A.; Software, J.-A.L.-A. and M.-Á.A.; Validation, J.-A.L.-A. and M.-Á.A.; Formal analysis, J.-A.L.-A. and M.-Á.A.; Investigation, J.-A.L.-A. and M.-Á.A.; Resources, J.-A.L.-A. and M.-Á.A.; Data curation, J.-A.L.-A. and M.-Á.A.; Writing–original draft, J.-A.L.-A. and M.-Á.A.; Writing–review & editing, J.-A.L.-A. and M.-Á.A.; Visualization, J.-A.L.-A. and M.-Á.A.; Supervision, J.-A.L.-A. and M.-Á.A.; Project administration, J.-A.L.-A. and M.-Á.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to they are the property of the administration that owns the structures.
Acknowledgments
The authors wish to express their gratitude to the Ministry for Transport and Sustainable Mobility of Spain, in particular to the General Directorate of Roads (DGC) and the Administrator of Railway Infrastructures (ADIF), for having facilitated access to the available data on the monitored structures; to those responsible for the companies Kinesia Data and IMC, for having provided the programs and knowledge necessary for the analysis of said information; and Ideam company for providing the computational model used during the construction of the E-1 structure.
Conflicts of Interest
Author Miguel-Ángel Astiz was employed by the company Carlos Fernández Casado, S.L. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Rymsza, J. Causes of the Collapse of the Polcevera Viaduct in Genoa, Italy. Appl. Sci. 2021, 11, 8098. [Google Scholar] [CrossRef]
- DNV. Technical Opinion of the Incident that Occurred on Line 12, in the Elevated Section between Olivos and Tezonco Stations, between Columns 12 and 13, and Root Cause Analysis. Available online: https://proteccioncivil.cdmx.gob.mx/storage/app/uploads/public/60c/a54/3b4/60ca543b4ac47042812476.pdf (accessed on 1 November 2023). (In Spanish).
- UN General Assembly. Transforming our World: The 2030 Agenda for Sustainable Development, A/RES/70/1. Available online: https://www.refworld.org/docid/57b6e3e44.html (accessed on 1 November 2023).
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Gomez, H.C.; Fanning, P.J.; Feng, M.Q.; Lee, S. Testing and long-term monitoring of a curved concrete box girder bridge. Eng. Struct. 2011, 33, 2861–2869. [Google Scholar] [CrossRef]
- Cross, J.; Koo, K.Y.; Brownjohn, J.M.W.; Worden, K. Long-term monitoring and data analysis of the Tamar Bridge. Mech. Syst. Signal Process. 2013, 35, 16–34. [Google Scholar] [CrossRef]
- Hasani, H.; Freddi, F. Operational Modal Analysis on Bridges: A Comprehensive Review. Infrastructures 2023, 8, 172. [Google Scholar] [CrossRef]
- Han, D.; Hosamo, H.; Ying, C.; Nie, R. A Comprehensive Review and Analysis of Nanosensors for Structural Health Monitoring in Bridge Maintenance: Innovations, Challenges, and Future Perspectives. Appl. Sci. 2023, 13, 11149. [Google Scholar] [CrossRef]
- Dong, C.; Bas, S.; Catbas, F.N. Applications of Computer Vision-Based Structural Monitoring on Long-Span Bridges in Turkey. Sensors 2023, 23, 8161. [Google Scholar] [CrossRef]
- Bai, Y.; Demir, A.; Yilmaz, A.; Sezen, H. Assessment and monitoring of bridges using various camera placements and structural analysis. J. Civ. Struct. Health Monit. 2023; in press. [Google Scholar] [CrossRef]
- Xu, J.; Zeng, J.; Chen, B.; Lu, R.; Zhu, Y.; Qi, L.; Chen, X. Spacecraft Segment Damage Identification Method Based on Fiber Optic Strain Difference Field Reconstruction and Norm Calculation. Sensors 2023, 23, 8822. [Google Scholar] [CrossRef]
- Ramón-Zamora, J.E.; Lliso-Ferrando, J.R.; Martínez-Ibernón, A.; Gandía-Romero, J.M. Corrosion Assessment in Reinforced Concrete Structures by Means of Embedded Sensors and Multivariate Analysis—Part 1: Laboratory Validation. Sensors 2023, 23, 8869. [Google Scholar] [CrossRef]
- Jia, J.; Li, Y. Deep Learning for Structural Health Monitoring: Data, Algorithms, Applications, Challenges, and Trends. Sensors 2023, 23, 8824. [Google Scholar] [CrossRef] [PubMed]
- Biondi, F.; Addabbo, P.; Ullo, S.L.; Clemente, C.; Orlando, D. Perspectives on the Structural Health Monitoring of Bridges by Synthetic Aperture Radar. Remote Sens. 2020, 12, 3852. [Google Scholar] [CrossRef]
- Wenzel, H. Health Monitoring of Bridges; Wiley: London, UK, 2009. [Google Scholar]
- Magalhães, F.; Cunha, A.; Caetano, E. Dynamic monitoring of a long span arch bridge. Eng. Struct. 2008, 30, 3034–3044. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, A.; Caetano, E. One-year dynamic monitoring of a bridge: Modal parameters tracking under the influence of environmental effects. In Proceedings of the 4th International Conference on Structural Health Monitoring on Intelligent Infrastructure (SHMII-4), Zurich, Switzerland, 22–24 July 2009. [Google Scholar]
- Magalhães, F.; Cunha, A.; Caetano, E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection. Mech. Syst. Signal Process. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Gentile, C.; Saisi, A. Dynamic monitoring of the Paderno iron arch bridge (1889). In Proceedings of the 6th International Conference on Arch Bridges (ARCH’10), Fuzhou, China, 2–4 October 2010. [Google Scholar]
- Soria, J.M.; Díaz, I.M.; García-Palacios, J.H.; Ibán, N. Vibration monitoring of a steel-plated stress-ribbon footbridge: Uncertainties in the modal estimation. J. Bridge Eng. 2016, 21, C5015002. [Google Scholar] [CrossRef]
- Soria, J.M. Damage Identification and Condition Assessment of Civil Engineering Structures through Response Measurement. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2019. [Google Scholar]
- Astiz, M.A. Towards a standard policy for structural monitoring in cable-stayed bridges. In Maintenance, Monitoring, Safety, Risk and Resilience of Bridges and Bridge Networks; Bittencourt, T.N., Frangopol, D.M., Beck, A., Eds.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Tan, D.; Guo, T.; Luo, H.; Ji, B.; Tao, Y.; Li, A.; Duan, J. Dynamic Threshold Cable-Stayed Bridge Health Monitoring System Based on Temperature Effect Correction. Sensors 2023, 23, 8826. [Google Scholar] [CrossRef]
- Kölling, M.; Resnik, B.; Sargsyan, A. Application of the Random Decrement Technique for Experimental Determination of Damping Parameters of Bearing Structures; BHS: Berlin, Germany, 2014. [Google Scholar]
- Llombart, J.A.; Revoltós, J. Alconétar Bridge over the River Tagus at Alcántara Reservoir, Cáceres, Spain. Struct. Eng. Int. 2010, 20, 200–205. [Google Scholar] [CrossRef]
- Llombart, J.A.; Revoltós, J.; Couto, S. Bridge over the river Tagus at Alcántara Reservoir («Arcos de Alconétar»). Hormigón Acero 2006, 242, 5–38. [Google Scholar]
- Ministry for Transportation, Mobility and Urban Agenda. Arch Bridge over the River Tagus (Extremadura). Available online: https://www.mitma.gob.es/el-ministerio/blog-mitma/puente-arco-sobre-el-tajo-extremadura (accessed on 1 November 2023). (In Spanish)
- López-Aragón, J.A.; Astiz, M.A. An experimental analysis of the evolution of dynamic parameters of a long-span metal arch bridge. Struct. Eng. Int. 2014, 24, 8–19. [Google Scholar] [CrossRef]
- Astiz, M.A. Wind-Induced Vibrations of the Alconétar Bridge, Spain. Struct. Eng. Int. 2010, 20, 195–199. [Google Scholar] [CrossRef]
- Lancha, J.C. Study of the aerolastic behaviour of the bridge over the Tajo River at the Alcántara Reservoir. Hormigón Acero 2008, 247, 55–67. (In Spanish) [Google Scholar]
- Barrero, A.; Alonso, G.; Meseguer, J.; Astiz, M.A. Wind tunnel tests on the «Arcos de Alconétar» arch bridge aerolastic model. Hormigón Acero 2007, 245, 33–40. (In Spanish) [Google Scholar]
- Puchol, V. Experimental analysis of the wind induced vibrations of the bridge over the river Tagus («Arcos de Alconétar»). Hormigón Acero 2007, 243, 51–66. (In Spanish) [Google Scholar]
- del Pozo Vindel, F.J.; Arrieta Torrealba, J.M.; Madrid Ramos, A.J.; Cerezo Macías, A.; Hernando Martín, A.; Higuera Antón, M.Á. Viaduct “Arroyo del Valle”, Madrid-Segovia-Valladolid High Speed Line. Available online: http://e-ache.com/modules/ache/ficheros/Realizaciones/Obra77.pdf (accessed on 1 November 2023). (In Spanish).
- Siegrist, C.; Siegrist, G.; Utrilla, M.A. Section of the High-Speed Line “Soto del Real-Miraflores”, Viaduct “Arroyo del Valle”. Available online: http://e-ache.com/modules/ache/ficheros/Realizaciones/Obra77.pdf (accessed on 1 November 2023). (In Spanish).
- Ministry for Transportation, Mobility and Urban Agenda. Adif Alta Velocidad. Line Madrid-Valladolid, Featured Structures. Available online: https://www.adifaltavelocidad.es/-/lav-madrid-valladolid-infraestructura (accessed on 1 November 2023). (In Spanish)
- Tifsa. Instrumentation and Monitoring of the Viaduct “Arroyo del Valle” (Miraflores de la Sierra); 2009. [Google Scholar]
- Apia XXI. Calibration of the Dynamic Computational Model of the Viaduct “Arroyo del Valle”; 2007. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures; Computer and Structures: Berkeley, CA, USA, 2003. [Google Scholar]
- López-Aragón, J.A.; Astiz, M.A. Influence of the modal damping ratio calculation method in the analysis of dynamic events obtained in Structural Health Monitoring of bridges. J. Civ. Struct. Health Monit. 2023; in press. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).