3D Dynamics Deduction and the Spatial Geometric Characteristics of Ball Balance Positioning in Automatic Ball Balancers

Abstract

In order to explore the geometric characteristics of the dynamic balance positions of balls in any orbit in space, this paper first deduces the dynamic equilibrium equations of an eccentric rotor system with the automatic ball balancer (ABB) skew, mounted with a deflection angle from the perspective of three-dimensional (3D) dynamics. The results obtained are consistent with those derived from the Euler–Lagrange equations. It is exciting that the spatial dynamics method reveals the spatial-geometric characteristics of dynamic balance positioning of the balls when the system is balanced with vibration suppression. Then, through spatial geometric inference, it is proved that the balance positioning of any ball in an arbitrary curved track is characterized. This characteristic indicates that the perpendicular line from any balance position to the rotating spindle of the system must pass through the central axis of curvature of the track at that position. Finally, spatial graphics and numerical analysis are used to verify the theoretical correctness. The characteristics are general rules that can explain the phenomena of the stable equilibrium positions of the balls in previous studies under ideal assumptions.

1. Introduction

For the vibration suppression of eccentric rotors, the passive balancing devices that are more widely applied and researched currently are Automatic Ball Balancers (ABBs) at present. The main components are composed of a circular orbit mechanism, mounted perpendicular to the spindle of the rotor and revolving with the rotor, and several balls that can freely move inside the track. In 1975, Sharp [1] established an ideally mounted two-ball balancer of a plane rotor system from the 2D viewpoint and derived the equations of motion to analyze stability. Lee [2] in 1996, Green [3] in 2006, and Lu [4] in 2009, etc., have explored the problems and phenomena of ABBs’ suppressing vibration in the model without assembly deviations.

However, when assembling the ABBs and eccentric rotor system, assembly deviations may include the deviations of the vertical and horizontal positions of the ABBs’ centroid and the centroid of the eccentric rotor as well as the deflections of the mounted angle. Regarding the discussions of vertical position deviation, Kim [5] in 2005 and Chao [6] in 2007 investigated the dynamic behavior of the system when the ABB is mounted at a small distance below the centroid of the plane eccentric rotor theoretically and experimentally, respectively. Numerical analysis and experimental results show that the system can still the approximate ideal-mounted (ABB is coplanar with the planar rotor) balance approach. The radial residual vibration under steady-state operation and the tilting angle during rotor balancing can be effectively reduced by positioning the balls at appropriate angular positions [5], where the radial amplitude can almost be suppressed, yet the tilting angle during balancing exists in a finite amount [6]. Furthermore, regarding the discussions of horizontal position deviation, Bykov in 2014 [7] and 2018 [8] proposed that the ABB and the planar rotor are coplanar, but the orbital center of the mounted ABB deviates horizontally from the rotor centroid along the rotor plane. In cases where the working speed is greater than the critical speed of the system, there are two types of incomplete balanced steady-state modes. Take the double ball ABB as an example, one is that two balls are gathered on the opposite side of the mass center of the rotor, and the other is half-balanced mode [7] or called almost balanced mode [8]. The second one is that two balls are spread by an appropriate amplitude spread angle to suppress (but not completely suppress) the eccentric imbalance of the planar rotor. As for the deflection of the mounting angle, in 2022, Huang [9] first established an angular deviation model between the plane of ABBs’ track and the plane of the eccentric rotor within the vibration suppression system. The examination principle of the skew-mounted ABB is proposed, comparing the differences in vibration suppression efficiency between skew-mounted and ideal-mounted systems, as well as the conditions of perfect balance.

For the research on ABBs’ vibration control system, across the past decade, many studies have proposed using springs or partitions along the track circumference to improve the ABBs’ performance or reduce the system amplitude at low speeds. Researchers such as Rezaee [10,11], Kim [12], and Haidar [13], etc., take into account the tangential force along the track, which in turn limits the movement of the balls in the track. However, in most of the literature, it is still assumed that the balls can rotate freely in the track except for viscous damping, and the balls in dynamic balance without any external forces acting along the tangential direction of the track. Additionally, the self-weight of the balls and friction in the track are ignored. Based on these assumed premises, which include single track [3,4,5,14,15,16,17], double track [18], radial spring [19], multiple balls [20,21], mounting offset [7,8], and mounting deflection [9] studies, there are various discussions regarding the dynamic characteristics and stability analysis of ABBs’ vibration suppression system. In these studies, the set of the dynamic equilibrium equations of the balls or their balance positions may seem to be different, but the balance mechanisms behind them are consistent.

Commonly seen in the derivation of the dynamic equilibrium equations of the vibration suppression system of the rotor, most use the Euler–Lagrangian method to obtain the governing equations of the system. Only under the condition that their differential terms are zero can we obtain the dynamic equilibrium equations of the system [1,2,3,4,5,6,9]. Pakuła (2022) [22] used 2D dynamics to deduce the equilibrium equations under the simultaneous action of multiple ABBs on the same plane and formulated the optimization of the vibration suppression of the system by the assembly locations of the ABBs. In 2023, Mirsaidov et al. presented two studies [23,24] on the subject of mounting an eccentric rotor tilted around the horizontal axis on a vertical rotor axis and an ABB with the angular deflection mounted on the eccentric rotor. The effect of two variables on the vibration suppression of the system, such as the amount of eccentricity of the rotor and the deflection angle of the ABB, is considered. The effect is proportional to the angular error of the ABB.

In this paper, in order to verify the dynamic equilibrium equations of the skew-mounted ABB eccentric rotor system, we utilize the 3D dynamics approach for derivation and mutual validation of the results with the Euler–Lagrangian method [9]. The process aids in finding out the spatial characteristics of the balance positions of the balls in space. Then the mechanical problem of the dynamic balance is converted into a spatial geometric problem for study, and the geometric characteristics of the dynamic balance positioning of the balls in an arbitrary curved track in space are proposed. Finally, the spatial and geographical presentation and numerical analysis are used to verify that the dynamic balance positioning of the balls should actually have a consistent balancing mechanism.

2. System Model

Figure 1 shows the skew-mounted model of the angular deviation between the plane of the balls moving in the ABB track and the rotor plane when the spindle speed is zero. The plane formed by the blue frame in Figure 1 is the plane where the eccentric rotor is located and C is its centroid, while the red frame represents the orbital plane of ABB. The ABB plane does not coincide with the rotor plane that is perpendicular to the spin axis of the system at rest. The deflection angle is shown as $\theta$. Suppose the skew-mounted ABB is only the angle deflection of the orbital plane without the position deviation of the centroid, then the ABB’s centroid coincides with the centroid C of the planar rotor at static. The intersection line of two planes should pass through the centroid C. As shown, the coordinate system $<\mathit{X}\mathit{Y}\mathit{Z}>$ is a space-fixed reference frame of the planar rotor, with the origin defined at the position of its centroid. The intersection line of two planes lies on the $\mathit{Y}$-axis.

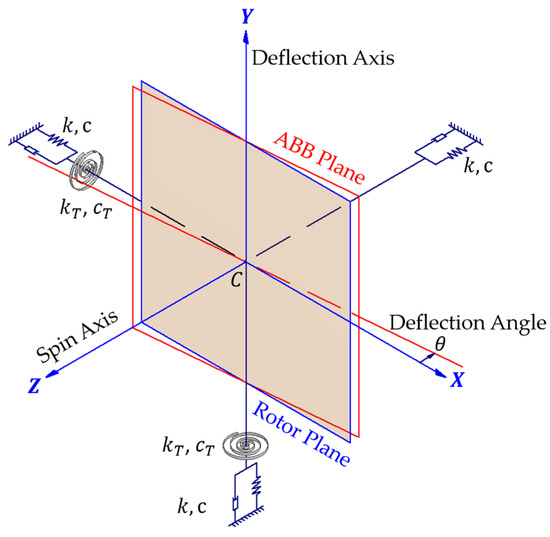
Figure 1. The support configurations of the rotor system equipped with skew-mounted ABB.

When the system operates as stable, due to the deflection of the orbital plane of ABB and the rotor plane, although the centrifugal forces acting on their respective planes both pass through the rotation axis, the intersection of each with the rotation axis is not necessarily the same, which may generate torques for the whole assembly system. In this paper, the spin axis ($\mathit{Z}$-axis) of the system is defined as the roll axis in a tri-axial system, and the pitch and yaw angles of the system should be considered for the phenomenon of torque. Therefore, in addition to the tri-axial isotropic linear spring k and viscous damper c, the elastic supports of the system should also consider the roles of the torsion spring $k_T$ and torsion damper $c_T$ in the other two axes except for the spin axis, as shown. The dynamic balance of this 3D model will be analyzed using spatial dynamics.

3. 3D Dynamics Deduction

3.1. Coordinate System

In order to understand and analyze the spatial position, attitude, and motion mechanism of the rotor system equipped with skew-mounted ABB, the coordinate systems of the ABB mechanism, eccentric rotor, and support device are constructed as shown in Figure 2. The rectangular coordinate ${<\mathit{X}\mathit{Y}\mathit{Z}>}_O$ is a space-fixed reference frame of the planar rotor, the origin O is defined at the centroid position of the eccentric rotor when the spindle speed is zero, the system is stationary, and the support springs are not deformed. The $\mathit{Y}$-axis is the deflection axis where mounting deviation occurs (refer to Figure 1). Moreover, the rotating reference frame ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ is defined with the origin located at point $O$ and $\mathit{z}=\mathit{Z}$ axis of the ${<\mathit{X}\mathit{Y}\mathit{Z}>}_O$ frame. The ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ coordinate system rotates around the spindle $\mathit{Z}$-axis of the system with a constant angular velocity $\omega$. The reference frame can be transformed to the rotating frame by a rotation matrix ${\mathbf{T}}_{\omega }$.

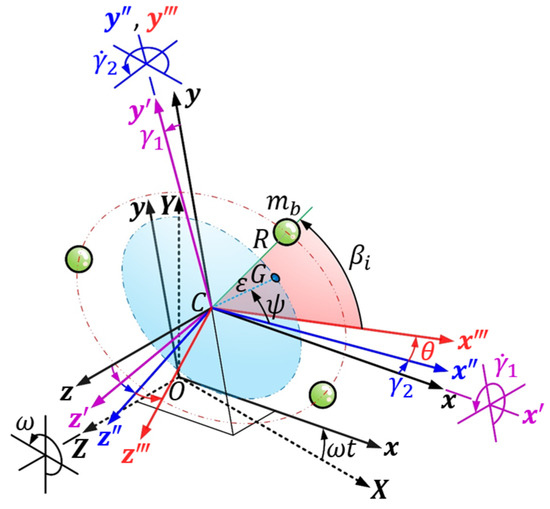
Figure 2. Configuration of the coordinate systems.

When the support spring is deformed, the position of the offset center $C$ is set to the origin of the ${<\mathit{x}\mathit{y}\mathit{z}>}_C$ coordinate system, which axes are always parallel to and in the same direction as the axes of ${<\mathit{x}\mathit{y}\mathit{z}>}_O$, except for the different position of the origin. Then rotating the pitch angle ${\gamma }_1$ around the $\mathit{x}$-axis, which is in the ${<\mathit{x}\mathit{y}\mathit{z}>}_C$ coordinate system, and the rotating coordinate system ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_C$, where ${\mathit{x}}^{\prime }=\mathit{x}$ can be obtained. Next, rotate the yaw angle ${\gamma }_2$ around the ${\mathit{y}}^{\prime }$-axis of ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_C$ coordinate system to obtain the rotating coordinate system ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_C$, where ${\mathit{y}}^{″}={\mathit{y}}^{\prime }$ and the ${\mathit{z}}^{″}$-axis passes through the rotor centroid and is perpendicular to the plane of the rotor (${\mathit{x}}^{″}{\mathit{y}}^{″}$ plane). Converting ${<\mathit{x}\mathit{y}\mathit{z}>}_C$ to ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_C$ and ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_C$ by rotation matrixes ${\mathbf{T}}_1$ and ${\mathbf{T}}_2$ in sequence. The mass center $G$ of the eccentric rotor with mass m is located on the plane of rotor and the eccentricity between $G$ and its centroid $C$ is $\epsilon$. The angle between $\overline{CG}$ and the ${\mathit{x}}^{″}$-axis is $\psi$.

The body-fixed coordinate system ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_C$ follows the rotor system in 3D space such that the ${\mathit{y}}^{″}$-axis is also the deflection axis of skew-mounted ABB. Rotating the deflection angle $\theta$ around the ${\mathit{y}}^{″}$-axis of the ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_C$ to obtain the coordinate system ${<{\mathit{x}}^{‴}{\mathit{y}}^{‴}{\mathit{z}}^{‴}>}_C$ of the orbital plane, where ${\mathit{y}}^{‴}={\mathit{y}}^{″}={\mathit{y}}^{\prime }$. It can convert ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_C$ to ${<{\mathit{x}}^{‴}{\mathit{y}}^{‴}{\mathit{z}}^{‴}>}_C$ by rotation matrix ${\mathbf{T}}_3$. The radius of the circular orbit of the ABB is $R$, there are $n$ balls moving in the orbit, and the mass of each ball is $m_b$. The angular position of the $i$-th ball from the ${\mathit{x}}^{‴}$-axis is denoted ${\beta }_i\left(i=1~n\right)$. The rotation matrices between the coordinates as

$$\begin{gathered} {\mathbf{T}}_{\omega }=\left[\begin{array}{ccc}\cos \omega t& \sin \omega t& 0\\ -\sin \omega t& \cos \omega t& 0\\ 0& 0& 1\end{array}\right], {\mathbf{T}}_1=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos {\gamma }_1& \sin {\gamma }_1\\ 0& -\sin {\gamma }_1& \cos {\gamma }_1\end{array}\right], \\ {\mathbf{T}}_2=\left[\begin{array}{ccc}\cos {\gamma }_2& 0& -\sin {\gamma }_2\\ 0& 1& 0\\ \sin {\gamma }_2& 0& \cos {\gamma }_2\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d} {\mathbf{T}}_3=\left[\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right]. \end{gathered}$$

(1)

3.2. Spatial Forces of Dynamic Balance

When the system is in dynamic balance, each particle of the system always maintains a fixed relative position to the observer of the rotating coordinate system which is attached to the spindle with the same angular velocity. The centripetal force required to maintain the constant angular velocity is provided by the constraint force generated by the deformation of the suspension or support device of the system. The plane of the ABB’s track of the rotor system with a skew-mounted ABB does not coincide with the plane of the rotor, as shown in Figure 3, Plane I, and Plane II. When the dynamic system is steadily balanced, the balls and the rotor centroid revolve around the spin axis, but each of them is on a different plane perpendicular to the spin axis. $B_1$ and $B_2$ in Figure 3 are any two balls in the same circular orbit but belong to two parallel planes III and V perpendicular to the spin axis; the other parallel plane IV is the plane of mass center $G$ of the eccentric rotor. From this corollary, n balls and the mass center of the eccentric rotor, the dynamic equilibrium analysis of (n + 1) planes perpendicular to the spin axis and parallel to each other needs to be explored to obtain the dynamic equilibrium equations.

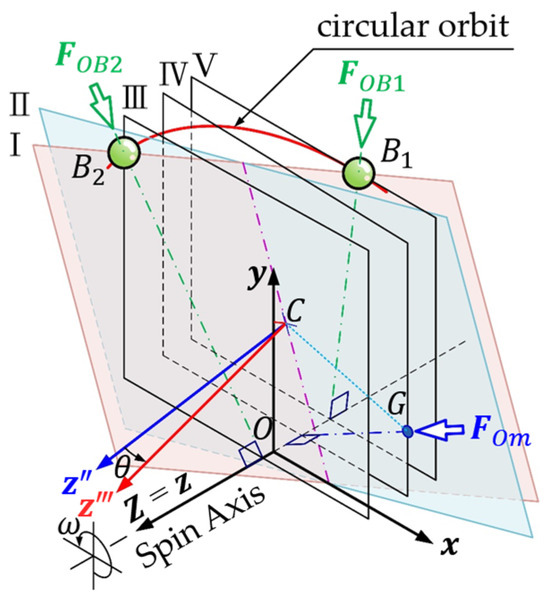
Figure 3. Each ball and the mass center of the rotor rotate around the spin axis in different parallel planes, respectively, at steady operation.

3.3. Dynamic Equilibrium Equations

3.3.1. Tri-Axial Force Balance of ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ Frame

The rotor system equipped with a skew-mounted ABB has a constant spindle speed ω. In the rotating reference frame ${<\mathit{x}\mathit{y}\mathit{z}>}_O$, the angular velocity of the system is denoted as ${\mathit{\Omega }}_O={\left[\begin{array}{ccc}0& 0& \omega \end{array}\right]}^T$, and the position of the offset centroid C after the deformations of the support springs can be expressed as the vector ${\mathit{r}}_{OC}={\left[\begin{array}{ccc}{x}_c& y_c& z_c\end{array}\right]}^T$. The system is in a dynamic balance, the equilibrium position of the rotor centroid C is expressed as the vector

$${\widehat{\mathit{r}}}_{OC}=\left[\begin{array}{c}{\widehat{x}}_c\\ {\widehat{y}}_c\\ {\widehat{z}}_c\end{array}\right].$$

(2)

Additionally, ${\widehat{\gamma }}_1$, ${\widehat{\gamma }}_2$, and ${\widehat{\beta }}_i(i=1~n)$ are the equilibrium pitch angle, equilibrium yaw angle, and $n$ balls’ equilibrium angular positions, respectively. From the definition of coordinate systems (Figure 2), the position vector of mass center $G$ of the rotor in ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_{\mathit{C}}$ as

$${\widehat{\mathit{r}}}_m^{″}=\left[\begin{array}{c}\epsilon \cos \psi \\ \epsilon \sin \psi \\ 0\end{array}\right].$$

(3)

The equilibrium position vector of the mass center of the i-th ball in ${<{\mathit{x}}^{‴}{\mathit{y}}^{‴}{\mathit{z}}^{‴}>}_C$ is ${\widehat{\mathit{r}}}_{Bi}^{‴}$, the reverse transformation is in ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_{\mathit{C}}$ as ${\widehat{\mathit{r}}}_{Bi}^{″}$, where

$${\widehat{\mathit{r}}}_{Bi}^{‴}=\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\\ R\sin {\widehat{\beta }}_i\\ 0\end{array}\right],i=1~n \mathrm{a}\mathrm{n}\mathrm{d}$$

(4)

$${\widehat{\mathit{r}}}_{Bi}^{″}={\mathbf{T}}_3^{-1}{\widehat{\mathit{r}}}_{Bi}^{‴}=\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\cos \theta \\ R\sin {\widehat{\beta }}_i\\ -R\cos {\widehat{\beta }}_i\sin \theta \end{array}\right] ,i=1~n.$$

(5)

Therefore, the equilibrium position vectors (Equations (3) and (5)) are inverted to the rotating reference frame ${<\mathit{x}\mathit{y}\mathit{z}>}_O$, which is

$$\begin{gathered} {\widehat{\mathit{r}}}_{Om}={\widehat{\mathit{r}}}_{OC}+{\mathbf{T}}_1^{-1}{\mathbf{T}}_2^{-1}{\widehat{\mathit{r}}}_m^{″}= \\ \left[\begin{array}{c}\epsilon \cos \psi \cos {\widehat{\gamma }}_2+{\widehat{x}}_c\\ \epsilon \sin \psi \cos {\widehat{\gamma }}_1+\epsilon \cos \psi \sin {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2+{\widehat{y}}_c\\ \epsilon \sin \psi \sin {\widehat{\gamma }}_1-\epsilon \cos \psi \cos {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2+{\widehat{z}}_c\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d} \end{gathered}$$

(6)

$${\widehat{\mathit{r}}}_{OBi}={\widehat{\mathit{r}}}_{OC}+{\mathbf{T}}_1^{-1}{\mathbf{T}}_2^{-1}{\widehat{\mathit{r}}}_{Bi}^{″}=\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\cos \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{x}}_c\\ R\sin {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1+R\cos {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{y}}_c\\ R\sin {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1-R\cos {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{z}}_c\end{array}\right].$$

(7)

The action forces of the steadily balanced system should include the centripetal force ${\mathit{F}}_{Om}$ and ${\mathit{F}}_{OBi}(i=1~n)$ acting on the system when the rotor mass center and $n$ balls revolve around the spin axis, as well as the supporting spring force ${\mathit{F}}_k$ and the supporting damping force ${\mathit{F}}_d$. ${\mathit{F}}_{Om}$ and ${\mathit{F}}_{OBi}(i=1~n)$ are all on parallel planes perpendicular to the spin axis (ref. Figure 3). By 3D dynamics [25], the above forces in the ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ frame can be obtained from the following equations, respectively.

$${\mathit{F}}_{Om}=m{\mathit{\Omega }}_O\times \left({\mathit{\Omega }}_O\times {\widehat{\mathit{r}}}_{Om}\right)=-m{\omega }^2\left[\begin{array}{c}\epsilon \cos \psi \cos {\widehat{\gamma }}_2+{\widehat{x}}_c\\ \epsilon \sin \psi \cos {\widehat{\gamma }}_1+\epsilon \cos \psi \sin {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2+{\widehat{y}}_c\\ 0\end{array}\right],$$

(8)

$${\mathit{F}}_{OBi}=m_b{\mathit{\Omega }}_O\times \left({\mathit{\Omega }}_O\times {\widehat{\mathit{r}}}_{OBi}\right)=-m_b{\omega }^2\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\cos \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{x}}_c\\ R\sin {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1+R\cos {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{y}}_c\\ 0\end{array}\right],i=1~n,$$

(9)

$${\mathit{F}}_k=-k{\widehat{\mathit{r}}}_{OC}=\left[\begin{array}{c}-k{\widehat{x}}_c\\ -k{\widehat{y}}_c\\ -k{\widehat{z}}_c\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d}$$

(10)

$${\mathit{F}}_d=-c{\mathit{\Omega }}_O\times {\widehat{\mathit{r}}}_{OC}=\left[\begin{array}{c}c\omega {\widehat{y}}_c\\ -c\omega {\widehat{x}}_c\\ 0\end{array}\right].$$

(11)

Through tri-axial force balance of the rotating reference frame ${<\mathit{x}\mathit{y}\mathit{z}>}_O$, ${\mathit{F}}_{Om}+{\sum }_{i=1}^n{\mathit{F}}_{OBi}={\mathit{F}}_k+{\mathit{F}}_d$, can list three dynamic equilibrium equations.

$$m{\omega }^2\left(\epsilon \cos \psi \cos {\widehat{\gamma }}_2+{\widehat{x}}_c\right)+m_b{\omega }^2\sum _{i=1}^n\left[R\cos {\widehat{\beta }}_i\cos \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{x}}_c\right]-k{\widehat{x}}_c+c\omega {\widehat{y}}_c=0,$$

(12)

$$\begin{array}{cc}\hfill m{\omega }^2(\epsilon \sin \psi \cos {\widehat{\gamma }}_1& +\epsilon \cos \psi \sin {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2+{\widehat{y}}_c)+m_b{\omega }^2{\displaystyle \sum _{i=1}^n}\left[R\sin {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1+R\cos {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{y}}_c\right]\hfill \\ & -k{\widehat{y}}_c-c\omega {\widehat{x}}_c=0 \mathrm{a}\mathrm{n}\mathrm{d}\hfill \end{array}$$

(13)

$$-k{\widehat{z}}_c=0.$$

(14)

3.3.2. Moment Balance around the x-Axis of the ${<\mathit{x}\mathit{y}\mathit{z}>}_C$ Coordinate System

The ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ and the ${<\mathit{x}\mathit{y}\mathit{z}>}_{\mathit{C}}$ are two parallel coordinate systems. In the coordinate system ${<\mathit{x}\mathit{y}\mathit{z}>}_{\mathit{C}}$, the angular velocity ${\mathit{\Omega }}_C$ around the $\mathit{z}$-axis, the centripetal forces ${\mathit{F}}_m$ and ${\mathit{F}}_{Bi}(i=1~n$) of the rotor mass center and the balls are the same as those in ${<\mathit{x}\mathit{y}\mathit{z}>}_O$, respectively. ${\mathit{\Omega }}_C={\mathit{\Omega }}_O={\left[\begin{array}{ccc}0& 0& \omega \end{array}\right]}^T$, ${\mathit{F}}_m={\mathit{F}}_{Om}$ (Equation (8)), and ${\mathit{F}}_{Bi}={\mathit{F}}_{OBi}$ (Equation (9)). The equilibrium position vector of the mass center of the rotor and the $i$-th ball in ${<\mathit{x}\mathit{y}\mathit{z}>}_{\mathit{C}}$ is ${\widehat{\mathit{r}}}_m$ and ${\widehat{\mathit{r}}}_{Bi}(i=1~n)$. To inverse transformation of ${\widehat{\mathit{r}}}_m^{″}$ and ${\widehat{\mathit{r}}}_{Bi}^{″}$ (Equations (3) and (5)) or to translation of ${\widehat{\mathit{r}}}_{Om}$ and ${\widehat{\mathit{r}}}_{OBi}$ (Equations (6) and (7)) can be obtained as

$${\widehat{\mathit{r}}}_m={\mathbf{T}}_1^{-1}{\mathbf{T}}_2^{-1}{\widehat{\mathit{r}}}_m^{″}={\widehat{\mathit{r}}}_{Om}-{\widehat{\mathit{r}}}_{OC}=\left[\begin{array}{c}\epsilon \cos \psi \cos {\widehat{\gamma }}_2\\ \epsilon \sin \psi \cos {\widehat{\gamma }}_1+\epsilon \cos \psi \sin {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2\\ \epsilon \sin \psi \sin {\widehat{\gamma }}_1-\epsilon \cos \psi \cos {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d}$$

(15)

$${\widehat{\mathit{r}}}_{Bi}={\mathbf{T}}_1^{-1}{\mathbf{T}}_2^{-1}{\widehat{\mathit{r}}}_{Bi}^{″}={\widehat{\mathit{r}}}_{OBi}-{\widehat{\mathit{r}}}_{OC}=\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\cos \left({\widehat{\gamma }}_2+\theta \right)\\ R\sin {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1+R\cos {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)\\ R\sin {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1-R\cos {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)\end{array}\right] ,i=1~n.$$

(16)

The absolute angular velocity $\widehat{\mathit{\Omega }}$ of the principal axis of inertia of the eccentric rotor in ${<{\mathit{x}}^{″}{\mathit{y}}^{″}{\mathit{z}}^{″}>}_{\mathit{C}}$ can transform by ${\mathit{\Omega }}_C$, and rotor angular momentum $\widehat{\mathit{H}}$ can be obtained from $\widehat{\mathit{\Omega }}$ and the principal moment of inertia tensor $\mathbf{J}$. The torque due to the angular momentum of the eccentric rotor is expressed in the cross-product term $\widehat{\mathit{\Omega }}\times \widehat{\mathit{H}}$, where

$$\widehat{\mathit{\Omega }}={\mathbf{T}}_2{\mathbf{T}}_1{\mathit{\Omega }}_C={\mathbf{T}}_2{\mathbf{T}}_1\left[\begin{array}{c}0\\ 0\\ \omega \end{array}\right]=\left[\begin{array}{c}-\omega \cos {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2\\ \omega \sin {\widehat{\gamma }}_1\\ \omega \cos {\widehat{\gamma }}_1\cos {\widehat{\gamma }}_2\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d}$$

(17)

$$\widehat{\mathit{H}}=\mathbf{J}\widehat{\mathit{\Omega }}=\left[\begin{array}{ccc}{\mathrm{J}}_T& 0& 0\\ 0& {\mathrm{J}}_T& 0\\ 0& 0& {\mathrm{J}}_P\end{array}\right]\widehat{\mathit{\Omega }}.$$

(18)

The support reaction moment of the torsion spring to the x-axis in dynamic balance is $k_T{\widehat{\gamma }}_1$. Therefore, the 3D spatial moment balanced on the x-axis in the coordinate system ${<\mathit{x}\mathit{y}\mathit{z}>}_{\mathit{C}}$ is expressed as

$$\left[{\widehat{\mathit{r}}}_m\times {\mathit{F}}_m+\sum _{i=1}^n{\widehat{\mathit{r}}}_{Bi}\times {\mathit{F}}_{Bi}+{\mathbf{T}}_1^{-1}{\mathbf{T}}_2^{-1}\left(\widehat{\mathit{\Omega }}\times \widehat{\mathit{H}}\right)\right]·{\left[\begin{array}{ccc}1& 0& 0\end{array}\right]}^T+k_T{\widehat{\gamma }}_1=0.$$

(19)

The moment equilibrium equation of the system for the x-axis in ${<\mathit{x}\mathit{y}\mathit{z}>}_{\mathit{C}}$ can be listed as

$$\begin{array}{cc}\hfill \frac{m{\epsilon }^2{\omega }^2}{2}\{-\sin \left(2\psi \right)& \cos \left(2{\widehat{\gamma }}_1\right)\sin {\widehat{\gamma }}_2+\sin \left(2{\widehat{\gamma }}_1\right)\left[{\sin }^2\psi -{\cos }^2\psi {\sin }^2{\widehat{\gamma }}_2\right]\}\hfill \\ & +m\epsilon {\omega }^2\left(\sin \psi \sin {\widehat{\gamma }}_1-\cos \psi \cos {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2\right){\widehat{y}}_c+{\omega }^2{\cos }^2{\widehat{\gamma }}_2\sin {\widehat{\gamma }}_1\cos {\widehat{\gamma }}_1\left({\mathrm{J}}_P-{\mathrm{J}}_T\right)\hfill \\ & +\frac{m_b{R}^2{\omega }^2}{2}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left\{-\sin \left(2{\widehat{\beta }}_i\right)\cos \left(2{\widehat{\gamma }}_1\right)\sin \left({\widehat{\gamma }}_2+\theta \right)+\sin \left(2{\widehat{\gamma }}_1\right)\left[{\sin }^2{\widehat{\beta }}_i-{\cos }^2{\widehat{\beta }}_i{\sin }^2\left({\widehat{\gamma }}_2+\theta \right)\right]\right\}\hfill \\ & +m_{b}R{\omega }^2{\displaystyle \sum _{i=1}^n}\left[\sin {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1-\cos {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)\right]{\widehat{y}}_c+k_T{\widehat{\gamma }}_1=0.\hfill \end{array}$$

(20)

3.3.3. Moment Balance around the y′-Axis of the ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_{\mathrm{C}}$ Coordinate System

${\mathit{F}}_m$ and ${\mathit{F}}_{Bi}(i=1~n)$ in ${<\mathit{x}\mathit{y}\mathit{z}>}_{\mathit{C}}$ are transformed to ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_{\mathit{C}}$ by the rotation matrix ${\mathbf{T}}_1$, described as follows, respectively:

$${\mathit{F}}_m^{\prime }={\mathbf{T}}_1{\mathit{F}}_m=-m{\omega }^2\left[\begin{array}{c}\epsilon \cos \psi \cos {\widehat{\gamma }}_2+{\widehat{x}}_c\\ \cos {\widehat{\gamma }}_1\left(\epsilon \sin \psi \cos {\widehat{\gamma }}_1+\epsilon \cos \psi \sin {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2+{\widehat{y}}_c\right)\\ -\sin {\widehat{\gamma }}_1\left(\epsilon \sin \psi \cos {\widehat{\gamma }}_1+\epsilon \cos \psi \sin {\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2+{\widehat{y}}_c\right)\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d}$$

(21)

$${\mathit{F}}_{Bi}^{\prime }={\mathbf{T}}_1{\mathit{F}}_{Bi}=-m_b{\omega }^2\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\cos \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{x}}_c\\ \cos {\widehat{\gamma }}_1\left(R\sin {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1+R\cos {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{y}}_c\right)\\ -\sin {\widehat{\gamma }}_1\left(R\sin {\widehat{\beta }}_i\cos {\widehat{\gamma }}_1+R\cos {\widehat{\beta }}_i\sin {\widehat{\gamma }}_1\sin \left({\widehat{\gamma }}_2+\theta \right)+{\widehat{y}}_c\right)\end{array}\right], i=1~n.$$

(22)

The equilibrium position vector of the mass center of the rotor and the i-th ball in ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_{\mathit{C}}$ is ${\widehat{\mathit{r}}}_m^{\prime }$ and ${\widehat{\mathit{r}}}_{Bi}^{\prime }(i=1~n)$. The inverse transformation of ${\widehat{\mathit{r}}}_m^{″}$ and ${\widehat{\mathit{r}}}_{Bi}^{″}$ (Equations (3) and (5)) or the transformation of ${\widehat{\mathit{r}}}_m$ and ${\widehat{\mathit{r}}}_{Bi}$ (Equations (13) and (14)) can be obtained.

$${\widehat{\mathit{r}}}_m^{\prime }={\mathbf{T}}_2^{-1}{\widehat{\mathit{r}}}_m^{″}={\mathbf{T}}_1{\widehat{\mathit{r}}}_m=\left[\begin{array}{c}\epsilon \cos \psi \cos {\widehat{\gamma }}_2\\ \epsilon \sin \psi \\ -\epsilon \cos \psi \sin {\widehat{\gamma }}_2\end{array}\right] \mathrm{a}\mathrm{n}\mathrm{d}$$

(23)

$${\widehat{\mathit{r}}}_{Bi}^{\prime }={\mathbf{T}}_2^{-1}{\widehat{\mathit{r}}}_{Bi}^{″}={\mathbf{T}}_1{\widehat{\mathit{r}}}_{Bi}=\left[\begin{array}{c}R\cos {\widehat{\beta }}_i\cos \left({\widehat{\gamma }}_2+\theta \right)\\ R\sin {\widehat{\beta }}_i\\ -R\cos {\widehat{\beta }}_i\sin \left({\widehat{\gamma }}_2+\theta \right)\end{array}\right], i=1~n.$$

(24)

Similarly, the support reaction moment of the torsion spring on the ${\mathit{y}}^{\prime }$-axis is $k_T{\widehat{\gamma }}_2$, and 3D spatial moment balance on the ${\mathit{y}}^{\prime }$-axis in the coordinate system ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_{\mathit{C}}$ is expressed as

$$\left[{\widehat{\mathit{r}}}_m^{\prime }\times {\mathit{F}}_m^{\prime }+\sum _{i=1}^n{\widehat{\mathit{r}}}_{Bi}^{\prime }\times {\mathit{F}}_{Bi}^{\prime }+{\mathbf{T}}_2^{-1}\left(\widehat{\mathit{\Omega }}\times \widehat{\mathit{H}}\right)\right]·{\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}^T+k_T{\widehat{\gamma }}_2=0.$$

(25)

The moment equilibrium equation of the system around the ${\mathit{y}}^{\prime }$-axis in ${<{\mathit{x}}^{\prime }{\mathit{y}}^{\prime }{\mathit{z}}^{\prime }>}_{\mathit{C}}$ can be written as

$$\begin{array}{cc}\hfill \frac{m{\epsilon }^2{\omega }^2}{4}[-\sin \left(2\psi \right)& \sin \left(2{\widehat{\gamma }}_1\right)\cos {\widehat{\gamma }}_2+2\sin \left(2{\widehat{\gamma }}_2\right){\cos }^2\psi {\cos }^2{\widehat{\gamma }}_1]+m\epsilon {\omega }^2\cos \psi \left({\widehat{x}}_c\sin {\widehat{\gamma }}_2-{\widehat{y}}_c\sin {\widehat{\gamma }}_1\cos {\widehat{\gamma }}_2\right)\hfill \\ & +{\omega }^2{\cos }^2{\widehat{\gamma }}_1\sin {\widehat{\gamma }}_2\cos {\widehat{\gamma }}_2\left({\mathrm{J}}_P-{\mathrm{J}}_T\right)\hfill \\ & +\frac{m_b{R}^2{\omega }^2}{4}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\left\{-\sin \left(2{\widehat{\beta }}_i\right)\sin \left(2{\widehat{\gamma }}_1\right)\cos \left({\widehat{\gamma }}_2+\theta \right)+2\sin \left[2\left({\widehat{\gamma }}_2+\theta \right)\right]{\cos }^2{\widehat{\beta }}_i{\cos }^2{\widehat{\gamma }}_1\right\}\hfill \\ & +m_{b}R{\omega }^2{\displaystyle \sum _{i=1}^n}\cos {\widehat{\beta }}_i\left[{\widehat{x}}_c\sin \left({\widehat{\gamma }}_2+\theta \right)-{\widehat{y}}_c\sin {\widehat{\gamma }}_1\cos \left({\widehat{\gamma }}_2+\theta \right)\right]+k_T{\widehat{\gamma }}_2=0.\hfill \end{array}$$

(26)

3.3.4. Moment Balance around the Central Axis Perpendicular to the Orbital Plane

The equilibrium position and the centripetal force vector of the mass center of the i-th ball in ${<{\mathit{x}}^{‴}{\mathit{y}}^{‴}{\mathit{z}}^{‴}>}_{\mathit{C}}$ is ${\widehat{\mathit{r}}}_{Bi}^{‴}(i=1~n)$ (Equation (4)) and ${\mathit{F}}_{Bi}^{‴}(i=1~n)$. ${\mathit{F}}_{Bi}^{‴}$ can be converted by the ${\mathit{F}}_{Bi}^{\prime }$ (Equation (20)) and written as

$${\mathit{F}}_{Bi}^{‴}={\mathit{T}}_3{\mathit{T}}_2{\mathit{F}}_{Bi}^{\prime }=-m_b{\omega }^2\left[\begin{array}{l}\begin{array}{l}\begin{array}{ll}\hfill R\mathit{cos}{\widehat{\beta }}_i[{\mathit{cos}}^2{\widehat{\gamma }}_1{\mathit{cos}}^2& \left({\widehat{\gamma }}_2+\theta \right)+{\mathit{sin}}^2{\widehat{\gamma }}_1]+\hfill \\ & R\mathit{sin}{\widehat{\beta }}_i\mathit{sin}{\widehat{\gamma }}_1\mathit{cos}{\widehat{\gamma }}_1\mathit{sin}\left({\widehat{\gamma }}_2+\theta \right)+\hfill \\ & \mathit{cos}\left({\widehat{\gamma }}_2+\theta \right){\widehat{x}}_c+\mathit{sin}{\widehat{\gamma }}_1\mathit{sin}\left({\widehat{\gamma }}_2+\theta \right){\widehat{y}}_c\hfill \end{array}\end{array}\\ R\mathit{cos}{\widehat{\gamma }}_1\left[\mathit{sin}{\widehat{\beta }}_i\mathit{cos}{\widehat{\gamma }}_1+\mathit{cos}{\widehat{\beta }}_i\mathit{sin}{\widehat{\gamma }}_1\mathit{sin}\left({\widehat{\gamma }}_2+\theta \right)\right]+\mathit{cos}{\widehat{\gamma }}_1{\widehat{y}}_c\\ \begin{array}{ll}\hfill R\mathit{sin}{\widehat{\beta }}_i\mathit{sin}{\widehat{\gamma }}_1\mathit{cos}{\widehat{\gamma }}_1& \mathit{cos}\left({\widehat{\gamma }}_2+\theta \right)-\hfill \\ & R\mathit{cos}{\widehat{\beta }}_i{\mathit{cos}}^2{\widehat{\gamma }}_1\mathit{sin}\left({\widehat{\gamma }}_2+\theta \right)\mathit{cos}\left({\widehat{\gamma }}_2+\theta \right)-\hfill \\ & \mathit{sin}\left({\widehat{\gamma }}_2+\theta \right){\widehat{x}}_c+\mathit{sin}{\widehat{\gamma }}_1\mathit{cos}\left({\widehat{\gamma }}_2+\theta \right){\widehat{y}}_c\hfill \end{array}\end{array}\right], i=1~n.$$

(27)

When the system is in dynamic balance, the sum of moments in 3D for the central axis (${\mathit{z}}^{‴}$-axis) perpendicular to the orbital plane is zero. Thus, the dynamic equilibrium equation of the i-th ball around the ${\mathit{z}}^{‴}$-axis of the orbital plane can be obtained.

$${\widehat{\mathit{r}}}_{Bi}^{‴}\times {\mathit{F}}_{Bi}^{‴}·{\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T=0,i=1~n.$$

(28)

$$\begin{array}{cc}\hfill m_b{R}^2{\omega }^2\{-\mathit{cos}\left(2{\widehat{\beta }}_i\right)& \mathit{sin}{\widehat{\gamma }}_1\mathit{cos}{\widehat{\gamma }}_1\mathit{sin}\left({\widehat{\gamma }}_2+\theta \right)+\mathit{sin}{\widehat{\beta }}_i\mathit{cos}{\widehat{\beta }}_i\left[{\mathit{sin}}^2{\widehat{\gamma }}_1-{\mathit{cos}}^2{\widehat{\gamma }}_1{\mathit{sin}}^2\left({\widehat{\gamma }}_2+\theta \right)\right]\}\hfill \\ & +m_{b}R{\omega }^2\left\{{\widehat{x}}_c\mathit{sin}{\widehat{\beta }}_i\mathit{cos}\left({\widehat{\gamma }}_2+\theta \right)-{\widehat{y}}_c\left[\mathit{cos}{\widehat{\beta }}_i\mathit{cos}{\widehat{\gamma }}_1-\mathit{sin}{\widehat{\beta }}_i\mathit{sin}{\widehat{\gamma }}_1\mathit{sin}\left({\widehat{\gamma }}_2+\theta \right)\right]\right\}=0,i=1~n.\hfill \end{array}$$

(29)

The above dynamic equilibrium equations (Equations (12), (18), (24) and (27)) from the 3D dynamics are compared with the equations derived from the Euler–Lagrange method [9], which can be verified to obtain exactly the same results. However, the spatial positioning of ball balancing during vibration suppression can be better described and understood through the analysis of spatial patterns in 3D dynamics inference.

3.4. Characteristic of Ball Balance Positioning

From the perspective of 3D dynamics, if the centripetal force ${\mathit{F}}_{Bi}^{‴}(i=1~n)$ of each ball can be decomposed into a component force in the tangential direction of the track, this component will cause the ball to move along the track direction. It can be seen from Equation (26) that the torque exerted by the centripetal force of each ball against the ${\mathit{z}}^{‴}$-axis perpendicular to the orbital plane is zero. It means that the centripetal force of each ball has no component in the tangential direction of the orbit and ${\mathit{F}}_{Bi}^{‴}$ must pass through the ${\mathit{z}}^{‴}$-axis. As shown in Figure 4, when the system exhibits dynamic balance, the balls revolve around the spin axis ($\mathit{Z}$-axis) of the system with their respective stable and balanced radius at a constant angular velocity $\omega$. At this time, the centripetal force ${\mathit{F}}_{Bi}^{‴}$ acting on the ball by the system should be on the perpendicular line from the mass center of the ball to the spin axis. In other words, when the system is in dynamic balance, the centripetal force acting on each ball must be perpendicular to the spin axis and pass through the central axis of the ball orbit.

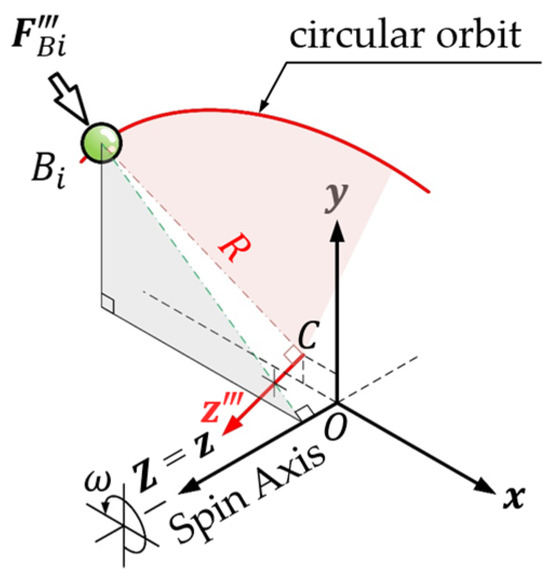
Figure 4. Centripetal force and attitude of ball positioning.

The aforementioned inferences reveal that the balls should have the spatial positioning characteristic in dynamic balance. Furthermore, Equation (14) expresses that the dynamic equilibrium displacement ${\widehat{z}}_c$ of the rotor centroid is zero. It shows that all forces acting on the system are on parallel planes perpendicular to the $\mathit{Z}$ (=z) axis during dynamic balance, so unforce in the rotation axis. This means that while the balls in the skew-mounted orbit may temporarily cause vibrations at the $\mathit{z}$-axis during the transient period of the system, once the steady-state balance and the balls are completely positioned, the vibration of the $\mathit{z}$-axis will eventually be attenuated to zero regardless of whether the system achieves a complete balance of vibration suppression.

4. Verification of Spatial Geometric Characteristic

In Section 3.4, the characteristic of ball positioning in the dynamic equilibrium state is stated. For rigor, the geometric relationship of the space vector is used to examine and verify it. As shown in Figure 5a, any two vectors ${\mathit{L}}_1$ and ${\mathit{L}}_2$ in space, where $P_1$ and $P_2$ are arbitrary points on the ${\mathit{L}}_1$ and ${\mathit{L}}_2$ vectors, respectively, and the displacement of point $P_1$ relative to point $P_2$ is the vector $\mathit{\Delta }$. When the shortest distance $d$ between ${\mathit{L}}_1$ and ${\mathit{L}}_2$ is zero, it means that vector ${\mathit{L}}_1$ and vector ${\mathit{L}}_2$ intersect in 3D space, where

$$d=\frac{\mathit{\Delta }·\left({\mathit{L}}_1\times {\mathit{L}}_2\right)}{‖{\mathit{L}}_1\times {\mathit{L}}_2‖}.$$

(30)

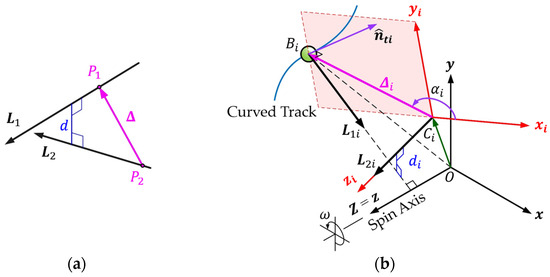
Figure 5. (a) Schematic diagram of spatial vectors and shortest distance; (b) Express the spatial vectors of the vibration suppression system.

Consider an arbitrary curved track in space rotating around a fixed $\mathit{Z}$-axis in space at constant angular velocity $\omega$, and the ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ coordinate synchronized with the spin axis is selected as the reference coordinate system, as shown in Figure 5b. First, the perpendicular line from the i-th ball $B_i$ to the spin $\mathit{Z}$-axis ($\mathit{Z}=\mathit{z}$) is described as the spatial vector ${\mathit{L}}_{1i}$. The curvature radius of the curved track at $B_i$ is $R_i$, the curvature center is $C_i$ and its unit tangent vector is ${\widehat{\mathit{n}}}_{ti}$. Define the vector pointing from $C_i$ to $B_i$ as ${\mathit{\Delta }}_i$, and the coordinate system ${<{\mathit{x}}_i{\mathit{y}}_i{\mathit{z}}_i>}_{C_i}$ with $C_i$ as the origin. The ${\mathit{x}}_i{\mathit{y}}_i$ is the plane formed by the two vectors ${\widehat{\mathit{n}}}_{ti}$ and ${\mathit{\Delta }}_i$, and the angular position of the vector ${\mathit{\Delta }}_i$ relative to the ${\mathit{x}}_i$-axis is denoted as ${\alpha }_i$. For the equilibrium position $B_i$ in the space-curved track, the vector ${\widehat{\mathit{n}}}_{ti}$ is perpendicular to ${\mathit{\Delta }}_i$. The ${\mathit{z}}^{‴}$-axis is the central axis of curvature perpendicular to the ${\widehat{\mathit{n}}}_{ti}{\mathit{\Delta }}_i$ plane, the unit vector of ${\mathit{z}}^{‴}$-axis is represented by the spatial vector ${\mathit{L}}_{2i}$.

Next, use the Euler coordinate transformation as in Section 3.1. Taking the $\mathit{z}$-axis as the roll axis, ${\varphi }_1$ as the pitch angle, and ${\varphi }_2$ as the yaw angle. The forms of matrices ${\mathit{T}}_{1i}$ and ${\mathit{T}}_{2i}$ are shown in Equation (1). Denote the vectors ${\mathit{\Delta }}_i$ and ${\mathit{L}}_{2i}$ in the ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ coordinate system as, respectively:

$${\mathit{\Delta }}_i={{\mathit{T}}_{1i}}^{-1}{{\mathit{T}}_{2i}}^{-1}\left[\begin{array}{c}{R}_i cos{\alpha }_i\\ R_i sin{\alpha }_i\\ 0\end{array}\right] \mathrm{and} {\mathit{L}}_{2i}={{\mathit{T}}_{1i}}^{-1}{{\mathit{T}}_{2i}}^{-1}\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right].$$

(31)

In the ${<\mathit{x}\mathit{y}\mathit{z}>}_O$ coordinate system, the position vector of $C_i$ is described as ${\mathit{r}}_{O{C}_i}={\left[\begin{array}{ccc}{x}_{C_i}& y_{C_i}& z_{C_i}\end{array}\right]}^T$ and the position vector of $B_i$ is described as ${\mathit{r}}_{O{B}_i}={\mathit{r}}_{O{C}_i}+{\mathit{\Delta }}_i$. ${\mathit{L}}_{1i}$ can be obtained from ${\mathit{r}}_{O{B}_i}$ and the unit vector $\widehat{\mathit{k}}$ of the $\mathit{z}$-axis.

$${\mathit{L}}_{1i}=\left({\mathit{r}}_{O{B}_i}\times \widehat{\mathit{k}}\right)\times \widehat{\mathit{k}},i=1~n.$$

(32)

Substitute Equations (29) and (30) into Equation (28), the shortest distance between ${\mathit{L}}_{1i}$ and ${\mathit{L}}_{2i}$ is

$$d_i=\frac{{\mathit{\Delta }}_i·\left({\mathit{L}}_{1i}\times {\mathit{L}}_{2i}\right)}{‖{\mathit{L}}_{1i}\times {\mathit{L}}_{2i}‖},i=1~n.$$

(33)

In general, it is impossible for the perpendicular of any position in the track to the spin axis of the system to be parallel to or coincide with its curvature center axis. So, $‖{\mathit{L}}_{1i}\times {\mathit{L}}_{2i}‖\ne 0$, calculate ${\mathit{\Delta }}_i·\left({\mathit{L}}_{1i}\times {\mathit{L}}_{2i}\right)$ to get

$$\begin{gathered} {\mathit{\Delta }}_i·\left({\mathit{L}}_{1i}\times {\mathit{L}}_{2i}\right)={R_i}^2\left[-\cos \left(2{\alpha }_i\right)\sin {\varphi }_1\cos {\varphi }_1\sin {\varphi }_2+\sin {\alpha }_i\cos {\alpha }_i\left({\sin }^2{\varphi }_1-{\cos }^2{\varphi }_1{\sin }^2{\varphi }_2\right)\right]+ \\ {R}_i\left[x_{C_i}\sin {\alpha }_i\cos {\varphi }_2-y_{C_i}\left(\cos {\alpha }_i\cos {\varphi }_1-\sin {\alpha }_i\sin {\varphi }_1\sin {\varphi }_2\right)\right],i=1~n. \end{gathered}$$

(34)

For the research of the ABB vibration suppression system, most of the assumptions are that the balls in the track can freely rotate except for viscous damping and that the balls are in dynamic balance without any external forces acting in the tangential direction of the track. At the same time, the self-weight of the balls and the friction within the track are ignored. This study uses Equation (32) to examine various previous research on ABB under the aforementioned assumptions, confirming that the equilibrium positions of the balls in each system all satisfy Equation (32) equal to zero. This means that after any ball in the track is balanced and positioned, the radial vector ${\mathit{L}}_{1i}$ of its stable rotation intersects with the vector ${\mathit{L}}_2$ of the curvature center axis of that position in the track. In other words, the balance positioning of the balls in the track must satisfy the spatial–geometric relationship of “the perpendicular from the ball stationing position to the system spin axis intersects with the curvature center axis of the track at that position”. The establishment of this geometric relationship helps to understand and predict the possible positioning of ABB balls.

4.1. Track and Rotor Coplanar

The dynamic balance system can be simplified into a two-dimensional system if the plane of the ABB’s track coincides with the rotor plane. It means that the central axis of the track and the spin axis of the system are always parallel or coincident, i.e., ${\varphi }_1={\varphi }_2=0$. Organize Equation (32) into

$$R_i\left(x_{c_i}\sin {\alpha }_i-y_{c_i}\cos {\alpha }_i\right)=0,i=1~n.$$

(35)

4.1.1. Ideal Installation

In addition to the track and the rotor coplanar, if the track center and the rotor centroid coincide with each other, ABB can be regarded as an ideal installation. First, to discuss under ideal installation conditions, the research into ABB with single track [3,4,5,14,15,16,17], multiple tracks [18], multiple balls [20,21], or radial springs [19]. After coordinate conversion and careful comparison of the equilibrium equations for ball positioning, we can confirm that each paper can reach the same conclusion and that the results shown can ensure that Equation (34) is satisfied. The geometric properties are described as follows:

(i)

When ABB can completely suppress the vibration of the rotor system, as shown in Figure 6a, where $x_{c_i}=y_{c_i}=0$, Equation (33) is necessarily satisfied. At this time, the central axis of the track completely coincides with the spin axis of the system, and the balls can be balanced to park at any position within the track. Therefore, regardless of the number of balls, track radius, and the number of tracks, the balls can balance at various corresponding positions in response to different rotor eccentricities.

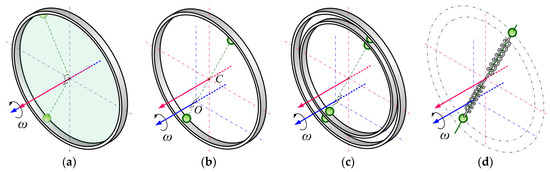Figure 6. The track is coplanar with the rotor: (a) Complete Vibration Suppression; (b) Incomplete Vibration Suppression; (c) Multiple Tracks; (d) Ball-Radial Spring.

(ii)

Regardless of whether the system is operating below or above the critical speed, if ABB cannot completely suppress the vibration of the rotor system, as shown in Figure 6b, the track center axis is parallel to but not coincident with the spin axis of the system. Equation (34) can be obtained by describing $\left(x_{c_i},y_{c_i}\right)$ in Equation (33) in polar coordinate form $\left(r_{c_i},{\theta }_{c_i}\right)$. Only if either ${\alpha }_i={\theta }_{c_i}$ or ${\alpha }_i={\theta }_{c_i}+\pi$ can the solution satisfy Equation (34).

$$R_i{ r}_{c_i}\sin \left({\alpha }_i-{\theta }_{c_i}\right)=0,i=1~n.$$

(36)

Discussed from the view of plane geometry, if one wants to make the perpendicular from the ball balance stationing point to the spin axis to intersect with the track center axis, as shown in Figure 6b, then the straight line passing through points O and C, which intersect the track at two points, can be both the possible and exclusive stationing positions for the balls. The phenomenon also applies to the ball positioning of ABB with multiple balls or multiple tracks or radial springs, as shown in Figure 6c,d.

4.1.2. Offset Installation

The mounting is offset along the rotor plane when mounting the ABB, then the center of the ABB track does not coincide with the rotor centroid. However, the orbital plane is still coplanar with the rotor plane, and the system in dynamic balance can also be simplified to a two-dimensional system. The equilibrium solutions of the system are as if the balanced steady-state mode described in [7] or the stationary balanced mode discussed in [8]. The rotor centroid, when balanced, is located on the spin axis and the balls are only balanced in the direction of the offset installation of the track center. Testing the results of the above two studies, the axis that is perpendicular from the ball to the rotation does intersect with the track center axis, and the geometric relationship inferred in this study is established. The balance positions of the balls are also shown in Figure 6b.

4.2. Track and Rotor Non-Coplanar (Skew-Mounted or Deflection Installation)

When the track and the rotor are not coplanar, the track center axis and the spin axis of the system are not parallel in space. Compare equilibrium Equation (27) of the system of the skew-mounted ABB and the spatial geometry Equation (32) of arbitrarily curved track: neither the system speed $\omega$ nor the ball mass $m_b$ is zero. If it is a circular orbit, the curvature radius $R_i$ at each equilibrium position in the track is the radius $R$ of the orbit, and the curvature center is located at the center of the orbit. Furthermore, if the Euler coordinate transformation and the ball phase angle variables are the same, i.e., ${\varphi }_1$=${\widehat{\gamma }}_1$, ${\varphi }_2$=${\widehat{\gamma }}_2+\theta$, and ${\alpha }_i$=${\widehat{\beta }}_i$, then the two equations are identical. The spatial geometry inference can be fully suited to describe the balance positions of the balls.

4.2.1. Balance Positions Based on Spatial Geometry

First, draw perpendiculars from each point in the track circumference to the spin axis of the system. It can be presented by the drawing to confirm the balance positions of ABB balls and know whether to satisfy the spatial geometry characteristic. When the system is in dynamic balance, Equation (14) shows that the orbit center is located on the $\mathit{x}\mathit{y}$ plane. In the inference of spatial geometry, the ${\mathit{x}}_i{\mathit{y}}_i$ plane is used to describe the orbital plane. For the sake of discussion, the ${\mathit{y}}_i$ axis is chosen as the intersection line between the orbital plane and the $\mathit{x}\mathit{y}$ plane when the system is dynamically balanced. Let ${\varphi }_1=0$ further simplify Equation (32) as follows:

$$R_i\left(\sin {\alpha }_i\cos {\alpha }_i{\sin }^2{\varphi }_2\right)-x_{c_i}\sin {\alpha }_i\cos {\varphi }_2+y_{c_i}\cos {\alpha }_i=0,i=1~n.$$

(37)

(i)

When the spin axis passes through the track center, due to the ABB installation deflection, the perpendiculars of each point on the circumference to the rotary axis intersect with the track center axis at only four positions ${\alpha }_i=0$, π and ±π/2, as shown in Figure 7a. This phenomenon aligns with the findings of the examination principle discussed in [9].

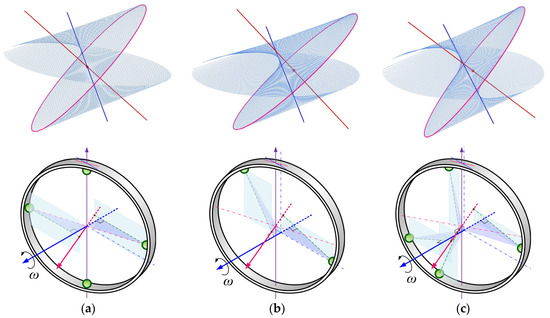Figure 7. Ball balance positions: When the spin axis (a) passes through the track center; and does not pass through the track center (b,c).

(ii)

If the spin axis does not pass through the track center, as long as the position of the track center ($x_{c_i},y_{c_i}$) and its equilibrium angle ${\varphi }_2$ can be determined, the intersections of the curved surface obtained by drawing perpendiculars to the spin axis at each point on the circumference of the track and the track center axis can be found. For two examples, (1) $R_i$ = 1, $x_{c_i}$ = −0.1, $y_{c_i}$ = 0.06 and ${\varphi }_2$ = 25° and (2) $R_i$ = 1, $x_{c_i}$ = −0.05, $y_{c_i}$ = 0.05 and ${\varphi }_2$ = 30° are shown in Figure 7b and Figure 7c, respectively, there may be two (${\alpha }_1$ = −12.77° and ${\alpha }_2$ = 111.87°) or four (${\alpha }_1$ = −165.91°, ${\alpha }_2$ = 102.58°, ${\alpha }_3$ = −9.79° and ${\alpha }_4$ = 98.28°) equilibrium positions of the balls.

4.2.2. Numerical Verification

For numerical verification, the dimensionless parameters used are defined as follows:

$$\begin{array}{c}x=\frac{x_c}{R}, y=\frac{y_c}{R}, M=m+2m_b, {\mu }_b=\frac{m_b}{M}, \eta =\frac{R m_b}{ϵ m}, {\omega }_n=\sqrt{\frac{k}{M}}, \Omega =\frac{\omega }{{\omega }_n},\\ \kappa =\frac{k_T}{R^2 k}, \zeta =\frac{c}{2 M {\omega }_n}, {\zeta }_T=\frac{c_T}{2 M R^2{ \omega }_n}, {\zeta }_b=\frac{c_T}{2 m_b R^2{ \omega }_n} \end{array}$$

(38)

Under the conditions of system parameters $\theta$ = 5°, $\varphi$ = 30°, $\Omega$ = 3, $\kappa$ = 0.2, ${\mu }_b$ = 0.1, $\zeta$ = 0.2 and ${\zeta }_b$ = ${ \zeta }_T$ = 0.1, the relationship between $\eta$ and the ball balance positioning numerically, as shown in Figure 8. The solid line is the solution obtained by satisfying the spatial-geometric relationship of the axis that is perpendicular to the balls and the track center axis. The part with η < 0.5 has two real solutions (and a pair of conjugate complex solutions). Starting from η ≥ 0.5, four real solutions appear, and as the value of $\eta$ gradually increases (about 1.93), two real solutions remain still. The hollow marked points in the figure are the ball balance positions obtained through numerical integration using the governing equation listed in [9]. It is worth noting that among the two equilibrium solutions in the η < 0.5 interval, only one is a stable solution, so the two balls gather together. When η = 0.5, although there are four equilibrium solutions, only one of them is stable. Two of the four equilibrium solutions in the interval 0.5 < η < 1.93 are stable. When η > 1.93, the only two equilibrium solutions are stable.

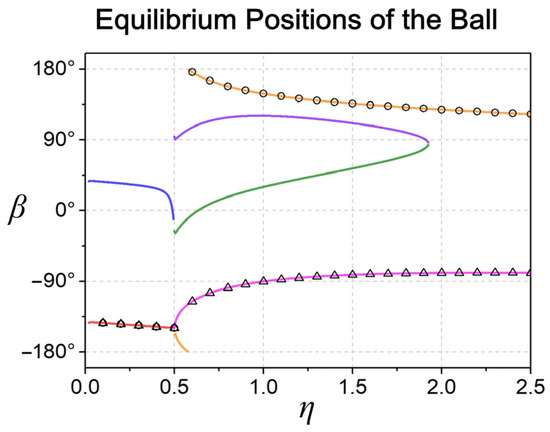
Figure 8. Ball balance positioning under different $\eta$ for the system with skew-mounted ABB.

In addition, take $\eta$ = 0.2 and $\eta$ = 1 in Figure 8 for numerical examination. Plot the transient responses of the system and label their steady-state equilibrium values, as illustrated in Figure 9 and Figure 10, respectively.

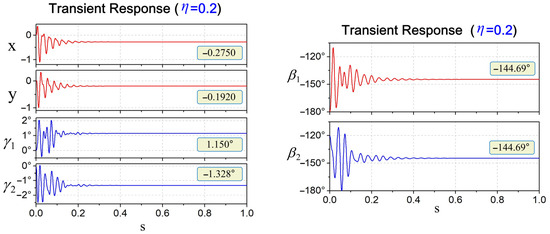
Figure 9. Transient response and steady-state equilibrium values of the system with η = 0.2.

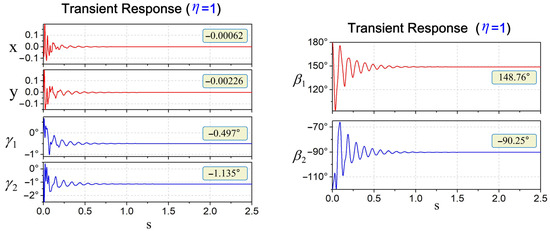
Figure 10. Transient response and steady-state equilibrium values of the system with η = 1.

Taking $\eta$ = 0.2 as an example, the numerical results when the system is in a steady state are described in the spatial coordinates mentioned in Section 4, it can be seen that the radius of curvature $R_i$, the positional coordinates of the curvature center ($x_{c_i}$, $y_{c_i}$, $z_{c_i}$), the pitch angle ${\varphi }_1$ and the yaw angle ${\varphi }_2$ of the ball track are $R_i$ = 1, $x_{c_i}$ = −0.275, $y_{c_i}$ = −0.192, $z_{c_i}$ = 0, ${\varphi }_1$ = 1.15° and ${\varphi }_2$ = 3.672°, respectively. By using the spatial geometric characteristic ${\mathit{\Delta }}_i·\left({\mathit{L}}_{1i}\times {\mathit{L}}_{2i}\right)$ = 0 of the ball positioning, the possible equilibrium positions of the balls can be found at 34.57° and −144.69°. Similarly, when η = 1, the possible equilibrium positions of the ball are found to be 30.10°, 120.70°, 148.76°, and −90.25°. Through comparison, it can be seen that the results derived from the spatial geometry can indeed denote the balls’ possible balance positions.

5. Conclusions

To explore the geometric characteristics of the dynamic balance positions of the balls in the ABB track for the eccentric rotor vibration suppression system with skew-mounted ABB, this paper analyzes the system model via 3D dynamics. All of the results verify complete consistency with the dynamic equilibrium equations derived from the Euler–Lagrange equation [9]. In particular, from the dynamic moment balance around the central axis of the orbit perpendicular to the orbital plane of the balls, list the $n$ dynamic equilibrium equations represented by the angular position of each ball’s balance positioning Equation (27). This helps to understand that the balls in dynamic balance do not rotate around the center axis of their tracks, but each rotate around the spindle of the system on different planes.

Through the discussion of 3D dynamics, it is especially important to analyze the dynamic equilibrium equations of ball positioning as this can help deduce the positioning conditions of the balls in dynamic balance. That is, the axis that is perpendicular from the balls to the rotating spindle of the system must pass through the central axis of the orbit perpendicular to the ABB plane. Upon the mathematical verification of the space geometry, we can confirm, with an arbitrary curved track, that the spatial geometric characteristic of ball balance positioning in broad terms of the ABB track is perpendicular from any balance positioning of the balls to the spin axis of the system intersects with the curvature center axis of the track at that position. Based on the ideal assumptions of ignoring the gravity of the balls, the friction of the track and the free moving of the balls without any external peripheral force except viscous damping, since the positioning characteristic of the balls in three-dimensional space during the dynamic balancing is only related to the relative position of the ball track to the spindle and the position of the curvature center of the track, the dynamic balanced positioning of the balls should comply with this spatial geometrical characteristic regardless of any spindle rotational speed, any rotor eccentricity, and whether the ABB has assembly deviations. This study applied this characteristic to the relevant research examples previously published on the stable balance positioning of the balls and obtained consistent results. Therefore, this characteristic is a necessary but insufficient condition for balanced positioning of the balls and can serve as a general rule.

The dynamic balanced positioning characteristic of the balls in the track of the ABB is completed in this study, based on some ideal assumptions. This could be used to explain the equilibrium positions of the balls in an arbitrary 3D curved track of the ABB. Further studies will find out the geometric relationship between the positioning of the ball and the peripheral constraints.