A Meta Reinforcement Learning-Based Task Offloading Strategy for IoT Devices in an Edge Cloud Computing Environment

Abstract

Developing an effective task offloading strategy has been a focus of research to improve the task processing speed of IoT devices in recent years. Some of the reinforcement learning-based policies can improve the dependence of heuristic algorithms on models through continuous interactive exploration of the edge environment; however, when the environment changes, such reinforcement learning algorithms cannot adapt to the environment and need to spend time on retraining. This paper proposes an adaptive task offloading strategy based on meta reinforcement learning with task latency and device energy consumption as optimization targets to overcome this challenge. An edge system model with a wireless charging module is developed to improve the ability of IoT devices to provide service constantly. A Seq2Seq-based neural network is built as a task strategy network to solve the problem of difficult network training due to different dimensions of task sequences. A first-order approximation method is proposed to accelerate the calculation of the Seq2Seq network meta-strategy training, which involves quadratic gradients. The experimental results show that, compared with existing methods, the algorithm in this paper has better performance in different tasks and network environments, can effectively reduce the task processing delay and device energy consumption, and can quickly adapt to new environments.

1. Introduction

Innovative mobile applications in a large number of IoT devices (e.g., face recognition, smart transportation, and AR/VR) are becoming an important part of today’s life as network communication technologies develop. According to the industry report by Cisco [1], by the end of 2023, about 3.5 billion people will have access to Internet services, which means that more than half of the world’s population will use one or more devices to connect to IP networks, and the number of devices connected to the network will be three times the global population, according to the European Telecommunications Standards Institute [2]. The Internet of everything age has arrived, and, with the increasing number of devices and the explosive growth of network traffic, the requirements for cloud computing resources from innovative mobile applications in IoT devices have skyrocketed, making it difficult to meet the basic needs of applications due to network latency caused by large network traffic and computational demand generated by offloading tasks. Mobile edge computing (MEC) [3] is a key technology that can help solve this problem. It does this by using edge servers with a certain type of computing power to move cloud computing and storage capacity to the edge, where it is not centralized [4].

Innovative IoT applications are frequently developed using modular programming in the mobile edge cloud computing environment [5], which contains many task modules internally that can be partially offloaded, and these task modules and their interdependencies can be well abstracted as a directed acyclic graph (DAG) [6], where the nodes represent tasks and the edges between the nodes represent task dependencies. This model has more task offload flexibility and can fully apply the heterogeneous parallel environment of MEC compared to the total offload model, but the resulting offload scheduling decisions are more difficult, mainly in terms of the following:

(1)

There are many subtasks, some of which can be processed concurrently, and there are more strategies to choose from. This makes the size of the problem several orders of magnitude bigger than the total offloading model, and it also makes the algorithm requirements higher.

(2)

The effect of the offloading strategy may be affected by various application types and subtask dependency characteristics, and the number of subtasks is inconsistent and not adaptive to all situations for conventional reinforcement learning algorithms.

Because mobile devices (MDs) have limited computational power and battery capacity, providing long-term steady services for various smart situations is difficult. Although the wireless power transfer (WPT) service can provide a stable power supply, the hybrid access point (HAP) technology in it provides both data transfer and energy transfer functions for MDs, and only one operation can be completed at a time; hence, a strategy to decide which subtasks need to be offloaded should be devised. The edge server and MD may collaborate to handle DAG tasks and improve service quality by offloading subtasks and WPT service times.

Much research is now being conducted by deep reinforcement learning (DRL), in which the DAG task offloading model is trained for a period of time and then utilized to select the optimum offloading solution, which is better than greedy algorithms, heuristic algorithms, and metaheuristics. However, this method requires a substantial quantity of sample data and suffers from low sample usage, slow learning speed, and low DRL adaptability. Different DAG tasks correspond to the DAG tasks considered in this paper, and, as users change applications, the MEC environment will change, making the relevant network settings incorrect. If the task offloading module is applied to multiple DAG tasks, it is necessary to retrain the network for different types of DAG tasks, which is very time-consuming and challenging to do in reality.

The meta reinforcement learning (MRL) framework may help accelerate the learning of new tasks by using the previous experience of different tasks to achieve quick adaptation to new tasks. MRL learns in two stages: an outer loop that learns a series of common experiences from multiple tasks to get the meta-strategy parameters, which requires more computational resources, and an inner loop that is based on meta-strategy parameters that can be adapted to new tasks with a small amount of experience-specific learning [7]. Using MRL to solve the computational offloading problem has several advantages for our MEC system. The meta-strategy learning in the system can be performed on the edge server, while the inner-loop training is performed on the MD. This is because the inner-loop training only requires a few simple steps and a small amount of sampled data; hence, it can be performed on the MD with limited computing power and data, so that the resources of the edge server and the MD can be utilized.

Considering the above, this paper conducts research around dynamic edge scenarios and proposes MTD3CO, a meta reinforcement learning-based task offloading strategy that takes into account DAG task types, subtask decisions, device power, WPT service time, task completion time, and other factors to solve the problem that conventional reinforcement learning algorithms are inefficient and cannot adapt to various types of mobile applications. In this paper, we first describe the process of unloading scheduling decisions for different types of DAG tasks as each different MDP, then modify the network of the TD3 algorithm to design a strategy and action network suitable for task unloading problems with different numbers of subtasks, and finally transform the DAG subtask decision process into a sequential prediction process. Each RNN network included in the algorithm is trained on the basis of the TD3 algorithm, with its training process primarily divided into inner-loop training and outer-loop training. Outer-loop training is primarily performed by the outer-loop learner of the edge server, which is uniformly trained for all applications in the system corresponding to the MDP environment and obtains the meta-strategy. The inner-loop learner on the edge device then downloads the meta-strategy parameters, initializes its own network, and performs a small number of training iterations to fine-tune the strategy according to its own task characteristics, achieving the goal of adapting to different tasks without requiring time-consuming retraining for general-purpose tasks. The following is a summary of this paper’s primary contributions:

• An edge system model, including a wireless charging module, is designed for the complicated edge computing environment for various types of mobile applications; on the basis of this architecture, a delay model, energy consumption model, and power model are built to quantify strategy performance.
• To address the problem of new tasks not being adapted quickly enough, a meta reinforcement learning-based task offloading decision (MTD3CO) is proposed. Among them, a Seq2Seq-based deep network suitable for the task offloading process is created to change the offloading decision into a sequential prediction process in order to accomplish adaptation for applications with different numbers of subtasks. To optimize the second-order gradient present in the meta-strategy solution, a first-order approximate optimization algorithm is proposed to accelerate the solution.
• Some simulation experiments were built on the basis of practical applications for tasks with different DAG topologies, including DAG topology, number of tasks, and transmission speed between MD and edge servers. After simulation experiments and comparing them to some baseline methods (e.g., improved DRL algorithm, HEFT-based heuristic algorithm, and greedy algorithm), it was shown that MTD3CO produced the highest results after only a few training steps.

The remainder of this paper is organized as follows: Section 2 introduces related academic research; Section 3 constructs the edge system model and models the task offloading problem; Section 4 describes the MTD3CO algorithm’s design and implementation; Section 5 presents simulated experiments and results; Section 6 concludes and reviews the paper’s work.

2. Related Work

2.1. Task Offloading Model

Because task offloading operations for MEC primarily consist of local execution, overall offloading, and partial offloading, the current study uses two task offloading models: the overall offloading model and the partial offloading model [8]. The overall offloading model and the partial offloading model both have advantages and disadvantages; the overall offloading model is relatively simple, and the algorithm is simple to implement, but resource utilization is low. However, the partial offloading model is more complex, and the algorithm has higher requirements; however, if the strategy is reasonable, it can fully utilize the resources.

The overall offload model assumes that the tasks to be offloaded cannot be partitioned, and that each task is independent of the other. The offload strategy needs to make the decision of local execution or offload execution for each task with a specific optimization goal and meet the needs of more applications by utilizing the computing and storage capacity of the edge server. Task offloading under the overall offloading model has been extensively studied in academia. Lin et al. [9] studied an edge server placement at the edge of a base station scenario, looked at the task execution cost problem between multiple users and an edge server in this area, and set up a cost model to minimize the overall task execution cost as the goal for overall task offloading decision. [10] added wireless charging to the system and developed an edge model of a device with wireless charging modules with task decisions consisting of charging times and offloading decisions, using alternating direction multiplier decomposition techniques to reduce the strong coupling between unloading decisions and charging times and to overall speed up the mobile device performing the task by jointly optimizing each choice. Fan et al. [11] studied the problem of collaboration between multiple edge server systems, finding that, when the server load is too high, the user experience suffers significantly, and that, by offloading the ineffective decisions to other systems, the overall system’s effectiveness improves and the user experience improves. Regarding the improvement of task processing speed in the Internet of things, Table 1 lists the differences between the approach proposed in this paper and existing methods.

Unlike the overall offload model, in the partial offload model, the application is able to offload some of the modules in the task for processing while the other part remains processed locally, and the two approaches can be performed in parallel [12]. The model assumes that each module of the application can be processed independently as a subtask. According to the backward and forward dependencies generated by the business logic, these subtasks must be processed in a certain order, and the offload strategy makes offload decisions for each subtask in a certain order, with the edge serv12er and the mobile device processing the tasks simultaneously. The partial offload model is more flexible and can use all of the heterogeneous parallel resources in MEC to get the most out of the performance of mobile devices and edge servers. Liu et al. [13] studied the MEC scenario of multiple edge servers collaborating on AR applications, first modeling the application as a directed acyclic graph (DAG) as a function of the connections between each module of the AR application task, and then investigating the performance of the particle swarm algorithm on real-time AR task offloading, despite the offloading scheme achieving optimal performance. The level of difficulty is high. As a result, the authors devised a heuristic algorithm to solve the problem, which produces a solution that is similar to particle swarm optimization but with less time complexity. Liang et al. [14] proposed a new blockchain-based secure task offloading framework for MEC systems with corresponding improvements in execution latency and energy consumption, as well as a deep reinforcement learning-based task offloading decision algorithm to efficiently derive near-optimal task offloading decisions to address the challenges of dimensionality and dynamic nature of the scenario.

Table 1. Comparison of differences in Internet of things task processing approaches.

Method	Research Focus	Research Method	Main Contribution	Differences from Other Papers
[10]	Rate maximization for wireless powered mobile-edge computing with binary computation offloading maximizing computation rate for wireless powered mobile-edge computing with binary computation offloading	Binary computation offloading	Maximizing computation rate	This paper uses meta reinforcement learning to handle more complex task offloading decision-making problems
[11]	Computation offloading based on cooperation among mobile edge computing-enabled base stations	Base station cooperation	Minimizing energy consumption	This paper uses meta reinforcement learning to adaptively make task offloading decisions
[13]	Code-partitioning offloading schemes for augmented reality in mobile edge computing	Code partitioning offloading	Minimizing latency	This paper uses meta reinforcement learning to handle different types of tasks and environments
[14]	Secure task offloading in blockchain-enabled mobile edge computing with deep reinforcement learning	Blockchain, deep reinforcement learning	Secure task offloading	This paper uses meta reinforcement learning to dynamically adjust task offloading strategies
This paper	Task offloading strategy for IoT devices in an edge cloud computing environment	Meta reinforcement learning	Improving task processing speed	This paper adopts a meta reinforcement learning approach to adaptively make task offloading decisions considering multiple factors, such as energy consumption, latency, and task types

Table 1. Comparison of differences in Internet of things task processing approaches.

Method	Research Focus	Research Method	Main Contribution	Differences from Other Papers
[10]	Rate maximization for wireless powered mobile-edge computing with binary computation offloading maximizing computation rate for wireless powered mobile-edge computing with binary computation offloading	Binary computation offloading	Maximizing computation rate	This paper uses meta reinforcement learning to handle more complex task offloading decision-making problems
[11]	Computation offloading based on cooperation among mobile edge computing-enabled base stations	Base station cooperation	Minimizing energy consumption	This paper uses meta reinforcement learning to adaptively make task offloading decisions
[13]	Code-partitioning offloading schemes for augmented reality in mobile edge computing	Code partitioning offloading	Minimizing latency	This paper uses meta reinforcement learning to handle different types of tasks and environments
[14]	Secure task offloading in blockchain-enabled mobile edge computing with deep reinforcement learning	Blockchain, deep reinforcement learning	Secure task offloading	This paper uses meta reinforcement learning to dynamically adjust task offloading strategies
This paper	Task offloading strategy for IoT devices in an edge cloud computing environment	Meta reinforcement learning	Improving task processing speed	This paper adopts a meta reinforcement learning approach to adaptively make task offloading decisions considering multiple factors, such as energy consumption, latency, and task types

2.2. Task Offloading Algorithm

In recent years, many studies have focused on the task offloading problem in mobile edge computing. In order to efficiently utilize limited resources, Arkian et al. [15] investigated the problems of data user association, task assignment, and data center-oriented virtual machine placement. The algorithm complexity is reduced, and the application response time is shortened by converting these nonlinear problems into a mixed-integer linear programming problem to solve, improving the user experience across a large number of tasks. Ma et al. [16] studied the problem of spectrum access, computational offloading, and radio resource allocation in a multiuser environment with multiple edge access points and proposed a genetic algorithm-based task offloading strategy. It divides the problem into two steps, offloading decisions and resource allocation, and then solves these two steps separately using an optimized genetic algorithm. Alhelaly et al. [17] proposed an efficient resource allocation and computation offloading model for a multiuser, multi-drone supported mobile edge cloud computing system that is scalable to support the increase in network traffic without degrading performance, considering computation offloading and resource allocation issues. In addition, the network deploys multistage mobile edge computing (MEC) technology to provide computing capabilities at the edge of the radio access network (RAN). The model problems presented in the article are transformed into various types of optimization problems, which are then solved using traditional optimization algorithms such as integer programming, nonlinear programming, convex optimization, and heuristic algorithms to obtain theoretical or approximate optimal solutions. The main problem is that the MEC environment needs to be modeled, and the algorithms are too complicated to be used directly in the real world, especially in situations where real-time performance is important.

Reinforcement learning is also widely used in task offloading problems because of its self-learning and adaptive features, as well as its better global search capability and advantages in solving large-scale complex problems. Zhang et al. [18] studied task scheduling strategies in MEC scenarios where the mobile device movement is unknown and proposed using a reinforcement learning technique called Deep Q-Network (DQN) to learn the optimal unloading strategy for mobile devices. The proposed DQN-based offloading algorithm does not require the mobile device’s movement pattern or the environment model, which eliminates the discretization error shown in previous work and allows the proposed algorithm to summarize previous experience, which is especially useful when dealing with a large number of states. Lu et al. [19] considered a graph offloading model with DAG dependencies for subtasks and used long short-term memory networks, post hoc experience playback, and candidate networks to improve the DQN algorithm separately in order to optimize the task offloading strategy. Given the inability of existing cloud computing paradigms to handle real-time and latency-sensitive ASA (automatic speech analysis) tasks, Li et al. [20] exploited mobile edge computing and deep learning (DL) to investigate the DL-enabled ASA task offloading problem in mobile edge cloud computing networks to minimize the total time to process ASA tasks, thus providing an agile service response, which enables edge servers to derive user tolerance limits through linear regression models, further improving the quality of user experience.

The above study achieved adaptation to the environment through deep reinforcement learning (DRL), which is able to summarize the optimal strategy through learning experience without knowing the state of the environment. After a certain number of learning sessions, the deep network parameters reach convergence, at which point the task offloading strategy achieves better results than greedy algorithms, heuristic algorithms, and metaheuristics and does not increase the time required for decision making due to the complexity of the model. However, this method relies on a large amount of sample data, having the same problems as traditional DRL of low utilization of samples, slow learning speed, and poor adaptability. In DAG task offloading, different applications correspond to different DAG applications, and, when users use other applications, the corresponding network parameters are invalidated because of the change in application characteristics. To use the task offloading module on different DAG tasks, the network must be retrained for each type of DAG task. This takes a long time and is hard to do in real life.

The meta reinforcement learning (MRL) framework [21] is able to use the experience of a series of different tasks to accelerate the learning of new tasks as a way to achieve rapid adaptation to different tasks. Generally speaking, MRL is a two-stage learning process: the first stage is outer-loop learning, which aims to learn the common experience of a series of different tasks and requires more computational resources; the second stage is inner-loop learning, which builds on the common experience learned in the outer loop and fine-tunes the experience according to the task under its responsibility to make the strategy better fit its task [22].

There are numerous advantages to using MRL to solve the computational offloading problem in MEC systems. First, because mobile devices run different applications, their offloading policies are not always the same, and MRL technology allows mobile devices to use the learning experience of other devices to quickly adjust their own offloading policies, unlike reinforcement learning, which requires retraining. Second, the system’s outer-loop learning, which is performed on the more powerful edge server, and the system’s inner-loop learning, which can be performed on mobile devices, are both performed on the more powerful edge server. This makes full use of the edge server’s and mobile devices’ resources. Inner-loop training can be performed on mobile devices with limited computation and data since it just requires a few simple steps and a small quantity of sampled data. This learning strategy makes full use of all the capabilities in the system and can speed up the training. As a result, this element of the research has great practical significance.

2.3. Task Scheduling Strategy

The current MEC research mostly focuses on task offloading and resource allocation optimization in different networking scenarios with different optimization targets. Some of the most common scenarios and objectives are outlined below.

2.3.1. Multiple Mobile Devices, Single Edge Server

Academics study the subsystems in complex MEC settings independently in this scenario, as well as in the case where a single edge server offers services to several mobile devices. Because the edge server’s computation and storage capacity cannot support all devices at the same time, task offloading should be based on the current resource situation, and resource optimization is dependent on the state of the system after all devices have offloaded their duties. As a result, many aspects inside the system influence and are coupled with the offloading choice, and an effective offloading strategy needs to be established in order for the system to operate efficiently.

2.3.2. Multiple Mobile Devices, Multiple Edge Servers

In this situation, mobile devices have multiple edge servers capable of providing offload services, leading to a one-level increase in the problem dimension of the offload strategy. The algorithm needs to account for the problem of multi-edge server collaboration; the selection of edge servers is based on the quality of the communication channel and the edge servers’ resources, and the offload decision of one task has an unpredictable impact on subsequent tasks, which are important research areas.

2.3.3. Strategic Optimization Objectives

Li et al. [23] used the sum of latency cost and energy consumption of all mobile devices as the algorithm’s optimization objective. This is because the offloading decision of mobile devices has an impact on subsequent offloading; thus, reinforcement learning’s long-term objective optimization can be a good fit for task offloading. The authors built a reinforcement learning-based task offloading framework on this basis and applied two reinforcement learning algorithms. Experiments showed that an offloading strategy with long-term aims can reduce the device’s overall energy consumption and average latency.

3. System Model

3.1. Problem Description

The face recognition program can express its submodules in DAG and has many calculations. Using the task offloading on MEC as an example, task offloading may be more easily understood. Modules such as stitching, detection, and feature merging work together to perform a single face recognition task. These modules are in charge of their own services, which run independently as application subtasks based on business processes. Some subtasks are uploaded to the edge server for processing through the mobile device’s decision module, and the results are then returned to the mobile device through the network, while other subtasks run on the mobile device. Each edge server runs numerous virtual machines to help process the tasks uploaded by each mobile device, and the computational capability of the edge server is represented by f_s (the number of CPU cores multiplied by the clock speed of each core). In this paper, we assume that virtual machine resource allocation is equal; thus, each virtual machine’s computing power can be represented as $f_{vm}=\frac{f_s}{k}$. Many innovative applications, including face recognition applications, can be executed collaboratively by a number of subtasks split by business processes. In this paper, face recognition is applied to a DAG representation, denoted as $G=\left(T,E\right)$, where the vertex set T denotes the set of subtasks, while the edge set E records the execution requirements of the business process for the subtasks. The edge set is made up of directed edges $\overrightarrow{e}=\left(t_i,t_j\right)$, where $\overrightarrow{e}$ denotes that task $t_j$ is a subtask of task $t_i$, and that task $t_i$ is a precursor task of task $t_j$. According to the edge constraint, a subtask cannot begin execution until all of its preceding tasks have been completed. Lastly, in the graph $G=\left(T,E\right)$, the tasks without subtasks are called exit tasks and represent the end of the application task.

As shown in Figure 1, each individual subtask can be offloaded to an edge server or executed locally on a mobile device, both of which have different processing latencies. If the task is executed locally, the task latency is defined as $T_i^{MD}=\frac{C_i}{f_{MD}}$, where $f_{MD}$ denotes the mobile device’s CPU frequency, and $C_i$ denotes the number of computation periods required for the task; if the task is executed on an edge server, the task latency is divided into three parts: task upload, task execution, and result download. The latency of these three elements is mostly determined by job execution metrics, as well as system upload and download speeds. Using task $t_i$ as an example, some task execution metrics include task data size ${data}_i^u$, received result data size ${data}_i^d$, immediate wireless uplink channel transmission speed $R_u$, wireless downlink channel transmission speed $R_d$ in edge environments, and edge server CPU frequency $f_{vm}$ to process the task. These factors have an impact on task latency. Therefore, when task $t_i$ is offloaded to an edge server for execution, the task delay may be expressed as

$$\begin{array}{c}{T}_i^{EDGE}=\frac{{data}_i^u}{R_u}+\frac{C_i}{f_{vm}}+\frac{{data}_i^d}{R_d}.\end{array}$$

(1)

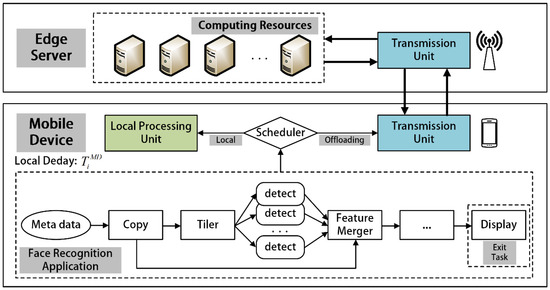
Figure 1. Example of face recognition in MEC.

Making appropriate offloading decisions for all subtasks so that they can minimize the total task processing latency while ensuring stable service is the goal of the edge task offloading strategy. To that aim, the latency, energy consumption, and device power in a single-edge-server multidevice MEC scenario are modeled in Section 3.2 in this paper.

3.2. Problem Modeling

The order of execution of a subtask-generated plan for a mobile application represented by $G=\left(T,E\right)$ is $A_{1:n}=\left\{a_1,a_n\dots a_n\right\}$, where $a_i$ is made up of the offloading decision $d_i$ of subtask $t_i$ and the mobile device’s WPT service time $T_i^{WPT}$. The offload decision of subtasks and the WPT service of mobile devices are performed sequentially according to the generated plan, and all precursor tasks in the plan are completed before the subtasks due to the dependencies between tasks. Therefore, the completion time of task $t_i$ depends on both the completion time of its precursor task and the resource availability time. In order to model the time delay of local processing and offloading processing, the upload completion time, edge server processing time, result download time, and local processing completion time of task $t_i$ are set as $F{T}_i^{upload}$, $F{T}_i^{compute}$, ${FT}_i^{download}$, and ${FT}_i^{MD}$, respectively. Moreover, if the WPT service shares a module with uplink and downlink, their available time has an impact, and the available time of uplink and downlink resources is denoted as $A{T}_i^{upload}$ and $A{T}_i^{download}$. $A{T}_i^{compute}$ and $A{T}_i^{MD}$ are used to describe the available time of edge server and mobile device computing resources. The available time of these resources is mostly determined by the end time of the preceding task that uses the resource, which in this paper is set to 0 if the resource is not utilized. According to the aforementioned definition, the task execution delay model, device energy consumption model, and device power model are created correspondingly.

3.2.1. Latency Model

If task $t_i$ is offloaded to the edge server for execution, then $t_i$ must not start execution until all its parent tasks are completed, the WPT service charging is performed, and the different resources required are accessible. Assuming that the set of parent tasks of task $t_i$ is $\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\left(t_i\right)$, the task upload completion time $F{T}_i^{upload}$ and uplink availability time $A{T}_i^{upload}$ may be calculated from the following equations according to the preceding requirements:

$$\begin{array}{c}\begin{array}{c}F{T}_i^{upload}=max\left\{A{T}_i^{upload},\underset{j\in \mathrm{p}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\left(t_i\right)}{max}\left\{F{T}_j^{\mathrm{M}\mathrm{D}},F{T}_j^{download}\right\}\right\}\hfill \\ +T_i^{\mathrm{u}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}+T_i^{WPT}\\ A{T}_i^{upload}=max\left\{A{T}_{i-1}^{upload},F{T}_{i-1}^{upload}\right\}\hfill \\ T_i^{\mathrm{u}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}=\frac{{data}_i^u}{R_u}\hfill \end{array}.\end{array}$$

(2)

The edge server computation completion time $F{T}_i^{compute}$ for task t_i relies on the time when computing resources are available $A{T}_i^{compute}$, the parent task completion time, and the actual computation time. Where the two requirements, parent task completion and computation resource availability, must be met at the same time, the bigger of these two values is picked. When the calculation is performed, the mobile device may start downloading the results only when the downlink is available. Hence, the time to start downloading is stated as the larger of the downlink availability time $A{T}_i^{download}$ and the computation completion time. In summary, the download completion time $F{T}_i^{download}$ may be introduced by the following equation:

$$\begin{array}{c}\begin{array}{c}F{T}_i^{compute}=max\left\{A{T}_i^{compute},max\left\{F{T}_i^{upload},\underset{j\in \mathrm{p}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\left(t_i\right)}{max}F{T}_j^{compute}\right\}\right\}\hfill \\ +T_i^{compute},\\ F{T}_i^{download}=max\left\{A{T}_i^{download},F{T}_i^{compute}\right\}+T_i^{download},\hfill \\ A{T}_i^{compute}=max\left\{A{T}_{i-1}^{compute},F{T}_{i-1}^{compute}\right\},\hfill \\ A{T}_i^{download}=max\left\{A{T}_{i-1}^{download},F{T}_{i-1}^{download}\right\},\hfill \\ T_i^{compute}=\frac{C_i}{f_{vm}},\hfill \\ T_i^{download}=\frac{{data}_i^d}{R_d}\hfill \\ \end{array}.\end{array}$$

(3)

If task $t_i$ is run locally, then the start time of task $t_i$ relies on the completion time of its parent task, the WPT service time, and the computational resources of the mobile device. ${FT}_i^{MD}$ may be obtained from the following equation:

$$\begin{array}{c}\begin{array}{c}{FT}_i^{MD}=max\left\{A{T}_i^{MD},\underset{j\in \mathrm{p}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}?\left(t_i\right)}{max}\left\{F{T}_j^{\mathrm{M}\mathrm{D}},F{T}_j^{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\right\}\right\}+T_i^{\mathrm{M}\mathrm{D}}+T_i^{WPT}\hfill \\ A{T}_i^{MD}=max\left\{A{T}_{i-1}^{MD},F{T}_{i-1}^{\mathrm{M}\mathrm{D}}\right\}.\hfill \end{array}.\end{array}$$

(4)

Finally, the total latency $T_{A_{1:n}}^{all}$ of the DAG tasks completed according to the execution plan $A_{1:n}$ may be described by the following equation:

$$\begin{array}{c}{T}_{A_{1:n}}^{all}=max\left[\underset{t_k\in \mathcal{K}}{max}\left(F{T}_k^{\mathrm{M}\mathrm{D}},F{T}_k^{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\right)\right],\end{array}$$

(5)

where $\mathcal{K}$ is the set of exit tasks of the DAG task G. The task is complete when the last completed exit task finishes. Overall, the purpose of the execution plan is to ensure the job completion rate and find the lowest execution delay and energy consumption while maintaining the power of the mobile device.

3.2.2. Energy Consumption Model

The WPT service time and energy consumption in the offload strategy of each subtask jointly affect device power, and this technique enables mobile devices with limited power to maintain consistent energy for task execution and data transfer. It can be described by the following equation:

$$\begin{array}{c}{CE}_i=\delta P^t{d}^{-\theta }g\cdot T_i^{WPT},\end{array}$$

(6)

where $\delta$ denotes the energy conversion efficiency and has a value between 0 and 1, $P^t$ denotes the charging power of the mobile device, d denotes the distance between the wireless charging modules, $\theta$ represents the distance loss, and $g$ represents the channel gain. Suppose the battery capacity of the gadget is $B^{cap}$ and the power after charging cannot exceed the battery capacity of $B^{cap}$. Then, after the WPT service time $T_i^{WPT}$ has passed, the power of the mobile device $B_i^{CE}$ can be figured out as follows:

$$\begin{array}{c}{B}_i^{CE}=\mathit{min}(B_{i-1}^{remain}+{CE}_i,B^{cap}),\end{array}$$

(7)

where $B_{i-1}^{remain}$ remaining is the remaining battery power of the mobile device after the previous task $t_{i-1}$ has been completed. In accordance with the energy consumption model, the remaining power of the device after the two policies of processing tasks, local execution and offloading to the edge server, can be expressed as follows:

$$\begin{array}{c}{B}_i^{MD}=\mathit{max}\left(B_i^{CE}-E_i^{MD},0\right),\end{array}$$

(8)

$$\begin{array}{c}{B}_i^{offload}=\mathit{max}\left(B_i^{CE}-E_i^{offload},0\right).\end{array}$$

(9)

If there is insufficient power, the processing task is considered unsuccessful. When the task offloading decision is denoted by $d_i\in \left\{\mathrm{0,1}\right\}$, the remaining processing power after task $t_i$ is expressed as

$$\begin{array}{c}{B}_i^{remain}=B_i^{MD}·d_i+B_i^{offload}·\left(1-d_i\right).\end{array}$$

(10)

In the edge environment, the offloading method of DAG tasks is highly flexible, but most of the tasks have very strict requirements for latency. Solving mixed-integer linear programming problems using standard heuristic algorithms demands a huge amount of processing resources, which is power-consuming, takes a long time to make decisions for edge devices, and does not match the real-time requirements. Deep reinforcement learning enhances the strategy by learning to support a large state space and action space, which is beneficial to solving such complex problems and meets the real-time requirements. However, deep reinforcement learning is sensitive to changes in the environment and DAG types, and, when the environment changes, relearning the strategy takes great time and computational resources, which hinders practical applications. Therefore, this paper proposes a task offloading algorithm called MTD3CO, which is based on meta reinforcement learning, to solve this problem. Table 2 shows the description of the main parameters in the text.

Table 2. Summary of main notations.

Notation	Description
$t_i$	The i-th task
$f_{vm}$	Computing power of virtual machines
${data}_i^u$$, {data}_i^d$	Data size of the task, data size of the received result
$f_{MD}$	CPU frequency of mobile devices
$T_i^{MD}$$,T_i^{EDGE}$	Task latency for local execution and edge-side execution
$F{T}_i^{upload}$	Upload completion time of task $t_i$
$F{T}_i^{compute}$	Edge server processing time
$F{T}_i^{download}$	Download completion time
$A{T}_i^{compute}$	Calculate resource availability time
$A{T}_i^{download}$	Downlink availability time
$\mathcal{K}$	Exit task set for DAG task G
$E_i^{MD}$$, E_i^{offload}$	Energy consumption generated by local execution, offloaded to the edge
$T_i^{upload}$$, T_i^{download}$	Task upload time, task download time

4. Design of Proposed Algorithm

In this section, we propose the edge task offloading method MTD3CO for MEC systems, which is based on meta reinforcement learning and uses the TD3 reinforcement learning algorithm. It explains the system components and the training process of the algorithm, then designs the MDP model under this architecture based on the model proposed in Section 3, and finally explains the algorithm’s design, principles, and pseudocode.

4.1. System Architecture

The MTD3CO algorithm makes full use of the MEC system capabilities by network training the algorithm on both mobile devices and edge servers. It splits the training process into two loops, with the inner-loop training for task-specific policies and the outer-loop training for meta-policies, with the inner-loop training performed on the mobile device and the outer-loop training performed on the edge server. Figure 2 shows a task offloading system that includes a mobile device and an edge server.

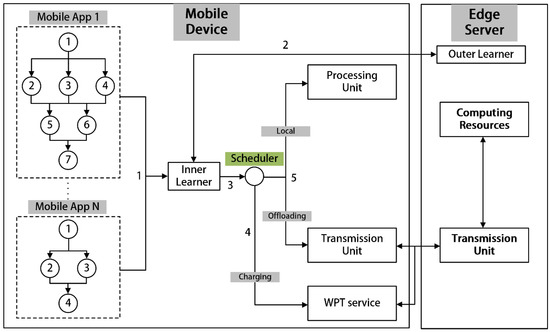
Figure 2. System architecture of MTD3CO task offloading.

Because mobile devices have a variety of different devices to perform application tasks with different foci, the DAGs used to describe the applications will change. Firstly, the inner-loop learner must download the meta-strategy from the outer-loop learner, initialize the strategy’s parameters to the inner-loop learner’s network, and then try some offloading with the specific application for which the device is responsible. Secondly, on the basis of these offloading experiences, the inner-loop learner’s network is trained to get its specific offloading strategy. Lastly, the edge server receives the inner-loop learner strategy for this device. This completes the inner-loop learning.

At the level of the edge server, it is responsible for collecting the inner-loop training experience of all inner-loop learners and extracting their shared characteristics. Using the collected data, the edge server trains the outer-loop learner network, gets the new meta-strategy, and performs the next round of training. Once a more stable meta-strategy has been obtained, outer-loop training can be stopped. The inner-loop learner can use the learning experience contained in this meta-strategy to quickly learn the specific offloading strategy for the task it is responsible for, and, because the meta-strategy contains experience shared by all inner-loop learners, only a few loops are required to achieve better results. With this fast iterative learning, the algorithm can adapt to different DAG tasks and environments.

4.2. MDP Modeling

For the different types of tasks in this chapter, we model them as multiple MDPs; each MDP corresponds to an individual task in meta-learning, and the aim of each task is to learn an effective offloading strategy for each MDP. We define the task distribution as $\rho \left(T\right)$, and the MDP for each task $T_i~\rho \left(T\right)$ is denoted as $T_i=\left(S,A,P,P_0,R,\gamma \right)$. To accommodate different task types, we divide the learning process into two parts: the first, in which each MDP learns its own specific strategy based on the meta-strategy; the second, in which all MDPs’ specific policies are extracted into a common meta-strategy and updated for the next learning loop. According to the system model, the status, action, and reward functions of the MDPs are defined below.

(1)

State Space

When offloading a subtask, the subtask’s execution latency is dependent on the CPU cycles required by the task, the size of the data being uploaded and downloaded, the DAG topology, the decision of the previous task, the transfer rate, the device power, and the MEC resources. The state space of subtask $t_i$ is denoted as $s_i=\left(G,A_{1:i-1},{data}_i^u,C_i,{data}_i^d,T_i^{max},B_{i-1}^{remain}\right)$, where G denotes the DAG topology of the task to which the subtask belongs. $A_{1:i-1}=\left\{a_1,a_n\dots a_{i-1}\right\}$ is the offload decision record of the task t_i predecessor; ${data}_i^u$, $C_i$, and ${data}_i^d$ are the amount of data uploaded by task $t_i$, the amount of computation of the task, and the amount of data downloaded, respectively; $T_i^{max}$ is the maximum tolerated delay of the task, and exceeding it is defined as task failure; $B_{i-1}^{remain}$ is the remaining power on the device before executing task $t_i$. To convert the set of subtasks represented by G into a sequence of subtasks and preserve the priority relationship, we add indices to the tasks using $rank\left(t_i\right)$, and then sort the tasks according to the indices. We define $rank\left(t_i\right)$ as follows:

$$\begin{array}{c}rank\left(t_i\right)=\left\{\begin{array}{cc}{T}_i^{EDGE}\hfill & \hfill \mathrm{i}\mathrm{f} t_i\in K\\ T_i^{EDGE}+\underset{t_j\in child\left(t_i\right)}{max}\left(rank\left(t_j\right)\right)& \hfill \mathrm{i}\mathrm{f} t_i\notin K\end{array}\right.,\end{array}$$

(11)

where $T_i^{EDGE}$ is the time interval between the start of offloading of task $t_i$ and the result obtained from the edge server, and $child\left(t_i\right)$ is the set of direct subtasks of task $t_i$. According to $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(t_i\right)$, $G$ is converted to a direct parent task index vector and a direct child task index vector of task $t_i$, and the size of this vector is set to the maximum value contained in all applications or filled with 0 if it is less than the maximum value.

(2)

Action Space

The offload strategy for each task includes the offload decision and WPT service time, $a_i=\left(d_i,T_i^{WPT}\right)$, where $d_i$ denotes the offload decision ($d_i=\left\{\mathrm{0,1}\right\}$, where 0 means local execution and 1 means offload execution), and $T_i^{WPT}$ represents the duration of WPT service before each task execution. Here, it is specified that $T_i^{WPT}=t$. To simulate discrete actions, t is taken as a multiple of 0.01. WPT service duration and offload decisions affect task latency and device energy consumption together.

(3)

Reward Function

The optimal task scheduling decision should have the lowest task processing latency and the lowest energy consumption for mobile devices. If a task fails to execute due to inadequate power or execution timeouts, it is called a “task failure”, which is defined as $T_i\left(fail\right)$. The power consumed by each task $t_i$ execution may be expressed as the difference of total energy consumption $\mathsf{\Delta }{E}_i=E_{A_{1:i}}^{total}-E_{A_{1:i-1}}^{total}$, and task latency can be expressed as $\mathsf{\Delta }{T}_i=E_{A_{1:i}}^{all}-E_{A_{1:i-1}}^{all}$. Task failure can be defined as

$$\begin{array}{c}{T}_i\left(fail\right)=1,\Delta E_i>B_{i-1}^{remain},\Delta T_i>T_i^{max},\end{array}$$

(12)

where $B_{i-1}^{remain}$ denotes the remaining power after the MD has completed task $t_{i-1}$, and $T_i^{max}$ denotes the task’s maximum processing time. To minimize the total energy consumption $E_{A_{1:n}}^{all}$ and the total delay $T_{A_{1:n}}^{all}$ of the task processing, and to improve the task processing success rate, the algorithm designs the reward function as the task $t_i$ negative increments of delay and energy consumption and punishments for task failure, which can be expressed as

$$\begin{array}{c}{r}_i=-\left(\left(\phi \mathsf{\Delta }{E}_i+\left(1-\phi \right)\mathsf{\Delta }{T}_i\right)\cdot \left(1-T_i\left(fail\right)\right)+\omega \cdot T_i\left(fail\right)\right),\end{array}$$

(13)

where $\omega$ is the punishment factor for task failure, and $\phi$ is able to control the weights of the two optimization objectives according to demand.

4.3. Algorithm Design

4.3.1. Seq2Seq

The strategy for offloading task $t_i$ is defined as $\pi \left(a_i|s_i\right)$ on the basis of the MDP setting in Section 3.2.2. This means that, when task $t_i$ arrives at the decision module, the decision module makes the task offloading decision $a_i$ according to the current state $s_i$. Assuming that a particular DAG task $\mathrm{G}$ can be represented by n subtasks, the strategy for these n subtasks can be expressed as $\pi \left(A_{1:n}|\mathrm{G}\right)$. Because each task’s offloading decision is linked to the task before it, the chain rule can be used to represent $\pi \left(A_{1:n}|\mathrm{G}\right)$ in terms of $\pi \left(a_i|s_i\right)$.

$$\begin{array}{c}\pi \left(A_{1:n}|\mathrm{G}\right)={\displaystyle \prod _{i=1}^n}\pi \left(a_i|s_i\right).\end{array}$$

(14)

The decisions taken by each of a task’s n subtasks affect how that task will be executed, and the number of subtasks differs from task to task. This difference can cause training difficulties for traditional neural networks. The Seq2Seq deep network is able to support the input of a different number of decisions, and it accepts and processes this chained strategy with recurrent neurons, whose structure is shown in Figure 3 and Figure 4, which contains an encoder and a decoder. Both parts are implemented by recurrent neural networks, where the encoder compresses the subtask sequences into uniform context vectors, and then the decoder decodes these vectors to output the policy.

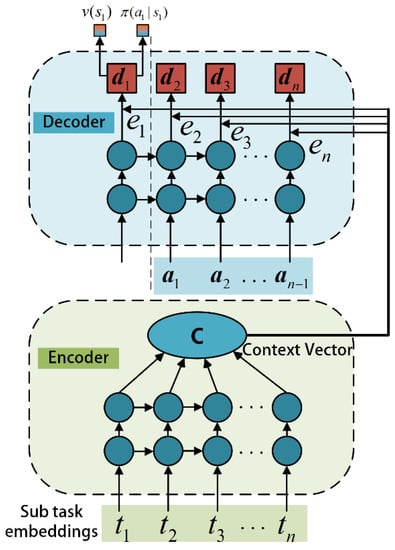
Figure 3. Task unloading network based on seq2seq.

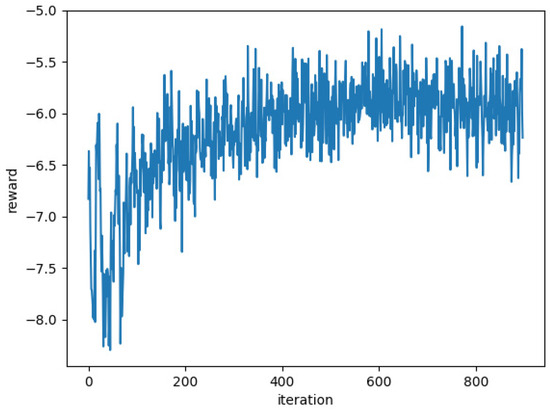
Figure 4. Training process of MTD3CO.

To keep the performance from going down because the context vector is too long, an attention mechanism is used. This makes the decoder focus on the parts that are closer to it when it is making the output. In the process of decoding and output, the context vector element is given greater weight the closer it is to the source. If the encoder’s input is the subtask state sequence $\left[s_1,s_2,\dots {,s}_n\right]$, the decoder’s output is the corresponding policy $\left[a_1,a_2,\dots {,a}_n\right]$, the encoder function is $f_{encoder}$, and the decoder function is $f_{decoder}$; then, the encoder of the i-th task hidden output may be represented as

$$\begin{array}{c}{e}_i=f_{encoder}\left(s_i,h_{i-1}\right).\end{array}$$

(15)

The context vector can be expressed as $c=\left[e_1,e_2,\dots ,e_n\right]$, and then the message is decoded by the decoder according to the last action $a_{j-1}$ in the context vector and the last decoder output $d_{j-1}$; its decoding formula can be expressed as

$$\begin{array}{c}{d}_j=f_{decoder}\left(c_j,d_{j-1},a_{j-1}\right),\end{array}$$

(16)

where $c_j$ is the weighted sum of partial context vectors by applying the attention mechanism, which is calculated as follows:

$$\begin{array}{c}{c}_j={\displaystyle \sum _{i=1}^n}{\mu }_{ji}{h}_i,\end{array}$$

(17)

where ${\mu }_{ji}$ is a probability distribution, which is calculated as follows:

$$\begin{array}{c}{\mu }_{ji}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(score\left(h_i,d_{j-1}\right)\right),\end{array}$$

(18)

where $score\left(h_i,d_{j-1}\right)$ is a function to determine the degree of matching between $h_i$ and $d_{j-1}$, and this function is defined as a trainable feedforward neural network in the literature. Lastly, the TD3 algorithm is improved by transforming the decoder output $d=\left[d_1,d_2,\dots ,d_n\right]$ into a policy and value network using two fully connected layers to make it applicable to the model of task offloading policy.

4.3.2. MTD3CO (Meta TD3 Computation Offloading) Implementation

In order to make the DAG task offloading adaptable to different tasks and, thus, achieve generalization, this chapter combines meta-learning and the TD3 algorithm [24] to improve the algorithm’s adaptability to the environment. After the initial training is complete, the algorithm can set up the outer-loop learner of the mobile device with a meta-strategy. The strategy can then be fine-tuned with a small number of specific tasks, and then the outer-loop learner strategy can be changed to fit the specific tasks of the mobile device.

For the actor–critic method, there is an unavoidable problem of overestimation due to cumulative errors. First, the TD3 algorithm uses the idea of double Q-learning by using two independent value functions, and using the smaller value between them in the update to reduce the deviation caused by overestimation. Second, when performing TD updates, the errors made at each step add up and make the estimation variance too high; thus, the TD3 algorithm uses the target network and delayed updates to solve this problem.

Lastly, the TD3 algorithm enhances the exploratory nature by adding noise to the target actions, which smoothens the values in the region near the value network actions and reduces the generation of errors. On the basis of the above improvements, assuming that the policy network in the TD3 algorithm is ${\pi }_{\varphi }\left(s\right)$, and the two value networks are $Q_{{\theta }_1}\left(s,a\right)$ and $Q_{{\theta }_2}\left(s,a\right)$ with parameters $\varphi$, ${\theta }_1$, and ${\theta }_2$, respectively, then the actions and expected rewards of the task unloading policy at each training can be expressed as

$$\begin{array}{c}\left\{\begin{array}{c}\tilde{a}={\pi }_{{\varphi }^{\prime }}\left(s^{\prime }\right)+\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\left(\mathcal{N}\left(0,\tilde{\sigma }\right),-c,c\right)\\ y\leftarrow r+\gamma \underset{i=\mathrm{1,2}}{min}{Q}_{{\theta }_i^{\prime }}\left(s^{\prime },\tilde{a}\right)\end{array},\right.\end{array}$$

(19)

where ${\varphi }^{\prime }$, ${\theta }_1^{\prime }$, and ${\theta }_2^{\prime }$ denote the parameters of the target policy network and the two target value networks, respectively, and $\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\left(\mathcal{N}\left(0,\tilde{\sigma }\right),-c,c\right)$ is the clipped noise function that makes the action fluctuate in a small range. $\gamma \in \left[\mathrm{0,1}\right]$ denotes the discount factor of learning. According to the expected reward, two value networks can use the same expected reward $y$ and the respective rewards of the current value network $Q_{{\theta }_1}\left(s,a\right)$ and $Q_{{\theta }_2}\left(s,a\right)$ to determine the TD error and update the current value network parameters, respectively, by minimizing the error as the objective, whose objective function formula can be defined as

$$\begin{array}{c}{J}_{critic}^{TD3}\left({\theta }_i\right)=N^{-1}\sum {\left(y-Q_{{\theta }_i}\left(s,a\right)\right)}^2,i=\left\{\mathrm{1,2}\right\}.\end{array}$$

(20)

For the update of the strategy network, the objective is to find the strategy parameter with the largest expected return, which can be updated in the actor–critic method using the deterministic strategy gradient algorithm, which uses gradient ascent to find the parameter with the largest return $\varphi$. Therefore, for the actor network in this section, the objective function can be expressed as

$$\begin{array}{c}{J}_{actor}^{TD3}\left(\varphi \right)={\left.N^{-1}\sum Q_{{\theta }_1}\left(s,a\right)\right|}_a{\pi }_{\varphi }\left(s\right).\end{array}$$

(21)

According to the model established in Section 3.2.2, we model the offloading tasks corresponding to different types of applications as multiple MDPs, each of which is responsible for generating an offloading policy for the same class of tasks. Formally, the task distribution is defined as $\rho \left(T\right)$, and each task follows the task distribution $T_i~\rho \left(T\right)$. MTD3CO and gradient-based meta reinforcement learning share a similar structure and also have two parts: inner-loop learning and outer-loop learning.

The inner-loop learning combines the Seq2Seq network with the TD3 algorithm, enabling its actor–critic network to adapt to training in environments with different numbers of subtasks. Compared with the VPG algorithm in the literature [25], it has better exploration ability and training stability. For each learning task $T_i$, according to the objective function above we define its value network objective function as $J_{critic}^{TD3}({\theta }_i^{T_i})$ with the objective of maximizing the expected gain, as shown in Algorithm 1, using the objective function gradient to update ${\theta }_1$ and ${\theta }_2$. Each task is updated a certain number of times to obtain the set of value network parameters; similarly, for the strategy network, we define the objective function as $J_{actor}^{TD3}\left({\varphi }^{T_i}\right),$ with the objective of minimizing the TD error by updating the parameters ${\varphi }^{T_i}$ with the gradient.

In outer-loop learning, following the theory of model-agnostic meta-learning proposed in the literature [5], the computation of the outer-loop learning objective function can be obtained; hence, for the meta critic network of outer-loop learning, its definition can be expressed as follows:

$$\begin{array}{c}{J}_{critic}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left({\theta }_{\mathrm{1,2}}\right)={\mathbb{E}}_{T_i~\rho \left(T\right)}\left[J_{critic}^{TD3}\left(U\left({\theta }_{\mathrm{1,2}}^{T_i},T_i\right)\right)\right],\end{array}$$

(22)

where $J_{critic}^{TD3}$ is the objective function of the inner-loop learning critic network for task $T_i$, and $U\left(\theta ,T_i\right)$ is the parameter after the task-set number of inner-loop learning gradient updates, which is defined as $U\left({\theta }_{\mathrm{1,2}}^{T_i},T_i\right)={\theta }_{\mathrm{1,2}}^{T_i}+\alpha {\sum }_{t=1}^k{{\nabla }_{{\theta }_{\mathrm{1,2}}^{T_i}}{J}_{critic}^{TD3}\left({\theta }_{\mathrm{1,2}}^{T_i}\right)}^t$, where k is the number of gradient updates for inner-loop learning and outer-loop learning with the objective of minimizing the objective function with gradient updates of the critic meta-parameters, but this objective function involves gradients of gradients that bring huge computational cost under a complex network such as Seq2Seq. To solve this problem, we use the first-order approximation method in [26]; the gradient of $J_{critic}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left({\theta }_{\mathrm{1,2}}\right)$ can be expressed as

$$\begin{array}{c}{{\nabla }_{{\theta }_{\mathrm{1,2}}}J}_{critic}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left({\theta }_{\mathrm{1,2}}\right)={grad}_{critic}^{MTD3CO}=\frac{1}{n}·\frac{1}{k}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{t=1}^k}{\nabla }_{{\theta }_{\mathrm{1,2}}^{T_i}}{J_{critic}^{TD3}\left({\theta }_{\mathrm{1,2}}^{T_i}\right)}_t,\end{array}$$

(23)

where n denotes the number of all tasks, k denotes the number of inner-loop training gradients, and similarly, for the meta-actor network with outer-loop learning, its objective function and approximate gradient can be obtained as

$$\begin{array}{c}{J}_{actor}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left(\varphi \right)={\mathbb{E}}_{T_i~\rho \left(T\right)}\left[J_{actor}^{TD3}\left(F\left({\varphi }^{T_i},T_i\right)\right)\right],\end{array}$$

(24)

$$\begin{array}{c}F\left({\varphi }^{T_i},T_i\right)={\varphi }^{T_i}+\alpha {\displaystyle {\sum }_{t=1}^k}{{\nabla }_{{\varphi }^{T_i}}{J}_{actor}^{TD3}\left({\varphi }^{T_i}\right)}^t,\end{array}$$

(25)

$$\begin{array}{c}{{\nabla }_{\varphi }J}_{actor}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left(\varphi \right)={grad}_{actor}^{MTD3CO}=\frac{1}{n}·\frac{1}{k}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{t=1}^k}{\nabla }_{{\varphi }^{T_i}}{J_{actor}^{TD3}\left({\varphi }^{T_i}\right)}_t.\end{array}$$

(26)

According to the objective function, we describe the overall training procedure in Algorithm 1.

Algorithm 1. Meta TD3 computation offloading

Input: Task distribution $\rho (T)$ Output: DAGs

The parameters of the random initialization policy network ${\pi }_{\varphi }$ and the two value networks $Q_{{\theta }_1}$ and $Q_{{\theta }_2}$ are $\varphi$, ${\theta }_1$, and ${\theta }_2$ Initialize the parameters of the target network ${\varphi }^{\prime }\leftarrow \varphi$, ${\theta }_1^{\prime }\leftarrow {\theta }_1$, ${\theta }_2^{\prime }\leftarrow {\theta }_2$ for iteration $k=\left\{\mathrm{1,2},\dots ,K\right\}$ do According to the task distribution $\rho \left(T\right)$, random sample of n tasks ${\{T}_1,T_2,T_3,\dots {,T}_n\}$ for task $T_i; i=\left\{\mathrm{1,2},\dots ,n\right\}$ do Initialize ${\varphi }^i\leftarrow \varphi$, ${\theta }_1^i\leftarrow {\theta }_1$, ${\theta }_2^i\leftarrow {\theta }_2 and {{\varphi }^i}^{\prime }\leftarrow \varphi$, ${{\theta }_1^i}^{\prime }\leftarrow {\theta }_1$, ${{\theta }_2^i}^{\prime }\leftarrow {\theta }_2$ Initialize experience pool $D_i$ Follow $a~{\pi }_{{\varphi }^i}+ϵ$, $ϵ~\mathcal{N}\left(0,\sigma \right)$, Sampling the task $T_i$ and storing the trajectory in $D_i$ for iterations $i=\left\{\mathrm{1,2},\dots ,k\right\}$ do Sampling $N$ trajectories from the experience pool $D_i$ According to the objective function $J_{critic}^{TD3}$, Update parameters using mini-batch gradient ${\theta }_1^i$, ${\theta }_2^i$ if i mod d then According to the objective function $J_{actor}^{TD3}$, Update parameters using mini-batch gradient ${\varphi }^i$ Update target network parameters ${{\varphi }^i}^{\prime }\leftarrow \tau {\varphi }^i+\left(1-\tau \right){{\varphi }^i}^{\prime }$ ${{\theta }_1^i}^{\prime }\leftarrow \tau {\theta }_1^i+{{\left(1-\tau \right)\theta }_1^i}^{\prime }$ ${{\theta }_2^i}^{\prime }\leftarrow {\tau {\theta }_2^i}^{\prime }+{(1-\tau )\theta }_2^i\prime$ end if Calculate ${grad}_{actor}^{MTD3CO}$, ${grad}_{critic}^{MTD3CO}$ end for Update meta-parameters $\varphi =\varphi +\beta {{\nabla }_{\varphi }J}_{actor}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left(\varphi \right)$ Update meta-parameters ${{{\theta }_{\mathrm{1,2}}={\theta }_{\mathrm{1,2}}+\mathsf{\beta }\nabla }_{{\theta }_{\mathrm{1,2}}}J}_{critic}^{\mathrm{M}\mathrm{T}\mathrm{D}3\mathrm{C}\mathrm{O}}\left({\theta }_{\mathrm{1,2}}\right)$ end for end for

The parameters of the meta-strategy and value network in the algorithm are _1 and _2, respectively, and the algorithm is a training process for the meta-parameters, which is mainly divided into inner-loop learning and outer-loop learning, where the learning task is first sampled once, followed by performing inner-loop training for each sampling task. When all inner-loop training is completed, we update the meta-parameters using the formula in lines 21 and 22 of Algorithm 1, and then proceed to the next inner- and outer-loop training.

4.4. Analysis of Algorithm Time Complexity

For the proposed MTD3CO offloading strategy, the main calculation lies in the inner cycle and the outer cycle. In the inner loop, the computational complexity is determined by the size of the state space and action space and the network. The computational complexity of the outer loop is O(nK), where n is the number of tasks, and K is the number of iterations.

5. Experimental Evaluation

In order to evaluate the proposed model and algorithm in this chapter, this section designs a simulated experimental environment, introduces the hyperparameters of the algorithm, and designs a set of experiments to evaluate the effect of the algorithm. In the simulation experiments, we designed an edge system simulator of the proposed model and generated some different applications represented by DAG in this simulation system to train and test the proposed algorithm.

5.1. Experimental Setup

5.1.1. Parameter Settings

The MTD3CO algorithm was implemented by TensorFlow, where the encoder–decoder network consisted of two layers of long short-term memory (LSTM) networks with 256 hidden units each, and a fully connected layer as the strategy network ${\pi }_{\varphi }$ in the algorithm, including two value networks $Q_{{\theta }_1}$ and $Q_{{\theta }_2}$. Both the inner-loop training and the outer-loop training learning rates were set to $5\times {10}^{-4}$ The algorithm’s noise parameter $\tilde{\sigma }$ was set to 0.2, and the clipping parameter $c$ was set to 0.5; thus, the noise was normally distributed in the range of $(-0.5,0.5)$. In inner-loop training, the gradient update number $k$ was set to 6, the parameter d for delayed update of the target network was set to 2, and the target network’s learning rate $\tau$ was set to 0.005. See Table 3 for related parameter settings.

Table 3. Parameters used in the MTD3CO algorithm.

Parameter	Value
Network architecture	Encoder–decoder network with 2 layers of LSTM networks (each with 256 hidden units) and a fully connected layer
Strategy network	${\pi }_{\varphi }$
Value networks	$Q_{{\theta }_1}$$\mathrm{and} Q_{{\theta }_2}$
Inner-loop and outer-loop training learning rates	$5\times {10}^{-4}$
Noise parameter	0.2
Clipping parameter	0.5
Range of noise	(−0.5,0.5)
Gradient update number in inner-loop training	6
Parameter d for delayed update of target network	2
Target network learning rate	0.005

5.1.2. Types of Tasks

Many real-world applications can be represented by DAGs having different topologies and different numbers of subtasks. When the features of topologies and the number of subtasks are comparable, they might represent similar applications, and the offloading techniques have many similarities. In this chapter, a DAG task generator is implemented in accordance with the literature [25] to generate different DAG datasets in order to simulate a variety of application tasks.

Four primary parameters control the DAG’s topology and characteristics: the number of subtasks N, the DAG width, the DAG density, and the task computation communication share. DAG width indicates the number of concurrent subtasks; when the number of subtasks is the same, the greater the width, the greater the number of subtasks that can be executed concurrently. DAG density shows how much subtasks depend on each other. Higher values mean that there are more backward and forward links between subtasks. The ratio of computational communication is used to control the task’s characteristics. The delay of task offloading is mainly composed of network communication and computational consumption time, where the larger the computational communication ratio, the larger the proportion of computational consumption time.

For the MEC environment, the upload and download speeds were set to $R_u$ and $R_d$ = 8 Mbps respectively, which would have some loss as the distance between the device and the signal source increased; the edge server $f_{vm}$ was set to 10 GHz; the clock speed of the mobile device was set to 1.5 GHz; the upload power and download power were $P^{upload}=0.5 \mathrm{W}$ and $P^{download}=0.6 \mathrm{W}$; the charging power of WPT service was $P^t=3 \mathrm{W}$; the battery capacity of the mobile device was 10 Wh.

5.1.3. Experimental Environment Settings

To evaluate the effectiveness of the MTD3CO algorithm proposed in this chapter, this section simulated a comparison experiment of task offloading strategies when the application and MEC environments changed. Three scenarios were created to evaluate the energy usage and latency of all algorithms. To make the problem simpler, the data size and required calculation for each subtask were assumed to be within a certain range. For example, assume that each subtask’s data size is between 5 kB and 50 kB, and that the CPU cycles required for each subtask are between 107 and 108 cycles. The computational communication ratio of the tasks is set to a random value between 0.5 and 0.8 since most mobile applications are computationally intensive. The time it takes to finish the computational part of a task depends on how high the computational communication ratio is.

In this paper, a task offloading model for MEC was developed by considering the computational performance, signal range, and geographical location of the edge server. The simulation environment used was deployed under the Ubuntu18 system, and, to implement the meta reinforcement learning model, the mainstream Tensorflow machine learning framework was used, using datasets from [23]. Throughout the experiments, we divided the dataset simulated by the DAG task generator into training and test datasets, with each set of DAG parameters differing in width, density, and number of subtasks. Each dataset had 100 DAG tasks with the same parameters but different topologies, simulating an application’s subtask relationships. The ultimate goal was to find the optimal offloading strategy for all offloading learning applications. The MTD3CO algorithm performed inner- and outer-loop training on multiple training datasets using Algorithm 1, and the DAG tasks in each dataset were trained to learn the strategy by the same inner-loop to obtain the optimal offloading strategy for this application. The outer-loop training summarized the commonality of the inner-loop training to obtain the meta-strategy, which was used as the algorithm’s initial strategy in the next inner-loop training to continue training specific policies for a specific DAG dataset, and the outer-loop training was continued until the meta-strategy converged. Lastly, the converged meta-strategy was used to set the initial network parameters for a test dataset that was used to see how effectively the offloading strategy worked.

5.2. Comparison Study and Discussion

We compared our approach MTD3CO with existing methods: (1) the improved deep reinforcement learning algorithm in [27], (2) the HEFT-based heuristic algorithm, and (3) the greedy algorithm. These methods were chosen because they are common algorithms when solving task offloading and are similar to our study.

To train the MTD3CO strategy, the DAG task generator was used to generate 20 training datasets with different DAG parameters and 100 DAG tasks with the same width and density in each set, each with 20 subtasks and density and width values of $\{0.5,0.6,0.7,0.8\}$. Each dataset represented a mobile device application preference, and finding an effective offloading strategy for each dataset was used as a learning task in the MTD3CO algorithm. Lastly, a training dataset was used to train the MTD3CO algorithm. In Algorithm 1, the number of sampling tasks n was set to 10, i.e., 10 training datasets were selected from 20 training datasets. Each dataset sampled N trajectories for gradient update with gradient number k = 6. Every two times the value network was updated, the target network and the strategy network were updated once.

Figure 4 shows the average reward during the training process. When the number of training times reached 200, it can be seen that the average reward increased substantially. This means that the strategy started to work and moved in a better direction. Finally, the average reward stabilized around −6 and converged. When the meta-strategy converges, the meta-strategy network at this point summarizes the commonality of different mobile application offloads so that effective task offloads can be performed for different applications. However, since all applications are considered at this time, the strategy is not the optimal strategy for a specific application at this time. For a specific application, only a small number of inner-loop learning iterations are needed to get the best strategy. Below, we make a few different changes to the environment that can be used to compare how well the meta-strategy adapts to the new environment.

When the meta-strategy training was completed, in order to verify the adaptability of the MTD3CO algorithm to new tasks and new environments, some test datasets different from the training dataset were randomly generated for testing. For a task that needs to be scheduled, the data points that users are most concerned about are latency and mobile device energy consumption performance. Thus, the experiments mainly compare the performance of the algorithm on these two metrics under the new task; three relevant experiments are described below.

5.2.1. Task Scenario Description

In the first experiment, to test the performance of the algorithm when the dependency situation between application subtasks changes, a test dataset with a different density than the training dataset was generated using the DAG task generator to simulate the offloading performance when a mobile device encounters this novel application. Subsequently, the performance of MTD3CO and the baseline algorithm was compared for a small number of tasks offloaded on the test dataset. The parameters of this test dataset were as follows: number of subtasks $N=20$, density = 0.4, and width = 0.8, where the density of DAG tasks did not appear in the training dataset, while both the number and the width of subtasks appeared. The energy consumption and latency for a small number of iterations are shown in Figure 5. HEFT could perform task offloading with a better strategy at the beginning because it predicts the partial offloading method and selects a better strategy, but it could not improve its strategy by increasing the number of iterations; hence, it remained at this performance, which was not the best. In this application, MTD3CO outperformed all algorithms in terms of energy consumption and time delay after five iterations, indicating that it achieved meta-strategy adaptation for this application. In general, because it only considers one factor, the greedy algorithm had the highest latency and relatively high energy consumption. The MTD3CO algorithm proposed in this paper outperformed the HEFT method in terms of latency and energy consumption after only a small amount of training, but the DRL method was still inferior to HEFT in both cases, and its energy consumption performance was less stable because the DRL method does not consider energy consumption. This shows that the MTD3CO method is more flexible and adaptive to new tasks and applications. Regarding the constant values for the greedy and HEFT schemes, they are not dependent on the number of iterations, and their results are expected to remain constant. In other words, the energy consumption and latency values for greedy and HEFT are not supposed to change with the number of iterations.

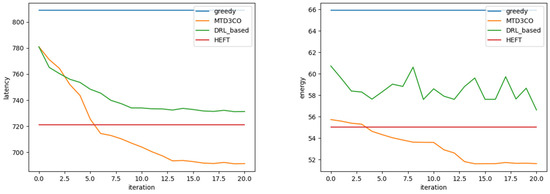
Figure 5. Scenario 1 comparison of delay and energy consumption after a few iterations.

The second experiment aimed to test the performance of the algorithm when the subtask concurrency varies. The DAG width of the test dataset was different from the training dataset, and the width in this scenario was 0.9, simulating the extreme case of application offloading with high subtask concurrency. As shown in Figure 6, at this point, HEFT did not perform as well as DRL and MTD3CO in terms of latency, and this fixed heuristic strategy tended to fall into suboptimal solutions when different applications were encountered. In terms of energy consumption performance, the DRL algorithm did not improve because it does not consider the energy consumption of the device and only takes the latency as the optimization objective. When faced with new applications, both MTD3CO and DRL algorithms outperformed HEFT after a small number of updates, because both algorithms are methods for updating the strategy, which adjusts the strategy in real time using reinforcement learning’s ability to adapt to the environment. They are more adaptable than algorithms with fixed policies like HEFT, and it can be seen that MTD3CO could adapt to new tasks faster than the conventional DRL algorithm because of its use of internal and external loop learning and its ability to use prior learning experience to guide the learning of new tasks.

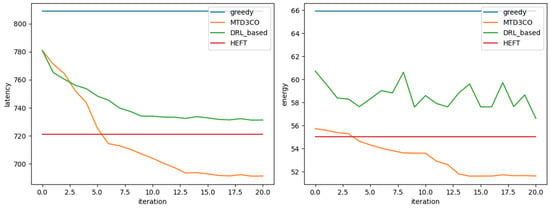
Figure 6. Scenario 2 comparison of delay and energy consumption after a few iterations.

5.2.2. Task Type Description

When the number of subtasks changes, the scale of the problem changes, and the algorithm becomes more demanding. In order to compare the performance of each algorithm when the scale of the problem increases, a scenario with the number of subtasks $N$ = 30, a density of 0.6, and a width of 0.6 was generated for experimentation. This application of width and density appeared in the training dataset, but the number of tasks increased, and, although the characteristics were the same, the problem was more complex. As shown in Figure 7, in terms of latency, the average latency of the DRL algorithm was only improved by 20 s after 20 iterations, indicating that the algorithm was still exploring the environment, with more strategies for poorer performance, not yet finding a better strategy, whereas MTD3CO surpassed DRL after two iterations, indicating that it successfully used meta-strategies to guide the learning and could adapt well to the increased complexity of the problem.

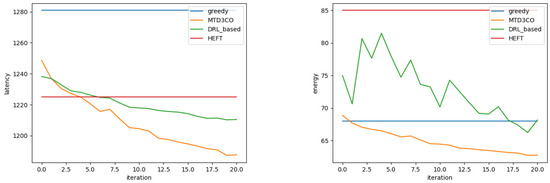
Figure 7. Comparison of delay and energy consumption when the number of subtasks changes.

6. Concluding Remarks and Future Directions

The task offloading problem of IoT devices in complex edge environments for various applications was investigated in this paper, assuming backward and forward connections between tasks and using DAG to represent subtask offloading. We proposed MTD3CO, a task offloading strategy based on meta reinforcement learning, in order to improve the algorithm’s adaptability to the environment and new applications. First, we studied the system model for mobile applications with different DAG types and mobile devices with different DAG types. The data and energy transfer system models were built, as well as the system’s latency model, energy consumption model, and MDP model. The concept of meta reinforcement learning was used to model the task offloading process in MEC as multiple MDPs based on the tasks, transform the unloading decision into a sequential prediction process based on the characteristics of subtask execution, design a seq2seq-based parameter sharing network to fit the optimal unloading decision, use this sharing network to improve the TD3 algorithm, and propose a meta reinforcement learning algorithm. Inner-loop training and outer-loop training are the two primary types of algorithm training. The outer-loop training network creates meta-parameters that are used to initialize the parameters for the inner-loop training network. The inner-loop training network then fine-tunes the parameters to quickly adapt to new applications based on their specific applications. Lastly, comparison experiments were used to assess the algorithm’s capability to adjust quickly in a variety of MEC environments and applications. The results show that the algorithm proposed in this paper could quickly adjust the strategy to adapt to the environment. Because the model in this paper ignores some signal effects and losses in the real world and uses a simplified problem model, future research will focus on how to design a more realistic problem model. Furthermore, the deep reinforcement learning algorithm employed is not cutting-edge; there are already some new algorithms under research, and how to apply more cutting-edge reinforcement learning algorithms will be a future focus of research. Lastly, achieving a unified system adaptation for heterogeneous IoT devices is a difficult future research area.