Abstract
In this paper, a nonlinear controller for tracking a desired trajectory for an underactuated hovercraft is considered. It is a modification of a method known from the literature. However, the control algorithm considered here has two important features that differ from the mentioned control strategy. First, it concerns the case when the center of mass does not coincide with the geometric center, which results in additional forces and moments of force. The lack of symmetry causes the original trajectory tracking method not to take this fact into account, while the proposed approach is a generalization of the known concept. Here, a diagonalization of the inertia matrix has been applied, by means of a velocity transformation, which made it possible to reduce the symmetric matrix to a diagonal form. Secondly, the transformed quasi-velocity equations of motion allow some insight into the dynamics of the vehicle as it moves, which was not shown in the source work. The offered approach was verified by numerical tests for a hovercraft model with three DOF and for two desired trajectories. The method can be useful in preliminary simulation studies at the controller selection stage without experimental validation.
1. Introduction
Underactuated vehicles, i.e., those that do not have all the control signals, have enjoyed growing interest for many years. This is due to the fact that their cost can be lower than fully actuated vehicles and their design can be simplified. To this group of vehicles belong hovercrafts. The control methods used can be divided from various points of view. They can be distinguished, for example, on the basis of the mathematical description, design or control task being carried out. Mostly considered is a model with three DOF for a vehicle moving horizontally. One of the criteria adopted here is the implementation of the controller into either the vehicle earth-fixed (inertial) frame or body-fixed body frame. Of the works concerning the first group, the following can be mentioned: [1] (nonlinear receding horizon control with real-time optimization), [2] (stabilization, fuzzy control), [3,4] (tracking control with two loops), [5] (LQR trajectory tracking), [6,7] (sliding mode control) and [8] (flatness-based tracking control). Trajectory tracking and path-following control schemes are discussed in the following: [9,10] (Lyapunov-based approach with backstepping) and [11] (Lyapunov-based approach with adaptive switching supervisory control). Despite the universality of the schemes, they have been applied to the hovercraft described in the inertial frame.
However, there are also many works belonging to the second group. An article on the stabilization of the hovercraft in [12] can be pointed out here. A modified genetic algorithm together with a fuzzy proportional integral derivative controller was presented in [13]. Trajectory tracking schemes based on a differential flatness property were proposed in [14,15,16]. Other methods used a flatness property with generalized proportional integral (GPI) control [17], backstepping [18], active disturbance rejection control, differential flatness or reinforcement learning [19]. Modified by disturbances, the model was used for tracking control in [20] (higher-order sliding mode control). A Lyapunov-based backstepping technique tracking algorithm was proposed in [9]. A strategy composed of the line-of-sight guidance law with a neural network-based adaptive dynamic inversion for the underactuated hovercraft following a prescribed path was found in [21]. The solution to the tracking control problem with simultaneous parameter identification was given in [22]. In [23], trajectory tracking and path following algorithms were developed for a hovercraft vehicle in the presence of uncertain parameters and unknown external disturbances, using the backstepping technique. An article [24] discussed and verified the design and trajectory tracking controller for an underactuated hovercraft using an observer, with unmeasured linear velocity and subject to time-varying disturbances. Another approach to trajectory tracking, namely based on the state transformation technique and cascade method, combined with a transverse function was proposed in [25]. In [26], it was shown that the quantitative feedback theory (QFT) technique provided an approach as well as a feasible control design methodology to solve the tracking problem of a nonlinear multivariable underactuated hovercraft, by using a manageable approach to nonlinear QFT synthesis based on the local linearization of the nonlinear plant about appropriate closed-loop outputs. It is also possible to adapt known control methods related to marine vehicles in horizontal motion. However, this requires careful verification because under some operating conditions such algorithms are unreliable, as was examined in [27].
Control methods can also be divided according to the design of the vehicle, that is, when only motors or motors and a rudder are used. If the vehicle has only thrusters, then schemes, e.g., from [4,5,6,9,17,19,20,25], can be proposed. On the other hand, when the hovercraft is equipped with a thruster and rudder, the relevant methods are as presented in [8,22,23,24]. The design of the vehicle is not a barrier to the applicability of methods with thrusters when equipped with a rudder because there are formulas for converting forces and moments of force as given in [23], recalling work from [28].
In this work, the trajectory tracking control scheme in the body-fixed frame for underactuated hovercrafts is considered. The proposed algorithm is a modification of the known controller developed in [22]. This modification extends the original scheme to non-symmetric vehicles. In the classical dynamics model, the vehicle is assumed to be symmetric which means that any inaccuracies in the model must be reduced using a controller. Furthermore, mutual interference between variables is also neglected in such a model. With this approach, we lose insight into the dynamics of the system, but we can effectively accomplish the task of trajectory tracking. The proposed algorithm addresses the trajectory tracking desired for a non-symmetric vehicle model. Such a model is closer to the real vehicle because it takes into account the fact of inaccuracy of the position of the center of mass as well as the external interactions on the individual variables. This is the case when the vehicle is not fully balanced or is carrying additional mass, which shifts the center of symmetry. The dynamics model is based on a velocity transformation which leads to a diagonalized inertia matrix. As a consequence, the new inertia matrix has a diagonal form and the unaccounted quantities are shifted to the other components of the dynamics equation. In addition, the control method by such a model can be used for simulation tests, which will help in later experimental studies. It can also be useful at the design phase when the model parameters can still be changed.
The contributions of this paper can be given as follows:
- (1)
- The proposed algorithm, unlike the scheme in [22] and many other algorithms, is suitable for asymmetric vehicles in the horizontal plane. Thus, it is an extension of the known control concept to a more general class of vehicles.
- (2)
- The theoretical development concerns the inclusion in the control algorithm of components related to the fact that the geometric center does not coincide with the center of mass. These components are then introduced into the stability proof of the system. In addition, the dynamic model of the vehicle is transformed to velocity space and, as a result of this transformation, new variables include the parameters of this model. Consequently, the combination consisting of a velocity transformation and a control algorithm yields a useful tool for estimating the behavior of a vehicle during trajectory tracking.
- (3)
- The simulation verification of the proposed trajectory tracking algorithm for estimating the effect of mutual coupling between velocities and evaluating the reduction in kinetic energy by each quasi-velocity (which includes coupling with other variables).
- (4)
- Pointing out some performance differences between the IQV-based control scheme and two other selected algorithms that use a diagonal inertia matrix model.
The remainder of this paper is organized as follows. In Section 2, the hovercraft model in terms of quasi-velocities is shown. The tracking control algorithm is presented in Section 3. Section 4 contains the simulation results of the confirmed effectiveness of the proposed controller. The conclusions are summarized in Section 5. At the end of the work, there is Appendix A.
2. Hovercraft Model
The model of a hovercraft moving horizontally that is considered in this work is shown in Figure 1.

Figure 1.
Underactuated hovercraft model sketch.
Using the North-East-Down (NED) frame (the inertial frame), the position and orientation of the vehicle is . Based on [22,29], the equations of motion of the hovercraft moving horizontally can be written as follows (symbols are explained in Appendix A):
where denotes the vector of velocities in the body frame (containing the surge velocity, the sway velocity and the yaw velocity). If the hovercraft is equipped with thrusters and a rudder, then the vector can be written as follows [22]:
. The remaining matrices and vectors have the following forms:
in which m, J are the vehicle mass and inertia, respectively; , are the mass displacements; mean the friction coefficients; and coefficients , represent linear drag.
Comment. In Equations (1)–(3), there are mass components, coefficients of friction linear drag and displacements. In the proposed method, it is not necessary to know the exact displacements (after transformation their influence is small but rather the mass components , are important). Although these are difficult to determine for a real vehicle, there are methods by which such information can be obtained. For example, one can use the parameter identification methods described in [22,30] for a hovercraft (a more detailed description of the general method is also known from [31]).
After velocity transformation, e.g., [32], the new equations instead of (2) are of the form
where is the vector of inertial quasi-velocities. Other symbols mean , , , , .
Finally, after dividing into two sub-systems, the set of Equations (6)–(11) can be given in the compact vector matrix form:
where is the linear velocity vector, is the corresponding quasi-velocity vector, , and
Assumption 1.
The presence of a discontinuous function ( denotes the argument of the function) in the system model makes the whole system a discontinuous system. Thus, in order to ensure the continuity condition of the system model, the condition (where c is a constant value that provides a good enough approximation) is assumed to be acceptable.
Assumption 2.
Considering Assumption 1, it is also assumed that the functions used for the controller design can also be approximated by functions. This approach to the approximation of signals of the controller is known from the literature, for example, [33,34]. In the functions, the constant c has the same value for both the model and the controller.
Comment. The notation of the function in the following work has been retained because of the symbolism used in the original paper [22]. Here, however, such notation should be understood as the function.
3. Control Scheme Using Quasi-Velocities
The proposed controller is a modification of the one coming from [22] and is an extension to vehicles with a model that takes into account the asymmetry caused by the shift of the center of mass. Thus, the goal is to also track the desired trajectory , which has a fixed point defined in the body frame . The disturbances are not taken into account. This means that the algorithm only considers the friction model as presented in Section 2, while it does not handle other types of external disturbances (deterministic or stochastic).
The tracking error is introduced as a measure of accuracy. Calculating its time derivative, one has
Recalling now (6) and (7), denoting , one obtains and its time derivative . Thus, the time derivative of has the following form:
The following LFC is proposed:
where , are some coefficients. Determining analogously as in [22] the time derivative of V, one obtains
with
and . Moreover, in order to guarantee that and are positively definite, it is assumed that [22]
Under such conditions, a stabilizing controller should be designed in order to track the system error.
Theorem 1.
It is assumed that the equations of motion of a hovercraft expressed in terms of quasi-velocities can be written as (6)–(11), with the external force (16) and (17) taking into consideration the states (18) and the bounded desired trajectory and bounded its time derivative. If an invertible matrix B (25) is selected, this means that
and the control thrust T as well as the rudder angle ψ are used in the form
with , , and then origin of the dynamical system of the system is globally exponentially stable.
Proof.
Taking into account (23), the LFC (20) is radially unbounded and positive definite function. Applying the controller (29) into (24), the closed-loop time derivative as well as the LFC lead to
Thus, from Lyapunov’s direct method (a simple convergence lemma [35] (p. 91)), one obtains
where is a real positive number. Hence, it can be concluded that the origin of the error system is globally exponentially stable. □
Zero dynamics question. Because , the analysis of the zero dynamics is thus analogous as in [22] but not direct. So, let us consider this issue.
The angular kinetic energy of the hovercraft is given in the form
Using (8), (11), the controller (29) and calculating the time derivative of , one obtains
Taking into account (18), , and denoting , it can be written as follows:
In addition, the inverse matrix to matrix B is of the form
where , , , ().
The sway velocity v (35) is applied in the time derivative . Thus, (34) can be rewritten as follows:
Denoting now
one obtains
The following theorem can now be proposed.
Theorem 2.
Consider the closed loop consisting of the system described by (12)–(15) together with the trajectory tracking controller (29). For any length of the arm a, there is a constant such that if the control point meets the condition , inequality (28) is true, and additionally , then the linear velocity and the vehicle angular velocity r are bounded.
Proof.
Based on Theorem 1, it can be concluded that tracking errors and , vehicle parameters in (2) and (3) (the mass, the inertia moment, the displacements and the drag coefficients) and the reference trajectory and its derivatives are bounded. If condition is satisfied, then and the boundedness of r is ensured. However, because component (38) has a complex form, it is necessary to pay attention to the design parameters and model parameters to guarantee this condition. Design parameters can be chosen small enough to reduce the impact of unwanted components. In addition, the values of the components for vehicle asymmetry , must not be too large (because it affects and ). The values of the drag due to asymmetry , and components and should also be small. To sum up this consideration, it can be said that the influence of components due to asymmetry should be limited. When such conditions are met, it is possible to guarantee that . In this case, r will be bounded. Given the definition of tracking error and the boundedness of and r, one can deduce that the linear velocities u, v are also bounded. □
4. Simulation Results
Proposed verification method. The simulation study was based on the following assumptions:
- (1)
- A hovercraft model with parameters similar to those of a vehicle known from the literature was selected;
- (2)
- Two curvilinear trajectories were selected for tracking;
- (3)
- Comparative tests were carried out for the proposed control algorithm based on quasi-velocities, the algorithm using the TSMC method and the original algorithm from [22];
- (4)
- The test results were compared on the basis of the assumed set of criteria and indexes.
Comment. The thrust saturation effect is sometimes taken into account in the control algorithm, such as [36,37]. However, when the thruster saturation effect is not significant, then this problem is ignored [38,39]. Such a situation occurs when the desired trajectories have an uncomplicated mathematical form, and the thrust saturation effect is only a temporary or sporadic phenomenon.
4.1. Hovercraft Model and Test Conditions
The purpose of the numerical simulations was to verify the effectiveness of the control algorithm under near-real conditions for two vehicles with different dynamics. This meant that the operating conditions had to be chosen so as not to exceed the maximum forces and torques that could be obtained from the thrusters. In addition, the velocity values could not exceed those that are achievable by each vehicle.
The parameters of the hovercraft adopted for testing are similar to those contained in [21]. They are collected in Table 1. The simulations were performed using the software from [40] (Matlab/Simulink source codes) but modified for an algorithm containing an asymmetric inertia matrix and for quasi-velocities. In this program, in order to avoid discontinuities in the system, the function was approximated by functions as used in the literature, e.g., [34,41].

Table 1.
Parameters of hovercraft.
The vehicle models under consideration have vastly different dynamics, which makes it possible to verify the suitability of the control algorithm for different vehicles.
Moreover, the center of mass is shifted, i.e., m, m, and the desired trajectory position profiles were selected as follows:
Other parameters applied are as follows: m, m and m. The first is the sine trajectory, whereas the second is a complex trajectory. The initial points for the hovercraft were . The saturation of the control signal was N, N. A comparison of the simulation results for two different set trajectories can be useful at the stage of trajectory design to perform the set task. The simulations were performed using Matlab/Simulink, the method ODE 3 (Bogacki–Shampine), the time of motion s and the time step s.
4.2. Performance Indexes and Evaluation Criteria
A performance test and a test of changes in motion dynamics were used to verify the proposed control scheme. The following quantities were applied to estimate the performance:
- (1)
- The mean integrated absolute error, i.e., , where ;
- (2)
- The mean integrated absolute control, i.e., , where ;
- (3)
- The root mean square of the tracking error, i.e., , with (, mean the position error in the reference frame).
The estimation of the effects of the dynamics is carried out by means of the following quantities [42,43]:
- (1)
- The kinetic energy for the total vehicle and corresponding to each quasi-velocity, i.e., .
- (2)
- The mean kinetic energy relating to each quasi-velocity and the total kinetic energy: .
- (3)
- The deformation of each velocity resulting from dynamic coupling, i.e., , where .
4.3. Simulation Tests Conducted
The parameters of the controllers were determined based on the method given in [27]. According to this procedure, the parameters are grouped according to the function played in the control algorithm. Their tuning and analysis of the results consists of visualizing the position errors of the values of the parameters in the same group (the other parameters have unit values of the values, and if they are too large, they should be reduced so that they are close to zero). If the values of several parameters (or one when it is enough) lead partially to the goal, e.g., the convergence of the position errors is acceptable, then the effect of other enhancements on the effectiveness of the controller can be studied. If the quality of the control improves, tuning is performed. With promising results, we change the values of the next group of parameters and check whether the position errors have improved.
4.3.1. Test of Quasi-Velocity Based Controller
The set of control parameters to ensure acceptable tracking results was (for both kind of desired trajectories)
These gains were obtained by tuning the control algorithm, i.e., increasing the values from 1 to such values that guaranteed acceptable trajectory tracking accuracy (taking into account the other operating conditions).
Sine trajectory. As is evident in Figure 2a, the set trajectory is tracking correctly and the position errors (presented in Figure 2b) in the x and y directions are tending to near zero after about 5 s. As can be observed in Figure 2c, the non-steady state for the control signals disappears after about 15 s of movement. Figure 2d demonstrates that at a similar time, this condition disappears for hovercraft velocities. Additional information about the effect of dynamic parameters on movement is obtained from changes in the value of as seen in Figure 2e. Because the displacement values of the center of mass position are the same in the x and y directions, are therefore symmetrical. Figure 2f presents the evolution of kinetic energy when the vehicle is in motion. Using this graph, it is possible to determine which variable causes more or less kinetic energy consumption, assuming dynamic parameters and a desired trajectory. This can be used to design the vehicle and for planning its movement.
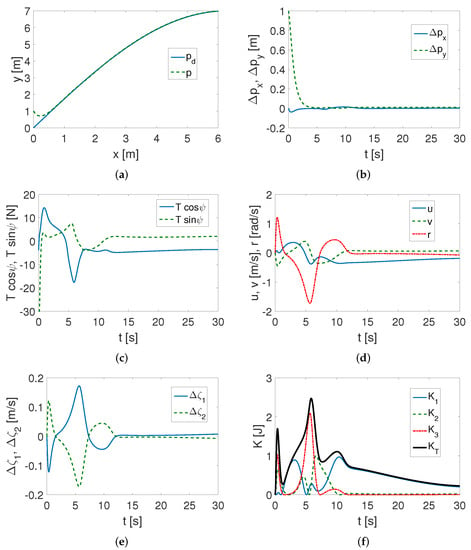
Figure 2.
Simulation results for sine trajectory: (a) desired () and realized (p) trajectory; (b) position errors (in inertial frame); (c) input signals components (applied force) ; (d) actual velocities ; (e) changes in quasi-velocity (); (f) changes in kinetic energy () during motion.
Complex trajectory. Figure 3 shows the results of the analogous tests conducted for the complex trajectory. It can refer, for example, to a situation in which the vehicle should avoid a fixed obstacle. As can be seen in Figure 3a, the algorithm works properly and the desired trajectory is tracked efficiently. This observation is also confirmed in Figure 3b. However, from Figure 3c, it is apparent that the values of the applied force components do not reach a steady state but are constantly changing and, moreover, are larger than for a sine trajectory. A similar phenomenon can be seen in Figure 3d, which shows the velocities of the vehicle. The changes in the values are larger than before but also symmetrical (for the same reason as previously), as observed in Figure 3e. The kinetic energy changes, as shown in Figure 3f, have larger values than for the sinus trajectory, and their waveforms are considerably different from the previous ones. So, the selection of the trajectory significantly affects the consumption of this energy.
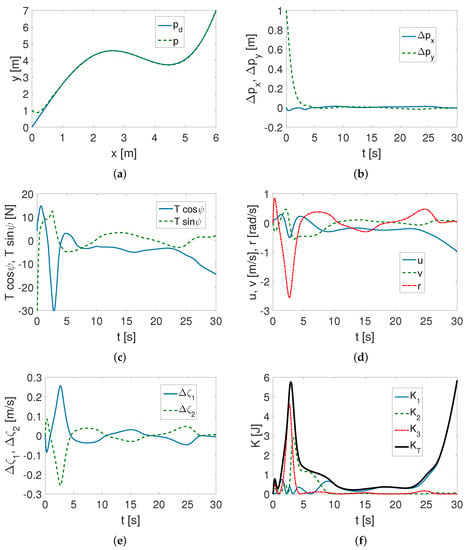
Figure 3.
Simulation results for complex trajectory: (a) desired () and realized (p) trajectory; (b) position errors (in inertial frame); (c) input signals components (applied force) ; (d) actual velocities ; (e) changes in quasi-velocity (); (f) changes in kinetic energy () during motion.
In order to obtain more objective information, other indexes were used to evaluate the achieved results. The corresponding values of the controller’s performance are summarized in Table 2.

Table 2.
Performance for IQV controller (with friction).
From the values of the MIA indexes, it can be seen that the tracking accuracy is comparable for both selected trajectories. The indexes have larger values for the complex trajectory, which means that the velocities are more deformed for such a trajectory. The observations regarding the larger values of the applied force components when using a complex trajectory instead of a sinus trajectory were confirmed. However, the RMS value was lower for this trajectory; therefore, it is somewhat more accurately tracked. On the other hand, the kinetic energy consumption was indeed higher for the complex trajectory (the observations from the graphs were confirmed). However, it is also interesting to know which quasi-variable is the reason for this energy consumption. For the sine trajectory, it was calculated that J, and for the complex trajectory J. As can be seen from the calculations, the most kinetic energy is consumed by the variable which corresponds to the movement in the longitudinal direction.
Robustness issue. In addition, the robustness of the proposed algorithm to changes in the hovercraft parameters was examined. The inaccuracy of the model parameters was assumed as W = 0.5 (50%).
It turned out that the controller was equally effective in this case (only small index values were obtained), except for kinetic energy, which had higher values (Figure 4) due to the fact that the vehicle had a greater mass and moment of inertia, or a greater displacement of the center of mass. The increase in the value of the kinetic energy is proportional to the increase in the value of the dynamic parameters. For the sine trajectory, it was calculated that J, and for the complex trajectory J.
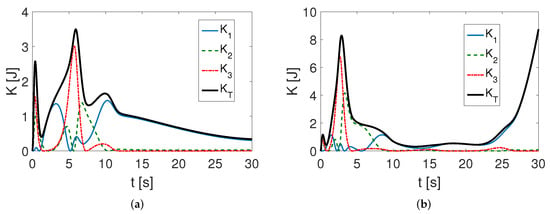
Figure 4.
Changes in kinetic energy () during motion—results with 50% parameter increase in parameter values: (a) sine trajectory; (b) complex trajectory.
4.3.2. Comparison with Terminal Sliding Mode Controller
In order to compare the performance and capabilities of the proposed control scheme, the simulation tests were conducted for the same hovercraft model and the same desired trajectories but using a different control method. An algorithm based on the terminal sliding mode control (TSMC) method proposed in [44] was chosen. The following considerations were followed:
- (1)
- According to the cited reference, the TSMC method provides robustness against unmodeled dynamics, model uncertainty and external interference from ocean currents and waves. It is also known to be superior to the conventional sliding mode control technique in terms of finite-time convergence and high-precision steady-state tracking. It has been successfully applied in many works.
- (2)
- Despite the fact that the approach based on TSMC is designed for underactuated underwater vehicles, it has been successfully implemented for the hovercraft in [27].
- (3)
- In the cited article, several algorithms based on different methods were investigated through simulation, and the mentioned TSMC method proved successful in tracking different trajectories while two others proved ineffective.
The comparative of the TSMC algorithm tests was performed taking into account three issues:
- (1)
- The model with diagonal inertia matrix and without friction.
- (2)
- The model with diagonal inertia matrix with friction.
- (3)
- The model with non-diagonal inertia matrix .
During the testing, it was noted that the TSMC algorithm is very sensitive to changes in control parameters, and numerical problems also arise (e.g., the integration step of the integration method). For this reason, the values of a set of these parameters were assumed similar to those given in [27] (the model of the tested vehicle has dynamics very similar to the model used in that paper). On the other hand, changing the gain of the controller led to a loss of trajectory tracking efficiency.
The control scheme of the TSMC algorithm was introduced and studied in [44]. The simulation investigation used software from [45] (Matlab/Simulink source codes). The following set of control parameters was assumed for the trials, which provided satisfactory trajectory tracking results:
and , . The saturation of the control signals was limited to N and Nm to obtain comparable constraints with the previous simulations.
Sine trajectory without friction and using . Due to numerical problems, acceptable results could not be obtained as in the case of the algorithm using IQV for the same step time. Therefore, this time was reduced to s (ODE 3 integration method). As can be seen in Figure 5a, the trajectory tracking is correct and the position errors are close to zero after about 10 s, as shown in Figure 5b. However, the time to obtain the error convergence is longer than with an IQV-type algorithm. The values of the force and torque decrease significantly after a short time (Figure 5c), but the torque suddenly increases and decreases after about 8 s, which is not good for the performance of the task. The velocity values are acceptable, as can be seen in Figure 5d.

Figure 5.
Simulation results for TSMC and sine trajectory (without friction): (a) desired () and realized (p) trajectory; (b) position errors (in inertial frame); (c) input signals components (applied force and torque) ; (d) actual velocities .
Sine trajectory with friction and using . The same step time s and ODE 3 integration method were applied. From Figure 6a,b, it can be observed that the sine trajectory tracking is not as accurate when frictional forces appear in the dynamics model. However, in this case, the force and torque have smaller values and the suddenly jumping value of the torque is clearly smaller, as shown in Figure 6c. The velocity values are now also slightly lower, as can be seen in Figure 6d.
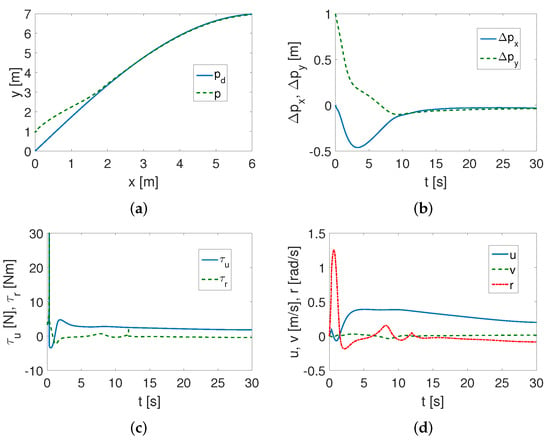
Figure 6.
Simulation results for TSMC and sine trajectory (with friction): (a) desired () and realized (p) trajectory; (b) position errors (in inertial frame); (c) input signals components (applied force and torque) ; (d) actual velocities .
Complex trajectory without friction and using . For this desired trajectory, the numerical problems were even greater than for the previous one. The ODE 3 method was adopted, but the time step was reduced 10 times, i.e., s. As can be noted in Figure 7a, and which is also confirmed by the results in Figure 7b, the algorithm works properly, ensuring trajectory tracking. The time to reach steady state is about 10 s, so the controller works quickly. Figure 7c shows that the force and moment values are acceptable. However, after about 15 s, there is a sharp change in the value of the moment due to a change in the shape of the desired trajectory. This also indicates the sensitivity of the algorithm when this situation occurs.
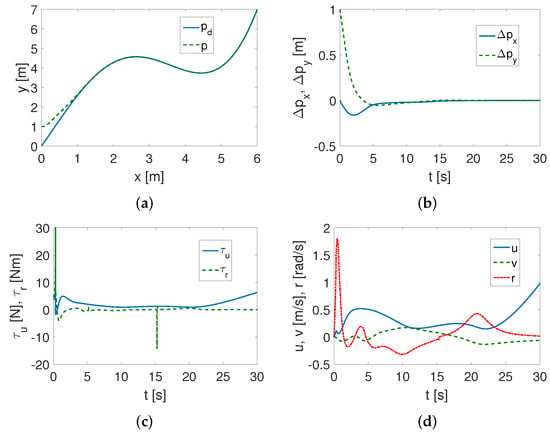
Figure 7.
Simulation results for TSMC and complex trajectory (without friction): (a) desired () and realized (p) trajectory; (b) position errors (in inertial frame); (c) input signals components (applied force and torque) ; (d) actual velocities .
Complex trajectory without friction and using . The algorithm did not provide any acceptable results even when reducing the integration step.
Sine and complex trajectory without friction and using . The algorithm proved to be completely useless and the task of trajectory tracking remained unsolved.
The performance parameters of the TSMC controller are shown in Table 3.

Table 3.
Performance for TSMC controller.
4.3.3. Comparison with Original Controller
The IQV-based control algorithm was also compared with the original algorithm in terms of performing the trajectory tracking task. The same trajectories, operating conditions and control coefficients (42) were assumed.
The performance parameters of the original controller are shown in Table 4. Comparing the parameter values in Table 2 and Table 4, it can be observed that the original algorithm gave better MIA results on the x direction than the IQV algorithm. However, this is an error difference of only 0.2 mm (sine) and 2.5 mm (complex). In the y direction, the error difference was 2.3 mm (sine). For the complex trajectory, the IQV controller delivered a lower value of 2.0 mm. The RMS index in both test cases had lower values after the IQV controller (2.7 mm—sine and 0.9 mm—complex). The smaller values of the MIAC and KE indexes are due to the fact that the original algorithm does not take into account the effect of vehicle asymmetry (additional mass components).

Table 4.
Performance for classical controller (with friction).
It is also worth noting that the favorable results from the original algorithm cannot be directly compared with those from the IQV algorithm, because the latter works under more difficult conditions resulting from vehicle asymmetry.
4.3.4. Discussion of Results
Tests were conducted on one hovercraft model and two desired trajectories selected for tracking. The goal was to compare the performance in both cases based on runs of different quantities, and to indicate the information possible with the criteria and indicators introduced. Based on the results obtained, the following was determined regarding the control algorithm:
- It provides information on the asymmetric movement of the hovercraft (with a displacement in the center of mass caused, for example, by an additional load);
- It makes it possible by simulating the effect of a set trajectory on the vehicle motion, velocity deformation and kinetic energy consumption for the vehicle and for the individual quasi-velocity corresponding to motion in each direction;
- A small effect of the inaccuracy of the model parameters (with a 50% increase in their values) on the tracking accuracy was noticed, except for the kinetic energy values;
- If possible for the realization of the set task of trajectory tracking, it is better to choose trajectories described by less complicated mathematical functions.
The fact that no differences were observed in the accuracy of tracking the set trajectory, but the dynamics indexes changed, can be explained by the reason that the proposed control scheme is based on the control of kinematic quantities, but at the same time it allows the detection of changes caused by modifications in vehicle dynamics.
Comment. Only an approximate friction model is included in the proposed control algorithm, which limits the controller’s applicability under conditions where disturbances may be negligible. Such a situation is the case, for example, in laboratory conditions or under favorable atmospheric conditions that will not disturb the work of the controller. In addition, a continuous function approximation was used in the simulations to avoid model discontinuities.
Based on the comparative tests conducted, some observations can be made about the performance of the proposed IQV algorithm and the TSMC method. The results relating to trajectory tracking errors are given in Table 5. The percentage increase UP was calculated according to the following formula:

Table 5.
Percentage increase in IQV tracking performance over TSMC.
As can be seen from this table, the IQV controller yielded lower values than the TSMC controller for all cases considered.
Table 6 shows a comparison of the percentages of the indexes used in the tests. The minus symbol for the IQV controller indicates that the values were worse. Although in 3 cases the IQV controller gave worse index values, these are position errors of 0.2 mm to 2.5 mm. It is also significant that the initial position in the y direction was 1 m.

Table 6.
IQV tracking performance vs. original algorithm [22].
Benefits of IQV controller compared to TSMC algorithm.
- The TSMC method can give satisfactory results but for a diagonal inertia matrix. For a symmetric matrix, the problem of tracking the desired trajectory, as shown by the tests performed, was not solved at all. This means that if the model errors are significant, the algorithm will be ineffective.
- For the proposed IQV algorithm, no such significant numerical problems arise as in the TSMC method.
- The applicability of the proposed IQV algorithm is greater than that of the TSMC scheme, because the former is suitable for both a model with a diagonal inertia matrix and a symmetric matrix, and it also takes into account functions representing friction.
- The selection of the control parameters in the case of the offered algorithm is intuitive, while the controller parameters in the TSMC method must be selected with a lot of time unless another selection method is added. Even then, when a set of parameters is selected correctly, a small change in them can lead to a loss of performance of the algorithm. Such an inconvenience is not present in the control scheme proposed in this paper.
Benefits of IQV controller compared to original algorithm.
- An IQV controller is suitable for asymmetric vehicles in the longitudinal and lateral directions, so the geometric center can be different from the center of mass.
- During the realization of the tracking task of the desired trajectory, information on changes in the behavior of the vehicle due to the displacement of the center of mass is obtained simultaneously. Thus, it is a combination of a control algorithm and a scheme for analyzing vehicle dynamics.
- It is possible to estimate the effect of dynamic parameters on changes in vehicle velocity and kinetic energy reduced by each quasi-velocity (taking into account couplings). In the classical algorithm, the effect of couplings is ignored.
Advantages, drawbacks and limitations of the IQV controller
- Because only two controller parameters and three design parameters are changed, it may therefore be difficult to achieve very accurate tracking (however, this may be because according to the mathematical proof only uniform stability is guaranteed).
- The control scheme is suitable for studying hovercraft with rudders, while so far there is no way to directly extrapolate to marine vehicle models with rudders.
The simulation verification involved testing a control algorithm using a model based on a velocity transformation containing components due to the fact that the geometric center does not coincide with the center of mass. New variables including the parameters of this model were incorporated into the control algorithm resulting in a useful tool for estimating vehicle behavior during trajectory tracking. Based on the comparison with the TSMC-type algorithm, better values of the adopted indicators were obtained, while in comparison with the original algorithm the results did not always yield a better performance. Nevertheless, a feature of the IQV controller is that it is a useful tool for estimating the impact of dynamic parameters during trajectory tracking.
5. Conclusions
This paper proposes a modified algorithm to track the desired trajectory. The original control scheme is designed for a hovercraft model described by a diagonal inertia matrix, whereas the design developed in this paper is for controlling a vehicle with an asymmetric dynamic model (caused, for example, by uneven load distribution). It is therefore more general than the classical version but does not allow the identification of model parameters because it is used to study the effect of dynamic parameters on the movement of the hovercraft. To achieve this, a velocity transformation using decomposition of the inertia matrix is utilized which leads to new equations but with a diagonal inertia matrix, and then only the control scheme is designed. It is also shown what mathematical conditions such a scheme must meet, and the performance criteria are adapted to evaluate its performance. The simulations performed for two different set trajectories allow comparing the performance of the algorithm under the assumed operating conditions. The presented approach can be helpful at the stage of motion planning when it is necessary to decide on the route of the vehicle, taking into account the kinetic energy consumption. Analogous tests as presented in this paper can be performed for different vehicle models.
Funding
This work was supported by the Poznan University of Technology Grant No. 0211/SBAD/0122.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Author would like to thank Dariusz Pazderski and Jakub Bernat for their comments on conducting stability proofs.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A

Table A1.
Explanation of symbols and abbreviations.
Table A1.
Explanation of symbols and abbreviations.
| Symbol | Explanation |
|---|---|
| DOF | degree of freedom |
| IQV | inertial quasi-velocities |
| LFC | Lyapunov function candidate |
| transformation matrix between the body frame and the inertial frame | |
| M | vehicle inertia matrix |
| Coriolis and centripetal forces vector | |
| drag vector | |
| vector of control inputs (the total force and torque) | |
| input scaling coefficient | |
| a | length of the arm from the measured center of mass to the surface of the rudder |
| N | diagonal vehicle inertia matrix in terms of IQV |
| velocity transformation matrix | |
| f | vector of total forces |
| total torque | |
| vector of IQV including the vehicle velocities and the inertial parameters | |
| tracking error in the inertial frame | |
| time derivative of the tracking error in the inertial frame | |
| second time derivative of the tracking error in the inertial frame | |
| arbitrary vector for the point to be controlled in the body frame | |
| B | control signal transformation matrix |
References
- Seguchi, H.; Ohtsuka, T. Nonlinear receding horizon control of an underactuated hovercraft. Int. J. Robust Nonlinear Control 2003, 13, 381–398. [Google Scholar] [CrossRef]
- Tanaka, K.; Iwasaki, M.; Wang, H.O. Switching Control of an R/C Hovercraft: Stabilization and Smooth Switching. IEEE Trans. Syst. Man Cybern. Part Cybern. 2001, 31, 853–863. [Google Scholar] [CrossRef] [PubMed]
- Chaos, D.; Moreno-Salinas, D.; Aranda, J. Control no lineal de un aerodeslizador no holonomico con acciones de control limitadas [Nonlinear control of an underactuated nonholonomic hovercraft with limited control inputs]. RIAI Rev. Iberoam. Autom. Inform. Ind. 2013, 10, 402–412. [Google Scholar] [CrossRef]
- Chaos, D.; Moreno-Salinas, D.; Munoz-Mansilla, R.; Aranda, J. Nonlinear Control for Trajectory Tracking of a Nonholonomic RC-Hovercraft with Discrete Inputs, Hindawi Publishing Corporation. Math. Probl. Eng. 2013, 2013, 589267. [Google Scholar] [CrossRef]
- Cremean, L.; William, B.; Dunbar, W.B.; van Gogh, D.; Hickey, J.; Klavins, E.; Meltzer, J.; Murray, R.M. The Caltech Multi-Vehicle Wireless Testbed. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; pp. 86–88. [Google Scholar]
- Jeong, S.; Chwa, D. Coupled Multiple Sliding-Mode Control for Robust Trajectory Tracking of Hovercraft with External Disturbances. IEEE Trans. Ind. Electron. 2018, 65, 4103–4113. [Google Scholar] [CrossRef]
- Jeong, S.; Eom, M.; Chwa, D. Disturbance-Estimation-Based Hierarchical Sliding Mode Control of Hovercraft with Wind Disturbance. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS 2015), in BEXCO, Busan, Republic of Korea, 13–16 October 2015; pp. 532–537. [Google Scholar]
- Pröhl, L.; Aschemann, H. Nonlinear Observer-Based Control of an Under-Actuated Hovercraft Vehicle. IFAC PapersOnLine 2020, 53-2, 8973–8978. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Cremean, L.; Hespanha, J.P. Position tracking for a nonlinear underactuated hovercraft: Controller design and experimental results. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 3858–3863. [Google Scholar]
- Aguiar, A.P.; Hespanha, J.P. Trajectory-Tracking and Path-Following of Underactuated Autonomous Vehicles with Parametric Modeling Uncertainty. IEEE Trans. Autom. Control 2007, 52, 1362–1379. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Hespanha, J.P. Logic-Based Switching Control for Trajectory-Tracking and Path-Following of Underactuated Autonomous Vehicles with Parametric Modeling Uncertainty. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 3004–3010. [Google Scholar]
- Fantoni, I.; Lozano, R.; Mazenc, F.; Pettersen, K.Y. Stabilization of a nonlinear underactuated hovercraft. Int. J. Robust Nonlinear Control 2000, 10, 645–654. [Google Scholar] [CrossRef]
- Tran, H.K.; Son, H.H.; Duc, P.V.; Trang, T.T.; Nguyen, H.N. Improved Genetic Algorithm Tuning Controller Design for Autonomous Hovercraft. Processes 2020, 8, 66. [Google Scholar] [CrossRef]
- Sira-Ramirez, H. Dynamic Second-Order Sliding Mode Control of the Hovercraft Vessel. IEEE Trans. Control Syst. Technol. 2002, 10, 860–865. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Ibanez, C.A. The Control of the Hovercraft System: A Flatness Based Approach. In Proceedings of the 2000 IEEE International Conference on Control Applications, Anchorage, AK, USA, 25–27 September 2000; pp. 692–697. [Google Scholar]
- Sira-Ramirez, H.; Ibanez, C.A. On the Control of the Hovercraft. Syst. Dyn. Control 2000, 10, 151–163. [Google Scholar] [CrossRef]
- Morales, R.; Sira-Ramirez, H.; Somolinos, J.A. Linear active disturbance rejection control of the hovercraft vessel model. Ocean Eng. 2015, 96, 100–108. [Google Scholar] [CrossRef]
- de Souza, W.F.; Rafikova, E.; Meza, M.E.M.; Gafurov, S. Backstepping Trajectory Tracking of Underactuated Hovercraft. In Proceedings of the 2018 Global Fluid Power Society PhD Symposium (GFPS), Samara, Russia, 18–20 July 2018. [Google Scholar] [CrossRef]
- Kong, X.; Xia, Y.; Hu, R.; Lin, M.; Sun, Z.; Dai, L. Trajectory Tracking Control for Under-Actuated Hovercraft Using Differential Flatness and Reinforcement Learning-Based Active Disturbance Rejection Control. J. Syst. Sci. Complex. 2022, 35, 502–521. [Google Scholar] [CrossRef]
- Defoort, M.; Floquet, T.; Kokosy, A.; Perruquetti, W. A novel higher order sliding mode control scheme. Syst. Control Lett. 2009, 58, 102–108. [Google Scholar] [CrossRef]
- Kim, K.; Lee, Y.K.; Oh, S.; Moroniti, D.; Mavris, D.; Vachtsevanos, G.J.; Papamarkos, N.; Georgoulas, G. Guidance, Navigation, and Control of an Unmanned Hovercraft. In Proceedings of the 2013 21st Mediterranean Conference on Control & Automation (MED), Platanias-Chania, Crete, Greece, 25–28 June 2013; pp. 380–387. [Google Scholar]
- Cabecinhas, D.; Batista, P.; Oliveira, P.; Silvestre, C. Hovercraft Control With Dynamic Parameters Identification. IEEE Trans. Control Syst. Technol. 2018, 26, 785–796. [Google Scholar] [CrossRef]
- Xie, W.; Cabecinhas, D.; Cunha, R.; Silvestre, C. Robust Motion Control of an Underactuated Hovercraft. IEEE Trans. Control Syst. Technol. 2019, 27, 2195–2208. [Google Scholar] [CrossRef]
- Xie, W.; Cabecinhas, D.; Cunha, R.; Silvestre, C. Global Practical Tracking for a Hovercraft with Unmeasured Linear Velocity and Disturbances. IFAC PapersOnLine 2020, 53, 8959–8964. [Google Scholar] [CrossRef]
- Yan, L.; Ma, B.; Xie, W. Robust practical tracking control of an underactuated hovercraft. Asian J. Control 2021, 23, 2201–2213. [Google Scholar] [CrossRef]
- Munoz-Mansilla, R.; Chaos, D.; Aranda, J.; Diaz, J.M. Application of quantitative feedback theory techniques for the control of a non-holonomic underactuated hovercraft. IET Control Theory Appl. 2012, 6, 2188–2197. [Google Scholar] [CrossRef]
- Herman, P. Assessing the Feasibility of Underwater Vehicle Controllers in Underactuated Hovercrafts via Simulations. Int. J. Model. Identif. Control 2021, 37, 45–56. [Google Scholar] [CrossRef]
- Sanders, R.M.W. Control of a Model Sized Hovercraft; DCT Rapporten; Technische Universiteit Eindhoven; University of New South Wales: Kensington, Australia, 2003; Volume 27. [Google Scholar]
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles; Springer: London, UK, 2009. [Google Scholar]
- Patelski, R.; Pazderski, D. Extended State Observer Based Parameter Identification of the Hovercraft System. In Proceedings of the 2022 26th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 22–25 August 2022; pp. 330–335. [Google Scholar] [CrossRef]
- Patelski, R.; Pazderski, D. Novel Adaptive Extended State Observer for Dynamic Parameter Identification with Asymptotic Convergence. Energies 2022, 15, 3602. [Google Scholar] [CrossRef]
- Loduha, T.A.; Ravani, B. On First-Order Decoupling of Equations of Motion for Constrained Dynamical Systems. Trans. ASME J. Appl. Mech. 1995, 62, 216–222. [Google Scholar] [CrossRef]
- Do, K.D. Global tracking control of underactuated ODINs in three-dimensional space. Int. J. Control 2013, 86, 183–196. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef]
- Slotine, J.J.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Huang, J.; Wen, C.; Wang, W.; Song, Y.D. Global stable tracking control of underactuated ships with input saturation. Syst. Control Lett. 2015, 85, 1–7. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, X.; Yin, B.; Liu, W. Adaptive terminal sliding mode based thruster fault tolerant control for underwater vehicle in time-varying ocean currents. J. Frankl. Inst. 2015, 352, 4935–4961. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Double-Loop Integral Terminal Sliding Mode Tracking Control for UUVs with Adaptive Dynamic Compensation of Uncertainties and Disturbances. IEEE J. Ocean. Eng. 2019, 44, 29–53. [Google Scholar] [CrossRef]
- Kicki, P.; Kozlowski, J. Software: Hovercraft Control With Dynamic Parameters Identification; Unpublished Project; Poznan University of Technology: Poznan, Poland, 2018. [Google Scholar]
- Mitchell, A.J.; McGookin, E.W.; Murray-Smith, D.J. Implementation of Sliding Mode Observer Based Reconfiguration in an Autonomous Underwater Vehicle. Acta Polytech. 2005, 45, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Herman, P. Application of nonlinear controller for dynamics evaluation of underwater vehicles. Ocean Eng. 2019, 179, 59–66. [Google Scholar] [CrossRef]
- Herman, P. Vehicle Dynamics Study Based on Nonlinear Controllers Conclusions and Perspectives. In Inertial Quasi-Velocity Based Controllers for a Class of Vehicles; Springer Tracts in Mechanical Engineering; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean Eng. 2017, 129, 613–625. [Google Scholar] [CrossRef]
- Gryczka, N.; Rychlewicz, K. Software: Terminal Sliding Mode Control for the Trajectory Tracking of Underactuated Autonomous Underwater Vehicles; Unpublished Project; Poznan University of Technology: Poznan, Poland, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).