Seismic Interferometry Method Based on Hierarchical Frequency Fusion and Its Application in Microtremor Survey

Abstract

Site velocity structure determination and stratigraphic division are important purposes of microtremor survey, and the precision of dispersion curves is an important factor affecting the accuracy of microtremor survey. In order to obtain more accurate dispersion curve and S-wave velocity structure, this paper proposed a dispersion curve processing method based on hierarchical frequency fusion of seismic interferometry. Analysis was performed on the link between station pair spacing and frequency component of the collected microtremor signal dependability and exploration depth. A mathematical model of station distances and reliable frequencies of the dispersion curves were achieved through a hierarchical relationship between station distances. Then, a fusion criterion was proposed to determine the fusion boundary based on the reliable frequency, and the dispersion curves of station pairs with different distances were fused to obtain the final dispersion curve. Finally, a more accurate velocity structure was obtained through s-wave velocity conversion from shallow layers to deep ones. The method was applied to the microtremor survey of the proposed high-rise building site in Xiamen. The rectangular observation array was arranged, and the dispersion curves were extracted and processed using hierarchical frequency fusion and traditional superimposed averaging method, and the S-wave velocity and stratigraphic structure were obtained. The experimental results show that the S-wave velocity and stratigraphic structure obtained using the hierarchical frequency fusion method are in better agreement with the borehole results than the superimposed averaging method, which shows its effectiveness and application prospect.

1. Introduction

Microtremor is a faint vibration that occurs naturally and is always present on the Earth’s surface; in the area of shallow surface wave investigation, it is often known as “ground pulsation”. The microtremor propagates through the ground as a wave with a frequency range of 0.1 to 50 Hz and a very modest amplitude, typically between 10⁻⁴ and 10⁻² mm. The origins of microtremor are numerous and diverse, ranging from man-made activities such as traffic and mechanical vibrations to natural occurrences such as tides, volcanic activity, wind, and rain [1,2,3]. Therefore, microtremor can be thought of as a collection of waves with various amplitudes and frequencies. These waves have different transmission characteristics in different media at the surface, so the microtremors contain a wealth of information about the surface media and can be analyzed to obtain geological structures [4,5]. The flow of the microtremor survey is shown in Figure 1, where the stations are positioned in an array to gather surface microtremor signals from all directions. Then, the dispersion curve is extracted from microtremor signals. Finally, the subsurface S-wave velocity structure and the underground geotechnical medium can be obtained using inversion or conversion with dispersion curve [6,7]. Due to the benefits of being rapid, ecologically friendly, devoid of electromagnetic interference, and having no artificial seismic source, the microtremor survey is crucial to urban subterranean surveys [8].

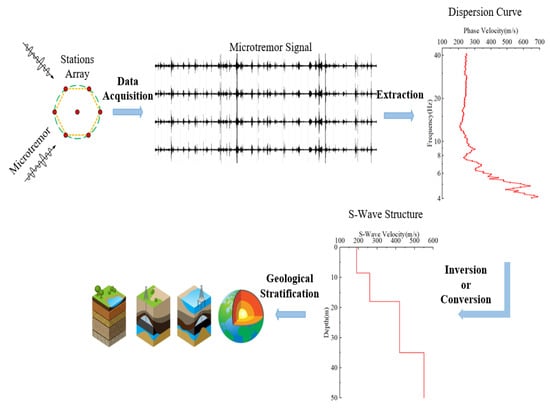
Figure 1. Flowchart of microtremor survey.

The extraction of the dispersion curve is the vital stage in the microtremor survey. At present, the algorithms of dispersion curve extraction that are commonly used include the spatial autocorrelation method(SPAC), the extended spatial autocorrelation method (ESPAC) [9,10], frequency-wavenumber method(FK) [11], and seismic interferometry method (SI). The SPAC needs to place the seismometers in triangular or circular arrays; however, the actual field is complex, and it may be difficult to meet its array conditions. For this reason, the ESPAC method was proposed to accommodate arbitrary arrangement of geometry. The FK method has no restrictions on arrangement of arrays, but it needs more seismometers to achieve better detection results [12]. The SI method extracts the dispersion curve from two microtremor signals. The arrangement of the array is flexible, and more dispersion information can be extracted through pairwise operation, which is helpful to obtain a higher resolution and more precise underground S-wave velocity structure [13]. Therefore, SI has been the subject of much investigation and application by numerous academics.

SI was often used in large-scale, deep geophysical exploration at first. In 2005, Shapiro used SI to analyze the data recorded by the US-Array station and successfully obtained the deep velocity structure in southern California [14]. Yao applied SI to the study of mantle-scale lithospheric structures in a dense array in Tibet [15]. Subsequently, some scholars introduced SI into shallow, small-scale surface wave exploration. Ridder detected the stratigraphic structure at 0–105 m depth in the Valhall area [16]. Liu compared the inversion results of the SI with the SPAC in YuXi and found that their velocity structure change trends are basically consistent [17].

In addition to the application practice, many academics concentrate their studies on the dispersion curve processing techniques. Zhou combined SI and signal-to-noise ratio theory, indicating that after signal-to-noise ratio compensation, the shape of the coherence coefficient curve obtained using SI is more similar to that of the Bessel function and more accurate [18]. Zhao investigated the effect of correlation between measurement points and common centroids on the quality of the dispersion curves in a double circular array and pointed out that the direct averaging method would reduce the depth of exploration [19]. Liu proposed a special point constraint processing method for the multiple dispersion curves produced by interference, fitting each multiple dispersion curve separately to produce a series of special dispersion points, and then fitting these special dispersion points with polynomial fitting to generate the ultimate dispersion curve [20]. Ekstrm found that in observed microtremor signal spectra, association of a given zero with a particular zero crossing of the zero-order Bessel curve may be difficult because noise in the spectrum can cause missed or extra zero crossings. To allow for this, he created a technique for estimating phase velocity to produce dispersion curves of superior quality by artificially adding the zero point [21].

Multiple dispersion curves will be obtained from two-station calculations when using SI to extract dispersion curves from a station array. These multiple dispersion curves need to be integrated into a single dispersion curve, which is thought of as a uniform response below the coverage of the station array. The superimposed averaging approach used in engineering may quickly obtain the final mean dispersion curve. The dispersion information of various spacing dispersion curves cannot, however, be fully utilized by this method, and there are certain mistakes. The zero poles of the coherence coefficients are generally less in small-scale exploration, and the results’ quality of special point constraint method are not always guaranteed. The zero-point add method depends more on the operator’s empirical understanding of spectrum analysis and may introduce additional errors if the zero-point location is incorrectly added. Thus, it is crucial to research a better extraction and processing technique for dispersion curves.

This paper studied the processing method of dispersion curves extracted using SI. Based on the correlation between station pair spacing and the frequency components of the gathered signals, the depth hierarchy of the concentrated dispersion curves was established, and a hierarchical frequency fusion criterion was proposed. The dependable frequency was utilized to establish the fusion boundary; then, station pair dispersion curves at various distances were fused to produce the final dispersion curve. A microtremor survey experiment was carried out in Xiamen City. The microtremor data were processed and analyzed using this method and a superimposed averaging approach. Compared to the superimposed averaging approach, the result of the hierarchical frequency fusion method more precisely achieved delicate depiction of the S-wave velocity structure. The accuracy and reliability of the method were verified by drilling results, and they can provide certain engineering significance for similar microtremor survey projects.

2. Principles and Methods

2.1. Seismic Interferometry

SI was proposed by Claerbout in 1968. According to the theory, the results of the cross-correlation of microtremor signals received at two different stations on the Earth’s surface can be regarded as a new signal record with one station as the virtual source and another station as the receiver [22,23]. The schematic diagram of SI is shown in Figure 2. a, b represents the microtremor signals recorded by two detectors at different locations on the surface. This record is similar to the Green’s function and can reflect the information of the subsurface medium between two stations.

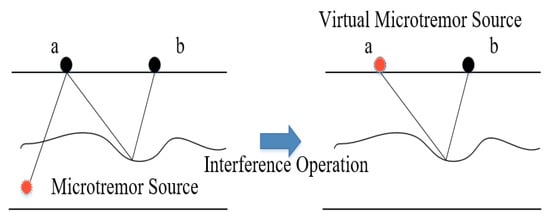
Figure 2. Schematic diagram of SI.

The basic method is to perform cross-correlation calculation on microtremor signals recorded by two stations to obtain the Green function and then use the Green function to extract the dispersion curve. The cross-correlation operation can be performed in the time domain or the frequency domain; convolution in the time domain corresponds to the conjugate dot product in the frequency domain. To extract the dispersion curves with the Green function, there are mainly three methods: traditional time-frequency analysis method, Yao method, and fitting the real part of spectrum of SI results with zero-order Bessel function method [24]. This study performed cross-correlation in frequency domain and extracted the dispersion curve by fitting the real part of spectrum of SI results with zero-order Bessel function.

In the frequency domain, the SI cross-correlation results of the microtremor signals between two stations a and b can be written as follows:

$${\gamma }_{a,b}(f)=\frac{\mathrm{Re}[S_{ab}(f)]}{\sqrt{S_a(f)S_b(f)}}$$

(1)

where ${\gamma }_{a,b}(f)$ is correlation coefficient, $S_{ab}(f)$ is the cross-correlation function of the microtremor signals between station a and station b, $S_a(f)$ and $S_b(f)$ refer to the autocorrelation function of microtremor signals collected at station a and station b, respectively.

According to the theoretical formula derived by Yokoi in proving the consistency between SI and SPAC [25], the vertical component of microtremor signals between two stations using SI can be cross-correlated as follows:

$${\gamma }_{a,b}(f)=J_0(k{r}_{ab})$$

(2)

where $J_0$ represents zero-order first-class Bessel function curve, $r_{ab}$ is the distance of station pair, k means the wavenumber and $k=2\pi f/v$, $v$ is the phase velocity, $f$ stands for the frequency, and Equation (2) can be obtained:

$${\gamma }_{a,b}(f)\frac{\mathrm{Re}[S_{ab}(f)]}{\sqrt{S_a(f)S_b(f)}}=J_0(\frac{2\pi f}{v}{r}_{ab})$$

(3)

By traversing the frequency and using the Newton iterative approach to determine the phase velocity corresponding to each value of the correlation function, the dispersion curve can be obtained. The algorithm of SI is shown below as Algorithm 1.

Algorithm 1: Algorithm of SI
	Input: Two microtremor signal files
	Output: Dispersion curve
	Function: Dispersion curve extraction by SI (signal1, signal2)
1	read signal files
2	data segmentation and windowing
3	for each seg in segments
4	Fourier transform
5	calculate correlation coefficient
6	for each freq in frequencies
7	solute phase velocity
8	find the median phase velocity of all windows
9	return dispersion curve

2.2. Hierarchical Frequency Fusion

2.2.1. Theoretical Analysis

In microtremor array survey, different pairs of stations can be combined according to the distribution characteristics of the stations. These station pairs vary in azimuth and distance. The microtremor array survey finally obtains a dispersion curve as a uniform response below the site. Therefore, it needs to process the dispersion curves from each station pair, and the final dispersion curves can be expressed as follows:

$$V=F(f,d,\theta )$$

(4)

where $V$ is phase velocity, $f$ is frequency, $d$ refers to distance between stations, and $\theta$ represents azimuth.

The oscillation source distribution at the observation site may not be uniform; the oscillation energy also varies in strength, so the response of different azimuth station pairs to the surface waves generated by different oscillation sources varies to some degree. In the SPAC method, the coherence coefficients of the center and circumference stations are azimuthally averaged to compensate for the effects of the inhomogeneity of the distribution of the oscillation sources. The azimuthal averaging treatment of SPAC can be expressed as follows:

$$\begin{array}{ll}\rho (r,f)& =\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\mathrm{Re}\{Coh((0,0),(r,\theta ),f)\}}d\theta \\ & \approx \frac{1}{M}{\displaystyle \sum _{m=1}^M\mathrm{Re}\{Coh((0,0),(r,\theta ),f)\}}\end{array}$$

(5)

where $r$ is the radius of the circular array, $f$ means angle frequency, $M$ is the number of stations on the circumference of the circle, and $\mathrm{Re}\{Coh((0,0),(r,\theta ),\omega )\}$ is the real part of coherence coefficient between the center station and the circumference station of the center.

Since SPAC and SI are both based on the correlation theory [25], and the spatial autocorrelation coefficient is the result of the operation of center-circumference stations, there is nevertheless no strict requirement for the division of center-circumference stations when using the SI method to extract the dispersion curves. In order to lessen the nonuniformity of the source distribution, the dispersion curves of each station pair are frequently extracted first when processing the dispersion curves of small-scale arrays using SI. The mean dispersion curve is then derived using superimposing averaging. The superimposed averaging of the dispersion curves of a microtremor array based on SI can be expressed as:

$$V(f,d)=\frac{1}{N}{\displaystyle \sum _{\begin{array}{l}n=1,m=1,\\ n\ne m\end{array}}^N{V}_{nm}(f,d_{nm})} (d_{nm}=d)$$

(6)

where $N$ is the total number of stations in the array, $n,m$ is the station number, $d_{nm}$ is the distance between station pairs, and $V_{nm}(f,d_{nm})$ is the dispersion curve extracted from microtremor signals from station pair.

The superimposed averaging approach of processing dispersion curves is simple and quick, and it can essentially suit the needs of small-scale station array microtremor surveys. However, the accuracy and reliability of dispersion curves are somewhat diminished by overlaid averaging since the dispersion information of various depth media carried by dispersion curves differs among stations at various distances. The correlation coefficient can be used to evaluate the reliability of the dispersion information.

$J_0$ is conceptually similar in shape to the correlation coefficient curve obtained through SI. The accuracy and interference factor influence are weaker in the initial segment of the correlation coefficient curve that is monotonically declining. As a result, the phase velocity produced by fitting the first monotonically declining section of both the correlation coefficient curve and $J_0$ is typically seen to be more accurate when extracting the dispersion curve. Figure 3a displays the correlation coefficient curves obtained using SI from the microtremor signals of station pairs with various spacing in a linear array, and Figure 3b displays $J_0$. For station pairings that are far apart, the correlation coefficient curve’s first monotonically falling interval is narrow and has an excessive number of oscillatory attenuation bands. When the frequency is higher than 6 Hz, the reliability falls. The correlation coefficient curve of the small spacing station pair has a more pronounced downward tendency overall in the high-frequency band. Furthermore, its effective frequency band range is broader. However, there is minimal change in its correlation coefficient in the low-frequency range of 1 to 4 Hz. The shape of the coherence coefficient in this band is different from the Bessel function curve, and it is less reliable.

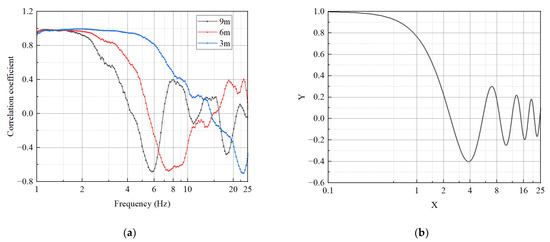
Figure 3. Correlation coefficient curves and zero-order first-class Bessel function curve. (a) Correlation coefficient curves; (b) $J_0$: Zero-order first-class Bessel function curve.

A great deal of studies and practical applications have shown that the distance between stations affects the depth of the microtremor survey [26,27]. As surface waves propagate at shallow ground surfaces, dispersion and attenuation features cause the energy of high-frequency signals to decay more quickly, penetrate to small depths, and have high resolution of shallow velocity patterns. Low-frequency signals decay slowly, travel long distances, penetrate to enormous depths, and contain more information about the deeper medium.

Pairs with a small station spacing record signals with a predominance of high-frequency components during station array observations, whereas pairings with large station spacing can capture more long-wavelength signals. The S-wave velocity structure of subsurface media at different depths can be inferred from surface waves of different frequencies [28]. The dispersion curves of various station spacing can be fused in bands according to the spacing size by combining the impact of station pair spacing on the form of the correlation coefficient curve. The frequency travels from high to low, the level goes from shallow to deep, and the sub-bands are fused to achieve a sharper dispersion curve and geological structure.

2.2.2. Fusion Criterion

The amplitude of surface waves decreases exponentially with depth during propagation. When the depth is approximately equal to the wavelength, its energy decays rapidly, and its penetration depth is about a wavelength range. According to the half-wavelength theory, the surface wave velocity measured using microtremor survey can be considered as the average elastic medium reflection of the medium within half a wavelength depth, and the surface wave survey depth is about half-wavelength [29]. So, the detection depth can be written as follows:

$$h_{\max }=\frac{{\lambda }_{\max }}{2}=\frac{V(f_{\min })}{2f_{\min }}$$

(7)

where $h_{\max }$ is the maximum detection depth, $f_{\min }$ refers to maximum reliable low frequency of the dispersion curve, ${\lambda }_{\max }$ and $V(f_{\min })$ are the wavelength and the surface wave phase velocity corresponding to the maximum reliable low frequency, respectively.

The ideal exploration depth for the SPAC is 3–5 times the station spacing [30], based on the theoretical agreement between the SPAC and SI; in this paper, 5 times the distance is taken as the maximum ideal detection depth, so the maximum wavelength that can be detected by a single station pair can be expressed as follows:

$${\lambda }_{\max }=\frac{V(f_{\min })}{f_{\min }}\le 10d$$

(8)

where $d$ is distance of two stations. Equation (8) shows the mathematical model for maximum reliable low frequency and station pair distance. Figure 4 shows the principle of maximum reliable low-frequency calculation. When one calculates the $V-f$ curve at 10 times the station distance according to Formula (8), the intersection point with the dispersion curve is the maximum reliable low frequency of the dispersion curve of the station pair.

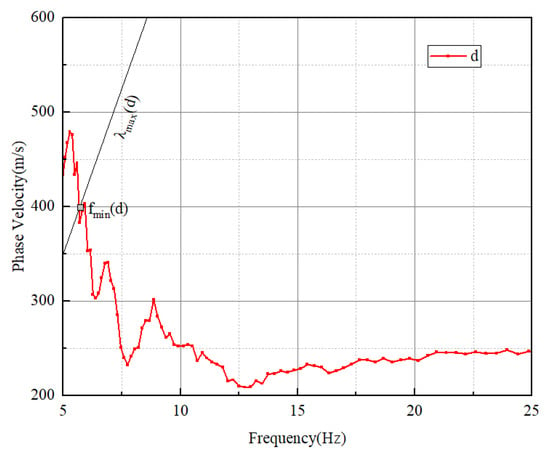
Figure 4. Principle of maximum reliable low-frequency calculation.

Calculating maximum reliable low frequencies of the dispersion curves for each distance and then using these frequencies as the fusion boundary to perform hierarchical frequency fusion, the final fused dispersion curve can be written as follows:

$$V(f)=\left\{\begin{array}{l}V(f,d_1) f\ge f_{\min }(d_1)\\ V(f,d_2) f_{\min }(d_1)<f\le f_{\min }(d_2)\\ \dots \dots .\\ V(f,d_n) f_{\min }(d_{n-1})<f\le f_{\min }(d_n)\end{array}\right.$$

(9)

The final dispersion curve consists of a fusion of reliable segments of the dispersion curve for each distance, each segment reflecting the relative accurate phase velocity structure at its corresponding reliable depth. The hierarchical frequency fusion schematic is shown in Figure 5.

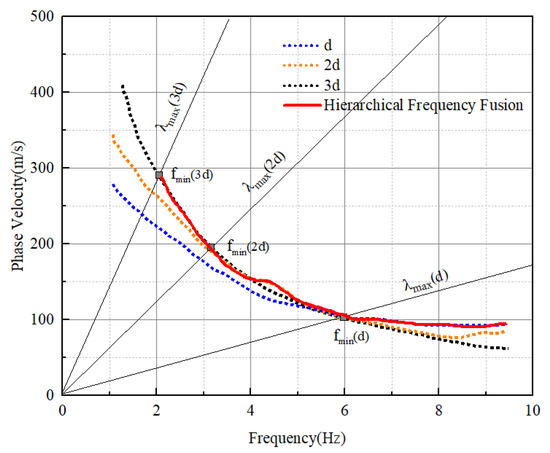
Figure 5. The schematic of hierarchical frequency fusion.

3. Microtremor Survey Application

3.1. Survey Area Overview

The survey area was located at HuBin East Road, Siming District, Xiamen City. Xiamen is located at the intersection of the north-east oriented Changle-Zhao’an Deep Fault Zone and the east-west oriented Nanjing-Xiamen Fault Zone. The regional tectonic position is part of the “Eastern Fujian Yanshan Fault Zone” and the “Southeast Fujian Coastal Metamorphic Zone”. The site is affected by fractures, and the local bedrock surface of the section to which it belongs is highly undulating.

An office building will be built on the site, and this experiment was the survey stage of the proposed project. One of the important objectives of this test was to determine the lithological characteristics of the strata to provide basic interpretation information for subsequent foundation design, engineering pile design, and seismic engineering design of the proposed building. The site was open, making it suitable for data acquisition.

3.2. Data Acquisition

In this experiment, VIDO micromotion detectors were used for data acquisition. Figure 6 shows a VIDO micromotion detector, and the main performance indicators of the detector are shown in Table 1.

Figure 6. VIDO intelligent micromotion detector.

Table 1. The main performance indicators of VIDO micromotion detector.

Name	Main Performance Indicators
Frequency bandwidth	0.2–500 Hz
Voltage output sensitivity	92 ± 7.5% V/m/s
Number of data channels	3
A/D conversion	24 bits
Sampling frequency	50 Hz, 100 Hz, 200 Hz, 500 Hz
Dynamic range	128 dB

9 sets of stations formed the observation array, the stations are numbered from 1 to 9, and the specific arrangement of the observation array is shown in Figure 7. The goal of this survey was to comprehend the geological conditions between 10 and 50 m beneath the site. So, in this experiment, the minimum spacing between adjacent stations was set at 3 m according to the ideal exploration depth of 3 to 5 times station spacing. The arrangement of the array was set as rectangle, which can be paired to generate station pairs of various distances and azimuths. Station pairs with multiple azimuths can attenuate the impact of dominant sources in certain directions. Station pairs with various distances receive signals of various wavelengths, reflecting the medium’s information at various depths.

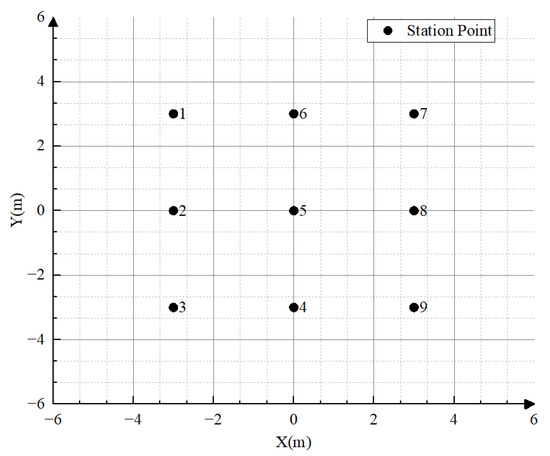
Figure 7. Arrangement of the observation array.

In this experiment, the micromotion detector’s sampling frequency was set to 250 Hz, and the microtremor signals were constantly gathered for 35 min. Figure 8 depicts the vertical component of waveforms of microtremor signals in this acquisition.

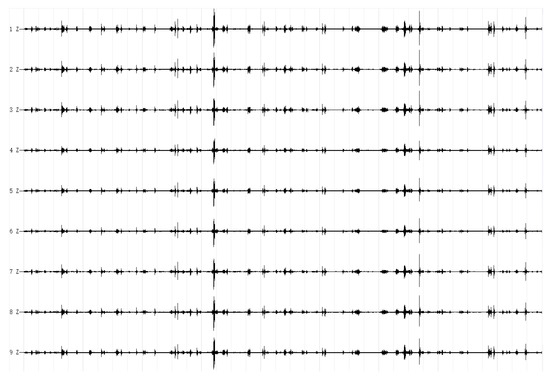
Figure 8. Waveforms of microtremor signals at observation stations in vertical direction.

4. Results

4.1. Data Processing

The seven station combinations with varying azimuths and distances that were formed from the stations in a rectangular array are depicted in Figure 9. The results of the microtremor survey can be viewed as the geological structure at the observation array’s center point, and station pairs that pass by or are close to the center can provide a better indication of the geology there. So, for analysis and computation in this study, the station combinations (a)~(e) were chosen to extract dispersion curves.

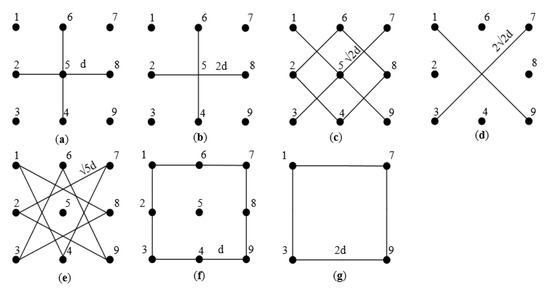
Figure 9. Schematic diagram of seven station combinations. (a) Combination of center and surrounding stations, distance is $d$, azimuth angles are 0°, 90°, 180°, 270°; (b) Combination of surrounding stations, distance is 2d, azimuth angles are 0°, 90°; (c) Combination of center and surrounding stations, distance is $\sqrt{2}d$, azimuth angles are 45°, 135°; (d) Combination of surrounding stations, distance is $2\sqrt{2}d$, azimuth angles are 45°, 135°; (e) Combination of surrounding stations, distance is $\sqrt{5}d$, azimuth angles are 26.5°, 63.5°, 116.5°, 153.5°; (f) Combination of surrounding stations, distance is d, azimuth angles are 0°, 90°; (g) Combination of surrounding stations, distance is 2d, azimuth angles are 0°, 90°.

First, the dispersion curve of the pair-wise station signals was extracted using SI. According to the geological laminar medium theory, the overall phase velocity of the surface waves should rise with falling frequency. When the high-frequency noise interference is too high or the low-frequency signal energy is too weak, the dispersion curve may exhibit high speed anomalies at high frequencies and velocity back inflection at low frequencies. These regions can be thought of as an anomalous frequency band. Abnormal frequency bands are removed according to this principle. All the dispersion curves extracted using SI are shown in Figure 10.

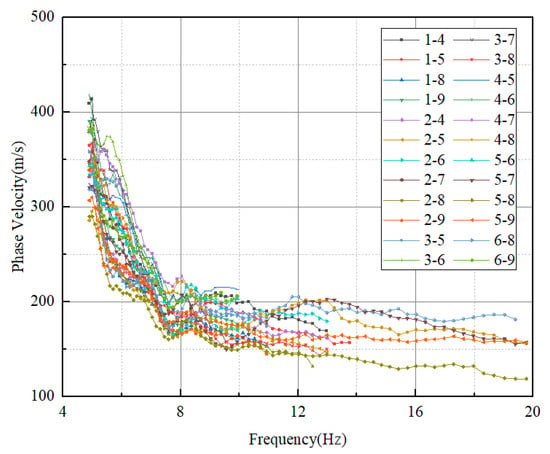
Figure 10. All dispersion curves extracted by SI.

Then, the dispersion curves of station pairs in the array with varying azimuths and equal station spacing were averaged using Formula (6) as a uniform effect under the site to weaken the influence of the wave field’s inhomogeneity. The average dispersion curves of the five different station distance combinations are shown in Figure 11.

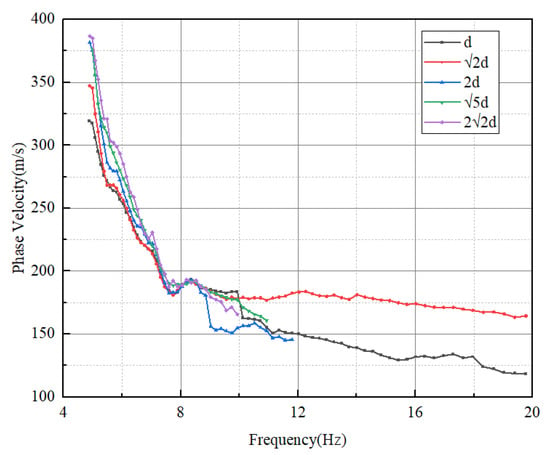
Figure 11. Average dispersion curves of five-station distance combinations.

Finally, we used the hierarchical frequency fusion method to fuse these averaged dispersion curves. ${\lambda }_{\max }$ curves were drawn according to Formula (8), and the maximum reliable low frequencies of a five-station combination were determined respectively. The results are shown in Figure 12. Based on the maximum reliable low frequencies, the dispersion curves of different spacing were refused. Mean dispersion curves were also calculated using the superimposed average method. The final dispersion curves for these two methods are shown in Figure 13.

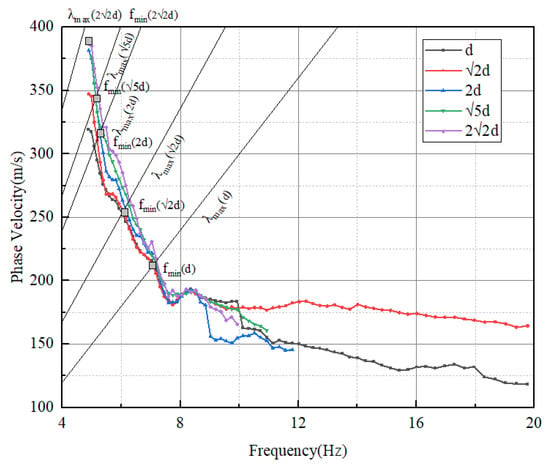
Figure 12. Maximum reliable low frequency of five-station distance combinations.

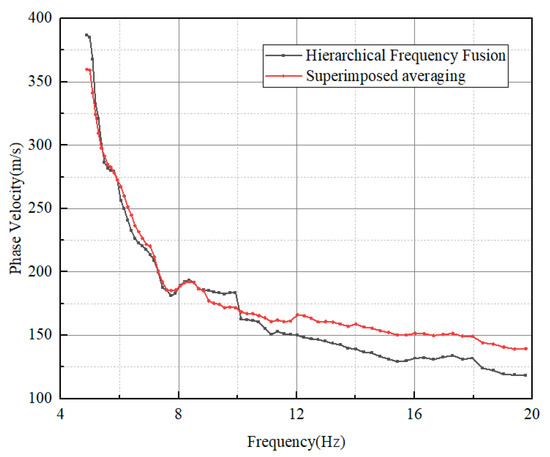
Figure 13. Dispersion curves of hierarchical frequency fusion and superimposed averaging method.

As shown in Figure 13, the dispersion curves obtained using the hierarchical frequency fusion approach have a wider overall phase velocity range, and the range of detection wavelengths determined from the half-wavelength formula is wider. The deeper information is larger and the equivalent shallow blind zone is smaller. The dispersion curves produced using the fusion method have a smoother velocity trend, whereas the dispersion curves produced by the superimposed averaging method may exhibit abnormal bumps or depressions at the dispersion curves’ starting frequencies at various distances, which may obstruct the analysis and discrimination of geological information that follows.

4.2. Results Interpretation

S-wave velocities are commonly used in engineering to reflect the density of geotechnical layers or for site classification and seismic calculations, so the surface wave dispersion curves at the measurement points need to be inverted or converted to obtain the S-wave velocity variation curve with depth. This paper used the Rayleigh surface wave phase velocity conversion S-wave velocity calculation method [31] to solve for S-wave velocity. The algorithm for the method is shown in Figure 14. The structure of the S-wave velocity obtained using these two methods is shown in Figure 15.

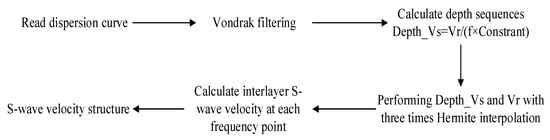
Figure 14. Algorithm of S-wave velocity conversion.

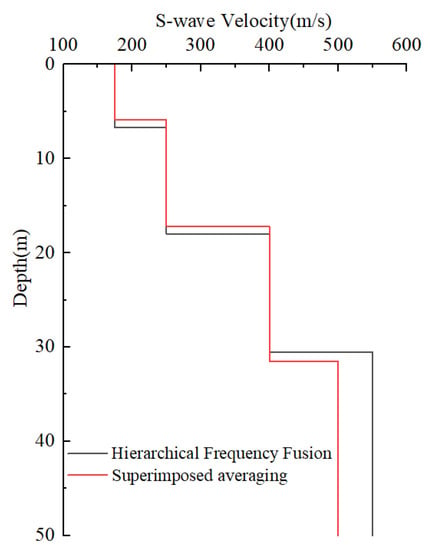
Figure 15. S-wave velocity structure of hierarchical frequency fusion and superimposed averaging.

According to the criteria for classifying soil types in the Code for Seismic Design of Buildings and the wave velocity test data from the geotechnical investigation boreholes close to the site to be tested in the Siming District, the stratigraphic structure of two methods at the test site was categorized. The stratigraphic delineation results of the two methods is shown in Table 2.

Table 2. Stratigraphic delineation results of two methods.

Lithology	Hierarchical Frequency Fusion(m)	Superimposed Averaging (m)	S-Wave Velocity (m/s)
Miscellaneous fill and silty clay	0–6.7	0–5.9	<175
Residual sandy clay	6.7–18	5.9–17.2	175–250
Fully weathered granite	18–30.5	17.2–31.5	250–400
Strongly–moderately weathered granite	>30.5	>31.5	>400

4.3. Drilling Verification

There was an engineering borehole located at the center of the detection array. In order to verify the accuracy of the detection results, the formation structure information obtained using the conversion of the dispersion curve can be compared with the borehole data. The engineering borehole drilling result is shown in Figure 16, and the core sample photo of the borehole is shown in Figure 17.

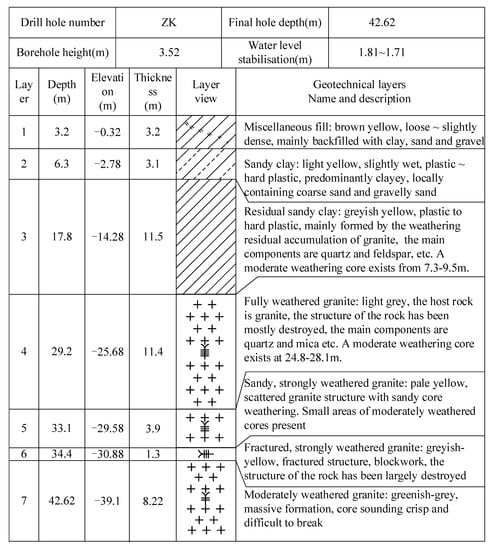
Figure 16. The engineering borehole drilling result.

Figure 17. Core sample photos of borehole.

In the field of shallow surface microtremor survey, the delineation errors usually need to be within 3 m. The borehole data shows that the delineation between residual sandy clay and fully weathered granite is 17.8 m, with a delineation error of 0.2 m for the hierarchical frequency fusion method and −0.6 m for the superimposed averaging method. The locations of the strongly weathered granite layers delineated using the hierarchical frequency fusion and the superimposed average are 30.5 m and 31.5 m, respectively, with the actual delayed upper interface of the strongly weathered granite being 29.2 m.

Figure 18 shows the stratigraphic delineation errors for the stratigraphic structures obtained using the two methods. The stratification error can be expressed using Formula (10):

$$error={depth}_{calc}-{depth}_{act}$$

(10)

where ${depth}_{calc}$ means the calculated stratification position, and ${depth}_{act}$ stands for the actual stratification position.

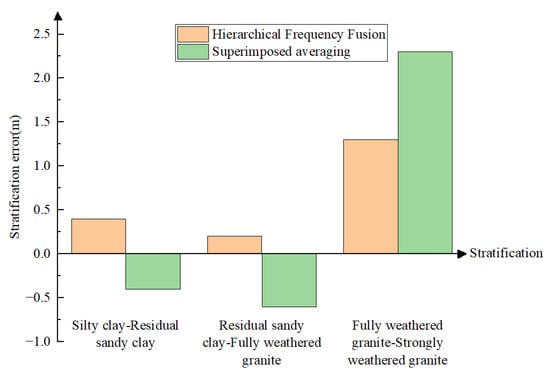
Figure 18. Stratification error of two methods.

It can be seen that the partitioning of the residual sandy clay–fully weathered granite and the partitioning of the fully weathered granite–strongly weathered granite using the hierarchical frequency fusion method is more accurate and has a smaller partitioning error.

In summary, it can be seen that hierarchical frequency fusion produces less error in the hierarchy and has a better match with the actual drilling data than the superimposed averaging method.

5. Conclusions

This paper investigated the extraction and processing method of dispersion curves from small-scale station array microtremor data based on SI. For multiple dispersion curves acquired using SI, the superimposed averaging method is quick but does not completely exploit the effective dispersion information of station pairs with varied distance, and the exploration accuracy is constrained. In response, this paper proposed a station-spacing-based dispersion curve processing method called hierarchical frequency fusion. Based on the correlation between the station pair spacing and the gathered signal frequency components, the reliable frequency intervals for dispersion curves were determined, and the fusion criterion was proposed. The dispersion curves of the various distance station pairs were fused in accordance with the fusion criteria to obtain the final dispersion curve. This method makes full use of the dispersion information of the various spacing station pairs and allows the dispersion curves of each distance station pair to be focused on their reliable frequency intervals to produce a more precise geological structure from shallow to deep.

Microtremor survey experiments were carried out in Xiamen City, with a rectangular exploration array arranged to explore and study the geological formations of the site. The station array’s dispersion curves were extracted and processed using the hierarchical frequency fusion method and superimposed averaging method, and the stratigraphic structures were determined using conversion of the subsurface transverse wave velocity structure. Compared with the superimposed averaging method, the stratigraphic structure obtained using the hierarchical frequency fusion method is in better agreement with the borehole data, which can effectively improve the accuracy of microtremor surveys and has certain guiding significance for similar projects in the future.