You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Applied Sciences
Download PDF
  • Communication
  • Open Access

21 March 2023

Tiling Photonic Topological Insulator for Laser Applications

,
,
and
1
Kirensky Institute of Physics, Federal Research Center KSC SB RAS, Krasnoyarsk 660036, Russia
2
Siberian Federal University, Krasnoyarsk 660041, Russia
*
Author to whom correspondence should be addressed.
Appl. Sci.2023, 13(6), 4004;https://doi.org/10.3390/app13064004
This article belongs to the Special Issue New Trends on Nonlinear Optics in Nanostructures and Plasmonics
Version Notes
Order Reprints

Abstract

A photonic topological insulator is a structure that isolates radiation in the bulk rather than at the edge (surface). Paradoxically, applications of such an insulator focus on its conducting edge states, which are robust against structural defects. We suggest a tiling photonic topological insulator constructed from identical prism resonators connected to each other. The light beam circulates inside the tiling bulk without propagation. However, we experimentally demonstrate a topologically-protected propagating state due to the disconnected faces of the edge resonators. The investigated state is robust against removing or attaching prism resonators. Moreover, the protection principle is phase-free and therefore highly scalable both in wavelength and resonator size. The tiling is suggested for active topological photonic devices and laser arrays.

1. Introduction

Recently, a topological insulator laser was demonstrated [,] which exhibits scatter-free edge-state transport of light in the laser cavity, immune to perturbations and disorder. The topological feature forces injection locking of many laser emitters to act as a single coherent laser. The concept led to a variety of configurations: electrical pumping of a quantum cascade laser with valley modes []; vertical emission []; and bulk and vortex lasing [,]. Simultaneously, one-dimensional active resonator arrays were described by a Su–Schrieffer–Heeger model [], and then implemented and optimized for robust single-mode high-power lasers [,,].
Topological invariance of a physical process means that it is described by some highly robust conserved quantity that does not change under continuous deformations in the parametric space []. For example, the number of holes of a connected smooth compact surface does not change as the surface deforms, without cutting or gluing. In particular, Emmy Noether’s theorem connects symmetries to the existence of the corresponding conserved quantities, such as energy, momentum, angular momentum, electric charge, and others. Parametric deformations can break the symmetry, still preserving the topological invariant. Almost forty years ago, a topological invariant was introduced for a single-particle electron state in a combined periodic potential and out-of-plane magnetic field [,]. The similar wave-like behavior is inherent to the photon state in the periodic potential of the photonic crystal []. As the Bloch wavenumber adiabatically passes the loop trajectory within the Brillouin zone of the crystal, its wave function acquires some topological phase that defines the topological invariant of the photonic band, separated by an insulating bandgap from neighboring bands. According to the bulk-edge correspondence principle [], the number of edge states in the bandgap is equal to the difference of topological invariants in neighboring bands. Here, one assumes the spatial edge of the array rather than frequency band edge. As usual, in the optical frequency range, the magnetic response is weak. Instead, a spin–orbit coupling [], dynamical modulation [], or gain-loss materials [] can also give rise to nonzero topological phases separated by an insulating bandgap. This idea was easily transferred from photonic crystal to waveguides, including ring resonator platforms [].
Quartz prism resonators serve well instead of ring resonators, as the excitation can propagate between prisms by the frustrated total internal reflection mechanism. For the latter structure, additional edge solutions arise at different incident angles []. Nonetheless, there is the question of realizing such a complex coupling utilizing synthetic dimensions [], or in the microring fashion [,]. If the structure period is comparable to radiation wavelength, then the description engages the topological phase. Otherwise, when the resonators are much larger than the wavelength, a phase-free explanation of the edge state is appropriate in terms of the edge trajectory of the beam [].
In this paper, we suggest a tiling photonic topological insulator (TPhTI) constructed from identical prism resonators. Compared to [], this new design suggests a continuous connection of neighboring resonators without spatial gaps. The light beam circulates within a few prisms inside the tiling bulk, penetrating through the mutual faces of the prisms or turning the propagation direction by total internal reflection at the open faces. However, a topologically-propagating state occurs at the edge of the array due to the disconnected faces of edge prisms. This propagating state persists against removing or attaching new prism resonators.
Furthermore, we fabricated the TPhTI and demonstrated the topologically-protected propagating state experimentally. We also speculated on laser applications of the TPhTI containing the gain material.

2. Materials and Methods

To fabricate the TPhTI we used a detailed concept similar to []. Rectangular prism resonators (Figure 1a) were manufactured from quartz glass with a refractive index of 1.43. Their linear dimensions of 12 × 12 × 8 mm3 were ensured by the Maksutov method [] with 10 um accuracy. To avoid accuracy problems with the half-wavelength gap and multilayer covering, we chose the zero gap. The immersion liquid infiltrated the unintentional air gaps between the prism resonators to suppress the parasitic reflection and to ensure the lossless beam penetration between the resonators. Therefore, a liquid with a refractive index close to the refractive index of quartz glass was selected.
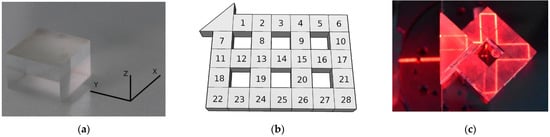
Figure 1. (a) The prism resonator made of quartz glass with a refractive index of 1.43. (b) A model of the tiling photonic topological insulator (TPhTI) composed of 28 prism resonators. (c) The TPhTI, composed of seven prism resonators.
The prism resonator tiling was precisely positioned on a flat platform, 200 × 200 mm2 in size. A rectangular triangular prism was used as a coupler to lead the light beam into and out of the quartz glass at the angle of total internal reflection. The angle of total internal reflection is 44.37° according to Snell’s law. The resonators were fixed on an adhesive composition of a mixture of vinyl acetate (30%) and acetone (70%) copolymers. The immersion liquid was an aqueous solution of glycerin with a density of 1.228 g per cubic centimeter. The refractive index of the immersion liquid was 1.45. No more than 0.01 mL of immersion liquid covered each face to avoid a meniscus on adjacent vertical faces, producing scattering and deviation of the beam. Before applying the immersion liquid, each prism was cleaned of dust and stains using crepe paper impregnated with a solution of water (80%), isopropanol (10%), metaxypropanol (5%), and nonionic surfactant (5%). Then, rectangular quartz prisms were connected, strictly in the order of numbering, as denoted in Figure 1b. After connecting each new segment, the operability of the tiling was checked using violet (405 nm) and red (650 nm) lasers (Figure 1c). Each prism was adjusted according to three degrees of freedom, namely one rotation and two translations along the axes X and Y (Figure 1a). The glass platform with assembled tiling and a triangular coupler was fixed on an optical bench next to the laser source.

3. Results

Figure 2 schematically demonstrates the stability of the beam trajectory; resonator #3, as denoted in Figure 1b, was removed in order to experimentally create the lattice defect of the TPhTI. Here, the green color indicates the trajectory of the beam. In and Out denote the entry and exit points of the beam, respectively. The input and output can be swapped; this does not affect the beam trajectory in any way. In the considered case, when removing nine resonators (#8–#9, #12–#16 and #19–#20), we observe an ordinary waveguide. However, while preserving the structure, we can observe robust beam trajectory relative to the removal of resonator #3 from the TPhTI. In this case, resonators #8, #9, and #13–15 are used to compensate for the absence of resonator #3. Obviously, all nine internal resonators have the same purpose with respect to other restructurings. For example, the removal of resonator #22 is compensated for by resonators #12, #13, and #19. This is the main topological insulator feature; an ordinary waveguide lacks this feature and behaves unstably with respect to the mentioned restructurings.
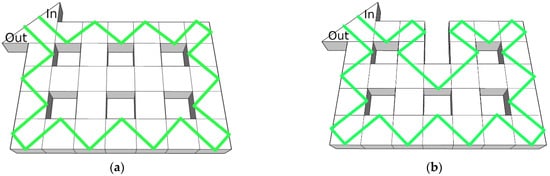
Figure 2. (a) The beam trajectory inside a smooth TPhTI model. (b) The corrected trajectory inside the TPhTI without prism resonator #3, as denoted in (b). The model shows that the light beam successfully bends around the defect of TPhTI.
The topological properties of the prism array yield a robustness to restructuring. Similar photonic topological insulators are theoretically described in [,,,], and practically implemented [,] on several platforms. Due to the angle of incidence of the beam trajectory, the prism array is a practical implementation of Rudner’s toy [], which provides a simple example of a topological insulator. As a class of restructuring, we chose the addition and removal of resonators from the array. Deeper explanations behind the topology are included in the Supplementary Materials.
Figure 3 shows that the laser beam bypasses the defect and exits the triangular coupler. The beam trajectory passes along the surface of the TPhTI structure due to the effect of total internal reflection on the faces of the prism resonators and exits back, as evidenced by the bright spot in the upper left corner of Figure 3b. The propagating state persists against removing (Figure 3b,d) or attaching new prism resonators (Figure 3e).
Figure 3. Beam trajectory photographs. The trajectory for smooth TPhTI (a,c) is robust against a defect obtained by removing prism resonator #3 (b,d) or attaching a new prism resonator below resonator #28 (e). Light beams for both a violet laser of 405 nm wavelength (a,b) and green laser of 532 nm (c–e) act in the same manner, proving the wavelength independence of the TPhTI principle.
Figure 4 shows that the presence of a topological state does not depend on prism resonator size. To demonstrate this scalability, the rectangular prism resonators were made in two versions. The first set was manufactured from quartz glass with a refractive index of 1.43, with linear dimensions 12 × 12 × 8 mm3 (Figure 4a). Their linear dimensions were ensured by the Maksutov method [] with 10 um accuracy. The second set was manufactured from Chinese crown glass K9 with a refractive index of 1.517 and linear dimensions 30 × 30 × 30 mm3, with 30 um accuracy (Figure 4b).
Figure 4. Scalability of the TPhTI is manifested by comparing two resonator sizes: (a) 12 × 12 × 8 mm3. (b) 30 × 30 × 30 mm3. Both trajectories are homothetic and proportional to prism linear dimensions.
In Figure 5, the scalability of the TPhTI principle is stressed. First, it works for every wavelength in the visible range, as long as the refractive index is sufficiently high. Second, the resonator size was fixed at the centimeter scale; nonetheless, the principle is valid for arbitrary sizes larger than the wavelength and the beam cross-section. Please see additional trajectories for different wavelengths, resonator sizes, and tiling configurations in the Supplementary Materials.
Figure 5. Wavelength-independent beam trajectory. Laser beams of RGB-colors pass the same trajectory through a TPhTI made of seven prism resonators: (a) red 650 nm, (b) green 532 nm, and (c) blue 405 nm.

4. Discussion

In practical implementation, the TPhTI turned out to be sensitive to the following parameters of the experiment:
  • Propagation of the light beam at the angle of total internal reflection; the intensity of the beam weakens with small deviations of the angle of incidence of the beam through a triangular coupler.
  • The presence of dust particles, air bubbles in the immersion liquid layer between the prism resonators, or remnants of immersion liquid on the side faces of prism resonators scatters the light beam. Violation of the parallelism of the faces when connecting prism resonators and inaccuracies in the manufacturing of prism resonators deflect the direction of the light beam, as well as changing its aperture and cross-section shape. With a strong deviation, splitting of the light beam on the vertical edges of the prism resonators is possible.
Quantitatively, TPhTI performance is proportional to the beam intensity along the trajectory, as shown in Table 1 for the smooth TPhTI (28 resonators, Figure 3a,c) and defective TPhTI, with one resonator taken away (27 resonators, Figure 3b,d). The relative intensity is normalized to the intensity of the beam passed through the reference waveguide, consisting of eight resonators (Figure 5). Throughout the visible range, the smooth TPhTI secures more than half of the radiation, while the defective TPhTI loses 10–20% more. The best performance is seen in the middle wavelength. The first reason for this is the refractive index dispersion for the prism material, coupler material, and immersion liquid. The second reason is the difference in beam cross-section of the used sources. Altogether, these reasons are technical and have no deep physical impact.
Table 1. TPhTI performance is measured as the relative beam intensity of the edge trajectory.
The effect of stability of the trajectory of the light beam relative to the defect introduced into the TPhTI is experimentally confirmed. Table 2 summarizes the stability of trajectories shown in Figure 3, Figure 4 and Figure 5. Figure 4 shows the perfect scalability of the phenomenon. Therefore, the minus sign ‘-’ declares that the linear dimensions of the prism resonator do not affect the trajectory stability. The refractive indices are not important until the total internal reflection and immersion conditions are satisfied. Therefore, they share the plus–minus sign ‘±’. The angle of beam incidence is exactly 45 degrees. This is critical, as the trajectory has to pass between certain corners or the beam will split and enter the array bulk. The partial impact of laser wavelength is shown in Table 1 and Figure 5.
Table 2. Experimental parameters and their impact on beam trajectory stability.

5. Conclusions

Here we focused on a new type of photonic topological insulator. We suggested a tiling photonic topological insulator constructed from identical prism resonators connected to each other. We experimentally demonstrated a topologically-protected propagating beam trajectory due to the disconnected faces of edge resonators. Then we removed or attached some prism resonators to destruct the trajectory. Nonetheless, the complete trajectory remained the same outside the destructed area. Overall, the main benefit is a novel platform for the practical implementation of Rudner’s toy []: a tiling photonic topological insulator. Other benefits are as follows: experimental demonstration of the novel platform, its robustness, phase-free concept, and laser array application. As a direction for possible further research, it is worth noting that, along with quadrangular TPhTIs, triangular and hexagonal prism resonator tiling can be experimentally implemented by zero gap, in accordance with the theoretical prediction []. One of the advantages of the hexagonal TPhTI is that the reflection angle is 60°. Therefore, this type of insulator can be experimentally implemented with optical material with a refractive index less than 1.43; hence, no less than 1.15. On the other hand, the simplest geometric considerations show that, under certain conditions in a hexagonal TPhTI, a diagonal transition occurs in fewer jumps between resonators than in a quadrangular TPhTI. The TPhTI can be described in the language of trajectories, as well as in the language of differential wave equations natural for graphene-like materials [], secondary quantization operators, or cellular automata []. For some certain incidence angles, the edge solutions reversed the direction upon scattering by edge defects. This case may be indicative of the existence of higher-order states [].
This tiling is suggested for active topological photonic devices and laser arrays, while topological features force unidirectional propagation. In the visible range, the magneto-optic effects are generally weak, which prohibits the conventional unidirectional propagation mechanism. Instead, the imbedding of gain and loss materials inside the resonator provides another type of unidirectionality [,]. The conducted research paves the way to transfer the gain–loss unidirectional mechanism from photonic crystals and waveguides to phase-free theory for macroscopic prism resonators.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app13064004/s1, Figures S1–S7: beam trajectory when passing through the TPhTI; Figures S4 and S5: trajectory that bends around the defect in the structure of the TPhTI; Figures S6 and S7: trajectory that bends around the defect in the structure of the TPhTI with resonators of a different size; Figures S8–S10: operation of Snell’s law; Figure S11: scattering matrix formalism to explain topological protection [,,,,,].

Author Contributions

Sample preparation, experimental setup, and measurement, P.N.K., N.V.R. and I.V.T.; software, D.P.F. and I.V.T.; validation, P.N.K.; conceptualization and methodology, D.P.F. and I.V.T.; writing—review and editing, P.N.K., D.P.F., N.V.R. and I.V.T.; supervision, I.V.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation (project no. 22-42-08003).

Data Availability Statement

The data presented in this study are available upon reasonable request from the corresponding author.

Acknowledgments

The authors are grateful to V.M. Sventitskii for useful discussions and materials used for experiment.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, eaar4005. [Google Scholar] [CrossRef] [PubMed]
  2. Harari, G.; Bandres, M.A.; Lumer, Y.; Rechtsman, M.C.; Chong, Y.D.; Khajavikhan, M.; Christodoulides, D.N.; Segev, M. Topological insulator laser: Theory. Science 2018, 359, eaar4003. [Google Scholar] [CrossRef] [PubMed]
  3. Zeng, Y.; Chattopadhyay, U.; Zhu, B.; Qiang, B.; Li, J.; Jin, Y.; Li, L.; Davies, A.G.; Linfield, E.H.; Zhang, B.; et al. Electrically pumped topological laser with valley edge modes. Nature 2020, 578, 246–250. [Google Scholar] [CrossRef] [PubMed]
  4. Dikopoltsev, A.; Harder, T.H.; Lustig, E.; Egorov, O.A.; Beierlein, J.; Wolf, A.; Lumer, Y.; Emmerling, M.; Schneider, C.; Höfling, S.; et al. Topological insulator vertical-cavity laser array. Science 2021, 373, 1514–1517. [Google Scholar] [CrossRef] [PubMed]
  5. Shao, Z.-K.; Chen, H.-Z.; Wang, S.; Mao, X.-R.; Yang, Z.-Q.; Wang, S.-L.; Wang, X.-X.; Hu, X.; Ma, R.-M. A high-performance topological bulk laser based on band-inversion-induced reflection. Nat. Nanotechnol. 2020, 15, 67–72. [Google Scholar] [CrossRef]
  6. Yang, Z.-Q.; Shao, Z.-K.; Chen, H.-Z.; Mao, X.-R.; Ma, R.-M. Spin-Momentum-Locked Edge Mode for Topological Vortex Lasing. Phys. Rev. Lett. 2020, 125, 013903. [Google Scholar] [CrossRef]
  7. Schomerus, H. Topologically protected midgap states in complex photonic lattices. Opt. Lett. 2013, 38, 1912. [Google Scholar] [CrossRef]
  8. St-Jean, P.; Goblot, V.; Galopin, E.; Lemaître, A.; Ozawa, T.; Le Gratiet, L.; Sagnes, I.; Bloch, J.; Amo, A. Lasing in topological edge states of a one-dimensional lattice. Nat. Photonics 2017, 11, 651–656. [Google Scholar] [CrossRef]
  9. Parto, M.; Wittek, S.; Hodaei, H.; Harari, G.; Bandres, M.A.; Ren, J.; Rechtsman, M.C.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Edge-Mode Lasing in 1D Topological Active Arrays. Phys. Rev. Lett. 2018, 120, 113901. [Google Scholar] [CrossRef]
  10. Ishida, N.; Ota, Y.; Lin, W.; Byrnes, T.; Arakawa, Y.; Iwamoto, S. A large-scale single-mode array laser based on a topological edge mode. Nanophotonics 2022, 11, 2169–2181. [Google Scholar] [CrossRef]
  11. Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
  12. Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef]
  13. Cheng, X.; Jouvaud, C.; Ni, X.; Mousavi, S.H.; Genack, A.Z.; Khanikaev, A.B. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 2016, 15, 542–548. [Google Scholar] [CrossRef]
  14. Haldane, F.D.M.; Raghu, S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef]
  15. Mong, R.S.K.; Shivamoggi, V. Edge states and the bulk-boundary correspondence in Dirac Hamiltonians. Phys. Rev. B 2011, 83, 125109. [Google Scholar] [CrossRef]
  16. Khanikaev, A.B.; Shvets, G. Two-dimensional topological photonics. Nat. Photonics 2017, 11, 763–773. [Google Scholar] [CrossRef]
  17. Rudner, M.S.; Lindner, N.H.; Berg, E.; Levin, M. Anomalous Edge States and the Bulk-Edge Correspondence for Periodically Driven Two-Dimensional Systems. Phys. Rev. X 2013, 3, 031005. [Google Scholar] [CrossRef]
  18. Leykam, D.; Yuan, L. Topological phases in ring resonators: Recent progress and future prospects. Nanophotonics 2020, 9, 4473–4487. [Google Scholar] [CrossRef]
  19. Fedchenko, D.P.; Kim, P.N.; Timofeev, I.V. Photonic Topological Insulator Based on Frustrated Total Internal Reflection in Array of Coupled Prism Resonators. Symmetry 2022, 14, 2673. [Google Scholar] [CrossRef]
  20. Yang, Z.; Lustig, E.; Harari, G.; Plotnik, Y.; Lumer, Y.; Bandres, M.A.; Segev, M. Mode-Locked Topological Insulator Laser Utilizing Synthetic Dimensions. Phys. Rev. X 2020, 10, 011059. [Google Scholar] [CrossRef]
  21. Liu, Y.G.N.; Wei, Y.; Hemmatyar, O.; Pyrialakos, G.G.; Jung, P.S.; Christodoulides, D.N.; Khajavikhan, M. Complex skin modes in non-Hermitian coupled laser arrays. Light Sci. Appl. 2022, 11, 336. [Google Scholar] [CrossRef] [PubMed]
  22. Liu, Y.G.N.; Jung, P.S.; Parto, M.; Christodoulides, D.N.; Khajavikhan, M. Gain-induced topological response via tailored long-range interactions. Nat. Phys. 2021, 17, 704–709. [Google Scholar] [CrossRef]
  23. Maksutov, D.D. New Catadioptric Meniscus Systems. J. Opt. Soc. Am. 1944, 34, 270. [Google Scholar] [CrossRef]
  24. Gao, F.; Gao, Z.; Shi, X.; Yang, Z.; Lin, X.; Xu, H.; Joannopoulos, J.D.; Soljačić, M.; Chen, H.; Lu, L.; et al. Probing topological protection using a designer surface plasmon structure. Nat. Commun. 2016, 7, 11619. [Google Scholar] [CrossRef] [PubMed]
  25. Grushevskaya, H.V.; Krylov, G.G.; Kruchinin, S.P.; Vlahovic, B.; Bellucci, S. Electronic properties and quasi-zero-energy states of graphene quantum dots. Phys. Rev. B 2021, 103, 235102. [Google Scholar] [CrossRef]
  26. Farrelly, T. A review of quantum cellular automata. Quantum 2020, 4, 368. [Google Scholar] [CrossRef]
  27. Li, M.; Zhirihin, D.; Gorlach, M.; Ni, X.; Filonov, D.; Slobozhanyuk, A.; Alù, A.; Khanikaev, A.B. Higher-order topological states in photonic kagome crystals with long-range interactions. Nat. Photonics 2020, 14, 89–94. [Google Scholar] [CrossRef]
  28. Pasek, M.; Chong, Y.D. Network models of photonic Floquet topological insulators. Phys. Rev. B—Condens. Matter Mater. Phys. 2014, 89, 075113. [Google Scholar] [CrossRef]
  29. Shalaev, M.I.; Walasik, W.; Tsukernik, A.; Xu, Y.; Litchinitser, N.M. Robust topologically protected transport in photonic crystals at telecommunication wavelengths. Nat. Nanotechnol. 2019, 14, 31–34. [Google Scholar] [CrossRef]
  30. Joannopoulos, J.; Johnson, S.; Winn, J.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University: Princeton, NJ, USA, 2008; p. 305. [Google Scholar]
  31. Vetrov, S.Y.; Timofeev, I.V.; Shabanov, V.F. Localized modes in chiral photonic structures. Physics-Uspekhi 2020, 63, 33. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Evaluation of Spring Stiffness of Resilience Pads for Booted Sleeper Track System Using a Pressure Sensor
Previous
Calculation Model of Compaction Coefficient of Soil among SP−PSC Pile Group on Collapsible Loess Foundation
Next