Abstract
An anterior cruciate ligament (ACL) tear is a severe sports injury that often occurs in young athletes. Besides the strong cumulative evidence on noncontact ACL tears, the injury mechanism (especially the contribution of external rotation) is still not well understood. The present work aims to evaluate which knee kinetics result in higher ACL stress and strain. A finite element model of the ACL was developed with a detailed geometry; the two distinct bundles (anteromedial and posterolateral) and the surrounding connective tissue were modelled based on medical anatomic measures and images. The model was validated using computational and cadaveric external data. Sixteen simulations were performed using different combinations of moments and axial loads applied to the knee model as boundary conditions. The results demonstrated that the peak stress (11.00 MPa) and strain (0.048) occurred at the midportion of the anteromedial bundle with the higher values being obtained under a combined knee valgus, flexion, tibial external rotation and high axial load. Anterior load showed low sensitivity in ACL stress and strain peaks. The tibial external rotation showed a higher contribution to the peak ACL stress and strain as compared to internal rotation. These results reinforce the role of axial load and highlight the importance of external rotation on ACL stress and strain, which may be suggestive of the ACL tear mechanism. The role of external rotation is often neglected and should be further explored in future cadaveric and experimental studies. The findings of this study provide data-driven insights to optimize the indications for prevention, diagnosis and treatment of ACL injuries in clinical practice and contribute to raising awareness of the injury mechanism among all relevant stakeholders.
1. Introduction
The anterior cruciate ligament (ACL) mechanism of injury is still debated and not well understood. The understanding of how the ACL is torn during a noncontact mechanism is crucial to determine which anatomical structures are ruptured and improve the knowledge on the tear mechanism for diagnostic and treatment purposes [1].
Most of the past clinical, experimental and computational studies highlight the importance of the tibial internal rotation (IR) to evaluate rotational instabilities of the knee joint. This framework arises from four main concepts that are well known in the literature: (1) the classic pivot–shift test that is performed with the tibia in IR [2]; (2) biomechanical studies showing the shift of the tibial centre of rotation towards the medial plateau in ACL-deficient knees [3]; (3) the bone-bruise patterns in magnetic resonance imaging (MRI) exams [4]; and (4) the anatomy of the ACL, suggesting that the ligament is tighter in IR than in external rotation (ER) [5]. For these reasons, the scientific literature considers that the noncontact ACL tear mechanism occurs mainly under 20–30 degrees of knee flexion combined with a valgus force and IR of the tibia, associated with posteroanterior and axial loads. Research has consequently been focused on the anterolateral structures of the knee [6,7,8,9,10,11,12], and surgical procedures have been developed with the aim of preventing the anterolateral displacement of the lateral tibial plateau, reducing the pivot–shift phenomenon and restoring the IR knee stability [7,9,10,11,12,13].
Despite the fact that IR plays an important role in the ACL noncontact mechanism of injury, the literature also suggests that the ER mechanism should be considered [14]. The ACL has a significant effect on isolated tibiofemoral ER at 20–30 degrees of knee flexion [15,16], and the tibial ER shows a significant increase after an ACL tear [16,17], suggesting that the ACL is also an ER restrictor and, consequently, is demanded during ER movement. Some authors have previously suggested that ER of the tibia can produce an equal or greater pivot–shift sign on physical examination [16,18,19]. The pivot–shift phenomenon, when evaluated intra-operatively or in cadaveric testing, has shown that the tibial centre of rotation is not identical in all isolated ACL-deficient knees with a significant medial plateau translation even with the pivot–shift test performed only in IR [20]. Despite the early evidence on the role of tibial ER in knee rotational stability, most experimental and simulation studies have solely focused on the IR when testing models of ACL injury [21,22,23,24,25,26]. The contribution of ER in the ACL tear mechanism has thus been undervalued and is still not well understood. The importance of the anteromedial knee structures and instability has been overlooked, and consequently, the potential of surgical procedures that are able to control the anteromedial biomechanical abnormality has been neglected.
Experimental procedures provide a good insight into the knee biomechanics and computational—based on the finite element method (FEM)—can serve as a complementary tool for a better understanding. The FEM modelling provides a fast and low-cost analysis of different biomechanical scenarios, especially when compared to cadaveric and clinical studies, which can be used to test and predict the behaviour of biological tissues under different conditions. The FEM allows for the simulation of the joint-kinetics behaviour under different boundary conditions of lower limb biomechanics. Indeed, the FEM can be a suitable tool to compute and simulate the cumulative damage to different tissues and materials [27,28] that are time-consuming and expensive to obtain experimentally [29,30]. The use of FEM simulations can test varying hypotheses and aid in understanding the complex cause–effect of the response of the soft tissues to different loading conditions [31].
There is a plethora of studies simulating the ACL response to different conditions after a reconstruction procedure [31]. However, accurate knee models are needed that mimic the average native ACL anatomy and the expected behaviour to common external forces that play a role during ACL injury (including ER). The simulation of soft tissues is a complex process due to the typical anisotropy of such biological materials. The soft tissue is, most of the time, simulated as an isotropic material (mainly the cartilage) or as a spring structure (mainly the ligaments) [31,32,33], which is not suitable for stress distribution calculation on the ACL [31]. The geometry of the ACL is often modelled as a spring structure [31] with a single bundle [31,34], which is not fit to test the response of the ACL to different loading conditions. The use of two bundles is important to best mimic the native anatomy of the ACL, especially considering each bundle may play a different role [35]. Moreover, most models collect data from a single individual/specimen that, although true for that single subject, is probably not adequate to be generalized to an average individual (lack of external validity). Therefore, it would be more accurate to use average data for both bone and soft structures, but especially to pinpoint the exact ligament insertions.
The present work focuses on a realistic geometry modelling that provides a detailed ACL structure with its two bundles and the surrounding connective tissue (instead of simulating the ACL as a single-spring structure). The material properties definition of the ACL model was applied to the bundles with the Holzapfel–Gasser–Ogden (HGO) to include the fibres and obtain a more realistic behaviour. The current study objective was to develop a realistic FEM model of the ACL (two bundles and exact morphometry of insertion points to the average population) and investigate which knee kinetics components result in a higher impact on ACL stress and strain during a simulated (FEM) ACL noncontact injury mechanism. We hypothesize that, contrary to the common literature, the tibial ER will have a more predominant impact than IR in ACL stress and strain.
2. Methods
The knee FEM model used in this study was adapted from the Open Knee Project [36], a valuable resource promoting scientific developments that is freely available. The model geometry was obtained from the MRI of a cadaveric body donation. The tri-dimensional right knee joint parts included in this work were the bones (femur and tibia), articular cartilages (femoral and tibial, lateral and medial), ligaments (anterior, posterior, medial and lateral) and menisci (lateral and medial). All the structures were assembled according to their anatomic location.
The femur and tibia were considered rigid bodies. A reference point was assigned to each of the bones to control their translational and rotational degrees of freedom. The articular cartilages were considered tied to the bones. A frictionless contact interaction was established between the menisci and the articular cartilages. Traction-only truss elements (E = 260 MPa, ν = 0.4 and cross-sectional area of 2 mm2) were added to the menisci (Figure 1) to simulate the ligaments in the horns of the menisci.
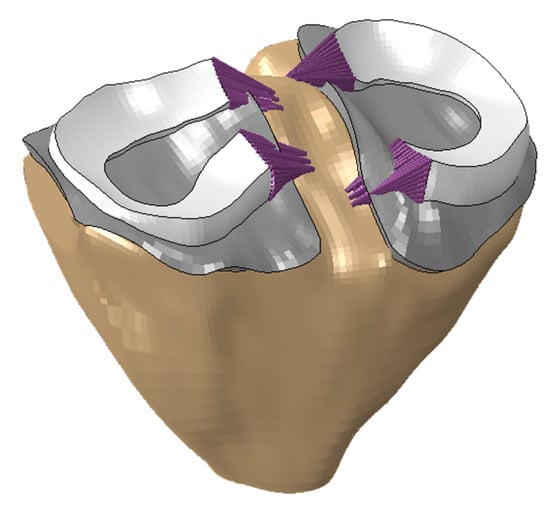
Figure 1.
Tibia, tibial cartilage, menisci and menisci ligaments.
The ACL was recreated from the ground up to improve and finetune its modelling features. The ACL was defined as close to real as possible, including accurate footprint locations and a global structure that contains the anteromedial (AM) and posterolateral (PL) bundles and the surrounding connective tissue. To build the new ligament, the geometry was first defined, and then, the mesh was assigned to the structure. The ACL geometric model was designed according to the femoral and tibial footprint locations measured in the anatomical work of Iriuchishima et al. [37]. All the proportions were applied to fit the open knee model dimensions, and the created sections are represented in yellow at their final location in Figure 2.

Figure 2.
ACL insertion dimensions in the model, (a) femoral, (b) tibial.
Six sections containing the edges of the bundles were defined between the two footprints (Supplement 1) based on the data from previous studies on the ACL anatomical dimensions [38,39]. All the sections were merged to shape the bundles, as shown in Figure 3a. The six ACL sections were built from five cross-sectional points based on previous MRI data [40]. Based on the presented geometry, all three ACL components were meshed (AM bundle, AL bundle and connective tissue). The ACL geometry was built using Rhinoceros software, and the simulations were performed with Abaqus-2020.
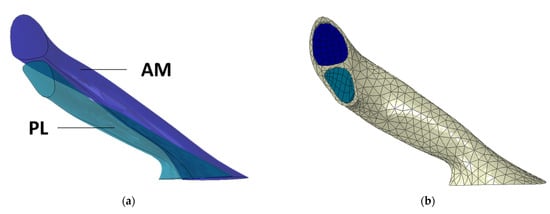
Figure 3.
(a) Geometry of the AM and PL bundles, (b) Complete ACL mesh (bundles and connective tissue).
The ACL model was built using two distinct bundles (AM and PL), represented in dark and light blue, respectively, in Figure 3a, and the surrounding connective tissue represented in greyish. The FEM mesh for the bundles was obtained using a sweep technique, which allowed for the use of hexahedral elements along their length. The usage of this type of element has several advantages and facilitates the definition of the HGO fibre directions. For the bundles’ connective tissue, a general technique was used based on tetrahedral elements. For the surrounding connective tissue, due to its geometry, it was not possible to create a suitable hexahedral based finite element mesh, and therefore, a general technique using tetrahedral elements was used. The mesh was defined by 3000 linear hexahedral elements (Abaqus-C3D8H) in the AM and PL bundles and 3875 linear tetrahedral (Abaqus-C3D4) elements in the surrounding tissue (Figure 3b).
The interfaces between the bundles and the connective tissue were defined and considered tied in order to maintain their position during the simulation. A soft hyperelastic material was used to model the connective tissue. Although a rupture of the connective tissue would expose the bundles, which would represent a risk factor for an eventual next failure of the ACL, the focus of the current work is on the bundles of the ACL. Therefore, it was considered that the connective tissue would be able to sustain large amounts of strain. The femoral and tibial ACL sections were fixed at their respective bony footprints to mimic their native anatomical role. A surface-to-surface general contact (with default interaction, contact pair with default thickness (1.0) and adjust 0.0) between the other ligaments, cartilage, menisci and bones was also defined.
The ACL bundles were modelled using the anisotropic HGO constitutive model, which takes into account the existence of the collagen fibres embedded in a soft matrix. The ACL connective tissue surrounding the bundles was modelled with the Neo–Hookean hyperelastic constitutive model. Table 1 describes all the structures comprised in the model, the constitutive models applied and the properties obtained from the literature.

Table 1.
Material properties.
Several uniaxial truss elements were used to simulate other relevant structural ligaments with a role in the knee kinetics. The added structures are highlighted in Figure 4a and Video 1 and modelled based on the properties and location described by Kiapour, Kiapour, Kaul, Quatman, Wordeman, Hewett, Demetropoulos and Goel [26]. The ligaments were defined with truss elements that have five elements each. The simulations were performed with the femur fixed, and all the boundary conditions (Figure 4c and Table 2) were imposed in the reference node of the tibia, node O in Figure 4c. All the boundary conditions followed the movement except one that was fixed in the initial axis direction, which was defined to simulate the quadricep and hamstring muscles’ action with a load of 600N [43] at the y-axis, as the femur position was fixed. Figure 4b shows the full model in the anterior view with the ACL bundles’ mesh highlighted in blue.

Figure 4.
(a) Posteromedial view of the truss elements representing the structural ligaments in the knee joint. The structures defined are the superficial (SM), deep (DM) and oblique (OM) bundles of the medial collateral ligament; the medial (APM), lateral (APL), oblique popliteal (APO) and arcuate popliteal (APA) bundles of the posterior capsule; the anterolateral structure (AL) and the popliteofibular ligament (PF); (b) anterior view of the FEM model with the ACL highlighted. Legend: M, medial side; L, lateral side; (c) Boundary conditions and loads imposed in the model: X-axis with anterior and valgus loads, Y-axis with knee flexion and Z representing the axial load IR/ER.

Table 2.
Simulations performed with the FEM model.
Despite the challenge related with the validation process in FEM models, mainly in such complex structures as the knee joint as described by some authors [44,45], an indirect validation was performed comparing the results obtained with the model developed in this study against those reported by Kiapour, Kiapour, Kaul, Quatman, Wordeman, Hewett, Demetropoulos and Goel [26]. The results compared were the tibial IR, as the knee was flexed up to 50 degrees, and the strain in the ACL and medial collateral ligament (MCL) during the abduction moment. The medial and lateral meniscus displacements were compared and validated based on the data from Vedi et al. [46]. The results obtained achieved similar values to those reported by Kiapour, Kiapour, Kaul, Quatman, Wordeman, Hewett, Demetropoulos and Goel [26] (Supplement 2), which led us to the next milestone. From a mechanical point of view, the goal of the present model is to be used as a reference model, which intends to represent a “normal” native biomechanical behaviour of the knee joint. The usage of such a model allows us to test different hypotheses.
An extended analysis of the knee joint was performed with a fixed 20 degrees of knee flexion and 50 Nm of abduction moment and compared, including several combinations of different magnitudes of tibial internal and external rotations and sagittal and axial loads (Table 2). The ACL most commonly tears with a low degree of knee flexion accompanied by an axial load (e.g., landing from a jump or cutting manoeuvres) [47,48,49,50,51,52,53,54]. It was decided to simulate two sets of axial forces to analyse the effects of a more demanding biomechanical scenario to the ACL (landing, 4000 N [55]) as compared to a less demanding scenario (walking, 700 N [56]). Moreover, most ACL tears are also associated with a dynamic valgus stress (knee abduction moment) [47,49,50,51,52,53], and thus, a 50 Nm knee abduction moment [26] was used in all testing sets. Anterior tibial stress loads are also commonly associated with ACL injury (134 N) [26]; therefore, the combination sets with and without anterior stress were tested. Lastly, tibial rotation also has an important impact on the ACL tear mechanism [47,48,49,50,51,52], and the model was thus tested with both internal and external rotations (separately) and used two different rotation magnitudes (15 Nm and 20 Nm) as suggested in a previous work [26].
The stress–strain distribution and peak values were obtained for the whole ACL and for each bundle in the fibres’ direction (Abaqus S11 and LE11). The peak stress and strain were tested in the 16 simulations combining different knee-kinetic scenarios. The locations (proximal, midportion and distal) of peak stress and strain for each of the ACL bundles were also registered.
3. Results
For the FE meshes used, a convergence study was not conducted, although different meshes were tested. Since the obtained results are in accordance with the literature, it can be assumed that the meshes used were reasonably refined. The maximum values of stress and strain obtained for the different structures of the ligament are shown in Figure 5 and Supplement 2. The whole ligament comprises the AM and PL bundles covered by the soft connective tissue. Although a large value of strain occurs on the connective tissue, this is not critical for the ligament rupture.
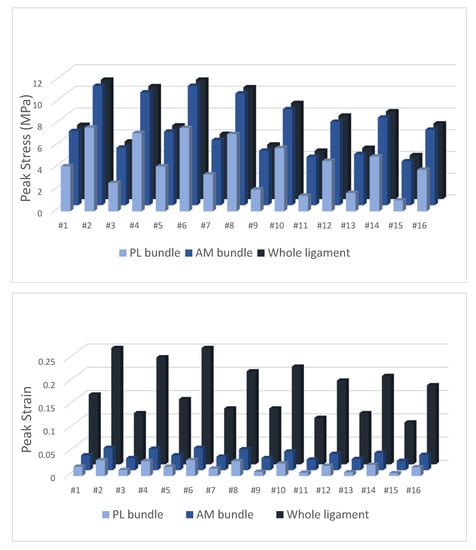
Figure 5.
Output of peak stress and strain for the whole ACL ligament and AM/PL bundles.
The peak stress (11 MPa) and strain (4.8%) were obtained at the AM bundle with the combined knee valgus (50 Nm abduction moment), 20-degree of knee flexion during landing (4000 N axial load) and with tibial ER (15 Nm and 20 Nm), corresponding to simulations #2 and #6. Under the same loading conditions but with a tibial IR instead of an ER, the simulations showed lower peak stress and strain values. The anterior tibial load had a minor role in both ACL stress and strain. The ACL stress and strain values were consistently higher when the axial load was 4000 N (simulation of landing) as compared to 700 N (simulation of walking).
The location of peak stress and strain was consistently at the AM bundle and always at the midportion of the ACL (Supplement 3). At the PL bundle, the location of peak stress and strain was also at the midportion when tibial ER momentum was applied; however, when the tibial IR momentum was applied coupled with 700 N axial load, the peak stress and strain were located at the distal and posterior portions of the PL bundle.
Figure 6 displays the location of the ACL strain evolution comparing the ER and IR under the same boundary conditions, #6 and #14 simulations, respectively. The highest strain values in both simulations are in the midportion of the AM bundle. An animation of simulations #6 and #14 can be viewed in videos 2 and 3. The peak strain location starts at the medial side of the midportion of the AM bundle and moves into the lateral side of the midportion of the PL bundle.
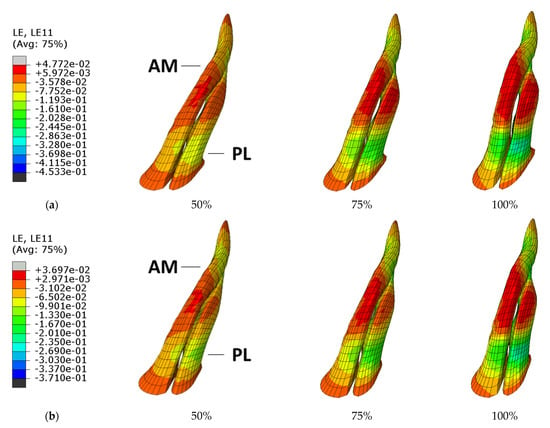
Figure 6.
Strain evolution in the ACL bundles during (a) simulation #6 [ER] and (b) simulation #14 [IR].
4. Discussion
The main finding of this study is that the location of peak stress and strain at the ACL is consistently at the AM bundle and always at the midportion of the ACL when the knee is under combined knee valgus, slight knee flexion, high axial load and with tibial ER. Our findings highlight the importance of ER in ACL injury, which is currently overlooked. Moreover, the finding that the ACL most probably begins to rupture at the AM bundle is also a novel finding. Our results were obtained using a knee model that uses a more realistic ACL model (two bundles) and is adjusted to the average individual (exact morphometry of ACL insertion points to the average population), which tested a multitude of different combinations of knee biomechanical kinetics to investigate which combinations would place the ACL at a higher risk of rupture. Our model and respective findings can be used for other different simulations and serve as the base model to further test the ACL behaviour under different conditions (for example, after ACL reconstruction or repair procedures).
The peak stress and strain at the ACL (either at the AM or PL bundles) were consistently higher when ER was applied as compared with the IR mechanism (under the same loading conditions). This finding goes against the common knowledge in testing the ACL tear with IR (because the PL bundle controls IR). Indeed, most cadaveric and simulation studies that evaluate the ACL tear are performed using a stress mechanism with IR and not ER [21,22,23,24,25,26]. There are several real-world examples of video analysis studies that support the ACL tear mechanism under ER. Many systematic video analysis studies have examined the moment of ACL injury in different sports and found that the tibia was most commonly externally rotated during the ACL noncontact mechanism of injury [47,48,49,52,57]. Waldén et al. [53] analysed the noncontact ACL injuries in 39 professional male football players and reported that the foot at the impact contact moment was in IR in six cases, in ER in six cases and neutral in 11 cases. Della Villa et al. [52] also analysed videos from 134 consecutive ACL injuries in football and found that the foot was externally rotated in 59% and 66% of the athletes at the initial contact and at the injury frame, respectively. Another video analysis study evaluated 69 noncontact ACL tears in professional American football athletes and found that the foot was externally rotated in 90% of the cases [47]. Similarly, Montgomery et al. [48] reported the systematic video analysis of 15 cases of noncontact ACL injuries in a professional rugby union with 11 cases showing an externally rotated foot at the initial contact. In team handball, Olsen et al. [49] evaluated the mechanisms for ACL injuries, and the tibia was either externally or internally rotated but most commonly externally rotated. Also, in skiing, where ACL injuries are frequent, the most common tear mechanism involves a combination of valgus and ER [57]. The tibiofemoral bone-bruise pattern after an ACL injury can also disclose the injury mechanism of an ACL tear. Although tibial IR is presented in most cases of injuries, there is large heterogeneity regarding the location of the tibial and femoral bone bruises [58,59,60] with approximately 25% of all bone bruises located exclusively in the medial tibial plateau and medial femoral condyle [60], suggesting that ER might be involved in an important proportion of the ACL mechanism of injuries. However, some caution is needed when interpreting the bone-bruise pattern to understand ACL injury dynamics because they can reflect the late phase of noncontact ACL injury rather than the injury mechanism leading to the ligament tear [61]. Some biomechanical studies also support an important role of ER in ACL injury. Park et al. [62] analysed the passive knee biomechanical properties in tibial rotation and suggested that there may be a greater risk of ACL injury resulting from impingement against the lateral wall of the intercondylar notch, which has been shown to be associated with tibial ER and knee abduction. Similarly, LaPrade and Burnett [63] reported a qualitative difference between placing the knee in external or internal rotation. When the knee was externally rotated past 15 degrees and flexed to between 30 and 40 degrees, the impingement occurred at the midportion of the ACL. No similar impingement was noted with internal rotation of the tibia on the fixed femur.
The tibiofemoral axial loads contributed significantly to the ACL tear, which was expected based on previous data from the literature [47,48,49,50,51,52,53,54]. This finding highlights the reliability of our model, which shows that higher axial load increases the peak stress and strain at the ACL. Axial loads often result from a landing situation [64,65] or when pivoting the foot at the ground (which has a higher axial load as compared to a walking load situation without impact). Indeed, video analysis studies show that the ACL often tears when there is an impact of the foot against the ground (for example, when landing) [49,51,66,67]. The simulations with the higher axial load (4000 N for landing [55] vs. 700 N for walking [56]) showed that the ACL stress and strain values were consistently higher when the 4000 N was applied.
The highest peak strain and stress values were located at the midportion of the AM and PL bundles, which suggests that the tear will probably occur at the midportion of the ACL. Combined data from 31 studies and 2088 individuals show that ACL tears occur mostly at the proximal third, but one third of these studies only included proximal ACL tears [68,69,70]. When more recent data are carefully analysed, the mid-substance tears account for half of the incidence of ACL tears [68]. Cadaveric testing also points to a tear mechanism starting at the mid-substance of the ACL [71].
A recent FEM study on the injury mechanism of ACL also tested the stress distribution at the ACL under three different loading conditions (134 N anterior tibial load, 5 Nm external tibial torque, 5 Nm internal tibial torque) [34]. They found that the peak stress was localized at the femoral insertion when under the anterior tibial load (14.9 MPa), at the mid-substance when under ER (0.8 MPa) and near the tibial insertion site when under IR (0.9 MPa). Their findings are similar to the present study when under ER, where we found that the peak stress was also at the mid-substance of the AM bundle. However, the findings for anterior tibial load and internal rotation, showing peak stress at the femoral and tibial insertions, were not corroborated in our study. One of the reasons for the diverging results might have arisen from the fact that the authors of the previous study tested the movement isolated, whereas we combined the knee movement under combining kinetic scenarios, which emulates better real-world conditions as shown by the video-analysis studies [47,48,49,52,57]. Moreover, it was not possible to compare which bundle was most affected, as the previous study modelled the ACL as a single structure. Side-to-side comparison of peak strain was also not possible because the previous study had not tested the ACL strain.
The native resistance of the ACL is described by the literature to be approximately 2160 ± 157 N among the young population. These values were tested using INSTROM in cadaveric knees submitted to axial and posteroanterior forces with the knee joint placed in a fixed 30° semiflexion [72]. The mechanism produced with the INSTROM device does not correspond to the reality of an ACL tear as it does not take into account the forces related to tibial rotation. In our study, the peak stress (11 MPa) and strain (4.8%) were obtained at the AM bundle with the combined knee valgus (50 Nm abduction moment), 20 degrees of knee flexion, during landing (4000 N axial load) and with tibial ER (15 Nm and 20 Nm). A study by Butler et al. [73] showed that the ACL bundles develop higher load-related material properties than the posterior bundles. The anterior bundles developed significantly larger moduli, maximum stresses and strain energy densities to maximum stress than the posterior subunits. The average stresses at rupture were, respectively, 38 MPa vs 15 MPa for the different bundles, which is in accordance with the present work. The tibial rotation plays an indisputable role in the ACL tear mechanism, but there was not a significant effect of the magnitude of the tibial rotation momentum (15 Nm vs 20 Nm) on the stress and strain values. This suggests that 15 Nm tibial rotation may be enough to cause an ACL tear (especially in cases of low energy injury mechanism) and increasing to 20 Nm may not lead to much further damage. The anterior tibial load showed low sensitivity in peak ACL stress and strain values in the FEM simulation, which suggests that, although the ACL has a major role in restricting posteroanterior tibial translation [74,75], an anterior load seems to have no significant effect on the ACL peak stress and strain values and probably a lesser role (than previously thought) in the ACL tear.
Our findings are clinically relevant and offer some directions for future studies. Upcoming cadaveric biomechanical studies should focus on ER when testing the ACL tear mechanism. The role of ER in ACL tears is undervalued and should be better understood as it may have important implications for the diagnosis, treatment and prevention of ACL injuries. Assuming that ER has an important role in ACL tears, orthopaedic surgeons also need to consider the anteromedial structures of the knee when performing ligament reconstructive or reparative surgery. Moreover, our model can be used in future studies to better understand the ACL and neighbouring structures (other knee ligament, meniscus and cartilage) and biomechanical behaviour under different kinematic and kinetic conditions [34,76,77]. Our ACL model and testing conditions can also serve as a base to simulate different orthopaedic procedures (such as ACL reconstruction [31,78,79,80] or ACL repair) [81], investigate the ACL stress and strain after these procedures and assess the potential risk of re-rupture. The use of FEM modelling can provide a faster and cheaper testing method than cadaveric, biomechanical or clinical studies [28] and, therefore, can be used as a predicting tool for both prevention and simulation of the potential results after an ACL reconstruction or repair procedure.
There are several limitations that need to be acknowledged. The FEM models simulate the behaviour of specific biomechanical conditions but are limited in their nature as it is not possible to simulate the true nature of real-world situations in which there are many factors that act in combination to predispose someone to an ACL injury [82]. Moreover, several potential confounders, such as interindividual varying anatomy and biomechanics, cannot be accounted for in FEM and may have influence on the results. However, we used average ACL footprint data to better adjust our model to the general population and thus increase the potential for external validity. Hence, FEM should be used to advance and complement experimental studies but not to override or replace them. The experimental data used in this study for validation purposes were not independently collected but extracted from a previous study [26] that used both cadaveric and computational testing. Our validation results varied from the work of Kiapour, Kiapour, Kaul, Quatman, Wordeman, Hewett, Demetropoulos and Goel [26], but they only varied slightly—which reflects the heterogeneity described in the literature [31]—and varied in the same direction and magnitude, which led us to consider the model close enough for validation purposes. It should also be noted that our results are limited, as we only evaluated one knee model, and the model’s stress and strain predictions were not validated against an experimental model. Although this model intends to represent the “normal” biomechanical behaviour of the knee joint, it can be adjusted for a specific patient by using a mesh-morphing technique. The patella was modelled with truss elements and not as the full structure, which could also influence the validation process, as the patella also controls the knee rotations and translations [83]. We did not conduct conventional mesh sensitivity analyses (convergence study); however, we used meshes that were obtained from the Open Knee Project [84] and tested different meshes that performed similarly to those described in the literature. Variations of the tibial slope were not considered in the present work. Tibial slope is shown to have an impact on the risk of ACL tear [85,86] but not on the ACL strain [87].
5. Conclusions
The peak stress and strain at the ACL are obtained when the knee is under slight knee flexion combined with high axial load, knee valgus and tibial ER. Peak stress and strain are consistently located at the midportion of the AM bundle of the ACL. These results are clinically relevant and should raise awareness for the important role of ER in ACL injury, which should be considered for the prevention, diagnosis and treatment of ACL injuries.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app13063802/s1, Supplement 1: Figure S1: FE model showing the five ACL section from its tibial to femoral footprint; Supplement 2: Figure S2.1: FE model comparison with literature data for tibiofemoral axial plane kinematics under abduction, internal rotation and sagittal load conditions; Figure S2.2: FE model comparison with Kiapour’s et al. FEM data for tibiofemoral axial plane kinematics under abduction, internal rotation and sagittal load conditions; Figure S2.3: FE model comparison with literature data for tibiofemoral frontal plane kinematics under 50 Nm abduction moment conditions; Figure S2.4: FE model comparison with Kiapour’s et al. FEM data for tibiofemoral frontal plane kinematics under 50 Nm abduction moment conditions; Figure S2.5: Comparison of the maximum strain values obtained in the current study, with literature data for the MCL and ACL structures, under 50 Nm abduction moment conditions; Figure S2.6: Comparison of the maximum strain values obtained in the current study, with Kiapour’s et al. FEM data for the MCL and ACL structures, under 50 Nm abduction moment conditions; Supplement 3: Table S1: Output and location of peak stress and strain for the whole ACL ligament and AM/PL bundles.
Author Contributions
Conceptualization, C.F.S., R.B., R.A., M.P.L.P., R.N.J. and J.E.-M.; Methodology, C.F.S., R.A., R.P. and M.P.L.P.; Analysis of data, C.F.S. and M.P.L.P.; Draft of results and manuscript, C.F.S., R.A. and M.P.L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received a funding from Arthrex with the grant number EMEA19065.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Arthrex for their support of this study.
Conflicts of Interest
A substantial part of this work was financially supported by Arthrex. Arthrex did not yield any role in the study design; in the collection, analysis and interpretation of data; in the writing of the manuscript and in the decision to submit the manuscript for publication.
References
- McLean, S.G.; Mallett, K.F.; Arruda, E.M. Deconstructing the anterior cruciate ligament: What we know and do not know about function, material properties, and injury mechanics. J. Biomech. Eng. 2015, 137, 020906. [Google Scholar] [CrossRef] [PubMed]
- Horvath, A.; Meredith, S.J.; Nishida, K.; Hoshino, Y.; Musahl, V. Objectifying the Pivot Shift Test. Sports Med. Arthrosc. Rev. 2020, 28, 36–40. [Google Scholar] [CrossRef] [PubMed]
- Noyes, F.R.; Jetter, A.W.; Grood, E.S.; Harms, S.P.; Gardner, E.J.; Levy, M.S. Anterior cruciate ligament function in providing rotational stability assessed by medial and lateral tibiofemoral compartment translations and subluxations. Am. J. Sports Med. 2015, 43, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.Y.; Spritzer, C.E.; Utturkar, G.M.; Toth, A.P.; Garrett, W.E.; DeFrate, L.E. Knee Kinematics During Noncontact Anterior Cruciate Ligament Injury as Determined From Bone Bruise Location. Am. J. Sports Med. 2015, 43, 2515–2521. [Google Scholar] [CrossRef] [PubMed]
- Amis, A.A.; Dawkins, G.P. Functional anatomy of the anterior cruciate ligament. Fibre bundle actions related to ligament replacements and injuries. J. Bone Jt. Surg. Br. Vol. 1991, 73, 260–267. [Google Scholar] [CrossRef]
- Xu, J.; Han, K.; Su, W.; Jiang, J.; Yan, X.; Yu, J.; Dong, S.; Zhao, J. A Secondary Injury of the Anterolateral Structure Plays a Minor Role in Anterior and Anterolateral Instability of ACL-Deficient Knees in the Case of Functional Iliotibial Band. Arthroscopy 2020, 37, 1182–1191. [Google Scholar] [CrossRef]
- Lee, J.K.; Seo, Y.J.; Jeong, S.Y.; Yang, J.H. Biomechanical function of the anterolateral ligament of the knee: A systematic review. Knee Surg. Relat. Res. 2020, 32, 6. [Google Scholar] [CrossRef]
- Smith, P.A.; Thomas, D.M.; Pomajzl, R.J.; Bley, J.A.; Pfeiffer, F.M.; Cook, J.L. A Biomechanical Study of the Role of the Anterolateral Ligament and the Deep Iliotibial Band for Control of a Simulated Pivot Shift With Comparison of Minimally Invasive Extra-articular Anterolateral Tendon Graft Reconstruction Versus Modified Lemaire Reconstruction After Anterior Cruciate Ligament Reconstruction. Arthroscopy 2019, 35, 1473–1483. [Google Scholar]
- Delaloye, J.R.; Hartog, C.; Blatter, S.; Schläppi, M.; Müller, D.; Denzler, D.; Murar, J.; Koch, P.P. Anterolateral Ligament Reconstruction and Modified Lemaire Lateral Extra-Articular Tenodesis Similarly Improve Knee Stability After Anterior Cruciate Ligament Reconstruction: A Biomechanical Study. Arthroscopy 2020, 36, 1942–1950. [Google Scholar] [CrossRef]
- Kittl, C.; El-Daou, H.; Athwal, K.K.; Gupte, C.M.; Weiler, A.; Williams, A.; Amis, A.A. The Role of the Anterolateral Structures and the ACL in Controlling Laxity of the Intact and ACL-Deficient Knee. Am. J. Sports Med. 2016, 44, 345–354. [Google Scholar] [CrossRef]
- Spencer, L.; Burkhart, T.A.; Tran, M.N.; Rezansoff, A.J.; Deo, S.; Caterine, S.; Getgood, A.M. Biomechanical analysis of simulated clinical testing and reconstruction of the anterolateral ligament of the knee. Am. J. Sports Med. 2015, 43, 2189–2197. [Google Scholar] [CrossRef]
- Inderhaug, E.; Stephen, J.M.; Williams, A.; Amis, A.A. Biomechanical Comparison of Anterolateral Procedures Combined With Anterior Cruciate Ligament Reconstruction. Am. J. Sports Med. 2017, 45, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Marom, N.; Ouanezar, H.; Jahandar, H.; Zayyad, Z.A.; Fraychineaud, T.; Hurwit, D.; Imhauser, C.W.; Wickiewicz, T.L.; Pearle, A.D.; Nawabi, D.H. Lateral Extra-articular Tenodesis Reduces Anterior Cruciate Ligament Graft Force and Anterior Tibial Translation in Response to Applied Pivoting and Anterior Drawer Loads. Am. J. Sports Med. 2020, 48, 3183–3193. [Google Scholar] [CrossRef] [PubMed]
- Csintalan, R.P.; Ehsan, A.; McGarry, M.H.; Fithian, D.F.; Lee, T.Q. Biomechanical and Anatomical Effects of an External Rotational Torque Applied to the Knee: A Cadaveric Study. Am. J. Sports Med. 2006, 34, 1623–1629. [Google Scholar] [CrossRef] [PubMed]
- Lorbach, O.; Pape, D.; Maas, S.; Zerbe, T.; Busch, L.; Kohn, D.; Seil, R. Influence of the anteromedial and posterolateral bundles of the anterior cruciate ligament on external and internal tibiofemoral rotation. Am. J. Sports Med. 2010, 38, 721–727. [Google Scholar] [CrossRef]
- Bull, A.M.; Andersen, H.N.; Basso, O.; Targett, J.; Amis, A.A. Incidence and mechanism of the pivot shift. An in vitro study. Clin. Orthop. Relat. Res. 1999, 363, 219–231. [Google Scholar] [CrossRef]
- Matsumoto, H.; Suda, Y.; Otani, T.; Niki, Y.; Seedhom, B.B.; Fujikawa, K. Roles of the anterior cruciate ligament and the medial collateral ligament in preventing valgus instability. J. Orthop. Sci. 2001, 6, 28–32. [Google Scholar] [CrossRef]
- Bach, B.R., Jr.; Warren, R.F.; Wickiewicz, T.L. The pivot shift phenomenon: Results and description of a modified clinical test for anterior cruciate ligament insufficiency. Am. J. Sports Med. 1988, 16, 571–576. [Google Scholar] [CrossRef]
- Jakob, R.P.; Stäubli, H.U.; Deland, J.T. Grading the pivot shift. Objective tests with implications for treatment. J. Bone Jt. Surg. Br. Vol. 1987, 69, 294–299. [Google Scholar] [CrossRef]
- Noyes, F.R.; Grood, E.S.; Cummings, J.F.; Wroble, R.R. An analysis of the pivot shift phenomenon. The knee motions and subluxations induced by different examiners. Am. J. Sports Med. 1991, 19, 148–155. [Google Scholar] [CrossRef]
- Meyer, E.G.; Baumer, T.G.; Slade, J.M.; Smith, W.E.; Haut, R.C. Tibiofemoral contact pressures and osteochondral microtrauma during anterior cruciate ligament rupture due to excessive compressive loading and internal torque of the human knee. Am. J. Sports Med. 2008, 36, 1966–1977. [Google Scholar] [CrossRef] [PubMed]
- Bates, N.A.; Schilaty, N.D.; Nagelli, C.V.; Krych, A.J.; Hewett, T.E. Multiplanar Loading of the Knee and Its Influence on Anterior Cruciate Ligament and Medial Collateral Ligament Strain During Simulated Landings and Noncontact Tears. Am. J. Sports Med. 2019, 47, 1844–1853. [Google Scholar] [CrossRef] [PubMed]
- Lo, J.; Müller, O.; Wünschel, M.; Bauer, S.; Wülker, N. Forces in anterior cruciate ligament during simulated weight-bearing flexion with anterior and internal rotational tibial load. J. Biomech. 2008, 41, 1855–1861. [Google Scholar] [CrossRef] [PubMed]
- Kiapour, A.M.; Demetropoulos, C.K.; Kiapour, A.; Quatman, C.E.; Wordeman, S.C.; Goel, V.K.; Hewett, T.E. Strain Response of the Anterior Cruciate Ligament to Uniplanar and Multiplanar Loads During Simulated Landings: Implications for Injury Mechanism. Am. J. Sports Med. 2016, 44, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Levine, J.W.; Kiapour, A.M.; Quatman, C.E.; Wordeman, S.C.; Goel, V.K.; Hewett, T.E.; Demetropoulos, C.K. Clinically relevant injury patterns after an anterior cruciate ligament injury provide insight into injury mechanisms. Am. J. Sports Med. 2013, 41, 385–395. [Google Scholar] [CrossRef]
- Kiapour, A.; Kiapour, A.M.; Kaul, V.; Quatman, C.E.; Wordeman, S.C.; Hewett, T.E.; Demetropoulos, C.K.; Goel, V.K. Finite element model of the knee for investigation of injury mechanisms: Development and validation. J. Biomech. Eng. 2014, 136, 011002. [Google Scholar] [CrossRef]
- Sága, M.; Vaško, M.; Ságová, Z.; Kuric, I.; Kopas, P.; Handrik, M. FEM Simulation of Non-proportional Multiaxial Fatigue Damage. In Proceedings of the MATEC Web of Conferences, Curtin, Malaysia, 12–13 December 2022; p. 02006. [Google Scholar]
- Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Wibowo, D.B.; Kurdi, O.; Tauviqirrahman, M.; Jamari, J. Minimizing risk of failure from ceramic-on-ceramic total hip prosthesis by selecting ceramic materials based on tresca stress. Sustainability 2022, 14, 13413. [Google Scholar] [CrossRef]
- Stanev, D.; Moustakas, K.; Gliatis, J.; Koutsojannis, C. ACL Reconstruction Decision Support. Personalized Simulation of the Lachman Test and Custom Activities. Methods Inf. Med. 2016, 55, 98–105. [Google Scholar] [CrossRef]
- Weiss, J.A.; Maker, B.N.; Govindjee, S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput. Methods Appl. Mech. Eng. 1996, 135, 107–128. [Google Scholar] [CrossRef]
- Benos, L.; Stanev, D.; Spyrou, L.; Moustakas, K.; Tsaopoulos, D.E. A Review on Finite Element Modeling and Simulation of the Anterior Cruciate Ligament Reconstruction. Front. Bioeng. Biotechnol. 2020, 8, 967. [Google Scholar] [CrossRef]
- Naghibi Beidokhti, H.; Janssen, D.; van de Groes, S.; Hazrati, J.; Van den Boogaard, T.; Verdonschot, N. The influence of ligament modelling strategies on the predictive capability of finite element models of the human knee joint. J. Biomech. 2017, 65, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Homyk, A.; Orsi, A.; Wibby, S.; Yang, N.; Nayeb-Hashemi, H.; Canavan, P.K. Failure locus of the anterior cruciate ligament: 3D finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 865–874. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; Shi, H.; Liu, Z.; Zhang, J.; Li, H.; Huang, H.; Ao, Y. Finite Element Analysis and Experimental Validation of the Anterior Cruciate Ligament and Implications for the Injury Mechanism. Bioengineering 2022, 9, 590. [Google Scholar] [CrossRef] [PubMed]
- Amis, A.A. The functions of the fibre bundles of the anterior cruciate ligament in anterior drawer, rotational laxity and the pivot shift. Knee Surg. Sports Traumatol. Arthrosc. 2012, 20, 613–620. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, A. Open Knee: Open Source Modeling and Simulation in Knee Biomechanics. J. Knee Surg. 2016, 29, 107–116. [Google Scholar] [CrossRef]
- Iriuchishima, T.; Ryu, K.; Aizawa, S.; Fu, F.H. Size correlation between the tibial anterior cruciate ligament footprint and the tibia plateau. Knee Surg. Sports Traumatol. Arthrosc. 2015, 23, 1147–1152. [Google Scholar] [CrossRef]
- Cohen, S.B.; VanBeek, C.; Starman, J.S.; Armfield, D.; Irrgang, J.J.; Fu, F.H. MRI measurement of the 2 bundles of the normal anterior cruciate ligament. Orthopedics 2009, 32, 687. [Google Scholar]
- Siebold, R.; Dejour, D.; Zaffagnini, S. Anterior Cruciate Ligament Reconstruction: A Practical Surgical Guide; Springer Science & Business: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Sohn, K.M.; Lee, M.J.; Hong, H.; Yoon, Y.C.; Park, C.D.; Wang, J.H. The Bow Tie Shape of the Anterior Cruciate Ligament as Visualized by High-Resolution Magnetic Resonance Imaging. Am. J. Sports Med. 2017, 45, 1881–1887. [Google Scholar] [CrossRef]
- Kubıcek, M.; Florian, Z. Stress strain analysis of knee joint. Eng. Mech. 2009, 16, 315–322. [Google Scholar]
- Li, L.; Yang, X.; Yang, L.; Zhang, K.; Shi, J.; Zhu, L.; Liang, H.; Wang, X.; Jiang, Q. Biomechanical analysis of the effect of medial meniscus degenerative and traumatic lesions on the knee joint. Am. J. Transl. Res. 2019, 11, 542–556. [Google Scholar]
- Kiapour, A. Non-Contact ACL Injuries During Landing: Risk Factors and Mechanisms. Ph.D. Thesis, University of Toledo, Toledo, OH, USA, 2013. [Google Scholar]
- Galbusera, F.; Freutel, M.; Dürselen, L.; D’Aiuto, M.; Croce, D.; Villa, T.; Sansone, V.; Innocenti, B. Material models and properties in the finite element analysis of knee ligaments: A literature review. Front. Bioeng. Biotechnol. 2014, 2, 54. [Google Scholar] [CrossRef] [PubMed]
- Cooper, R.J.; Wilcox, R.K.; Jones, A.C. Finite element models of the tibiofemoral joint: A review of validation approaches and modelling challenges. Med. Eng. Phys. 2019, 74, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Vedi, V.; Williams, A.; Tennant, S.J.; Spouse, E.; Hunt, D.M.; Gedroyc, W.M. Meniscal movement. An in-vivo study using dynamic MRI. J. Bone Jt. Surg. Br. Vol. 1999, 81, 37–41. [Google Scholar] [CrossRef]
- Johnston, J.T.; Mandelbaum, B.R.; Schub, D.; Rodeo, S.A.; Matava, M.J.; Silvers-Granelli, H.J.; Cole, B.J.; ElAttrache, N.S.; McAdams, T.R.; Brophy, R.H. Video Analysis of Anterior Cruciate Ligament Tears in Professional American Football Athletes. Am. J. Sports Med. 2018, 46, 862–868. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, C.; Blackburn, J.; Withers, D.; Tierney, G.; Moran, C.; Simms, C. Mechanisms of ACL injury in professional rugby union: A systematic video analysis of 36 cases. Br. J. Sports Med. 2018, 52, 994–1001. [Google Scholar] [CrossRef]
- Olsen, O.E.; Myklebust, G.; Engebretsen, L.; Bahr, R. Injury mechanisms for anterior cruciate ligament injuries in team handball: A systematic video analysis. Am. J. Sports Med. 2004, 32, 1002–1012. [Google Scholar] [CrossRef] [PubMed]
- Carlson, V.R.; Sheehan, F.T.; Boden, B.P. Video Analysis of Anterior Cruciate Ligament (ACL) Injuries: A Systematic Review. JBJS Rev. 2016, 4, e5. [Google Scholar] [CrossRef]
- Krosshaug, T.; Nakamae, A.; Boden, B.P.; Engebretsen, L.; Smith, G.; Slauterbeck, J.R.; Hewett, T.E.; Bahr, R. Mechanisms of anterior cruciate ligament injury in basketball: Video analysis of 39 cases. Am. J. Sports Med. 2007, 35, 359–367. [Google Scholar] [CrossRef]
- Della Villa, F.; Buckthorpe, M.; Grassi, A.; Nabiuzzi, A.; Tosarelli, F.; Zaffagnini, S.; Della Villa, S. Systematic video analysis of ACL injuries in professional male football (soccer): Injury mechanisms, situational patterns and biomechanics study on 134 consecutive cases. Br. J. Sports Med. 2020, 54, 1423–1432. [Google Scholar] [CrossRef]
- Waldén, M.; Krosshaug, T.; Bjørneboe, J.; Andersen, T.E.; Faul, O.; Hägglund, M. Three distinct mechanisms predominate in non-contact anterior cruciate ligament injuries in male professional football players: A systematic video analysis of 39 cases. Br. J. Sports Med. 2015, 49, 1452–1460. [Google Scholar] [CrossRef]
- Kimura, Y.; Ishibashi, Y.; Tsuda, E.; Yamamoto, Y.; Tsukada, H.; Toh, S. Mechanisms for anterior cruciate ligament injuries in badminton. Br. J. Sports Med. 2010, 44, 1124–1127. [Google Scholar] [CrossRef] [PubMed]
- Kiapour, A.M.; Wordeman, S.C.; Paterno, M.V.; Quatman, C.E.; Levine, J.W.; Goel, V.K.; Demetropoulos, C.K.; Hewett, T.E. Diagnostic value of knee arthrometry in the prediction of anterior cruciate ligament strain during landing. Am. J. Sports Med. 2014, 42, 312–319. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, J. A comparative study on different walking load models. Struct. Eng. Mech. 2017, 63, 847–856. [Google Scholar]
- Järvinen, M.; Natri, A.; Laurila, S.; Kannus, P. Mechanisms of anterior cruciate ligament ruptures in skiing. Knee Surg. Sports Traumatol. Arthrosc. 1994, 2, 224–228. [Google Scholar] [CrossRef] [PubMed]
- Bastos, R.; Andrade, R.; Vasta, S.; Pereira, R.; Papalia, R.; van der Merwe, W.; Rodeo, S.; Espregueira-Mendes, J. Tibiofemoral bone bruise volume is not associated with meniscal injury and knee laxity in patients with anterior cruciate ligament rupture. Knee Surg. Sports Traumatol. Arthrosc. 2019, 27, 3318–3326. [Google Scholar] [CrossRef] [PubMed]
- Kim-Wang, S.Y.; Scribani, M.B.; Whiteside, M.B.; DeFrate, L.E.; Lassiter, T.E.; Wittstein, J.R. Distribution of Bone Contusion Patterns in Acute Noncontact Anterior Cruciate Ligament-Torn Knees. Am. J. Sports Med. 2021, 49, 404–409. [Google Scholar] [CrossRef]
- Zhang, L.; Hacke, J.D.; Garrett, W.E.; Liu, H.; Yu, B. Bone Bruises Associated with Anterior Cruciate Ligament Injury as Indicators of Injury Mechanism: A Systematic Review. Sports Med. 2019, 49, 453–462. [Google Scholar] [CrossRef]
- Grassi, A.; Agostinone, P.; Di Paolo, S.; Lucidi, G.A.; Macchiarola, L.; Bontempi, M.; Marchiori, G.; Bragonzoni, L.; Zaffagnini, S. Knee position at the moment of bone bruise could reflect the late phase of non-contact anterior cruciate ligament injury rather than the mechanisms leading to ligament failure. Knee Surg. Sports Traumatol. Arthrosc. 2021, 29, 4138–4145. [Google Scholar] [CrossRef]
- Park, H.S.; Wilson, N.A.; Zhang, L.Q. Gender differences in passive knee biomechanical properties in tibial rotation. J. Orthop. Res. 2008, 26, 937–944. [Google Scholar] [CrossRef]
- LaPrade, R.F.; Burnett, Q.M. Femoral intercondylar notch stenosis and correlation to anterior cruciate ligament injuries. A prospective study. Am. J. Sports Med. 1994, 22, 198–202. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, X.; Yu, T. Simulation Analysis of Knee Ligaments in the Landing Phase of Freestyle Skiing Aerial. Appl. Sci. 2019, 9, 3713. [Google Scholar] [CrossRef]
- Xu, D.; Jiang, X.; Cen, X.; Baker, J.S.; Gu, Y. Single-Leg Landings Following a Volleyball Spike May Increase the Risk of Anterior Cruciate Ligament Injury More Than Landing on Both-Legs. Appl. Sci. 2021, 11, 130. [Google Scholar] [CrossRef]
- Takahashi, S.; Nagano, Y.; Ito, W.; Kido, Y.; Okuwaki, T. A retrospective study of mechanisms of anterior cruciate ligament injuries in high school basketball, handball, judo, soccer, and volleyball. Medicine 2019, 98, e16030. [Google Scholar] [CrossRef] [PubMed]
- Koga, H.; Nakamae, A.; Shima, Y.; Iwasa, J.; Myklebust, G.; Engebretsen, L.; Bahr, R.; Krosshaug, T. Mechanisms for noncontact anterior cruciate ligament injuries: Knee joint kinematics in 10 injury situations from female team handball and basketball. Am. J. Sports Med. 2010, 38, 2218–2225. [Google Scholar] [CrossRef] [PubMed]
- van der List, J.P.; Mintz, D.N.; DiFelice, G.S. The Location of Anterior Cruciate Ligament Tears: A Prevalence Study Using Magnetic Resonance Imaging. Orthop. J. Sports Med. 2017, 5, 2325967117709966. [Google Scholar] [CrossRef]
- Henle, P.; Röder, C.; Perler, G.; Heitkemper, S.; Eggli, S. Dynamic Intraligamentary Stabilization (DIS) for treatment of acute anterior cruciate ligament ruptures: Case series experience of the first three years. BMC Musculoskelet. Disord. 2015, 16, 27. [Google Scholar] [CrossRef]
- van der List, J.P.; DiFelice, G.S. Role of tear location on outcomes of open primary repair of the anterior cruciate ligament: A systematic review of historical studies. Knee 2017, 24, 898–908. [Google Scholar] [CrossRef]
- Paschos, N.K.; Gartzonikas, D.; Barkoula, N.M.; Moraiti, C.; Paipetis, A.; Matikas, T.E.; Georgoulis, A.D. Cadaveric study of anterior cruciate ligament failure patterns under uniaxial tension along the ligament. Arthroscopy 2010, 26, 957–967. [Google Scholar] [CrossRef]
- Woo, S.L.; Hollis, J.M.; Adams, D.J.; Lyon, R.M.; Takai, S. Tensile properties of the human femur-anterior cruciate ligament-tibia complex. The effects of specimen age and orientation. Am. J. Sports Med. 1991, 19, 217–225. [Google Scholar] [CrossRef]
- Butler, D.L.; Guan, Y.; Kay, M.D.; Cummings, J.F.; Feder, S.M.; Levy, M.S. Location-dependent variations in the material properties of the anterior cruciate ligament. J. Biomech. 1992, 25, 511–518. [Google Scholar] [CrossRef]
- Zantop, T.; Herbort, M.; Raschke, M.J.; Fu, F.H.; Petersen, W. The role of the anteromedial and posterolateral bundles of the anterior cruciate ligament in anterior tibial translation and internal rotation. Am. J. Sports Med. 2007, 35, 223–227. [Google Scholar] [CrossRef] [PubMed]
- Limbert, G.; Middleton, J.; Taylor, M. Finite element analysis of the human ACL subjected to passive anterior tibial loads. Comput. Methods Biomech. Biomed. Eng. 2004, 7, 1–8. [Google Scholar] [CrossRef]
- Hodel, S.; Postolka, B.; Flury, A.; Schütz, P.; Taylor, W.R.; Vlachopoulos, L.; Fucentese, S.F. Influence of Bone Morphology on In Vivo Tibio-Femoral Kinematics in Healthy Knees during Gait Activities. J. Clin. Med. 2022, 11, 5082. [Google Scholar] [CrossRef]
- Knapp, A.; Williams, L.N. Predicting the Effect of Localized ACL Damage on Neighbor Ligament Mechanics via Finite Element Modeling. Bioengineering 2022, 9, 54. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, B.; Cheng, C.-K. Stiffness and shape of the ACL graft affects tunnel enlargement and graft wear. Knee Surg. Sports Traumatol. Arthrosc. 2020, 28, 2184–2193. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.G.; Kang, K.T.; Wang, J.H. Biomechanical Difference between Conventional Transtibial Single-Bundle and Anatomical Transportal Double-Bundle Anterior Cruciate Ligament Reconstruction Using Three-Dimensional Finite Element Model Analysis. J. Clin. Med. 2021, 10, 1625. [Google Scholar] [CrossRef]
- Wang, H.; Tao, M.; Shi, Q.; He, K.; Cheng, C.-K. Graft Diameter Should Reflect the Size of the Native Anterior Cruciate Ligament (ACL) to Improve the Outcome of ACL Reconstruction: A Finite Element Analysis. Bioengineering 2022, 9, 507. [Google Scholar] [CrossRef]
- Bartolin, P.B.; Boixadera, R.; Hudetz, D. Experimental testing and finite element method analysis of the anterior cruciate ligament primary repair with internal brace augmentation. Med. Eng. Phys. 2021, 95, 76–83. [Google Scholar] [CrossRef]
- Bittencourt, N.F.N.; Meeuwisse, W.H.; Mendonça, L.D.; Nettel-Aguirre, A.; Ocarino, J.M.; Fonseca, S.T. Complex systems approach for sports injuries: Moving from risk factor identification to injury pattern recognition—Narrative review and new concept. Br. J. Sports Med. 2016, 50, 1309. [Google Scholar] [CrossRef]
- Dhaher, Y.Y.; Kwon, T.-H.; Barry, M. The effect of connective tissue material uncertainties on knee joint mechanics under isolated loading conditions. J. Biomech. 2010, 43, 3118–3125. [Google Scholar] [CrossRef]
- Chokhandre, S.; Schwartz, A.; Klonowski, E.; Landis, B.; Erdemir, A. Open Knee(s): A Free and Open Source Library of Specimen-Specific Models and Related Digital Assets for Finite Element Analysis of the Knee Joint. Ann. Biomed. Eng. 2023, 51, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.; Vasta, S.; Sevivas, N.; Pereira, R.; Leal, A.; Papalia, R.; Pereira, H.; Espregueira-Mendes, J. Notch morphology is a risk factor for ACL injury: A systematic review and meta-analysis. J. ISAKOS 2016, 1, 70–81. [Google Scholar] [CrossRef]
- Bayer, S.; Meredith, S.J.; Wilson, K.; de Sa, D.; Pauyo, T.; Byrne, K.; McDonough, C.M.; Musahl, V. Knee Morphological Risk Factors for Anterior Cruciate Ligament Injury: A Systematic Review. J. Bone Jt. Surg. Am. 2020, 102, 703–718. [Google Scholar] [CrossRef]
- Nelitz, M.; Seitz, A.M.; Bauer, J.; Reichel, H.; Ignatius, A.; Dürselen, L. Increasing posterior tibial slope does not raise anterior cruciate ligament strain but decreases tibial rotation ability. Clin. Biomech. (Bristol Avon) 2013, 28, 285–290. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).