Abstract
The p-y curve method can be used to describe the stress–strain relationship of soil under elastic, elastoplastic, and plastic states, and is more accurate than other methods in dealing with the nonlinearity of pile–soil interaction. However, the p-y curve method also has several limitations. First, when constructing the p-y curve, undrained shear strength Cu is taken to be constant, and the diversity of soil layers around the pile side are also not considered. Second, in the analysis of the internal forces and deformation of the pile, the influence of the vertical load from the top of the pile and the self-weight of the pile, are both ignored. Third, in the analysis of internal forces and deformation, the pile side soil is set equivalent to a homogeneous soil layer, and the layering of the soil is not considered at all. In order to study the nonlinear problem of internal forces and deformation of a single pile in layered soil in greater detail, this paper analyzes a calculation model based on Wang’s calculation model, and compares several commonly used p-y curve calculation models. An internal force and deformation analysis model for a laterally loaded single pile, that explicitly considers the second-order effect is then established, by considering the differences between p-y curves of different soil types, as well as the change in Cu with depth. The differential equation of pile deflection for a single pile in layered soil is also presented, together with the corresponding finite differential solution algorithm program. This model was validated using a horizontal load test of a pile, and comparison of the calculated results with the measured results shows that the method outperforms existing p-y curve methods for deformation and internal force analysis of horizontally loaded piles.
1. Introduction
A p-y curve depicts the relationship between soil horizontal resistance p, at a certain depth under the ground and pile deflection y, at the corresponding position under the lateral load (horizontal force and bending moment) of the pile. This curve can help engineers understand the nonlinear state of pile–soil interaction, which is why it is the most used method globally for calculating the large deformation of a horizontally loaded pile. In 1970, Matlock [1] established the formula for a p-y curve for soft clay under a horizontal load, in the form of a subsection function, based on field tests. Then, Reese et al. [2] established the p-y curve for hard clay. Both of these papers laid the foundations for the p-y curve method, but the method still had limitations. In order to make the p-y curve method more broadly applicable, Sullivan et al. [3] proposed a unified method suitable for arbitrary clay, and Wang et al. [4] proposed a unified method suitable for clay, based on the constitutive relationship of the soil. Along the same lines, Zhang et al. [5] proposed a calculation method for a p-y curve suitable for soft clay in the middle and lower reaches of the Yangtze River in China, through field pile testing, and Zhang et al. [6] expanded upon this, by considering the weakening effect of soil. These authors constructed p-y curves of saturated sand under different weakening states. Additionally, based on field tests and a theoretical analysis, Luo et al. [7] and others combined the “m method” with the s hyperbolic p-y curve, to modify the calculation of p-y curves in layered soil.
Zou et al. [8] dealt with pile side soil resistance by using the stress distribution law of the pile side soil, and considered the influence of the longitudinal stress of the soil, in order to establish a p-y curve model based on the stress state of the pile side soil. Lei et al. [9] went further, and used the finite difference method to solve the deflection differential equation, based on the combination of load transfer and p-y curve methods for layered soil foundations, and validated the model’s feasibility with real-world engineering examples. Similarly, Xing et al. [10] adopted a hyperbolic horizontal load transfer model, based on a consideration of the layering of the surrounding soil, and obtained the nonlinear solution of the deformation and internal forces of the pile body under a composite load. Their results show that the large deformation of horizontally loaded piles cannot be ignored. Lu et al. [11] studied the mechanism of composite loads on piles in sandy soil, and indicated that they are caused by the superposition of the soil compaction and second-order effect. Thieken et al. [12] also studied a p-y curve method of piles in layered sandy soil, based on numerical analysis, and compared it to the iso-depth method proposed by Georgiadis [13], and the results showed little difference. Finally, Cao et al. [14] used a model test that considered the influence of pile top constraints, and constructed the hyperbolic p-y curve of an inclined pile in sand, using the two parameters of initial foundation reaction modulus and ultimate soil reaction at the pile side.
At present, there are still some problems that are generally ignored by the p-y curve method. First, Cu is taken as fixed, ignoring the influence of its change with depth on the p-y curve. Second, when the p-y curve is used to calculate the forces on a laterally loaded pile, the influence of the vertical load on the pile top is not considered. Third, the soil mass is divided into soft clay (Cu < 96 kPa) and hard clay (Cu ≥ 96 kPa) only, according to the undrained shear strength Cu value, and then analyzed assuming a uniform soil layer, which ignores the possible coexistence of soft and hard clay, as well as other cohesionless soil that is often observed in practice. Based on field tests and Wang’s method, this paper corrects for the above three problems, in order to study the nonlinear problem of internal forces and deformation of a single pile in layered soil in greater detail. A calculation method for the internal forces and displacement of the pile body in layered soil is proposed, based on the improved p-y curve method, and an engineering application analysis is also conducted.
2. Calculation Model and Solution Method
2.1. Calculation Model and Basic Equation
For a single pile set in layered soil, the pile top is assumed to be flush with the ground, and the horizontal load H0, bending moment M0, and vertical load N0 are assumed to be applied to the pile top. The other basic assumptions are enumerated below.
(1) The pile is regarded as a vertical foundation beam, and the deformation and internal forces of the pile body under the elastic state can be determined according to beam bending theory.
(2) The pile, and the soil around the pile, are always in contact, and the displacement of the soil around the pile is the same as that of the pile body.
(3) The soil is an elastic–plastic body, and the relationship between the pile side soil resistance and deformation is described by a p-y curve.
(4) The pile side friction is uniformly distributed along the pile body.
Since the dead weight of the pile varies linearly with its depth, the axial force, N, of the pile at any depth, z, from the ground is [15]:
where is the axial force growth coefficient. For cast-in-place piles, the pile side friction is assumed to be rectangular, . Here, is the side friction per unit area at depth z; is the weight of the pile; A is the cross-sectional area of the pile, and U is the circumference of the pile.
The stress of the micro-element, with a length of dz at the depth of z, is shown in Figure 1. Based on the above assumptions and the static equilibrium conditions of this element, the horizontal displacement y of the pile body follows the fourth-order differential equation:
where b0 is the calculated width of the pile; and cz is the horizontal resistance coefficient of the foundation. When the p-y curve is used to describe the pile side resistance, cz is the secant modulus of the p-y curve, , kN/m3.
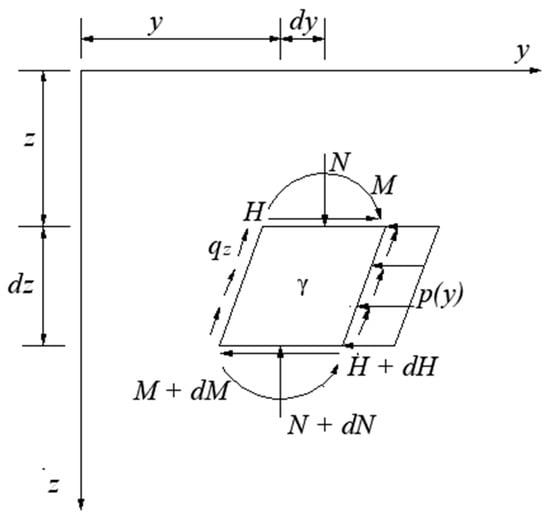
Figure 1.
Force analysis of a single pile micro-element.
2.2. Establishment and Solution of the Difference Equation
In order to facilitate the analysis of a single pile in layered soil, Equation (2) must be converted into differential form.
2.2.1. The Difference Equation
To establish the difference equation, the pile length is first divided into n equal parts, of length λ. For layered soil, attention should be paid to the disposal of sections at the soil layer interface, as shown in Figure 2, and this allows for the following system to be established:
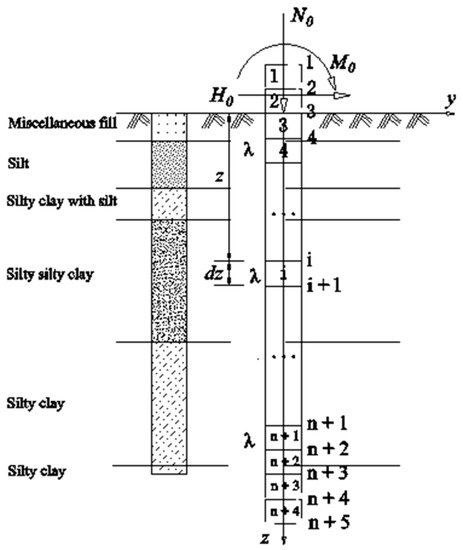
Figure 2.
Schematic diagram of single pile stress calculation in layered soil.
Equation (3) is substituted into Equation (2) to obtain the deflection difference equation for the pile shaft, with section i:
where , , , , and .
2.2.2. Boundary Conditions
As shown in Figure 2, in order to facilitate programming and avoid zeros and negative signs, 1, 2, n + 4, and n + 5 virtual units are set at both ends of the pile, so that the pile top number is 3 and the pile bottom number is n + 3.
(1) Pile top boundary conditions
At the pile top, there is a horizontal force H0, bending moment M0, and axial force .
From , there is
and from , there is
(2) Pile bottom boundary conditions
Free bearing at the pile bottom:
When the lower end of the pile is supported in the general soil layer and the conversion depth is αl ≥ 2.5, or when the pile end is supported on the rock surface and αl ≥ 3.5, the bending moment and shear force are both zero.
From ,
is obtained, and from ,
is likewise obtained.
Fixed support at the pile bottom:
For this case the pile bottom displacement and rotation angle are both zero.
so that
2.2.3. Solution Ideas
Taking the free pile bottom as the boundary condition in (7) and (8) gives
When i = n + 3, Equations (11) and (12) can be substituted into the pile deflection difference equation (Equation (4)) to obtain
where, .
By analogy with the above method, the intermediate node displacements yn+2 to y3, can be obtained, and then the expressions for node displacements y3, y4, and y5 obtained by the above method can be substituted into the boundary condition, Equations (5) and (6), for the pile top, to obtain the expressions of node displacements y1 and y2, so that all node displacements, yi, can be inversely deduced.
2.2.4. Solving Steps
The first step for solving the system is to divide the pile into n segments, according to the geometric dimensions of the pile foundation and the distribution conditions of each of the soil layers. The second step, is to preset the initial value of the foundation resistance coefficient, cz0, of the soil at the node of the pile element. In the third step, the finite difference method is used to solve the displacement of each node, yi, and the fourth step is to determine the pile side soil resistance, pi, from yi, according to the p-y curve of the different soil layers. Next, step 5 is to obtain a new czi from . Finally, the sixth step is to use the finite difference method to calculate the new node displacements according to the new czi. If the displacement difference of each node obtained by two iterations is within the error limit ε, then the process is stopped, otherwise steps 4 to 6 are repeated until the error limit is reached.
2.2.5. Programming
The flow chart for the calculation procedure according to the above calculation methods and steps, is shown in Figure 3.
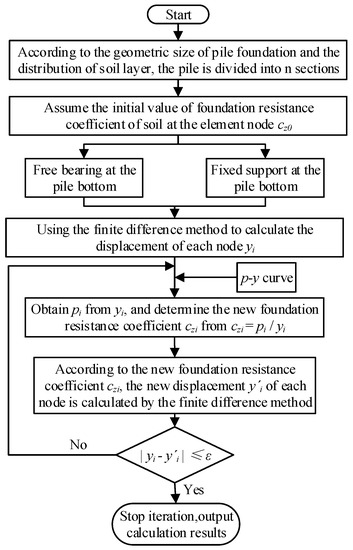
Figure 3.
The flow chart of the p-y curve programming method.
2.3. p-y Curve Characteristics and Selection
The relationship between pile side resistance, p, and displacement, y, directly affects the working characteristics of the pile. The current Chinese pile foundation design code assumes elastic resistance that is divided into the “m method”, “k method”, and “C method”, according to different assumptions about how the proportional coefficient of the foundation, cz, varies with depth. When the soil displacement at the pile side is large, the nonlinear relationship between resistance, p, and displacement, y, is often best described by a p-y curve.
2.3.1. Characteristics and Application of Common p-y Curves
Existing p-y curves mostly apply to soft and hard clay soils. The following four specific types of p-y curves are among the most widely used [16], and their characteristics and applications are listed in Table 1.

Table 1.
Typical p-y curves.
In the table, pu is the standard value of the ultimate horizontal soil resistance per unit area at a depth below the surface, and y50 is the lateral horizontal displacement of the pile when the soil around the pile reaches half of the ultimate horizontal soil resistance.
2.3.2. Comparison of Applications of p-y Curves for Homogeneous Soil
The above calculation method and program can also be applied to homogeneous soil layers. In this paper, site horizontal load test conditions are used for the calculation conditions (see Section 3 for details), and the soil around the pile is regarded as a uniform soil layer. Four p-y curve models, the Matlock, Sullivan, Wang, and Zhang methods, are used to analyze the internal forces and deformation of the pile body. Table 5 shows that the undrained shear strength of the test site was less than 96 kPa and consisted of soft clay. The soil mass weight was 18.1 kN/m3, and the undrained shear strength, Cu, was 17 kPa. Comparisons of the theoretical pile top displacement and the maximum pile shaft bending moment with the measured results are shown in Table 2 and Table 3.

Table 2.
Comparisons of theoretical pile top displacement and actual measurements.

Table 3.
Comparison of theoretical maximum pile bending moment and actual measurements.
Table 2 and Table 3 show that the pile top displacements and pile shaft bending moments calculated by different methods can differ greatly. Under different horizontal loads (H = 200, 300, 350 kN), the pile top displacement obtained by the Matlock method is close to the measured value, as is the maximum pile shaft bending moment obtained by the Wang method. Further analysis shows that both Wang’s method and Matlock’s method are more suitable than other methods in calculating relevant parameters for horizontally loaded piles in soft clay areas. However, Wang’s method was selected as the basis for improvement and application. In Wang’s p-y curve, y50 = Aε50D, A = 0.05(1/D + 4), and ε50 is the strain value when the maximum principal stress difference is half: pu = KACuD, .
3. Improvement of Wang’s p-y Curve
3.1. The Change in Undrained Shear Strength, Cu, with Depth
For cohesive soil, because the pu in Table 1 is often described by Cu, the undrained shear strength Cu, has a great influence on the results, when a p-y curve is used to calculate the internal forces and lateral displacement of piles. The Code for Pile Foundations of Port Engineering [16] gives the p-y curve for Cu < 96 kPa and Cu > 96 kPa, respectively. ε50 and Cu is taken as a fixed value during calculation. According to the basic principle of soil mechanics [17], even for the same soil, undrained shear strength Cu increases with depth, and so is not a fixed value. At present, there are three main ways to obtain the undrained shear strength, Cu: (1) direct measurement by field or indoor test; (2) the effective consolidation stress method [18], which considers the failure of a soil mass to be a sudden undrained shear process, where the water content and strength of soil elements remain unchanged; here, the undrained shear strength can be measured by the effective consolidation stress on the potential fracture surface before failure; and (3) the empirical fitting method, which is based on the main factors that affect the undrained shear strength, Cu, of the soil mass, and can give the Cu according to several parameters that are easy to measure, hence this method’s name.
Guo [19] compared the undrained shear strength measured by in situ field tests and indoor tests, with the undrained shear strength obtained by an empirical formula. The results obtained from the empirical fitting method and the tests were consistent, but the calculated results from the effective stress method were roughly twice the measured ones. The main reason for this was that the undrained cohesion, c, had a large impact. Duan [20], Chen [21], and others found that the undrained shear strength of cohesive soil increases linearly with depth.
In this paper, the authors adopt the empirical fitting method due to a lack of measured data. That is, the undrained shear strength is assumed to follow a linear growth rule along the depth, and the reference value of ε50 is obtained from Table 4:
where, is the effective weight of the soil, and a is the effective coefficient, which is 0.244 [19].

Table 4.
ε50 value [22].
3.2. The Case of Layered Soil
The Code for Pile Foundations of Port Engineering divides all soil types into soft clay, hard clay, and sandy soil, according to the size of the soil’s Cu, and puts forward the construction method of p-y curve clusters for dealing with different types of soils. However, most current studies do not consider the coexistence of the three types of soil. Thus, a p-y curve cluster in layered soil can be established by considering the differences in p-y curves between different soil layers, as follows.
(1) Soft and hard clay
For p-y curves in soft clay, hard clay, and other soil layers, this paper adopts the Wang method, that is applicable to clay.
(2) Sand
In the absence of field test data, the p-y curve of sand can be determined by the following formula [18]:
where, k is the initial modulus of soil resistance (kN/m3); ψ is the calculation coefficient; and d is the pile diameter or pile width.
4. Application of the Improved p-y Curve Method in Layered Soil
4.1. Overview of the Site Horizontal Load Test
The horizontal load test was a 1:1 field prototype test, using a loading mode of double piles pushing against each other. The bored pile of the test foundation pile was 1 m in diameter and 45 m in length. The cap of the pile was 1.8 m in length, 1.4 m in width, and 1 m in height. C40 concrete was used, and the weight of the foundation pile was 25 kN/m3. The test device is shown in Figure 4, which shows that the horizontal displacement of piles on the ground was measured with a dial indicator. Two dial indicators were installed symmetrically on the horizontal force action surface, at heights of 10 cm, 60 cm, and 95 cm above the bottom of the pile cap, with a spacing of 1.0 m. Pile A was a test pile, where a reinforcement meter was symmetrically arranged on the reinforcement cage, to measure the strain on the pile body. A total of 10 test sections were set up at a depth of 34 m below the ground, with 20 elements in total, according to the principle of “upper dense” and “lower sparse”. The strain gauge on the top layer was 50 cm from the ground, and the spacing below was 200 cm, 250 cm, 300 cm, and 400 cm.
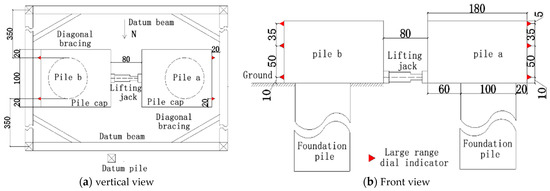
Figure 4.
Pile horizontal load test.
The test was carried out using the slow sustained load method. According to the relevant specifications [23,24], 100 kN was taken as the initial load and, according to the change in pile top displacement and pile foundation conditions, 25 kN or 50 kN were taken as the incremental load, step-by-step, until the pile foundation was damaged. The soil layer in the test site was distributed from top to bottom as follows: 0 to 4.80 m was miscellaneous fill with loose structure and poor uniformity; 4.80 to 13.10 m was flow-plastic sludge with high void ratio and high compressibility; 13.10 to 17.90 m was soft plastic silty clay, with high mass fraction of local silt particles and medium–high compressibility; 17.90 to 30.50 m was flow-soft plastic silty clay with high compressibility; and below 30.50 m was soft plastic silty clay with medium compressibility. The soil layer distribution and physical and mechanical property parameters of the test site are shown in Table 5.

Table 5.
Soil physical and mechanical property parameters.
4.2. Validation
The improved p-y curve method was applied to the above tests, and the displacement and bending moment of the pile were compared with the measured results.
(1) Pile displacement
The comparison between the calculated and measured value of pile displacement along with depth is shown in Figure 5a, and the comparison between the calculated and measured value of pile top displacement is shown in Figure 5b.
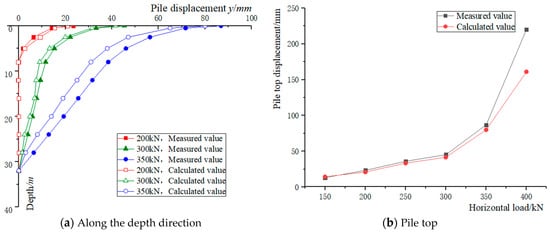
Figure 5.
Comparison between the calculated and measured value of the pile body displacement with depth.
Figure 5a shows that the calculated value of pile displacement was consistent with the measured value. When the load was below 300 kN, the pile displacement mainly occurred within 10 m underground. When the load increased to 350 kN, however, the displacement value and the depth of displacement influence, increased rapidly. Similarly, Figure 5b shows that when the load increased from 150 kN to 350 kN, the error between the calculated value of pile top displacement and the measured value was between −9.8% and 10.3%. When the load reached 400 kN, however, the calculated and measured values of pile top displacement increased sharply, to 161.2 mm and 220.4 mm, respectively, and the error increased to 26.9%. This may have been because the pile foundation had been damaged and the measured value of the pile top displacement was thus too large. Thus, within a certain allowable range, the improved p-y curve method has good applicability in calculating the internal forces and deformation of piles loaded at large displacement levels, before a pile foundation is likely to be damaged.
(2) The bending moment of the pile shaft
The comparison between the calculated and measured value of the pile shaft bending moment with depth is shown in Figure 6a, and the comparison between the calculated and measured value of the pile shaft maximum bending moment is shown in Figure 6b.
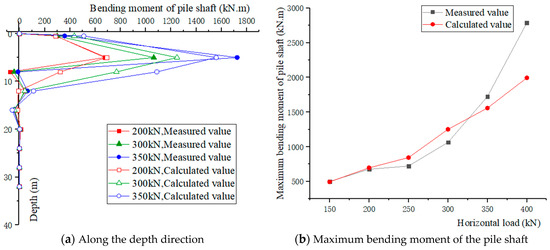
Figure 6.
Comparison between the calculated and measured value of the pile bending moment with depth.
According to Figure 6a, the calculated and measured bending moment values were mainly distributed within 12 m below the ground. With an increase in load, the calculated depth of the maximum pile bending moment appeared about 5 m below the ground, which was consistent with the measured value. Figure 6b shows that when the load increased from 150 kN to 350 kN, the error between the calculated value of the maximum pile shaft bending moment and the measured value was −17.4% to 9.8%. When the load was increased to 400 kN, however, the calculated and measured values of the maximum pile bending moment increased to 1995 kN and 2789 kN, respectively, with an error of 28.5%. Combined with the comparative analysis of the pile top displacement, the improved p-y curve method also has good applicability in calculating the internal forces and deformation of a pile loaded at a displacement level, within a certain allowable error range, in addition to when the pile foundation is not damaged.
5. Conclusions
Through theoretical analysis and field tests, this paper analyzed the internal forces and deformation of laterally loaded piles, based on an improved p-y curve framework. The highlights are enumerated below.
(1) Taking into account the simultaneous presence of soft clay, hard clay, and sand, as well as the change in undrained shear strength, Cu, in the clay layer with depth, the p-y curve of the Wang method was the most applicable to our model and was therefore used for subsequent analysis.
(2) A new calculation method for pile internal forces and deformation in layered soil, that also considered vertical load, was established, and the corresponding difference solution program was put forth.
(3) The calculation method in this paper was then applied to an analysis of the results of field horizontal load tests. These results showed that the trends in the change in the pile top displacement and the maximum bending moment of the pile body calculated by our improved p-y curve method in layered soil, were consistent with the measured values. When the horizontal load was between 150 kN and 350 kN, the absolute values of the relative error of the maximum displacement and the maximum bending moment of the pile body were less than 10.3% and 17.4%, respectively. This demonstrated that our method has good applicability for the analysis of deformation and internal forces of horizontally loaded piles with large displacements.
Author Contributions
Conceptualization, J.W.; Methodology, J.W.; Software, S.Z.; Validation, S.Z.; Formal analysis, L.W. and J.W.; Resources, Q.H.; Data curation, S.Z.; Project administration, S.Z. and Q.H.; Funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Grant No. 51878671).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Matlock, H. Correlation for Design of Laterally Loaded Piles in Soft Clay. In Offshore Technology in Civil Engineering; ASCE: Reston, VA, USA, 1970; pp. 77–94. [Google Scholar]
- Reese, L.; Cox, W.; Koop, F. Field Testing and Analysis of Laterally Loaded Piles om Stiff Clay. In Offshore Technology in Civil Engineering; ASCE: Reston, VA, USA, 1975; pp. 106–125. [Google Scholar]
- Sullivan, W.R.; Reese, L.C.; Fenske, C.W. Unified Analysis Method of Horizontally Loaded Piles in Clay; Hu Yaoyi Water Transport Engineering (Numerical Calculation Album of Pile Foundation Engineering); Thomas Telford Publishing: London, UK, 1980; pp. 110–121. [Google Scholar]
- Huichu, W.; Dongqing, W.; Ping, T. A new unified method for P-Y curve of lateral static piles in clay. J. Hohai Univ. 1991, 1, 9–17. [Google Scholar]
- Lianyang, Z.; Zhuchang, C. Method for calculating p-y curve of cohesive soil. Ocean. Eng. 1992, 4, 50–58. [Google Scholar]
- Xiaoling, Z.; Dongzhi, Z.; Chengshun, X.; Xiuli, D. Study on p-y curve of pile-soil interaction in saturated sandy soil under the condition of weakened strength. Rock Soil Mech. 2020, 41, 2252–2260. [Google Scholar]
- Lunbo, L.; Yuan, W.; Endi, Z.; Zhongbo, H.; Xingguang, Y.; Qingwen, L. Study on p-y curves of monopile in layered soil based on field test. Acta Energ. Sol. Sin. 2019, 40, 3258–3264. [Google Scholar]
- Kangyu, X.; Hongzhi, L.; Yaochun, C.; Xinguo, W.; Kaishun, Z.; Wenbing, W. Nonlinear solution of horizontal response of laterally loaded piles in layered soil. Bull. Geol. Sci. Technol. 2021, 40, 166–174. [Google Scholar]
- Haocheng, L.; Lianheng, Z.; Pengpeng, Z.; Qiuliang, L. Analysis of the internal force and displacement of the laterally combined loaded pile in the layered soft soil foundation. Chin. J. Railw. Sci. Eng. 2021, 18, 2907–2915. [Google Scholar]
- Xinjun, Z.; Siqing, N.; Qiong, H. Analysis model of single pile p-y curve based on the stress state of soil at the pile side. J. Railw. Sci. Eng. 2019, 16, 2716–2724. [Google Scholar]
- Lu, W.; Zhang, G. Influence mechanism of vertical-horizontal combined loads on the response of a single pile in sand. Soils Found. 2018, 58, 1228–1239. [Google Scholar] [CrossRef]
- Thieken, K.; Achmus, M.; Terceros, M.; Lemke, K. Evaluation of p-y approaches forlarge-diameter piles in layered sand. Int. J. Offshore Polar Eng. 2018, 28, 318–327. [Google Scholar] [CrossRef]
- Georgiadis, M. Development of p-y curves for layered soils. In Geotechnical Practice in Offshore Engineering; ASCE: Reston, VA, USA, 1983; pp. 536–545. [Google Scholar]
- Weiping, C.; Bing, X.; Xin, G. Construction and application of hyperbolic p-y curve of horizontal loaded inclined pile. J. Zhejiang Univ. 2019, 53, 1946–1954. [Google Scholar]
- Minghua, Z.; Longgang, W.; Jianhua, L. Finite difference decomposition of load-bearing anti-slip pile considering P-∆ effect. Eng. Mech. 2008, 3, 102–106. [Google Scholar]
- The Third Harbor Engineering Survey and Design Institute of the Ministry of Communications. JTS 167-4 2012; Code for Pile Foundation of Port Engineering; People’s Communications Press: Beijing, China, 2012. [Google Scholar]
- Baili, Z. Computational Soil Mechanics; Shanghai Science and Technology Press: Shanghai, China, 1990. [Google Scholar]
- Yuan, T.; Kuihua, W.; Jian, Z.; Anfeng, H. Application of effective stress method and effective consolidation pressure method in strength calculation of precompressed foundations. Geotech. Mech. 2020, 41, 645–654. [Google Scholar]
- Guo, X.; Zhu, B.; Liu, J.; Xiong, G.; Huang, G. Experimental study on undrained shear strength and cyclic weakening characteristics of marine soft soil in the Pearl River Estuary. Geotech. Mech. 2016, 37, 1005–1012. [Google Scholar]
- Duan, W.; Cai, G.J.; Liu, S.Y.; Puppala, A.J. Correlations between shear wave velocity and geotechnical parameters for Jiangsu Clays of China. Pure Appl. Geophys. 2018, 176, 669–684. [Google Scholar] [CrossRef]
- Fu, C.; Ning, L. Undrained Shear Strength Analysis of Vacuum Preloaded Surface Hard Shell Based on Modified Cambridge Model. Found. Treat. 2021, 3, 271–276. [Google Scholar]
- Compilation Committee of Pile Foundation Engineering Manual. Pile Foundation Engineering Manual; China Construction Industry Press: Beijing, China, 1995. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. JGJ 94-2008; Technical Specifications for Building Pile Foundations; China Construction Industry Press: Beijing, China, 2008. [Google Scholar]
- China Academy of Building Research. JGJ 106-2014; Technical Specification for Building Pile Foundation Detection; China Building Industry Press: Beijing, China, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).