MFFNet: A Building Extraction Network for Multi-Source High-Resolution Remote Sensing Data

Abstract

The use of deep learning methods to extract buildings from remote sensing images is a key contemporary research focus, and traditional deep convolutional networks continue to exhibit limitations in this regard. This study introduces a novel multi-feature fusion network (MFFNet), with the aim of enhancing the accuracy of building extraction from high-resolution remote sensing images of various sources. MFFNet improves feature capture for building targets by integrating deep semantic information from various attention mechanisms with multi-scale spatial information from a spatial pyramid module, significantly enhancing the results of building extraction. The performance of MFFNet was tested on three datasets: the self-constructed Jilin-1 building dataset, the Massachusetts building dataset, and the WHU building dataset. Notably, experimental results from the Jilin-1 building dataset demonstrated that MFFNet achieved an average intersection over union (MIoU) of 89.69%, an accuracy of 97.05%, a recall rate of 94.25%, a precision of 94.66%, and an F1 score of 94.82%. Comparisons with the other two public datasets also showed MFFNet’s significant advantages over traditional deep convolutional networks. These results confirm the superiority of MFFNet in extracting buildings from different high-resolution remote sensing data compared to other network models.

1. Introduction

Building extraction using high-resolution remote sensing images is a current focus in research. High-resolution remote sensing imaging can achieve commendable results in geographical mapping, coastline extraction, land classification, and geological disaster monitoring. Shao, Z. et al. summarized the latest advancements in extracting urban impervious surfaces using high-resolution remote sensing images and provided recommendations for high-resolution imagery [1]. Cheng, D. et al. applied deep convolutional neural networks to the land–sea segmentation problem in high-resolution remote sensing images, significantly improving the segmentation results [2]. Investigating land use monitoring, Zhang, B. et al. achieved favorable outcomes using a framework based on conditional random fields and fine-tuned CNNs [3]. Park, N.W. et al. also employed high-resolution remote sensing images to assess landslide susceptibility [4]. High-resolution remote sensing datasets have become widely used in the remote sensing field and can primarily be categorized into drone remote sensing and satellite remote sensing varieties. Both types of high-resolution remote sensing images offer satisfactory display results. The aerial imagery is clearer since drone remote sensing images can be captured more flexibly, effectively avoiding weather impacts. Researchers such as Qiu, Y. et al. and Wang, H. et al. have preferred using high-resolution drone remote sensing images to build extraction [5,6]. In practical applications, issues regarding UAV remote sensing coverage and aerial photography costs must still be resolved. Satellite remote sensing images provide large-area coverage, enabling long-term monitoring of large territories in the process of urbanization. However, the quality of the images is still insufficient compared with aerial images. Since the two data sources are inconsistent, some methods of building extraction are difficult to simultaneously consider.

The extraction of buildings from remote sensing images was initially based on the features of the buildings. Sirmaçek, B. et al. utilized the color, shape, texture, and shadow of buildings for extraction [7]. This method primarily relies on the features of facilities for extraction, making it inefficient and imprecise. As such, it requires personnel with extensive professional knowledge. In the early 21st century, the concept of machine learning was introduced into remote sensing. Chen, R. et al. significantly improved the results of building extraction by designing unique feature maps and using random forest and support vector machine algorithms [8]. Using the random forest algorithm, Du, S.H. et al. achieved the semantic segmentation of buildings by combining features such as the image’s spectrum, texture, geometry, and spatial distribution [9]. Although traditional machine learning methods have improved segmentation accuracy, the manual selection of essential features remains an inevitable challenge [10].

Deep learning models have addressed the issue of feature selection inherent in traditional machine learning, and many researchers are keen on using deep convolutional networks for building extraction. Huang, L. et al. designed a deep convolutional network based on an attention mechanism [11]. They significantly improved the rough-edge segmentation of buildings in high-resolution remote sensing images drawn from the WHU dataset. Wang, Y. et al. added a spatial attention mechanism to the intermediate layers of the deep convolutional network and adopted a residual structure to deepen the network [12]. This method achieved higher accuracy on the WHU and INRIA datasets than other mainstream networks. Liu, J. et al. proposed an efficient deep convolutional network with fewer parameters for building extraction and this model achieved commendable results on the Massachusetts and Potsdam datasets [13]. The segmentation accuracy of traditional deep convolutional networks for high-resolution remote sensing images of buildings needs to be further improved, and the details of the segmentation results are not sufficient. To address this, we designed a small-sample deep convolutional network tailored for high-resolution remote sensing imagery, achieving the precise extraction of buildings from high-resolution remote sensing images from different sources. To validate our model’s adaptability to various high-resolution remote sensing images, we conducted tests on a self-built Jilin-1 dataset and two publicly available high-resolution remote sensing datasets.

The main contributions of this paper are as follows: we introduced semantic segmentation models related to remote sensing applications in the Related Work section. Based on the advantages of these models, we designed a multi-feature fusion net (MFFNet) and tested it against traditional convolutional networks for assessing three different datasets. Whether in terms of MIoU, accuracy, or F1 score, MFFNet outperformed other models. In the discussion section, we elaborated on the advantages and disadvantages of MFFNet compared to other traditional models and contrasted it with ViT (visual transformer) models. Through comparisons between different models, we validated the superiority of MFFNet.

2. Related Work

2.1. Development of DCNNs

In the 2012 ImageNet Large Scale Visual Recognition Challenge (ILSVRC), AlexNet triumphed with an error rate significantly lower than that of other competing models, marking the rise of deep learning in image classification [14]. Subsequently, deeper convolutional neural networks, such as VGG [15], shone brightly in the visual domain. However, in traditional deep neural networks, increasing the depth of the network might lead to issues such as vanishing gradients and exploding gradients, making the training of the network challenging. GoogLeNet introduced the inception block to widen the network, ensuring more comprehensive information extraction and significantly improving classification accuracy [16]. The idea behind the inception block shifted researchers’ focus from increasing network depth to achieving better results, although deeper networks remain the primary method of obtaining deep features. Nevertheless, in deeper structures, as information propagates across multiple layers, gradients might diminish over time, leading to minuscule updates in network weights and resulting in a decline in network performance. ResNet effectively addressed this issue with the design of residual blocks [17]. ResNet introduced the concept of residual blocks to tackle the degradation problem in deep neural networks, enabling the network to efficiently learn deep feature representations. This innovation has significantly impacted the successful application of deep learning in fields such as computer vision.

To address the shortcomings of traditional computer vision methods in pixel-level segmentation tasks, earlier researchers drew inspiration from the characteristics of classification networks. In 2015, Long, J. et al. first introduced the FCN (fully convolutional network) concept for per-pixel classification tasks [18]. FCN eliminated the fully connected layers found in classification networks, extending the convolutional neural network to handle input images of any size and output pixel-level segmentation results. The introduction of FCN marked a breakthrough in deep learning in semantic segmentation. It realized end-to-end feature learning and segmentation, greatly simplifying the entire process. FCN has been widely applied in various domains, including medical image segmentation, autonomous driving, and satellite image analysis [19].

End-to-end semantic segmentation networks have been widely adopted, and these methods have evolved from the foundational FCN. This includes prominent networks such as SegNet [20], UNet [21], the Deeplab [22,23] series, and PSPNet [24]. SegNet introduced the encoder–decoder structure and employed skip connections and hierarchical softmax for pixel classification, aiming to retain more detailed information. UNet, with its encoder–decoder and skip connection architecture, improved classification accuracy when applied to small datasets, leading to its widespread use in scientific research. Subsequent variations, including UNet++ and others, have also become classic models in semantic segmentation. However, the UNet series is not without its limitations. As training iterations increase, the network may experience degradation, and UNet struggles to achieve satisfactory results when segmenting complex categories. Addressing the challenges of complex segmentation categories, both DeeplabV3+ and PSPNet introduced a pyramid structure to handle features of different scales. This design aims to capture contextual information from various scales, better addressing different object sizes and details within images. In summary, these networks, primarily designed for semantic segmentation, have been widely recognized and accepted across various domains.

2.2. DCNN in the Remote Sensing Domain

In recent years, an increasing number of deep learning methods have been applied to remote sensing image segmentation. Although the evolution of deep convolutional networks in remote sensing has been rapid, most of these models are variants of traditional segmentation networks. Li, X. et al. found that small objects tend to be overlooked when applying Deeplabv3+ to drone datasets. As a result, they proposed EMNet, which is based on edge feature fusion and multi-level upsampling [25]. Wang, X. et al. achieved promising results when applied to high-resolution remote sensing images using a joint model constructed from improved UNet and SegNet [26]. Daudt, R.C. et al. employed a structure similar to FCN with skip connections, merging the image representation information and global information of the network, and achieving more accurate segmentation precision [27]. Multi-level cascaded networks have also been widely adopted. Chen, Z. et al. introduced a method similar to Adaboost, cascading multiple lightweight UNets. The results demonstrated higher accuracy than those obtained with a single UNet [28].

In addition to improvements in some standard networks, the attention mechanism of DCNN has also caught the attention of researchers. Such methods utilize transformations of different scales to extract multi-scale features of segmentation targets. Chen, H. et al. enhanced the UNet structure by adding a SE (squeeze-and-excitation) module [29], allowing the network to focus more on the most crucial feature maps in the upsampling section, thereby improving landslide detection results [30]. Yu, Y. et al. also used the channel attention mechanism to achieve impressive results in building extraction [31]. Eftekhari, A. et al. incorporated both channel and spatial attention mechanisms into the network to address the issues of inadequate boundary and detail extraction in building detection from drone remote sensing images [32]. In summary, DCNN and its variants have been widely accepted by scholars in the remote sensing domain [33].

To recap and summarize, the current methods deployed to enhance segmentation accuracy in the remote sensing domain are as follows:

(i)

Employing skip connections to link the encoder and decoder modules of the network, effectively merging global and local features.

(ii)

Adopting the spatial pyramid approach, capturing semantic information of different scales through receptive fields of varying sizes, as seen in modules such as ASPP (atrous spatial pyramid pooling) and SPP (spatial pyramid pooling).

(iii)

Integrating attention mechanisms, allowing the network to fuse information across multiple scales.

(iv)

Enhancing the model using multi-level cascading methods. However, this is achieved under the cascade of various networks and does not necessarily indicate an enhancement in the segmentation accuracy of a single network.

2.3. Datasets

In order to verify the effectiveness of our deep convolutional network on different high-resolution remote sensing images, we used three high-resolution remote sensing datasets for the experiments. One was the Jilin-1 satellite high-resolution remote sensing dataset we produced, and the images were derived from Jilin-1 satellite remote sensing images; another was the Massachusetts building remote sensing dataset derived from aerial images; and the last set was the fusion of drone and satellite high-resolution large-scale remote sensing WHU datasets.

2.3.1. Jilin-1 Dataset

The Jilin-1 dataset is a satellite dataset that we constructed ourselves. Jilin-1 satellite remote sensing images possess characteristics such as high resolution and wide swath, being capable of obtaining high-definition remote sensing imagery with a panchromatic resolution better than 0.75 m, a multispectral resolution better than 3 m, and a swath width exceeding 40 km. Compared to drone remote sensing images, the Jilin-1 high-resolution remote sensing images can rapidly capture large-area land object information.

The study area for the dataset was designated as the Chang’an District of Xi’an City, China (Figure 1). This region boasts a thriving economy, a high degree of urbanization, and diverse building types. Regarding area delineation, we aimed to select regions where buildings are relatively concentrated, particularly in the urban city center. The chosen date for the imagery was 13 July 2023, a day with clear weather, which minimizes the impact of weather conditions on image quality.

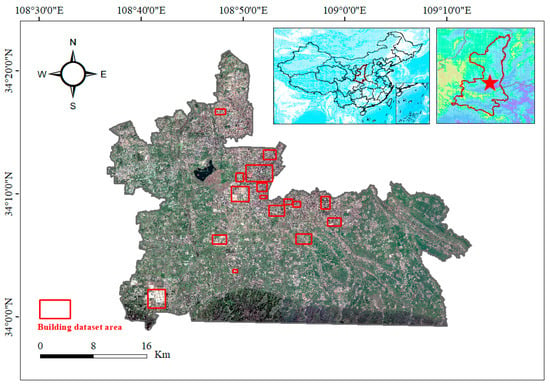
Figure 1. Building dataset sample area for Jilin-1.

We fused the panchromatic and multispectral images of the study area to obtain remote sensing images with a spatial resolution of 0.75 m. The images had three channels: red, green, and blue. In addition, with pixel values ranging from 0 to 255. We selected 16 areas with a high concentration of buildings to annotate the samples, ensuring a diverse range of building types and avoiding areas with too few building categories. We used a sliding window approach to segment the images and labels into samples of size 256 × 256. All samples were then divided into training, validation, and testing sets at a ratio of 8:1:1. This resulted in 4005 training images, 500 validation images, and 502 testing images.

Our dataset presents challenges for segmentation networks. The Jilin-1 remote sensing images are captured at a certain tilt angle, resulting in large shadow areas obscuring buildings. Additionally, the side contours of buildings are clearly visible. Drawing from the annotation standards of other public datasets and real-world cases, our annotation process disregarded shadow obstructions. At the same time, we considered precise side contours to be part of the building. The segmentation considered the entire building in the 2D image, as opposed to just the rooftop area. Furthermore, factors such as atmospheric radiation impacted the imaging of Jilin-1.

2.3.2. Massachusetts Building Dataset

The public Massachusetts building dataset is used by a large number of scholars [34,35]. The Massachusetts buildings dataset consists of 151 aerial images of the Boston area. Each image is 1500 × 1500 pixels and covers an area of 2.25 square kilometers. The entire dataset covers approximately 340 square kilometers. The image is clearly captured, with some shadow-related obstruction. The data are divided into a training set of 137 images, a test set of 10 images, and a validation set of 4 images. In order to prevent the GPU memory from overflowing during the training process, the Massachusetts building dataset was sliced. We used sliding windows to cut the training, verification, and test sets into multiple 512 × 512 images.

2.3.3. WHU Building Dataset

The WHU building dataset is a large-scale remote sensing dataset comprising both drone and satellite image datasets [36]. The drone dataset consists of over 220,000 individual buildings from Christchurch, New Zealand. These buildings were extracted from drone images with a spatial resolution of 0.075 m, covering an area of 450 ${\mathrm{k}\mathrm{m}}^2$. Most aerial images (including 187,000 buildings) were downsampled to a ground resolution of 0.3 m and then cropped into 8189 tiles of 512 × 512 pixels each.

The satellite image dataset is made up of two subsets. One subset was collected from cities worldwide and various remote sensing resources, including QuickBird, the Worldview series, IKONOS, ZY-3, and more. The other satellite building subset comprises six adjacent satellite images, covering 550 square kilometers in East Asia with a ground resolution of 2.7 m. The satellite image dataset was also cropped into tiles of 512 × 512 pixels. Without further processing, we directly used the cropped datasets from WHU, which were already divided into training, validation, and testing sets.

3. Model and Evaluation Metrics

3.1. MFFNet

We designed the multi-feature fusion net (MFFNet), a network structure capable of fusing multiple features. The fused features include the representational information extracted from shallow convolutional blocks, the semantic information from deep convolutional blocks, and the semantic information extracted from various attention mechanisms and spatial pyramid modules. The representative information retains the geometric shape of the segmentation target, while the semantic information retains information such as the target’s spatial position. The detailed model diagram is shown in Figure 2.

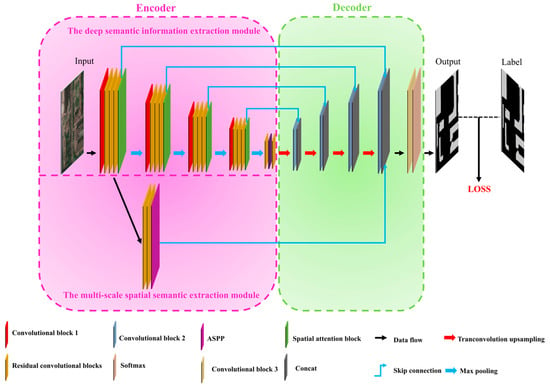
Figure 2. MFFNet model architecture.

The multi-feature fusion net (MFFNet) accepts a three-channel remote sensing image as input. MFFNet is composed of an encoder and a decoder. The encoder of MFFNet includes two parts: the deep semantic information extraction module and the multi-scale spatial semantic extraction module. The deep semantic information extraction module can extract deep features through multiple convolutional layers and attention mechanisms and skip-connects the shallow representational information to the decoder. The multi-scale spatial semantic extraction module extracts features from images of different scales through atrous spatial pyramid pooling (ASPP). The decoder consists of upsampling and feature fusion modules, and is used with the primary goal of restoring the size of the segmented image and fusing various feature information from the encoder.

In the deep semantic information extraction module, after four sets of identical feature extraction operations, a learnable self-attention feature extraction is performed to enhance the effect of deep semantic information extraction. The image size is downsampled by 1/2 via max pooling between every two sets of identical feature extraction operations. In each set of feature extraction operations, the feature map goes through a convolutional layer 1, three residual convolution blocks, and a spatial attention extraction block. Convolutional layer 1 includes a 3 × 3 convolution operation, batch normalization, and a ReLU activation function operation. During the convolution process, the size of the feature map remains unchanged. Except for the convolutional layer 1 in the first group, which maps the original three-band image to a 32-channel feature map, the convolutional layer 1 in other groups doubles the number of feature maps. In the residual convolution block, the input feature map is directly added to the feature map obtained after two sets of identical 3 × 3 convolution operations, BathNormalize, and ReLU activation functions. Then, a ReLU nonlinear activation is performed to obtain the output of the residual convolution block (Figure 3). Our designed spatial attention extraction block is shown in Figure 4. First, the input feature map X separately calculates the average and maximum values on the channel dimension. After concatenating the calculation results, the map undergoes a 3 × 3 convolution operation to change the channel dimension to 1. The sigmoid nonlinear activation function is converted into a weight value, which is then multiplied by the input feature map to obtain the output result of the spatial attention block (Equation (1)). The learnable self-attention feature extraction operation contains a self-attention learning module and residual convolution blocks before and after this module. The self-attention learning module is shown in Figure 5. First, the batch feature map X goes through q, k, and v, which are three different 1 × 1 convolutions, to change the scale, obtaining three different sets of matrices: $W^q$, $W^k$, and $W^v$. These three different matrices can all be regarded as multi-channel feature maps. The original feature map dimension before the self-attention learning module is (B,C*H,W). After q processing, the dimensions become (B,H*W,C/8) for $W^q$, (B,C/8,H*W) for $W^k$ after k processing, and (B,C,H*W) for $W^v$ after v processing. $W^q$ and $W^k$ are matrix-multiplied on the channel dimension to obtain the matrix qk. After the matrix qk goes through the softmax layer to obtain the weight value between the two feature maps, it is matrix-multiplied with $W^v$ on the channel dimension and returns to the original batch feature map size to obtain the matrix qkv. Finally, the matrix qkv is multiplied by the learnable parameter gamma and the product is added to the original input feature map after the self-attention learning module to obtain the result. The initial value of the learnable parameter gamma is 1. As training progresses, the gamma parameter adaptively obtains the optimal gamma value within the learnable range (Equation (2)).

$$Output=sigmoid\left(conv3\times 3\left(concatenate\left(mean\left(X\right),max\left(X\right)\right)\right)\right)\times X$$

(1)

where $Output$ is the output feature map, $conv3\times 3$ is a 3 × 3 convolution, and $concatenate$ represents splicing in the same dimension.

$$Attention=gamma\times softmax\left(W^q\times {\left(W^k\right)}^T\right)\times W^v+X$$

(2)

where $Attention$ represents the output feature map, $gamma$ is a learnable parameter, $X$ represents the input feature map, and $W^q$, $W^v$, and $W^k$ are conditional feature maps generated through deformation.

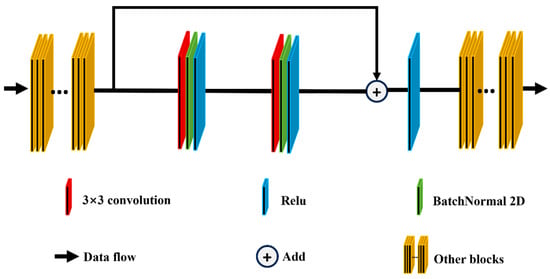
Figure 3. Residual block.

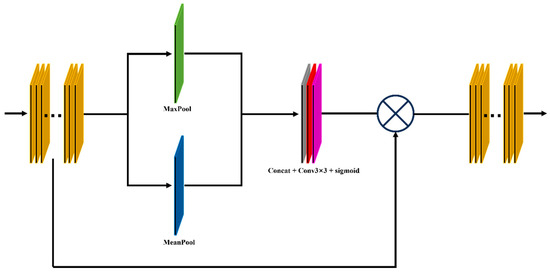
Figure 4. Spatial attention module.

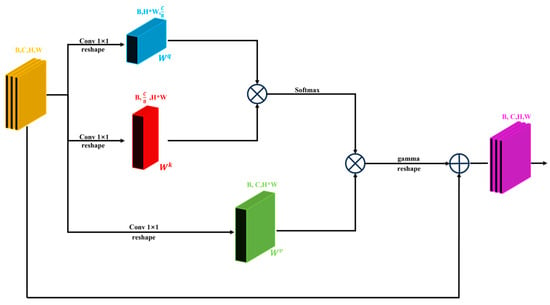
Figure 5. Learnable self-attention module.

The multi-scale spatial semantic extraction module differs from the deep semantic information extraction module in that the latter does not downsample and will not cause changes in the feature map size. The deep semantic information extraction module branches the feature map before the spatial attention block of the first operation of the multi-scale spatial semantic extraction module, obtaining a feature map parallel to the deep semantic information extraction module. This feature map will go through two consecutive residual convolution blocks and then be connected to an atrous spatial pyramid pooling (ASPP) block. The specific structure of ASPP blocks is shown in Figure 6. The feature map entering ASPP blocks will undergo five parallel operations. These five operations are a 1 × 1 convolution, three 3 × 3 convolutions with dilation rates of 6, 12, and 18, respectively, and a global average pooling followed by a 1 × 1 convolution and upsampling. The results of these five parallel operations are concatenated and then passed through a 3 × 3 convolution, after which they are subjected to batch normalization and a ReLU activation function.

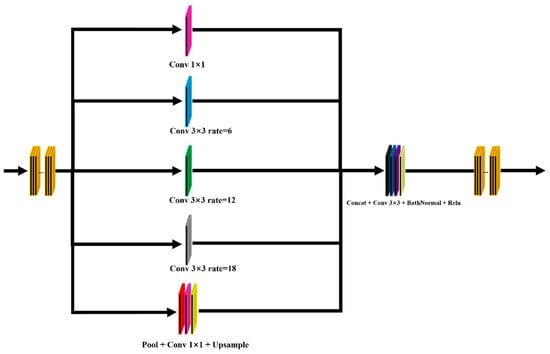
Figure 6. ASPP module structure.

The decoder part of MFFNet consists of an upsampling layer, convolutional layer, multi-feature concatenation layer, and segmentation output layer. The upsampling layer, convolutional layer, and multi-feature concatenation layer together form a group. To integrate multi-scale features, it is ensured that the number of groups in the decoder is the same as in the encoder. The upsampling layer in the decoder uses a 2 × 2 transposed convolution, followed by batch normalization and a ReLU activation function. The convolutional layer includes a 3 × 3 convolution operation, batch normalization, and a ReLU activation function. Before ReLU activation, a dropout layer with a rate of 0.5 is added to prevent overfitting. After this convolutional layer, the image size remains unchanged, but the number of feature map channels is reduced to half of the input. The multi-feature concatenation layer concatenates the feature map from the corresponding spatial attention extraction block in the encoder with the feature map after upsampling and convolution. Notably, the fourth group of the multi-feature concatenation layer concatenates the feature map extracted from the encoder of the corresponding size, the feature map after multi-scale spatial semantic extraction, and the feature map after upsampling and convolution. After undergoing four similar group operations, two sets of 3 × 3 convolutions, batch normalization, and ReLU activations are applied. The original feature map number is compressed to one-third in the first convolutional layer. The second convolutional layer changes the output feature map number to the number of categories during pixel-level classification. After these two convolutions, the softmax layer is used to obtain the segmentation result, which is then compared with the actual annotated data to calculate the loss value via the loss function.

3.2. Evaluation Metrics

For a comprehensive evaluation of model performance, we employed six commonly used metrics in semantic segmentation: MIOU (mean intersection over union), PA (pixel accuracy), precision, recall, F1-score, and kappa. The calculation of these six metrics is aided by the binary confusion matrix (Figure 7). First, we consider buildings as positive and the background as negative. TP (true positive) represents samples predicted to be positive and labeled as positive. FN (false negative) represents samples predicted as negative but labeled positive. FP (false positive) represents samples predicted as positive but labeled as negative. TN (true negative) represents samples predicted as negative and labeled as negative. In the metric calculation process, both buildings and backgrounds are considered positive instances and negative instances, respectively, and their average values are used to determine MIOU, precision, recall, and F1-score. However, for the accuracy and kappa metrics, the results remain consistent regardless of whether a particular target is considered a positive or negative instance, as determined via the inherent calculation equation.

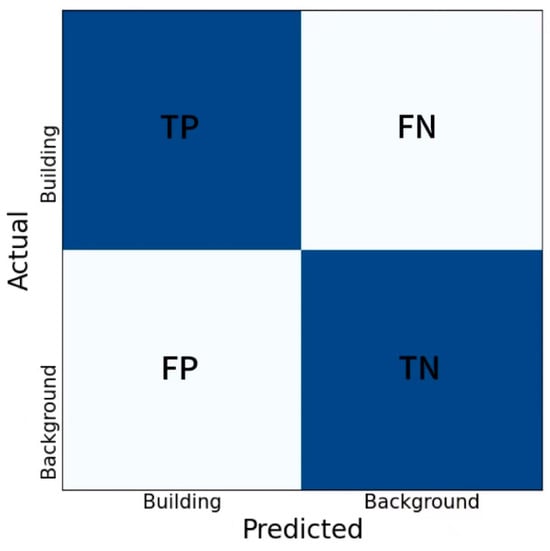
Figure 7. Confusion matrix (with buildings considered as positive instances).

The detailed evaluation index is described as follows:

$$IoU=\frac{TP}{TP+FN+FP}$$

(3)

$$MIoU=\frac{1}{N}\sum \left({IoU}_{class}\right)$$

(4)

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$

(5)

$$Precision=\frac{TP}{TP+FP}$$

(6)

$$Recall=\frac{TP}{TP+FN}$$

(7)

$$F1-score=\frac{2\times Precision\times Recall}{Precision+Recall}$$

(8)

$$Po=\frac{TP+TN}{TP+TN+FP+FN}$$

(9)

$$Pe=\frac{(TP+FN)\times (TP+FP)+(FN+TN)\times (FP+TN) }{{(TP+TN+FP+FN)}^2}$$

(10)

$$Kappa=\frac{Po-Pe}{1-Pe}$$

(11)

where $TP$ represents samples predicted as positive and labeled as positive, $FN$ represents samples predicted as negative but labeled as positive, $FP$ represents samples predicted as positive but labeled as negative, and $TN$ represents samples predicted as negative and labeled as negative. ${IoU}_{class}$ represents the $IoU$ of each type.

MIoU reflects the ratio of the pixel intersection to the union between the predicted results and the actual annotations, indicating the degree of pixel overlap between the predictions and the ground truth. Accuracy measures the proportion of pixels correctly classified by the model in pixel-level classification tasks; precision quantifies the number of samples correctly classified into the positive category in pixel-level classification tasks; and recall assesses the model’s capability to identify positive category samples in pixel-level classification tasks. To provide a comprehensive evaluation of both precision and recall, the F1-score is employed to harmonize the significance of precision and recall; and kappa is a metric used to evaluate the consistency of pixel-level classification tasks. Considering the influence of random allocation, besides the mentioned evaluation using the above metrics, the final imaging results of the output images are also considered. Given that there might be a small number of mislabeled pixels during sample annotation, the display of imaging results can help us to evaluate a model’s ability to resist noise.

4. Results

4.1. Experimental Environment and Configuration

During the experiment, in addition to the proposed model, we also compared four segmentation models commonly used in remote sensing: UNet, UNet++, PSPNet, and DeepLabV3+. PSPNet and DeepLabV3+ use Resnet50 as the feature extraction module in their encoder parts to achieve better segmentation results. Throughout the experimental process, we trained the models using the training set of each dataset. Within a fixed number of iterations, we identified the best MioU index through the validation set to save the model parameters. Ultimately, we tested the trained models on the test set and compared the evaluation metrics across different models. Moreover, during the training process, each image had a 70% probability of undergoing horizontal and vertical flipping and random 90° rotations to perform data augmentation on the training set. No additional processing was conducted for testing and validation.

We use the PyTorch framework to implement our model. The version number of PyTorch is 1.13.1. The initial learning rate is 0.0001, and the models are trained within 100 epochs. The learning rate drops to 0.00002 after 50 cycles. The optimizer we use is Adam, and the loss function is cross-entropy loss. In addition, all programs use a consistent random seed number 707.

In terms of hardware, we use a single CPU (12th Gen Intel(R) Core(TM) i5-12400F) and two GPUs (GeForce RTX 3060 12 G) to accelerate training. Our memory is 32 G, and the hard drive capacity is 1.5 T.

4.2. Experimental Results

4.2.1. Jilin-1 Dataset

We visualized the results after segmentation, as shown in Figure 8. We displayed eight sets of typical images to observe the segmentation differences among various models. The red rectangular boxes highlight the areas we focused on for comparison. Sets 1, 2, 3, and 6 demonstrate that the edges of the segmentation targets subjected to MFFNet are regular and continuous. In contrast, networks such as UNet, UNet++, PSPNet, and DeepLabV3+ tend to misclassify or omit boundaries, resulting in irregular geometries at the edges. Sets 4 and 7 show that when segmenting buildings of different sizes, MFFNet can better delineate smaller structures than other networks, which often confuse multiple small targets. Set 8 reveals that MFFNet still achieves commendable results when segmenting very small targets in a satellite image. This indicates that MFFNet can achieve excellent segmentation results for buildings of various sizes and accurately delineate the edges of structures.

Figure 8. Comparison of experimental results on the Jilin-1 dataset. Each row represents a set of the same image segmented by different models, with the red rectangular boxes highlighting areas of particular interest.

We evaluated the segmentation results of various networks using the assessment metrics. MFFNet outperforms the comparison networks in MIoU, achieving an MIoU of 89.69%, which is 3.03%, 3.58%, 4.63%, and 2.72% higher than those values obtained via UNet++, UNet, PSPNet, and DeepLabV3+, respectively. The accuracy value reaches 97.05%, which surpasses UNet++, UNet, PSPNet, and DeepLabV3+ by 1.59%, 1.39%, 1.65%, and 0.93%, respectively. The precision, recall, and F1-score values reached 94.66%, 94.25%, and 94.82%, respectively, all of which are superior to the values of the comparison networks. As illustrated in Table 1, MFFNet achieves the best results across all evaluation metrics, including the Kappa metric. MFFNet exhibits exemplary segmentation performance when applied to the Jilin-1 building dataset.

Table 1. Segmentation Results on the Jilin-1 Dataset.

Model	MIoU	Accuracy	Precision	Recall	F1-Score	Kappa
UNet++	86.66%	95.46%	92.91%	92.70%	92.85%	90.21%
UNet	86.51%	95.66%	92.81%	92.53%	92.68%	90.05%
PSPNet	85.06%	95.40%	91.26%	92.16%	91.81%	89.06%
DeepLabV3+	86.97%	96.12%	93.01%	92.74%	92.99%	90.48%
MFFNet	89.69%	97.05%	94.66%	94.25%	94.82%	92.63%

4.2.2. Massachusetts Building Dataset

We observed that some conventional networks, when applied to the Massachusetts building dataset, tend to inaccurately segment boundaries, as illustrated in groups 1, 2, and 5 (Figure 9). Traditional segmentation models often merge small buildings, whereas MFFNet mitigates this issue. For buildings located in shadowed areas, MFFNet also achieves effective segmentation, as shown in groups 3 and 7. The fourth and sixth groups of images collectively attest to MFFNet’s proficiency in delineating the edges of buildings, even for smaller targets. The eighth group demonstrates that UNet and UNet++ are prone to misclassifying terrain with similar characteristics to buildings, while PSPNet, DeepLabV3+, and MFFNet can avoid this phenomenon. These sets of images indicate that MFFNet is capable of independently segmenting each small building in densely populated areas, and MFFNet can alleviate the impact of complex environments, such as shadows, on building segmentation.

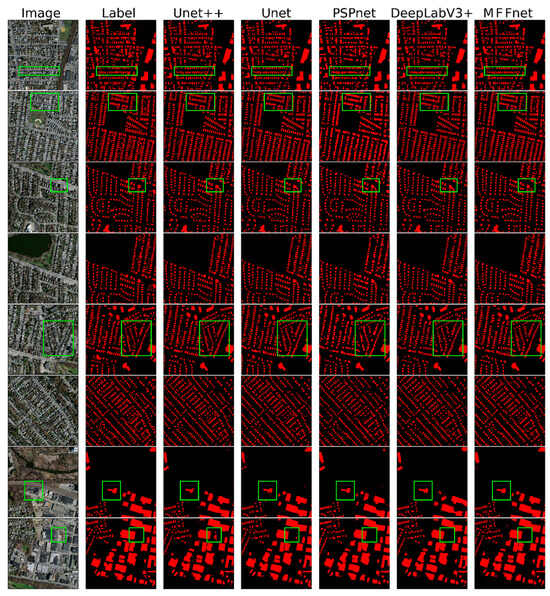
Figure 9. Comparative segmentation results on the Massachusetts dataset, with each row representing a set of images segmented by different models. The green rectangles highlight areas of particular interest.

As shown in Table 2, our model achieved the best results and far outperformed other models. MFFNet’s MIoU and accuracy reached 81.76% and 94.00% on the Massachusetts building dataset, respectively. It was 1.12% and 0.4% higher than UNet++’s MIoU and accuracy, 1.4% and 0.52% higher than UNet’s MIoU and accuracy, 5.57% and 1.95% higher than PSPNet’s MIoU and accuracy, and 1.95% higher than DeepLabV3+. The MIoU and accuracy were 3.68% and 1.26% higher. In addition, MFFNet’s precision, recall rate, F1-score, and kappa indicators were also higher than those of the other models, which were 94.66%, 94.25%, 94.82%, and 92.63%, respectively.

Table 2. Segmentation Results on the Massachusetts Dataset.

Model	MIoU	Accuracy	Precision	Recall	F1-Score	Kappa
UNet++	80.64%	93.60%	87.94%	89.76%	88.79%	86.54%
UNet	80.36%	93.48%	87.50%	89.94%	88.58%	86.32%
PSPNet	76.19%	92.05%	84.70%	87.18%	85.48%	82.74%
DeepLabV3+	78.08%	92.74%	85.49%	88.92%	86.99%	84.47%
MFFNet	81.76%	94.00%	89.02%	90.11%	89.50%	87.43%

4.2.3. WHU Building Dataset

As shown in Figure 10, with a large amount of sample data, various models achieve commendable segmentation results in groups 4, 5, and 8. However, MFFNet has a distinct advantage in terms of capturing the contours of smaller structures. In the annotations of group 7, none of the five networks accurately segmented the entire tiny house. However, MFFNet delineated a portion of the house’s area, while the other models categorized it as background. Simultaneously, UNet++, UNet, PSPNet, and DeepLabV3+ mistakenly segmented the complex background below as a building. In groups 2, 3, and 6, UNet++, UNet, PSPNet, and DeepLabV3+ all exhibited varying degrees of misclassification. In group 1, at the corner of the building, the manual annotation was at a right angle. However, intuitively, it can be determined that the original image had a certain degree of curvature. The segmentation results of all five networks seem more in line with reality than the manual annotation.

Figure 10. Comparison of experimental results on the WHU dataset. Each row represents a set of images segmented by different models. The red rectangle highlights areas of particular interest.

Table 3 presents the evaluation metrics for each model on the WHU dataset. The MIoU of MFFNet stands at 91.82%, with an accuracy of 98.73%, a precision of 95.69%, a recall rate of 95.50%, an F1-score of 96.22%, and a kappa value of 94.22%. Compared to other models, MFFNet’s MIoU surpasses UNet++, UNet, PSPNet, and DeepLabV3+ by 0.94%, 1.18%, 2.15%, and 0.70%, respectively. Furthermore, MFFNet’s accuracy exceeds that of UNet++, UNet, PSPNet, and DeepLabV3+ by margins of 0.19%, 0.23%, 0.51%, and 0.21%, respectively. It is evident that, while MFFNet’s MIoU and accuracy are marginally superior to those of other models, the distinctions are not substantial for other evaluation metrics. When applied to the WHU building dataset, it is apparent that MFFNet’s segmentation capability is superior to that of traditional remote sensing segmentation models.

Table 3. Segmentation Results on the WHU Dataset.

Model	MIoU	Accuracy	Precision	Recall	F1-Score	Kappa
UNet++	90.88%	98.54%	95.40%	94.63%	95.82%	93.53%
UNet	90.64%	98.50%	95.23%	94.64%	95.61%	93.38%
PSPNet	89.67%	98.22%	93.66%	95.18%	95.05%	92.74%
DeepLabV3+	91.12%	98.52%	95.23%	95.09%	95.88%	93.89%
MFFNet	91.82%	98.73%	95.69%	95.50%	96.22%	94.22%

5. Discussion

Our experiments on three datasets showed that MFFNet delivers impressive results in the extraction of buildings. There were slight variations in the segmentation results of MFFNet across these three datasets, which could be attributed to the differences in building materials and scales in different regions. However, when compared to other deep convolutional networks on the same dataset, MFFNet consistently achieved the best segmentation results. This indicates that MFFNet can be effectively used to extract buildings from high-resolution remote sensing images of various sources.

When working on the Jilin-1 dataset, since this dataset was manually annotated based on satellite images, some buildings in the images were difficult to identify, leading to various degrees of mislabeled results or omitted labels becoming mixed into the training, validation, and test sets. Among the five comparison models, MFFNet achieved the highest evaluation metrics (as shown in Figure 11), indicating that MFFNet possesses superior noise resistance. Even when the training, validation, and test sets contain certain noise levels, MFFNet still delivers superior segmentation results on complex buildings. As illustrated in group 3 of Figure 8, we highlighted a rectangular area in the original image where the top of the building was slightly covered by vegetation. MFFNet segmented the target more accurately than other models. Satellite data cannot provide more apparent detailed expressions, and other comparison networks tend to mistakenly segment the middle road as part of the building, whereas MFFNet largely avoids this issue. Additionally, the shooting angle of satellite remote sensing images is not vertical, resulting in larger shadows of buildings. MFFNet can accurately segment buildings under shadows. Due to various factors affecting satellite remote sensing images, their imaging quality is inferior compared to drone data, leading to slight noise in the data. The experiments show that MFFNet can mitigate the impact of noise on segmentation results, making MFFNet highly effective for extracting buildings from high-resolution satellite remote sensing images.

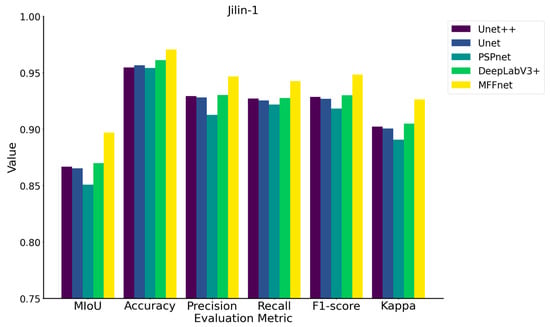
Figure 11. Comparison of evaluation metrics across multiple models on the Jilin-1 dataset.

As shown in Figure 12, MFFNet achieved the best evaluation metrics in the multi-model comparison applied to the Massachusetts dataset. The UNet series networks also commendably performed, with their evaluation metrics consistently surpassing those of networks characterized by spatial pyramid structures. As can be observed from Figure 9, networks with spatial pyramid structures tend to produce “sticky” results when segmenting the Massachusetts building dataset, where buildings are often merged. This phenomenon might be attributed to the high density and quantity of buildings within the spatial scope of the Massachusetts dataset. The spatial pyramid structure struggles to capture the information of these small buildings, whereas the UNet series networks excel at integrating semantic information from different scales, effectively extracting the buildings. This capability is one of the reasons why the UNet series networks have garnered widespread attention among researchers. MFFNet, possessing both the characteristics of the spatial pyramid structure and the UNet series networks, achieves higher accuracy than the UNet series networks, making it highly effective for extracting buildings from high-resolution remote sensing images.

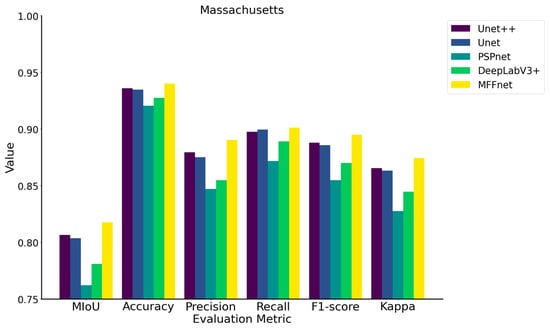
Figure 12. Comparison of evaluation metrics across multiple models on the Massachusetts dataset.

The WHU building dataset comprises high-resolution satellite remote sensing images and drone high-resolution remote sensing images. Moreover, it is a large-scale remote sensing dataset. Supported by big data, the segmentation performance of each network is commendable (as shown in Figure 13). However, MFFNet has a more distinct segmentation advantage. On the one hand, MFFNet can fuse multiple features, delineating more accurate building boundaries. Conversely, MFFNet can extract deep features that other models fail to capture, reducing misclassifications and omissions. It can be said that MFFNet achieves outstanding segmentation results on large-scale integrated building datasets.

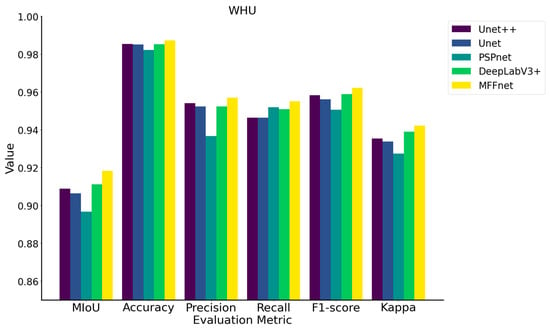
Figure 13. Comparison of evaluation metrics across multiple models on the WHU dataset.

Our model encounters challenges in comprehensively segmenting small objects in complex scenes. When applied to the Massachusetts dataset, due to the dense and small-sized buildings, some small-scale structures are easily overlooked. Similarly, on the WHU building dataset, fine details of small building contours are often missed. However, MFFNet still demonstrates superior segmentation performance compared to other networks. Considering that networks represented by the spatial pyramid structure show significantly lower segmentation performance on the Massachusetts dataset compared to others, and also underperform on the other two datasets, we hypothesized that the spatial pyramid structure might not enhance MFFNet’s segmentation capability. We conducted a new set of experiments, testing the MFFNet without the multi-scale spatial semantic extraction module on all three datasets. We found that the network without this module yielded significantly lower evaluation metrics on small-sample datasets (Table 4) compared to our MFFNet, but still performed exceptionally well. This indicates that our multi-scale spatial semantic extraction module is not an arbitrary addition. Rather, it enhances the feature fusion capability of MFFNet, especially when applied to small-sample building datasets, thereby improving segmentation results. On the WHU large building dataset, MFFNet’s segmentation capability is slightly weaker than the network without the multi-scale module, but the minor differences in evaluation metrics are acceptable. Considering that ViT consistently achieves good results on large datasets, we compared segmentation models with ViT as the backbone. On small-sample datasets, MFFNet outperformed ViT in several evaluation metrics. On the WHU large building dataset, ViT’s MIoU was higher than that of MFFNet by 0.28%, and ViT also slightly exceeded MFFNet in precision, recall, and kappa, but MFFNet was superior in terms of accuracy and F1-score. Overall, segmentation models with ViT as the backbone perform better on large datasets compared to traditional convolutional networks such as MFFNet, but MFFNet excels in segmenting small datasets. In practical work, due to the time and effort required for data annotation, the use of extensive annotated samples is not the first choice of method and training on small-sample data, as MFFNet is more reasonable.

Table 4. Segmentation results of MFFNet, MFFNet (without ASPP), and ViT.

Datasets	Model	MIoU	Accuracy	Precise	Recall	F1-Score	Kappa
Jilin-1	MFFNet	89.69%	97.05%	94.66%	94.25%	94.82%	92.63%
	MFFNet (without ASPP)	88.70%	96.66%	94.14%	93.63%	94.22%	91.90%
	ViT	89.27%	95.60%	94.42%	94.10	94.12%	92.62%
Massachusetts	MFFNet	81.76%	94.00%	89.02%	90.11%	89.50%	87.43%
	MFFNet (without ASPP)	81.07%	93.69%	88.61%	89.61%	89.04%	86.86%
	ViT	79.15%	93.07%	86.78%	88.91%	87.76%	85.35%
WHU	MFFNet	91.82%	98.73%	95.69%	95.50%	96.22%	94.22%
	MFFNet (without ASPP)	91.94%	98.78%	95.81%	95.55%	96.42%	94.28%
	ViT	92.10%	98.50%	95.71%	95.83%	95.72%	95.18%

6. Conclusions

In this paper, we introduce a novel multi-feature fusion network (MFFNet) that significantly enhances the accuracy of building extraction from high-resolution remote sensing images using deep convolutional networks and improves the detail of the extraction results. The network utilizes an encoder–decoder architecture, merging modules for deep semantic information extraction with those for multi-scale spatial semantic extraction. It employs various attention mechanisms and the atrous spatial pyramid pooling (ASPP) module to effectively capture diverse feature information, enabling precise building extraction. The experimental results on the Jilin-1 building dataset, Massachusetts building dataset, and WHU building dataset indicate that MFFNet outperforms other traditional models in critical evaluation metrics such as mean intersection over union (MIoU), accuracy, and F1-score. MFFNet’s successful deployment across multiple datasets highlights its exceptional performance and utility in extracting buildings from high-resolution remote sensing images from diverse sources. Notably, in datasets with small samples, MFFNet demonstrates remarkable noise resistance and accuracy, underscoring its substantial potential for real-world applications. Despite MFFNet’s significant advancements in processing high-resolution remote sensing data, it still encounters challenges in handling particularly complex terrains and urban landscapes, signifying a direction for future enhancement.