A Large-Class Few-Shot Learning Method Based on High-Dimensional Features

Abstract

Large-class few-shot learning has a wide range of applications in many fields, such as the medical, power, security, and remote sensing fields. At present, many few-shot learning methods for fewer-class scenarios have been proposed, but little research has been performed for large-class scenarios. In this paper, we propose a large-class few-shot learning method called HF-FSL, which is based on high-dimensional features. Recent theoretical research shows that if the distribution of samples in a high-dimensional feature space meets the conditions of compactness within the class and the dispersion between classes, the large-class few-shot learning method has a better generalization ability. Inspired by this theory, the basic idea is use a deep neural network to extract high-dimensional features and unitize them to project the samples onto a hypersphere. The global orthogonal regularization strategy can then be used to make samples of different classes on the hypersphere that are as orthogonal as possible, so as to achieve the goal of sample compactness within the class and the dispersion between classes in high-dimensional feature space. Experiments on Omniglot, Fungi, and ImageNet demonstrate that the proposed method can effectively improve the recognition accuracy in a large-class FSL problem.

1. Introduction

The problem of few-shot learning (FSL) attracted the attention of E. G. Miller et al., in 2000 [1]. With the development of deep learning [2,3,4], since 2015, some few-shot learning methods based on deep features have been proposed, which have achieved remarkable results in fewer-class scenarios. In 2016, the matching network [5] proposed by O Vinyals et al. achieved a 98.9% recognition accuracy under an experimental setup using a 5-way 5-shot setting on Omniglot; the prototype network [6] proposed by J Snell et al., in 2017 achieved a 99.7% recognition accuracy with the same dataset and experimental settings. These methods were aimed at scenarios with a very small number of target classes (5 or 20 classes). The recognition accuracy declines significantly when the number of target classes increases. Under an experimental setup using a 2636-way 5-shot setting on Omniglot, the accuracy of the matching network and prototype network decreased to 68.04% and 69.90%, respectively [7]. However, there are a large number of categories in the real world, and it is difficult to achieve a practical level using the existing few-shot learning methods in large-class scenarios. Compared with a traditional few-shot learning task, large-class few-shot learning tasks contain hundreds or thousands of target classes, which is more challenging. This paper proposes a large-class few-shot learning method for an image recognition task. We use a global regularization strategy to make different classes of samples as orthogonal as possible. In addition, we apply AM-Softmax Loss to the final cost function in order to describe the relationships between samples distributed on a hypersphere.

At present, little research for large-class few-shot learning has been performed. As far as we know, there are only a few studies [7,8,9,10,11]. Recently, theoretical research on few-shot learning in a high-dimensional feature space has been carried out [11,12,13,14,15]. As reported by [11], with certain conditions, the precision of few-shot classification can improve as the number of classes grows. Ref. [15] conducted theoretical research on high-dimensional space and proved that as long as samples of different classes are scattered and samples of the same class are distributed compactly in high-dimensional space, a large-class FSL learner can achieve a better generalization ability. Inspired by this theory, this paper proposes a large-class few-shot learning method based on high-dimensional features. The basic idea is to use convolutional neural networks to extract high-dimensional features and unitize them to project samples onto a feature sphere. The global orthogonal regularization strategy is then used to make the samples in different categories as orthogonal as possible on the hypersphere, so as to achieve the purpose of compactness within the class and dispersion between classes in high-dimensional space. To describe the relationships between samples distributed on a sphere, we employ an angle metric-based loss function. Our source code is available at: https://github.com/jwdang/HF-FSL (accessed on 30 October 2023).

The main contribution of this paper consists of two parts:

(1)

A large-class few-shot learning method, HF-FSL, based on high-dimensional features is proposed. On the high-dimensional feature sphere, HF-FSL uses a regularization strategy to make different classes of samples as orthogonal as possible, so as to achieve the purpose of homogeneous compactness and heterogeneous dispersion. In addition, HF-FSL uses AM-Softmax Loss to describe the relationships between samples distributed on a hypersphere.

(2)

The experimental results from three public large-class few-shot datasets, Omniglot [16], Fungi, and ImageNet [17], show that HF-FSL can effectively improve the recognition accuracy of a large-class FSL task.

2. Related Work

Few-shot learning: In recent years, many few-shot learning methods have been proposed, which have achieved excellent results in fewer-class classification tasks. These methods are mainly divided into three categories: data-augmentation methods, metric learning-based methods, and metalearning methods based on optimization strategies.

Data augmentation is an intuitive way to increase the number of training samples and enhance diversity in data. In the field of computer vision, some basic augmentation operations have been applied, such as rotation, flipping, cropping, translation, and adding noise to an image [18,19,20]. For few-shot learning tasks, these naive augmentation methods cannot improve generalization in the FSL method. Recently, data augmentation based on the generation model has aroused people’s interest as it can learn the distribution of data. Ref. [21] built a generator joint classifier model that combined the generation model with the classification algorithm and used a metalearning idea to generate additional samples to achieve an end-to-end metatraining optimization strategy. This greatly improved the credibility of additional images in the classification task. Ref. [22] proposed a data-augmentation method, f-DAGAN, based on GAN, which can generate high-quality training data. Ref. [23] proposed a model for orthogonal regularization of convolutional kernels called DBT, and they combined the DBT-based orthogonal regularizer with a data-augmentation strategy in order to improve the recognition accuracy of the few-shot learning method.

Metric learning [24] aims to measure the similarity among samples while using an optimal distance metric for learning tasks. Methods based on metric learning are more concise and efficient. By learning the mapping between samples and features, the samples can be mapped onto the feature space and the nearest neighbor in the space can be found in order to achieve better classification. The goal of metric learning is to learn the paired similarity metric. Under this metric, pairs from the same class obtain higher similarity scores, while pairs from different classes obtain lower similarity scores. Ref. [5] proposed matching networks, which predicted the category of query samples by measuring the cosine similarity between query samples and each supporting sample. Ref. [6] proposed prototypical networks, which project samples into a metric space, calculate the center of each category, and classify query samples by comparing the distance between the query sample and the center of each category.

The goal of meta-learning is to train a model on a variety of learning tasks so that it can solve new learning tasks using only a small number of training samples. Ref. [25] proposed a very general optimization algorithm that can be used for any model based on gradient descent learning. Ref. [26] proved that MAML with hyperparametric DNN can converge to the global optimal solution at a linear rate.

These three types of methods have their own advantages, and this paper adopts the method based on metric learning for modeling. HF-FSL projects samples onto a hypersphere and applies AM-Softmax Loss, which is based on an angular distance metric, to describe the relationships between samples distributed on a hypersphere.

Large-class few-shot learning: The above methods have shown good results in fewer-class few-shot learning tasks, but it is difficult to extend them to solve problems in large-class scenarios. At present, there is a paucity of literature on large-class few-shot learning. Facebook AI Research (FAIR) [10] proposed a large-class few-shot learning method based on shrinking and transformation features. First, inter class augmentation is used to expand data, and, then, square gradient loss is introduced in the representation learning stage to improve the representation ability of the large-class few-shot learning model. Ref. [8] put forward a class hierarchy that uses the semantic relationships between classes to guide the network to learn more transferable feature information, thereby helping the nearest neighbor algorithm to obtain more accurate classification results. Ref. [9] proposed a multimodal knowledge-discovery method. The foreground image and background image of a sample are obtained through saliency detection. The original image, foreground image, and background image are respectively input into the corresponding network to extract features. The three feature maps obtained are spliced into a visual feature, and the semantic weak supervision information of the class is used. Ref. [7] introduced a confusion matrix to analyze the easily confused categories in a dataset, so as to improve the recognition accuracy of neural networks for large-class few-shot learning. These methods can improve recognition accuracy in large-class few-shot learning tasks to a certain extent; however, there is still much room for improvement in practical applications.

Continuous learning: Continuous learning [27] refers to the ability of a system to continuously learn and adapt when processing new data without forgetting what it has learned. A representative scenario is few-shot continual learning (FSCL). FSCL requires CNN models to incrementally learn new classes from very few labelled samples, without forgetting the previously learned ones. Ref. [28] represents previously learned knowledge using a neural gas (NG) network, which can learn and preserve the topology of the feature manifold formed by different classes. The model first learns some base classes for initialization with a large number of training samples, and, then, learns a sequence of novel classes with only a small number of training samples. Ref. [29] introduces a data-free replay method based on entropy regularization to solve the FSCL problem. It proves that the data-replay method is effective in solving the FSCL problem, and it proposes a data-independent replay method to avoid privacy issues.

High-dimensional feature space learning: Recently, some scholars have conducted FSL theoretical research based on a high-dimensional feature space [11,12,13,14,15]. Ref. [11] proposed that, with certain conditions, the precision of few-shot classification can improve as the number of classes grows. Ref. [15] presents theoretical research on high-dimensional space, and the authors prove that, as long as samples from the same class can be distributed compactly in the high-dimensional space and samples from different classes can be fully dispersed, the model of large-class FSL can achieve better generalization. This theoretical research give us some proof that the large-class FSL problem could be solved in high-dimensional space. First, we normalized the feature embedding to unit length, projected the samples onto the unit sphere, and then used the global orthogonal regularization strategy to make the samples from different categories as orthogonal as possible on the hypersphere, so as to achieve the goal of compactness within the class and the dispersion between classes in high-dimensional space.

The classification loss function: softmax loss is the most commonly used loss function. It maps the flattened output of the feature map to (0, 1) and outputs the probability of each class. Many variants of the softmax loss function have been proposed to maximize the distance between classes and reduce the distance within a class. Ref. [30] proposed center loss, which is used to constrain the intraclass compactness of features. With the development of face recognition technology, A-Softmax Loss [31], CosFace Loss [32], AM-Softmax Loss [33], and other loss functions based on the angular distance metric in high-dimensional feature space have been proposed, and have achieved remarkable classification performances. Since HF-FSL distributes the samples on the hypersphere, it is more appropriate to use the loss function based on the angular distance metric; hence, AM-Softmax Loss was adopted in this study.

3. Methodology

3.1. The Large-Class FSL Definition and Symbol Representation

Formally, we use x to represent input data and y to represent the supervision target. A few-shot classification task, T, usually consists of a T-independent auxiliary dataset, $D_{base}$, and a T-dependent dataset, $D_{novel}$. The goal of few-shot learning is to transfer knowledge learned from $D_{base}$ to $D_{novel}$, where $D_{novel}$ contains limited amounts of available data per category. $D_{novel}$ consists of support sets, $S_{spt}$, and query sets, $S_{qry}$, i.e., $D_{novel}=\{S_{spt},S_{qry}\}$, where $S_{spt}={\left\{(x_i,y_i)\right\}}_{i=1}^n$, $S_{qry}={\left\{x_j\right\}}_{j=1}^{N_{qry}}$. If $S_{spt}$ contains C categories, and each category contains K samples, T is called a C-way K-shot task. Common settings for traditional few-shot learning are 5-way 1-shot and 20-way 1-shot. When the value of C reaches hundreds or thousands it is called a large-class few-shot learning task. In this paper, $\varphi \left(x\right)$ represents the feature embedding of sample x, where ${\left\{(x_i,\overline{x_i})\right\}}_{i=1}^n$ is the sample pair formed by pairs of samples from different categories.

3.2. The Basic Idea of Model Building

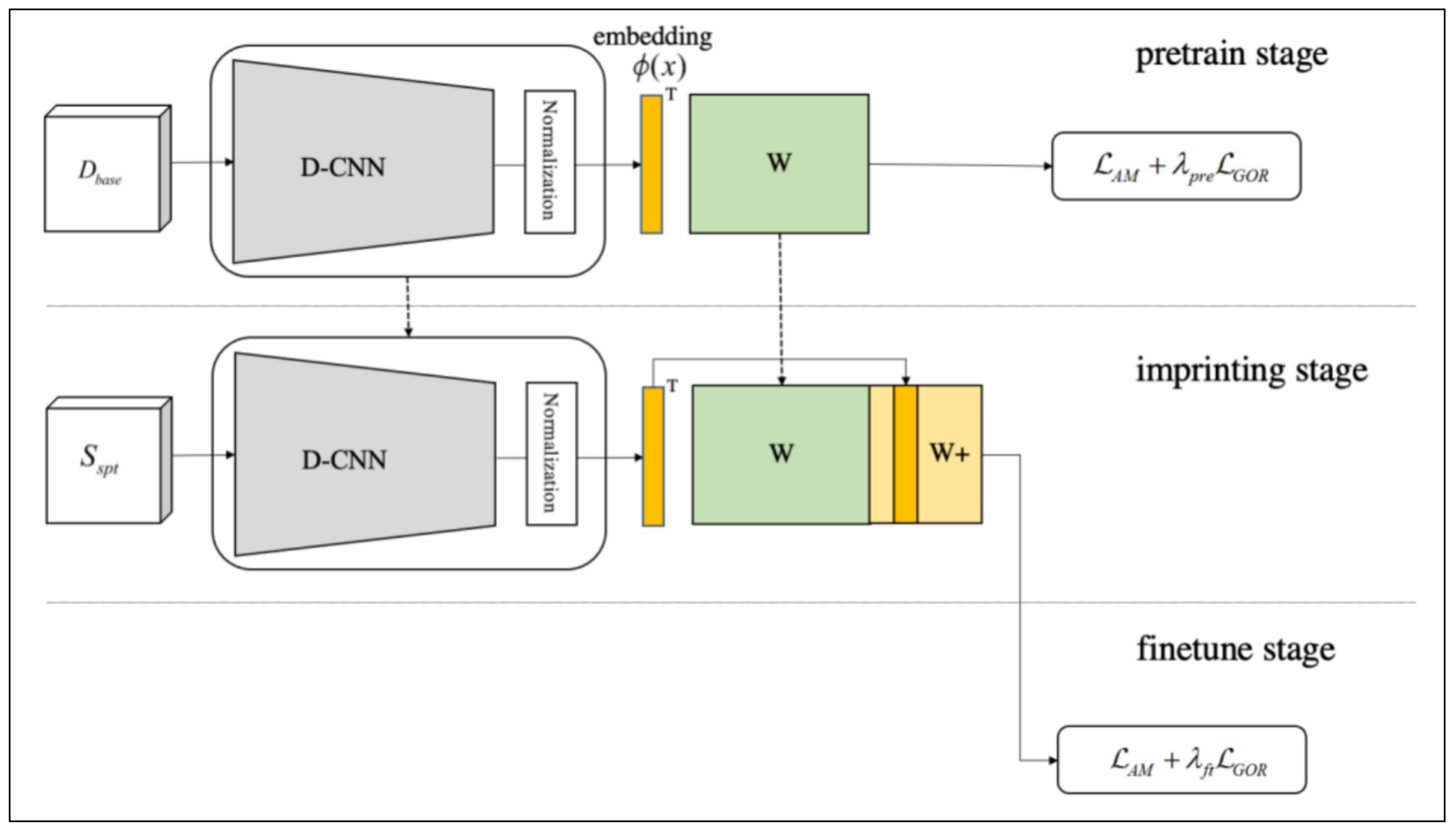
Ref. [15] proved that as long as samples from the same class are compactly distributed in the high-dimensional space and the heterogeneous samples are sufficiently dispersed, the large-class FSL learning model can achieve better generalization. Drawing on this theory, we propose a large-class FSL method based on high-dimensional features. As shown in Figure 1, we first use a deep convolutional neural network to extract high-dimensional features, we then unitize the obtained high-dimensional features, project the sample onto the hypersphere, and then use the global orthogonal regularization strategy to make different categories of samples as orthogonal as possible on the hypersphere, so as to achieve the purpose of compactness within the class and the dispersion between classes.

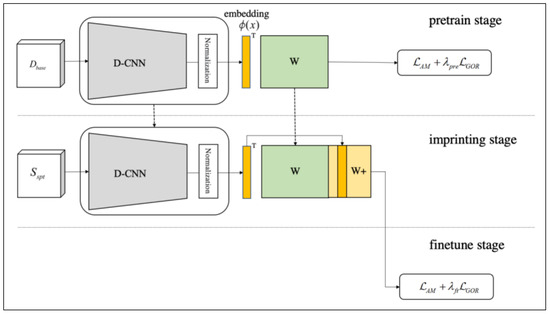
Figure 1. HF-FSL architecture. HF-FSL uses an task-independent auxiliary dataset, $D_{base}$, for pretraining. In the imprinting stage HF-FSL only uses support set, $S_{spt}$. The feature extractor trained in the pretraining stage is used to extract the feature embedding, and, after unitization, it is spliced into the classifier weight matrix in the pretraining stage as a classifier weight vector. In the end, $D_{novel}$ is used for fine-tuning.

Ref. [34] proves that two independent and uniformly sampled points on the unit sphere are orthogonal with high probability. Let $x_i$ and ${\overline{x}}_i$ be two points from different classes sampled from the unit sphere in d-dimensional space. The mean and the second moment of $\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right)$ are, respectively,

$$\mathbb{E}\left(\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right)\right)=0\mathrm{and}\mathbb{E}\left({\left(\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right)\right)}^2\right)=\frac{1}{d}.$$

(1)

This paper draws on this idea and characterizes the orthogonality of two samples on the sphere through Equation (1). We define a global orthogonal regularization term as follows:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{GOR}=& (\frac{1}{n}\sum _{i=1}^n\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right){)}^2\hfill \\ \hfill & +max\{0,\frac{1}{n}\sum _{i=1}^n{\left(\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right)\right)}^2-\frac{1}{d}\}.\hfill \end{array}$$

(2)

It can be seen that the regular term tries to make the mean value of $\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right)$ equal to zero, and the second moment equal to the reciprocal of the dimension number of the feature space, that is, the feature embedding of different classes are orthogonal to each other. In this way, the samples from different classes are fully dispersed, and those from same class are compactly distributed on the feature sphere.

Since the normalized feature embeddings are distributed on a hypersphere, in order to describe the relationships between the samples distributed on the sphere, we adopt AM-Softmax Loss [33], which is based on the angular distance metric. The AM-Softmax Loss function can be formalized as follows:

$${\mathcal{L}}_{AM}=-\frac{1}{n}\sum _{i=1}^{n}log\frac{e^{s·(cos{\theta }_{y_i,i}-m_{ft})}}{e^{s·(cos{\theta }_{y_i,i}-m_{ft})}+{\mathrm{\Sigma }}_{k=1,k\ne y_i}^{}{e}^{s·cos{\theta }_{k,i}}}$$

(3)

where $cos{\theta }_{y_i,i}$ represents the angular distance between the feature vector of the i-th sample in the support set, $S_{spt}$, and the weight vector corresponding to the ground truth class of the i-th sample in the classifier weight matrix. The value $m_{ft}$ represents the hyperparameter of the angular interval, and we set the scaling factor, s, to a learnable parameter. Combining Equations (2) and (3), the loss function of HF-FSL is

$$\begin{array}{cc}\hfill \mathcal{L}=& {\mathcal{L}}_{AM}+{\lambda }_{ft}·{\mathcal{L}}_{GOR}\hfill \\ \hfill =& -\frac{1}{n}\sum _{i=1}^{n}log\frac{e^{s·(cos{\theta }_{y_i,i}-m_{ft})}}{e^{s·(cos{\theta }_{y_i,i}-m_{ft})}+{\mathrm{\Sigma }}_{k=1,k\ne y_i}^{}{e}^{s·cos{\theta }_{k,i}}}\hfill \\ \hfill & +{\lambda }_{ft}·((\frac{1}{n}\sum _{i=1}^n\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right){)}^2\hfill \\ \hfill & +max\{0,\frac{1}{n}\sum _{i=1}^n{\left(\varphi {\left(x_i\right)}^T\varphi \left({\overline{x}}_i\right)\right)}^2-\frac{1}{d}\}),\hfill \end{array}$$

(4)

where the hyperparameter, ${\lambda }_{ft}$, is the weight coefficient of the regular term.

3.3. Model Training Strategy

As shown in Algorithm 1, this paper adopts the training strategy of imprinting [35], which consists of three stages: a pretraining stage, an imprinting stage, and a fine-tuning stage. Below is the specific introduction of the three stages:

(1)

Pretraining stage.

This stage uses a task-independent auxiliary dataset, $D_{base}$, for pretraining. For an input image, x, first use a CNN feature extractor to extract a d-dimensional embedding, $\varphi \left(x\right)$, and, then, unitize $\varphi \left(x\right)$ and the classifier weight matrix, respectively. The loss is then computed according to Equation (4). the values ${\lambda }_{pre}$ and $m_{pre}$ are the hyperparameters in Equation (4) in the pretraining stage.

(2)

Imprinting stage.

The imprinting stage uses only the support set, $S_{spt}$. The feature extractor trained in the pretraining stage is used to extract the feature embedding, and, after unitization, it is spliced into the classifier weight matrix in the pretraining stage as a classifier weight vector.

(3)

Fine-tuning stage.

This stage uses $D_{novel}$ fine-tuning, and the calculation process is similar to that of the pretraining stage. It is worth noting that they all use Equation (4) to calculate the loss; however, the hyperparameters used by each are not necessarily the same. The values ${\lambda }_{ft}$ and $m_{ft}$ are the hyperparameters in Equation (4) in the fine-tuning stage.

Algorithm 1 HF-FSL.

Input: Auxiliary dataset $D_{base}$, support set $S_{spt}$, query set $S_{qry}$      Parameter: Feature extractor $f_{ex}$, classifier $f_{cl}$      Hyper-parameter: ${\lambda }_{pre},m_{pre},{\lambda }_{ft},m_{ft}$  1: procedure Pre-train  2:     Initialize $f_{ex}$ and $f_{cl}$  3:     while $Modeldoesnotconverge$ do  4:         for $batch$ in $D_{base}$ do  5:            $embedding\leftarrow L_{2}Norm\left(f_{ex}\left(batch\right)\right)$  6:            $f_{cl}\leftarrow L_{2}Norm\left(f_{cl}\right)$  7:            Compute $loss$ with ${\lambda }_{pre},m_{pre}$ in Equation (4)  8: procedure Imprinting  9:     $f_{novel}\leftarrow f_{ex}\left(S_{spt}\right)$ 10:     $f_{cl}\leftarrow$ concat($f_{cl}$, $L_{2}Norm\left(f_{novel}\right)$) 11: procedure finetune 12:     load $f_{ex}$ from procedure PRE-TRAIN and $f_{cl}$ from procedure IMPRINTING 13:     while $Modeldoesnotconverge$ do 14:         for $batch$ in $S_{spt}$ do 15:            $embedding\leftarrow L2norm\left(f_{ex}\left(batch\right)\right)$ 16:            $f_{cl}\leftarrow L_{2}Norm\left(f_{cl}\right)$ 17:            Compute $loss$ with ${\lambda }_{ft},m_{ft}$ in Equation (4)

4. Experimental Results and Analysis

This paper verifies the effectiveness of HF-FSL on three public large-class few-shot datasets. Next, we introduce the datasets and experimental settings, comparative analysis, ablation experiments, and parameter sensitivity analysis, in turn.

4.1. Dataset and Experimental Setup

In order to prove the effectiveness of the proposed method, HF-FSL, on large-class and FSL tasks, experiments were performed on three public large-scale datasets: Omniglot, Fungi, and ImageNet. The number of novel classes in the experimental setting ranged from hundreds to thousands. Table 1 lists the number of base classes and novel classes in the three large-class few-shot datasets that were used.

Table 1. Classification of the number of categories of base classes and novel classes in the different datasets.

Dataset	Num. of Base Classes	Num. of Novel Classes
Omniglot	3856	2636
Fungi	632	674
ImageNet	522	410

The Omniglot dataset is often used for few-shot learning. It contains 1623 different handwritten characters from 50 different alphabets, which are written by 20 different people. To increase the number of classes, all images were rotated by 90, 180, and 270 degrees. Each spin generated an extra class, so the total number of classes became 6492 ($1623\times 4$). We adopted 3856 classes as base classes and the remaining 2636 classes as novel classes.

Fungi is a fine-grained fungal image dataset that was originally introduced by the 2018 FGVCx Fungal Classification Challenge. We randomly sampled 632 classes for the base class, 674 classes for the novel class, and 88 classes for the validation set.

ImageNet is a widely used image dataset. We conducted experiments using the ImageNet64 × 64 dataset, which is a downsampled version of the original ImageNet used in ILSVRC, with images resized to 64 × 64 pixels. We used WordNet to divide the original 1000 classes into three groups, namely Living Thing, Artifact, and Rest. Among them, 522 classes that were classified as Living Thing were used as base classes, 410 classes classified as Artifacts were used as novel classes, and the remaining 68 classes were used for the validation set.

4.2. Analysis of Comparative Results

This study used ResNet-50 as the backbone network for extracting high-dimensional features and adopted the experimental setting of 5-shot on Omniglot, Fungi, and ImageNet. It was compared with several few-shot learning methods, namely the Prototype Network (PN), the Matching Network (MN), the Prototype Matching Network (PMN), the Ridge Regression Differentiable Discriminator (R2D2), and their combination using the confusion learning method variant [7] (denoted by “w/CL”). Table 2 shows the Top-1 accuracy comparison of these methods on three large-class datasets. It is easy to see that the method proposed in this paper obtained the highest accuracy compared with other methods. Overall, HF-FSL significantly improved recognition accuracy compared with other methods.

Table 2. Top-1 accuracy comparison table of different methods on three large-class datasets.

Method	Omniglot	Fungi	ImageNet
PN	69.90%	6.96%	6.02%
PN w/CL	73.21%	7.29%	6.27%
MN	68.04%	7.26%	4.79%
MN w/CL	71.07%	7.92%	5.41%
PMN	69.73%	6.96%	5.90%
PMN w/CL	73.68%	7.28%	6.41%
R2D2	66.12%	7.92%	7.78%
R2D2 w/CL	74.72%	8.04%	8.46%
HF-FSL	82.39%	21.75%	9.36%

4.3. Ablation Study

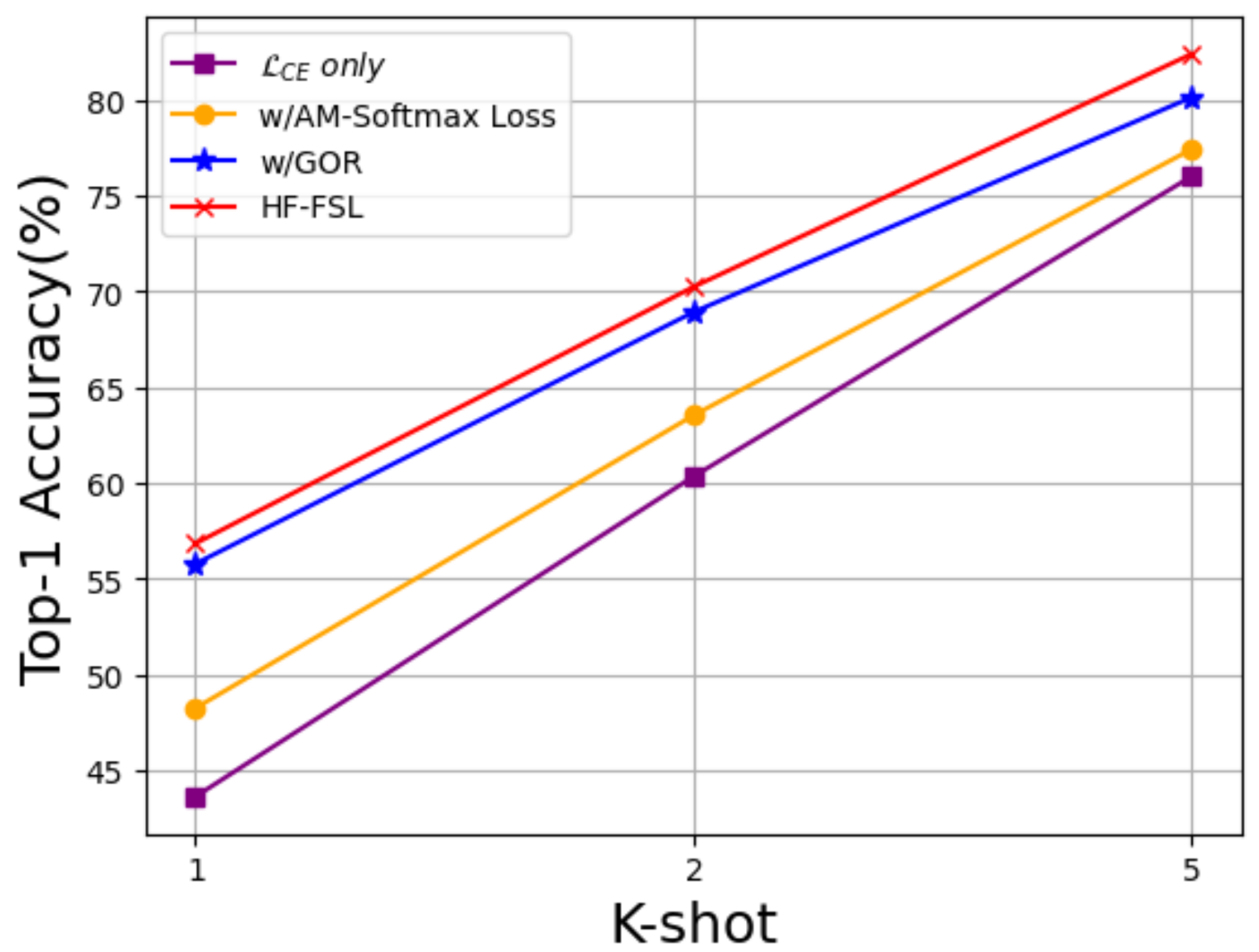
In order to verify the effectiveness of the two core modules, AM-Softmax Loss and GOR in the proposed HF-FSL method, we conducted ablation experiments on Omniglot using the setting 2636-way K-shot, where K = 1, 2, 5, see Figure 2. The first row in Table 3 is the result of using the traditional cross-entropy loss function, denoted by $L_{CE}$, only. The second line shows results when the AM-Softmax function based on the angular distance metric was used, which is represented by AM-Softmax. The third line shows results when the traditional cross-entropy loss function and the global orthogonal regularization term proposed in this paper were used, which is represented by w/GOR. By comparing the first row with the second row and the first row with the third row, respectively, it can be seen that using AM-Softmax Loss and GOR greatly improved the accuracy of the ordinary cross-entropy loss function. Comparing these rows with the fourth row, it can be seen that, compared with the traditional method, the recognition accuracy of HF-FSL under the experimental setting of K = 1, 2, 5 brought improvements of 13.21%, 9.90%, and 6.39%, respectively.

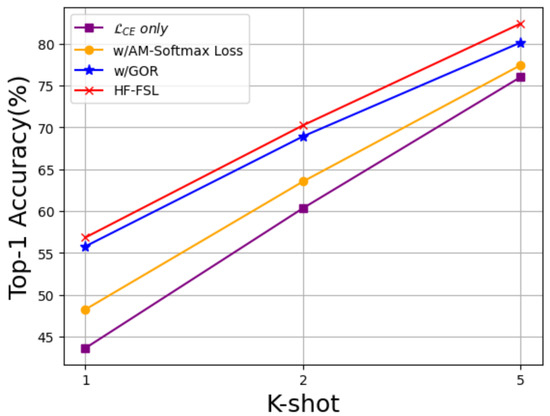
Figure 2. Ablation study on Omniglot.

Table 3. Ablation experiment results (based on Omniglot dataset).

Method	K = 1	K = 2	K = 5
$L_{CE}$ only	43.61%	60.33%	76.00%
w/AM-Softmax	48.23%	63.52%	77.42%
w/GOR	55.77%	68.91%	80.13%
HF-FSL	56.83%	70.23%	82.39%

4.4. Parameter Sensitivity Analysis

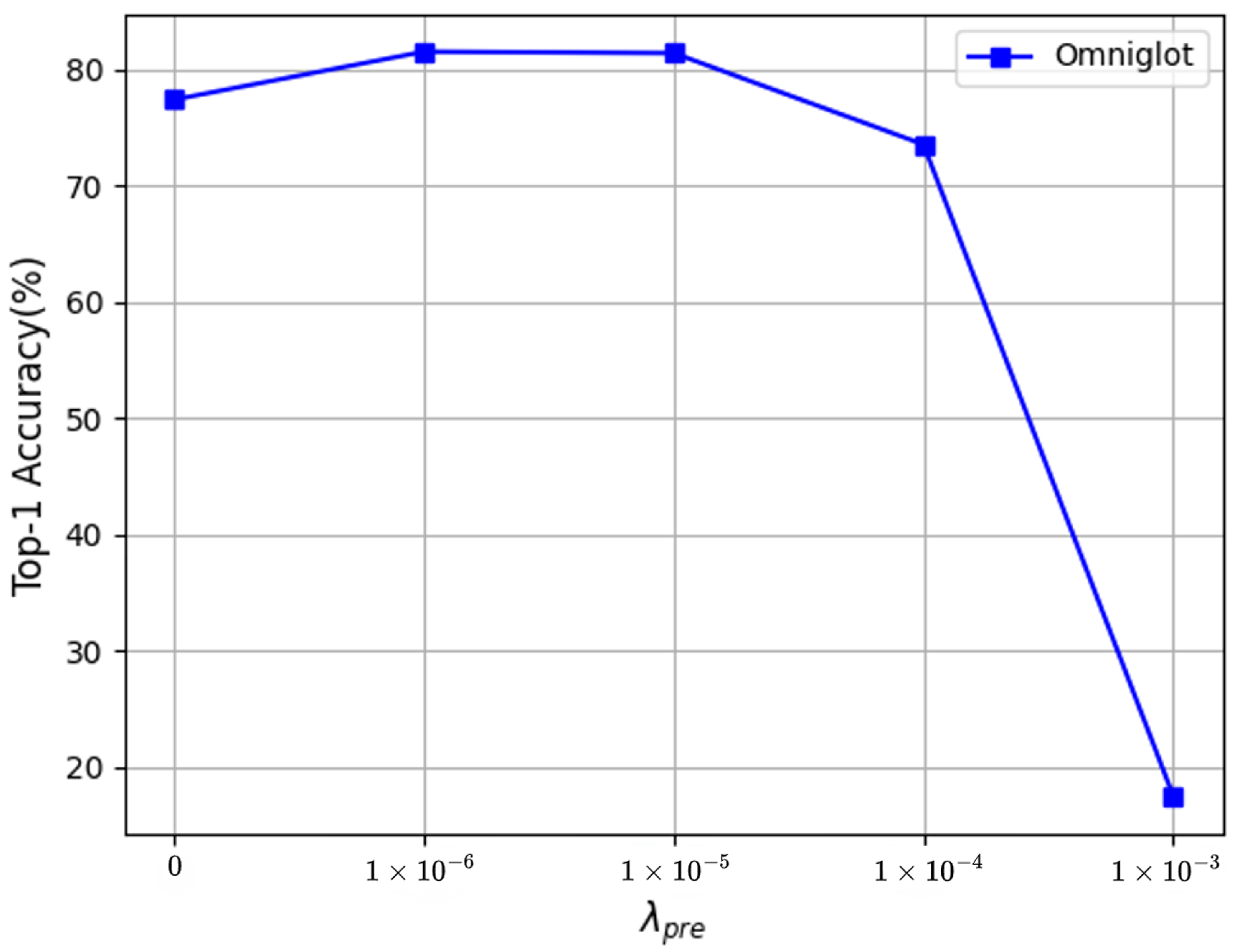
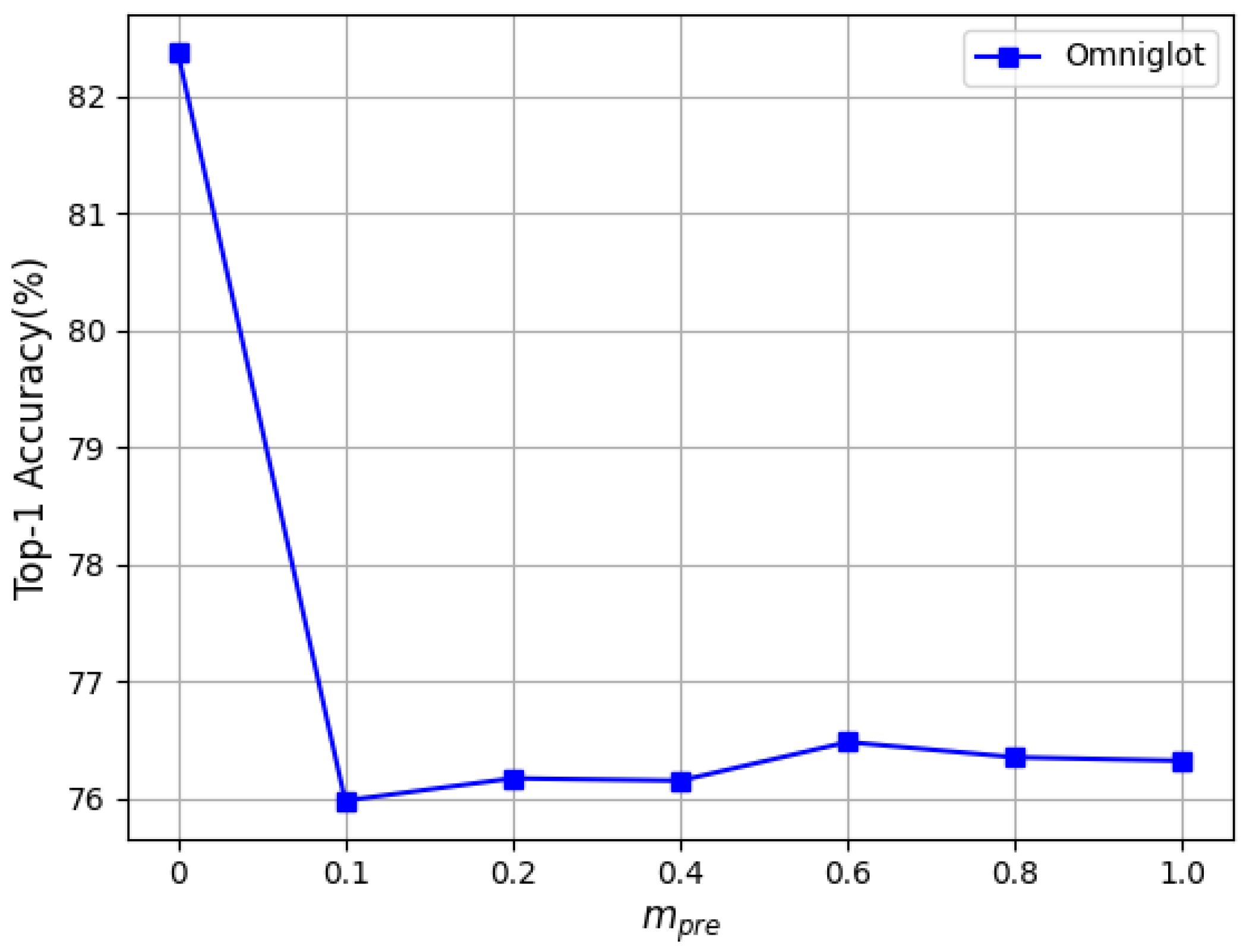
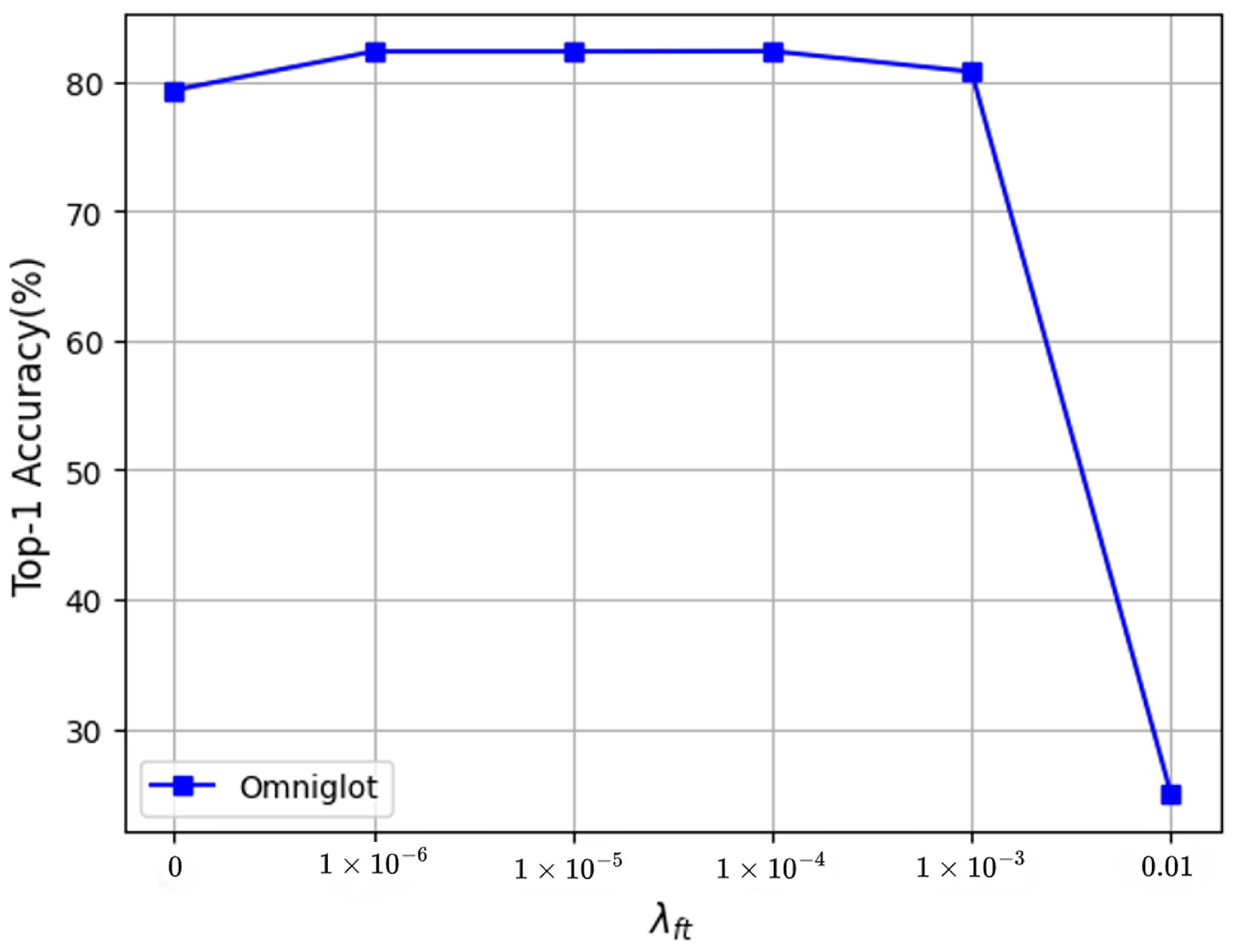
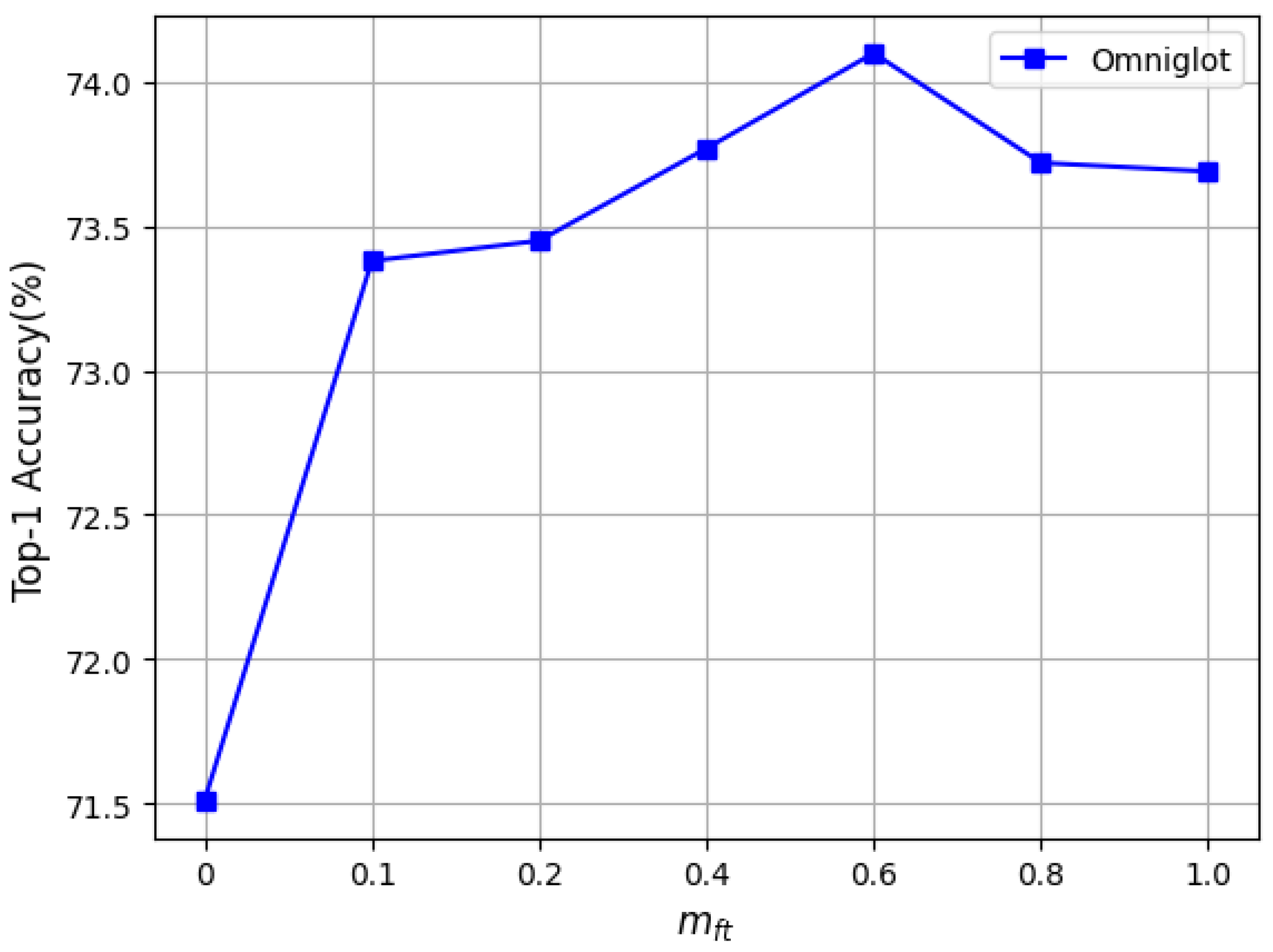
We adjusted these four hyperparameters on Omniglot separately (one hyperparameter was adjusted each time, and the remaining three hyperparameters were kept fixed). In Figure 3, when ${\lambda }_{pre}$ changed from 0 to 1 $\times {10}^{-5}$, the recognition accuracy significantly improved, and when ${\lambda }_{pre}$ was greater than 1 $\times {10}^{-4}$, the accuracy began to drop sharply. It can be seen in Figure 4 that the change in $m_{pre}$ in the pretraining stage did not have a positive effect on the recognition accuracy; hence, it is recommended to set $m_{pre}$ to 0 in the experiment. Figure 5 shows that ${\lambda }_{ft}$ in the fine-tuning stage changed from 0 to $1\times {10}^{-3}$, the recognition accuracy was improved by varying degrees, and the accuracy dropped sharply when it was greater than $1\times {10}^{-3}$. Therefore, we recommend that the value of ${\lambda }_{ft}$ be chosen from the interval 0 to $1\times {10}^{-3}$. In Figure 6, with the change in the value of $m_{ft}$ in the fine-tuning stage, the accuracy steadily improved compared to when $m_{ft}$ was set to 0. It can be concluded that the proposed HF-FSL method can achieve better recognition accuracy without much parameter adjustment.

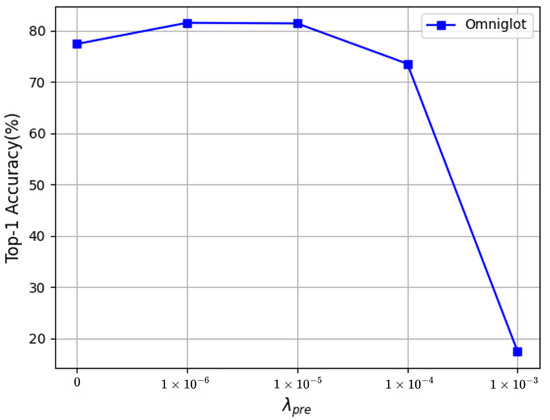
Figure 3. Tuning ${\lambda }_{pre}$.

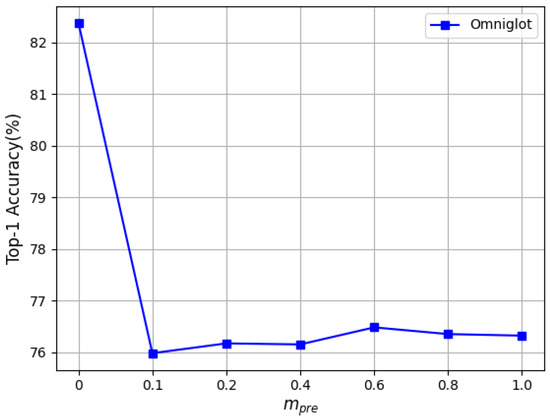
Figure 4. Tuning $m_{pre}$.

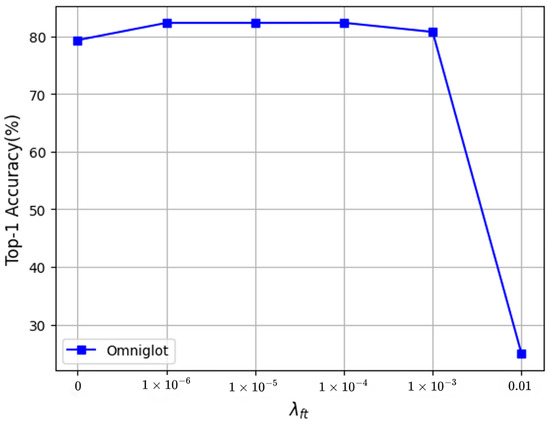
Figure 5. Tuning ${\lambda }_{ft}$.

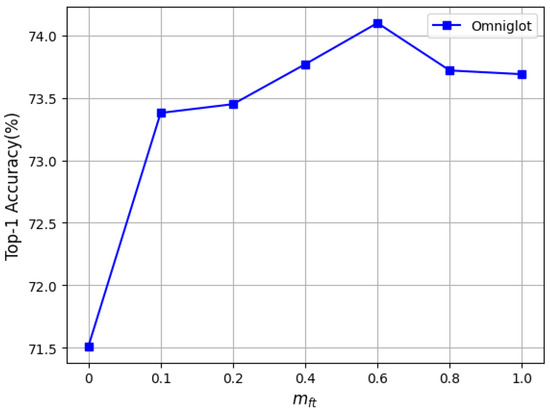
Figure 6. Tuning $m_{ft}$.

5. Conclusions

This paper proposes a large-class few-shot learning method called HF-FSL. First, we projected samples onto a hypersphere, and, then, used the global orthogonal regularization strategy to make samples from different categories as orthogonal as possible, so as to achieve the purpose of compactness within the class and the dispersion between classes. Moreover, the angle metric-based loss function was applied in order to characterize the relationships between the samples distributed on the hypersphere. Experimental results using three public large-class few-shot datasets showed that HF-FSL could effectively improve the recognition accuracy of large-class few-shot learning methods.