A Study of Reciprocal Job Recommendation for College Graduates Integrating Semantic Keyword Matching and Social Networking

Abstract

With the surge in college graduate numbers, a disparity has emerged where the supply of jobs falls short of demand, intensifying employment pressures annually. College graduates, due to their lack of historical employment data compared with job seekers in the broader society, encounter a ‘cold start’ issue in the job recommendation process. Additionally, the nature of job recommendations, which differs fundamentally from unilateral recommendations, requires consideration of reciprocity between both parties involved. This article introduces a new approach to job recommendations using college graduates as the object of study. In the screening stage, a semantic keyword iterative algorithm is applied to compute the similarity between the resume and recruitment texts. This algorithm enhances the intersectionality of keywords in the calculation process, maximizing the utilization of resume information to enhance the accuracy of text similarity calculations. The ranking phase utilizes in-school data to build a social network between college graduates and graduated students and solves the system’s cold-start problem using the social network to recommend jobs for college graduates where graduated students are employed. We introduce a dual-dimensional matching approach that incorporates both specialty and salary, building upon the amalgamated semantic keyword iterative algorithm and the social network job recommendation method, to enhance the reciprocity of job recommendations. The job recommendation method introduced herein outperforms other methods in terms of the average satisfaction rate (AR) and normalized discounted cumulative gain (NDCG), thereby confirming its superior ability to meet the job-seeking preferences of graduates and the recruitment criteria of employers. This job recommendation method offers effective assistance to graduates lacking employment experience and historical employment data, facilitating their search for more suitable job opportunities.

1. Introduction

The advancement of higher education has facilitated an expansion in student enrollment within colleges and universities, consequently leading to a yearly increase in the number of graduates. According to statistics, the number of college graduates in China for the year 2023 reached 11.58 million, which represents a year-on-year growth of 820,000. This substantial influx of new graduates has entered the job market, intensifying the competition for employment [1,2]. Concurrently, some graduates encounter challenges due to undefined employment goals, decision-making difficulties, and information overload [3,4]. These factors contribute to a decline in the overall employment rate. To assist graduates in securing employment, colleges offer career guidance; however, tailored recommendations for individual cases are often lacking [5]. Current job search platforms predominantly cater to social job seekers, while the exploration and implementation of personalized recommendations for graduates remain underdeveloped. Additionally, given the multitude of majors and diverse employment fields, providing tailored job recommendations for graduates becomes a more intricate challenge [6]. The following issues afflict the current job recommendation methodology: (a) The content-based approach heavily depends on semantic matching technology, while the current technology still faces limitations in understanding and extracting semantics. This results in poor accuracy when calculating the relevance of resumes to jobs. (b) Collaborative filtering-based methods rely on user behavioral data to model interest preferences, but the sparsity of user data for first-time graduates makes it challenging to accurately capture their interests. (c) The specific group of graduates differs from the richness of historical behavioral data that social users have, and the system faces the cold-start problem, thus limiting the effectiveness of the recommendation model.

In addressing the aforementioned issues, this study proposes an enhanced semantic matching algorithm. This algorithm uses keyword expansion and iterative computation to prevent the loss of semantic information when calculating the similarity between a resume and job text. Building upon this foundation and leveraging the social network relationships among graduates, personalized suggestions are deduced by relying on the recommendation results of similar users. This approach aims to address the cold-start problem in graduate recommendations and provide accurate and reliable recommendation results. The approach integrates information from both semantic and social network dimensions, with the goal of enhancing the performance of graduate job recommendation methods. Moreover, this article emphasizes professional matching and salary matching, aspects of considerable concern for both parties in job search and recruitment. It incorporates the calculation of dimensions related to “professional matching and salary matching,” thereby further fortifying the reciprocity of job recommendations.

2. Related Works

2.1. Research on Job Recommendation Based on Keyword Matching

The keyword matching-based job recommendation method is fundamentally a content-based approach. It uncovers job seeker preferences and job recruitment requirements by extracting keywords and calculating the similarity between them, ultimately generating a list of job recommendations. Bansal [7] utilized an LDA model to extract keywords for mining job seekers’ preferences and recommending optimal jobs. Lacic [8] used a self-encoder architecture to encode a job seeker’s session within the session domain and used k-nearest neighbor methods for inference, analyzing potential jobs to provide recommendations. While keyword matching has advantages over traditional methods, it also faces limitations in semantic matching and effectively processing sparse texts. For instance, the Boolean search-based model utilizes a keyword-matching technique to align job posting requirements with the qualification information from the user’s resume. However, this model encounters semantic extraction limitations [9]. Moreover, the limited information in resumes and recruitment texts challenges the effective extraction of job seekers’ personality preferences. This has led to the development of behavioral preference models for users, constructed with the collection of their implicit data, and these models are used to recommend jobs that satisfy users’ preferences [10]. On this foundation, the development of constructing user profiles by analyzing the behavioral data of job seekers on e-recruitment platforms to extract personality preferences, with the aim of establishing a unidirectional job recommendation model for job seekers, began to unfold [11]. At present, the keyword matching used in job recommendation involves extracting keywords from text for a basic match. However, the information within the job seeker’s resume is limited, resulting in the extraction of fewer keywords. This limitation impedes the accurate alignment of resume information with recruitment details, thereby lowering the accuracy and satisfaction levels of job recommendations. In addition, the current keyword matching does not start from semantic matching and reciprocal matching [12].

2.2. Research on Job Recommendations Based on Social Networks

Social networks are essentially the fusion of social elements and network structures, representing virtual networks established with the primary intent of facilitating social interaction [13,14]. In the era of the Internet’s evolution, numerous third-party suites have been integrated into social networking platforms, enhancing the diversity and integration of these social platforms. The integration of job recommendations with social networks is intended to assist job seekers in identifying more suitable and satisfying employment opportunities [15,16,17]. Integrating social networks into the process of generating job recommendations not only diminishes operational costs but also enhances the precision of job recommendations [15]. With his research, Alejandro [18] illustrates that engaging in recruiting and job searching on social networks can effectively address issues such as the low accuracy of job recommendations stemming from sparse user data. Zhao et al. [19] introduced an algorithm that leverages academic social networks to facilitate job transitions by extracting data from publications, a method that not only preserves privacy but also addresses the issue of data sparsity. Job recommendation methods established on career-oriented social networks exhibit superior performance in suggesting satisfactory jobs for job seekers by effectively capturing their preferences [20]. Moreover, disseminating job postings via social networking platforms and suggesting vacancies to friends within social networks can significantly enhance the accuracy of recommendations [21]. The greater the activity level of social network users and the extent of their contacts, the higher the precision of job recommendations [22]. Social networks not only facilitate efficient job searching for job seekers but also assist employers in identifying more suitable candidates for recruitment. Social networks can furnish more dependable hiring references for recruiting employers, as they commonly utilize platforms like Facebook to acquire information about potential candidates [23]. Given that information posted on social networks, such as Facebook, is typically personal rather than professional, employers can form a more precise assessment of a candidate’s character [24]. While the integration of social networks can enhance the effectiveness of job recommendations, college graduates, as newcomers in the workplace, often lack a well-established professional social circle. Hence, there is significant research significance in integrating the academic data of college graduates with the employment information of graduated students to establish a social network for college graduates, thereby facilitating the recommendation of satisfactory job opportunities for them.

2.3. Research on Job Recommendations Based on Reciprocity

Reciprocal recommendation is to provide recommendations based on the common preferences of both users [25]. Reciprocal recommendations have been successfully used in various domains, including online dating systems [26], online mentoring systems [26], and online recruitment systems [27]. Reciprocity-based job recommendation implies that the recommended job not only aligns with the preferences of the job seeker but also meets the requirements and preferences of the recruiter [12,28]. To achieve reciprocity in job recommendation, existing research predominantly uses distinct recommendation methods tailored to the characteristics of diverse users. For instance, Malinowski [28] devised two job recommendation systems tailored to the distinct preferences of both job seekers and recruiters, effectively addressing the requirements of each party. Li [29] proposes a job guidance system for college students that integrates ideological and political education with a recommendation algorithm. This algorithm aggregates the preferences and needs of both students and employers to enhance the reciprocity of job recommendations. A job recommender system that utilizes latent factors derived from the explicit profile information of both job seekers and jobs can achieve notable reciprocity [30,31]. Integrating hybrid recommendation methods with reciprocal approaches can further refine the precision of job recommendations. For instance, using Support Vector Machine (SVM) predictive modeling to estimate the likelihood of a company’s response to an application, within a hybrid recommendation method that integrates content and collaborative filtering, can enhance the accuracy of job recommendations [32]. These personalized job recommendation systems take into account the mutual preferences of both job seekers and recruiters, overcoming the limitations of reciprocal recommendations and thereby increasing the success rate. However, the evaluation is solely focused on the accuracy of one-way recommendation results and does not provide a side-by-side comparison with other one-way job recommendation methods.

2.4. The Application of Job Recommendation in the Field of Colleges

Currently, established personalized employment platforms, such as ‘Wisdom Link Recruitment Network’ and ‘58job’, target social users. Nevertheless, the research and application of job recommendations tailored specifically for college graduates are limited. There exist collaborative filtering-based job recommendation algorithms that cluster graduates based on their characteristics and recommend jobs in line with their preferences [33]. Moreover, content-based job recommendation algorithms utilize historical employment data to determine the relevance between graduates and jobs, offering targeted job recommendations [34]. However, these algorithms tend to produce recommendations with a limited focus, which may not be suitable for suggesting a wide range of job types. To address this, Shi [35] proposes to integrate key technologies, such as graduate feature technology, similarity algorithms, and neighbor selection mechanisms, to establish a graduate employment recommendation system, with the aim of broadening the scope of recommendation results. Li [36] combines recommendation and machine learning algorithms to match and optimize job options for college students based on their major types, interests, specialties, preferred employment areas, and other job-related characteristics. This integration improves the diversity and satisfaction of job recommendations simultaneously. Assudani [37] underscores the difficulties in expanding job recommendation diversity and creating a multi-category job database as significant obstacles in the recommendation process. Leveraging existing campus employment portals has become a novel research focus for recommending suitable graduate candidates to companies from the recruiter’s perspective. Given that college graduates, as newcomers to the job recommendation system, lack historical behavioral data, the system faces difficulty in capturing graduates’ job search preferences [10,35]. Thus, job recommendation research for college graduates could utilize campus data to better understand their job search preferences and suggest more fulfilling employment opportunities.

3. Proposed Job Recommendation Method

The job recommendation model comprises three distinct phases, as illustrated in Figure 1. In the screening stage, a semantic keyword iterative algorithm calculates the text similarity between resumes and job postings, which is then used to filter the pool of potential jobs. The second stage is the ranking stage, in which entropy aggregation is conducted using three dimensions: professional similarity, salary matching, and social network. Based on the calculated values, the set of job recommendations is determined, and subsequently, the jobs are returned to college graduates for scoring. The final evaluation stage measures the satisfaction and reciprocity of the job recommendation results using metrics such as average satisfaction (AR) and normalized discounted cumulative gain (NDCG).

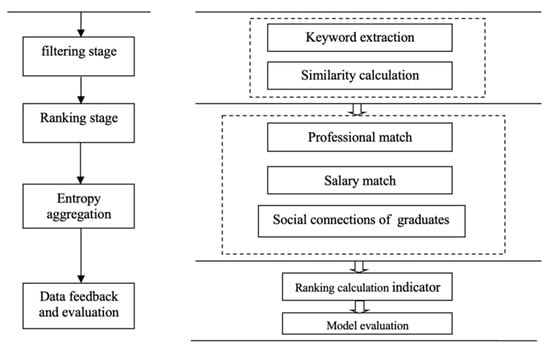
Figure 1. Job recommendation model framework.

3.1. Screening Phase

3.1.1. Text Information Extraction and Processing Filtering Stage

Examples of resume texts of college graduates and job recruitment texts are presented in Table 1 and Table 2, respectively. The resume text includes essential information, such as gender, hometown, graduation college, major, research direction, and job preferences. The job recruitment text encompasses details on job positions, workplaces, salary levels, and company nature (state-owned or private enterprises), as well as academic, skill, and professional requirements.

Table 1. Resume information of a logistics graduate.

Logistics Graduate Resume Information
Name: Zhang Gender: Female Graduate school: xx university, logistics engineering Research direction: supply chain management supervisor: Li xx Address: Kunming, Yunnan Province	Expected salary CNY: 3000–5000 Expected work location: Southwest Desired position: engaged in logistics-related work Expected working environment: office environment; corporate culture; work prospects; and so on

Table 2. Job recruitment Information.

Job Recruitment Information
Recruitment company: xxx Salary level CNY: 5000–6000 Job responsibilities: manage supply chain; cost control Working environment: office environment; corporate culture; employment prospects… Working location: Kunming, Yunnan	Education requirements: graduate degree or above English level: College English Level 6 Job requirements: applicants are logistics-related majors, supply chain research direction is preferred, candidates should be skilled in using matlab software, and so on

In this study, the Jieba precise mode was used to perform word segmentation on both the resume and job recruitment texts. To enhance the precision of word segmentation, specialized vocabulary related to a profession was incorporated. We removed punctuation marks and stop words from the texts. Then, Term Frequency-Inverse Document Frequency (TFIDF) values were calculated, and keywords were extracted based on these values.

3.1.2. The Semantic Keyword Iterative Algorithm

Quattrone et al. [38] pointed out that traditional similarity calculation methods, such as cosine similarity, suffer from low utility when dealing with sparse data. Traditional methods rely solely on word frequency to calculate text similarity, making them susceptible to discarding keywords with low frequency, thus resulting in reduced calculation accuracy [38,39]. In light of the sparse data and lack of historical information for college graduates as new users of job recommendation systems, this study uses a semantic keyword iterative algorithm. This algorithm leverages a keyword correlation matrix to calculate text similarity, thereby countering the accuracy issues associated with low-frequency keywords. This approach enhances the accuracy of the job recommendation system, enabling it to provide more reliable recommendations to college graduates, despite their limited historical data.

The keyword correlation matrix is calculated using Equations (1)–(5). First, the TFIDF algorithm was used to calculate the ‘keyword-text’ matrix, referred to as the $\mathrm{K}\mathrm{D}$ matrix. KD is an ${\mathrm{n}}_{\mathrm{k}}\times {\mathrm{n}}_{\mathrm{d}}$ matrix, where ${\mathrm{n}}_{\mathrm{k}}$ represents the number of keywords, ${\mathrm{n}}_{\mathrm{d}}$ represents the number of texts, and $\mathrm{K}\mathrm{D}$ represents the number of times the keyword appears in the text; for example, ${\mathrm{K}\mathrm{D}}_{\mathrm{i}\mathrm{m}}$ represents the number of times the keyword ${\mathrm{k}}_{\mathrm{i}}$ appears in the text ${\mathrm{D}}_{\mathrm{m}}$.

The keyword correlation matrix is calculated based on the KD matrix. The specific calculation process is as follows:

Step 1:

$${sk}^0\left(k_m, { k}_n\right)={\theta }_{mn}, { sd}^0\left(d_m, { d}_n\right)={\delta }_{mn}$$

(1)

The first step is to define the initial similarity value of the keyword ${\mathrm{s}\mathrm{k}}^0\left({\mathrm{k}}_{\mathrm{m}},{\mathrm{k}}_{\mathrm{n}}\right)$ and the text ${\mathrm{s}\mathrm{d}}^0\left({\mathrm{d}}_{\mathrm{m}}, {\mathrm{d}}_{\mathrm{n}}\right)$. The principle of definition is that each keyword or text is the same as itself and has certain differences from other keywords and texts. ${\mathrm{s}\mathrm{k}}^0\left({\mathrm{k}}_{\mathrm{m}}, {\mathrm{k}}_{\mathrm{n}}\right)$ represents the initial similarity value between keywords ${\mathrm{k}}_{\mathrm{m}}$ and ${\mathrm{k}}_{\mathrm{n}}$, and ${\mathrm{s}\mathrm{d}}^0\left({\mathrm{d}}_{\mathrm{m}}, {\mathrm{d}}_{\mathrm{n}}\right)$ represents the initial similarity value between text ${\mathrm{d}}_{\mathrm{m}}$ and ${\mathrm{d}}_{\mathrm{n}}$.

Step n:

$${sk}^n\left(k_m,k_n\right)=\frac{{SKK}^n(k_m, k_n)}{\sqrt{{SKK}^n(k_m,k_m)}·\sqrt{{SKK}^n(k_n,k_n)}}$$

(2)

$${sd}^n\left(d_m,d_n\right)=\frac{{SDD}^n(d_m,d_n)}{\sqrt{{SDD}^n(d_m,d_m)}·\sqrt{{SDD}^n(d_n,d_n)}}$$

(3)

where ${\mathrm{s}\mathrm{k}}^{\mathrm{n}}\left({\mathrm{k}}_{\mathrm{m}},{\mathrm{k}}_{\mathrm{n}}\right)$ represents the similarity value between keywords ${\mathrm{k}}_{\mathrm{m}}$ and ${\mathrm{k}}_{\mathrm{n}}$ in the nth iteration, and ${\mathrm{s}\mathrm{d}}^{\mathrm{n}}\left({\mathrm{d}}_{\mathrm{m}},{\mathrm{d}}_{\mathrm{n}}\right)$ represents the similarity value between text ${\mathrm{d}}_{\mathrm{m}}$ and ${\mathrm{d}}_{\mathrm{n}}$ in the nth iteration. The definitions of ${\mathrm{S}\mathrm{K}\mathrm{K}}^{\mathrm{n}}\left({\mathrm{k}}_{\mathrm{m}},{\mathrm{k}}_{\mathrm{n}}\right)$ and ${\mathrm{S}\mathrm{D}\mathrm{D}}^{\mathrm{n}}\left({\mathrm{d}}_{\mathrm{m}},{\mathrm{d}}_{\mathrm{n}}\right)$ are given in Equations (4) and (5):

Where

$${SKK}^n\left(k_m,k_n\right)={\sum }_{i,j=1}^{n_d}{KD}_{mi}·{\phi }_{ij}·{sd}^{n-1}(d_i,d_j)·{KD}_{nj}$$

(4)

$${SDD}^n\left(d_m,d_n\right)={\sum }_{i,j=1}^{n_k}{KD}_{im}·{\phi }_{ij}·{sk}^{n-1}(k_i,k_j)·{KD}_{jn}$$

(5)

The calculated value of ${\mathrm{S}\mathrm{K}\mathrm{K}}^{\mathrm{n}}\left({\mathrm{k}}_{\mathrm{m}},{\mathrm{k}}_{\mathrm{n}}\right)$ in step n must be incorporated into the text similarity calculation of ${\mathrm{s}\mathrm{d}}^{\mathrm{n}-1}({\mathrm{d}}_{\mathrm{i}},{\mathrm{d}}_{\mathrm{j}})$ in step $(\mathrm{n}-1)$. The calculated value of ${\mathrm{S}\mathrm{D}\mathrm{D}}^{\mathrm{n}}\left({\mathrm{d}}_{\mathrm{m}},{\mathrm{d}}_{\mathrm{n}}\right)$ in step n must be incorporated into the keyword similarity calculation of ${\mathrm{s}\mathrm{k}}^{\mathrm{n}-1}({\mathrm{k}}_{\mathrm{i}},{\mathrm{k}}_{\mathrm{j}})$ in step $(\mathrm{n}-1)$, and the iterative calculation is carried out in turn. ${\mathrm{K}\mathrm{D}}_{\mathrm{m}\mathrm{i}}$, ${\mathrm{K}\mathrm{D}}_{\mathrm{n}\mathrm{j}}$, ${\mathrm{K}\mathrm{D}}_{\mathrm{i}\mathrm{m}}$, and ${\mathrm{K}\mathrm{D}}_{\mathrm{j}\mathrm{n}}$ in Equations (4) and (5) are elements of the $\mathrm{K}\mathrm{D}$ matrix. ${\mathsf{\phi }}_{\mathrm{i}\mathrm{j}}$ is the mutual reinforcement factor. When keywords ${\mathrm{k}}_{\mathrm{i}}$ and ${\mathrm{k}}_{\mathrm{j}}$ represent the same document, the mutual reinforcement factor ${\mathsf{\phi }}_{\mathrm{i}\mathrm{j}}=1$. In the other cases, the value range of ${\mathsf{\phi }}_{\mathrm{i}\mathrm{j}}$ is (0,1). The value of ${\mathsf{\phi }}_{\mathrm{i}\mathrm{j}}$ was experimentally obtained. In this study, the best result was obtained when ${\mathsf{\phi }}_{\mathrm{i}\mathrm{j}}=0.4$.

To further address the issue of data sparsity, the resume text of graduates was expanded with additional keywords. Specifically, the two most similar keywords, excluding those already present in the resume text, were added to enhance their content. This expanded resume text was then used to match the job recruitment text. A keyword relevance matrix was obtained using the iterative process described above. Finally, the match degree (MD) between the graduates’ resume text and the job recruitment text was calculated using Equation (6).

$$MD\left(s_n, w_m\right)={\sum }_{i=1}^{n_k}{TF}_{s_n}\left(k_i\right)·{TF}_{w_m}\left(k_i\right)·sin\left(k_i\right)$$

(6)

where ${\mathrm{n}}_{\mathrm{k}}$ indicates the number of extended-resume document keywords. ${\mathrm{T}\mathrm{F}}_{{\mathrm{k}\mathrm{s}}_{\mathrm{n}}}\left(\mathrm{i}\right)$ represents the frequency score of keyword $\mathrm{i}$ in the nth resume document, and ${\mathrm{T}\mathrm{F}}_{{\mathrm{k}\mathrm{w}}_{\mathrm{m}}}\left(\mathrm{i}\right)$ represents the frequency score of keyword $\mathrm{i}$ in the ${\mathrm{m}}^{\mathrm{t}\mathrm{h}}$ job document. $\sin \left(\mathrm{i}\right)$ is a parameter used to determine whether the keyword in the resume document is the original keyword. When $\sin \left(\mathrm{i}\right)=1$, $\mathrm{i}$ is the original keyword in the document. When $\mathrm{i}$ is a rich keyword, the value of $\sin \left(\mathrm{i}\right)$ is equal to the calculated value of the keyword correlation matrix. The candidate working set was obtained according to the similarity value calculated using the keyword correlation matrix.

3.2. Ranking Stage

In employment, the degree of professional alignment between job seekers and job positions is a crucial factor influencing job search outcomes. With the growing gap between job availability and the demand for skilled workers, employers are emphasizing professional compatibility between job roles and candidates [36]. Rational choice theory posits that individuals are rational decision-makers who weigh the costs and potential benefits when arriving at decisions [40]. Researchers, such as Jung et al. [41], have used the potential Dirichlet distribution method online to extract themes from a substantial volume of employee comments, and their analysis has highlighted salary as a pivotal factor influencing job satisfaction. Hence, salary alignment emerges as a significant determinant affecting the satisfaction of job recommendations. Regular equivalence theory, a fundamental doctrine within communication theory, posits that an individual’s behavior is influenced by the information, attitudes, and actions of others within a network [37]. When two individuals share more common social circles, their behavioral preferences tend to exhibit greater similarity, fostering a propensity to establish connections [42]. Thus, this study applies social networks in recommending jobs to recent college graduates, drawing on the employment decisions of alumni to effectively enhance satisfaction and reciprocity in job recommendations.

In the ranking stage, this study used three critical dimensions: professional matching, salary matching, and social network, to perform entropy-based aggregation. The recommended job set is generated by calculating the entropy aggregation. Professional matching assesses the compatibility between college graduates’ skills and qualifications and the requirements specified in job postings. Salary matching evaluates the level of correspondence between the expected salary of college graduates and the actual salary offered by the employing companies. Social networks analyze the social connections and relationships between college graduates and other graduate students, taking into consideration potential networking opportunities or affiliations that may influence job recommendations.

3.2.1. Professional Matching

First, random walk probability was used to calculate the connection between graduated students and work, and then the professional matching score between the target and graduated students was calculated. We organized all the professional attributes of the job, job, and graduated students into a graphic$\mathrm{G}(\mathrm{V},\mathrm{E})$. Professional job attributes include professional skills. In the figure, ${\mathrm{V}}_{\mathrm{p}\mathrm{t}}$ represents the set of nodes of the graduated students, ${\mathrm{V}}_{\mathrm{w}}$ represents the set of working nodes, and ${\mathrm{V}}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{t}}$ represents the set of professional attribute nodes of the work, that is, $\mathrm{V}={\mathrm{V}}_{\mathrm{p}\mathrm{t}}+{\mathrm{V}}_{\mathrm{w}}+{\mathrm{V}}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{t}}$, as shown in Figure 2 and Figure 3.

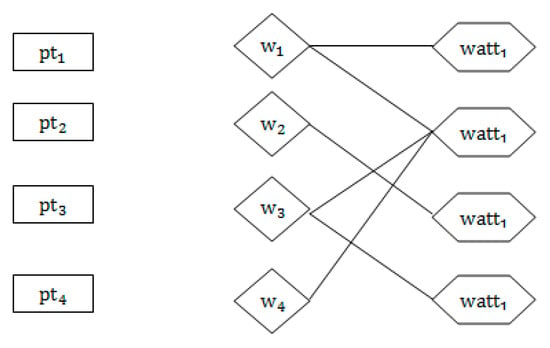
Figure 2. Initial correlation model.

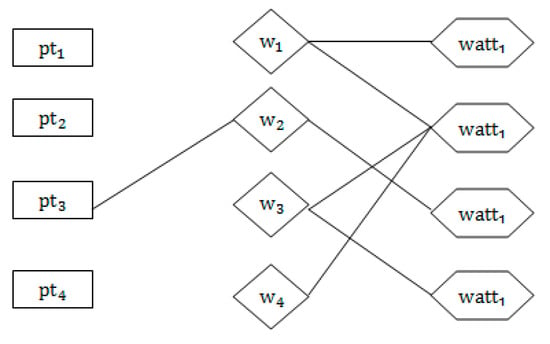
Figure 3. Correlation model.

Figure 2 depicts the initial correlation, which represents the graduated student node and its associated job node without any inserted edges. Starting with wandering, the edges connecting the node ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$ of the graduated student and the node ${\mathrm{w}}_{\mathrm{q}}$ of the signed job of this graduate are inserted, as illustrated in Figure 3. The next step is to randomly travel from the graduated student node ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$ and, according to the probability ∂, decide whether to continue to travel or stop this travel to return to the starting node ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$. Based on the above principle, if every job and job specialty attribute node is visited, the probability will converge to a number, and then the edge of the graduated student node to the job node will be removed.

The algorithm terminates once every starting node ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$ has been visited; if not, the random walk proceeds from the initial graduated student node. In this study, the value of ∂ is set to 0.7 based on experimental findings, and the calculation formula is defined as follows:

$$PR\left(r\right)=\left\{\begin{array}{c} \partial {\sum }_{r^{,}\in in\left(r\right)}\frac{PR\left(r^{,}\right)}{\left|\left.out\left(r^{,}\right)\right|\right.} (r\ne {s_p}^{\prime })\\ \left(1-\partial \right)+\partial {\sum }_{r^{,}\in in\left(r\right)}\frac{PR\left(r^{,}\right)}{\left|\left.out\left(r^{,}\right)\right|\right.} (r={s_p}^{\prime })\end{array}\right.$$

(7)

where $\mathrm{P}\mathrm{R}\left(\mathrm{r}\right)$ denotes the probability of visiting node $\mathrm{r}$, PR$\left({\mathrm{r}}^{,}\right)$denotes the probability of ${\mathrm{r}}^{,}$ being visited, and ∂ denotes the probability of random wandering. $\mathrm{o}\mathrm{u}\mathrm{t}\left({\mathrm{r}}^{,}\right)$ denotes the set of nodes pointing from ${\mathrm{r}}^{,}$, and $\mathrm{i}\mathrm{n}\left(\mathrm{r}\right)$denotes the set of nodes pointing to node $\mathrm{r}$. PR$({{\mathrm{s}}_{\mathrm{p}}}^{\prime },{\mathrm{w}}_{\mathrm{q}})$ denotes the probability that the start node ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$ visits job node${\mathrm{w}}_{\mathrm{q}}$. If ${\mathrm{w}}_{\mathrm{q}}$ is a job signed by the graduated student ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$, then PR $\left({{\mathrm{s}}_{\mathrm{p}}}^{\prime },{\mathrm{w}}_{\mathrm{q}}\right)=1$.

The professional matching value between the graduate student ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$ and the graduate ${\mathrm{s}}_{\mathrm{p}}$ is calculated using Equation (8).

$$sim\left(s_p, {s_p}^{\prime }\right)=\frac{\left|{tr}_p\cap {TR}_p\right|}{\left|{tr}_p\right|+\left|{TR}_p\right|}$$

(8)

where $\mathrm{s}\mathrm{i}\mathrm{m}\left({\mathrm{s}}_{\mathrm{p}},{{\mathrm{s}}_{\mathrm{p}}}^{\prime }\right)$ represents the professional matching value between college graduates and graduate students. ${\mathrm{t}\mathrm{r}}_{\mathrm{p}}$ denotes the set of specialized attributes of college graduate $\mathrm{p},$ and ${\mathrm{T}\mathrm{R}}_{\mathrm{p}}$ denotes the set of specialized attributes of graduated student ${{\mathrm{s}}_{\mathrm{p}}}^{\prime }$. The wandering probability, starting with the graduate most similar to the college graduate, is considered the specialty match value. For example, if the match value between ${{\mathrm{s}}_3}^{\prime }$ and ${\mathrm{s}}_2$ is the highest, then the wandering probability with graduated students ${{\mathrm{s}}_3}^{\prime }$ as the starting node is used as the professional match value for college graduates ${\mathrm{s}}_2$.

3.2.2. Salary Matching

In this study, salary matching is conducted using a two-dimensional Euclidean metric that considers the job’s average and maximum salary against the graduate’s desired entry and incentive salary. The average salary is the monthly pay received by an employee, while the maximum salary is the highest amount offered by the company. Entry-level salary refers to the minimum salary required for college graduates, and incentive salary refers to the maximum salary desired by college graduates. The job’s average and maximum salaries are viewed as a two-dimensional point $\mathsf{\alpha }=({\mathrm{x}}_{\mathrm{w}},{\mathrm{y}}_{\mathrm{w}})$, where ${\mathrm{x}}_{\mathrm{w}}$ represents the average salary for the job, and ${\mathrm{y}}_{\mathrm{w}}$ represents the maximum salary for the job. Similarly, the graduate’s entry and incentive salaries are viewed as two-dimensional points $\mathsf{\beta }=({\mathrm{x}}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})$, where ${\mathrm{x}}_{\mathrm{s}}$ denotes the entry salary and ${\mathrm{y}}_{\mathrm{s}}$ denotes the incentive salary.

$$dis\left(\alpha ,\beta \right)=\sqrt[2]{{(x_w-x_s)}^2+{(y_w-y_s)}^2}$$

(9)

$$\mathit{if}:\left(x_w-x_s\right)<0,default{\left(x_w-x_s\right)}^2=0$$

(10)

$$\mathit{if}:\left(y_w-y_s\right)<0,default{\left(y_w-y_s\right)}^2=0$$

(11)

The value of ${\mathrm{x}}_{\mathrm{w}}-{\mathrm{x}}_{\mathrm{s}}$ defaults to zero when the average salary of the job is lower than the entry salary expected by college graduates. Similarly, the value of ${\mathrm{y}}_{\mathrm{w}}-{\mathrm{y}}_{\mathrm{s}}$ defaults to zero when the maximum salary of the job is lower than the incentive salary desired by college graduates. When choosing a job, college graduates look at the average and highest salary of the job with a bias, so when calculating the weight, δ is added to improve the accuracy of the calculation, and the value of δ ranges from 0 to 1. In this study, δ is experimentally set to 0.6, and is calculated as follows:

$$dis\left(\alpha ,\beta \right)=\sqrt[2]{{(x_w-x_s)}^2·\delta +{(y_w-y_s)}^2·(1-\delta )}$$

(12)

3.2.3. Social Relationship

Interactive behaviors such as contacting and interacting between college graduates and those who have graduated can constitute a social network structure. In this paper, social networks between college graduates and graduated students are quantified using the “common friend set” and “intersection group” metrics. The common friends set pertains to the friends shared by college graduates and graduated students from the same hometown and college. The common intersection group refers to individuals with the same major and tutor. To account for differences in economic and consumption levels across cities, grouping based on hometown helps minimize variations in the salary requirements of graduates. Moreover, if a college graduate and a graduated student share the same major and mentor, it indicates a high degree of similarity in research interests and, consequently, job search preferences. This study also accounts for the potential impact of the annual economic climate on employment by incorporating the timing of graduation into the job recommendation process.

$$<s_p:f_1,f_2,f_3\cdots >,<s_p^{\prime }:f_1^{\prime },f_2^{\prime },f_3^{\prime },\cdots >$$

(13)

$$<s_p:g_1,g_2,g_3\cdots >,<s_p^{\prime }:g_1^{\prime },g_2^{\prime },g_3^{\prime },\cdots >$$

(14)

$$c\left(s_p,s_p^{\prime }\right)=({\sum }_{p=1}^{n_f}{x}_p{y}_p^{\prime }+{\sum }_{q=1}^{n_g}{x}_q{y}_q^{\prime })·\frac{1}{\left|T-T^{\prime }\right|}$$

(15)

Equation (13) represents the social network common friend set of college graduate ${\mathrm{s}}_{\mathrm{p}}$ and graduated student ${\mathrm{s}}_{\mathrm{p}}^{\prime }$. Equation (14) represents the common intersection group of college graduates ${\mathrm{s}}_{\mathrm{p}}$ and graduated students ${\mathrm{s}}_{\mathrm{p}}^{\prime }$. $\sum _{\mathrm{p}=1}^{{\mathrm{n}}_{\mathrm{f}}}{\mathrm{x}}_{\mathrm{p}}{\mathrm{y}}_{\mathrm{p}}^{\prime }$ represents the summation of the number of common friends between college graduates and graduated students, and $\sum _{\mathrm{q}=1}^{{\mathrm{n}}_{\mathrm{g}}}{\mathrm{x}}_{\mathrm{q}}{\mathrm{y}}_{\mathrm{q}}^{\prime }$ represents the summation of the common intersection group of college graduates and graduated students. ${\mathrm{n}}_{\mathrm{f}}$ represents the total number of friends of the college graduates and graduated students. If ${\mathrm{f}}_{\mathrm{p}}$ is a friend of college graduate ${\mathrm{s}}_{\mathrm{p}}$, ${\mathrm{x}}_{\mathrm{p}}$ equals one; otherwise, it equals zero. If ${\mathrm{f}}_{\mathrm{p}}$ is also a friend of a graduated student ${\mathrm{s}}_{\mathrm{p}}^{\prime }$, ${\mathrm{y}}_{\mathrm{p}}^{\prime }$ equals 1; otherwise, it equals 0. $\left|\mathrm{T}-{\mathrm{T}}^{\prime }\right|$ denotes the time difference between graduation time $\mathrm{T}$ of college graduates and graduation time ${\mathrm{T}}^{\prime }$of graduated students.

3.2.4. Entropy Aggregation

Entropy aggregation is used to convert professional match values, salary match values, and social networks into a decision matrix, which is computed to produce a recommended job set. The calculation process is illustrated in Figure 4.

$$A=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ ⋮& ⋮& ⋮\\ a_{n1}& a_{n2}& a_{n3}\end{array}\right]$$

(16)

where $\mathrm{n}$ in the above matrix represents a total of $\mathrm{n}$ jobs, and ${\mathrm{a}}_{\mathrm{i}\mathrm{j}}$ represents the score value of the ith job in the jth column. There are three columns in the matrix: professional, salary, and social relationships. Decision matrix A is obtained using entropy aggregation. The decision matrix is normalized to obtain matrix B. Finally, the entropy values are obtained using Equations (17)–(19).

$$B=\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\\ ⋮& ⋮& ⋮\\ b_{n1}& b_{n2}& b_{n3}\end{array}\right]$$

(17)

$$E_j=-\frac{({\sum }_{i=1}^n{b}_{ij}{\mathit{ln}b}_{ij})}{\mathit{ln}n}$$

(18)

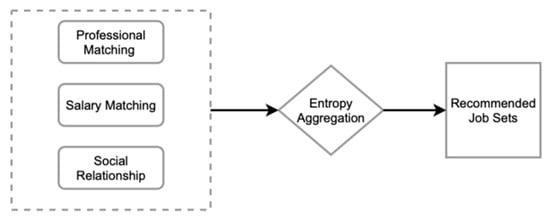
Figure 4. Ranking calculation process.

Let ${\mathrm{d}}_{\mathrm{j}}=1-{\mathrm{E}}_{\mathrm{j}}(1\le \mathrm{j}\le \mathrm{m})$, where $\mathrm{m}$ is the number of column dimensions of the matrix (there are three dimensions in this study: professional matching, salary matching, and social relationship), and the entropy weight of the jth column is obtained using the calculation of Equation (19).

$$w_j=\frac{d_j}{\sum _{j=1}^m{d}_j}$$

(19)

Finally, the entropy weights of each column of the work attributes are summarized to obtain the final ranking score ${\mathrm{F}\mathrm{R}\mathrm{S}}_{\mathrm{i}}$.

$${FRS}_i={\sum }_{j=1}^m{w}_j{b}_{ij}$$

(20)

3.3. Experimental Evaluation

3.3.1. Recommendation Method

To rigorously assess the efficacy of the job recommendation approach proposed in this study, it underwent evaluation and comparison with existing recommendation methods. The description of the recommended method is provided as follows:

TF-C [38]: This method employs cosine similarity to compute the resemblance between the text within a college graduate’s resume and the content of the job posting. The system then produces a list of job recommendations based on similarity scores for college graduates to evaluate. The rating scale ranges from 1 (unsatisfactory) to 5 (satisfactory), with a total score of 5.

MS [43]: In the screening stage, a semantic keyword-matching approach is used to evaluate the likeness between the content of the college graduate’s resume and the text of the job posting. Subsequently, a list of job recommendations is generated based on similarity and submitted to college graduates for scoring.

GERS [35]: Employment characteristics of graduates are analyzed using a two-dimensional matrix of graduate preferences. Subsequently, the system calculates the similarity between graduates to identify jobs chosen by neighboring graduates, generating a recommendation list.

RSCF [44]: The similarity between graduates’ resumes and job descriptions is integrated with a collaborative filtering algorithm based on graduates’ similarity to calculate a list of job recommendations. The recommended jobs are then provided to college graduates for scoring.

JRSR: Utilizing the job recommendation method introduced in this paper, the screening stage uses a semantic keyword iterative algorithm to compute the similarity between resume text and recruitment text. In the ranking stage, three dimensions—”professional matching, salary matching, and social network”—are used to generate a set of job recommendations using entropy aggregation. This collection is then returned to college graduates for scoring.

To assess the impact of each dimension of the job recommendation method (JRSR) on the computational method’s performance, this study disaggregates the system into its constituent components—semantic keyword matching, professional matching, salary matching, and social networking—and conducts an experimental evaluation of each. RSR omits the semantic keyword-matching method, relying solely on professional alignment, salary comparison, and social network inputs for its calculations. JSR excludes professional alignment, utilizing only semantic keyword matching, salary comparison, and social networks. JRR discards salary comparison, operating with semantic keyword matching, professional alignment, and social networks. In contrast, JRS disregards social networking elements, conducting analyses strictly with semantic keyword matching, professional alignment, and salary matching components. The aforementioned methods were individually applied to the dataset, which comprised 110 target graduates, 320 total graduates, and 280 work samples, to perform calculations, with the recommendation list set at a length of five.

To evaluate the impact of graduates’ historical employment information on recommendation performance, this study categorizes the employment data into two sets: one for logistics engineering and another for management and science work samples. Subsequently, the job recommendation method (JRSR) proposed in this study was applied separately to each work sample set, generating two sets of recommendation results. Finally, the performance of the job recommendation method is assessed and compared based on the evaluation results from both sets of work samples.

3.3.2. Evaluation of Indicators

In this study, the recommendation outcomes were evaluated using the average satisfaction rate (AR) and normalized discounted cumulative gain (NDCG). AR was used to assess the average satisfaction of college graduates with recommended jobs. NDCG was used to assess the reciprocity of job referral methods.

The average satisfaction rate (AR) indicator was calculated using the ratings of college graduates for recommended jobs. The calculation formula is as follows:

$$AR@n=\frac{1}{\left|U\right|}{\sum }_{j=1}^{\left|U\right|}\frac{1}{\left|n\right|}{\sum }_{i=1}^n{s}_j\left(i\right)$$

(21)

where ${\mathrm{s}}_{\mathrm{j}}\left(\mathrm{i}\right)$ represents the rating (on a scale of 1–5) of graduate ${\mathrm{s}}_{\mathrm{j}}$ for job ranked $\mathrm{i}$ in the recommendation set. $\mathrm{i}$ denotes the ranking of the job in the recommendation set (the rankings are 1, 2, 3, 4, and 5; the value of i is an integer between 1 and 5). $\mathrm{N}$ denotes the number of jobs in the recommendation set (the number of recommended jobs in this study was five). $\left|\mathrm{U}\right|$ is the number of graduates.

The normalized discounted cumulative gain (NDCG) calculates the reciprocity of the recommendation results based on the ranking and rating of the job in the recommendation list. The calculation formula is as follows:

$$NDCG@n=\frac{1}{\left|U\right|}{\sum }_{j=1}^{\left|U\right|}\frac{{DCG}_j@n}{{maxDCG}_j@n}$$

(22)

where

$${ DCG}_j@n={\sum }_{i=1}^n\left[\right(2^{s_j\left(i\right)}-1)/log(1+i)$$

(23)

$${maxDCG}_j@n={\sum }_{i=1}^n\left[\right(2^{s_j\left(i\right)}-1)/log(1+e)$$

(24)

The $\mathrm{i}$ in the equation ${\mathrm{D}\mathrm{C}\mathrm{G}}_{\mathrm{j}}@\mathrm{n}$ represents the rank of the recommended job in the recommendation set; for example, job ${\mathrm{w}}_1$ is ranked 3 in the recommendation set, and the value of $\mathrm{i}$ equals 3. The $\mathrm{e}$ in the equation ${\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{D}\mathrm{C}\mathrm{G}}_{\mathrm{j}}@\mathrm{n}$ is the ranking from highest to lowest based on the ratings of the college graduates for the recommended jobs. For example, job ${\mathrm{w}}_5$, where the target graduates rated the lowest and ranked 5; therefore, the value of e is 5. There are a total of five candidate jobs in the recommended list, so the rankings are a total of five places.

4. Analysis and Discussion of Experimental Results

4.1. Experimental Settings

Logistics engineering, management, and science represent a multidisciplinary domain that bridges the realms of management and technology, integrating engineering and scientific principles. It maintains strong connections with fields such as transportation engineering, industrial engineering, computer technology, mechanical engineering, environmental engineering, architecture, and civil engineering. Consequently, this study focuses on graduates in logistics engineering, management, and science, given their versatile qualifications and adaptability. The data on graduates’ resumes come from the personal contents of university graduates registered in the university employment program, and the data on job samples come from the information on jobs signed by graduated students at several universities. For the experimental data in this paper, the total number of target graduates is 110, the total number of graduated graduates is 320, and the total number of remaining work samples after screening out the same jobs is 280. All the above data are from the two majors of logistics engineering and management and science. To assess the generalizability of the recommended methods proposed in this paper, additional experimental data is incorporated for comparative evaluation. This paper includes employment data for students who graduated from five colleges in the last five years, encompassing a total of 1200 graduates and 1027 jobs across various majors under the management disciplines of business management, accounting, financial management, marketing, and tourism management.

During the screening stage, a semantic keyword iterative algorithm is used to assess the similarity between the resume text of college graduates and the job recruitment text. In the ranking stage, the top 110 jobs with the highest degree of similarity undergo entropy aggregation, using the three dimensions of “professional matching, salary matching, and social network” to generate a list of job recommendations. Finally, the jobs in the job recommendation list are returned to the college graduates for scoring from 1 (indicating dissatisfaction) to 5 (indicating satisfaction). This rating process serves as the means to evaluate the efficacy of the job recommendation method proposed in this paper.

4.2. Social Network Visualization of Experimental Data

The primary focus of this paper is to investigate the employment situation of students majoring in logistics engineering, management, and science. Therefore, the employment data related to these two majors, including 110 targeted graduates, 320 graduated students, and a total of 280 work samples, were analyzed for data visualization. Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the percentage distribution of college graduates and graduated hometowns, secondary colleges, majors, and mentors, respectively. The horizontal axis represents the percentage of college graduates in the dataset, while the vertical axis represents the percentage of graduated students in the dataset.

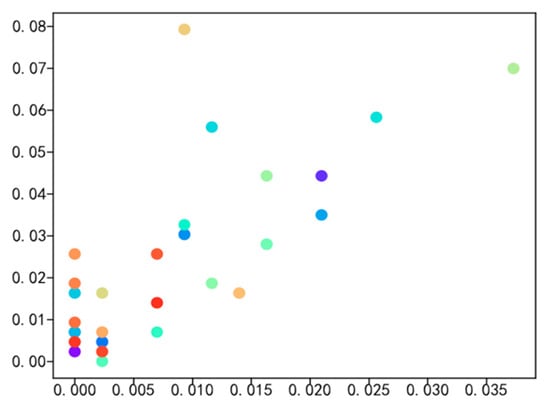
Figure 5. Comparison of high school graduates and graduated students’ hometown datasets.

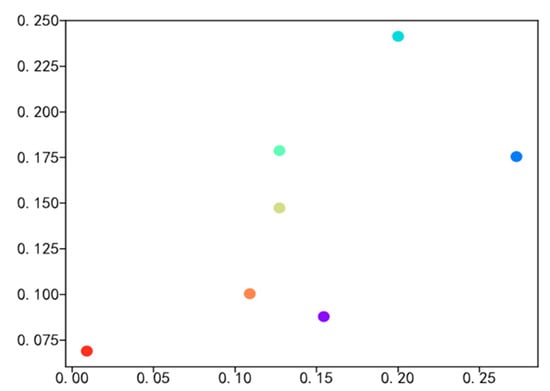
Figure 6. Comparison of high school graduates’ and graduated students’ secondary college datasets.

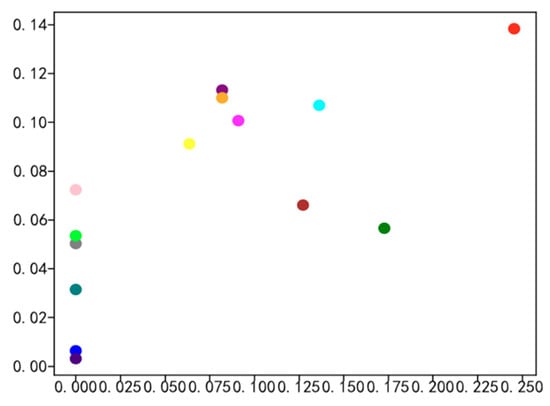
Figure 7. Comparison of high school graduates and graduated students’ major datasets.

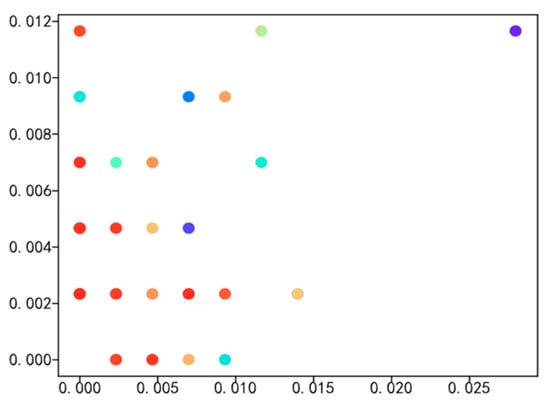
Figure 8. Comparison of high school graduates and graduated students’ mentor datasets.

Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the distribution of hometown, secondary college, major, and advisor proportions for college graduates and graduated students. The horizontal axis represents the percentage of college graduates’ hometowns within the dataset of college graduates, while the vertical axis represents the percentage of graduated students’ hometowns within the dataset of graduated students. The highest proportion of hometowns in the college graduate dataset is 3.6%, compared with 7% in the graduated student dataset. For the secondary college with the highest proportion in the college graduate dataset, it accounts for 20%, while in the graduated student dataset, it is 24%. The major with the highest proportion in the college graduate dataset is 17.5%, in contrast with 11% in the graduated student dataset. Additionally, the top advisor proportion in the college graduate dataset is 28%, while in the graduated student dataset, it is merely 1.18%. With meticulous data analysis, a notable and substantial social interconnection emerges between college graduates and graduated students, encompassing facets such as hometowns, secondary colleges, majors, and advisors. This interconnectedness serves as the bedrock for cultivating a closely woven social network, which in turn provides the fundamental groundwork for calculating probabilities in the context of random walks.

To analyze the social connections between college graduates and those who already graduated more clearly, this paper subdivides into four dimensions—hometown, secondary college, major, and mentor—to generate a social relationship network, depicted in Figure 9. The analysis demonstrates a strong social connection across the four dimensions of hometowns, secondary colleges, majors, and mentors between college graduates and graduated students. This emphasizes the viability of utilizing social networks to facilitate the recommendation of job opportunities endorsed by graduated students to college graduates.

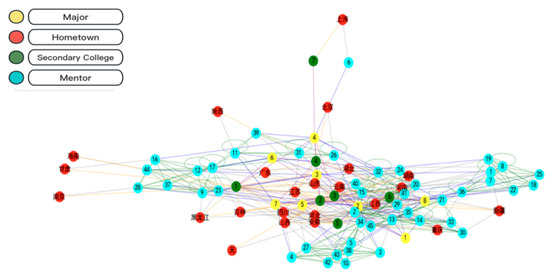
Figure 9. Social network for college graduates and graduated students.

4.3. Result Analysis

This article uses five job recommendation methods (TF-C, MS, GERS, RSCF, JRSR) to compute the recommended work set and subsequently conducts an analysis of the outcomes utilizing evaluation metrics.

4.3.1. Evaluation Analysis of the Average Satisfaction Rate

Figure 10 presents a comparative chart illustrating the average satisfaction rates among the five job recommendation methods. The graph clearly indicates that JRSR attains a notably higher average satisfaction rate when contrasted with the remaining four job recommendation methods. Among these five approaches, TF-C demonstrates the lowest average satisfaction rate, registering at a mere 2.631. Meanwhile, the average satisfaction rates for the other three job recommendation methods, namely, MS, GERS, and RSCF, exhibit relatively close values. The job recommendation method introduced in this paper, JRSR, records an average satisfaction rate of 3.743. In comparison to the four benchmark methods, it showcases a maximum improvement of 1.112 and a minimum improvement of 0.502. This compellingly suggests that the job recommendation method presented in this study, JRSR, excels in discerning the job preferences of college graduates, ultimately resulting in more gratifying job recommendations.

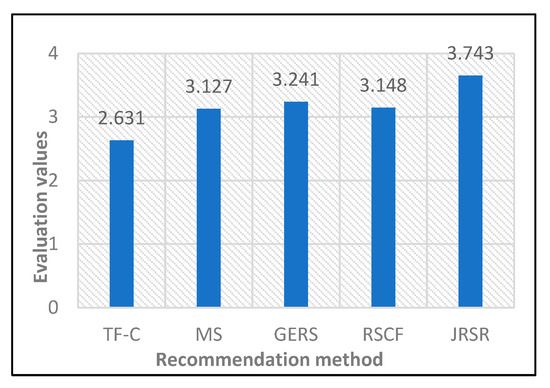
Figure 10. Average satisfaction rate.

The experimental data in this paper were non-normally distributed. To test for a significant difference in the AR@5 assessment values of the JRSR, TF-C, MS, GERS, and RSCF methods, the Wilcoxon signed-rank test was used. As indicated in Table 3 (p < 0.05), there is a significant difference between the assessed values of JRSR and the other four methods.

Table 3. Wilcoxon signed rank test for AR@5.

Recommendation Model	TF-C	MS	GERS	RSCF
JRSR	0.000	0.000	0.000	0.000

4.3.2. Evaluation Analysis of Normalized Discounted Cumulative Gain

Figure 11 illustrates the results of normalized discounted cumulative gain (NDCG@5) for the five job recommendation methods. The graph clearly demonstrates that among these methods, JRSR attains the highest NDCG@5 score, reaching 0.938. Among the four benchmark methods, TF-C achieves the lowest NDCG@5 score at 0.675, while GERS reaches the highest score at 0.859. When compared with TF-C and GERS, the proposed JRSR method exhibits a remarkable improvement in NDCG@5, with enhancements of 38.96% and 9.19%, respectively. This emphasizes the effectiveness of the JRSR job recommendation method presented in this paper in aligning the preferences and requirements of college graduates with job opportunities.

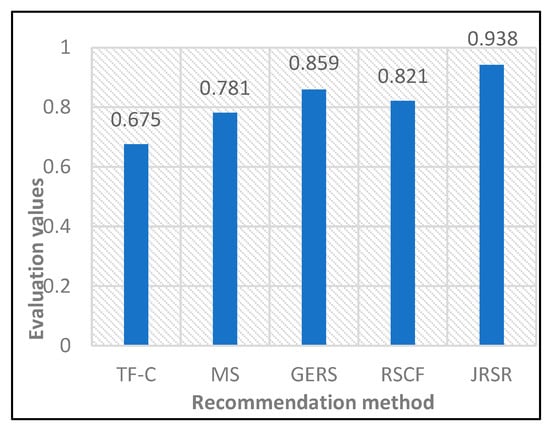
Figure 11. Normalized discounted cumulative gain.

The experimental data were non-normally distributed. In this paper, the Wilcoxon signed-rank test was used to assess whether there was a significant difference in the NDCG@5 assessment values of the JRSR, TF-C, MS, GERS, and RSCF methods. As evident in Table 4, with p < 0.05, there is a significant difference between the assessment values of JRSR and the other four methods.

Table 4. Wilcoxon signed rank test for NDCG@5.

Recommendation Model	TF-C	MS	GERS	RSCF
JRSR	0.002	0.001	0.000	0.001

4.3.3. Comparative Analysis of the Recommendation Results under Different Job Sample Sets

To assess the impact of historical employment information on recommendation outcomes, this study categorizes the job placements of graduates into two groups: the “Logistics Engineering Job Sample Set” and the “Management and Science Job Sample Set”, as illustrated in Figure 12. The AR@5 evaluation score for the Logistics Engineering sample set is 3.728, surpassing that of the Management and Science sample set by 0.467. This indicates a stronger preference among college graduates for jobs closely aligned with their majors. In terms of NDCG@5, the Logistics Engineering sample set achieves a score of 0.971, while the Management and Science sample set scores 0.866, resulting in a 0.105 higher NDCG@5 score for the Logistics Engineering sample set. This demonstrates the potential for major alignment to enhance the mutual effectiveness of job recommendations.

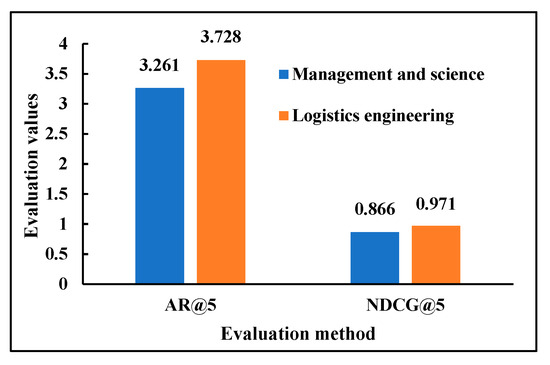
Figure 12. Evaluation results of separate use of historical employment information for the logistics and management section.

4.3.4. Comparative Analysis of Evaluation Values in Different Dimensions

This article dissects each dimension of the job recommendation method (JRSR) to analyze its impact on the system’s recommendation performance. The dimensions are individually assessed to calculate the recommendation outcomes, which are then evaluated using the average satisfaction rate and the normalized discounted cumulative gain. Figure 13 reveals that RSR has the lowest average satisfaction rate and normalized discounted cumulative gain, suggesting that dimensionality reduction in the semantic keyword iteration algorithm adversely affects satisfaction and validity. This indicates a superior filtering capability of the semantic keyword iteration algorithm when fully utilized. The data indicate that JRR’s average satisfaction rate and normalized discounted cumulative gain are second to last and third to last, respectively, which suggests that salary is a critical concern for graduates during their job search. Conversely, JSR registers the highest values in both average satisfaction rate and normalized discounted cumulative gain, signifying that the alignment of graduates’ majors is not a predominant consideration in their employment pursuits.

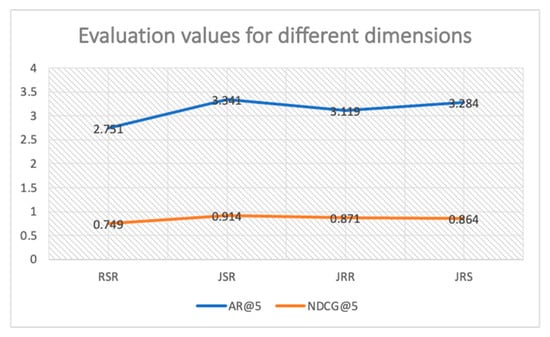
Figure 13. Evaluated values of AR@5 and NDCG@5 for different dimensional approaches.

4.3.5. Comparative Analysis of Evaluated Values for Different Recommendation List Lengths

To assess the performance of job recommendation methods across different sample sizes and recommendation list lengths, this paper expands the experimental sample size and generates recommendation lists of different lengths. The experimental dataset used for this comparative analysis comprises 110 targeted graduates, 1200 graduated students, and 1027 job positions. It encompasses various specializations within the management disciplines, including business management, accounting, financial management, marketing, and tourism management.

By examining Figure 10, Figure 14, and Table 5, it is evident that the assessed values of AR@5 for the five recommended methods exhibited a decline with the augmentation of data. The most substantial decrease occurred in the case of JRSR, dropping from 3.743 to 3.462, which represents a 7.5% reduction. As the length of the recommendation lists increases for the five methods, their AR evaluations correspondingly decrease. In Figure 14, it is evident that the assessed value of AR@20 significantly exceeds that of AR@5, with the MS value-added reaching its peak at 0.301 and the TF-C value-added registering its lowest at 0.114. These findings indicate that both the size of the experimental data sample and the length of the recommendation list directly impact the recommendation satisfaction rate.

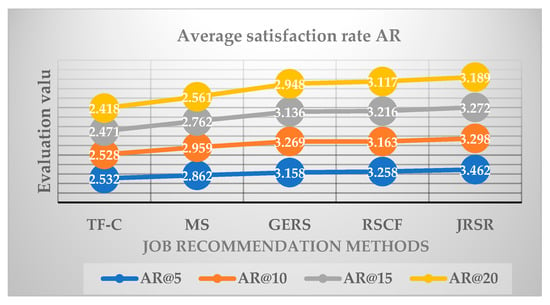
Figure 14. Analysis of AR evaluation values for different recommendation list lengths.

Table 5. AR assessment values for different recommended list lengths.

	AR@5	AR@10	AR@15	AR@20
TF-C	2.532	2.528	2.471	2.418
MS	2.862	2.959	2.762	2.561
GERS	3.158	3.269	3.136	2.948
RSCF	3.258	3.163	3.216	3.117
JRSR	3.462	3.298	3.272	3.189

By examining Figure 11, Figure 15, and Table 6, it is apparent that as the sample size of the experimental data expands, the assessed values of NDCG@5 for the five recommended methods decrease. The most substantial decrease is observed in MS, where it is 0.089, while the smallest decrease is in RSCF, where it is 0.03. Moreover, with the increase in the length of the recommended list, there is a decrease in its NDCG assessment. The most significant decrease is observed for GERS at 12.81%, while the smallest decrease is for MS at 4.9%. These findings indicate that both the size of the experimental data sample and the length of the recommendation list directly impact the normalized discounted cumulative gain assessment value.

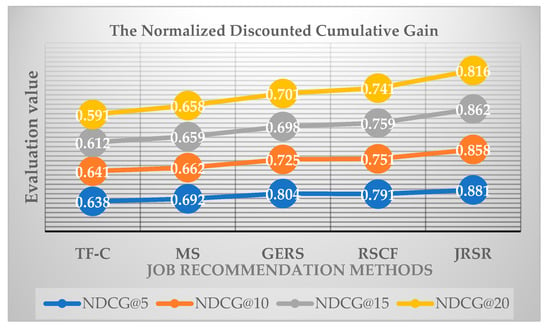
Figure 15. Analysis of NDCG evaluation values for different recommended list lengths.

Table 6. NDCG assessment values for different recommended list lengths.

	NDCG@5	NDCG@10	NDCG@15	NDCG@20
TF-C	0.638	0.641	0.612	0.591
MS	0.692	0.662	0.659	0.658
GERS	0.804	0.725	0.698	0.701
RSCF	0.791	0.751	0.759	0.741
JRSR	0.881	0.858	0.862	0.816

4.4. Discussion

In Figure 10 and Figure 11, both the average satisfaction rate and the normalized discounted cumulative gain (NDCG) of the JRSR job recommendation method, as proposed in this paper, outperform the other four recommendation methods. This robustly underscores the effectiveness and superiority of the JRSR approach in job recommendation. In contrast with the TF-C and MS methods, JRSR uses a keyword iterative calculation approach to determine the similarity between the resume text of college graduates and the job recruitment text. This methodology not only mitigates the problem of neglecting low-frequency keywords but also enhances inter-keyword cross-referencing, resulting in a more robust semantic matching of text similarity. The job recommendation method GERS recommends job selections for graduates by calculating the similarity of employment characteristics among graduates and suggesting the choices of neighboring graduates as pre-recommended items [35]. This method is a collaborative filtering recommendation approach, which narrows down the recommendation scope. However, it simplifies the calculation of similarity in employment characteristics among graduates. In contrast, the JRSR recommendation method, when calculating the similarity in employment characteristics among graduates, establishes a social network based on academic data from graduates. This approach not only effectively computes the similarity in employment characteristics among graduates but also addresses the system cold-start problem caused by a lack of employment data for college graduates. Compared with the recommendation method RSCF, which combines content-based and collaborative filtering approaches [44], the JRSR recommendation method adds dimensions of major matching and salary matching. By using multiple methods and dimensions, JRSR matches the preferences and job requirements of college graduates, thereby enhancing the reciprocity of job recommendations.

The empirical evaluation demonstrates that the job recommendation method introduced in this study exhibits superior performance relative to the benchmark method. Nonetheless, job recommendation for college graduates is a multifaceted and applied discipline, and this study acknowledges certain limitations. (a) While the semantic keyword iterative algorithm enhances the accuracy of text similarity calculations, its iterative nature results in time-consuming processing with large datasets. Future research should, therefore, focus more on improving the scalability of this computational method. (b) The dataset used in this study is not diverse, which limits the consideration of data variability. Consequently, future work will aim to increase the sample size to broaden the assessment indicators. (c) This paper focuses on the two most prevalent employment characteristics, major and salary; future studies should encompass a broader range of employment attributes. (d) This study does not utilize a range of career assessment tools to aid graduates in gaining a more objective and comprehensive understanding of their employment aspirations. Future research could incorporate ideological education to enhance graduates’ awareness of their career intentions, thereby improving the overall quality of job recommendations.

5. Conclusions

(a)

In response to the issue of low accuracy resulting from the omission of low-frequency keywords during the keyword matching calculation, this study used a text similarity calculation method based on a semantic keyword iteration algorithm during the filtering phase. This method effectively mitigated the problem of discarding low-frequency keywords, thereby enhancing calculation accuracy. This study addressed the issues of major structure matching and salary matching between college graduates and jobs, leading to a significant improvement in job recommendation satisfaction.

(b)

For the first time, this study introduces graduate social networks and historical employment information of past graduates. Jobs held by previous graduates are recommended to recent graduates, serving as a strategy to address the cold-start problem of the system. With the augmentation of both the sample size in the experimental data and the length of the job recommendation list, there is a concurrent decrease in the average satisfaction rate (AR) and the normalized discounted cumulative gain (NDCG) of the job recommendation method.

(c)

Evaluation based on the average satisfaction rate (AR) and normalized discounted cumulative gain (NDCG) metrics demonstrated that the job recommendation method for college graduates proposed in this study outperforms baseline recommendation methods in terms of recommendation performance.